EXPERIMENTAL STUDY ON MECHANICAL PROPERTIES OF TWO TYPES OF VISCOELASTIC DAMPERS
-
摘要: 该文通过不同应变幅值、不同加载频率以及疲劳荷载下的低周往复试验,对A、B两种具有不同耗能特征的黏弹性阻尼器的基本力学性能进行了研究,并对其储能剪切模量、耗能剪切模量、损耗因子等力学性能进行比较分析。试验结果表明:在相同变形幅值下,A、B两种黏弹性阻尼器的损耗因子和等效阻尼比的值比较接近,其中A种黏弹性阻尼器的单位体积材料的耗能量较大,提供的刚度也更大,但是加载过程中材料内部的升温效应比较明显,疲劳荷载下的各力学性能指标的衰减量也较大;B种黏弹性阻尼器的单位体积材料的耗能量和刚度较小,但是其力学性能受材料内部升温效应以及累积疲劳损伤的影响较小,疲劳荷载下各力学性能指标的衰减量较小。因此,在实际工程应用中,A种黏弹性阻尼器适合应用于有较高的刚度需求和耗能需求的结构,而B种黏弹性阻尼器适用于对力学性能稳定性以及抗震疲劳性能要求较高的结构。另外,采用Bouc-Wen模型得到的模拟结果与试验数据吻合良好。
-
关键词:
- 黏弹性阻尼器 /
- 低周往复试验 /
- 耗能特性 /
- 力学性能 /
- Bouc-Wen模型
Abstract: Low cycle tests of A-type and B-type viscoelastic dampers are carried out with different energy dissipating characteristics, and shear storage module, shear loss module, loss factor and other parameters are compared under different strain amplitudes, under different loading frequencies and under fatigue loads. Experimental results show that the loss factor and equivalent damping ratio have little difference between two types of dampers. Besides, the A-type viscoelastic damper dissipates more energy per unit volume and has larger stiffness, but the temperature of the material increases obviously during the loading process which leads to a significant mechanical property attenuation under fatigue loading. Furthermore, B-type is less affected by heating effect of viscoelastic material and cumulative fatigue damage and has more stable mechanical performance and more excellent seismic fatigue property. Therefore, in practical structural engineering application, A-type viscoelastic damper is suitable for the structure with higher stiffness requirement and larger energy dissipation requirement, while the B-type is suitable for the structure with less stiffness requirement and more stable energy dissipation requirement. Besides, the simulated results using Bouc-Wen model are well consistent with the experimental results. -
黏弹性阻尼器是一种性能优良的被动控制装置,通常由钢板和黏弹性材料层粘结制成。外荷载作用下,结构中黏弹性阻尼器的黏弹性材料层发生剪切变形,耗散输入结构中的能量,增加结构的附加阻尼,从而减小结构的动力响应。由于黏弹性阻尼器耗能能力优良、构造简单、造价经济,目前已广泛应用于建筑结构的消能减振工程中[1-4]。
黏弹性阻尼器的研究在国外起步比较早,近些年国内许多学者也对不同黏弹性材料制成的阻尼器进行了研究。吴波等[5]对两种国产黏弹性阻尼器的基本力学性能进行了试验研究,并确定了考虑材料内部升温效应的四参数力学模型。周云等[6-7]对某高阻尼型以及改善疲劳性能的黏弹性阻尼器进行了试验研究,结果表明:阻尼器耗能性能良好,并分别采用五单元模型和Bouc-Wen模型对试验滞回曲线进行了模拟。赵刚等[8]对某黏弹性阻尼器,在大变形下的基本力学性能以及疲劳性能等进行了试验研究,试验结果表明:该黏弹性阻尼器在大变形下的力学性能依然稳定,具有良好的变形能力。周颖等[9-15]对某黏弹性阻尼器的基本力学性能进行了试验研究,研究推导了不同尺寸和温度下滞回曲线的相似关系,揭示了多种非线性力学特征的来源及规律,并根据现行规范的不足提出了改进的黏弹性阻尼器抗震疲劳加载制度。
许多研究表明:虽然不同黏弹性材料制成的阻尼器均具有良好的滞回耗能能力,但是其力学性能特征还是有所不同的。目前关于不同耗能特性黏弹性阻尼器的比较研究较少,基于此本文对两种不同耗能特性的黏弹性阻尼器进行了试验研究,并对它们的基本力学性能等进行比较与分析。
1 试验概况
1.1 试件设计
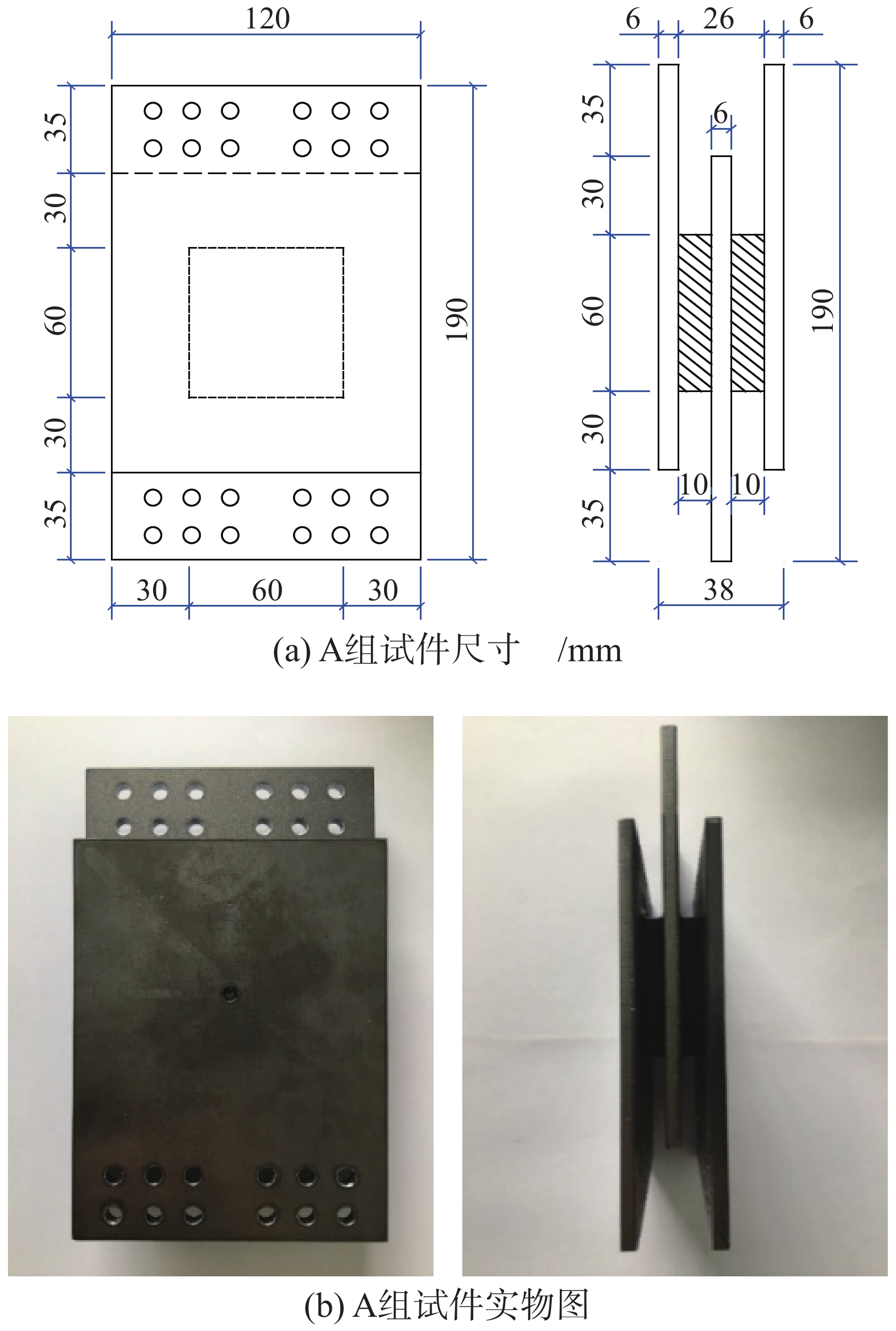
本次试验中的黏弹性阻尼器试件分为A、B两组,分别由日本CONSTEC株式会社和日本住友理工株式会社提供。每组均有3个试件,分别为A1~A3和B1~B3。每组三个试件的几何尺寸和黏弹性材料均相同,A、B两组试件的黏弹性材料层尺寸分别为60 mm×60 mm×10 mm,70 mm×40 mm×5 mm。A、B两组试件的具体尺寸和实物图如图1、图2所示。由于B组试件的构造原因,其最外侧两钢板之间放置有垫块。
1.2 试验加载
试验加载装置采用MTS拉压试验机(如图3所示),其最大出力为250 kN,空载时最大加载位移约为800 mm。试验时采用位移控制方式加载,位移为正弦波形式。加载时的力和位移数据均由该装置采集输出,试验室的环境温度以及黏弹性材料层的温度由电子测温计和测温仪测得,并人工记录。
基于我国现行相关规范[16-18],本文对不同应变幅值、不同加载频率以及疲劳荷载下两组黏弹性阻尼器试件的力学性能进行了试验研究。其中,A组试件由于连接加载装置部分的构造问题,允许加载的最大应变幅值为200%。两组试件具体的加载制度如表1所示。
2 试验结果
2.1 试验现象
试验加载前后,A组试件中,试件A1、试件A3无明显变化,黏弹性材料与钢板粘结完好,黏弹性材料无明显撕裂破坏,也无明显残余变形。在加载频率1.5 Hz、应变幅值100%的加载工况中,由于超出了加载装置最大加载速率,试件A2未能完成该工况的加载,且由于加载装置的颤动产生了约5 mm的残余变形(约50%残余应变)。重新安装后,以50%的应变幅值重新进行变频率(0.25 Hz~2.5 Hz)加载。各试件加载过程中,试验室温度保持在(21±1)℃。在加载过程中部分试件出现了明显的升温现象,其中试件A1升温最为明显(约7 ℃),试件A3升温幅度要小一些(约4 ℃),试件A2的升温现象不明显。
B组试件加载前后均无明显变化,黏弹性材料与钢板黏结完好,黏弹性材料无明显撕裂破坏,也无明显残余变形。各试件加载过程中,试验室温度保持在(21±2)℃。在加载过程中B组各试件均未出现明显的升温现象。
表 1 黏弹性阻尼器试验加载制度Table 1. Test scheme of viscoelastic dampers试件编号 应变幅值/(%) 频率/Hz 加载圈数 测试性能 A1 50、100、110、120、130、140、150、180、200 0.1 5 变形幅值相关性 B1 50、100、110、120、130、140、150、180、200、250、300 0.1 5 变形幅值相关性 A2、B2 100 0.25、0.5、0.75、0.85、1.0、1.5、2.0、2.5 5 加载频率相关性 A3、B3 100 0.1 30 抗震疲劳性能 2.2 基本力学性能
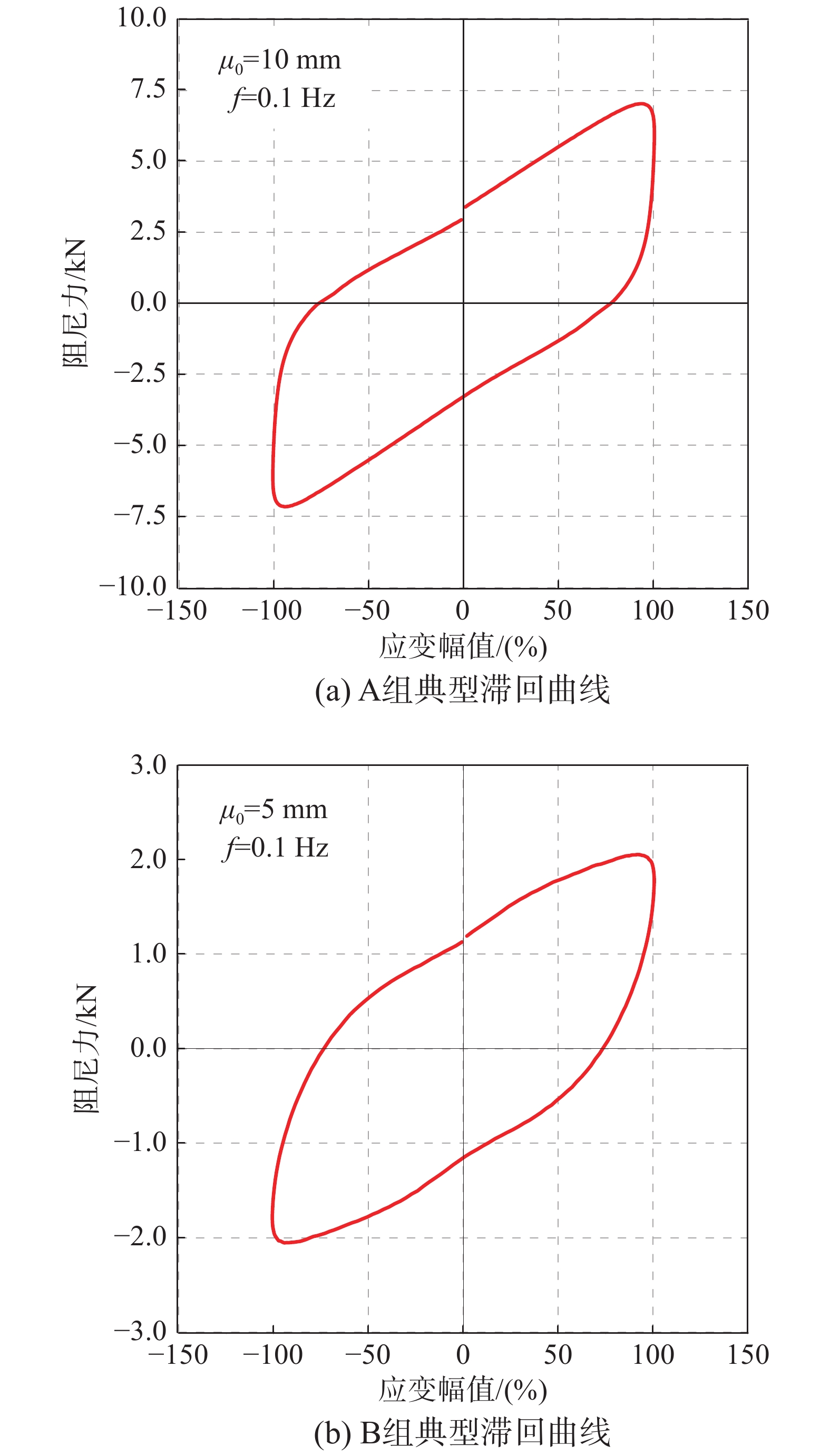
根据现行规范,取100%应变幅值、0.1 Hz加载频率下,A、B两组试件的典型滞回曲线进行基本力学性能分析,如图4所示。与B组试件相比,A组试件滞回曲线的硬化特征更加明显。由于两组试件的黏弹性材料层尺寸不同,为便于比较分析,将最大阻尼力除以黏弹性材料层的总面积,进行归一化处理,并计算该应变幅值下单位体积黏弹性材料每圈加载(应变幅值为100%)的耗能量。A、B两组试件的基本力学性能参数如表2所示。B组试件的损耗因子和等效阻尼比略大于A组,但是其归一化的最大阻尼力、储能剪切模量和耗能剪切模量比A组小很多,其中B组试件归一化的阻尼力仅为A组试件的38%,这表明在相同的加载频率和加载幅值下,A组试件等效刚度更大。每圈加载中A组试件单位体积黏弹性材料的耗能量为1.79 N·mm,为B组试件的2.63倍,这可能是加载过程中A组试件升温现象比较明显的原因。
表 2 基本力学性能Table 2. Basic mechanical properties项目 A组 B组 比值B/A 单位体积每圈耗能量/(N·mm) 1.79 0.68 0.38 归一化最大阻尼力/N 0.98 0.37 0.38 储能剪切模量/MPa 0.81 0.31 0.38 耗能剪切模量/MPa 0.47 0.21 0.44 损耗因子 0.58 0.68 1.17 等效阻尼比 0.34 0.37 1.08 2.3 应变幅值相关性
为研究应变幅值对两组试件力学性能的影响,取试件A1、试件B1各工况第3圈的滞回曲线,进行力学性能参数分析。图5、图6给出了不同应变幅值下,两试件的滞回曲线、最大阻尼力、储能剪切模量、耗能剪切模量和等效阻尼比等参数的变化情况。
从图5(a)可以看到,试件A1在不同应变幅值下,滞回曲线均比较饱满。如图5(b)所示,随着应变幅值增加,最大阻尼力的变化趋势为先增大,后减小,再增大。在110%~150%应变幅值范围内,加载工况比较密集,相邻两加载工况之间的应变幅值差距比较小,因此疲劳累积损伤以及材料内部的升温效应等影响比较明显,导致最大阻尼力明显降低。如图5(c)~图5(d)所示,储能剪切模量和耗能剪切模量均随应变幅值的增加而降低,并且随着应变幅值的增大,下降趋势变缓。从图5(e)~图5(f)可以看出,应变幅值为100%时,损耗因子和等效阻尼比最大,表明100%应变幅值下该黏弹性阻尼器的耗能能力较强。
从图6可以看到,试件B1在不同应变幅值下的滞回曲线均饱满稳定、光滑无异常,具有稳定的滞回耗能能力。图6(b)中,最大阻尼力随应变幅值的增加而增加,增加趋势大致呈线性。储能剪切模量、耗能剪切模量均随应变幅值的增加而降低,并且随着应变幅值的增大,下降趋势变缓,如图6(c)~图6(d)所示。如图6(e)~图6(f)所示在应变幅值为100%~300%时,损耗因子和等效阻尼比比较稳定。与应变幅值为100%时相比,应变幅值为300%时,损耗因子和等效阻尼比增大了1.3%和3.7%,表明该黏弹性材料的耗能性能非常稳定。
在50%~200%的应变幅值范围内,试件A1与试件B1采用了相同的加载制度。由图5(a)、图6(a)可以看到,与试件A1相比,试件B1在不同应变幅值下的滞回曲线形状更加稳定。在加载工况密集的110%~150%应变幅值范围内,B组试件的最大阻尼力也未出现大幅降低的情况,变化趋势比较稳定,受累积疲劳损伤以及材料内部升温效应等影响小。与试件A1相比,试件B1在不同应变幅值下的力学性能更加稳定。
2.4 加载频率相关性
为研究加载频率对两组黏弹性阻尼器基本力学性能的影响,分别取试件A2、试件B2各加载工况下第3圈滞回曲线进行力学性能分析。
取100%应变幅值下,0.25 Hz~1.0 Hz加载频率范围内试件A2的数据进行分析。从图7(a)中可以看出,不同加载频率下的滞回曲线均比较饱满,随着加载频率逐渐增大,滞回曲线包围的面积逐渐减小。各力学性能参数均随加载频率的增大而减小,如图7(b)~图7(f)所示。由于在100%应变幅值下加载装置难以实现1.5 Hz及以上频率的加载,所以在50%应变幅值下重新对试件A2进行变频率加载。取各工况第3圈的滞回曲线进行各力学性能参数分析,结果如图8所示。由于残余变形的影响,各滞回曲线关于坐标原点不对称,但是几何中心基本一致。加载频率越大,滞回曲线包围的面积越大,如图8(a)所示。在试验数据处理过程中,同时考虑了正、负两个加载方向的力,例如最大阻尼力的取值为正方向和负方向最大阻尼力绝对值的平均值。如图8(b)~图8(d)所示,随着加载频率的增大,最大阻尼力、储能剪切模量、耗能剪切模量逐渐增大,这与100%应变幅值下的结果相反。加载频率增大会提高阻尼器的散热效率,从而提高其力学性能,但是大应变下黏弹性阻尼器耗能产生的热量较多,材料内部的升温效应影响更加明显,因此在大应变幅值下,黏弹性阻尼器的部分力学性能随加载频率的增大而降低。在小应变幅值下,材料内部累积耗能带来的升温效应的影响要小于加载频率对散热效率的影响,从而使黏弹性阻尼器的部分力学性能随加载频率的增大而提升。
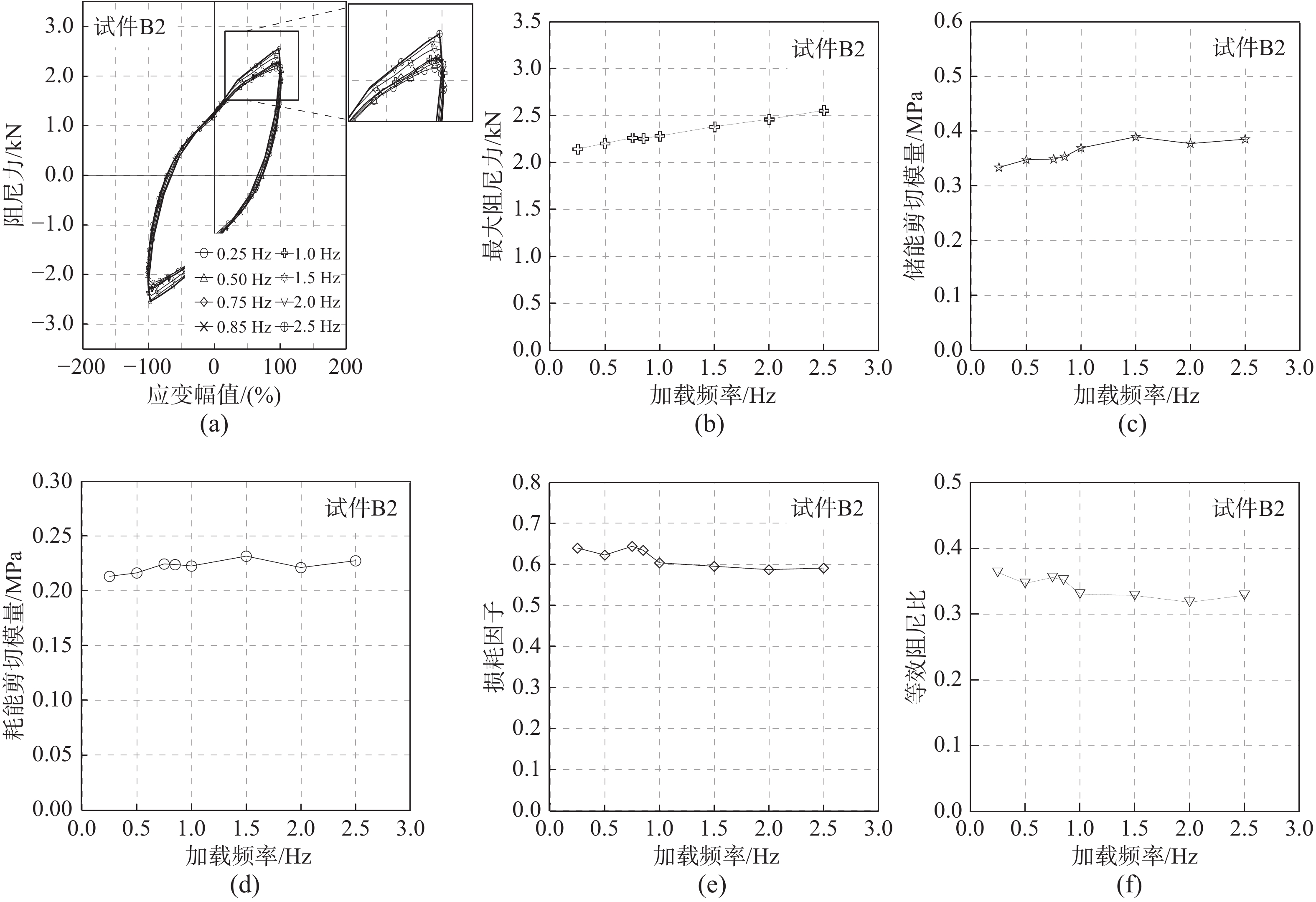
为研究加载频率对该B组黏弹性阻尼器力学性能的影响,取试件B2不同加载频率下第3圈的滞回曲线进行力学性能分析。在100%应变幅值下、0.25 Hz~2.5 Hz的加载频率范围内,试件B2的滞回曲线、最大阻尼力、储能剪切模量、耗能剪切模量、损耗因子和等效阻尼比如图9所示。从图9(a)中可以看出,不同加载频率下的滞回曲线均比较饱满、稳定。随着加载频率逐渐增大,该黏弹性阻尼器的最大阻尼力、储能剪切模量、耗能剪切模量均呈增大趋势,如图9(b)~图9(d)所示。从图9(e)~图9(f)中可以看到,随着加载频率的增大,损耗因子和等效阻尼比下降幅度不大,表明在不同的加载频率下,该黏弹性阻尼器耗能能力比较稳定。
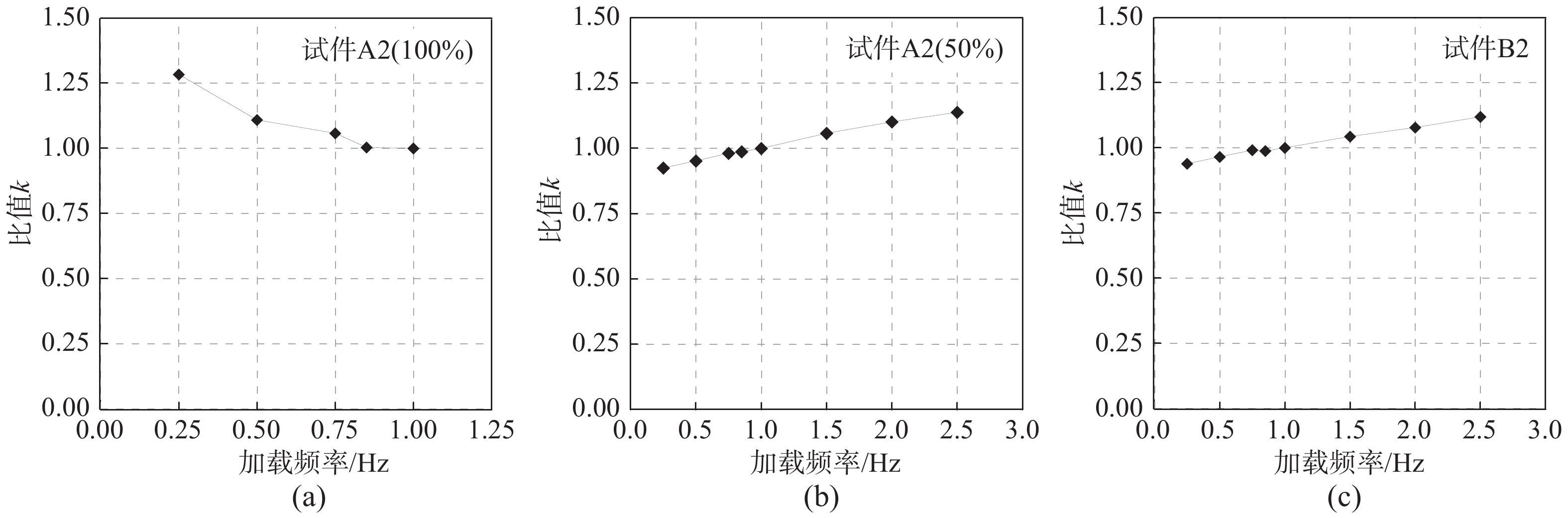
为比较A、B两组试件力学性能的加载频率相关性,分别计算试件A2、试件B2在各加载频率下的最大阻尼力与1 Hz下的最大阻尼力的比值k,结果如图10所示。在100%应变幅值下,相同的加载频率范围内(0.25 Hz~1.0 Hz),试件A2的比值k随加载频率的增大而减小,试件B2的比值k随加载频率的增大而增大。当试件A2应变幅值为50%时,其最大阻尼力与加载频率的相关性与100%应变幅值下的试件B2基本一致,最大阻尼力随加载频率的增大而增大,这应该是由于在小应变幅值下,试件A2的累积疲劳损伤以及材料内部的升温效应的影响减小引起的。
2.5 抗震疲劳性能
基于现行疲劳加载制度,取试件A3连续加载30圈的试验数据进行分析。试件A3各加载圈次的滞回曲线以及最大阻尼力、储能剪切模量、耗能剪切模量等基本力学性能如图11所示。由图11(a)可知,该黏弹性阻尼器的初始刚度比较大,随着加载圈次的增加,滞回曲线一直比较饱满,但是滞回曲线包围的面积不断减小。前2圈加载后,滞回曲线的形状以及各项基本力学性能参数的变化趋势趋于平缓。随着加载圈次的增加,各力学性能参数均呈下降趋势。对第3圈次和第30圈次的力学性能参数进行比较,结果见表3。最大阻尼力、储能剪切模量、耗能剪切模量、损耗因子的衰减量分别为35.6%、34.2%、46.1%、18.1%远超出现行规范15%的限值要求。
表 3 抗震疲劳性能指标变化量Table 3. Variances of seismic fatigue performance力学性能指标 A组衰减量/(%) B组衰减量/(%) 最大阻尼力 35.6 16.8 储能剪切模量 34.2 13.0 耗能剪切模量 46.1 15.7 损耗因子 18.1 3.1 等效阻尼比 12.8 2.9 试件B3各加载圈次的滞回曲线以及最大阻尼力、储能剪切模量等力学性能如图12所示。由图12(a)可知,疲劳加载过程中,该黏弹性阻尼器的滞回曲线一直比较饱满,初始刚度略大。前2圈加载后,滞回曲线的形状以及各项基本力学性能参数基本稳定下来。随着加载圈次的增加,最大阻尼力、储能剪切模量、耗能剪切模量均呈明显下降趋势。损耗因子和等效阻尼比的下降趋势不明显,前3圈加载后,基本处于比较稳定的状态,略有波动。比较第3圈与第30圈的基本力学性能,结果见表3。其中最大阻尼力、耗能剪切模量的衰减量分别为16.8%、15.7%,略超出现行规范15%的限值要求。
由表3可以看出,基于现行规范进行疲劳加载后,试件B3各力学性能的降低幅值均明显小于试件A3。在相同应变幅值和加载频率下,与A组试件相比,B组试件黏弹性材料的抗震疲劳性能更加优越。
3 滞回曲线模拟
考虑到两种黏弹性阻尼器滞回曲线的非线性特征,本文采用OpenSees中的TwoNodeLink单元和Bouc-Wen材料来进行模拟。Bouc-Wen模型的计算公式为:
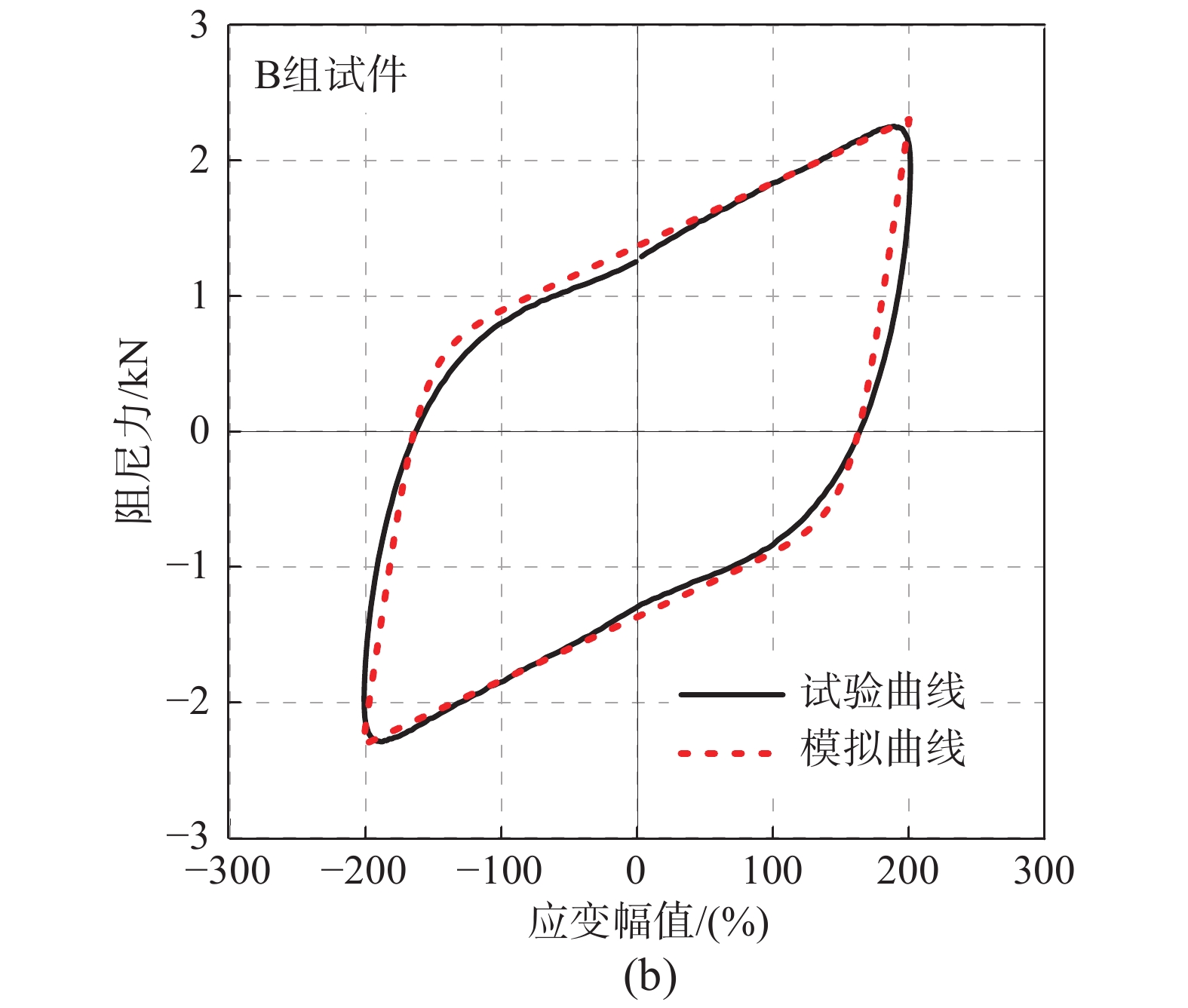
R=αkx+(1−α)Fz (1) 式中:R为恢复力;x为位移;k为初始弹性刚度;α为屈服后刚度与初始弹性刚度的比值;F为屈服力;z为内部的滞回变量。除α,k外,OpenSees中的Bouc-Wen模型还需要定义线性过渡到非线性的控制参数n,滞回曲线形状的控制参数γ和β,切线刚度的控制参数A0。根据A组和B组黏弹性阻尼器在200%应变幅值下的滞回曲线,对OpenSees中的Bouc-Wen模型进行参数识别,在kN-mm单位下,A组试件的各参数为:α=0.047,k=4.819,n=1.666,γ=1.198,β=1.883,A0=1.406;B组试件的各参数为:α=0.123,k=0.762,n=1.790,γ=0.223,β=0.272,A0=1.791。滞回曲线的模拟结果与试验结果的对比如图13所示。从图13可以看出两组黏弹性阻尼器的模拟结果与试验结果吻合良好。
4 结论
本文主要对两种黏弹性阻尼器在不同应变幅值、不同加载频率和疲劳荷载下得基本力学性能进行试验研究,分析得出的主要结论如下:
(1) A组黏弹性阻尼器初始刚度较大;在100%应变幅值下的等效阻尼比达0.34,滞回耗能能力较好;相同应变幅值和加载频率下,单位面积黏弹性材料阻尼力和等效刚度较大,单位体积耗能量较高,但是材料内部升温效应比较明显,因此其在连续加载下的力学性能稳定性差一些。
(2) B组黏弹性阻尼器初始刚度较小;100%应变幅值下等效阻尼比为0.37,滞回耗能能力良好;相同应变幅值和加载频率下,单位面积黏弹性材料阻尼力较小,耗能量较小,材料内部升温效应不明显,连续加载下的力学性能稳定性好。
(3) 经过上述比较分析可知,A、B两组试件的损耗因子和等效阻尼比差别不是很大,但是在相同应变幅值下,A组试件的单位体积材料耗能量更大,提供的刚度也比较大,适合有刚度需求和较大耗能需求的结构。与A组试件相比,B组试件受材料内部升温效应以及累积疲劳损伤影响较小,其力学性能稳定性以及抗震疲劳性更好,适合刚度需求小以及力学性能稳定性要求高的结构。
(4) 两组黏弹性阻尼器的滞回曲线均可采用OpenSees中的Bouc-Wen材料模型进行模拟,模拟结果与试验结果吻合良好,但更适用于不同黏弹性阻尼器耗能特征的力学模型还有待进一步开发研究。
-
表 1 黏弹性阻尼器试验加载制度
Table 1 Test scheme of viscoelastic dampers
试件编号 应变幅值/(%) 频率/Hz 加载圈数 测试性能 A1 50、100、110、120、130、140、150、180、200 0.1 5 变形幅值相关性 B1 50、100、110、120、130、140、150、180、200、250、300 0.1 5 变形幅值相关性 A2、B2 100 0.25、0.5、0.75、0.85、1.0、1.5、2.0、2.5 5 加载频率相关性 A3、B3 100 0.1 30 抗震疲劳性能 表 2 基本力学性能
Table 2 Basic mechanical properties
项目 A组 B组 比值B/A 单位体积每圈耗能量/(N·mm) 1.79 0.68 0.38 归一化最大阻尼力/N 0.98 0.37 0.38 储能剪切模量/MPa 0.81 0.31 0.38 耗能剪切模量/MPa 0.47 0.21 0.44 损耗因子 0.58 0.68 1.17 等效阻尼比 0.34 0.37 1.08 表 3 抗震疲劳性能指标变化量
Table 3 Variances of seismic fatigue performance
力学性能指标 A组衰减量/(%) B组衰减量/(%) 最大阻尼力 35.6 16.8 储能剪切模量 34.2 13.0 耗能剪切模量 46.1 15.7 损耗因子 18.1 3.1 等效阻尼比 12.8 2.9 -
[1] Tsai C S, Lee H H. Applications of viscoelastic dampers to high-rise buildings [J]. Journal of Structural Engineering, 1993, 119(4): 1222 − 1233. doi: 10.1061/(ASCE)0733-9445(1993)119:4(1222)
[2] 周云, 徐赵东, 赵鸿铁. 粘弹性阻尼结构的性能、分析方法及工程应用[J]. 地震工程与工程振动, 1998, 18(3): 96 − 107. doi: 10.3969/j.issn.1000-1301.1998.03.013 Zhou Yun, Xu Zhaodong, Zhao Hongtie. Performance, analysis method and engineering application of the structure with viscoelastic dampers [J]. Earthquake Engineering and Engineering Vibration, 1998, 18(3): 96 − 107. (in Chinese) doi: 10.3969/j.issn.1000-1301.1998.03.013
[3] Mahmoodi P, Robertson L E, Yontar M, et al. Performance of viscoelastic dampers in world trade center towers [C]// Dynamics of Structures. ASCE, Orlando, 1987: 632 − 644.
[4] Nielsen E J, Lai M L, Soong T T, et al. Viscoelastic damper overview for seismic and wind applications [C]// Smart Structures and Materials 1996: Passive Damping and Isolation. International Society for Optics and Photonics, San Diego, 1996, 2720: 138 − 144.
[5] 吴波, 郭安薪. 粘弹性阻尼器的性能研究[J]. 地震工程与工程振动, 1998(2): 108 − 116. doi: 10.3969/j.issn.1000-1301.1998.02.014 Wu Bo, Guo Anxin. Performance study of viscoelastic dampers [J]. Earthquake Engineering and Engineering Vibration, 1998(2): 108 − 116. (in Chinese) doi: 10.3969/j.issn.1000-1301.1998.02.014
[6] 周云, 林绍明, 吴从晓, 等. 高阻尼黏弹性阻尼器性能与力学模型研究[J]. 振动与冲击, 2015, 34(7): 1 − 7. Zhou Yun, Lin Shaoming, Wu Congxiao, et al. Performance and mechanical model of high damping viscoelastic dampers [J]. Journal of Vibration and Shock, 2015, 34(7): 1 − 7. (in Chinese)
[7] 周云, 林绍明, 吴从晓, 等. 新型高阻尼黏弹性阻尼器性能试验研究[J]. 工程力学, 2016, 33(7): 92 − 99. doi: 10.6052/j.issn.1000-4750.2014.08.0732 Zhou Yun, Lin Shaoming, Wu Congxiao, et al. Research on experimental properties of novel high damping viscoelastic dampers [J]. Engineering Mechanics, 2016, 33(7): 92 − 99. (in Chinese) doi: 10.6052/j.issn.1000-4750.2014.08.0732
[8] 赵刚, 潘鹏, 钱稼茹, 等. 黏弹性阻尼器大变形性能试验研究[J]. 建筑结构学报, 2012, 33(10): 126 − 133. Zhao Gang, Pan Peng, Qian Jiaru, et al. Experimental study of viscoelastic dampers subjected to large deformation [J]. Journal of Building Structures, 2012, 33(10): 126 − 133. (in Chinese)
[9] 周颖, 李锐, 吕西林. 粘弹性阻尼器性能试验研究及参数识别[J]. 结构工程师, 2013, 29(1): 83 − 91. doi: 10.3969/j.issn.1005-0159.2013.01.013 Zhou Ying, Li Rui, Lü Xilin. Experimental study and parameter identification of viscoelastic dampers [J]. Structural Engineers, 2013, 29(1): 83 − 91. (in Chinese) doi: 10.3969/j.issn.1005-0159.2013.01.013
[10] 周颖, 龚顺明. 新型黏弹性阻尼器性能试验研究[J]. 结构工程师, 2014, 30(1): 137 − 142. doi: 10.3969/j.issn.1005-0159.2014.01.022 Zhou Ying, Gong Shunming. Experimental study of advanced viscoelastic dampers [J]. Structural Engineers, 2014, 30(1): 137 − 142. (in Chinese) doi: 10.3969/j.issn.1005-0159.2014.01.022
[11] 龚顺明, 周颖. 黏弹性阻尼器耗能特征的温度影响分析[J]. 地震工程与工程振动, 2014(增刊 1): 801 − 809. Gong Shunming, Zhou Ying. Analysis of temperature effect on energy dissipation characteristics of viscoelastic dampers [J]. Earthquake Engineering and Engineering Vibration, 2014(Suppl 1): 801 − 809. (in Chinese)
[12] 周颖, 龚顺明, 吕西林. 黏弹性阻尼器滞回曲线及特征参数的相似准则[J]. 中南大学学报: 自然科学版, 2014, 45(12): 4317 − 4324. Zhou Ying, Gong Shunming, Lü Xilin. Similarity of hysteretic loops and characteristic parameters of viscoelastic dampers [J]. Journal of Central South University (Science and Technology), 2014, 45(12): 4317 − 4324. (in Chinese)
[13] Gong S, Zhou Y. Experimental study and numerical simulation on a new type of viscoelastic damper with strong nonlinear characteristics [J]. Structural Control and Health Monitoring, 2017, 24(4): e1897. doi: 10.1002/stc.1897
[14] 周颖, 平添尧, 龚顺明, 等. 黏弹性阻尼器抗震疲劳性能试验加载制度研究[J]. 建筑结构学报, 2019, 41(6): 101 − 107, 118. Zhou Ying, Ping Tianyao, Gong Shunming, et al. Research on the loading protocol in the seismic fatigue performance test of viscoelastic dampers [J]. Journal of Building Structures, 2019, 41(6): 101 − 107, 118. (in Chinese)
[15] 周颖, 龚顺明. 混合非线性黏弹性阻尼器非线性特征与力学模型研究[J]. 工程力学, 2018, 35(6): 132 − 143. doi: 10.6052/j.issn.1000-4750.2017.02.0156 Zhou Ying, Gong Shunming. Study on nonlinear characteristics and mechanical model of hybrid nonlinear viscoelastic damper [J]. Engineering Mechanics, 2018, 35(6): 132 − 143. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.02.0156
[16] GB 50011−2010, 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2016. GB 50011−2010, Code for seismic design of buildings [S]. Beijing: China Architecture & Building Press, 2016. (in Chinese)
[17] JGJ 297−2013, 建筑消能减震技术规程[S]. 北京: 中国建筑工业出版社, 2013. JGJ 297−2013, Technical specification for seismic energy dissipation of buildings [S]. Beijing: China Architecture & Building Press, 2013. (in Chinese)
[18] JG/T 209−2012, 建筑消能阻尼器[S]. 北京: 中国标准出版社, 2012. JG/T 209−2012, Dampers for vibration energy dissipation of buildings [S]. Standards Press of China, 2012. (in Chinese)
-
期刊类型引用(11)
1. 王道航,吴桂香,孙博,黄兆明. 纤维增强黏弹性阻尼器力学性能试验研究. 建筑结构. 2025(04): 52-58 .  百度学术
百度学术
2. 尚峰,刘文光,许浩,张强. 单层与多层放大型黏弹阻尼器力学性能研究. 建筑结构学报. 2024(04): 86-96 .  百度学术
百度学术
3. 武大洋,张璐,杨国涛,赵斌. 可恢复功能复合结构体系基于复模态叠加法的响应分析和应用. 工程力学. 2024(07): 147-162 .  本站查看
本站查看
4. 王伟,陈俊百. 温度相关型结构地震风险评估方法. 工程力学. 2023(05): 93-103+139 .  本站查看
本站查看
5. 马乾瑛,李帅,高晓敏,吴宗欢. 复合橡胶基磁流变弹性体的动态力学特性研究与模型验证. 复合材料科学与工程. 2023(09): 5-12+20 .  百度学术
百度学术
6. 徐业守,徐赵东,郭迎庆,黄兴淮,葛腾,贺琪. 基于RVE方法的炭黑填充黏弹性材料力学行为研究. 工程力学. 2023(12): 245-256 .  本站查看
本站查看
7. 朱云青,吴京,童超,柳东森,谢鲁齐. 带可更换耗能钢棒的装配式混凝土单侧屈服梁柱节点抗震性能试验研究. 工程力学. 2022(07): 205-216+256 .  本站查看
本站查看
8. 孙利民,狄方殿,陈林,邹易清. 考虑垂度影响的拉索-双粘滞阻尼器系统振动分析. 工程力学. 2022(08): 49-60 .  本站查看
本站查看
9. 卜海峰,蒋欢军,和留生. 剪切型金属阻尼器恢复力模型研究. 工程力学. 2022(10): 131-139 .  本站查看
本站查看
10. 徐业守,徐赵东,郭迎庆,黄兴淮,李强强,贺琪. 管约束和分子链缠结作用下黏弹性材料力学行为. 东南大学学报(自然科学版). 2022(06): 1023-1031 .  百度学术
百度学术
11. 李旭,赵应龙,朱成华,杨一凡,陈美霞. 不同结构特征的STF阻尼器性能试验对比分析. 中国造船. 2022(05): 233-244 .  百度学术
百度学术
其他类型引用(10)



 下载:
下载: