Processing math: 0%

可恢复功能复合结构体系基于复模态叠加法的响应分析和应用

武大洋, 张璐, 杨国涛, 赵斌

武大洋, 张璐, 杨国涛, 赵斌. 可恢复功能复合结构体系基于复模态叠加法的响应分析和应用[J]. 工程力学, 2024, 41(7): 147-162. DOI: 10.6052/j.issn.1000-4750.2022.06.0502
引用本文: 武大洋, 张璐, 杨国涛, 赵斌. 可恢复功能复合结构体系基于复模态叠加法的响应分析和应用[J]. 工程力学, 2024, 41(7): 147-162. DOI: 10.6052/j.issn.1000-4750.2022.06.0502
shu
WU Da-yang, ZHANG Lu, YANG Guo-tao, ZHAO Bin. RESPONSE ANALYSIS AND APPLICATION OF EARTHQUAKE RESILIENT DUAL-SYSTEMS UPON COMPLEX MODE SUPERPOSITION METHOD[J]. Engineering Mechanics, 2024, 41(7): 147-162. DOI: 10.6052/j.issn.1000-4750.2022.06.0502
Citation: WU Da-yang, ZHANG Lu, YANG Guo-tao, ZHAO Bin. RESPONSE ANALYSIS AND APPLICATION OF EARTHQUAKE RESILIENT DUAL-SYSTEMS UPON COMPLEX MODE SUPERPOSITION METHOD[J]. Engineering Mechanics, 2024, 41(7): 147-162. DOI: 10.6052/j.issn.1000-4750.2022.06.0502
shu

可恢复功能复合结构体系基于复模态叠加法的响应分析和应用

  • 1.

    青岛理工大学土木工程学院，山东，青岛 266520

  • 2.

    同济大学土木工程防灾国家重点实验室，上海 200092

基金项目: 国家自然科学基金项目(51978351)；山东省自然科学基金项目(ZR2020QE277)
详细信息
    作者简介:

    张　璐(1998−)，女，山东人，硕士生，主要从事工程结构抗震研究(E-mail: zhanglu_199808@163.com)

    杨国涛(1986−)，男，山东人，教授，博士，博导，主要从事组合结构和结构非线性方面的研究(E-mail: yangguotao@qut.edu.c)

    赵　斌(1967−)，男，四川人，教授，博士，博导，主要从事工程结构抗震研究(E-mail: binzh@tongji.edu.cn)

    通讯作者:

    武大洋(1985—)，男，山东人，副教授，博士，硕导，主要从事工程结构抗震研究(E-mail: wudayang@qut.edu.cn)

  • 中图分类号: TU352.1

RESPONSE ANALYSIS AND APPLICATION OF EARTHQUAKE RESILIENT DUAL-SYSTEMS UPON COMPLEX MODE SUPERPOSITION METHOD

  • 1.

    College of Civil Engineering, Qingdao University of Technology, Qingdao, Shandong 266520, China

  • 2.

    State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China

摘要

    摘要
  • 摘要:

    可恢复功能复合结构体系利用黏滞阻尼等耗能机制可显著提高抗震韧性水平，同时导致其非比例阻尼特征更加突出，采用传统振型叠加法进行响应计算会产生较大误差。为建立该类体系面向抗震韧性的设计方法，该文在前期研究基础上，推导得到可恢复功能复合结构体系分布参数模型复模态正交性条件，建立了该类体系基础激励下动力响应的复模态叠加计算方法。在验证推导正确性后，将该方法应用于两个方面：传统振型叠加法响应计算误差分析和复合体系的设计参数选择。结果表明：相比于振型叠加法只在非比例阻尼不显著的情况具备较好的计算精度，复模态叠加法不仅可以更加准确地计算地震响应，而且可以量化黏滞阻尼对结构响应的控制效果，对于指导该类体系的设计具有参考价值。

    Abstract:

    Energy dissipation mechanism, such as viscous damping, is dramatically beneficial to improve seismic resilience of earthquake resilient dual-systems. At the same time, large amounts of viscous damping make this system have more significant non-proportional damping characteristics, which leads to a large error when calculating response by using the traditional mode superposition method. Aiming at establishing a seismic resilience-oriented design method for this system with previous research, the complex mode orthogonality conditions are derived first for the distributed parameter model of the system, and then the complex mode superposition method is developed for computing its dynamic response under base excitations. Two applications are conducted with this method after verification: response calculation error analysis of the traditional mode superposition method, and choice of design parameters. It is found that: compared with the mode superposition method which only has fairly good calculation accuracy provided that the non-proportional damping is not significant, the complex mode superposition method performs better on calculation accuracy and on quantifying the control effect of viscous damping, which is helpful to design this system.

    • HTML全文

  • 可恢复功能结构在结构体系方面已经具备较为丰富的解决方案可供选择，包括适用于多层结构的自复位框架结构和摇摆结构体系，以及适用于高层建筑结构的可更换构件/部件结构体系[1]。同时，初步的工程实践和实际的地震检验也证明了这类体系在保护生命安全方面具有出色的抗震性能。更为重要的是，这类结构体系在震后的快速恢复中展示了非常显著的韧性水平，在提升结构体系抗震韧性方面具有非常大的潜力和应用前景[2]。

    尽管可恢复功能结构体系在实现方式上具备多种形式，但是其主要的工作机制包括：摇摆机制、自复位机制、耗能机制和可更换机制。其中，耗能机制是可恢复功能结构的核心机制之一。作为一种速度相关型耗能机制，黏滞阻尼机制在结构抗震中得到广泛应用[3]。黏滞阻尼的加入和布置的非均匀性使得结构体系由比例阻尼体系转变为非比例阻尼体系。由于非比例阻尼体系独特的动力学特性，在精确计算其响应时需要采取区别于传统比例阻尼体系的求解方法，而复模态叠加理论就是解决该问题的一种有效途径。同时，将计算比例阻尼体系响应的振型叠加法拓展到非比例阻尼体系的复模态叠加法，既具有方法的连续性，也便于工程技术人员掌握和运用。

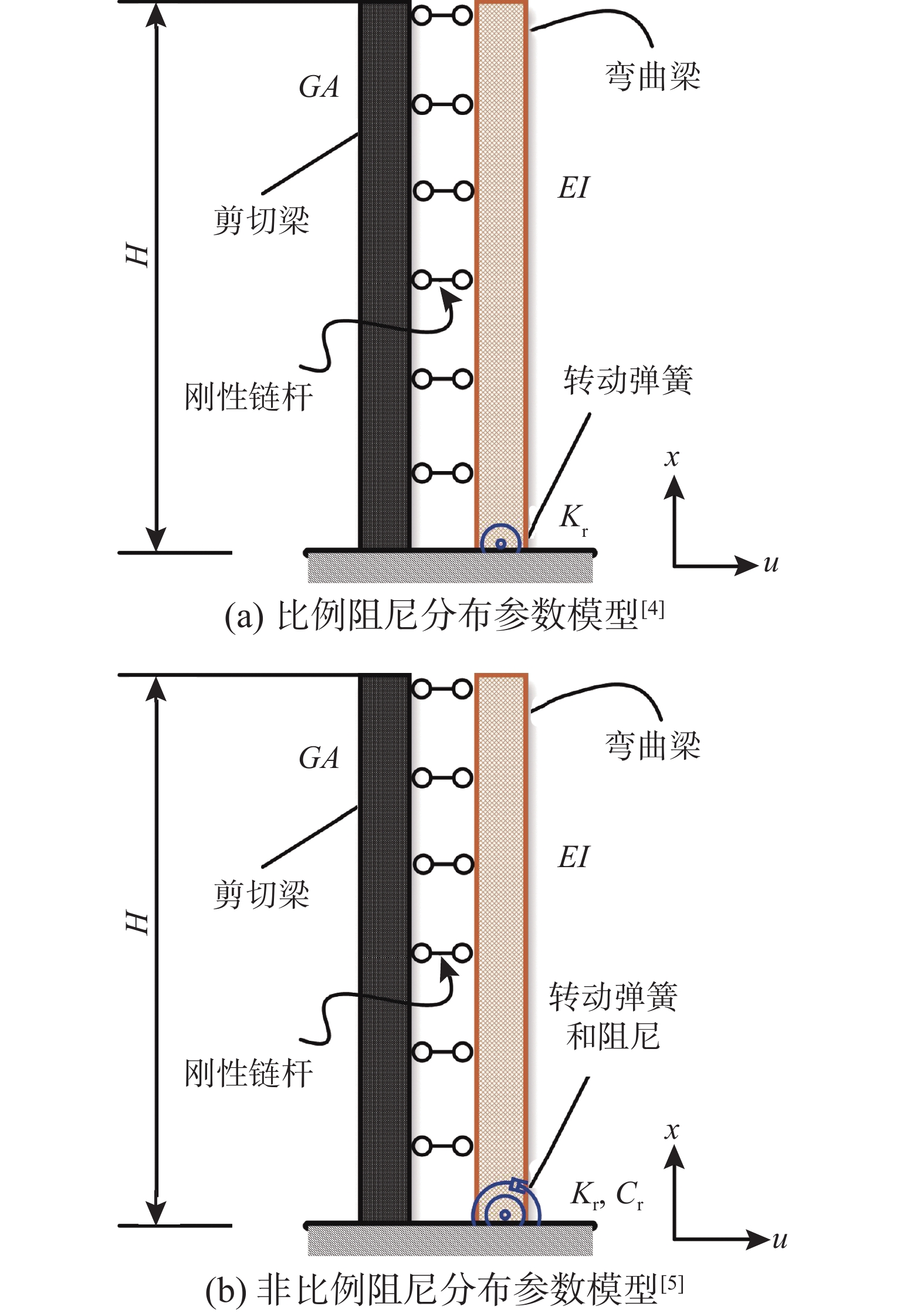
    作为一种可恢复功能结构体系，可恢复功能复合结构体系也同时包含上述四种工作机制。图1所示即为可恢复功能复合结构体系的一种实现方式，主体系采用框架结构，次体系采用摇摆墙和黏滞阻尼器的组合构件，振动台试验结果验证了这种体系的有效性。为建立包含可恢复功能复合结构体系在内的可恢复功能结构体系的面向抗震韧性的设计方法，需要准确量化耗能机制对体系动力特性的影响并建立快速计算体系动力响应的方法。在前期工作中，我们建立了可恢复功能复合结构体系比例阻尼体系的分布参数模型，将剪切变形为主的框架主体系和弯曲变形为主的摇摆次体系分别简化为剪切梁和弯曲梁，并采用经典的振型叠加法计算出体系的动力响应[4]。最近，在该比例阻尼分布参数模型的基础上进一步提出了非比例阻尼分布参数模型，将复合体系中的自复位机制和耗能机制分别简化为弹性转动弹簧和线性转动黏滞阻尼，进行了包括模态阻尼比和复模态在内等基本动力特性和频域响应的参数分析[5]。同时，将均匀刚度模型拓展到适用范围更广的非均匀刚度分布参数模型[6]。但是，目前针对复合体系尚未建立基于复模态叠加法的响应计算方法。

    为进一步分析复合体系在地震作用下的时域响应特征，本文在上述研究的基础上，首先推导得到可恢复功能复合结构体系采用复模态叠加法的时域响应正交性条件，建立该体系在基础激励下的体系动力响应方程；然后与采用分布传递函数法计算的响应对比[7]，验证推导的正确性；最后是两个方面的应用：与传统振型叠加法计算结果对比，分析采用振型叠加法计算非比例阻尼体系的响应误差；采用本文的复模态叠加法完成可恢复功能复合结构体系的弹性响应计算分析和设计参数选择。

    图  1  可恢复功能复合结构体系振动台试验模型
    Figure  1.  Shaking-table test model of an earthquake resilient dual-system
    下载: 全尺寸图片 幻灯片

    1   基于复模态叠加法的响应计算

    结构体系的多自由度(MDOF)集中质量模型已经广泛用于分析和设计，具有比例阻尼和非比例阻尼的MDOF模型已有较为完善的计算理论。对于具有非比例阻尼的MDOF模型，不同结构体系采用复模态叠加法均可给出一致模态正交性解耦条件[8-9]。与MDOF模型不同，由于分布参数模型的质量和刚度沿结构高度连续分布，需要针对不同分布参数模型推导其对应的模态正交性解耦条件[10]。为此，本节在分布参数模型及其动力方程的基础上，重点介绍复模态解耦正交性条件的推导和响应计算方法。

    1.1   可恢复功能复合结构体系分布参数模型

    可恢复功能复合结构体系的比例阻尼分布参数模型(图2(a))，将自复位机制简化为转动弹簧置于次体系的底部，转动弹簧的转动刚度为Kr，而将耗能机制以整体阻尼比的形式体现在动力方程中，该整体阻尼比包含结构的固有阻尼比和黏滞阻尼机制提供的附加阻尼比。基于该比例阻尼模型，得到了可恢复功能复合结构体系的层间位移角谱并以此谱为工具进行了大量的参数分析[11-12]。为进一步分析耗能机制对体系动力特性和响应的影响，在比例阻尼分布参数模型的基础上提出了非比例阻尼分布参数模型(图2(b))。在该模型中，自复位机制依然简化为转动刚度为Kr的弹簧置于次体系的底部，耗能机制以局部的转动线性阻尼体现在次体系的底部，转动阻尼的线性阻尼系数为Cr。因此，相比于比例阻尼分布参数模型，非比例阻尼分布参数模型可以直接分析耗能机制对体系动力特性和响应的影响。更为重要的是，可以直接建立附加阻尼与抗震韧性目标的量化关系，从而建立面向抗震韧性的设计方法。

    图  2  可恢复功能复合结构体系比例阻尼和非比例阻尼分布参数模型
    Figure  2.  Distributed parameter model with proportional and non-proportional damping of earthquake resilient dual-systems
    下载: 全尺寸图片 幻灯片

    1.2   动力方程

    非比例阻尼分布参数体系的动力方程为[4-5]：

    ρ¨u(x,t)+c˙u(x,t)+u(4)(x,t)EI/H4−u″ (1)

    对应的边界条件为：

    1)顶部弯矩为0 (x=1)

    u''\left( {1,t} \right){{EI} / {{H^2}}} = 0 (2)

    2)顶部剪力为0 (x=1)

    u'''\left( {1,t} \right) - {\alpha ^2}u'\left( {1,t} \right) = 0 (3)

    其中：

    \alpha = H\sqrt {{{GA} \mathord{\left/ {\vphantom {{GA} {EI}}} \right. } {EI}}} (4)

    式中：α为无量纲参数，剪弯刚度比，量化复合结构中框架主体系与摇摆次体系之间的相对刚度关系，变化范围是(0, +∞)。α从零增加到+∞时，体系由纯弯曲梁转变为纯剪切梁；α≤1时，弯曲梁占主导，体系变形中弯曲变形居多；1<α≤3时，二者比较均衡，呈现出弯剪变形模式；α>3时，剪切变形逐渐主导整体变形。

    3)底部位移为0 (x=0)

    u\left( {0,t} \right) = 0 (5)

    4)弯曲梁底部弯矩平衡 (x=0)

    u''\left( {0,t} \right) = {R_{\text{f}}}u'\left( {0,t} \right) + {D_{\text{f}}}\dot u'\left( {0,t} \right) (6)

    其中：

    {R_{\text{f}}} = {{{K_{\rm{r}}}H} \mathord{\left/ {\vphantom {{{K_{\rm{r}}}H} {EI}}} \right. } {EI}},{D_{\text{f}}} = {{{C_{\rm{r}}}H} \mathord{\left/ {\vphantom {{{C_{\rm{r}}}H} {EI}}} \right. } {EI}} (7)

    式中：Rf为无量纲参数，转动刚度参数，用于量化自复位机制(如预应力筋和自复位支撑等装置[13-14])的相对刚度，变化范围为(0, +∞)。Rf从零增加到+∞时，转动约束由铰接转变为固接；Rf取值介于二者之间时，表示对转动具有一定的约束能力。Df为阻尼机制的中间参数。

    式(1)对应的无阻尼齐次方程为：

    \kappa \ddot u\left( {x,t} \right) + {u^{\left( 4 \right)}}\left( {x,t} \right) - {\alpha ^2}u''\left( {x,t} \right) = 0 (8)

    式中，\kappa = {{\rho {H^4}} / {EI}}。

    采用分离变量法，令：

    u\left( {x,t} \right) = \phi \left( x \right){\rm{e}^{\rm{i}\omega t}} (9)

    将式(9)代入式(8)，得到：

    {\phi ^{\left( 4 \right)}}\left( x \right) - {\alpha ^2}\phi {{''}}\left( x \right) - \kappa {\omega ^2}\phi \left( x \right) = 0 (10)

    式中：ω为体系的圆频率；i=\sqrt { - 1} 。同时，边界条件变为：

    \phi {{''}}\left( 1 \right) = 0 (11)
    \phi {{'''}}\left( 1 \right) - \alpha _0^2\phi '\left( 1 \right) = 0 (12)
    \phi \left( 0 \right) = 0 (13)
    \phi {{''}}\left( 0 \right) = {R_{\text{f}}}\phi '\left( 0 \right) + {D_{\text{f}}}{\rm{i}}\omega \phi '\left( 0 \right) (14)

    \phi ( x ) 体系的振型模态位移：

    \begin{split} \phi \left( x \right) =& {A_1}\sin \left( {\gamma x} \right) + {A_2}\cos \left( {\gamma x} \right) + \\& {A_3}\sinh ( {\sqrt {{\alpha ^2} + {\gamma ^2}} x} ) + {A_4}\cosh ( {\sqrt {{\alpha ^2} + {\gamma ^2}} x} ) \end{split} (15)

    式中：A1~A4为需要根据边界条件确定的常数；γ为确定圆频率ω的特征值参数。

    1.3   正交性条件推导

    非比例阻尼分布体系的复模态叠加计算响应首先需要解决的问题是正交性条件的推导，通过得到的正交条件实现复模态响应的解耦[9, 13]。基于式(10)，可得到第n阶和第m阶模态控制方程：

    {\phi _{n}^{\left( 4 \right)}} - {\alpha ^2}{\phi _n''} - \kappa {\omega _n^2}{\phi _n} = 0 (16)
    {\phi _{m}^{\left( 4 \right)} }- {\alpha ^2}{\phi _m''} - \kappa {\omega _m^2}{\phi _m} = 0 (17)

    式(16)× \phi_{m} ，式(17)× \phi_{n}，得到：

    \mathop \int \nolimits_0^1 {\phi _{n}^{\left( 4 \right)}}{\phi _m}{\text{d}}x - {\alpha ^2}\mathop \int \nolimits_0^1 {\phi _n''}{\phi _m}{\text{d}}x - \kappa {\omega _n^2}\mathop \int \nolimits_0^1 {\phi _n}{\phi _m}{\text{d}}x = 0 (18)
    \mathop \int \nolimits_0^1 {\phi _{m}^{\left( 4 \right)}}{\phi _n}{\text{d}}x - {\alpha ^2}\mathop \int \nolimits_0^1 {\phi _m''}{\phi _n}{\text{d}}x - \kappa {\omega _m^2}\mathop \int \nolimits ^1 {\phi _n}{\phi _m}{\text{d}}x = 0 (19)

    通过利用分部积分和边界条件，得到：

    \begin{split} & \phi {'_m}( 0 )\phi {'_n}( 0 )( {{R_{\text{f}}} + {\text{i}}\mu {\gamma _n}\sqrt {{\gamma _{n}^2} + {\alpha ^2}} } ) + \\ &\;\;\; \mathop \int \nolimits_0^1 {\phi _n''}{\phi _m''}{\text{d}}x + {\alpha ^2}\mathop \int \nolimits_0^1 {\phi _n'}{\phi _m'}{\text{d}}x - \kappa {\omega _n^2}\mathop \int \nolimits_0^1 {\phi _n}{\phi _m}{\text{d}}x = 0 \end{split} (20)
    \begin{split} & \phi {'_m}( 0)\phi {'_n}( 0 )( {{R_{\text{f}}} + {\text{i}}\mu {\gamma _m}\sqrt {{\gamma _{m}^2} + {\alpha ^2}} }) + \\&\;\;\; \mathop \int \nolimits_0^1 {\phi _n''}{\phi _m''}{\text{d}}x + {\alpha ^2}\mathop \int \nolimits_0^1 {\phi _n'}{\phi _m'}{\text{d}}x - \kappa {\omega _m^2}\mathop \int \nolimits_0^1 {\phi _n}{\phi _m}{\text{d}}x = 0 \end{split} (21)

    式中： \mu=R_{\mathrm{f}} / \sqrt{\kappa} ，为无量纲参数，耗能参数，用于量化速度相关型耗能机制(如黏滞阻尼器或黏弹性阻尼器等耗能装置[15-16])对体系动力特性的影响，变化范围为(0, +∞)。μ从零增加到+∞时，转动约束由铰接转变为固接；μ取值介于二者之间时，表示对转动产生一定的约束。利用关系 \sqrt \kappa \omega = \gamma \sqrt {{\gamma ^2} + {\alpha ^2}} ，式(20)、式(21)进一步整理为：

    \begin{split} & \phi {'_m}\left( 0 \right)\phi {'_n}\left( 0 \right)( {{R_{\text{f}}} + {\text{i}}\mu \sqrt \kappa {\omega _n}} ) + \mathop \int \nolimits_0^1 {\phi _n''}{\phi _m''}{\text{d}}x + \\&\qquad {\alpha ^2}\mathop \int \nolimits_0^1 {\phi _n'}{\phi _m'}{\text{d}}x - \kappa {\omega _{n}^2}\mathop \int \nolimits_0^1 {\phi _n}{\phi _m}{\text{d}}x = 0 \end{split} (22)
    \begin{split}& \phi {'_m}\left( 0 \right)\phi {'_n}\left( 0 \right)( {{R_{\text{f}}} + {\text{i}}\mu \sqrt \kappa {\omega _m}} ) + \mathop \int \nolimits_0^1 {\phi _n''}{\phi _m''}{\text{d}}x + \\&\qquad {\alpha ^2}\mathop \int \nolimits_0^1 {\phi _n'}{\phi _m'}{\text{d}}x - \kappa {\omega _{m}^2}\mathop \int \nolimits_0^1 {\phi _n}{\phi _m}{\text{d}}x = 0 \end{split} (23)

    将式(23)与式(22)相减得到第一个正交条件：

    {\text{i}}\mu \phi {'_m}\left( 0 \right)\phi {'_n}\left( 0 \right) - \sqrt \kappa \left( {{\omega _n} + {\omega _m}} \right)\mathop \int \nolimits_0^1 {\phi _n}{\phi _m}{\text{d}}x = 0 (24)

    式(22)× \phi_{m} ，式(23)× \phi_{n} ，得到第二个正交条件：

    \begin{split} & \phi {'_m}\left( 0 \right)\phi {'_n}\left( 0 \right){R_{\text{f}}} + \mathop \int \nolimits_0^1 {\phi _n''}{\phi _m''}{\text{d}}x + \\&\qquad {\alpha ^2}\mathop \int \nolimits_0^1 {\phi _n'}{\phi _m'}{\text{d}}x + \kappa {\omega _m}{\omega _n}\mathop \int \nolimits_0^1 {\phi _n}{\phi _m}{\text{d}}x = 0 \end{split} (25)

    1.4   基础激励下体系动力响应计算推导

    基础激励下非比例阻尼分布参数体系的动力方程为：

    \kappa \ddot u + {u^{\left( 4 \right)}} - {\alpha ^2}u{{''}} = - \kappa {\ddot u_{\rm{g}}} (26)

    其解答可以表示为：

    u\left( {x,t} \right) = \mathop \sum \limits_{n = 1}^\infty {u_n}\left( t \right){\phi _n}\left( x \right) (27)

    第n阶模态位移响应为：

    {u_n}\left( t \right) = {C_n}{{\text{e}}^{{\text{i}}{\omega _n}t}} (28)

    式中：Cn为待定系数。则式(26)可以重写为：

    \mathop \sum \limits_{n = 1}^\infty [ {\kappa {{\ddot u}_n}( t ){\phi _n}( x ) + {u_n}( t ){\phi _n^{( 4 )}} - {\alpha ^2}{u_n}( t ){\phi _n''}} ] = - \kappa {{\ddot u}_{\rm{g}}}( t ) (29)

    式(29)× \phi_{m} ，并0到1进行积分，得到：

    \begin{split} & \mathop \sum \limits_{n = 1}^\infty \left( {\kappa {{\ddot u}_n}\left( t \right)\mathop \int \nolimits_0^1 {\phi _n}\left( x \right){\phi _m}{\text{d}}x} \right){{ + }} \\&\qquad \mathop \sum \limits_{n = 1}^\infty {u_n}\left( t \right)\left( {\mathop \int \nolimits_0^1 {\phi _n}^{\left( 4 \right)}{\phi _m}{\text{d}}x - {\alpha ^2}\mathop \int \nolimits_0^1 {\phi _n''}{\phi _m}{\text{d}}x} \right) = \\&\qquad - \kappa {{\ddot u}_{\rm{g}}}\left( t \right)\mathop \int \nolimits_0^1 {\phi _m}{\text{d}}x \end{split} (30)

    观察式(18)和(20)可以发现，式(30)左边第二项中括号内表达式可用式(31)替代：

    \begin{split} & \mathop \int \nolimits_0^1 {\phi _n^{\left( 4 \right)}}{\phi _m}{\text{d}}x - {\alpha ^2}\mathop \int \nolimits_0^1 {\phi _n''}{\phi _m}{\text{d}}x = \\&\qquad \phi {'_m}\left( 0 \right)\phi {'_n}\left( 0 \right)\left( {{R_{\text{f}}} + {\text{i}}\mu {\gamma _n}\sqrt {{\gamma _n}^2 + {\alpha ^2}} } \right) + \\&\qquad \mathop \int \nolimits_0^1 {\phi _n''}{\phi _m''}{\text{d}}x + {\alpha ^2}\mathop \int \nolimits_0^1 {\phi _n'}{\phi _m'}{\text{d}}x \end{split} (31)

    得到：

    \begin{split} & \mathop \sum \limits_{n = 1}^\infty \left( {\kappa {{\ddot u}_n}\left( t \right)\mathop \int \nolimits_0^1 {\phi _n}\left( x \right){\phi _m}{\text{d}}x} \right) + \\&\qquad \mathop \sum \limits_{n = 1}^\infty {u_n}\left( t \right)( {\phi {'_m}\left( 0 \right)\phi {'_n}\left( 0 \right)( {{R_{\text{f}}} + {\text{i}}\mu \sqrt \kappa {\omega _n}} )} ) + \\&\qquad \mathop \sum \limits_{n = 1}^\infty {u_n}\left( t \right)\left( {\mathop \int \nolimits_0^1 {\phi _n''}{\phi _m''}{\text{d}}x + {\alpha ^2}\mathop \int \nolimits_0^1 {\phi _n'}{\phi _m'}{\text{d}}x} \right) = \\&\qquad - \kappa {{\ddot u}_{\rm{g}}}\left( t \right)\mathop \int \nolimits_0^1 {\phi _m}{\text{d}}x \end{split} (32)

    由刚度正交条件得到：

    \begin{split} & \int_0^1 {\phi ''{_n}} \phi ''{_m}\text{d}x + {\alpha ^2}\int_0^1 {\phi {'_n}} \phi {'_m}\text{d}x = \\ &\qquad \phi {'_n}\left( 0 \right)\phi {'_m}\left( 0 \right){R_{\text{f}}} - \kappa {\omega _m}{\omega _n}\int_0^1 {{\phi _n}} {\phi _m}\text{d}x \end{split} (33)

    将式(33)等号左边代入式(32)，得到：

    \begin{split} & \mathop \sum \limits_{n = 1}^\infty \left( {\kappa {{\ddot u}_n}\left( t \right)\mathop \int \nolimits_0^1 {\phi _n}{\phi _m}{\text{d}}x} \right) + \\&\qquad \mathop \sum \limits_{n = 1}^\infty {u_n}\left( t \right)( {\phi {'_m}\left( 0 \right)\phi {'_n}\left( 0 \right){\text{i}}\mu \sqrt \kappa {\omega _n}} ) - \\&\qquad \mathop \sum \limits_{n = 1}^\infty {u_n}\left( t \right)\left( {\kappa {\omega _m}{\omega _n}\mathop \int \nolimits_0^1 {\phi _m}{\phi _n}{\text{d}}x} \right) = \\&\qquad - \kappa {{\ddot u}_{\rm{g}}}\left( t \right)\mathop \int \nolimits_0^1 {\phi _m}{\text{d}}x \end{split} (34)

    由式(28)可知：

    {\ddot u_n}\left( t \right) = - \omega _n^2{C_n}{{\text{e}}^{{\text{i}}{\omega _n}t}} = - \omega _n^2{u_n}\left( t \right) (35)

    将式(35)代入式(34)，整理得到：

    \begin{split} & \mathop \sum \limits_{n = 1}^\infty \left[ {\frac{{{{\ddot u}_n}\left( t \right)}}{{{\omega _n}}}\left( { - \phi {'_m}\left( 0 \right)\phi {'_n}\left( 0 \right){\text{i}}\mu \sqrt \kappa } \right)} \right] + \\&\qquad \mathop \sum \limits_{n = 1}^\infty \left[ {\frac{{{{\ddot u}_n}\left( t \right)}}{{{\omega _n}}}\left( {\kappa \left( {{\omega _n} + {\omega _m}} \right)\mathop \int \nolimits_0^1 {\phi _n}{\phi _m}{\text{d}}x} \right)} \right] = \\&\qquad - \kappa {{\ddot u}_{\rm{g}}}\left( t \right)\mathop \int \nolimits_0^1 {\phi _m}{\text{d}}x \end{split} (36)

    此时，引入第二个正交条件，对于ωn≠ωm，式(36)括号内表达式的值为零，由此得到解耦的动力方程：

    {{\ddot u}_n}( t )2\mathop \int \nolimits_0^1 {\phi _n^2}{\text{d}}x + {{\dot u}_n}( t )\frac{\mu }{{\sqrt \kappa }}{( {\phi {'_n}( 0 )} )^2} = - {{\ddot u}_{\rm{g}}}( t )\mathop \int \nolimits_0^1 {\phi _n}{\text{d}}x (37)

    将式(37)在区间[0−,0+]进行积分，得到：

    {{\dot u}_n}( {{0^ + }} )2\mathop \int \nolimits_0^1 {\phi _n^2}{\text{d}}x + {u_n}( {{0^ + }} )\frac{\mu }{{\sqrt \kappa }}{( {\phi {'_n}( 0 )} )^2} = - I\mathop \int \nolimits_0^1 {\phi _n}{\text{d}}x (38)

    将{\dot u_n}\left( {{0^ + }} \right) = {\rm i}{\omega _n}{C_n},{u_n}\left( {{0^ + }} \right) = {C_n}代入式(38)，得到：

    {C_n} = \frac{{ - I \displaystyle\int \nolimits_0^1 {\phi _n}{\text{d}}x}}{{2 \displaystyle\int \nolimits_0^1 {\phi _n^2}{\text{d}}x \times {\text{i}}{\omega _n} + \dfrac{\mu }{{\sqrt \kappa }}{{\left( {\phi {'_n}\left( 0 \right)} \right)}^2}}} = I{B_n} (39)

    其中：

    {B_n} = \frac{{ - \displaystyle\int \nolimits_0^1 {\phi _n}{\text{d}}x}}{{2 \displaystyle\int \nolimits_0^1 {\phi _n^2}{\text{d}}x \times {\text{i}}{\omega _n} + \dfrac{\mu }{{\sqrt \kappa }}{{\left( {\phi {'_n}\left( 0 \right)} \right)}^2}}} (40)

    参考文献[8]、文献[9]和文献[17]，体系的动力响应可以采用脉冲响应函数的复响应和实响应表达，分别为：

    h_n^c\left( {x,t} \right) = {B_n}{\phi _n}{{\text{e}}^{{\text{i}}{\omega _n}t}} (41)
    h_n^r\left( {x,t} \right) = 2{{\rm{Re}}} [ {{B_n}{\phi _n}{{\text{e}}^{{\text{i}}{\omega _n}t}}} ] (42)

    进一步整理如下：

    {\beta _n}\left( x \right) = 2{{\rm{Re}}} \left[ {{B_n}{\phi _n}} \right] (43)
    {\gamma _n}\left( x \right) = 2{\text{Im}}\left[ {{B_n}{\phi _n}} \right] (44)
    {\alpha _n}\left( x \right) = {\xi _n}{\beta _n}\left( x \right) - \sqrt {1 - \xi _n^2} {\gamma _n}\left( x \right) (45)
    h_n^r\left( {x,t} \right) = {\alpha _n}\left( x \right){\omega _n}{h_n}\left( t \right) + {\beta _n}\left( x \right){\dot h_n}\left( t \right) (46)

    其中，hn(t)为脉冲响应函数：

    {h_n}\left( t \right) = \frac{1}{{{\omega _{D_{n}}}}}{{\text{e}}^{ - {\xi _n}{\omega _n}t}}\sin \left( {{\omega _{D_{n}}}t} \right) (47)

    式中， {\omega _{D_{n}}} = \left| {{\omega _n}} \right|\sqrt {1 - \xi _n^2} 为有阻尼圆频率。

    由此得到了可恢复功能复合结构体系采用复模态叠加法计算得到的地震响应：

    \begin{split} u\left( {x,t} \right) = &\sum \limits_{n = 1}^\infty \int \nolimits_0^t {{\ddot u}_{\rm{g}}}\left( \tau \right)h_n^r\left( {x,t - \tau } \right){\text{d}}\tau = \\& \sum \limits_{n = 1}^\infty [ {{\alpha _n}\left( x \right){\omega _n}{D_n}\left( t \right) + {\beta _n}\left( x \right){{\dot D}_n}\left( t \right)} ] \end{split} (48)

    其中：

    {D_n}\left( t \right) = \int \nolimits_0^t {\ddot u_{\rm{g}}}\left( \tau \right){h_n}\left( {t - \tau } \right){\text{d}}\tau (49)
    {\dot D_n}\left( t \right) = \int \nolimits_0^t {\ddot u_{\rm{g}}}\left( \tau \right){\dot h_n}\left( {t - \tau } \right){\text{d}}\tau (50)

    需要说明的是，此处计算时域响应采用的是杜哈梅积分，仅适用于外部激励为显式函数的情况。采用逐步积分法计算单自由度体系的响应，不仅可以提高计算效率，而且会使计算公式同时适用于离散的地震动时程记录数据，后续计算均采用逐步积分法计算地震动响应。

    2   方法验证

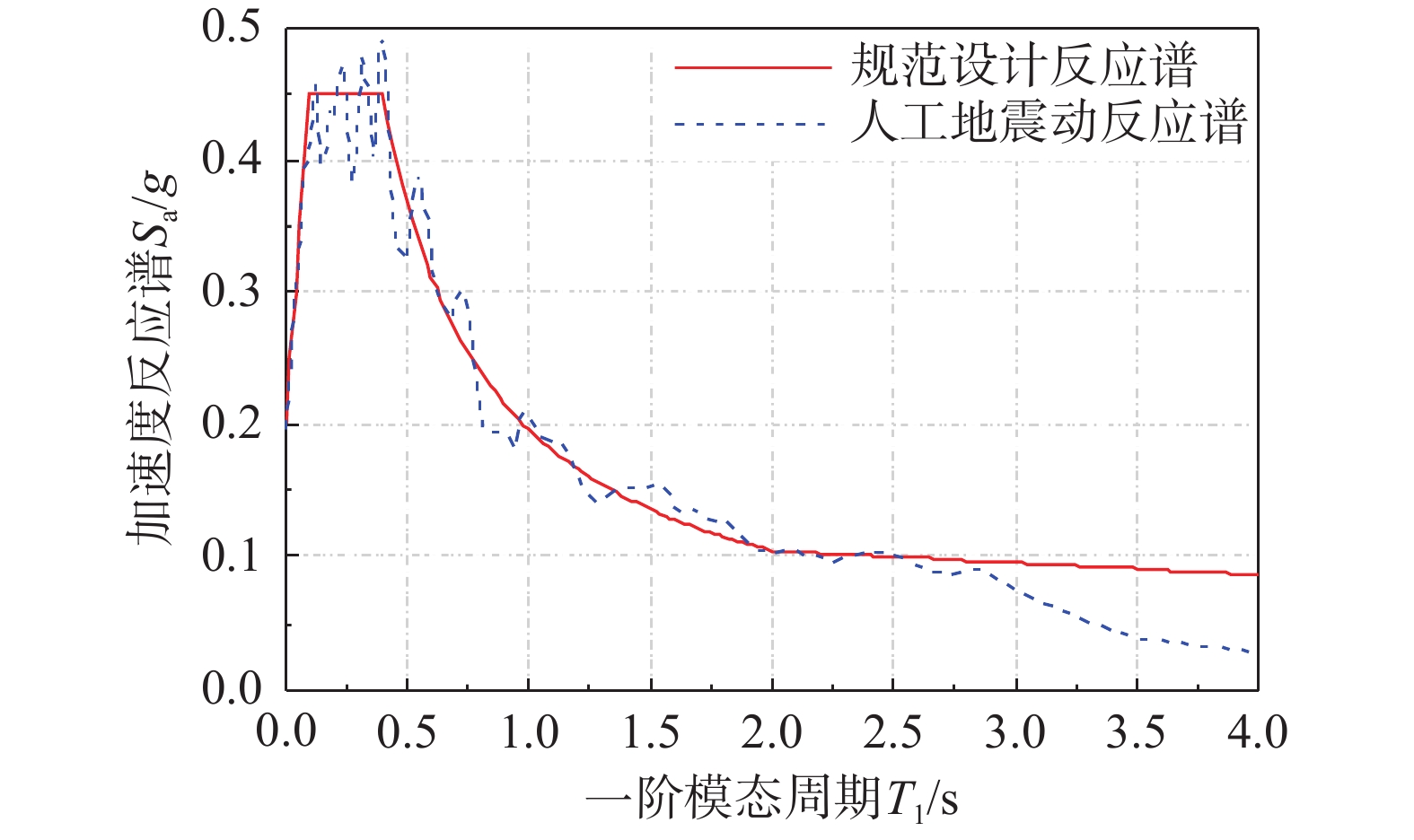
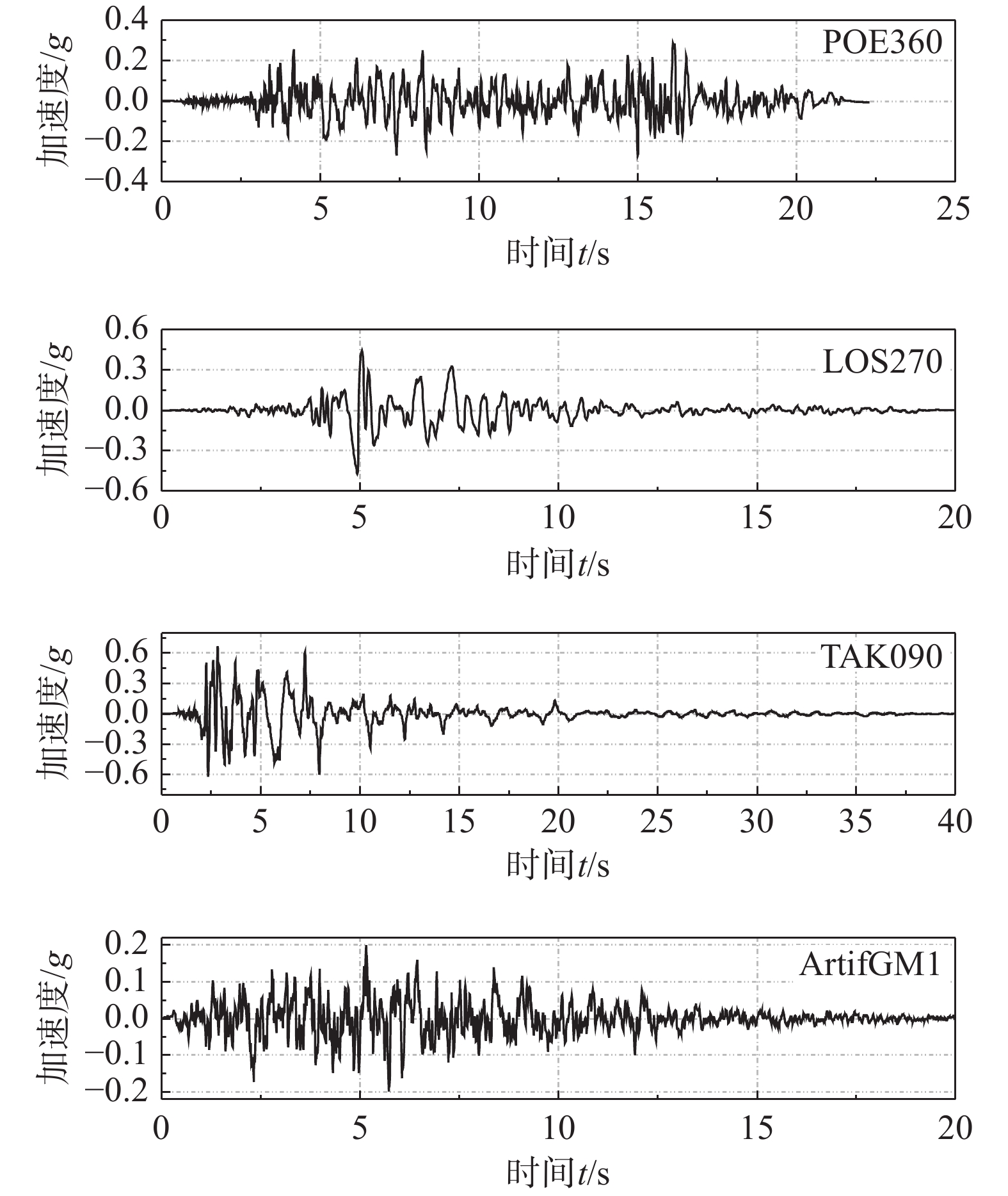
    为验证推导正确性，我们将在相同参数下对比复模态法和分布传递函数法(Distributed Transfer Function Method，DTFM)计算非比例阻尼分布参数模型动力特性和响应的差异。采用分布传递函数法计算非比例阻尼分布参数模型动力特性和响应的过程详见文献[5]，本文不再赘述。本节将对比两种方法计算的复频率和地震作用下的动力响应，以验证本文推导的正确性。如图3和图4所示，地震响应计算采用四条地震动，其中POE360分量、LOS270分量和TAK090分量，均下载自PEER，人工地震动ArtifGM1由软件SeismoArtif根据规范设计反应谱生成。

    图  3  由规范设计反应谱生成的人工地震动时程反应谱
    Figure  3.  Response spectra of artificial ground motion generated with code design response spectra
    下载: 全尺寸图片 幻灯片
    图  4  天然地震动和人工地震动时程曲线
    Figure  4.  Time histories of natural and artificial ground motions
    下载: 全尺寸图片 幻灯片

    表1列出了由复模态法和DTFM法分别计算出的不同参数下体系前三阶圆频率。图5则给出了在天然地震动POE360和人工地震动ArtifGM1作用下由三种计算方法得到的部分工况顶部位移时程结果，表2则给出了全部工况三种方法计算结果的误差，计算工况和参数见表3。

    表  1  复模态法和DTFM法计算的复频率及其对比
    Table  1.  Comparison of complex frequencies computed with the complex mode method and DTFM method
    工况第n阶模态第n阶圆频率ωn/(rad·s−1)对比误差/(%)
    复模态法DTFM法
    α=11−2.102+0.264i−2.102+0.264i0.0
    μ=0.22−17.501+2.627i−17.501+2.627i0.0
    Rf=0.53−56.606+6.643i−56.606+6.643i0.0
    α=31−5.199+0.346i−5.199+0.346i0.0
    μ=0.22−23.272+2.641i−23.272+2.641i0.0
    Rf=0.53−61.893+6.227i−61.893+6.227i0.0
    α=51−8.323+0.619i−8.323+0.619i0.0
    μ=0.32−32.614+3.119i−32.614+3.119i0.0
    Rf=0.23−73.385+4.851i−73.385+4.851i0.0
    下载: 导出CSV 
    | 显示表格
    图  5  天然和人工地震动作用下三种计算方法顶部位移时程结果对比
    Figure  5.  Comparison of roof displacement time histories computed with three methods under two ground motions
    下载: 全尺寸图片 幻灯片

    通过对比可以发现两种方法圆频率的计算结果一致。通过对比复模态叠加法(CMSM)、振型叠加法(RMSM)与分布传递函数法(DTFM)的时程计算结果可以发现，考虑前六阶模态三者的计算结果吻合较好。相比于Df=0.20的情况，Df为其他值的情况相符更好。其中，四条地震动下三种方法(CMSM、RMSM和DTFM)计算得到的最大顶部位移分别为：POE360分量，58.98 mm、60.25 mm和55.73 mm；LOS270分量，156.56 mm、153.51 mm和146.97 mm；TAK090分量，306.98 mm、327.28 mm和286.50 mm，ArtifGM1，42.40 mm、43.06 mm和39.92 mm。相比于分布传递函数法的计算结果，复模态叠加法的计算结果偏大，说明采用该方法进行计算得到的结果偏于保守。同时，对比复模态叠加法和振型叠加法的结果，二者之间数值大致接近。

    表  2  三种方法各工况顶层位移沿高度最大误差
    Table  2.  Maximum story displacement and interstory drift ratio errors along the height for the three methods
    地震动响应类别对比类别误差CvsD=(CMSM-DTFM)/DTFM×100/(%)误差RvsD=(RMSM-DTFM)/DTFM×100/(%)
    工况1工况2工况3工况4工况5工况6工况7工况8工况9工况10工况11工况12
    POE360顶层位移CvsD0.135.8312.3435.87−0.61−0.370.501.79−0.020.611.482.48
    RvsD−0.778.1113.4634.36−0.90−1.24−1.12−0.910.180.971.432.80
    LOS270顶层位移CvsD1.456.5216.0630.860.551.412.574.47−0.270.521.402.93
    RvsD0.644.4512.1026.24−0.02−0.25−0.49−0.27−0.520.170.290.66
    TAK090顶层位移CvsD1.687.1517.4435.620.191.122.554.620.110.561.362.51
    RvsD4.0314.2428.8866.82−0.081.624.047.65−0.020.000.230.79
    ArtifGM1顶层位移CvsD2.596.2212.0224.290.471.112.714.580.380.650.532.63
    RvsD3.697.8620.3737.60−0.01−0.271.263.380.09−0.13−1.91−1.97
    下载: 导出CSV 
    | 显示表格
    表  3  三种方法的计算参数
    Table  3.  Computing parameters for the three methods
    工况 复合体系参数 复合体系参数 模态阻尼比
    α Rf Df/s κ/s2 µ T1/s T2/s T3/s T4/s T5/s T6/s ξ1 ξ2 ξ3 ξ4 ξ5 ξ6
    工况1 1 0.5 0.05 0.1210 0.1438 1.037 0.127 0.040 0.019 0.011 0.007 0.089 0.111 0.109 0.082 0.058 0.042
    工况2 1 0.5 0.10 0.1210 0.2875 1.019 0.116 0.037 0.018 0.011 0.007 0.179 0.186 0.099 0.054 0.034 0.023
    工况3 1 0.5 0.15 0.1210 0.4313 0.986 0.105 0.036 0.018 0.011 0.007 0.271 0.175 0.071 0.037 0.023 0.015
    工况4 1 0.5 0.20 0.1210 0.5750 0.933 0.101 0.035 0.018 0.011 0.007 0.365 0.142 0.054 0.028 0.017 0.012
    工况5 2 0.5 0.05 0.4839 0.0719 1.209 0.229 0.081 0.040 0.023 0.015 0.030 0.051 0.061 0.061 0.057 0.051
    工况6 2 0.5 0.10 0.4839 0.1438 1.204 0.224 0.077 0.038 0.022 0.015 0.060 0.099 0.103 0.080 0.057 0.041
    工况7 2 0.5 0.15 0.4839 0.2156 1.195 0.216 0.073 0.037 0.022 0.015 0.090 0.138 0.108 0.066 0.043 0.029
    工况8 2 0.5 0.20 0.4839 0.2875 1.182 0.206 0.071 0.036 0.022 0.015 0.119 0.158 0.093 0.052 0.033 0.022
    工况9 3 0.5 0.05 1.0887 0.0479 1.272 0.295 0.115 0.059 0.035 0.023 0.016 0.031 0.039 0.042 0.042 0.041
    工况10 3 0.5 0.10 1.0887 0.0958 1.269 0.292 0.113 0.057 0.034 0.022 0.032 0.061 0.074 0.071 0.061 0.050
    工况11 3 0.5 0.15 1.0887 0.1438 1.265 0.287 0.110 0.055 0.033 0.022 0.048 0.088 0.096 0.076 0.055 0.040
    工况12 3 0.5 0.20 1.0887 0.1917 1.259 0.281 0.106 0.054 0.033 0.022 0.064 0.110 0.101 0.068 0.046 0.032
    注：α为剪弯刚度比；Rf为转动刚度参数；Df为阻尼机制的中间参数；κ为复合体系的中间参数；μ为耗能参数；Ti为模态周期；ξi为模态阻尼比。
    下载: 导出CSV 
    | 显示表格

    3   结果对比分析和设计参数选择

    3.1   结果对比分析

    实模态叠加法也称为模态叠加法、振型叠加法，是目前地震响应计算中应用最为广泛的方法之一。对于比例阻尼结构体系，基于振型正交性解耦不同模态的响应，大大降低了计算难度，提高了计算效率。对于非比例阻尼结构体系，当非比例阻尼较低时，采用比例阻尼的振型叠加法进行强行解耦计算，可在一定误差范围内得到满足工程精度的计算结果。为此，本节将对比复模态叠加法、DTFM法与振型叠加法在位移、层间位移角、层剪力和层弯矩等响应的计算结果，计算中均考虑前六阶振型对总响应的贡献。根据设计中常采用的附加阻尼比建议值，非比例阻尼提供的附加阻尼比的范围为2%~40%。考虑12种工况：1)~4) α=1, Rf=0.5, Df=0.05~0.20; 5)~8) α=2, Rf=0.5, Df=0.05~0.20; 9)~12) α=3, Rf=0.5, Df= 0.05~0.20。三种方法采用的计算参数列于表3，模态周期(表3中T1~T6)和模态阻尼比(表3中ξ1~ξ6)均采用DTFM法的计算结果，其他两种方法均采用该计算结果作为输入参数进行计算。

    在第2节选取的三条天然地震动和一条人工地震动(图3和图4)作用下分别采用三种计算方法进行地震响应计算。虽然四条地震动不同，但是分析结果得到的规律和趋势相近。因此，本节以POE360分量为代表进行讨论，结合其他三条地震动给出总结性描述。图6~图8给出了由三种计算方法得到的POE360地震动作用下部分工况的层位移、层间位移角、剪力和弯矩的结果及其沿高度的误差分布情况。图9和图10分别给出了POE360和ArtifGM1地震动作用下全部工况的最大误差对比概况，全部地震动的详细结果列于表4~表6。

    图  6  α=1时POE360地震动作用下三种计算方法层位移、层间位移角、剪力和弯矩结果对比
    Figure  6.  Story displacement, interstory drift ratio, shear and moment response computed with three methods for α=1 POE360
    下载: 全尺寸图片 幻灯片
    图  7  α=2时POE360地震动作用下三种计算方法层位移、层间位移角、剪力和弯矩结果对比
    Figure  7.  Story displacement, interstory drift ratio, shear and moment response computed with three methods for α=2 POE360
    下载: 全尺寸图片 幻灯片
    图  8  POE360地震动作用下三种计算方法地震响应误差沿高度分布对比
    Figure  8.  Errors of seismic responses along the height computed with three methods for POE360
    下载: 全尺寸图片 幻灯片
    图  9  POE360地震动作用下三种计算方法地震响应沿高度最大误差对比
    Figure  9.  Maximum errors of seismic responses along the height computed with three methods for POE360
    下载: 全尺寸图片 幻灯片
    图  10  ArtifGM1地震动作用下三种计算方法地震响应沿高度最大误差对比
    Figure  10.  Maximum errors of seismic responses along the height computed with three methods for ArtifGM1
    下载: 全尺寸图片 幻灯片
    表  4  三种方法各工况层位移和层间位移角沿高度最大误差
    Table  4.  Maximum story displacement and interstory drift ratio errors along the height for the three methods
    地震动响应类别对比类别误差CvsD=|CMSM−DTFM|/DTFM/(%)误差RvsD=|RMSM−DTFM|/DTFM/(%)
    工况1工况2工况3工况4工况5工况6工况7工况8工况9工况10工况11工况12
    POE360层位移CvsD2.9812.6019.0250.851.914.708.3912.790.611.663.836.02
    RvsD1.008.5113.4634.360.901.332.474.400.781.914.347.59
    层间位移角CvsD3.4813.2421.3749.501.975.089.4713.860.622.054.516.19
    RvsD3.108.5214.8736.101.663.535.157.010.672.335.268.52
    LOS270层位移CvsD2.009.9325.5746.860.551.484.128.681.311.613.285.26
    RvsD0.724.4512.1126.260.360.390.490.751.410.832.063.67
    层间位移角CvsD2.1210.7527.2248.000.321.255.8111.221.421.953.926.23
    RvsD0.774.5412.1026.090.601.121.431.661.511.442.634.63
    TAK090层位移CvsD2.8811.9730.8655.770.602.315.349.740.111.052.504.39
    RvsD4.7216.4235.5876.530.562.375.8411.210.180.291.012.29
    层间位移角CvsD3.1813.2234.2352.850.702.666.1611.240.141.242.804.84
    RvsD4.7916.8536.8676.680.592.506.1911.870.550.331.092.42
    ArtifGM1层位移CvsD2.5912.2221.8133.031.731.497.108.332.264.025.657.25
    RvsD3.6911.9622.7139.781.631.142.473.381.341.892.683.95
    层间位移角CvsD3.8112.5322.6634.011.691.328.159.692.324.175.726.97
    RvsD4.2612.1324.0540.871.701.332.973.511.391.903.976.10
    下载: 导出CSV 
    | 显示表格
    表  5  三种方法各工况剪力沿高度最大误差
    Table  5.  Maximum shear errors along the height for the three methods
    地震动体系类别对比类别误差CvsD=|CMSM−DTFM|/DTFM/(%)误差RvsD=|RMSM−DTFM|/DTFM/(%)
    工况1工况2工况3工况4工况5工况6工况7工况8工况9工况10工况11工况12
    POE360复合结构整体CvsD17.5236.3241.9650.852.145.718.359.093.084.857.368.12
    RvsD23.6237.6147.5048.033.327.1114.4520.393.035.426.768.93
    框架主体系CvsD3.4813.2421.3749.501.975.089.4713.860.622.054.516.19
    RvsD3.108.5214.8736.101.663.535.157.010.672.335.268.52
    摇摆次体系CvsD27.8457.7547.4355.255.8511.2118.6823.816.339.5918.9530.70
    RvsD25.6247.1262.2467.5611.0926.5041.9551.677.9419.0027.3732.23
    LOS270复合结构整体CvsD31.2547.3555.5659.093.064.564.844.124.461.583.034.05
    RvsD29.3244.6450.3953.243.667.6210.8911.025.342.845.387.91
    框架主体系CvsD2.1210.7527.2248.000.321.255.8111.221.421.953.926.23
    RvsD0.774.5412.1026.090.601.121.431.661.511.442.634.63
    摇摆次体系CvsD29.0591.6168.3458.757.7317.7727.3628.175.6011.5013.8919.08
    RvsD45.1549.9062.0472.688.6719.9033.2946.608.8113.9925.2236.63
    TAK090复合结构整体CvsD6.1715.1526.2635.570.560.991.321.680.380.832.515.03
    RvsD4.4214.1821.4935.070.861.141.631.951.081.422.423.46
    框架主体系CvsD3.1813.2234.2352.850.702.666.1611.240.141.242.804.84
    RvsD4.7916.8536.8676.680.592.506.1911.870.550.331.092.42
    摇摆次体系CvsD36.1646.5543.5553.2020.6529.4830.8229.6712.6120.5227.4133.84
    RvsD14.3132.6345.0457.033.6210.1520.3331.974.2211.9318.9727.64
    ArtifGM1复合结构整体CvsD18.6637.8049.0153.873.095.215.8712.963.355.999.028.96
    RvsD17.8836.1646.0854.464.679.1713.0819.782.164.4310.9316.60
    框架主体系CvsD3.8112.5322.6634.011.691.328.159.692.324.175.726.94
    RvsD4.2612.1324.0540.871.701.332.973.511.391.903.976.10
    摇摆次体系CvsD26.88102.1689.6262.219.9045.2873.0257.717.8319.5027.3841.39
    RvsD30.6552.3768.3975.5512.4731.8844.9252.396.3720.8328.3735.75
    下载: 导出CSV 
    | 显示表格
    表  6  三种方法各工况弯矩沿高度最大误差
    Table  6.  Maximum moment errors along the height for the three methods
    地震动体系类别对比类别误差CvsD=|CMSM−DTFM|/DTFM/(%)误差RvsD=|RMSM−DTFM|/DTFM/(%)
    工况1工况2工况3工况4工况5工况6工况7工况8工况9工况10工况11工况12
    POE360复合结构整体CvsD25.6143.6656.9964.884.456.667.767.893.574.746.979.38
    RvsD31.0550.5260.8962.562.725.998.7711.483.253.035.728.46
    框架主体系CvsD3.445.8312.3435.870.860.910.682.060.180.611.923.62
    RvsD3.088.1114.1534.361.653.525.136.980.401.521.432.80
    摇摆次体系CvsD20.3425.0464.8174.9811.7134.7447.9151.707.6636.4648.2470.20
    RvsD20.5844.6867.4976.4637.2353.8763.1772.8626.8146.4356.5966.94
    LOS270复合结构整体CvsD40.8057.3164.8568.002.974.618.806.105.281.272.824.07
    RvsD39.5455.5061.2763.772.484.936.388.845.952.074.106.68
    框架主体系CvsD1.456.5216.0630.860.551.412.574.470.850.771.402.93
    RvsD0.644.4612.1026.240.601.121.421.651.251.471.100.67
    摇摆次体系CvsD32.2250.1471.8388.518.8315.3648.2342.505.2622.8744.0269.28
    RvsD27.4543.1960.3872.1814.9628.7155.4967.4815.7433.2347.7563.56
    TAK090复合结构整体CvsD7.2426.1045.7456.480.510.510.761.360.270.952.755.48
    RvsD7.1627.1246.5856.600.800.820.660.841.111.332.032.38
    框架主体系CvsD1.687.1517.4435.620.191.122.554.620.190.581.362.51
    RvsD4.0314.2428.8866.820.321.624.047.650.550.170.400.79
    摇摆次体系CvsD33.0957.3367.1466.8824.0019.4828.5340.022.5413.1024.3423.78
    RvsD25.0748.6460.4467.7930.8857.9167.0673.5124.2546.4061.6271.44
    ArtifGM1复合结构整体CvsD24.5946.3659.3163.763.065.363.826.103.971.963.234.08
    RvsD23.5944.4156.6960.334.213.702.529.352.314.5511.8117.46
    框架主体系CvsD3.816.4512.0224.290.471.132.714.580.400.661.412.77
    RvsD4.347.8620.3737.600.430.371.263.510.541.513.946.06
    摇摆次体系CvsD39.1995.3876.5658.2517.0867.2387.1685.5112.3629.9347.0756.01
    RvsD22.1247.7062.2371.2819.1447.4464.3472.8325.7943.4159.0768.74
    下载: 导出CSV 
    | 显示表格

    表3中，剪弯刚度比α从1增加到3，意味着摇摆次体系的刚度逐渐降低；阻尼中间参数Df从0.05增加到0.20，阻尼参数μ从0.048增加到0.575，意味着非比例阻尼的程度逐渐增强。例如，当α=1时，从工况1到工况4，一阶模态阻尼比从0.089增加到0.365。虽然α为2和3时，一阶模态和高阶阻尼比较小，但是增加的趋势一致，即工况4、工况8和工况12非比例特性均较强。因此，模态阻尼比较高的这些工况是本节分析的重点。

    以POE360地震动为例，图6~图8分别给出了工况2、工况4、工况6、工况8和工况12地震响应及其误差沿高度的分布情况。首先，层位移和层间位移角的详细结果列于表4。作为一阶模态绝对主导的层位移响应，工况4由于一阶非比例阻尼比达到了0.365，DTFM法与复模态叠加法和振型叠加法的计算结果相差较大，顶部位移误差为50.85%。但是，其他工况下采用复模态叠加法和振型叠加法方法计算的结果相符较好，最大为工况8的12.79%。同时，随着工况9~工况12非比例阻尼程度的降低，三种计算方法结果误差进一步降低。其次，对于层间位移角，与层位移的趋势一致，非比例阻尼对工况2和工况4的层间位移角影响较大，这种影响沿结构全高均较明显，最大为49.5%。但是，从工况1到工况12，剪弯刚度比α的增大导致非比例阻尼的降低，相应的误差也逐渐降低，例如α=3时工况12为6.19%。

    其次，相比于层位移和层间位移角，剪力和弯矩响应更多的受到高阶模态效应的影响，同样以POE360地震动为例进行分析，详细结果列于表5和表6。由三种方法计算得到的复合体系整体、框架主体系和摇摆次体系的剪力和弯矩响应及其误差变化趋势较为相近，随着剪弯刚度比的增大，误差幅值逐渐减小。但是，相比于框架主体系，摇摆次体系中下部剪力和弯矩响应幅值和分布相差较大(如图7和图8所示)，并且这种差异在非比例阻尼较低时依然显著。例如，结合表3、图7、表5和表6分析工况8，即α=3且一阶模态阻尼比为0.119时，复模态叠加法和振型叠加法与DTFM法计算摇摆次体系剪力响应的相差分别达到了23.81%和51.67%，弯矩响应分别相差51.70%和72.86%。相比之下，三种方法框架主体系剪力响应计算误差仅在非比例阻尼较大的工况2和工况4时较大。随着剪弯刚度比的增大和模态阻尼比的降低，框架主体系的计算误差逐渐降低。例如，同样对于工况8，复模态叠加法和振型叠加法与DTFM法计算框架主体系剪力响应的误差分别为13.86%和7.01%，弯矩响应分别为2.06%和6.98%。这在一定程度上说明，相比于振型叠加法，采用复模态叠加法可以更为准确地计算出剪力和弯矩等高阶效应影响较为显著的响应，而这些响应对于结构设计至关重要。

    为更全面地反映更多参数和不同地震动的计算结果并进行分析，图9和图10分别给出了POE360和ArtifGM1作用下三种方法计算得到的响应误差最大值的变化情况，全部地震动的详细计算结果列于表4~表6。从整体上看，虽然两条地震动存在差异，但是图9和图10反映出的趋势一致，同时表4~表6中数据也表明其他两条地震动也具有如下趋势：1)随着剪弯刚度比的增大，非比例阻尼程度的降低，复模态叠加法和振型叠加法与DTFM法之间的结果差异降低，此时采用复模态叠加法和振型叠加法均可以得到较为准确的计算结果。2)由于给出的是沿高度的最大误差，图9和图10呈现出的趋势是复模态叠加法在计算响应时并不比振型叠加法更具优势。这是由于有些部位的幅值小但是差异大，其误差计算值较大，如体系中上部的剪力响应等。3)需要重点说明是，复模态叠加法在计算摇摆次体系的剪力和弯矩响应时具有更高的精度。如图6和图7所示，在摇摆次体系底部，复模态叠加法与DTFM法的计算结果更接近。但是，振型叠加法由于忽略了局部非比例阻尼的影响，无法准确体现局部附加阻尼对于摇摆次体系动力特性和响应的影响。同时，这也将导致计算得到的摇摆次体系底部剪力和弯矩等响应偏小，对于该类体系的设计偏于不安全。

    综上分析可以得知，采用振型叠加法可以较为准确地计算非比例阻尼复合体系的整体和框架主体系剪力和弯矩响应，较难准确计算摇摆次体系的剪力和弯矩响应。相比之下，复模态叠加法可以在不显著增加计算成本的前提下较为准确地计算出复合体系整体、框架主体系和摇摆次体系的剪力和弯矩等响应。

    3.2   设计参数选择

    将复合体系的非比例阻尼分布参数模型与复模态叠加法结合起来，可以直接计算复合体系在地震动作用下的位移、层间位移角、层剪力和层弯矩响应，对于该类体系面向抗震韧性的设计和优化具有参考价值。作为本文方法的重要应用，本节将进行复合体系算例的设计参数选择和优化。利用人工地震动生成软件SeismoArtif基于规范反应谱生成具有代表性的人工地震动，作为外部激励作用于复合体系，规范反应谱和人工地震动反应谱示于图3和图4。

    面向抗震韧性的设计目标要求结构在设防水准地震动作用下不需修复即可恢复正常使用功能，即结构构件和非结构构件保持无损伤状态[1]。对于混凝土框架结构，规范给出的层间位移角限值为1/550。因此，以该层间位移角限值为设计目标，采用复模态叠加法进行设计参数的选择和优化，包括摇摆次体系刚度、自复位装置刚度和黏滞阻尼参数。在复合结构的设计中，剪弯刚度比α、转动刚度参数Rf和转动阻尼参数μ分别表征主次体系相对刚度、自复位机制和耗能机制，对应的控制指标为层间位移集中系数DCF、模态阻尼比和层间位移角。在前期研究中[5]，通过参数分析确定了三个参数的建议取值范围：1≤α≤7，0≤Rf≤3，0≤μ≤3。当三个参数处于更小的范围1≤α≤3，0≤Rf≤0.5，0≤μ≤0.35时，DCF可控制在1.2以下，即层间位移沿高度接近于均匀分布。

    本文采用文献[5]的算例，基本布置如图11所示。算例结构为8层4跨的平面框架结构，层高均为3600 mm，跨度均为6000 mm。梁、柱和摇摆墙均为矩形截面，尺寸分别为：300 mm×600 mm，600 mm×600 mm和600 mm×4000 mm，混凝土弹性模量为Ec=3.0×107 kN/m2，框架结构的剪切刚度GA为2.9×105 kN。

    图  11  算例结构基本信息[5]
    Figure  11.  Information of the example structure[5]
    下载: 全尺寸图片 幻灯片

    首先，基于前述建议取值范围，根据DCF的控制目标可以初步确定剪弯刚度比α的取值，本节取α=1.5。根据剪弯刚度比的定义可得到摇摆次体系的刚度EI=2.9×105×28.82/1.52 kN·m2=1.07×108 kN·m2。

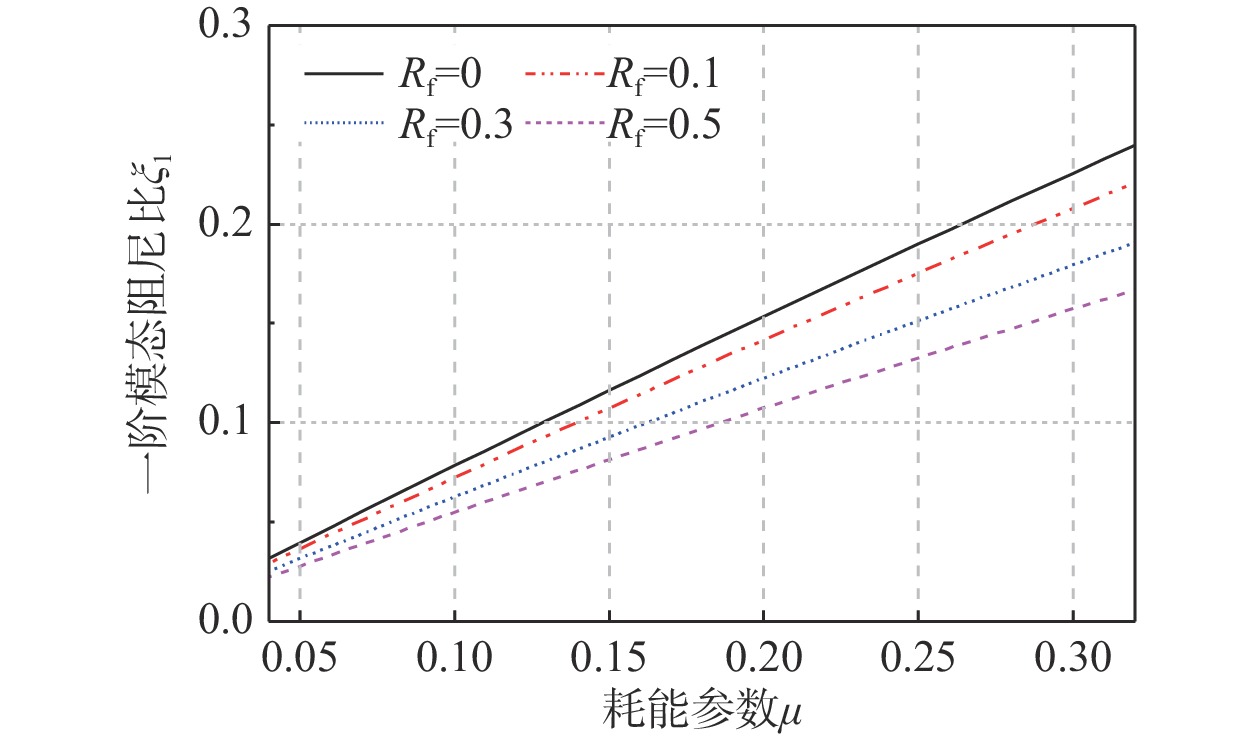
    其次，要确定转动刚度参数Rf和阻尼参数μ，这两个参数将显著影响模态阻尼比，进而影响地震响应的控制效果。前期研究中已经建立了模态阻尼比与三个无量纲参数之间的量化关系[5]。其中，针对α=1.5的复合体系，一阶模态阻尼比ξ1与参数Rf和μ之间的关系曲线为图12所示。

    图  12  α=1.5一阶模态阻尼比ξ1与Rf和μ之间的关系曲线
    Figure  12.  Relationship curve between ξ1 and Rf, μ when α=1.5
    下载: 全尺寸图片 幻灯片

    从图12中可以发现，为实现特定的一阶模态阻尼比取值，存在多种Rf和μ组合，而且当Rf取更大值时需要更大的μ值与之匹配。为此，我们采用本文的复模态叠加法直接计算出层间位移角、层位移、层剪力和层弯矩完成复合结构的初步设计和参数优选，计算结果如图13所示。从图13(a)和图13(b)可以发现，增大阻尼参数可以显著提升模态阻尼比，从而降低最大层间位移角响应，从μ=0.05，ξ1=0.029时的0.442%到μ=0.3，ξ1=0.177时的0.194%，非常接近规范位移角限值；最大层位移也从119.569 mm降到50.022 mm；DCF从1.06增加到1.12，但始终控制在1.2以下。

    图  13  α=1.5时μ和ξ1与响应之间的关系曲线
    Figure  13.  Relationship curve between μ, ξ1 and response when α=1.5
    下载: 全尺寸图片 幻灯片

    由3.1节可知，采用振型叠加法和复模态叠加法计算位移和层间位移角结果相近，重点是剪力和弯矩的计算，这会对结构的设计产生重要影响，因此图13(c)和图13(d)给出了复合结构整体、框架主体系和摇摆次体系层剪力和层弯矩随阻尼参数的增加的变化规律。对于复合结构整体和框架主体系，随着阻尼参数的增加这二者的剪力和弯矩响应单调降低，框架主体系的基底剪力和基底弯矩从1.283 MN和34.706 MN·m降至0.808 MN和14.519 MN·m，降幅分别达到37.0%和58.2%。与此不同，摇摆次体系的剪力和弯矩，随着阻尼参数的增大会出现先降低后增大的变化趋势。通过复模态叠加法可以直接得到摇摆次体系底部黏滞阻尼装置的设计需求，进而通过阻尼参数和黏滞阻尼器的换算关系得到实际阻尼器的设计参数，完成摇摆次体系的初步设计，为下一步建立有限元模型进行精细分析奠定基础。

    4   结论

    可恢复功能复合结构体系面向抗震韧性的设计需要建立摇摆、自复位和耗能机制与层间位移角、剪力和弯矩等地震需求参数之间的量化关系，本文基于分布参数模型建立了地震动作用下该类体系基于复模态叠加法的响应计算方法，主要结论为：

    (1)剪弯刚度比较小(α≤1)且非比例阻尼较大(ξ1≥0.20)时，复模态叠加法和振型叠加法与分布传递函数法的计算结果相差较大；剪弯刚度比较大(α>1)时，复合体系基于复模态叠加法的响应在位移、层间位移角、主体系剪力和弯矩等响应计算方面精度与分布传递函数法相当，可以较为准确地计算出非比例阻尼导致的复合体系整体和主体系响应。但是，次体系剪力和弯矩的计算结果相差较大。

    (2)相比于实模态叠加法，复模态叠加法可以更为准确地计算出摇摆次体系的剪力和弯矩，尤其是自复位和耗能装置导致的局部非比例阻尼引起的摇摆次体系的基底剪力和弯矩。

    (3)采用复模态叠加法可以直接计算复合体系参数与响应之间的量化关系，进行设计参数优选和结构初步设计，为结构深度设计奠定基础。

  • 图  1   可恢复功能复合结构体系振动台试验模型

    Figure  1.   Shaking-table test model of an earthquake resilient dual-system

    下载: 全尺寸图片 幻灯片

    图  2   可恢复功能复合结构体系比例阻尼和非比例阻尼分布参数模型

    Figure  2.   Distributed parameter model with proportional and non-proportional damping of earthquake resilient dual-systems

    下载: 全尺寸图片 幻灯片

    图  3   由规范设计反应谱生成的人工地震动时程反应谱

    Figure  3.   Response spectra of artificial ground motion generated with code design response spectra

    下载: 全尺寸图片 幻灯片

    图  4   天然地震动和人工地震动时程曲线

    Figure  4.   Time histories of natural and artificial ground motions

    下载: 全尺寸图片 幻灯片

    图  5   天然和人工地震动作用下三种计算方法顶部位移时程结果对比

    Figure  5.   Comparison of roof displacement time histories computed with three methods under two ground motions

    下载: 全尺寸图片 幻灯片

    图  6   α=1时POE360地震动作用下三种计算方法层位移、层间位移角、剪力和弯矩结果对比

    Figure  6.   Story displacement, interstory drift ratio, shear and moment response computed with three methods for α=1 POE360

    下载: 全尺寸图片 幻灯片

    图  7   α=2时POE360地震动作用下三种计算方法层位移、层间位移角、剪力和弯矩结果对比

    Figure  7.   Story displacement, interstory drift ratio, shear and moment response computed with three methods for α=2 POE360

    下载: 全尺寸图片 幻灯片

    图  8   POE360地震动作用下三种计算方法地震响应误差沿高度分布对比

    Figure  8.   Errors of seismic responses along the height computed with three methods for POE360

    下载: 全尺寸图片 幻灯片

    图  9   POE360地震动作用下三种计算方法地震响应沿高度最大误差对比

    Figure  9.   Maximum errors of seismic responses along the height computed with three methods for POE360

    下载: 全尺寸图片 幻灯片

    图  10   ArtifGM1地震动作用下三种计算方法地震响应沿高度最大误差对比

    Figure  10.   Maximum errors of seismic responses along the height computed with three methods for ArtifGM1

    下载: 全尺寸图片 幻灯片

    图  11   算例结构基本信息[5]

    Figure  11.   Information of the example structure[5]

    下载: 全尺寸图片 幻灯片

    图  12   α=1.5一阶模态阻尼比ξ1与Rf和μ之间的关系曲线

    Figure  12.   Relationship curve between ξ1 and Rf, μ when α=1.5

    下载: 全尺寸图片 幻灯片

    图  13   α=1.5时μ和ξ1与响应之间的关系曲线

    Figure  13.   Relationship curve between μ, ξ1 and response when α=1.5

    下载: 全尺寸图片 幻灯片

    表  1   复模态法和DTFM法计算的复频率及其对比

    Table  1   Comparison of complex frequencies computed with the complex mode method and DTFM method

    工况第n阶模态第n阶圆频率ωn/(rad·s−1)对比误差/(%)
    复模态法DTFM法
    α=11−2.102+0.264i−2.102+0.264i0.0
    μ=0.22−17.501+2.627i−17.501+2.627i0.0
    Rf=0.53−56.606+6.643i−56.606+6.643i0.0
    α=31−5.199+0.346i−5.199+0.346i0.0
    μ=0.22−23.272+2.641i−23.272+2.641i0.0
    Rf=0.53−61.893+6.227i−61.893+6.227i0.0
    α=51−8.323+0.619i−8.323+0.619i0.0
    μ=0.32−32.614+3.119i−32.614+3.119i0.0
    Rf=0.23−73.385+4.851i−73.385+4.851i0.0
    下载: 导出CSV

    表  2   三种方法各工况顶层位移沿高度最大误差

    Table  2   Maximum story displacement and interstory drift ratio errors along the height for the three methods

    地震动响应类别对比类别误差CvsD=(CMSM-DTFM)/DTFM×100/(%)误差RvsD=(RMSM-DTFM)/DTFM×100/(%)
    工况1工况2工况3工况4工况5工况6工况7工况8工况9工况10工况11工况12
    POE360顶层位移CvsD0.135.8312.3435.87−0.61−0.370.501.79−0.020.611.482.48
    RvsD−0.778.1113.4634.36−0.90−1.24−1.12−0.910.180.971.432.80
    LOS270顶层位移CvsD1.456.5216.0630.860.551.412.574.47−0.270.521.402.93
    RvsD0.644.4512.1026.24−0.02−0.25−0.49−0.27−0.520.170.290.66
    TAK090顶层位移CvsD1.687.1517.4435.620.191.122.554.620.110.561.362.51
    RvsD4.0314.2428.8866.82−0.081.624.047.65−0.020.000.230.79
    ArtifGM1顶层位移CvsD2.596.2212.0224.290.471.112.714.580.380.650.532.63
    RvsD3.697.8620.3737.60−0.01−0.271.263.380.09−0.13−1.91−1.97
    下载: 导出CSV

    表  3   三种方法的计算参数

    Table  3   Computing parameters for the three methods

    工况 复合体系参数 复合体系参数 模态阻尼比
    α Rf Df/s κ/s2 µ T1/s T2/s T3/s T4/s T5/s T6/s ξ1 ξ2 ξ3 ξ4 ξ5 ξ6
    工况1 1 0.5 0.05 0.1210 0.1438 1.037 0.127 0.040 0.019 0.011 0.007 0.089 0.111 0.109 0.082 0.058 0.042
    工况2 1 0.5 0.10 0.1210 0.2875 1.019 0.116 0.037 0.018 0.011 0.007 0.179 0.186 0.099 0.054 0.034 0.023
    工况3 1 0.5 0.15 0.1210 0.4313 0.986 0.105 0.036 0.018 0.011 0.007 0.271 0.175 0.071 0.037 0.023 0.015
    工况4 1 0.5 0.20 0.1210 0.5750 0.933 0.101 0.035 0.018 0.011 0.007 0.365 0.142 0.054 0.028 0.017 0.012
    工况5 2 0.5 0.05 0.4839 0.0719 1.209 0.229 0.081 0.040 0.023 0.015 0.030 0.051 0.061 0.061 0.057 0.051
    工况6 2 0.5 0.10 0.4839 0.1438 1.204 0.224 0.077 0.038 0.022 0.015 0.060 0.099 0.103 0.080 0.057 0.041
    工况7 2 0.5 0.15 0.4839 0.2156 1.195 0.216 0.073 0.037 0.022 0.015 0.090 0.138 0.108 0.066 0.043 0.029
    工况8 2 0.5 0.20 0.4839 0.2875 1.182 0.206 0.071 0.036 0.022 0.015 0.119 0.158 0.093 0.052 0.033 0.022
    工况9 3 0.5 0.05 1.0887 0.0479 1.272 0.295 0.115 0.059 0.035 0.023 0.016 0.031 0.039 0.042 0.042 0.041
    工况10 3 0.5 0.10 1.0887 0.0958 1.269 0.292 0.113 0.057 0.034 0.022 0.032 0.061 0.074 0.071 0.061 0.050
    工况11 3 0.5 0.15 1.0887 0.1438 1.265 0.287 0.110 0.055 0.033 0.022 0.048 0.088 0.096 0.076 0.055 0.040
    工况12 3 0.5 0.20 1.0887 0.1917 1.259 0.281 0.106 0.054 0.033 0.022 0.064 0.110 0.101 0.068 0.046 0.032
    注：α为剪弯刚度比；Rf为转动刚度参数；Df为阻尼机制的中间参数；κ为复合体系的中间参数；μ为耗能参数；Ti为模态周期；ξi为模态阻尼比。
    下载: 导出CSV

    表  4   三种方法各工况层位移和层间位移角沿高度最大误差

    Table  4   Maximum story displacement and interstory drift ratio errors along the height for the three methods

    地震动响应类别对比类别误差CvsD=|CMSM−DTFM|/DTFM/(%)误差RvsD=|RMSM−DTFM|/DTFM/(%)
    工况1工况2工况3工况4工况5工况6工况7工况8工况9工况10工况11工况12
    POE360层位移CvsD2.9812.6019.0250.851.914.708.3912.790.611.663.836.02
    RvsD1.008.5113.4634.360.901.332.474.400.781.914.347.59
    层间位移角CvsD3.4813.2421.3749.501.975.089.4713.860.622.054.516.19
    RvsD3.108.5214.8736.101.663.535.157.010.672.335.268.52
    LOS270层位移CvsD2.009.9325.5746.860.551.484.128.681.311.613.285.26
    RvsD0.724.4512.1126.260.360.390.490.751.410.832.063.67
    层间位移角CvsD2.1210.7527.2248.000.321.255.8111.221.421.953.926.23
    RvsD0.774.5412.1026.090.601.121.431.661.511.442.634.63
    TAK090层位移CvsD2.8811.9730.8655.770.602.315.349.740.111.052.504.39
    RvsD4.7216.4235.5876.530.562.375.8411.210.180.291.012.29
    层间位移角CvsD3.1813.2234.2352.850.702.666.1611.240.141.242.804.84
    RvsD4.7916.8536.8676.680.592.506.1911.870.550.331.092.42
    ArtifGM1层位移CvsD2.5912.2221.8133.031.731.497.108.332.264.025.657.25
    RvsD3.6911.9622.7139.781.631.142.473.381.341.892.683.95
    层间位移角CvsD3.8112.5322.6634.011.691.328.159.692.324.175.726.97
    RvsD4.2612.1324.0540.871.701.332.973.511.391.903.976.10
    下载: 导出CSV

    表  5   三种方法各工况剪力沿高度最大误差

    Table  5   Maximum shear errors along the height for the three methods

    地震动体系类别对比类别误差CvsD=|CMSM−DTFM|/DTFM/(%)误差RvsD=|RMSM−DTFM|/DTFM/(%)
    工况1工况2工况3工况4工况5工况6工况7工况8工况9工况10工况11工况12
    POE360复合结构整体CvsD17.5236.3241.9650.852.145.718.359.093.084.857.368.12
    RvsD23.6237.6147.5048.033.327.1114.4520.393.035.426.768.93
    框架主体系CvsD3.4813.2421.3749.501.975.089.4713.860.622.054.516.19
    RvsD3.108.5214.8736.101.663.535.157.010.672.335.268.52
    摇摆次体系CvsD27.8457.7547.4355.255.8511.2118.6823.816.339.5918.9530.70
    RvsD25.6247.1262.2467.5611.0926.5041.9551.677.9419.0027.3732.23
    LOS270复合结构整体CvsD31.2547.3555.5659.093.064.564.844.124.461.583.034.05
    RvsD29.3244.6450.3953.243.667.6210.8911.025.342.845.387.91
    框架主体系CvsD2.1210.7527.2248.000.321.255.8111.221.421.953.926.23
    RvsD0.774.5412.1026.090.601.121.431.661.511.442.634.63
    摇摆次体系CvsD29.0591.6168.3458.757.7317.7727.3628.175.6011.5013.8919.08
    RvsD45.1549.9062.0472.688.6719.9033.2946.608.8113.9925.2236.63
    TAK090复合结构整体CvsD6.1715.1526.2635.570.560.991.321.680.380.832.515.03
    RvsD4.4214.1821.4935.070.861.141.631.951.081.422.423.46
    框架主体系CvsD3.1813.2234.2352.850.702.666.1611.240.141.242.804.84
    RvsD4.7916.8536.8676.680.592.506.1911.870.550.331.092.42
    摇摆次体系CvsD36.1646.5543.5553.2020.6529.4830.8229.6712.6120.5227.4133.84
    RvsD14.3132.6345.0457.033.6210.1520.3331.974.2211.9318.9727.64
    ArtifGM1复合结构整体CvsD18.6637.8049.0153.873.095.215.8712.963.355.999.028.96
    RvsD17.8836.1646.0854.464.679.1713.0819.782.164.4310.9316.60
    框架主体系CvsD3.8112.5322.6634.011.691.328.159.692.324.175.726.94
    RvsD4.2612.1324.0540.871.701.332.973.511.391.903.976.10
    摇摆次体系CvsD26.88102.1689.6262.219.9045.2873.0257.717.8319.5027.3841.39
    RvsD30.6552.3768.3975.5512.4731.8844.9252.396.3720.8328.3735.75
    下载: 导出CSV

    表  6   三种方法各工况弯矩沿高度最大误差

    Table  6   Maximum moment errors along the height for the three methods

    地震动体系类别对比类别误差CvsD=|CMSM−DTFM|/DTFM/(%)误差RvsD=|RMSM−DTFM|/DTFM/(%)
    工况1工况2工况3工况4工况5工况6工况7工况8工况9工况10工况11工况12
    POE360复合结构整体CvsD25.6143.6656.9964.884.456.667.767.893.574.746.979.38
    RvsD31.0550.5260.8962.562.725.998.7711.483.253.035.728.46
    框架主体系CvsD3.445.8312.3435.870.860.910.682.060.180.611.923.62
    RvsD3.088.1114.1534.361.653.525.136.980.401.521.432.80
    摇摆次体系CvsD20.3425.0464.8174.9811.7134.7447.9151.707.6636.4648.2470.20
    RvsD20.5844.6867.4976.4637.2353.8763.1772.8626.8146.4356.5966.94
    LOS270复合结构整体CvsD40.8057.3164.8568.002.974.618.806.105.281.272.824.07
    RvsD39.5455.5061.2763.772.484.936.388.845.952.074.106.68
    框架主体系CvsD1.456.5216.0630.860.551.412.574.470.850.771.402.93
    RvsD0.644.4612.1026.240.601.121.421.651.251.471.100.67
    摇摆次体系CvsD32.2250.1471.8388.518.8315.3648.2342.505.2622.8744.0269.28
    RvsD27.4543.1960.3872.1814.9628.7155.4967.4815.7433.2347.7563.56
    TAK090复合结构整体CvsD7.2426.1045.7456.480.510.510.761.360.270.952.755.48
    RvsD7.1627.1246.5856.600.800.820.660.841.111.332.032.38
    框架主体系CvsD1.687.1517.4435.620.191.122.554.620.190.581.362.51
    RvsD4.0314.2428.8866.820.321.624.047.650.550.170.400.79
    摇摆次体系CvsD33.0957.3367.1466.8824.0019.4828.5340.022.5413.1024.3423.78
    RvsD25.0748.6460.4467.7930.8857.9167.0673.5124.2546.4061.6271.44
    ArtifGM1复合结构整体CvsD24.5946.3659.3163.763.065.363.826.103.971.963.234.08
    RvsD23.5944.4156.6960.334.213.702.529.352.314.5511.8117.46
    框架主体系CvsD3.816.4512.0224.290.471.132.714.580.400.661.412.77
    RvsD4.347.8620.3737.600.430.371.263.510.541.513.946.06
    摇摆次体系CvsD39.1995.3876.5658.2517.0867.2387.1685.5112.3629.9347.0756.01
    RvsD22.1247.7062.2371.2819.1447.4464.3472.8325.7943.4159.0768.74
    下载: 导出CSV
    • 参考文献(17)
  • [1] 吕西林, 武大洋, 周颖. 可恢复功能防震结构研究进展[J]. 建筑结构学报, 2019, 40(2): 1 − 15.

    LYU Xilin, WU Dayang, ZHOU Ying. State-of-the-art of earthquake resilient structures [J]. Journal of Building Structures, 2019, 40(2): 1 − 15. (in Chinese)
    [2] 周颖, 吴浩, 顾安琪. 地震工程: 从抗震、减隔震到可恢复性[J]. 工程力学, 2019, 36(6): 1 − 12. doi: 10.6052/j.issn.1000-4750.2018.07.ST09

    ZHOU Ying, WU Hao, GU Anqi. Earthquake engineering: From earthquake resistance, energy dissipation, and isolation, to resilience [J]. Engineering Mechanics, 2019, 36(6): 1 − 12. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.07.ST09
    [3] 周云, 商城豪, 张超. 消能减震技术研究与应用进展[J]. 建筑结构, 2019, 49(19): 33 − 48.

    ZHOU Yun, SHANG Chenghao, ZHANG Chao. Progress in research and application of energy-dissipated technology [J]. Building Structure, 2019, 49(19): 33 − 48. (in Chinese)
    [4] 武大洋, 吕西林. 基于分布参数模型的复合自复位结构参数分析[J]. 工程力学, 2018, 35(6): 78 − 87. doi: 10.6052/j.issn.1000-4750.2017.02.0160

    WU Dayang, LYU Xilin. Parametric analysis of a self-centering dual system based on a distributed parameter model [J]. Engineering Mechanics, 2018, 35(6): 78 − 87. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.02.0160
    [5]

    WU D Y, LU X L, ZHAO B. Parametric study of rocking cores-moment frames with supplemental viscous damping and self-centering devices using a distributed parameter model [J]. Soil Dynamics and Earthquake Engineering, 2019, 123: 304 − 319. doi: 10.1016/j.soildyn.2019.04.034
    [6] 武大洋, 杨国涛, 赵斌, 等. 刚度非均匀分布对可恢复功能复合结构体系动力特性的影响[J]. 建筑结构学报, 2023, 44(10): 49 − 61. doi: 10.14006/j.jzjgxb.2021.0707

    WU Dayang, YANG Guotao, ZHAO Bin, et al. Influence of nonuniform stiffness distribution on dynamic characteristics of earthquake resilient dual-systems [J]. Journal of Building Structures, 2023, 44(10): 49 − 61. (in Chinese) doi: 10.14006/j.jzjgxb.2021.0707
    [7] 武大洋. 可恢复功能防震复合体系基于层间位移角谱的设计方法[D]. 上海: 同济大学, 2019.

    WU Dayang. Interstory drift ratio spectra-based design method of earthquake resilient dual-systems [D]. Shanghai: Tongji University, 2019. (in Chinese)
    [8]

    VELETSOS A S, VENTURA C E. Modal analysis of non-classically damped linear systems [J]. Earthquake Engineering & Structural Dynamics, 1986, 14(2): 217 − 243.
    [9]

    CHOPRA A K. Dynamics of structures: Theory and applications to earthquake engineering [M]. Upper Saddle River, NJ: Prentice Hall, 2012: 622 − 647
    [10] 陈华霆, 谭平. 非经典阻尼分布参数系统复振型叠加方法[J]. 振动工程学报, 2021, 34(1): 48 − 59.

    CHEN Huating, TAN Ping. Complex mode superposition method for distributed-parameter systems with non-classical damping [J]. Journal of Vibration Engineering, 2021, 34(1): 48 − 59. (in Chinese)
    [11]

    WU D Y, ZHAO B, LU X L. Dynamic behavior of upgraded rocking wall-moment frames using an extended coupled-two-beam model [J]. Soil Dynamics and Earthquake Engineering, 2018, 115: 365 − 377. doi: 10.1016/j.soildyn.2018.07.043
    [12] 武大洋, 吕西林, 赵斌. 近场脉冲型地震作用下复合自复位结构刚度需求的谱分析[J]. 建筑结构学报, 2018, 39(8): 130 − 137.

    WU Dayang, LYU Xilin, ZHAO Bin. Stiffness demand of self-centering dual systems under near-field pulse-type ground motions based on spectral analysis [J]. Journal of Building Structures, 2018, 39(8): 130 − 137. (in Chinese)
    [13] 韩建平, 章全才. 新型自复位黏弹性阻尼支撑力学性能研究[J]. 工程力学, 2021, 38(1): 195 − 204. doi: 10.6052/j.issn.1000-4750.2020.03.0168

    HAN Jianping, ZHANG Quancai. The investigation on mechanical behavior of a new-type self-centering viscoelastic damping brace [J]. Engineering Mechanics, 2021, 38(1): 195 − 204. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.03.0168
    [14]

    ZHONG C Y, CHRISTOPOULOS C. Self-centering seismic-resistant structures: Historical overview and state-of-the-art [J]. Earthquake Spectra, 2022, 38(2): 1321 − 1356. doi: 10.1177/87552930211057581
    [15]

    ZHU R Z, GUO T, MWANGILWA F. Development and test of a self-centering fluidic viscous damper [J]. Advances in Structural Engineering, 2020, 23(13): 2835 − 2849. doi: 10.1177/1369433220920464
    [16] 周颖, 刘晓芳, 汪盟. 不同耗能特征的黏弹性阻尼器性能对比试验研究[J]. 工程力学, 2021, 38(增刊 1): 167 − 177. doi: 10.6052/j.issn.1000-4750.2020.06.S030

    ZHOU Ying, LIU Xiaofang, WANG Meng. Experimental study on mechanical properties of two types of viscoelastic dampers [J]. Engineering Mechanics, 2021, 38(Suppl 1): 167 − 177. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.06.S030
    [17]

    OLIVETO G, SANTINI A, TRIPODI E. Complex modal analysis of a flexural vibrating beam with viscous end conditions [J]. Journal of Sound and Vibration, 1997, 200(3): 327 − 345. doi: 10.1006/jsvi.1996.0717
    • 相关文章
    • 施引文献(1)

  • 期刊类型引用(0)

    其他类型引用(1)

    • 资源附件(0)
图(13)  /  表(6)
计量
  • 文章访问数:  265
  • HTML全文浏览量:  48
  • PDF下载量:  34
  • 被引次数: 1
出版历程
  • 收稿日期:  2022-06-01
  • 修回日期:  2022-08-22
  • 网络出版日期:  2022-09-01
  • 刊出日期:  2024-07-08

目录

摘要
HTML全文

  • 1   基于复模态叠加法的响应计算

  • 1.1   可恢复功能复合结构体系分布参数模型

  • 1.2   动力方程

  • 1.3   正交性条件推导

  • 1.4   基础激励下体系动力响应计算推导

  • 2   方法验证

  • 3   结果对比分析和设计参数选择

  • 3.1   结果对比分析

  • 3.2   设计参数选择

  • 4   结论

参考文献(17)
相关文章
施引文献
资源附件(0)

/

返回文章
返回

京ICP备18030614号

版权所有 © 《工程力学》编辑部

地址：北京清华大学新水利馆114室邮政编码：100084

电话：(010)62788648传真：021-64253812电子信箱：gclxbjb@tsinghua.edu.cn

本系统由北京仁和汇智信息技术有限公司开发  百度统计