减少地震作用下主体结构构件损伤和非结构构件失效带来的人员伤亡和经济损失，并进一步提高城市强震后恢复韧性，是新一代结构体系设计的发展趋势和重点^[1]。形状记忆合金(SMA)^[1]、粘弹性材料^[2]等因其优良的力学特性，在近年来被广泛应用于以新型支撑^[3]、阻尼器^[4]和隔震支座^[5]等为代表的高性能结构韧性设计领域中。

尽管大量研究已经验证了SMA和粘弹性材料等应用于结构韧性设计的优良性能，但对于其构件和结构体系的评估通常基于某一特定设计温度，而环境温度变化的影响往往被忽视。事实上，SMA和粘弹性材料等的力学行为存在显著的温度相关性。例如，SMA材料的相变应力值随温度降低而降低^[6]；而粘弹性材料^{[2, 7]}的滞回耗能能力则会随温度升高而出现显著下降。温度所引起的材料力学行为变化会进一步影响结构体系的地震响应，即结构响应存在温度相关性。

为了考虑环境温度变化对温度相关型结构性能的影响，部分学者开展了不同环境温度下的结构地震响应研究。QIU等^[8]以SMA自复位支撑钢框架结构为研究对象，结果表明温度变化对整体结构的位移需求影响较小。OZBULUT等^[5]研究了应用SMA-叠层橡胶隔震支座(SRB)的高速公路桥梁在近场地震作用下的响应，发现温度降低将可能引起桥面板位移增大。CHANG等^[7]通过缩尺振动台试验对采用粘弹性阻尼器的建筑结构进行研究，研究发现温度升高将降低结构阻尼比，并削弱粘弹性阻尼器对楼层加速度和层间位移的控制效果。

可以看出，已有针对温度相关型结构的研究重点聚焦于结构在特定环境温度下的确定性响应特性。然而，由于地震发生存在不确定性，同时不同地区的区域温度分布特性存在明显差异。若仅以确定性结果为依据进行结构性能判定，则难以对位于不同地区的温度相关型结构进行全面的性能评估。

为此，本文利用第二代基于性能的抗震性能评估框架并结合区域温度分布特性，提出了一种考虑温度影响和区域温度分布的温度相关型结构地震风险评估方法。该方法将传统结构地震易损性扩展为地震动强度-温度联合易损性，在此基础上得到包含区域温度分布信息的结构修正区域易损性，并进一步用于评估位于不同区域的结构地震风险。利用该方法，本文将以基于SMA材料的自复位支撑钢框架为研究对象，并选取我国北京和文昌地区为案例地区，计算对象结构的地震风险和倒塌概率。此外，对于应用SMA丝材、棒材和拉索等拉力型元件的结构性能评估，已有研究通常采用不考虑材料大变形断裂行为的理想旗帜型SMA材料模型^[8]。而实际情况下，当材料变形超过极限应变时，将可能出现断裂并引起结构承载力的大幅降低，因此材料的断裂行为不应忽视。对此，本文将进一步结合温度影响，考虑材料失效对结构性能的影响，进而为温度相关型结构的性能评估提供参考依据。

1   区域温度分布特性及其表征方法

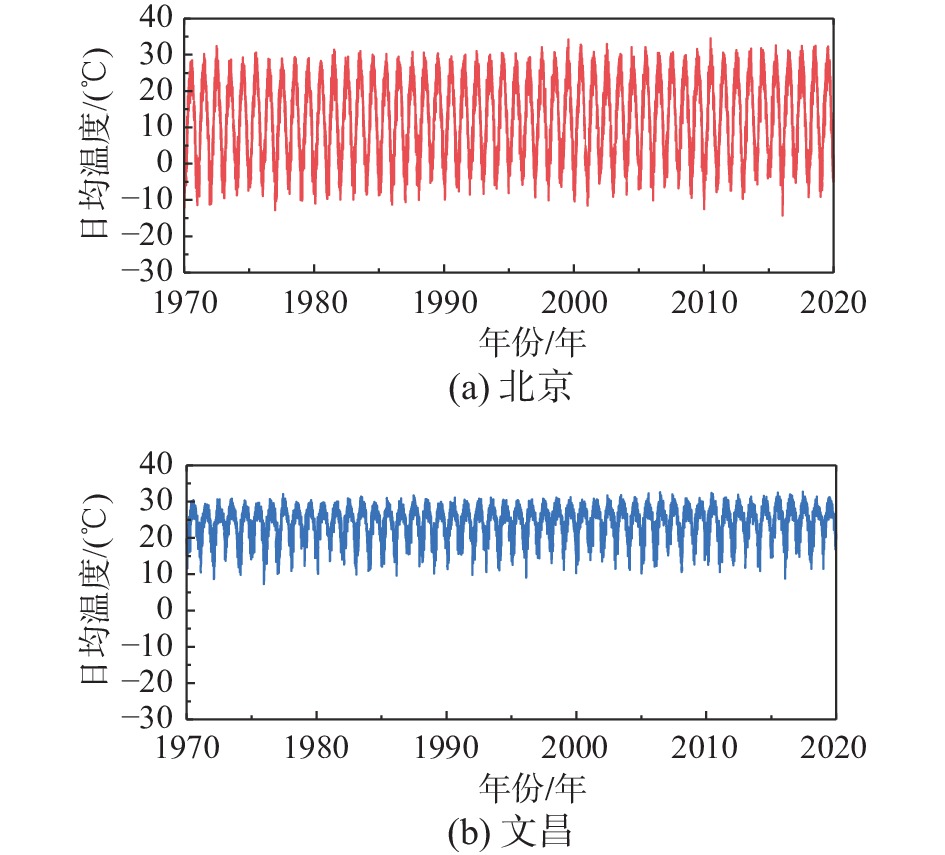
为对比研究不同地区的温度分布特性，本文选取分属温带季风性和热带季风性气候区的北京(北纬39.9°)和文昌(北纬19.6°)， 从国家气象科学数据中心获取了两个地区50年(1970年−2019年)的日平均气温数据^[9]，如图1所示。根据气温数据，两个地区50年记录最高温度与最低温度的平均值分别为10.1 ℃和20.0 ℃，温差分别为48.8 ℃和25.5 ℃。可以看出，北京的平均温度较低，气温波动更为剧烈；而文昌的平均温度较高且波动平缓。不同地区温度分布存在显著差异。

图  1  50年日平均气温数据

Figure  1.  50-year daily mean temperature data

下载: 全尺寸图片 幻灯片

为描述各地区温度分布的统计特性，首先考虑采用离散形式的相对频率对温度分布Θ的分布概率P^Θ进行估计。以Δθ作为相对频率统计的区间范围，可以将地区温度分布概率用下式进行表示：

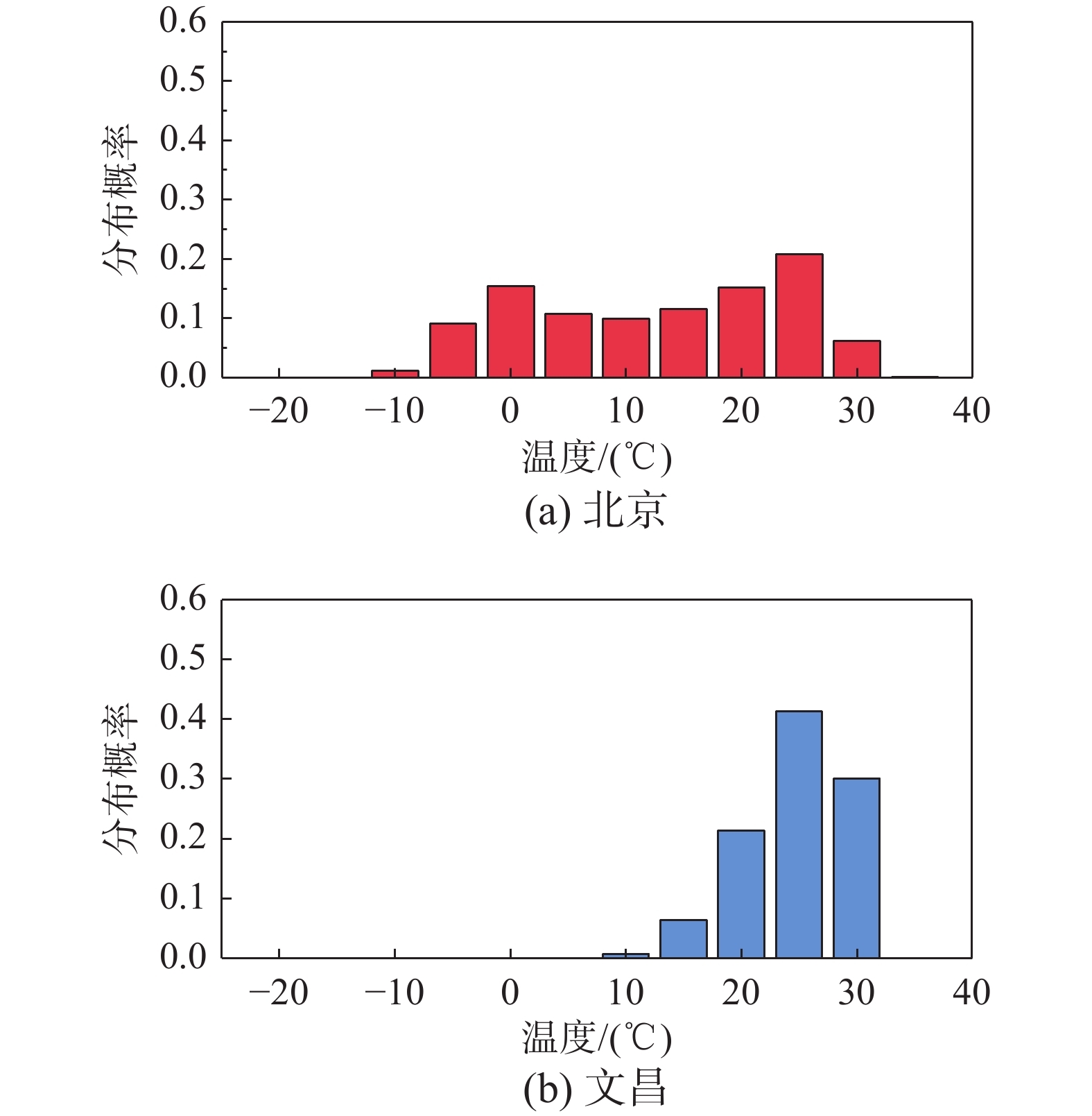
式中，N_θ、m和n_i分别为温度数据总量、温度区间划分数和属于各区间的数据点数。根据式(1)给出的温度分布概率的基本表达式，以Δθ=5 ℃作为相对频率统计的间隔范围，得到各地区的温度分布概率如图2所示。可以看出，北京地区的气温主要分布在−10 ℃~30 ℃区间，而文昌地区的气温分布则主要集中于10 ℃~30 ℃。

图  2  各地区温度分布概率

Figure  2.  Probability of temperature distribution in different regions

下载: 全尺寸图片 幻灯片

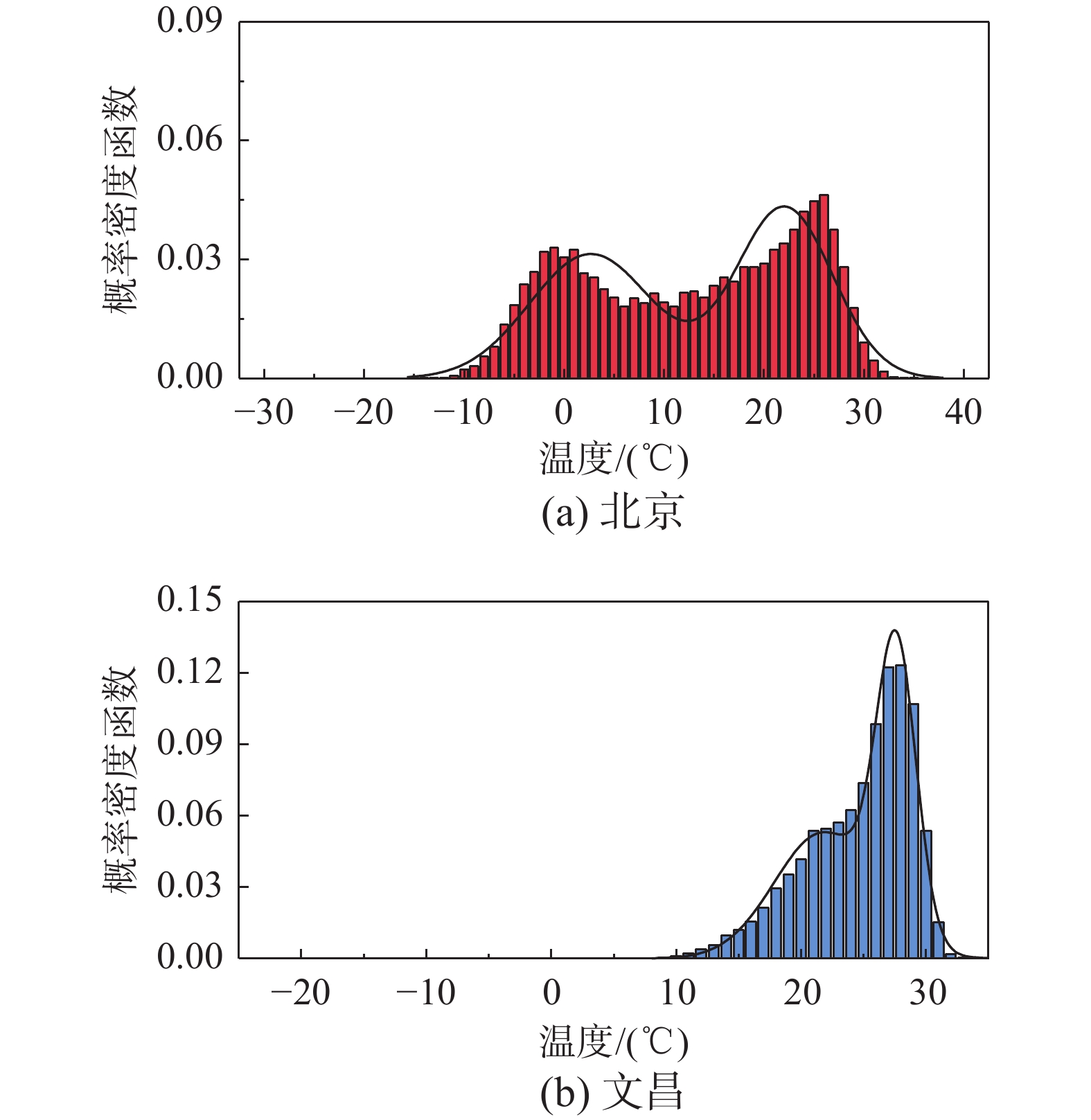
进一步的，考虑到温度在实际情况中是连续变化的，可以采用概率密度函数形式对各地区的温度分布进行连续性表达，如图3所示。可以发现，温度分布近似服从双峰正态分布，将其概率密度函数用下式表示为：

式中：p_m为双峰分布比例；φ(ˑ)为标准正态分布的概率密度函数；μ₁、μ₂和σ₁、σ₂分别为双峰正态分布的均值和标准差，分别代表了低温天气和高温天气的温度均值和波动程度，用于表征地区温度分布的统计特性。表1给出了利用式(2)的概率密度函数形式，通过极大似然估计所得到的不同地区的温度分布参数。

图  3  各地区温度分布概率密度函数

Figure  3.  Probability density function of temperature distribution in different regions

下载: 全尺寸图片 幻灯片

表  1  各地区温度分布概率密度函数参数

Table  1.  Parameters of probability density function of temperature distribution in different regions

地区	双峰分布比例pm	均值μ1	均值μ2	标准差σ1	标准差σ2
北京	0.48	2.7	22.0	6.1	4.8
文昌	0.52	21.8	27.6	3.9	1.6

下载: 导出CSV 

| 显示表格

实际上，式(2)中采用了双峰正态分布假设，对于其合理性需要进行检验。由于某一地区环境温度Θ的总体分布函数F(θ)及其参数未知，因此，对于Θ的分布类型及其参数的检验属于一般非参数假设检验问题。考虑到Kolmogorov-Smirnov (K-S)检验并不能直接适用于分布函数参数未知的一般非参数检验问题，故本文采用自引重取样(bootstrap resampling)方法结合K-S检验对式(2)所对应的分布函数形式进行检验^[10]，结果表明：在置信水平95%下，案例地区的温度分布均满足所给出的分布函数形式。

由表1可以进一步看出，北京地区的温度波动明显大于文昌地区，同时低温天气的温度波动也大于高温天气(σ₁>σ₂)。利用上述温度分布特性，本文将提出考虑区域温度分布的地震风险评估方法，用于全面评估温度相关型结构性能。

2   考虑区域温度分布特性的结构地震风险评估方法

第二代基于性能的地震工程(performance-based earthquake engineering, PBEE)以控制地震风险和地震损失为目标，考虑地震动和工程结构响应的随机性和不确定性，采用基于概率表达的概率决策框架为结构性能评估提供参考^[11-12]。PBEE评估框架将结构概率抗震性能评估分为四个部分：地震危险性分析、结构地震需求分析、结构损伤分析和结构损失分析。具体表达为：

式中：IM为地震动强度参数；EDP为工程需求参数；DM为结构损伤变量；DV为涉及修复时间和修复费用的决策变量；λ(A)为变量A超越某一特定值a的年超越概率，而G(A |B)则为变量A的条件超越概率。

由式(3)可知，最终的损失分析和损失决策依赖于待分析结构的损伤状态及对应的损伤风险。考虑到结构损伤风险与环境温度直接相关，故以损伤风险分析为基础，对地震危险性，区域温度分布特性和考虑温度影响的结构易损性进行积分，得到结构达到或超过某一损伤状态(damage state, DS)的损伤风险，表达为：

式中： λ(IM) 即为地震危险性；${F}_{\rm{DS}}^{\varTheta }\left(im\right)$则为考虑区域温度分布特性的结构修正区域易损性，其含义与常用的结构地震易损性相同，为结构在特定地震动强度im下对某一DS的条件超越概率。修正区域易损性包含了特定区域的温度分布信息，可通过下式计算为：

式中，F_DS(im, θ_i)为地震动强度-温度联合易损性(以下简称“联合易损性”)，为在特定地震动强度im和环境温度θ下对某一DS的条件超越概率。联合易损性F_DS(im, θ_i)可以全面反映考虑温度影响的结构概率抗震性能，并为修正区域易损性${F}_{\rm{DS}}^{\varTheta }\left(im\right)$的计算提供基础。

为便于计算修正区域易损性${F}_{\rm{DS}}^{\varTheta }\left(im\right)$，可以结合区域温度分布概率P^Θ和联合易损性F_DS(im, θ_i)，采用全概率公式，将修正区域易损性${F}_{\rm{DS}}^{\varTheta }\left(im\right)$表示为：

对于结构联合易损性，结合需求分析和损伤分析，在随机的地震动作用下，假设EDP和DM仍服从对数正态分布的随机变量，可将联合易损性表达为：

式中：Φ(ˑ)为标准正态分布的累积分布函数；${\beta }_{C}$和${\beta }_{D|IM}^{{\theta }_{i}}$分别为随机变量DM 和${EDP}_{{\theta }_{i}}$的离差。式中将DM及其离差${\beta }_{C}$近似认为与温度无关；而${EDP}_{{\theta }_{i}}$和${\beta }_{D|IM}^{{\theta }_{i}}$则表征在特定温度θ_i下的结构需求和考虑地震动记录不确定性的结构需求不确定性，可以通过概率地震需求模型计算得到结构需求与地震动强度的关系。

对于联合易损性的求解，也可以通过对某一DS的条件超越概率的累计分布函数进行对数正态累积分布拟合，得到结构在不同温度和地震动强度下的易损性曲线，即：

式中，N_g和n_g分别为分析中所采用的地震动记录总数和超过特定DS的地震动记录数量。

综上，通过式(7)或式(8)可以求得结构的联合易损性F_DS(im, θ_i)，并利用式(5)或式(6)得到结构考虑区域温度分布特性的修正区域易损性${F}_{\rm{DS}}^{\varTheta }\left(im\right)$，即可利用式(4)得到所考虑地区的结构损伤风险 λ_DS。此外，利用泊松分布，可以进一步计算得到结构服役期n年内结构对某一特定DS的超越概率为：

3   温度相关型结构设计实例与响应特性研究

3.1   SMA材料温度相关性

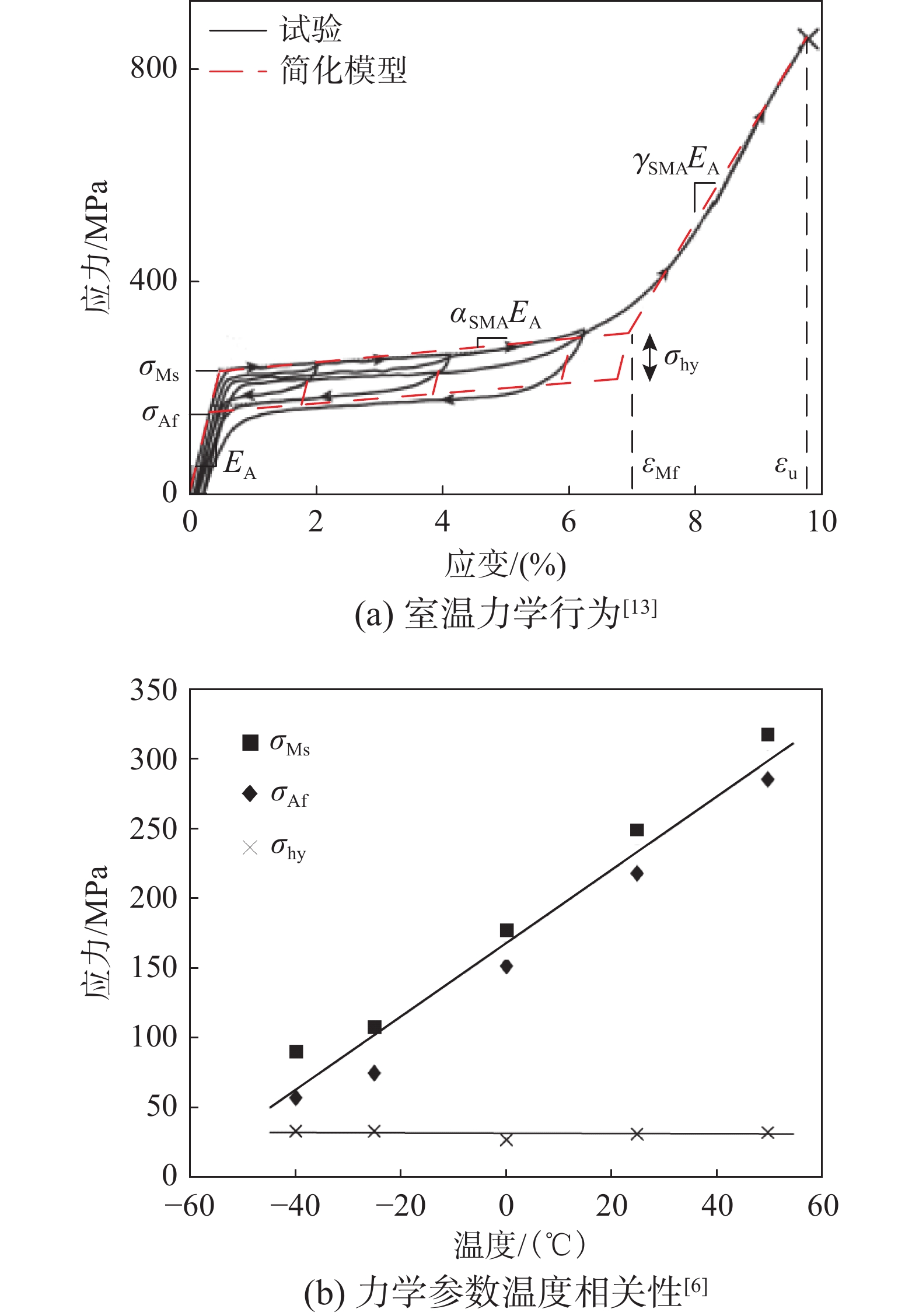
NiTi合金和Cu-Al-Mn合金等SMA材料具备良好的超弹性，但其力学特性存在温度相关性。相对于NiTi合金， Cu-Al-Mn合金具有较低的马氏体逆相变结束温度(A_f ≈ −50 ℃)，在绝大部分地区均能保持超弹性状态^[6]。室温下(20 ℃)Cu-Al-Mn合金力学行为如图4(a)所示^[13]，其主要力学参数包括正相变开始应力σ_Ms，逆相变结束应力σ_Af，应力滞回σ_hy=β_SMAσ_Ms=σ_Ms−σ_Af，奥氏体弹性模量E_A，相变模量E_T=α_SMAE_A。同时，当变形超过相变结束应变ε_Mf，材料会表现出显著强化，对应的马氏体弹性模量E_M=γ_SMAE_A；而当变形超过极限应变ε_u时，材料发生破坏。提取室温下的力学参数如表2所示。

图  4  Cu-Al-Mn热力学行为

Figure  4.  Thermal-mechanical properties of Cu-Al-Mn alloy

下载: 全尺寸图片 幻灯片

表  2  Cu-Al-Mn合金材料参数

Table  2.  Mechanical parameters of Cu-Al-Mn alloy

正相变 开始应力 σMs/MPa	逆相变 结束应力 σAf/MPa	应力滞回 σhy/MPa	奥氏体 弹性模量 EA/GPa	相变 模量比 αSMA	相变结束 应变εMf	马氏体 模量比 γSMA	极限 应变 εu
237	180	57	60	0.02	0.065	0.2	0.095

下载: 导出CSV 

| 显示表格

相关试验研究表明^[6]，Cu-Al-Mn合金的温度相关力学参数主要为正逆相变应力，且相变应力与温度变化近似满足正相关的线性关系：

式中：Δσ_cr为(正逆)相变应力变化量；K_σ为相变应力变化量与温度变化量的比率。对于Cu-Al-Mn合金，如图4(b)所示，K_σ约为2.6 MPa/℃。其他力学参数则认为与温度无关。

3.2   SMA自复位支撑框架

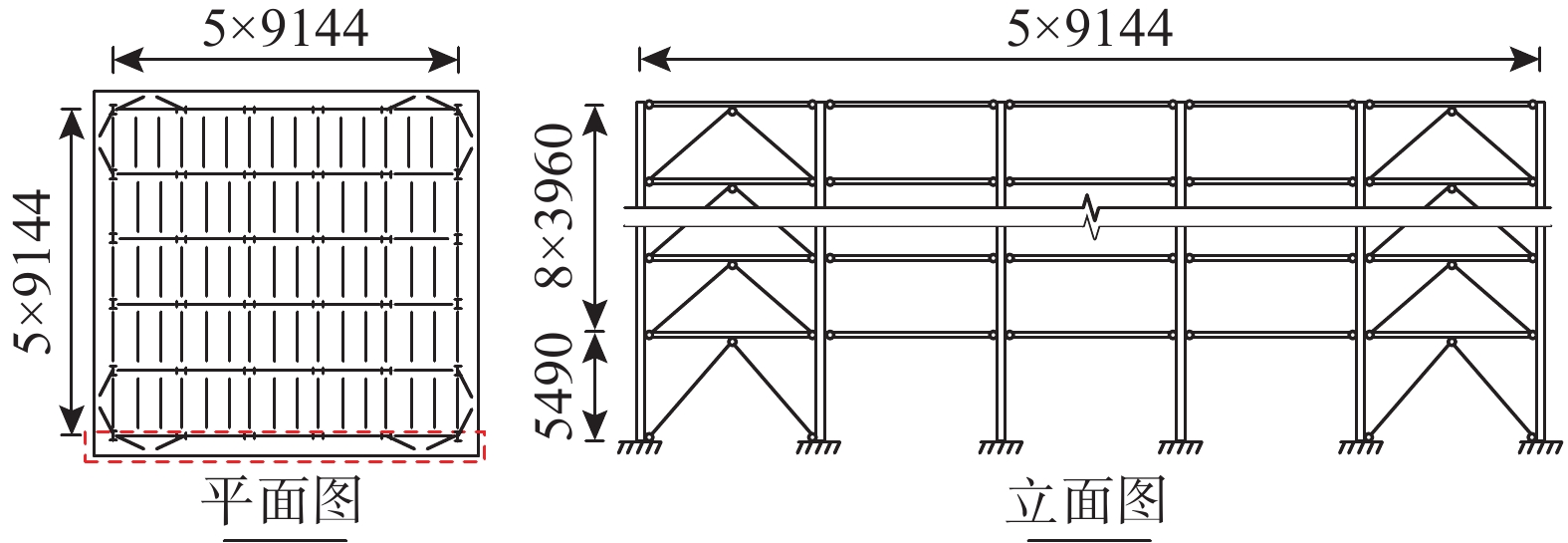
本研究中所考虑的研究对象为一典型的9层中心支撑钢框架结构^[14]，具体结构布置和楼层信息如图5所示。该钢框架采用柱贯通、梁分跨的梁柱铰接连接形式，以支撑系统作为抗侧体系，将支撑系统布置于外围框架。本研究选择北京和文昌为案例地区。根据建筑抗震设计规范(GB 50011−2010)^[15]，案例地区抗震设防烈度为8度，设计基本地震加速度为0.20 g。

图  5  原型结构 　/mm

Figure  5.  Prototype building

下载: 全尺寸图片 幻灯片

以本文作者所提出的新型自复位支撑(SCB)作为支撑系统的核心抗侧力构件^[3]，支撑构造如图6所示。支撑包括提供自复位能力的SMA轴心拉力元件和提供附加耗能能力的新型摩擦装置。通过对拉力元件施加一定的初始预拉力T_SMA，可以克服摩擦力F_f对复位的阻碍作用，实现支撑拉压对称的旗帜型自复位行为，如图6(b)所示。支撑的主要滞回参数包括屈服力F_y=T_SMA+F_f，初始刚度K₁，屈服刚度K₂=αK₁，耗能系数β，强化刚度K₃= γK₁。其中，β可通过改变T_SMA和F_f进行调整，本研究设定支撑β=0.90。对于拉力元件，设初始预应力大小等于马氏体相变开始应力σ_Ms，即可得到总截面面积为A_SMA=T_SMA/σ_Ms；而长度L_SMA则以材料断裂时对应约4%层间位移角确定。对于支撑刚度，K₂和K₃可以根据拉力元件总面积A_SMA，长度L_SMA和材料模量计算得到；由于支撑初始刚度与加工误差等因素相关^[16]，假定初始屈服位移为3 mm，即可通过屈服力F_y和初始屈服位移的比值确定初始刚度K₁。

图  6  自复位支撑构造和滞回行为

Figure  6.  Configuration and hysteretic behavior of SCB

下载: 全尺寸图片 幻灯片

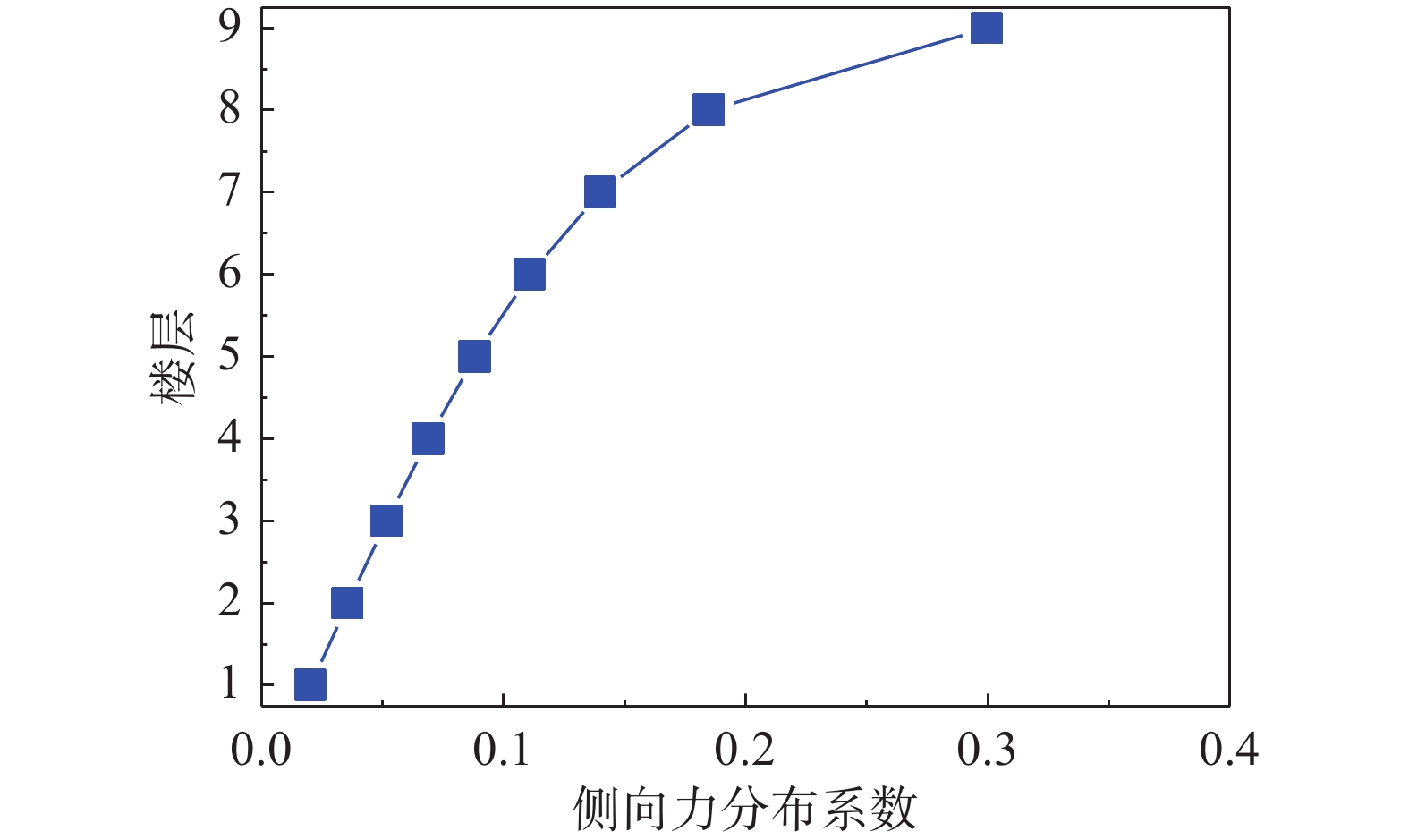
以室温温度20 ℃作为设计基准温度，根据上述设计信息和表2所示Cu-Al-Mn合金材料参数，参考CHAO等学者研究^[17]，采用如图7所示的近似倒三角的侧向力分布模式对结构梁柱构件和支撑系统进行设计。梁柱构件采用Q345材料，假定温度变化对钢材性能的影响可以忽略不计^[18]。得到设计梁柱截面尺寸和支撑设计信息如表3所示。

图  7  侧向力分布模式

Figure  7.  Lateral force pattern

下载: 全尺寸图片 幻灯片

3.3   模型建立

从原型结构中选取平面支撑框架作为简化分析对象，Rayleigh阻尼比为0.02，并通过附加重力柱考虑重力带来的二阶效应，建立相应的有限元分析模型。非线性有限元分析基于开源有限元分析程序OpenSees。梁柱构件采用Steel01材料，使用基于柔度法的非线性梁柱(dispBeamColumn)单元，控制截面采用纤维单元进行模拟。重力柱采用弹性梁柱(elasticBeamColumn)模拟。框架采用刚性楼板假定，并采用零长度(Zerolength)单元模拟铰接节点。

表  3  自复位支撑设计信息

Table  3.  Design information of SCBs

楼层	SMA元件				摩擦		支撑				结构柱截面	结构梁截面	楼层质量/kg
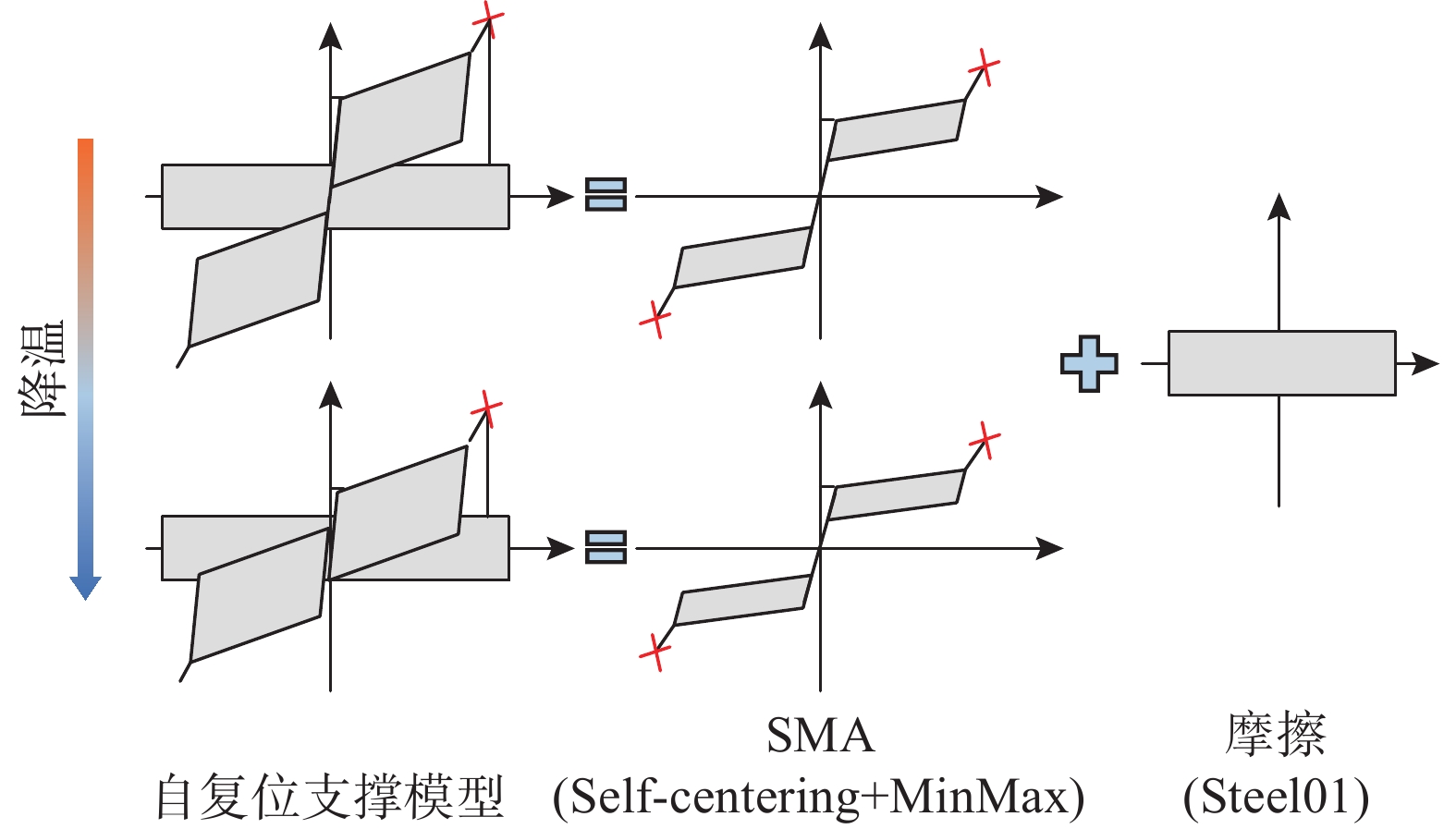
	初始预拉力 TSMA/kN	面积 ASMA/mm2	长度 LSMA/mm		摩擦力 Ff/kN		屈服力 Fy /kN	初始刚度 K1/(kN/mm)	屈服刚度 K2/(kN/mm)	强化刚度 K3/(kN/mm)
1	965.4	4073.5	1479.3		578.8		1544.2	514.7	3.3	33.0	HW500×500	HN700×300	9.06×105
2	800.6	3378.1	1260.3		480.0		1280.6	426.9	3.2	32.2
3	771.5	3255.1	1260.3		462.5		1234.0	411.3	3.1	31.0
4	729.2	3077.0	1260.3		437.2		1166.5	388.8	2.9	29.3	HW400×400
5	673.0	2839.5	1260.3		403.5		1076.4	358.8	2.7	27.0
6	600.9	2535.6	1260.3		360.3		961.2	320.4	2.4	24.1
7	510.3	2153.3	1260.3		306.0		816.3	272.1	2.1	20.5	HW350×350
8	395.9	1670.5	1260.3		237.4		633.3	211.1	1.6	15.9
9	244.8	1033.1	1260.3		146.8		391.6	130.5	1.0	9.8			8.19×105

下载: 导出CSV 

| 显示表格

自复位支撑复位和耗能系统分别使用自复位(Self-Centering)材料和Steel01材料模拟。其中，不同环境温度的影响通过改变复位系统温度相关的力学参数进行研究，而材料断裂失效行为则通过附加MinMax材料实现。当支撑变形超过限值时，拉力元件断裂破坏，支撑力学行为转变为摩擦装置行为。自复位支撑模型和温度对荷载-位移关系的影响如图8所示。

图  8  自复位支撑荷载-位移关系模拟

Figure  8.  Modelling of force-displacement responses of SCBs

下载: 全尺寸图片 幻灯片

3.4   静力推覆分析

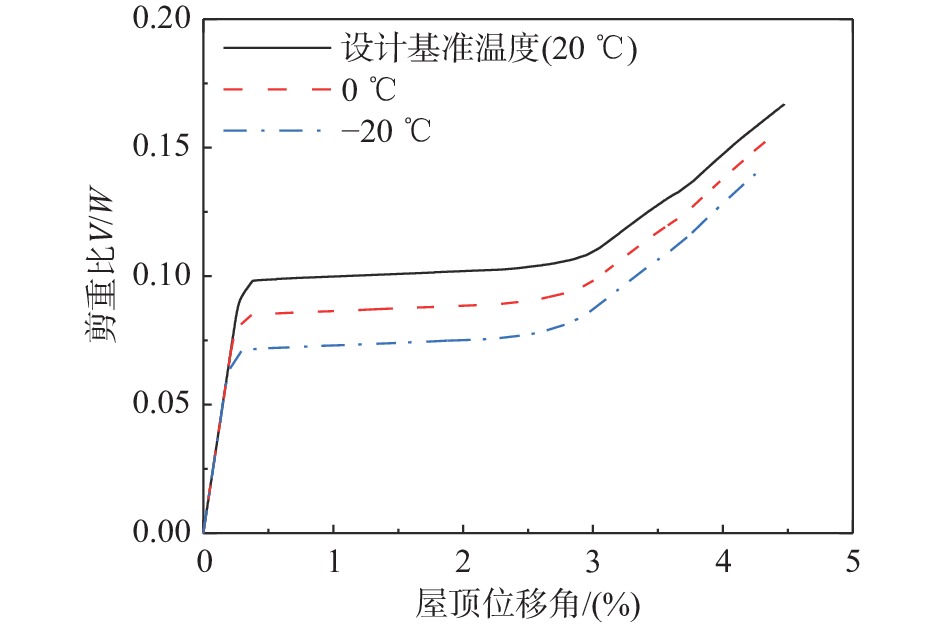
采用静力推覆方法(pushover)对所设计的框架模型进行分析，并与−20 ℃和0 ℃环境温度下的结构进行对比。各框架的静力推覆结果如图9所示。图中横坐标为屋顶位移角(顶点水平位移比结构总高)，纵坐标V/W为剪重比。

对比模型结果可知，温度降低将引起整体结构承载力的降低。相对于设计基准温度(20 ℃)，温度每降低10 ℃，结构屈服剪重比下降约8%； −20 ℃下结构屈服剪重比约为设计剪重比的70%。随着侧向位移进一步增大，由于支撑的强化行为，各结构推覆曲线在约3%屋顶位移角出现明显强化，并在约4%屋顶位移角处达到峰值。此后由于复位元件变形超过极限应变破坏失效，结构承载力下降发生倒塌。

图  9  框架静力推覆曲线对比

Figure  9.  Comparison of pushover curves

下载: 全尺寸图片 幻灯片

3.5   非线性时程分析

3.5.1   地震动选择

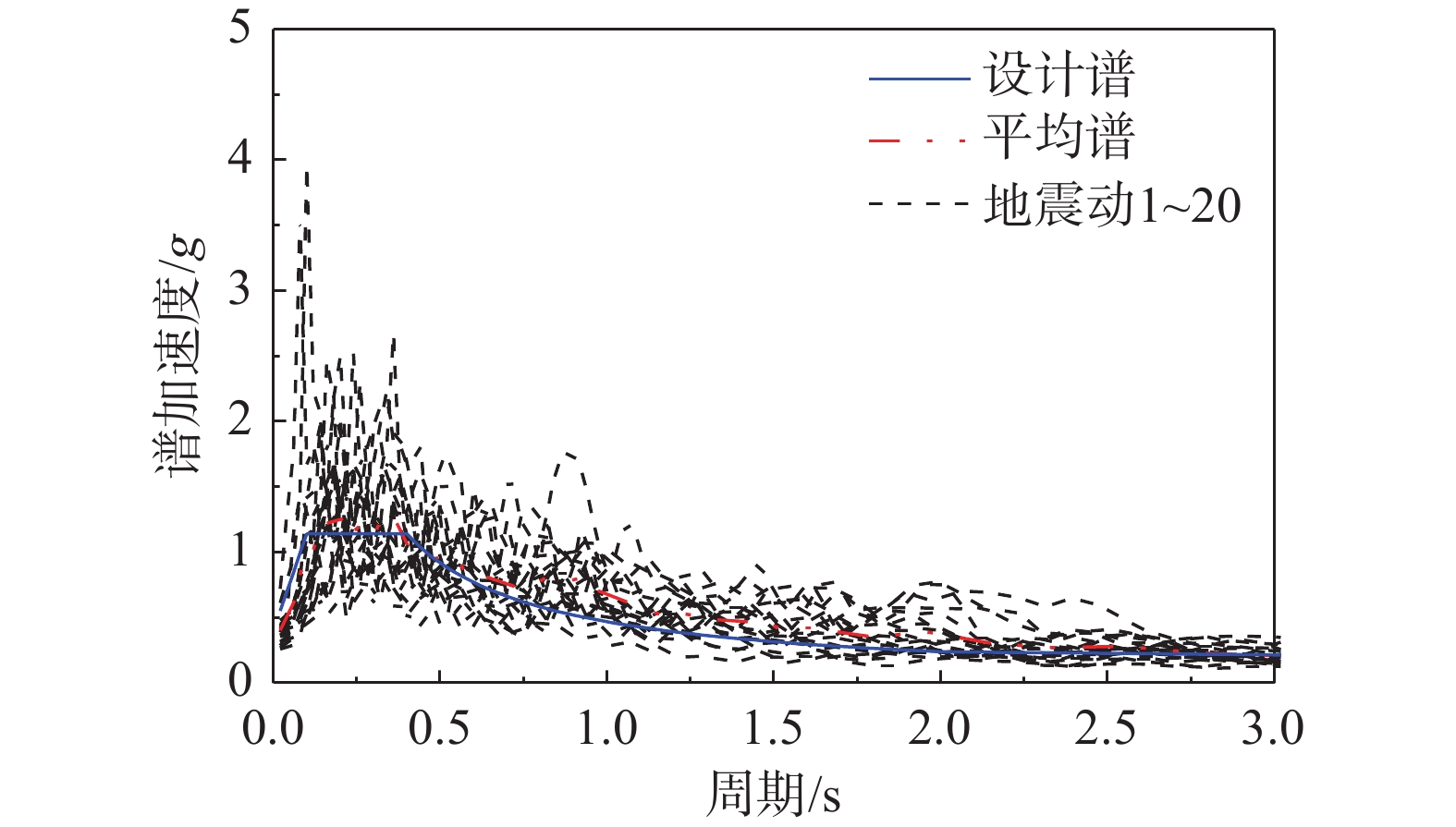
根据建筑抗震设计规范^[15]，考虑案例地区所属抗震设计分组及场地土类型^[19]，从PEER NGA数据库中选取震级范围为M6.5~M7.4，剪切波速范围为250 m/s~500 m/s，断层距大于15 km的20条无脉冲远场地震波记录，并调幅至罕遇地震水平。地震具体信息如表4所示，设计反应谱和所选地震动记录的加速度反应谱如图10所示。

表  4  地震动记录信息

Table  4.  Ground motion records

序号	地震名称	震级	PGA/g	调幅系数
1	Kern County, 1952	7.36	0.159	1.32
2	Parkfield, 1966	6.19	0.060	3.64
3	Borrego Mtn, 1968	6.63	0.041	5.42
4	San Fernando, 1971	6.61	0.026	5.18
5	San Fernando, 1971	6.61	0.009	19.82
6	San Fernando, 1971	6.61	0.012	17.81
7	San Fernando, 1971	6.61	0.225	0.86
8	San Fernando, 1971	6.61	0.007	17.60
9	San Fernando, 1971	6.61	0.008	18.05
10	San Fernando, 1971	6.61	0.006	25.12
11	San Fernando, 1971	6.61	0.013	11.96
12	San Fernando, 1971	6.61	0.155	1.91
13	San Fernando, 1971	6.61	0.101	2.34
14	Friuli_ Italy-01, 1976	6.5	0.029	12.17
15	Tabas_ Iran, 1978	7.35	0.106	1.69
16	Tabas_ Iran, 1978	7.35	0.027	7.53
17	Trinidad, 1980	7.2	0.062	3.19
18	Irpinia_ Italy-01, 1980	6.9	0.047	4.38
19	Irpinia_ Italy-02, 1980	6.2	0.018	9.83
20	Coalinga-01, 1983	6.36	0.225	0.89

下载: 导出CSV 

| 显示表格

图  10  地震动反应谱

Figure  10.  Response spectra of selected ground motions

下载: 全尺寸图片 幻灯片

3.5.2   结构响应特性

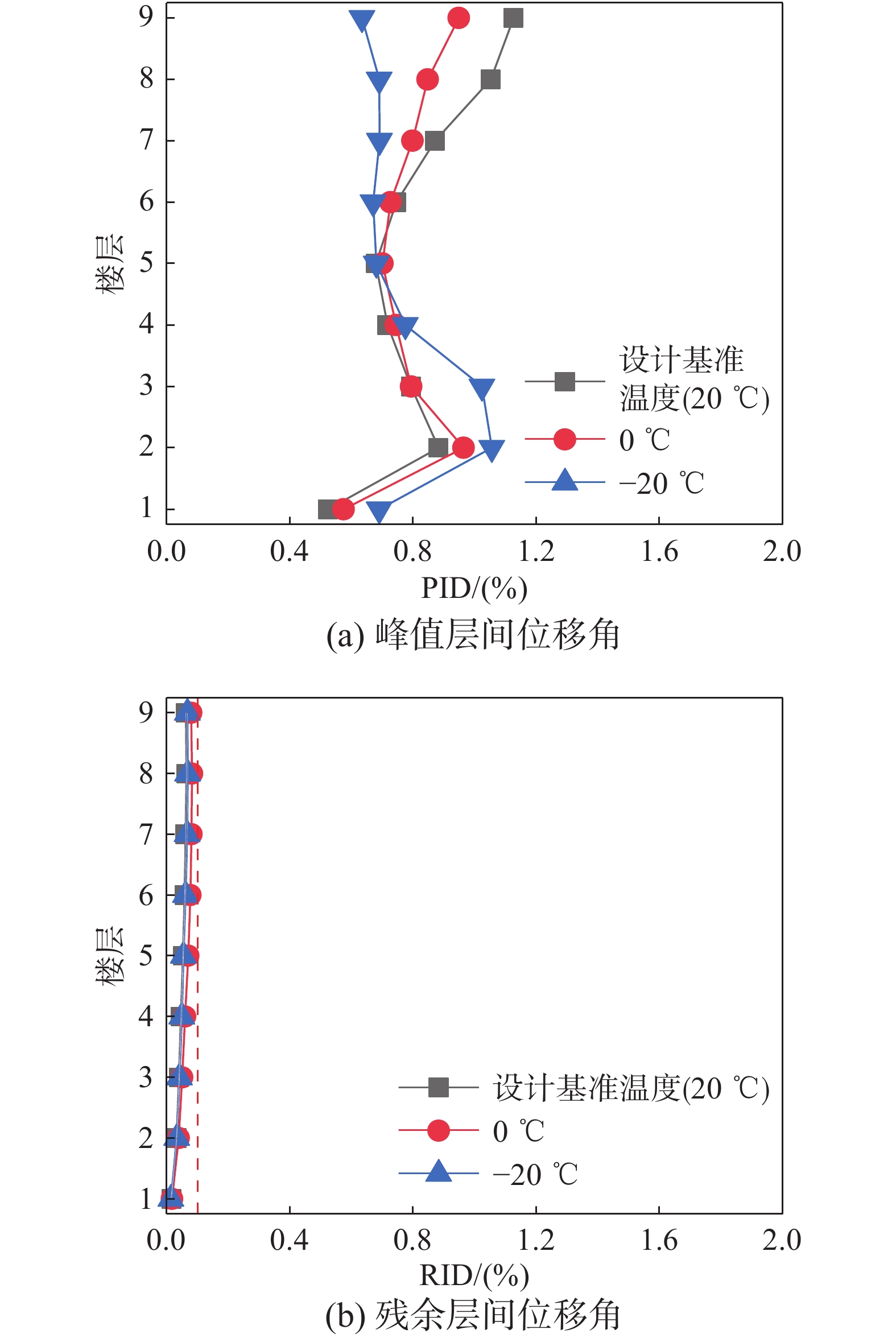
选取各层峰值层间位移角(PID)和残余层间位移角(RID)作为关键抗震需求指标进行对比。根据建筑抗震设计规范 ^[15]，PID需满足2%的层间位移角限值要求；而对于作为评价结构可修复性重要指标之一的RID，相关研究^[20]认为当RID小于0.2%时，可认为结构损坏轻微，基本能够实现震后自复位功能。

选取−20 ℃和0 ℃作为环境温度与设计基准温度进行对比。对结构进行非线性时程分析，每一次时程分析在地震动记录作用结束后均添加5 s自由振动时间以获得较为准确的残余层间位移角响应。

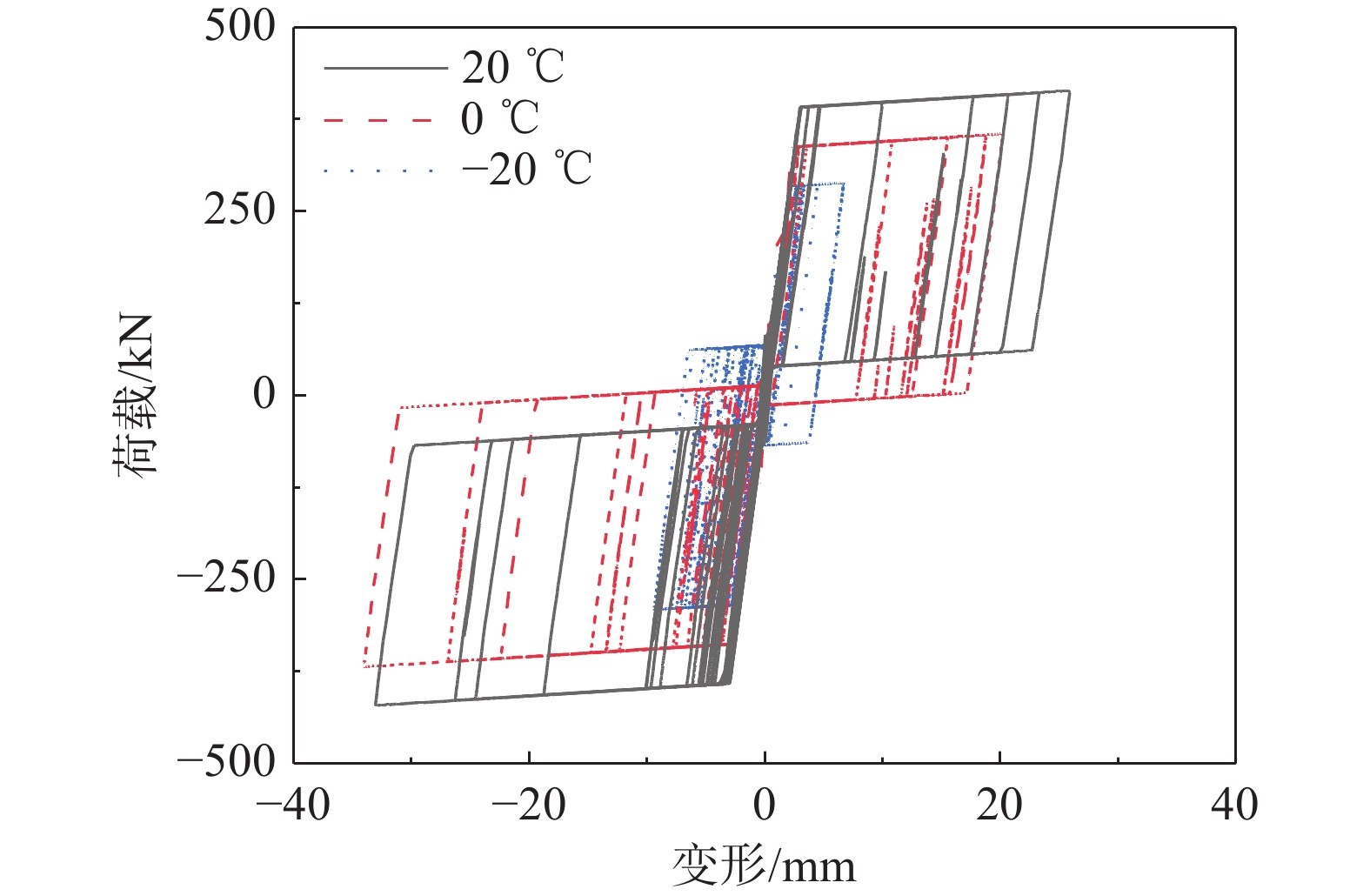
图11为九层支撑框架结构各层的PID和RID响应的中值分布曲线。对于PID响应，如图11(a)所示，各结构PID响应均满足2%的最大层间位移角限值要求。可以看出，处于较低环境温度的结构低层段(1层~3层)层间位移角设计基准温度，温度降低将引起下部结构峰值响应的提升；但另一方面，处于设计基准温度的结构高层段(7层~9层)响应较其他结构放大，最大PID响应与−20 ℃下的结构相当。统计各结构在20条地震动记录作用下最大PID响应的楼层分布如图12所示；可以发现，随环境温度升高，结构最大PID响应逐渐由低层段向高层段发展，结构变形模式发生变化。该现象与自复位支撑的滞回行为变化有关。提取第18号地震动作用下结构顶层支撑荷载-变形关系如图13所示，−20 ℃、0 ℃和20 ℃环境温度下所对应的支撑耗能系数β分别为1.24、1.04和0.90。处于较高环境温度的结构具备更高的承载力，但同时耗能系数β会相应降低。

图  11  非线性时程分析结果

Figure  11.  Deterministic results from NRHA

下载: 全尺寸图片 幻灯片

图  12  最大PID响应分布

Figure  12.  Distribution of maximum PID response

下载: 全尺寸图片 幻灯片

对于RID响应，如图11(b)所示，不同结构模型的RID均小于0.2%，处于各环境温度的结构在罕遇水准地震作用下均能实现预期的自复位功能。

图  13  支撑荷载-变形关系

Figure  13.  Force-deformation relationship of SCBs

下载: 全尺寸图片 幻灯片

4   温度相关型结构地震风险评估

4.1   增量动力分析

作为目前用于确定不同地震作用下结构响应和结构易损性最有效的方法之一^{[14, 19]}。增量动力分析(incremental dynamic analysis, IDA)方法将地震动记录按IM进行调幅输入结构进行非线性时程分析，得到一系列地震动强度指标和结构损伤指标的关系曲线，并对IDA结果进行统计分析，进而评价结构概率抗震性能。

选用表4所示的地震动记录，以最大层间位移角作为损伤指标，以结构基本周期对应的谱加速度值S_a(T₁)作为IM进行调幅。每条地震动记录调幅12次以获得对应的IDA曲线。考虑从−20 ℃~35℃的环境温度变化，以5℃为分析间隔，对各结构进行IDA分析。提取各结构的IDA中值曲线如图14所示。

图  14  IDA中值曲线

Figure  14.  Median IDA curves

下载: 全尺寸图片 幻灯片

根据IDA曲线可以看出，在S_a(T₁)≤1.2 g时，各结构IDA曲线基本一致，环境温度变化对结构性能影响不大。而当S_a(T₁)>1.2 g时，各环境温度下结构IDA曲线均出现“变平”趋势，即地震动强度的微小增加引起了结构位移响应的无限增大，说明结构在地震动作用下由于支撑拉力元件失效出现承载力下降，进而引起了结构的动力失稳和倒塌。随环境温度逐渐降低，结构的“变平”趋势将会更早出现。上述结果表明，结构倒塌行为存在显著的温度相关性。若不考虑环境温度变化的影响，仅以室温下的材料力学特性对结构进行设计，将可能偏于不安全地评估结构性能。

4.2   区域易损性分析

利用IDA曲线结果，即可得到结构在不同地震动强度和环境温度下各损伤状态的地震易损性。针对结构的PID响应，定义三种损伤状态，分别为立即使用(immediate occupation, IO)，生命安全(life safety, LS)和防止倒塌(collapse prevention, CP)，所对应PID限值如表5所示。其中，IO点和LS点参考建筑抗震设计规范^[15]中所给定的多高层钢结构弹性和弹塑性层间位移角限值；CP点对应于SMA材料发生断裂时的结构层间位移角。

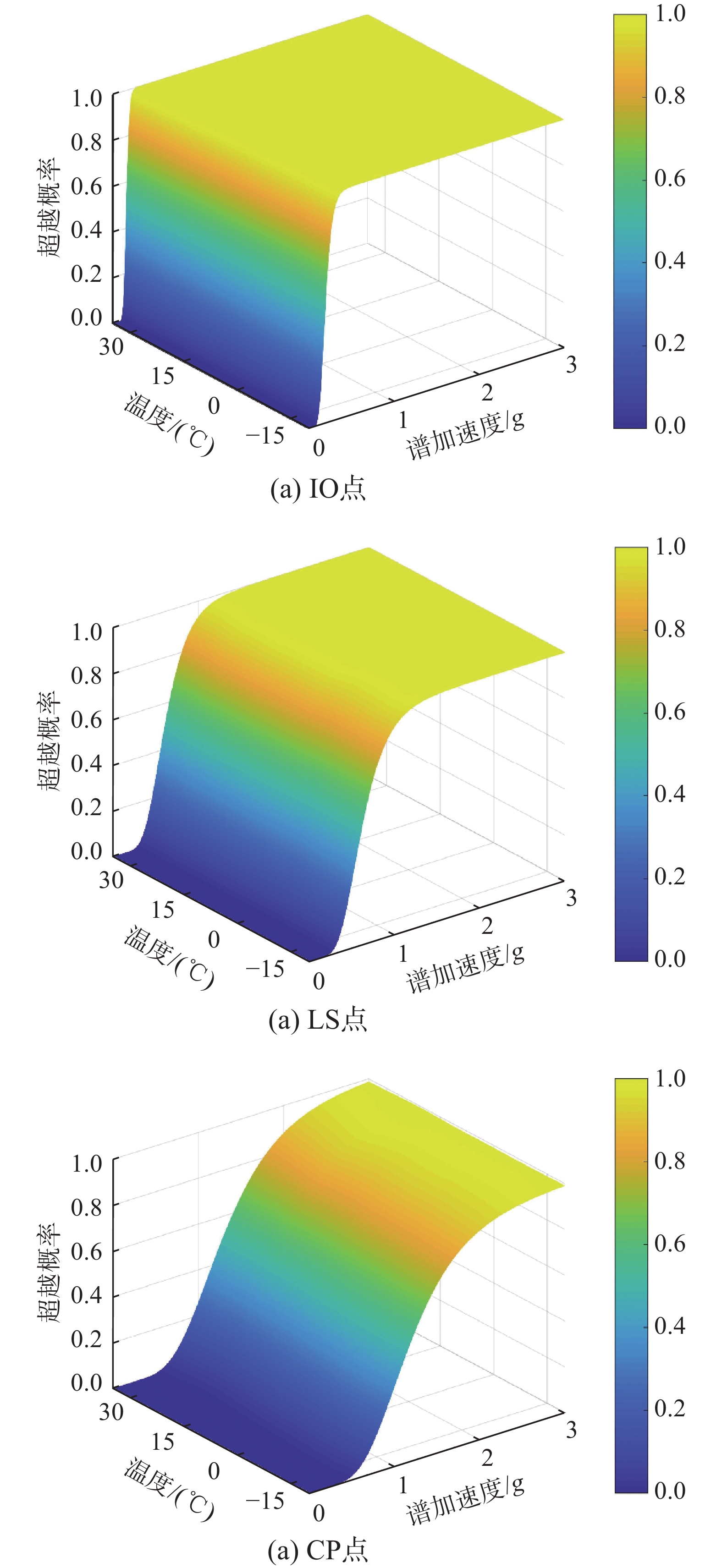
表  5  损伤状态定义

Table  5.  Definition of damage states

损伤状态DS	峰值层间位移角PID/(%)
DS1：立即使用(IO)	0.5
DS2：生命安全(LS)	2.0
DS3：防止倒塌(CP)	4.0

下载: 导出CSV 

| 显示表格

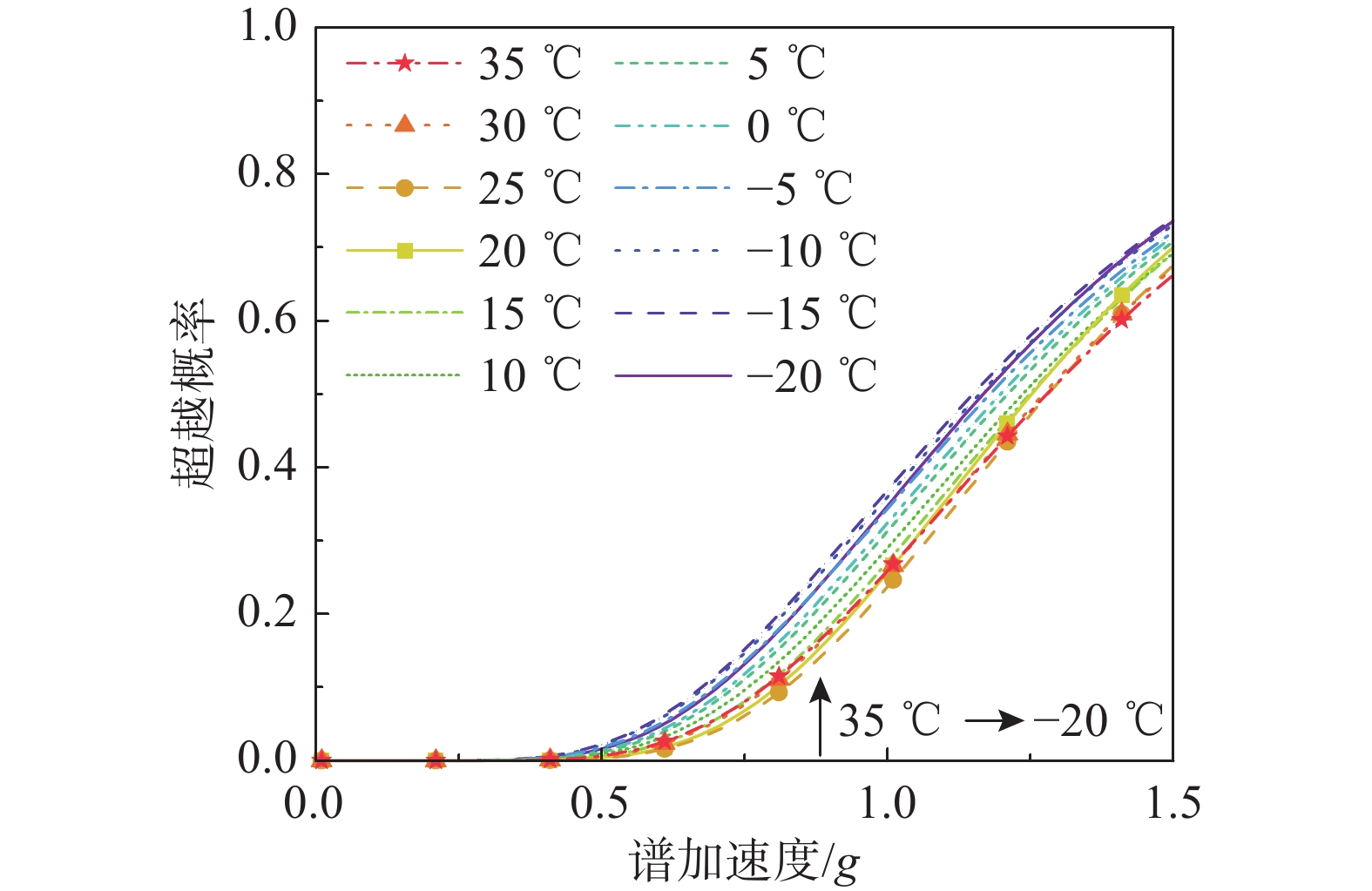
根据损伤状态定义，可以得到结构各损伤状态超越概率的累计分布，通过式(8)拟合得到对应的联合易损性${F}_{\rm{DS}}(im,{\theta }_{i})$，分析结果如图15所示。从图15中提取不同环境温度下，CP极限状态对应的结构倒塌易损性曲线，如图16所示。由结果可知，随温度降低，结构的倒塌概率逐渐提升。以地震动强度水平为S_a(T₁)=1.0 g下的结构倒塌概率为例，当结构温度从35 ℃降至−20 ℃时，结构倒塌概率从25%提升至35%。

图  15  联合易损性曲线

Figure  15.  Joint seismic fragility curves

下载: 全尺寸图片 幻灯片

图  16  不同环境温度结构倒塌易损性曲线

Figure  16.  Seismic fragility curves at different temperatures

下载: 全尺寸图片 幻灯片

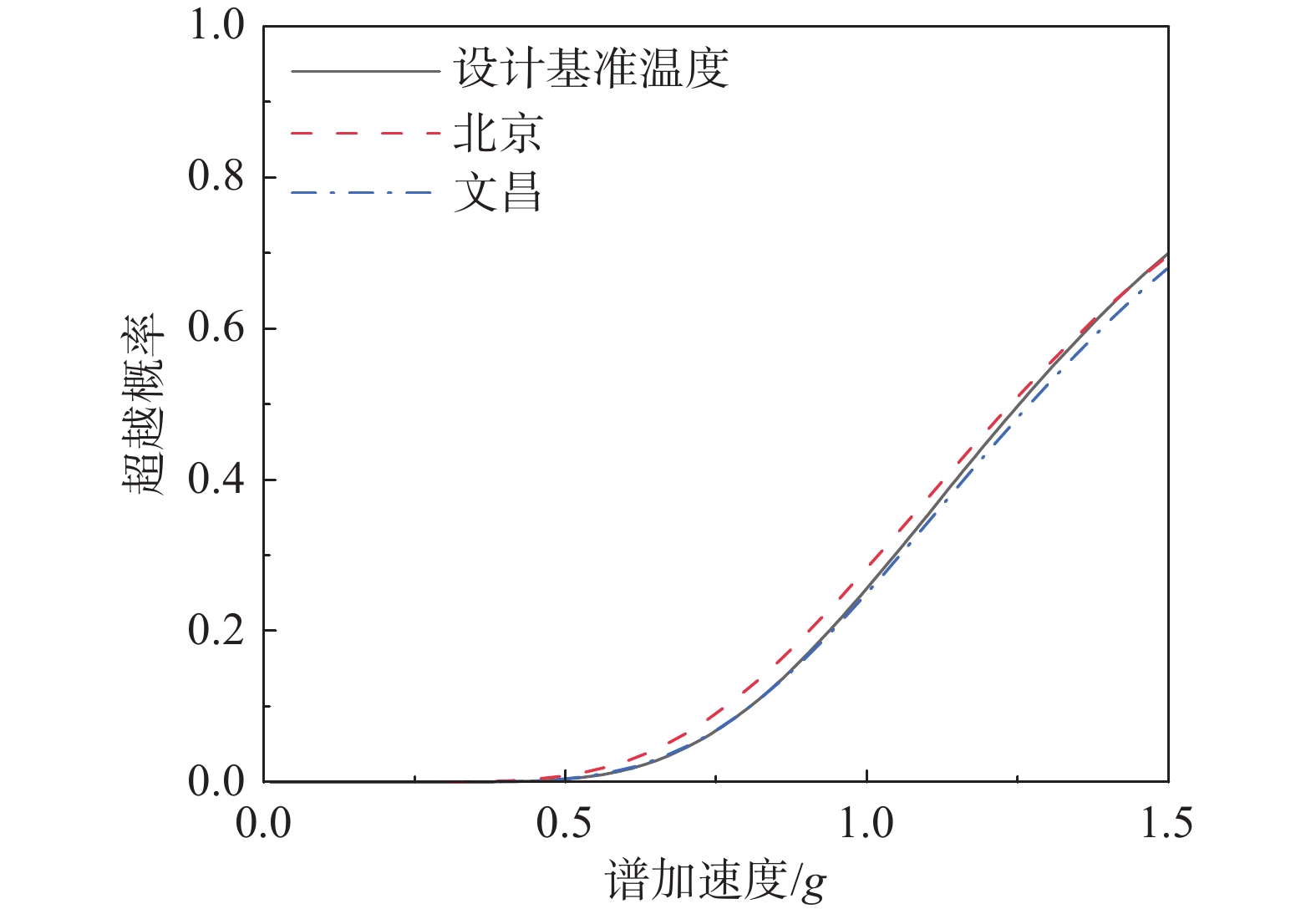
利用联合易损性${F}_{\rm{DS}}(im,{\theta }_{i})$和区域温度分布概率P^Θ，即可计算得到结构位于案例地区的修正区域倒塌易损性${F}_{\rm CP}^{\varTheta }\left(im\right)$，如图17所示。相对于文昌地区和设计基准温度，位于北京地区的对象结构具有更高的地震倒塌易损性。该现象与各地区的区域温度分布特性相关。由表1可知，北京的区域温度分布均值均低于文昌，且温度波动幅度较大，更易出现低温天气；故在相同地震动强度水平作用下，对象结构更易出现倒塌。

图  17  区域倒塌易损性曲线

Figure  17.  Regional fragility curves

下载: 全尺寸图片 幻灯片

4.3   风险分析

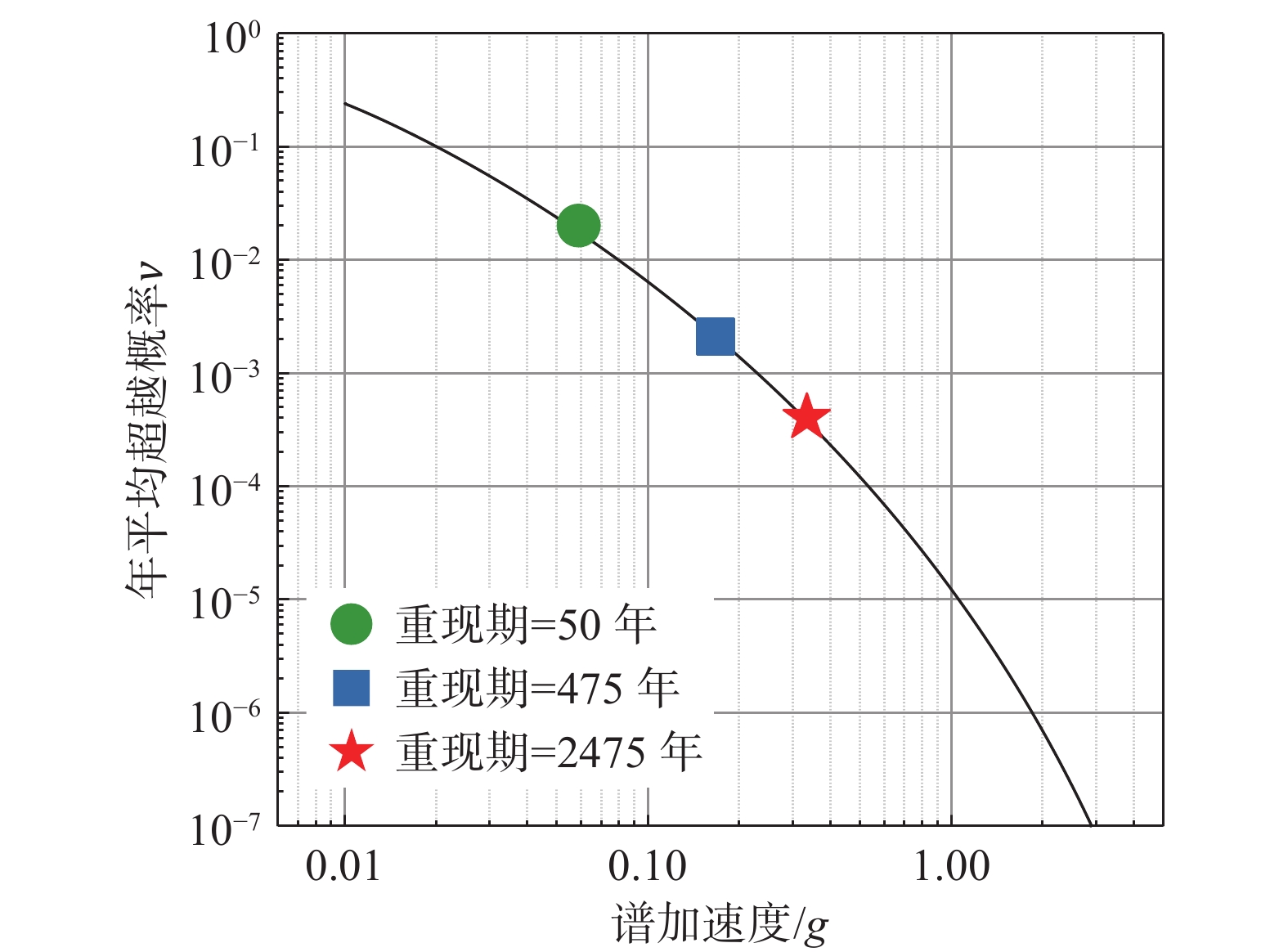
结合修正区域易损性和地震危险性，即可通过式(4)得到结构损伤状态的超越概率λ_DS。为获得案例地区的地震危险性曲线，根据建筑抗震设计规范^[15]，确定多遇地震、设防地震和罕遇地震(重现期分别为50年、475年和2475年)对应的地震动强度水平作为地震危险性数据，如表6所示。

表  6  地震危险性数据

Table  6.  Seismic hazard data

地震动强度	地震动强度水平/g	年平均超越概率值$\mathrm{\nu }$
多遇地震	0.059	2.0×10−2
设防地震	0.167	2.1×10−3
罕遇地震	0.333	4.0×10−4

下载: 导出CSV 

| 显示表格

考虑到常用的基于对数线性关系的概率地震危险模型会高估较小和较大IM下的地震危险性，本文采用BRADLEY等^[21]所给出的改进地震危险性模型，以对更大IM范围的地震危险性进行合理估计，该模型如下式所示：

式中：$\nu$为不同地震动强度值对应的年平均超越概率；η_i(i=1, 2, 3)为基于地震危险性数据拟合得到的参数。根据式(11)得到地震危险性曲线，如图18所示。

图19给出了不同案例地区的结构地震风险曲线，并与设计基准温度下的结构模型进行对比。各损伤状态对应的结构风险可以直接根据图19得到。当最大PID响应小于4%时，对象结构在各区域的地震风险接近；且当最大PID响应大于2%时，结构风险曲线由下凸转变为上凸，表明支撑的强化行为提高了结构的整体性能。而当最大PID响应超过4%时，由于材料发生断裂支撑承载力下降，结构发生倒塌。考虑到所选取的案例地区出现极端环境温度的概率较小，同时Cu-Al-Mn材料的温度相关性相对较小，从概率意义而言案例地区区域温度分布对本文所研究的SMA自复位支撑钢框架结构地震风险影响较小。

图  18  地震危险性数据

Figure  18.  Seismic hazard data λ(IM)

下载: 全尺寸图片 幻灯片

图  19  地震风险曲线

Figure  19.  Seismic risk curve of PID

下载: 全尺寸图片 幻灯片

提取DS3损伤状态所对应的结构地震倒塌风险，计算结构在50年服役期内的倒塌概率对比如表7所示。可以发现，当对象结构位于北京地区时，其倒塌风险将高于设计基准温度和位于文昌地区的评估结果。同时，对于对象结构，其考虑温度影响的结构地震风险可以得到有效的量化评估。

表  7  倒塌风险评估结果

Table  7.  Results of collapse risk assessment

地区	年平均超越概率${\mathit{\lambda } }_{{\rm CP} }$	50年超越概率${\mathit{P} }_{{\rm CP} }^{50}$/(%)
设计基准温度 (20℃)	4.0×10−4	1.97
北京	4.5×10−4	2.23
文昌	3.9×10−4	1.95

下载: 导出CSV 

| 显示表格

5   结论

当前针对温度相关型结构的性能评估，并未充分考虑环境温度变化影响和区域温度分布特性的不确定性。本文结合地震危险性分析、结构地震需求分析、结构损伤分析和区域温度分布特性，提出了温度相关型结构的地震风险评估方法；并以SMA自复位支撑钢框架结构为分析对象，得出主要结论如下：

(1) 对于本文所研究的SMA自复位支撑钢框架结构，较低温度环境会降低支撑和整体结构的承载力，同时增大支撑的耗能系数。根据罕遇水平地震动作用下的结构响应结果可以发现，随温度变化结构整体变形模式发生变化，最大PID响应逐渐由低层段向高层段发展；同时各结构均能实现预期的自复位功能。

(2) IDA分析结果表明，较大地震动强度水平下出现的材料断裂将引起支撑承载力下降，进而引发支撑框架结构倒塌；该现象在处于低温环境下的结构中更易发生。同时，结构倒塌概率随温度降低而出现升高的趋势。若仅以室温下的材料力学特性对结构进行设计而不考虑环境温度变化的影响，将可能偏于不安全地评估结构性能。

(3) 利用所提出的地震风险评估方法得到了SMA自复位支撑钢框架结构的修正区域易损性曲线和结构地震风险曲线，并进一步求解了结构服役期内的倒塌概率。

(4) 分析结果表明，不同地区的区域温度分布特性将会影响结构地震风险，应在温度相关型结构的评估和设计中予以考虑。