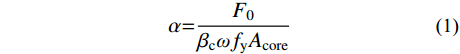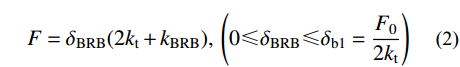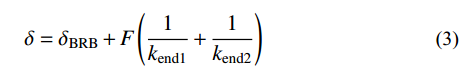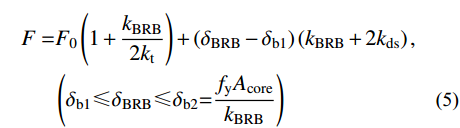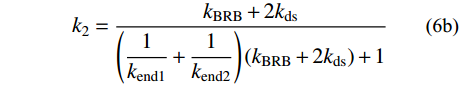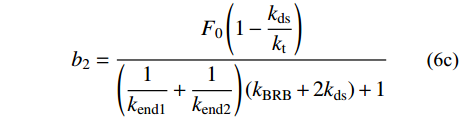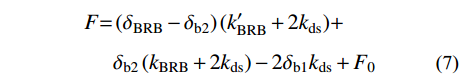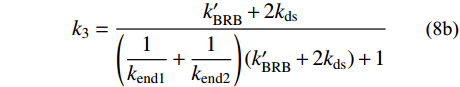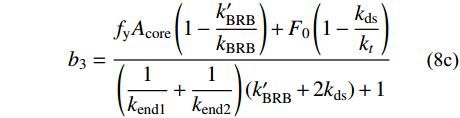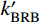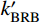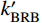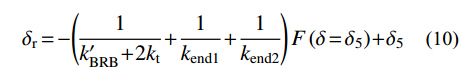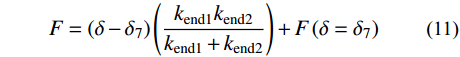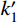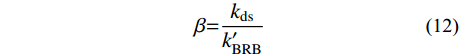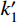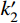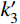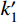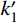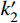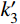THE HYSTERETIC BEHAVIOR AND WORKING MECHANISM OF SELF-CENTERING STEEL BUCKLING-RESTRAINED BRACES
-
摘要: 该文提出一种新型自复位全钢型防屈曲支撑(SC-SBRB),主要由防屈曲耗能系统和预压组合碟簧自复位系统并联组成。对其基本构造和工作原理进行了介绍,建立了能够准确描述支撑滞回特性的恢复力模型。采用ABAQUS有限元软件建立了具有不同设计参数的4个SC-SBRB实体模型,研究了支撑在低周往复荷载作用下的滞回特性及复位性能,并与恢复力模型计算结果进行了对比分析。结果表明,低周往复荷载作用下,SC-SBRB的滞回响应呈现稳定饱满的类“旗形”特征,建立的恢复力模型能够准确地预测支撑各阶段的力学性能。SC-SBRB的自复位性能随碟簧初始预压力的增大而逐渐得到发挥,残余变形同步减小。当复位率达到1.0时,支撑最大残余变形率为0.039%,复位性能和耗能能力匹配合理。Abstract: A novel self-centering steel buckling-restrained brace (SC-SBRB) is proposed, which is mainly comprised of a buckling-restrained energy-dissipation system and a self-centering system of pre-pressed disc springs in parallel. The fundamental configuration and working mechanism of the SC-BRB are introduced. A restoring force model that accurately describes the unique hysteretic behavior of the SC-SBRB is established. Four solid numerical models of SC-SBRBs with different design parameters are built using ABAQUS finite element software. The hysteretic behavior and self-centering performance of the SC-SBRB under cyclic loading are studied and compared with the calculation results of the restoring force model. The results demonstrate that the SC-SBRB exhibits a stable and full flag-shaped hysteretic response under cyclic loadings, and that the proposed restoring force model is capable of accurately predicting the mechanical properties at different stages. The self-centering performance of the SC-SBRB is gradually exerted as the initial pre-pressed force of disc springs increases, while the residual deformation is reduced simultaneously. The maximum residual deformation ratio of the brace is decreased to 0.039% when the self-centering ratio is 1.0, indicating a good coordination of the self-centering and energy-dissipation performance.
-
防屈曲支撑(buckling-restrained brace, BRB)作为一种具有稳定拉、压承载能力和良好延性的结构构件[1],已被广泛地应用于新建建筑结构和既有结构的加固改造中[2],其不仅可为结构提供有效的抗侧刚度,同时亦可在地震作用下减少结构的整体响应和损伤[3-4]。国内外学者就BRB的约束机理、耗能机理和失效机理[5-6]已进行了充分的研究和论证。
然而,BRB的优异性能是依靠钢材的塑性累积变形获得,势必使得支撑耗能后产生较大残余变形。对于设置BRB的结构,中大震作用后结构同样会产生明显的残余变形[7],残余变形作为评价建筑结构韧性的重要指标[8],其大小直接影响结构的震后安全性能评估和修复成本[9]。
近年来,国内外学者基于性能化地震工程的发展需求[10],提出了多种具有自复位功能的耗能支撑。Christopoulos等[11]提出一种在内外钢管两端锚固预应力筋的方式提供复位能力,辅以摩擦装置进行耗能的支撑构件,并通过试验验证了支撑的耗能能力和复位性能。Qiu等[12-13]采用形状记忆合金作为支撑的复位元件,通过振动台试验验证了该种支撑框架结构的优异抗震性能。徐龙河等[14-15]基于碟簧不同的组合方式及碟簧自身的承载和复位特性,提出预压碟簧自复位阻尼耗能和摩擦耗能支撑,试验证明了支撑的旗形滞回耗能和良好的复位能力。Wang等[16]在复位BRB的内、中管端部采用多束交错锚固的预应力钢绞线作为自复位系统,对其进行了低周往复加载试验,结果证明该构造能够有效减小支撑的残余变形。
前述所研究的具有自复位功能的耗能支撑基本都采用内、外管配合、内置自复位系统的构造形式,支撑本身的构造比较复杂,装配过程较为繁琐。本文基于碟簧的受力和变形特点,提出一种新型自复位全钢型防屈曲支撑(self-centering steel buckling-restrained brace, SC-SBRB),支撑由防屈曲耗能系统和预压组合碟簧自复位系统并联组成。对支撑的构造和工作原理进行了阐述,并进一步建立了SC-SBRB的恢复力模型。采用ABQUAS软件建立了具有不同设计参数的支撑数值模型,对SC-SBRB的滞回特性和复位性能进行了研究。
1 SC-SBRB基本构造
SC-SBRB的基本构造如图1所示。SC-SBRB由支撑内核单元、外包约束单元、侧向传力单元、盖板单元和内嵌于外包约束单元内的自复位系统组成。
支撑内核单元可分为端部连接段、过渡段、核心耗能段和非屈服延伸段。在内核单元两端部连接段开设多个螺栓孔,形成螺栓群,以便将支撑内核单元与外包约束单元在相应位置处通过螺栓进行连接;在非屈服延伸段范围内设置多个仅用于安装固定而非传递荷载的短槽型螺栓孔。
外包约束单元(或称“双槽钢单元”)由两个C型槽钢组成具有双轴对称的截面形式,在其近端范围内设置相应数量的长槽孔,该长槽孔可保证支撑内核单元在轴向自由拉伸、压缩。此外,由于内核单元两端有翼缘伸出,腹板处需预留出外伸翼缘所需的空间。将支撑内核单元安装于外包约束单元内,并与上、下盖板单元通过螺栓连接紧固后,已可形成全钢型BRB构件。
侧向传力单元由一块短板和垂直于板面的碟簧推进翼缘组成。在传力单元表面设置与外包约束单元腹板处同等数量的标准圆形螺栓孔,通过螺栓连接将该单元紧贴于外包约束单元的腹板处,使其与外包约束单元腹板,内核单元的非屈服延伸段和右侧端部连接段形成整体。
自复位系统由两组以叠合和对合方式组合而成的预压碟簧、碟簧导管、碟簧端板和碟簧限位单元组成。将自复位系统安置于外包约束单元内,通过螺栓将碟簧限位单元与外包约束单元的上下翼缘连接,预压的组合碟簧处于碟簧限位单元之间,形成具有自复位功能的SC-SBRB构件。
2 工作原理和恢复力模型
2.1 简化的力学模型
支撑内核单元中的核心耗能段用于提供对称饱满的滞回耗能能力,同时利用安装于外包约束单元内的自复位系统,对支撑提供足够的复位能力,将支撑的残余变形极大减小甚至完全消除。
由于SC-SBRB在正向(受拉)加、卸载以及反向(受压)加、卸载过程中的受力机理较为复杂,因此描述支撑的工作原理和对应的恢复力模型前,需对支撑的力学模型做一定程度的简化。简化后的力学模型如图2所示,其特点如下:
1) 将支撑沿全长共分为两端部连接段、BRB区段(不包括自复位系统)三段;
2) 受荷传力过程中,碟簧端板始终保持挺直状态,不发生弯曲和剪切变形。与之接触传力的碟簧推进单元和碟簧限位单元同样不考虑变形;
3) 碟簧压缩产生的荷载在外包约束单元中传递时,忽略外包单元的压缩和拉伸变形;
4) 支撑受拉时,一旦碟簧的初始预压力被克服后,侧向传力臂的拉伸变形不再考虑。
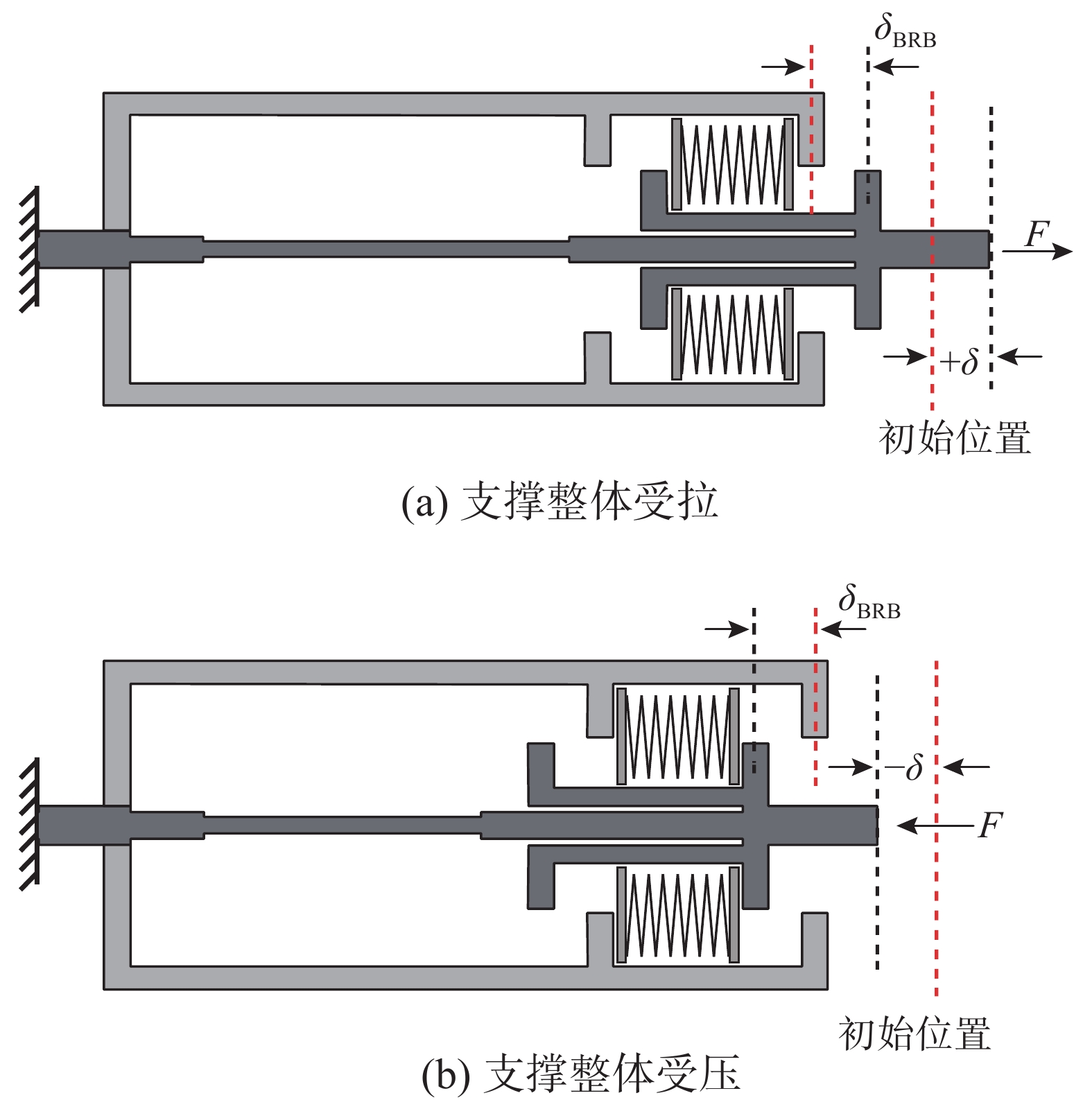
2.2 工作原理及恢复力表达式
根据图2,BRB区段由核心耗能段及两侧过渡段组成。根据其串联关系可得BRB区段屈服前刚度为kBRB,屈服后刚度为
k′BRB ;支撑两端部加强区刚度分别为kend1、kend2;侧向传力臂刚度为kt;碟簧刚度为kds,支撑受拉或受压的工作原理如图3所示。根据支撑工作性能的设计要求,碟簧的初始预压荷载F0与核心耗能段屈服荷载的比值是影响支撑复位效果的关键参数[17],为:
α=F0βcωfyAcore (1) 式中:α为复位率;fy为核心耗能段的屈服强度;Acore为核心耗能段的截面面积;ω为屈服后强化系数;βc为支撑受压时的摩擦影响系数。若复位率太小,则支撑将无法提供足够的复位能力,致使支撑产生很大的残余变形;复位率太高,则支撑各传力部件之间的设计将难以匹配,造成支撑局部变形和附加作用过大。
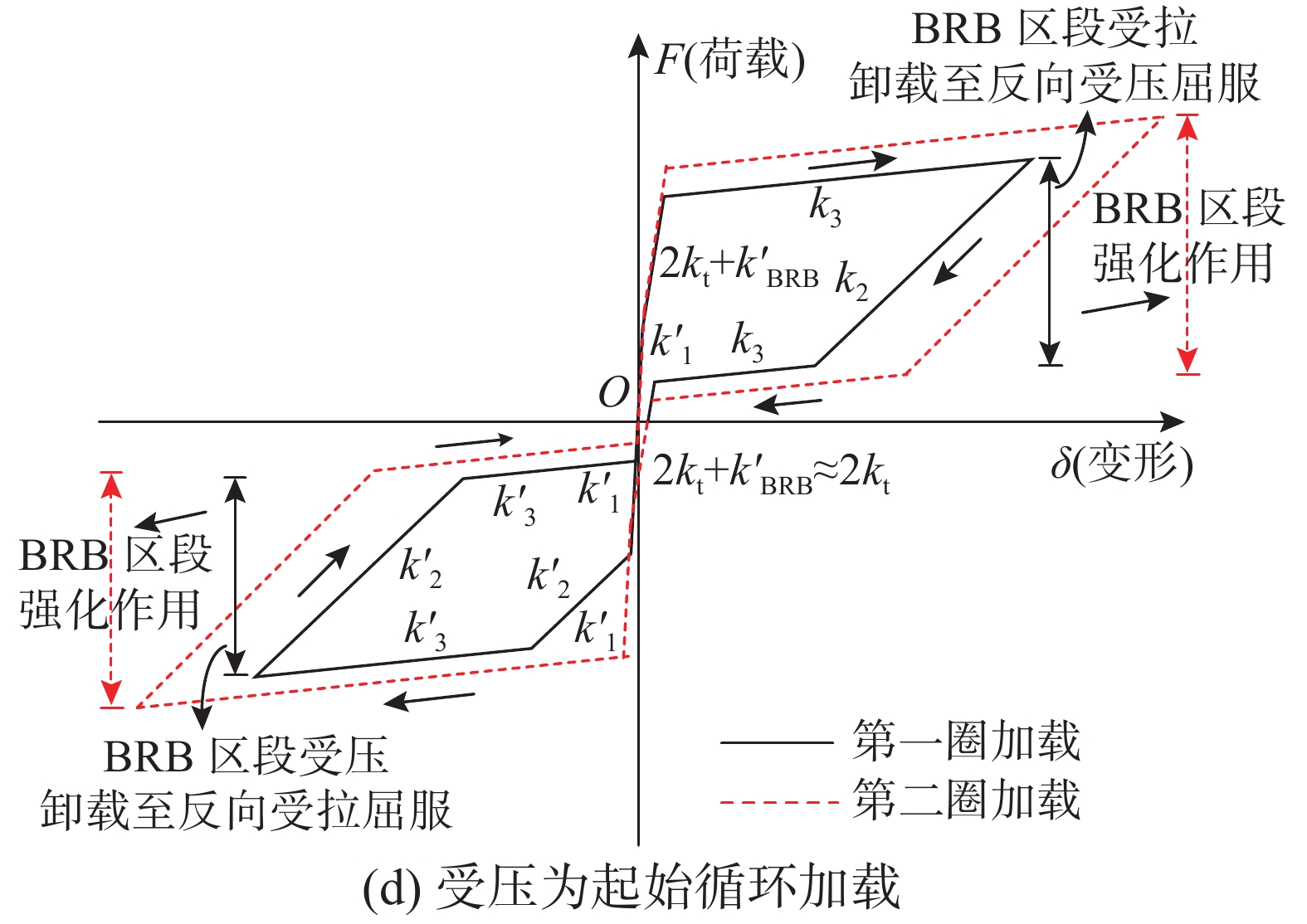
基于简化力学模型中的假设和合理的复位率α,图4(a)和图4(c)分别给出了SC-SBRB以受拉或受压为起始作用顺序下单圈的恢复力模型,并分离出BRB区段在全过程中的受力和变形,以供对比;同时图4(b)和图4(d)分别给出了SC-SBRB以受拉或受压为起始作用顺序下循环荷载作用时的恢复力模型。图中以BRB区段为力学模型基础,增加了碟簧力学特性的自复位系统[18],支撑整体表现出理想的类“旗形”滞回特征。根据其受力特点,恢复力模型可分为12个阶段。
以支撑起始受拉为例,第1阶段(OA),开始加载至支撑两侧左端的碟簧推进单元刚好克服碟簧初始预压力F0。此时,由于两侧传力臂与支撑右端部连接,需保持变形协调,即BRB区段产生与侧向传力臂相同的变形。以BRB区段的变形为控制变量,外部总荷载为:
F=δBRB(2kt+kBRB),(0⩽ (2) 支撑总变形由BRB区段和两端部共同组成,可表示如下:
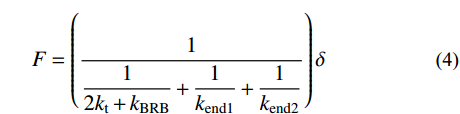
\delta = {\delta _{{\rm{BRB}}}} + F\left( {\dfrac{1}{{{k_{{\rm{end1}}}}}} + \dfrac{1}{{{k_{{\rm{end2}}}}}}} \right)\qquad\qquad\qquad\quad\;\; (3) 式中:F为支撑外部施加的总荷载;δ为支撑总变形量;δBRB为BRB区段的变形量。将式(2)代入式(3)中可建立支撑总荷载与总变形的关系:
F = \left({\dfrac{1}{{\dfrac{1}{{2{k_{\rm{t}}} + {k_{{\rm{BRB}}}}}} + \dfrac{1}{{{k_{{\rm{end1}}}}}} + \dfrac{1}{{{k_{{\rm{end2}}}}}}}}}\right)\delta \qquad\qquad (4) 该阶段支撑受拉的第一刚度为k1,如果两端部的刚度远大于BRB区段和侧向传力臂的刚度,则k1=2kt+kBRB。
第2阶段(AB),碟簧推进单元克服碟簧初始预压力后,将进一步推动碟簧压缩变形,直至BRB区段中的核心耗能段受拉屈服。同样以BRB区段的变形为控制变量,则支撑总荷载与BRB区段的变形关系为:
\begin{split} F =& {F_0}\left( {1 + \dfrac{{{k_{{\rm{BRB}}}}}}{{2{k_{\rm{t}}}}}} \right) + \left( {{\delta _{{\rm{BRB}}}} - {\delta _{{\rm{b1}}}}} \right)\left( {{k_{{\rm{BRB}}}} + 2{k_{{\rm{ds}}}}} \right),\\ &\left( {{\delta _{{\rm{b1}}}} \leqslant {\delta _{{\rm{BRB}}}} \leqslant {\delta _{{\rm{b2}}}}{\rm{ = }}\dfrac{{{f_{\rm{y}}}{A_{{\rm{core}}}}}}{{{k_{{\rm{BRB}}}}}}} \right) \end{split} (5) 支撑总变形同式(3)。将式(5)代入式(3)中,可改写得到如下关系:
\tag{6a} F{\rm{ = }}{k_2}\delta + {b_2} \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \tag{6b} {k_2} = \dfrac{{{k_{{\rm{BRB}}}} + 2{k_{{\rm{ds}}}}}}{{\left( {\dfrac{1}{{{k_{{\rm{end1}}}}}} + \dfrac{1}{{{k_{{\rm{end2}}}}}}} \right)\left( {{k_{{\rm{BRB}}}} + 2{k_{{\rm{ds}}}}} \right) + 1}} \tag{6c} {b_2} = \dfrac{{{F_0}\left( {1 - \dfrac{{{k_{{\rm{ds}}}}}}{{{k_{\rm{t}}}}}} \right)}}{{\left( {\dfrac{1}{{{k_{{\rm{end1}}}}}} + \dfrac{1}{{{k_{{\rm{end2}}}}}}} \right)\left( {{k_{{\rm{BRB}}}} + 2{k_{{\rm{ds}}}}} \right) + 1}} 支撑受拉的第二刚度为k2,若两端部的刚度远大于BRB区段和碟簧的刚度,则k2=2kds+kBRB。
第3阶段(BC),核心耗能段屈服后,进入应变强化阶段,碟簧继续被压缩,如图3(a),则有:
\begin{split} F{\rm{ = }}&\left( {{\delta _{{\rm{BRB}}}} - {\delta _{{\rm{b2}}}}} \right)( {k'_{{\rm{BRB}}} + 2{k_{{\rm{ds}}}}} ) + \\ &{\delta _{{\rm{b2}}}}\left( {{k_{{\rm{BRB}}}} + 2{k_{{\rm{ds}}}}} \right) - 2{\delta _{{\rm{b1}}}}{k_{{\rm{ds}}}} + {F_0} \end{split} 经变换,支撑总荷载与总变形的关系为:
\tag{8a} F{\rm{ = }}{k_3}\delta + {b_3} \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \tag{8b} {k_3} = \dfrac{{k'_{{\rm{BRB}}} + 2{k_{{\rm{ds}}}}}}{{\left( {\dfrac{1}{{{k_{{\rm{end1}}}}}} + \dfrac{1}{{{k_{{\rm{end2}}}}}}} \right)( {k'_{{\rm{BRB}}} + 2{k_{{\rm{ds}}}}} ) + 1}} \tag{8c} {b_3} = \dfrac{{{f_{\rm{y}}}{A_{{\rm{core}}}}\left( {1 - \dfrac{{k'_{{\rm{BRB}}}}}{{{k_{{\rm{BRB}}}}}}} \right) + {F_0}\left( {1 - \dfrac{{{k_{{\rm{ds}}}}}}{{{k_t}}}} \right)}}{{\left( {\dfrac{1}{{{k_{{\rm{end1}}}}}} + \dfrac{1}{{{k_{{\rm{end2}}}}}}} \right)( {k'_{{\rm{BRB}}} + 2{k_{{\rm{ds}}}}} ) + 1}} 支撑受拉的第三刚度为k3,由于两端部的刚度远大于
k'_{{\rm{BRB}}} 和kds,则k3=2kds+k'_{{\rm{BRB}}} 。第4阶段(CD),支撑开始卸载。卸载过程时,已压缩的碟簧逐渐恢复变形。BRB区段在此过程中经历两个阶段,首先是受拉荷载完全卸载至零,然后开始反向加载受压,直至核心耗能段受压屈服,反向加载的荷载源于压缩碟簧的恢复力。此过程中,支撑外荷载始终保持为正,卸载刚度为k2,可得:
F = - \left( {{\delta _{{\rm{BRB}}}} - {\delta _{{\rm{b4}}}}} \right)\left( {{k_{{\rm{BRB}}}} + {\rm{2}}{k_{{\rm{ds}}}}} \right) + F\left( {\delta = {\delta _{\rm{3}}}} \right) 第5阶段(DE),支撑外荷载持续卸载,BRB区段进入受压强化阶段,直至碟簧端板与碟簧限位单元刚好开始接触,此时BRB区段的变形基本恢复至零,此过程卸载刚度为k3。
第6阶段(EG),碟簧与限位单元接触后,支撑外荷载持续卸载至零,总体存在残余变形δr=δ6,对应表达式如下,如近似考虑的话,支撑卸载刚度为2kt+
k'_{{\rm{BRB}}} 。{\delta _{\rm{r}}} \!= \!-\! \left( \!{\dfrac{1}{{k'_{{\rm{BRB}}}\! +\! 2{k_{\rm{t}}}}} \!+\! \dfrac{1}{{{k_{{\rm{end}}1}}}} \!+\! \dfrac{1}{{{k_{{\rm{end2}}}}}}} \!\right)F\left( {\delta \!=\! {\delta _5}} \right) \!+\! {\delta _{\rm{5}}} (10) 以上6个阶段为支撑总体受拉加载、卸载的全过程。此后支撑将进入受压状态,与初始状态不同,支撑此刻外部荷载虽已卸载归零,但BRB区段是处于受压屈服且经历了一段应变强化的受荷状态,维持该状态所需的受压荷载完全来自于碟簧的预压力。因此,支撑由受拉转变为受压时,恢复力模型中的荷载路径会发生变化。
第7阶段(GH),支撑端部首先需要承担BRB区段的屈服强化荷载,建立与BRB区段的荷载传递路径。BRB区段完全恢复到初始零变形状态,加载刚度与第6阶段相同。
第8阶段(HJ),右侧碟簧推进单元与碟簧端板刚好接触。支撑端部逐渐克服碟簧的初始预压力,BRB区段变形保持不变。可直接建立总荷载与总变形的关系为:
F = \left( {\delta - {\delta _7}} \right)\left( {\dfrac{{{k_{{\rm{end1}}}}{k_{{\rm{end2}}}}}}{{{k_{{\rm{end1}}}} + {k_{{\rm{end2}}}}}}} \right) + F\left( {\delta = {\delta _7}} \right) (11) 往后支撑受压的9至12阶段与支撑受拉的3至6阶段基本一致,恢复力表达式亦相近,不再赘述。不同的是,最终外部受压荷载完全卸载后,支撑整体变形将准确回归零点,如图4(a)中受压加、卸载过程所示。
如果以受压为起始作用顺序,如图4(c),同样具有12阶段,各阶段对应的表达式与起始受拉时基本相同,但初始受压的第一刚度不同,可表示为
k'_1 =kend1kend2/(kend1+kend2),其工作原理与图4(a)中的第8阶段类似,但此时BRB区段不参与受力,变形量为零。最终支撑第12阶段受拉卸载后,会产生与图4(a)中第6阶段相同的残余变形。3 SC-SBRB滞回特性分析
3.1 支撑设计参数
为验证本文所提出的SC-SBRB的恢复力模型和工作性能,根据文献[16]所给复位率α的建议取值范围,以及考虑碟簧刚度与BRB区段屈服后刚度比值β对支撑性能的影响,如式(12),共设计了4个支撑模型,设计参数列于表1。
\beta {\rm{ = }}\dfrac{{{k_{{\rm{ds}}}}}}{{k'_{{\rm{BRB}}}}} (12) 表 1 SC-SBRB设计参数Table 1. Design parameters of SC-SBRB支撑编号 核心耗能段
屈服荷载/kN复位率α {k'_{{\rm{BRB}}}} /(kN·mm−1) 刚度比β SC-SBRB-1 260 0.0 4.3 1.3,2.3 SC-SBRB-2 260 0.5 4.3 1.3,2.3 SC-SBRB-3 260 1.0 4.3 1.3,2.3 SC-SBRB-4 260 1.5 4.3 1.3,2.3 3.2 分析模型
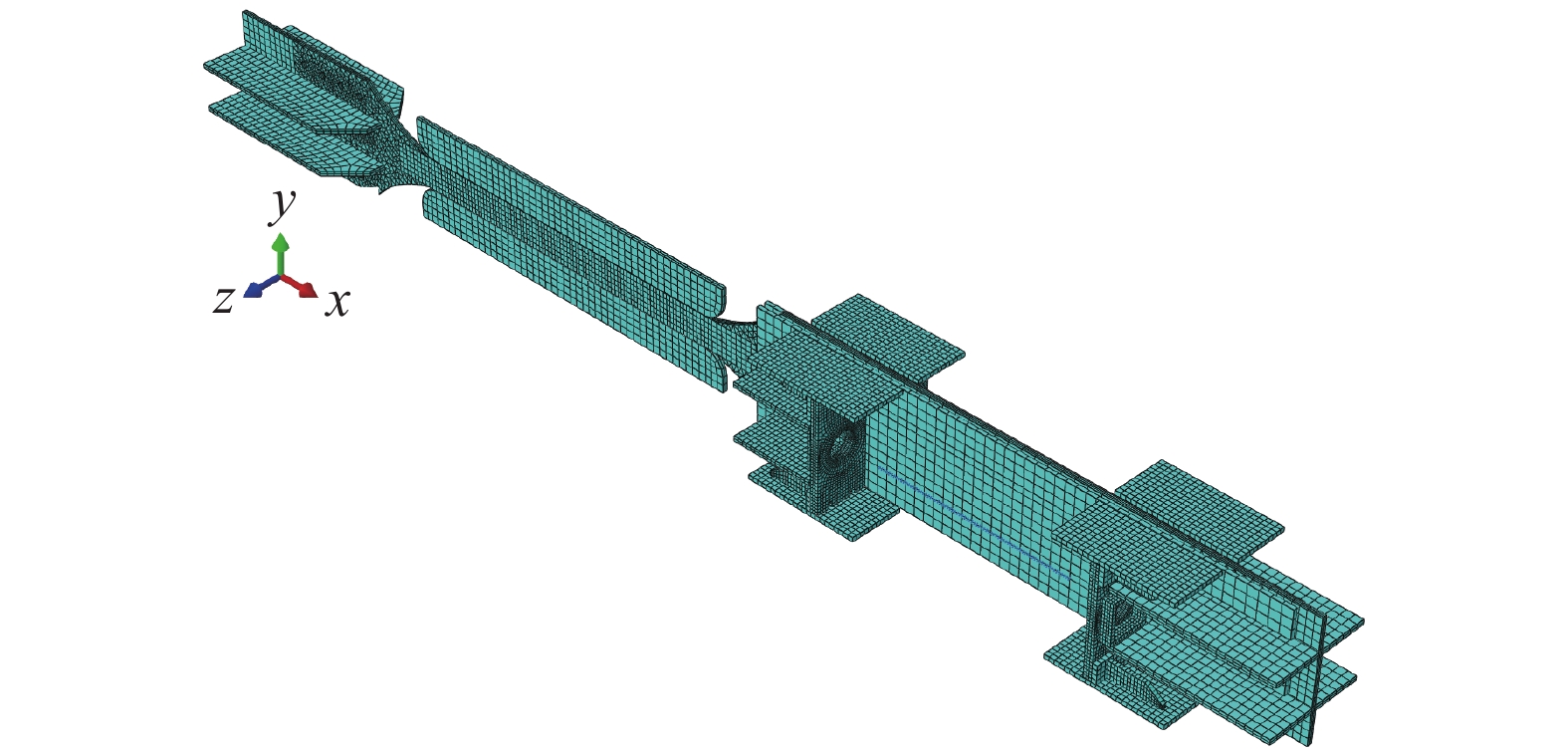
采用ABAQUS有限元分析软件,分别建立了不同参数下的SC-SBRB数值模型,如图5所示。模型主要包括了支撑内核单元、侧向传力单元和提供复位能力的自复位系统。为减少计算成本,模型中省略了双槽钢单元,需指出,此简化会造成部分碟簧荷载无法传递至支撑远端,但对结构整体变形和承载力几乎没有影响。模型中各部件的主要单元类型为C3D8I,以及少量不规则区域的C3D6单元,组合碟簧采用非线性弹簧单元进行模拟。弹簧单元两端分别与对应碟簧端板表面的局部面积进行耦合传力,该面积为碟簧与端板接触时所形成的圆环面积。模型中碟簧推进翼缘与各自的碟簧端板为硬接触关系。双槽钢单元省略后,为保证支撑受压时的稳定性,同样以非线性弹簧单元沿着核心耗能段两侧间隔均匀布置,作为侧向约束抑制受压时产生的屈曲行为。
钢材采用Q235,屈服强度取285 MPa,采用二折线本构模型,考虑2%的应变强化[19],弹性模量Es=2.06×105 MPa,泊松比为0.3。加载方式以位移控制施加往复荷载,加载幅值为支撑变形率的0.6%、1.0%、1.5%、2%。
3.3 计算结果对比和分析
支撑恢复力模型采用MATLAB进行编程计算。图6为SC-SBRB不同设计参数时,单向受压、受拉作用下的骨架曲线。可以看出,数值模拟结果和恢复力模型计算所得的正、负向三阶段刚度值k1、k2、k3、(
k' _1 、k' _2 、k' _3 )趋势一致且各阶段承载力基本相等。特别地,当复位率α为0时,支撑只表现出后两阶段刚度。数值模拟与恢复力模型计算所得的三阶段刚度对比如表2所示,以定量分析数值模型中省略双槽钢单元的影响。第一阶段受拉刚度k1误差在35%左右,且随着碟簧初始预压力的增大而增大,受压刚度
k'_1 具有同样趋势。误差来源于两个方面,首先,省略双槽钢单元,导致本应传递至远端的部分荷载无法达至,因而支撑拉、压时的总体变形减小,即刚度偏大;其次,有限元分析时,无法忽略各传力单元之间的局部变形,且不同参数条件下局部变形不尽相同,该因素会导致支撑变形偏大,即总体刚度偏小。表 2 SC-SBRB拉压三阶段刚度数值模拟与恢复力模型计算对比Table 2. Comparison of SC-SBRB stiffnesses in first three phases under tension and compression between simulation and restoring force model calculation复位率 刚度k1(k_1')/(kN·mm−1) 刚度k2(k_2' )/(kN·mm−1) 刚度k3(k_3' )/(kN·mm−1) β=1.3 β=2.3 β=1.3 β=2.3 β=1.3 β=2.3 数值
模拟恢复力
模型误差/
(%)数值
模拟恢复力
模型误差/
(%)数值
模拟恢复力
模型误差/
(%)数值
模拟恢复力
模型误差/
(%)数值
模拟恢复力
模型误差/
(%)数值
模拟恢复力
模型误差/
(%)α=0.0 − − − − − − 140.8
(142.2)133.5
(133.5)5.4
(6.5)150.6
(151.5)140.7
(140.7)7.0
(7.6)15.3
(16.3)15.8
(15.8)3.1
(3.1)23.1
(23.8)23.8
(23.8)2.9
(0)α=0.5 1197.1
(1766.4)909.3
(2705.4)31.6
(34.7)1184.8
(1782.1)909.3
(2705.4)30.2
(30.4)141.8
(142.2)6.2
(6.5)149.0
(149.3)5.8
(6.1)15.7
(16.3)0.6
(3.1)23.1
(23.9)2.9
(0.4)α=1.0 1228.4
(1764.3)35.1
(34.8)1214.3
(1707.7)33.5
(36.8)141.7
(141.8)6.1
(6.2)149.1
(149.7)5.9
(6.3)15.5
(16.2)1.8
(2.5)23.0
(23.8)3.3
(0)α=1.5 1285.9
(1605.3)41.4
(40.7)1289.5
(1614.3)41.8
(40.3)141.5
(141.7)5.9
(6.1)148.1
(149.6)5.2
(6.3)15.3
(16.0)3.1
(1.2)22.7
(23.6)4.4
(0.8)本质上,前述两个因素相互影响,以α=1.0、β=1.3设计参数为例,第一刚度范围内理论计算所得支撑受拉变形0.49 mm,受压变形0.14 mm。数值计算时,所有传力单元间的局部变形使受拉变形增大约为0.15 mm,受压变形增大约为0.32 mm。由于省略了外包约束单元,将使受拉、受压变形同时减少约为0.24 mm,因此造成支撑受拉时刚度总体偏大,受压时总体刚度偏小。随着支撑进入至第二刚度k2(
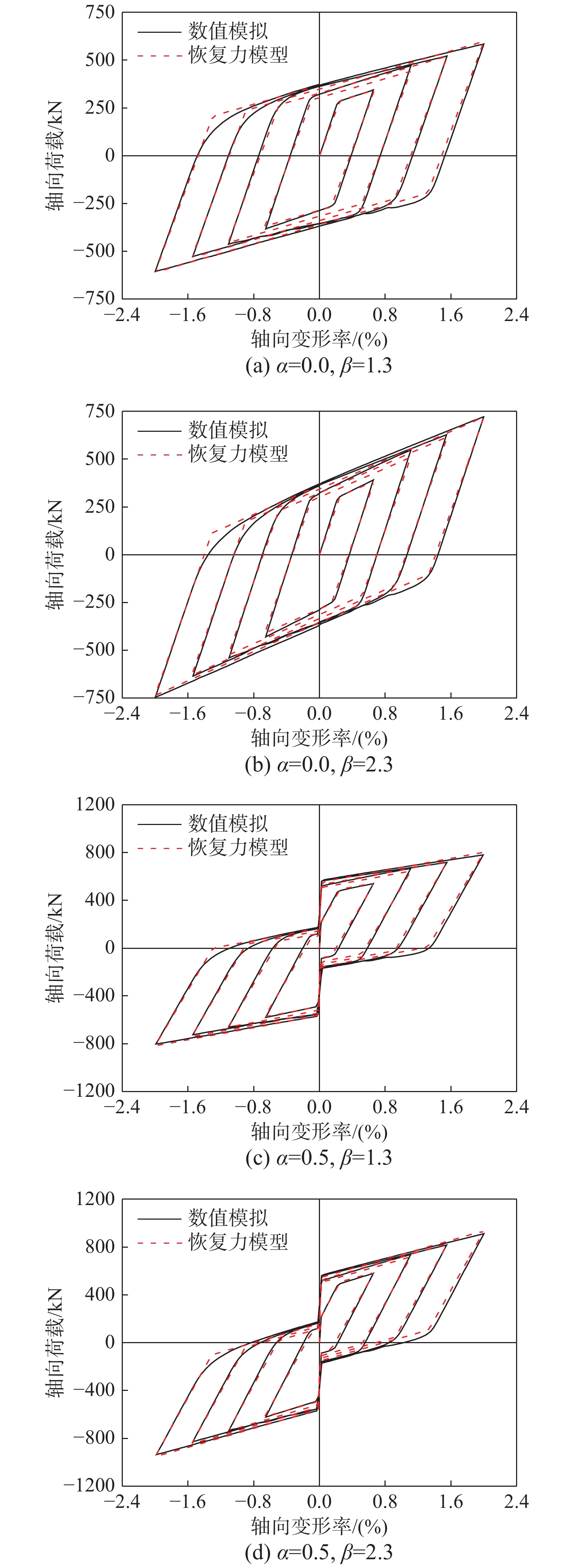
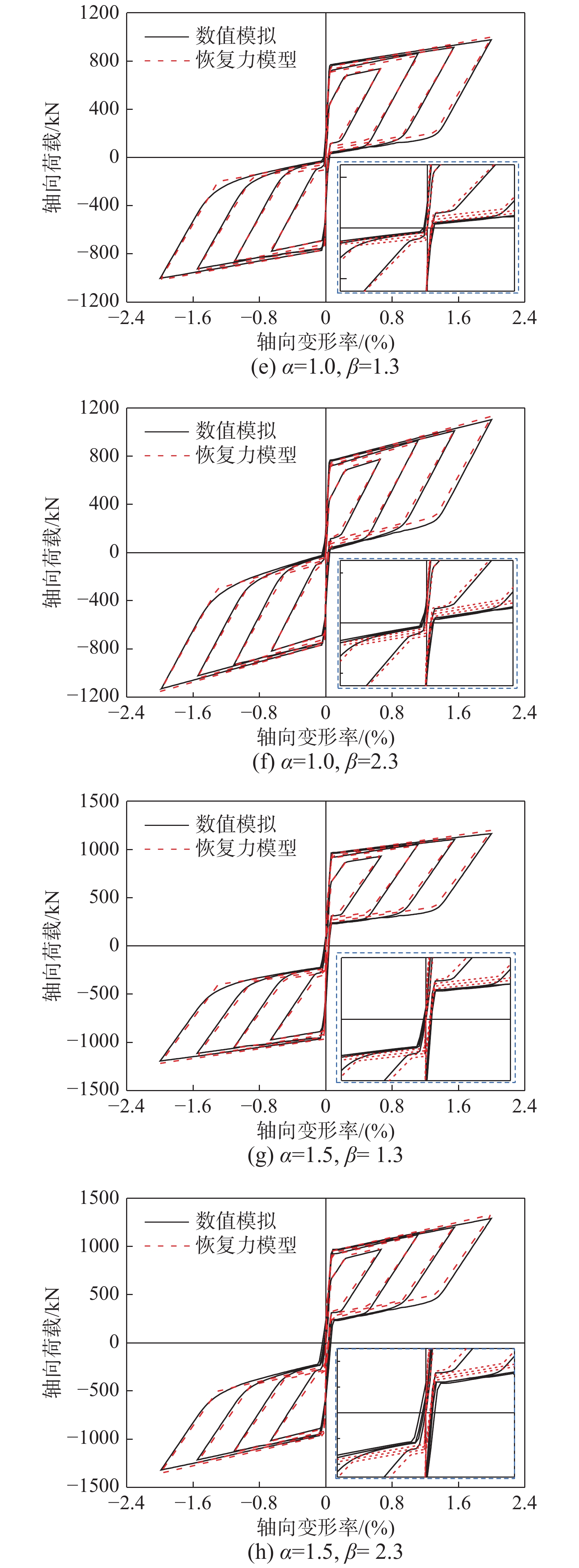
k_2' )后,支撑总体变形有较大幅度增大,误差大幅降低,最大为7.6%。支撑进入第三刚度k3(k'_3 )后,误差进一步降低。由此可见支撑模型的简化对支撑刚度的影响范围有限。图7给出了不同设计参数下,有限元和各阶段恢复力表达式计算所得的支撑滞回响应结果对比。采用恢复力模型计算时,额外考虑了反向加载时的强化效应。由图可知,支撑恢复力模型能够比较准确地预测数值模拟的计算结果。
当复位率α=0时,SC-SBRB直接退化成普通BRB构件,但支撑屈服前后刚度为支撑内核单元屈服前后刚度与碟簧刚度的叠加,并随着参数β的增大而增大。支撑2%变形率时,对应的最大承载力分别为604.8 kN、745.1 kN。
当复位率α=0.5时,已对碟簧施加了一定程度的初始预压力,但不够充分,导致支撑的复位功能不能充分发挥,完全卸载后残余变形很大,对应的最大承载力和残余变形率为801.8 kN和1.33%。当β=2.3时,支撑的最大承载力提高至935.3 kN,同时最大残余变形率减小至1.01%。
当复位率α=1.0时,碟簧施加的初始预压力较为合适,除核心耗能段进入塑性耗能外,支撑内其余单元均保持为弹性。数值模拟结果验证了与恢复力模型计算结果的一致性,包括滞回过程中支撑所经历阶段数、各阶段加、卸载趋势、承载力以及残余变形的大小。当β=1.3时,支撑正、负向最大残余变形率为0.039%和0.017%。支撑的耗能能力和复位性能匹配合理,均得到充分发挥。
当复位率α=1.5时,支撑整体响应与α=1.0类似,但认为碟簧上施加的初始预压力是过大的。支撑受拉克服碟簧初始预压力后,对应一侧的碟簧端板局部已进入了屈服状态,且随着支撑变形率的增大,碟簧进一步压缩,端板上的压力持续累加,塑性变形开始发展。当β=2.3时,其不利影响更为显著,如图8(b),变形率达到2%时,碟簧端板已经屈服并经历了少量塑性变形,端板跨中最大挠度为1.93 mm,且相应的碟簧限位单元(图8(c))在局部应力集中处也进入塑性状态。传力部件的屈服和变形导致残余变形有增大的趋势,支撑的最大残余变形率为0.06%。
图9为支撑各设计参数下的残余变形率。由图可见,无论碟簧初始预压力是否充足,支撑的残余变形率总体上随支撑拉、压变形率的增大而增大;当碟簧初始预压力不足时,即SC-SBRB-1/2,碟簧初始预压力的增大对减小支撑残余变形有明显效果,同样碟簧刚度的增大也可进一步降低支撑残余变形,但对于退化成BRB的SC-SBRB-1而言,其作用有限。当α从0到0.5,β从1.3到2.3时,支撑残余变形率在正、负向的最大降幅可达33.4%和43.6%。
当碟簧的初始预压力适宜时,即SC-SBRB-3,支撑的复位功能得到充分发挥,总体的残余变形已相当小,受拉向略大于受压向,但都远小于文献[9]中0.5%的限值,并与式(6)计算所得的残余变形率相差较小。当β进一步增大时,传力部件之间的弹性变形相应增加,反而导致支撑的残余变形率有所增大。
当碟簧初始预压力已充足时,继续提高α,即支撑SC-SBRB-4,碟簧的高预压力将导致各传力部件之间的变形同时增大,甚至进入塑性变形阶段,不利于支撑复位性能的发挥。对于β=1.3,支撑的残余变形率总体上略小于α=1.0时同等β条件下的值,但效果甚微。从图9(b)又可见,β继续增大所导致的反效果开始显现,各传力单元的相继屈服变形使得支撑残余变形率随支撑变形率的增大而加速增大。
4 结论
本文提出了一种新型自复位全钢型防屈曲支撑,阐释了其基本工作原理,提出了支撑简化力学模型,并建立了支撑的恢复力模型及其主要阶段的恢复力表达式。通过数值模拟对恢复力模型加以验证,对比分析了支撑在不同设计参数下的工作性能和参数影响,得到以下结论:
(1) 数值模拟与各阶段恢复力表达式结果具有一致性,验证了本文所提出的恢复力模型的合理性与正确性。
(2) 支撑单调受拉或受压时,均表现出三个不同阶段的刚度。分别对应于克服碟簧初始预压力的刚度k1(
k' _1 ),核心耗能段受力至屈服与碟簧的并联刚度k2(k' _2 ),核心耗能段屈服后应变强化与碟簧的并联刚度k3(k' _3 )。(3) 碟簧初始预压力不足时,支撑的复位性能随碟簧预压力的增大逐渐得到发挥,相应的残余变形同步减小,效果显著;碟簧预压力充足时,支撑具有饱满的类“旗形”滞回响应,支撑残余变形基本消除,支撑表现出优异的耗能能力和自恢复能力。
(4) 分别增大碟簧预压力和碟簧刚度都可提高支撑整体的承载能力和复位性能,但过度增加,支撑内部传力单元的设计难以匹配,且不经济,传力单元的局部变形甚至塑性变形不利于支撑复位效果,导致残余变形增大。
-
表 1 SC-SBRB设计参数
Table 1 Design parameters of SC-SBRB
支撑编号 核心耗能段
屈服荷载/kN复位率α {k'_{{\rm{BRB}}}} /(kN·mm−1) 刚度比β SC-SBRB-1 260 0.0 4.3 1.3,2.3 SC-SBRB-2 260 0.5 4.3 1.3,2.3 SC-SBRB-3 260 1.0 4.3 1.3,2.3 SC-SBRB-4 260 1.5 4.3 1.3,2.3 表 2 SC-SBRB拉压三阶段刚度数值模拟与恢复力模型计算对比
Table 2 Comparison of SC-SBRB stiffnesses in first three phases under tension and compression between simulation and restoring force model calculation
复位率 刚度k1(k_1')/(kN·mm−1) 刚度k2(k_2' )/(kN·mm−1) 刚度k3(k_3' )/(kN·mm−1) β=1.3 β=2.3 β=1.3 β=2.3 β=1.3 β=2.3 数值
模拟恢复力
模型误差/
(%)数值
模拟恢复力
模型误差/
(%)数值
模拟恢复力
模型误差/
(%)数值
模拟恢复力
模型误差/
(%)数值
模拟恢复力
模型误差/
(%)数值
模拟恢复力
模型误差/
(%)α=0.0 − − − − − − 140.8
(142.2)133.5
(133.5)5.4
(6.5)150.6
(151.5)140.7
(140.7)7.0
(7.6)15.3
(16.3)15.8
(15.8)3.1
(3.1)23.1
(23.8)23.8
(23.8)2.9
(0)α=0.5 1197.1
(1766.4)909.3
(2705.4)31.6
(34.7)1184.8
(1782.1)909.3
(2705.4)30.2
(30.4)141.8
(142.2)6.2
(6.5)149.0
(149.3)5.8
(6.1)15.7
(16.3)0.6
(3.1)23.1
(23.9)2.9
(0.4)α=1.0 1228.4
(1764.3)35.1
(34.8)1214.3
(1707.7)33.5
(36.8)141.7
(141.8)6.1
(6.2)149.1
(149.7)5.9
(6.3)15.5
(16.2)1.8
(2.5)23.0
(23.8)3.3
(0)α=1.5 1285.9
(1605.3)41.4
(40.7)1289.5
(1614.3)41.8
(40.3)141.5
(141.7)5.9
(6.1)148.1
(149.6)5.2
(6.3)15.3
(16.0)3.1
(1.2)22.7
(23.6)4.4
(0.8) -
[1] Black C J, Makris N, Aiken I D. Component testing, seismic evaluation and characterization of buckling-restrained braces [J]. Journal of Structural Engineering, 2004, 130(6): 880 − 894. doi: 10.1061/(ASCE)0733-9445(2004)130:6(880)
[2] Sutcu F, Takeuchi T, Matsui R. Seismic retrofit design method for RC buildings using buckling-restrained braces and steel frames [J]. Journal of Constructional Steel Research, 2014, 101: 304 − 313. doi: 10.1016/j.jcsr.2014.05.023
[3] Fahnestock L A, Ricles J M, Sause R. Experimental evaluation of a large-scale buckling-restrained braced frame [J]. Journal of Structural Engineering, 2007, 133(9): 1205 − 1214. doi: 10.1061/(ASCE)0733-9445(2007)133:9(1205)
[4] 杨青顺, 甄伟, 解琳琳, 陆新征. 耗能伸臂桁架抗震性能的试验研究[J]. 工程力学, 2016, 33(10): 76 − 85. Yang Qingshun, Zhen Wei, Xie Linlin, Lu Xinzheng. Experimental study on the seismic performance of energy dissipation outriggers [J]. Engineering Mechanics, 2016, 33(10): 76 − 85. (in Chinese)
[5] Wu A C, Lin P C, Tsai K C. High-mode buckling responses of buckling-restrained brace core plates [J]. Earthquake Engineering & Structural Dynamics, 2014, 43(3): 375 − 393.
[6] Jiang Z Q, Guo Y L, Tong J Z, et al. Design method of the pinned external integrated buckling-restrained braces with extended core. Part I: theoretical derivation [J]. Journal of Zhejiang University-SCIENCE A, 2015, 16(10): 781 − 792. doi: 10.1631/jzus.A1400325
[7] Sabelli R, Mahin S A, Chang C. Seismic demands on steel braced frame buildings with buckling-restrained braces [J]. Engineering Structures, 2003, 25(5): 655 − 666. doi: 10.1016/S0141-0296(02)00175-X
[8] Takewaki I, Moustafa A, Fujita K. Improving the earthquake resilience of buildings: the worst case approach[M]. London: Springer Science & Business Media, 2012.
[9] Erochko J, Christopoulos C, Tremblay R, et al. Residual drift response of SMRFs and BRB frames in steel buildings designed according to ASCE 7-05 [J]. Journal of Structural Engineering, 2011, 137(5): 589 − 599. doi: 10.1061/(ASCE)ST.1943-541X.0000296
[10] Ghobarah A. Performance-based design in earthquake engineering: state of development [J]. Engineering Structures, 2001, 23(8): 878 − 884. doi: 10.1016/S0141-0296(01)00036-0
[11] Christopoulu C, Tremblay R, Kim H J, et al. Self-centering energy dissipative bracing system for the seismic resistance of structure: development and validation [J]. Journal of Structural Engineering, 2008, 134(1): 96 − 107. doi: 10.1061/(ASCE)0733-9445(2008)134:1(96)
[12] Qiu C, Zhu S. Shake table test and numerical study of self-centering steel frame with SMA braces [J]. Earthquake Engineering & Structural Dynamics, 2017, 46(1): 117 − 137.
[13] Qiu C, Du X. Seismic performance of multistory CBFs with novel recentering energy dissipative braces [J]. Journal of Constructional Steel Research, 2019: 105864. doi: 10.1016/j.jcsr.2019.105864
[14] 徐龙河, 谢行思, 李忠献. 自复位变阻尼耗能支撑的力学原理与性能研究[J]. 工程力学, 2018, 35(1): 201 − 208. Xu Longhe, Xie Xingsi, Li Zhongxian. Mechanics and performance study of self-centering variable damping energy dissipation brace [J]. Engineering Mechanics, 2018, 35(1): 201 − 208. (in Chinese)
[15] 徐龙河, 樊晓伟, 逯登成, 李忠献. 预压弹簧自恢复耗能支撑恢复力模型与滞回特性研究[J]. 工程力学, 2016, 33(10): 116 − 122. Xu Longhe, Fan Xiaowei, Lu Dengcheng, Li Zhongxian. Study on restoring force model and hysteretic behaviors of pre-pressed spring self-centering energy dissipation brace [J]. Engineering Mechanics, 2016, 33(10): 116 − 122. (in Chinese)
[16] Wang H S, Nie X, Pan P. Development of a self-centering buckling restrained brace using cross-anchored pre-stressed steel strands [J]. Journal of Constructional Steel Research, 2017, 138: 621 − 632. doi: 10.1016/j.jcsr.2017.07.017
[17] Eatherton M R, Fahnestock L A, Miller D J. Computational study of self-centering buckling-restrained braced frame seismic performance J]. Earthquake Engineering & Structural Dynamics, 2014, 43(13): 1897―1914.
[18] 徐龙河, 孙雨生, 要世乾, 等. 装配式自复位耗能支撑恢复力模型与试验验证[J]. 工程力学, 2019, 36(6): 119 − 127. Xu Longhe, Sun Yusheng, Yao Shiqian, et al. Restoring force model and experimental verification of an assembled self-centering energy dissipation brace [J]. Engineering Mechanics, 2019, 36(6): 119 − 127. (in Chinese)
[19] Xu L H, Zhang G, Xiao S J, et al. Development and experimental verification of damage controllable energy dissipation beam to column connection [J]. Engineering Structures, 2019, 199: 109660. doi: 10.1016/j.engstruct.2019.109660
-
期刊类型引用(12)
1. 王德斌,王英豪,付兴,孙治国,张昕岳. 新型TDAB力学性能及其在双柱式桥墩减震中的应用. 工程力学. 2025(03): 128-142 .  本站查看
本站查看
2. 徐龙河,黄楚城,谢行思. 自复位支撑钢框架摩擦装配式节点性能研究. 振动工程学报. 2024(07): 1239-1249 .  百度学术
百度学术
3. 刘玮博. 基于ABAQUS对自复位防屈曲支撑简化模型的验证与参数分析. 科技资讯. 2024(16): 131-133 .  百度学术
百度学术
4. 张城,王敦强. 碟簧式自复位防屈曲支撑滞回性能数值模拟. 计算机辅助工程. 2024(03): 57-61 .  百度学术
百度学术
5. 李文鹏,鲁军凯. 碟簧-钢绞线组合自复位防屈曲支撑滞回性能分析. 黑龙江交通科技. 2024(10): 75-80+84 .  百度学术
百度学术
6. 王德斌,何杰,孙治国,王东升. 具有位移放大功能的摩擦自复位支撑及其在双柱式桥墩中的应用. 振动与冲击. 2023(02): 51-59 .  百度学术
百度学术
7. 马立成,史庆轩,王秋维,王斌. 预压碟簧自复位装配式混凝土梁柱节点滞回特性研究. 建筑结构学报. 2023(03): 70-78 .  百度学术
百度学术
8. 胡宝琳,徐世安,徐庆,吴仁杰. 三阶屈服屈曲约束支撑耗能机理及设计方法研究. 工程力学. 2023(08): 105-114 .  本站查看
本站查看
9. 丁振坤,胡宝琳,田华,胡吴彪,闵昱钧,徐世安. 核岛钢平台支撑框架抗震性能试验对比及支撑优化布置研究. 振动与冲击. 2023(22): 60-70 .  百度学术
百度学术
10. 王涛,侯明珠,孟丽岩,钱悦. 支撑自复位能力对框架节点受力性能的影响. 黑龙江科技大学学报. 2022(03): 301-305 .  百度学术
百度学术
11. 金双双,李盈开,周建庭,杜轲,白久林. 全装配式自复位防屈曲支撑滞回模型及其性能试验研究. 工程力学. 2022(07): 49-57 .  本站查看
本站查看
12. 吴山,何浩祥,兰炳稷,陈建伟. 分级屈服型金属套管阻尼器减震理论与试验研究. 工程力学. 2022(07): 147-157 .  本站查看
本站查看
其他类型引用(13)



 下载:
下载: