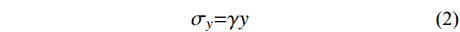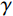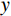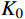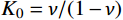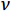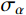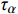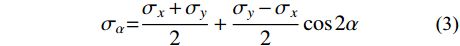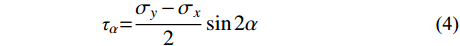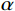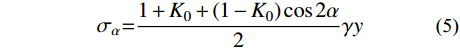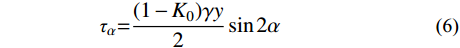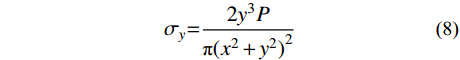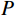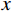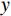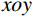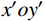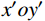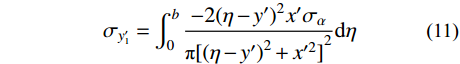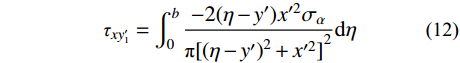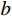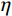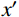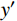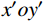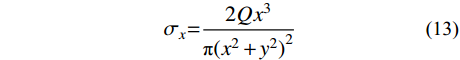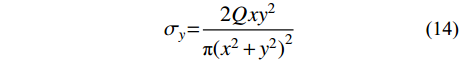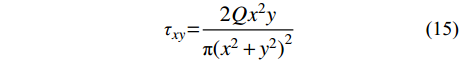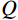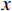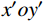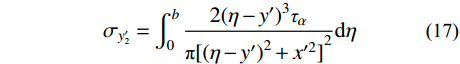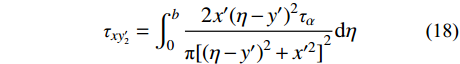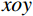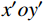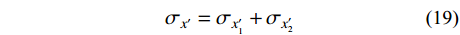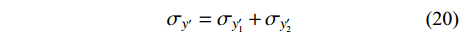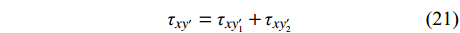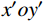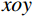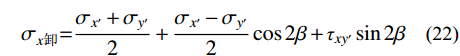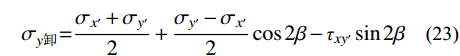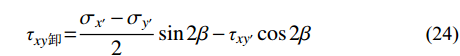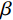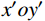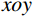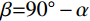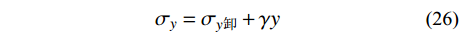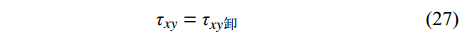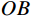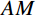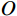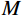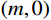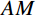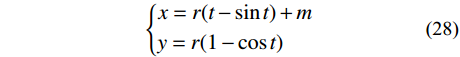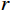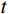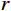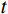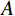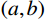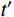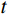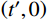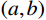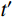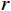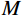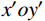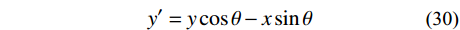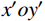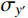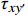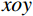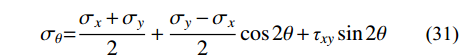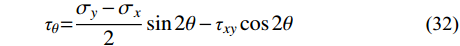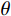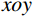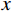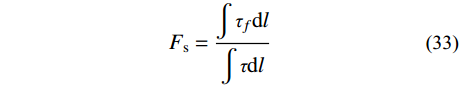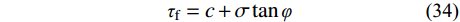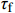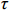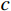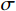基于坡面卸荷的土质边坡应力状态及稳定性分析

杨奎斌; 朱彦鹏

doi:10.6052/j.issn.1000-4750.2020.10.0753

基于坡面卸荷的土质边坡应力状态及稳定性分析

杨奎斌^{1, 2, ,},
朱彦鹏^{1, 2,}

1.
兰州理工大学土木工程学院，甘肃，兰州 730050
2.
西部土木工程防灾减灾教育部工程研究中心，甘肃，兰州 730050

基金项目: 国家自然科学基金面上项目(51978321)；教育部长江学者和创新团队支持计划项目(IRT_17R51)

详细信息

作者简介:
朱彦鹏(1960−)，男，甘肃人，教授，硕士，博导，从事岩土与结构相互作用、工程事故分析与处理研究(E-mail: zhuyp1@163.cn)

通讯作者:
杨奎斌(1993−)，男，陕西人，博士生，从事边坡稳定性研究(E-mail: ykbin93@163.com)

中图分类号: U213.1+3
计量
- 文章访问数: 636
- HTML全文浏览量: 206
- PDF下载量: 109
出版历程
- 收稿日期: 2020-10-19
- 修回日期: 2021-01-04
- 网络出版日期: 2021-01-20
- 刊出日期: 2021-11-17

SOIL SLOPE STRESS STATE AND STABILITY ANALYSIS BASED ON UNLOADING EFFECT OF SLOPE SURFACES

YANG Kui-bin^{1, 2, ,},
ZHU Yan-peng^{1, 2,}

1.
School of Civil Engineering, Lanzhou University of Technology, Lanzhou, Gansu 730050, China
2.
Western Engineering Research Center of Disaster Mitigation in Civil Engineering of Ministry of Education, Lanzhou, Gansu 730050, China

摘要

摘要: 边坡稳定性分析中极限平衡法难以考虑土体应力状态，坡体滑面应力计算又长期停留在数值方法上。为解决这一问题，提出坡面卸荷应力等效思路，将坡面按半无限边界考虑后利用弹性理论求解坡体应力，并根据滑面应力进行稳定性安全系数计算，最后结合多个算例将潜在滑动面位置、滑面应力分布、安全系数与已有理论进行比较。研究结果表明：坡面卸荷应力等效思路概念清晰，符合边坡受力特征，且通过该思路求得的滑面应力与有限元分计算结果基本一致，搜索得到的潜在滑动面位置，以及对应的稳定性安全系数与有限元强度折减法、极限平衡法计算结果十分接近。此外，该计算方法还能有效与支护结构预应力结合，体现预应力的加固作用。
- 边坡 /
- 坡面卸荷 /
- 稳定性分析 /
- 潜在滑动面 /
- 安全系数
Abstract: In the limit equilibrium method for slope stability analysis, it is difficult to consider the stress state of the soil and the calculation of slope sliding surface stress has relied on the finite element numerical method for a long time. To solve this problem, the idea of slope surface unloading and equivalent stress is proposed. After considering the slope surface as a semi-infinite boundary, the slope stress is solved by the elastic theory. Then the stability safety factor is calculated according to the slip surface stress. Finally, the position of the potential sliding surface, the stress distribution of the sliding surface and the safety factor are compared with the existing theories based on the several example. The research results show that the concept of slope surface unloading and equivalent stress is clear and conforms to the slope force characteristics. The sliding surface stress obtained by this method is basically consistent with the finite element calculation results. The searched potential sliding surface position and the corresponding stability safety factor are very close to the finite element strength reduction method and the limit equilibrium method calculation results. In addition, the calculation method can be effectively combined with prestressed support structures, reflecting the reinforcing effect of prestressing.
- slope /
- slope surface unloading /
- stability analysis /
- potential sliding surface /
- safety factor

HTML全文

边坡稳定性分析是土力学中的经典问题之一，而坡体应力状态作为影响边坡稳定性的一个重要因素，长期以来备受专家学者关注。卢应发等^[1]根据坡体变形和力的传递特征，认为边坡滑面在不同位置表现出不同的应力状态特征；苏杭等^[2]基于边坡施工后坡体位移的相对变化趋势，给出了边坡开挖松弛区和预压区的明确定义；王浩等^[3]解释了路堑高边坡开挖卸荷松弛的力学机理，模拟重现了边坡失稳破坏阶段的全过程应力调整规律及发展趋势；冷伍明等^[4]、艾希等^[5]为有效改善路堤填土应力状态，提出了一种新型预应力路基结构，并分析了坡面法向、水平向附加应力扩散规律；李丽华等^[6]对废旧轮胎加筋路堤边坡进行模型试验，认为轮胎加筋可显著改变坡体应力状态，有利于增强边坡稳定性；陈金锋和宋二祥^[7]在山区机场高填方边坡建设中提出了单级反压护道的优化设计方法，其理念实质也是通过反压改变坡体受力状态，进而提高边坡稳定性。由此可见，无论是边坡开挖卸荷还是支护加载，均与坡体应力重分布密切相关，基于应力状态对边坡稳定性进行研究很有实际意义。

在现有边坡稳定分析方法中，利用条分法建立的极限平衡理论最早产生，根据条间力假设的不同，相继又有多种不同方法被提出，这些方法概念清晰、计算简便，在工程中被广泛应用，然而刚性土条假设无法反映坡体应力场分布情况，且条间力假设所产生的分析误差始终难以避免。为解决这一问题，部分学者在不引入条间力的情况下，取整个滑体为研究对象，并基于滑面应力假设和修正建立平衡方程进行安全系数求解^[8-12]。与此同时，一些学者还借助数值软件获取坡体真实应力场，进而根据滑面应力进行边坡稳定性分析。其中邵龙潭等^[13]基于有限元滑面应力分析法对重力式挡土墙进行研究，搜索确定了最危险滑动面和对应的安全系数；吴顺川等^[14]根据滑面应力状态提出了边坡安全系数新解法，能够有效解决非等比强度折减方案中边坡稳定性评价指标的确定；张海涛等^[15]给出了矢量和的滑面应力抗滑稳定分析新思路以及矢量和形式的安全系数；李忠等^[16-17]通过建立边坡非线性有限元计算模型，提出了基于滑面应力控制的边坡主动加固计算方法，并将有限元计算与多种群遗传算法结合，建立了一种基于MPGA的复杂应力状态边坡稳定性分析通用模型；Stianson等^[18]利用有限元所得应力对边坡稳定性进行研究，总结了土体泊松比和弹性模量对稳定性安全系数的影响规律；Liu等^[19]将有限元应力场用于多种不同类型边坡，进一步拓宽其在边坡稳定性分析中的适用性。显然，以上这些方法为边坡稳定性研究提供了很好的思路，但利用条分法建立的极限平衡理论始终难以考虑土体应力状态，坡体滑面应力计算又长期停留在数值方法上。

为了有效获取坡体应力状态，本文基于坡面卸荷应力等效思路，将边坡视为水平地面经开挖后形成的坡体，并利用弹性理论对坡内土体任一点进行应力求解，进而根据滑面应力计算边坡稳定性安全系数，最后结合多个算例对潜在滑动面位置及稳定性安全系数进行比较来验证其合理性。

1 坡面卸荷应力等效分析思路

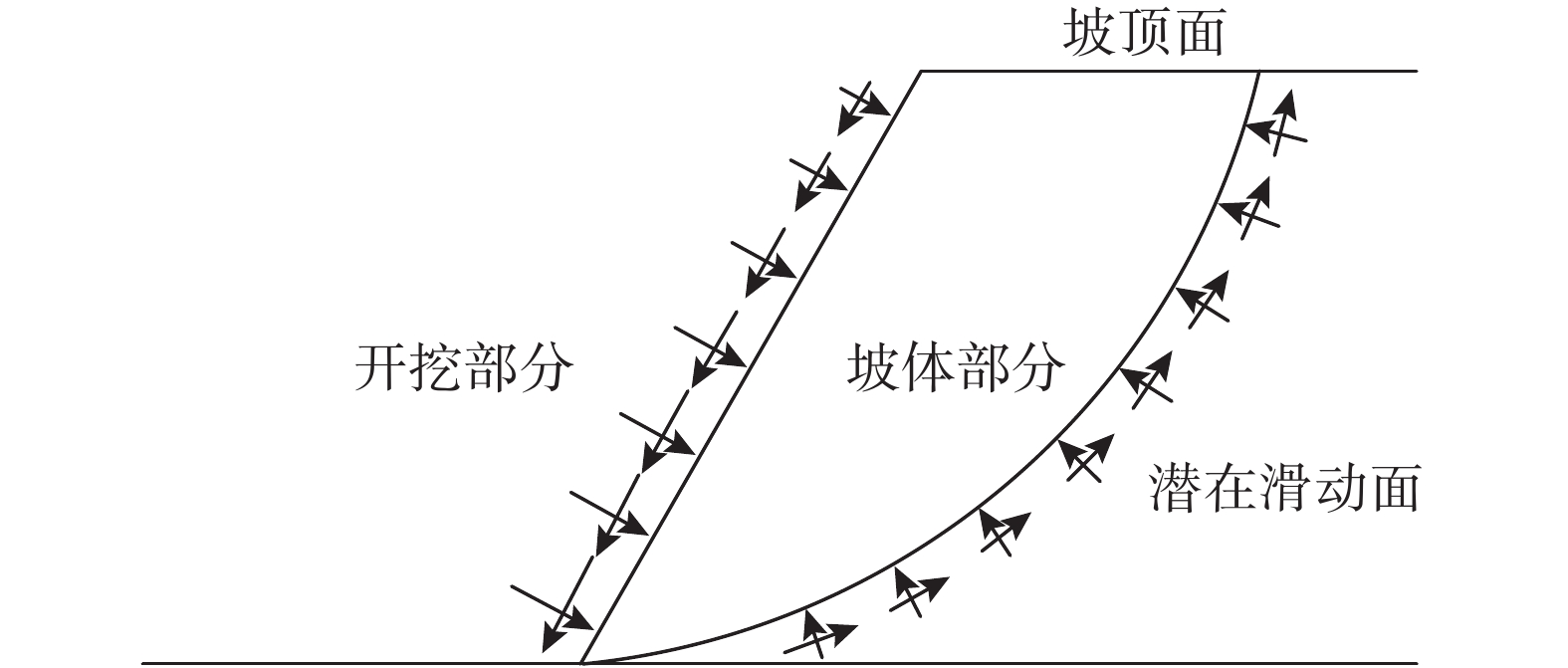
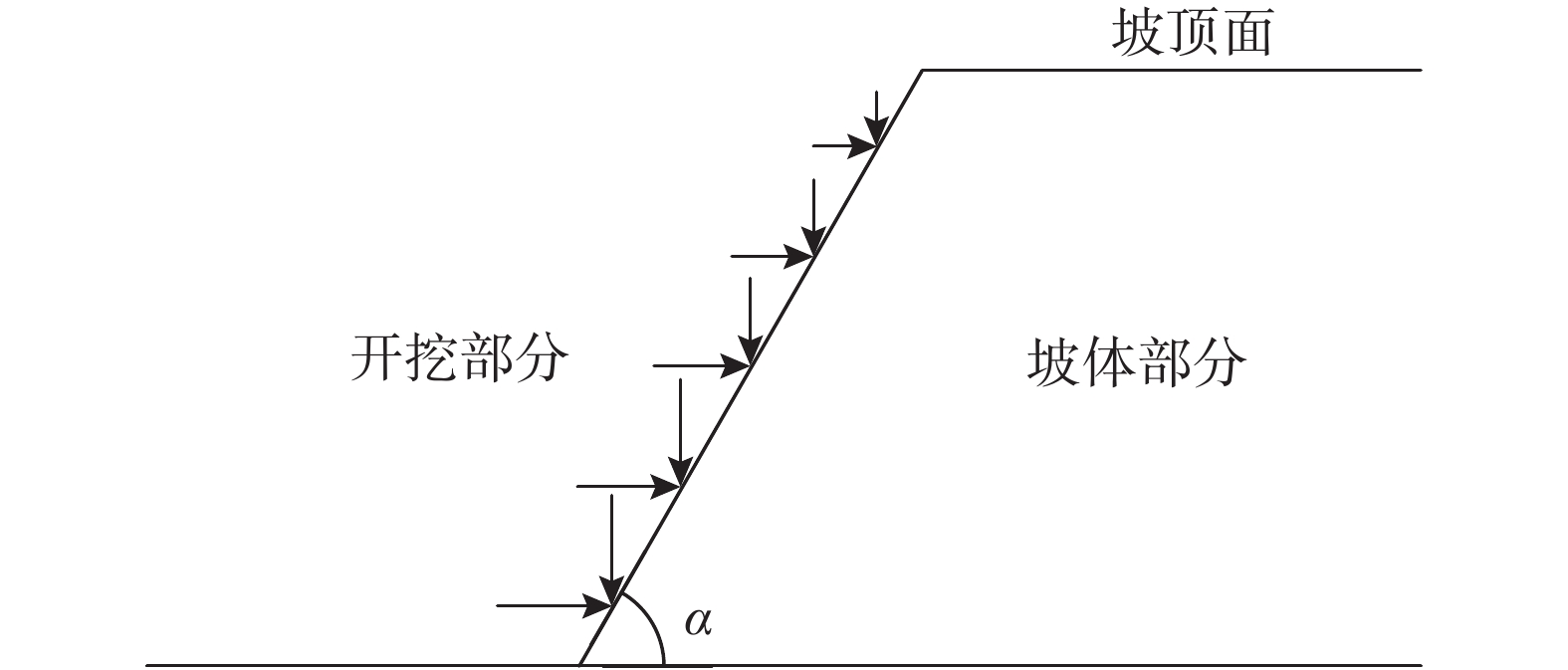
具有一定高度和坡度，存在临空面的坡体，可以将其认为是自然水平地面经开挖后形成的斜坡。当开挖部分挖除卸荷后，原本作用在坡面上的应力将得到释放，所以坡体内任一点应力由两部分组成：一部分是开挖前自然水平地面所对应的竖向自重应力和水平自重应力；另一部分则是卸荷引起的应力改变量。

需要说明的是，坡面卸荷是一个应力释放、应力重分布过程，在坡面处的卸荷等效应该采用应力等效，而非荷载等效，如图1所示。后者被苏联专家弗洛林 B·A^[20]在《土力学原理(第一卷)》中提到，笔者认为两者在本质上存在不同，应力等效较荷载等效更为合理。

图 1 坡面卸荷应力等效示意图

Figure 1. Stress equivalent diagram of slope unloading

下载: 全尺寸图片幻灯片

坡面上任一点竖向和水平向卸荷应力可根据土力学按深度求得，其中均质土按下式计算，成层土则进一步考虑每层土性质。

${\sigma _x}{\rm{ = }}{K_0}\gamma y$

(1)

${\sigma _y}{\rm{ = }}\gamma y\quad$

(2)

式中： $\gamma$ 为土体重度； $y$ 为坡顶面以下深度； ${K_0}$ 为土的侧压力系数，理论上有 ${K_0} = \nu /(1 - \nu )$ ， $\nu$ 为土的泊松比。

为方便计算，取坡面土单元进行受力分析时，可将卸荷等效应力转换为作用于坡面的法向应力 ${\sigma _{\alpha} }$ 和切向应力 ${\tau _{\alpha} }$ ，其沿坡面分布如图2所示。

${\sigma _{\alpha} }{\rm{ = }}\frac{{{\sigma _x} + {\sigma _y}}}{2} + \frac{{{\sigma _y} - {\sigma _x}}}{2}\cos 2\alpha$

(3)

${\tau _{\alpha} }{\rm{ = }}\frac{{{\sigma _y} - {\sigma _x}}}{2}\sin 2\alpha \qquad\qquad\quad$

(4)

式中， $\alpha$ 为边坡坡度。

图 2 坡面等效应力分布

Figure 2. Equivalent stress distribution of slope surface

下载: 全尺寸图片幻灯片

显然，只要计算出图2中坡面卸荷应力对坡体内应力的改变量，即可获得重分布后的坡体应力场，进而以此得到潜在滑动面上的应力状态。

2 坡体内一点应力计算

对于二维边坡而言，可以将其视为平面应变问题，这样在进行坡面卸荷应力释放量计算时，能够将坡面按弹性半无限边界考虑，并采用弹性理论进行附加应力积分处理，具体计算过程如下。

2.1 计算模型与参数

根据式(1)~式(4)可将坡面线上任一点切向力和法向力简化如下：

${\sigma _{\alpha} }{\rm{ = }}\frac{{1 + {K_0} + (1 - {K_0})\cos 2\alpha }}{2}\gamma y$

(5)

${\tau _{\alpha} }{\rm{ = }}\frac{{(1 - {K_0})\gamma y}}{2}\sin 2\alpha\qquad\qquad$

(6)

2.2 坡面法向卸荷应力作用下的附加应力

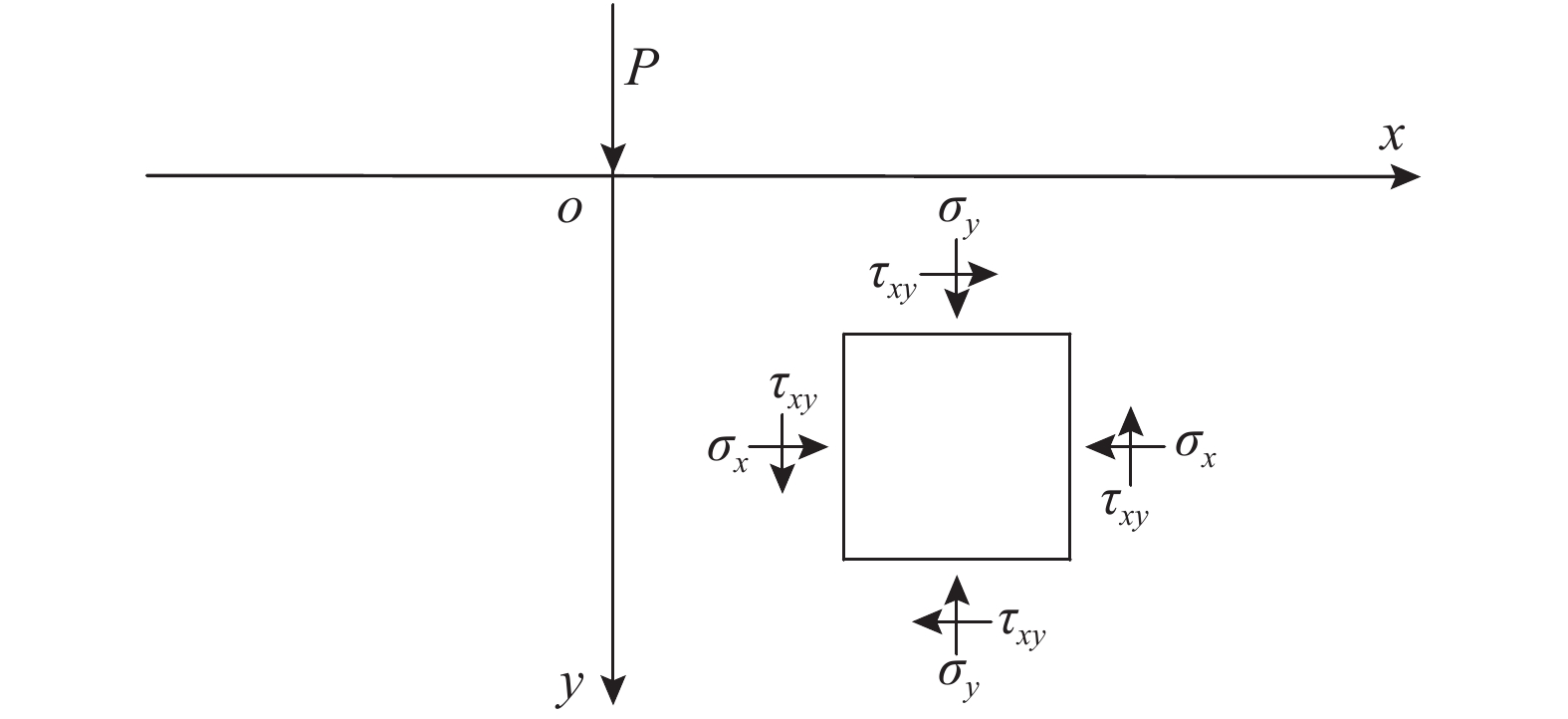
本文以压应力为正，剪应力则以使单元体逆时针旋转为正，反之为负，半无限体在边界上受法向集中力时如图3所示。

图 3 半无限体边界受法向集中力

Figure 3. Normal force on boundary of semi-infinite body

下载: 全尺寸图片幻灯片

图3中任一点附加应力计算公式可根据弹性半无限体在边界上受法向集中力作用的Boussinesq解^[21]在无限长范围内积分得到的Flamant解^[22]确定，也可利用楔形体楔顶受集中荷载作用的弹性应力解^[23]确定：

${\sigma _x}{\rm{ = }}\frac{{2{x^2}yP}}{{{\rm{\pi }}{{({x^2} + {y^2})}^2}}}$

(7)

${\sigma _y}{\rm{ = }}\frac{{2{y^3}P}}{{{\rm{\pi }}{{({x^2} + {y^2})}^2}}}$

(8)

${\tau _{xy}}{\rm{ = }}\frac{{2x{y^2}P}}{{{\rm{\pi }}{{({x^2} + {y^2})}^2}}}$

(9)

式中： $P$ 为法向集中力； $x$ 、 $y$ 分别为半无限体内一点距法向集中力作用点的水平、竖向距离。

为方便表示坡体内应力以及进行坡面附加应力计算，以坡顶为坐标原点分别建立 $xoy$ 和 ${x'}o{y'}$ 平面直角坐标系，如图4所示。

图 4 坡面受法向应力作用分析模型

Figure 4. Analysis model of normal stress on slope surface

下载: 全尺寸图片幻灯片

在 ${x'}o{y'}$ 坐标系下对式(7)~式(9)进行坡面范围内积分，可得坡面法向卸荷应力作用下坡体内附加应力值，具体求解根据积分式采用MATLAB中的int函数进行。

${\sigma _{x_1'}} = \int_0^b {\frac{{ - 2{x^{\prime 3}}{\sigma _{\alpha} }}}{{{\rm{\pi }}{{[ {{{(\eta - {y'})}^2} + {x^{\prime 2}}} ]}^2}}}} {\rm d}\eta$

(10)

${\sigma _{y_1'}} = \int_0^b {\frac{{ - 2{{(\eta - {y'})}^2}{x'}{\sigma _{\alpha} }}}{{{\rm{\pi }}{{[ {{{(\eta - {y'})}^2} + {x^{\prime 2}}} ]}^2}}}} {\rm d}\eta$

(11)

${\tau _{xy_1'}} = \int_0^b {\frac{{ - 2(\eta - {y'}){x^{\prime 2}}{\sigma _{\alpha} }}}{{{\rm{\pi }}{{[ {{{(\eta - {y'})}^2} + {x^{\prime 2}}}]}^2}}}} {\rm d}\eta$

(12)

式中： $b$ 为坐标原点至坡脚的距离； $\eta$ 为坡面任一法向应力作用点至坐标原点的距离； ${x'}$ 、 ${y'}$ 为 ${x'}o{y'}$ 坐标系内任一点坐标。

2.3 坡面切向卸荷应力作用下的附加应力

同理，半无限体在边界上受切向集中力时如图5所示，任一点的应力计算公式为^[23]：

${\sigma _x}{\rm{ = }}\frac{{2Q{x^3}}}{{{\rm{\pi }}{{({x^2} + {y^2})}^2}}}$

(13)

${\sigma _y}{\rm{ = }}\frac{{2Qx{y^2}}}{{{\rm{\pi }}{{({x^2} + {y^2})}^2}}}$

(14)

${\tau _{xy}}{\rm{ = }}\frac{{2Q{x^2}y}}{{{\rm{\pi }}{{({x^2} + {y^2})}^2}}}$

(15)

式中： $Q$ 为切向集中力； $x$ 、 $y$ 分别为半无限体内一点距切向集中力作用点的水平、竖向距离。

图 5 半无限体边界受切向集中力

Figure 5. Tangential force on boundary of semi-infinite body

下载: 全尺寸图片幻灯片

坡面受切向力作用分析模型如图6所示，在 ${x'}o{y'}$ 坐标系下对式(13)~式(15)进行坡面范围内积分，可得到坡面切向卸荷应力作用下坡体内任一点应力附加值，具体求解根据积分式采用MATLAB中的int函数进行。

${\sigma _{x_2'}} = \int_0^b {\frac{{2{x'}^2(\eta - {y'}){\tau _{\alpha} }}}{{{\rm{\pi }}{{[ {{{(\eta - {y'})}^2} + {x^{\prime 2}}} ]}^2}}}} {\rm d}\eta$

(16)

${\sigma _{y_2'}} = \int_0^b {\frac{{2{{(\eta - {y'})}^3}{\tau _{\alpha} }}}{{{\rm{\pi }}{{[ {{{(\eta - {y'})}^2} + {x^{\prime 2}}} ]}^2}}}} {\rm d}\eta$

(17)

${\tau _{xy_2'}} = \int_0^b {\frac{{2{x'}{{(\eta - {y'})}^2}{\tau _{\alpha} }}}{{{\rm{\pi }}{{[ {{{(\eta - {y'})}^2} + {x^{\prime 2}}} ]}^2}}}} {\rm d}\eta$

(18)

图 6 坡面受切向应力作用分析模型

Figure 6. Analysis model of tangential stress on slope surface

下载: 全尺寸图片幻灯片

2.4 $xoy$ 坐标系内坡体应力转化

在 ${x'}o{y'}$ 坐标系内，坡体内任一点卸荷应力改变量为坡面法向、切向卸荷应力所引起的附加应力之和。

${\sigma _{{x'}}} = {\sigma _{x_{_1}'}} + {\sigma _{x_2'}}$

(19)

${\sigma _{{y'}}} = {\sigma _{y_1'}} + {\sigma _{y_2'}}$

(20)

${\tau _{x{y'}}} = {\tau _{xy_1'}} + {\tau _{xy_2'}}$

(21)

通过对坡体内土单元进行受力分析，可以将 ${x'}o{y'}$ 坐标系内计算得到的卸荷应力改变量按下式转化至 $xoy$ 坐标系内。

${\sigma _{x{\text{卸}}}}{\rm{ = }}\frac{{{\sigma _{{x'}}} + {\sigma _{{y'}}}}}{2} + \frac{{{\sigma _{{x'}}} - {\sigma _{{y'}}}}}{2}\cos 2\beta + {\tau _{x{y'}}}\sin 2\beta$

(22)

${\sigma _{y{\text{卸}}}}{\rm{ = }}\frac{{{\sigma _{{x'}}} + {\sigma _{{y'}}}}}{2} + \frac{{{\sigma _{{y'}}} - {\sigma _{{x'}}}}}{2}\cos 2\beta - {\tau _{x{y'}}}\sin 2\beta$

(23)

${\tau _{xy{\text{卸}}}}{\rm{ = }}\frac{{{\sigma _{x'}} - {\sigma _{y'}}}}{2}\sin 2\beta - {\tau _{x{y'}}}\cos 2\beta \qquad\qquad\;\;$

(24)

式中， $\beta$ 为 ${x'}o{y'}$ 坐标系与 $xoy$ 坐标系之间的夹角，根据几何关系易知 $\beta {\rm{ = }}90^{\circ} - \alpha$ 。

综上，坡体内任一点应力为卸荷应力改变量与卸荷前土体应力之和：

${\sigma }_{x}={\sigma }_{x{\text{卸}}}+{K}_{0}\gamma y$

(25)

${\sigma }_{y}={\sigma }_{y{\text{卸}}}+\gamma y\quad\;$

(26)

${\tau }_{xy}={\tau }_{xy{\text{卸}}}\qquad\quad\;$

(27)

3 稳定性分析方法

3.1 潜在滑动面形式选择

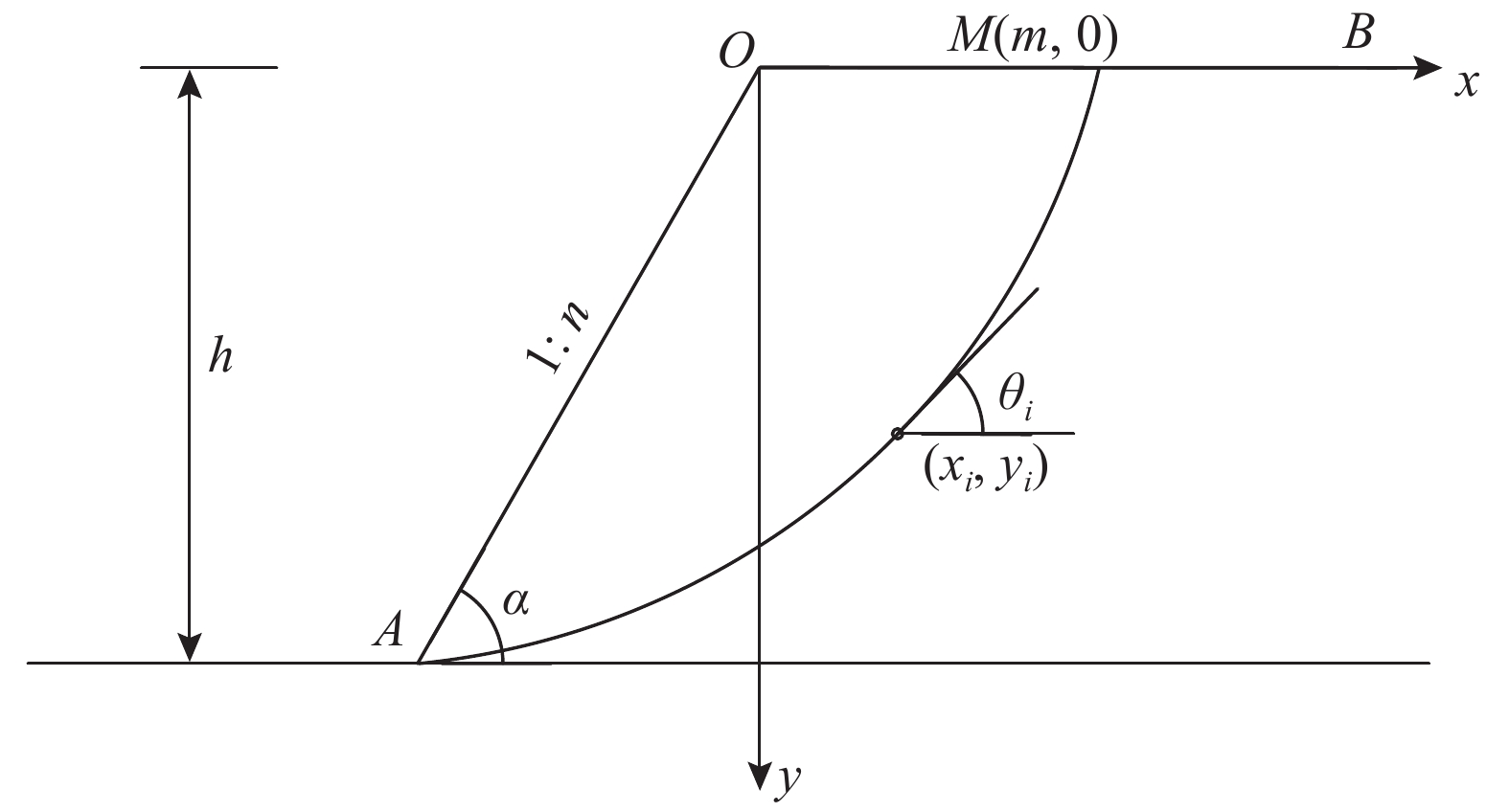
通过对圆弧、对数螺旋线等现有潜在滑动面曲线形式，以及相应搜索方法的比较，笔者提出了搜索量小，易于编程，且具有一定物理意义的最速降线形滑动面，由于篇幅有限，在此不再赘述，具体搜索模型如图7所示。

图 7 边坡潜在滑动面搜索模型简图

Figure 7. Sketch of searching model for potential sliding surface of slope

下载: 全尺寸图片幻灯片

图7中线段 $OA$ 、 $OB$ 为边坡表面，曲线 $AM$ 为最速降线滑动面，以点 $O$ 为坐标系原点，当 $M$ 点的坐标为 $\left( {m,0} \right)$ 时，潜在滑动面曲线 $AM$ 的参数方程如下：

$\left\{ \begin{aligned} & x = r(t - \sin t) + m \\& y = r(1 - \cos t) \end{aligned} \right.$

(28)

式中： $r$ 为最速降线对应的旋转圆半径； $t$ 为旋转圆转动经过的角度。

显然，要确定最速降线滑动面参数方程需要求得 $r$ ，以及自变量 $t$ 的取值范围，其求解过程如下：

1) 将滑出位置 $A$ 点坐标 $\left( {a,b} \right)$ 代入滑动面参数方程可求得滑出点处自变量的边界值 ${t'}$ ，由此得出自变量 $t$ 的取值范围为 $\left( {{t'},0} \right)$ 。

2) 再将滑出点坐标 $\left( {a,b} \right)$ 及滑出点处自变量的边界值 ${t'}$ 代入参数方程，即可求得 $r$ 值。

搜索过程中，假定滑动面经过坡脚，由此便可通过移动 $M$ 点位置进行潜在滑动面搜索。

3.2 滑面应力计算

由滑动面曲线方程得到滑面坐标后，经以下变换方程将其转换至 ${x'}o{y'}$ 坐标系内。

${x'} = x\cos \theta + y\sin \theta$

(29)

${y'} = y\cos \theta - x\sin \theta$

(30)

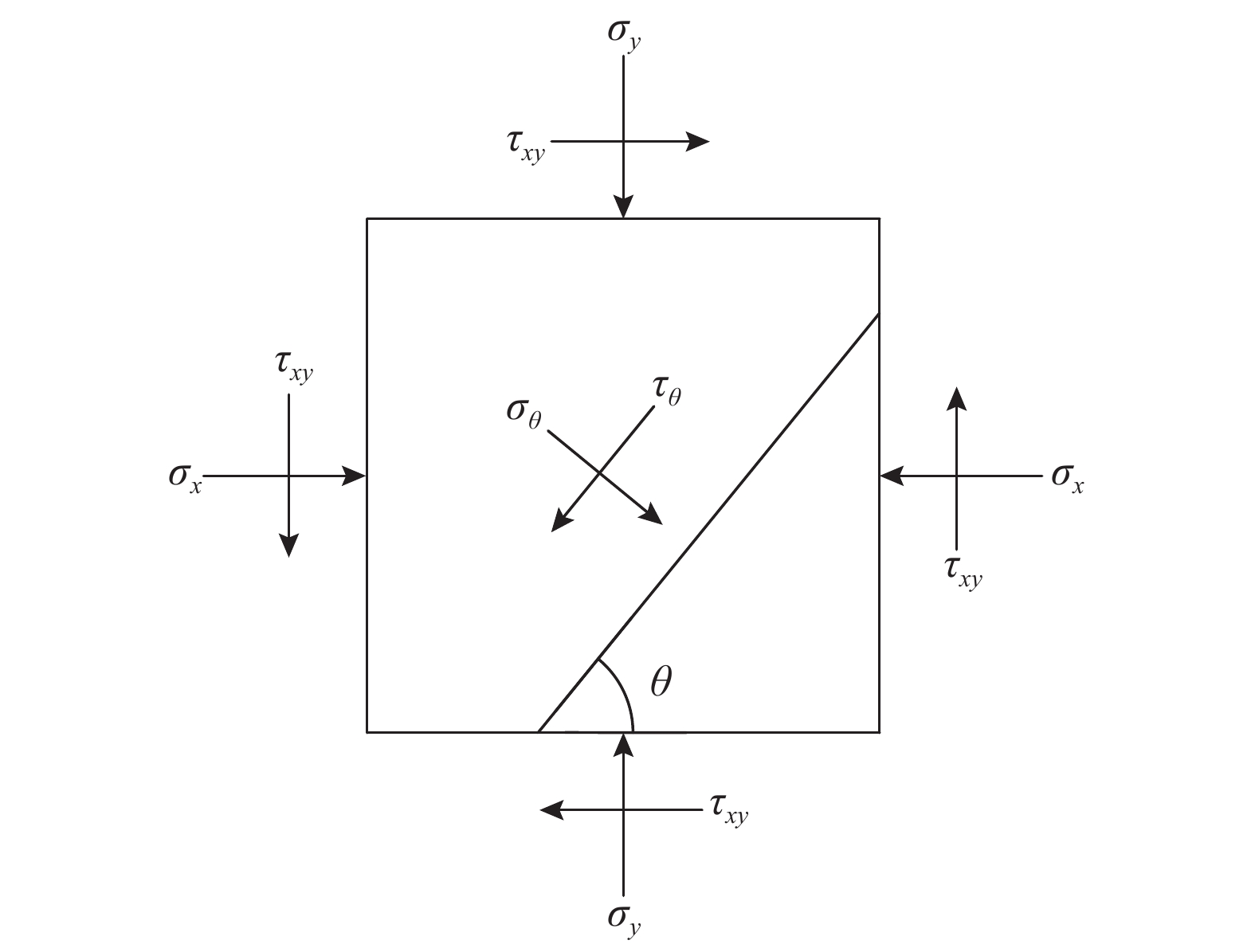
然后，在 ${x'}o{y'}$ 坐标系内计算卸荷应力改变量 ${\sigma _{{x'}}}$ 、 ${\sigma _{{y'}}}$ 和 ${\tau _{x{y'}}}$ ，并按式(22)~式(27)得到 $xoy$ 坐标系内滑面应力状态，再取滑面土体单元进行受力分析，如图8所示，可求得滑面上任一点法向、切向应力如下：

图 8 滑面单元应力分析模型

Figure 8. Analysis model of stress on an element of slip surface

下载: 全尺寸图片幻灯片

${\sigma _\theta }{\rm{ = }}\frac{{{\sigma _x} + {\sigma _y}}}{2} + \frac{{{\sigma _y} - {\sigma _x}}}{2}\cos 2\theta + {\tau _{xy}}\sin 2\theta$

(31)

${\tau _\theta }{\rm{ = }}\frac{{{\sigma _y} - {\sigma _x}}}{2}\sin 2\theta - {\tau _{xy}}\cos 2\theta \qquad\qquad\;\;$

(32)

式中， $\theta$ 为 $xoy$ 坐标系内滑动面切线与 $x$ 轴夹角。

3.3 安全系数计算

得到滑面法向应力和切向应力后，可根据滑面土体抗剪强度和实际剪应力求解对应的安全系数。

${F_{\rm{s}}} = \frac{{\displaystyle \int {{\tau _f}{\rm d}l} }}{{\displaystyle \int {\tau {\rm d}l} }}\quad$

(33)

${\tau _{\rm f}} = c + \sigma \tan \varphi$

(34)

式中： ${\tau _{\rm f}}$ 为土体抗剪强度； $\tau$ 为实际剪应力； $c$ 为粘聚力； $\sigma$ 为滑面法向应力； $\varphi$ 为土的内摩擦角。

4 算例分析

4.1 未支护均质土坡

4.1.1 算例概况

为说明坡面卸荷应力等效思路在边坡稳定性分析中的可行性，选用多个文献[24-26]中均用到的一个经典边坡算例进行分析比较，边坡高度20 m，坡度为45°。这里为便于观察比较，取坡脚处为坐标原点，滑面应力计算仍按2.2节和2.3节坐标系进行，具体计算模型如图9所示，岩土材料参数如表1所示。

图 9 算例1的边坡尺寸　/m

Figure 9. Slope size of classical Model 1

下载: 全尺寸图片幻灯片

表 1 算例1的材料参数

Table 1. Material parameters of Model 1

重度γ/(kN/m³)	黏聚力c/kPa	内摩擦角φ/(°)	弹性模量E/kPa	泊松比ν
20	42	17	100 000	0.3

下载: 导出CSV

| 显示表格

4.1.2 滑动面位置及安全系数比较

借助MATLAB编制计算程序，实现沿坡顶面移动滑入点位置进行滑动面搜索，最终寻找出最小安全系数对应的潜在滑动面，经搜索得到安全系数随滑入点位置变化情况，如图10所示。

从图10中可以看出，当滑入点距坡顶边缘8 m左右时安全系数最小，通过进一步提高搜索精度，得到边坡潜在滑动面滑入点位置为(27.7，20)，稳定性安全系数为1.148。

图 10 安全系数与搜索位置关系曲线

Figure 10. Relationship curve between safety factor and search location

下载: 全尺寸图片幻灯片

与此同时，为验证计算结果的合理性，将其与已有文献和极限平衡法相应结果进行比较，其中潜在滑动面位置比较如图11所示，稳定性安全系数对比如表2所示。

图 11 不同方法潜在滑动面位置比较

Figure 11. Comparison of potential sliding surface positions obtained by different methods

下载: 全尺寸图片幻灯片

表 2 不同计算方法所得安全系数对比

Table 2. Comparison of safety factor from different calculating methods

计算方法	滑入点距坡顶边缘距离/m	安全系数
郑颖人等^[24]/强度折减法	−	1.20~1.40
赵尚毅等^[25]/强度折减法	−	1.12或1.36
裴利剑等^[26]/强度折减法	−	1.16~1.20
圆弧/极限平衡法	9.0	1.244
最速降线/极限平衡法	8.7	1.220
最速降线/本文	7.7	1.148

下载: 导出CSV

| 显示表格

结合图11和表2可以看出，基于坡面卸荷应力等效思路所得结果与传统方法计算结果基本一致，其中潜在滑动面位置吻合度较好，滑入点较极限平衡法所得位置略有前移。稳定性安全系数方面，较已有文献以及极限平衡法结果略微偏小，分析认为有以下几点原因：

1)坡体内应力求解时将坡面按弹性半无限边界进行假设，所得滑面应力存在一定偏差，会影响到稳定性安全系数值。

2)有限元方法虽然能够充分考虑土体应力-应变关系，但在边坡稳定性分析时采用的强度折减法却存在着一些不足^[27]，尤其在折减方法及失稳别标准上，尚未形成统一，受人为因素影响较大。

由上述分析可以看出，经典算例所得结果与强度折减法、极限平衡法吻合度较好，但坡面按弹性半无限边界假设对计算结果有一定影响。为说明其影响程度，并充分验证坡面卸荷应力等效思路在边坡稳定性分析中合理性，有必要在经典算例基础上继续对滑面应力进行比较，以及采用更多衍生算例对安全系数影响因素作进一步讨论。

4.1.3 滑动面应力比较

选用有限元软件Plaxis开展数值模拟，进行坡体内应力值对比，尤其是滑面应力比较，其中土体材料模型采用Mohr-Coulomb，考虑到计算精度要求，模型下边界为坡脚以下10 m，左边界为坡脚向左10 m，右边界为坡顶向右30 m，网格密度为很细，有限元模型如图12所示。

图 12 经典算例有限元模型

Figure 12. FE model of classical example

下载: 全尺寸图片幻灯片

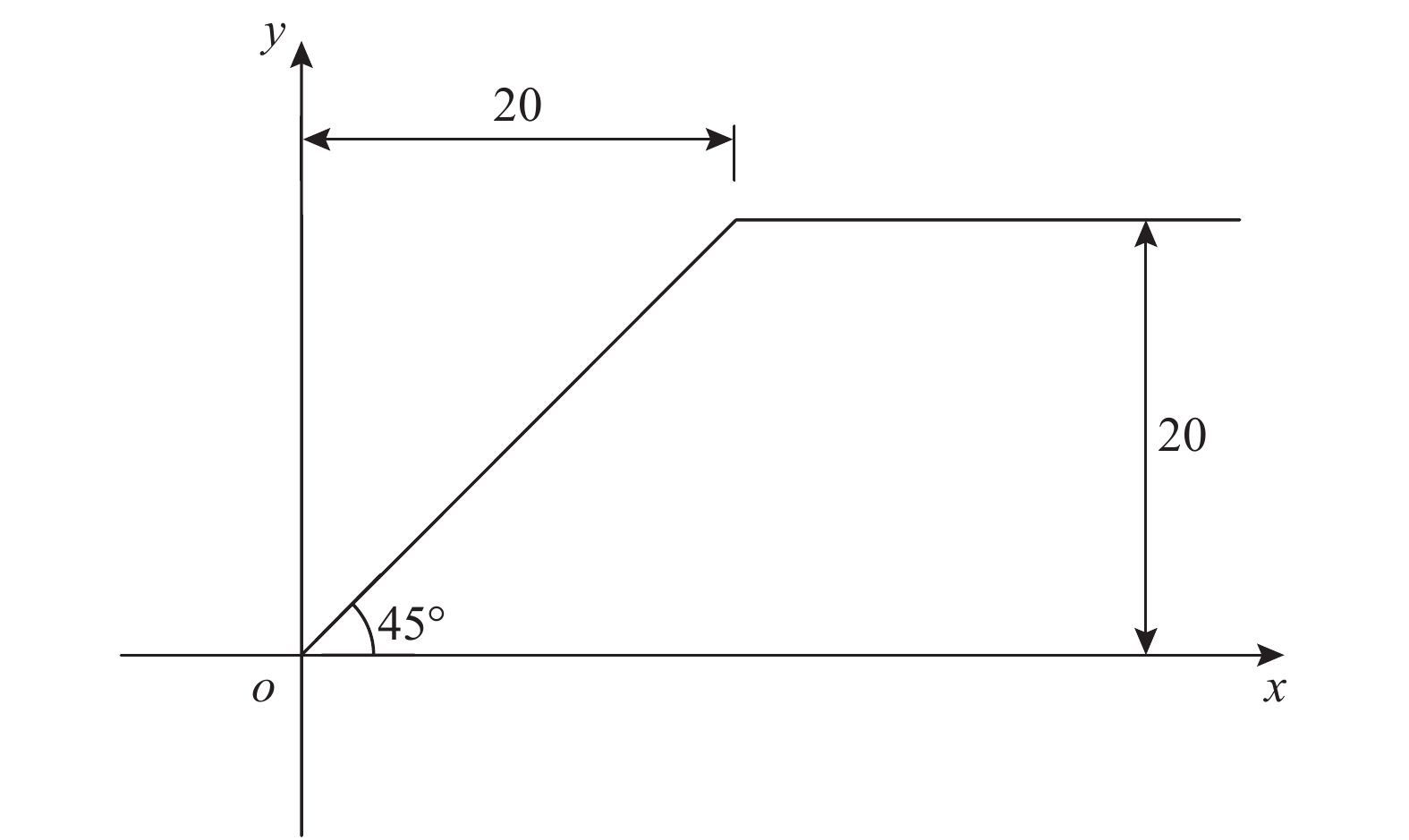
经计算，得到能够反映潜在滑动面特征的增量位移云图，如图13所示，对应的稳定性安全系数为1.157，这与4.1.2节分析的滑动面位置和安全系数大小一致，说明基于此模型进行滑面应力比较合理可行。因此，在基于坡面卸荷应力等效思路搜索得到的潜在滑动面上选取3个参考点，与有限元模型相应位置应力进行比较，其中point1位于滑面下部，point2位于滑面中部，point3位于滑面上部，如图14所示，所得参考点应力值如表3所示。

图 13 模型增量位移云图

Figure 13. Incremental displacement nephogram of model

下载: 全尺寸图片幻灯片

图 14 滑面应力参考点选取

Figure 14. Selection of reference points of stress on sliding surface

下载: 全尺寸图片幻灯片

从表3中可以看出，坡体按弹性半无限体计算得到的竖向应力和滑面中下部剪应力与有限元结果接近，水平向应力与有限元结果存在偏差。分析认为这种偏差由坡面卸荷应力等效和坡面半无限体假设共同造成，主要是因为边坡临空面的存在使得水平向应力计算受假定条件影响较大。但总体来看，竖向应力相较于水平向应力、剪应力而言数值明显偏大，在应力状态中具有主导作用，经变换后得到的滑面法向应力、切向应力与有限元结果相差不大。

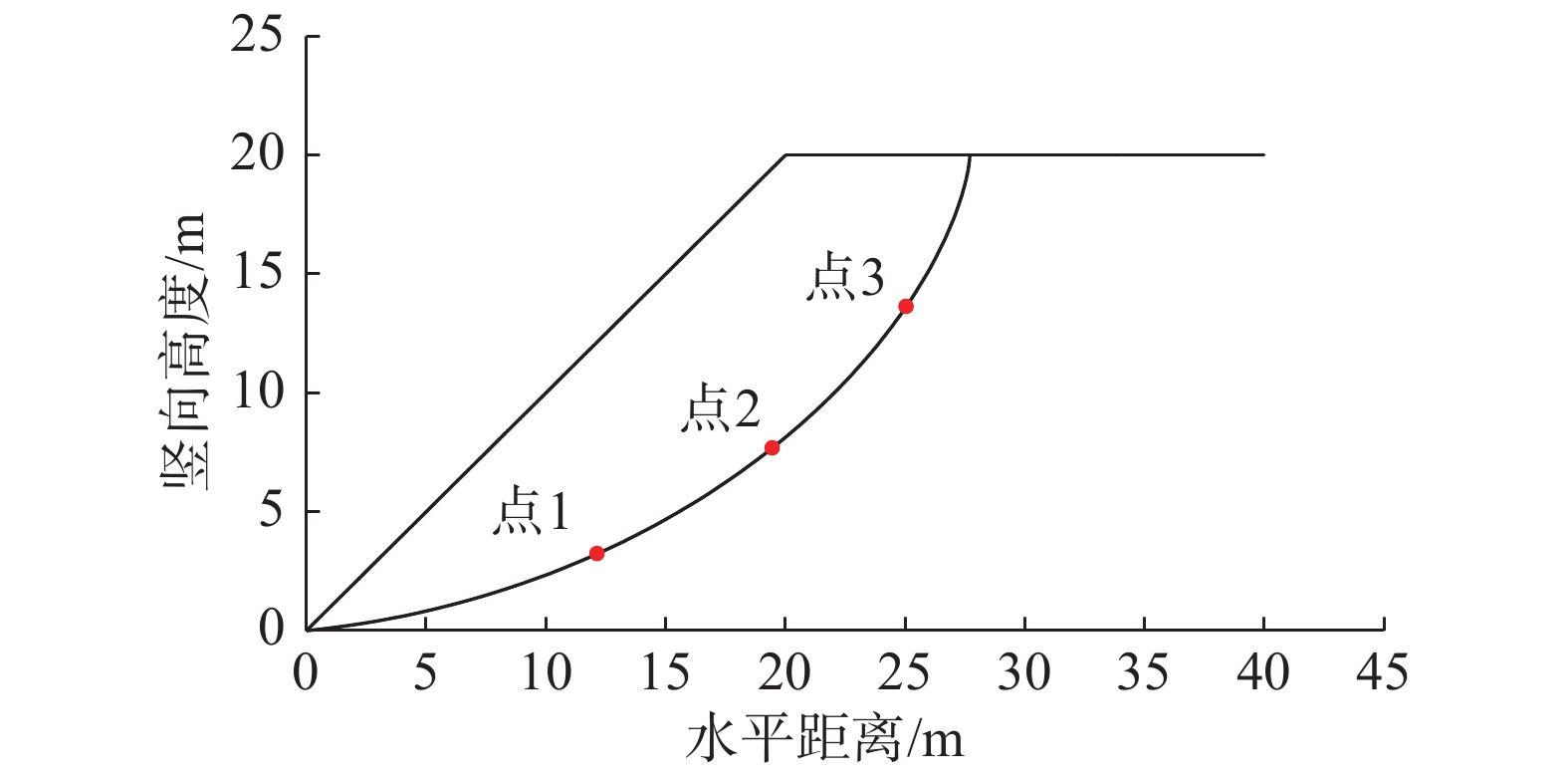
表 3 参考点应力对比

Table 3. Stress comparison at reference points /kPa

参考点	计算方法	水平向应力	竖向应力	剪应力	滑面处法向应力	滑面处切向应力
点1	Plaxis有限元法	80.58	190.43	−42.91	139.49	73.52
点1	本文	39.62	219.48	−47.38	153.27	98.84
点2	Plaxis有限元法	61.48	190.93	−18.52	122.28	81.23
点2	本文	36.97	212.54	−24.74	119.81	91.07
点3	Plaxis有限元法	15.22	117.41	9.79	56.48	38.37
点3	本文	30.01	124.98	−3.83	56.34	42.69

下载: 导出CSV

| 显示表格

为全面掌握滑面应力分布情况，沿滑面将计算得到的法向、切向应力与自重应力、有限元相应结果进行比较，其中自重应力由滑面以上土体自重沿滑面法向和切向分解后得到。由此滑面法向应力分布如图15所示，滑面切向应力分布如图16所示。

图 15 滑面法向应力比较

Figure 15. Comparison of normal stress on sliding surface

下载: 全尺寸图片幻灯片

经图15、图16比较可以看出，三种计算方法得到的滑面法向应力与切向应力变化规律相同，均是在滑面中部应力最大，但应力分量数值大小存在一定差异。总体看来，按弹性半无限体求得的滑面应力介于自重应力分量与有限元所得应力之间，与有限元结果接近，与自重应力分量相差甚远。由此说明，不能将滑面应力简单的视为自重应力分量，而按弹性半无限体进行滑面应力计算实际可行，这一点也验证了王邓峮等^[28]、雷军和肖世国^[29]将坡面视为弹性半无限边界后按弹性理论进行预应力锚杆附加应力分析是正确的。

图 16 滑面切向应力比较

Figure 16. Comparison of tangential stress on sliding surface

下载: 全尺寸图片幻灯片

4.1.4 坡率对安全系数影响比较

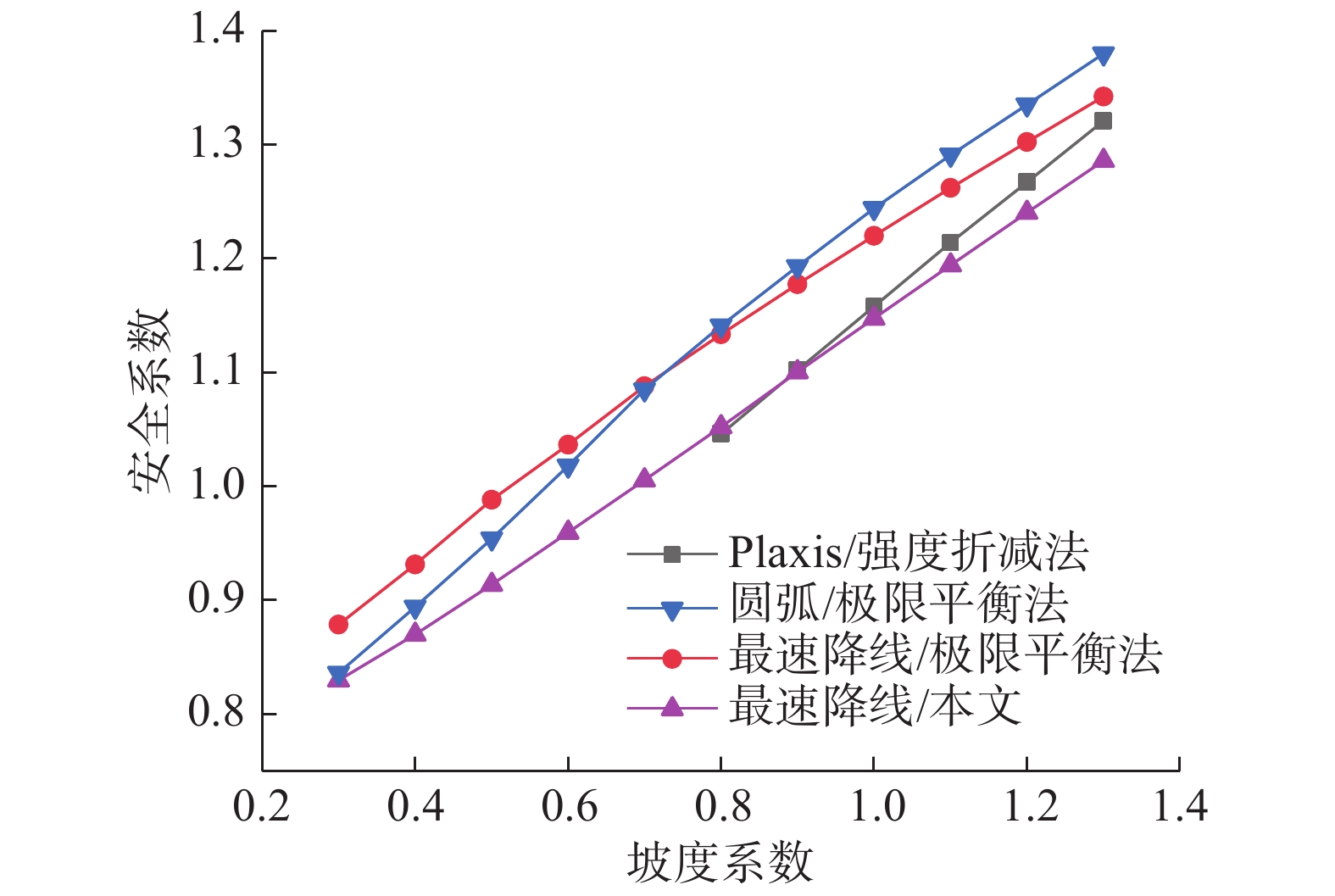
取高度为20 m，坡率依次为1∶0.3、1∶0.4、1∶0.5、1∶0.6、1∶0.7、1∶0.8、1∶0.9、1∶1.0、1∶1.1、1∶1.2、1∶1.3的边坡进行比较分析，岩土材料参数仍然采用4.1.1节中给出的参数。经计算，得到安全系数随坡率变化的对比关系如图17所示。

图 17 坡率变化时安全系数比较

Figure 17. Comparison of safety factor with slope rate change

下载: 全尺寸图片幻灯片

从图17中可以看出，当滑面曲线形式同为最速降线时，基于坡面卸荷应力等效思路所得安全系数较极限平衡法偏小，相差在8%以内，有限元强度折减法计算结果则介于两者之间。当坡度系数小于0.8时，Plaxis显示土体将要坍塌，只能说明安全系数小于1，无法得到具体数值，这一点与本文计算所得安全系数小于1相一致；当坡度系数大于0.8时，有限元结果也与本文计算所得安全系数十分接近，相差在3%以内。

4.1.5 坡高对安全系数影响比较

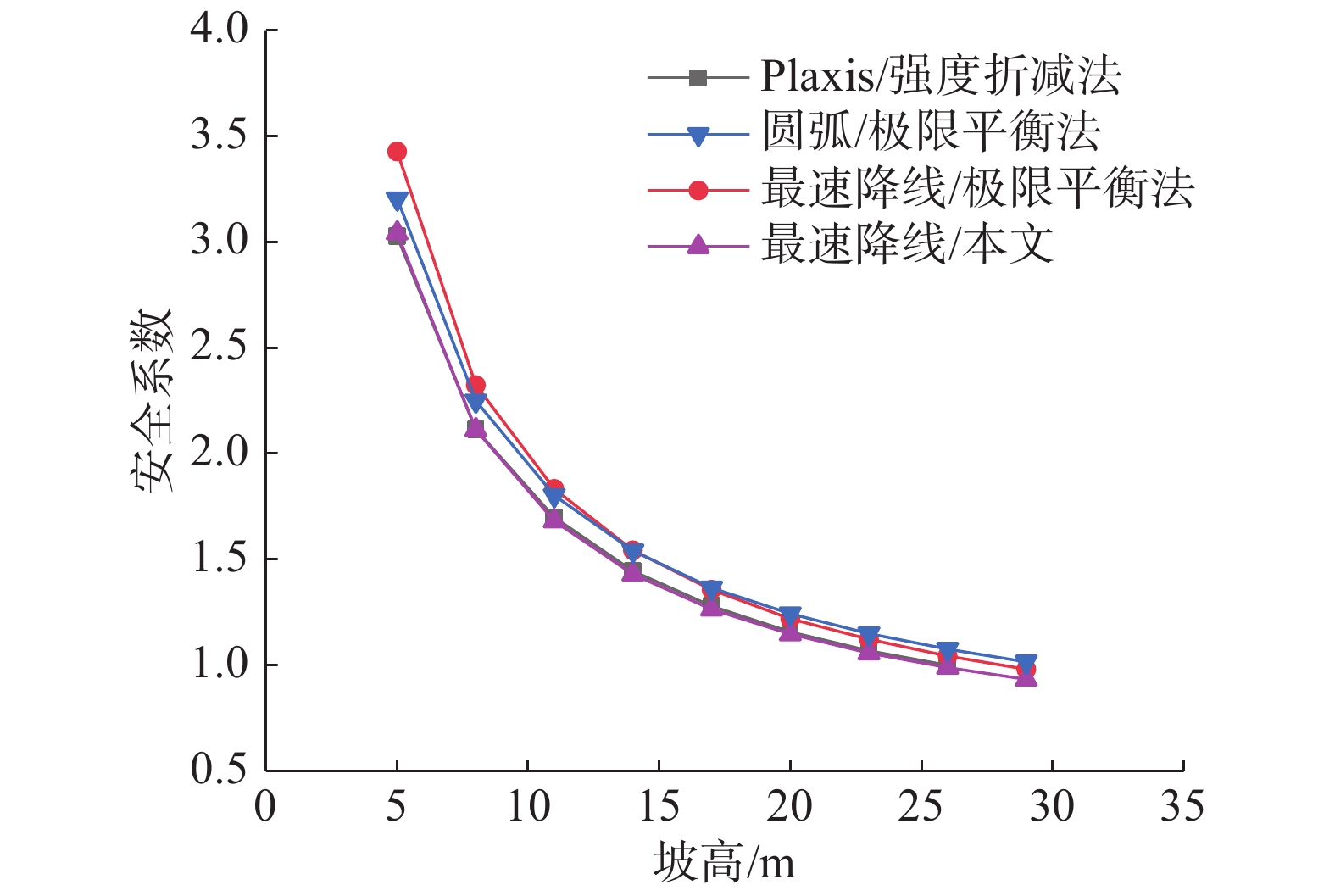
取坡度为45°，坡高依次为5 m、8 m、11 m、14 m、17 m、20 m、23 m、26 m和29 m进行比较分析，岩土材料参数仍然采用4.1.1节中给出的参数。经计算，得到安全系数随坡高变化的对比关系如图18所示。

图 18 坡高变化时安全系数比较

Figure 18. Comparison of safety factors with slope height change

下载: 全尺寸图片幻灯片

从图18中可以看出，基于坡面卸荷应力等效思路所得安全系数始终与有限元强度折减法计算结果接近，相较于极限平衡法而言偏小，但随着坡高的增加，计算值越来越接近。

4.2 预应力锚杆支护边坡

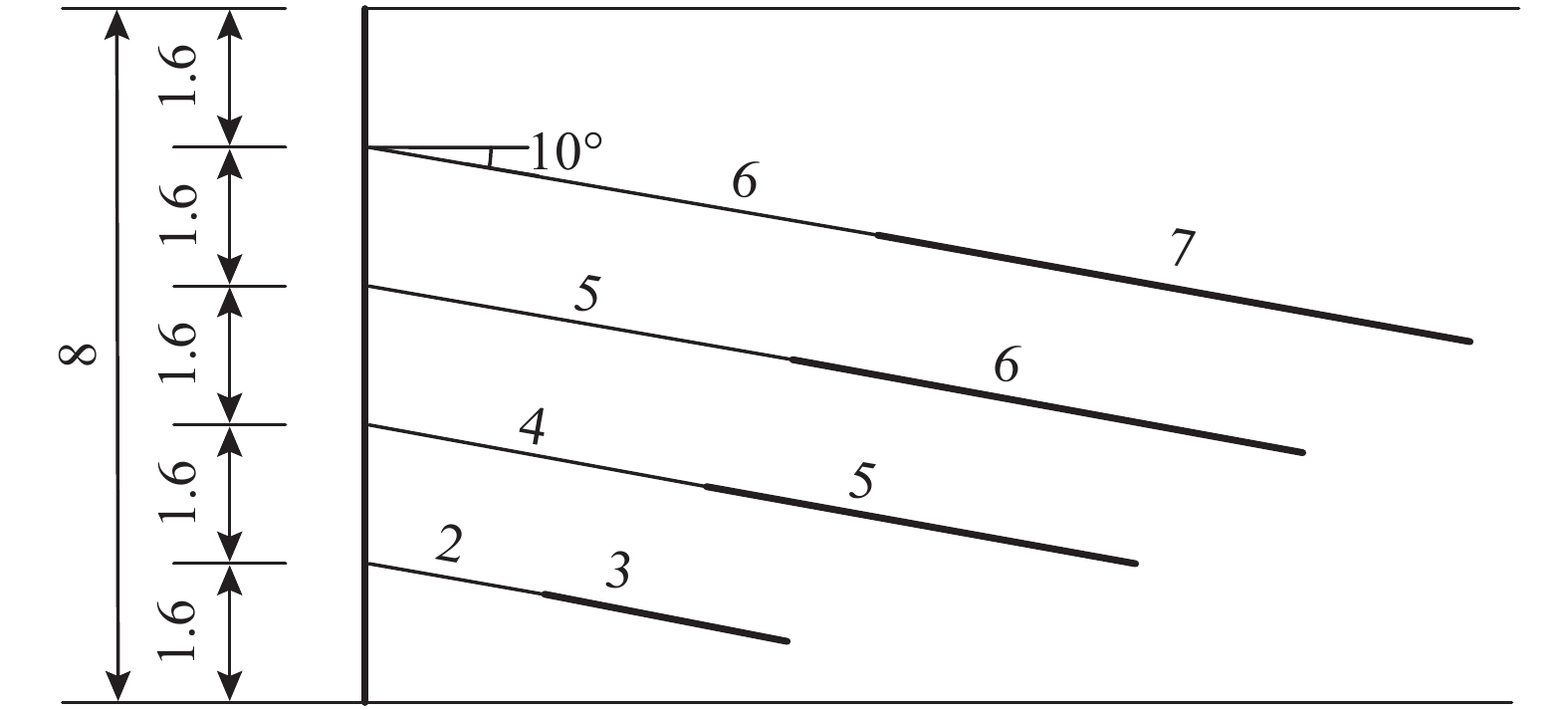
选用文献[28]中用到的一个预应力锚杆支护边坡进行分析比较，边坡高度8 m，坡度为90°，土体参数如表4所示，锚杆布置如图19所示，每根锚杆施加相同的预应力。

表 4 算例2的土体参数

Table 4. Material parameters of Model 2

${\text{ 重度} }\gamma /({\rm{kN}}/{{\rm{m}}^3})$	${\text{ 内摩擦角} }c/{\rm{kPa}}$	${\text{ 粘聚力} }\varphi /(^{\circ} )$
17	20	24

下载: 导出CSV

| 显示表格

图 19 算例2的边坡锚杆布置图　/m

Figure 19. Prestressed anchor rod layout of slope in Model 2

下载: 全尺寸图片幻灯片

该算例中除了要计算坡面卸荷引起的应力改变量，还要考虑预应力锚杆作用，因此将预应力分解为水平方向及竖直方向两个集中力后，按半无限体进行附加应力计算。

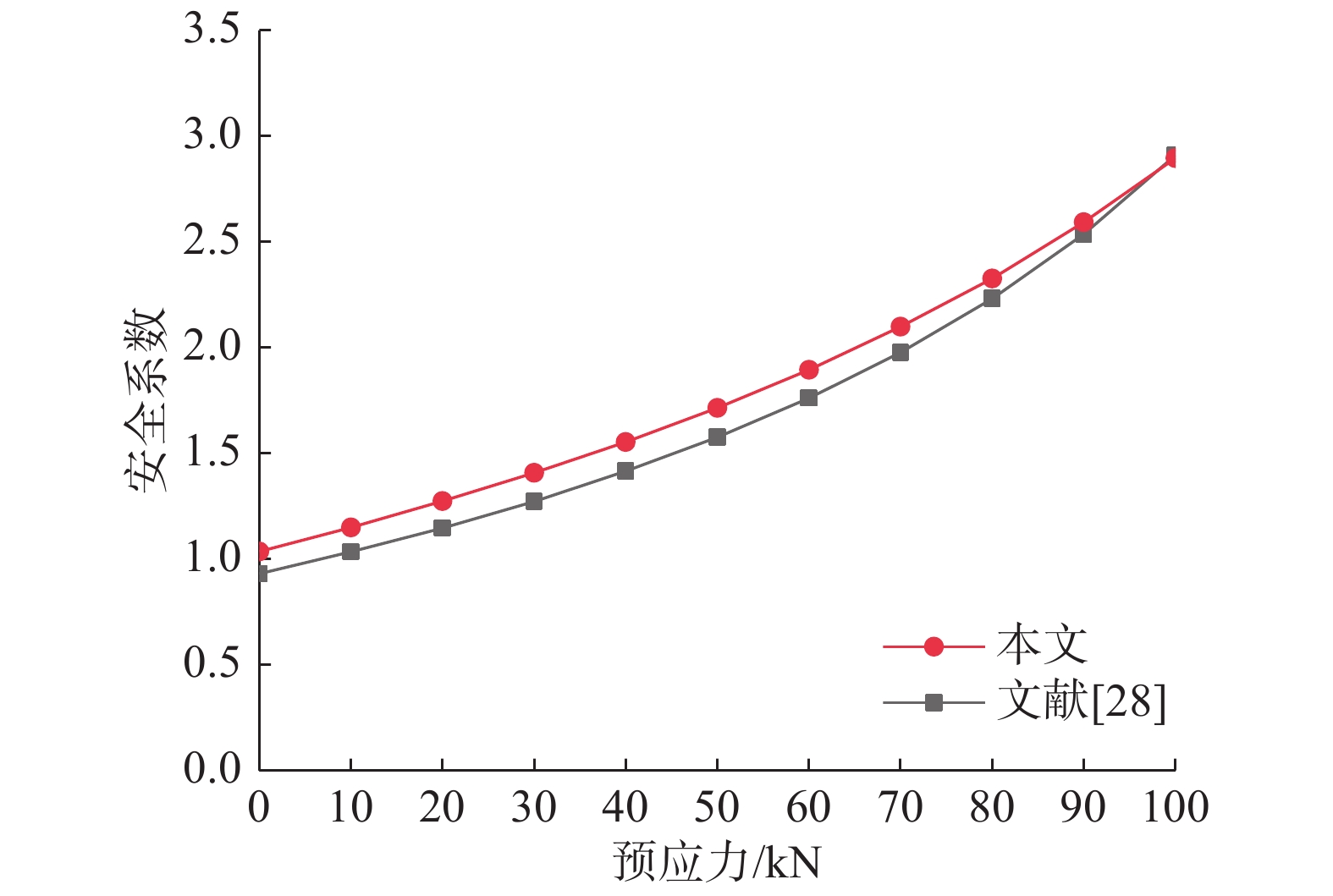
当预应力从10 kN增加到100 kN，对算例2进行稳定性安全系数计算，并将计算结果与文献[28]进行比较，如图20所示。

图 20 预应力变化时安全系数比较

Figure 20. Comparison of safety factors with prestress change

下载: 全尺寸图片幻灯片

从图20中可以看出，随着预应力的增加，安全系数提高明显，说明锚杆预应力对提高边坡稳定性十分有效。同时，所得稳定性安全系数整体与已有研究结果十分接近。对比图17中采用极限平衡法所得圆弧和最速降线结果可知，安全系数受坡度影响，当坡度较大时，最速降线所得安全系数略小于圆弧相应结果，当坡度较小时，最速降线所得安全系数略大于圆弧相应结果。本算例中安全系数略大于文献[28]中的相应结果与坡度为90°有关。

5 结论

通过坡面卸荷应力等效思路的提出，将坡面按弹性半无限边界考虑进行坡体内应力求解和稳定性安全系数计算，并多个算例对其合理性验证，得出以下几点结论。

(1)坡面卸荷应力等效思路概念清晰，符合边坡受力特征，能够体现临空面这一决定边坡稳定性的实质特征，同时，将坡面按弹性半无限边界考虑可以有效求得坡体内任一点应力释放值，从而使得边坡稳定性分析不再局限于条分极限平衡法和数值有限元法。

(2)基于坡面卸荷应力等效思路求得的滑面应力与有限元分计算结果基本一致，搜索得到的潜在滑动面位置，以及对应的稳定性安全系数与有限元强度折减法、极限平衡法计算结果十分接近。

(3)在锚杆支护边坡稳定性分析中，该计算方法可以有效与支护结构预应力结合，将坡面卸荷与锚杆预应力施加一并考虑，既能反映坡体临空面的存在，又能体现锚杆预应力的加固作用。

(4)基于坡面卸荷应力等效思路进行的边坡应力计算及稳定性分析主要适用于土质边坡，包括均质土边坡、成层土边坡和预应力锚杆支护土质边坡，对于含有顺坡结构面的岩、土复合边坡并不适用。

图 1 坡面卸荷应力等效示意图

Figure 1. Stress equivalent diagram of slope unloading

下载: 全尺寸图片幻灯片

图 2 坡面等效应力分布

Figure 2. Equivalent stress distribution of slope surface

下载: 全尺寸图片幻灯片

图 3 半无限体边界受法向集中力

Figure 3. Normal force on boundary of semi-infinite body

下载: 全尺寸图片幻灯片

图 4 坡面受法向应力作用分析模型

Figure 4. Analysis model of normal stress on slope surface

下载: 全尺寸图片幻灯片

图 5 半无限体边界受切向集中力

Figure 5. Tangential force on boundary of semi-infinite body

下载: 全尺寸图片幻灯片

图 6 坡面受切向应力作用分析模型

Figure 6. Analysis model of tangential stress on slope surface

下载: 全尺寸图片幻灯片

图 7 边坡潜在滑动面搜索模型简图

Figure 7. Sketch of searching model for potential sliding surface of slope

下载: 全尺寸图片幻灯片

图 8 滑面单元应力分析模型

Figure 8. Analysis model of stress on an element of slip surface

下载: 全尺寸图片幻灯片

图 9 算例1的边坡尺寸　/m

Figure 9. Slope size of classical Model 1

下载: 全尺寸图片幻灯片

图 10 安全系数与搜索位置关系曲线

Figure 10. Relationship curve between safety factor and search location

下载: 全尺寸图片幻灯片

图 11 不同方法潜在滑动面位置比较

Figure 11. Comparison of potential sliding surface positions obtained by different methods

下载: 全尺寸图片幻灯片

图 12 经典算例有限元模型

Figure 12. FE model of classical example

下载: 全尺寸图片幻灯片

图 13 模型增量位移云图

Figure 13. Incremental displacement nephogram of model

下载: 全尺寸图片幻灯片

图 14 滑面应力参考点选取

Figure 14. Selection of reference points of stress on sliding surface

下载: 全尺寸图片幻灯片

图 15 滑面法向应力比较

Figure 15. Comparison of normal stress on sliding surface

下载: 全尺寸图片幻灯片

图 16 滑面切向应力比较

Figure 16. Comparison of tangential stress on sliding surface

下载: 全尺寸图片幻灯片

图 17 坡率变化时安全系数比较

Figure 17. Comparison of safety factor with slope rate change

下载: 全尺寸图片幻灯片

图 18 坡高变化时安全系数比较

Figure 18. Comparison of safety factors with slope height change

下载: 全尺寸图片幻灯片

图 19 算例2的边坡锚杆布置图　/m

Figure 19. Prestressed anchor rod layout of slope in Model 2

下载: 全尺寸图片幻灯片

图 20 预应力变化时安全系数比较

Figure 20. Comparison of safety factors with prestress change

下载: 全尺寸图片幻灯片

表 1 算例1的材料参数

Table 1 Material parameters of Model 1

重度γ/(kN/m³)	黏聚力c/kPa	内摩擦角φ/(°)	弹性模量E/kPa	泊松比ν
20	42	17	100 000	0.3

下载: 导出CSV

表 2 不同计算方法所得安全系数对比

Table 2 Comparison of safety factor from different calculating methods

计算方法	滑入点距坡顶边缘距离/m	安全系数
郑颖人等^[24]/强度折减法	−	1.20~1.40
赵尚毅等^[25]/强度折减法	−	1.12或1.36
裴利剑等^[26]/强度折减法	−	1.16~1.20
圆弧/极限平衡法	9.0	1.244
最速降线/极限平衡法	8.7	1.220
最速降线/本文	7.7	1.148

下载: 导出CSV

表 3 参考点应力对比

Table 3 Stress comparison at reference points /kPa

参考点	计算方法	水平向应力	竖向应力	剪应力	滑面处法向应力	滑面处切向应力
点1	Plaxis有限元法	80.58	190.43	−42.91	139.49	73.52
点1	本文	39.62	219.48	−47.38	153.27	98.84
点2	Plaxis有限元法	61.48	190.93	−18.52	122.28	81.23
点2	本文	36.97	212.54	−24.74	119.81	91.07
点3	Plaxis有限元法	15.22	117.41	9.79	56.48	38.37
点3	本文	30.01	124.98	−3.83	56.34	42.69

下载: 导出CSV

表 4 算例2的土体参数

Table 4 Material parameters of Model 2

${\text{ 重度} }\gamma /({\rm{kN}}/{{\rm{m}}^3})$	${\text{ 内摩擦角} }c/{\rm{kPa}}$	${\text{ 粘聚力} }\varphi /(^{\circ} )$
17	20	24

下载: 导出CSV

参考文献(29)

[1]	卢应发, 黄学斌, 刘德富. 边坡力的分布特征和稳定性分析[J]. 岩土工程学报, 2017, 39(7): 1321 − 1329. doi: 10.11779/CJGE201707019 Lu Yingfa, Huang Xuebin, Liu Defu. Distribution characteristics of force and stability analysis of slope [J]. Chinese Journal of Geotechnical Engineering, 2017, 39(7): 1321 − 1329. (in Chinese) doi: 10.11779/CJGE201707019
[2]	苏杭, 周海清, 武松. 多级边坡施工效应的模型试验研究[J]. 岩土力学, 2017, 38(8): 2261 − 2269. Su Hang, Zhou Haiqing, Wu Song. Model test research on construction effect of the multi-stage slope [J]. Rock and Soil Mechanics, 2017, 38(8): 2261 − 2269. (in Chinese)
[3]	王浩, 王晓东, 泮俊. 超高路堑边坡治理工程案例研究Ⅰ: 边坡失稳机制模拟分析[J]. 岩石力学与工程学报, 2017, 36(4): 899 − 909. Wang Hao, Wang Xiaodong, Pan Jun. A case study of super-high cut slope I: Simulation and analysis of instability mechanism of slopes [J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(4): 899 − 909. (in Chinese)
[4]	冷伍明, 张期树, 徐方, 等. 新型预应力路基坡面法向附加应力扩散规律分析[J]. 岩土力学, 2019, 40(10): 3987 − 4000. Leng Wuming, Zhang Qishu, Xu Fang, et al. Diffusion behavior of additional stress perpendicular to the slope surface in a new prestressed subgrade [J]. Rock and Soil Mechanics, 2019, 40(10): 3987 − 4000. (in Chinese)
[5]	艾希, 冷伍明, 徐方, 等. 新型预应力路基水平附加应力计算的图表法[J]. 岩土力学, 2020, 41(1): 253 − 266, 277. Ai Xi, Leng Wuming, Xu Fang, et al. Graphic method for computing horizontal additional stress in a new prestressed subgrade [J]. Rock and Soil Mechanics, 2020, 41(1): 253 − 266, 277. (in Chinese)
[6]	李丽华, 肖衡林, 郑俊杰, 等. 废旧轮胎加筋路堤边坡模型试验研究[J]. 工程力学, 2015, 32(11): 79 − 85. doi: 10.6052/j.issn.1000-4750.2014.03.0244 Li Lihua, Xiao Henglin, Zheng Junjie, et al. The model test of waste tire reinforced slope [J]. Engineering Mechanics, 2015, 32(11): 79 − 85. (in Chinese) doi: 10.6052/j.issn.1000-4750.2014.03.0244
[7]	陈金锋, 宋二祥. 西南山区机场高填方边坡反压护道优化设计[J]. 工程力学, 2012, 29(6): 85 − 91, 97. doi: 10.6052/j.issn.1000-4750.2010.08.0610 Chen Jinfeng, Song Erxiang. Optimized design of loading berm for high fill slope of airport in mountainous area of southwest China [J]. Engineering Mechanics, 2012, 29(6): 85 − 91, 97. (in Chinese) doi: 10.6052/j.issn.1000-4750.2010.08.0610
[8]	Bell J M. General slope stability analysis [J]. Journal of the Soil Mechanics and Foundations Division, ASCE, 1968, 94(SM6): 1253 − 1270.
[9]	Zhu D Y, Lee C F. Explicit limit equilibrium solution for slope stability [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2002, 26(15): 1573 − 1590. doi: 10.1002/nag.260
[10]	朱大勇, 李焯芬, 姜弘道, 等. 基于滑面正应力修正的边坡安全系数解[J]. 岩石力学与工程学报, 2004, 23(16): 2788 − 2791. doi: 10.3321/j.issn:1000-6915.2004.16.023 Zhu Dayong, Lee C F, Jiang Hongdao, et al. Solution of slope safety factor by modifying normal stresses over slip surface [J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(16): 2788 − 2791. (in Chinese) doi: 10.3321/j.issn:1000-6915.2004.16.023
[11]	郑宏, 谭国焕, 刘德富. 边坡稳定性分析的无条分法[J]. 岩土工程学报, 2007, 28(7): 1285 − 1291. Zheng Hong, Tham Leslie George, Liu Defu. A slice-free method for stability analysis of slopes [J]. Chinese Journal of Geotechnical Engineering, 2007, 28(7): 1285 − 1291. (in Chinese)
[12]	赵四汉, 刘鑫, 单浩, 等. 均质地基路堤无条分稳定安全系数计算和临界滑动面确定[J]. 工程科学与技术, 2018, 50(5): 122 − 129. Zhao Sihan, Liu Xin, Shan Hao, et al. Non-slice calculation of safety factor and the determination of critical sliding surface of homogeneous ground embankment [J]. Rock and Soil Mechanics, 2018, 50(5): 122 − 129. (in Chinese)
[13]	邵龙潭, 刘士乙, 李红军. 基于有限元滑面应力法的重力式挡土墙结构抗滑稳定分析[J]. 水利学报, 2011, 42(5): 602 − 608. Shao Longtan, Liu Shiyi, Li Hongjun. Analysis of stability against sliding for gravity retaining wall structure based on finite element slip surface stress method [J]. Journal of Hydraulic Engineering, 2011, 42(5): 602 − 608. (in Chinese)
[14]	吴顺川, 韩龙强, 李志鹏, 等. 基于滑面应力状态的边坡安全系数确定方法探讨[J]. 中国矿业大学学报, 2018, 47(4): 719 − 726. Wu Shunchuan, Han Longqiang, Li Zhipeng, et al. Discussion on the methods for determining slope safety factor based on stress state of the sliding surface [J]. Journal of China University of Mining& Technology, 2018, 47(4): 719 − 726. (in Chinese)
[15]	张海涛, 罗先启, 沈辉, 等. 基于矢量和的滑面应力抗滑稳定分析方法[J]. 岩土力学, 2018, 39(5): 1691 − 1698, 1708. Zhang Haitao, Luo Xianqi, Shen Hui, et al. Vector-sum-based slip surface stress method for analysing slip mass stability [J]. Rock and Soil Mechanics, 2018, 39(5): 1691 − 1698, 1708. (in Chinese)
[16]	李忠, 朱彦鹏, 余俊. 基于滑面上应力控制的边坡主动加固计算方法[J]. 岩石力学与工程学报, 2008, 27(5): 979 − 989. doi: 10.3321/j.issn:1000-6915.2008.05.014 Li Zhong, Zhu Yanpeng, Yu Jun. Calculation methods for active slope reinforcement based on stress control in critical slip surface [J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(5): 979 − 989. (in Chinese) doi: 10.3321/j.issn:1000-6915.2008.05.014
[17]	李忠, 杨俊. 基于MPGA的复杂应力状态边坡稳定性分析[J]. 岩土力学, 2015, 36(5): 1488 − 1495, 1504. Li Zhong, Yang Jun. Stability analysis of slope under complex stress conditions based on multi-population genetic algorithm [J]. Rock and Soil Mechanics, 2015, 36(5): 1488 − 1495, 1504. (in Chinese)
[18]	Stianson J R, Chan D, Fredlund D G. Role of admissibility criteria in limit equilibrium slope stability methods based on finite element stresses [J]. Computers and Geotechnics, 2020, 66(5): 113 − 125.
[19]	Liu S Y, Su Z N, Li M, et al. Slope stability analysis using elastic finite element stress fields [J]. Engineering Geology, 2020, 273(8): 1 − 13.
[20]	弗洛林 B·A. 土力学研究原理(第一卷) [M]. 北京: 中国工业出版社, 1965. Флорин B A. Principles of soil mechanics (Volume 1) [M]. Beijing: China Industrial Press, 1965. (in Chinese)
[21]	沈珠江. 理论土力学[M]. 北京: 中国水利水电出版社, 2000. Shen Zhujiang. Theory of soil mechanics [M]. Beijing: China National Water Resources and Hydropower Press, 2000. (in Chinese)
[22]	袁聚云, 钱建固, 张宏鸣, 等. 土质学与土力学[M]. 第4版. 北京: 人民交通出版社, 2009. Yuan Juyun, Qian Jiangu, Zhang Hongming, et al. Soil properties and soil mechanics [M]. The Fourth Edition. Beijing: China Communications Press, 2009. (in Chinese)
[23]	高家美, 顿志林. 楔形体应力理论及其在工程中的应用 [M]. 北京: 煤炭工业出版社, 2001. Gao Jiamei, Dun Zhilin. Wedge stress theory and its application in engineering [M]. Beijing: China Coal Industry Publishing House, 2001. (in Chinese)
[24]	郑颖人, 陈祖煜, 王恭先, 等. 边坡与滑坡工程治理 [M]. 北京: 人民交通出版社, 2007. Zheng Yingren, Chen Zuyu, Wang Gongxian, et al. Engineering treatment of slope & landslide [M]. Beijing: China Communications Press, 2007. (in Chinese)
[25]	赵尚毅, 郑颖人, 时卫民, 等. 用有限元强度折减法求边坡稳定安全系数[J]. 岩土工程学报, 2002, 24(3): 343 − 346. doi: 10.3321/j.issn:1000-4548.2002.03.017 Zhao Shangyi, Zheng Yingren, Shi Weimin, et al. Analysis on safety factor of slope by strength reduction FEM [J]. Chinese Journal of Geotechnical Engineering, 2002, 24(3): 343 − 346. (in Chinese) doi: 10.3321/j.issn:1000-4548.2002.03.017
[26]	裴利剑, 屈本宁, 钱闪光. 有限元强度折减法边坡失稳判据的统一性[J]. 岩土力学, 2010, 31(10): 3337 − 3341. doi: 10.3969/j.issn.1000-7598.2010.10.049 Pei Lijian, Qu Benning, Qian Shanguang. Uniformity of slope instability criteria of strength reduction with FEM [J]. Rock and Soil Mechanics, 2010, 31(10): 3337 − 3341. (in Chinese) doi: 10.3969/j.issn.1000-7598.2010.10.049
[27]	朱彦鹏, 杨晓宇, 马孝瑞, 等. 边坡稳定性分析双折减法的几个问题[J]. 岩土力学, 2018, 39(1): 331 − 338, 348. Zhu Yanpeng, Yang Xiaoyu, Ma Xiaorui, et al. Several questions of double reduction method for slope stability analysis [J]. Rock and Soil Mechanics, 2018, 39(1): 331 − 338, 348. (in Chinese)
[28]	王邓峮, 朱彦鹏. 附加应力法在预应力锚杆支护结构稳定性分析中的应用[J]. 工程力学, 2014, 31(4): 196 − 202. doi: 10.6052/j.issn.1000-4750.2012.11.0824 Wang Dengqun, Zhu Yanpeng. Calculation of stability of anchor support considering prestress [J]. Engineering Mechanics, 2014, 31(4): 196 − 202. (in Chinese) doi: 10.6052/j.issn.1000-4750.2012.11.0824
[29]	雷军, 肖世国. 考虑滑体中锚拉力扩散效应的锚固边坡稳定性分析方法[J]. 岩土工程学报, 2019, 41(9): 1724 − 1730. Lei Jun, Xiao Shiguo. A stability analysis method for anchored slopes considering stress dispersion effect in sliding mass due to anchor tensile forces [J]. Chinese Journal of Geotechnical Engineering, 2019, 41(9): 1724 − 1730. (in Chinese)

施引文献(12)

期刊类型引用(7)

1.	涂义亮，陈晓虎，王星驰，柴贺军，张立舟，张瑞. 基于连续-离散耦合强度折减法的边坡稳定性分析. 工程力学. 2025(03): 238-249 . 本站查看
2.	邓东平，石柱，彭文耀. 卸荷损伤效应下开挖边坡稳定性极限平衡分析. 工程地质学报. 2025(01): 327-340 . 百度学术
3.	王建国，孙郡庆，李卫鹏，张凯亮. 地下水作用下含软弱岩层露天矿边坡稳定性分析. 科技通报. 2025(03): 36-41 . 百度学术
4.	彭普，李泽，张小艳，申林方，许芸. 土质边坡的单元失效概率与失效模式研究. 工程力学. 2024(01): 193-207 . 本站查看
5.	梁京涛，赵聪，张肃，董继红，铁永波，高延超，撒兰鹏，杨磊，鄢圣武. 西南山区巨型古滑坡体发育演化特征与城镇空间扩张关联机制分析. 沉积与特提斯地质. 2024(03): 510-522 . 百度学术
6.	陈强，张雪萍. 采动作用下黑岱沟露天矿区岩土边坡稳定性研究. 能源与环保. 2023(05): 137-143 . 百度学术
7.	李学锋，宋勇军，李和群，梁莉，向进伟，李坤光. 露天矿边坡岩体强度参数确定及稳定性分析. 广西大学学报(自然科学版). 2022(06): 1682-1691 . 百度学术

其他类型引用(5)

资源附件(0)

图(20) / 表(4)

计量

文章访问数: 636
HTML全文浏览量: 206
PDF下载量: 109
被引次数: 12

1 坡面卸荷应力等效分析思路
2 坡体内一点应力计算
2.1 计算模型与参数
2.2 坡面法向卸荷应力作用下的附加应力
2.3 坡面切向卸荷应力作用下的附加应力
2.4 $xoy$ 坐标系内坡体应力转化
3 稳定性分析方法
3.1 潜在滑动面形式选择
3.2 滑面应力计算
3.3 安全系数计算
4 算例分析
4.1 未支护均质土坡
4.1.1 算例概况
4.1.2 滑动面位置及安全系数比较
4.1.3 滑动面应力比较
4.1.4 坡率对安全系数影响比较
4.1.5 坡高对安全系数影响比较
4.2 预应力锚杆支护边坡
5 结论

1 坡面卸荷应力等效分析思路
2 坡体内一点应力计算
2.1 计算模型与参数
2.2 坡面法向卸荷应力作用下的附加应力
2.3 坡面切向卸荷应力作用下的附加应力
2.4 $xoy$ 坐标系内坡体应力转化
3 稳定性分析方法
3.1 潜在滑动面形式选择
3.2 滑面应力计算
3.3 安全系数计算
4 算例分析
4.1 未支护均质土坡
4.1.1 算例概况
4.1.2 滑动面位置及安全系数比较
4.1.3 滑动面应力比较
4.1.4 坡率对安全系数影响比较
4.1.5 坡高对安全系数影响比较
4.2 预应力锚杆支护边坡
5 结论

参考文献(29)

施引文献(12)

资源附件(0)

基于坡面卸荷的土质边坡应力状态及稳定性分析

作者简介: 朱彦鹏(1960−)，男，甘肃人，教授，硕士，博导，从事岩土与结构相互作用、工程事故分析与处理研究(E-mail: zhuyp1@163.cn)

通讯作者: 杨奎斌(1993−)，男，陕西人，博士生，从事边坡稳定性研究(E-mail: ykbin93@163.com)

计量

出版历程

SOIL SLOPE STRESS STATE AND STABILITY ANALYSIS BASED ON UNLOADING EFFECT OF SLOPE SURFACES

1 坡面卸荷应力等效分析思路

2 坡体内一点应力计算

2.1 计算模型与参数

2.2 坡面法向卸荷应力作用下的附加应力

2.3 坡面切向卸荷应力作用下的附加应力

2.4 xoyxoy坐标系内坡体应力转化

3 稳定性分析方法

3.1 潜在滑动面形式选择

3.2 滑面应力计算

3.3 安全系数计算

4 算例分析

4.1 未支护均质土坡

4.1.1 算例概况

4.1.2 滑动面位置及安全系数比较

4.1.3 滑动面应力比较

4.1.4 坡率对安全系数影响比较

4.1.5 坡高对安全系数影响比较

4.2 预应力锚杆支护边坡

5 结论

期刊类型引用(7)

其他类型引用(5)

计量

出版历程

目录

1 坡面卸荷应力等效分析思路

2 坡体内一点应力计算

2.1 计算模型与参数

2.2 坡面法向卸荷应力作用下的附加应力

2.3 坡面切向卸荷应力作用下的附加应力

2.4 xoyxoy坐标系内坡体应力转化

3 稳定性分析方法

3.1 潜在滑动面形式选择

3.2 滑面应力计算

3.3 安全系数计算

4 算例分析

4.1 未支护均质土坡

4.1.1 算例概况

4.1.2 滑动面位置及安全系数比较

4.1.3 滑动面应力比较

4.1.4 坡率对安全系数影响比较

4.1.5 坡高对安全系数影响比较

4.2 预应力锚杆支护边坡

5 结论

作者简介:
朱彦鹏(1960−)，男，甘肃人，教授，硕士，博导，从事岩土与结构相互作用、工程事故分析与处理研究(E-mail: zhuyp1@163.cn)

通讯作者:
杨奎斌(1993−)，男，陕西人，博士生，从事边坡稳定性研究(E-mail: ykbin93@163.com)

2.4 $xoy$ 坐标系内坡体应力转化

2.4 $xoy$ 坐标系内坡体应力转化