ANALYSIS OF SWELL CHARACTERISTICS AND SPECTRA BASED ON IN SITU MEASUREMENTS
-
摘要:
基于太平洋沿岸秘鲁某海域的海浪观测资料，对得到的波浪数据进行了波浪特征以及波浪谱研究。结果表明，该海域主要受到来自太平洋的长周期涌浪作用，最大谱峰周期达到了20 s以上。根据相关性分析以及波高周期联合分布，得到了涌浪的特征波高和平均周期之间存在较强的线性关联，拟合得到了涌浪的各特征波高与平均周期之间的关系，可用于对涌浪的特征波高进行估计。采用了3种波浪谱模型，利用非线性最小二乘法对实测波浪谱进行了拟合分析，发现Ochi-Hubble谱模型的拟合结果与实测谱更加一致，相关系数分布在1.0附近，有效波高和谱峰周期的拟合结果整体误差均在2%以内。通过对比波浪谱型、相关系数和波浪特征参数的综合结果，认为Ochi-Hubble谱模型能够较好地描述长周期涌浪波谱。
Abstract:Swell characteristics and wave spectra were studied based on in situ measurements in a Peru sea area off the Pacific coast. The sea is mainly affected by long-period swells from the Pacific Ocean, with a maximum spectral peak period of more than 20 s. A strong linear correlation between the characteristic wave heights and the mean period of swell was obtained by correlation analysis. The joint distribution of wave heights and periods, and the relationship between each characteristic wave heights and the mean period of swell were fitted, which can be used to estimate the characteristic wave heights of swell. Three wave spectral models were adopted to fit the measured wave spectra using the nonlinear least squares method, and it is found that the fitting results of the Ochi-Hubble spectra are more consistent with the measured spectra, with a correlation coefficients around 1.0, and the overall errors of the fitting results for the significant wave heights and the spectral peak periods are all within 2%. Comparing the combined results of wave spectra shape, correlation coefficients and wave characteristic parameters, it is concluded that the Ochi-Hubble spectrum is better to describe the swell spectra.
-
Keywords:
- in situ measurements /
- swell /
- nonlinear least squares method /
- wave characteristics /
- wave spectrum
-
波浪作为海洋中最主要的动力荷载，是在进行海洋工程设计和建设过程中主要的影响因素。波高、周期和波谱等，是描述波浪特征的基本信息，正确地认识和理解这些基本波浪特征，对海洋工程的结构设计和安全运维具有重大意义[1 − 4]。
海洋中的波浪分为风浪和涌浪。风浪是当海面上持续受到风的作用时而产生的波浪；而涌浪是指当波浪传播至风区以外时，遗留在海面上的波浪或是其他海区传来的波浪，常说的“无风三尺浪”指的就是涌浪。涌浪的传播是一个复杂的过程，包括非线性相互作用、色散以及衰减等，这导致涌浪和风浪的特性截然不同，具有较规则的外形，波长和周期较大，以及波浪谱窄而尖锐等典型特点。涌浪对船舶和海洋工程均会造成较大的危害。在深远海工程中，由于涌浪的频率与海洋平台导管架和漂浮式基础等结构物频率相近，容易与其发生共振，具有极强的破坏力，造成巨大的经济损失与人身危害[5]；对于航行中的船舶，当涌浪的波长与船舶本身的长度相近时，相邻的两个波峰分别出现在船首和船尾，受到船舶自身重量的影响，很容易在中部发生断裂；若波峰出现在船舶中部，则出现在波谷位置的船头和船尾很容易发生悬空，导致船舶出现较大的倾斜甚至倾覆，严重影响船舶的航行安全[6]；当涌浪传播到港内时，由于其周期较大的特点，容易造成系泊船横摇与垂荡的幅度加大，加剧系泊船缆绳的磨损，严重时甚至导致缆绳断裂，影响港内船只的安全作业以及工人的生命安全[7]。随着涌浪进一步传向近岸，在近岸缓坡地形上发生浅化现象，波高增大，会对防波堤等近岸防护结构物造成冲击，进而发生破坏[8 − 10]。国内外学者们针对涌浪的特性及其波浪谱，开展了一系列相关研究。裴晔等[11]采用数值模拟的方法，研究了特定海域涌浪在不同气候条件下的产生机理和演变特性，分析了涌浪的波高和周期特性。在发生台风的极端天气条件下，往往会产生显著的涌浪[12]。韩晓伟等[13]利用WAVEWATCH-III海浪数值模式对台风“浣熊”进行了模拟，并分析了台风浪的发展和涌浪场的分布特征。周昳鸣等[12]和杨斌等[14]根据台风期间波浪观测资料，研究了长周期涌浪的波浪特征和波谱特点，分析了波浪几种特征波高之间的规律和波谱形状的变化规律。波浪谱是一种从频域角度来描述波浪的重要方法[15]，对于风浪谱，研究者们针对不同的风距和波浪发展阶段提出了许多对应的风浪谱模型[16 − 21]。GODA[22]对已经传播了几千公里的涌浪记录进行了分析，提出JONSWAP谱可近似的描述涌浪谱模型。OLAGNON等[23]提出了一种采用高斯概率函数定义的高斯波浪谱模型来描述涌浪谱。LUCAS和GUEDES SOARES[24]对比了JONSWAP谱模型和高斯模型在拟合实测涌浪谱的表现，相比于高斯模型，认为JONSWAP谱能够更好地描述涌浪谱，但拟合得到的有效波高整体上偏小。GAO等[25]根据谱型特征将实测谱分为单峰谱与双峰谱，对比了多种单峰波浪谱模型在拟合实测波浪谱中的表现，并提出了一种新的单峰波浪谱模型。对于双峰谱，采用了2种典型的双峰谱模型进行拟合和特征分析，发现Ochi-Hubble谱能够更好的描述双峰谱。然而在谱型分类时受到人为判断影响，难以客观准确，且在应用时较为复杂，因此需要根据单、双峰谱选择波浪谱模型。受观测资料有限的影响，当前对涌浪的基本特征和波谱的研究还存在不足，对于工程所在特定海域涌浪的产生原因及运动特性等研究还很少[5]，且还未提出专门的涌浪谱模型[26]。因此，基于现场观测数据对涌浪特征与波谱进行深入研究，对海上航行、海洋资源开发利用、防止和减少海浪灾害都具有重要意义。
本文基于太平洋沿岸秘鲁某海域的海浪观测资料，对涌浪的统计特征参数和波浪谱开展研究。根据相关性分析和拟合分析，得到了涌浪特征波高和平均周期之间的关系；此外，采用3种常用的波浪谱模型对实测波谱进行了拟合分析，得到了可用于同时描述单峰和双峰涌浪谱的推荐谱型，便于工程应用。
1 数据介绍与处理
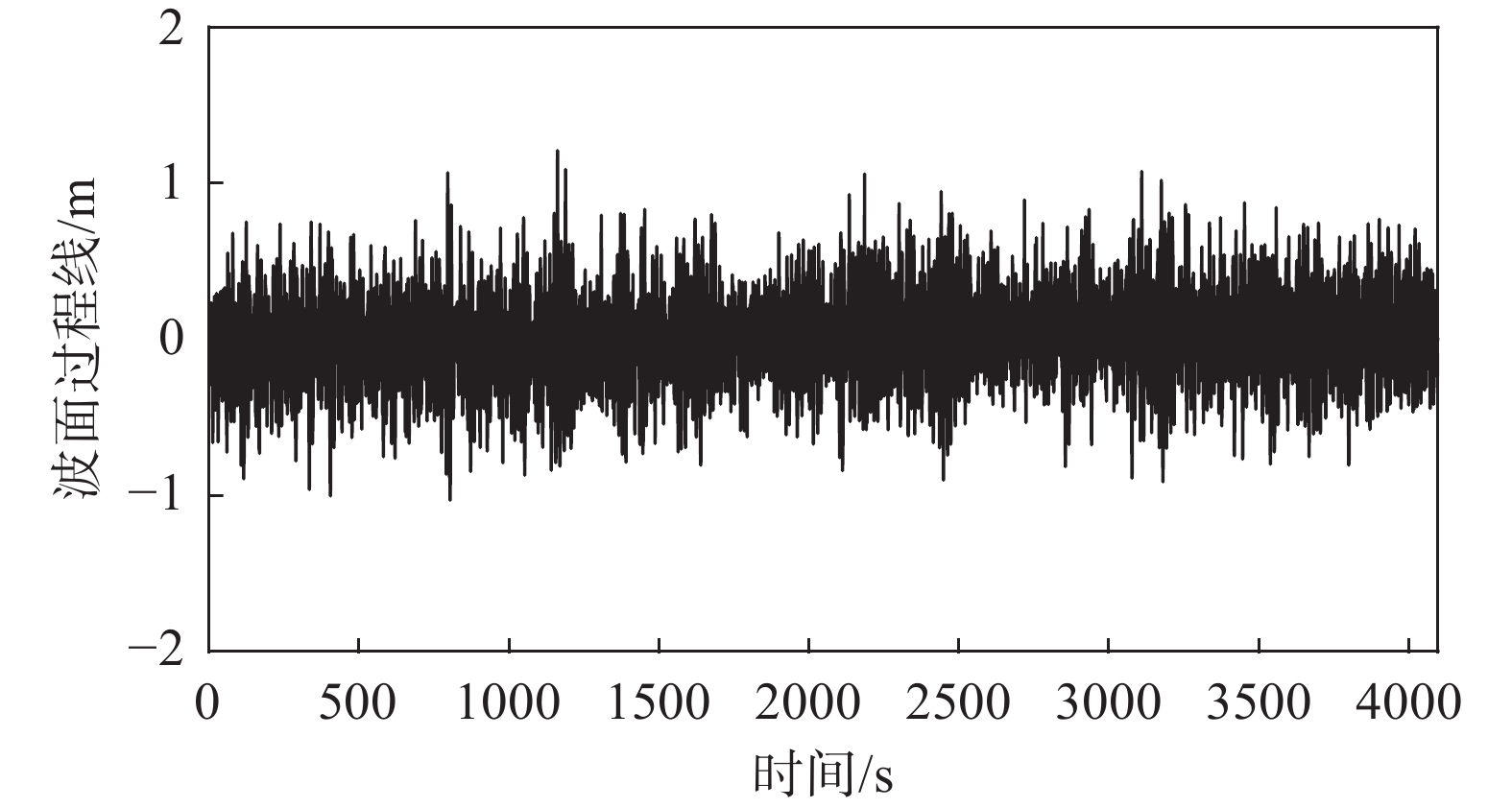
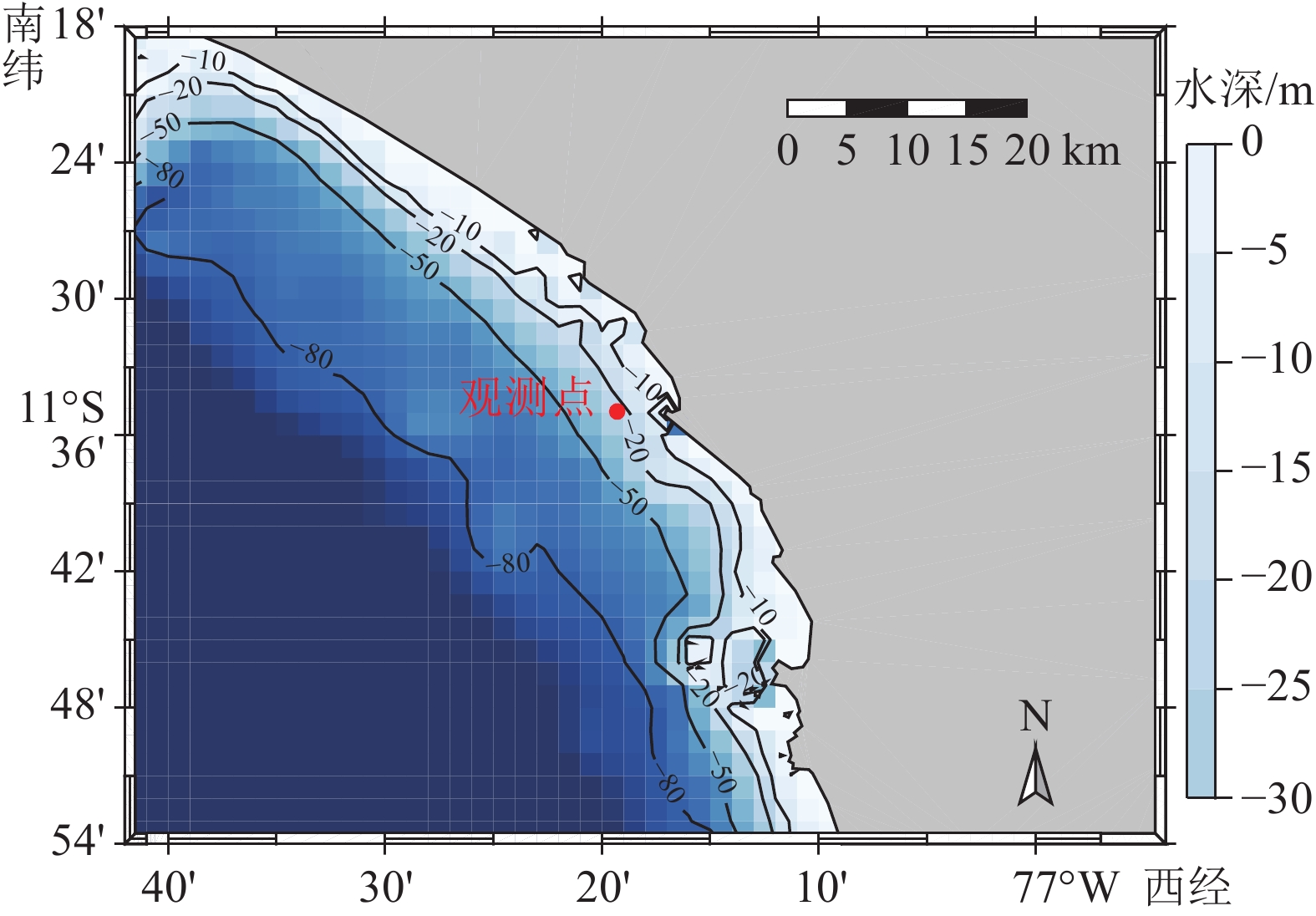
测点位于太平洋沿岸秘鲁某海域，测点位置水深为25 m，观测位置如图1所示。相比于我国典型海域的主要波浪类型为风浪[27 − 29]，该观测位置受到咆哮西风带的影响，全年都会受到长周期涌浪的影响[30 − 33]，弥补了涌浪观测资料有限的局限，有助于对涌浪的波浪特征以及波浪谱进行研究。采用坐底式声学多普勒流速剖面仪(acoustic Doppler current profiler, ADCP)进行观测，现场安放及布置情况见图2。采集数据时间跨度为2018年7月7日—2018年12月7日。每2 h测量一次波面过程，每次采集时间持续4096 s，采样频率为4 Hz。
在波浪采集过程中，由于受到外部环境以及仪器稳定性的影响，个别时段的波面过程线会出现大量毛刺现象，无法通过滤波等手段获得有效数据，有效波面数据见图3。异常数据量较少，由于分布于不同日期的个别时段，且未出现连续分布的现象，认为不会影响整体数据的统计结果。为了保证波浪特征分析的准确性，在分析过程中剔除这部分异常数据，异常数据约为40段，最终得到的有效数据为1757段，数据有效率为97.8%，每个月份的有效数据情况见表1。
表 1 各月份有效数据次数Table 1. The number of effective data of every month月份 异常数据次数 有效数据次数 7 19 276 8 5 356 9 4 347 10 5 355 11 3 345 12 3 78 2 涌浪特征分析
2.1 涌浪特征参数与判别标准
对观测数据进行处理，有效波高Hs和谱峰周期Tp的表达式如下：
Hs=4.0√∫∞0S(f)df (1) Tp=1/fp (2) 式中：S(f)为波浪谱；fp为波浪谱谱峰对应的谱峰频率。
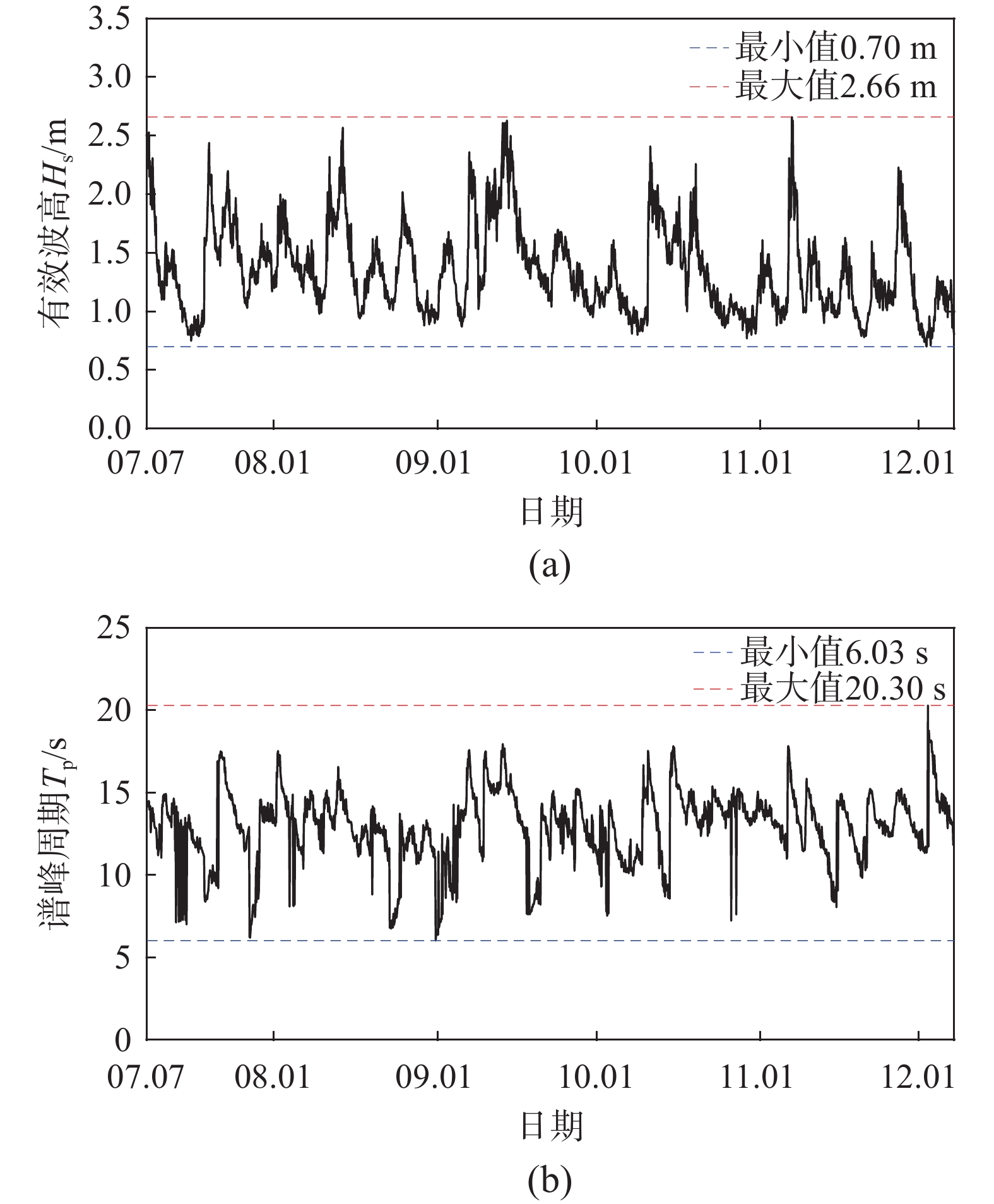
观测位置处的有效波高Hs和谱峰周期Tp随时间的变化情况如图4所示。
![]()
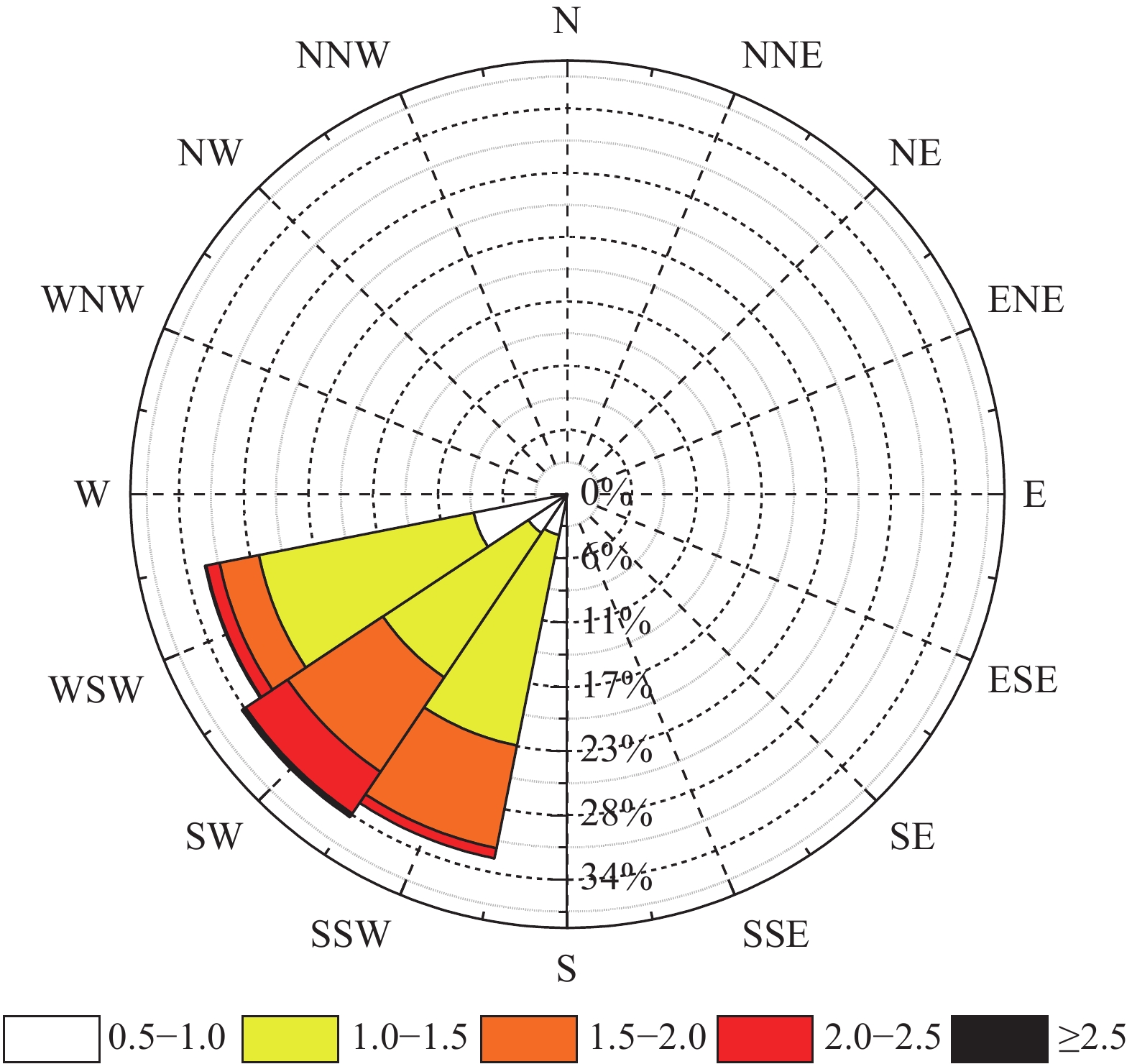
图 4 观测时间段内，(a)有效波高Hs和(b)谱峰周期Tp随时间的变化曲线Figure 4. Variation of (a) significant wave height and (b) spectral peak period during the observation period结果显示：在观测时段内，有效波高分布在0.70 m~2.66 m，谱峰周期分布在6.03 s~20.30 s，有效波高和谱峰周期的均值分别为1.35 m和12.94 s。可以发现，观测时间段内，有效波高随时间变化较平稳，未出现台风等极端天气而导致的极端大值；然而波浪的谱峰周期较大，平均值达到了10 s以上。由波浪玫瑰图(图5)可知，观测位置海域主要受到来自西南方向波浪的影响，常浪向和强浪向均为SW向。
对于风涌浪的判别标准，通常认为周期超过7 s或8 s(对应的波浪频率分别为0.14 Hz和0.125 Hz)的波浪为涌浪[34]，然而这种判断方法过于简略，不能很好地结合当点海域环境条件给出更加真实可信的结果。TORSETHAUGEN等[35]提出了一种结合风距判断海域以风浪或涌浪为主的分类标准：
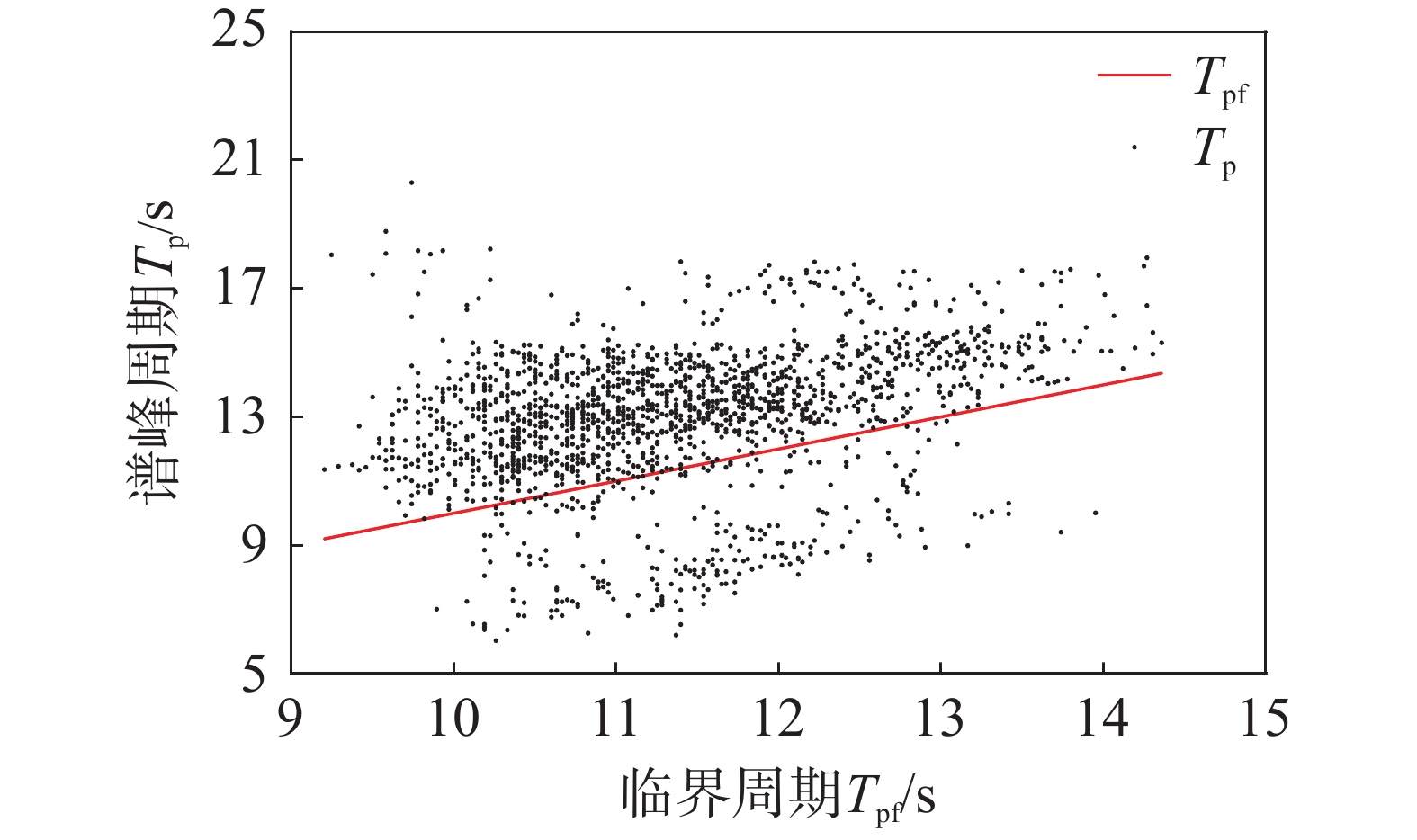
Tpf=afHs1/3 (3) 式中：Tpf为临界周期；af为一个与风距Fe有关的经验常数：
af=0.78F1/6e (4) 若谱峰周期Tp≤Tpf，则表明海域是以风浪系统为主导的；反之，则表明该海域是以涌浪系统为主。风距Fe很难精确的估计，为保守起见，将咆哮西风带到测点位置的最大距离代入式(4)，可得到af =10.4，进而得到实测波浪数据的两种周期之间的关系，见图6。由图6可知，测点位置处的谱峰周期总体上大于临界周期，因此，可认为该海域主要以长周期涌浪为主。
![]()
图 6 实测的谱峰周期Tp与临界周期Tpf对比情况Figure 6. Comparisons between the measured spectra peak periods Tp and the critical periods Tpf基于线性波假设和大量的观测结果表明，对于深水中的波浪，波高分布基本符合瑞利(Rayleigh)分布[26]：
f(H)=π2H¯H2exp{−π4(H¯H)2}, (5) 式中，¯H为波列平均波高。
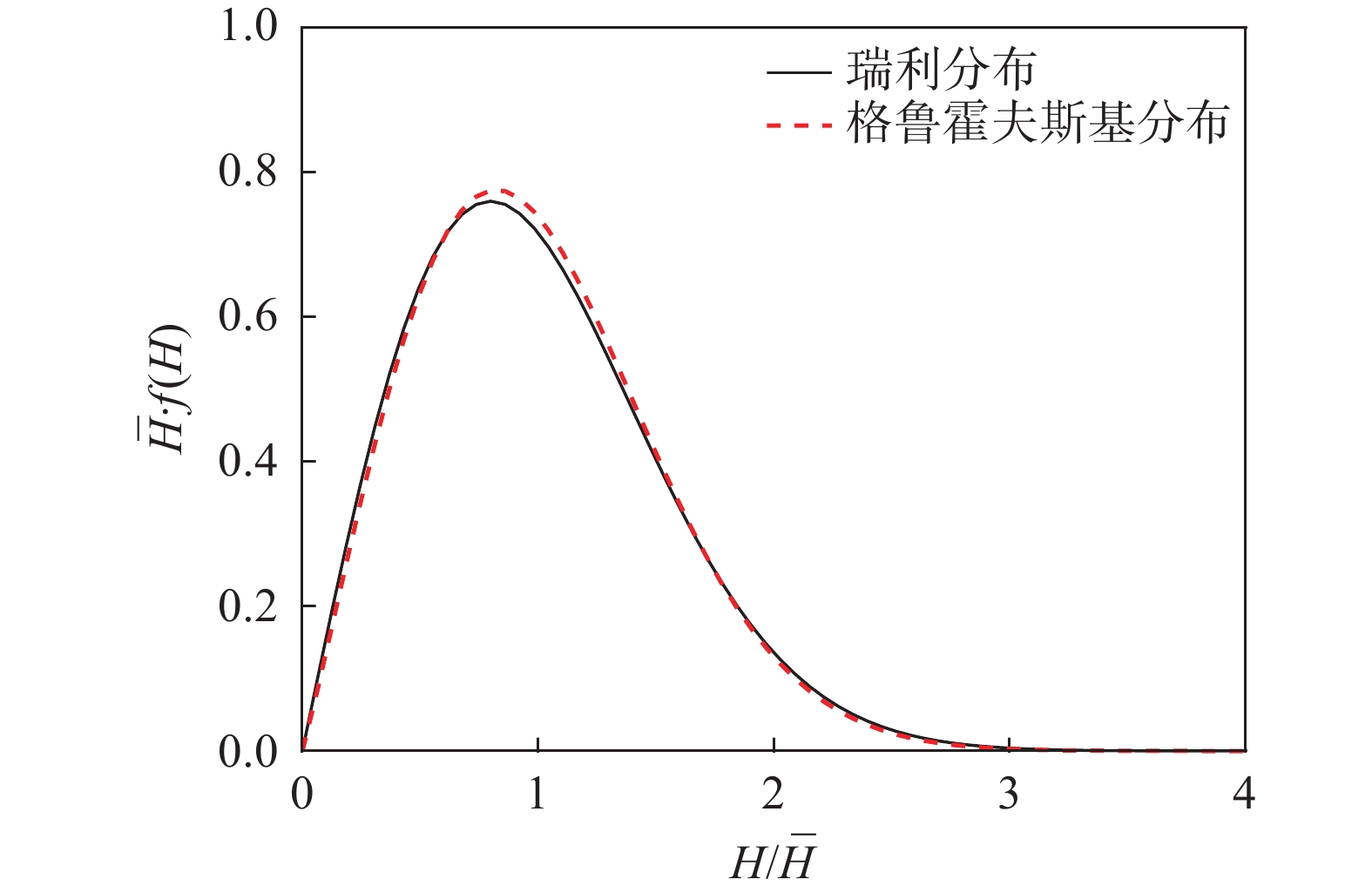
苏联格鲁霍夫斯基(Глуховский)系统地观测和分析了浅水中的海浪波高分布，提出了与水深有关的波高分布的概率密度函数[26]：
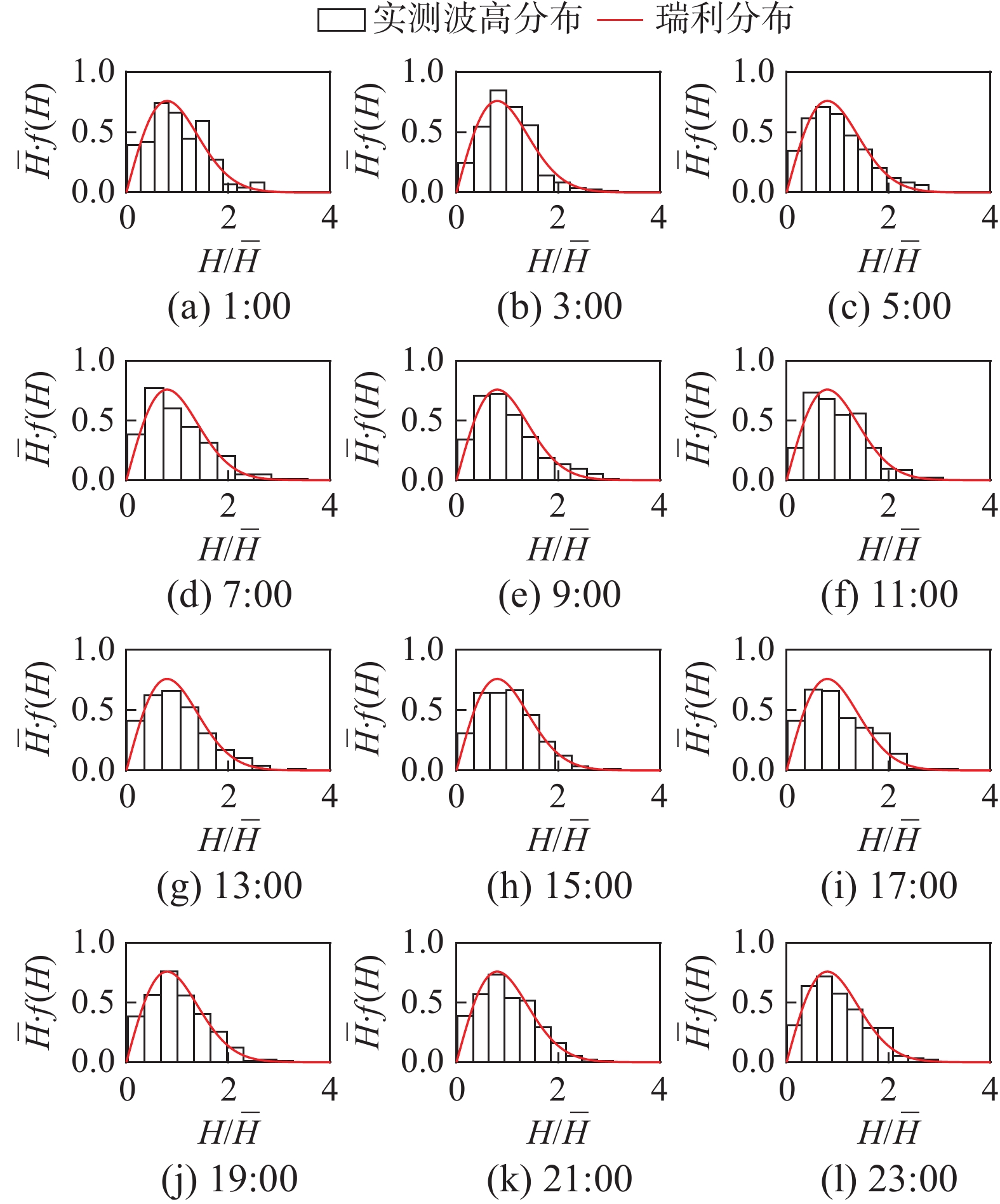
f(H)=π2¯H(1−H∗)(1−H∗/√2π)(H¯H)(1+H∗)/(1−H∗)⋅exp[−π4(1+H∗/√2π)(H¯H)2/(1−H∗)] (6) 对于本次观测位置，选择8月20日4:00的观测数据为代表，得到该段平均波高对应的两种理论波高分布如图7所示。由图7可见，两种理论分布几乎重合。此时H* = 0.0423，趋近于0。8月20日各个时段的波高概率分布情况如图8所示。结果显示：该海域处波高分布基本符合瑞利分布，虽然该观测位置已处于有限水深位置，可认为还未发生显著的浅水变形和浅化效应。因此，后续可基于观测位置数据，进行涌浪特征参数之间定量关系的研究。
![]()
图 7 观测位置处波高的瑞利分布与格鲁霍夫斯基分布对比Figure 7. The comparison between the Rayleigh distribution of wave height and that of the Глуховский distribution at the observation site![]()
图 8 8月20日各时段的波高概率分布情况Figure 8. The probability distribution of wave height at different times on August 202.2 涌浪波高与周期的关系
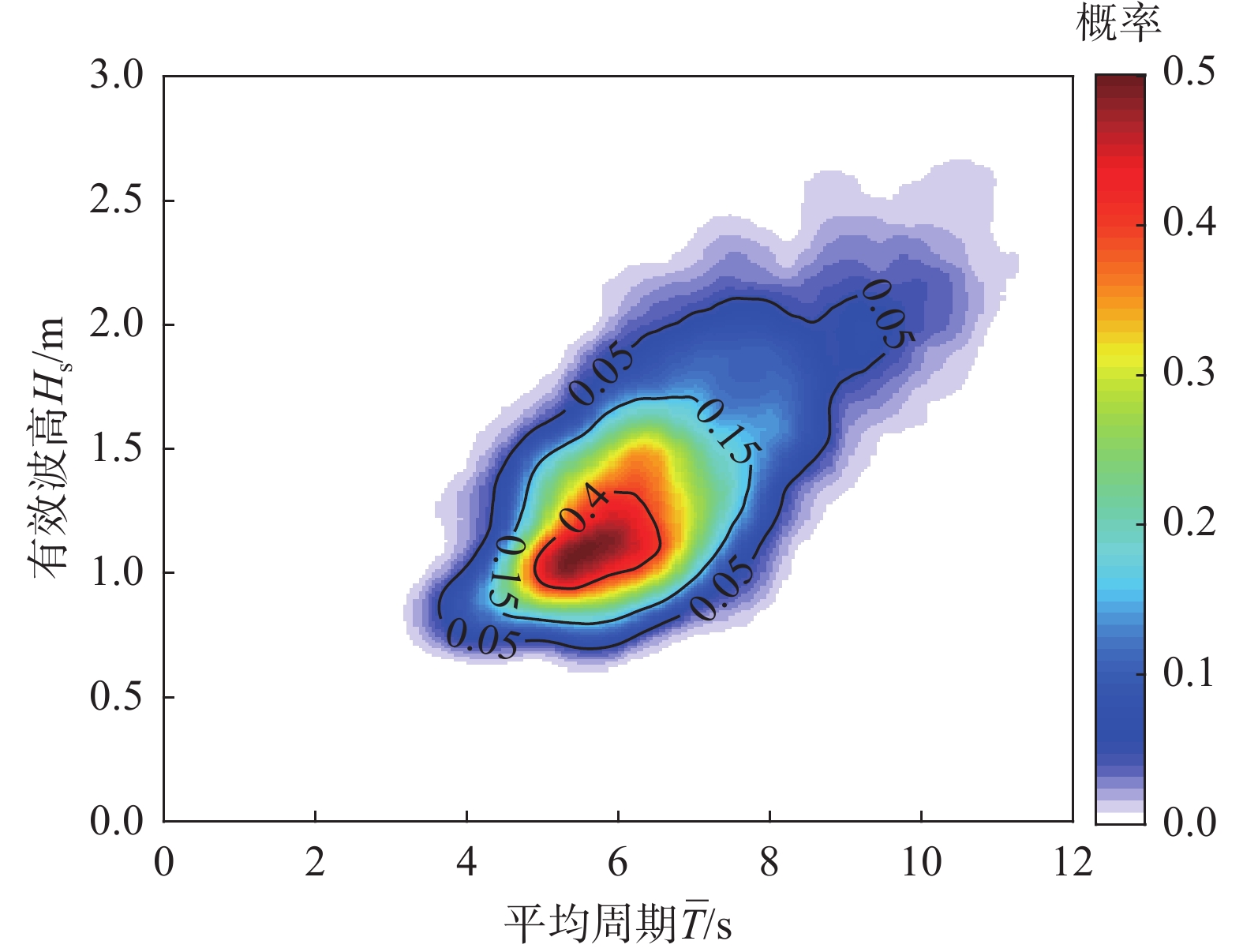
波高和周期作为随机波浪过程的两个重要特征，两者之间并非是完全独立的。根据本次的观测资料，可得到波浪的波高周期的联合分布如图9所示，最大概率对应的有效波高为1.06 m，对应的平均周期为5.42 s。根据波高周期联合分布的整体变化趋势可知，随着平均周期的增大，其对应的有效波高也在增大。
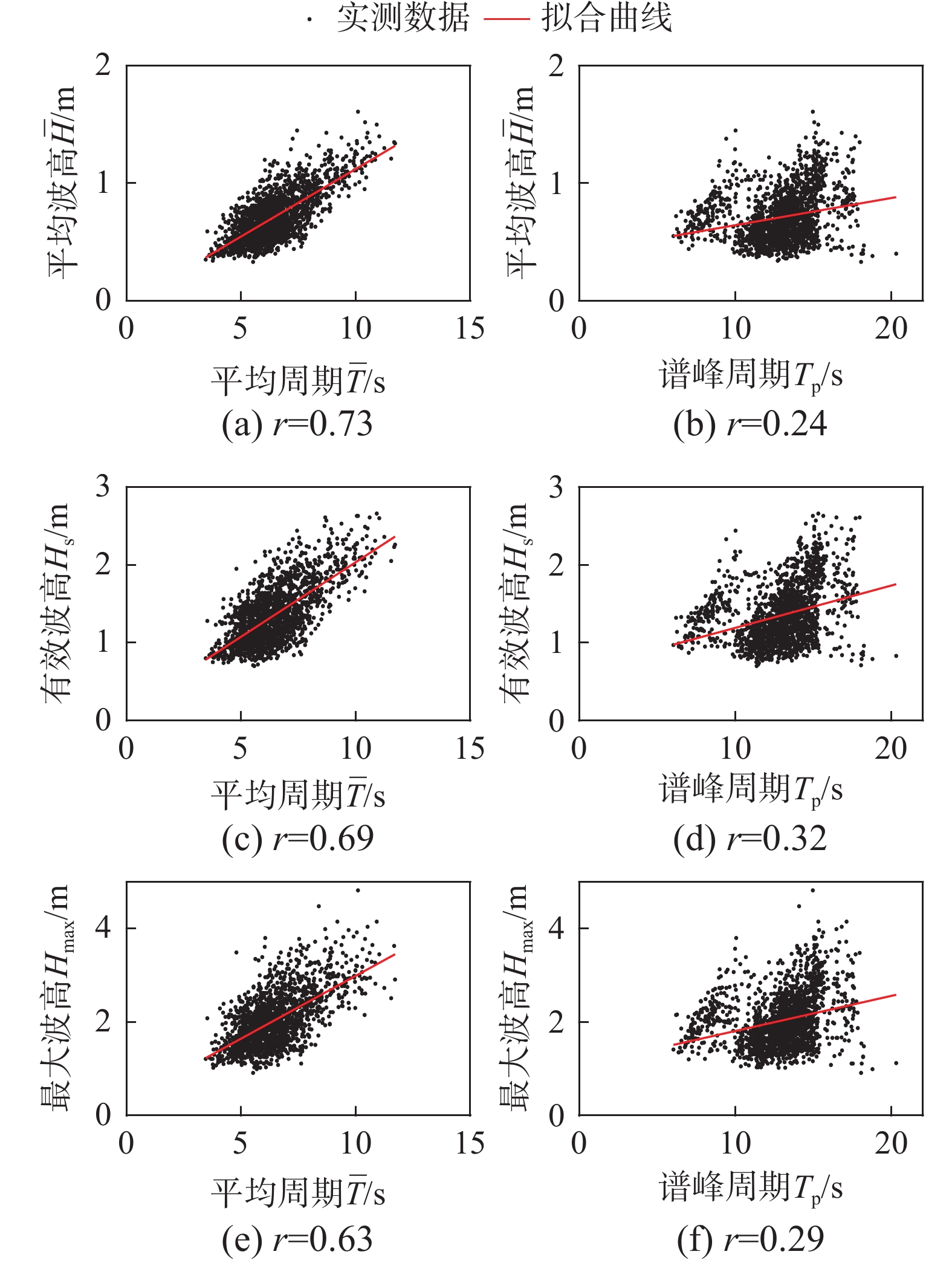
计算得到谱峰周期Tp和平均周期¯T与各特征波高(平均波高¯H，有效波高Hs和最大波高Hmax)之间的相关性见图10。计算得到的相关系数及置信度水平见表2，由表2可知，显著性水平P均远小于0.05，置信度超过99%，因此波浪的波高和周期之间是存在线性关联的。采用相关系数来衡量各个波浪特征参数之间的相关性程度：
r=n∑i=1(xi−¯x)(yi−¯y)n σxσy (7) 式中，σx和σy为变量标准差。
谱峰周期与各特征波高之间的相关系数均在0.4以下，表明谱峰周期与各特征波高之间相关性较弱；而平均周期与各特征波高与相关系数均大于0.6，说明每对变量之间都是强相关的。分析产生这一现象的原因，谱峰周期是在对波浪进行谱分析之后得到的谱型峰值对应的周期，受到谱分析方法和谱型光滑程度等多方面的影响，导致谱峰周期波动较大。而平均周期的定义如下：
T02=√m0/m2 (8) 式中，m0和m2分别为波浪谱的0阶矩和2阶矩：
mn=∫∞0fnS(f)df (9) ![]()
图 10 涌浪平均周期和谱峰周期与特征波高之间的相关性Figure 10. Correlation between the mean period and the spectral peak period and the characteristic wave heights of swell表 2 波浪周期与各特征波高之间的相关性Table 2. Correlation between the wave period and characteristic wave heights波浪周期/s 特征波高/m 显著性水平P 置信度水平 相关系数r 平均周期¯T 平均波高¯H < 10-8 > 99% 0.73 有效波高Hs < 10-8 > 99% 0.69 最大波高Hmax < 10-8 > 99% 0.63 谱峰周期Tp 平均波高¯H < 10-8 > 99% 0.24 有效波高Hs < 10-8 > 99% 0.32 最大波高Hmax < 10-8 > 99% 0.29 根据计算表达式可知，平均周期与有效波高(见式(1))均与谱面积密切相关，而波谱面积与谱分析方法和波谱光滑程度无关，因此平均周期在描述波浪周期时更加稳定。在分析波浪的波高和周期之间的关系时，采用平均周期更加合理。采用最小二乘法对各特征波高和平均周期进行回归分析，得到的拟合曲线的参数及与实测数据的均方根误差见表3，可为涌浪控制海域的特征波高估计提供参考。
表 3 平均周期与各特征波高的拟合参数Table 3. Fitting parameters of mean wave period and characteristic wave heights特征波高/m 斜率k 截距b 均方根误差RMSE 平均波高¯H 0.115 −0.03 0.15 有效波高Hs 0.191 0.12 0.26 最大波高Hmax 0.269 0.30 0.45 3 波谱拟合与分析
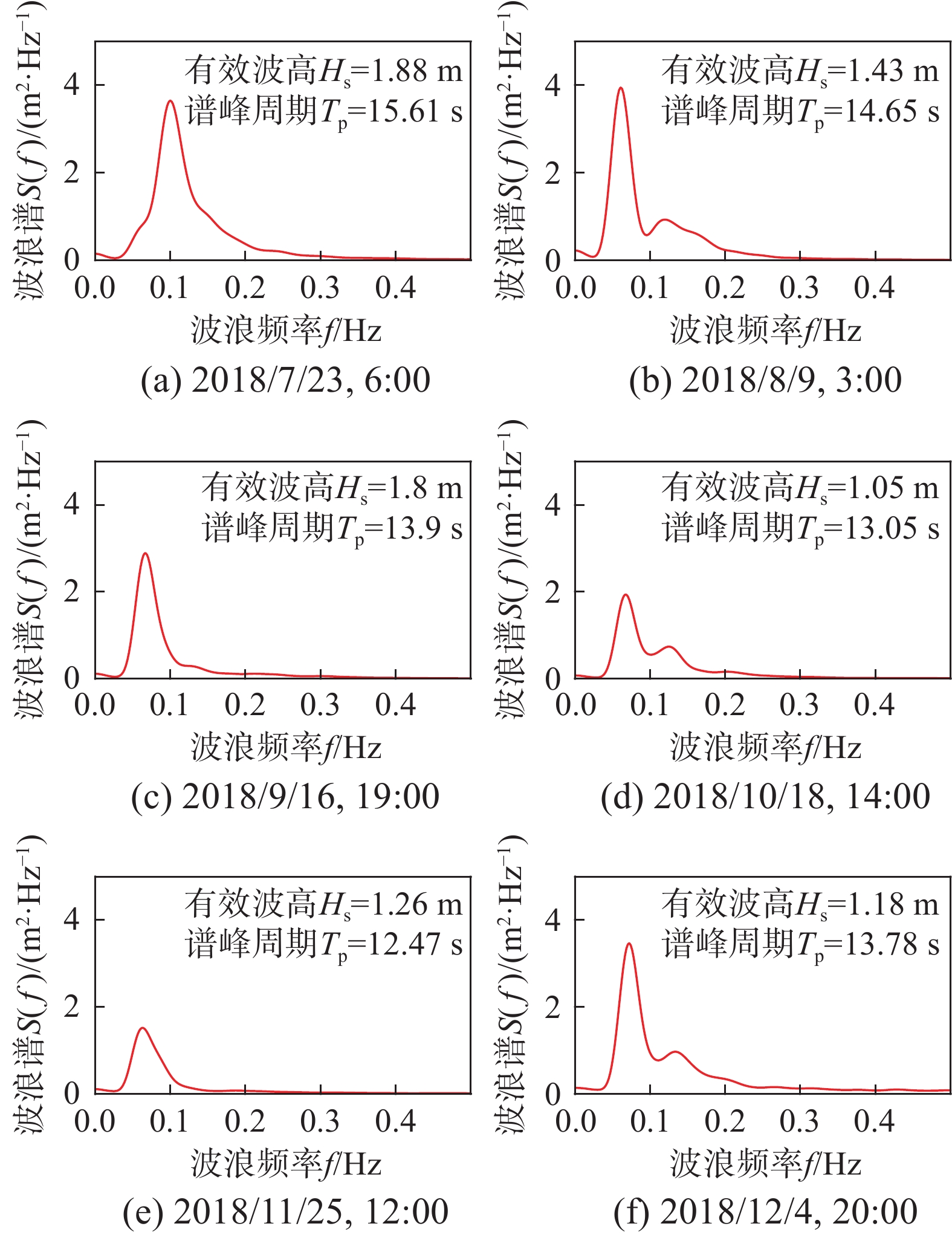
采用快速傅里叶变换方法(FFT)可得到各个时段实测波浪过程的波浪谱，选取代表时刻的波浪谱型如图11所示，观测位置处主要以单峰谱和双峰谱为主。由图11可知，对于单峰谱，谱峰周期均在10 s以上，波浪能量主要集中在涌浪部分；对于双峰谱，涌浪部分的谱峰高度远大于风浪，进一步说明该海域为涌浪主导海域。
采用以下三种常用的波浪谱模型来拟合实测波浪谱，寻求一种能够较好的描述该以长周期涌浪为主的海域的波浪谱。
ITTC谱：
S(f)=0.0081g2K−4f−5exp(−0.0324g2K4H−2sf−4) (10) 式中：f为波浪频率；K=Tp√g/Hs/2.492。
JONSWAP谱：
S(f)=βJH2sT−4pG(f)f−5exp(−1.25T−4pf−4) (11) 对于JONSWAP谱，其中的系数βJ和谱峰升高项的表达式为：
βJ=0.06238(1.094−0.01915lnγ)0.23+0.0336γ−0.185(1.9+γ)−1 (12) G(f)=γexp(−(Tpf−1)2/2σ2) (13) 式中：γ为谱峰升高因子；σ为峰形参数，当f < fp时，σ = 0.07，当f > fp时，σ = 0.09。
Ochi-Hubble谱：
S(f)=2∑j=114H2sjTpjΓ(λj)(λj+0.25)λj(Tpjf)(4λj+1)exp{−(λj+0.25)(Tpjf)4} (14) 该波浪谱模型由2个波浪谱系统组成，每个波系的频谱包含3个参数：有效波高 Hs、谱峰周期Tp以及和频谱形状参数λ。其中的系数j=1和2分别代表涌浪系统和风浪系统。
利用非线性最小二乘法，分别采用上述三种波浪谱模型来拟合实测的波浪谱，在拟合时未对单峰谱和双峰谱进行区分，拟合结果如图12所示。由图12可知，当谱型为单峰谱时，三种波浪谱模型的拟合结果只存在轻微差异，JONSWAP谱拟合结果在谱峰位置处与实测谱更加一致，这表明JONSWAP谱模型中的谱峰升高因子在调节谱峰高度上具有良好的效果；在高频尾部，ITTC谱和JONSWAP谱的拟合结果与实测谱存在差异，根据谱模型表达式可知，这两种谱模型的高频侧恒正比于f−5，无法进行谱型调节；而Ochi-Hubble谱由两个波浪谱系统组成，可以对高频侧谱型进行调节，因此在高频尾部的拟合效果较好。当谱型为双峰谱时，根据谱型可知Ochi-Hubble谱模型具有显著优势。
![]()
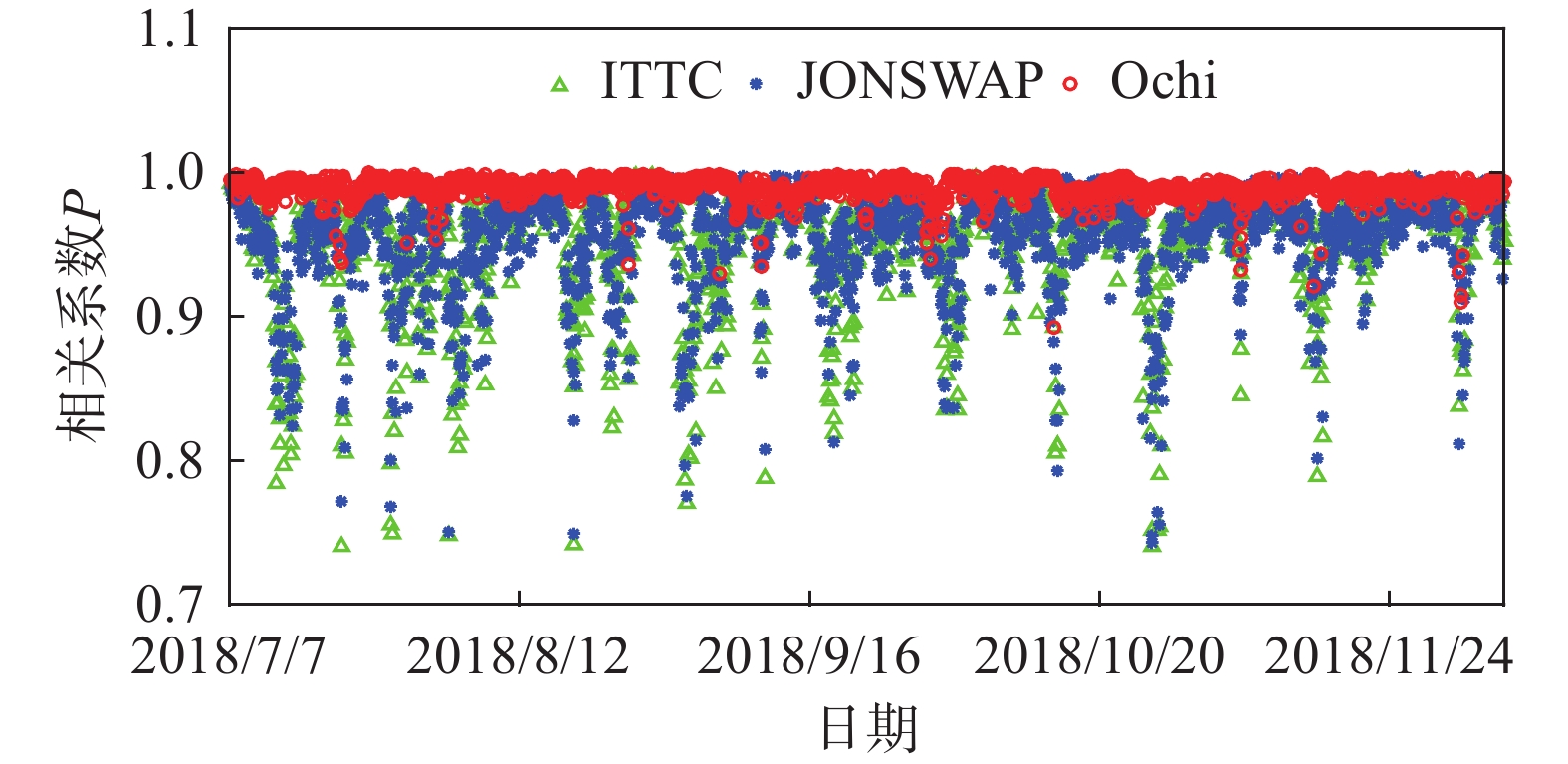
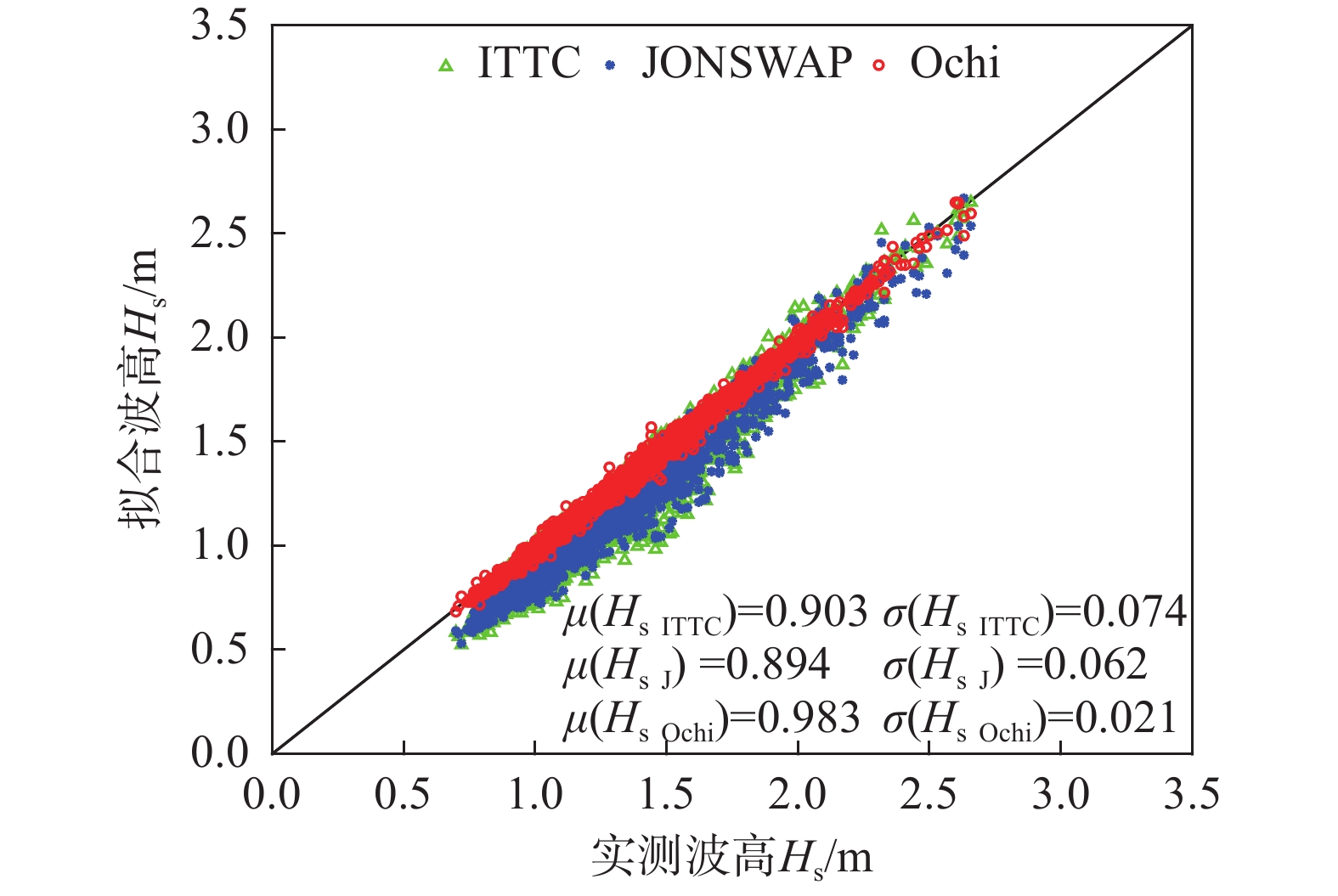
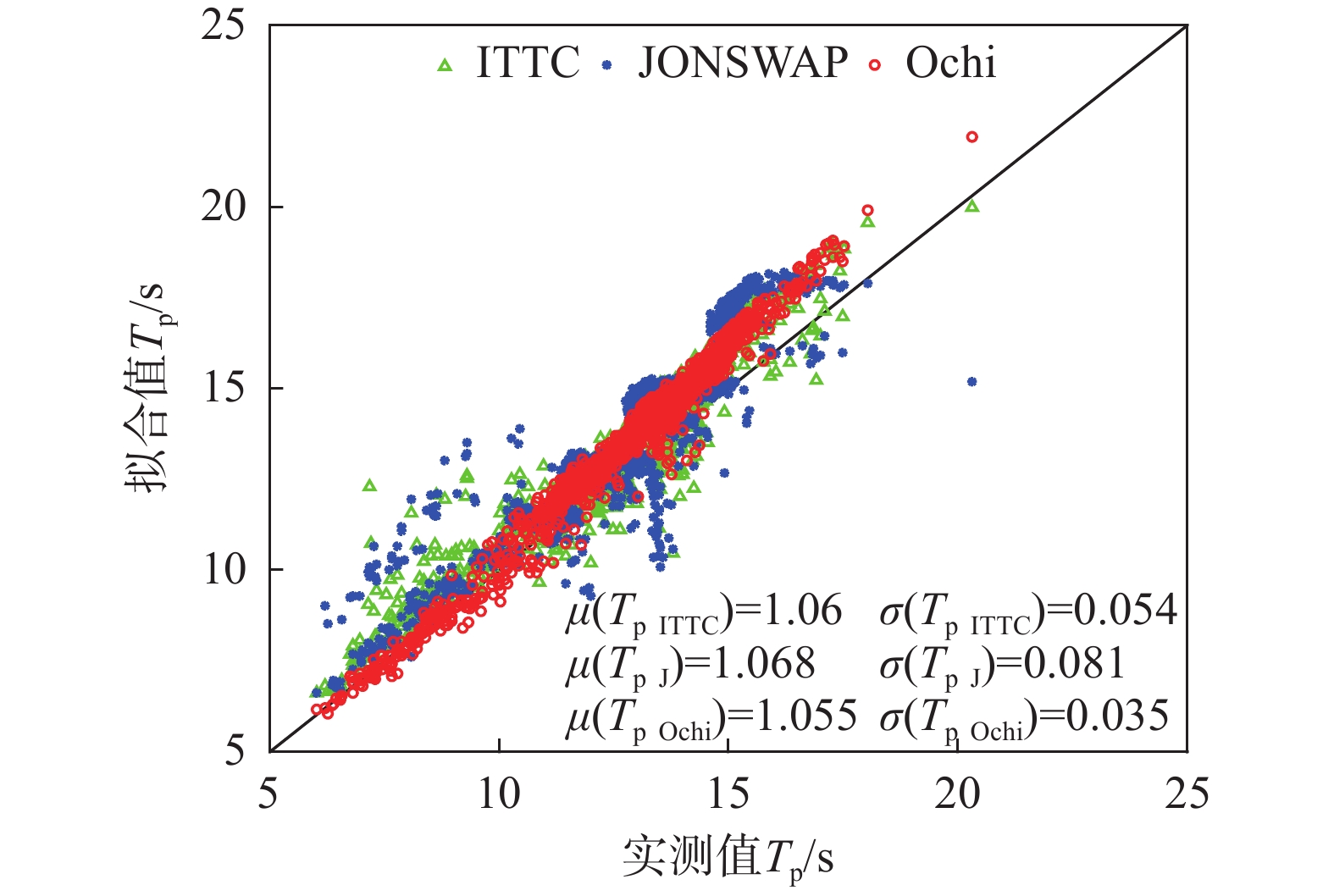
图 12 实测谱与拟合谱对比Figure 12. Comparisons between the fitted spectra and the measured spectra采用相关系数来衡量拟合谱与实测谱之间的吻合程度，见图13，可以发现Ochi-Hubble谱拟合结果的相关系数更接近1.0且保持稳定。对比拟合得到的有效波高结果见图14，其中μ和σ分别代表均值和标准差。由图14可知，JONSWAP谱拟合得到的有效波高偏小，这与LUCAS和GUEDES SOARES[24]得到的结论相同，分析产生这种误差的原因主要在于谱型高频侧的偏差，而Ochi-Hubble谱的拟合有效波高与实测值更加一致且具有更小的标准差。对比谱峰周期拟合结果见图15，同样Ochi-Hubble谱的拟合结果均值更接近于1.0且标准差最小，具有良好的效果。只有在较大谱峰周期时，拟合结果会偏大。综合考虑拟合曲线的相关性以及波浪特征参数的拟合结果，认为Ochi-Hubble谱模型能够较好的描述单峰和双峰涌浪谱。
![]()
图 13 各波浪谱模型与实测波浪谱之间的相关系数Figure 13. Correlation coefficients between modeled spectra and measured spectra![]()
图 14 有效波高拟合结果与实测结果对比注：μ和σ分别代表均值和标准差。Figure 14. Comparison between fitted significant wave height and that of measured![]()
图 15 谱峰周期拟合结果与实测结果对比注：μ和σ分别代表均值和标准差。Figure 15. Comparison between fitted spectrum peak period and that of measured4 结论
本文基于太平洋沿岸秘鲁某海域2018年7月—2018年12月的涌浪观测资料，根据TORSETHAUGEN等[35]提出的涌浪判据条件，该海域主要受到长周期涌浪的影响，对涌浪的统计特征参数和波浪谱进行了研究，得到以下主要结论：
(1) 根据波高周期联合分布以及相关性分析可知，在分析波浪的波高与周期之间的关系时，采用平均周期更加合理。利用实测数据拟合得到了各特征波高与波浪平均周期之间的关系式，可用于对涌浪的特征波高进行估计。
(2) 采用多种波浪谱模型拟合实测波谱，通过对比波浪谱型，相关系数和波浪特征参数的拟合结果，得到Ochi-Hubble谱的拟合谱型与实测波浪谱基本吻合，且相关系数均分布在1.0附近。因此，认为在观测海域Ochi-Hubble谱模型能够较好的描述涌浪谱，在单峰谱和双峰谱时，都能够保证具有较好的拟合结果，无需预先对实测谱进行单峰谱与双峰谱的分离，便于工程应用。
-
![]()
图 4 观测时间段内，(a)有效波高Hs和(b)谱峰周期Tp随时间的变化曲线
Figure 4. Variation of (a) significant wave height and (b) spectral peak period during the observation period
![]()
图 6 实测的谱峰周期Tp与临界周期Tpf对比情况
Figure 6. Comparisons between the measured spectra peak periods Tp and the critical periods Tpf
![]()
图 7 观测位置处波高的瑞利分布与格鲁霍夫斯基分布对比
Figure 7. The comparison between the Rayleigh distribution of wave height and that of the Глуховский distribution at the observation site
![]()
图 8 8月20日各时段的波高概率分布情况
Figure 8. The probability distribution of wave height at different times on August 20
![]()
图 10 涌浪平均周期和谱峰周期与特征波高之间的相关性
Figure 10. Correlation between the mean period and the spectral peak period and the characteristic wave heights of swell
![]()
图 12 实测谱与拟合谱对比
Figure 12. Comparisons between the fitted spectra and the measured spectra
![]()
图 13 各波浪谱模型与实测波浪谱之间的相关系数
Figure 13. Correlation coefficients between modeled spectra and measured spectra
![]()
图 14 有效波高拟合结果与实测结果对比
注：μ和σ分别代表均值和标准差。
Figure 14. Comparison between fitted significant wave height and that of measured
![]()
图 15 谱峰周期拟合结果与实测结果对比
注：μ和σ分别代表均值和标准差。
Figure 15. Comparison between fitted spectrum peak period and that of measured
表 1 各月份有效数据次数
Table 1 The number of effective data of every month
月份 异常数据次数 有效数据次数 7 19 276 8 5 356 9 4 347 10 5 355 11 3 345 12 3 78 
下载: 导出CSV
表 2 波浪周期与各特征波高之间的相关性
Table 2 Correlation between the wave period and characteristic wave heights
波浪周期/s 特征波高/m 显著性水平P 置信度水平 相关系数r 平均周期¯T 平均波高¯H < 10-8 > 99% 0.73 有效波高Hs < 10-8 > 99% 0.69 最大波高Hmax < 10-8 > 99% 0.63 谱峰周期Tp 平均波高¯H < 10-8 > 99% 0.24 有效波高Hs < 10-8 > 99% 0.32 最大波高Hmax < 10-8 > 99% 0.29
下载: 导出CSV
表 3 平均周期与各特征波高的拟合参数
Table 3 Fitting parameters of mean wave period and characteristic wave heights
特征波高/m 斜率k 截距b 均方根误差RMSE 平均波高¯H 0.115 −0.03 0.15 有效波高Hs 0.191 0.12 0.26 最大波高Hmax 0.269 0.30 0.45
下载: 导出CSV
-
[1] 李淑江, 李泽文, 范斌, 等. 海南岛东南近岸海浪观测及统计特征 [J]. 海洋科学进展, 2016, 34(1): 1 − 9. doi: 10.3969/j.issn.1671-6647.2016.01.001 LI Shujiang, LI Zewen, FAN Bin, et al. Wave observation and statistical analysis in the southeast coast of Hainan island [J]. Advances in Marine Science, 2016, 34(1): 1 − 9. (in Chinese) doi: 10.3969/j.issn.1671-6647.2016.01.001
[2] 冯兴如, 李近元, 尹宝树, 等. 海南东方近岸海域海浪观测特征研究 [J]. 热带海洋学报, 2018, 37(3): 1 − 8. FENG Xingru, LI Jinyuan, YIN Baoshu, et al. Characteristics of ocean waves in coastal area of Dongfang, Hainan Island based on observations [J]. Journal of Tropical Oceanography, 2018, 37(3): 1 − 8. (in Chinese)
[3] 魏凯, 钟茜, 沈忠辉, 等. 台风作用下风-浪-潮三维环境等值面模型[J]. 工程力学, 2021, 38(11): 189 − 198. doi: 10.6052/j.issn.1000-4750.2020.11.0831 WEI Kai, ZHONG Xi, SHEN Zhonghui, et al. Environmental contour of wind-wave-storm surges induced by typhoons [J]. Engineering Mechanics, 2021, 38(11): 189 − 198. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.11.0831
[4] 刘章军, 张文远, 彭辉. 多向不规则波浪模拟的降维方法 [J]. 工程力学, 2023, 40(4): 12 − 20. doi: 10.6052/j.issn.1000-4750.2021.09.0753 LIU Zhangjun, ZHANG Wenyuan, PENG Hui. Dimension-reduction method for mutidirectional irregular wave simulation [J]. Engineering Mechanics, 2023, 40(4): 12 − 20. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.09.0753
[5] 周延东, 雷震名, 孙国民, 等. 涌浪基本理论研究综述 [J]. 水道港口, 2016, 37(1): 1 − 6. doi: 10.3969/j.issn.1005-8443.2016.01.001 ZHOU Yandong, LEI Zhenming, SUN Guomin, et al. A review on basic theory research of swell [J]. Journal of Waterway and Harbor, 2016, 37(1): 1 − 6. (in Chinese) doi: 10.3969/j.issn.1005-8443.2016.01.001
[6] 郑崇伟, 周林, 周立佳. 西沙、南沙海域波浪及波浪能季节变化特征 [J]. 海洋科学进展, 2011, 29(4): 419 − 426. doi: 10.3969/j.issn.1671-6647.2011.04.001 ZHENG Chongwei, ZHOU Lin, ZHOU Lijia. Seasonal variation of wave and wave energy in Xisha and Nansha sea area [J]. Advances in Marine Science, 2011, 29(4): 419 − 426. (in Chinese) doi: 10.3969/j.issn.1671-6647.2011.04.001
[7] 严明宇, 马小舟, 郑振钧, 等. 涌浪作用下港内大型集装箱船运动特性数值研究 [J]. 海洋工程, 2023, 41(6): 100 − 111. YAN Mingyu, MA Xiaozhou, ZHENG Zhenjun, et al. Numerical research on motion characteristics of a large container ship moored at a port under swell [J]. The Ocean Engineering, 2023, 41(6): 100 − 111. (in Chinese)
[8] 陈晓斌, 周林, 史文丽, 等. 台风“梅花”风浪场和涌浪场特征分析 [J]. 海洋科学进展, 2013, 31(1): 22 − 30. doi: 10.3969/j.issn.1671-6647.2013.01.003 CHEN Xiaobin, ZHOU Lin, SHI Wenli, et al. Characteristics of wave and surge fields of typhoon MUIFA [J]. Advances in Marine Science, 2013, 31(1): 22 − 30. (in Chinese) doi: 10.3969/j.issn.1671-6647.2013.01.003
[9] 魏凯, 沈忠辉, 吴联活, 等. 强台风作用下近岸海域波浪-风暴潮耦合数值模拟 [J]. 工程力学, 2019, 36(11): 139 − 146. doi: 10.6052/j.issn.1000-4750.2018.12.0646 WEI Kai, SHEN Zhonghui, WU Lianhuo, et al. Coupled numerical simulation on wave and storm surge in coastal areas under strong typhoons [J]. Engineering Mechanics, 2019, 36(11): 139 − 146. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.12.0646
[10] 季新然, 邹丽, 柳淑学, 等. 多向不规则波浪作用下群墩结构所受波浪力的实验研究 [J]. 工程力学, 2019, 36(10): 238 − 243. doi: 10.6052/j.issn.1000-4750.2018.07.0399 JI Xinran, ZOU Li, LIU Shuxue, et al. Experimental study on the multidirectional wave force on an array of cylinders [J]. Engineering Mechanics, 2019, 36(10): 238 − 243. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.07.0399
[11] 裴晔, 陶爱峰, 张义丰, 等. 东海E3海域低频涌浪生成机制研究 [J]. 海洋湖沼通报, 2016(1): 17 − 24. PEI Ye, TAO Aifeng, ZHANG Yifeng, et al. The generation mechanisms of low-frequency well in the E3 sea area of the East China sea [J]. Transactions of Oceanology and Limnology, 2016(1): 17 − 24. (in Chinese)
[12] 周昳鸣, 杨立华, 郇彩云, 等. 浙江苍南近岸海域实测波浪特征分析 [J]. 海洋学研究, 2023, 41(3): 43 − 55. ZHOU Yiming, YANG Lihua, HUAN Caiyun, et al. Analysis of measured wave characteristics in the coastal waters of Cangnan, Zhejiang Province [J]. Journal of Marine Sciences, 2023, 41(3): 43 − 55. (in Chinese)
[13] 韩晓伟, 周林, 游大鸣, 等. 0801号台风风浪场和涌浪场的数值模拟 [J]. 大气科学学报, 2011, 34(5): 597 − 605. doi: 10.3969/j.issn.1674-7097.2011.05.010 HAN Xiaowei, ZHOU Lin, YOU Daming, et al. Numerical simulation of wind wave and swell fields generated by 0801 typhoon [J]. Transactions of Atmospheric Sciences, 2011, 34(5): 597 − 605. (in Chinese) doi: 10.3969/j.issn.1674-7097.2011.05.010
[14] 杨斌, 施伟勇, 叶钦, 等. 舟山岛东北部沿海实测台风浪特性 [J]. 水科学进展, 2017, 28(1): 106 − 115. YANG Bin, SHI Weiyong, YE Qin, et al. Characteristics of waves in coastal waters of northeast Zhoushan Island during typhoons [J]. Advances in Water Science, 2017, 28(1): 106 − 115. (in Chinese)
[15] GHAZANGIAN R, SHAFIEEFAR M, PANAHI R, et al. An appropriate unidirectional wave spectrum model for the Strait of Hormuz [J]. Journal of Marine Science and Application, 2015, 14(3): 261 − 269. doi: 10.1007/s11804-015-1313-y
[16] BRETSCHNEIDER C L. Wave variability and wave spectra for wind generated gravity waves [R]. Texas, U.S.: Texas A & M University, 1959: 192.
[17] PIERSON W J JR, MOSKOWITZ L. A proposed spectral form for fully developed wind seas based on the similarity theory of S. A. Kitaigorodskii [J]. Journal of Geophysical Research, 1964, 69(24): 5181 − 5190. doi: 10.1029/JZ069i024p05181
[18] MITSUYASU H. The one-dimensional wave spectra at limited fetch [C]// Proceedings of the 13th International Conference Coastal Engineering. Vancouver: ASCE, 1972: 289 − 306.
[19] HUANG N E, LONG S R, TUNG C C, et al. A unified two-parameter wave spectral model for a general sea state [J]. Journal of Fluid Mechanics, 1981, 112: 203 − 224. doi: 10.1017/S0022112081000360
[20] ITTC. The specialist committee on waves, final report and recommendations to the 23rd ITTC [C]// Proceedings of the 23th International Towing Tank Conference.Venice, Italy: ITTC, 2002: 544 − 551.
[21] LEE H S, KIM S D. A comparison of several wave spectra for the random wave diffraction by a semi-infinite breakwater [J]. Ocean Engineering, 2006, 33(14/15): 1954 − 1971.
[22] GODA Y. A unified nonlinearity parameter of water waves [J]. Report of the Port and Harbour Research Institute, 1983, 22(3): 3 − 30.
[23] OLAGNON M, EWANS K, FORRISTALL G, et al. West africa swell spectral shapes [C]// Proceedings of the 32nd International Conference on Ocean, Offshore and Arctic Engineering. Nantes: ASME, 2013: V02BT02A029.
[24] LUCAS C, GUEDES SOARES C. On the modelling of swell spectra [J]. Ocean Engineering, 2015, 108: 749 − 759. doi: 10.1016/j.oceaneng.2015.08.017
[25] GAO X, MA X Z, MA Y X, et al. Spectral characteristics of swell-dominated seas with in situ measurements in the coastal seas of peru and sri lanka [J]. Journal of Atmospheric and Oceanic Technology, 2022, 39(6): 755 − 770. doi: 10.1175/JTECH-D-21-0143.1
[26] 俞聿修, 柳淑学. 随机波浪及其工程应用 [M]. 4版. 大连: 大连理工大学出版社, 2011: 154 − 155. YU Yuxiu, LIU Shuxue. Random wave and its applications to engineering [M]. 4th ed. Dalian: Dalian University of Technology Press, 2011: 154 − 155. (in Chinese)
[27] 孙连成. 渤海湾西部海域波浪特征分析 [J]. 黄渤海海洋, 1991, 9(3): 50 − 58. SUN Liancheng. Analysis of wave characteristics of the west offshore area of the Bohai Bay [J]. Journal of Oceanography of Huanghai & Bohai Seas, 1991, 9(3): 50 − 58. (in Chinese)
[28] 陈红霞, 华锋, 袁业立. 中国近海及临近海域海浪的季节特征及其时间变化[J]. 海洋科学进展, 2006, 24(4): 407 − 415. doi: 10.3969/j.issn.1671-6647.2006.04.001 CHEN Hongxia, HUA Feng, YUAN Yeli. Seasonal characteristics and temporal variations of ocean wave in the Chinese offshore waters and adjacent sea areas [J]. Advances in Marine Science, 2006, 24(4): 407 − 415. (in Chinese) doi: 10.3969/j.issn.1671-6647.2006.04.001
[29] 孙庆颖. 基于ERA5的中国海域波浪能资源时空特征分析[D]. 烟台: 鲁东大学, 2020. SUN Qingying. Analysis of spatial and temporal characteristics of wave energy resources along the coast of China based on ERA5 [D]. Yantai: Ludong University, 2020. (in Chinese)
[30] PREVOSTO M, EWANS K, FORRISTALL G Z, et al. Swell genesis, modelling and measurements in west africa [C]// Proceedings of the 32nd International Conference on Ocean, Offshore and Arctic Engineering. Nantes: ASME, 2013: V02BT02A028.
[31] ZHENG K W, SUN J, GUAN C L, et al. Analysis of the global swell and wind sea energy distribution using WAVEWATCH III [J]. Advances in Meteorology, 2016, 2016: 8419580.
[32] DONG G H, ZHENG Z J, MA X Z, et al. Characteristics of low-frequency oscillations in the Hambantota Port during the southwest monsoon [J]. Ocean Engineering, 2020, 208: 107408. doi: 10.1016/j.oceaneng.2020.107408
[33] ZHENG Z J, MA X Z, MA Y X, et al. Wave estimation within a port using a fully nonlinear Boussinesq wave model and artificial neural networks [J]. Ocean Engineering, 2020, 216: 108073. doi: 10.1016/j.oceaneng.2020.108073
[34] MAHMOUDOF S M. Investigation of infragravity waves dependency on wind waves for breaking and nonbreaking conditions in the sandy beaches of southern Caspian Sea (Nowshahr Port) [J]. International Journal of Coastal and Offshore Engineering, 2018, 1(4): 13 − 20. doi: 10.29252/ijcoe.1.4.13
[35] TORSETHAUGEN K, HAVER S. Simplified double peak spectral model for ocean waves [C]// Proceedings of the Fourteenth International Offshore and Polar Engineering Conference. Toulon: ISOPE, 2004: ISOPE-I-04-289.
计量
- 文章访问数: 19
- HTML全文浏览量: 8
- PDF下载量: 4
