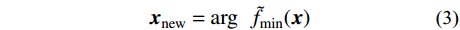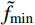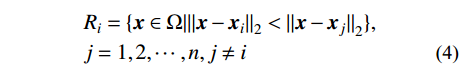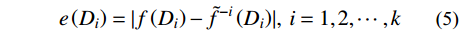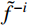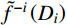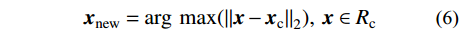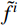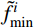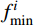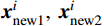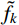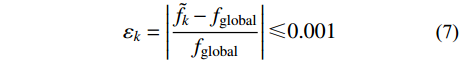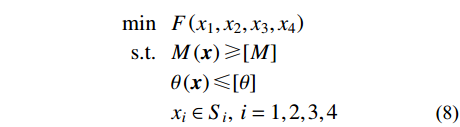A SURROGATE-BASED OPTIMIZATION DESIGN METHOD BASED ON HYBRID INFILL SAMPLING CRITERION
-
摘要: 在工程优化设计中,采用数值仿真模拟计算结构响应需耗费大量的时间和计算成本,给计算密集型的优化设计带来了巨大挑战,因此基于代理模型的序列优化设计方法得到了深入研究和广泛应用。对代理模型的序列优化方法框架进行了简要的概述;针对现有方法中存在的不足,发展了一类模型无关的混合加点准则,使优化循环过程中产生的新样本点分布在当前最小值邻域以及设计空间中交叉验证误差较大的区域,局部开发与全局搜索并行,能够更加准确地找到全局最优解;将发展的混合加点准则引入到代理模型优化框架中,并结合粒子群优化算法,提出了一种高效的代理模型优化设计方法;通过数学算例和工程算例对建议方法进行了验证。算例结果表明,与基于传统加点准则的代理模型优化设计方法比较,建议方法能够兼顾计算精度与效率,具有更好的全局寻优特性。Abstract: In engineering optimization design, numerical simulation calculation of structural response is expensive and time-consuming, which brings great challenges to compute-intensive optimization design. Therefore, the surrogate-based sequential optimization method has been well studied and widely used. Firstly, the framework of the surrogate-based sequence optimization is summarized at first. Secondly, a model-independent hybrid infill sampling criterion is developed in view of the insufficiency in existing methods. The new sample points generated during optimization process are distributed in the neighborhood of the current minimum value and the region with largest cross-validation error in the design space. The local exploitation and global exploration can be carried out simultaneously to find accurate global optimal solution. Thirdly, hybrid infill sampling criterion is introduced into the surrogate-based optimization framework combined with particle swarm optimization algorithm, and an efficient surrogate-based optimization design method is proposed. Finally, the proposed method is verified by mathematical and engineering examples. Compared with the optimization method by the grounds of traditional criterions, the proposed method can keep the tradeoff of accuracy and efficiency, which has better global optimization characteristics.
-
随着计算机建模分析能力的不断提高,在工程优化设计领域中,采用有限元分析或计算流体动力学技术进行结构分析成为获取实际响应的主要手段。然而,数值仿真模型缺乏与设计变量相关的目标函数及约束函数的显式表达式,属于“黑箱问题”,基于显式、连续函数梯度信息的传统优化算法不再适用;且数值仿真模拟往往需要耗费大量的时间,使得遗传算法[1]、粒子群算法[2]等一系列现代启发式群算法在优化设计中的计算成本变得难以接受。
幸运的是,随着代理模型的发展以及代理模型技术在优化设计中的应用,上述问题在一定程度上得以缓解[3]。代理模型技术通过一定数量的设计变量样本及相应的响应值,建立输入与输出的近似函数关系。将代理模型与优化算法相结合,形成了一类基于代理模型的优化(surrogate-based optimization, SBO)方法,能大幅减少优化过程中的计算量,提高优化设计的效率。最初这一方法被应用于“一步”优化设计框架中[4],直接使用一次抽样所得样本建立代理模型进行优化求解,不涉及加点过程,所得代理模型精度往往难以保证,且优化结果偏差较大。而序列优化设计能够通过自适应地添加新样本,提高代理模型精度、降低优化误差,因此,基于代理模型的序列优化方法得到了广泛的认可和应用[5-6]。
基于代理模型的序列优化方法首先采用少量初始样本建立代理模型,在优化过程中根据加点准则进行自适应采样,不断更新代理模型并进行优化求解,直至满足收敛条件。这一过程中,加点准则的选择将直接影响代理模型精度、最终优化结果以及优化设计效率,显得尤为重要,因此探究和发展性能更佳的加点策略成为现阶段工程优化设计领域的研究热点[7-18]。
现有加点策略中,经典的加点准则是将每次优化的最优设计直接加入样本集中更新模型,即最小化模型预测准则[7]。这一加点准则以最优解为导向,能使算法迅速地收敛,但它过分依赖于已有模型的预测结果,没有考虑代理模型精度较低带来的误差,相关研究[8]表明,此种做法会使算法难以搜寻到全局最优解,优化进程陷于局部最小值。为了更好地在整个设计空间进行全局优化设计,Jones等[9]基于Kriging模型提出了期望提高(expected improvement, EI)准则,并与序列优化相结合得到一种高效全局优化(efficient global optimization, EGO)算法。随后许多学者针对EI准则进行了改进,发展了q-EI[10]、广义期望提高[11]、加权EI 函数[12]等,拓展了该方法的适用范围。同时,一系列兼顾局部开发和全局搜索能力的加点准则被陆续提出,如PI(probability of improvement)准则[13]、MSE (mean square error)准则[14]、LBC (low-bounding confidence)准则[15]等。除此之外,用于并行计算的多点加点准则由于计算效率颇高受到一些学者的青睐,高月华等[16]、Hamza等[17]、Zhan等[18]对此展开了深入的研究。
然而,上述加点准则仍存在一些不足之处:一方面,上述优化设计方法和采样策略均基于贝叶斯估计的Kriging模型,不适用于缺乏方差估计的代理模型,如径向基函数[19]等,发展具有普适性的加点准则有待进一步研究;另一方面,Kriging模型中预测方差是样本空间距离的相关函数,基于方差的加点策略侧重在样本稀疏的区域进行抽样,这将使样本趋于空间均匀分布,背离自适应采样的初衷,不利于优化效率的提高。因此,如何进一步提高代理模型优化设计的全局寻优能力和优化效率,仍是目前亟待解决的问题[19]。
据此,针对复杂黑箱问题的优化设计,本文提出了一种适用于任意代理模型的混合加点序列优化方法。该方法在优化循环过程中使用混合加点准则添加新的样本点,对设计空间进行全局搜索和局部开发,寻找最优解邻域的同时搜索模型预测偏差较大的区域,以期能够最大程度地寻到全局最优点,提高优化算法的精度和效率。
1 代理模型优化设计方法概述
对于任意的约束优化问题,其数学模型为[20]:
\begin{split} \min \;\;\;&f({\boldsymbol{x}}) \\[-2pt] {\rm{s}}{\rm{.t}}{\rm{. }}\;\;\;&{g_i}({\boldsymbol{x}}) = 0,\;\;\;i = 1, 2, \cdots ,{m_1} \\[-2pt] \;\;\;\;\;\;\;\;\;&{h_j}{\rm{(}}{\boldsymbol{x}}{\rm{)}} \leqslant 0,\;\;\;j = 1, 2, \cdots ,{m_2} \\[-2pt] \;\;\;\;\;\;\;\;\;&{{\boldsymbol{x}}_L} \leqslant {\boldsymbol{x}} \leqslant {{\boldsymbol{x}}_R} \end{split} (1) 其中,f(x)为优化目标函数,须服从m1个等式约束方程和m2个不等式约束,d维设计变量x的取值范围为[xL, xR]。将代理模型技术引入优化设计中,式(1)可转化为如下形式:
\begin{split} \min \;\;\;&\tilde f({\boldsymbol{x}}) \\[-2pt] {\rm{s}}{\rm{.t}}{\rm{. }}\;\;\;&{{\tilde g}_i}({\boldsymbol{x}}) = 0,\;\;\;i = 1, 2, \cdots ,{m_1} \\[-2pt] \;\;\;\;\;\;\;\;\;&{{\tilde h}_j}{\rm{(}}{\boldsymbol{x}}{\rm{)}} \leqslant 0,\;\;\;j = 1, 2, \cdots ,{m_2} \\[-2pt] \;\;\;\;\;\;\;\;\;&{{\boldsymbol{x}}_L} \leqslant {\boldsymbol{x}} \leqslant {{\boldsymbol{x}}_R} \end{split} (2) 式中,上标“~”表示采用一定数量样本建立的代理模型函数。
为求解上述优化问题,一般的代理模型序列优化设计流程如图1所示。在序列优化过程中,样本的选取决定了代理模型的精度以及优化进行的方向,因此加点准则对实现高效的全局优化具有重要影响。
2 基于混合加点准则的代理模型序列优化方法
2.1 混合加点准则
本文提出了一种与代理模型无关的混合加点准则,其核心思想是保证优化算法具备较好的局部开发和全局搜索能力。混合加点准则在一次序列优化循环中通过局部加点和全局加点同时产生2个样本,下面将对这两个加点过程展开详细描述。
1)局部加点过程
最小化模型预测准则[7]是最早应用于序列优化设计的一种加点方法,具有操作简单、易于实现的特点,可以引导优化算法很快地收敛,表现出较强的局部开发能力。因此,本文采用该准则进行局部加点:在每次循环中对当前代理模型进行优化求解,将所得最优设计加入样本集中,更新代理模型。该准则可表示为:
{{\boldsymbol{x}}_{\rm{new}}} = \arg \;\;{\tilde f_{\min }}({\boldsymbol{x}}) (3) 式中,"arg"表示自变量与因变量之间的映射关系,返回值为当前模型最小值
{\tilde f_{\min }} 对应的输入参数。但由于研究对象往往具有多峰、非线性等复杂特点,代理模型拟合的精度较低,导致全局最优点很容易被忽略,仅使用局部加点准则的优化结果往往难以满足要求。
2)全局加点过程
全局加点的目的是探究设计空间中最优解的潜在区域,进一步提高模型精度,使优化朝着全局最优的方向进行。Xu等[21]基于泰森图解法和LOO(leave-one-out)交叉验证提出了用于构造全局代理模型CV-Voronoi采样方法,为序列优化设计的全局探索提供了可借鉴的思路。基于此,本文引入k-fold交叉验证(k-fold cross validation)方法,发展了一种高效的全局加点方法,该方法可根据误差追踪对整个设计空间进行探索,在预测误差较大的区域采样,能够有效减少计算成本,提高代理模型精度。其加点过程可大致分为设计空间的划分、预测误差的计算以及新样本的选取3个步骤。
首先采用泰森图解法划分设计空间,以便更直观地研究目标函数在局部区域的特性。假设d维设计空间中存在一组样本点X={x1, x2,···, xn},泰森图解法根据这组样本将设计空间分割为n个泰森多边形{R1, R2, ···, Rn},Ri的定义为:
\begin{split} & {R_i} = \{ {{\boldsymbol{x}} \in \Omega | {{{\| {{\boldsymbol{x}} - {{\boldsymbol{x}}_i}} \|}_2} < {{\| {{\boldsymbol{x}} - {{\boldsymbol{x}}_j}} \|}_2}} } \} ,\\& j = {1,2, \cdots ,n} ,j \ne i \end{split} (4) 式中:Ω代表整个设计空间;x为空间中任意一向量点;||·||2表示向量的二范数。图2展示了一个二维的泰森多边形(Voronoi图),明显看出多边形Ri内任意一点到其中心点xi的距离是最近的,因此可以将多边形区域Ri视为中心点xi的影响范围。由于Voronoi图形状不规则,且对于高维度问题难以表达,实际操作中采用大量随机点来近似描述多边形的形状。
然后,对各个样本点及其所在区域进行误差评价。交叉验证被视为一种非常有效的误差计算方法,可以从有限的数据中获取尽可能多的信息,采用计算简单高效的k-fold交叉验证方法计算误差。在k-fold交叉验证中,将n个样本点随机地分为k组互斥的子集{D1, D2, ···, Dk},样本的预测误差由下式可得:
e\left({{D_i}} \right) = | {f\left({{D_i}} \right) - {{\tilde f}^{ - i}}\left({{D_i}} \right)} |,\;i = 1, 2, \cdots , k (5) 式中:f(Di)为Di集合中所有样本的实际响应值;
{{{\tilde f}^{ - i}}} 是由除Di组以外样本构建的代理模型;{{{\tilde f}^{ - i}}\left( {{D_i}} \right)} 表示Di中样本的预测响应值。将样本的交叉验证误差进行排序,选出预测误差最大的点xc,其所在的多边形Rc被记为“敏感多边形”[21],在该区域内进行采样。为了让样本具有较好的空间分布均匀性,且最大程度地获取函数的局部特征,应使敏感多边形Rc内产生的新样本点距中心点xc较远,根据最大化最小距离准则筛选样本,即:
{{\boldsymbol{x}}_{\rm{new}}} = \arg \;\max ({\left\| {{\boldsymbol{x}} - {{\boldsymbol{x}}_{\rm{c}}}} \right\|_2}),\;{\boldsymbol{x}} \in {R_{\rm{c}}} (6) 式中,“arg”含义与式(3)中一致,计算得到与最大化函数最优解对应的输入向量 x 。
2.2 基于混合加点准则的优化方法及其实现
基于上述混合加点准则,本文发展了一种通用的代理模型序列优化方法,其优化设计流程如图3所示,图中右侧虚线框内为混合加点过程。
选择适当的代理模型、优化算法,确定相关计算参数后,基于混合加点准则的代理模型序列优化设计的具体实施步骤为:
1)根据给定的试验设计方法,在设计空间中选取少量初始样本 X 0,此时循环次数i=0;
2)进行数值计算或结构分析,获取样本X i对应的实际响应f(X i);
3)基于已有样本X i及其响应值f(X i),运用代理模型技术构建近似函数
{\tilde f^i} (X i);4)采用优化算法对当前代理模型进行优化求解,得到第i次循环的最优解
{\tilde f^i_{\rm{min}}} 并计算其实际响应值f^i_{\rm{min}} ;5)核查优化是否收敛:若优化结果已满足收敛条件,则优化停止,并输出最优设计{xmin, fmin};否则i=i+1,继续下一步骤;
6)采用混合加点准则进行选点:根据等式(3)计算第一个候选样本点
{\boldsymbol{x}}_{{\rm{new}}1}^i ;同时,使用式(5)计算已有样本X i−1的k-fold交叉验证误差e,依据式(6)在产生最大误差的多边形区域Rc内挑选第二个候选样本{\boldsymbol{x}}_{{\rm{new}}2}^i ;7)将候选样本
{\boldsymbol{x}}_{{\rm{new}}1}^i ,\;{\boldsymbol{x}}_{{\rm{new}}2}^i 加入总样本中,得到集合X i,转至步骤2),继续进行迭代。建议的序列优化方法可采用任意代理模型技术进行建模,在循环过程中通过添加样本对当前代理模型最小值附近的局部地区展开细致搜索,同时在设计空间中函数变化波动大、非线性程度较强的区域进行自适应采样,减少模型的预测偏差,引导优化进行的方向。故该方法能够在序列迭代中不断进行全局搜索与局部开发,具有较好的全局寻优能力。
3 算例分析
本节选用如表1所示的三个典型数学优化算例验证所提优化设计方法,并将建议的混合加点准则与通用的EI准则[9]、PI准则[13]及LBC准则[15]进行对比。
表 1 测试函数信息表Table 1. The information of test functions函数序号 函数名 取值范围 维度 全局最优解 F1 Hump camel [−2,2]2 2 −1.0316 F2 Shekel5 [0,5]4 4 −10.1532 F3 Hartman6 [0,1]6 6 −3.3224 试验中,采用拉丁超立方抽样(Latin hypercube sampling, LHS)选取少量初始样本;调用MATLAB中的DACE工具箱[22]建立Kriging代理模型;在优化循环过程中,采用简单易实现、可调参数少的粒子群优化(PSO)算法[23]进行寻优。但需强调文中建议的基于混合加点准则的序列优化设计方法也能与其他代理模型方法相结合,适用于多种工程优化问题。
在初始样本数量、循环次数相同的情况下,不同测试函数在序列优化过程中的收敛情况如图4所示。从图中看出,当函数维度较低时,少量优化迭代后的结果已经非常接近全局最优;随着维度的增加,函数空间分布特征变得复杂,所需优化迭代次数随之增加。对比几种不同的加点准则,容易发现:在序列优化过程中,基于混合加点准则的优化设计方法能以较少的迭代次数迅速逼近全局最小值;对于所有测试函数,使用建议的混合加点准则能得到更加精确的优化结果,其相对误差均控制在0.01%以内。相比之下,基于EI准则、PI准则及LBC准则的优化设计收敛速度较慢,易陷于最优解附近的局部最小值,难以收敛到全局最优解。
根据表1中所给数学优化算例,进一步比较不同加点准则在优化收敛时的计算成本和优化效率。设置优化收敛准则为第k次优化结果
{{{\tilde f}_k}} 与理论值全局最优解fglobal的相对误差小于0.1%,即:{\varepsilon _k} = \left| {\frac{{{{\tilde f}_k} - {f_{{\rm{global}}}}}}{{{f_{{\rm{global}}}}}}} \right| \leqslant 0.001 (7) 测试结果如表2 所示,为避免偶然性,表中数据取50次序列优化设计结果的平均值。可以观察到,对于所有测试函数,采用混合加点准则时NIteration较小,表明该加点策略能有效减少优化循环次数,优化效果好,相应地,PSO算法调用代理模型计算响应的次数Nmcall也相应较少。从样本数量来看,由于一次循环过程中混合加点准则的加点数目是其他加点准则的2倍,因此二维函数F1在基于混合加点准则的优化设计中总样本数和原函数调用次数Nfcall略大;但随着维度的上升,对于函数F2、F3,使用EI准则、PI准则及LBC准则所需优化循环次数和样本数量都远超过混合加点准则,调用原函数进行计算的次数也大幅度上升,而此时混合加点准则表现出较强的全局寻优能力,计算效率高。
表 2 优化结果对比Table 2. Comparison of optimization results函数序号 加点准则 初始样本数量Nini 新增样本点数量Nnew 优化循环次数NIteration 原函数调用次数Nfcall 代理模型调用次数Nmcall 相对误差ɛ/(%) F1 混合加点准则 10 30.96 15.48 40.96 9288 0.0126 EI准则 10 25.16 25.16 35.16 15096 0.0330 PI准则 10 15.64 15.64 25.64 9384 0.0320 LBC准则 10 23.40 23.40 33.40 14040 0.0368 F2 混合加点准则 20 144.40 72.20 164.40 98640 0.0414 EI准则 20 1548.20 1548.20 1568.20 928920 0.0886 PI准则 20 1376.50 1376.50 1396.50 825900 0.0978 LBC准则 20 322.50 322.50 342.50 193500 0.0816 F3 混合加点准则 30 121.52 60.76 182.28 109368 0.0611 EI准则 30 483.55 483.55 503.55 290130 0.0734 PI准则 30 332.02 332.02 352.02 199212 0.0735 LBC准则 30 172.50 172.50 192.50 103500 0.0615 4 工程算例
以某输电塔连接节点的优化设计为例,对连接构件进行截面优化设计。节点由主角钢、左右两肢角钢以及节点板组成,各部分通过高强承压型螺栓连接。通过ANSYS软件的Solid单元建模,节点的有限元模型如图5所示,定义角钢、节点板、螺栓之间的相互接触关系,考虑几何非线性和材料非线性,采用Newton-Raphson法进行分析计算。
在输电塔节点优化设计中,选取主角钢肢厚tm、肢角钢肢厚tn、节点板厚度tp、螺栓直径d 这4个主要影响参数作为离散设计变量,优化目标函数为节点用钢量总成本F(x),同时应满足承载力约束及位移约束条件,该优化问题表述为:
\begin{split} \min \;\;\; & F\left({{x_1},{x_2},{x_3},{x_4}} \right) \\ {\rm{s}}{\rm{.t}}{\rm{. }}\;\;\;&M\left({\boldsymbol{x}} \right) \geqslant [M] \\ \;\;\;\;\;\;\;\;\;&\theta \left({\boldsymbol{x}} \right) \leqslant [\theta ] \\ \;\;\;\;\;\;\;\;\;&{x_i} \in {S_i},\;i = 1,2,3,4 \end{split} (8) 式中:Si为设计变量xi的设计尺寸取值集合;M(x)为输电塔节点的极限抗弯承载力;θ(x) 表示弯矩作用下节点产生的最大转角位移;[M]、[θ]分别为给定的抗弯承载力下限值和转角位移上限值。
采用拉丁超立方抽样方法选取初始样本,通过精细化有限元模型获取节点的弯矩和位移,建立相应的Kriging代理模型,根据基于混合加点准则的代理模型序列优化方法进行优化设计。
表3中展示了优化前后节点的不同设计,其中初始设计为初始样本中满足约束条件且目标函数最小的设计。通过对比可以发现,采用建议方法进行离散优化设计后的输电塔节点在抗弯承载能力和位移变形情况在满足要求的情况下,用钢量总成本降低了20.78%。
表 3 节点优化设计结果Table 3. Optimization results of joint节点设计 主角钢肢厚/mm 肢角钢肢厚/mm 节点板厚度/mm 螺栓直径/mm 总成本/€ 极限抗弯承载力/(kN·m) 最大转角位移/rad 优化前设计 12 14 12 22 64.05 77.45 0.1382 初始设计 14 16 16 22 66.91 81.69 0.0790 优化设计 12 14 12 20 50.74 71.38 0.1016 5 结论
针对黑箱优化设计存在的问题,本文提出了一种与代理模型无关的混合加点准则,从而发展了一类基于混合加点的代理模型序列优化设计方法。该方法在序列优化迭代中通过全局搜索与局部开发协同搜索最优解,自适应地提高模型精度。通过数值算例表明,与经典的基于EI准则、PI准则以及LBC准则的优化设计结果相比,建议方法表现出良好的稳健性,且能够兼顾精度与效率。将建议方法应用于输电塔节点设计,对节点几何尺寸进行优化,有效地减少了用钢量成本。
-
表 1 测试函数信息表
Table 1 The information of test functions
函数序号 函数名 取值范围 维度 全局最优解 F1 Hump camel [−2,2]2 2 −1.0316 F2 Shekel5 [0,5]4 4 −10.1532 F3 Hartman6 [0,1]6 6 −3.3224 表 2 优化结果对比
Table 2 Comparison of optimization results
函数序号 加点准则 初始样本数量Nini 新增样本点数量Nnew 优化循环次数NIteration 原函数调用次数Nfcall 代理模型调用次数Nmcall 相对误差ɛ/(%) F1 混合加点准则 10 30.96 15.48 40.96 9288 0.0126 EI准则 10 25.16 25.16 35.16 15096 0.0330 PI准则 10 15.64 15.64 25.64 9384 0.0320 LBC准则 10 23.40 23.40 33.40 14040 0.0368 F2 混合加点准则 20 144.40 72.20 164.40 98640 0.0414 EI准则 20 1548.20 1548.20 1568.20 928920 0.0886 PI准则 20 1376.50 1376.50 1396.50 825900 0.0978 LBC准则 20 322.50 322.50 342.50 193500 0.0816 F3 混合加点准则 30 121.52 60.76 182.28 109368 0.0611 EI准则 30 483.55 483.55 503.55 290130 0.0734 PI准则 30 332.02 332.02 352.02 199212 0.0735 LBC准则 30 172.50 172.50 192.50 103500 0.0615 表 3 节点优化设计结果
Table 3 Optimization results of joint
节点设计 主角钢肢厚/mm 肢角钢肢厚/mm 节点板厚度/mm 螺栓直径/mm 总成本/€ 极限抗弯承载力/(kN·m) 最大转角位移/rad 优化前设计 12 14 12 22 64.05 77.45 0.1382 初始设计 14 16 16 22 66.91 81.69 0.0790 优化设计 12 14 12 20 50.74 71.38 0.1016 -
[1] 寇峥, 李宁. 基于NSGA-Ⅱ的城市桥梁系统震后可恢复性分析与优化[J]. 工程力学, 2021, 3(38): 148 − 158, 180. doi: 10.6052/j.issn.1000-4750.2020.05.0290 Kou Zheng, Li Ning. Earthquake resilience analysis and optimization for urban bridge network system based on NSGA-II algorithm [J]. Engineering Mechanics, 2021, 3(38): 148 − 158, 180. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.05.0290
[2] 胡进军, 张辉, 靳超越, 等. 基于PCA及PSO智能算法的地震动合成方法——以中国西部中强地震为例[J]. 工程力学, 2021, 3(38): 159 − 168. doi: 10.6052/j.issn.1000-4750.2020.05.0293 Hu Jinjun, Zhang Hui, Jin Chaoyue, et al. A method to simulate ground motion based on PCA and intelligent algorithms—A case study of moderate magnitude earthquakes in western China [J]. Engineering Mechanics, 2021, 3(38): 159 − 168. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.05.0293
[3] Wang L, Shan S, Wang G G. Mode-pursuing sampling method for global optimization on expensive black-box functions [J]. Engineering Optimization, 2004, 36(4): 419 − 438. doi: 10.1080/03052150410001686486
[4] Simpson T W, Mauery T M, Korte J J, Mistree F. Comparison of response surface and Kriging models for multidisciplinary design optimization [C]. St. Louis, MO, USA: 7th Symposium on Multidisciplinary Analysis Optimization , 1998.
[5] Jones D R. A taxonomy of global optimization methods based on response surfaces [J]. Journal of Global Optimization, 2001, 21(4): 345 − 383. doi: 10.1023/A:1012771025575
[6] 曲杰, 苏海赋. 基于代理模型的通风盘式制动器制动盘结构优化设计[J]. 工程力学, 2013, 30(2): 332 − 339. doi: 10.6052/j.issn.1000-4750.2011.07.0459 Qu Jie, Su Haibin. Self-adaptive constraint optimization algorithm based on multiple surrogates and its application in the design of rivet head [J]. Engineering Mechanics, 2013, 30(2): 332 − 339. (in Chinese) doi: 10.6052/j.issn.1000-4750.2011.07.0459
[7] Forrester A I J, Keane A J. Recent advances in surrogate-based optimization [J]. Progress in Aerospace Science, 2009, 45(1/2/3): 50 − 79. doi: 10.1016/j.paerosci.2008.11.001
[8] Gutmann H M. A radial basis function method for global optimization [J]. Journal of Global Optimization, 2001, 19(3): 201 − 227. doi: 10.1023/A:1011255519438
[9] Jones D R, Schonlau M, Welch W J. Efficient global optimization of expensive black-box functions [J]. Journal of Global Optimization, 1998, 13(4): 445 − 492. doi: 10.1023/A:1008354314309
[10] Ginsbourger D, Riche R L, Carraro L. Kriging is well-suitable parallelize optimization [M]. Berlin: Computational Intelligence in Expensive Optimization Problems, Springer-Verlag, 2010.
[11] Schonlau M, Welch W J, Jones R D. Global versus local search in constrained optimization of computer models [M]. Hayward, California: Institute of Mathematical Statistics, 1998.
[12] Sobester A, Leary S J, Keane A J. On the design of optimization strategies based on global response surface approximation models [J]. Journal of Global Optimization, 2005, 33(1): 31 − 59. doi: 10.1007/s10898-004-6733-1
[13] Viana F A C, Haftka R T. Surrogate-based optimization with parallel simulations using the probability of improvement [C]. Fort Worth, TX, USA: 13th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, AIAA, 2010.
[14] Sasena M J, Papalambros P, Goovaerts P. Exploration of metamodeling sampling criteria for constrained global optimization [J]. Engineering Optimization, 2002, 34(3): 263 − 278. doi: 10.1080/03052150211751
[15] Cox D D, John S. A statistical method for global optimization [C]. Philadelphia, USA: Multidisciplinary Design of Optimization: State of Art, 1997.
[16] 高月华, 王希诚. 基于Kriging代理模型的多点加点序列优化方法[J]. 工程力学, 2012, 29(4): 90 − 95. Gao Yuehua, Wang Xicheng. A sequential optimization method with multi-point sampling criterion based on Kriging surrogate model [J]. Engineering Mechanics, 2012, 29(4): 90 − 95. (in Chinese)
[17] Hamza K, Shalaby M. A framework for parallelized efficient global optimization with application to vehicle crashworthiness optimization [J]. Engineering Optimization, 2014, 46(9): 1200 − 1221. doi: 10.1080/0305215X.2013.827672
[18] Zhan D, Qian J, Cheng Y. Balancing global and local search in parallel efficient global optimization algorithms [J]. Journal of Global Optimization, 2017, 67(4): 873 − 892. doi: 10.1007/s10898-016-0449-x
[19] 龙腾, 郭晓松, 彭磊, 等. 基于信赖域的动态径向基函数代理模型优化策略[J]. 机械工程学报, 2014, 50(7): 184 − 190. doi: 10.3901/JME.2014.07.184 Long Teng, Guo Xiaosong, Peng Lei, et al. Optimization strategy using dynamic radial basis function metamodel based on trust region [J]. Journal of Mechanical Engineering, 2014, 50(7): 184 − 190. (in Chinese) doi: 10.3901/JME.2014.07.184
[20] 彭磊, 刘莉, 龙腾. 基于动态径向基函数代理模型的优化策略[J]. 机械工程学报, 2011, 47(7): 164 − 170. doi: 10.3901/JME.2011.07.164 Peng Lei, Liu Li, Long Teng. Optimization strategy using dynamic radial basis function metamodel [J]. Journal of Mechanical Engineering, 2011, 47(7): 164 − 170. (in Chinese) doi: 10.3901/JME.2011.07.164
[21] Xu S, Liu H, Wang X, et al. A robust error-pursuing sequential sampling approach for global metamodeling based on Voronoi diagram and cross validation [J]. Journal of Mechanical Design, 2014, 136(7): 69 − 74.
[22] Lophaven S N, Nielsen H B, Søndergaard J. Dace—A matlab kriging toolbox—version 2.0 [R]. Lyngby: IMM Technical University of Denmark, 2002.
[23] Kennedy J, Eberhart R. Particle swarm optimization [C]. Honolulu, HI, USA: Icnn95-international Conference on Neural Networks, IEEE, 2002.
-
期刊类型引用(12)
1. 袁子淇,黄腾龙,林敏,杨双有,陈久吾. 基于PSO-SVM的尾砂仓储浓密机放砂稳定性分析. 矿业研究与开发. 2025(01): 95-102 .  百度学术
百度学术
2. 邵泽山,关成启,吴东涛. 加筋薄壳结构多层级自适应代理优化算法研究. 空天技术. 2025(01): 68-81 .  百度学术
百度学术
3. 高培根,锁斌. 基于加权犹豫模糊集的实验设计与分阶段PSO-Kriging建模. 计算机应用. 2024(07): 2144-2150 .  百度学术
百度学术
4. 齐晓轩,王欣宇. 基于IKrJaya算法的激光熔覆参数优化. 制造技术与机床. 2024(10): 110-118 .  百度学术
百度学术
5. 戴雅雪,应培,王波,马晓平. 带下表面射流的超临界翼型优化. 工程力学. 2024(11): 248-256 .  本站查看
本站查看
6. 姜峰,洪林雄,李华聪. 基于自适应径向基函数模型的区间不确定性分析方法. 航空动力学报. 2024(11): 73-82 .  百度学术
百度学术
7. 李二超,崔添超. 基于标签传播引导和区域自适应集成的代理辅助进化算法. 南京师范大学学报(工程技术版). 2024(04): 1-16 .  百度学术
百度学术
8. 张纯,何君儒,周宇轩,林莹. 基于深度神经网络代理模型的盾构隧道密封垫断面优化. 工程力学. 2023(07): 137-144 .  本站查看
本站查看
9. 罗建男,李雪利,王鹤,马溪,宋卓. 基于局部-全局混合自适应替代模型的地下水污染源反演识别. 中国环境科学. 2023(07): 3664-3671 .  百度学术
百度学术
10. 李云全,曹阳,智鹏鹏,毋高峰. 基于多权值优化代理模型的撒砂装置稳健可靠性设计. 机械设计. 2023(08): 113-120 .  百度学术
百度学术
11. 孙晓旺,孙魁远,秦伟伟,张绍彦,付条奇,王显会. 功能梯度下肢保护装置设计与优化. 工程力学. 2023(10): 190-203 .  本站查看
本站查看
12. 李正良,王成,王涛,汪之松,李佳鸿. 基于主动学习Kriging模型的直立锁缝屋面系统抗风揭可靠度分析. 工程力学. 2022(10): 111-119 .  本站查看
本站查看
其他类型引用(16)




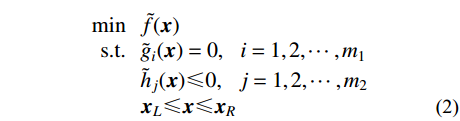

 下载:
下载: