改善与提高飞机的气动性能，一直是航空人孜孜不倦的追求，其中，翼型是影响飞机气动性能的关键因素，翼型的每一次气动性能的革命性优化都大幅提升了航空飞行器性能^[1]，翼型的设计是飞机设计中重要的不可或缺的第一环。翼型设计起初依赖风洞试验和专家经验，需要耗费大量的人力与时间，随着20世纪80年代计算机技术的快速发展，数值计算方法的成熟和代理模型的提出，发展了高效的基于代理模型的优化设计方法(surrogate-based optimization, SBO)^[2]，该方法利用代理模型技术，建立输入与输出的近似函数关系来替代翼型数值仿真的黑箱模型，能有效减少优化过程中的计算量，提高优化设计效率^[3-4]，进而实现在给定工况和给定设计空间中以较小的CFD计算代价快速找出全局目标气动性能接近最优的翼型^[5-6]。段焰辉等^[7]基于代理模型的两步优化方法大幅提升了跨声速下RAE2822翼型的升阻比；VAVALLE等^[8]基于改进响应面代理模型的优化方法消除了激波；吴宽展等^[9]采用多输出高斯过程回归模型结合模拟退火算法的翼型优化设计方法，在升力系数一定的条件下实现阻力系数减小30%。

传统的翼型优化设计对翼型气动性能的提高有一定局限。近年来，通过局部能量输入，或者微尺度的扰动达到对整体流动特性的控制的主动流动控制(active flow control, AFC)技术让翼型气动性能提升又向上一个台阶。研究表明，主动流动控制能有效增升减阻，实现抑制分离、延迟转捩及扩大飞机失速裕度，相比于被动流动控制，主动流动控制具有应用更灵活且气动性能更优的特点^[10]。目前，主动流动控制技术已发展了环量控制(circulation control, CC)、合成射流(synthetic jet, SJ)、协同射流(co-flow jet, CFJ)、表面吹吸气等方式。LI等^[11]使用后掠射流驱动的环量控制技术有效提高了翼型升力。ZHA等^[12]通过风洞实验分析了低来流速度下协同射流翼型的气动性能，研究发现CFJ可显著提高翼型升力，并改善失速迎角到40°；陈诚等^[13]将协同射流技术与翼型变弯度技术结合，将薄翼型的最大升力系数提升至3.3127。表面吹吸气技术也是一种发展相对成熟的主动流动控制方式。相比于以上两种方式，表面吹吸气技术不改变翼型的流线型形状，不会产生额外的阻力，且控制方式更简单，易于实施，并能带来不错的气动效益^[14]。GENÇ等^[15]利用翼型表面吹吸气联合控制技术，研究低雷诺数翼型的流动分离控制。段会申等^[16]利用吸气可实现转捩控制、吹气可实现湍流减阻的特点，分析上翼面单吹/吸气和联合吹吸气对翼型阻力系数的影响，发现单吹/吸气和联合吹吸气都能降低阻力系数，但联合吹吸气的减阻效果更大。付云豪等^[17]提出了一种新型表面吹吸气方式，即下表面射流(射流从翼型下表面靠近后缘处喷出)，并以带下表面射流的NACA0012翼型为对象进行了来流马赫数Ma=0.155 的工况下的气动性能数值研究，研究表明带下表面射流的NACA0012翼型的增升减阻效果比基准翼型更好。目前下表面射流的相关研究主要集中在低亚声速工况下^[17]，最高也是0.6Ma工况下的气动性能研究^[18]，尚未研究跨声速翼型上表面出现激波时射流的作用效果。且目前的主动流动控制研究主要集中于机理性研究，侧重射流控制参数的定性优化，未考虑射流以外的翼型形状带来的影响。

基于上述问题，本文采用基于雷诺平均Navier-Stokes方程的数值方法，研究了来流速度达到临界马赫数时，下表面射流技术对超临界翼型RAE2822的气动特性影响。为了进一步提高气动效果，提出将下表面射流控制与翼型优化设计相结合，构建基于Kriging代理模型的带下表面射流的翼型一体优化设计方法，分析该方法优化效果。

1   数值模拟方法

1.1   计算模型

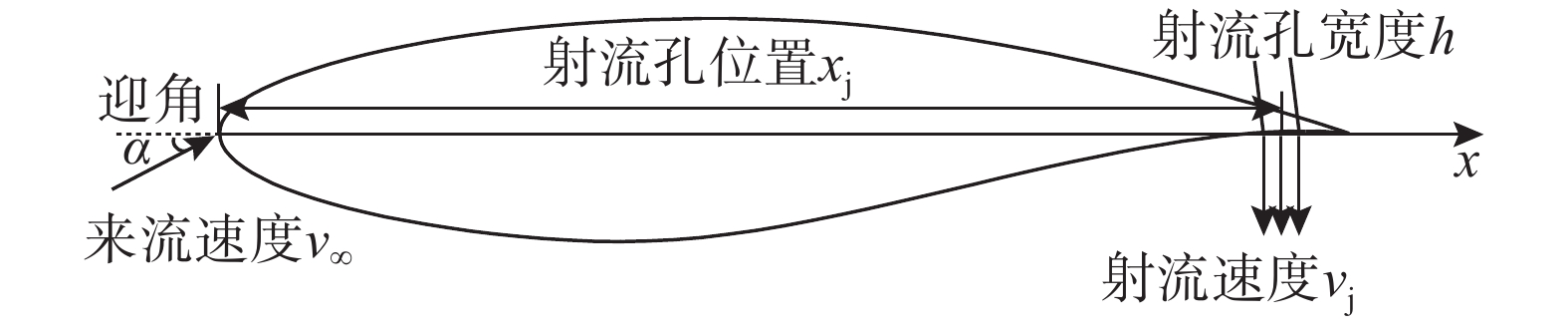
本文选取RAE2822翼型为研究对象，弦长c=1 m，基于弦长的雷诺数Re=6.5×10⁶，在翼型下表面靠近后缘处开孔，射流孔位于x_j=0.98c处，孔径h=0.01c，射流从翼型内垂直孔表面向外喷出，为定常连续射流，速度为v_j，远场来流速度为v_∞，α为来流迎角，翼型带下表面射流参数示意见图1。

图  1  RAE2822翼型下表面射流参数示意

Figure  1.  Schematic diagram of RAE2822 airfoil with LSTE jet

下载: 全尺寸图片 幻灯片

射流强度通过引入无量纲化的射流动量系数来表示^[17]：

式中：ρ为射流口气体密度；${\rho _\infty }$为自由来流密度。

1.2   下表面射流能耗计算

由于下表面喷出的射流消耗能量，故衡量带下表面射流翼型的气动性能时需要考虑功耗代价，借用文献[19]的思想计算射流功耗并引入等效升阻比。其中功率消耗取决于射流质量流量与总焓损失，具体表示为：

式中：${\dot m_{\rm j}}$为射流质量流量；$\eta$为能量转化效率；${T_{{\rm t}\infty }}$、${P_{{\rm t}\infty }}$分别为当地高度下总温与总压；${P_{\rm tj}}$为射流孔总压。

等效升阻比在原本的升阻比定义下修改得到，将功率消耗折合成阻力项，其定义如下：

式中：L、D分别代表翼型产生的升力和阻力；${v_\infty }$为自由来流速度；P为功率消耗。关闭射流或无射流时，P=0，此时等效升阻比与常用的升阻比K一致。

1.3   数值方法与网格

为求解跨声速粘性流，采用二维稳态可压缩RANS方程为控制方程，控制方程为：

数值求解采用有限体积法，空间离散采用二阶迎风格式，湍流模型采用Spalart-Allmaras单方程模型，该模型能够很好地模拟强表面激波与边界层之间的相互作用。翼型表面采用无滑移壁面，远场条件采用压力远场条件，带下表面射流时，由于本文所选取射流速度较小(Ma < 0.3)，可视为不可压缩流，故射流边界条件设为速度入口边界。

翼型网格采用O型结构网格，计算域的远场半径为30倍弦长，且第一层网格高度为4×10⁻⁶ m，使得${y^ + } < 1$，并在翼型前缘、后缘、上表面中部和射流口周围区域进行网格加密，以便捕捉上表面激波与射流流动细节，网格生成如图2所示。

1.4   数值计算方法及网格无关性验证

为了验证上述数值计算方法的准确性，将RAE2822翼型仿真结果与文献[20]中的风洞试验数据作对比并进行网格无关性验证。

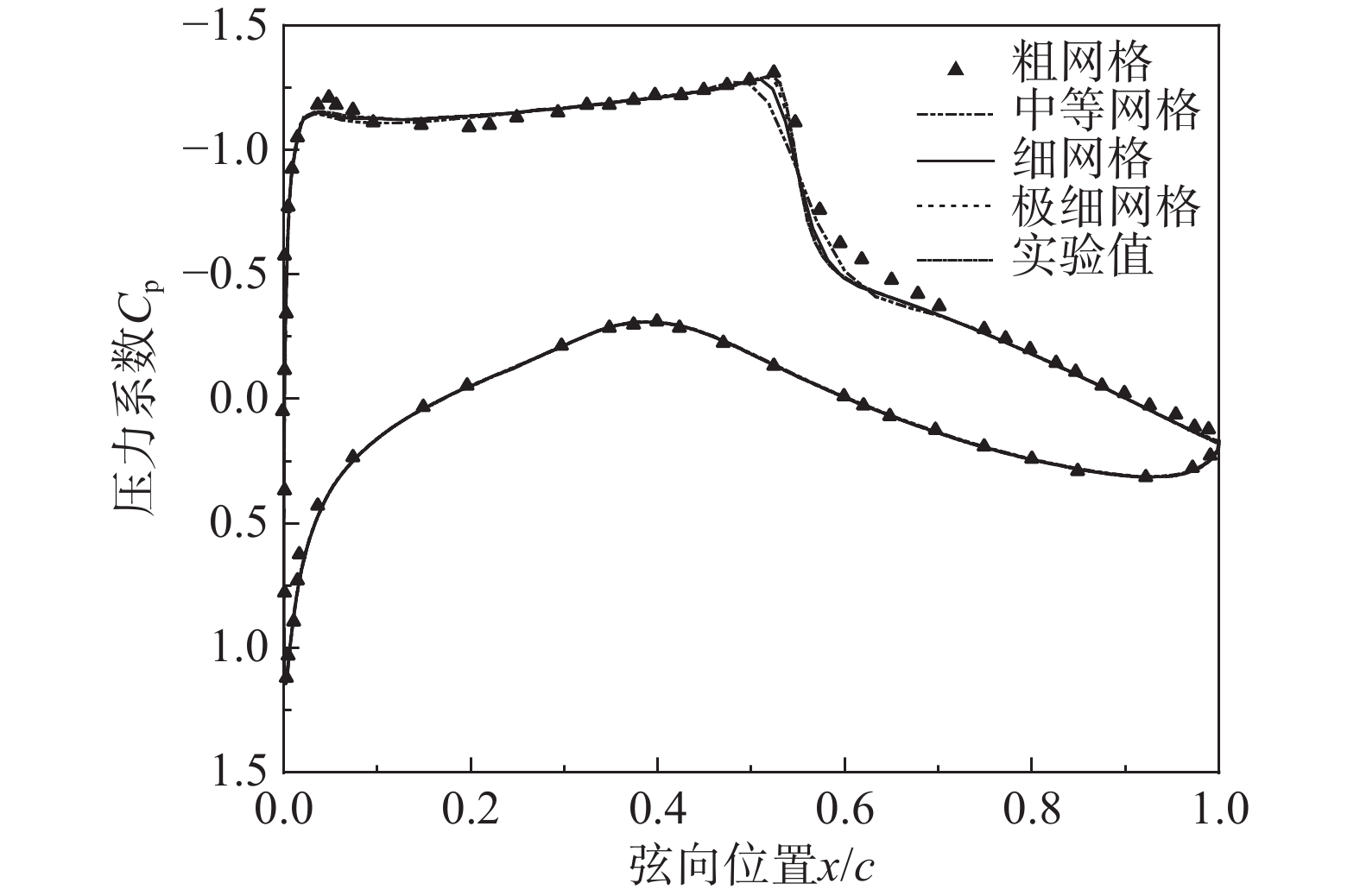
数值计算工况Ma=0.73、Re=6.5×10⁶、α=2.79°。分别选取3万粗网格(396×92)、6万中等网格(460×130)、12万细网格(650×184)和20万极细网格(800×250)4套网格进行气动数值仿真，计算得到的翼型表面压力分布如图3所示。由图可知，四套网格的数值计算结果与实验数据整体吻合较好，主要区别在上翼面0.5c~0.6c之间的激波部分，在0.55c之前网格越密越接近实验值，在0.55c之后网格越疏越接近实验值。气动力数据对比见表1，由表可知网格规模对气动力系数数值的影响不大，升力系数与风洞实验值的最大误差为−1.89%，阻力系数与实验值的最大误差为3.3%，误差水平较小，故该数值计算方法是可靠的，其中由中等网格计算得到阻力系数误差最小。故下表面射流翼型将选取中等网格进行计算。

图  2  RAE2822下表面射流翼型计算网格

Figure  2.  Computing grids of RAE2822 airfoil with LSTE jet

下载: 全尺寸图片 幻灯片

图  3  RAE2822翼型表面压力系数分布对比

Figure  3.  Pressure coefficient distribution of RAE2822 airfoil by numerical simulation compared with experiment results

下载: 全尺寸图片 幻灯片

表  1  RAE2822翼型网格参数与气动力系数的对比

Table  1.  Comparison of grid parameters and aerodynamic coefficients of RAE2822 airfoil

网格	网格数量	升力系数CL	阻力系数CD
实验值	−	0.8030	0.01680
粗网格	326×92	0.7878(−1.89%)	0.01735(+3.30%)
中等网格	460×130	0.7922(−1.34%)	0.01723(+2.56%)
细网格	650×184	0.7940(−1.11%)	0.01727(+2.79%)
极细网格	800×250	0.7954(−0.95%)	0.01729(+2.92%)

下载: 导出CSV 

| 显示表格

2   代理模型优化方法

为了进一步提高翼型气动性能，本文构建了基于Kriging代理模型的优化框架。

2.1   CST参数化方法

本文采用Kulfun提出的CST参数化方法^[21]，翼型形状使用以下方程表达：

上翼面：${ \zeta _{\rm u}} = C_{N2}^{N1}(\psi )S_{\rm u}(\psi ) + \psi \Delta {\xi _{\rm u}}$

下翼面：${ \zeta _{\rm l}} = C_{N2}^{N1}(\psi )S_{\rm l}(\psi ) + \psi \Delta {\xi _{\rm l}}$

式中：

式中：ζ、ψ分别为x轴和y轴方向上的坐标相对于弦长c的无量纲化；∆ξ_u、∆ξ_l为后缘厚度项；C函数用于确定翼型类别，当N₁=1、N₂=0.5时用于描述常规圆头尖尾翼型；S_u、S_l函数描述上、下翼面曲线具体的形状；K为伯恩斯坦多项式(Bernstein polynomial, BPO)；n、m分别为上、下翼面选取的BPO阶数；X_ui、X_lj为每个BPO分量对应的权重系数，当X_u、X_l参数给定，对应的翼型就确定。对某个翼型的拟合权重系数，可通过最小二乘法求解得到。在翼型的优化设计中，权重系数即为优化设计变量。

本文对目标翼型上、下翼面均采用6阶BPO多项式的CST参数化，即共使用14个参数变量描述翼型形状，拟合的权重参数取值见表2。

表  2  拟合RAE2822翼型对应的CST权重系数

Table  2.  CST weight coefficient for fitting the RAE2822 airfoil

序号i	上翼面Xui	下翼面Xli
1	0.1266	−0.1289
2	0.1379	−0.1426
3	0.1614	−0.1312
4	0.1647	−0.2614
5	0.2195	−0.0253
6	0.1728	−0.1145
7	0.2123	0.0728

下载: 导出CSV 

| 显示表格

2.2   拉丁超立方试验设计

样本的合理选取是影响基于代理模型的优化方法的关键环节。既需要能充分表达设计空间，又要考虑尽量降低计算成本。本文采用拉丁超立方试验设计方法。该方法具有以下2个特点：① 每一个维度都划分成N个区间，每个区间都有一个样本点；② 每个区间的样本点是随机产生的。因此，该方法兼具全局性和随机性，相比于全试验设计能大幅减少所需样本点，进而减少计算量。在基准翼型权重系数上下浮动30%基础上，本文的优化方法基于拉丁超立方抽样原则选取1000个样本点。

2.3   基于Kriging代理模型优化方法

代理模型通过由CFD计算得到的一定数量样本进行训练得到。它可以近似模拟翼型控制参数和气动性能之间的函数关系，故使用代理模型可以替代大量复杂的、高精度的CFD计算。在目前已发展的多种代理模型中，Kriging代理模型是一种无偏估计模型，并且对高维度非线性具有很好的拟合能力，能同时给出估计值与估计值的均方误差(mean square error, MSE)，MSE误差可用于指导加入新样本点^[2]。

Kriging代理模型假定响应值与自变量之间的函数关系为：

式中：f(x)为多个函数的线性组合；β为每个函数对应的系数，则f(x)^Tβ视为回归模型；z(x)视为附加在回归模型上的高斯随机过程误差，其均值为0，均方差为σ²，协方差为σ²R(θ, xⁱ, x^j)。其中R(θ, xⁱ, x^j)具体表示为：

式中：d_l为两个样本点在多维空间中的距离关系；θ_l为样本点在第l维上的相关参数；R_l(θ_l, d_l)为选定的核函数。在给定回归模型和核函数的条件下，相关参数θ的求解是确定Kriging代理模型的关键^[22]。通过构造极大似然函数，将求解θ的问题转化为最优化问题，进而采用寻优算法得到最优的θ^[23]。

采用全局寻优算法粒子群算法在Kriging代理模型基础上寻优，每一轮优化的结果是基于代理模型的预测值，因此与CFD流体解算的真实值存在一定误差。通过将每轮优化的结果进行校正，并将新的数据点加入样本点集，实时更新代理模型，以提高预测精度。

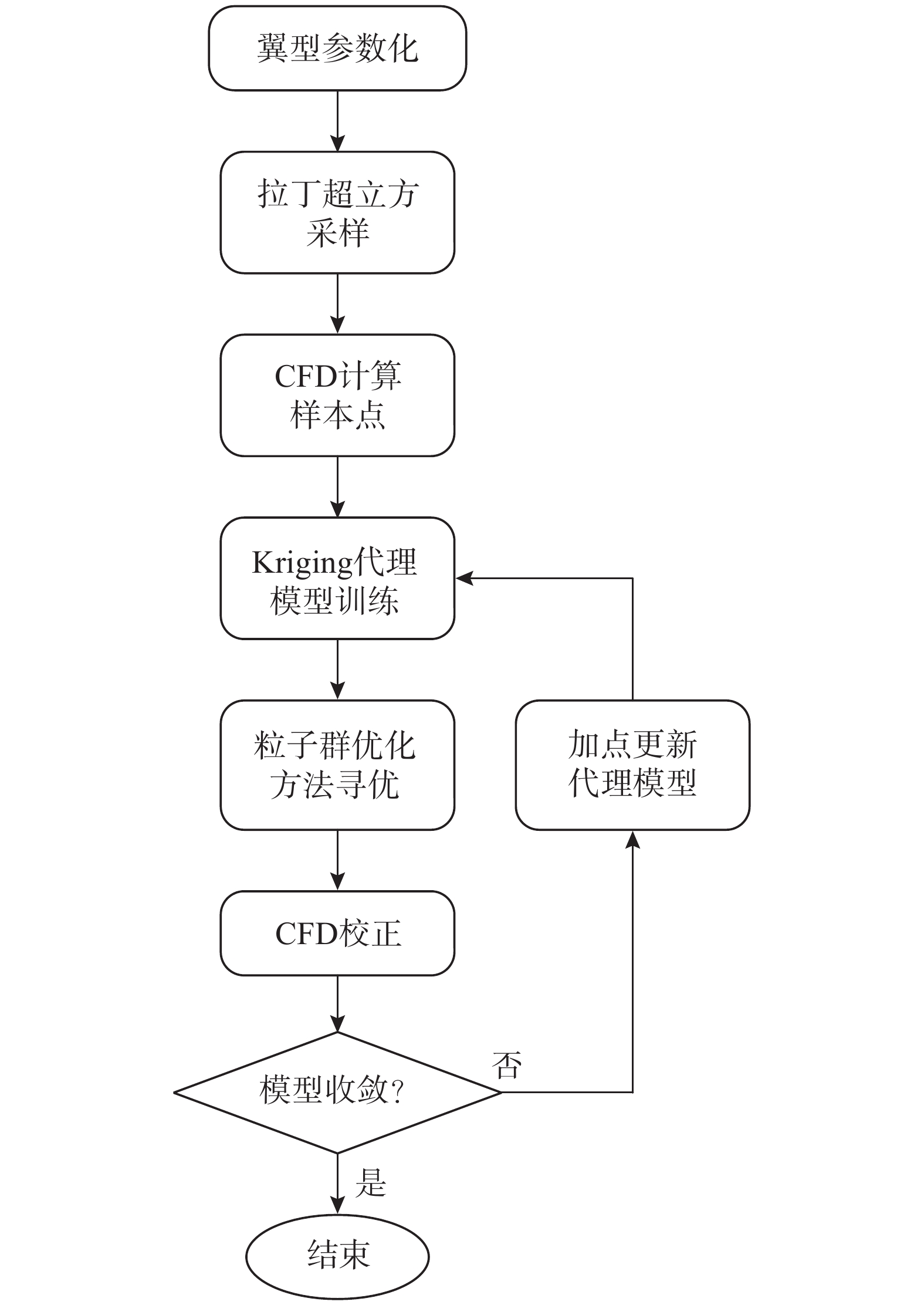
综上所述，本文采用基于Kriging代理模型的优化方法流程如图4所示。

优化目标为升阻比最大，约束条件为翼型厚度大于等于基准翼型厚度，射流动量系数c_μ为定值。其优化设计问题可以表示为：

其中：

式中：C_L为翼型升力系数；C_D为阻力系数；C_L0为RAE2822基准翼型在设计工况下的升力系数，用以引入罚函数项；t₀为基准翼型厚度；X_l、X_u为优化变量上下边界，CST权重系数变化范围为在基准翼型拟合权重系数X₀上下浮动30%。每一次优化迭代次数100，粒子数50，自我学习因子和社会学习因子都取2，采用线性变化惯性权重，以实现寻优初期重全局、后期重局部，进而实现全局高效寻优。将每一次的优化结果进行CFD解算来校正升阻比，然后将该优化翼型及对应的实际升阻比加入样本点集进行代理模型的更新，直至代理模型预测值与实际值误差收敛。

图  4  优化设计流程

Figure  4.  The flow chart of optimization

下载: 全尺寸图片 幻灯片

3   结果及分析

3.1   下表面射流影响分析

在RAE2822翼型下表面射流影响分析中，分别设置射流动量系数c_μ=0.0002, 0.0004, 0.0006, 0.0008和0.0010进行模拟。计算工况为Ma=0.73、Re=6.5×10⁶、α=2°。

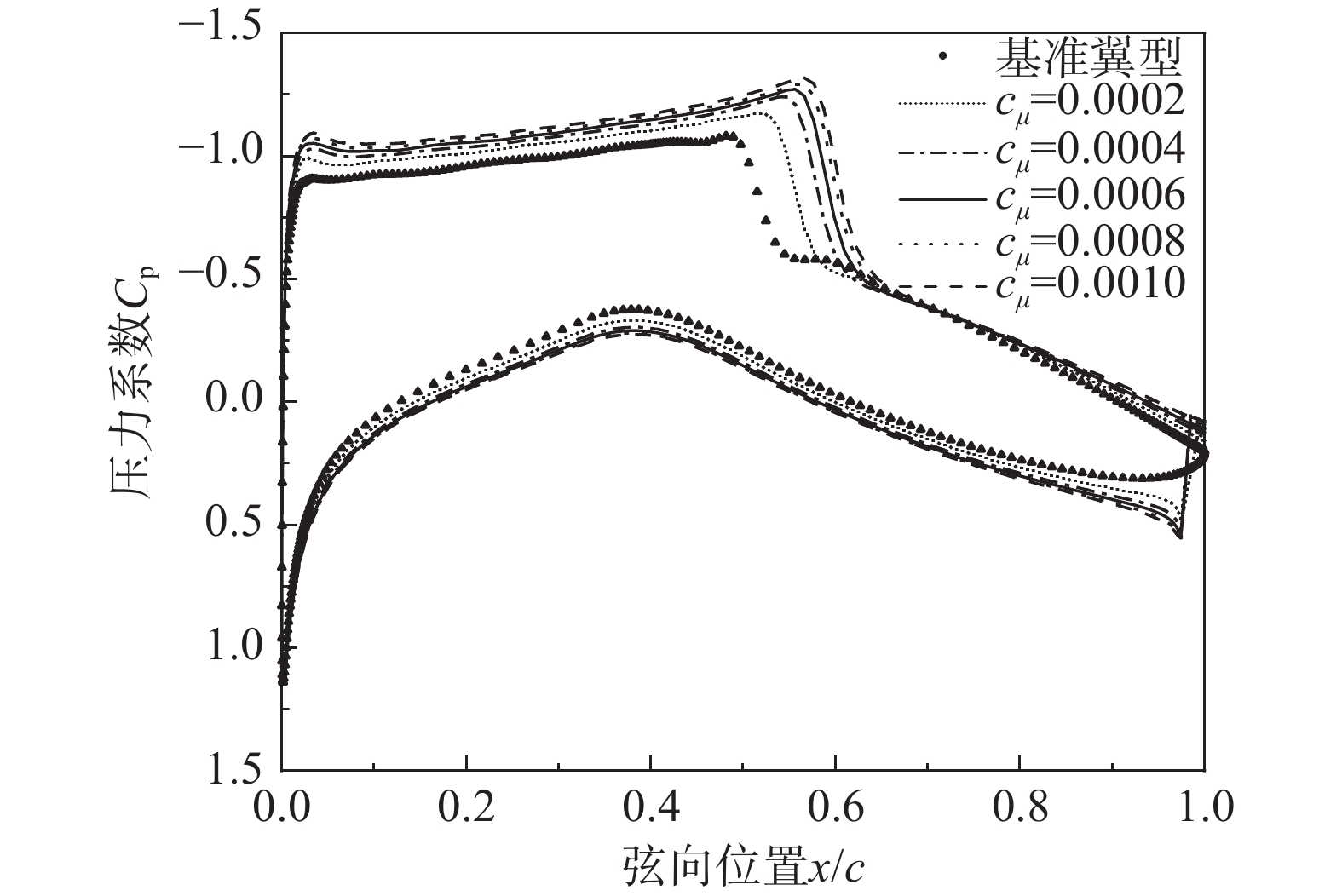
图5给出了基准翼型和具有不同射流动量系数的下表面射流翼型的表面压力系数分布对比，图6是对应翼型的压力分布云图。通过压力系数分布对比和压力分布可以看出，射流导致上表面激波发生后移，扩大了激波前的低压区范围，并增大了低压强度；受益于翼型环量提高，射流翼型下表面压力有一定增大，有助于提高升力系数。从图5还可以看出，随着射流动量系数增大，上、下表面压差越大，这将带来翼型升力系数提升。

图  5  基准翼型与下表面射流翼型表面压力系数分布

Figure  5.  Pressure coefficient distribution of the baseline airfoil with and without LSTE jet

下载: 全尺寸图片 幻灯片

图  6  有无下表面射流的翼型的压力分布

Figure  6.  Pressure distribution of the baseline airfoil with and without LSTE jet

下载: 全尺寸图片 幻灯片

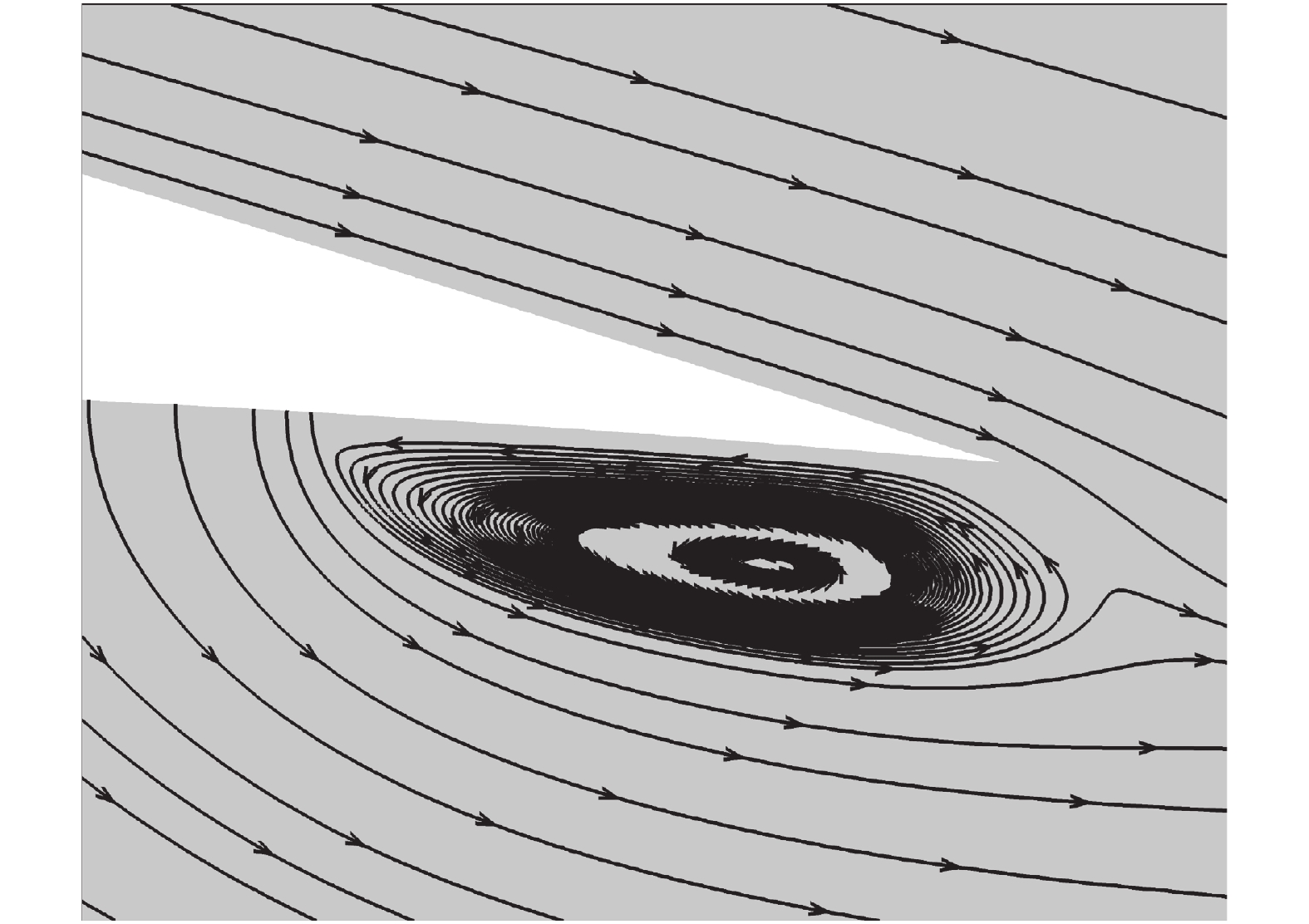
图7给出了基准翼型和下表面射流翼型的马赫云图。结合图8的后缘流场流线图可知，下表面射流后产生了逆时针旋涡，该低压区吸引后缘绕流，促进气流加速，因而增大了翼型环量^[24]。

图  7  下表面射流翼型(c_μ=0.0010)马赫云图及流线图

Figure  7.  Mach cloud and streamlines of airfoil with LSTE jet

下载: 全尺寸图片 幻灯片

图  8  下表面射流翼型(c_μ=0.0010)后缘流线图

Figure  8.  Flow streamline diagram of trailing edge of airfoil with LSTE jet

下载: 全尺寸图片 幻灯片

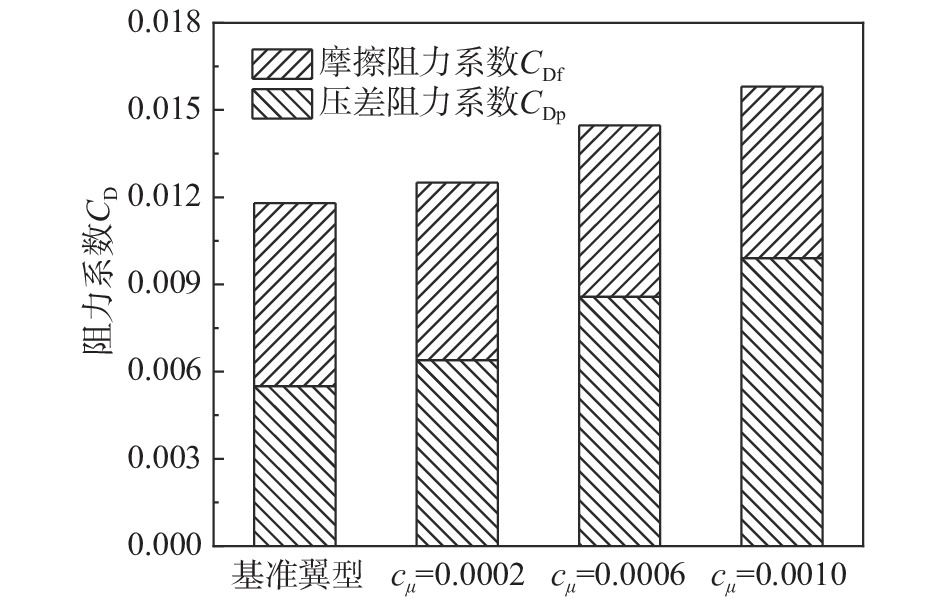
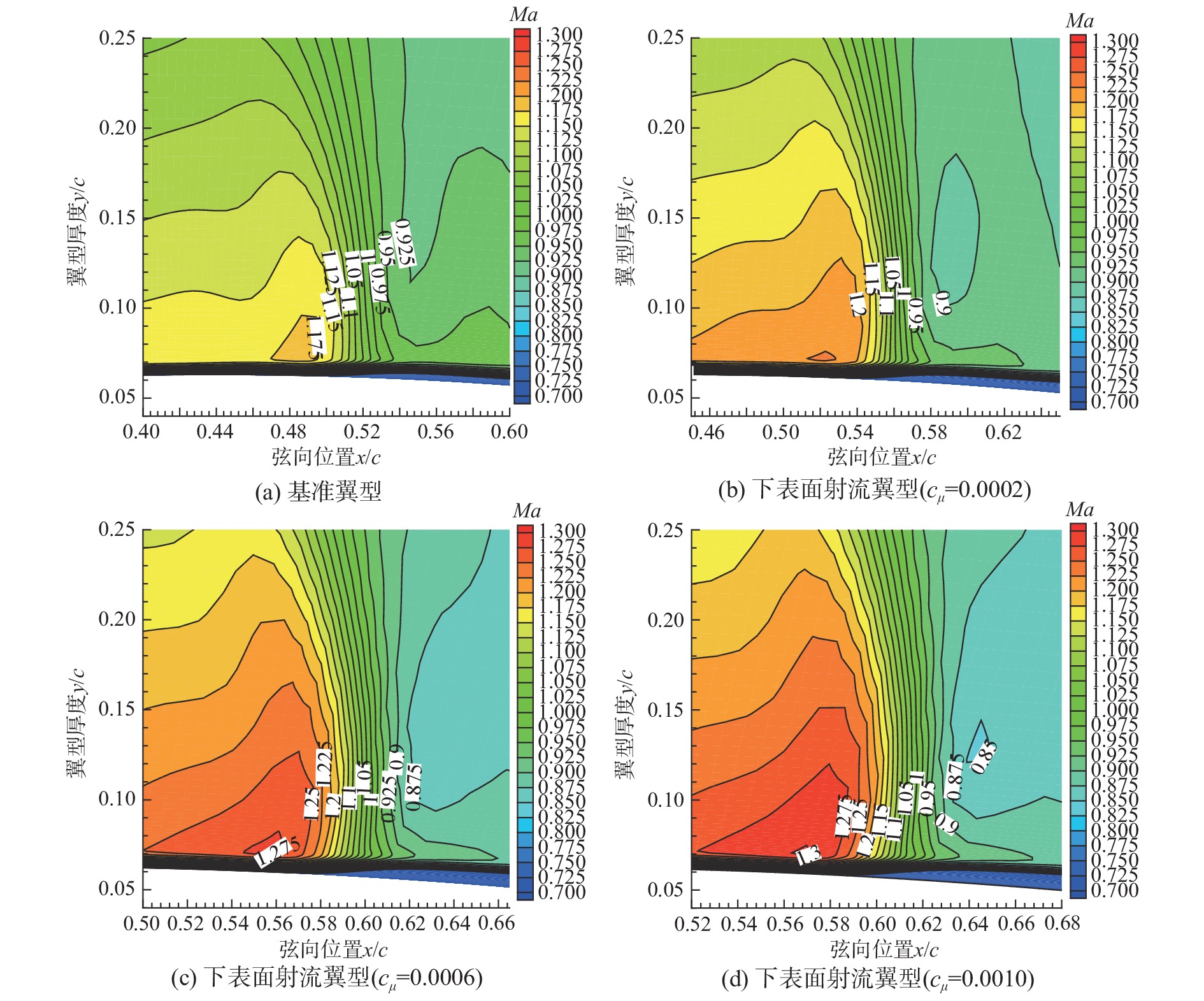
表3是基准翼型与下表面射流翼型具体的气动力数据对比。结果显示出，相较于基准翼型，射流翼型能够获得更高的升力系数和升阻比，随着射流动量系数的增加，增大升力系数的同时也增大了阻力系数。考虑射流功耗后，当射流动量系数c_μ=0.0002时，等效升阻比高于基准翼型升阻比4.9%，显示出获得正收益；当c_μ=0.0006时，等效升阻比与基准翼型升阻比基本持平；当c_μ=0.0010时，其等效升阻比低于基准翼型升阻比4.6%，此时射流注入能量代价高于升阻比提升，显示出获得负收益。通过分析基准翼型和下表面射流翼型的阻力系数组成(图9)及激波马赫数等值线图(图10)可知，带下表面射流翼型的阻力较基准翼型增加主要源于上翼面激波产生的压差阻力，且激波强度随射流动量系数的增加而增大，这将导致激波阻力随之增大。

表  3  基准翼型与下表面射流翼型的气动力特性

Table  3.  Aerodynamic characteristics of baseline and baseline airfoil with LSTE jet

翼型	升力系数CL	阻力系数CD	升阻比K	等效升阻比Kc
基准翼型	0.6447	0.0118	54.68	54.68
cμ=0.0002	0.7373(+14.4%)	0.0125(+5.9%)	58.94	57.36(+4.9%)
cμ=0.0004	0.7955(+23.4%)	0.0137(+16.1%)	58.24	56.14(+2.7%)
cμ=0.0006	0.8294(+28.6%)	0.0145(+22.9%)	57.22	54.69(+0.0%)
cμ=0.0008	0.8554(+32.7%)	0.0152(+28.8%)	56.37	53.50(-2.2%)
cμ=0.0010	0.8748(+35.7%)	0.0158(+33.9%)	55.30	52.18(-4.6%)

下载: 导出CSV 

| 显示表格

图  9  基准翼型和下表面射流翼型的阻力系数组成

Figure  9.  Composition of drag coefficient of baseline and baseline airfoil with LSTE jet

下载: 全尺寸图片 幻灯片

3.2   优化设计及分析

基于3.1节分析可知，跨声速工况下带下表面射流的RAE2822翼型的确实现了升力的大幅增加，但同时伴随着气动阻力的增大。因此本节将对RAE2822翼型分别进行基准翼型优化和带下表面射流翼型优化，以进一步提高带下表面射流翼型的气动性能，并将下表面射流优化翼型与基准优化翼型进行对比。由3.1节带下表面射流翼型气动数值模拟结果可知，射流动量系数c_μ=0.0002时等效升阻比较优。因此本节优化设计工况同3.1节一致的情况下, 选取c_μ=0.0002进行带下表面射流一体的翼型优化，射流方向始终垂直于射流孔表面。带下表面射流翼型的优化方法与基准翼型优化方法一致，通过撰写相应的网格生成脚本实现迭代过程中带下表面射流翼型网格的变形。

图  10  激波底部马赫数等值线图

Figure  10.  Contours of Mach number at the bottom of the shock

下载: 全尺寸图片 幻灯片

3.2.1   优化结果

在分别加点181次和283次得到了基准优化翼型与下表面射流优化翼型，表4给出了两种优化翼型与基准翼型的气动力特性对比。基准优化翼型和下表面射流优化翼型的升力系数较基准翼型都有所提高，阻力系数降低，但下表面射流优化翼型提高或降低的幅度更大，尤其在提高升力系数方面。因而基准优化翼型升阻比较基准翼型提高了8.6%，考虑到射流消耗的功率，下表面射流优化翼型的等效升阻比提高了26.2%，下表面射流优化翼型相较于基准优化翼型具有更高的气动力效率。

表  4  基准翼型与优化翼型的气动力特性对比

Table  4.  Comparison of aerodynamic characteristics of the baseline and optimized airfoil

翼型	升力系数CL	阻力系数CD	升阻比K	等效升阻比Kc
基准翼型	0.6447	0.0118	54.68	54.68
基准优化翼型	0.6707(+4.0%)	0.0113(−4.2%)	59.39(+8.6%)	59.39(+8.6%)
下表面射流优化翼型	0.7728(+19.9%)	0.0109(−7.6%)	71.05(+29.9%)	69.00(+26.2%)

下载: 导出CSV 

| 显示表格

3.2.2   结果分析

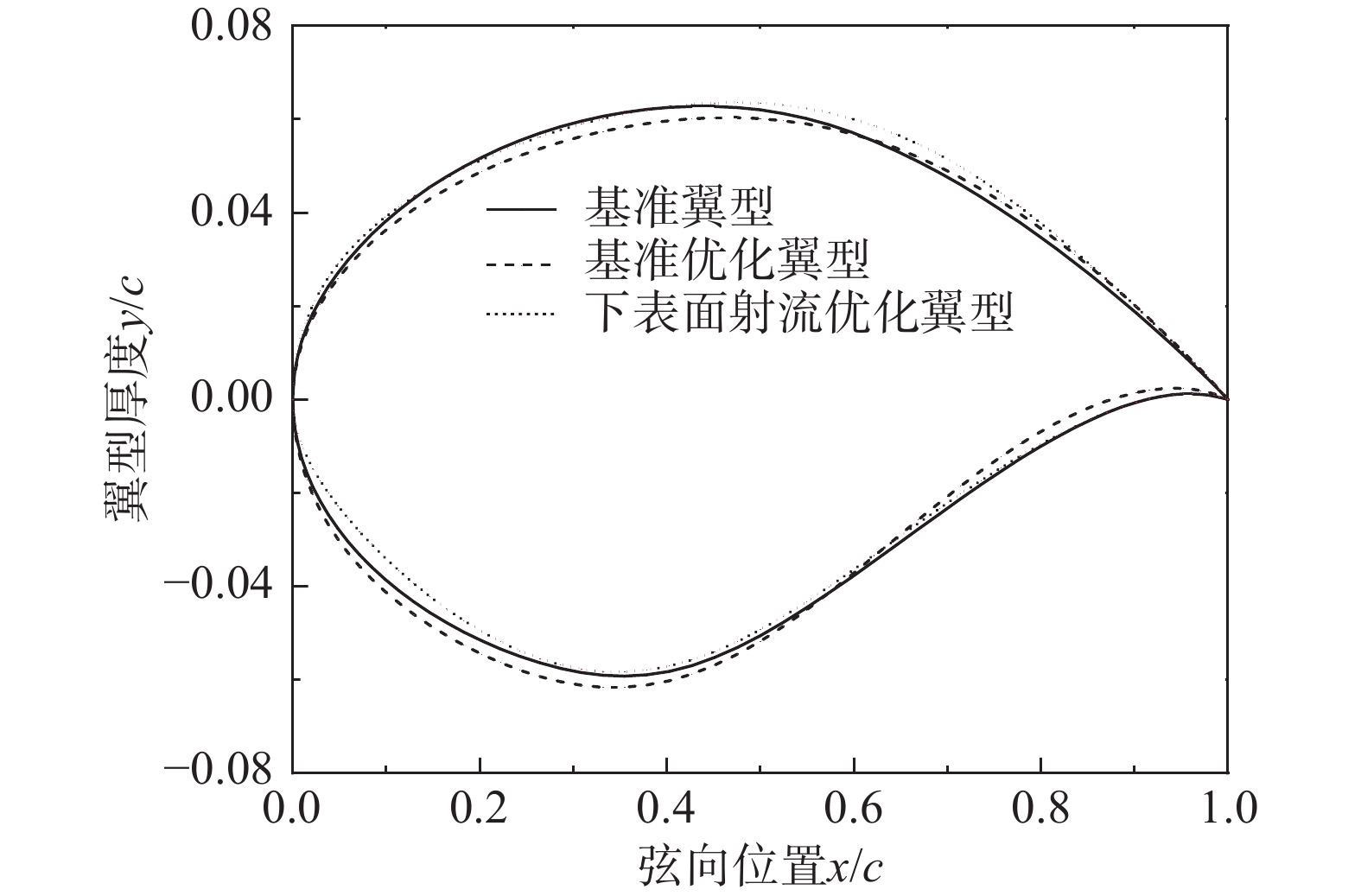
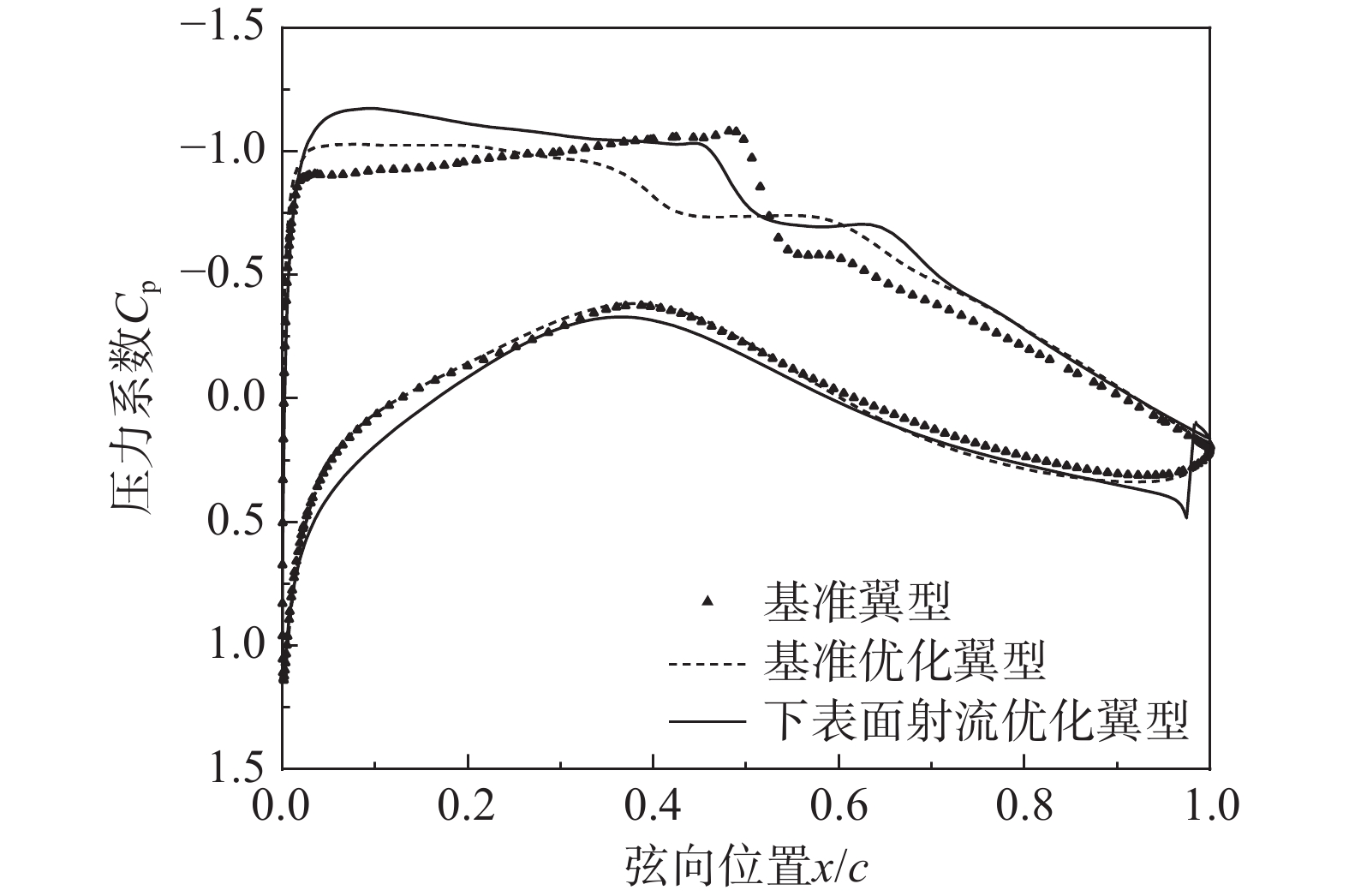
图11和图12分别是基准翼型、基准优化翼型和下表面射流优化翼型的形状对比和表面压力系数分布对比图。结合两图分析可知，相较于基准翼型，在减小阻力方面，两种优化翼型都具有更平坦的上表面，这有助于减弱激波强度，降低激波阻力。其中，下表面射流优化翼型具有更平缓的下表面，厚度分布均匀，这有助于进一步减小形状阻力。在增加升力方面，基准优化翼型具有更大的弯度，下表面靠近后缘处内凹，该处气压上升，这使上下表面压差增大，进而升力增加；下表面射流优化翼型弯度变化不大，其升力的增加的主要机制是，通过下表面射流加快上表面激波前方的外流流动，提高前缘负压强度，同时阻滞了下表面射流口前的流动，增大下表面压力，实现压差的扩大。

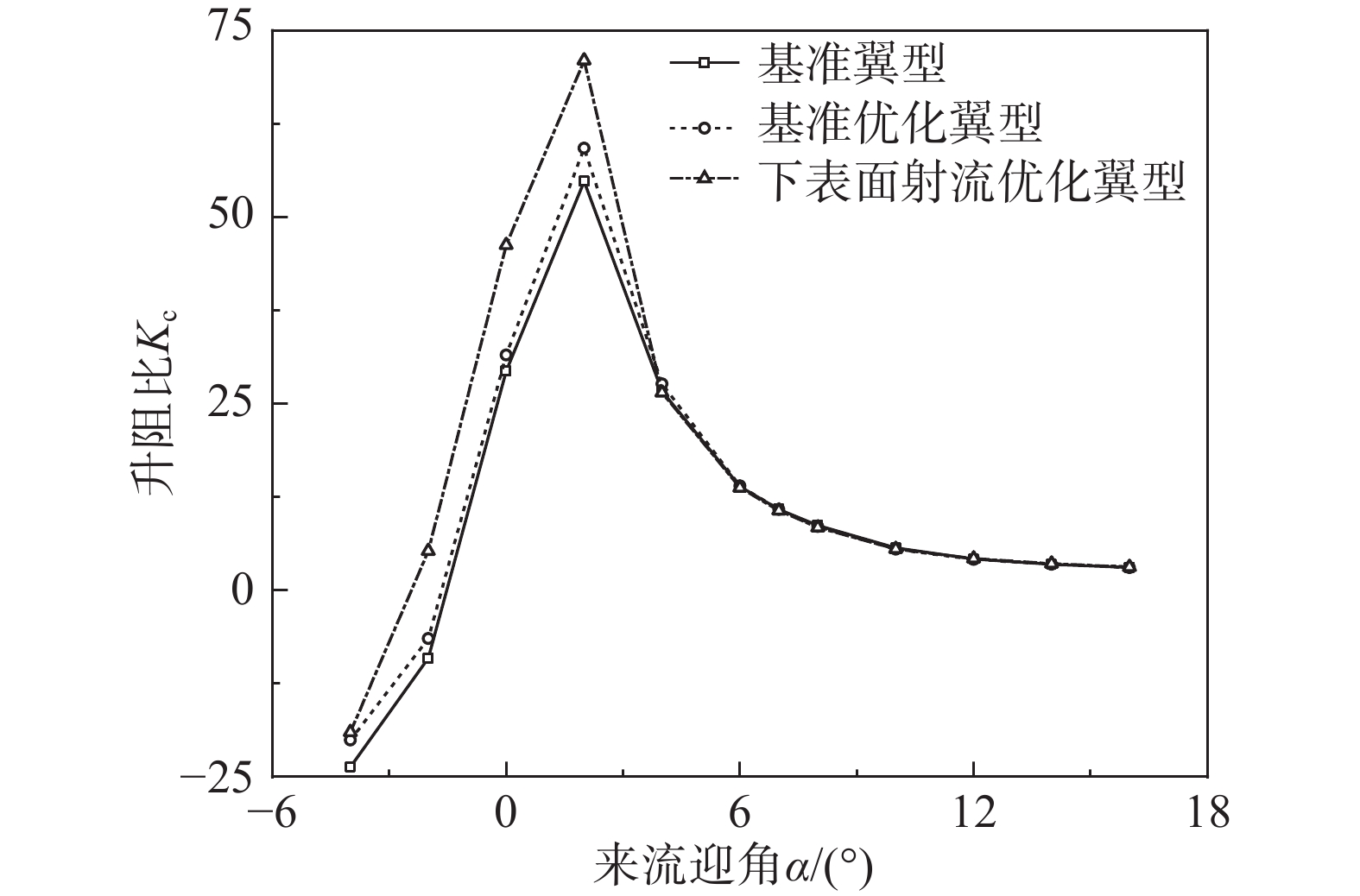
进一步分析下表面射流优化翼型在一定迎角范围内的气动力特性，结果如图13所示。结果显示出，下表面射流和翼型的整体优化方法主要提高了0°~3°小迎角范围内的等效升阻比，适用于飞机亚声速巡航飞行工况，能够有助于提高航程航时。

图  11  基准翼型与优化翼型的形状对比

Figure  11.  Comparison of the shapes of the baseline and optimized airfoil

下载: 全尺寸图片 幻灯片

图  12  基准翼型与优化翼型的表面压力系数分布对比

Figure  12.  Comparison of pressure distribution of the baseline and optimized airfoil

下载: 全尺寸图片 幻灯片

图  13  基准翼型与优化翼型的气动力特性对比

Figure  13.  Comparison of aerodynamic characteristics of the baseline and optimized airfoil

下载: 全尺寸图片 幻灯片

4   结论

本文采用RANS方程，结合SA湍流模型的数值仿真方法，模拟了Ma=0.73、Re=6.5×10⁶、α=2°工况下的带下表面射流的RAE2822翼型气动性能。基于CST参数化方法、Kriging代理模型和改进权重粒子群优化算法，构建了下表面射流的翼型优化方法，进一步提升了下表面射流气动效果。得出主要结论如下：

(1) 研究发现，使用下表面射流技术能够有效提高翼型升力，但是射流会增强上表面激波，进而增大翼型阻力；当c_μ=0.0002时，下表面射流能够提高翼型等效升阻比4.9%。

(2) 通过射流翼型一体优化方法进一步优化得到的下表面射流优化翼型，其具有更平坦的上表面，几何弯度比基准优化翼型更小，能有效提高翼型升力，同时减小激波和形状阻力，等效升阻比提高了26.2%。

(3) 带下表面射流优化翼型在小迎角范围内具有较好的等效升阻比提升效果，有助于飞机巡航飞行。