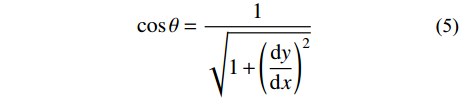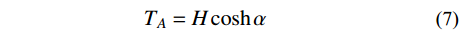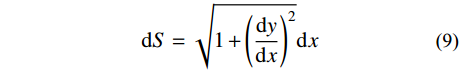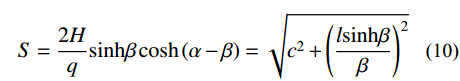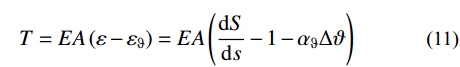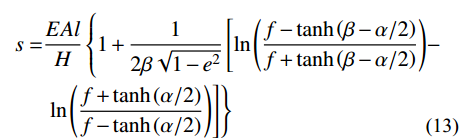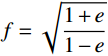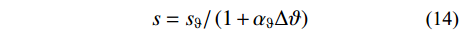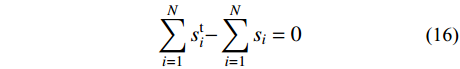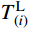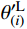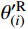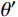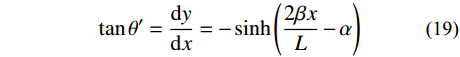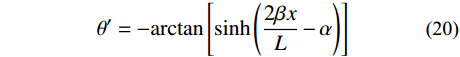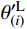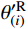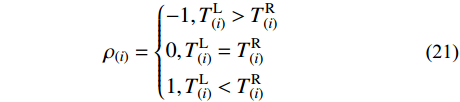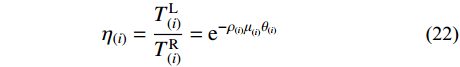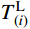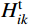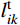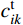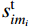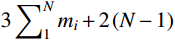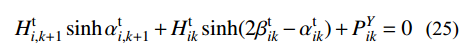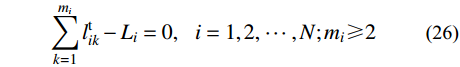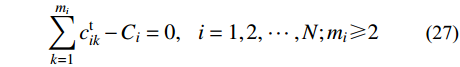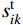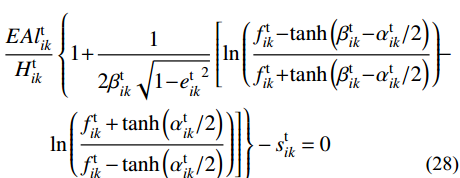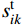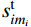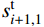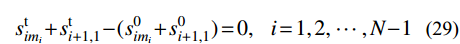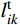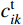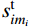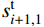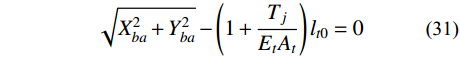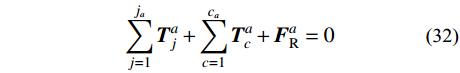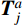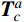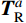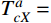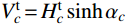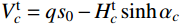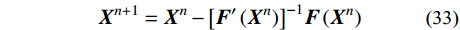THEORETICAL SOLUTION OF SLIDING CABLE STRUCTURES CONSIDERING FRICTIONAL EFFECT
-
摘要: 滑移索结构在工程中有广泛的应用,目前分析此类结构仍主要以数值方法为主,缺乏理论解析计算方法。且其滑移计算分析时必须充分计入几何非线性和考虑摩擦的影响。该文基于悬链线理论,推导了单索无应力索长的一元解析表达式;在此基础上,引入Euler摩擦公式,根据滑移时总无应力索长不变和张力平衡特性,分别建立了自重和集中荷载下的多跨连续滑移索的解析方程组,并将其拓展到索杆滑移结构;采用精度可控的Newton-Raphson迭代法求解方程组,并运用编制程序对四个算例进行了计算分析。算例结果表明:该文提出的考虑摩擦的滑移索结构的理论分析方法不仅具有较高的计算精度,而且还有较好的工程适应性和有效性,可为多跨滑移索结构的设计与分析提供理论依据。Abstract: Sliding cable structures are widely used in engineering practice. The analyses of such structures are still mainly based on numerical methods at present, which is a lack of theoretical methods. The effects of geometrical nonlinearity and friction on sliding need to be taken into account in the analysis simultaneously. Based on the catenary theory, the one-dimensional analytical expression of the unstressed length for a single cable is deduced. After the introduction of Euler equation, the analytical equations of multi-span continuous cables under self weight and concentrated loads are respectively established, according to the characteristics of the invariant total unstressed length and balanced tension at the sliding point. The analytical equations of continuous cables are extended to cable-supported trusses. The Newton-Raphson scheme with controllable accuracy is used to solve the equations, and four examples are analyzed by the program. The results show that the theoretical solution is accurate with high adaptability in engineering, which can provide a theoretical basis for the design and analysis of sliding cable structures.
-
Keywords:
- cable structure /
- sliding /
- friction /
- geometric nonlinearity /
- unstressed cable length /
- analytical method
-
索结构由于轻质高强、造型美观、经济合理,在工程中具有广泛的应用。索在工程应用中往往存在滑移行为,比如缆索吊装系统、悬索桥主缆架设、穹顶结构、高压输电结构、索道等。滑移索结构由于张拉或者外荷载的改变,在支点处存在滑移行为,滑移后两侧索原长发生改变,从而影响结构的内力及位移。索结构本身具有高度的几何非线性,可根据变形关系准确得到变形协调方程[1]。索在滑移时不可避免地会受到摩擦力的影响。为了准确分析滑移索结构,需要合理考虑几何非线性、滑移特性及滑动摩擦。
索的几何非线性使得计算变得复杂,滑移问题的求解一般采用数值方法进行,主要以有限元法为主。一些学者简化了几何非线性的处理,采用直线索单元模拟拉索,把关注点集中于滑移的分析。Aufaure[2]和Zhou等[3]提出了三节点折线单元处理滑移;Lee等[4]通过直线型整体滑移单元来进行滑移摩擦结构的分析;Chen等[5]提出了考虑几何非线性的多折线单元用于分析穹顶结构的滑移问题。基于直线索假定的索单元大大简化了计算过程,但是这类单元对于松弛索滑移的模拟精度不足。
此外,一些学者同样采用直线索的假定,利用逐步逼近的办法来获得滑移平衡态,比如冷冻-升温法[6]、拉力分配法[7]、角平分线法[8]。这类方法的优势体现在避免了复杂的迭代过程,然而为了结果更准确,也需要更多单元数。近年来,一些研究基于直线索的假定建立新型有限元法。俞锋等[9-10]使用有限质点法建立了索杆梁膜结构的滑移分析方法,Kan等[11-12]利用多体动力学方法分析滑移索结构,他们的方法[9-12]都适用于滑移体系的线性动力分析。
为了达到更高的精度和使用更少的单元数,滑移分析的数值模拟普遍采用悬链线单元。许多学者基于弹性悬索解析解推导了索在支点处的滑移刚度[13-15],利用悬链线索有限元法和滑移刚度分析滑移索结构。魏建东等[16-17]直接建立悬链线型滑移单元分析缆索吊装系统。滑移往往涉及接触摩擦问题,悬链线理论使得摩擦力可以准确使用Euler摩擦公式进行描述。因此,采用悬链线理论分析滑移结构,不仅可以大大提高了计算精度,减少了单元数,还能准确考虑摩擦损失。
上述数值方法的计算结果存在一定差异,目前也没有专门的理论解评价其精度。因此,滑移摩擦索结构理论解的研究具有十分重要的意义。滑移索结构理论解的研究很少,唐建民和卓家寿[18]提出了一种近似理论解,只能求解两跨连续索,变形协调条件采用了近似处理,且不考虑滑移点的摩擦,因而具有较大的局限性。Such等[19]指出索和杆的变形和滑移行为都可利用解析方法描述,但其方法无法处理多点滑移和摩擦问题。
为了建立考虑摩擦的滑移索结构的理论解,本文首先推导了单索无应力索长的解析表达式;利用该表达式、Euler摩擦公式,结合滑移的总无应力索长不变(Invariant total unstressed length, 简称ITUL)特性和张力平衡条件,分别建立自重下和集中荷载下的多跨连续索、索杆滑移结构的解析平衡方程组;利用Newton-Raphson迭代求解该方程组,得到滑移平衡态。对两个经典算例进行分析,以对现有方法进行精度评价;利用本文方法对缆索吊装系统和预应力钢桁架进行计算分析,验证本文方法的有效性和可靠性。
1 单索的非线性分析
单索的分析是索结构分析的基础,而无应力索长是单索分析的关键因素。目前,单索的无应力索长主要通过近似计算得到。本节基于索曲线方程推导了无应力索长的解析表达式。
索本身具有一定的特性,本文采用以下的基本假定:1) 拉索在弹性阶段工作,并满足虎克定律;2) 索具有理想柔性,只能受拉,无抗压、抗弯刚度。
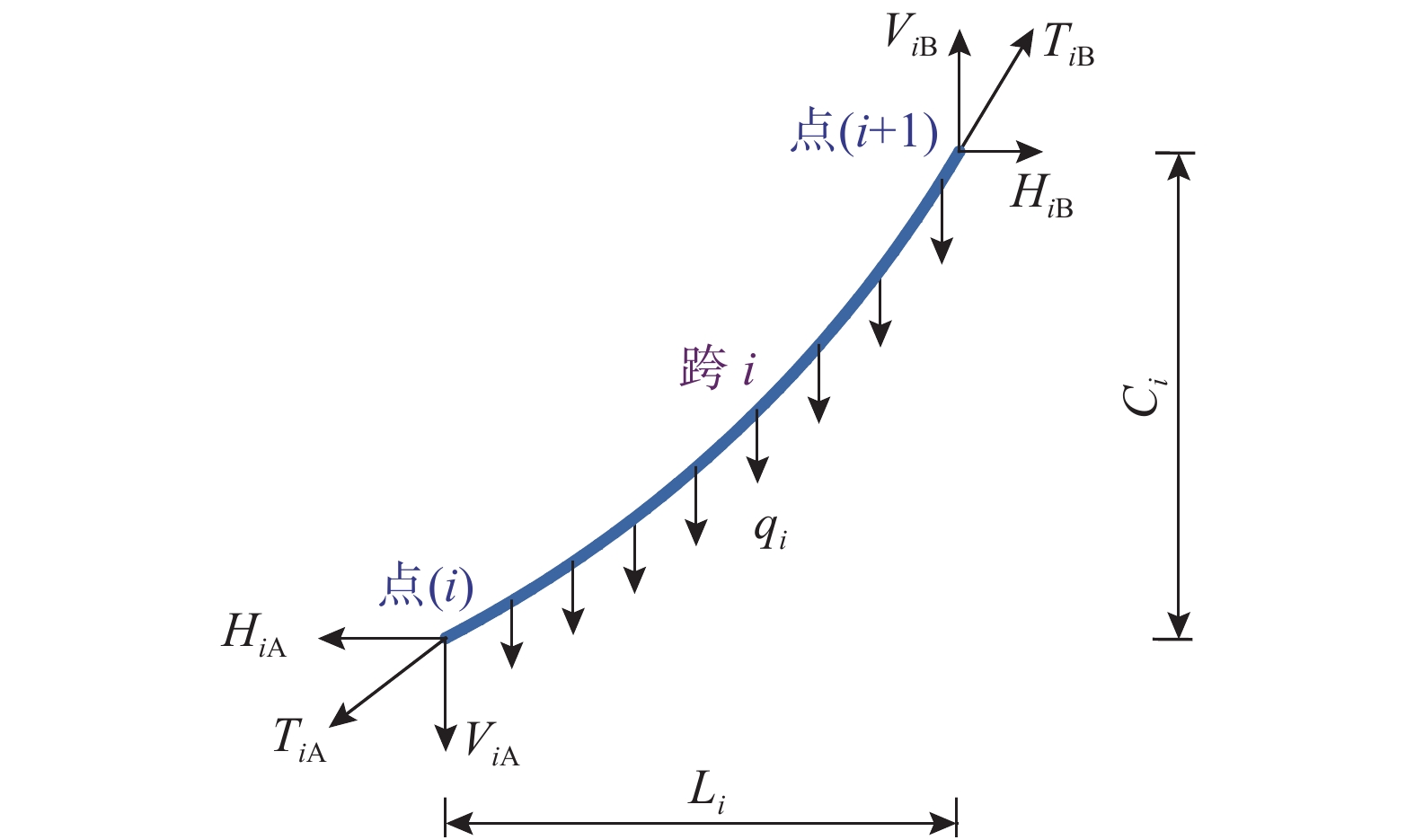
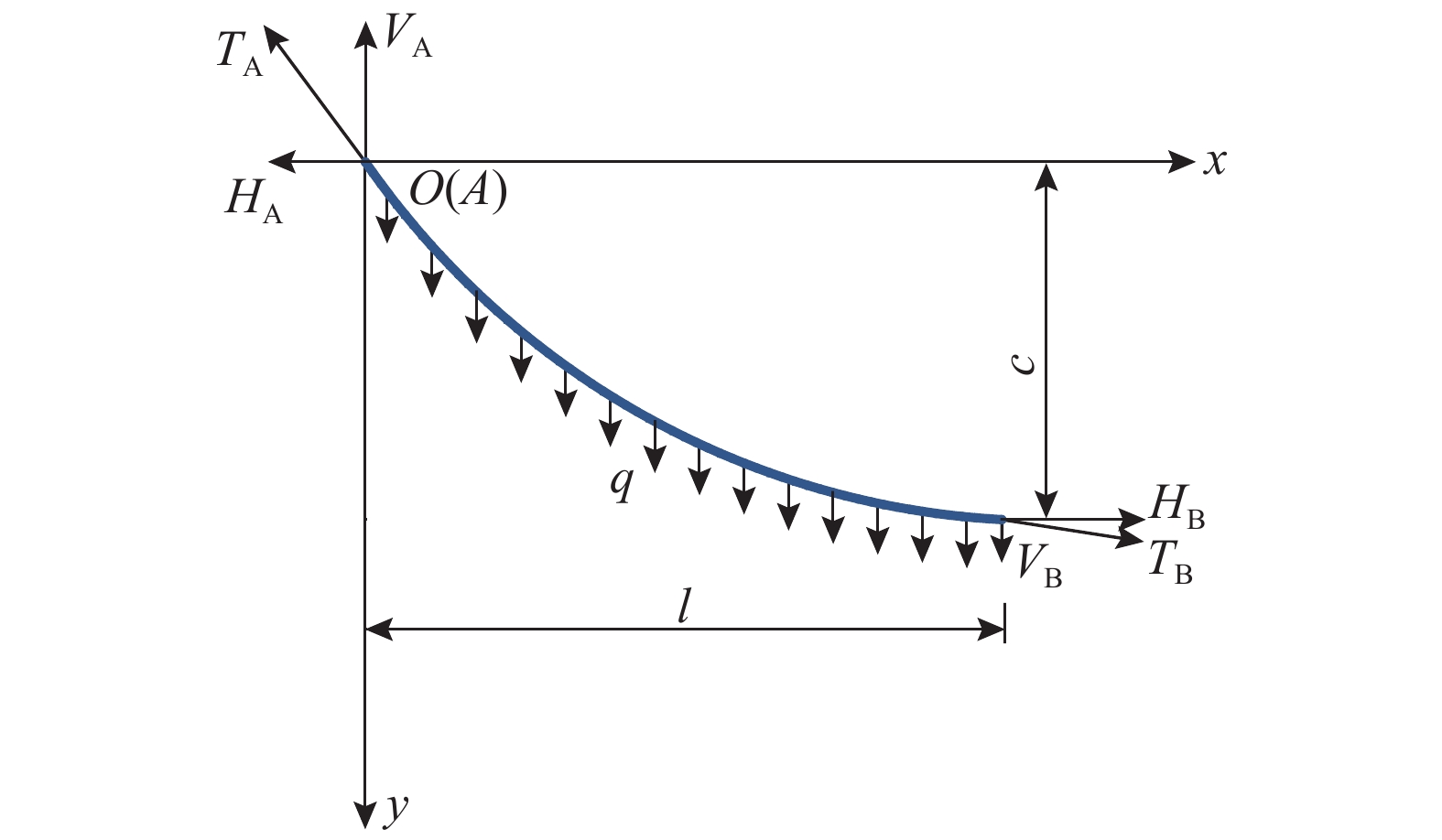
图1为沿索曲线分布的均布荷载q作用下的单索简图,y轴与q方向相同。其中TA和TB是端点A和B的索力;HA、VA、HB和VB是x和y方向上相应的索端力分量。悬链线索曲线方程如下[20]:
y=Hq[coshα−cosh(2βxl−α)] (1) 式中:
α=arcsinh(βclsinhβ)+β (2) β=ql2H (3) 其中:H=HA=HB为索的水平张力;l为索终点与起点x坐标的差值;c为索终点与起点y坐标的差值。
索力T和水平张力H之间的关系为:
T=Hcosθ (4) 式中:
cosθ=1√1+(dydx)2 (5) dydx=−sinh(2βxl−α) (6) 将式(6)代入式(5),再代入式(4),可以得到索力T与坐标x的关系式,将A点、B点的坐标代入该关系式,即可得到TA、TB的表达式。
TA=Hcoshα (7) TB=Hcosh(2β−α) (8) 受力后索长的微分dS可以表示为:
dS=√1+(dydx)2dx (9) 将式(6)代入式(9),通过积分得索长表达式:
S=2Hqsinhβcosh(α−β)=√c2+(lsinhββ)2 (10) 索长的微分dS与无应力索长的微分ds的关系可用索力T建立,表示为:
T=EA(ε−εϑ)=EA(dSds−1−αϑΔϑ) (11) 式中:E、A分别是索的弹性模量、横截面积;ε和εϑ分别为总应变和温度应变;αϑ为线膨胀系数;Δϑ为温度变化量,升温为正,降温为负。
式(11)可以被改写为:
ds=dSTEA+1+αϑΔϑ (12) 将式(4)~式(6)、式(9)代入式(12),积分可以得到设计温度下的无应力索长的解析表达式:
s=EAlH{1+12β√1−e2[ln(f−tanh(β−α/2)f+tanh(β−α/2))−ln(f+tanh(α/2)f−tanh(α/2))]} (13) 式中:
e=HEA(1+αϑΔϑ) ;f=√1+e1−e 。通过以上分析,得到了以水平张力为变量的单索无应力索长的解析表达式。式(13)可用于计算给定水平张力下的无应力索长,给定无应力索长时同理可得水平张力,只要给定上述两个参数之一便可确定单索构型。
2 考虑摩擦的滑移索结构的理论解
为了直观评价数值方法的精度,保证理论解的可靠性,本文的方法选择在平面内建立。
2.1 自重下的多跨连续索的解析方程组
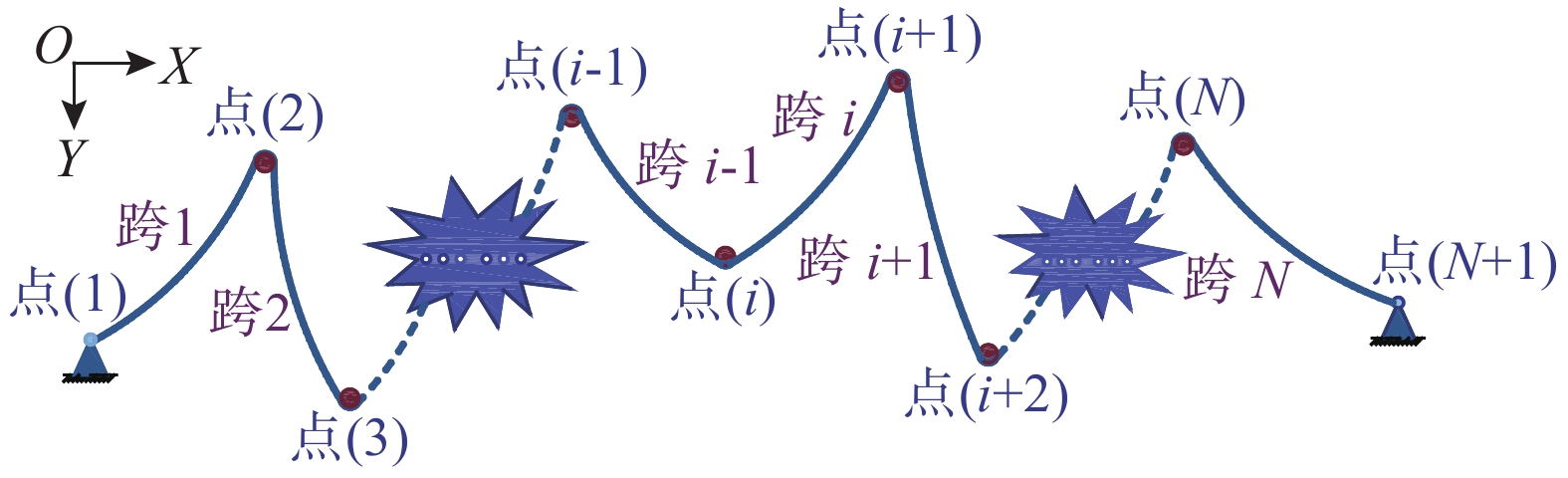
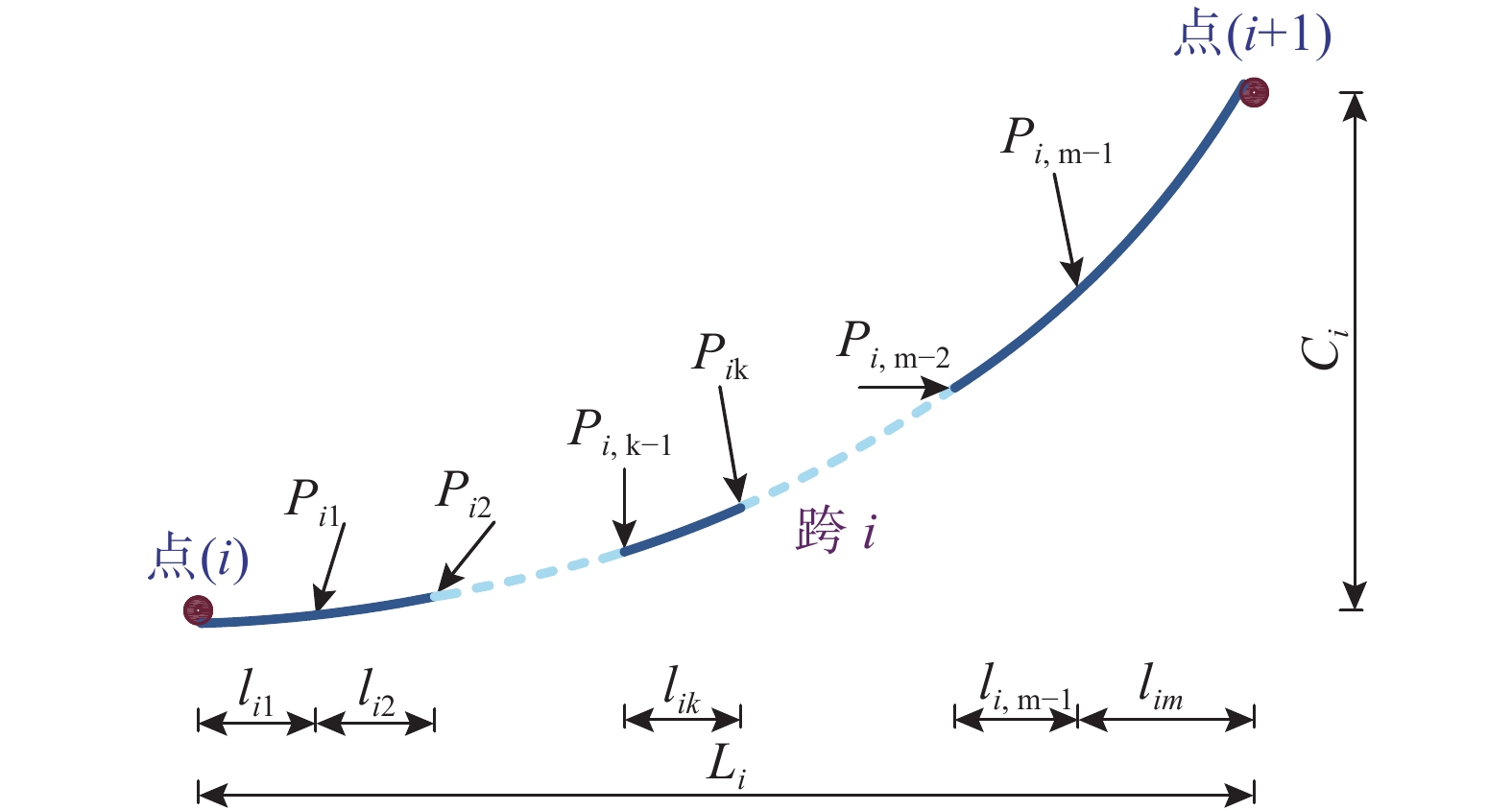
图2为N跨连续滑移索的示意图,各跨索曲线由第1节的公式描述。本文不考虑滑轮体积,将滑轮简化成一个点。图2中除第一个和最后一个点外,所有点都是可滑动的。第i跨(i=1, 2, 3,···, N)的受力如图3所示。
对于温度荷载下的索滑移,由于ITUL特性在当前温度下更加合理,将设计温度的无应力索长换算至当前温度下,再根据本节的方法求解:
s=sϑ/(1+αϑΔϑ) (14) q=qϑ(1+αϑΔϑ) (15) 式中:sϑ是当前温度下的无应力索长,即式(13)取Δϑ为0;qϑ为当前温度下的荷载。
因此以下公式不含温度相关的参数。另外,以下公式中,上标“t”代表滑动平衡状态。
基于ITUL特性,可以得到滑移前后总无应力索长不变方程:
N∑i=1sti−N∑i=1si=0 (16) 式中:si表示初始状态下第i跨的无应力索长;
sti 由式(13)计算。为了考虑滑移索结构中的滑移点摩擦,引入应用广泛的Euler公式。点(i)左侧的张力
TL(i) 和右侧的张力TR(i) 之间的关系由Euler公式建立(假设TR(i) 大于TL(i) ):η(i)=TL(i)TR(i)=e−μ(i)θ(i) (17) 式中,θ(i)可由索切线与X轴的夹角差值表示:
θ(i)=θ′R(i)−θ′L(i) (18) 式中:
θ′L(i) 是点(i)左侧索切线与X轴之间的夹角;θ′R(i) 同理。索的切线斜率(
tanθ′ )及其与X轴的夹角(θ′ )可以通过式(1)对x求导得到:tanθ′=dydx=−sinh(2βxL−α) (19) θ′=−arctan[sinh(2βxL−α)] (20) 因此,
θ′L(i) 和θ′R(i) 可以分别通过将x=Li−1和x=0代入式(20)中得到。摩擦力的方向由张拉或者后期荷载的行为决定。为了进一步在计算中考虑摩擦方向,在式(17)中引入符号函数ρ:
ρ(i)={−1,TL(i)>TR(i)0,TL(i)=TR(i)1,TL(i)<TR(i) (21) 然后式(17)可以被重写为:
η(i)=TL(i)TR(i)=e−ρ(i)μ(i)θ(i) (22) 考虑到式(8)中TB相当于
TL(i) ,式(7)中的TA相当于TR(i) ,可通过将式(7)和式(8)代入式(22),得出考虑摩擦的张力平衡方程:Htie−ρ(i)μ(i)θ(i)coshαti−Hti−1cosh(αti−1−2βti−1)=0 (23) 式中:i和i−1为相邻的两跨编号;(i)为滑移点编号。
对于自重下的N跨连续滑移索结构,存在由式(16)和式(23)组成的N元解析方程组。通过求解N个未知数(各跨水平张力Hit)的方程组,可以得到各跨在滑移平衡状态下的水平张力,进而可以根据第1节得到各跨索的其他参数。
2.2 集中荷载下的多跨连续索的解析方程组
为了给工程中带集中力的索滑移问题提供可靠的理论方法进行支撑,本节基于解析法建立相应的多元方程组。当受集中力的连续索在支点处滑移时,与滑移点相连索段的无应力索长也为变量,因此2.1节的自重下多跨连续索的方程组需要被进一步拓展。由于集中力的参与,2.1节的ITUL只在滑移点两侧索段成立,不再包含全部索段。N跨连续索的示意图仍为图2,区别在于内部索段的受力,其中第i跨索的受力图示见图4。
N跨连续索中,第i跨被(mi−1)个集中力分成mi (mi ≥2)个索段。对于整个结构,所有未知数包含:
Htik 、ltik 、ctik (下标“ik”代表第i跨的第k个索段,上标“t”代表滑移平衡态)、滑移点两侧索段的无应力索长stimi 与sti+1,1 ,共3∑N1mi+2(N−1) 个。而方程有:集中力作用点处的受力平衡方程、各索段变形协调方程、各跨水平和竖向相容方程、滑移点张力平衡方程、滑移点两侧索段ITUL方程,共3∑N1mi+2(N−1) 个。方程组数与未知量数相等,故方程组闭合。当第p跨无集中力时,mp=1,同理也可得到闭合的方程组。与2.1节同理,下标“(i)”代表点(i)的特性;上标“0”代表集中力作用前的平衡态。为了准确考虑摩擦,需进行分步加载,集中荷载在后期施加。集中荷载作用前的平衡态可根据2.1节计算。
第i跨的第k个集中力Pik作用点处在X和Y方向受力平衡,可得:
Hti,k+1−Htik+PXik=0 (24) Hti,k+1sinhαti,k+1+Htiksinh(2βtik−αtik)+PYik=0 (25) 式(24)和式(25)中:i=1, 2, ···, N;k=1, 2, ···, mi−1;mi≥2。
各索段的lik、cik始终满足位移相容条件,由此可得:
mi∑k=1ltik−Li=0,i=1,2,⋯,N;mi⩾ (26) \sum\limits_{k = 1}^{{m_i}} {c_{ik}^{\rm{t}}} - {C_i} = 0, \;\;\; {i = 1,{\rm{ }}2,{\rm{ }} \cdots ,N;{m_i} \geqslant {\rm{ }}2} (27) 式中:Li=X(i+1)−X(i);Ci=Y(i+1)−Y(i);均为常数。
由索段k的无应力索长
s_{ik}^{\rm{t}} 得变形协调方程:\begin{split} & \frac{{EAl_{ik}^{\rm{t}}}}{{H_{ik}^{\rm{t}}}}\left\{ {1 + \frac{1}{{2\beta _{ik}^{\rm{t}}\sqrt {1 - e{{_{ik}^{\rm{t}}}^2}} }}\left[ {\ln \left( {\frac{{f_{ik}^{\rm{t}} - \tanh \left( {\beta _{ik}^{\rm{t}} - {{\alpha _{ik}^{\rm{t}}} / 2}} \right)}}{{f_{ik}^{\rm{t}} + \tanh \left( {\beta _{ik}^{\rm{t}} - {{\alpha _{ik}^{\rm{t}}} / 2}} \right)}}} \right)} - \right.} \right.\\&\qquad \left. {\left. {\ln \left( {\frac{{f_{ik}^{\rm{t}} + \tanh \left( {{{\alpha _{ik}^{\rm{t}}} / 2}} \right)}}{{f_{ik}^{\rm{t}} - \tanh \left( {{{\alpha _{ik}^{\rm{t}}} / 2}} \right)}}} \right)} \right]} \right\} - s_{ik}^{\rm{t}}=0 \\[-18pt] \end{split} (28) 式中:i=1, 2, ···, N; k=1, 2, ···, mi;不与滑移点连接索段的
s_{ik}^{\rm{t}} 为常数,直接由初始态给出,与滑移点相连的索段的s_{i{m_i}}^{\rm{t}} 与s_{i + 1,1}^{\rm{t}} 为变量。各滑移点两侧的索段满足ITUL特性,可得:
s_{i{m_i}}^{\rm{t}} + s_{i + 1,1}^{\rm{t}} - ( {s_{i{m_i}}^0 + s_{i + 1,1}^0} ) = 0,\;\;\; {i = 1,{\rm{ }}2,{\rm{ }} \cdots ,N - 1} (29) 式中,括号中的两项为初始值,由已知条件确定。
与2.1节同理,在滑移点处张力平衡,可得:
\begin{split} & H_{i + 1,1}^{\rm{t}}{{\rm e}^{ - {\rho _{\left( i \right)}}{\mu _{\left( i \right)}}{\theta _{\left( i \right)}}}}\cosh \alpha _{i + 1,1}^{\rm{t}} - H_{i{m_i}}^{\rm{t}}\cosh ( {2\beta _{i{m_i}}^{\rm{t}} - \alpha _{i{m_i}}^{\rm{t}}} ) = 0,\\&\qquad\qquad {i = 1,{\rm{ }}2,{\rm{ }} \cdots ,N - 1} \\[-16pt] \end{split} (30) 式(24)~式(30)构成了以
l_{ik}^{\rm{t}} 、c_{ik}^{\rm{t}} 、H_{ik}^{\rm{t}} (i=1, 2, ···, N; k=1, 2, ···, mi)、s_{i{m_i}}^{\rm{t}} 与s_{i + 1,1}^{\rm{t}} (i=1, 2, ···, N−1)为变量的多元方程组,通过求解该方程组,即可得到集中力作用后的滑移平衡态。2.3 索杆滑移结构的解析方程组
2.1节和2.2节都不考虑滑轮中心设置在杆系上,只考虑连续索本身,这种做法只能满足部分工程结构,比如塔架刚度较大的缆索吊装系统、索道、起重机、海上升降机等。对于工程中的张弦桁架、张拉穹顶等滑移索结构[21],往往需要考虑杆件对结构整体的贡献,这时候就需要加入杆件的参数和变形协调方程。
索杆滑移结构如图5所示,连续索搭接在杆件上形成整体,共同受力和变形。受集中力的多跨连续索的方程组已在2.2节给出,无集中力作用时,退化为2.1节的方程组。由于加入了杆件,需要在2.2节的基础上增加杆件的变量和方程。对于索杆滑移结构,连续索的变形方程同式(24)~式(30)。增加杆件的端点坐标变量(Xk, Yk)共2n个(n为杆件节点数,k=1, 2, ···, n),杆件的轴力变量Tj共p个(p为杆件节点数,j=1, 2, ···, p)。每根杆件变形前后可根据定义建立p个变形协调方程[19]:
\sqrt {X_{ba}^2 + Y_{ba}^2} - \left( {1 + \frac{{{T_j}}}{{{E_t}{A_t}}}} \right){l_{t0}} = 0 (31) 式中:Xba=Xb−Xa, Yba=Yb−Ya(注:索节点也有此等式);下标“b”和“a”代表杆件的两个端点号;Et、At分别为杆件的弹性模量和横截面积;lt0为杆件的原长。
在杆件的端点处受力平衡,可以建立2n个方程(下式为矢量形式):
\sum\limits_{j = 1}^{{j_a}} {{{\boldsymbol{T}}_j^a}} + \sum\limits_{c = 1}^{{c_a}} {{{\boldsymbol{T}}_c^a}} + {\boldsymbol{F}}_{\rm{R}}^a = 0 (32) 式中:
{{\boldsymbol{T}}_{j}^{a}} 、{{\boldsymbol{T}}_{c}^{a}} 、{{\boldsymbol{T}}_{\rm{R}}^{a}} 分别为端点a处的杆端力、索端力、等效节点外力;ja、ca分别为端点a处的杆件数、单索数。写为分量形式时(杆件自重为qt):T_{jX}^a = T_j^a\dfrac{{{X_{ba}}}}{{\sqrt {X_{ba}^2 + Y_{ba}^2} }};\;T_{jY}^a = T_j^a\dfrac{{{Y_{ba}}}}{{\sqrt {X_{ba}^2 + Y_{ba}^2} }} + \dfrac{{{q_t}{l_{t0}}}}{2} ;T_{cX}^a = H_c^{\rm{t}}\dfrac{{{X_{ba}}}}{{\sqrt {X_{ba}^2} }};T_{cY}^a = V_c^{\rm{t}} , 点a为索起点时,V_c^{\rm{t} } = H_c^{\rm{t}}\sinh {\alpha _c} ;若为索终点,V_c^{\rm{t}}=q{s_0} - H_c^{\rm{t}}\sinh {\alpha _c} 。另外,注意到引入杆件端点坐标变量后,2.2节式中的Li和Ci可能受到其影响,不再为常数。此时Li和Ci由(Xk, Yk)替换式(26)和式(27)中的相应端点坐标表示。
2.2节的式(24)~式(30)和本节的式(31)和式(32)组成了索杆滑移结构的基本方程组。由于新增的式(31)~式(32)的数量与新增变量数相等,方程组闭合。
2.4 解析方程组的求解技术
对于非线性方程组的求解,现有数学方法已经比较成熟,精度可以定量控制。本文采用Newton-Raphson迭代求解方程组。另外,也可使用MATLAB自带的方程组求解函数fsolve等直接求解非线性方程组。
对于平面索杆滑移结构的方程组,将变量写为列向量形式X=[H s l c X Y T]T。注意到自重下的多跨连续索只包含上述X中的第一项,集中力下的多跨连续索只包含前4项。将方程组改写为函数形式F(X),使用Newton-Raphson迭代法求解非线性方程组,需要相应的Jacobi矩阵,可根据定义推导。方程组形式统一,Jacobi矩阵F′(X)形式简洁,为了方便,也可直接使用MATLAB的jacobian函数直接推导。利用下式进行迭代:
{{\boldsymbol{X}}^{n + 1}}={{\boldsymbol{X}}^n} - {\left[ {{\boldsymbol{F}}'\left( {{{\boldsymbol{X}}^n}} \right)} \right]^{{\rm{ - }}1}}{\boldsymbol{F}}\left( {{{\boldsymbol{X}}^n}} \right) (33) 式中,n为迭代次数。
迭代时,以X增量的二范数作为精度的控制参数。由于各个方程组和变量的明确性和统一性,本文的理论计算方法与文献[19]同理,可以编制通用分析程序。与通用有限元软件类似,在可视化界面定义索段、坐标等信息后,由软件自动形成方程组,并分析求解。
3 算例分析与讨论
3.1 两跨滑移索结构
一个两跨滑移索结构如图6所示。在结构中,索只能在点(2)处滑动。跨1和跨2的无应力索长分别为8.02 m和12.02 m。索的弹性模量E为170 GPa,横截面积A为67.4 mm2。两跨均承受沿索曲线的均布荷载q=0.2 kN/m。本例不考虑滑移点处的摩擦力,求该结构的滑移平衡态。
根据本文方法,编制了MATLAB程序,得到滑动平衡状态下该结构的计算结果如表1所示。表1也给出了唐建民和卓家寿[18]两跨理论解和其他数值模拟方法的结果。其中,Liu等[22]的方法基于直线索单元;而聂建国等[13]和Cai等[15]基于悬链线索单元;俞锋等[9]利用的是有限质点法。
文献[18]理论解与本文的误差主要是其对单索几何非线性分析的近似处理。结果表明,聂建国等[13]和Cai等[15]的数值方法具有较高的精度,而Liu等[22]的方法的精度相对较低。这主要是由于Liu等[22]的方法利用杆单元代替悬链线单元,与索实际构型不同。Cai等[15]的方法中,采用无应力索长的高精度近似算法,造成了与本文方法很小的误差。相比文献[9, 22]的数十个直线单元,本文只需要三个变量和方程组,省去了索内部单元划分的步骤。此外,由于每跨的对称性,各跨左右两端的张力应该相等。表1的结果表明,本文和Cai等[15]的方法计算的结果均满足这一点。
表 1 两跨滑移索结构的计算结果Table 1. Calculated results of the two-span sliding cables方法 位置 左端张力 右端张力 值/kN 误差/(‰) 值/kN 误差/(‰) 本文理论解 第1跨 8.3541 − 8.3541 − 第2跨 8.3541 − 8.3541 − 理论解[18] 第1跨 8.3562 0.25 8.3562 0.25 第2跨 8.3562 0.25 8.3562 0.25 Liu等[22] 第1跨 8.2945 −7.13 8.3063 −5.72 第2跨 8.2873 −8.00 8.2896 −7.72 聂建国等[13] 第1跨 8.3478 −0.75 8.3488 −0.63 第2跨 8.3488 −0.63 8.3490 −0.61 Cai等[15] 第1跨 8.3534 −0.08 8.3534 −0.08 第2跨 8.3534 −0.08 8.3534 −0.08 俞锋等[9] 第1跨 8.3491 −0.60 8.3493 −0.57 第2跨 8.3493 −0.57 8.3490 −0.61 注:本文所有表格中的误差均是相对于本文理论解。 3.2 三跨滑移索结构
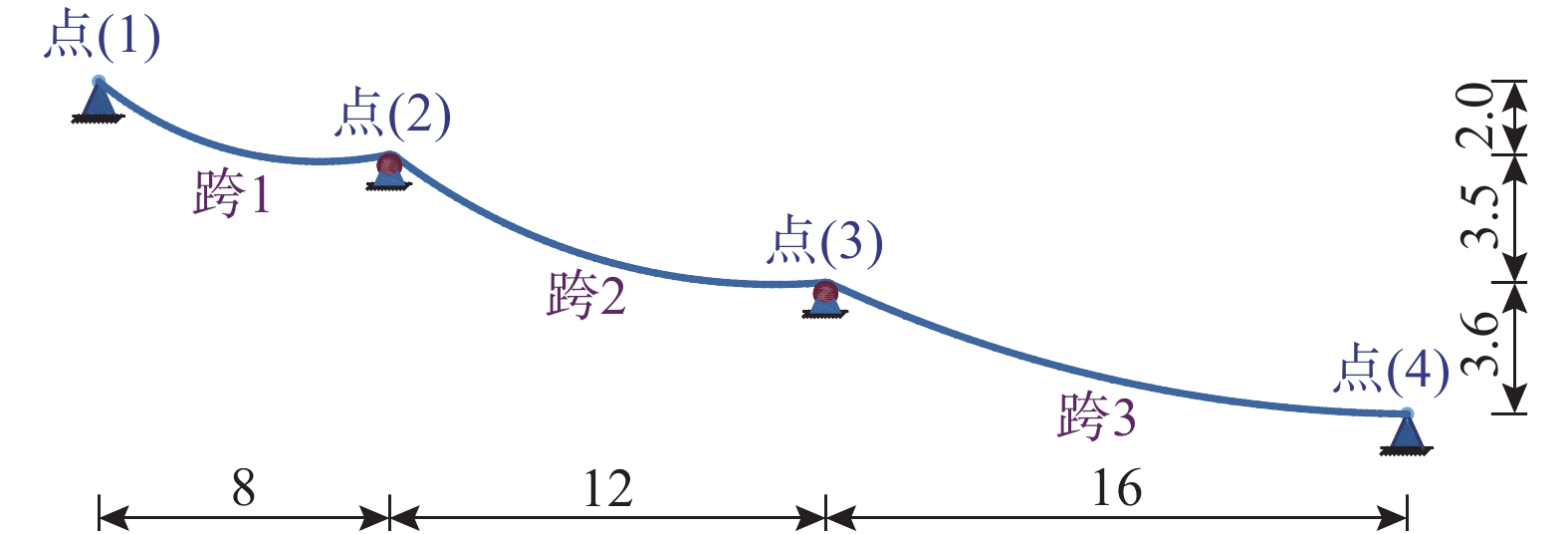
图7为三跨滑移索结构,其中点(1)和点(4)是锚固点,连续索可以在点(2)和点(3)处滑动。索的横截面积、弹性模量、自重q均同例3.1。跨1、跨2和跨3的无应力索长分别为8.26 m、12.52 m和16.64 m。本例中考虑滑动摩擦时,假定两个滑移点处的摩擦系数μ1=μ2=0.1。索在点(1)左端张拉,由此可以确定摩擦力方向。
为了便于比较,表2首先给出了不考虑摩擦的三跨滑移索结构的计算结果。表2也列出了魏建东[14]和Cai等[15]基于悬链线索单元和滑移刚度的有限元法的计算结果。结果表明,他们的两者的计算结果与本文方法非常接近。这主要是因为他们都使用悬链线理论,并基于ITUL特性。
表 2 不考虑摩擦的三跨索结构的计算结果Table 2. Calculated results of the three-span sliding cables without considering friction表3列出了该结构考虑摩擦的滑动平衡状态下的计算结果。对比表2和表3,得出考虑摩擦后,第一跨的左端张力增大了5.4%,且连续索索力变得更不均匀。表3也给出了有限质点法的计算结果,发现其结果与其他方法有明显不同,这是由于它不考虑张拉引起摩擦力方向改变引起的。在文献[10]中,说明了摩擦力作为非保守力,其对结构响应的影响与加载路径有关,滑移索分析应准确考虑施工过程。因此,摩擦对滑移索结构的内力峰值和分布有明显影响,实际工程中应根据施工准确考虑。
表 3 考虑摩擦的三跨索结构的计算结果Table 3. Calculated results of the three-span sliding cables considering friction方法 位置 左端张力 右端张力 值/kN 误差/(‰) 值/kN 误差/(‰) 本文理论解 第1跨 7.8895 − 7.4895 − 第2跨 7.2573 − 6.5573 − 第3跨 6.3098 − 5.5898 − 魏建东[14] 第1跨 7.8853 −0.53 7.4856 −0.52 第2跨 7.2535 −0.52 6.5539 −0.52 第3跨 6.3066 −0.51 5.5870 −0.50 Cai等[15] 第1跨 7.8907 0.15 7.4907 0.16 第2跨 7.2585 0.17 6.5585 0.18 第3跨 6.3093 −0.08 5.5893 −0.09 俞锋等[10] 第1跨 7.4438 −56.49 7.0459 −59.23 第2跨 7.2757 2.54 6.5761 2.87 第3跨 6.3290 3.04 5.6091 3.45 3.3 缆索吊装系统模拟
宜宾小南门金沙江大桥施工的缆索吊装系统的简图如图8所示。该结构的主缆在两个塔架顶部可以滑动。主缆的弹性模量75.6 GPa,横截面积33.73 cm2,自重31.716 kg/m。设计起吊重量为40 t,包含吊具重6 t。设计的最大垂度23.42 m,最大索力1470 kN。文献[16]采用两个三节点滑移单元近似模拟了该结构。已知吊具安装后位于跨中,吊点垂度16.047 m。现有文献未考虑接触摩擦,本文考虑摩擦时,两个摩擦系数均取0.2。
缆索吊装系统通常已知吊具安装后吊点的垂度,而非无应力索长。对于有限元法[16],只能通过假设,反复试算得到设计参数。而本文的理论方法可直接求解方程组,准确得到。本文2.2节的方程组中,由于索的参数l、c全部已知,方程组剩下式(24)、式(25)、式(28)、式(30)中的8个方程,变量为8个各索段水平张力及其无应力索长。求解方程组,迭代4次收敛。表4给出了本文和文献[16]吊具安装后的状态参数。考虑摩擦时,由于吊重较大,两个边跨向中跨滑动,由此可确定摩擦力方向。由表4可知本文与文献[16]的结果较接近;考虑摩擦与不考虑摩擦的静力响应差别较大。
表 4 缆索吊装系统吊具安装后的状态参数Table 4. Parameters of cable lifting system afterinstallation of the spreader方法 总无应力
索长/m边跨无应力
索长力/m地锚处索力 值/kN 误差/(%) 本文-无摩擦 650.0035 174.3840 478.27 − 本文-摩擦 650.1275 174.4460 441.50 −7.69 文献[16] 649.9893 174.3828 479.00 0.15 图9和图10分别为左锚固点索力与吊点位置的关系。由图可知,本文和文献[16]的结果高度一致,文献[16]的精度较高;摩擦对索力的影响较大,对垂度的影响较小,实际工程应准确考虑。
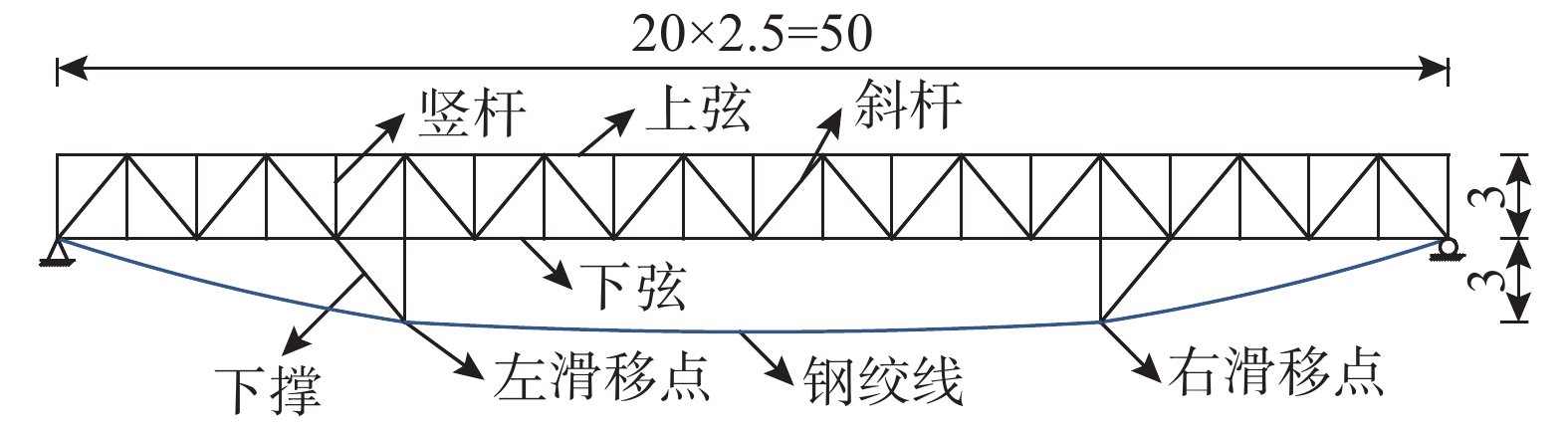
3.4 平行式预应力钢桁架模拟
平行式预应力钢桁架由两片平面结构组成,计算时取一侧的平面结构进行,如图11所示。杆件采用箱形截面,面积为46.79 cm2,弹性模量为200 GPa,钢材重度为78.5 kN/m3。下部由一根连续拉索施加预应力,拉索横截面积为9.186 cm2,弹性模量为170 GPa,自重荷载为80 N/m。施工时,在左锚固点左侧张拉,张拉完成后在每个上弦节点施加竖直向下20 kN的后期荷载,参考文献[14],两个滑移点的摩擦系数取0.4。
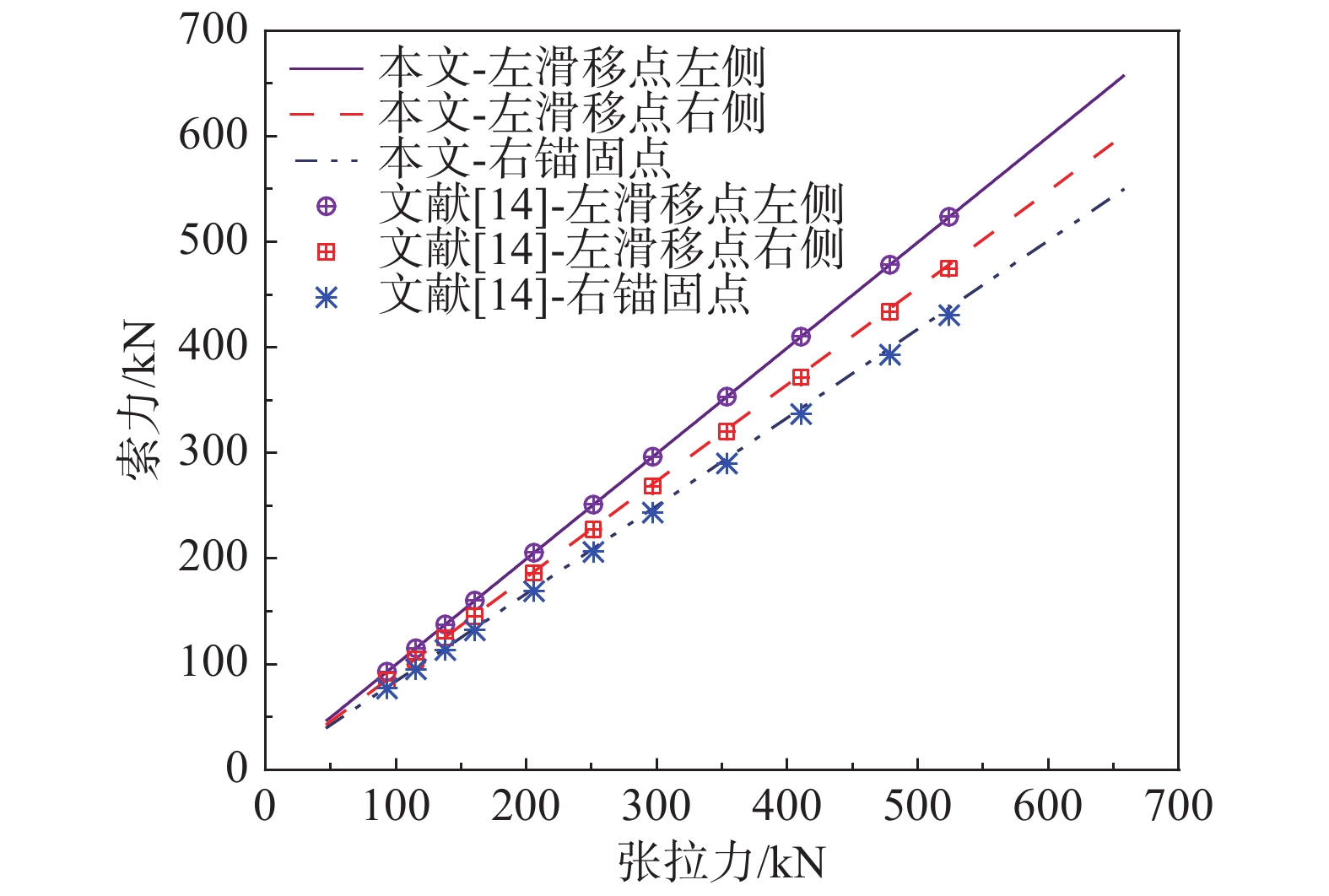
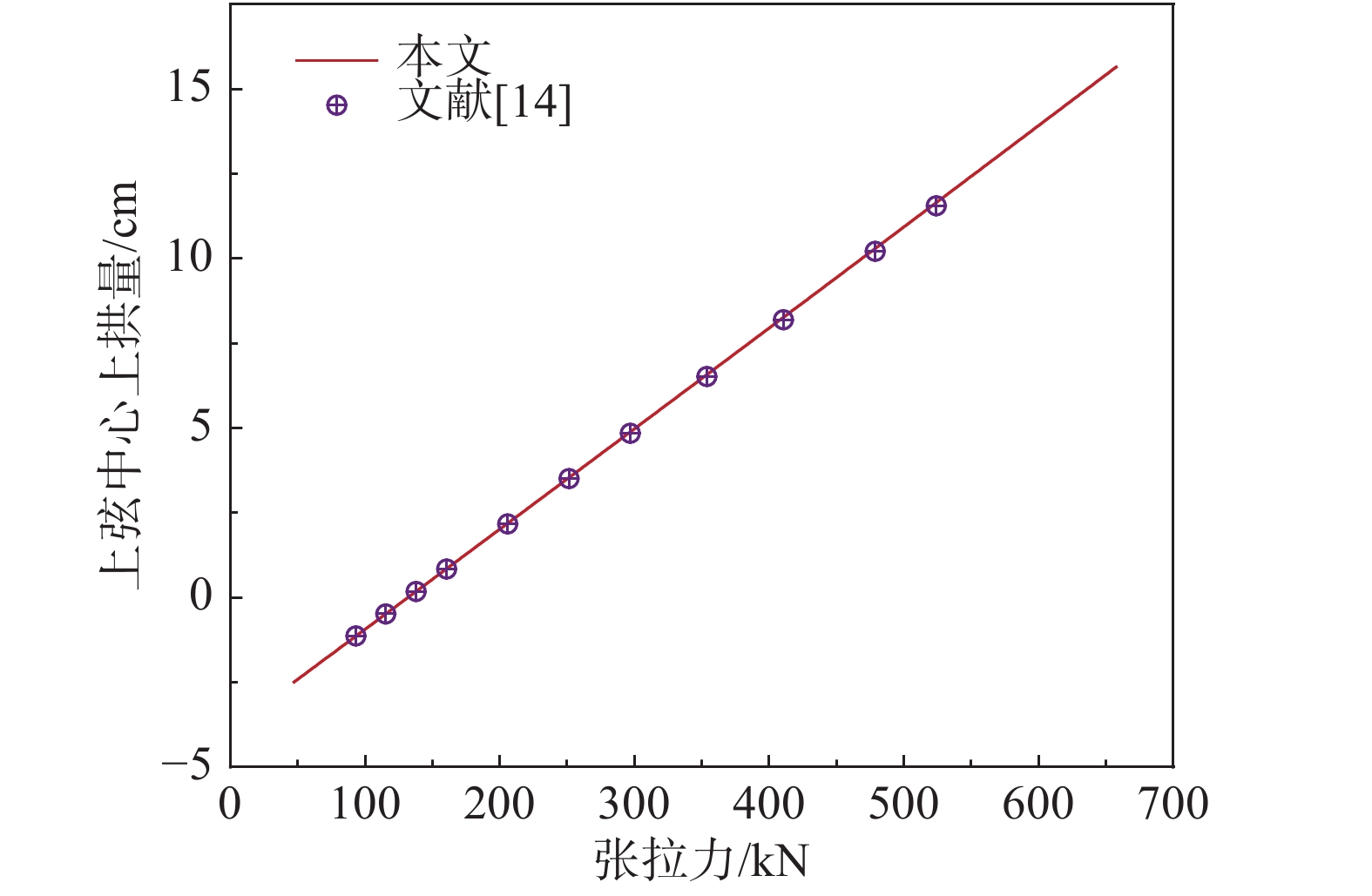
图12和图13分别为索力与上弦中心上拱量随张拉力变化的关系图。由图可知,随着张拉力的增大,索力与上拱量均呈增大趋势;本文的结果与文献[14]高度吻合。后期荷载作用后的结构响应如表5所示。由表可知,文献[14]的内力和位移响应均略大于本文的计算结果,但其精度较高。此外,通过该复杂结构的模拟,发现本文方法对迭代初值依赖很低。迭代十次左右即可达到0.000 01%的迭代精度。因此,可以得出:本文的理论解分析索杆滑移结构时,准确可靠、效率较高,能给有限元方法提供精度评价。
表 5 后期荷载作用后的结构响应Table 5. Structural responses under service loads方法 张拉端
索力/kN左滑移点
左侧索力/kN左滑移点
右侧索力/kN锚固端
索力/kN上弦中心
上拱量/cm本文 701.083 700.844 638.647 581.958 0.57 文献[14] 720.181 719.943 650.753 588.432 0.99 4 结论
本文基于悬链线理论、Euler摩擦公式,采用解析法建立了滑移索结构的解析方程组。利用精度可以定量控制的Newton-Raphson迭代求解方程组,通过编程对算例进行验证。结果表明:
(1) 本文建立的考虑温度效应的单索无应力索长解析式只包含水平张力一个变量,方便用于索结构分析理论的建立。以该解析式为核心建立的滑移索结构的理论解合理可行。
(2) 本文建立的自重、集中荷载下的多跨连续索结构和索杆滑移结构的解析方程组形式统一,变量意义明确,易于编程。
(3) 摩擦对结构内力峰值有明显的影响,使得内力分布更不均匀,实际工程中应根据施工方案在结构分析时准确计入摩擦。
(4) 本文的理论计算方法克服了数值模拟方法的误差及一般解析法的局限性,计算精度高,具有较好的适应性和可靠性,可为索支承桥及预应力张拉结构等的滑移问题分析提供理论依据。
-
表 1 两跨滑移索结构的计算结果
Table 1 Calculated results of the two-span sliding cables
方法 位置 左端张力 右端张力 值/kN 误差/(‰) 值/kN 误差/(‰) 本文理论解 第1跨 8.3541 − 8.3541 − 第2跨 8.3541 − 8.3541 − 理论解[18] 第1跨 8.3562 0.25 8.3562 0.25 第2跨 8.3562 0.25 8.3562 0.25 Liu等[22] 第1跨 8.2945 −7.13 8.3063 −5.72 第2跨 8.2873 −8.00 8.2896 −7.72 聂建国等[13] 第1跨 8.3478 −0.75 8.3488 −0.63 第2跨 8.3488 −0.63 8.3490 −0.61 Cai等[15] 第1跨 8.3534 −0.08 8.3534 −0.08 第2跨 8.3534 −0.08 8.3534 −0.08 俞锋等[9] 第1跨 8.3491 −0.60 8.3493 −0.57 第2跨 8.3493 −0.57 8.3490 −0.61 注:本文所有表格中的误差均是相对于本文理论解。 表 2 不考虑摩擦的三跨索结构的计算结果
Table 2 Calculated results of the three-span sliding cables without considering friction
表 3 考虑摩擦的三跨索结构的计算结果
Table 3 Calculated results of the three-span sliding cables considering friction
方法 位置 左端张力 右端张力 值/kN 误差/(‰) 值/kN 误差/(‰) 本文理论解 第1跨 7.8895 − 7.4895 − 第2跨 7.2573 − 6.5573 − 第3跨 6.3098 − 5.5898 − 魏建东[14] 第1跨 7.8853 −0.53 7.4856 −0.52 第2跨 7.2535 −0.52 6.5539 −0.52 第3跨 6.3066 −0.51 5.5870 −0.50 Cai等[15] 第1跨 7.8907 0.15 7.4907 0.16 第2跨 7.2585 0.17 6.5585 0.18 第3跨 6.3093 −0.08 5.5893 −0.09 俞锋等[10] 第1跨 7.4438 −56.49 7.0459 −59.23 第2跨 7.2757 2.54 6.5761 2.87 第3跨 6.3290 3.04 5.6091 3.45 表 4 缆索吊装系统吊具安装后的状态参数
Table 4 Parameters of cable lifting system afterinstallation of the spreader
方法 总无应力
索长/m边跨无应力
索长力/m地锚处索力 值/kN 误差/(%) 本文-无摩擦 650.0035 174.3840 478.27 − 本文-摩擦 650.1275 174.4460 441.50 −7.69 文献[16] 649.9893 174.3828 479.00 0.15 表 5 后期荷载作用后的结构响应
Table 5 Structural responses under service loads
方法 张拉端
索力/kN左滑移点
左侧索力/kN左滑移点
右侧索力/kN锚固端
索力/kN上弦中心
上拱量/cm本文 701.083 700.844 638.647 581.958 0.57 文献[14] 720.181 719.943 650.753 588.432 0.99 -
[1] 杨孟刚, 陈政清. 两节点曲线索单元精细分析的非线性有限元法[J]. 工程力学, 2003, 20(1): 42 − 47. doi: 10.3969/j.issn.1000-4750.2003.01.008 Yang Menggang, Chen Zhengqing. Nonlinear analysis of cable structures using a two-node curved cable element of high precision [J]. Engineering Mechanics, 2003, 20(1): 42 − 47. (in Chinese) doi: 10.3969/j.issn.1000-4750.2003.01.008
[2] Aufaure M. A three-node cable element ensuring the continuity of the horizontal tension: a clamp-cable element [J]. Computers and Structures, 2000, 74(2): 243 − 251. doi: 10.1016/S0045-7949(99)00015-2
[3] Zhou B, Accorsi M L, Leonard J W. Finite element formulation for modeling sliding cable elements [J]. Computers and Structures, 2004, 82(2/3): 271 − 280.
[4] Lee K H, Choo Y S, Ju F. Finite element modeling of frictional slip in heavy lift sling systems [J]. Computers and Structures, 2003, 81(30/31): 2763 − 2690.
[5] Chen Z H, Wu Y J, Yin Y, et al. Formulation and application of multi-node sliding cable element for the analysis of suspend-dome structures [J]. Finite Elements in Analysis and Design, 2010, 46(9): 743 − 750. doi: 10.1016/j.finel.2010.04.003
[6] 郭彦林, 崔晓强. 滑动索系结构的统一分析方法—冷冻-升温法[J]. 工程力学, 2003, 20(4): 156 − 160. doi: 10.3969/j.issn.1000-4750.2003.04.028 Guo Yanlin, Cui Xiaoqiang. An unified analytical method for gliding cable structures—frozen-heated method [J]. Engineering Mechanics, 2003, 20(4): 156 − 160. (in Chinese) doi: 10.3969/j.issn.1000-4750.2003.04.028
[7] 彭伟贤, 陈春雷, 梁佶, 等. 一种滑移索的简捷计算方法[J]. 结构工程师, 2005, 21(1): 30 − 33. doi: 10.3969/j.issn.1005-0159.2005.01.008 Peng Weixian, Chen Chunlei, Liang Ji, et al. A simplified method for dealing with sliding cable [J]. Structural Engineering, 2005, 21(1): 30 − 33. (in Chinese) doi: 10.3969/j.issn.1005-0159.2005.01.008
[8] Yu X, Chen D, Bai Z. A new method for analysis of sliding cable structures in bridge engineering [J]. KSCE, Journal of Civil Engineering, 2018, 22(11): 4483 − 4489. doi: 10.1007/s12205-017-0151-7
[9] 俞锋, 罗尧治. 索杆结构中索滑移行为分析的有限质点法[J]. 工程力学, 2015, 32(6): 109 − 116. Yu Feng, Luo Yaozhi. The finite particle method for analysing cable sliding in cable-strut structures [J]. Engineering Mechanics, 2015, 32(6): 109 − 116. (in Chinese)
[10] 俞锋, 尹雄, 罗尧治, 等. 考虑接触点摩擦的索滑移行为分析[J]. 工程力学, 2017, 34(8): 47 − 55. Yu Feng, Yin Xiong, Luo Yaozhi, et al. Cable sliding analysis considering frictional effect [J]. Engineering Mechanics, 2017, 34(8): 47 − 55. (in Chinese)
[11] Kan Z, Peng H, Chen B, et al. A sliding cable element of multibody dynamics with application to nonlinear dynamic deployment analysis of clustered tensegrity [J]. International Journal of Solids and Structures, 2018, 130-131: 61 − 79. doi: 10.1016/j.ijsolstr.2017.10.012
[12] Kan Z, Peng H, Chen B. A simple linear complementarity approach for sliding cable modeling considering friction [J]. Mechanical Systems and Signal Processing, 2019, 130: 293 − 314. doi: 10.1016/j.ymssp.2019.05.012
[13] 聂建国, 陈必磊, 肖建春. 多跨连续长索在支座处存在滑移的非线性静力分析[J]. 计算力学学报, 2003, 20(3): 320 − 324. doi: 10.3969/j.issn.1007-4708.2003.03.012 Nie Jianguo, Chen Bilei, Xiao Jianchun. Nonlinear static analysis of continuous cables with sliding at the middle supporting [J]. Chinese Journal of Computational Mechanics, 2003, 20(3): 320 − 324. (in Chinese) doi: 10.3969/j.issn.1007-4708.2003.03.012
[14] 魏建东. 预应力钢桁架结构分析中的摩擦滑移索单元[J]. 计算力学学报, 2006, 23(6): 800 − 806. doi: 10.3969/j.issn.1007-4708.2006.06.030 Wei Jiandong. Friction sliding cable element for structural analysis of prestressed steel truss [J]. Chinese Journal of Computational Mechanics, 2006, 23(6): 800 − 806. (in Chinese) doi: 10.3969/j.issn.1007-4708.2006.06.030
[15] Cai Jianguo, Lim James, Feng Jian. Elastic catenary cable element considering frictional slip effect [J]. Science China Technological Sciences, 2012, 55(6): 1489 − 1495. doi: 10.1007/s11431-012-4833-6
[16] 魏建东. 索结构分析的滑移索单元法[J]. 工程力学, 2004, 21(6): 172 − 176. doi: 10.3969/j.issn.1000-4750.2004.06.028 Wei Jiandong. Sliding cable element for the analysis of cable structures [J]. Engineering Mechanics, 2004, 21(6): 172 − 176. (in Chinese) doi: 10.3969/j.issn.1000-4750.2004.06.028
[17] 魏建东. 缆索吊装系统有限元分析中的滑轮单元[J]. 力学与实践, 2007, 29(1): 58 − 63. doi: 10.3969/j.issn.1000-0879.2007.01.012 Wei Jiandong. Cable-pulley element in finite element analysis of cableway erection system [J]. Mechanics in Engineering, 2007, 29(1): 58 − 63. (in Chinese) doi: 10.3969/j.issn.1000-0879.2007.01.012
[18] 唐建民, 卓家寿. 在中支座可滑动的两跨连续索的静[J]. 计算力学学报, 1999, 16(4): 483 − 488. doi: 10.3969/j.issn.1007-4708.1999.04.016 Tang Jianming, Zhuo Jiashou. Nonlinear static analysis of two-span continuous cables sliding on the middle supporting [J]. Chinese Journal of Computational Mechanics, 1999, 16(4): 483 − 488. (in Chinese) doi: 10.3969/j.issn.1007-4708.1999.04.016
[19] Such M, Jimenez-Octavio J R, Carnicero A, et al. An approach based on the catenary equation to deal with static analysis of three-dimensional cable structures [J]. Engineering Structures, 2009, 31: 2162 − 2170. doi: 10.1016/j.engstruct.2009.03.018
[20] Krishna P. Cable-suspended roofs (second edition)[M]. New York: McGraw, 2013.
[21] 董石麟, 陈伟刚, 涂源, 等. 蜂窝三撑杆型索穹顶结构构形和 预应力态分析研究[J]. 工程力学, 2019, 36(9): 128 − 135. doi: 10.6052/j.issn.1000-4750.2018.08.0438 Dong Shilin, Chen Weigang, Tu Yuan, et al. Configuration and prestressing distribution of the honeycomb-type cable dome with three struts [J]. Engineering Mechanics, 2019, 36(9): 128 − 135. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.08.0438
[22] Liu Y, Qian Z, Xia K. Mechanical response of transmission lines based on sliding cable element [J]. Journal of Central South University, 2014, 21(8): 3370 − 3377. doi: 10.1007/s11771-014-2311-y
-
期刊类型引用(1)
1. 陈诗再,杨孟刚. 滑移索结构分析的精确三维有限元法. 工程力学. 2023(02): 135-144+189 .  本站查看
本站查看
其他类型引用(2)




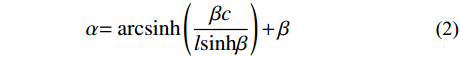

 下载:
下载: