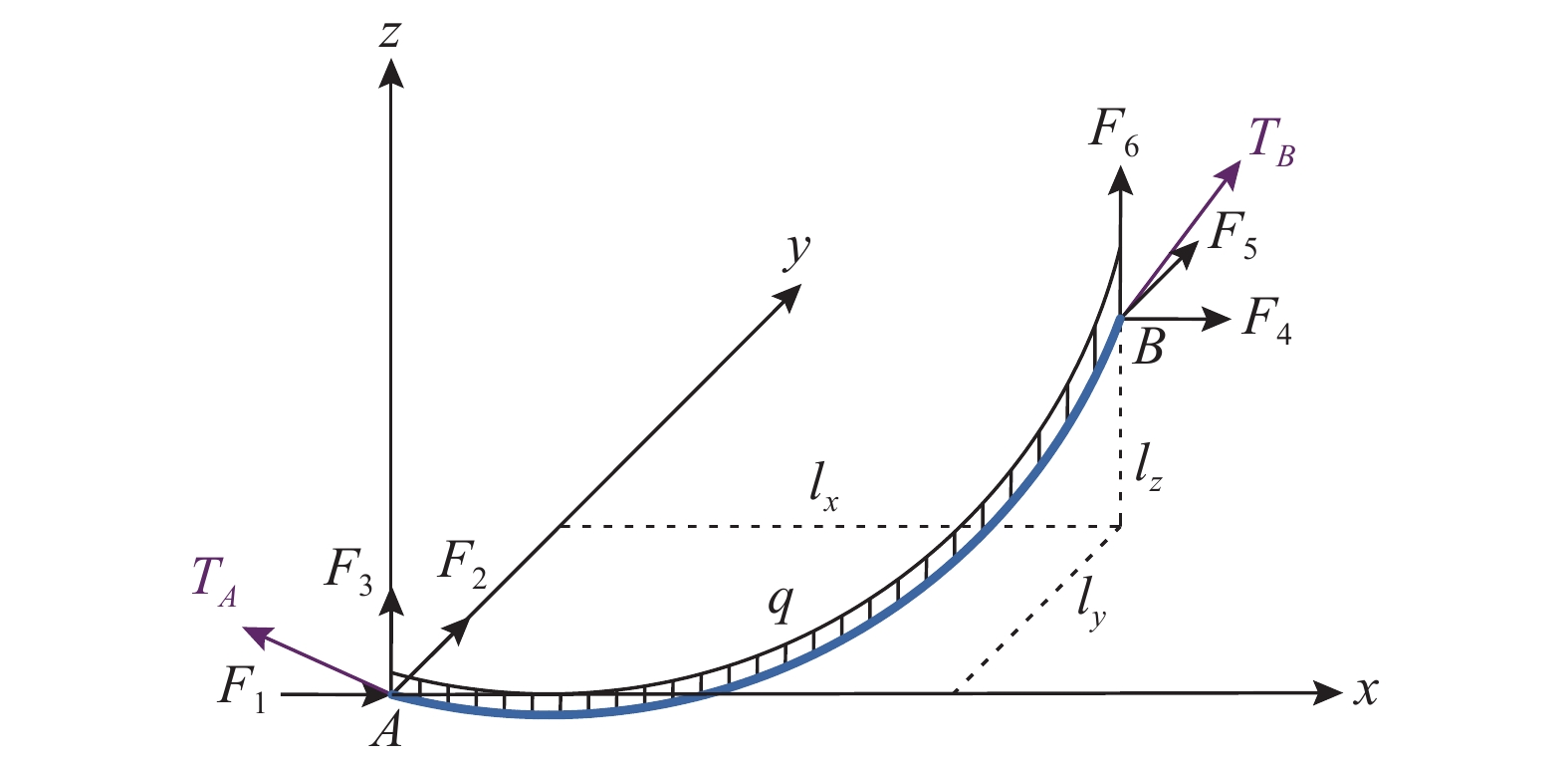
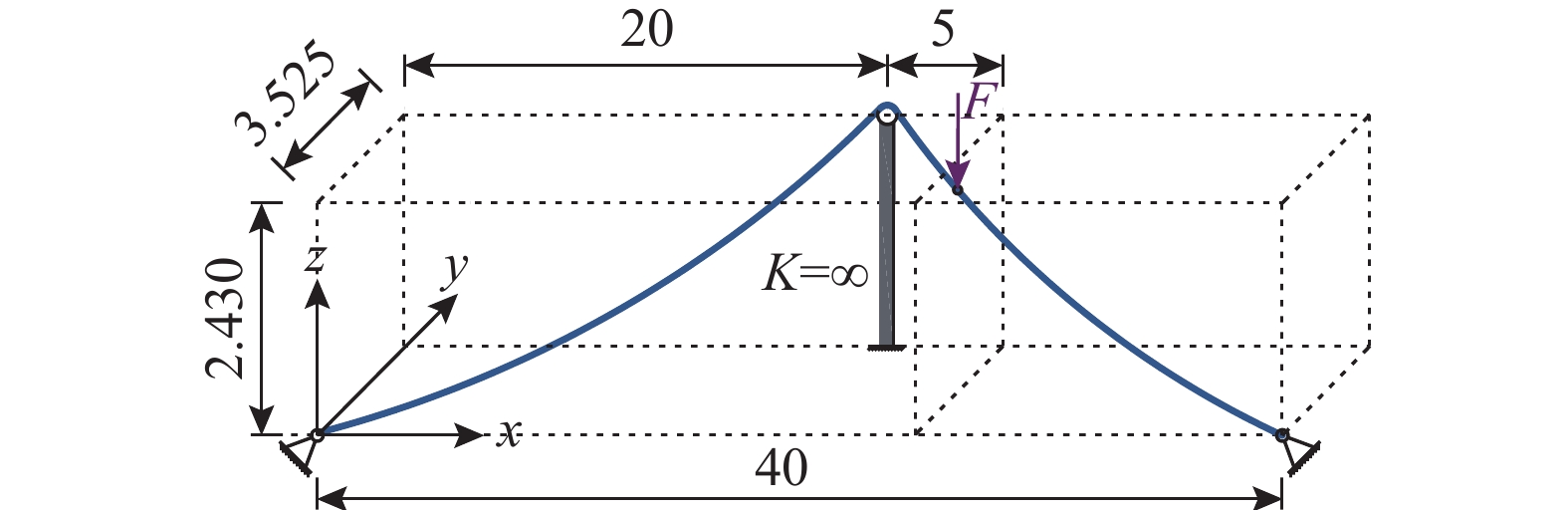
HIGH-PRECISION THREE-DIMENSIONAL FINITE ELEMENT METHOD FOR ANALYSIS OF SLIDING CABLE STRUCTURES
-
摘要: 针对现有滑移索结构分析方法适用范围有限、精度不高的缺点，提出了一种通用、高精度的三维滑移索单元法。基于悬链线理论和Euler-Eytelwein公式，同时考虑了温度效应和滑动摩擦，分别建立了已知单元无应力索长和已知张拉力的三维滑移索单元的基本方程组；利用矩阵微分从单元基本方程组导出了单元的切线刚度矩阵；建立了滑移索结构从张拉到后期加载的全过程精细化分析流程，可实现自动调用建立的各类索单元，准确分析各滑移点的摩擦；通过3个算例的计算及与现有理论解、数值解和试验结果的比较来验证该文所提出方法的可靠性和有效性。结果表明，该文提出的三维有限元法准确可靠，计算效率较高，适用于工程中各种滑移索结构的高精度非线性分析。Abstract: To overcome the shortcomings of limited application range and low precision in the existing analysis methods for sliding cable structures, a general and high-precision three-dimensional finite element method for sliding cables is proposed. Based on the catenary theory and Euler-Eytelwein equation, the governing equations of the three-dimensional sliding cable elements with known unstressed cable length and with known tensile forces are respectively developed, accounting for the thermal effect and sliding friction. The tangent stiffness matrix of the element is derived directly from the governing equations by using matrix differential. A refined analysis procedure of sliding cable structures for the whole process from tensioning to later loadings is proposed, with the capability of automatically using all types of cable elements and accurately analyzing the friction at each sliding point. The reliability and effectiveness of the proposed method are verified by three computational examples and, by the comparison with the pertinent existing theoretical solutions and, with the pertinent numerical results and experimental ones. The computational results show that the three-dimensional finite element method proposed is accurate and reliable with high computational efficiency and is very suitable for the high-precision nonlinear analysis of various sliding cable structures in engineering practice.
-
Keywords:
- sliding cable structures /
- friction /
- temperature /
- geometric nonlinearity /
- finite element method
-
-
![]()
图 1 一种穹顶结构空间型滑移索节点的构造
Figure 1. Composition of a spatial sliding cable joint in the suspen-dome structure
![]()
图 2 两节点三维悬链线索单元示意图
Figure 2. Schematic diagram of the two-node three-dimensional catenary cable element
![]()
图 4 三维滑移索单元内部受力图
Figure 4. Internal forces of the three-dimensional sliding cable element
![]()
图 9 无摩擦的两跨三维滑移索数值和试验结果
Figure 9. Numerical and experimental results of the two span three-dimensional sliding cable without friction
![]()
图 10 考虑摩擦的两跨三维滑移索数值和试验结果
Figure 10. Numerical and experimental results of the two-span three-dimensional sliding cable with friction
![]()
图 12 索力与张拉力关系的比较
Figure 12. Comparison of the relationship between cable force and tensile force
![]()
图 13 上弦中心上拱量与张拉力关系的比较
Figure 13. Comparison of the relationship between the camber on the center of the top chord and tensile force
表 1 不考虑温度效应的平面移动索-轮体系的平衡构型
Table 1 Equilibrium configurations of the plan transport pulley system without thermal effect
平衡构型 方法 滑移点索力(T/g)/kg 坐标xo/m 无应力索长s1/m C1 文献[15] 1478.000 47.6700 111.070 文献[22] 1481.230 47.2500 110.833 文献[21] 1479.510 47.2530 110.830 本文 1481.180 47.3300 110.957 C2 文献[15] 1830.000 282.810 446.370 文献[22] 1833.020 283.150 447.295 文献[21] 1830.780 283.155 447.300 本文 1833.440 283.125 447.226 C3 文献[22] 1083.680 136.530 221.518 文献[21] 1082.770 136.540 221.530 本文 1083.920 136.519 221.497 C4 文献[15] 278 059.0 199.960 219.780 本文 264 225.8 200.197 220.174 
下载: 导出CSV
表 2 考虑温度效应的平面移动索-轮体系的平衡构型
Table 2 Equilibrium configurations of the plan transport pulley system with thermal effect
平衡构型 方法 滑移点索力(T/g)/kg 坐标xo/m 无应力索长s1/m C1 本文 1481.190 47.2930 110.907 C2 本文 1833.270 283.136 447.245 C3 本文 1083.770 136.532 221.512 C4 本文 259 396.3 200.201 220.177
下载: 导出CSV
表 3 三维移动索-轮的平衡构型
Table 3 Equilibrium configurations of the three-dimensional transport pulley system
下载: 导出CSV
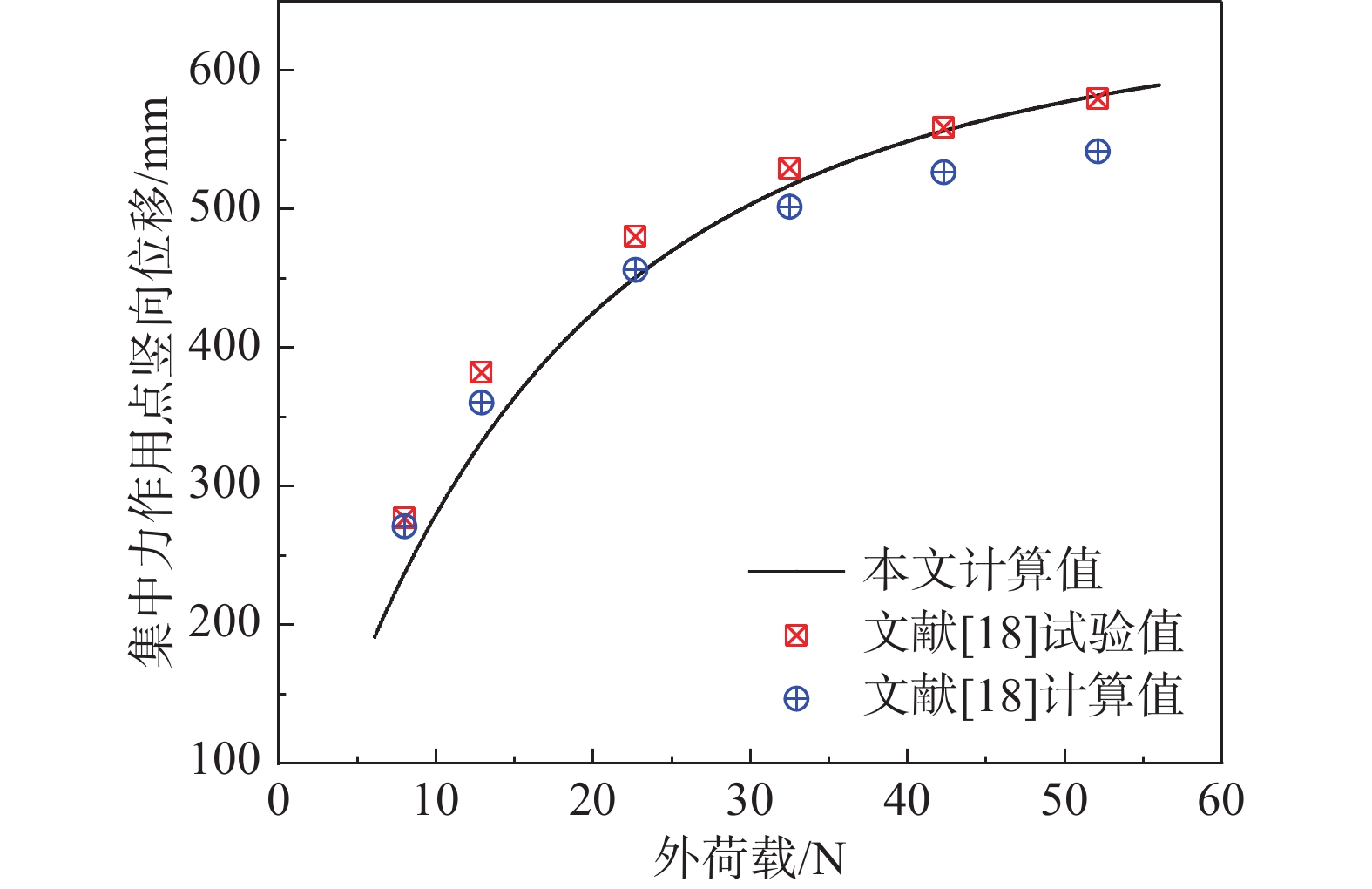
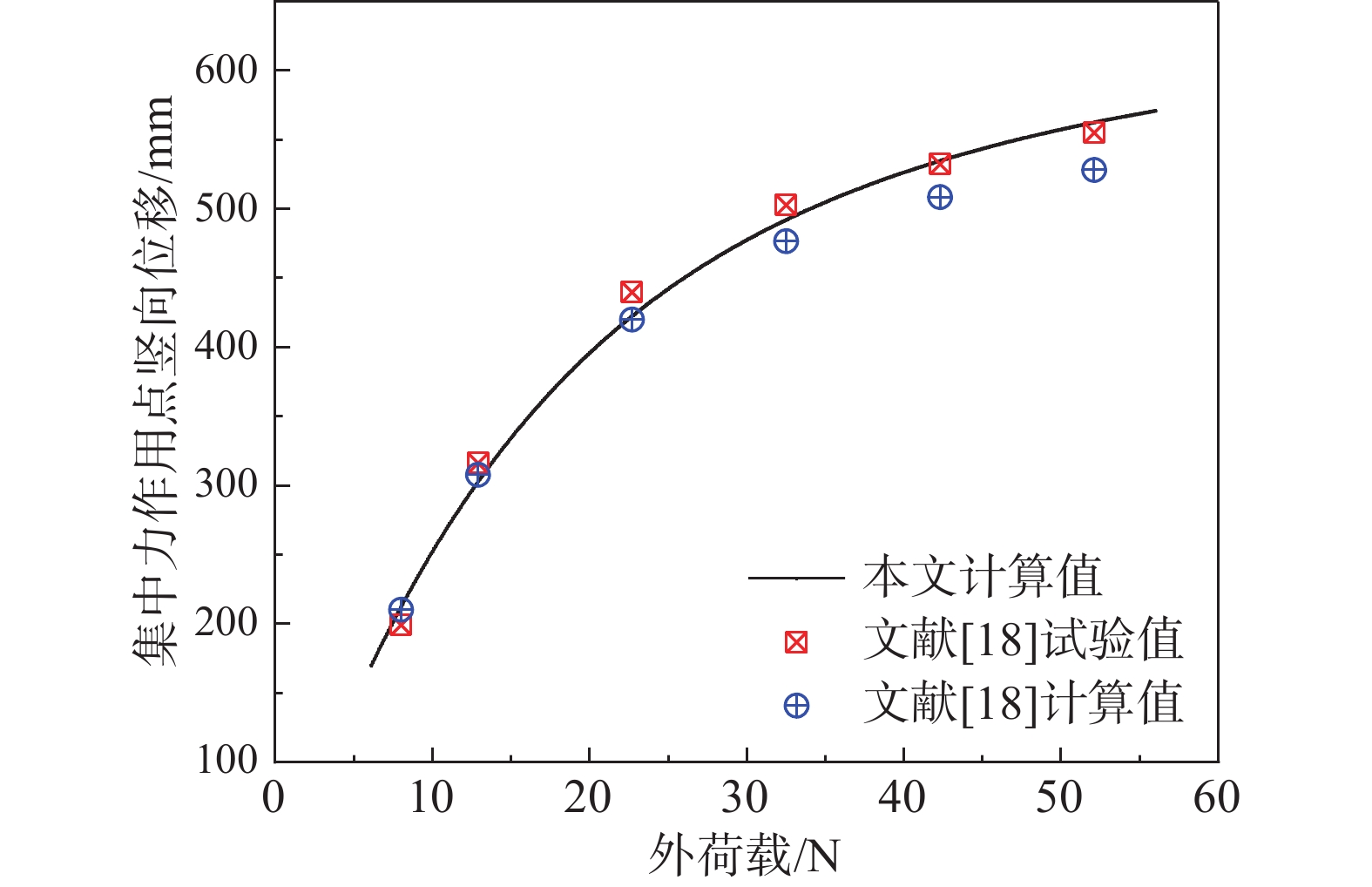
表 4 施加后期荷载后的结构响应(相对初始态)
Table 4 Structural response under later loadings (relative to the initial state)
下载: 导出CSV
-
[1] 杨孟刚, 陈政清. 基于UL列式的两节点悬链线索元非线性有限元分析[J]. 土木工程学报, 2003, 36(8): 63 − 68. doi: 10.3321/j.issn:1000-131X.2003.08.012 YANG Menggang, CHEN Zhengqing. The non-linear finite element analysis for two-node catenary element of cable structure based on UL formulation [J]. China Civil Engineering Journal, 2003, 36(8): 63 − 68. (in Chinese) doi: 10.3321/j.issn:1000-131X.2003.08.012
[2] 蔡建国, 杨晶文, 汪凯, 等. 考虑摩擦滑移拉索的张拉过程研究[J]. 土木工程学报, 2013, 46(11): 54 − 62. CAI Jianguo, YANG Jingwen, WANG Kai, et al. Study on the cable pretension process considering friction slip [J]. China Civil Engineering Journal, 2013, 46(11): 54 − 62. (in Chinese)
[3] AUFAURE M. A three-node cable element ensuring the continuity of the horizontal tension: a clamp-cable element [J]. Computers and Structures, 2000, 74(2): 243 − 251. doi: 10.1016/S0045-7949(99)00015-2
[4] CHEN Z H, WU Y J, YIN Y, et al. Formulation and application of multi-node sliding cable element for the analysis of suspend-dome structures [J]. Finite Elements in Analysis and Design, 2010, 46(9): 743 − 750. doi: 10.1016/j.finel.2010.04.003
[5] CHEN S Z, YANG M G, MENG D L, et al. Theoretical solution for multi-span continuous cable structures considering sliding [J]. International Journal of Solids and Structures, 2020, 207: 42 − 54. doi: 10.1016/j.ijsolstr.2020.09.024
[6] 陈诗再, 杨孟刚. 考虑摩擦的滑移索结构理论计算方法[J]. 工程力学, 2021, 38(2): 92 − 100. doi: 10.6052/j.issn.1000-4750.2020.03.0201 CHEN Shizai, YANG Menggang. Theoretical solution of sliding cable structures considering frictional effect [J]. Engineering Mechanics, 2021, 38(2): 92 − 100. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.03.0201
[7] ZHOU B, ACCORSI M L, LEONARD J W. Finite element formulation for modeling sliding cable elements [J]. Computers and Structures, 2004, 82: 271 − 280. doi: 10.1016/j.compstruc.2003.08.006
[8] JU F, CHOO Y S. Super element approach to cable passing through multiple pulleys [J]. International Journal of Solids and Structures, 2005, 42: 3533 − 3547. doi: 10.1016/j.ijsolstr.2004.10.014
[9] KAN Z, PENG H, CHEN B, et al. A sliding cable element of multibody dynamics with application to nonlinear dynamic deployment analysis of clustered tensegrity [J]. International Journal of Solids and Structures, 2018, 130/131: 61 − 79. doi: 10.1016/j.ijsolstr.2017.10.012
[10] CUI X Q, GUO Y L. Influence of gliding cable joint on mechanical behavior of suspend-dome structures [J]. International Journal of Space Structures, 2004, 19(3): 149 − 154. doi: 10.1260/0266351042886658
[11] 俞锋, 尹雄, 罗尧治, 等. 考虑接触点摩擦的索滑移行为分析[J]. 工程力学, 2017, 34(8): 47 − 55. doi: 10.6052/j.issn.1000-4750.2016.03.0150 YU Feng, YIN Xiong, LUO Yaozhi. Cable sliding analysis considering frictional effect [J]. Engineering Mechanics, 2017, 34(8): 47 − 55. (in Chinese) doi: 10.6052/j.issn.1000-4750.2016.03.0150
[12] YU X, CHEN D, BAI Z. A New Method for Analysis of Sliding Cable Structures in Bridge Engineering [J]. KSCE Journal of Civil Engineering, 2018, 22(11): 4483 − 4489.
[13] 魏建东. 预应力钢桁架结构分析中的摩擦滑移索单元[J]. 计算力学学报, 2006, 23(6): 800 − 806. doi: 10.3969/j.issn.1007-4708.2006.06.030 WEI Jiandong. Friction sliding cable element for structural analysis of prestressed steel truss [J]. Chinese Journal of Computational Mechanics, 2006, 23(6): 800 − 806. (in Chinese) doi: 10.3969/j.issn.1007-4708.2006.06.030
[14] CAI J, LIM J, FENG J. Elastic catenary cable element considering frictional slip effect [J]. Science China Technological Sciences, 2012, 55(6): 1489 − 1495. doi: 10.1007/s11431-012-4833-6
[15] BRUNO D, LEONARDI A. Nonlinear structural models in cableway transport systems [J]. Simulation Modelling Practice and Theory, 1999, 7(3): 207 − 218. doi: 10.1016/S0928-4869(98)00024-X
[16] 魏建东, 许惟国. 滑轮在索上滑行分析的索一轮单元法[J]. 力学学报, 2005, 37(3): 322 − 328. WEI Jiandong, XU Weiguo. Cable-pulley element to analyze pulley sliding on cable [J]. Chinese Journal of Theoretical and Applied Mechanics, 2005, 37(3): 322 − 328. (in Chinese)
[17] LIU H, CHEN Z. Influence of cable sliding on the stability of suspend-dome with stacked arches structures [J]. Advanced Steel Construction, 2012, 8(1): 54 − 70.
[18] CHUNG K S, CHO J, PARK J I, et al. Three-dimensional elastic catenary cable element considering sliding effect [J]. Journal of Engineering Mechanics, 2011, 137(4): 276 − 283. doi: 10.1061/(ASCE)EM.1943-7889.0000225
[19] THAI H T, KIM S E. Nonlinear static and dynamic analysis of cable structures [J]. Finite Elements in Analysis and Design, 2011, 47: 237 − 246. doi: 10.1016/j.finel.2010.10.005
[20] SALEHI AHMAD ABAD M, SHOOSHTARI A, ESMAEILI V, et al. Nonlinear analysis of cable structures under general loadings [J]. Finite Elements in Analysis and Design, 2013, 73: 11 − 19. doi: 10.1016/j.finel.2013.05.002
[21] CRUSELLS-GIRONA M, FILIPPOU F C, TAYLOR R L. A mixed formulation for nonlinear analysis of cable structures [J]. Computers and Structures, 2017, 186: 50 − 61.
[22] IMPOLLONIA N, RICCIARDI G, SAITTA F. Statics of elastic cables under 3D point forces [J]. International Journal of Solids and Structures, 2011, 48: 1268 − 1276.
[23] 俞锋. 索滑移分析的计算理论及其在索杆梁膜结构的应用研究 [D]. 浙江: 浙江大学, 2015. YU Feng. Research on Computational theory for slide cable and applications in cable-strut-beam-membrane structures [D]. Zhejiang: Zhejiang University, 2015. (in Chinese)
[24] 俞锋, 许贤, 罗尧治. 索强化剪式铰机构力学性能研究[J]. 工程力学, 2021, 38(5): 151 − 160. doi: 10.6052/j.issn.1000-4750.2020.06.0390 YU Feng, XU Xian, LUO Yaozhi. Research on mechanical properties of cable-strengthened scissor-hinge mechanism [J]. Engineering Mechanics, 2021, 38(5): 151 − 160. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.06.0390
[25] 孙利民, 狄方殿, 陈林, 等. 考虑垂度影响的拉索-双粘滞阻尼器系统振动分析[J]. 工程力学, 2022, 39(8): 49 − 60. doi: 10.6052/j.issn.1000-4750.2021.04.0262 SUN Limin, DI Fangdian, CHEN Lin, et al. Free vibrations of a shallow cable with two viscous dampers [J]. Engineering Mechanics, 2022, 39(8): 49 − 60. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.04.0262
计量
- 文章访问数: 561
- HTML全文浏览量: 199
- PDF下载量: 106
