DAMAGE IDENTIFICATION OF CIVIL STRUCTURES BASED ON FINITE ELEMENT MODEL UPDATING
-
摘要: 基于有限元模型修正的结构损伤识别方法计算过程直观、物理意义明确,能同步识别结构损伤位置和损伤程度,是结构损伤评估最直接的依据。该文介绍了基于有限元模型修正的损伤识别方法基本原理与过程,总结近三十年来有限元模型修正技术的发展。土木工程结构模型复杂性(包含大量单元、节点、待修正参数等)导致有限元模型修正过程效率低,详细介绍了基于子结构有限元模型修正的土木工程损伤识别方法在提高计算效率方面的优势。将两种有限元模型修正方法应用于一栋超高层建筑数值模型的损伤识别,说明两类方法在土木结构损伤识别中的特点。土木工程尺度大而结构损伤通常发生在局部区域,子结构方法将整体结构的分析转换为对若干独立子结构的分析,通过少数局部子结构的模型修正实现损伤识别,避免重复分析大尺寸整体结构,为大型结构基于有限元模型修正的损伤识别开辟高精度和高效率的途径。Abstract: The finite element model updating is advantageous in damage identification because it is physically meaningful and simultaneously identifies the damage location and extent. It provides a direct and important basis for structural safety assessment. We firstly present the background and basic process of model updating based damage identification, and summarize its development in the past thirty years. A finite element model of a civil structure is usually large in scale and contains many parameters to update. It makes the model updating process time consuming. Therefore, substructure-based model updating methods are developed to identify the damage of large-scale civil structures to improve the efficiency of the model updating process. The two methods are applied to the damage identification of a high-rise building model to illustrate their advantages in practical damage assessment. A civil structure is large in scale while the damage is localized. The substructuring method divides the global structure into several independent substructures for the analysis. The substructure-based damage identification is achieved by updating a few substructures, avoiding repeated analysis of the large whole structures, and therefore improving the accuracy and efficiency of the model updating process.
-
土木工程有限元模型广泛应用于抗震抗风模拟、振动控制、损伤识别及优化设计等方面。有限元模型修正方法的基本思想是以结构静动力试验数据为基础[1],将试验得到的信息与原始有限元模型分析结果进行综合比较。通过优化约束,不断修正模型物理参数,使理论值与试验值基本吻合,从而获取更精确反映实际结构特性的有限元模型。通过对比损伤前后有限元模型参数的变化,实现结构损伤识别。基于有限元模型修正的损伤识别方法,计算过程直观、物理意义明确,能同步识别损伤位置和损伤程度,被广泛应用于实际工程。多项标准规程中也明确规定结构安全二级评估必须实施有限元模型修正[2]。近三十年,有限元模型修正方法迅速发展[1-19],在土木工程损伤识别与健康评估中发挥着越来越重要的作用。
有限元模型修正是一个约束优化问题,属于反问题的一种。土木工程损伤识别通常需要建立精细化的有限元模型,包含上万乃至百万自由度,且待修正参数多。有限元模型修正过程,需要重复计算整体结构模型的特征解,即使少数甚至一个修正参数发生改变(局部损伤),也需要重新分析整体结构模型。大量修正参数使优化过程容易出现病态或者收敛缓慢的问题,效率极低。特别是在考虑参数不确定性、结构非线性等问题时,土木工程的有限元模型修正和损伤识别更是难以完成。例如,Xia等[3]对西澳大利亚州的Balla Balla桥进行了模型修正,该小型桥梁有限元模型包含4200个自由度、1200单元和1039个修正参数,优化过程迭代155次收敛,花费约420 h。对于大型土木工程,例如青马桥[4]、广州塔[5]包含上百万自由度、上万修正参数,即使使用功能强大的计算机,使用常规方法修正有限元模型也非常困难。
用于有限元模型修正的动态测量数据反映整体结构信息,但是结构损伤通常只是发生在结构的局部区域。子结构方法根据分界面上的位移协调条件和力平衡条件将整体结构分解为若干个独立子结构,将对整体结构的模型修正转换为对独立子结构的模型修正。特别是在应用于损伤识别时,只需要重复分析某些特定(损伤区域)的子结构,避免重复计算整体结构特性。此外,子结构包含的待修正参数远少于整体结构,有助于加速大规模优化问题的收敛。从而有效地减轻大型结构动力分析和有限元模型修正的计算负担,在大型土木工程结构损伤识别中具有显著的优势。
本文将首先介绍基于有限元模型修正的损伤识别原理与过程。然后,详细阐述用于土木工程损伤识别的子结构有限元模型修正方法,包括正向子结构方法和逆向子结构方法;总结基于子结构有限元模型修正的损伤识别方法在频域、时域、不确定性分析、非线性分析中的研究进展。最后,将传统有限元模型修正方法和子结构有限元模型方法用于一个实际超高层建筑数值模型的损伤识别中,对比分析损伤识别的精度和效率。
1 基于有限元模型修正的结构损伤识别方法
对于土木工程这一类体积庞大、参数多,且存在各类不确定性和非线性的结构,按照结构设计详细建立的有限元模型不可避免存在各种偏差,如边界误差、材料参数误差、离散化误差等。必须采用有限元模型修正技术使得有限元模型能真实反映实际工程结构动静力特性[5]。
现有的有限元模型修正方法可分为矩阵型修正方法和参数型修正方法。在此基础上,针对土木工程中参数不确定性问题和非线性问题,建立了有限元模型修正的不确定性分析方法和非线性模型修正方法。
1.1 矩阵型有限元模型修正方法
矩阵型有限元模型修正方法直接修正有限元模型的刚度、质量、阻尼等系统矩阵,使得修正后的系统矩阵计算的响应与实测响应吻合。为保证系统矩阵原有的带状、稀疏特性,同时对矩阵优化问题施加一些约束,例如振型的正交性[6],矩阵的对称性或正定性[7],使得修正后系统矩阵与实测的系统矩阵尽可能接近。为保持目标方程的一些特性,对修正矩阵的参数也施加约束,如最小范数[7]或最小秩[8]。目标方程通常是由质量、刚度、阻尼矩阵的摄动矩阵和施加约束的拉格朗日乘子的叠加[1]。杨朋超等[9]总结了各种矩阵型有限元模型修正方法,考虑对称性、模态正交性及模态参与因子等约束,采用拉格朗日乘子算法,推导了质量矩阵和刚度矩阵的最优解。
矩阵型有限元模型修正方法具有修正结果准确和计算量小的优势,修正后的模型能够精确“复制”试验测试数据[10]。其缺点是结点的连续性、修正后矩阵的稀疏性、对称性不能得到保证;修正后的结构系统矩阵难以解释、物理意义不明确;修正后的模型只在数学结果上与实际结构相近而不具备实际工程意义。因此,近三十年,针对矩阵型有限元模型修正方法的研究逐步减少,在结构损伤识别应用中的报道较少。
1.2 参数型有限元模型修正方法
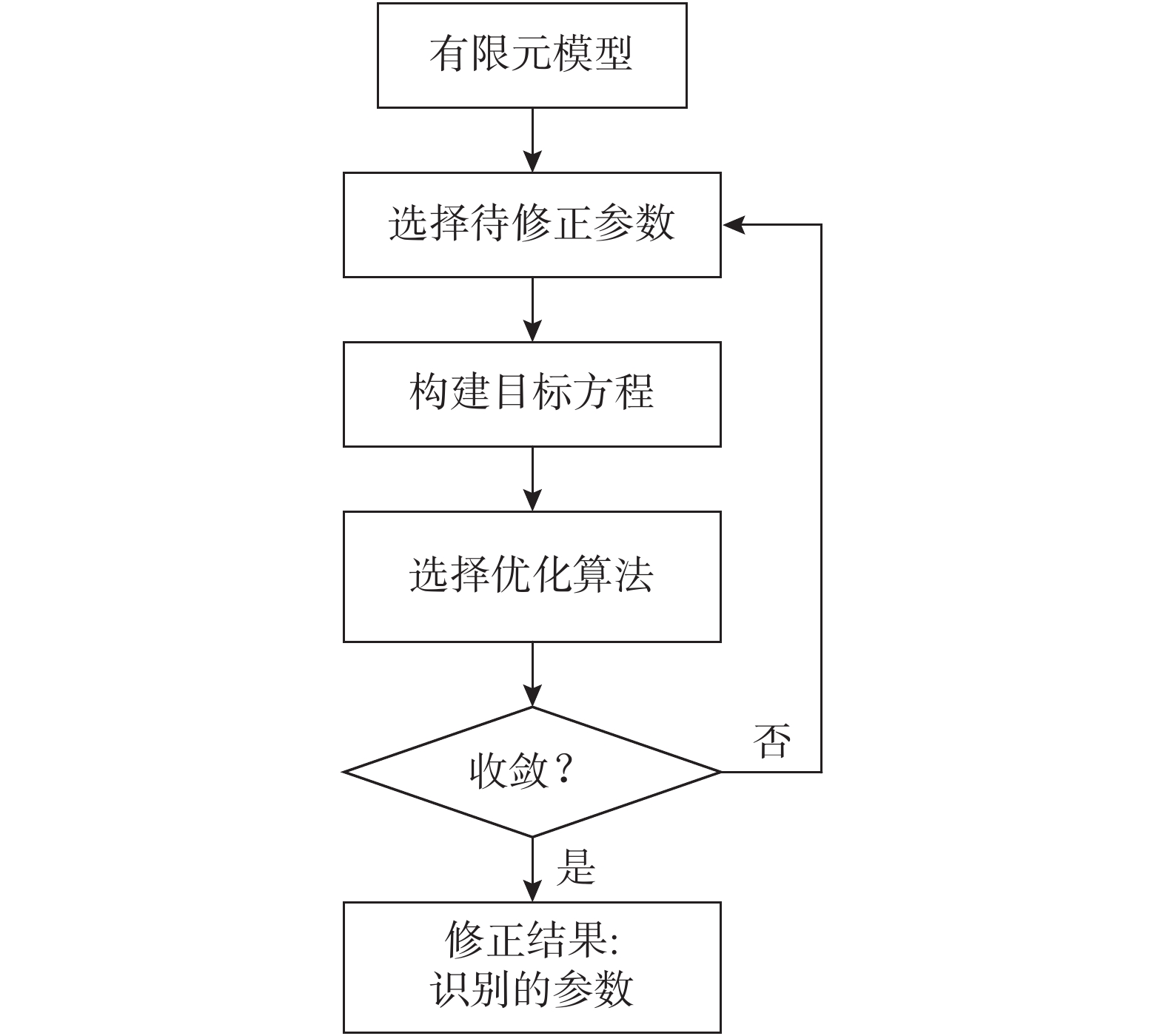
参数型有限元模型修正方法选取结构自身物理参数(密度、单元刚度、材料参数等)作为修正参数,以有限元模型的动力响应特征值与实际结构试验值的残差为目标函数,重复迭代调整物理参数取值,使目标函数最小化,有限元模型修正的流程图如图1所示。由于修正参数通常为结构物理参数,该类方法的修正结果具有明确的物理意义,修正后的参数可用于损伤识别、状态评估。参数型有限元模型修正方法能够克服矩阵型模型修正方法的局限性,因此得到了更加广泛的应用。选取修正参数、构建目标函数、迭代优化算法和计算灵敏度矩阵是参数型有限元模型修正方法的关键步骤。
1.2.1 修正参数
修正参数的选择是有限元模型修正的首要关键步骤[11]。选择过多的修正参数不仅导致结构动力分析和灵敏度分析中的计算负荷增加,而且可能导致模型修正过程中的不适定或溢出问题[12]。因此,通常选择不确定性较大、且对结构动静力特性影响较大的部分参数进行修正。参数选择方法主要分为三种:1) 综合考虑物理意义和工程经验的情况下选择修正参数,通常选择对结构特性影响大的参数,如材料特性(弹性模量、密度等),几何特性(截面面积、截面惯性矩)和边界条件等[5];2) 基于灵敏度分析方法,求解结构响应相对于参数的灵敏度,选取灵敏度大的参数作为待修正参数[12-13];3) 参数子集选择方法,从各种组合的参数子集中挑选让目标方程残差最小的参数子集[14-15]。
1.2.2 目标方程
目标函数量化了实际结构与有限元模型之间动态特性的差异,通常定义为实际结构实验数据与有限元模型计算特征之间的残差,例如:
f(r)=XE−XA(r) (1) 式中:XE为实际结构试验测量得到的特征;XA(r)为有限元模型的计算特征,可表达为修正参数r的函数;r为包含所有修正参数的向量。
根据测试的数据类型分类,用于构建目标函数的特征包括静力数据(位移、应变、应力等)和动力数据(频率、振型、频响函数等)[16]。静力数据精度高,但对大型土木工程施加较大的静力荷载难以实施,且测试会妨碍工程正常运营。因此,基于静力数据的模型修正方法在实时在线结构损伤识别中应用较少[10-11]。大量研究集中在基于动态数据的有限元模型修正方法上[1, 10-11]。
用于构建目标函数的动态数据包括频域特征和时域特征。在频域内,频率和振型是最早和最广泛应用于有限元模型修正和损伤识别的特征指标。实测频率可以直接运用到有限元模型修正中。限于传感器数目,实测振型的自由度要少于计算振型,需要通过模态缩聚或模态扩展技术与振型自由度相匹配[17-18]。频率和振型可以分别用于构建目标方程[19-20],也可以通过权重系数[20-21]联合构建目标函数。由于频率和振型往往对局部小损伤不敏感,且受噪声影响大,导致损伤识别的精度较低[19-20]。Meruane[22]用从传递矩阵中识别反共振频率代替振型来构建目标方程,反共振频率的识别难度小且精度高,同时包括了频率和振型的结构信息。一些模态参数的衍生指标,如模态应变能[23]、模态柔度[24]、应变振型[21]、小波时频数据[25]等,比频率、振型对结构局部变化更为敏感,也常用来构建目标方程。除模态参数外,频响函数也用于构建目标函数[26]。Lin和Zhu[27]通过推导频响函数对结构参数的灵敏度,提出自动选择有限频率点方法,让目标函数包含尽可能多的信息,并将基于频响函数的有限元模型修正方法应用到有阻尼结构。Gang等[28]通过恰当选择测量频率点和扩充自由度,改进有限元模型修正的精度和收敛性。
时域指标直接运用实测响应数据及其衍生量作为目标函数。最直接的时域指标为直接测量的结构加速度、速度、位移等指标[29],以实测时域数据与模型时域数据的残差构建目标方程。与频域指标相比,时域指标避免了数据时频转换的误差,适用于非线性结构等没有表现模态特征的结构;并且时域数据点较多,有利于保证有限元模型修正中优化方程式的正定性[16]。
一些研究将动力数据和静力数据联合起来构建目标方程,增加了数据样本点,同时也使有限元修正模型更能真实全面反映实际结构特性。张启伟和范立础[30]采用基于静动力数据的有限元模型修正对一个悬臂梁进行了损伤识别。
1.2.3 优化算法
有限元模型修正是一个参数优化过程,即寻找一组最优参数使目标方程最小化。常用的优化算法,包括灵敏度算法[5]、神经网络方法[31]、仿生优化算法[32-34]等。其中,基于灵敏度分析的优化算法[5],利用结构特征解对结构参数变化的敏感程度,根据解的搜索方向进行迭代优化,具有搜索速度快、超线性收敛等优点,被广泛应用于实际工程的损伤识别和健康评估。其缺点是计算灵敏度矩阵耗时,且在非平滑连续处结构的灵敏度不存在。基于神经网络的优化算法是一种类似于人类神经系统的信息处理技术,它通过学习有限元模型数据推出输入与输出的关系。虽然神经网络具有超强的学习能力和非线性映射能力,但是其学习的准确度需要大量的学习样本来保证[31]。仿生优化算法包括遗传算法[32]、粒子群算法[33]、蚁群算法[34]等。这种优化算法依据生物智能选择能耗最小、资源安排最高效得到启发,仿生优化算法的发展依托处理设备计算速度与功能的提高。
1.2.4 灵敏度矩阵
灵敏度即是目标方程关于修正参数的偏导数,其一方面可以用于选取最优的修正参数,另一方面可给优化目标方程提供快速的搜索方向,加快优化过程收敛。
以频域指标构建目标函数时,计算特征值(频率)和特征向量(振型)灵敏度主要包括三类方法:1) 有限差分法,估计特征解灵敏度为设计点特征解与其附近有限步长点的特征解关于步长的斜率[35]。该方法的误差与步长的选取有关;2) 模态法[36],将特征向量灵敏度表达为所有特征向量的线性组合,该方法需要计算所有特征向量,大型结构通常采用模态截断的方法取部分模态,会影响计算精度;3) Nelson的方法[37],是将特征向量灵敏度表达为一个齐次项和非齐次项之和,精度和效率较高。在这三种方法的基础上,还发展出其他的计算方法,包括几何法[38]、Lanczos法[39]、迭代法[40]、奇异分解法[41]、摄动法[42]、子结构法[43]、模型缩聚法[44]等。频响函数灵敏度的计算可通过模态叠加法,将频响函数灵敏度表示为所有模态的叠加,进而通过模态截断的方法提高计算效率,通过补充舍弃模态的贡献以提高计算精度[45]。时域内动力响应灵敏度的计算,可对运动方程求偏导,通过Newmark方法或者Newton Rapson方法计算偏导方程的响应,作为时域内动力响应灵敏度[46]。
参数型有限元模型修正方法优化结构物理参数,物理意义明确,对实际工程损伤评估具有指导意义;灵敏度分析为参数优化提供快速搜索方向,是一种被广泛应用于实际工程的有限元模型修正方法。该类方法的进步在一定程度上得益于优化算法、灵敏度计算等数学方法的发展,以及硬件设备计算能力的提高,未来将在大型土木工程损伤评估中发挥越来越重要的作用。
1.3 不确定性有限元模型修正方法
有限元模型和测试数据都存在不确定性。模型不确定包括材料制作误差、材料本构关系建模误差、边界条件建模误差、单元划分误差、非结构特性建模误差等[47]。测量不确定性主要包括测量噪声和数据处理误差。常用三种方法来考虑模型修正过程中的不确定性:蒙特卡洛法、摄动法、贝叶斯法。
蒙特卡洛法生成大量服从特定概率密度分布的样本点,对每个样本点参数分别进行有限元模型修正,然后从修正结果中估计修正参数的统计特性[48]。Mares等[49]详细阐述了蒙特卡洛法及其在概率参数估计上的应用。蒙特卡洛法需要生成大量的分析数据来保证其修正结果的精度,计算效率低。
摄动法通过引入微小变化量考虑不确定性[50],给有限元模型修正方程的每个变量一个微小变化量,推导一个近似的微分方程来求解函数的不确定性,参数的一阶矩和二阶矩常用来估计参数的均值和方差。与传统的基于灵敏度的有限元模型修正方法一样,摄动法要求修正参数的初值要接近真实值,当摄动量较大时会产生误差,需要使用高阶摄动方程[51]。
基于贝叶斯理论的有限元模型修正方法,根据主观已知修正参数先验分布信息和测试数据信息,识别修正参数的后验概率密度分布。Beck和Karafygiotis[52-53]详细阐述了基于贝叶斯理论的模型修正过程,该方法不仅能获得修正参数的最优解,还能从它们联合概率分布中评估参数不确定性水平。Lam等[54]从环境数据中评估参数不确定性水平,并基于贝叶斯模型修正方法对IASC–ASCE基准模型进行了损伤识别。Yuen和Katafygiotis[55]将该方法扩展到随机模型输入未知的情况。该方法不需要响应是平稳的,也不需要基于输入谱密度的参数先验信息。Cheung和Beck[56]提出利用混合蒙特卡洛来求解贝叶斯模型修正问题,适合于求解高纬度参数空间的优化问题,且不局限于模型的类别(线性或非线性)和测试数据的类型。
有限元模型和测试数据的不确定性会影响有限元模型修正和损伤识别的结果,研究参数识别过程中的不确定性问题势在必行。随着统计理论与大数据分析方法的发展,为不确定性分析提供新的契机,这也将为考虑不确定性分析的有限元模型修正和损伤识别创造良好的条件。
1.4 非线性有限元模型修正方法
严格来讲土木工程结构是非线性的,线性只是特例或一种简化方法。例如,混凝土等材料本身的非线性引起的结构非线性、结构发生大变形时产生的几何非线性、结构阻尼耗散的非线性、结构边界条件及状态的非线性等。结构的各种损伤也呈现出典型的非线性特征,如裂缝的产生和发展、节点的松动和滑移、刚度退化等。土木工程结构遭受地震、强风等较强的荷载激励时,表现出较强的非线性特征,必须采用非线性模型。目前,线性系统的模态分析理论并不适用于非线性系统,非线性有限元模型修正方法的发展没有线性模型修正方法成熟,非线性有限元模型修正技术尚待进一步发展[16]。
非线性模型修正方法主要包括频域内的谐波平衡方法[57]、本构方程误差法[58-59]和时域内的恢复力面法[60]、本征正交分解[61]。频域方法一般将非线性特征表达为线性贡献和非线性贡献的叠加[59],或将非线性贡献的多维度高阶特征线性化[58]。由于线性化过程损失了一些结构信息,该方法不适用于复杂的非线性结构的有限元模型修正[62]。时域方法通过输入输出振动方程识别出非线性方程的恢复力[60],或者将时间序列数据分解为非线性系统的正交基[61],进而以恢复力或非线性正交基构建目标函数来修正非线性参数。Silva等[63]比较了频域的非线性模型修正方法(谐波平衡法、本构方程误差法)和时域的非线性模型修正方法(恢复力面法、本征正交分解),认为时域方法比频域方法计算效率高,其中恢复力面法是耗时最小且识别结果精度最高的模型修正方法。
土木工程结构实质是非线性的,非线性有限元模型修正和损伤识别更能反映土木工程的本质特征。随着非线性动力分析的发展和设备计算能力的提高,非线性有限元模型修正将为土木工程损伤评估提供更贴切、更可靠的信息。
1.5 基于有限元模型修正的结构损伤识别方法
当结构损伤导致其刚度参数发生变化,运用有限元模型修正方法来识别损伤前后结构的刚度参数变化,从而根据刚度参数变化的位置和程度实现损伤的定位和定量。基于有限元模型修正的损伤识别过程分为两个阶段,具体流程如图2所示。
第一个过程,建立结构未损状态下的有限元模型,即基准模型。初始有限元模型尚不能准确反映真实结构的特性,需要通过对其材料参数、截面尺寸、约束条件进行修正,避免初始建模误差对第二个过程中损伤识别结果的影响。当第一个过程的有限元模型修正完成,将修正好的模型作为精准的未损状态结构有限元模型。在第二个过程中,由于第一个过程已经对结构质量约束等进行修正,则认为只有损伤造成刚度变化,其他因素是不变的。因此,以单元刚度作为待修正参数,利用现场实测的损伤结构的试验数据对基准模型进行模型修正,得到损伤后的刚度参数,从而识别损伤位置和损伤程度。
Brownjohn等[64]利用实测振型和频率,采用基于灵敏度的有限元模型修正方法识别了实际桥梁的损伤状况。Fritzen等[65]利用基于频响函数灵敏度的有限元修正方法识别实际结构损伤位置和损伤程度。Abdel[66]、Jaishi和Ren[23]分别推导了模态曲率灵敏度和模态柔度灵敏度的计算方法,建立了基于模态曲率和模态柔度的有限元模型修正方法,完成实际桥梁的损伤识别。Lu和Law[67]提出了基于动力响应灵敏度的模型修正方法,识别了一个小型桥梁的损伤状况。针对实际工程的损伤识别中,为提高有限元模型修正计算效率,通常会采用简化的有限元模型,或者从有限元模型的众多不确定性参数中选取少数待修正参数,在不同程度上通过牺牲有限元模型的精度来提高模型修正过程的效率,修正后的模型难以准确地反映结构的一些真实损伤状况。
基于有限元模型修正的损伤识别方法,计算过程直观、物理意义明确,能识别结构损伤发生的位置和损伤程度,并根据模型物理参数的变化评估结构安全状况,是了解和掌握结构安全状况最直接、最准确的途径。然而,土木工程结构有限元模型庞大,不确定性参数多,导致基于有限元模型修正的损伤识别过程效率低、精度差,特别是在考虑不确定性和非线性后,耗时巨大甚至是无法实施。虽然现有硬件设备具有日益强大的计算能力,为大型土木工程有限元模型修正计算创造了良好的条件,但是大型土木工程精细化有限元模型修正和损伤识别仍然难以实现[3-5],计算方法上的突破仍然是土木工程研究者与实践者需要努力的方向。
2 基于子结构有限元模型修正的结构损伤识别方法
为保证损伤识别的精度,土木工程通常需要建立比较精细的有限元模型,包含大量单元、节点、自由度和待修正参数。有限元模型修正属于结构动力学中的逆问题,大尺寸模型的动力分析精度极低,大量待识别参数使参数识别过程容易出现病态或者收敛缓慢的问题。
用于有限元模型修正的动态测量数据反映整体结构信息,但是结构损伤通常只是发生在结构的局部区域。子结构方法将整体结构分解为独立的子结构,通过协调条件将对整体结构的分析转换为对独立子结构的分析,是解决有限元模型修正精度低、效率低的有效方法。子结构方法应用于大型土木工程结构有限元模型修正有如下优势[68-70]:
1) 各子结构之间相互独立,采用不同的方法独立分析,独立存储,并行计算;
2) 将对整体结构的分析转换为对独立子结构的分析,子结构模型尺寸远小于整体结构模型,将减少模型分析时间,从而降低对分析计算设备的需求;
3) 独立子结构修正参数的数量远小于整体结构修正参数的数量,从而加速优化过程的收敛,获取更精确的参数优化结果。
4) 子结构有限元模型修正方法用于损伤识别中,由于损伤往往发生在结构的局部区域,只需对少数关键子结构进行分析,避免了对整体结构进行反复运算。
子结构有限元模型修正方法分为两类:第一类为正向子结构方法,通过子结构特征参数组集得到整体结构特征参数,进而修正结构参数使得整体模型特征参数与测量得到的整体特征参数相吻合;第二类为逆向子结构方法,将整体结构试验特征参数分解为独立子结构试验特征参数,进而修正独立子结构模型。
2.1 正向子结构有限元模型修正方法
正向子结构方法的核心思想是将整体结构特征参数表达为独立子结构特征参数的叠加。该方法的过程是[70]:首先,将整体结构有限元模型划分为若干个独立的子结构模型,计算子结构模型的振动特性;然后,组集子结构振动特性得到整体结构的振动特性;最后,通过优化过程调整子结构物理参数,使得整体结构振动特性与实测结构试验数据相吻合,进而实现损伤识别(如图3所示)。用作有限元模型修正的振动特性包括频域特性(频率、振型、频响函数等)和时域特性(加速度、位移等时程响应)。
1) 基于子结构的频域特征计算方法
频域子结构方法主要用来快速计算结构的特征解(频率)和特征向量(振型)。Kron子结构[68]方法通过拉格朗日乘子和虚功原理在相邻子结构界面施加位移约束组集各个子结构特征参数。该方法精度高,且适用于复杂的分界面,但是Kron子结构方法需要计算每个子结构所有阶模态,效率极低,对较大子结构难以完成。Weng等[69]只保留了部分模态来改进Kron子结构方法的计算效率,同时通过剩余柔度补充舍弃模态的贡献来保证方法的精度,该方法也被扩展到快速计算特征解灵敏度[71]。模态综合法是将结构特征解表达为子结构模态的叠加[72-75]。子结构模态分为正交模态、刚体模态、约束模态和附加模态。根据子结构界面约束类型,模态综合法分为固定界面模态综合法和自由界面模态综合法。子结构方法也被用来通过子结构特征参数快速计算整体结构频响函数[75-80]。Klerk等[75]综述了基于子结构的频响函数计算方法,包括阻抗耦合法[76]、导纳耦合法[77]、拉格朗日乘子耦合法[78]。Lim和Li[79]用最小二乘法和缩聚的奇异值分解法来改进子结构方法计算频响函数的精度。Law和Ihlenfeldt[80]将基于子结构的频响函数计算方法拓展到计算结构多点柔度特征。
2) 基于子结构的时域特征计算方法
时域子结构方法快速计算结构时程响应[81, 82]和脉冲响应函数[83]。Zhu等[82]基于Kron子结构方法将整体结构时程响应表达为独立子结构模态参数的叠加,为提高计算效率只保留了部分子结构低阶模态,舍弃的高阶模态的贡献通过考虑一阶效应和二阶效应的指标来补偿,并推导了基于子结构的动态响应灵敏度计算方法,应用于超高层建筑的损伤识别。Gruber等[84-85]将模态综合法拓展到时域计算结构位移,并转换到状态域计算非比例阻尼线性系统时程响应。时域子结构方法通过一定约束条件组集子结构的脉冲响应函数,也被用于快速计算整体结构脉冲响应函数。Gordis[83, 86]通过对子结构脉冲响应函数进行杜哈梅积分和模态叠加法得到整体结构脉冲响应函数,用于瞬时冲击或敲击荷载作用下的动力分析和模型修正。基于子结构的脉冲响应函数计算方法也被应用到刚性-弹性混合节点的结构的有限元模型修正中[87]。
在正向子结构有限元模型修正过程中,当结构损伤引起局部参数发生改变,只需要重新计算一个或者几个子结构的模态参数,其他子结构保持不变,即可快速计算整体结构振动特性,通过修正少数子结构模型实现损伤识别,极大地提高了有限元模型修正的效率。
2.2 逆向子结构有限元模型修正方法
逆向子结构方法通过探索整体结构与独立子结构的位移、力等参数的相似性,以及子结构分界面处位移平衡、力协调等约束条件,建立整体结构振动特性与独立子结构振动特性之间的联系。进而,将整体结构的试验特征参数分解为独立子结构的试验特征参数。将子结构完全从整体结构中分离出来,成为独立自由的个体。最后,建立独立子结构有限元模型,以独立子结构模型的特征参数和子结构试验特征参数的残差作为优化目标,以独立自由的子结构模型为修正对象,其他的子结构并不参与模型修正过程,基于逆向子结构的有限元模型修正过程如图4所示。逆向子结构方法的实质是将整体结构上测得的特征参数通过建立数学方程分解为局部区域的特征参数,进而对某一个子结构进行有限元模型修正。从整体结构试验数据中提取的子结构特征参数包括频域特征参数和时域特性参数。
1) 频域内逆向子结构法
频域逆向子结构方法的关键是建立子结构特征解和整体结构特征解的关系,然后再从整体结构的模态试验数据中提取出子结构频域特征参数。Doebling等[88]根据预先假定的子结构连接性和应变能量分布从整体刚度和柔度矩阵中提取出了子结构的刚度矩阵,进而从形状方程和几何关系中计算子结构特征向量,并通过线性最小二乘法求解子结构特征值。Alvin和Park[89]依据力法基本原理,基于力转换矩阵从整体柔度矩阵中提取出子结构柔度矩阵。由于转换矩阵的计算非常耗时,这种方法主要用于简单梁结构的计算。Park和Reich[90]综述了从整体测量数据中提取子结构特征的柔度法,包括自由-自由子结构柔度法、基于变形的柔度法、基于应变的柔度法。Hou等[91]根据虚拟变形方法推导了子结构隔离方法,将其他子结构对目标子结构的作用等效为一个虚拟力,利用分界面的虚拟力变形隔离出一个不受其余子结构影响的目标子结构。
Weng等[92]根据位移协调条件和力平衡方程从整体模态数据提取出了子结构柔度矩阵,并建立正交投影算子剔除子结构刚体模态用于自由子结构的分析[93]。从子结构柔度矩阵中提取子结构频率和振型,以独立子结构为对象构建目标函数,计算灵敏度矩阵,并修正独立子结构模型[94]。由于结构损伤通常发生在局部区域,子结构模态参数比整体结构模态参数对损伤更加敏感。该方法用于广州塔的有限元模型修正和损伤识别[94],局部小损伤对子结构模态参数的改变量为1.84%,而对整体结构模态参数的改变量仅为0.01%,证实了子结构模态参数比整体结构模态参数对局部损伤更加敏感。以所提取的子结构试验模态参数修正目标子结构有限元模型,系统方程的尺寸从21 690×21 690缩小为2736×2736,基于逆向子结构的有限元模型修正时间为整体有限元模型修正时间的10%,极大地提高了基于有限元模型修正的损伤识别的精度和效率。
2) 时域内逆向子结构法
在时域内,如果能提取目标子结构与其他子结构的界面力,那么就可以将界面力当作输入力作用在目标子结构上,将目标子结构从整体结构中分离出来,作为一个独立的结构进行动力分析[95],并对该独立子结构进行有限元模型修正和损伤识别。因此,时域内逆向子结构方法的关键是获取目标子结构与其他子结构的界面力。
获取子结构界面力最直接的方法是测量界面处的响应,通过界面处的响应来计算界面力。Koh等[95]测量每个子结构分界面结点的位移、速度、加速度,通过参数优化方法识别其他子结构对目标子结构的界面力。Yun和Lee[96]构建界面处加速度响应与界面力的时间序列模型,通过神经网络算法从复杂结构中提取子结构特征参数和子结构界面力[97]。这些方法需要测量界面处所有自由度的响应数据,在实验室模型试验中取得较好的结果。在实际工程中,测量目标子结构所有界面结点的所有响应难以实施。一些研究试图通过数学变换来消除目标子结构振动方程中与界面结点有关的项,以避免测量子结构界面处所有结点响应。Koh和Shankar[98]使用传递方程来关联一个结点的响应和另一个结点的激励,测量同样激励条件下目标子结构上多组响应数据,建立转换矩阵将子结构界面上未测量的响应转换为已测响应的函数。Tee等[99]将模型缩聚和恢复方法融合,解决子结构界面处不完备测量的问题。
针对实际工程中目标子结构界面处测量不完备的难题,另一种处理方法是将子结构界面力当作未知参数,在有限元模型修正过程中与其余待识别参数同步识别。Li和Law[100]融合响应重构方法和传递方程,采用基于灵敏度的有限元模型修正方法同步识别子结构界面力和损伤参数。Zhu等[101]将移动荷载和子结构界面力表示为切比雪夫多项式,推导了在状态域内结构动力响应关于结构单元刚度参数和切比雪夫多项式因子的灵敏度,通过子结构响应重构和灵敏度分析方法同步识别移动列车荷载作用下轨道参数和列车荷载。
逆向子结构方法建立整体结构动态特征与独立子结构动态特征的联系,将子结构完全从整体结构中分离出来,成为独立自由的个体,对独立自由的子结构模型进行有限元模型修正。用于大型土木工程的损伤识别时,只需要建立局部损伤区域的有限元模型,修正独立的局部子结构模型,而其他大部分未损区域不参与有限元建模和修正过程,是提高大型结构有限元模型修正计算效率最理想的途径。由于整体结构动态参数包含测量噪声等误差,且整体结构特征参数与子结构特征参数关系复杂,在提取子结构特征参数时这些误差会被放大和积累,因此,如何在数学方法上降低整体-子结构关系的复杂性,提高子结构试验特征参数的精度,是目前逆向子结构方法亟待解决的难题。
2.3 考虑不确定性的子结构有限元模型修正方法
大型结构有限元模型修正过程非常耗时,考虑不确定性分析后,需要对大量统计数据进行重复分析,势必进一步增加计算负担。一方面,子结构方法可以对独立子结构分别建立统计模型,对包含支座、损伤等不确定性较大的子结构进行重复统计分析,避免了反复分析整个结构。另一方面,对每个子结构分别建立统计模型,而不是对整体结构建立统一的统计模型,精度更高。
Beck等[102]将贝叶斯方法引入子结构方法中,通过子结构参数的先验概率估计整体结构参数的不确定性,减少了不确定性有限元模型修正的时间。Tran等[103]将子结构模态综合法与蒙特卡洛方法相结合,Chentouf等[104]评估了两种模态综合法在基于蒙特卡洛不确定分析中的鲁棒性。蒙特卡洛方法产生大量样本点,并对大量样本点统计数据进行重复有限元模型修正和损伤识别计算,子结构方法有效减少了大量重复计算负担。梁锋[105]将子结构方法与摄动法相结合,建立子结构物理参数、子结构模态参数、整体结构模态参数、整体结构统计参数的定量关系,基于摄动法推导了不确定性参数的一阶和二阶统计矩,提高了大型结构不确定性分析的效率。
子结构方法可以对各独立子结构分别建立统计模型,不仅精度更高,而且将重复的统计计算限制在少数子结构内,为大型结构损伤识别及其概率估计提供了高效率、高精度的途径。
2.4 非线性子结构有限元模型修正方法
土木工程非线性通常存在于结构的局部位置,例如非线性支撑或非线性连接,结构损伤也是一种局部非线性发展过程。局部非线性特征使整个结构呈现非线性行为,必须对整体结构进行非线性动力分析。常用直接积分法、谐波平衡法求解非线性方程,大型结构的非线性计算非常耗时。子结构方法考虑局部非线性特征分别建立非线性子结构和线性子结构,对线性子结构采用线性叠加、动态缩聚等高效的动力分析方法,将耗时的非线性动力分析限制在局部子结构内,极大地提高非线性动力分析及有限元模型修正的效率。
Praveen和Padmanabhan[106]依据整体结构的非线性特征,将刚度矩阵和质量矩阵分为主自由度和从自由度,与非线性区域和外力自由度相关的部分作为主自由度,其余的线性区域作为从自由度。对主自由度进行耗时的非线性动力分析,非线性修正力施加到线性部分作为非线性效应影响,以提高计算效率。Weng等[107]将整体非线性结构分解为线性子结构和非线性子结构,将线性子结构表达为低阶模态的叠加从而缩减线性子结构方程尺寸,非线性结构保持原状。由于土木工程中大部分区域为线性,耗时的非线性动力分析和参数识别被限制在少数非线性子结构内,所计算的地震荷载作用下的动力响应被用于非线性参数识别中。Apiwattanalunggarn等[108]引入子结构非线性正交模态,通过模态综合法缩减线性子结构的运动方程,通过非线性正交模态缩减非线性子结构的运动方程,非线性正交模态是线性正交模态的拓展,它们通过线性约束模态耦合起来[109]。
非线性子结构方法将耗时的非线性动力分析限制在局部子结构内,并极大地缩聚线性子结构尺寸,为土木工程局部非线性动力分析、参数识别和损伤识别开辟了一个高效的途径。
2.5 基于子结构有限元模型修正的结构损伤识别方法
由于土木工程损伤通常发生在局部区域,在判定结构损伤区域后,可只对发生损伤的子结构进行有限元模型修正,而其他大部分未损结构保持不变,将提高损伤识别的精度和效率。
Weng等[70]推导了基于正向子结构的特征解和特征解灵敏度求解方法,建立了基于子结构有限元模型修正的损伤识别方法,完成澳大利亚Balla Balla桥的损伤识别;并进一步提取独立子结构试验柔度矩阵,建立了逆向子结构有限元模型修正方法,应用于广州塔的损伤识别[92, 94]。Zhu等[83]利用子结构方法推导结构位移和位移灵敏度的快速计算方法,通过子结构有限元模型修正过程对武汉长江航运中心进行损伤识别。Yu等[110]推导了固定界面模态综合法、自由界面模态综合法[111]计算结构特征灵敏度,并基于特征解和特征灵敏度对一框架建筑进行了损伤识别。Lam和Yang[112]综合贝叶斯模型修正和子结构方法,依据试验模态数据实现了钢塔的损伤识别。Jensen等[113]在时域内建立了贝叶斯模型修正和损伤识别方法,其中子结构模态综合法用来缩小模型的尺寸。Xu等[29]提出了多尺度子结构模型修正方法,首先在子结构层面识别出损伤的子结构,然后在单元层面识别出损伤发生的单元和程度。
土木工程结构庞大而损伤往往只是发生在局部区域,子结构方法将对整体结构的分析转换为对独立子结构的分析,将耗时的优化计算、不确定性分析和非线性计算限制在局部子结构内,避免对整体结构大尺寸方程实施各类耗时的运算,在保证损伤识别高精度的同时提高损伤识别的效率,为土木工程基于有限元模型修正的损伤识别开辟了新的途径。
3 工程应用
本节将上述有限元模型修正方法和子结构有限元模型修正方法用于超高层建筑武汉长江航运中心模型的损伤识别。武汉长江航运中心大楼地上66层,建筑高度335 m,如图5所示。主体结构为第1层~第64层,高度306 m,采用外框架-核心筒结构体系。外框架由4根钢管混凝土柱和16根型钢混凝土柱构成,截面尺寸50 m×50 m。核心筒为钢筋混凝土剪力墙,截面尺寸30 m×30 m。
依据施工图纸建立该实际工程有限元模型,包含9112个单元、3950个结点、23 364个自由度。首先,采用现场模态试验测得的频率和振型修正有限元模型的刚度参数,完成第一阶段有限元模型修正。然后,以修正后的有限元模型为基础,进行第二阶段有限元模型修正,即损伤识别。
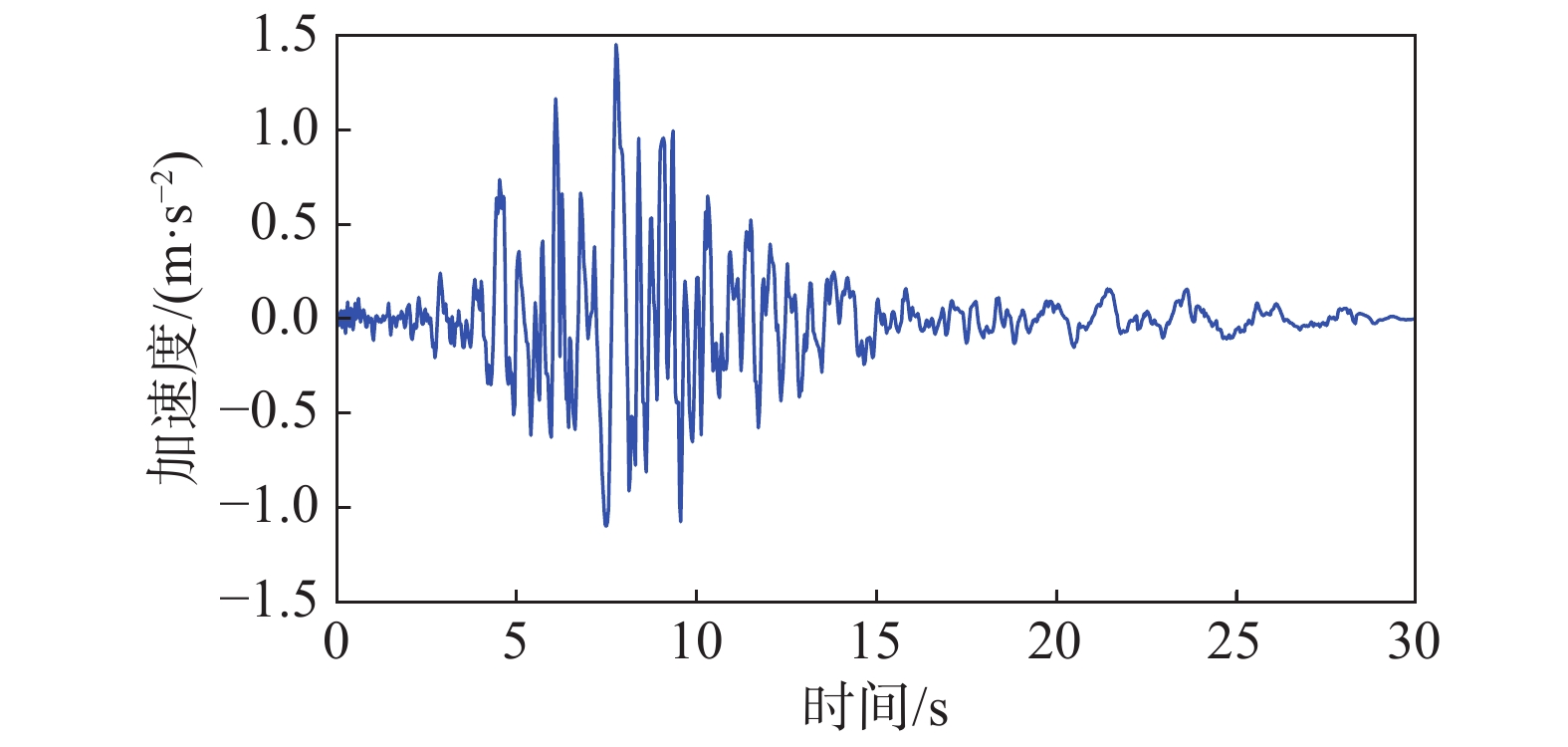
在第二阶段有限元模型修正过程中,分别采用传统的有限元模型修正和子结构有限元模型修正方法作对比分析。在采用子结构方法时,将有限元模型划分为9个子结构。由于该实际工程目前没有发生损伤,因此数值模拟结构损伤。对局部区域(子结构3)中单元21和单元77(剪力墙单元)的单元刚度分别折减20%和30%来模拟损伤,对整体有限元模型施加如图6所示水平地震荷载作用,地震荷载持续30 s,采样频率是0.03 s,总的时间步为1001,采用Newmark法计算损伤后模型的动位移作为现场试验数据。有限元模型修正过程中,目标方程为试验动位移和有限元模型计算位移的残差,当目标方程小于2 × 10−15时,模型修正过程停止。有限元模型修正的待修正参数选为第三个子结构对应所有单元的刚度,共336个刚度参数。传统以整体结构为对象进行有限元模型修正时,一般取所有单元刚度参数为待修正参数,即9112个单元参数,现有计算设备难以完成对9112个单元参数的优化。因此,本算例中两种有限元模型修正方法均采用336个修正参数,即以整体结构为对象进行损伤识别时只取局部336个参数进行优化。
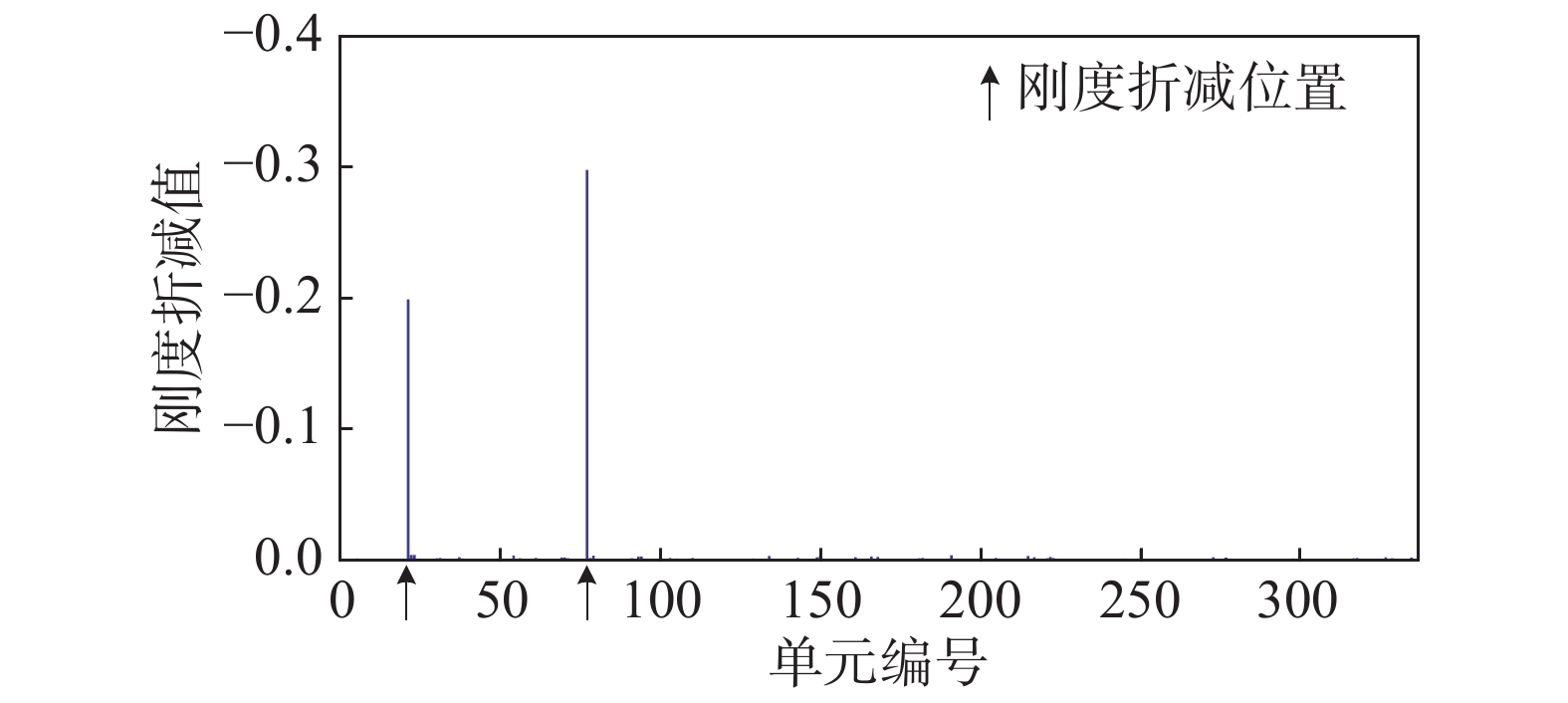
首先采用基于正向子结构有限元模型修正的损伤识别方法,每个子结构只保留了少量的低阶模态来组集得到缩聚的振动方程,进而计算出整体结构的动位移,并对缩聚的振动方程求偏导计算动位移灵敏度。在振动方程中补充一个额外项来考虑舍弃的高阶模态的贡献。保留的模态数量会影响子结构方法的精度,保留的模态越多,精度越高。但是,保留模态的数目越多,计算效率会大大降低。模型修正越接近最优解,对位移和位移灵敏度的精度要求越高。因此,为了同时保证子结构模型修正的精度和效率,在不同模型修正阶段保留不同数量的模态。最初的前6阶迭代中,保留30阶模态。随着有限元模型修正过程逐渐接近收敛,保留模态的数目不断增加。在最后的3次迭代中,保留130阶模态。有限元模型修正过程在满足目标方程小于2 × 10−15时完成运算。基于子结构有限元模型修正的损伤识别结果如图7所示,识别出单元21和77的刚度折减值分别为0.2和0.3,而其他单元识别的刚度折减值均为0,该方法高精度地识别出预先设定的损伤位置和损伤程度。同样也应用传统的基于整体结构有限元模型修正的损伤识别方法,采用相同的目标函数、灵敏度计算和优化过程。由于本算例数值模拟结构损伤,且未考虑不确定性和噪声影响,传统的基于整体结构有限元模型修正的损伤识别方法同样能高精度地识别结构损伤位置和损伤程度。
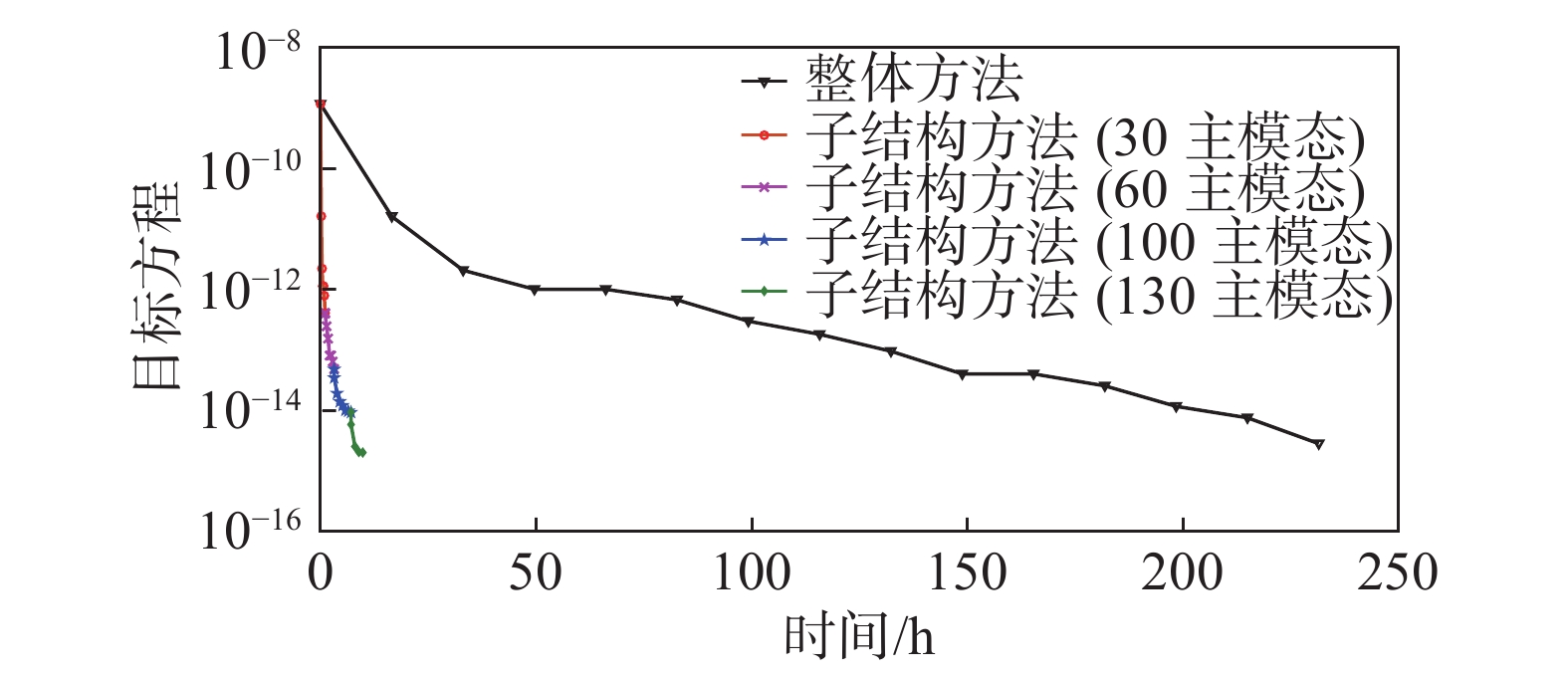
表1比较了两种方法的迭代过程和计算时间,图8对比了两种方法的收敛曲线。基于子结构有限元模型修正的损伤识别方法,当模态保留30阶时,振动方程和灵敏度方程的尺寸被缩聚为270×270,每次迭代花费时间为0.18 h。在最后3次迭代,振动方程/灵敏度方程的尺寸为1170×1170,每次迭代花费时间为0.90 h。子结构方法总共需要23个迭代步和9.78 h收敛。整体结构方法计算整体模型的动力响应与灵敏度,振动方程/灵敏度方程尺寸为23 364×23 364,每个迭代步花费14.17 h,一共花费了14个迭代步和198.38 h达到收敛。综上所述,在相同收敛条件、相同计算精度的前提下,基于子结构有限元模型修正的损伤识别方法花费的时间是传统整体模型修正方法的4.93%。
表 1 有限元模型修正计算时间和迭代步数的比较Table 1. Comparison of computational time and iterations by finite element model updating方法类型 系统矩阵尺寸 每步迭代时间/h 迭代步数 总迭代步数 总时间/h 相对值/(%) 整体结构方法 23 364×23 364 14.17 14 14 198.38 100.00 子结构方法 30 模态 270×270 0.18 6 23 9.78 4.93 60 模态 540×540 0.35 6 100 模态 900×900 0.65 6 130 模态 1170×1170 0.90 3 子结构有限元模型修正能极大地提高损伤识别的效率,原因主要在如下三个方面:1) 子结构方法极大地缩减了模型尺寸,当子结构模态保留30阶时,振动方程和灵敏度方程的尺寸由23 364×23 364缩减为270×270;2) 计算灵敏度是一个比较耗时的过程,在采用子结构方法计算灵敏度时,各个子结构是相互独立的,通过计算第3个子结构的灵敏度矩阵来组集得到整体结构的灵敏度,而其余8个子结构的灵敏度矩阵为零,对独立子结构计算灵敏度比对整体结构计算灵敏度效率高;3) 局部子结构的待修正参数远小于整体结构,本算例中对子结构方法和整体结构方法均取局部336个修正参数,整体结构有限元模型修正消耗198.38 h。在实际结构损伤识别中,以整体结构为对象时,一般取所有单元刚度参数为待修正参数,也即9112个单元参数。可以预测,同时优化9112个单元参数的耗时将成级数倍增加,现有的计算设备难以完成。
4 结论
本文详细介绍了有限元模型修正方法及其在土木工程损伤识别中的应用,并总结了不确定性和非线性有限元模型修正方法。土木工程结构庞大而损伤往往发生在局部区域,针对大型土木工程有限元模型修正效率低的难题,详细阐述了子结构有限元模型修正方法,并介绍了适合于土木结构损伤识别的正向子结构方法和逆向子结构方法。主要结论如下:
(1)基于有限元模型修正的损伤识别方法计算过程直观、物理意义明确,能同步识别结构损伤位置和损伤程度,是一种直接、有效的土木工程损伤识别技术。然而,土木工程有限元模型包含大量节点、单元和待修正参数,大型结构有限元模型修正效率极低,甚至无法完成。
(2)土木工程尺寸庞大而损伤通常发生在局部区域,子结构方法将对整体结构的分析转换为对独立子结构的分析,将耗时的优化计算、不确定性分析和非线性计算限制在局部子结构内,通过局部子结构有限元模型修正实现损伤识别,有效提高了损伤识别的精度和效率,为传统基于有限元模型修正的损伤识别技术开辟了新的途径。
基于有限元模型修正的结构损伤识别方法在结构健康监测领域已经取得了较好的理论成果和工程应用,多个结构健康评估规范中均规定结构二次评估需要实施基于有限元模型修正的损伤识别,该方法正在为结构安全评估提供越来越重要的信息。基于有限元模型修正的损伤识别方法与子结构方法、贝叶斯方法、人工智能与大数据方法等先进方法的深入融合,以及计算设备的高速化、智能化,将推动土木工程安全评估进一步向高精高效、智能化、信息化的可持续方向发展。
注:该文在第29届结构工程学术会议(2020 武汉)应邀作特邀报告
-
表 1 有限元模型修正计算时间和迭代步数的比较
Table 1 Comparison of computational time and iterations by finite element model updating
方法类型 系统矩阵尺寸 每步迭代时间/h 迭代步数 总迭代步数 总时间/h 相对值/(%) 整体结构方法 23 364×23 364 14.17 14 14 198.38 100.00 子结构方法 30 模态 270×270 0.18 6 23 9.78 4.93 60 模态 540×540 0.35 6 100 模态 900×900 0.65 6 130 模态 1170×1170 0.90 3 -
[1] Friswell M I, Mottershead J E. Finite element model updating in structural dynamics [M]. Netherlands: Kluwer Academic Publishers, 1995.
[2] JT/T 1037−2016, 中华人民共和国交通运输行业标准: 公路桥梁结构安全监测系统技术规程[S]. 北京: 中国建筑工业出版社, 2016. JT/T 1037−2016, Standards of the People's Republic of China for the transportation industry: Technical specification for structural monitoring systems of highway bridges [S]. Beijing: China Building Industry Press, 2016. (in Chinese)
[3] Xia Y, Hao H, Deeks A J, et al. Condition assessment of shear connectors in slab-girder bridges via vibration measurements [J]. Journal of Bridge Engineering, 2008, 13(1): 43 − 54. doi: 10.1061/(ASCE)1084-0702(2008)13:1(43)
[4] Duan Y F, Xu Y L, Fei Q G, et al. Advanced finite element model of the Tsing Ma Bridge for structural health monitoring [J]. International Journal of Structural Stability and Dynamics, 2011, 11(2): 313 − 344. doi: 10.1142/S0219455411004117
[5] Ni Y Q, Xia Y, Lin W, et al. SHM benchmark for high-rise structures: a reduced-order finite element model and field measurement data [J]. Smart Structures and Systems, 2011, 10(4/5): 411 − 426.
[6] Baruch M, Bar-Itzhack I Y. Optimal weighted orthogonalization of measured modes [J]. AIAA Journal, 1987, 16(4): 346 − 351.
[7] Berman A, Nagy E J. Improvement of large analytical model using test data [J]. AIAA Journal, 1983, 21(8): 1168 − 1173. doi: 10.2514/3.60140
[8] Zimmerman D C, Kaouk M. Structural damage detection using a minimum rank update theory [J]. Journal of Vibration and Acoustics, 1994, 116(2): 222 − 230. doi: 10.1115/1.2930416
[9] 杨朋超, 薛松涛, 谢丽宇. 结构动力模型的改进直接修正方法及工程应用[J]. 建筑结构学报, 2020: 1 − 7. Yang Pengchao, Xue Songtao, Xie Liyu. An improved direct method for dynamic model updating and its practical engineering applications [J]. Journal of Building Structures, 2020: 1 − 7. (in Chinese)
[10] Abdullah N A Z, Sani M S M, Rahman M M, et al. A review on model updating in structural dynamics [C]// 3rd International Conference of Mechanical Engineering Research. Brisol: Iop Publishing Ltd, 2015.
[11] 范立础, 袁万城, 张启伟. 悬索桥结构基于敏感性分析的动力有限元模型修正[J]. 土木工程学报, 2000, 33: 9 − 14. doi: 10.3321/j.issn:1000-131X.2000.01.003 Fan Lichu, Yuan Wancheng, Zhang Qiwei. Sensitivity-based FE model updating of a suspension bridge [J]. China Civil Engineering Journal, 2000, 33: 9 − 14. (in Chinese) doi: 10.3321/j.issn:1000-131X.2000.01.003
[12] Yuan Z X, Liang P, Silva T, et al. Parameter selection for model updating with global sensitivity analysis [J]. Mechanical Systems and Signal Processing, 2019, 115: 483 − 496. doi: 10.1016/j.ymssp.2018.05.048
[13] Jafari M, Akbari K. Global sensitivity analysis approaches applied to parameter selection for numerical model-updating of structures [J]. Engineering Computations, 2019, 36(4): 1282 − 1304. doi: 10.1108/EC-08-2018-0336
[14] Millar A J. Subset selection in regression. Series: Monographs on statistics and applied probability [J]. London, England: Chapman and Hall, 1990.
[15] Lallement G, Piranda J. Localization methods for parameter updating of finite element models in elastodynamics [C]// 8th International Modal Analysis Conference, Orlando, Chichester, Florida, John Wiley & Sons, Ltd, 1990: 579 − 585.
[16] 张皓, 李东升, 李宏男. 有限元模型修正研究进展: 从线性到非线性[J]. 力学进展, 2019, 49(1): 542 − 575. Zhang Hao, Li Dongsheng, Li Hongnan. Recent progress on finite element model updating: From linearity to nonlinearity [J]. Advances in Mechanics, 2019, 49(1): 542 − 575. (in Chinese)
[17] 李伟明. 有限元模型修正方法及自由度匹配迭代技术研究[D]. 上海: 上海交通大学, 2011. Li Weiming. Study on finite element model updating method and iterative technique for degree of freedom matching [D]. Shanghai: Shanghai Jiao Tong University, 2011. (in Chinese)
[18] Weng S, Tian W, Zhu H, et al. Dynamic condensation approach to calculation of structural responses and response sensitivities [J]. Mechanical Systems and Signal Processing, 2017, 88: 302 − 317. doi: 10.1016/j.ymssp.2016.11.025
[19] 费庆国, 张令弥, 李爱群, 等. 基于不同残差的动态有限元模型修正的比较研究[J]. 振动与冲击, 2005, 24: 24 − 26, 135. doi: 10.3969/j.issn.1000-3835.2005.06.007 Fei Qingguo, Zhang Linmi, Li Aiqun, et al. Evaluation of FE model updating using four kinds of residues [J]. Journal of Vibration and Shock, 2005, 24: 24 − 26, 135. (in Chinese) doi: 10.3969/j.issn.1000-3835.2005.06.007
[20] 郭勤涛, 张令弥. 结构动力学有限元模型确认方法研究[J]. 应用力学学报, 2005, 22: 572 − 578, 678. doi: 10.3969/j.issn.1000-4939.2005.04.015 Guo Qintao, Zhang Lingmi. Fnite element model validation in structural dynamics [J]. Chinese Journal of Applied Mechanics, 2005, 22: 572 − 578, 678. (in Chinese) doi: 10.3969/j.issn.1000-4939.2005.04.015
[21] Guo, N, Yang Z C, Wang L, et al. Dynamic model updating based on strain mode shape and natural frequency using hybrid pattern search technique [J]. Journal of Sound and Vibration, 2018, 422: 112 − 130. doi: 10.1016/j.jsv.2018.02.013
[22] Meruane V. Model updating using antiresonant frequencies identified from transmissibility functions [J]. Journal of Sound and Vibration, 2013, 332(4): 807 − 820. doi: 10.1016/j.jsv.2012.10.021
[23] Jaishi B, Ren W X. Damage detection by finite element model updating using modal flexibility residual [J]. Journal of Sound and Vibration, 2006, 290(1/2): 369 − 387. doi: 10.1016/j.jsv.2005.04.006
[24] Jaishi B, Kim H J, Kim M K, et al. Finite element model updating of concrete-filled steel tubular arch bridge under operational condition using modal flexibility [J]. Mechanical Systems and Signal Processing, 2007, 21(6): 2406 − 2426. doi: 10.1016/j.ymssp.2007.01.003
[25] Marwala T. Finite element model updating using wavelet data and genetic algorithm [J]. Journal of Aircraft, 2002, 39(4): 709 − 711. doi: 10.2514/2.2985
[26] Kwon K S, Lin R M. Frequency selection method for FRF-based model updating [J]. Journal of Sound and Vibration, 2004, 278(1-2): 285 − 306. doi: 10.1016/j.jsv.2003.10.003
[27] Lin R M, Zhu J. Model updating of damped structures using FRF data [J]. Mechanical Systems and Signal Processing, 2006, 20(8): 2200 − 2218. doi: 10.1016/j.ymssp.2006.05.008
[28] Gang X Y, Chai S, Allemang R J, et al. A new iterative model updating method using incomplete frequency response function data [J]. Journal of Sound and Vibration, 2014, 333(9): 2443 − 2453. doi: 10.1016/j.jsv.2013.12.008
[29] Xu Y L, Zhang C D, Zhan S, et al. Multi-level damage identification of a bridge structure: A combined numerical and experimental investigation [J]. Engineering Structures, 2018, 156: 53 − 67. doi: 10.1016/j.engstruct.2017.11.014
[30] 张启伟, 范立础. 利用动静力测量数据的桥梁结构损伤识别[J]. 同济大学学报(自然科学版), 1998, 26(5): 528 − 532. Zhang Qiwei, Fan Lichu. Based on dynamic and static measurements of the damage identification of bridge structures [J]. Journal of Tongji University: Natural Science Edition, 1998, 26(5): 528 − 532. (in Chinese)
[31] 胡俊亮, 余晓琳, 郑恒斌, 等. 基于优化BP神经网络的梁结构有限元模型修正[J]. 华南理工大学学报(自然科学版), 2013, 41(8): 67 − 73. Hu Junliang, Yu Xiaolin, Zheng Hengbin, et al. Beam structure finite element model updating via BP neural network optimized [J]. Journal of South China University of Technology: Natural Science Edition, 2013, 41(8): 67 − 73. (in Chinese)
[32] 谢海龙. 遗传算法在桥梁有限元模型修正中的应用[J]. 石家庄铁道大学学报(自然科学版), 2018, 31(1): 33 − 38. Xie Hailong. Application of genetic algorithm in bridge finite element model updating [J]. Journal of Shijiazhuang Tiedao University (Natural Science Edition), 2018, 31(1): 33 − 38. (in Chinese)
[33] 夏志远, 李爱群, 李建慧, 等. 基于GMPSO的有限元模型修正方法验证[J]. 工程力学, 2019, 36(10): 66 − 74. Xia Zhiyuan, Li Aiqun, Li Jianhui, et al. Validation of finite element model updating methodology based on GMPSO [J]. Engineering Mechanics, 2019, 36(10): 66 − 74. (in Chinese)
[34] 张宏怡, 韩建松. 蚁群算法优化策略及其仿真研究[J]. 计算机工程与应用, 2006(25): 48 − 49, 97. doi: 10.3321/j.issn:1002-8331.2006.25.015 Zhang Hongyi, Han Jiansong. Strategy of optimization in ant colony algorithm and simulation research [J]. Computer Engineering and Applications, 2006(25): 48 − 49, 97. (in Chinese) doi: 10.3321/j.issn:1002-8331.2006.25.015
[35] Adelman H M, Haftka R T. Sensitivity analysis of discrete structural systems [J]. AIAA Journal, 1986, 24(5): 823 − 832. doi: 10.2514/3.48671
[36] Fox R L, Kapoor M P. Rates of change of eigenvalues and eigenvectors [J]. AIAA Journal, 1968, 6(12): 2426 − 2429. doi: 10.2514/3.5008
[37] Nelson R B. Simplified calculation of eigenvector derivatives [J]. AIAA Journal, 1976, 14(9): 1201 − 1205. doi: 10.2514/3.7211
[38] Lee I W, Jung G H. An efficient algebraic method for the computation of natural frequency and mode shape sensitivities-Part 1. Distinct natural frequencies [J]. Computers and Structures, 1997, 62(3): 429 − 435. doi: 10.1016/S0045-7949(96)00206-4
[39] Li S, Wang B, Hu J Z. Sensitivity analysis based on Lanczos algorithm in structural dynamics [J]. Applied Mathematics and Mechanics-English Edition, 2003, 24(1): 92 − 98. doi: 10.1007/BF02439382
[40] Andrew A L. Convergence of an iterative method for derivatives of eigen-systems [J]. Journal of Computational Physics, 1978, 26(1): 107 − 112. doi: 10.1016/0021-9991(78)90102-X
[41] Burchett B T, Costello M. QR-based algorithm for eigenvalue derivatives [J]. AIAA Journal, 2002, 40(11): 2319 − 2322. doi: 10.2514/2.1569
[42] Lin R M, Lim M K, Wang Z. Improved calculation of eigenvector sensitivities using matrix perturbation analysis [J]. Journal of Mechanical Design, 1997, 119(1): 137 − 141. doi: 10.1115/1.2828777
[43] Tian W, Weng S, Xia Y, et al. An iterative reduced-order substructuring approach to the calculation of eigensolutions and eigensensitivities [J]. Mechanical Systems and Signal Processing, 2019, 130: 361 − 377. doi: 10.1016/j.ymssp.2019.05.006
[44] 田炜. 基于动态缩聚的有限元模型修正方法研究[D]. 武汉: 华中科技大学, 2018. Tian Wei. Finite element model updating using dynamic condensation methods [D]. Wuhan: Huazhong University of Science and Technology, 2018. (in Chinese)
[45] 朴思扬, 祁峰, 张亚辉. 基于模态综合法的大型结构模型修正技术[J]. 应用数学和力学, 2018, 39(9): 989 − 998. doi: 10.21656/1000-0887.390065 Pu Siyang, Qi Feng, Zhang Yahui. Model updating for large structures based on the modal synthesis method [J]. Applied Mathematics and Mechanics, 2018, 39(9): 989 − 998. (in Chinese) doi: 10.21656/1000-0887.390065
[46] 张立涛, 李兆霞, 费庆国. 基于加速度时域信息的结构损伤识别方法研究[J]. 振动与冲击, 2007, 26(9): 138 − 141. Zhang Litao, Li Zhaoxia, Fei Qingguo. Experimental investigation of piezoelectric shunt damped vibration control based on optimal placement [J]. Journal of Vibration and Shock, 2007, 26(9): 138 − 141. (in Chinese)
[47] 张纯, 宋固全, 吴光宇. 改进的正则化模型修正方法在结构损伤识别中的应用[J]. 工程力学, 2012, 29(2): 29 − 33, 44. Zhang Chun, Song Guquan, Wu Guangyu. Structural damage identification by finite element model updated with improved Tikhonov regularization [J]. Engineering Mechanics, 2012, 29(2): 29 − 33, 44. (in Chinese)
[48] Mosegaard K, Tarantola A. Probabilistic approach to inverse problems [M]. New York: International Handbook of Earthquake and Engineering Seismology, Academic Press, 2002.
[49] Mares C, Mottershead J E, Friswell M I. Stochastic model updating: Part 1—Theory and simulated example [J]. Mechanical Systems and Signal Processing, 2006, 20(7): 1674 − 1695. doi: 10.1016/j.ymssp.2005.06.006
[50] 姜东, 费庆国, 吴邵庆. 基于摄动法的不确定性有限元模型修正方法研究[J]. 计算力学学报, 2014, 31(4): 431 − 437, 445. doi: 10.7511/jslx201404004 Jiang Dong, Fei Qingguo, Wu Shaoqing. A study on stochastic finite element model updating based on perturbation approach [J]. Chinese Journal of Computational Mechanics, 2014, 31(4): 431 − 437, 445. (in Chinese) doi: 10.7511/jslx201404004
[51] Hua X G, Ni Y Q, Chen Z Q, et al. An improved perturbation method for stochastic finite element model updating [J]. International Journal for Numerical Methods in Engineering, 2008, 73(13): 1845 − 1864. doi: 10.1002/nme.2151
[52] Beck J L, Katafygiotis L S. Updating models and their uncertainties I: Bayesian statistical framework [J]. Journal of Engineering Mechanics, 1998, 124(4): 455 − 462.
[53] Katafygiotis L S, Beck J L. Updating models and their uncertainties II: Model identifiability [J]. Journal of Engineering Mechanics, 1998, 124(4): 463 − 467. doi: 10.1061/(ASCE)0733-9399(1998)124:4(463)
[54] Lam H F, Katafygiotis L S, Mickleborough N C. Application of a statistical model updating approach on Phase I of the IASC-ASCE structural health monitoring benchmark study [J]. Journal of Engineering Mechanics, 2004, 130(1): 34 − 48. doi: 10.1061/(ASCE)0733-9399(2004)130:1(34)
[55] Yuen K V, Katafygiotis L S. Model updating using noisy response measurements without knowledge of the input spectrum [J]. Earthquake Engineering and Structural Dynamics, 2005, 34(2): 167 − 187. doi: 10.1002/eqe.415
[56] Cheung S H, Beck J L. Bayesian model updating using hybrid monte carlo simulation with application to structural dynamic models with many uncertain parameters [J]. Journal of Engineering Mechanics, 2009, 135(4): 243 − 255.
[57] Meyer S, Link M. Modeling and updating of local non-linearity using frequency response residues [J]. Mechanical Systems & Signal Processing, 2003, 17(1): 219 − 226.
[58] Nguyen H M, Allix O, Feissel P. A robust identification strategy for rate-dependent models in dynamics [J]. Inverse Problems, 2008, 24(6): 065006. doi: 10.1088/0266-5611/24/6/065006
[59] Philippe B, Bruce S S, Da S S. Updating of a nonlinear finite element model using discrete-time Volterra series [J]. Latin American Journal of Solids & Structures, 2017, 14(7): 1183 − 1199.
[60] Kerschen G, Lenaerts V, Golinval J C. VTT Benchmark: Application of the restoring force surface method [J]. Mechanical Systems and Signal Processing, 2003, 17(1): 189 − 193. doi: 10.1006/mssp.2002.1558
[61] Lenaerts V, Kerschen G, Golinval J C. Proper orthogonal decomposition for model updating of non-linear mechanical systems [J]. Mechanical Systems and Signal Processing, 2001, 15(1): 31 − 43. doi: 10.1006/mssp.2000.1350
[62] Peng Z K, Lang Z Q, Billings S A, et al. Comparisons between harmonic balance and nonlinear output frequency response function in nonlinear system analysis [J]. Journal of Sound and Vibration, 2008, 311(1/2): 56 − 73. doi: 10.1016/j.jsv.2007.08.035
[63] Silva S D, Cogan S, Emmanuel F, et al. Metrics for nonlinear model updating in structural dynamics [J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2009, 31(1): 27 − 34. doi: 10.1590/S1678-58782009000100005
[64] Brownjohn J M W, Xia P Q, Hao H, et al. Civil structure condition assessment by FE model updating: Methodology and case studies [J]. Finite Elements in Analysis and Design, 2001, 37(10): 761 − 775. doi: 10.1016/S0168-874X(00)00071-8
[65] Fritzen C P, Jennewein D, Kiefer T. Damage detection based on model updating methods [J]. Mechanical Systems and Signal Processing, 1998, 12(1): 163 − 186. doi: 10.1006/mssp.1997.0139
[66] Abdel W M M. Effect of modal curvatures on damage detection using model updating [J]. Mechanical Systems and Signal Processing, 2001, 15(2): 439 − 445. doi: 10.1006/mssp.2000.1340
[67] Lu Z R, Law S S. Features of dynamic response sensitivity and its application in damage detection [J]. Journal of Sound and Vibration, 2007, 303(1/2): 305 − 329. doi: 10.1016/j.jsv.2007.01.021
[68] Kron G. Diakoptics-piecewise solution of large-scale systems [M]. London: Macdonald and Co., 1963.
[69] Weng S, Xia Y, Xu Y L, et al. Improved substructuring method for eigensolutions of large-scale structures [J]. Journal of Sound and Vibration, 2009, 323(3): 718 − 736.
[70] Weng S, Xia Y, Xu Y L, et al. Substructure based approach to finite element model updating [J]. Computers and Structures, 2011, 89(9/10): 772 − 782. doi: 10.1016/j.compstruc.2011.02.004
[71] Xia Y, Weng S, Xu Y L, et al. Calculation of the eigenvalue and eigenvector derivatives using an improved kron’s substructuring method [J]. Structural Engineering and Mechanics, 2010, 36(1): 37 − 55. doi: 10.12989/sem.2010.36.1.037
[72] Craig R R, Bampton M M C. Coupling of substructures for dynamic analysis [J]. AIAA Journal, 1968, 6(7): 1313 − 1319. doi: 10.2514/3.4741
[73] MacNeal R H. A hybrid method of component mode synthesis [J]. Computers and Structures, 1971, 1: 581 − 601. doi: 10.1016/0045-7949(71)90031-9
[74] Rubin S. Improved component-mode representation for structural dynamic analysis [J]. AIAA Journal, 1975, 8(8): 995 − 1005.
[75] Klerk D, Rixen D J, Voormeeren S N. General Framework for dynamic substructuring: History, review, and classification of techniques [J]. AIAA Journal, 2008, 46(5): 1169 − 1181. doi: 10.2514/1.33274
[76] D’Ambrogio W, Sestieri A. Unified approach to substructuring and structural modification problems [J]. Shock and Vibration, 2004, 11(3): 295 − 309.
[77] Gordis J H, Bielawa R, Flannelly W. General theory for frequency domain structural synthesis [J]. Journal of Sound and Vibration, 1991, 150(1): 139 − 158. doi: 10.1016/0022-460X(91)90407-B
[78] Crowley J, Klosterman A, Rocklin G, et al. Direct structure modification using frequency response functions [C]// Proceedings of the Second International Modal Analysis Conference, Society for Experimental Mechanics, Bethel, CT, Schenectad: Union Coll, 1984: 58 − 65.
[79] Lim T, Li J. Theoretical and computational study of the FRF-based substructuring technique applying enhanced least square and TSVD approaches [J]. Journal of Sound and Vibration, 2000, 231(4): 1135 − 1157. doi: 10.1006/jsvi.1999.2724
[80] Law M, Ihlenfeldt S. A frequency-based substructuring approach to efficiently model position-dependent dynamics in machine tools [J]. Journal of Multi-Body Dynamics, 2015, 229(3): 304 − 317.
[81] Zhu H P, Li J J, Weng S, et al. Calculation of structural response and response sensitivity with improved substructuring method [J]. Journal of Aerospace Engineering, 2019, 32(3): 04019016. doi: 10.1061/(ASCE)AS.1943-5525.0000996
[82] Zhu H P, Li J J, Tian W, et al. An enhanced substructure-based response sensitivity method to finite element model updating of large-scale structures [J]. Mechanical Systems and Signal Processing, Accepted.
[83] Gordis J H. Integral equation formulation for transient structural synthesis [J]. AIAA Journal, 1995, 33(2): 320 − 324.
[84] Gruber F M, Gille M, Rixen D J. A strategy to stabilize the transient analysis and increase the approximation accuracy of dual Craig-Bampton reduced systems [J]. Finite Elements in Analysis and Design, 2019, 160: 32 − 45. doi: 10.1016/j.finel.2019.03.003
[85] Gruber F M, Rixen D J. Dual Craig-Bampton component mode synthesis method for model order reduction of nonclassically damped linear systems [J]. Mechanical Systems and Signal Processing, 2018, 111: 678 − 698. doi: 10.1016/j.ymssp.2018.04.019
[86] Gordis J H. Fast transient analysis for locally nonlinear structures by recursive block convolution [J]. Journal of Vibration and Acoustics, 2011, 123(4): 545 − 547.
[87] Dong W L, Liu L, Zhou S D, et al. Substructure synthesis in time domain with rigid-elastic hybrid joints [J]. AIAA Journal, 2015, 53(2): 504 − 509. doi: 10.2514/1.J053630
[88] Doebling S W, Peterson L D, Alvin K F. Experimental determination of local structural stiffness by disassembly of measured flexibility matrices [J]. Journal of Vibration and Acoustics, 1998, 120(4): 949 − 957. doi: 10.1115/1.2893925
[89] Alvin K F, Park K C. Extraction of substructural flexibility from global frequencies and mode shapes [J]. AIAA Journal, 1999, 37(37): 1444 − 1451.
[90] Park K C, Reich G W. Structural damage detection using localized flexibilities [J]. Journal of Intelligent Material Systems and Structures, 1998, 9(9): 911 − 919.
[91] Hou J L, Jankowski L, Ou J P. Frequency-domain substructure isolation for local damage identification [J]. Advances in Structural Engineering, 2015, 18(1): 137 − 153.
[92] Weng S, Xia Y, Zhou X Q, et al. Inverse substructure method for model updating of structures [J]. Journal of Sound and Vibration, 2012, 331(25): 5449 − 5468. doi: 10.1016/j.jsv.2012.07.011
[93] Weng S, Zhu H P, Li P H, et al. Construction of orthogonal projector for the damage identification by measured substructural flexibility [J]. Measurement, 2016, 88: 441 − 455. doi: 10.1016/j.measurement.2015.12.047
[94] Weng S, Zhu H P, Xia Y, et al. Damage detection using the eigenparameters decomposition of substructural flexibility matrix [J]. Mechanical Systems and Signal Processing, 2013, 34(1/2): 19 − 38.
[95] Koh C G, See L M, Balendra T. Estimation of structural parameters in time domain: A substructure approach [J]. Earthquake Engineering and Structural Dynamics, 1991, 20(8): 787 − 801. doi: 10.1002/eqe.4290200806
[96] Yun C B, Lee H J. Substructural identification for damage estimation of structures [J]. Structural Safety, 1997, 19(1): 121 − 140. doi: 10.1016/S0167-4730(96)00040-9
[97] Yun C B, Bahng E Y. Substructural identification using neural networks [J]. Computers and Structures, 2000, 77(1): 41−52.
[98] Koh C G, Shankar K. Substructural identification method without interface measurement [J]. Journal of Engineering Mechanics, 2003, 129(7): 769 − 776. doi: 10.1061/(ASCE)0733-9399(2003)129:7(769)
[99] Tee K F, Koh C G, Quek S T. Numerical and experimental studies of a substructural identification strategy [J]. Structural Health Monitoring, 2009, 8(5): 397 − 410. doi: 10.1177/1475921709102089
[100] Li J, Law S S. Substructural damage detection with incomplete information of the structure [J]. Journal of Applied Mechanics, 2012, 79(4): 041003. doi: 10.1115/1.4005552
[101] Zhu H P, Mao L, Weng S. Calculation of dynamic response sensitivity to substructural damage identification under moving load [J]. Advances in Structural Engineering, 2013, 16(9): 1621 − 1631. doi: 10.1260/1369-4332.16.9.1621
[102] Beck J L, Vanik M W, Katafygiotis L S. Determination of stiffness changes from modal parameter changes for structural health monitoring [C]// First World Conference on Structural Control, Elsevier Science Limited, Great Britain, 1994: 122 − 125.
[103] Tran Q H, Ouisse M, Bouhaddi N. A robust component mode synthesis method for stochastic damped vibroacoustics [J]. Mechanical Systems and Signal Processing, 2010, 24(1): 164 − 181. doi: 10.1016/j.ymssp.2009.06.016
[104] Chentouf S A, Bouhaddi N, Laitem C. Robustness analysis by a probabilistic approach for propagation of uncertainties in a component mode synthesis context [J]. Mechanical Systems and Signal Processing, 2011, 25: 2426 − 2443.
[105] 梁锋. 基于摄动分析和子结构的有限元模型修正方法[D]. 武汉: 华中科技大学, 2014. Liang Feng. Perturbation analysis and substructure technique based finite element model updating method [D]. Wuhan: Huazhong University of Science and Technology, 2014. (in Chinese)
[106] Praveen K I R, Padmanabhan C. Improved reduced order solution techniques for nonlinear systems with localized nonlinearities [J]. Nonlinear Dynamics, 2011, 63(4): 561 − 586. doi: 10.1007/s11071-010-9820-5
[107] Weng S, Gao F, Zhu H P, et al. System identification of nonlinear structures by a substructuring method [C]// The 24th Australasian Conference on the Mechanics of Structures and Materials, CRC Press, Boca Raton, 2017: 1381 − 1387.
[108] Apiwattanalunggarn P, Shaw S W, Pierre C. Component mode synthesis using nonlinear normal modes [J]. Nonlinear Dynamics, 2005, 41: 17 − 46. doi: 10.1007/s11071-005-2791-2
[109] Huang X R, Jezequel L, Besset S, et al. Noninear hybrid modal synthesis based on branch modes for dynamic analysis of assembled structure [J]. Mechanical Systems and Signal Processing, 2018, 99: 624 − 646. doi: 10.1016/j.ymssp.2017.07.002
[110] Yu J X, Xia Y, Lin W, et al. Element-by-element model updating of large-scale structures based on component mode synthesis [J]. Journal of Sound and Vibration, 2016, 362: 72 − 84. doi: 10.1016/j.jsv.2015.10.019
[111] Chen S H, Lin W, Yu J X, et al. Free-interface modal synthesis based substructural damage detection method [J]. Shock and Vibration, 2014: 741697-1 − 741697-13.
[112] Lam H F, Yang J H. Bayesian structural damage detection of steel towers using measured modal parameters [J]. Earthquakes and Structures, 2015, 8(4): 935 − 956. doi: 10.12989/eas.2015.8.4.935
[113] Jensen H A, Esse C, Araya V, et al. Implementation of an adaptive meta-model for Bayesian finite element model updating in time domain [J]. Reliability Engineering and System Safety, 2017, 160: 174 − 190. doi: 10.1016/j.ress.2016.12.005
-
期刊类型引用(48)
1. 罗大明,李凡,牛荻涛. 人工智能时代混凝土结构耐久性诊断研究进展. 建筑结构学报. 2024(02): 1-13 .  百度学术
百度学术
2. 万能,黄民水,朱宏平. 基于卷积神经网络和交叉模型交叉模态方法的钢框架两阶段损伤识别研究. 工业建筑. 2024(01): 123-129 .  百度学术
百度学术
3. 周宇,甘露一,狄生奎,贺文宇,李宁波. 基于应变影响线的桥梁模型修正试验. 浙江大学学报(工学版). 2024(03): 537-546 .  百度学术
百度学术
4. 夏恒,崔鸿知. 贝叶斯理论在既有砌体损伤定位中的应用研究. 重庆建筑. 2024(04): 54-57+60 .  百度学术
百度学术
5. 黄怡颖. 智能算法在结构损伤识别与评估优化中的应用. 电子技术. 2024(03): 298-299 .  百度学术
百度学术
6. 叶玲,江宏康,陈华鹏,冯宇轩,王力骋. 基于多链竞争差分进化算法的无砟轨道结构有限元模型修正. 交通运输工程学报. 2024(02): 112-124 .  百度学术
百度学术
7. 秦世强,苏晟,杨睿. 基于多标签卷积神经网络的结构损伤识别. 建筑科学与工程学报. 2024(03): 108-119 .  百度学术
百度学术
8. 余恒,殷红,彭珍瑞. 基于变分模态提取的动力响应重构方法研究. 噪声与振动控制. 2024(03): 43-49 .  百度学术
百度学术
9. 单伽锃,周子杰,王律己,余桦,苏金蓉. 考虑实测信息的既有规则建筑状态识别与抗震性能快速评估. 振动工程学报. 2024(05): 802-811 .  百度学术
百度学术
10. 梅冲,宋任贤,周云飞,霍学晋,秦世强. 基于静动力试验的铁路连续刚构-拱桥模型修正. 铁道标准设计. 2024(07): 108-117 .  百度学术
百度学术
11. 李宾宾,朱伟,谢炎龙,朱作. 基于最小二乘法的振动监测系统测量噪声现场标定. 噪声与振动控制. 2024(04): 110-117 .  百度学术
百度学术
12. 曹明明,彭珍瑞. 考虑不确定性的高速列车车轮有限元模型修正. 兰州交通大学学报. 2024(04): 45-52 .  百度学术
百度学术
13. 于虹,文望青,严爱国,余兴胜,闫俊锋. 高速铁路桥梁车致加速度响应监测数据分类方法研究. 世界桥梁. 2024(05): 83-89 .  百度学术
百度学术
14. 周雪文,彭珍瑞. 改进Tikhonov正则化方法在结构激励识别与响应重构中的应用. 机械科学与技术. 2024(09): 1469-1476 .  百度学术
百度学术
15. 苏子献,韩东,崔钊. 基于灵敏度分析的直升机旋翼桨叶模型修正方法. 航空动力学报. 2024(11): 118-125 .  百度学术
百度学术
16. 王磊,黄杜康,马亚飞,黄可. 基于元学习的结构损伤定位与量化. 中国公路学报. 2024(11): 38-51 .  百度学术
百度学术
17. 李整,李奥利,陈代海,许世展,张宇. 基于车桥耦合振动和深度学习的悬索桥损伤识别分析. 国外电子测量技术. 2024(10): 26-35 .  百度学术
百度学术
18. 侯亚琨,彭珍瑞. 未知激励下基于改进强跟踪卡尔曼滤波的结构响应重构. 机械强度. 2024(06): 1271-1278 .  百度学术
百度学术
19. 李整,李奥利,陈代海,许世展,张宇. 基于小波包分解和优化BP神经网络的桥梁结构损伤识别试验研究. 国外电子测量技术. 2024(11): 94-102 .  百度学术
百度学术
20. 江守燕,杜成斌,孙立国. 基于数据驱动的大体积结构裂缝深度反演. 工程力学. 2023(04): 215-225 .  本站查看
本站查看
21. 王慧,王乐,田鑫海. 基于相关函数矩阵及卷积神经网络的结构健康监测研究. 工程力学. 2023(05): 217-227 .  本站查看
本站查看
22. 杨根源,李国生. 基于有限元模型修正的悬臂梁桥长期挠度研究分析. 建筑技术. 2023(08): 927-930 .  百度学术
百度学术
23. 余洁歆,林伟,陈欣,谢本飞. 基于灵敏度分析的结构损伤识别方法研究. 黑龙江工业学院学报(综合版). 2023(05): 86-93 .  百度学术
百度学术
24. 黄斌,刘雨欣,吴志峰,李烨君. 基于同伦分析方法的梁结构静力随机损伤识别. 华中科技大学学报(自然科学版). 2023(07): 69-76 .  百度学术
百度学术
25. 任现才,孙伟明,葛福冲,柴山清,杨乐华. 基于确定性的结构损伤识别方法研究进展. 低温建筑技术. 2023(06): 29-33 .  百度学术
百度学术
26. 夏志远,陈鹏,唐柏鉴,史慧媛. 基于不同MCMC抽样子集模拟的模型修正方法对比研究. 力学季刊. 2023(03): 662-672 .  百度学术
百度学术
27. 王俊,辛宇,王佐才,戈壁. 改进生成对抗网络及其在结构非线性模型修正中的应用. 振动工程学报. 2023(04): 934-945 .  百度学术
百度学术
28. 周林仁,叶文许. 空间桁架结构特征响应信息对模型修正的影响机理分析. 振动与冲击. 2023(17): 1-8 .  百度学术
百度学术
29. 付君健,彭铁川,李然,李帅虎,周祥曼,李响. 考虑刚度和质量耦合效应的结构弹性成像方法. 力学学报. 2023(09): 1971-1982 .  百度学术
百度学术
30. 曹震雄,翁顺,李佳靖,陈志丹,于虹,闫俊锋,余兴胜. 基于时域残余力向量特征分解的结构损伤识别方法研究. 振动工程学报. 2023(06): 1516-1526 .  百度学术
百度学术
31. 彭珍瑞,史鹏程. 基于状态空间模型的结构外部激励计算与响应重构. 铁道学报. 2023(12): 182-188 .  百度学术
百度学术
32. 王慧,郭晨林,王乐,张敏照. 基于内积矩阵及深度学习的结构健康监测研究. 工程力学. 2022(02): 14-22+75 .  本站查看
本站查看
33. 丁一凡,刘宇飞,樊健生,刘家豪. 基于空间位形的在役索膜结构有限元模型修正与安全评估. 工程力学. 2022(05): 44-54 .  本站查看
本站查看
34. 王宁波,赵雨森,贺政,黄天立. 基于转角数据的梁式桥挠度响应重构方法. 振动与冲击. 2022(10): 284-291 .  百度学术
百度学术
35. 林光伟,张熠. 不同结构复杂度下结合集成学习的模型修正方法. 工程力学. 2022(S1): 153-157 .  本站查看
本站查看
36. 刘纲,陈奇,雷振博,熊军. 基于改进萤火虫算法的有限元模型修正. 工程力学. 2022(07): 1-9 .  本站查看
本站查看
37. 罗辉,周剑锋,朱宏平. 基于间接测量法的盾构隧道损伤识别. 华中科技大学学报(自然科学版). 2022(08): 124-130 .  百度学术
百度学术
38. 邹云峰,卢玄东,阳劲松,何旭辉. 基于应变模态响应重构的损伤识别方法. 工程力学. 2022(09): 225-233 .  本站查看
本站查看
39. 单伽锃,王律己,余桦,苏金蓉. 结构强震观测与评估研究现状与展望. 工程力学. 2022(11): 1-12 .  本站查看
本站查看
40. 刘洋,刘冲,王丽霞. 基于小波包变换的框架剪力墙结构健康监测研究. 工业建筑. 2022(10): 211-218 .  百度学术
百度学术
41. 李佳靖,朱宏平,翁顺,宋晓东,杨国静,颜永逸. 动力特征解灵敏度分析的结构关键区域判别. 振动工程学报. 2022(05): 1181-1187 .  百度学术
百度学术
42. 丁雅杰,王佐才,辛宇,戈壁,袁子青. 基于贝叶斯理论的非线性结构模型修正及其动力可靠度分析. 工程力学. 2022(12): 13-22+59 .  本站查看
本站查看
43. 顾箭峰,向春燕,陶甫先,黄民水,贾文坤,王枫. 基于深度学习和IHPO的桥梁结构模型修正方法. 广西大学学报(自然科学版). 2022(05): 1147-1159 .  百度学术
百度学术
44. 张前进,李德巧,宫亚峰,林思远. 基于响应面法的基坑有限元模型修正. 现代隧道技术. 2022(S2): 69-76 .  百度学术
百度学术
45. 董晴晴,赵腾飞,倪浩冉,吴志伟,王爱森. 浅议古建筑木结构损伤识别方法. 广东建材. 2021(08): 71-73 .  百度学术
百度学术
46. 卓德兵,曹晖. 基于小波时频图与轻量级卷积神经网络的螺栓连接损伤识别. 工程力学. 2021(09): 228-238 .  本站查看
本站查看
47. 史京晶,王功臣,张萧. 基于BP神经网络的多响应斜拉桥模型修正. 市政技术. 2021(09): 62-67+77 .  百度学术
百度学术
48. 王凌波,王秋玲,朱钊,赵煜. 桥梁健康监测技术研究现状及展望. 中国公路学报. 2021(12): 25-45 .  百度学术
百度学术
其他类型引用(91)



 下载:
下载: