钢管混凝土组合柱结合了钢结构和混凝土结构的优点，取得了良好的经济效益^[1]。圆形钢管混凝土柱对核心混凝土提供均匀的约束，使组合柱强度高、塑性好^[2-5]。方形或矩形钢管混凝土柱惯性矩和抗弯刚度较大，且利于梁柱连接^[6-9]。随着现代高层、超高层建筑及铁路桥梁墩柱等结构向大跨、高耸、重载方向发展需求的增加^[10]，众多学者开展了对复式钢管混凝土柱的研究。蔡绍怀等^[11]、WAN等^[12]和YAN等^[13]通过对同心圆钢管的复式钢管混凝土柱轴压试验得出，在含钢率相同的情况下，双层钢管混凝土柱较单钢管混凝土柱具有更高的极限承载力和延性。池思源^[14]、史艳莉等^[15]、徐海俭^[16]和GUO等^[17]对外方内圆的复式钢管混凝土短柱进行了轴压试验研究。复式钢管混凝土柱破坏形式呈现腰鼓形破坏，内圆钢管的设置能有效增强方钢管对核心混凝土的约束，提高整体极限承载力和延性。刘礼等^[18]对矩形钢管混凝土柱和矩形钢管内配同心单圆钢管混凝土柱进行的轴压对比试验得出，内置圆钢管也能有效增加整个结构的极限承载力和延性。

随着我国高速铁路高架桥的发展，独柱墩结构发挥着重要作用，而独柱墩结构对于抗横向倾覆能力及稳定性要求更高^[19]。采用矩形截面可以增大桥墩顶面支座的横向间距，减小因偏压引起的支座反力变化，从而可提高桥梁独柱墩抗倾覆能力^[20]。矩形单钢管混凝土柱外钢管极易锈蚀和腐蚀，而且耐火性和抗撞性能差^[21]。复式钢管混凝土墩柱可以在不增加截面尺寸的情况下，提高墩柱的鲁棒性^[22]，当墩柱受到剪切、周期性震动效应等不利作用时，可以提高墩柱的抗力储备，有利于提高结构长期服役性能。因此，结合复式钢管混凝土柱优越的力学性能，本文提出矩形钢管内套异心双圆的新型复式钢管混凝土墩柱截面形式，截面如图1所示。该类型截面可发挥矩形钢管混凝土惯性矩和抗弯刚度大的特点，兼有圆钢管混凝土良好的塑性与韧性。内钢管在加载初期即可对混凝土产生约束作用^[23]，既可以改善矩形钢管仅在角部约束好、截面中部约束差的缺点^{[7, 24]}，又可以发挥圆钢管对混凝土约束好的优点^[15]。新型复式钢管混凝土墩柱可以减少混凝土变形，降低大尺寸构件中混凝土收缩、徐变等对试件力学性能的不利影响^[21]，同时获得较普通钢管混凝土柱优异的极限承载力、延性和耐火性能，防止试件发生剪切破坏^[17]。可用于高墩柱且不受轴压比限制^[25]，适合桥梁墩柱强弱轴方向抗弯刚度不同的情况和大型公共建筑、厂房、高层和超高层等大跨重载结构^{[3, 26]}。本文通过轴压试验分析矩形钢管内套异心双圆的复式钢管混凝土墩柱轴压工作机理，通过对比空钢管柱、矩形墩柱和夹层墩柱分析其破坏形态、延性和钢管应变变化情况，并利用钢管和混凝土的组合效应原理进行墩柱轴压承载力提高分析。

图  1  新型复式钢管混凝土墩柱截面形式

Figure  1.  New composite CFST pier column

下载: 全尺寸图片 幻灯片

1   试验概况

1.1   试件设计与制作

试验共设计7个试件，变化参数为内置圆钢管、混凝土浇筑截面和试件高度，具体参数见表1，试件矩形截面宽厚比和圆钢管径厚比符合设计规范^[27]。其中D₀、B₀、t₀分别为矩形钢管截面的宽度、高度和厚度。d_i、t_i分别为内圆钢管截面的直径和厚度，H为试件的高度。试件编号中R-L为矩形钢管混凝土墩柱(简称矩形墩柱)、RC88-L为新型复式钢管混凝土墩柱(简称新型墩柱)、RC88-L(S-C)为新型夹层复式钢管混凝土墩柱(简称夹层墩柱)、RC88-L(N-C)为空钢管柱、RC88-S为新型复式钢管混凝土矮墩柱(简称新型矮墩柱)。为防止试验数据的离散型，对矩形墩柱和新型墩柱各制作2个试件。试件制作完成照片见图2，其中新型夹层复式钢管混凝土墩柱是指双圆钢管内不浇筑混凝土，仅在矩形钢管和圆钢管中间浇筑混凝土。钢材强度等级设计为Q345，混凝土强度等级设计为C60。试件底部垫板采用4 mm厚的Q345钢板，与内外钢管定位焊接并预留孔洞引出应变片数据线，现场浇筑混凝土采用分层灌入法，混凝土配合比见表2。试件养护方法为自然养护。

表  1  试件参数

Table  1.  Parameters of specimens

试件编号	矩形钢管截面D0×B0×t0/mm	圆钢管截面di×ti/mm	柱高度H/mm	简称
R-L	300×150×6	—	900	矩形墩柱
R-L1	300×150×6	—	900	矩形墩柱
RC88-L	300×150×6	88×4	900	新型墩柱
RC88-L1	300×150×6	88×4	900	新型墩柱
RC88-L(S-C)	300×150×6	88×4	900	夹层墩柱
RC88-L(N-C)	300×150×6	88×4	900	空钢管柱
RC88-S	300×150×6	88×4	450	新型矮墩柱

下载: 导出CSV 

| 显示表格

图  2  试件制作完成

Figure  2.  Specimens

下载: 全尺寸图片 幻灯片

表  2  C60混凝土配合比

Table  2.  C60 concrete mix proportion /(kg/m³)

设计强度	水	水泥	砂子	石子	水灰比	砂率/(%)
C60	205	500	538	1144	0.41	32.0

下载: 导出CSV 

| 显示表格

1.2   材性试验

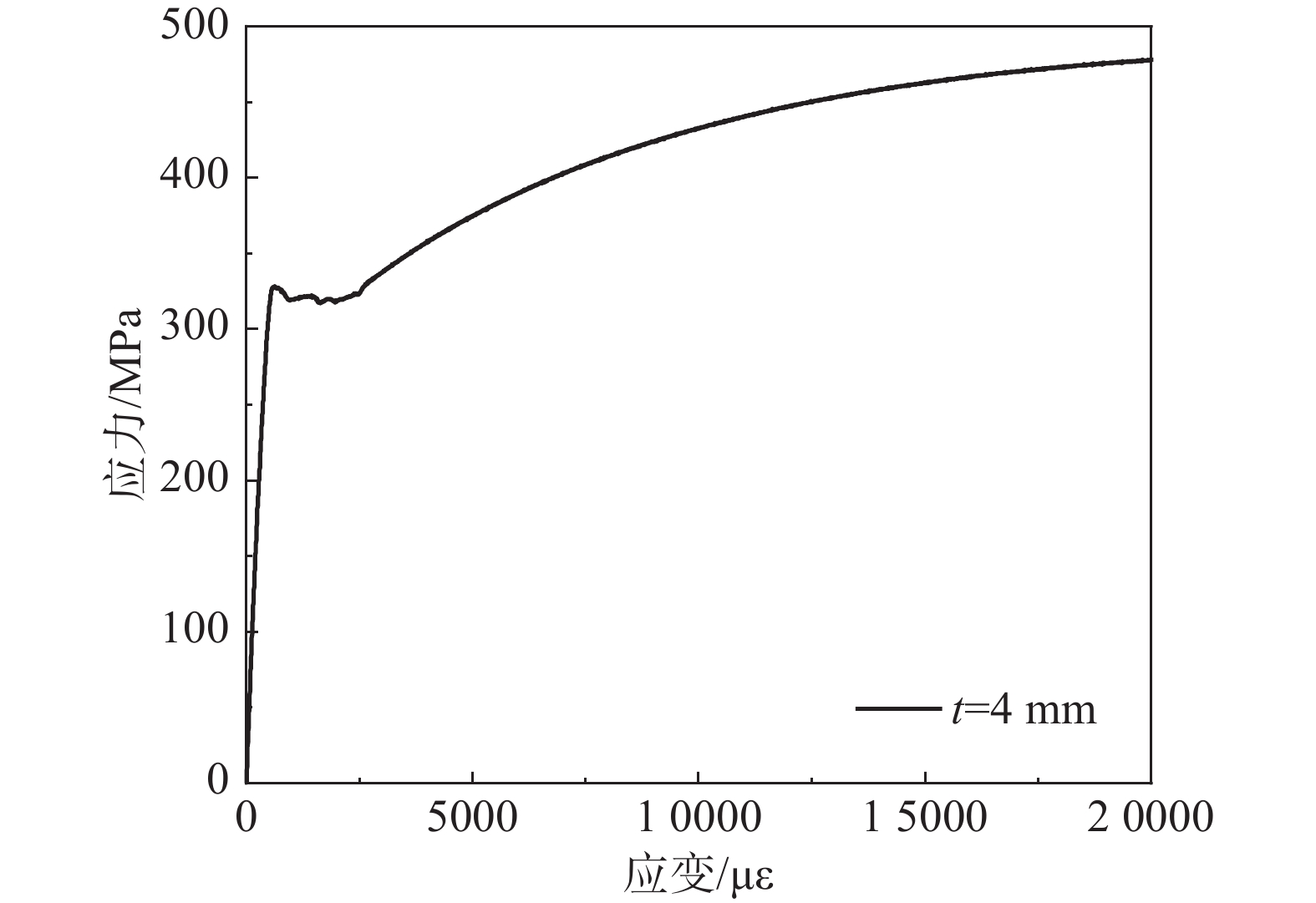
根据规范^[28-29]，分别对钢管和混凝土进行拉伸和抗压材性试验。钢管材性试验结果见表3，试验测得的Q345钢(内钢管)应力-应变曲线如图3所示。混凝土立方体抗压强度为59.1 MPa，弹性模量为35 971 GPa。

表  3  钢材材性试验实测值

Table  3.  Measured values of steel tubes

名义厚度 t/mm	实测厚度 t/mm	屈服强度 fy/MPa	抗拉强度 fu/MPa	屈服应变/ με	弹性模量 Es/GPa
6	6.08	312.8	444.9	1553	212
4	4.08	317.0	443.2	1637	210

下载: 导出CSV 

| 显示表格

图  3  Q345钢应力-应变曲线

Figure  3.  Stress-strain curve of Q345 steel

下载: 全尺寸图片 幻灯片

1.3   加载装置和量测方案

试验在结构试验室进行，采用5000 kN电液伺服压力试验机，加载装置见图4。全程采用位移控制加载，首先进行预加载，然后卸载。正式加载保持0.2 mm/min的速率，每加载1 mm停顿进行检查。当试件轴向位移较大或者试件出现明显变形后，停止加载^[15]。竖向位移由试验机和试件上端部一侧布置的竖向位移计共同测定。矩形钢管的横向位移计和应变片设置在距端板H/4和H/2处的长短边中间位置^[30]，并且在相同高度的矩形钢管长边同侧角部布置应变片；内圆钢管的应变片布置位置与矩形钢管长短边中间位置相同，具体布置如图5所示。位移计和应变片数据由DHDAS动态信号采集分析系统进行采集。

图  4  加载装置

Figure  4.  Loading device

下载: 全尺寸图片 幻灯片

图  5  位移计和应变片布置图

Figure  5.  Displacement meter and strain gauge layout

下载: 全尺寸图片 幻灯片

2   试验现象和破坏形态

2.1   试验现象

各墩柱轴压试验的破坏过程大致分为以下3个阶段。① 弹性阶段：随着荷载的增加，钢管横向、竖向应变片值上升较快，而横向位移计数值变化较慢，因为此时组合墩柱矩形钢管泊松比大于混凝土，二者处于单独工作状态^[1]，相互挤压作用很小。空钢管柱并未发生局部屈曲，横向变形较小。② 弹塑性阶段：承载力达到0.5N_u(N_u极限承载力)时，空钢管柱矩形钢管靠近垫板处出现起皮和掉渣现象，比组合墩柱较早发生。组合墩柱承载力达到0.7N_u~0.8N_u时，钢管横向应变增长幅度变大，矩形钢管靠近垫板处才有起皮和掉渣现象，此时组合墩柱还伴有混凝土的轻微开裂声。承载力达到0.9N_u左右时，除新型墩柱外其他墩柱在距垫板约H/4处矩形钢管长边出现轻微鼓曲，空钢管柱短边还出现轻微内凹。新型墩柱延缓了矩形钢管发生局部屈曲，在达到极限承载力时，矩形钢管长边才出现轻微鼓曲。③ 塑性破坏阶段：试件达到极限承载力后，荷载-位移曲线出现陡降，说明组合墩柱混凝土裂缝发展加剧；空钢管柱荷载-位移曲线并未出现陡降，可见钢管变形逐渐增大发生屈曲。荷载降至0.95N_u左右时，组合墩柱矩形钢管短边在与长边相同高度出现轻微鼓曲。随着位移不断增加，各试件矩形钢管长、短边鼓曲和内凹逐渐增大，混凝土被压碎。荷载降至0.85N_u时，新型墩柱内外钢管横向应变增长迅速，此时承载力开始出现缓慢回升。之后，各试件鼓曲和内凹现象逐渐加剧，甚至出现严重的褶皱破坏现象。新型墩柱由于内套双圆钢管，而矩形钢管长边中部对混凝土约束较差，导致两圆钢管之间混凝土出现平行于矩形长边方向产生受拉裂缝，见图6。所有试件最终破坏形态见图7。新型墩柱矩形钢管褶皱现象更为严重，由于内层混凝土受到内圆钢管及外部约束较强，承载力下降缓慢，试件发生较大轴向位移。而且后期承载力下降到0.85N_u时，新型墩柱的混凝土此时在内外钢管包裹下在保持强度的前提下，随着竖向位移增加横截面增大，荷载-位移曲线出现回升现象。

图  6  混凝土开裂

Figure  6.  Concrete cracking

下载: 全尺寸图片 幻灯片

图  7  各试件整体破坏图

Figure  7.  Overall failure diagram of each specimen

下载: 全尺寸图片 幻灯片

2.2   试件破坏形态

试件的破坏形态根据组合柱构造不同存在较大差异，破坏形态对比见图8，试件破坏与其他类型组合柱^{[3, 31]}相似基本发生在两端。对于空钢管柱由于没有混凝土的支撑，矩形钢管出现长边鼓曲和短边内凹型破坏，见图8(a)，其中内圆钢管因长径比较大整体发生微弯。矩形墩柱和夹层墩柱均是在距垫板约H/4处矩形钢管长、短边出现水平鼓曲，钢管屈曲范围较大且长边鼓曲严重，矩形墩柱和夹层墩柱破坏形态分别见图8(b)、图8(c)。其中夹层墩柱内圆钢管还发生了向内凹曲^[32]，说明没有内层混凝土，内圆钢管缺乏较强的稳定支撑。对于新型墩柱，矩形钢管同样发生了鼓曲严重的现象(图8(d))，内钢管在矩形钢管长边相同高度处也发生局部鼓曲(图8(e))。外层混凝土的破坏面与其他墩柱的混凝土明显不同，矩形墩柱和夹层墩柱混凝土受到的约束效果较均匀，破坏是主应力面先达到抗压强度，表现为混凝土全截面压溃；新型墩柱由于内圆钢管和内层混凝土的存在，外层混凝土受到内部的支撑约束强于外部的矩形钢管，使得外层混凝土压剪危险面先达到压剪强度，并沿压剪斜面产生了斜裂缝，又因矩形钢管长边约束小于短边小于角点，故由图8(d)可以看出，外层混凝土垂直长边方向发生了斜向滑移破坏，新型矮墩柱也出现了类似破坏现象。

图  8  破坏形态

Figure  8.  Failure modes

下载: 全尺寸图片 幻灯片

3   试验结果及其分析

3.1   荷载-位移曲线

试件轴向荷载-位移曲线如图9所示，两个矩形墩柱和两个新型墩柱荷载与变形发展过程基本相同，故仅选取试件R-L和RC88-L的试验数据。所有曲线在弹性阶段荷载与位移基本呈线性增加，在达到峰值荷载前荷载上升较快，进入下降段后荷载下降缓慢，而变形发展迅速。依据是否内置圆钢管、混凝土浇筑截面和试件高度进行分组分析：

1) 由图9(a)可见，新型墩柱和矩形墩柱相比，双圆钢管使截面含钢率提高5%，而新型墩柱初始刚度提高了18%，极限承载力提高了22%。可见，在不改变横截面面积的前提下，内置异心双圆钢管墩柱能显著提高轴压承载能力。新型墩柱的曲线下降段比矩形墩柱要平缓，后期承载力还有回升现象，剩余承载力高于85%极限承载力，表明内置异心双圆钢管后组合柱在发生较大变形后仍能承受较高的轴向压力。

2) 新型墩柱、夹层墩柱和空钢管柱的轴向荷载-位移曲线比较如图9(b)所示，三个试件的初始刚度相同，说明钢管内是否浇筑混凝土对试件的初始刚度影响不大，初始受力主要由内、外钢管承受。空钢管柱到夹层墩柱再到新型墩柱，混凝土浇筑面积占全截面比由0%、61%到84%，极限承载力提高了102%和144%，说明钢管内浇筑混凝土后组合柱承载力翻倍增加，且随着浇筑截面的增大，极限承载力也明显提升。比较图9(a)中新型墩柱和矩形墩柱两试件峰值荷载对应的位移基本相当，而空钢管柱、夹层墩柱和新型墩柱峰值荷载对应的位移逐渐增大，说明组合墩柱极限承载力主要由混凝土破坏决定，柱内约束混凝土达到极限状态时的应变量相当，约束的强弱最终体现在应力的提高上，故新型墩柱比矩形墩柱因混凝土体量相差很小峰值点位移相差不大，而极限承载力明显提高；对空钢管柱、夹层墩柱和新型墩柱因混凝土体量增加明显极限承载力明显增大，对应的峰值点位移也增大。

3) 不同高度新型墩柱的轴向荷载-位移曲线比较如图9(c)所示，矮墩柱高度减小1/2，但在与新型墩柱相同承载力点时的竖向位移比新型墩柱的1/2略小，说明因试件高度降低，受到加载两端摩擦、约束效应的影响增大，试件的轴压刚度也略增，极限承载力也提高了4%。新型墩柱试件在极限承载力后均出现较长的平缓下降段，后期破坏阶段还出现承载力二次上升现象，说明，在破坏阶段，新型墩柱在保证较大变形情况下仍具有较好的后期剩余承载能力。

图  9  荷载-位移曲线

Figure  9.  Load-displacement curves

下载: 全尺寸图片 幻灯片

3.2   试件延性

延性体现了结构的变形能力，会影响结构的安全性和耐久性。引入延性系数DI研究墩柱在轴压作用下的变形能力，计算如式1所示。其中${\varepsilon _{\text{u}}}$为极限承载力N_u时对应的应变，${\varepsilon _{85{\text{% }}}}$为下降到85%极限承载力时对应的应变，应变为试件的轴向压缩位移与试件变形后高度的比值^[33]。得到的延性系数见表4，表中Δ_u为极限承载力时对应的试件轴向压缩位移，Δ_85%为下降到85%极限承载力时对应的试件轴向压缩位移，h_u为极限承载力时对应的试件变形后高度，h_85%为下降到85%极限承载力时对应的试件变形后高度。

表4中空钢管柱延性系数较高，由于没有混凝土材料，钢管产生的竖向位移较大，发挥了纯钢材延性较好的特性。而新型墩柱的延性系数仅略小于空钢管柱，说明在双层钢管的约束下，混凝土这一脆性材料性质得到了明显改善，组合柱变形能力较强。由图9(b)看出，在荷载从峰值点降低15%后新型墩柱的轴向变形较空钢管柱要大很多，因空钢管柱发生的是失稳破坏，没有充分发挥钢管材料的强度，而新型墩柱中钢管和混凝土因组合协调工作充分利用了材料强度。新型墩柱的延性系数是矩形墩柱的2.8倍、夹层墩柱的2.5倍，说明新型墩柱发生较大变形后，内置圆钢管能够减缓内层混凝土的裂缝发展，反之内层混凝土也可以增大对内圆钢管的支撑，延缓内圆钢管屈曲。所以新型墩柱承载力降低较缓，而且保证了其后期剩余承载力，延性较好。因此，复式钢管混凝土墩柱可用于对延性性能要求较高的桥墩及大跨厂房结构中。

表  4  试件轴压承载力及延性系数

Table  4.  Axial compressive bearing capacity and ductility coefficient

试件编号	极限承载力 Nu/kN	0.85Nu/kN	试件轴向压缩 位移Δu/mm	试件变形后 高度hu/mm	试件轴向压缩 位移Δ85%/mm	试件变形后 高度h85%/mm	应变 εu/με	应变 ε85%/με	延性系数 DI
R-L(矩)	3328	2829	6.3	893.7	8.1	891.9	7049.4	9081.7	1.29
R-L1(矩)	3300	2805	6.2	893.8	7.9	892.1	6936.7	8855.5	1.28
RC88-L(新)	4075	3464	6.6	893.4	23.7	876.3	7387.5	27 045.5	3.66
RC88-L1(新)	4012	3410	6.4	893.6	22.8	877.2	7162.0	25 991.8	3.63
RC88-L (S-C)(夹)	3372	2866	3.9	896.1	5.7	894.3	4352.2	6373.7	1.46
RC88-L (N-C)(空)	1669	1419	2.3	897.7	8.5	891.5	2562.1	9534.5	3.72
RC88-S(矮)	4228	3594	3.5	446.5	12.2	437.8	7838.7	27 866.7	3.56

下载: 导出CSV 

| 显示表格

3.3   荷载-钢管应变曲线

钢管混凝土组合墩柱的优势在于钢管可以约束混凝土的横向变形，从而提高其竖向承载能力。为了解钢管对混凝土的约束作用，对轴向压力作用下钢管应变发展趋势进行分析。由于试件破坏集中在离端部H/4处，故取该处钢管的应变变化情况来分析，因矩形钢管长短边中部应变发展规律大致相同，故以长边为例，内圆钢管的应变位置取与矩形钢管同一高度同一侧。得到如图10所示的荷载-钢管应变曲线，竖向应变为负，横向应变为正，图中虚线为对应钢材的屈服应变(ε_yo、ε_yi分别为外、内钢管屈服应变)。新型墩柱、夹层墩柱、矩形墩柱和空钢管柱的荷载-外钢管应变曲线如图10(a)所示。新型墩柱、夹层墩柱和空钢管柱的荷载-内钢管应变曲线如图10(b)所示。所有曲线在弹性阶段呈线性增长，钢管屈服后应变增长加剧，破坏阶段因钢管发生屈曲，应变均达到了较大值，但本文忽略了应变值发生瞬间增值突变甚至应变片失灵后的数据。钢管应变发展规律及分析如下：

1) 空钢管柱内外钢管的荷载-应变曲线初始斜率均最小，说明无混凝土填充时钢管应变发展较快；在达到峰值荷载时钢管未屈服，说明因钢管壁薄，内外钢管均发生了失稳破坏，故试验中发生了外钢管鼓曲和内凹、内钢管微弯现象，且空钢管柱极限承载力较低。

2) 对于新型墩柱，承载力在0.76N_u左右时，外钢管竖向、内钢管横、竖向应变即达到屈服应变，而外钢管横向应变在承载力达到0.97N_u才达到屈服应变，说明矩形钢管尤其在长边中部对混凝土的横向约束发挥作用较晚。

3) 夹层墩柱在矩形钢管应变达到屈服值左右达到极限承载力，说明内外钢管中间填充混凝土后也能避免其发生局部屈曲；但内钢管横向应变较小未达到屈服，说明内圆钢管因整体支撑刚度大于外矩形钢管，混凝土横向变形主要往约束较小的外钢管发展，故内钢管在没有内层混凝土情况下发挥作用不如新型墩柱充分。

4) 新型墩柱和夹层墩柱在极限承载力时，内外钢管的竖向应变均达到了屈服应变，根据Q345钢应力-应变曲线(图3)，可知内外钢管在有混凝土支撑下均能保持其对竖向承载力的贡献。新型墩柱外钢管横向应变略大于夹层墩柱，但新型墩柱内钢管横向应变明显大于夹层墩柱，说明夹层墩柱仅外钢管发挥较好的约束夹层混凝土作用，内钢管材料强度没有得到充分发挥，因没有内层混凝土内钢管在夹层墩柱极限承载力时横向应力较小未达到屈服点。新型墩柱中混凝土面积比夹层墩柱增加36%，轴压承载力提高20%。

5) 新型墩柱和矩形墩柱的外钢管竖向应变发展大致相同，在极限荷载时矩形墩柱外钢管刚好屈服，而新型墩柱外钢管提前屈服，同理可认定外钢管在混凝土支撑下对组合柱的竖向承载力贡献相当；但外钢管横向应变发展新型墩柱明显大于矩形墩柱，说明新型墩柱中内混凝土在内双圆钢管包裹下，外钢管对外层混凝土约束作用也能得到充分发挥，所以新型墩柱承载力提高。此外，内钢管在混凝土的双侧约束挤压下，钢管横向应变在加载初期就发展较快，同时内钢管竖向和横向应变在新型墩柱未到达极限荷载前较早屈服，说明增加内钢管不仅体现在对轴向承载力的贡献，还包括对混凝土的约束作用增强，尤其在破坏阶段内钢管应变发展连续稳定，说明其仍能较好约束混凝土，故组合柱承载力下降缓慢且后期出现承载力回升。

图  10  荷载-钢管应变曲线

Figure  10.  Load-strain curves

下载: 全尺寸图片 幻灯片

4   新型墩柱轴压承载力提高分析

综上试验研究得出，钢管中填充混凝土后可以防止其发生失稳破坏，增大其竖向承载能力；而混凝土在钢管的约束下其截面应力得到显著提高，故组合柱的承载力实现“1+1>2”^[34-35]。下面就钢管和混凝土各自受力情况及承载力提高进行分析。

4.1   钢管承载力

钢管中填充混凝土后，混凝土会对钢管产生侧向支撑而延缓钢管屈曲变形，防止钢管的平面外失稳，从而达到提高其竖向承载力的作用^[36]。新型墩柱中圆钢管处于内、外层混凝土的双侧约束，能够保证钢管平面内的竖向承载能力，故按照屈服强度乘以截面面积来计算圆钢管承载力贡献，这一计算依据在复式钢管混凝土柱整体与各部分荷载分配^{[15, 37]}中已得到了验证。而矩形钢管仅处于外层混凝土的单侧约束，且矩形钢管宽厚比较大，不能完全保证钢板平面内的竖向承载能力，故引入钢板的正则化宽厚比^[38]来计算其在单侧约束下发生屈曲时的竖向应力，并根据矩形钢管长短边的受力差异，分别对长短边进行屈曲强度折减和应力有效宽度计算，从而得出矩形钢管在混凝土单侧约束情况下的承载力贡献。正则化宽厚比$\lambda$计算公式如式2所示，其中，b为钢板宽度，t为钢板厚度，$\nu$为钢材泊松比，${k_0}$为单侧约束板的弹性屈曲系数，取10.67^[39]。

计算得出本文矩形钢管长边钢板正则化宽厚比为0.619，短边钢板正则化宽厚比为0.309。正则化宽厚比公式根据钢材屈服强度和焊接残存应力的影响^[38]，得出钢板发生弹性屈曲和弹塑性屈曲的界限正则化宽厚比为1.348，故矩形钢管长边钢板发生弹塑性屈曲，即在应力超过钢材的比例极限后发生局部屈曲；钢板发生弹塑性屈曲和塑性屈曲的界限正则化宽厚比为0.500，故短边钢板发生塑性屈曲，即钢板达到屈服应力后发生屈曲。根据Mises屈服准则，单侧支撑的钢板受压发生屈曲时，纵向和横向应力可用图11表示。长边钢板发生弹塑性屈曲时，在钢板发生初始局部屈曲(A点)后，钢板对混凝土产生横向拉应力，钢板很快达到屈服(B点)，但是由于应力水平较低，纵向压应力增加较少，因此长边钢板屈曲应力取为钢材的比例极限；短边钢板发生塑性屈曲时，短边纵向应力在达到屈服应力之前不会发生局部屈曲，因此短边屈曲应力取为钢材的屈服强度，此时钢板不会产生横向应力。

图  11  钢板纵向、横向应力变化

Figure  11.  Vertical and transverse stress changes of steel plates

下载: 全尺寸图片 幻灯片

新型墩柱加载初期过后，矩形钢管会受到混凝土的挤压产生横向拉应力，从而降低了其竖向应力。根据矩形钢管长短边钢板受力不同，对长短边钢板竖向抗压强度进行不同系数折减。故引入长、短边宽厚比参数R:

式中，${f_{\text{y}}}$对于矩形钢管中长边钢板屈服应力取为钢材的比例极限(0.85${f_{\text{y}}}$)，短边钢板屈服应力取为屈服强度。当R>0.85时，钢板强度为：

其中，若f<0.89f_y，按式(4)进行计算，若f>0.89f_y，则直接取f=0.89f_y；当R<0.85，则钢板强度f=0.89f_y ^[40]。本文试验得出矩形钢管角部的竖向应力较大，说明其在角部约束支撑较好，而长边中间应力较小，为计算钢管屈曲后的竖向承载力，用钢板有效宽度来计算钢管屈曲后的等效应力分布范围。钢板在有效宽度范围内应力达到屈服应力，其余部分认为不承受压力，图12为矩形钢管长边有效宽度示意图。有效宽度b_e的计算公式^[41]见式(5)。因此，根据正则化宽厚比的计算值，可以得出本文矩形钢管长边有效宽度为264 mm，短边有效宽度为150 mm。综上计算过程，根据单侧支撑钢板受压后屈曲强度以及考虑其混凝土相互挤压的强度折减，得出矩形钢管提供的极限承载力为1251 kN，内圆钢管在混凝土双侧约束下极限承载力为669 kN，所以新型墩柱中内外钢管竖向承载力贡献应为1920 kN，与试验空钢管柱承载力(1669 kN)相比提高了15%，说明新型墩柱内外层混凝土的存在延缓了内、外钢管发生局部屈曲，钢管在受到混凝土支撑后提供的竖向承载力提高幅度较大。

图  12  长边钢板有效宽度

Figure  12.  Effective width of long side plate

下载: 全尺寸图片 幻灯片

4.2   混凝土抗压强度

极限状态时，钢管混凝土中混凝土处于三向受压受力状态，混凝土受到钢管侧压力可以约束混凝土的横向变形，减少混凝土内部裂缝的产生和发展从而提高抗压强度^[42]，新型墩柱外、内层混凝土受力图可以用图13表示。外层混凝土受到外钢管的侧向约束力，内层混凝土受到内外钢管及外层混凝土的包裹侧向约束力较强。为分析新型墩柱中混凝土提供的竖向承载力提高幅度，定义混凝土强度提高系数k，为构件中混凝土实际抗压强度和混凝土轴心抗压强度标准值${f_{{\text{ck}}}}$的比值。${f_{{\text{ck}}}} = 0.88{\alpha _{{\text{c}}1}}{\alpha _{{\text{c}}2}}{f_{{\text{cu}}}}$，其中${\alpha _{{\text{c}}1}}$为棱柱强度与立方体强度之比，${\alpha _{{\text{c2}}}}$为混凝土考虑脆性折减系数^[43]，试验混凝土按照线性差值计算，${\alpha _{{\text{c}}1}}$=0.78，${\alpha _{{\text{c2}}}}$=0.935，计算得出试验混凝土的${f_{{\text{ck}}}}$=37.9 MPa。夹层墩柱中内钢管侧向刚度较强，故其混凝土认定与新型墩柱中外层混凝土所受到的约束相同^[44]。因此，根据新型墩柱和夹层墩柱的截面形式，新型墩柱外层混凝土的计算抗压强度为夹层墩柱的试验承载力值减去4.1节中内外钢管承载力贡献值；内混凝土计算抗压强度为新型墩柱试验承载力减去夹层墩柱试验承载力。为方便和新型墩柱内外层混凝土对比，将矩形墩柱混凝土按照面积分配，计算出与新型墩柱相对应的内外层混凝土承载力贡献。计算结果如表5所示，其中N_co、N_ci为外、内层混凝土承载力贡献，f_co、f_ci为外、内层混凝土抗压强度，k_co、k_ci为外、内层混凝土抗压强度提高系数。

图  13  混凝土受力

Figure  13.  Confining concrete

下载: 全尺寸图片 幻灯片

表5得出混凝土在钢管的约束作用下抗压强度均有明显提高。新型墩柱的外层混凝土抗压强度提高系数为1.39，略大于矩形墩柱的外层混凝土抗压强度提高系数平均值1.37，但是其内层混凝土抗压强度提高系数平均值为1.93，内层混凝土的抗压强度提高系数平均值相较其外层混凝土提高39%，说明内层混凝土在内外钢管和外层混凝土的约束下，显著增大了其侧向约束，这也说明了圆钢管对混凝土的约束效果最好的特性^[15]。故综合起来看，新型墩柱混凝土受到的约束明显大于矩形墩柱混凝土，尤其内混凝土受到了较大的侧向约束力，从而明显提高试件的极限承载力。

表  5  承载力提高系数计算表

Table  5.  Calculation table of bearing capacity improvement coefficient

试件编号	外层 混凝土 承载力 贡献Nco/kN	内层 混凝土 承载力 贡献Nci/kN	钢管 承载力 贡献 Ns/kN	混凝土 截面 面积Ac/mm2	混凝土 轴心 强度抗压 标准值fck/MPa	外层 混凝土 抗压强度 fco/MPa	内层 混凝土 抗压强度 fci/MPa	不考虑 相互作用 的计算 承载力N0/kN	组合柱 承载力 试验值 Nu/kN	外层 混凝土 抗压强度 提高系数kco	内层 混凝土 抗压强度 提高系数kci	组合 柱承载 力提高 系数SI	复式 钢管混 凝土等效 套箍系数${\xi _{{\text{ssc}}}}$
R-L(矩)	1442	525	1145	39744	37.9	52.3	52.3	2651	3328	1.38	1.38	1.26	0.71
R-L1(矩)	1422	518	1145	39744	37.9	51.6	51.6	2651	3300	1.36	1.36	1.24	0.71
RC88-L(S-C)(夹)	1452	−	1669	27586	37.9	52.6	−	2715	3372	1.39	−	1.24	1.66
RC88-L(新)	1452	703	1669	37634	37.9	52.6	70.0	3095	4075	1.39	1.85	1.32	1.22
RC88-L1(新)	1452	640	1669	37634	37.9	52.6	63.7	3095	4012	1.39	1.68	1.30	1.22
RC88-S(矮)	1452	856	1669	37634	37.9	52.6	85.2	3095	4228	1.39	2.25	1.37	1.22

下载: 导出CSV 

| 显示表格

4.3   组合效应

引入承载力提高系数SI ^[45] 通过比较不考虑钢管和混凝土相互作用效应下的承载力情况，从而分析出二者的组合效应，如式(6)所示。其中，N₀为不考虑钢管及混凝土相互作用计算的承载力之和，如式(7)所示，式中N_s为组合柱中空钢管承担的轴压承载力，A_c为混凝土截面面积。对于矩形墩柱，空心的矩形钢管长边钢板竖向承载力根据文献[41]中宽厚比为50的钢板在无约束情况下屈曲后强度与屈服强度比为0.58，对于短边钢板宽厚比为25时屈曲后强度与屈服强度比约为1，故可以算出空心矩形钢管的竖向承载力为1145 kN。各组合墩柱的承载力提高系数为试验承载力N_u除以N₀后的比值，如表5所示，承载力提高系数均大于1，说明组合墩柱均发挥了钢、混凝土二者相互协调作用。新型墩柱的承载力提高系数平均值为1.31，夹层墩柱承载力提高系数为1.24，与矩形墩柱值相当。说明浇筑内混凝土后，受到钢管约束的混凝土面积增大，而且圆钢管可以充分发挥其对内层混凝土提供的均匀约束，由内钢管应变发展趋势也可以得出相同规律。所以，矩形钢管内套双圆的新型墩柱钢管和混凝土二者的相互作用发挥明显，组合效应较好。

组合墩柱中钢管和混凝土的相互作用也可以用套箍系数来表示，引入复式钢管混凝土等效套箍系数(${\xi _{{\text{ssc}}}}$)^[46]来分析组合效应与承载力提高系数之间的关系，计算式见式(8)，其中${A_{{\text{so}}}}$、${A_{{\text{si}}}}$为外、内钢管的面积，${f_{{\text{so}}}}$、${f_{{\text{si}}}}$为外、内钢管的屈服强度，${k_0}$、${k_{\text{i}}}$为矩形、圆钢管套箍约束效应系数。矩形钢管由于长宽比较大，其套箍约束效应系数较小，取相同面积方形截面套箍约束效应系数并用套箍影响系数$\theta$来折减，计算式见式(9)，${k_{\text{c}}}$为方形截面套箍约束效应系数，取k_c=0.73，k_i=1^[47-48]。计算组合墩柱的套箍系数见表5。

图14为等效套箍系数和承载力提高系数的关系图。由图可见，夹层墩柱因含钢率最大，计算的等效套箍系数也最大，但其承载力提高系数却和等效套箍系数最小的矩形墩柱相似。原因在于，如4.1节所述钢管在混凝土单侧支撑下竖向强度提高比率相同，而如4.2节所述混凝土承载力强度提高比率也相差不大，故组合柱整体的承载力提高也基本一致，说明夹层墩柱中内钢管主要是提供了竖向承载力贡献。实际上，内钢管对夹层混凝土套箍约束较弱使组合柱实际承载力提高较小，故钢管的套箍约束作用不明显，导致夹层墩柱承载力提高系数并不理想。而新型墩柱比矩形墩柱等效套箍系数提高较大，同时承载力提高系数也明显提高，原因在于，虽然钢管和外层混凝土强度提高相似，但是内层混凝土强度提高较大。综合来看，新型复式钢管混凝土墩柱真实的套箍作用较强，能够真正发挥混凝土和钢管之间的协同工作效应，达到节省材料、减少用钢量的有益效果。

图  14  承载力提高系数与等效套箍系数

Figure  14.  Bearing capacity improvement coefficient and confinement coefficient

下载: 全尺寸图片 幻灯片

钢管混凝土统一理论^[49]认为钢管和混凝土因它们之间的组合效应也可视为一种统一的组合材料，可用约束套箍系数来分析轴压承载力，计算公式如式(11)所示。计算出试件的承载力计算值(N_y)见表6所示，N_u为试验值。本文另选取了5个夹层墩柱^[50]进行承载力验算，其中后三个试件双内圆钢管间距不同。得出N_y/N_u的平均值为1.01，均方差为0.04，故钢管混凝土统一理论计算值和试验值结果吻合较好，验证了钢管混凝土统一理论公式在现有常规薄壁钢管混凝土柱的设计中均可取得较好的精度^[51]。采用等效套箍系数计算的新型墩柱承载力与试验误差在4%以内，平均绝对误差为3%，但本文数据中计算值略大于试验值，因为轴压试验中高的试件可能存在压弯破坏趋势或受压构件的初始缺陷影响较大而导致试验结果略低^[52]，而本文矮墩柱和引用夹层墩柱的承载力计算值和试验值结果吻合较好。所以，用等效套箍系数可以准确地计算出钢管和混凝土在组合效应作用下的新型复式钢管混凝土墩柱强度，这种内套异心双圆钢管的新型复式钢管混凝土结构也符合钢管混凝土统一理论，为后续组合柱性能研究提供了一个简单且实用的承载力计算方法。

式中：A为构件截面面积；a、b分别为钢管和混凝土所起的作用，计算式如下：

式中，$f_{{\text{ss}}}^{\rm y}$为复式钢管混凝土内外钢管屈服强度加权平均值，即：

表  6  复式钢管混凝土轴压承载力及理论计算结果

Table  6.  Axial compression bearing capacity and theoretical calculation results of composite concrete filled steel tube

试验构件	矩形钢管 截面尺寸 D0×B0×t0/mm	内圆钢管 截面尺寸 di×ti/mm	试件高度 H/mm	外钢管屈服 强度fso/MPa	内钢管屈服 强度fsi/MPa	混凝土立方体 抗压强度 fcu/MPa	复式钢管 混凝土等效 套箍系数${\xi _{ {\text{ssc} }} }$	试件承载力 试验值 Nu/kN	试件承载力 计算值 Ny/kN	计算值/ 试验值 Ny/Nu	文献
R-L	300×150×6.00	−	900	312.8	−	59.1	0.71	3328	3387	1.02	本文
R-L1	300×150×6.00	−	900	312.8	−	59.1	0.71	3300	3387	1.03
RC88-L(S-C)	300×150×6.00	88×4.00	900	312.8	317.0	59.1	1.66	3372	3645	1.08
RC88-L	300×150×6.00	88×4.00	900	312.8	317.0	59.1	1.22	4075	4161	1.02
RC88-L1	300×150×6.00	88×4.00	900	312.8	317.0	59.1	1.22	4012	4161	1.04
RC88-S	300×150×6.00	88×4.00	450	312.8	317.0	59.1	1.22	4228	4161	0.98
C0.48-30	300×150×5.65	48×3.55	600	346.5	265.2	61.3	0.92	3910	3792	0.97	[52]
C0.48-38	300×150×5.65	60×3.55	600	346.5	329.8	61.3	1.09	4065	3894	0.96
C0.48-48	300×150×5.65	76×3.54	600	346.5	293.6	61.3	1.25	3600	3781	1.05
C0.40-48	300×150×5.65	76×3.54	600	346.5	293.6	61.3	1.25	4010	3781	0.94
C0.35-48	300×150×5.65	76×3.54	600	346.5	293.6	61.3	1.25	3886	3781	0.97

下载: 导出CSV 

| 显示表格

5   结论

对7个组合墩柱进行了轴压试验，通过对比矩形墩柱、夹层墩柱和空钢管柱，分析了新型复式钢管混凝土墩柱的破坏形态、钢管应变、延性和钢-混组合效应，得到以下结论：

(1) 新型复式钢管混凝土墩柱轴压破坏形态为鼓曲型破坏，内置异心双圆钢管能够显著提高墩柱极限承载力，延缓荷载下降速率，在破坏阶段新型墩柱在保证较大变形情况下后期剩余承载力大于85%的极限承载力。

(2) 新型墩柱极限承载力较夹层墩柱提高20%，较矩形墩柱轴压承载力提高22%；新型墩柱延性是夹层墩柱的2.5倍，是矩形墩柱的2.8倍；在达到极限承载力时，内外钢管应变均超过其屈服应变，尤其内钢管在混凝土双侧约束情况下，较早达到屈服应变，说明新型墩柱可以充分发挥钢管竖向承载和横向约束混凝土的能力。

(3) 在钢管和混凝土在组合效应作用下，内、外钢管承载力提高15%，混凝土承载力提高49%，新型墩柱整体承载力比不考虑组合效应时提高31%，承载力提高系数较大，说明新型墩柱的组合效应最好；采用等效套箍系数计算的新型墩柱承载力与试验值平均绝对误差为3%，说明新型复式钢管混凝土墩柱也可视为一种组合材料，符合钢管混凝土统一理论。本文研究成果可促进钢管混凝土组合结构新的应用和发展。