下肢动脉支架在植入血管后受到肢体体位的影响，会发生轴向拉伸、压缩、弯曲、扭转以及多种组合的复杂变形，当支架无法承受外载荷产生过大的变形时，可能会导致断裂失效，甚至引起支架内再狭窄和炎症等并发症，因此研究多级载荷下的疲劳强度具有重要的临床意义。

目前国内外学者针对血管支架在不同载荷下的疲劳性能做了一些研究。QIU等^[1]通过试验方法对镍钛合金支架在单轴拉伸和扭转载荷下的疲劳性能进行研究，发现单轴拉伸比扭转对疲劳性能的影响更显著。CARVALHO等^[2]设计了一种可以调节角度的旋转弯曲试验机，通过试验和有限元法对镍钛合金圆管的弯曲力学性能进行研究，得到有限元分析的最大应力应变位置与实验结果一致的结论。EARLY等^[3]基于GOODMAN曲线分析支架在轴向弯曲和压缩载荷下的疲劳性能，揭示了弯曲和压缩载荷对支架断裂失效的影响规律。MEOLI等^[4]分析两款不同长度的镍钛合金支架在完全扩张状态下分别承受周期性轴向压缩和弯曲载荷，发现了支架长度对其安全性具有显著影响。LONG等^[5]对自膨胀支架在治疗腘动脉时考虑生理脉动载荷和动脉粥样硬化斑块影响，基于支架上各个节点的平均应变和交变应变分析了疲劳性能，揭示了这两个因素对支架疲劳寿命的影响规律。DORDONI等^[6]探究周期性轴向压缩和弯曲载荷对支架疲劳性能的影响，发现了压缩比弯曲载荷更容易产生疲劳断裂的现象。徐江等^[7]对支架承受脉动载荷和血管弯曲变形下进行疲劳性能研究，发现支架在血管弯曲变形时更容易发生断裂失效。胡章頔等^[8]模拟W 型和 V 型支架在血管内服役随血管脉动载荷的过程，采用疲劳极限理论对两种支架的疲劳寿命进行预测，得出W型支架的疲劳寿命优于 V 型支架的结论。

一些临床研究^[9]表明，自膨胀支架可提高下肢动脉病变治疗的有效性，但下肢动脉支架植入术的疗效仍然受到支架内再狭窄相关临床并发症的影响，这些并发症是支架植入术的主要临床问题，2年内再狭窄率高达46%^[10-11]。而以上绝大多数研究只考虑了支架在单一载荷变形下的疲劳性能，对于复杂载荷是否影响支架的疲劳强度和寿命预测鲜有研究。因此考虑支架植入血管后可能会受到多级载荷的影响，本文对支架在一级载荷(生理脉动循环、轴向拉伸、压缩、弯曲、扭转)、二级载荷(拉-弯、拉-扭、压-弯、压-扭、弯-扭)和三级载荷(拉-弯-扭、压-弯-扭)分别进行疲劳强度和寿命预测的研究，揭示多级载荷对支架疲劳失效的影响规律。

1   材料和方法

1.1   材料模型

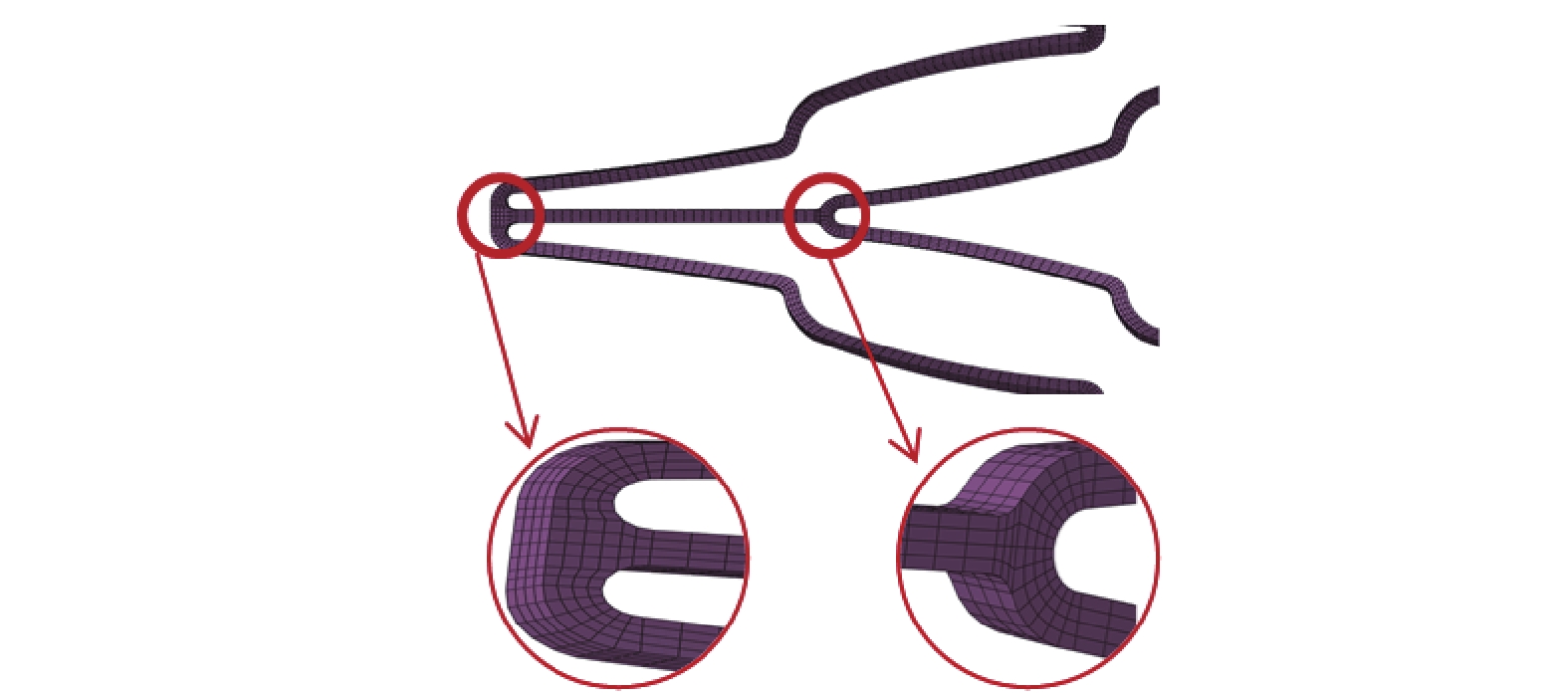
支架模型参考Absolute Pro(Abbott Vascular，美国)支架。采用三维软件SolidWorks建立支架模型，如图1所示。支架的最大外径均为6 mm，长度为30 mm，其他尺寸为实际测量所得。Absolute Pro支架结构是由单圆弧支撑筋与双圆弧支撑筋轴向交替排列，轴向双圆弧支撑筋和单圆弧由连接筋连接，两端呈花冠状。支架材料为镍钛合金，镍钛合金是一种超弹性的记忆合金材料，采用有限元软件内嵌的Ogden本构模型，通过实际测量镍钛合金单轴拉伸卸载得到的应力-应变曲线^[12]。弹性模量E = 80 GPa，泊松比0.33，抗拉强度1290 MPa，屈服强度390 MPa^[13]。简化血管模型为圆筒形^[14]，直径5.4 mm，壁厚0.1 mm，长为20 mm，弹性模量为1.75 MPa，泊松比为0.495，压握壳弹性模量为300 MPa，泊松比为0.495^[15]。

图  1  支架模型

Figure  1.  Model of stent

下载: 全尺寸图片 幻灯片

1.2   网格划分

有限元分析中网格的质量会影响计算精度、效率及可行性。网格尺寸过大影响仿真结果的准确性，网格过小使仿真时间变长，因此要保证网格尺寸的合理性。

应用Hypermesh软件对血管和支架进行六面体网格划分，确保网格质量雅克比在0.7以上，通过网格灵敏性分析发现，支架厚度设置4×4单元，对结果分析的准确性和计算时间最合适，与于文博等^[16]分析的结果一致，支架和血管均设置单元类型是线性减缩积分单元C3D8R，节点数为402 809和16 200。支架圆弧进行加密处理，如图2所示。压握壳设置为四节点曲面薄壳缩减积分单元S4R，采用增强型沙漏抑制算法控制沙漏的传播来保证合理的计算精度^[17-18]。

图  2  支架局部网格区域

Figure  2.  Stent local mesh area

下载: 全尺寸图片 幻灯片

1.3   边界条件

根据真实情况将支架的植入下肢动脉过程简化为压握和释放两个过程。在压握阶段，约束支架一端的周向和轴向自由度，另一端约束支架的周向自由度，支架和压握壳之间采用通用接触，压握壳的表面施加径向均匀位移载荷，将支架压握到2 mm，支架植入血管图如图3所示；在释放阶段，支架外表面和血管内表面同样采用通用接触，约束血管两端的周向和轴向自由度，支架的约束条件不变，撤去压握壳的位移约束，支架发生自膨胀扩张到直径为5.4 mm的血管模型中，于支架内表面施加压强模拟生理脉动循环载荷^[19]，根据正常人的下肢动脉血压情况，舒张压是8.8 kPa，收缩压17.1 kPa。

图  3  支架植入图

Figure  3.  Stent implantation diagram

下载: 全尺寸图片 幻灯片

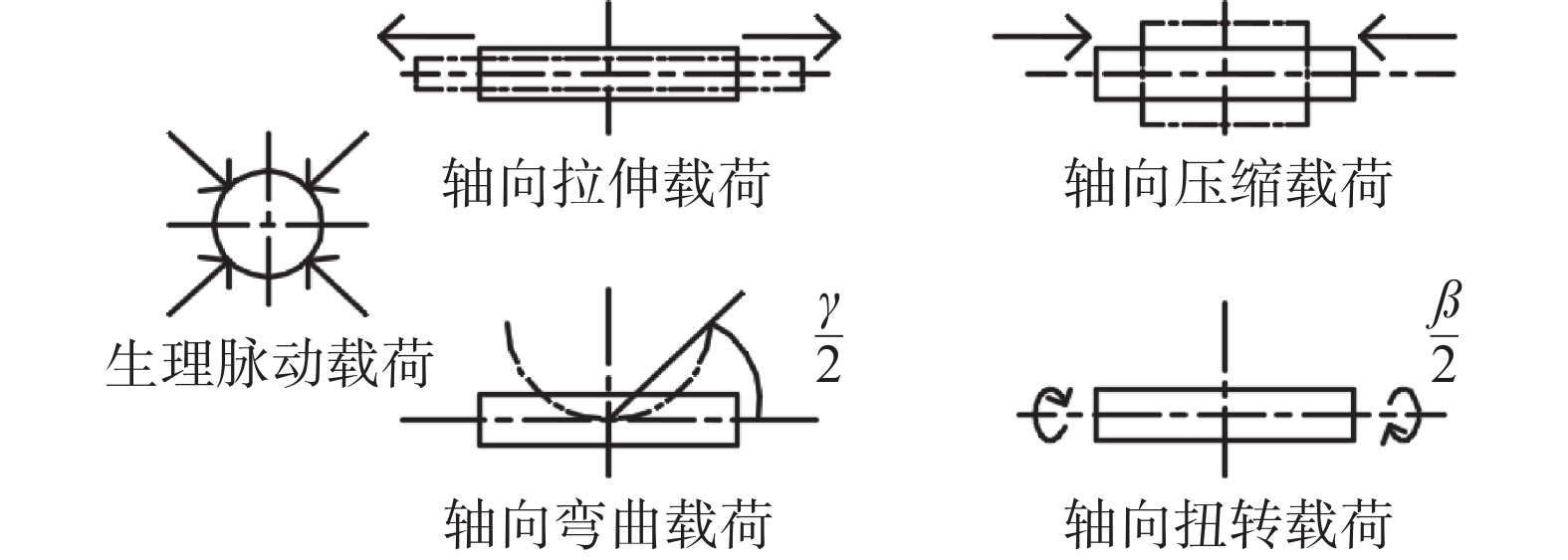
本文研究的一级载荷包括上述生理脉动载荷及支架植入下肢动脉后会受到轴向拉伸(5 mm)、压缩(5 mm)^[20]、弯曲(γ = 120°)^[21]和扭转(β = 90°)^[22]载荷的作用，选取支架拉伸、压缩、弯曲和扭转规整的极限值进行研究，更有利于分析支架疲劳失效原因，除脉动载荷外，本文不考虑血管对支架的影响。载荷示意图如图4所示，将支架两端的表面耦合在其中心点上，对两端中心点施加均匀载荷(所对应轴向载荷的1/2)，约束支架两端的所有旋转自由度以及周向自由度；二级载荷包括拉-弯、拉-扭、压-弯、压-扭、弯-扭，通过两种载荷耦合的形式施加，如弯-扭载荷是同时施加扭转和弯曲载荷，并约束支架两端的旋转自由度；三级载荷包括拉-弯-扭和压-弯-扭，其加载方式与二级载荷相似，但是只施加对应载荷值，不对支架两端中心点的自由度进行约束，防止影响支架的自由变形，并同时在每种变形前施加一个周期的生理脉动循环载荷，脉动载荷加载的幅值曲线是周期性正弦曲线，幅值为1，其余多级载荷为线性过渡幅值曲线，初始为(0, 0)，结束值为(1, 1)。

图  4  支架加载示意图

Figure  4.  Stents loading diagram

下载: 全尺寸图片 幻灯片

1.4   分析方法

1.4.1   疲劳性能

美国食品和药物管理局(FDA)和欧盟规定^[23]，血管支架应该能承受至少4亿次的脉动循环载荷，即满足10年以上的疲劳寿命要求。目前血管内支架的疲劳检测有两种方式：一是应变检测疲劳；二是应力检测疲劳。对于医用镍钛合金自膨胀支架而言，镍钛合金支架植入后一般受到两种形变：一种是因尺寸过大受到血管壁的约束限制，从而保持恒定的平均应变；另一种是由于肌肉的收缩和扩张引起的支架直径较大的脉动变化，因此支架的疲劳行为属于应变检测疲劳^[24-25]。PELTON 等^[25]通过对镍钛合金的实验得出，当支架的平均应变小于2% 时，其疲劳极限一般为 0.4%，若测试值小于疲劳极限值，则证明支架是安全的，反之，则会增加断裂失效的风险。当平均应变超出 2% 后，由于镍钛合金受应力诱发相变，使得支架疲劳极限会增大，但本文因支架的平均应变未超出2%，所以暂不考虑平均应变大于2%的疲劳极限。利用有限元方法模拟得出支架服役过程中受到周期性载荷下产生的应变幅值ε^α和平均应变值ε^m，如式(1)和式(2)所示^[25]。

式中：ε^m为平均应变；$\varepsilon_{ij}^{\text{L}}$为支架上各节点的最大应变量；ε^α为交变应变；$\varepsilon_{ij}^{\text{U}}$为支架上各节点的最小应变量。

1.4.2   名义应力法预测疲劳寿命

血管支架在长期循环脉动工作时间大于10⁷，名义应力法是以S-N寿命曲线为依据计算结构的高周疲劳常用方法^[26]，因此本文通过名义应力法预测支架的全寿命。

联合ABAQUS和FESAFE进行寿命计算。由于支架是多个载荷受力方向同时作用，裂纹产生的位置与其所受的应力方向的剪切力和正应力有关，因此在进行FESAFE进行计算时选择“stress based on Brown-Miller”算法，主要原理是“Brown-Miller”算法^[27]：即90°的平面可以在0°~180°变化，采用10°的增量进行寿命计算，其误差相比1°增量小2%，并循环计算平面上的剪切(法向)应变历程，理论公式如式(3)所示：

式中：γ_max为最大剪切应变；ε_n为法向正应变；${\sigma }_{\rm f}'$为疲劳强度系数；b为疲劳强度指数；$\varepsilon _{\rm f}'$为疲劳延展系数；c为疲劳延展指数。

1.4.3   基于断裂力学疲劳寿命预测

从断裂力学的角度来看，表面疲劳破坏通常经历裂纹萌生、裂纹稳定扩展和裂纹失稳扩展三个阶段，本文主要研究初始裂纹在扩展阶段的寿命。考虑到支架预先存在裂纹缺陷(激光制造或者过度扩张时产生的裂纹)对其疲劳寿命的影响，利用线弹性断裂力学对有缺陷的支架进行寿命预测。初始裂纹在疲劳载荷作用下，低于材料断裂韧性的应力强度会出现裂纹扩展。这种现象用裂纹尖端小范围屈服条件下的Paris公式 ^[28]预测寿命。具体表达公式如式(4)所示：

式中：ΔK为应力强度因子幅值 ； a为裂纹长度；N为循环次数；C和m为材料参数。

式中：f为受力载荷决定的形状系数；a_c为裂纹断裂临界尺寸；K_IC为断裂韧性准则的临界条件。

根据式(5)、式(6)代入式(4)即可得出式(7)：

在外界因素作用下，血管支架上不可避免地会产生裂纹缺陷，这无疑增加了疲劳失效甚至断裂的风险，而传统的名义应力寿命很难评估裂纹缺陷产生的影响，断裂力学方法可以有效地量化缺陷对支架的安全可靠性。依据MARREY等^[29]在血管支架加工制造中过度扩张导致裂纹缺陷，选取初始裂纹极限值为13 μm和46 μm。根据ROBERTSON等^[30]对超弹性镍钛合金材料进行的裂纹扩展实验分析结果，得到裂纹扩展参数为：C=2.96×10⁻¹⁰(m/cycle/(${\rm{MPa}}\cdot \sqrt {\rm m}$)^m，m=3.43，K_IC=34 MPa∙$\sqrt{\rm m}$。裂纹尖端形状因子根据 《应力强度因子手册》^[31]得到f值，将这些参数代入式(7)预测其寿命。

2   结果与分析

2.1   多级载荷下的疲劳强度

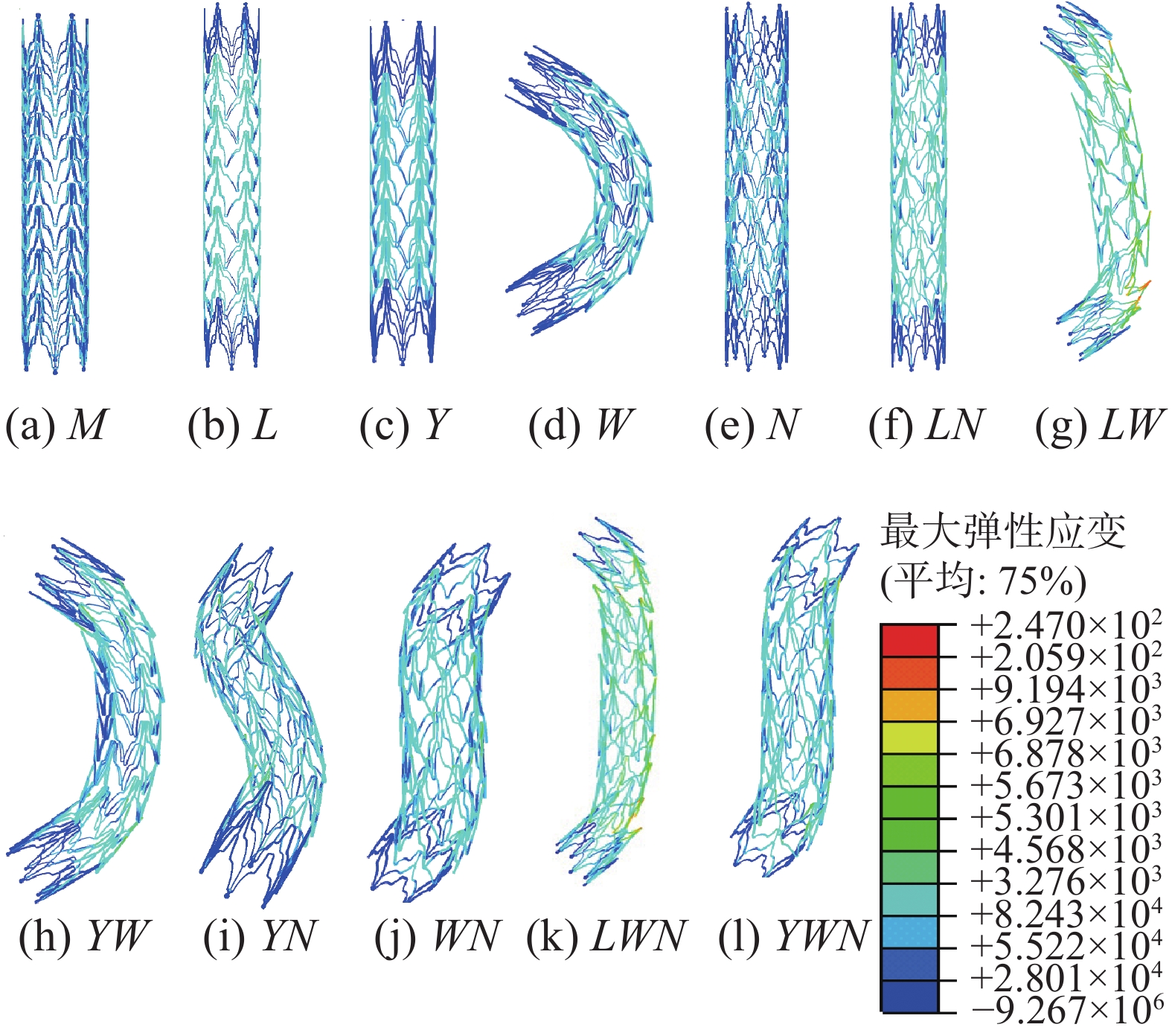
图5表示Absolute Pro支架承受多级载荷下的疲劳极限图。M、L、Y、W、N分别表示生理脉动、轴向拉伸、压缩、弯曲和扭转载荷，LW表示拉-弯载荷，以此类推。在一级载荷下，支架的交变应变均位于疲劳极限下方，其疲劳强度均满足美国FDA血管支架10年疲劳寿命要求；二级和三级载荷下，拉-弯和拉-弯-扭载荷作用时支架部分单元的交变应变处于疲劳极限上方，这些危险点位于支架弯曲变形的圆弧部位，易产生应力集中导致断裂失效，这是由于支架承受载荷时支撑筋发生过大的弯曲变形导致；其余多级载荷下应变分布比较均匀，不会对支架的疲劳强度造成影响。

图  5  Absolute Pro支架在多级载荷下的疲劳极限图

Figure  5.  Fatigue strength diagram of the Absolute Pro stents under multi-level loads

下载: 全尺寸图片 幻灯片

图6是Absolute Pro支架在多级载荷下的弹性应变分布云图。结果显示，支架在承受一级载荷时，支架的应变主要集中在中央部位；在拉伸和压缩载荷作用下支撑筋结构(阶梯型)不稳定，易产生变形导致应变比较集中；在弯曲变形中，支架的双圆弧支撑筋端部翘起产生夹角，易对血管壁造成损伤；在扭转变形中，轴向排列的双圆弧支撑筋随着扭转角的改变，沿轴线形成螺旋线状。

支架在承受二级载荷时，应变集中分布在支架变形处。拉-弯载荷下，支架呈现“月牙”形状，应变主要分布在支架两端，支撑筋链接处翘起较明显；拉-扭载荷下，支架整体呈细长直线型，应变集中分布在支架中央段；压-弯载荷下支架整体的弯曲角度介于拉-弯和弯曲载荷之间；压-扭载荷下，整体呈“S”形；弯-扭载荷下，支架整体呈现佝偻型的 “S”形，弯曲段应变较大。

图  6  支架多级载荷下的弹性应变分布云图

Figure  6.  Elastic strain distribution cloud diagram of the Absolute Pro stents under multi-level loads

下载: 全尺寸图片 幻灯片

支架承受三级载荷时。压-弯-扭载荷下，整体呈幅度较小的“S”形，拉-弯-扭载荷下，整体呈弯曲幅度较小的“月牙”形状，三级载荷变形程度小于二级和一级载荷的变形，但两端连接筋翘起的角度相对较大，易对血管壁产生损伤。

2.2   多级载荷下的寿命预测

图7是支架在多级载荷下的寿命分布云图。一级载荷下，支架在脉动载荷的寿命最长，为8.4×10¹⁰(840亿次)，在压缩载荷作用下的寿命最短，为8.9×10⁸(8.9亿次)，Absolute Pro支架的疲劳寿命影响从大到小依次是压缩>拉伸>弯曲>扭转>脉动，可以看出，在一级载荷其余载荷对支架疲劳寿命影响均大于脉动载荷。FROTSCHER等^[32]通过微型试验台对镍钛合金支架在拉伸载荷下进行试验，发现在支架连接筋圆弧处出现断裂，这与等仿真结果分析的结果一致。

图  7  Absolute Pro支架多级载荷下的寿命分布云图

Figure  7.  Fatigue life distribution diagram of the Absolute Pro stents under multi-level loads

下载: 全尺寸图片 幻灯片

二级载荷下，支架在弯-扭载荷下的寿命最长，为7.4×10⁸(7.4亿次)，在拉-弯载荷下的寿命最短，为2.5×10⁷(0.2亿次)，说明在二级载荷中拉-弯载荷对支架疲劳寿命影响最大，弯-扭载荷影响最小。二级载荷对支架疲劳寿命影响从大到小依次是拉-弯>压-弯>压-扭>拉-扭>弯-扭，在一级载荷中，对支架的疲劳寿命影响最大是压缩载荷，而二级载荷中拉-弯载荷相比压-弯载荷较大，从力学角度分析，拉-弯载荷在支架两端施加的外力方向相同，导致支架弯曲部分的变形出现翘起现象；而压-弯载荷外力方向相反，一部分作用力相互抵消，因此拉-弯载荷对支架疲劳寿命影响最大，对于Absolute Pro支架，弯-扭载荷下的变形行为明显比拉-扭更加复杂，然而后者对疲劳失效的影响更显著，这是因为该支架结构在一级载荷中弯曲和扭转载荷对支架的影响较小。

三级载荷中，拉-弯-扭载荷对支架的疲劳寿命影响最显著，为8.3×10⁶，在压-弯-扭载荷作用下，支架折弯部处(双圆弧连接筋附近)的寿命最短，为9.5×10⁷。压-弯-扭对支架的疲劳寿命影响低于拉-弯和拉-弯-扭载荷，因此，得出在Absolute Pro支架中与拉伸和弯曲耦合下的外力对疲劳失效的影响最显著。

从图7可以看出，在脉动载荷下在圆弧内侧容易发生疲劳失效，其余多级载荷最危险位置位于连接筋圆弧区域，易产生应力集中，而容易发生疲劳失效的位置经过外力的持续作用及损伤的累积，是造成寿命较低的主要原因。支架在多级载荷作用下寿命差异较大，说明外载荷的性质对支架寿命有显著影响。

图8是支架在多级载荷下的安全系数。结果显示，在一级载荷下支架安全系数均大于1，表明在一级载荷下支架的结构是安全的，支架在一级载荷作用下的安全系数大小依次为：生理脉动>扭转>弯曲>拉伸>压缩载荷；在二级载荷下，只有在弯-扭载荷作用下支架的安全系数大于1，其安全系数大小依次为：弯-扭>拉-扭>压-扭>压-弯>拉-弯载荷；支架在拉-弯-扭载荷作用下的安全系数小于压-弯-扭，且都小于1，说明三级载荷对支架疲劳强度的安全性影响最显著。

图  8  支架在多级载荷下的安全系数

Figure  8.  Safety factor of stent under multi-level loads

下载: 全尺寸图片 幻灯片

2.3   基于断裂力学的寿命预测

多级载荷的断裂力学寿命结果如图9所示，柱状图的寿命值遵从左边纵轴数据，点线图的寿命值遵从右边纵轴数据。采用名义应力法与断裂力学方法预测支架的寿命时，前者结果相对要大，主要是断裂力学方法考虑了初始裂纹的存在，故采用名义应力方法评估其寿命相对保守。利用上述两种方法预测了支架在一级和二级载荷下的寿命，发现变化规律一致，在一级载荷作用下，压缩载荷对支架在裂纹扩展下的寿命影响最大，在二级载荷作用下，拉-弯载荷对支架在裂纹扩展下的寿命影响最大。

图  9  支架在多级载荷下的断裂力学寿命值

Figure  9.  Fracture mechanical life of stent under multi-level loads

下载: 全尺寸图片 幻灯片

3   结论

针对镍钛合金支架植入下肢动脉后可能产生疲劳失效问题，利用数值模拟分析支架在多级载荷下的疲劳性能，并对支架的疲劳寿命进行预测，得到结论如下：

(1) 经疲劳强度分析结果表明，支架的疲劳强度与外载荷的性质有关。支架承受一级载荷时最大交变应变均小于疲劳极限，满足10年疲劳寿命要求；支架承受二/三级载荷时，拉-弯和拉-弯-扭载荷下的最大交变应变超出疲劳极限，不满足疲劳寿命要求，其它载荷下均满足要求，其中受拉-弯和拉-弯-扭多级载荷对支架的疲劳强度有显著的影响。

(2) 对支架寿命预测发现，支架变形时圆弧连接筋和圆弧内侧附近更容易产生应力集中，从而导致疲劳失效。在一级载荷下，压缩载荷对支架的寿命影响最大，脉动载荷影响最小；在二级载荷下，拉-弯载荷对支架的寿命影响最大，拉-扭载荷影响最小；在三级载荷中，拉-弯-扭对支架寿命的影响大于压-弯-扭载荷。

(3) 基于断裂力学研究发现初始裂纹是造成支架发生疲劳失效的主要原因，尤其支架产生初始裂纹时，压缩和拉-弯载荷对支架的疲劳寿命影响较大，因此在支架的使用和制造过程中减少裂纹的发生和明确载荷的性质尤为重要。