PVC-FRP管混凝土是一种新型组合结构，它是在预制的PVC-FRP管内配筋、浇筑混凝土所形成的组合结构，具有承载力高、耐久性好、施工方便等优点^[1-2]。目前，这种新型组合结构已取得较多有价值的研究成果，主要集中在PVC-FRP管混凝土构件的静力性能^[3-4]、抗震性能^[5-6]、抗弯性能^[7]、耐久性能^[8-9]等方面，这些研究成果对于促进PVC-FRP管混凝土向结构体系方向发展奠定良好的基础。

作为结构的薄弱环节，节点的研究比一般结构更具有意义。在地震作用下，节点同时承受弯矩、剪力和轴压力的共同作用，其受力性能直接影响到框架结构整体的抗震性能。目前，国内外对钢筋混凝土节点、钢管混凝土节点开展深入系统的研究，取得丰硕的研究成果^[10-20]。这些已有研究成果为PVC-FRP管混凝土结构节点的研究提供有益参考。

为促进PVC-FRP管混凝土从构件层次向结构体系方向发展，本课题组系统开展PVC-FRP管混凝土柱与钢筋混凝土梁节点连接方式^[21]，节点静力性能^[22-23]等方面研究，提出环梁连接、钢筋网片连接和芯钢管连接等三种节点连接方式，验证节点连接方式可行性，建立了轴向荷载作用下节点的相关计算理论。但对于PVC-FRP管混凝土柱-钢筋混凝土梁节点的抗震性能还未开展相关研究。

因此，为深入研究PVC-FRP管钢筋混凝土柱-钢筋混凝土梁节点抗震性能，探究其破坏机理，本文开展11根PVC-CFRP管钢筋混凝土柱-钢筋混凝土环梁T型节点低周反复荷载试验，分析环梁配筋率、CFRP条带间距、环梁宽度、轴压比和梁纵筋配筋率等因素对其破坏形态、滞回性能和骨架曲线的影响，提出环梁节点骨架曲线各特征点计算方法，确定其滞回规则，建立弯矩-曲率恢复力模型。研究成果为PVC-CFRP管混凝土结构设计和工程应用提供科学依据。

1   试验概况

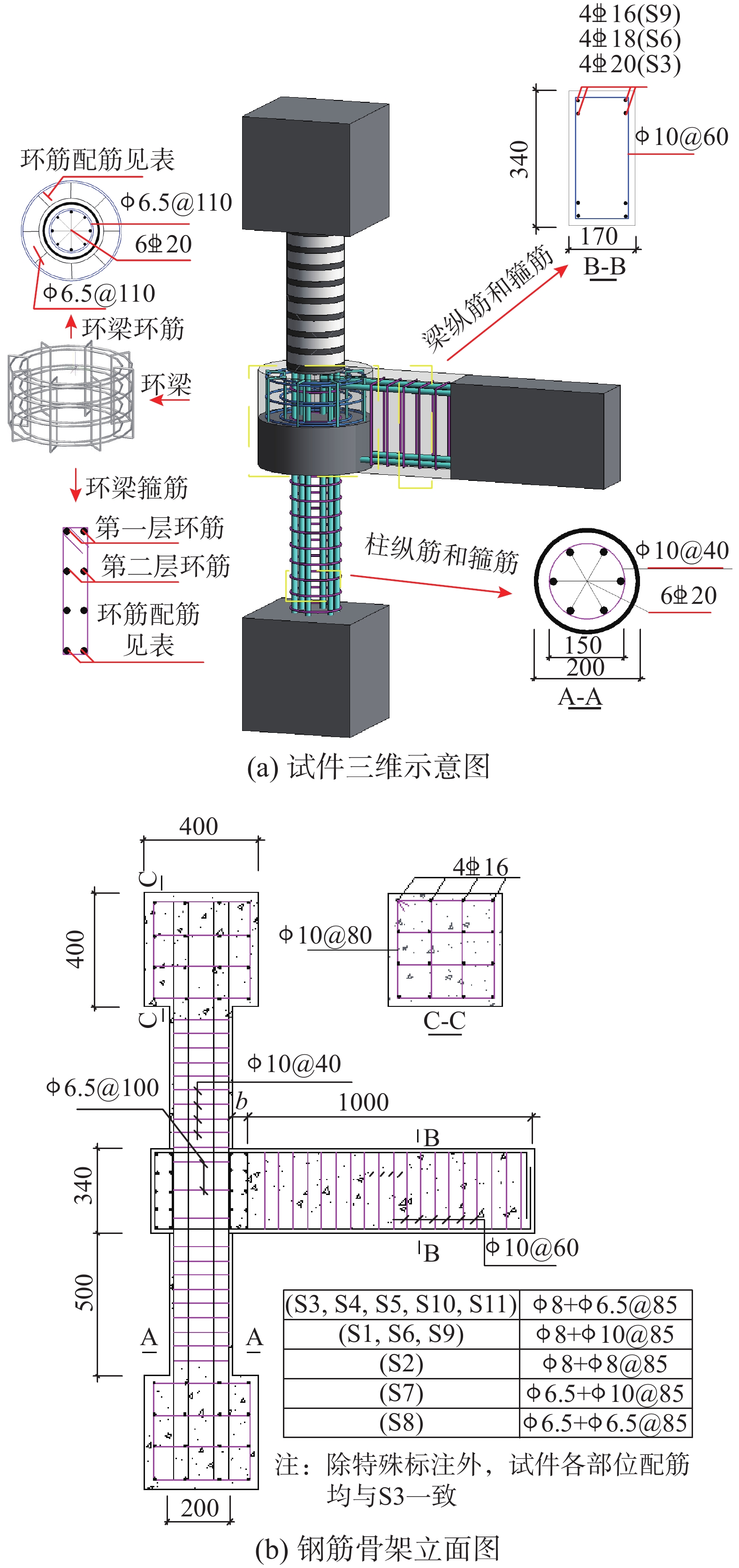
本文设计11根PVC管钢筋混凝土柱-钢筋混凝土环梁T型节点试件，试件上、下柱高度和直径分别为500 mm和200 mm，钢筋混凝土梁跨度为1000 mm、截面尺寸为170 mm×340 mm，详见图1所示。柱纵筋为620，配筋率为6%；柱节点区和非节点区箍筋分别为6.5@100和10@40，体积配箍率为0.09%和0.55%；梁纵筋采用上、下对称配筋，配筋率包括1.39%、1.76%和2.17%；梁箍筋为10@60，配箍率为1.54%。环梁节点截面高度为340 mm，环梁宽度包括75 mm、100 mm和125 mm三种，其内部布置内、外2层的环形钢筋，直径较大的环形钢筋位于内层，在节点高度方向布置4层环形钢筋，每层环形钢筋间距为85 mm，环筋配筋率包括0.98%、1.27%和1.51%三种，环梁箍筋在环梁360°范围内均匀布置，环梁配箍率为0.06%。试件具体试验参数如表1所示。

图  1  试件尺寸和配筋^[24]

Figure  1.  Size and reinforcement of specimens^[24]

下载: 全尺寸图片 幻灯片

混凝土采用C30商品混凝土，按照《普通混凝土力学性能试验方法标准》(GB/T 50081−2002)^[25]规定的方法测得混凝土轴心抗压强度为22.9 MPa，弹性模量为3.12×10⁴ MPa；CFRP条带宽度和层数分别为20 mm和2层，为防止PVC管与环梁连接处(柱端)提前发生破坏，PVC管柱端部缠绕3层CFRP条带，CFRP条带间距分别为20 mm、40 mm、60 mm和不缠，依据《定向纤维增强聚合物基复合材料拉伸性能试验方法》(GB/T 3354−2014)^[26]的规定试验方法测得CFRP条带的抗拉强度为3795.6 MPa，弹性模量为2.74×10⁵ MPa，极限拉应变为1.52%；PVC管外径为200 mm，管壁厚7.8 mm，参照《热塑性塑料管材拉伸性能测定》(GB/T 8804.1−2003)^[27]中建议方法测得PVC管抗压强度为57.0 MPa，抗拉强度为69.6 MPa，弹性模量为2590 MPa，泊松比为0.4。依据《金属材料拉伸试验室温试验方法》(GB/T 228.1−2010)^[28]的规定试验方法测得钢筋的主要力学性能如表2所示。

表  1  环梁节点试验参数

Table  1.  Experimental parameters of ring beam joints

试件编号	环梁尺寸b×h /mm	CFRP条带层数${n_{\text{f}}}$/间距$s_{\text{f} }'$/mm	环筋配筋率${\rho _{\text{r}}}$	梁纵筋配筋率${\rho _{\text{b} }}$/(%)	轴压比n
S1	100×340	2/40	1.51%(410/48)	2.17(420)	0.2
S2	100×340	2/40	1.27%(48/48)	2.17(420)	0.2
S3	100×340	2/40	0.98%(48/46.5)	2.17(420)	0.2
S4	100×340	2/20	0.98%(48/46.5)	2.17(420)	0.2
S5	100×340	2/60	0.98%(48/46.5)	2.17(420)	0.2
S6	100×340	2/40	1.51%(410/48)	1.76(318)	0.2
S7	125×340	2/40	1.05%(410/46.5)	2.17(420)	0.2
S8	75×340	2/40	1.04%(46.5/46.5)	2.17(420)	0.2
S9	100×340	2/40	1.51%(410/48)	1.39(316)	0.2
S10	100×340	−	0.98%(48/46.5)	2.17(420)	0.2
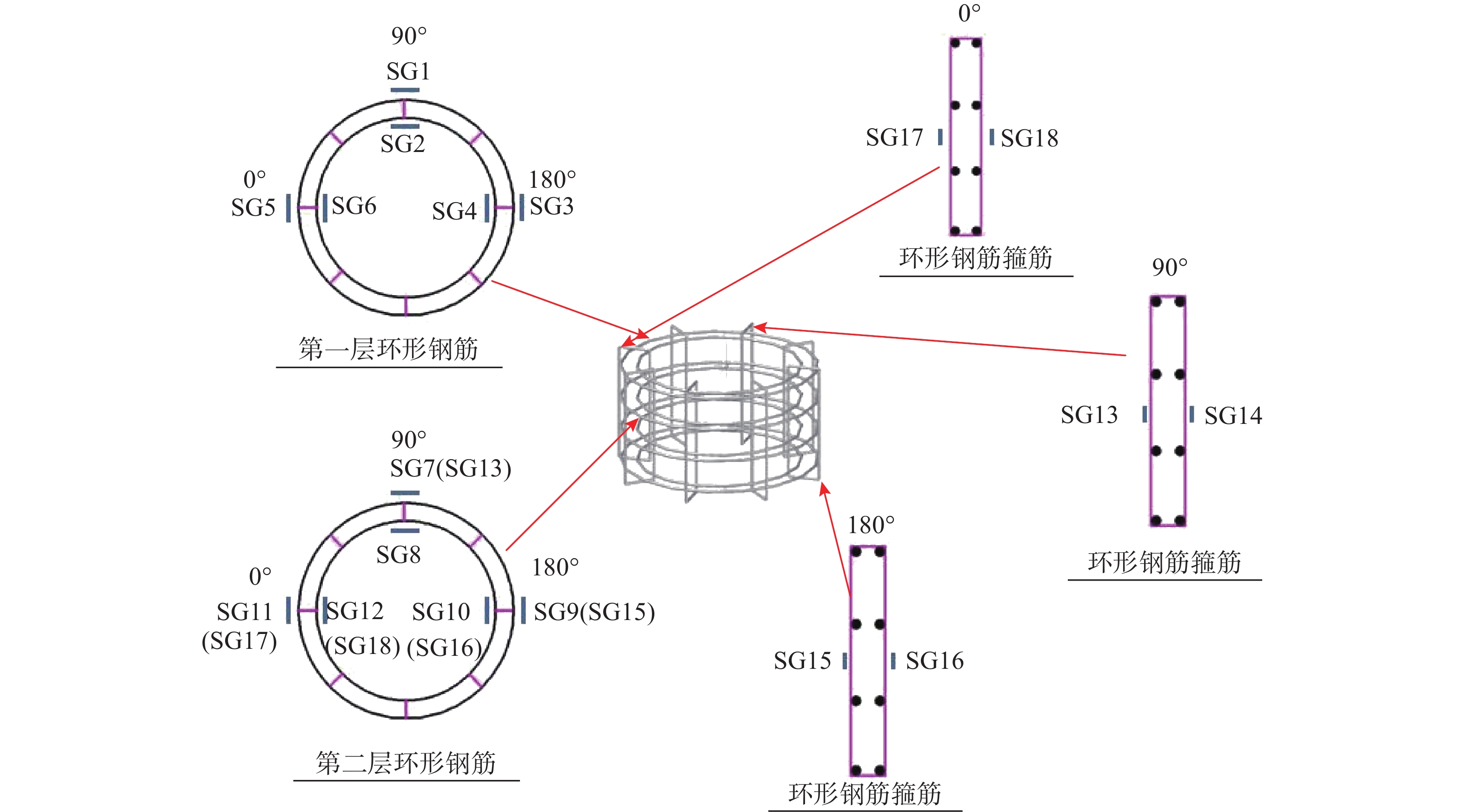
S11	100×340	2/40	0.98%(48/46.5)	2.17(420)	0.4
注：1)环筋配筋率${\rho _{{ {\rm{r} } } } } = { { {A_{ {\text{rs} } } } } / {bh} }$，其中：${A_{{\text{rs}}}}$为环梁环形钢筋的总面积；$b$和$h$分别为环梁截面宽度和高度；2)梁纵筋配筋率${\rho _{\text{b} } } = { { {A_{ {\text{bs} } } }}/ { {b_{\text{b} } }{h_{\rm{b}}} } }$，其中：${A_{{\text{bs}}}}$为纵向受拉钢筋的截面面积；$b_{\text{b}}^{}$和${h_{\text{b}}}$分别为梁截面宽度和高度；3)柱体积配箍率${\rho _{{\text{vc}}}} = {{4{A_{{\text{svc}}}}} / {{s_{\text{c}}}{d_{\text{c}}}}}$，其中：${A_{{\text{svc}}}}$、${s_{\text{c}}}$和${d_{\text{c}}}$分别为箍筋截面积、间距和所围成圆直径；4)—表示PVC管表面不缠绕CFRP条带。

下载: 导出CSV 

| 显示表格

表  2  钢筋的基本性能

Table  2.  Basic mechanical properties of reinforcement

钢筋种类和直径/mm	屈服强度/MPa	极限强度/MPa	弹性模量/GPa
HPB300/6	323	542	197
HPB300/8	308	426	201
HPB300/10	313	432	197
HRB400/16	451	620	195
HRB400/18	465	633	195
HRB400/20	446	611	199

下载: 导出CSV 

| 显示表格

试验加载装置及测试仪器布置如图2所示^[24]，在整个试验过程中，主要通过荷载传感器、位移计和应变片量测试件各部位的荷载、位移及应变。梁端施加的低周反复荷载由MTS电液伺服作动器的荷载传感器直接采集，试件的轴压荷载、应变及位移则通过TDS530静态数据采集仪获得。位移测量主要包括塑性铰区梁柱相对转角测量、节点核心区剪切变形测量以及梁与柱端位移测量(见图3)，应变测量主要包括混凝土及CFRP条带应变测量(见图3)、环形钢筋及其箍筋应变测量(见图4)、柱与梁钢筋应变测量(见图5)。试验采用全过程位移控制加载，试件屈服前位移加载每级循环一次，位移增幅为1 mm，试件屈服后位移加载每级循环三次，位移幅值以屈服位移为基数倍数增加。

图  2  试验加载装置及测试仪器布置^[24]

Figure  2.  Test loading device and measurement instrument layout^[24]

下载: 全尺寸图片 幻灯片

图  3  试件位移计布置与混凝土、CFRP条带应变片布置^[24]

Figure  3.  Displacement meter arrangement of specimen and strain gauge arrangement of concrete and CFRP strips^[24]

下载: 全尺寸图片 幻灯片

图  4  环形钢筋及其箍筋应变片布置^[24]

Figure  4.  Strain gauge arrangement of ring reinforcement and stirrups^[24]

下载: 全尺寸图片 幻灯片

图  5  柱与梁的钢筋应变片布置^[24]

Figure  5.  Reinforcement strain gauge arrangement of columns and beams^[24]

下载: 全尺寸图片 幻灯片

2   试验结果分析

2.1   破坏形态

试验研究表明，试件的破坏形态分为三类，即环梁节点剪切破坏、框架梁受弯破坏以及梁与节点交界处破坏。大部分试件(如：S1-S5、S7、S8和S11)的破坏形态为典型的节点剪切破坏(如图6)，其破坏过程经历初裂、通裂、极限和破坏四个阶段。加载初期，试件表面没有明显变化，钢筋和混凝土的应变近似呈线性增长，试件处于弹性状态，此阶段各因素对节点破坏形态影响不明显。随后，框架梁与环梁交界处侧面逐渐出现弯曲裂缝，试件进入初裂阶段；随着梁端位移增加，环梁侧面不断出现交叉斜裂缝，节点核心区被分割成若干菱形区域，试件进入通缝阶段；随着环筋配筋率和环梁宽度的减小，节点核心区混凝土裂缝发展更加显著，这主要是因为环梁对节点核心区的约束作用随着环筋配筋率和环梁宽度的减小而削弱。随着CFRP条带间距的减小，PVC-CFRP管对柱内核心混凝土的约束作用增强，CFRP条带环向应变增大。随着梁端位移进一步增加，节点核心区斜裂缝宽度继续增大，斜裂缝交汇处混凝土有轻微起皮现象，试件进入极限阶段；随着梁端位移的进一步增大，梁与环梁交界处上下表面混凝土开始大块剥落，节点剪切变形急剧增大，试件进入最终破坏阶段。试件最终破坏形态表现为：环梁环筋和箍筋受拉屈服，节点区柱钢筋受拉屈服，梁与环梁交界处和节点区梁纵筋受拉屈服。环梁节点靠近梁侧出现多条交叉斜裂缝，斜裂缝交汇处混凝土剥落；节点区靠近梁侧混凝土受压起皮脱落，梁与节点交界处混凝土被压碎。环梁上下表面出现多条径向裂缝，梁上出现多条弯曲裂缝，柱根部出现环向裂缝。

图  6  环梁节点典型破坏形态^[24]

Figure  6.  Typical failure modes of the ring beam joints^[24]

下载: 全尺寸图片 幻灯片

梁纵筋配筋率为1.39%的S9试件发生框架梁受弯破坏，主要表现为：大部分非节点区梁钢筋受拉屈服，仅有靠近梁侧环梁环筋和箍筋以及节点区柱钢筋受拉屈服，非节点区柱钢筋未屈服，PVC管和CFRP条带应变较小。梁上出现多条弯曲裂缝，梁与环梁交界处上表面混凝土被压碎。节点区靠近梁侧混凝土受压起皮脱落，梁与环梁交界处下表面混凝土剥落。梁纵筋配筋率为1.76%的S6试件发生梁与节点交界处破坏，主要表现为：环梁环筋和箍筋大部分受拉屈服，节点区柱钢筋和梁纵筋受拉屈服，非节点区柱钢筋、梁钢筋均未屈服，PVC管和CFRP条带应变较小。环梁侧面靠近梁侧和上下表面出现多条交叉斜裂缝和径向裂缝，斜裂缝交汇处混凝土剥落。节点区靠近梁侧混凝土受压起皮脱落，梁与环梁交界处上表面混凝土被压碎。梁上出现多条弯曲裂缝，柱根部出现环向裂缝。

2.2   弯矩-曲率滞回曲线

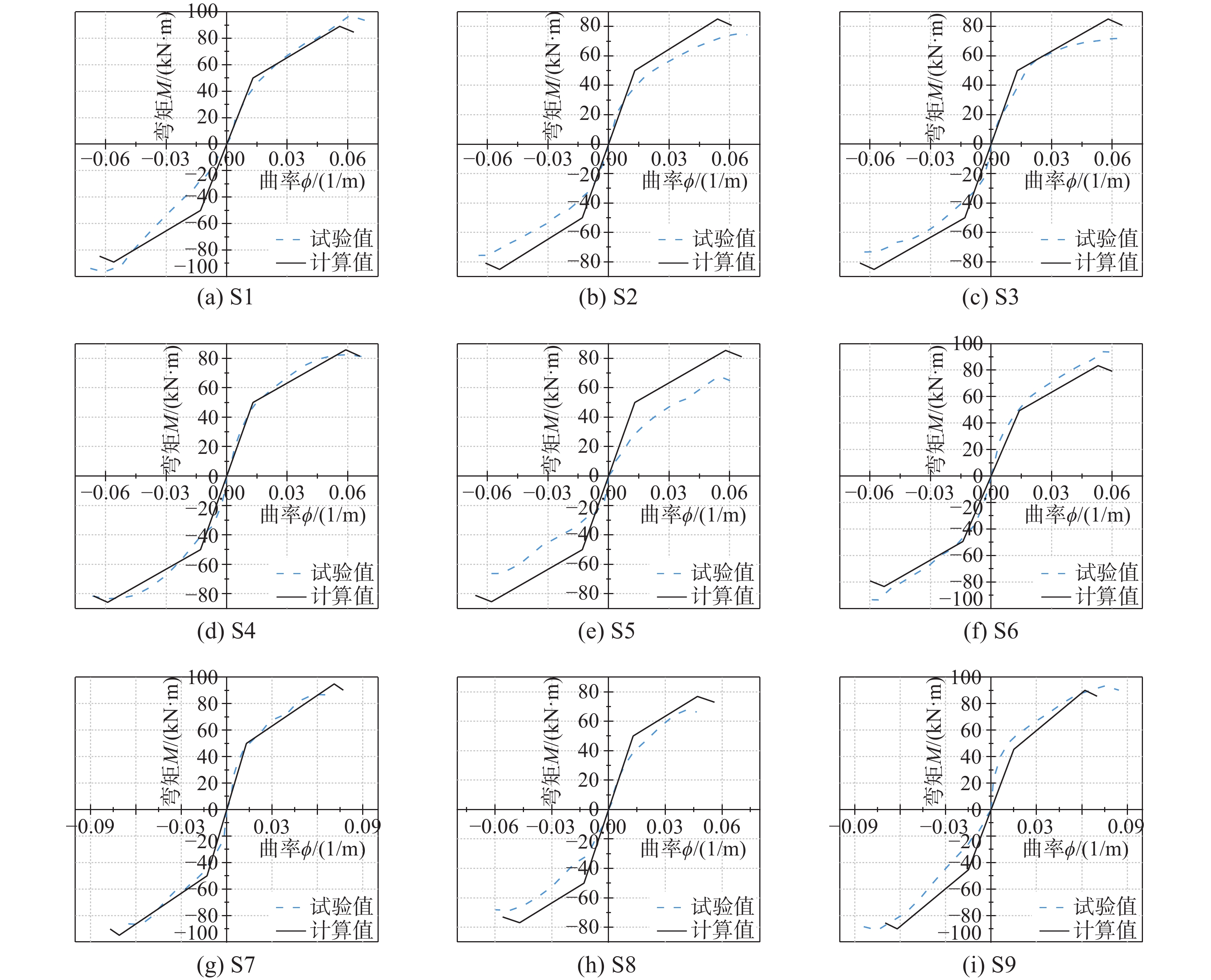
图7描述了各因素对试件弯矩-曲率曲线($M{\text{-}}\phi$)滞回性能的影响，图中：$M$为弯矩；$\phi$为曲率，由梁柱相对转角推算而得，梁柱的相对转角由布置的上下位移计的变形量所确定。由图7可知，环梁节点的$M{\text{-}}\phi$曲线主要经历弹性、弹塑性和平稳三个阶段。加载初期，试件的弯矩和曲率基本呈线性增长，试件刚度和强度基本没有退化，试件处于弹性阶段。此阶段试件刚度较大，曲率增长速度较慢，弯矩增长速度较快，滞回环形状为梭形；随着弯矩增加，试件不同位置先后出现裂缝，节点区部分钢筋屈服，试件曲率偏离线性增长，弯矩增长速度减小，试件进入弹塑性阶段。在此阶段，曲线所围成的面积逐渐增大，当弯矩卸为零时，试件曲率不再降为零，出现一定量残余变形；随着框架梁与环梁上裂缝不断发展，钢筋与混凝土之间发生一定量的粘结滑移，曲线出现“捏缩”现象，滞回环形状逐渐变为反S形，试件曲率继续增加，弯矩增长减缓，试件进入平稳阶段。随着曲率进一步增加，试件弯矩变化不明显，曲线上形成较为明显的曲率延性平台。

图  7  环梁节点弯矩-曲率滞回曲线

Figure  7.  Moment-curvature hysteretic curves of ring beam joints

下载: 全尺寸图片 幻灯片

2.2.1   环筋配筋率的影响

由图7(a)~图7(c)可知，不同环筋配筋率试件的$M{\text{-}}\phi$滞回曲线基本一致，随着环筋配筋率增大，$M{\text{-}}\phi$滞回曲线变得更加饱满，滞回环所围成的面积增加，且各阶段的$M$和$\phi$增加，$M{\text{-}}\phi$曲线“捏缩”程度降低，试件的承载力和延性提高。这是因为环梁对节点核心区混凝土的约束作用随环筋配筋率的增大而增强，节点区钢筋与混凝土之间的粘结滑移量减少，$M{\text{-}}\phi$曲线“捏缩”程度削弱。

2.2.2   CFRP条带间距的影响

由图7(c)~图7(e)可知，CFRP条带间距对$M{\text{-}}\phi$滞回曲线的影响不明显。这主要是因为CFRP条带间距主要影响柱的力学性能，对环梁节点力学性能的影响相对较小。

2.2.3   环梁宽度的影响

如图7(b)、图7(g)和图7(h)所示，与环梁配筋率影响类似，试件$M{\text{-}}\phi$滞回曲线随着环梁宽度增加而趋于饱满，滞回环所围成的面积增加，且试件在各阶段的弯矩、曲率增加，试件整体刚度增大，$M{\text{-}}\phi$曲线“捏缩”程度降低。这是因为，随着环梁宽度增加，环梁对节点核心区混凝土的约束作用增强，钢筋在节点区的锚固性能提高，节点区钢筋与混凝土之间的粘结滑移量减少，试件的承载能力和刚度提高。

2.2.4   轴压比的影响

如图7(c)和图7(k) 所示，在弹性阶段，试件$M{\text{-}}\phi$滞回曲线近似呈线性增长，轴压比对其影响不明显。随着弯矩的增大，试件$M{\text{-}}\phi$滞回曲线逐渐偏离线性增长，试件进入弹塑性阶段。节点核心区混凝土横向变形随轴压比的增大而增大，环梁对节点核心区的约束作用增强，试件的承载能力提高，但变形能力降低。在平稳阶段，提高轴压比将导致试件$M{\text{-}}\phi$滞回曲线变得陡峭。

2.2.5   梁纵筋配筋率的影响

如图7(a)、图7(f)和图7(i)所示，随着梁纵筋配筋率的增大，试件的$M{\text{-}}\phi$滞回曲线更加饱满，滞回环所围成的面积增大，$M{\text{-}}\phi$滞回曲线“捏缩”程度降低。这是因为随着梁纵筋配筋率降低，一方面试件由节点剪切破坏变为梁弯曲破坏，节点区钢筋与混凝土之间的粘结滑移量减少；另一方面试件的抗弯刚度减小，其抵抗变形的能力相应减弱。

2.3   弯矩-曲率骨架曲线

如图8(a)所示，环筋配筋率对试件$M{\text{-}}\phi$骨架曲线的前两个阶段影响不明显，但提高环筋配筋率有利于增大试件的极限弯矩和极限曲率，缩短试件的平稳阶段。例如，相较于S3试件，试件S1的极限弯矩和极限曲率分别增加了26.0%和4.4%。这是因为环梁对节点核心区混凝土的约束作用随环筋配筋率的增大而增强，节点刚度相应增加，梁与环梁交界处塑性铰转动能力减弱，试件的承载和抵抗变形能力提高。

由图8(b)可知，CFRP条带间距对$M{\text{-}}\phi$骨架曲线的影响也不明显。如图8(c) 所示，随着环梁宽度的增大，试件的极限弯矩与极限曲率增大。与试件S8相比，试件S7的极限弯矩和极限曲率分别提高了22.4%和32%。这主要是因为增大环梁宽度导致环梁对节点核心区混凝土的约束作用增强，节点区的钢筋锚固性能提高，节点区钢筋与混凝土之间的粘结滑移量减少，梁与环梁交界处塑性铰转动能力提高，试件刚度退化减缓，抵抗变形能力增强。

如图8(d)所示，加载初期，轴压比对试件$M{\text{-}}\phi$骨架曲线的影响不明显，但随着轴压比增加，试件承载力提高，变形能力降低，试件的平稳阶段缩短，极限弯矩增加而极限曲率明显减少。与试件S3相比，试件S11的极限弯矩增加16%，而极限曲率减少31%。这是因为，提高试件的轴压比，节点核心区混凝土横向变形增大，环梁对节点核心区的约束效应增强，试件的承载能力提高，但节点区混凝土的主压应力和应变增大，一定程度上削弱了混凝土后期塑性变形能力，使得混凝土脆性增加，试件极限曲率降低。

如图8(e)所示，梁纵筋配筋率对试件$M{\text{-}}\phi$骨架曲线的影响不明显。改变梁的纵筋配筋率对试件破坏形态有影响，但对节点的承载和变形能力影响较小。在平稳阶段，随着梁纵筋配筋率减小，试件的抗弯刚度与抵抗变形能力降低，试件平稳阶段延长，梁端传递弯矩的能力减弱，试件极限弯矩基本不变，但极限曲率增长明显，试件S9的极限曲率相较于试件S1的极限曲率增加了17.6%。

图  8  各因素对弯矩-曲率骨架曲线的影响

Figure  8.  Influence of various factors on moment-curvature skeleton curves

下载: 全尺寸图片 幻灯片

3   弯矩-曲率关系恢复力模型

3.1   骨架曲线简化计算方法

3.1.1   基本假定

1)不考虑出平面外的荷载和位移；

2)假定钢筋与混凝土之间无粘结滑移；

3)不考虑核心混凝土收缩、徐变的影响；

4)不考虑混凝土斜裂缝之间骨料咬合作用以及纵筋销栓作用；

5)混凝土及钢筋的应力-应变关系分别采用式(1)的软化混凝土本构关系模型^[29]和式(2)的理想弹塑性模型。

式中：${\sigma _{\text{d}}}$为混凝土平均主压应力(斜压杆方向)；$\zeta$为软化效应系数，$\zeta=\dfrac{5.8}{\sqrt{f_{\mathrm{c}}^{\prime}}} \dfrac{1}{\sqrt{1+400 \varepsilon_{\mathrm{r}}}} \leqslant \dfrac{0.9}{\sqrt{1+400 \varepsilon_{\mathrm{r}}}}$；$f_{\mathrm{c}}^{\prime}$为圆柱体试块抗压强度，$f_{\rm{c}}^\prime = 0.79{f_{{\rm{cu}}}}$，${f_{{\text{cu}}}}$为立方体试块抗压强度；${\varepsilon _{\text{r}}}$和${\varepsilon _{\text{d}}}$为混凝土平均主拉应变和主压应变；${\varepsilon _{\text{0}}}$为$f_{\rm{c}}^\prime$对应的峰值应变，${\varepsilon _{\text{0}}} = - {\text{0}}.002 - 0{\text{.001}}\left( {\dfrac{{f_{\text{c}}' - 20}}{{80}}} \right)$^[30]。

式中：${E_{\text{s}}}$为钢筋弹性模量；${f_{\text{s}}}$和${\varepsilon _{\text{s}}}$分别为钢筋应力和应变；${f_{\text{y}}}{\text{ }}$和${\varepsilon _{\text{y}}}$分别为钢筋屈服强度和屈服应变。

3.1.2   弯矩-曲率骨架曲线简化计算方法

如图9所示，将环梁节点的$M{\text{-}}\phi$骨架曲线进行无量纲化处理。从图中可以看出，试件的$M{\text{-}}\phi$骨架曲线可近似简化为正反向对称三折线模式。

图  9  试件规格化骨架曲线

Figure  9.  Normalized skeleton curves of specimens

下载: 全尺寸图片 幻灯片

1)屈服弯矩和屈服曲率

在大量试验研究的基础上，PANAGIOTAKOS^[31]提出环梁节点屈服弯矩和屈服转角的计算方法，如下所示：

式中：${\phi _{\rm{y}}}$为截面屈服曲率；${f_{{\text{ybs}}}}$、${\varepsilon _{{\text{ybs}}}}$和${d_{\text{b}}}$为梁纵筋的屈服强度、屈服应变和直径；${h_{{\rm{b0}}}}$为梁有效高度；${a'}$为梁受压区边缘至受压钢筋合力作用点的距离；${a_{{\text{sl}}}}$为粘结滑移系数。与普通梁柱节点相比，本文中环梁节点为增大节点，截面尺寸较大，钢筋的锚固性能较好，钢筋粘结滑移量很小，因此本文建议取${a_{{\text{sl}}}} = 0$，则环梁节点截面屈服曲率可表示为：

式中：${\xi _{\text{y}}}$为梁截面相对受压区高度(节点屈服)，基于截面分析法，可得${\xi _{\text{y}}} = {( {{\eta ^{\text{2}}}{A^{\text{2}}} + {\text{2}}\eta B} )^{{\text{1/2}}}} - \eta A$^[31]，参数的取值和意义详见文献[31]。利用式(3)和式(5)可以得出环梁节点的屈服弯矩和屈服曲率，如表3所示。由表可知，试件的屈服弯矩试验值与计算值之比$M_{\text{y}}^{\text{t}}{\text{/}}M_{\text{y}}^{\text{c}}$偏差较大。这可能是因为，一方面试验中大部分试件的梁纵筋配筋率较大(除试件S6和S9外)，当节点发生剪切破坏时，梁仍处于弹性工作状态，除节点区内的梁纵筋屈服以外，非节点区梁纵筋并没有发生屈服，而式(3)是在梁纵筋全部屈服的基础上提出的，导致式(3)计算值偏大；另一方面，所有试件(包括试件S6和S9外)计算获得的屈服弯矩试验值为屈服荷载与对应梁长的乘积而得，梁长的取值并未考虑增大的环梁节点部分，导致计算的试验值偏低。从表3可以看出，$M_{\text{y}}^{\text{t}}{\text{/}}M_{\text{y}}^{\text{c}}$与梁配筋率特征值${\lambda _{{\text{bs}}}}$有较大的相关性，这是因其破坏形态由节点剪切破坏转变为梁弯曲破坏。通过试验数据回归分析，可以得到环梁节点修正后屈服弯矩计算公式为：

式中：${k_{{\text{rb}}}}$为节点尺寸影响系数，${k_{{\text{rb}}}} = {{D_{\text{c}}}} / {({\text{2}}b + {D_{\text{c}}})}$；${D_{\text{c}}}$为PVC-CFRP管混凝土柱截面直径；${\lambda _{{\text{bs}}}}$为梁配筋特征值，${\lambda _{{\text{bs}}}} = {\rho _{\text{b}}}{{{f_{{\text{ybs}}}}} /{{f_{\text{c}}}}}$，${\rho _{\text{b}}}$为梁配筋率。

表  3  环梁节点屈服弯矩和曲率试验值与计算值比较

Table  3.  Comparison of experimental and calculated yield moment and curvature of ring beam joints

试件编号	$屈服弯矩试验值M_{\rm{y} }^{\rm{t } }/{\rm{kN} }$	$屈服曲率试验值\phi_{\rm{y} }^{\rm{t} } /{\rm{mm} }$	$屈服弯矩计算值M_{\rm{y} }^{\rm{c} } /{\rm{kN} }$			$屈服曲率计算值\phi_{\rm{y} }^{\rm{c} } /{\rm{mm} }$			$M_{\rm{y}}^{\rm{t}}/M_{\rm{y}}^{\rm{c}}$			$\phi_{\rm{y}}^{\rm{t}}/\phi_{\rm{y}}^{\rm{c}}$
			式(3)	式(6)		式(5)	式(7)		式(3)	式(6)		式(5)	式(7)
S1	57.5	0.014	110.5	50.0		0.008	0.013		0.520	1.150		1.750	1.077
S2	45.8	0.015	110.5	50.0		0.008	0.013		0.414	0.916		1.875	1.154
S3	51.4	0.013	110.5	50.0		0.008	0.013		0.465	1.028		1.625	1.000
S4	47.7	0.015	110.5	50.0		0.008	0.013		0.432	0.954		1.875	1.154
S5	40.5	0.013	110.5	50.0		0.008	0.013		0.367	0.810		1.625	1.000
S6	53.5	0.013	90.6	49.4		0.007	0.014		0.591	1.083		1.857	0.929
S7	49.0	0.014	110.5	50.0		0.008	0.013		0.443	0.980		1.750	1.077
S8	44.6	0.012	110.5	50.0		0.008	0.013		0.404	0.892		1.500	0.923
S9	50.5	0.016	72.5	45.5		0.007	0.015		0.697	1.110		2.286	1.067
S10	49.9	0.012	110.5	50.0		0.008	0.013		0.452	0.998		1.500	0.923
S11	53.6	0.014	110.5	50.0		0.008	0.013		0.485	1.072		1.750	1.077
均值									0.479	0.999		1.763	1.035

下载: 导出CSV 

| 显示表格

同理，式(5)屈服曲率的试验值与计算值$\phi _{\text{y}}^{\text{t}}{\text{/}}\phi _{\text{y}}^{\text{c}}$相差较大。这可能是因为：式(5)计算环梁节点屈服曲率时，认为环梁节点为增大节点，截面尺寸较大，钢筋的锚固性能较好，钢筋粘结滑移量很小，计算屈服曲率时未考虑钢筋粘结滑移的影响，导致节点屈服曲率计算值偏低，与此同时，本研究试验实测曲率值为梁端部截面的曲率，与环梁增大节点处相比，试验实测曲率值偏大。类似地，从表3可以看出，$\phi _{\text{y}}^{\text{t}}{\text{/}}\phi _{\text{y}}^{\text{c}}$与梁配筋率特征值${\lambda _{{\text{bs}}}}$有较大的相关性。随着梁纵筋配筋率减小，梁端抗弯刚度降低，试件由节点剪切破坏转变为梁弯曲破坏。通过试验数据回归分析，可以得到环梁节点修正后的屈服曲率计算公式为：

式中：${{\lambda} _{{\text{rs}}}} = {\rho _{\text{r}}}{{{f_{{\text{yrs}}}}} /{{f_{\text{c}}}}}$，${f_{{\text{yrs}}}}$为环筋屈服强度。本文提出的环梁节点屈服弯矩和屈服曲率的计算值与试验值对比如表3所示。环梁节点$M_{\text{y}}^{\text{t}}{\text{/}}M_{\text{y}}^{\text{c}}$的平均值为0.999，标准差为0.102。环梁节点$\phi _{\text{y}}^{\text{t}}{\text{/}}\phi _{\text{y}}^{\text{c}}$的平均值为1.035，标准差为0.086。由此可见，本文提出环梁节点屈服弯矩和屈服曲率的计算值与试验值吻合较好。

2)峰值弯矩和峰值曲率

环梁节点的峰值曲率可由其弯矩-曲率骨架曲线平稳段的刚度计算得到，其表达式为：

式中：${M_{\text{m}}}$为环梁节点峰值弯矩^[28]；$k_{\rm{1}}'$为平稳段刚度。试验结果表明：$k_{\rm{1}}'$与环梁配筋特征值${\lambda _{{\text{rs}}}}$、节点尺寸影响系数${k_{{\text{rb}}}}$、梁配筋特征值${\lambda _{{\text{bs}}}}$和轴压比$n$相关，由试验数据回归分析，可得：

3)极限弯矩和极限曲率

根据环梁节点静力平衡条件和弯矩-曲率骨架曲线下降段刚度，可得环梁节点极限曲率计算公式为：

式中：${M_{\text{u}}}$为环梁节点极限弯矩^[28]；${k'_{\text{2}}}$为下降段刚度，由本文试验数据回归分析，可得：

图10为环梁节点弯矩-曲率骨架曲线计算值与试验值对比情况，从图中可以看出，本文提出环梁节点弯矩-曲率骨架曲线简化计算方法的计算精度较高，与试验结果吻合较好。

下载: 全尺寸图片 幻灯片

  10  环梁节点弯矩-曲率骨架曲线计算值和试验值比较

  10.  Comparison between calculated and experimental results of moment-curvature skeleton curve of ring beam joints

下载: 全尺寸图片 幻灯片

3.2   弯矩-曲率恢复力模型

3.2.1   滞回规则

试验研究表明，在环梁节点屈服前，环梁节点试件加载和卸载弯矩-曲率骨架曲线近似为直线，刚度变化较小，加卸载刚度与弹性段刚度$k_{\rm{0}}'$基本相同，即$k_{0}^{\prime}=M_{\mathrm{y}} / \phi_{\mathrm{y}}$。在试件屈服后，其卸载刚度逐渐退化，卸载刚度与弹性刚度之比$k_{\rm{u}}'/k_{\rm{0}}'$随着$\phi {\text{/}}{\phi _{\text{y}}}$变化呈幂函数形式。其中，卸载刚度$k_{\rm{u}}'$取滞回环正反向峰值点与卸载至弯矩零点直线斜率的平均值，且与环梁配筋特征值${\lambda _{{\text{rs}}}}$、节点尺寸影响系数${k_{{\text{rb}}}}$、梁配筋特征值${\lambda _{{\text{bs}}}}$和轴压比$n$呈一定的相关性。通过文中试验数据回归分析可得：

式中，$b$、$d$为试验数据回归得到的参数。

对环梁节点正反两方向卸载刚度取平均值，可得不同曲率幅值下环梁节点的卸载刚度，如表4所示。

表  4  不同曲率幅值下的卸载刚度

Table  4.  Unloading stiffness under different curvature amplitudes

试件编号	曲率/屈服曲率卸载刚度/屈服曲率	各级曲率卸载刚度
S1	$\phi /{\phi _{\text{y}}}$	0.83	0.93	1.04	1.14	1.25	1.87	2.49	2.90	3.11	3.73	4.35	4.97
	$k_{\text{u}}'/k_{\text{0}}'$	5.73	5.48	5.30	4.69	3.87	4.12	3.30	2.86	2.25	1.40	1.13	0.83
S2	$\phi /{\phi _{\text{y}}}$	0.42	0.52	0.63	0.73	0.84	1.25	1.67	2.09	2.50	2.92	3.34	3.76
	$k_{\text{u}}'/k_{\text{0}}'$	1.77	1.76	1.74	1.72	1.69	1.56	1.29	1.12	0.98	0.90	0.80	0.77
	$\phi /{\phi _{\text{y}}}$	4.17	4.59	−	−	−	−	−	−	−	−	−	−
	$k_{\text{u}}'/k_{\text{0}}'$	0.77	0.75	−	−	−	−	−	−	−	−	−	−
S3	$\phi /{\phi _{\text{y}}}$	0.69	0.81	0.92	1.27	1.58	2.30	2.87	3.45	3.59	4.11	4.61	5.13
	$k_{\text{u}}'/k_{\text{0}}'$	1.80	1.77	1.75	1.50	1.41	0.88	0.73	0.61	0.64	0.56	0.54	0.51
S4	$\phi /{\phi _{\text{y}}}$	0.13	0.25	0.38	0.50	0.63	0.76	0.88	1.01	1.51	2.01	2.52	3.02
	$k_{\text{u}}'/k_{\text{0}}'$	8.63	8.44	8.42	8.29	4.52	5.15	5.72	7.43	2.40	1.73	1.53	1.34
	$\phi /{\phi _{\text{y}}}$	3.53	4.03	4.54	−	−	−	−	−	−	−	−	−
	$k_{\text{u}}'/k_{\text{0}}'$	1.21	1.18	0.99	−	−	−	−	−	−	−	−	−
S5	$\phi /{\phi _{\text{y}}}$	0.74	0.85	0.84	1.26	1.69	2.11	2.53	2.95	3.80	4.21	4.64	−
	$k_{\text{u}}'/k_{\text{0}}'$	8.84	8.52	8.16	6.92	4.20	2.20	1.68	1.36	1.10	1.08	1.00	−
S6	$\phi /{\phi _{\text{y}}}$	0.72	0.84	0.97	1.44	1.92	2.41	2.89	3.37	3.85	4.33	4.82	−
	$k_{\text{u}}'/k_{\text{0}}'$	3.11	3.05	2.85	1.59	1.17	0.98	0.83	0.73	0.66	0.67	0.59	−
S7	$\phi /{\phi _{\text{y}}}$	0.61	0.72	0.82	1.23	1.63	2.05	2.45	2.86	3.27	3.68	4.08	4.49
	$k_{\text{u}}'/k_{\text{0}}'$	3.65	3.58	3.27	1.70	1.27	1.09	0.90	0.80	0.77	0.72	0.68	0.65
	$\phi /{\phi _{\text{y}}}$	4.91	−	−	−	−	−	−	−	−	−	−	−
	$k_{\text{u}}'/k_{\text{0}}'$	0.63	−	−	−	−	−	−	−	−	−	−	−
S8	$\phi /{\phi _{\text{y}}}$	0.89	1.00	1.11	1.67	2.23	2.78	3.34	3.89	−	−	−	−
	$k_{\text{u}}'/k_{\text{0}}'$	2.19	2.14	2.11	1.29	1.01	0.88	0.79	0.70	−	−	−	−
S9	$\phi /{\phi _{\text{y}}}$	0.10	0.39	0.49	0.59	0.69	0.78	0.88	0.98	1.18	1.76	2.35	2.93
	$k_{\text{u}}'/k_{\text{0}}'$	3.02	2.85	2.54	2.16	2.13	2.09	2.00	1.96	1.92	1.84	1.72	1.65
	$\phi /{\phi _{\text{y}}}$	3.52	4.69	5.28	−	−	−	−	−	−	−	−	−
	$k_{\text{u}}'/k_{\text{0}}'$	1.61	0.94	0.76	−	−	−	−	−	−	−	−	−
S10	$\phi /{\phi _{\text{y}}}$	0.94	1.06	1.18	1.30	1.41	2.12	2.82	3.52	4.23	4.94	5.64	−
	$k_{\text{u}}'/k_{\text{0}}'$	2.51	2.49	2.48	2.47	2.18	1.31	1.02	0.83	0.75	0.72	0.62	−
S11	$\phi /{\phi _{\text{y}}}$	0.66	0.77	0.88	0.99	1.10	1.65	2.20	2.75	3.30	0.66	−	−
	$k_{\text{u}}'/k_{\text{0}}'$	1.52	1.53	1.48	1.43	1.36	1.26	0.95	0.89	0.75	1.52	−	−

下载: 导出CSV 

| 显示表格

在确定环梁节点不同位移幅值卸载刚度后，考虑环梁配筋特征值${\lambda _{{\text{rs}}}}$、节点尺寸影响系数${k_{{\text{rb}}}}$、梁配筋特征值${\lambda _{{\text{bs}}}}$和轴压比$n$对卸载刚度的影响，本文提出如图11所示的环梁节点滞回规则，具体规定如下：

图  11  环梁节点弯矩-曲率关系滞回规则

Figure  11.  Hysteretic rule of moment-curvature relationship for the ring beam joints

下载: 全尺寸图片 幻灯片

1)在试件屈服前，试件处于弹性阶段，试件的加载刚度和卸载刚度均等于试件的弹性刚度$k_{\text{0}}'$，在此阶段，加卸载路径均在直线0-1-2上；

2)当试件达到屈服位移以后，骨架曲线由3点以卸载刚度正向卸载至4点(即3→4)，随后反向加载指向反向屈服点5(即4→5)，沿着骨架曲线到达下一级位移幅值点(即5→6)，再从位移幅值点以卸载刚度反向卸载到7点(即6→7)；

3)当试件卸载到反向卸载零点(7点)以后，骨架曲线由7点正向加载至8点(即7→8)，随后沿着骨架曲线加载至下一级位移幅值点9点(8→9)，再以卸载刚度反向卸载到10点(9→10)；

4)同理，试件的加卸载按照10 → 11 → 12 → 13 → 14 →15→16 →17 →18 →19 → 20→ 21→ 22路线连续进行，最终得到环梁节点的恢复力模型。

3.2.2   模型验证

图12为环梁节点$M{\text{-}}\phi$恢复力模型计算值与试验值的比较。由对比可知，本文提出的$M{\text{-}}\phi$恢复力模型计算结果与试验结果吻合较好，表明该预测模型能较好地反映环梁节点的恢复力特性。

图  12  环梁节点恢复力模型计算值和试验值对比

Figure  12.  Comparison between the calculated and experimental values of restoring force model for ring beam joints

下载: 全尺寸图片 幻灯片

4   结论

本文开展11根PVC-CFRP管钢筋混凝土柱-钢筋混凝土环梁T型节点低周反复加载试验，重点对环梁节点弯矩-曲率滞回性能进行研究，主要得出以下结论：

(1)典型的环梁节点试件破坏过程经历初裂、通裂、极限和破坏四个阶段，最终试件发生节点剪切破坏。环梁环筋和箍筋受拉屈服，梁与环梁交界处和节点区梁纵筋受拉屈服，环梁上下表面出现多条径向裂缝，梁上出现多条弯曲裂缝，环梁节点靠近梁侧出现多条交叉斜裂缝，斜裂缝交汇处混凝土剥落，梁与节点交界处混凝土被压碎，试件破坏前有明显的破坏预兆；

(2)环梁节点弯矩-曲率滞回曲线包括弹性段、弹塑性段和平稳段。随着环筋配筋率、环梁宽度或梁纵筋配筋率的增大，$M{\text{-}}\phi$滞回曲线所围成滞回环的面积增加，滞回曲线“捏缩”程度降低。提高环筋配筋率、环梁宽度有利于增大试件的极限弯矩与极限曲率，随着轴压比的增加，试件极限弯矩增加而极限曲率减少，CFRP条带间距对$M{\text{-}}\phi$骨架曲线的影响不明显；

(3)基于软化混凝土本构关系模型，考虑环筋配筋率、环梁宽度、轴压比和梁纵筋配筋率等对骨架曲线特征点的影响，提出环梁节点弯矩-曲率骨架曲线特征点简化计算公式。基于退化三线型恢复力模型，考虑轴压比、环梁配筋特征值、节点尺寸影响系数和梁配筋特征值的影响，确定卸载刚度计算公式，提出环梁节点滞回规则，建立精度较高的环梁节点弯矩-曲率恢复力模型。