自升式钻井平台是海洋能源开发领域应用较为广泛的一种平台形式，而桩靴作为支承结构常运用于其中，但桩靴构造的特异性导致传统的等直径桩的理论分析方法无法直接套用，因此需要重新构建理论模型或试验研究。在桩靴承载机制的研究方面，LEE^[1]对桩靴贯入软黏土-砂土复合层导致的破坏面进行积分，得到桩靴的剪切阻力，并计算出剪切阻力的峰值；HU等^[2-5]根据大量的模型试验和数值模拟，改进了LEE^[1]提出的阻力计算方法，在已有基础上考虑了土体相对密实度等因素；MEYERHOF^[6]通过极限平衡原理得到桩靴承载力的解析式；MICHALOWSKI^[7]分析砂土-粘土复合地基极限承载力，发现当砂土层承载力未达极限值时，承载力与下层粘土的强度呈正比关系；当砂土层承载力达到极限值后，地基承载力不再受下层粘土的强度变化影响。季春群等^[8]对桩靴承载力与抗倾覆性进行研究，分析桩靴承载力与贯入深度的关系，探讨桩靴结构稳定性。范怡飞等^[9]基于Poulos法推导得出受邻近桩靴贯入影响的桩靴p-y曲线，将离心试验数据与理论结果对比验证，结果基本一致。YI等^[10]采用大变形有限元技术，模拟桩靴的安装与加固并预测桩靴安装后固结沉降，通过与离心机试验结果对比，首次验证了数值分析在桩靴沉降研究方面的可行性。关于桩靴承载机制的研究，多数围绕于桩靴在受压时的承载力，或通过数值模拟研究桩靴的荷载-沉降预测，但静载作用下桩靴的荷载-沉降预测缺乏理论方面的研究。

在桩靴贯入土体的试验研究方面：TANI和CRAIG^[11]通过模型试验研究发现当桩靴贯入土体时，桩靴上方土体将会出现回流现象；HOSSAIN等^[12]利用离心机模型试验研究桩靴贯入土体过程的机理时，发现土体变形存在两个明显阶段，第一阶段土体向桩靴两侧挤压，桩靴上方出现孔穴；第二阶段为桩靴上方两侧土体回流进孔穴。王阳等^[13]设计筒型桩靴贯入粘土与砂土模型试验，对比两种工况下桩靴的受力性能，发现桩靴阻力随桩靴贯入深度的增加而增加，且阻力极限值近似。王冬石等^[14]研究加载速度对桩靴贯入土体的影响，发现加载速度越快，桩靴下沉越快，且土体固结速度也提高；双层土条件下，加载速度越快会增大桩靴穿刺的风险。无论是模型试验或者现场试验，都无法直观地获得桩靴贯入时桩侧土体的位移场，进而导致变形理论与内部变形试验结果的对比分析不足。

当前，土体变形理论主要有圆孔扩张法、应变路径法和浅应变路径法。圆孔扩张法(CEM)^[15]是解决沉桩对周围土体影响应用最为广泛的一种方法，其形式简单，易于求解。张小玲等^[16]基于Vesic圆孔扩张理论，分析水平荷载作用下桩侧土体的实际受力状态，推导出基于应力增量的桩侧土抗力的计算公式，进而提出了考虑摩擦效应的桩土相互作用的计算方法；由于CEM只考虑径向变形，为此BALIGH^[17]提出了应变路径法(SPM)，可反映土体的二维变形，通常适用于深基础问题。而SPM在预测桩土作用时，地表土体变形与实际变形不符合，为此SAGASETA和WHITTLE^[18]在SPM的基础上提出了浅应变路径法(SSPM)，该法不仅可以预测隧道开挖引起的地表沉陷量，也可以预测桩体打设作用引起的土体变形。HU和RANDOLPH^[19]采用的大变形有限元(FEM)在理论方面相对完善，但难以准确模拟沉桩过程，其求解比应变路径法更复杂，而且本构模型及本构参数的选取对计算结果影响大。考虑到现场试验易受环境影响且费用昂贵这一点，周健等^[20]以及LEHANE和GILL^[21]通过模型试验来研究沉桩过程周围土体的位移场，但只得到土体内部少数离散点位移，并非桩周土体整体连续变化的位移场。这类变形理论在桩基方面得到了很多应用，然而应用于桩靴的有效性仍值得商榷。

综上，为研究桩靴贯入饱和砂土的承载机制和桩靴周围砂土变形机理，开展了桩靴的抗压承载模型试验和透明土试验，分别运用圆孔扩张理论、分段位移迭代算法以及浅应变路径法推导得到桩靴静载作用下的荷载-沉降变化规律和桩靴周围砂土水平位移理论值，并与模型试验结果进行对比分析，探讨圆孔扩张理论以及浅应变路径法应用于桩靴的有效性，解决桩靴贯入砂土研究不全面的问题。

1   试验介绍

1.1   桩靴抗压承载特性模型试验

1)抗压承载模型试验装置

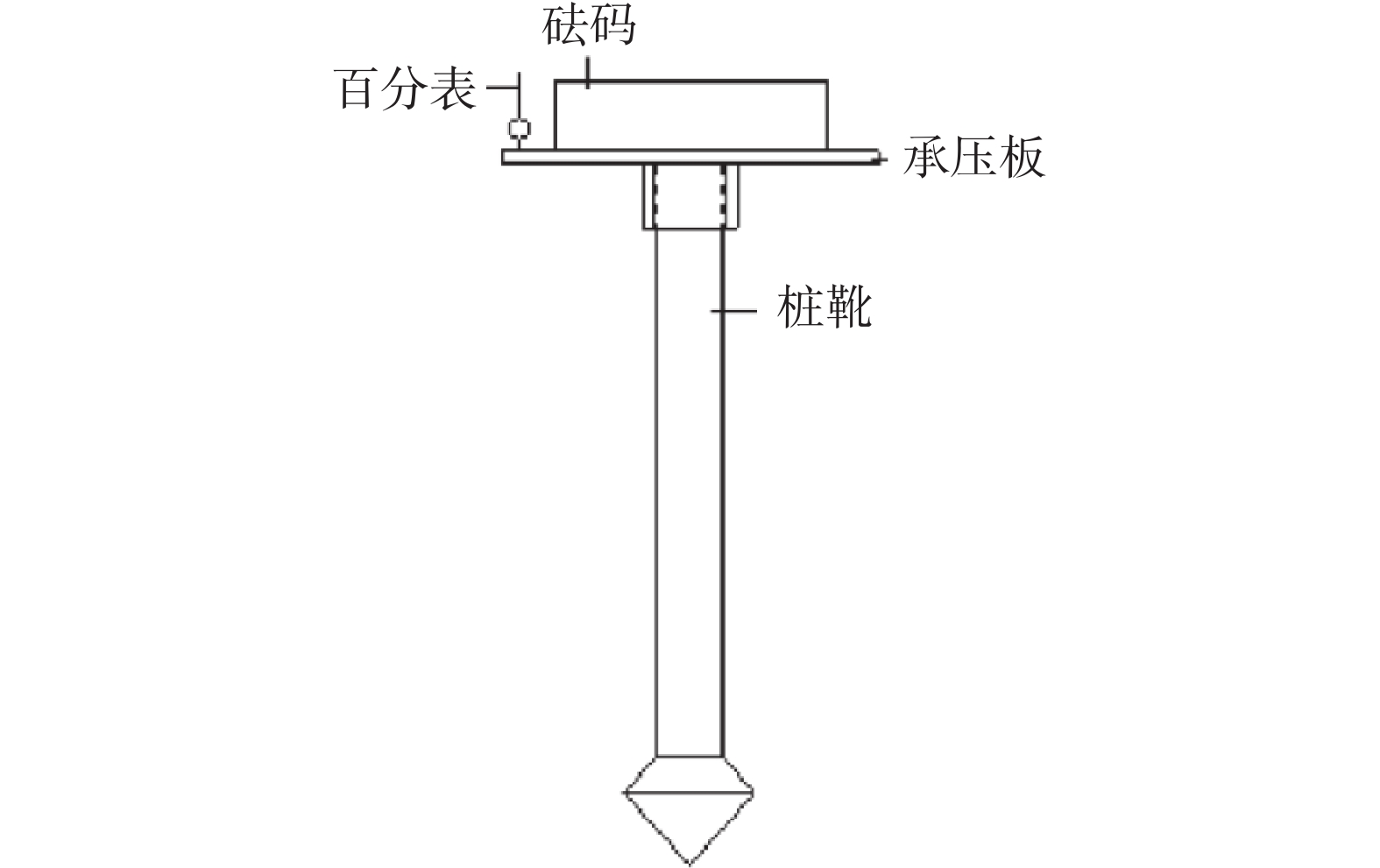
桩靴抗压试验装置如图1所示，主要包括模型箱、承载系统两部分。模型箱内部尺寸长×宽×高=2.0 m×1.2 m×1.2 m。承载系统如图2所示，包括承压板、百分表、砝码。承压板由空心圆管与钢板焊接而成，上部钢板承接砝码，下部空心圆管承接桩靴。

2)测量系统

测量系统包括DH3816N静态应变测试系统与哈量百分表等组件构成的荷载-沉降量测系统，试验开始前将BK120-3AA(11)型电阻应变片粘贴于桩身，并将应变片与应变采集仪相连，确保试验开始即可自动获取桩身应变数据。

图  1  桩靴抗压试验装置

Figure  1.  Spudcan compression test device

下载: 全尺寸图片 幻灯片

图  2  承载系统

Figure  2.  Bearing system

下载: 全尺寸图片 幻灯片

在进行抗压静载荷试验时，荷载直接施加在桩顶，因而可以直接计算荷载的质量和获取载荷荷载数据。

3)模型桩

本组试验所用桩靴模型由钢材预制而成。桩身直径分别为50 mm与100 mm，桩长505 mm，具体桩型如图3所示，图3(a)中从左至右分别为桩尖角75°的倒三角桩靴，桩尖角75°的100 mm等直径桩，桩尖角45°、60°、75°的圆台桩靴，桩尖角60°的50 mm等直径桩。

图  3  预制桩靴

Figure  3.  Prefabricated spudcan

下载: 全尺寸图片 幻灯片

4)砂土参数

模型试验用土为宁波某地的砂土，进行直接剪切试验以及三轴压缩试验，测得相关砂土土性参数见表1。

表  1  砂土土性参数

Table  1.  Parameters of sand

密度/(kg·m−3)	最小干密度/(kg·m−3)	最大干密度/(kg·m−3)	含水率/(%)	相对密实度	泊松比	弹性模量/(MPa)	摩擦角/(°)
1.441	1.311	1.778	28.02	0.323	0.3	0.2	15

下载: 导出CSV 

| 显示表格

1.2   桩靴贯入透明土试验

在桩靴抗压承载特性模型试验的基础上，发现此类传统岩土模型试验无法精确认识桩-土相互作用。因此，通过结合图像测量、透明土和PIV三种技术建立测量内部土体变形的透明土试验，并揭示桩靴的贯入机理。

1)透明土

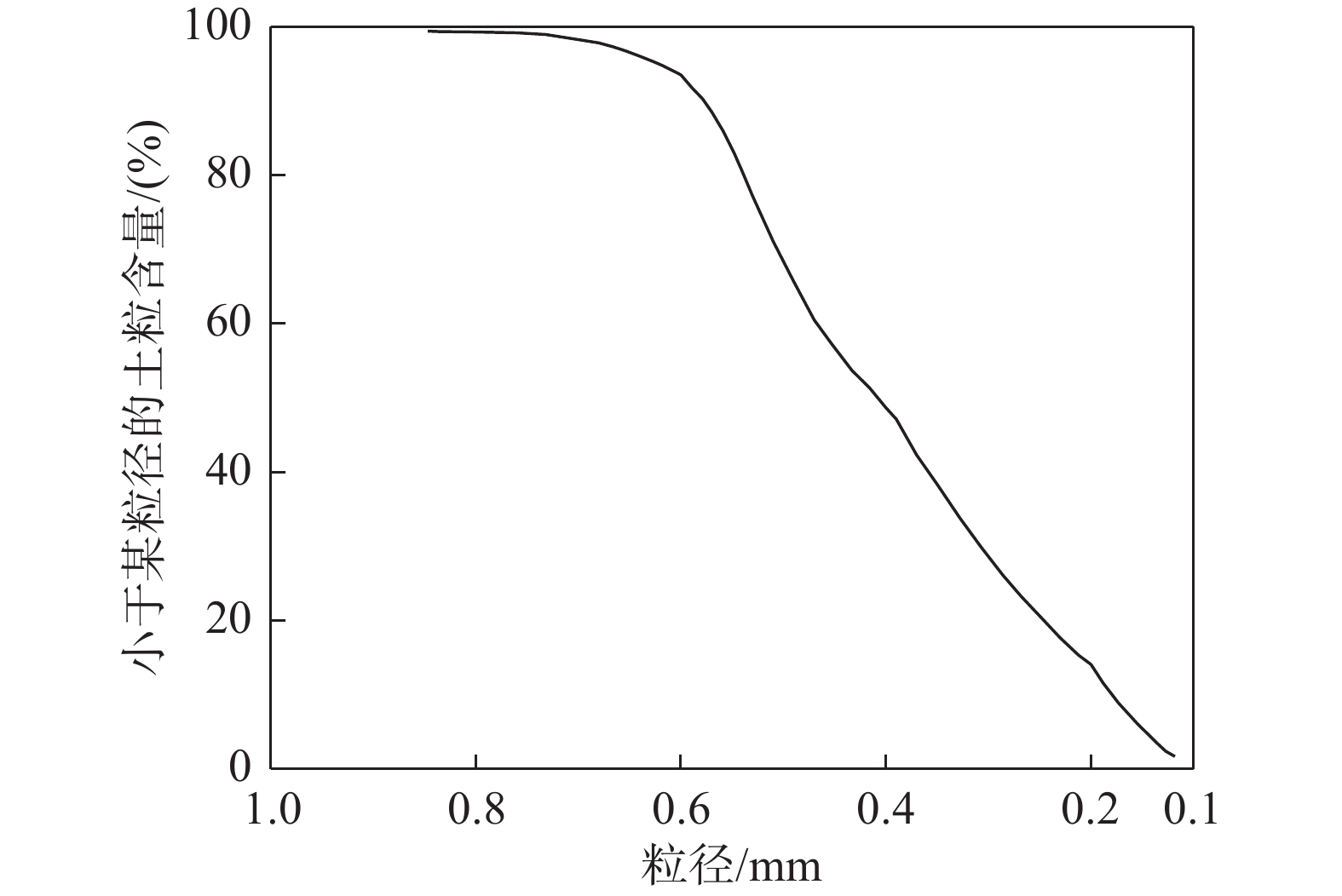
本试验采用由EZZEIN等^[22]研发的新式透明土，即由骨料(熔融石英)与孔隙溶液(Puretol7和Krystol40的混合液)混合构成。熔融石英的颗粒级配如图4所示。孔隙溶液由Puretol7与Krystol40按照1∶2.77的体积比配置得到。在20℃时，配置得到的孔隙溶液与熔融石英的折射率分别为1.458和1.459。根据齐昌广等^[23]、EZZEIN等^[22]和GUZMAN等^[24]所做的试验证明，本试验所采用的新式透明土的物理指标可基本视为与对应级配条件下的天然饱和砂土一致。通过试验测得配制完成的透明土最大干密度为1.222 g/cm³，最小干密度为0.963 g/cm³，相对密实度分别为0.231、0.665、0.821、0.930，分别模拟松散砂、中密砂以及密实砂的试验条件，通过图5的透明度检测，结果表明配置完成的透明土透明性符合预期，满足试验要求。透明土试验工况如表2所示。

图  4  熔融石英的颗粒级配

Figure  4.  Particle size distribution of fused quartz

下载: 全尺寸图片 幻灯片

图  5  透明性检测

Figure  5.  Transparency detection

下载: 全尺寸图片 幻灯片

表  2  模型试验工况

Table  2.  Model test conditions

试验编号	土样相对密实度	贯入深度记录点
T1	0.930	1.3R	2.1R
T2	0.821	1.3R	2.1R
T3	0.665	1.3R	2.1R
T4	0.231	1.3R	2.1R

下载: 导出CSV 

| 显示表格

2)试验设备

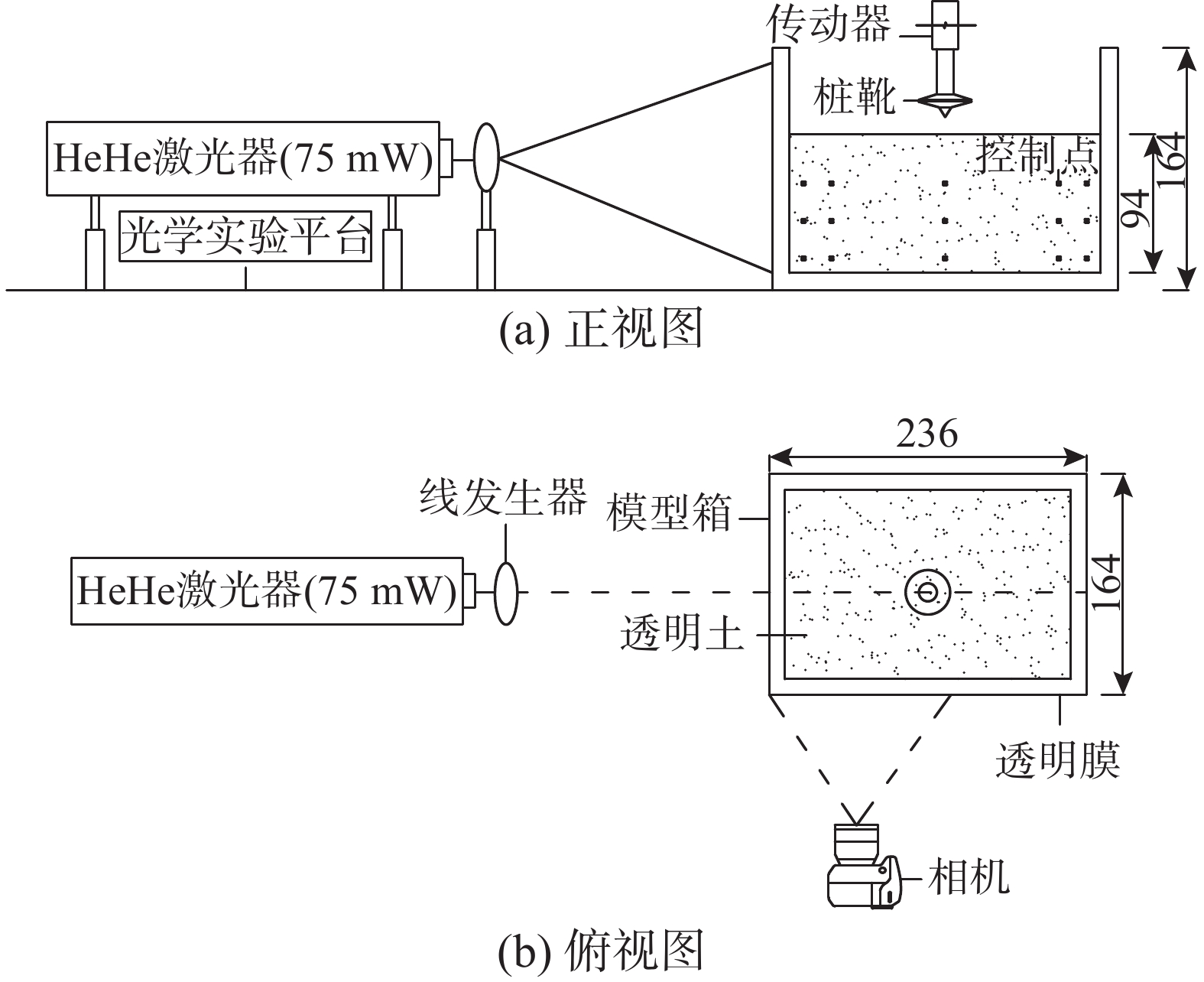
桩靴透明土模型如图6所示。模型试验装置包括模型箱、透明土、桩靴基础、数码相机、激光器、传动器，模型箱采用20 mm厚的有机玻璃制作而成，其尺寸：长×宽×高=236 mm×164 mm×164 mm。模型槽左侧设置氦氖型激光器，通过线发生器，将激光器上发射的激光束投射为激光面，增强透明土颗粒的可视化效果。桩靴模型通过其上的传动器施压而贯入透明土，在贯入过程中，用正前方架设的数码相机拍摄记录桩靴贯入的全过程，试验实物如图7所示。

3)模型桩尺寸

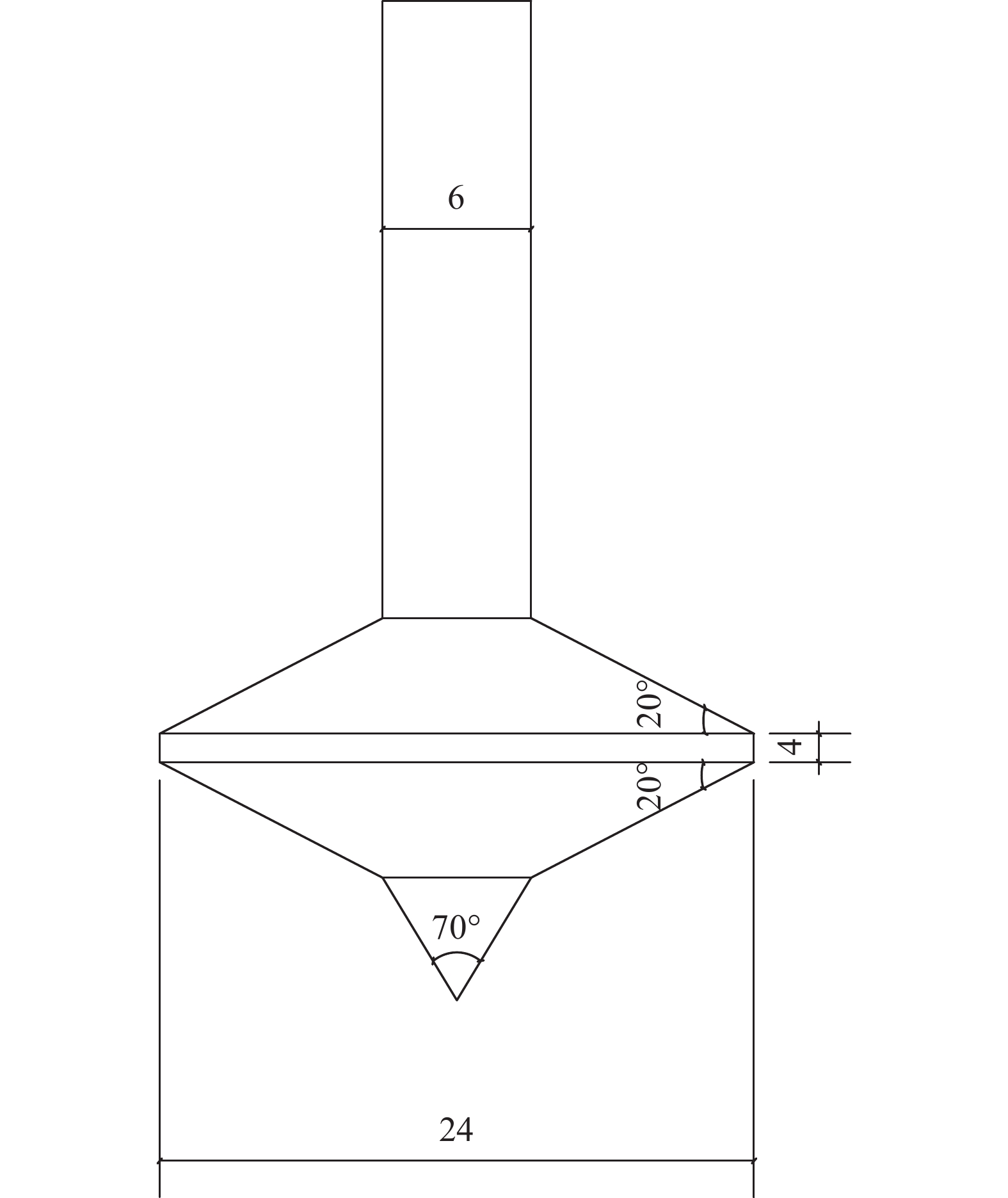
通过亚克力塑材制作与实际桩靴缩略比为1∶1000的桩靴模型，尺寸如图8所示，桩靴模型最大截面直径为24 mm，桩尖角为70°，中部两侧锥形内夹角为20°，中部隔板厚度为4 mm。

图  6  桩靴透明土模型示意图

Figure  6.  Schematic diagram of spudcan model experiment in transparent soil

下载: 全尺寸图片 幻灯片

图  7  桩靴透明土试验

Figure  7.  Spudcan experiment in transparent soil

下载: 全尺寸图片 幻灯片

图  8  桩靴尺寸示意图

Figure  8.  Schematic diagram of spudcan size

下载: 全尺寸图片 幻灯片

4)试验图像处理

常用的材料变形场测量技术有数字图像相关技术(DIC)^[25]和粒子图像测速法(PIV)。本试验图像处理采用GEO-PIV软件，该软件是由WHITE等^[26]利用PIV研究沉桩过程引起的土体变形过程中研发得出。其结合PIV原理，以MATLAB模块为基础，分析数字图像以得到变形位移场。另外，由于模型玻璃槽和透明土的折射率以及镜头畸变均会不同程度地影响分析结果，因此需注意提前修正处理。

2   试验结果与分析

2.1   承载特性试验结果分析

1)荷载-沉降曲线

根据不同桩尖角桩靴以及等直径桩的静载荷试验获得的荷载-沉降曲线如下图9所示。从图9可得知桩靴的荷载-沉降曲线与传统桩类似，均为缓变型，在曲线上没有出现拐点。桩靴的曲线介于50 mm与100 mm等直径桩之间，施加同等大小的荷载，桩靴的沉降小于50 mm的等直径桩，大于100 mm等直径桩，说明桩靴的设置在一定程度上增加了桩的下沉难度。

图  9  荷载-沉降曲线

Figure  9.  Load settlement curve

下载: 全尺寸图片 幻灯片

取沉降40 mm时50 mm等直径桩以及不同桩尖角桩靴承载力进行横向对比，分析数据得到桩尖角为45°、60°、75°桩靴承载力分别比50 mm等直径桩承载力提高了9.98%、16.95%以及22.03%。

而不同大小的桩靴的桩尖角度在静载荷过程中，不难分析得出桩尖角度的大小将影响桩的沉降，同样取沉降40 mm时承载力进行横向对比，桩尖角为75°桩靴承载力相比60°、45°桩尖角桩靴提高了10.96%和4.35%。

在45°~75°，随着角度的增加，桩的沉降愈加困难。

2)桩身轴力

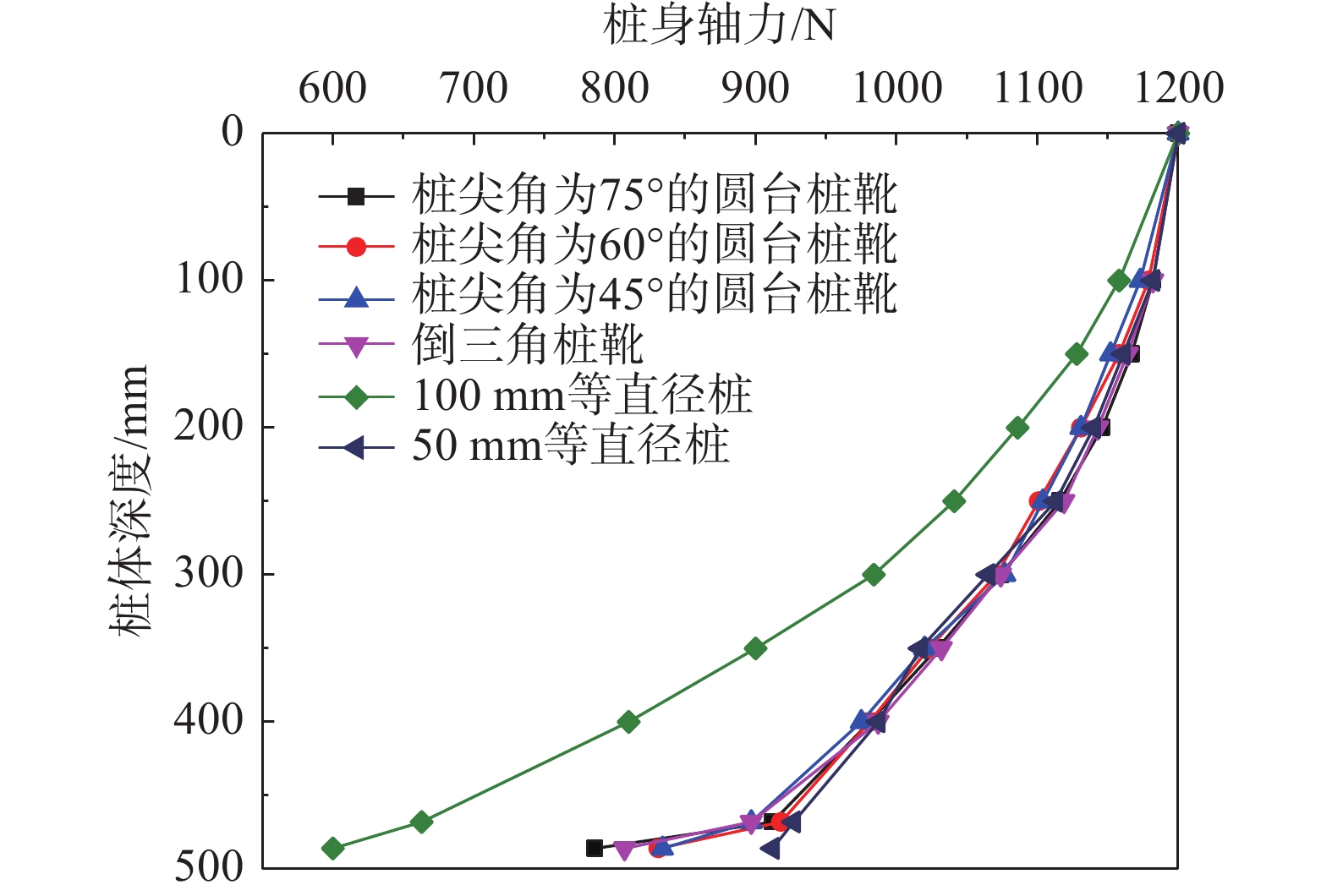
选取桩顶总荷载为1200 N时的轴力图进行分析，如图10所示。从整体上观测，由于桩身直径相同，桩侧摩阻力基本相同。而在桩端处，桩靴的轴力出现“台阶型”突变，减小的速度明显比50 mm等直径桩的速度快，可见桩靴结构增大了侧摩阻力。

图  10  桩身轴力

Figure  10.  Axial force of pile shaft

下载: 全尺寸图片 幻灯片

从局部上观测，可以发现桩尖角度对于桩端处的荷载传递也存在一定的影响。桩尖角75°桩靴及倒三角桩靴的轴力减小速度相比桩尖角45°和60°桩靴要快。这是由于桩尖角的增大，意味着桩端表面积的增大，与土体的接触面积也就更大，导致了桩端处的侧摩阻力存在一定的差别。

3)桩端阻力

根据图10发现不同桩尖角的桩靴的轴力变化相似，因此选用桩尖角为75°的桩靴与直径为50 mm的等直径桩进行桩端阻力对比分析。

图11为桩顶施加分级荷载时，桩端阻力所占桩顶荷载的比例。分析图11发现桩靴的桩端阻力占比明显高于等直径桩，说明桩靴结构能发挥更多的桩端阻力，提高桩的载荷能力。

在逐级加载过程中，桩靴桩端阻力占比前期增长缓慢，中后期呈跳跃式增长。这是由于前期施加荷载较小，桩靴侧摩阻力先于桩端阻力发挥。在施加荷载后期，桩端阻力占比跳跃式增长，由于荷载作用下桩靴对下部土体进行挤压，土体变得更加密实，促进桩端阻力的发挥。

图  11  各级荷载作用下桩端阻力占桩顶荷载的比例

Figure  11.  Ratio of pile end resistance to pile top load under various loads

下载: 全尺寸图片 幻灯片

2.2   贯入挤土效应试验结果分析

1)桩靴周围砂土位移向量

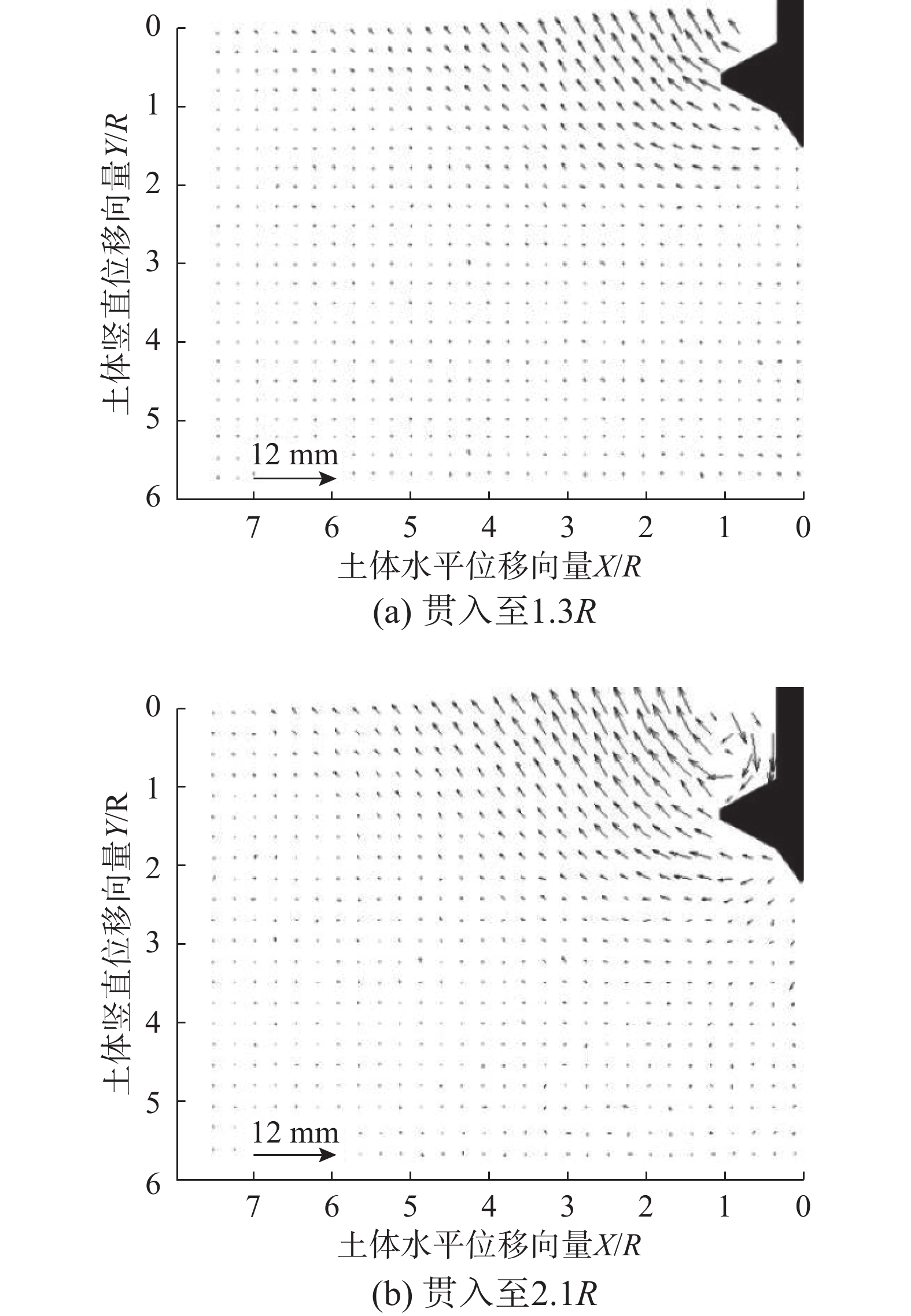
桩靴贯入相对密实度为0.821与0.930(密实砂)的透明土的位移向量如图12与图13所示。分析图12、图13得知，随着贯入深度的增加，桩靴周围土体扰动范围也随之扩大。贯入1.3R时，周围土体在水平方向上受影响范围为2.5R~3.5R，竖直方向上，受影响范围为1R~1.5R。而当贯入深度增加至2.1R时，周围土体在水平方向上受影响范围扩大至3.5R~5R，竖直方向上，受影响范围则为1.5R~2.5R。

图  12  桩靴贯入密实砂(相对密实度为0.821)的位移向量图

Figure  12.  Displacement vector diagram of supdcan penetrating dense sand (relative compaction is 0.821)

下载: 全尺寸图片 幻灯片

图  13  桩靴贯入密实砂(相对密实度为0.930)的位移向量图

Figure  13.  Displacement vector diagram of supdcan penetrating dense sand (relative compaction is 0.930)

下载: 全尺寸图片 幻灯片

以桩靴周围土体为研究对象，具体分析其位移趋势。从整体上观测，在桩靴贯入过程中施加的水平力和土颗粒间咬合摩擦的共同作用下，桩靴周围土体呈现倾斜向上的总体位移趋势。在竖直方向上，桩端上部的土体在靠近地表的方向位移较大。在水平方向上，桩靴周围土体的位移随着土体与桩距离的增大而减小。

从局部上观测，桩靴贯入深度为1.3R时，由于桩靴结构的特异性，土体往两侧偏移并在桩靴顶部形成空腔，这是因为贯入深度较浅且贯入时间较短，土颗粒未能及时回流导致的。随着桩靴的进一步贯入，当贯入深度逐步达到2.1R时，桩靴上部明显出现回流现象，回流土颗粒的位移相较于桩靴周围土颗粒较小。

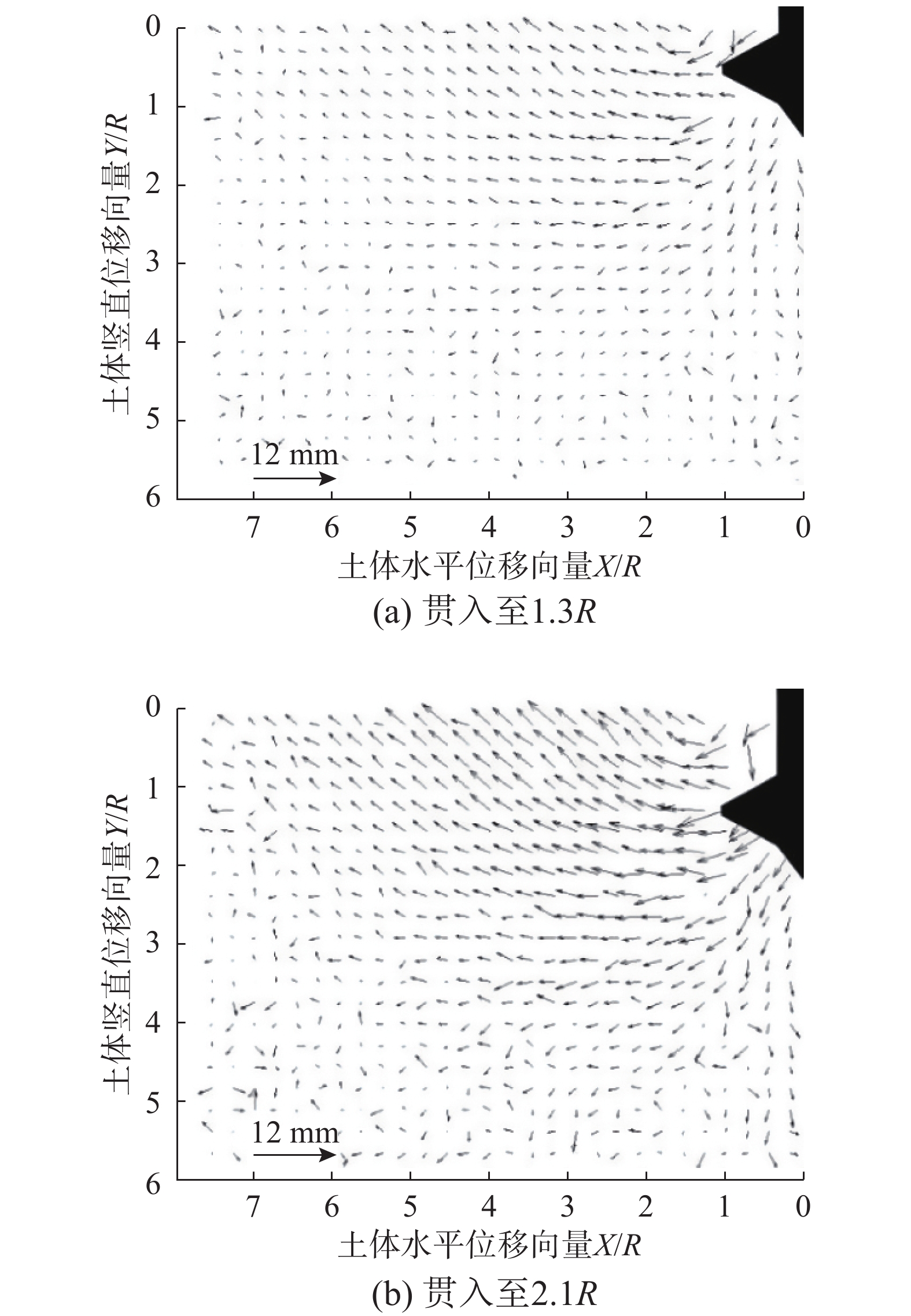
桩靴贯入相对密实度为0.665(中密砂)、0.231(松散砂)的透明土的位移向量如图14和图15所示。与图12、图13进行对比，图14、图15所观测到的土体位移向量更为混乱，其原因为随着土体相对密实度减小，土体颗粒之间的咬合摩擦作用也随之减小，导致桩靴贯入砂土所引起的挤压力在传递过程中减小的愈加缓慢，从而扩大了土体影响范围和土体位移程度。

图  14  桩靴贯入中密砂(相对密实度为0.665)的位移向量图

Figure  14.  Displacement vector diagram of supdcan penetrating medium dense sand (relative compaction is 0.665)

下载: 全尺寸图片 幻灯片

图  15  桩靴贯入松散砂(相对密实度为0.231)的位移向量图

Figure  15.  Displacement vector diagram of supdcan penetrating loose sand (relative compaction is 0.231)

下载: 全尺寸图片 幻灯片

2)桩靴周围砂土水平位移等值线图

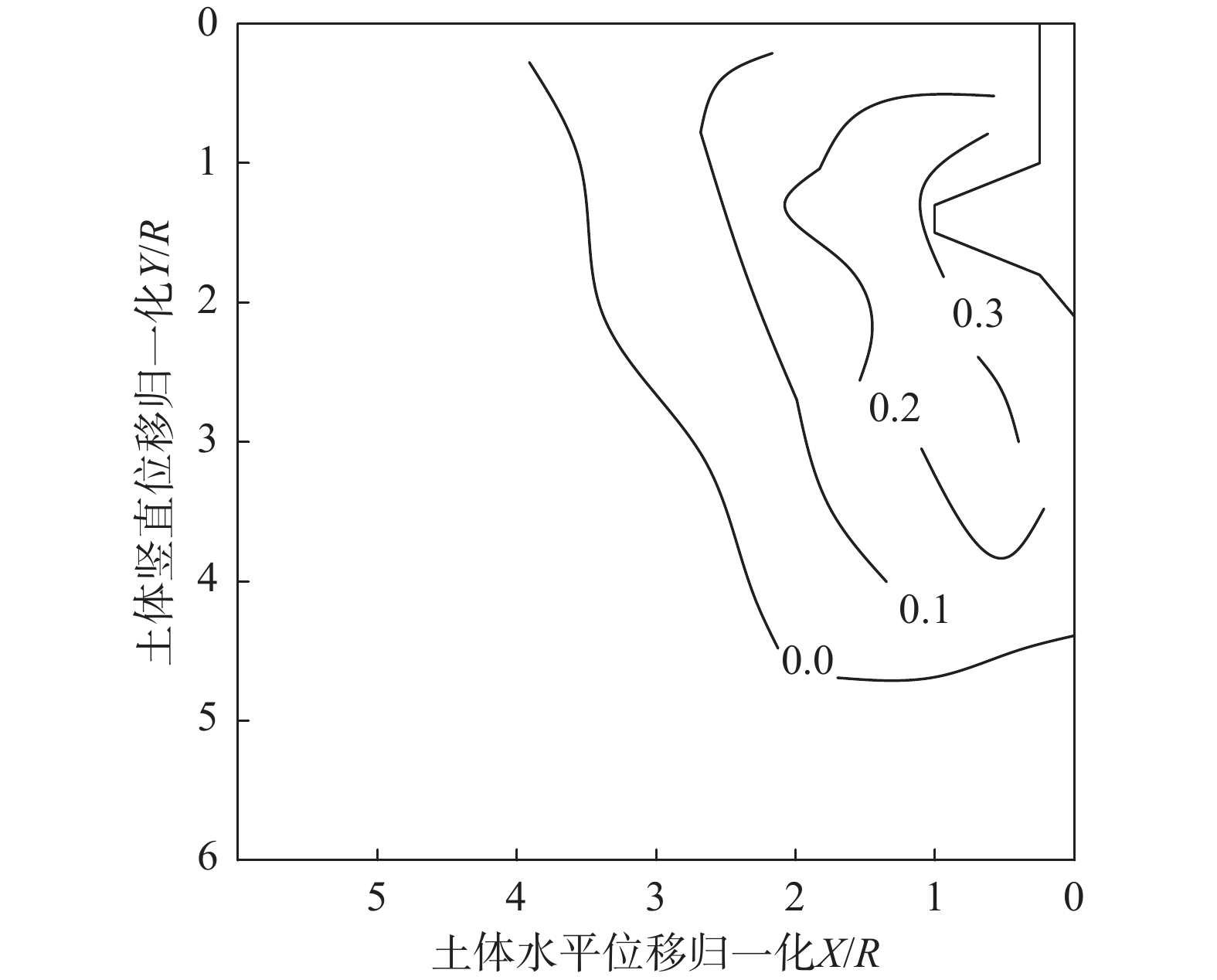
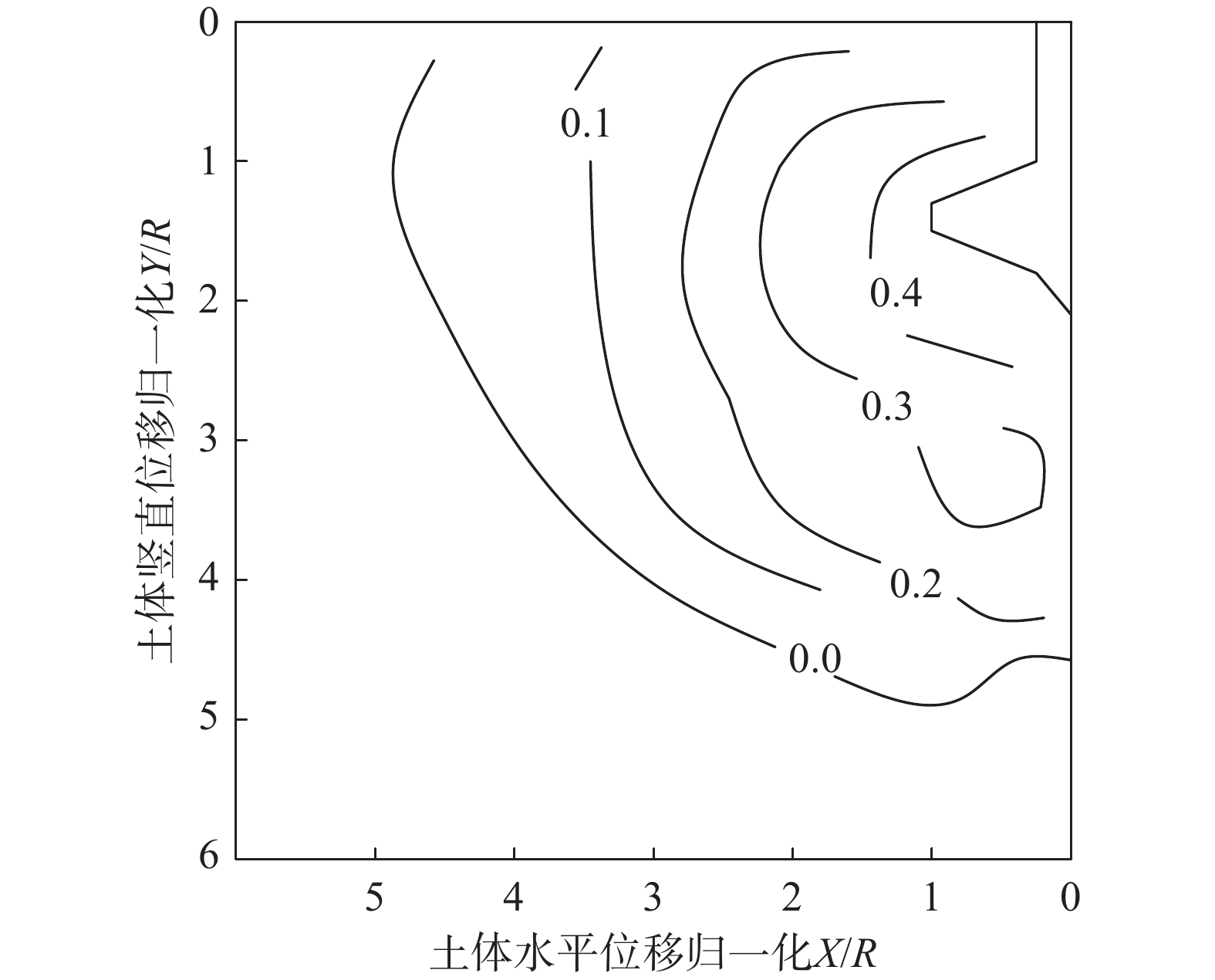
为定量地描述桩靴周围土体的位移，图16给出了桩靴贯入密实砂(相对密实度为0.930)至2.1R时，周围土体归一化水平位移等值线图。分析图16，桩靴周围土体的水平位移随着与桩靴距离的增大而减小，且越靠近地表的土层位移消减的趋势越慢。同时，桩靴上部的土体由于回流现象，回流土颗粒的位移相对桩靴周围土体较小。

图  16  桩靴贯入密实砂至2.1R时水平位移归一化等值线

Figure  16.  Normalized contour of horizontal displacement of spudcan penetrating dense sand to 2.1R

下载: 全尺寸图片 幻灯片

图17、图18则分别是桩靴贯入中密砂与松散砂至2.1R时，归一化桩靴周围土体水平位移等值线图。各组土体位移趋势大致相似，但由于土体相对密实度的减小，土体之间的咬合摩擦力大幅减小，使得桩靴在贯入土体时产生的水平挤压力影响土体的范围更大，相应的，土体水平位移也大幅增加。

图  17  桩靴贯入中密砂至2.1R时水平位移归一化等值线

Figure  17.  Normalized contour of horizontal displacement of spudcan penetrating medium dense sand to 2.1R

下载: 全尺寸图片 幻灯片

图  18  桩靴贯入松散砂至2.1R时水平位移归一化等值线

Figure  18.  Normalized contour of horizontal displacement of spudcan penetrating loose dense sand to 2.1R

下载: 全尺寸图片 幻灯片

3   理论与试验对比分析

3.1   理论介绍

1)桩靴荷载-沉降(Q-s)预测理论

通过圆孔扩张理论，可计算得到土体扩张弹塑性区域的土体内压力，从而得到桩靴在受压情况下的桩端阻力。通过桩侧阻力作为媒介，将桩体分为多段，采用分段位移迭代算法，便可求导得到桩靴的荷载-沉降曲线。

① 桩端荷载传递函数

圆孔扩张示意图如图19所示。

图  19  圆孔扩张示意图

注：${r_0}$为桩体半径；${r_{\text{u}}}$为圆孔扩张半径； ${\sigma _r}$为法向应力；${\sigma _\theta }$为切向应力。

Figure  19.  Schematic diagram of cavity expansion

下载: 全尺寸图片 幻灯片

周航等^[27]将圆孔扩张理论与弹性理论结合应用，推导得到圆孔内压与扩张半径的关系：

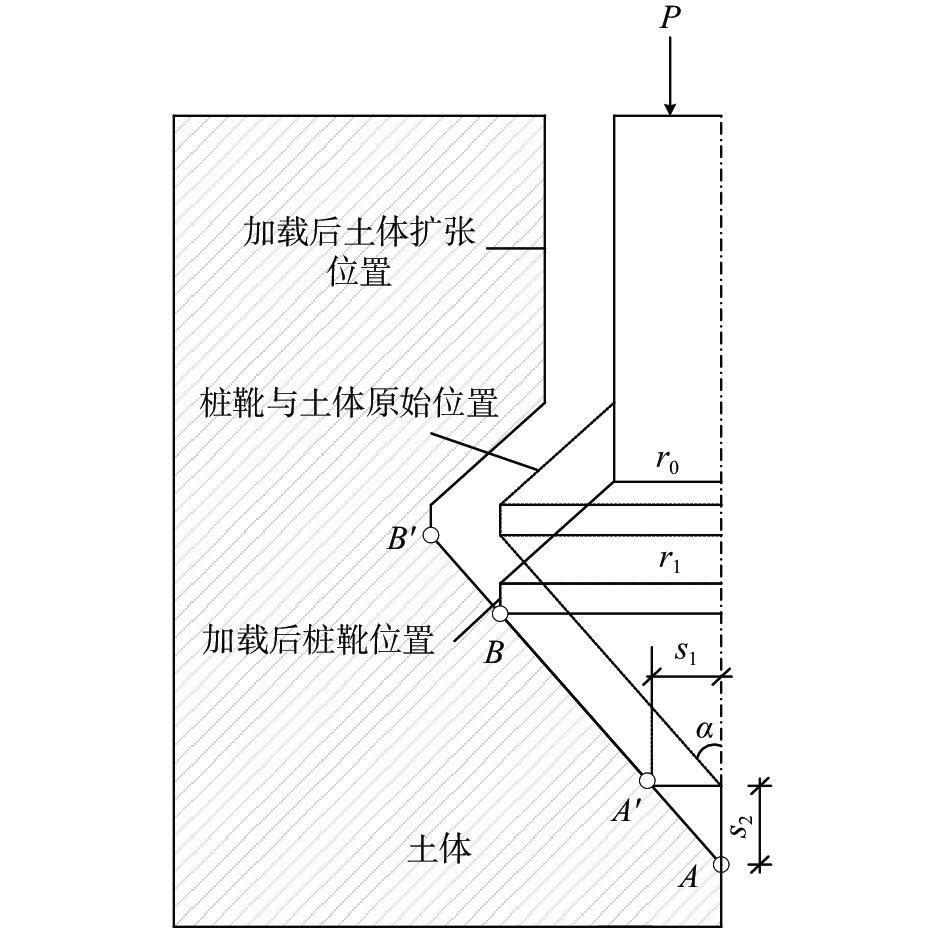
式中，$G$为剪切模量。

加压时桩靴-土体位移示意图如图20所示。在顶部施加大小为$P$的荷载后，桩靴从虚线位置下移至图中实线位置，并对桩侧土体产生大小为$p$的内压力，桩侧土体在此压力作用下往外扩张，此时土体相对桩靴，从A点移动至A′，从B移动至B′。

图  20  加压时桩靴-土体位移示意图

注：${r_0}$为桩身半径；${r_1}$为桩靴最大半径；$\alpha$为桩靴半桩尖角；${S_1}$为桩侧土体扩张水平位移；${S_2}$为竖直位移。

Figure  20.  Schematic diagram of spudcan displacement under pressure

下载: 全尺寸图片 幻灯片

从图20的几何关系可求出以下几何关系：

将式(2)代入式(1)可求得桩侧点A与点B的内压力：

假设平面AB内压力呈线性分布，因此将平面AB的平均内压力取作平面AB的实际内压力，即：

如图21所示，平面AB的切向应力与法向应力的大小应当满足摩尔-库仑强度理论，即：

式中：$c$为土体粘聚力；$\varphi$为土体内摩擦角。

图  21  平面AB受力分析

Figure  21.  Force analysis of surface AB

下载: 全尺寸图片 幻灯片

根据应力平衡定理，可求得平面AB的法向内压力与切向内压力，如式(7)：

式中：${p_{\text{v}}}$为竖向内压力；${p_{\text{h}}}$为水平内压力。

圆孔扩张理论中，假设挤土桩在桩土界面每个“平面”、每个单元同时都在进行着水平向外的扩张，由此可以推论得到，桩靴-土体界面的实际内压力应与土体水平内压力相等，即：

解得：

竖向内压力的公式中，需先计算得到切向应力与法向应力，根据文献[28]中的应力表达式即可求得，即：

式中：$\gamma$为土体重度；$H$为桩体深度；${K_0}$为土体侧压力系数；$\varphi$为土体内摩擦角。

计算竖向应力所占用投影面积：

将竖向内压力乘以竖向应力所占用投影面积即可得到桩端阻力。

②桩侧荷载传递函数

刘方成等^[29]通过单剪试验，设置不同法向压力，分析得到不同粗糙度界面下，桩侧接触面的剪应力随桩体位移的变化曲线，如图22所示。为将得到的变化曲线应用于桩靴荷载-沉降中，将相应的见剪应力-位移函数拟合成对数函数，如式(13)所示。

式中，$n$为桩侧摩阻调整系数。

图  22  剪应移曲线^[29]

Figure  22.  Shear stress and displacement curve^[29]

下载: 全尺寸图片 幻灯片

考虑到桩土界面的粗糙度的不确定，应结合实际工况来确定。在下文算例分析中，由于采用的桩由钢材料制成，并在稍松砂土中进行试验，因而$n$值取的相对较小，为1.5。

③分段位移迭代算法预测桩靴沉降

通过张乾青等^[30]采用的公式来求得桩身位移，即式(14)：

式中：${w_{\rm t}}$为桩顶沉降；${\varepsilon _j}$为第j段桩的桩身应变；${\varepsilon _{j + 1}}$为第j+1段桩的桩身应变；$L_j$为第j段桩长。

采用分段迭代法进行桩靴沉降预测计算，步骤如下所示：

1)将桩身分割成“$n$”份，桩端扩颈处单独分割为1份。

2)假设桩端位移为$w$并代入式(12)，求得桩端轴力，桩端轴力记作记作${p_{\text{n}}}$，随后将位移与求得的轴力用于递推。

3)将步骤2)求解出的轴力作为第$n - 1$段桩的底部轴力，即${p_{{{(n}} - {\text{1)b}}}} = {p_{{n}}}$。

4)求解出第$n - 1$段下半段的压缩量为：

式中：${E_{\text{p}}}$为桩体的弹性模量；${A_{{{n}} - {\text{1}}}}$为第$n - 1$段桩身截面面积。

5)步骤2)求解出的位移量作为第$n - 1$段桩底部的位移${w_{{{(n}} - {\text{1)b}}}}$，将位移相加，即可得到第$n - 1$段中点的位移，即：${w_{{{(n}} - {\text{1)d}}}} = {w_{{{(n}} - {\text{1)b}}}} + {w_{{{(n}} - {\text{1)c}}}}$。

6)将步骤5)求解出的位移代入式(13)，求出第$n - 1$段桩侧摩阻力${\tau _{{{{\rm{s}}{\rm{(}}{{n}}}} - {{1{\rm{)}}}}}}$，则根据式(15)可计算得到第$n - 1$段桩的总侧摩阻力：

将第$n - 1$段的总侧摩阻力与桩端轴力相加即可得到$n - 1$段桩顶的力：

7)假设第$n - 1$段桩轴力线性分布，取第$n - 1$段桩的平均轴力，可得到$n - 1$段桩体下半段的压缩量修正值：

8)将步骤7)求得的压缩量修正值代回步骤5)，得到第$n - 1$段的位移修正值：

9)将修正的位移值${w'_{{{(n}} - {\text{1)d}}}}$代入式(13)，得到桩的修正侧摩阻力，再将所求得的修正侧摩阻力代入式(15)，得到修正后的桩侧总侧摩阻力${p'_{{{(n}} - {\text{1)s}}}}$，代入式(16)，得到第$n - 1$段修正后桩顶轴力${p'_{{{(n}} - {\text{1)t}}}}$，通过下式求出第$n - 1$段桩总位移：

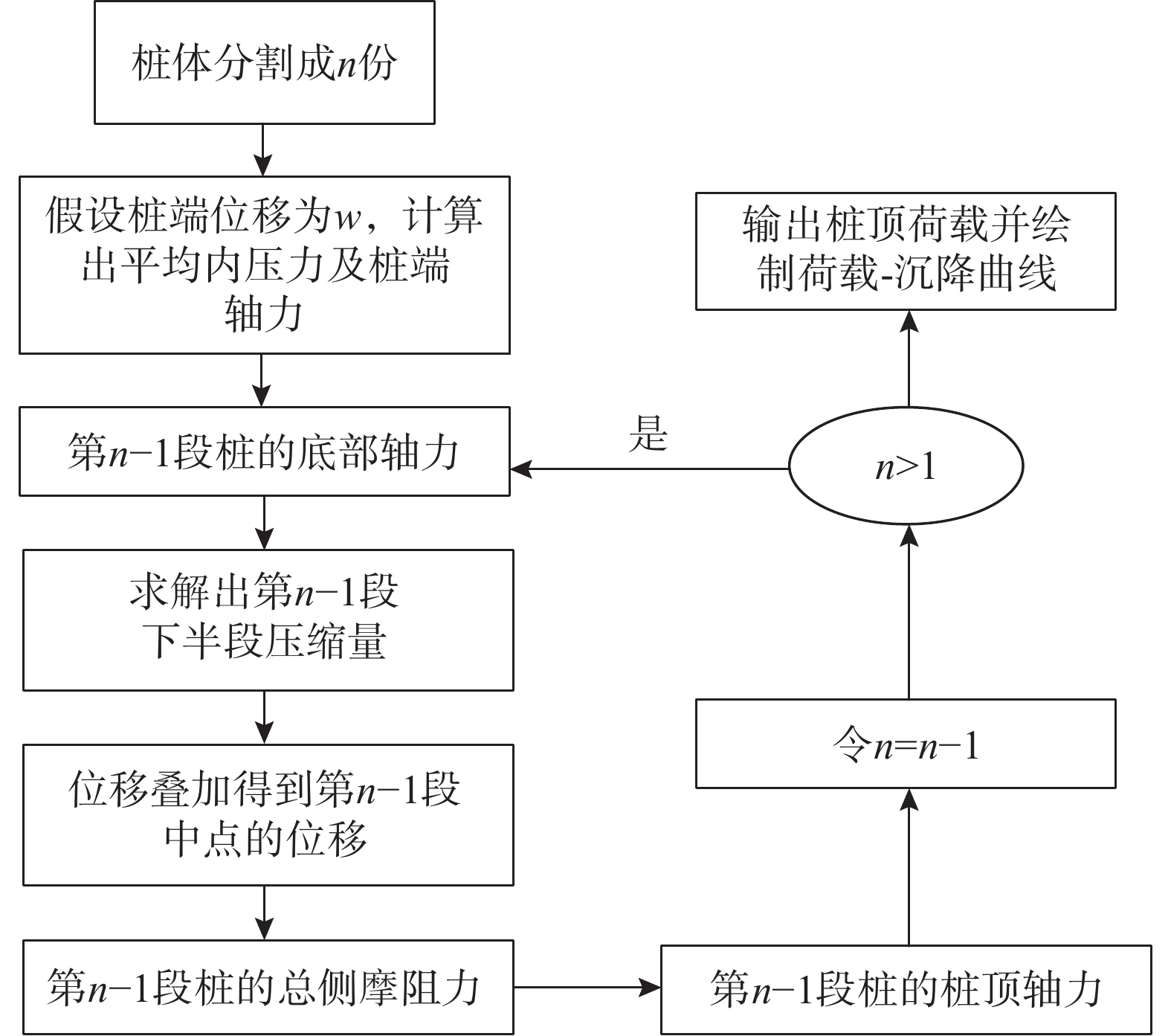
第$n - 1$段桩的位移与力求解完成后，再去求解第$n - 2$段的底部桩力${p_{{{(n}} - {\text{2)b}}}} = {p'_{{{(n}} - {\text{1)t}}}}$，底部位移${w_{{{(n}} - {\text{2)b}}}} = {w_{{{(n}} - {\text{1)t}}}}$再重复步骤4)~步骤9)，为减小位移累计过程中的计算误差，此时假设桩侧摩阻力与第$n - 1$段的阻力相同，再求解出第$n - 2$段的位移与轴力。随后经过同样步骤，不断向上迭代递推，最后获得第1段的位移与桩顶荷载，绘制出荷载-沉降曲线。

迭代流程如图23所示。

图  23  迭代流程图

Figure  23.  Iteration flow chart

下载: 全尺寸图片 幻灯片

④算例分析

桩靴材料采用弹性模量为206 GPa得钢材，桩尖角为60°，桩长为505 mm，预埋深度为450 mm，桩身直径为50 mm，桩端最大直径为100 mm。土体性质为均质松散砂土，泊松比为0.3，切内摩擦角为15°，土体的弹性模量为0.2 MPa，剪模量为$G = \dfrac{E}{{{\text{2(1}} + \nu {\text{)}}}} = 0.077{\text{ MPa}}$，土体重度为20 kN/m³。

将桩靴分成9段，第9段位桩端扩颈部分，每段长50 mm。

从上述工况可知，桩端位移为4 mm，将其代入式(15)，解得：

下面求解法向应力${\sigma _{\text{n}}}$和切向应力$\tau$：土体侧压力系数${K_0} = 1 - \sin \varphi = 1 - \sin {15^ \circ } = 0.741$，代入式(10)求得切向应力。

将内压力与切向应力代入式(12)，解得桩端阻力：

将上述求解得到的桩端阻力作为第8段底部力${p_{{\text{8b}}}} = 153.59\;{\text{N}}$，将其代入步骤3)，求解该段下半段的压缩量，如下所示：

由此可知，桩体自身因荷载产生得桩身压缩量极小，可忽略不计。因此，总位移量可视为不发生变化，即${w_{{\text{8d}}}} = {w_{{\text{8t}}}} = {S_2} = 4{\text{ mm}}$。

桩侧摩阻力求解：

将所求得的位移代入式(13)得：

计算第8段桩侧总摩阻力：

将第8段总侧摩阻力与底部力相加，即可得到第8段桩顶轴力：

考虑到桩身本身压缩量可忽略不计，因此步骤7)~步骤9)的压缩量修正可以省略不计算。因此第7段桩总位移量与第8段相同，桩侧摩阻力及桩侧总摩阻力均相同，所以第7段桩顶的轴力大小为：

同理可通过计算得到第6段~第1段的轴力大小分别是：178.28 N、186.51 N、194.74 N、202.97 N、211.2 N、219.43 N。

通过计算，当桩体沉降量达到4 mm时，桩顶荷载为219.43 N。

按照同样的计算步骤，可求得不同沉降量的桩顶荷载，即可绘制荷载-沉降曲线，具体算例分析过程不再赘述。

2) SSPM

SSPM通过源、汇在z=0处，以速度U分别向h、−h方向运动，以此确定各处土体所产生的速度，再考虑地表应力自由面，利用一个修正的剪切应力来抵消源、汇共同作用下在地表产生的两倍剪应力，最终将源、汇以及修正剪切应力单独作用下得到的土体速度沿源、汇运动方向积分得到位移场，土体位移的最终解是通过三部分位移场相互叠加所得，表达式如下：

式中：$({x_0},{{\textit{z}}_0})$为土颗粒初始坐标；${v_{xi}}(x,{\textit{z}},h)$为土颗粒产生的径向速度，$i = 1,2,3$分别对应源、汇和修正剪应力单独作用；${v_{{\textit{z}}i}}(x,{\textit{z}},h)$为土颗粒产生的径向速度，$i = 1,2,3$分别对应源、汇和修正剪应力单独作用；$h$、$- h$为源、汇所处的竖向位置。

3.2   对比分析

1)桩靴荷载-沉降(Q-s)曲线

由圆孔扩张理论、分段位移迭代算法推导出桩靴静载荷作用下的荷载-位移变化规律，进行理论计算，再与模型试验结果进行对比，得到荷载-沉降曲线对比图如图24所示。

图  24  荷载沉降曲线实测值与理论值对比

Figure  24.  Comparison between measured and theoretical load-settlement curve

下载: 全尺寸图片 幻灯片

分析图24可得，理论结果与试验结果相近，曲线皆为缓变型，计算误差约为11.6%，一定程度上可验证所推导理论的准确性。

2)桩靴周围土体水平位移

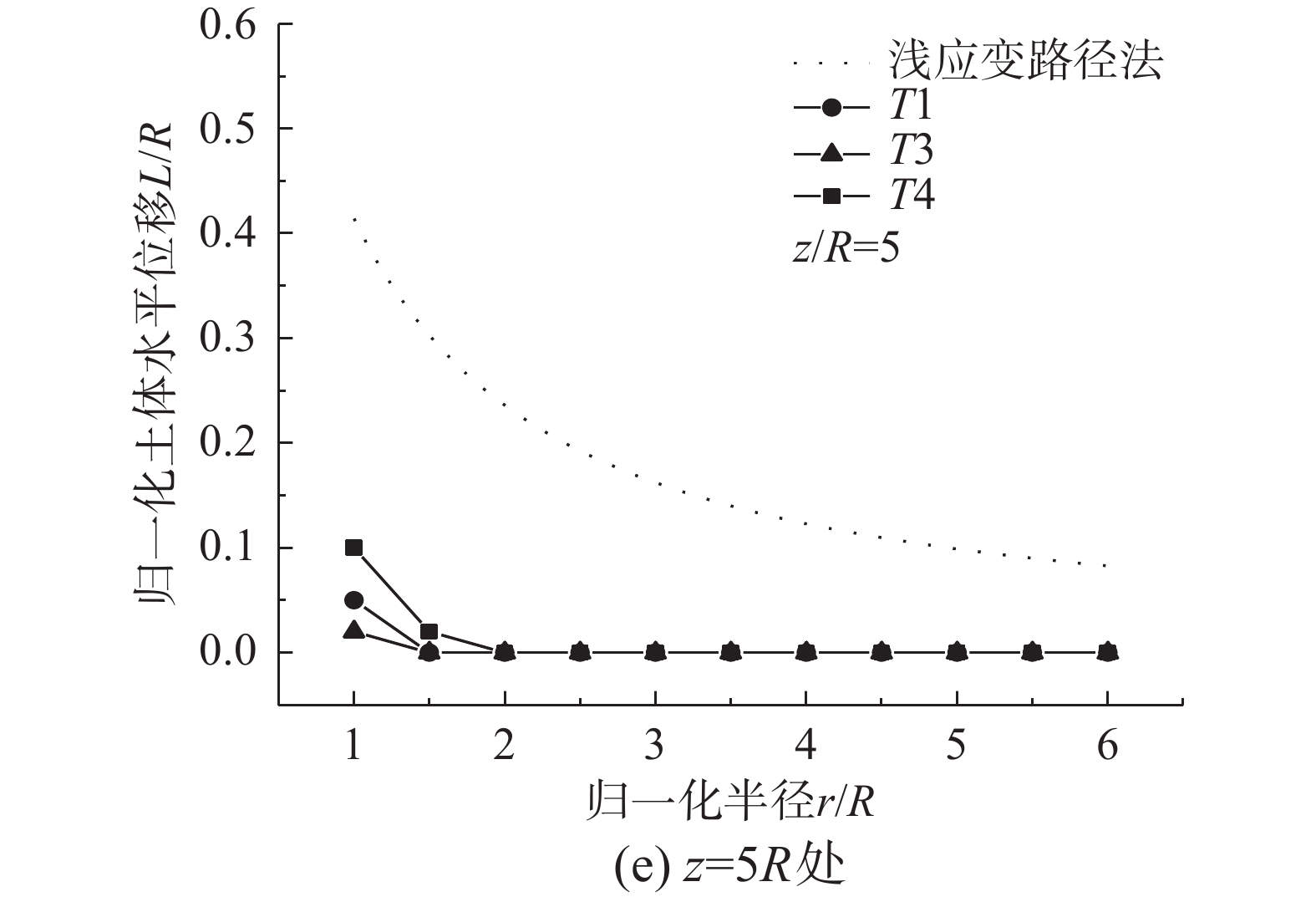
将T1、T3、T4试验中的桩靴周围土体水平位移与进行归一化处理后的SSPM结果进行比较。如图25所示，选取桩靴贯入深度H等于2.1R，沿桩靴高度z分别选取1R、2R、3R、4R、5R处的土体水平位移与理论结果进行比较，图中横坐标为归一化半径$r/R$，纵坐标为归一化的水平位移$L/R$。

下载: 全尺寸图片 幻灯片

  25  桩靴贯入至2.1R时各深度的水平向位移

  25.  Horizontal displacement at different depth caused by spudcan penetration to 2.1R

下载: 全尺寸图片 幻灯片

分析图25可得，各组试验结果和浅应变路径理论解关于水平位移的变化规律基本一致，考虑到桩靴结构的特异性以及模型试验存在边界效应，当${\textit{z}}/R = 2$且$r/R \lt 4$时，T1、T3、T4三组水平位移变化规律与理论解的计算误差为16.7%~26.3%。

从整体分析，显然随着土体密实度的减小，桩靴贯入对周围土体位移产生的影响愈加显著，且影响范围也更大。从局部分析，当${\textit{z}}/R = 1$且$r/R < 4.5$时，T4的试验数据大于浅应变路径法，这是低相对密实度土体颗粒间咬合摩擦作用微弱而引起的；当${\textit{z}}/R = 1$且$r/R > 4.5$时，T1、T3、T4的水平位移均小于浅应变路径法，这主要是由于模型试验的边界效应；当${\textit{z}}/R = 5$时，T1、T3、T4的水平位移基本相同，接近于0，说明桩靴贯入过程对于桩端底部土体的影响范围大致为3R。

4   结论

基于桩靴的抗压模型试验，研究桩靴的荷载-位移曲线及桩身轴力传递规律，后续对相关理论进行推导；基于数码摄影/摄影测量、透明土和PIV设计桩靴贯入砂土的透明土试验，研究桩靴周围砂土的变形机理，主要结论如下：

(1)桩靴的抗压性能比等直径桩的相对更好，桩尖角为45°、60°、75°桩靴承载力分别比50 mm等直径桩承载力提高了9.98%、16.95%以及22.03%；且随着桩尖角的增大，桩靴的抗压效果增大，桩尖角为75°桩靴承载力相比60°、45°桩尖角桩靴提高了10.96%、4.35%；桩身轴力自桩顶向下缓慢减小，在桩端处出现突变，原因是桩端阻力较大；逐级加载过程中，桩靴桩端阻力占比前期增长缓慢，后期跳跃式增长。

(2)基于圆孔扩张理论的分段位移迭代预测桩靴沉降的研究，绘制桩靴荷载-沉降理论值曲线图，并与承载试验结果进行对比分析，计算误差约为11.6%，一定程度上说明所推导理论的可行性。

(3)从透明土试验中观测到桩靴周围土体呈倾斜向上运动，贯入深度为1.3R时，桩靴上部土体往两侧挤压，在上部形成空腔，当贯入深度逐步达到2.1R时，桩靴上部明显出现回流现象，回流土颗粒的位移相较于桩靴周围土颗粒较小。桩靴周围土体的位移变化与土体的相对密实度有关，随着土体相对密实度的减小，桩靴周围土体的影响范围增大，土体颗粒的位移减小趋势缓慢。

(4)通过透明土模型试验，得到桩靴贯入过程中桩靴周围土体水平位移向量与等值线图，将试验结果与浅应变路径理论解进行对比，两者变化规律大致相同，当${\textit{z}}/R = 2$且$r/R \lt 4$时,各组水平位移变化与理论值的误差在16.7%~26.3%，一定程度上验证了模型试验的准确性。