随着人口和经济活动不断向沿海地区聚集，避免海啸对沿海地区造成破坏变的越来越重要。海啸是一种长波，通常由地震或海啸产生，为了模拟海啸波，孤立波常被用来作为海啸波^[1-2]近似值。因此以孤立波为参考，从数值方面研究了孤立波与防波堤相互作用的水动力特性。防波堤是一种常见的海岸防护工程结构，分为直立式防波堤^[3]、斜坡式防波堤、潜堤^[4-5]、浮式防波堤^[6]、透空式防波堤等。帷幕式防波堤，属于透空式防波堤的一种，其上部是由垂直的刚性薄板构成，从水面上方一直延伸到水面下方，距离海底有一定的距离，下部是透空的，如图1所示。由于波浪能量主要集中在水面附近，此结构可阻挡水面附近的大部分波能，小部分能量由下部透过。帷幕式防波堤不仅能够抵御外浪保护临海的建筑，也能实现外部海水和内部海水之间的交换，从而维持港内外水域生态平衡，因此越来越受到研究界和工程界的关注。

图  1  帷幕式防波堤三维结构图

Figure  1.  Three-dimensional structure drawing of curtain breakwater

下载: 全尺寸图片 幻灯片

学者对帷幕式防波堤开展了研究，URSELL^[7]初步研究了波浪与帷幕式防波堤相互作用，求解了无限水深情况下薄板帷幕式防波堤的透射和反射的解析解。WIEGEL^[8]针对其透反射系数的求解，开发了一种基于Power transmission的理论，并以实验数据来验证。REDDY和NEELAMANI^[9]改进了Power transmission理论，并通过实验研究了深水波的波陡度和浸没深度的特性与透射系数K_t和反射系数K_r的关系。LOSADA等^[10]通过特征函数展开法分析了帷幕式防波堤的K_t，并与WIEGEL的结果进行了比较。K_t随着浸入屏障相对长度的增加而减小，K_t的衰减率随着kd的减小而减小(k为波数，d为水深)。ABUL-AZM^[11]提出了基于二维势流理论的特征函数解来估计波的透射和反射，K_t和K_r随浸入屏障长度的变化趋势与LOSADA等^[12]一致。COOKER等^[13]使用边界积分法来求解孤立波与垂直墙壁的碰撞，并引入波峰停留时间，即波峰附着在壁上的时间的概念。MADSEN等^[14]提出一种新的Boussinesq方法用来模拟孤立波与垂直墙壁的相互作用。LIU和LI^[15]基于线性波势能理论下，利用本征函数展开法和最小二乘法，分析波浪透过两列帷幕式防波堤的水动力特性。岳景云等^[16]利用多领域边界元素法(Multi-domain BEM)，研究了传统帷幕墙与水平空隙板相结合的复合式帷幕式防波堤的消浪特性。

由于疏忽了粘度，基于势流的研究难以准确预测涡量场和强非线性，例如波浪破碎和空气滞留。随着计算技术的发展，基于Navier-Stokes(N-S)方程的数值模型广泛应用于波浪与海岸工程结构的相互作用的研究，数值模型又分为网格法和无网格法^[17-18]。GOTOH等^[19]用SPH-LES模型研究了规则波与帷幕式防波堤的相互作用，自由面大变形与实验吻合较好。波浪能耗散的主要原因是湍流产生和涡旋脱落。SHAO^[20]利用ISPH模拟了孤立波与帷幕式防波堤的相互作用，研究了帷幕式防波堤的冲击力和反射、透射特性。如果浸入深度超过一半水深，帷幕式防波堤在消散波浪能方面更有效。

基于网格点物理值及其空间导数值的紧致差分格式，CIP具有结构稳定、数值耗散低的特点^[21-22]，因此广泛应用于许多流体问题的求解，如波浪破碎、气液混掺等。HU和KASHIWAGI^[23]利用CIP模拟了不同波周期波浪与浮式结构的相互作用，发现了当周期为0.7 s时有甲板上浪现象，ZHAO和HU^[24]基于CIP模拟了规则波、聚焦波以及它们的组合波与浮体之间相互作用，HU等^[25]基于CIP模拟了不同角度的楔块在入水过程的不同现象，ZHENG等^[26]对复杂几何形状的入水问题进行了模拟，提高了精度。WEN和QIU^[27]使用改进的CIP算法进行三维物体入水模拟，YOU等^[28]使用CIP法模拟了孤立波与水下水平板的相互作用，韩新宇等^[29]通过CIP方法模拟了二阶斯托克斯波在不同坡度的复式防波堤下的爬高情况，何广华和油锐^[30]利用CIP分析了孤立波与斜坡上的梯形防波堤作用的过程，陈更和董胜^[31]基于CIP方法模拟了液舱晃荡，分析了隔板对液体晃荡的抑制作用。

本文基于N-S方程建立数值模型，对流项采用高阶紧致差分格式CIP求解，自由液面的捕捉采用WLIC-THINC方法^[32]。建立固-液-气三相流的二维数值水槽模拟孤立波的产生及其冲击帷幕式防波堤的演变过程，并与文献结果进行对比，结果表明CIP方法可以有效地模拟波浪与防波堤之间的强非线性作用。因此本文将采用CIP数值方法讨论帷幕式防波堤尺度对消波的影响。

1   控制方程和数值算法

1.1   控制方程组

模型基于不可压缩的二维N-S方程如下：

式中：x_i(i=1,2)为笛卡尔坐标系；${s_{{ij}}} = \dfrac{1}{2}\left( {\dfrac{{\partial {u_{{i}}}}}{{\partial {x_{{j}}}}} + \dfrac{{\partial {u_{{i}}}}}{{\partial {x_{{i}}}}}} \right)$；t为时间；ρ为流体密度，取1000 kg/m^3；p为压强；μ为动力粘度系数，取0.001 N·s/m²；f_i为质量力。

为了区分不同计算区域内的不同介质，如水，固体与空气，引入体积函数${\varphi _{{m}}} ( {{{m = 1,2,3}}} )$，满足方程：

式中，m=1,2,3分别为液体、气体以及固体，同一网格中固液气三相之和为1。计算区域内的固体处理为内部单元，视其为密度无限大的流体，将问题转化为多相流的问题。

式中，λ为网格内特征参数，可为流体密度或黏性系数。

1.2   造波方法和消波边界

造波方法采用边界造波，其基本原理是造波机推板运动的速度赋值给位于造波边界的流体。故在孤立波周期内，造波机推板运动由下式控制：

HAMMACK和SEGUR^[33]通过理论和实践证明，高于静止水位的水体释放至少会产生一个孤立波和一系列的弥散波。为了保证在数值模拟孤立波的时候尽量产生更少的拖尾波并保持稳定的波形，故使用GRIMSHAW^[34]推导出的孤立波三阶解。

式中：η为波面；U和W分别为水平速度和垂直速度；${{S = {\rm sech}}}\vartheta \psi$，$T = \tanh \vartheta \psi$和${\vartheta ^2} = 3/4{d^{ - 3}}$。

在数值水槽中，因为水槽的长度是有限的，所以当波浪到达计算的边界时会产生反射波，反射波会影响模拟结果的准确性，为了在数值模拟的过程中减少反射波，需要在数值水槽的末端设置阻尼消波层，在消波阻尼区里加入人工黏性耗散项，来达到阻尼消波的目的。本文采用的人工粘性系数如下：

式中：$x_1^{\rm{s}}$、$x_1^{\rm{e}}$和$x_3^{\rm{t}}$、$x_3^{\rm{b}}$为人工阻尼消波区的边界；$x_3^{\rm{f}}$为自由表面的平均位置。其中$\alpha = 0.5/\Delta t$，r=1和n=1，由HU和KASHIWAGI^[35]给出。

1.3   浸入体边界处理

在笛卡尔网格中刚体上的受力计算由下式给出：

式中：$F_{{i}}^{( {\rm{p}} )}$为与压力相关的力；$F_{{i}}^{( {\rm{v}} )}$为与摩擦相关的力；$A$为物体的表面；${{\boldsymbol n}_{{k}}}$为物体表面第k部分的单位法向量。本研究仅需考虑与压力相关的力，与摩擦相关的力很小，忽略不计。

模型采用浸入边界法(Immersed Boundary Method)处理流固耦合问题，将固体边界由虚拟粒子标记，通过积分法获得每个单元的${\varphi _3}$值。在固体边界耦合固体速度场与流体速度场，从而得到固体覆盖区域的速度场。在数值计算中质量力为重力加速度g，将其设为g = [0, 9.81] m/s²。

式中：$u_{{{\rm B}i}}^{{{n}} + 1}$为固体的局部速度；$u_{{{\rm F} i}}^{{{n}} + 1}$为流场求解后得到的流体速度场；$u_{{i}}^{{{n}} + 1}$为未知速度。

1.4   网格收敛验证

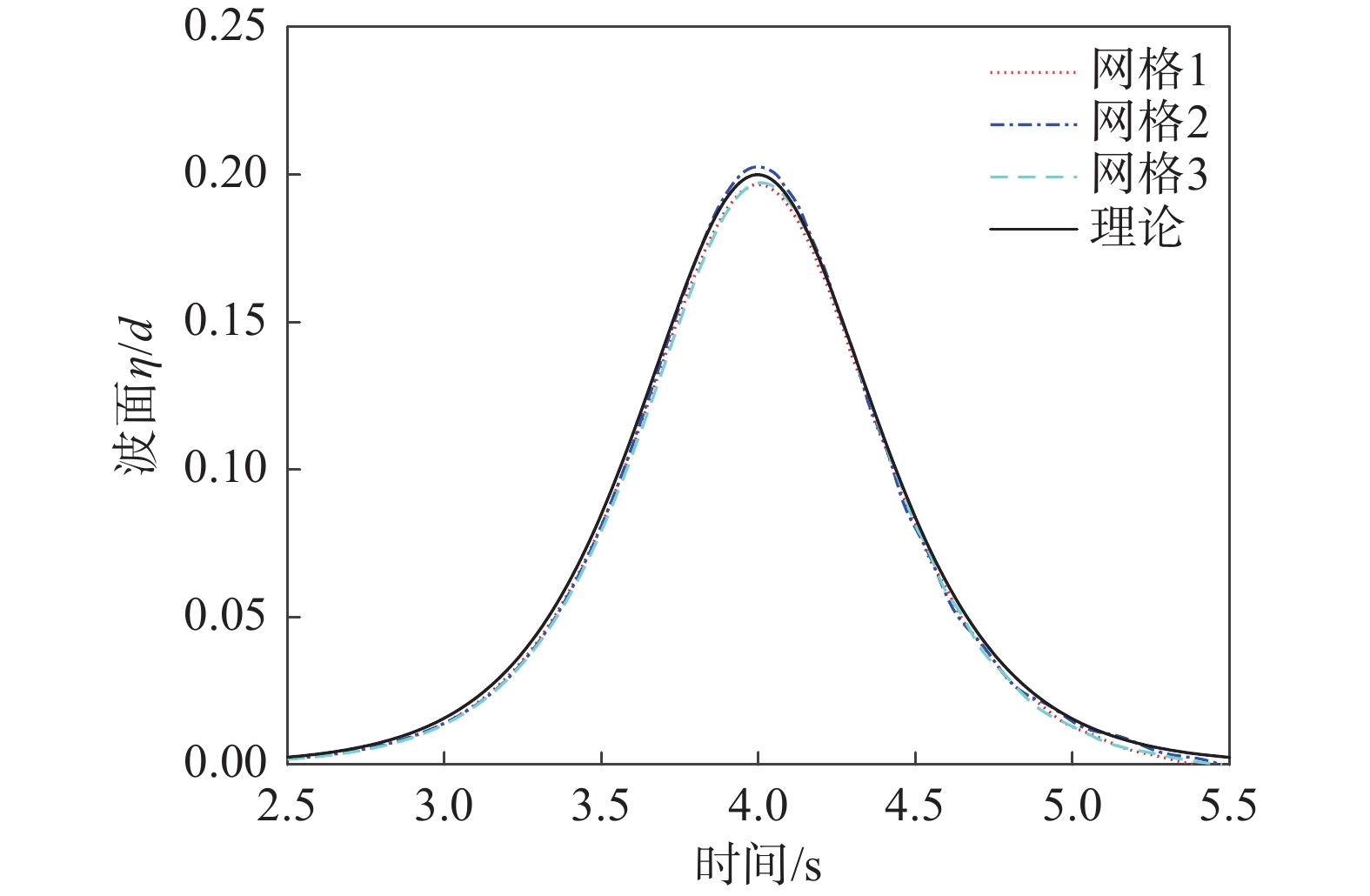
计算网格采用均匀的交错网格系统，表1是不同尺寸网格的信息。将孤立波通过数值水槽x=6 m处随时间的变化过程与孤立波解析解做对比，用于验证网格质量和收敛性。由图2可知，在不同的网格密度的情况下，计算的波形结果与解析解是相近的，因此选取的三种网格尺寸都具有收敛性。数值模拟时选用网格1网格尺度。

表  1  不同的网格参数

Table  1.  Parameters of different meshes

网格划分	网格长度Δx/m	网格宽度Δy/m
网格1	0.0050	0.0050
网格2	0.0100	0.0100
网格3	0.0025	0.0025

下载: 导出CSV 

| 显示表格

图  2  验证网格收敛

Figure  2.  Verification of grid convergence

下载: 全尺寸图片 幻灯片

1.5   数值计算方法

计算网格采用基于笛卡尔坐标系的交错网格系统，可以避免非交错网格在求解不可压N-S方程时出现数值压力分布异常的情况。对于动量方程采用分步式算法，将其分为对流项和两个非对流项进行求解。其中，对流项的求解采用三阶精度CIP算法，之后采用中心差分方法求解扩散项，而压力项则采用SOR迭代法进行压力-速度耦合计算，完成速度场和压力场的求解，最后采用WLIC-THINC方法重构自由液面。

2   数值模型验证

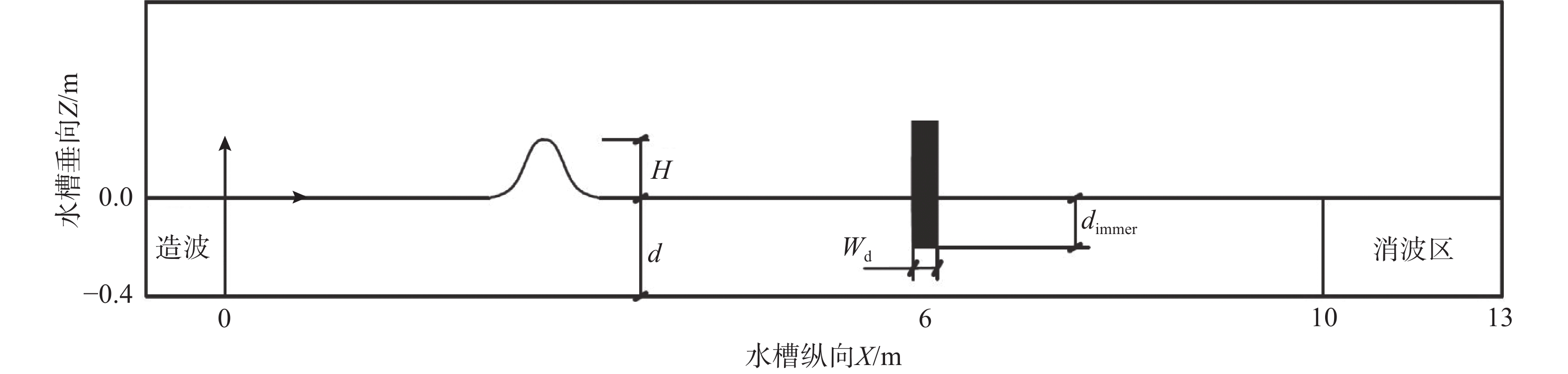
图3为构建的数值水槽，采用二维正交笛卡尔坐标系，以静止水面与数值水槽的最左边界的交界点为零点，波浪前进方向为x轴正向，以x轴逆时针旋转90°后方向为y轴的正向，其中数值水槽的长度为11 m，水深为0.4 m，设置无量纲波幅ε=H/d取值为0.1、0.2、0.3、0.4。帷幕式防波堤安装在距离数值水槽左侧x=6.0 m处，静水面以上的长度为0.6 m，帷幕式上端距离静止水面0.4 m，如图3所示。在计算中，数值水槽采用不均匀交错网格，网格在帷幕式防波堤周围和表面附近具有更精细的间距，时间步长取为0.001 s，模拟的总时间为12 s。评价不同尺寸下的帷幕式防波堤对透射系数、反射系数和耗散系数的影响，设置相对浸没深度为d_immer/d=0、0.25、0.5、0.75；帷幕式防波堤相对宽度为W_b/d=1/4、3/8、1/2、5/8。

图  3  数值水槽及变量定义示意图

Figure  3.  Schematic diagram of numerical water tank and variable definition

下载: 全尺寸图片 幻灯片

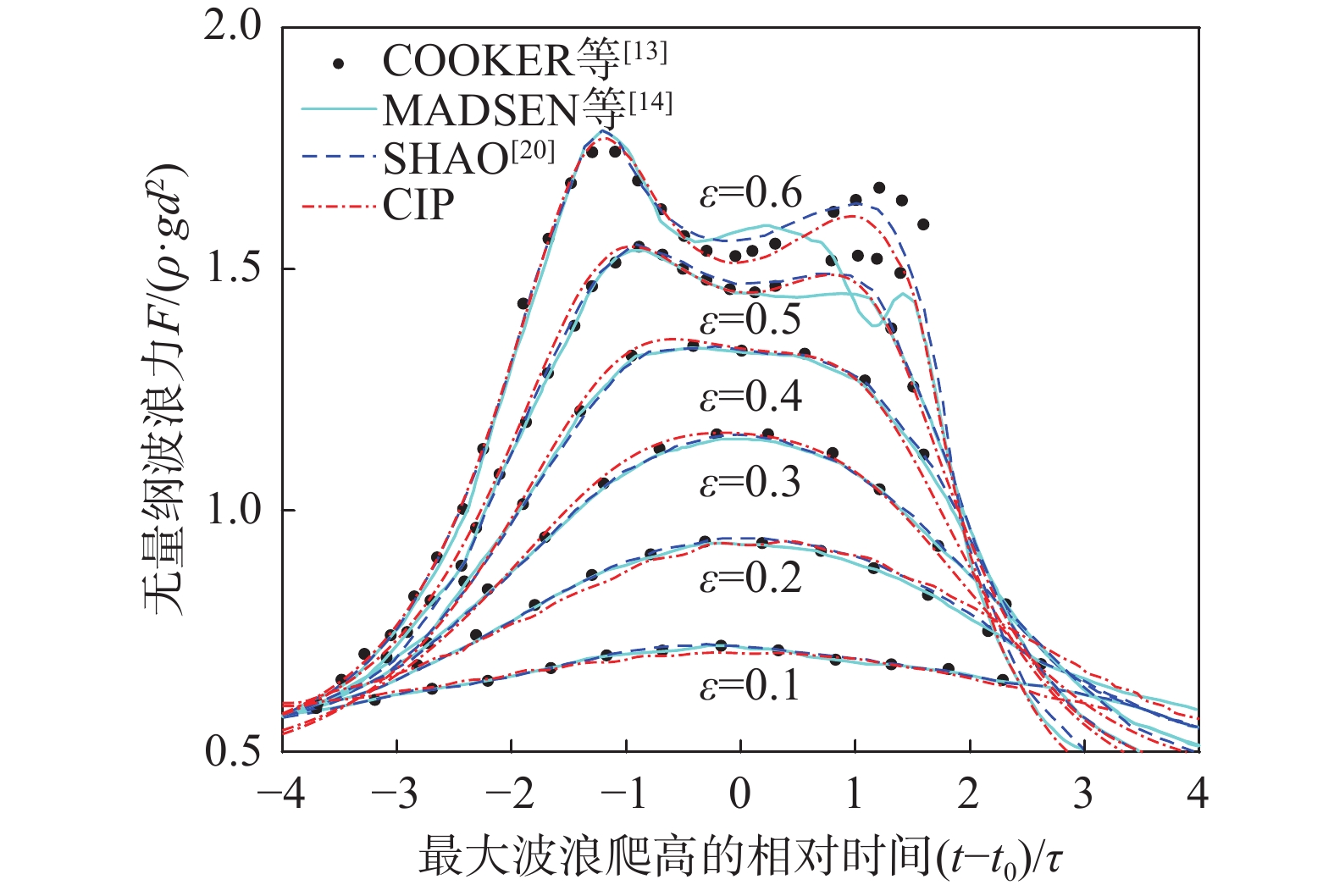
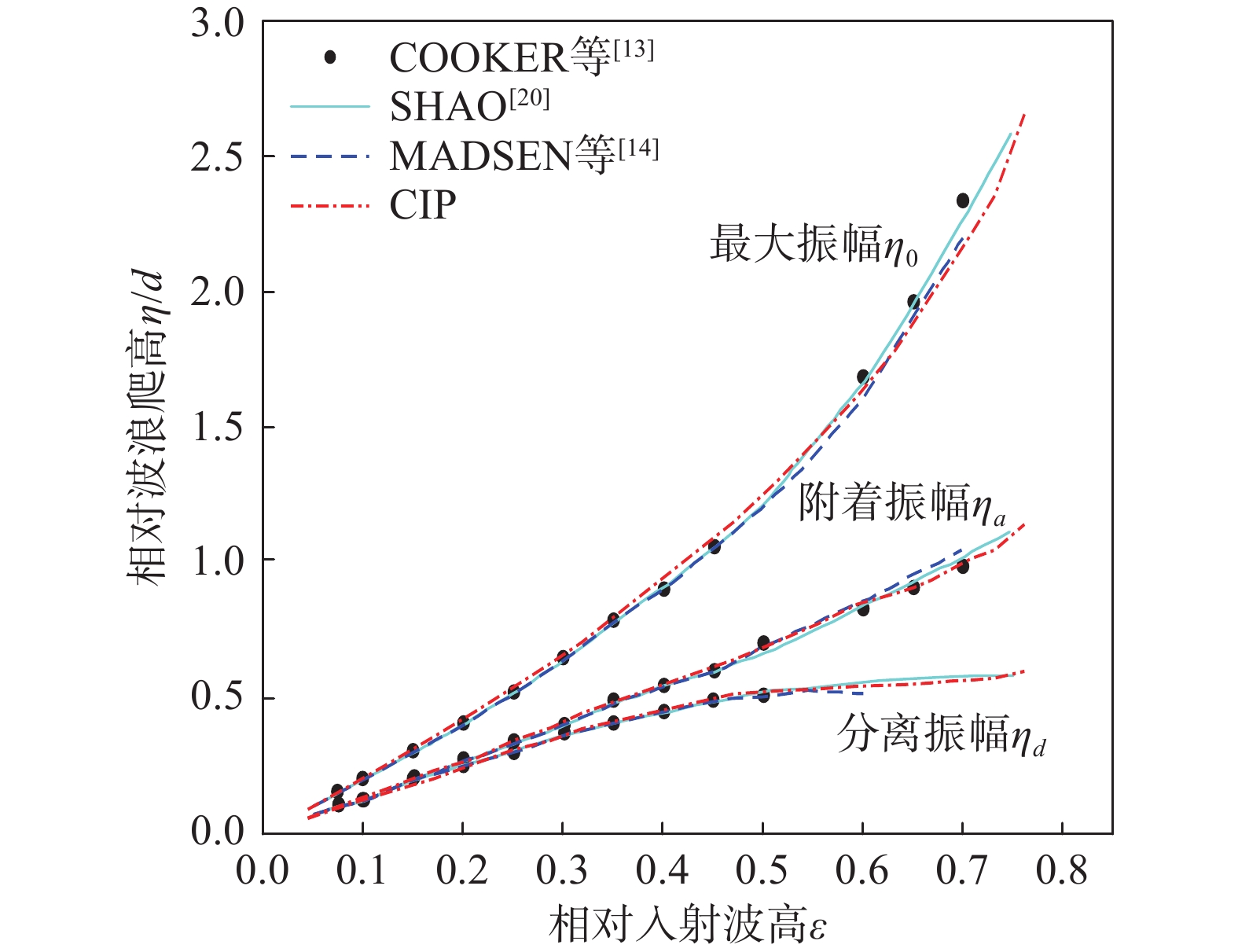
在完全浸没的帷幕式防波堤的迎浪面设置压力器，记录迎浪面所受的压力随时间的变化过程，然后进行积分求解迎浪面所受的力，将其结果和时间归一化后，再跟文献[20]中的结果进行比较，得到图4。图中$\left( {t - {t_0}} \right)/\tau$为无量纲时间，其中$\tau = {(h/g)^{1/2}}$。

图  4  防波堤迎浪面压力变化比较图

Figure  4.  Comparison chart of pressure changes on the face of the breakwater

下载: 全尺寸图片 幻灯片

当波峰距离墙面不到水深的两倍时，波峰会显著加速。至t_a时刻(附着时间)，波峰已经到达墙面，其相应波峰高程为附着振幅η_a。到t₀时刻，波峰爬到最大高度，高度可能是入射波波高的几倍，此时波峰的高度为最大振幅η₀。波峰在t_d时刻离开墙面，此时波峰的高度为分离振幅η_d。CIP数值模拟的结果与文献[20]的结果比较可得图5。通过对比，在分析不同的相对孤立波波高在冲击完全浸没的帷幕式防波堤的过程中，CIP方法可以有效地模拟孤立波冲击帷幕式防波堤的过程和现象。因此后续将采用CIP方法，来探究帷幕式防波堤在不同浸没深度和宽度与不同高度的孤立波相互作用下透射系数，反射系数和耗散系数的变化规律和波浪力随时间的变化规律。

图  5  附着振幅、分离振幅和最大振幅与入射孤立波振幅的关系

Figure  5.  Attachment amplitude, detachment amplitude and maximum run-up versus incoming solitary wave amplitude

下载: 全尺寸图片 幻灯片

3   帷幕式防波堤水动力分析

3.1   流场分析

图6是选取的帷幕式防波堤相对浸没深度d_immer/d=0.5，相对宽度W_b/d=0.2和孤立波相对波高H/d=0.4的情况。1)孤立波刚遇到帷幕式防波堤，从图中可以明显的看到一部分水体正在不断沿着帷幕式防波堤继续的爬高，少部分水体则绕过帷幕式防波堤的下端，进入防波堤的右侧，在绕过帷幕式防波堤下方的同时逐渐在帷幕式防波堤的下方产生了逆时针方向的涡流。2)在帷幕式防波堤左侧的流体主要分为了两种不同的流向，一部分靠近水面的水体在惯性的作用下继续沿着防波堤向上爬高，在波面形成逆时针的涡流运动，而另一部分水体则在压力差的作用下向下运动，在运动的过程中形成顺时针涡流。同时在帷幕式防波堤后面已经产生了一个比较完整的逆时针旋转的涡流，而这个涡流是从帷幕式防波堤的下方脱落而成的。3)此时水面附近的水体已经不再爬高，防波堤左侧的水体在压力差的作用下向下运动，在帷幕式防波堤的下方有大量水体继续向右运动，为透射波的形成提供能量。而在最靠近防波堤的下端的位置流体的速度方向不明显，形成了紊流区，波浪能在这个位置被大量消耗。4)此时帷幕式防波左侧的水面已经降到最低点的位置，比防波堤右侧的水面还要低，防波堤后面的逆时针涡流发展的所占范围比较大，而且相较于上一个时刻涡流离帷幕式防波堤的距离更远了。观察防波堤右侧的水体，可以发现因为帷幕式防波堤两侧的压强差将导致一部分水体从防波堤的右侧运动到左侧。5)在帷幕式防波堤的右侧，除了上一时刻的逆时针的大漩涡外，在大漩涡的右下方还产生了相比于它较小的顺时针旋涡，同时逆时针大旋涡继续向右移动。在帷幕式防波堤的下方已经形成了顺时针的涡流，在这股涡流的影响下，在其左下方向也产生了一个逆时针的小涡流。6)上一时刻逆时针大涡流右下方的顺时针涡流逐渐发展壮大，涡流的中心也逐渐上移，其涡流的中心位置与逆时针大涡流中心几乎位于同一水平位置上。同时在逆时针大涡流的左上方产生了又产生了一个顺时针小涡流，且涡流的中心存在着气泡。在防波堤的左下方产生两个涡流，是从帷幕式防波堤的下方脱落形成的。可以看出在一个孤立波冲击帷幕式防波堤的过程中，存在着涡流的产生、脱落、液面的变形与破碎以及气液掺混等复杂的现象，正是这些现象消耗大量的波浪能，从而达到削弱透射波能量的目的。第一，因为帷幕式防波堤上方是薄板刚体结构，可以直接将部分孤立波的波浪能以反射波的形式消耗掉；第二、在帷幕式防波堤的下方是透空的，因为帷幕式防波堤两侧压力差的缘故，导致水体的运动，运动的同时将产生大量的涡流以及紊流区域从而不断的消耗孤立波的波浪能。而且帷幕式两侧的压力差往复变化也增加了波浪能的消耗。

图  6  孤立波冲击帷幕式防波堤的波面变形过程

Figure  6.  Wave surface deformation process of solitary wave impacting curtain breakwater

下载: 全尺寸图片 幻灯片

3.2   透射系数、反射系数和耗散系数

波浪能耗散是防波堤研究的主要课题。在孤立波与帷幕式防波堤相互作用过程中，由于波浪破碎、上升和下降过程中产生的湍流，因此一部分能量被反射，另一部分入射波能量会因屏障底部尖端的涡旋脱落而消散，如图7所示。将透射系数定义为${K_{\rm{t}}} = {H_{\rm{t}}}/{H_{{i}}}$和反射系数${K_{\rm{r}}} = {H_{\rm{r}}}/{H_{{i}}}$和耗散系数${K_{\rm{d}}} = {H_{\rm{d}}}/{H_{{i}}}$，其中H_t、H_r、H_d和H_i分别是透射、反射、耗散和入射波的高度，利用能量守恒定律可以建立以下关系：

图7中的四幅图分别为帷幕式防波堤相对浸没深度为0、0.25、0.5和0.75时，透射系数、反射系数和耗散系数随不同相对波高的变化趋势，以及不同宽度的帷幕式防波堤之间的对比。

图  7  透射系数、反射系数和耗散系数

Figure  7.  Transmission coefficient, reflection coefficient and dissipation coefficient

下载: 全尺寸图片 幻灯片

帷幕式防波堤相对浸没深度d_immer/d=0时，反射系数随着相对波高增加而增加，但增加的幅度相对较小。当相对波高从0.1增加到0.3的时候，反射系数增加趋势不明显，这说明帷幕式防波堤浸没深度d_immer/d=0时，对于相对波高小于0.3的入射波的阻挡效果较弱，因此不能形成有效地反射波。而且透射系数则会随着相对波高的增加而减小，两者呈现出一定的线性关系，说明在帷幕式防波堤相对宽度不变时，相对波高越高会引起更大更多的涡流，有更多的波浪能会被消耗掉，因此帷幕式防波堤能对相对波高更高的波浪有更好的消浪作用。从图7也能看出，入射波的波浪能更多的被以涡流的形式消耗掉。

当帷幕式防波堤的相对浸没深度d_immer/d=0.25的时候，从图7可以清晰的看出，在相对波高小于0.3的时候，不同宽度的帷幕式防波堤透射系数和耗散系数是基本上重合的，但是当相对波高大于0.3时，可以发现防波堤相对宽度为1/4的透射系数大于其他宽度的防波堤，而耗散系数则要偏小。表明在相对波高大于0.3的情况下，帷幕式防波堤的相对宽度会对反射系数和耗散系数产生比较明显的影响，但对反射系数并没有很大的影响，这也与我们的认知是相符的。从图中还可以看出当相对宽度到达3/8的时候再增加宽度，对耗散系数和透射系数影响不大。因此当帷幕式防波堤相对浸没深度d_immer/d=0.25和相对波高H/d=0.4时，宽度较小的透射系数更大、耗散系数更小。通过图8分析了产生这种现象的原因。在图8中展示了在H/d=0.4和d_immer/d=0.25的条件下，帷幕式防波堤相对宽度分别为W_b/d=1/4和W_b/d=1/2的涡流变化。可以看出在帷幕式防波堤相对宽度较小的时候，形成的多数的涡流随着时间的变化，脱落的位置是位于防波堤中心线靠后的位置，所以涡流主要的发生区域也位于帷幕式防波堤的中后区。而当帷幕式宽度较大的时候，脱落的位置是位于防波堤中心靠前的位置，因此涡流区域主要是在防波堤位置的中部偏前区域。说明较宽的帷幕式防波堤可以影响涡流脱落的位置，从而影响了透射系数和耗散系数。因为防波堤宽度比较宽，导致在防波堤下端产生的涡流不能被通过下端的流体将涡流完全带到帷幕式防波堤的后方，从而使留在帷幕式防波堤下端涡流进一步阻碍流体通过防波堤的下端，以至于透射系数的减小。因此在一定情况下，宽度较大的防波堤对港湾有更好的保护作用。

图  8  不同宽度帷幕式防波堤的涡流

Figure  8.  Eddy currents of curtain breakwaters of different widths

下载: 全尺寸图片 幻灯片

帷幕式防波堤相对浸没深度d_immer/d=0.5时，透射系数、反射系数和耗散系数随相对波高的变化趋势跟相对浸没深度d_immer/d=0的变化趋势是一致的，但在相同的波高条件下，透射系数更小，反射系数和耗散系数更大。以相对波高H/d=0.1为例，相对浸没深度d_immer/d=0时，透射系数接近于1，反射系数和耗散系数小于0.1；相对浸没深度d_immer/d=0.5时，透射系数接近于0.9，反射系数和耗散系数约为0.2。表明随着浸没深度的增加，透射系数是变小的，而反射系数和耗散系数是增大的，这充分说明帷幕式防波堤的浸没深度越大，对孤立波的消减作用越好。另一方面，当相对波高0.4时，帷幕式防波堤相对宽度1/4和3/8的透射系数大小一致，而相对宽度1/2和5/8的透射系数大小一致，且两者之间的差距比较明显。这种现象与相对浸没深度d_immer/d=0.25和相对波高H/d=0.4时的现象类似，说明帷幕式防波堤的宽度在一定程度上可以消减波浪能。但跟帷幕式防波堤相对浸没深度d_immer/d=0.25不同的是，透射系数是在帷幕式防波堤相对宽度从3/8增加到1/2时降幅加大，说明在不同的浸没深度下，帷幕式防防波堤的宽度对透射系数影响最大的临界点是不一样的。

当帷幕式防波堤相对浸没深度d_immer/d=0.75时，在波高相同的情况下，与其他不同的浸没深度相比透射系数更小，反射系数和耗散系数更大。当相对波高H/d=0.4时，透射系数系数的变化是随着帷幕式防波堤的宽度增加而减少，但跟其他浸没深度不同的是透水系数降低趋势中并没有出现大幅度的减少的情况(例如：相对浸没深度d_immer/d=0.5、相对波高H/d=0.4时，帷幕式防波堤相对宽度从3/8增加到1/2时透射系数大幅减少)。

总的来说，在帷幕式防波堤的浸没深度下和宽度相同的情况下，透射系数随着波高的增大而减小，反射系数和耗散系数都随着波高的增大而增大，说明帷幕式防波堤对波高更高的波浪有更好的消浪效果。通过四幅图对比可以发现，当相对浸没深度d_immer/d小于0.5时，透射系数都是比较大的，有超过一半的入射波的能量可以传递到防波堤的后方，但当其相对浸没深度d_immer/d超过0.5时，可以看出透射系数相比于其他的浸没深度有着明显的下降。SHAO^[20]研究孤立波与薄壁帷幕式防波堤的水动力特性的结果与本文结果一致。

另一方面，当帷幕式防波堤浸没深度一样时，且孤立波波高H/d=0.4时，发现不同的帷幕式防波堤的相对宽度对透射系数和耗散系数影响是不同的。其中当相对浸没深度为0、0.25时，防波堤的相对宽度从1/4增加到3/8时，会使透射系数大幅度降低和耗散系数大幅度升高，而帷幕式防波堤的相对宽度继续从3/8增加到5/8时，则对透射系数和耗散系数没有显著的变化。其中当相对浸没深度为0.5时，防波堤的相对宽度从1/4增加到3/8时，其系数并没有发生显著的变化，相对宽度从3/8增加到1/2时可以很清楚的发现透射系数较大幅度的降低和耗散系数较大幅度的升高，而当相对宽度从1/2增加到5/8时，变化幅度再一次变得比较小了。该现象表明随着宽度的增大，透射系数逐渐减少，消浪效果增强，但在不同的浸没深度下，透射系数的变化情况是不一样的，说明了宽度因素在消波过程中发挥的作用会受到浸没深度的影响。

3.3   迎面波浪力和背面波浪力

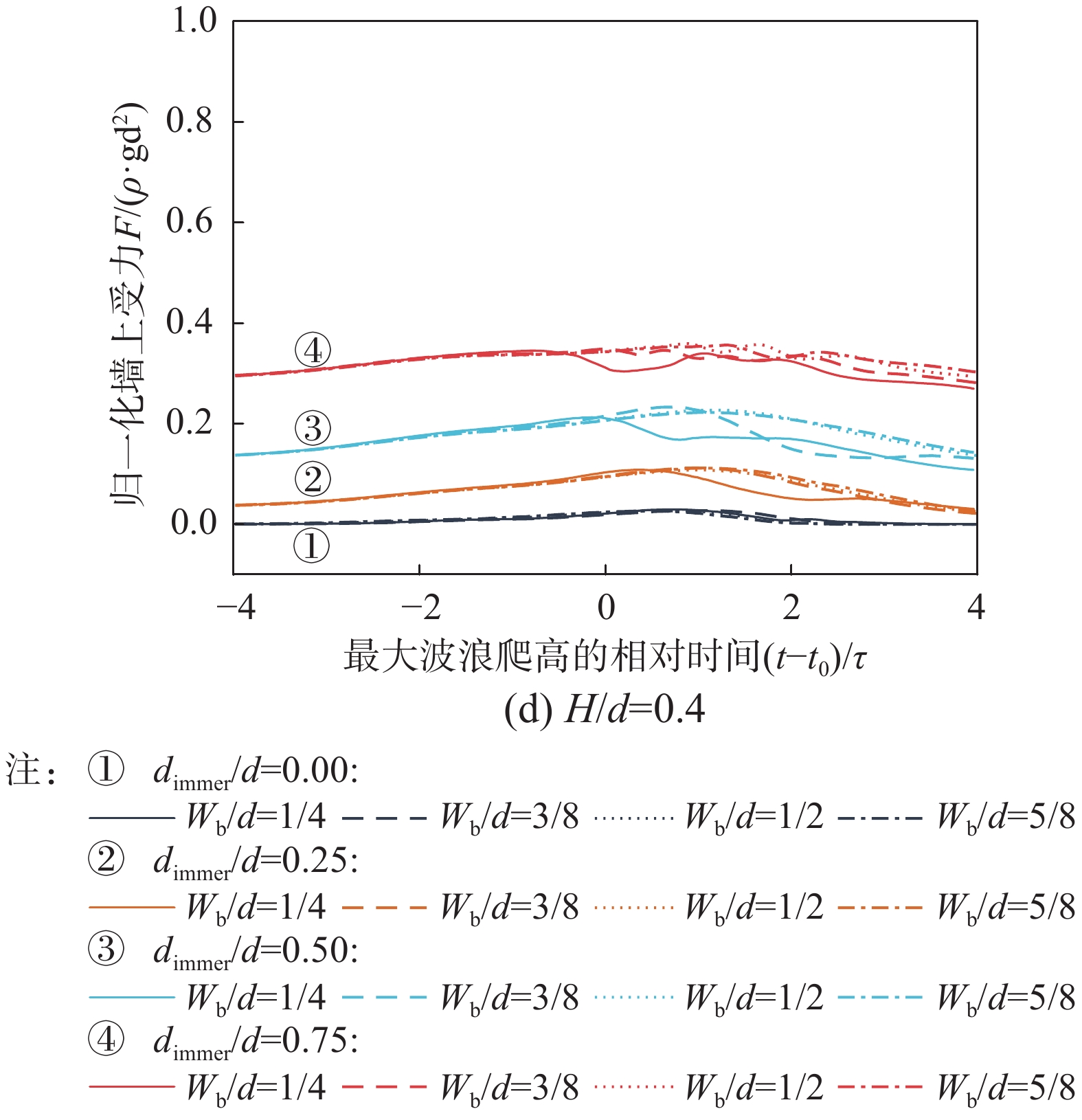
在波浪两侧，帷幕式防波堤也会经历随时间变化的波浪力，图9和图10分别是迎浪面和背浪面波浪力时程与帷幕式防波堤结构尺寸和波高的关系。采用无量纲波浪力，波浪力通过压力积分得到，并除以ρgd²进行归一化。

图  9  防波堤迎浪面无量纲波浪力随无量纲时间的变化

Figure  9.  Variation of dimensionless wave force with dimensionless time on the facing surface of breakwater

下载: 全尺寸图片 幻灯片

从图9可以发现，迎浪面波浪力的变化都是遵循相似的规律，即力突然增加到峰值，然后迅速衰减，最大的波浪力发生在波浪爬坡高度最大的期间，并且波浪力随着浸没深度的增加而增加，这与COOKER等^[13]、MADSEN等^[14]和SHAO^[20]的特征一致。但是与COOKER等^[13]和MADSEN等^[14]的数据相比，可以观察到最大波浪力的持续时间更短，而且幅度也小，这是因为他们使用的帷幕式防波堤时完全浸没水中，下方没有空隙。可见帷幕式防波堤下方空隙的传输可以大大降低流体的能量。当帷幕式防波堤相对浸没深度不变时以及波高相同的情况下，相对宽度对波浪力的影响较小。

从图10中发现在孤立波冲击帷幕式防波堤的过程中，背浪面压力变化规律跟迎浪面变化规律并不一样。总的来说，随着时间的增加，背浪面波浪力先略有上升，然后再回落。当相对波高较大时(例如H/d=0.4)，随着孤立波穿过防波堤，背浪面波浪力出现非稳定的波动，它们变化规律主要是先陡然的减小，在缓慢的增加。但这种现象并不是在所有的情况下都出现，当相对波高较大以及相对宽度较小的时候更容易发生。因为防波堤相对宽度越小，导致涡流发生的区域就在帷幕式防波堤的右侧，让右侧的水体运动更剧烈，甚至发生水汽混掺的现象，如图8所示。

下载: 全尺寸图片 幻灯片

  10  防波堤背浪面无量纲波浪力随无量纲时间的变化

  10.  The change of dimensionless wave force on the back wave surface of breakwater with dimensionless time

下载: 全尺寸图片 幻灯片

4   结论

通过数值建模的对比分析，得到结论如下：

(1) 当传统帷幕式防波堤的宽度和孤立波波高不变，浸没深度对透射系数、反射系数和耗散系数有比较明显的影响，随着浸没深度的增加透射系数逐渐减小，反射系数和耗散系数逐渐增加。当传统帷幕式防波堤的宽度和浸没深度不变，随着孤立波波高的增加透射系数逐渐减小，反射系数和耗散系数逐渐增加，且呈现一定的线性特征。

(2) 当传统帷幕式防波堤的浸没深度和孤立波波高不变，传统帷幕式防波堤的宽度对透射、反射和耗散系数的影响较小。在不同的浸没深度下，传统帷幕式防波堤相对宽度对其的影响是不一样的。当相对浸没深度d_immer/d=0、0.25时，相对宽度W_b/d=3/8的传统帷幕式防波堤消浪效果较好，随着相对宽度的增大，消浪效果没有明显提高。当相对浸没深度d_immer/d=0.5时，相对宽度W_b/d=1/2的传统帷幕式防波堤消浪效果好而且经济。宽度因素在消波过程中发挥的作用会受到浸没深度的影响，浸没深度越大传统帷幕式防波堤宽度对消波的作用越明显。

(3) 传统帷幕式防波堤相对宽度对波浪力的影响不大，但相对宽度较大的防波堤背浪面波浪力变化幅度更小，更稳定。