模态识别是确定结构模态参数直接有效的方法，模态识别的精度评价贯穿于模态识别研究的全过程。新的模态识别方法产生时，需要通过识别精度来验证所提识别方法的可行性，LI等^[1]用合成结构响应时程的算例，验证了增强HVD方法的模态识别精度；陈永高等^[2]通过振动台实验识别结果与有限元模拟结果的对比，验证了CS-CDSI识别算法在桥梁模态识别中的可靠性。对实验结构进行模态识别前，往往也需要对选定模态识别方法的识别精度进行评估，以确定识别方法的适用性，刘威等^[3]通过五自由度弹簧-质量-阻尼系统的数值算例，验证了随机子空间法的模态识别精度。

评价模态识别的精度和适用性，一方面，目前常见的方法是构建算例，通过一个或少数几个算例的识别结果来确定模态识别的精度，进行适用性和可行性的评估^[4-15]。通过识别结果与模态参数理论值的对比，确实可以得到识别精度的估计，但单一或少数几个算例得到的结论存在偶然性；另一方面，一个或少数几个算例有时无法满足研究的需求，例如探究采样时长^[16]或噪声^[17]对识别结果的影响时。因此，提出一种基于数据库评价模态识别方法适用性和识别精度的方法(简称：数据库方法)，即根据“目标”构建包含结构响应和模态参数理论值的数据库(即一系列数值算例)，通过模态识别方法对数据库中算例的识别结果与理论值的对比，获得模态识别精度的评价。

数据库方法中，构建数据库是一个关键环节，而数据库的构建又可分为两个部分：参数取值和结构响应获取。参数的取值需要根据研究目的和“目标结构”确定；结构响应的获取方法有三种常见的形式：第一种是构造法，即通过正(余)弦函数构造结构的响应时程曲线给出结构的响应和模态参数理论值^{[1, 18]}；第二种是计算法，即通过构建模型，计算结构的模态参数和给定激励下结构的响应时程；对于简单的集中质量系统，结构的模态参数理论值和结构响应可以通过求解运动方程的方式获得^[3]，对于复杂结构，模态参数理论值和结构响应可以用过建立有限元模型的方式获得^[19]；第三种方法是实验法，即结构的响应时程由实验获得，结构的模态参数理论值由数值模拟给出^[20-25]。构造法比较难实现结构的阻尼特性；实验法和有限元数值模拟方法获得结构响应和模态参数理论值的过程复杂，效率不高。因此，通过集中质量模型建立数据库的方法是比较准确而又高效的选择。故对于集中质量模型，建立数据库的核心问题是基于模态参数计算结构响应。

结构的动力响应计算方法可分为4类^[26]，分别为运动方程法、状态方程法、脉冲响应函数法、频响函数法。由于这4种途径均需要结构的物理参数(本文中特指：质量、刚度、阻尼)参与运算，因此，推导并提出了一种基于集中质量系统，由模态参数(频率、振型和阻尼比)构建结构物理参数的方法，并用数值算例验证了该方法的可行性。基于数据库评价模态识别方法适用性和识别精度时，数据库构建过程中引入的误差大小，直接影响识别精度的评价结果的误差；以五自由度弹簧、质量、阻尼系统为基础，构建数据库，对比了4种途径下，中心差分法(Difference)、Houbolt方法、Newmark-β方法、威尔逊θ方法(Wilson)、精细积分法(Precise)、状态空间法、频响函数法(FRF)、脉冲响应函数法(IRF)8种响应计算方法的计算精度和计算效率，给出了集中质量模型兼顾计算精度和计算效率的数据库构建方案。针对随机子空间法定阶难、虚假模态剔除难的问题，提出一种基于奇异熵增量定阶和稳态图两阶段虚假模态剔除的优化随机子空间法，并基于数据库方法对优化的随机子空间法进行了识别精度评价。

1   基于数据库的模态识别精度评价方法

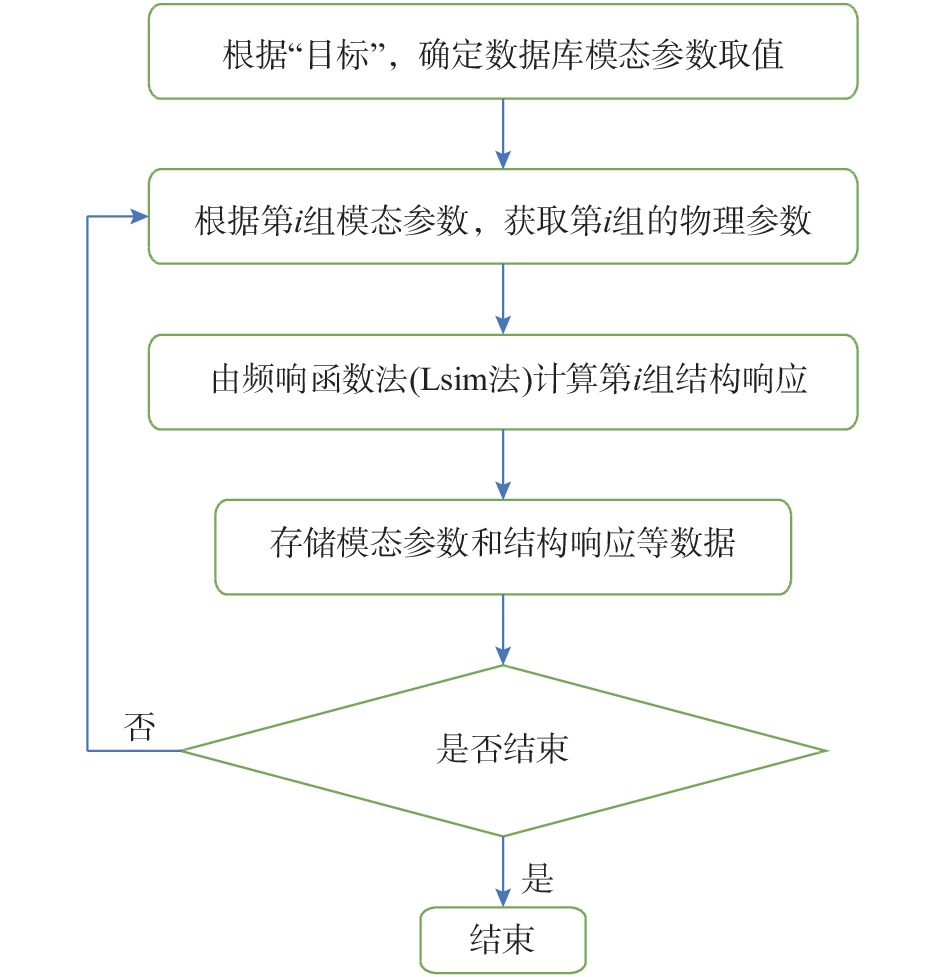
现有的模态识别精度评价的思路可以归纳为：构建算例，通过对比模态参数识别结果与模态参数理论值，获得模态识别精度的评价结果。但单一或少量的算例得到的识别精度评价结果存在偶然性，因此提出模态识别精度评价的数据库方法，即：由大量算例构建数据库，通过数据库中所有算例识别精度的统计结果获得对应的模态识别精度评价。通过集中质量模型计算结构响应，获取算例的方法是构建数据库最简单高效的方法。对于集中质量模型，现有的结构响应计算方法可归为：运动方程法、状态空间法、频响函数法和脉冲响应函数法4类。无论哪一类方法，计算的起点都是结构物理参数，即：质量、刚度和阻尼。但基于数据库的模态识别精度评价方法中，结构的物理参数并不是关键参数；仅有结构的模态参数理论值和结构响应是必需的，换而言之，数据库构建的起终点应该为结构的模态参数和响应，计算流程如图1所示。实现图1所示的计算流程，需要利用模态参数获得结构的物理参数，本文提出一种基于模态参数构建结构物理模型的方法。

图  1  基于模态参数的结构响应计算流程

Figure  1.  Structural response calculation process based on modal parameters

下载: 全尺寸图片 幻灯片

1.1   基于模态参数构建结构物理模型

基于振型矩阵关于质量矩阵带权正交，可由完整的振型信息获得集中质量系统的质量分布(各集中质量的比值)。在质量分布已知时，选取合理的质量矩阵，结合频率和阻尼比，可以获得结构的刚度矩阵和阻尼矩阵，实现结构物理参数模型的构建。

1.1.1   理论推导

记结构的质量矩阵和振型矩阵分别为${\boldsymbol{M}}$和${\boldsymbol{\varPhi}}$：

式中，${m_i}$和${\varphi _i}$分别为第$i$个集中质量和第$i$阶振型，$i = 1, 2, \cdots ,n$，$n$为系统的自由度数。

由于振型关于质量正交可得：

式中，${{\boldsymbol{M}}^*}$为广义质量矩阵：

将式(2)展开，可得非齐次方程和齐次方程：

记：

则式(4)和式(5)可改写为：

对于多自由度结构($n \geqslant 2$)，当结构的刚度矩阵${\boldsymbol{K}}$不能准对角化时(即刚度矩阵不能通过列之间的交换变换为准对角矩阵)，齐次方程组式(9)的解空间维数为1，式(9)有唯一的解向量$\vec m$，记作：

式(8)和式(9)联立后与式(2)等价，且式(2)和式(8)的解均为式(7)，因此，式(8)和式(9)解的交集为式(7)，故：

式中，$k$为非零实数。

综上，齐次方程组式(9)的解为质量的比值向量，故可以根据完整的振型矩阵，获得质量分布(各集中质量的比值)，从而结合频率和阻尼比信息，可以构建出包含对应振型、频率和阻尼的结构系统。值得注意的是，上述推导是基于集中质量系统的，该方法只能用于计算已知模态参数的集中质量系统的质量比。

1.1.2   算法流程

通过完整振型、频率和阻尼比信息构建结构系统的计算流程如下：

1)根据完整振型信息$\{ {\varphi _1}, \cdots ,{\varphi _i}, \cdots ,{\varphi _n}\} \;,\;\;i = 1, 2, \cdots ,n$，构建并求解齐次方程组$\varphi _i^{\rm{T}}{\rm diag}({\varphi _j})\vec m = 0, \; i,j = 1,2, \cdots ,n;\;i \ne j$，获得质量比向量$[m_1', \cdots , m_i', \cdots, m_n']^{\rm{T}},\;i = 1,2, \cdots ,n$；根据质量比向量和任意正数$c$选取质量矩阵${\boldsymbol{M}}$：

2)由以下方程根据质量、振型、频率和阻尼比矩阵计算结构的刚度和阻尼矩阵：

式中：${{\boldsymbol{M}}}^{*}、{{\boldsymbol{K}}}^{*}、{{\boldsymbol{C}}}^{*}$分别为结构的广义质量、刚度、阻尼矩阵；${\boldsymbol{\varPhi}} 、{\bf\textit{ω}} 、{\boldsymbol{\xi}}$分别为结构的振型矩阵、频率矩阵和阻尼比矩阵；${{{\boldsymbol{M}}、{\boldsymbol{K}}、{\boldsymbol{C}} }}$结构的质量、刚度和阻尼比。

1.1.3   数值算例

参考经典算例^[27]，建立一个五自由度质量_弹簧_阻尼系统数值模型(如图2)，验证该计算流程的可行性。每个单元质量、刚度、阻尼系数分别为：${m_n} = 50{\text{ kg}}$，${k_n} = 2.9 \times {10^7}{\text{ N/m}}$，${c_n} = 1000{\text{ N}} \cdot {\text{s/m}}$。计算可得的振型、频率、阻尼比如表1和表2所示。

图  2  五自由度质量_弹簧_阻尼系统示意图

Figure  2.  Schematic diagram of a 5 degree-of-freedom mass-spring-dashpot system

下载: 全尺寸图片 幻灯片

表  1  算例结构的振型向量表

Table  1.  Mode Shape Vector Table of Example Structure

阶次	振型向量
1	0.1699	0.3260	0.4557	0.5485	0.5969
2	−0.4557	−0.5969	−0.3260	0.1699	0.5485
3	0.5969	0.1699	−0.5485	−0.3260	0.4557
4	0.5485	−0.4557	−0.1699	0.5969	−0.3260
5	−0.3260	0.5485	−0.5969	0.4557	−0.1699

下载: 导出CSV 

| 显示表格

计算可得质量比向量：$[0.4472\;,\;0.4472\;,\; 0.4472\;,\; 0.4472\;,\;0.4472]^{\rm{T}}$；按照1.1.2节中的算法流程，取${\boldsymbol{M}} = {\rm diag}({[50,50,50,50,50]^{\rm{T}}})$，计算得到的刚度矩阵和阻尼矩阵如式(14)、式(15)所示；计算获得的刚度矩阵、阻尼矩阵与理论值一致，上述1.1.2节中的算法流程可行。

表  2  算例结构的频率和阻尼比表

Table  2.  Frequency and Damping Ratios Table of Example Structures

阶次	1	2	3	4	5
频率/Hz	34.50	100.70	158.75	203.93	232.60
阻尼比/(%)	0.0037	0.0109	0.0172	0.0221	0.0252

下载: 导出CSV 

| 显示表格

1.2   结构响应数据库构建算例

通过模态识别方法对数据库的识别效果，来评价不同识别方法对特定结构的适用性，需要先构建与特定结构模态参数相似的结构响应数据库。数据库的构建思路如图3所示。

1.2.1   参数选取及参数取值

构建结构响应数据库，一个值得关注的问题是如何确保所构建的数据库与目标结构的动力特性相似或者包含目标结构的动力特性，即数据库构建时模态参数如何取值。为此需要先确定结构模态参数的大致范围，可以先通过数值模拟或实验测试，获取结构模态参数的大致范围，然后在结构模态参数的基础上，扩大参数取值范围即可获得数据库构建模态参数的取值。

图  3  结构响应数据库构建思路示意图

Figure  3.  Schematic diagram of the construction idea of structural response database

下载: 全尺寸图片 幻灯片

可能影响结构响应计算结果的参数主要有：结构物理(动力特性)参数、激励信息参数两类。选取结构自由度数为5，以最小质量、基频、阻尼比、激励时间间隔(采样频率)和激励时长(采样点数)作为变量，进行数值算例实验设计。王德鑫^[28]指出，激励幅值不影响频响函数，因此不考虑激励(响应)幅值的影响。以五自由度系统为例构建数据库，有两方面的原因：一方面五自由度系统能包含两组密集频率；另一方面又不会因为自由度太多而使计算量暴增。采样频率不小于结构基频的2.56倍；由结构的激励和响应计算频响函数的过程中，采样时长(采样点数)会影响频响函数的分辨率，为了减小该过程中由采样时长引起的误差，采样点数的取值使得频响函数的分辨率不小于基频的0.1%；为了便于之后的模态识别，取采样点数为1024的整倍数。

以图2所示的五自由度系统为目标结构的系统简图，假定前5阶频率在0.5 Hz~10 Hz，且可能存在密频现象；假定目标结构的阻尼比约为1%~4%。采样频率和采样点数各取满足前述条件的3个不同的值，其余参数取值如表3所示。

表  3  数据库建立参数取值表

Table  3.  Structure response database parameter value table

是否密频	最小质量/kg	基频/Hz	阻尼比/(%)
否、单组密频、双组密频	1、100、10 000	0.5、5、50	0.5、2.5、5

下载: 导出CSV 

| 显示表格

1.2.2   结构响应计算方法

不同的结构响应计算方法，计算结果也会有所差异，而结构响应计算的结果中所包含的模态信息与理论值越接近，则该过程引入的误差越小，越有利于通过数据库评价模态识别方法的识别精度，因此，本算例中对四类结构响应计算方法进行对比，分析整理8种响应计算方法的计算精度，为建立结构响应数据库做参考。

运动方程法中，求解运动方程的常见方法有：中心差分法(Difference)、Houbolt方法、Newmark-β方法^[29]、威尔逊θ方法(Wilson)、精细积分法(Precise)^[30-32]等；状态空间法可用Lsim函数求解状态空间方程，获得结构响应；频响函数法(FRF)中时频域转换由傅里叶变换实现，脉冲响应函数法(IRF)中结构响应计算由杜哈梅积分实现。

如表3所示为数据库建立时各参数的取值范围，用白噪声激励作为结构激励，为简化计算量，激励方式采用单点加速度激励(加载点均为${m_1}$对应的质点，结构示意图如图2所示)，保存结构的模态参数(振型、频率和阻尼矩阵)、激励信息(荷载指示向量、激励时程)和结构响应(位移、速度和加速度时程)，构成结构响应数据库。

1.2.3   结构响应计算比较

选取位移响应为对比对象，以表3中包含“双组密频”的数据为基础，研究运动方程法、状态方程法、频响函数法和脉冲响应函数法4类(共计8种方法)响应计算方法的计算精度。

1.3   频域特征对比

对比响应计算方法计算结构响应的精度，需要有客观的评价指标，相比于时域特征，在此研究中，频域特征更加重要。一方面，频响函数不仅包含全部模态信息，同时频响函数曲线能直观地描述结构的频域信息；另一方面，频响函数的理论值可以轻松获取。因此，将频响函数作响应计算方法精度评价的基础。

响应计算方法频响函数与频响函数理论值的对比，可以从相似性和差异性两个方面进行。频响函数相关系数^[33](Frequency response assurance criterion, FRAC)可评价两条频响函数曲线形状的相似程度，幅值相关系数(Frequency amplitude assurance criterion, FAAC)可用于评价两条频响函数曲线幅值的相关性，频响函数残差(Frequency response residual error, FRRE)和频响函数均方根误差^[34](Frequency response function square, FRFRMS)可以用评价频响函数曲线的差异程度。

表4中：${H}_{{\rm{e}}}(\omega )、{H}_{{\rm{s}}}(\omega )$分别为通过结构激励与相应数据计算得到的频响函数和结构的理论频响函数；此研究中涉及的频响函数均中指位移频响函数，计算式如式(16)：

式中：${G}_{fx}(\omega )、{G}_{ff}(\omega )$分别为激励与相应的互功率谱和激励的自功率谱^[35-36]；${\rm{j}}$为虚数单位。由于有阻尼系统的频响函数为复函数，其频响函数曲线一般指幅频曲线、实频曲线、虚频曲线和相频曲线的统称，且可由幅频曲线确定结构的自振频率和振型，故本文中提到的频响函数曲线特指幅频曲线，表4中用于计算的频响函数值均取频响函数的模。

表  4  频响函数曲线对比参数信息表

Table  4.  Comparative parameter table of frequency response function curve

名称	计算公式	描述
频响函数相关系数	${\rm{FRAC}} = \dfrac{ { { {[H_{\rm{e} }^{\rm{T} }(\omega ) \cdot {H_{\rm{s} } }(\omega )]}^2} } }{ {[H_{\rm{e} }^{\rm{T} }(\omega ) \cdot {H_{\rm{e} } }(\omega )][H_{\rm{s} }^{\rm{T} }(\omega ) \cdot {H_{\rm{s} } }(\omega )]} }$	能够评价两条频响函数曲线形状相似程度的归一化指标
幅值相关系数	${\rm{FAAC}} = \dfrac{ {2\left| {H_{\rm{e} }^{\rm{T} }(\omega ) \cdot {H_{\rm{s} } }(\omega )} \right|} }{ {[H_{\rm{e} }^{\rm{T} }(\omega ) \cdot {H_{\rm{e} } }(\omega )] + [H_{\rm{s} }^{\rm{T} }(\omega ) \cdot {H_{\rm{s} } }(\omega )]} }$	可用于评价两条频响函数曲线幅值相似程度的归一化指标
频响函数残差	${\rm{FRRE}} = \displaystyle\sum\limits_{i = 1}^N {\left| {\dfrac{ {\log \left| { {H_{\rm{e} } }({\omega _i})} \right| - \log \left| { {H_{\rm{s} } }({\omega _i})} \right|} }{ {\log \left| { {H_{\rm{e} } }({\omega _i})} \right|} } } \right|}$	衡量两条频响函数的差异程度，值越小，两条曲线差异越小
频响函数均方根误差	${\rm{FRFRMS}} = \sqrt {\displaystyle\sum\limits_{i = 1}^N {\dfrac{ { { {(\log \left| { {H_{\rm{e} } }({\omega _i})} \right| - \log \left| { {H_{\rm{s} } }({\omega _i})} \right|)}^2} } }{ { { {(\log \left| { {H_{\rm{e} } }({\omega _i})} \right|)}^2} } } } }$

下载: 导出CSV 

| 显示表格

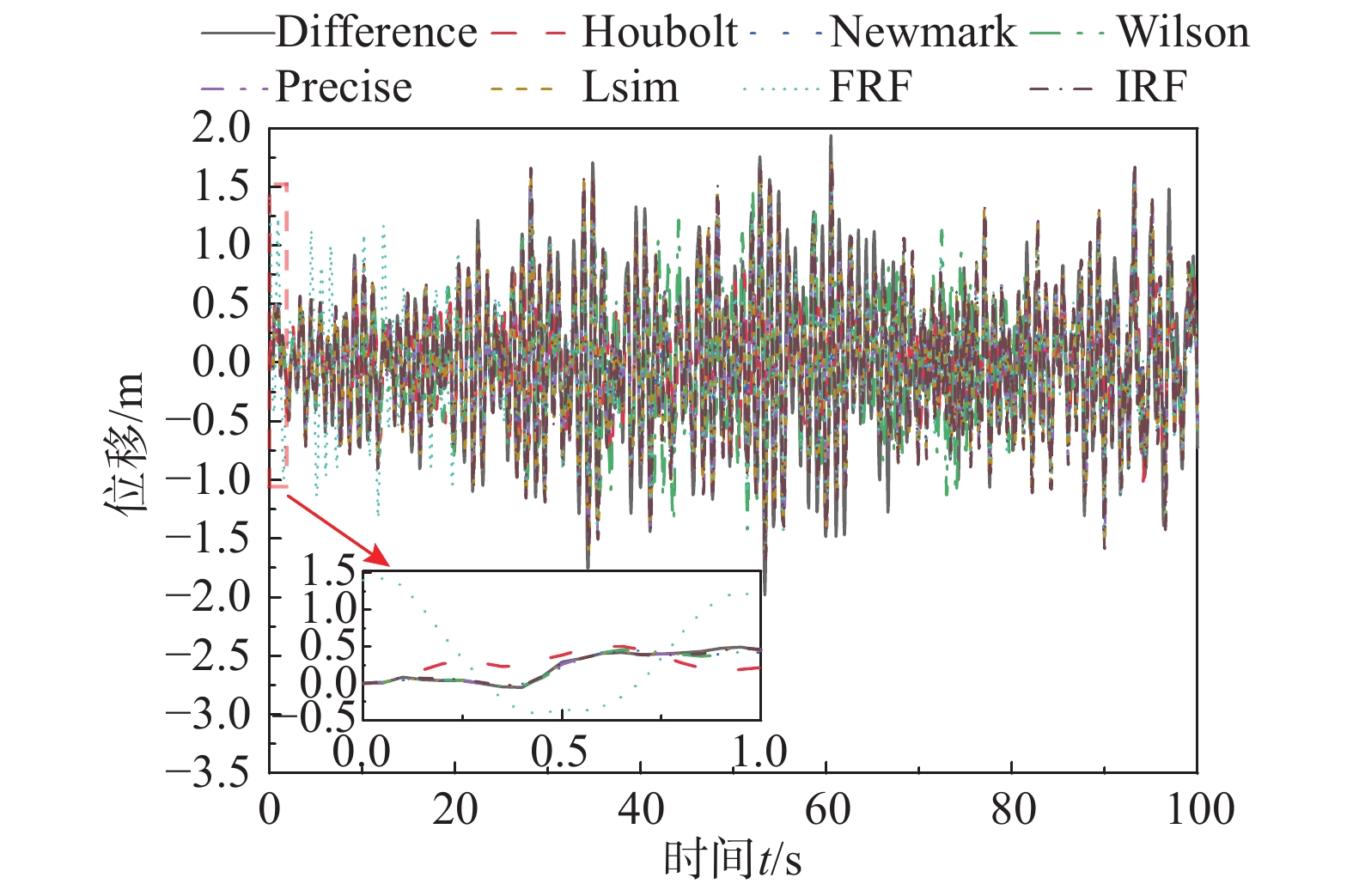
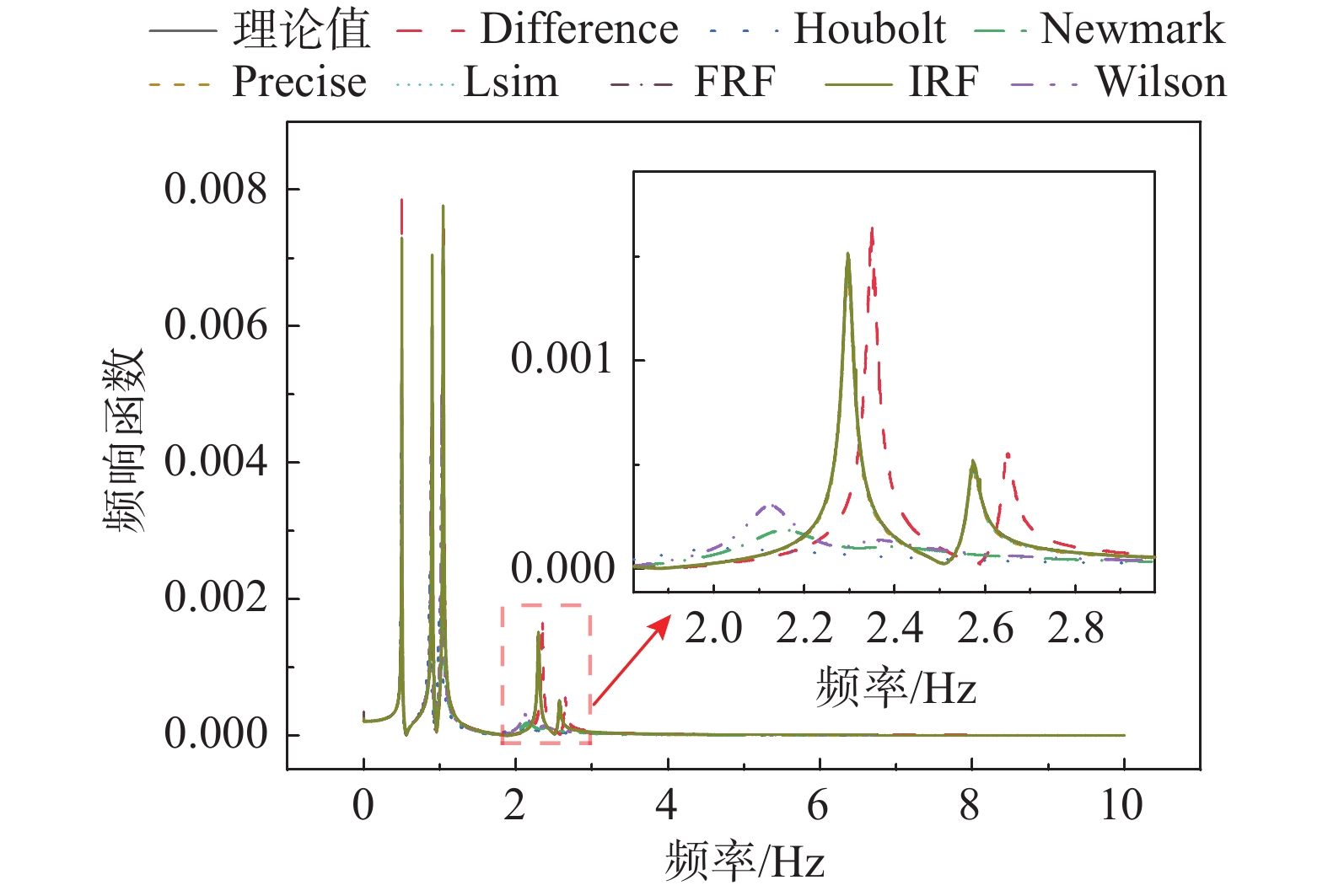
通过编程实现结构响应的计算，并进行如下对比，所有对比中对比的参数均为${m_1}$质点对应的参数。如图4和图5所示，8种响应计算方法计算的位移时程和频响函数均存在差异；如图4所示，频响函数法(FRF)的位移时程曲线起点位移不为零，Houblt方法的时程曲线与其余曲线的差异较大，除Houblt方法和频响函数方法以外，其余方法的时程曲线基本重合；如图5所示，精细积分法(Precise)、状态空间法(Lsim函数方法)、频响函数法以及脉冲响应函数法计算结果对应的频响函数基本一致，且与理论频响函数曲线基本重合。

图  4  位移时程曲线对比图

Figure  4.  Contrast diagram of displacement time history curve

下载: 全尺寸图片 幻灯片

图  5  频响函数曲线对比图

Figure  5.  Contrast diagram of frequency response function curve

下载: 全尺寸图片 幻灯片

由以上对比可知：8种响应计算方法获得的位移响应时程和频响函数曲线均存在差异；为了更直观地展现这8种响应计算方法的精度，将从一致性和差异性两个方面，对比频响函数相关系数(FRAC)、幅值相关系数(FAAC)、频响函数残差(FRRE)和频响函数均方根误差(FRFRMS)4个参数，获取8种响应计算方法对应的频响函数与理论频响函数之间的一致程度和偏差大小。

1.3.1   一致性对比

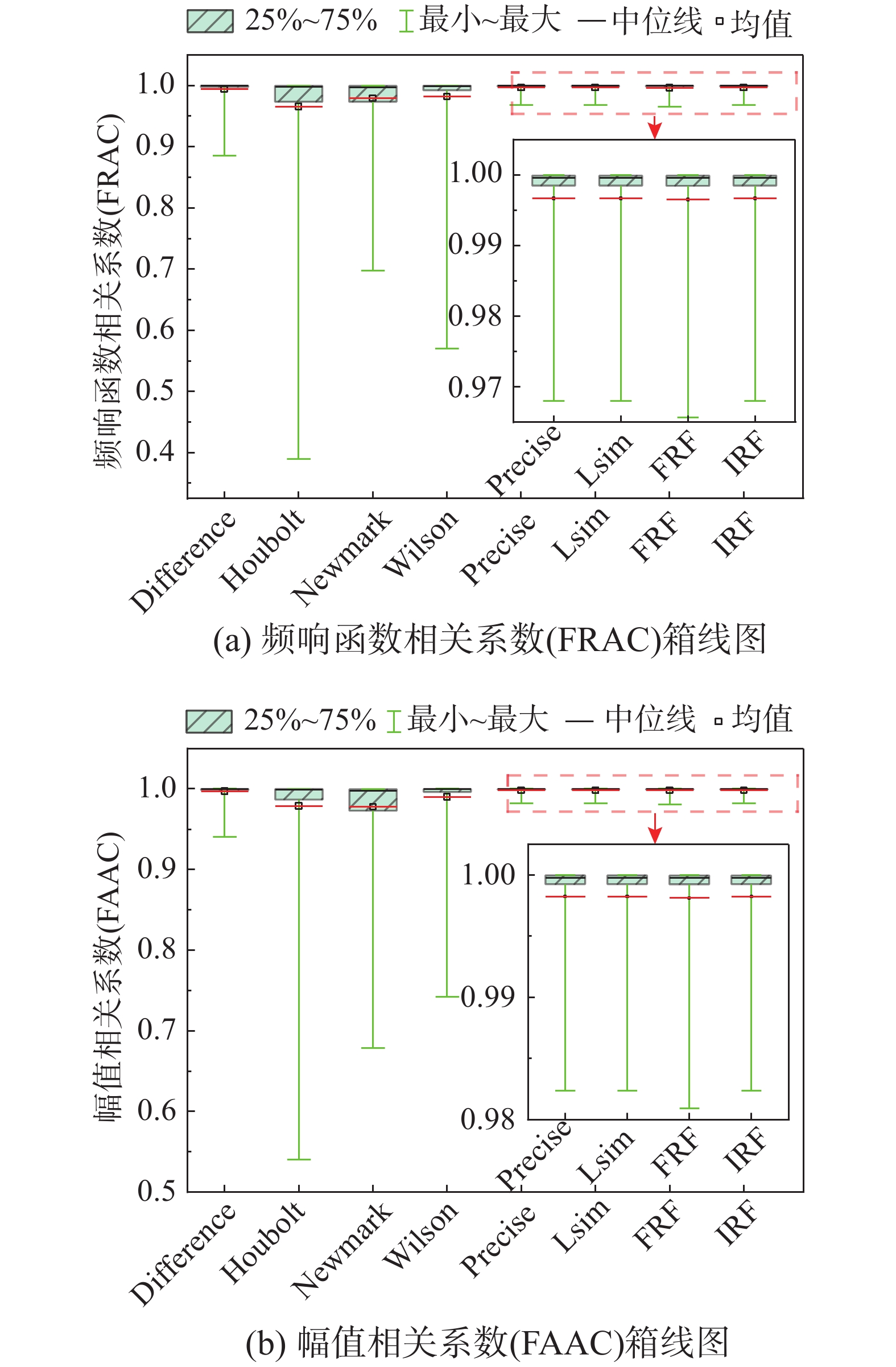
通过频响函数相关系数(FRAC)和频响函数幅值相关系数(FAAC)来评价两条频响函数曲线的一致性(相似性)，两个参数的值越接近1，则对应的频响函数与理论频响函数越接近，反之FRAC与FAAC的值越接近0，说明对应的频响函数曲线与理论频响函数曲线的一致性越低。

如图6所示，8种响应计算方法的FRAC和FAAC的均值都大于0.96，说明多数情况下这8种响应计算方法均能获得结构较为准确的响应。对比图6中Precise、Lsim函数、FRF和IRF方法箱线图的放大图，发现4种方法的FRAC与FAAC的均值和分布基本一致；观察FRAC和FAAC值的25%~75%分布区间，发现Precise、Lsim函数、FRF和IRF方法的FRAC和FAAC的分布区间最集中，且FRAC值均大于0.96，FAAC值均大于0.98；而Houbolt方法的FRAC和FAAC最小值约为0.4和0.55。如表5、表6所示，8种方法FRAC和FAAC的均值和中位数十分接近，且均大于0.994，说明8种响应计算方法的频响函数与理论频响函数的形状和峰值都十分接近，Precise、Lsim函数、FRF和IRF方法的FRAC和FAAC的标准差相近，且标准差约为其余4种方法的50%；即Precise、Lsim函数、FRF和IRF方法计算的结构响应对应的频响函数曲线与理论频响函数曲线相似程度较高，且相似程度的离散性较低。

图  6  8种响应计算方法频响函数一致性对比图

Figure  6.  Consistency chart of frequency response function of eight response calculation methods

下载: 全尺寸图片 幻灯片

表  5  频响函数相关系数统计分析表

Table  5.  Statistical parameter list of FRAC

方法	Difference	Houbolt	Newmark	Wilson	Precise	Lsim	FRF	IRF
中位数	0.9940	0.9660	0.9790	0.9820	0.9970	0.9970	0.9960	0.9970
均值	0.9944	0.9662	0.9795	0.9822	0.9969	0.9969	0.9965	0.9966
标准差	0.0150	0.0975	0.0462	0.0610	0.0073	0.0073	0.0079	0.0073

下载: 导出CSV 

| 显示表格

表  6  频响函数幅值相关系数统计分析表

Table  6.  Statistical parameter list of FAAC

方法	Difference	Houbolt	Newmark	Wilson	Precise	Lsim	FRF	IRF
中位数	0.9970	0.9790	0.9780	0.9900	0.9980	0.9980	0.9980	0.9980
均值	0.9971	0.9789	0.9778	0.9901	0.9983	0.9983	0.9982	0.9982
标准差	0.0078	0.0681	0.0513	0.0354	0.0040	0.0040	0.0043	0.0040

下载: 导出CSV 

| 显示表格

1.3.2   差异性对比

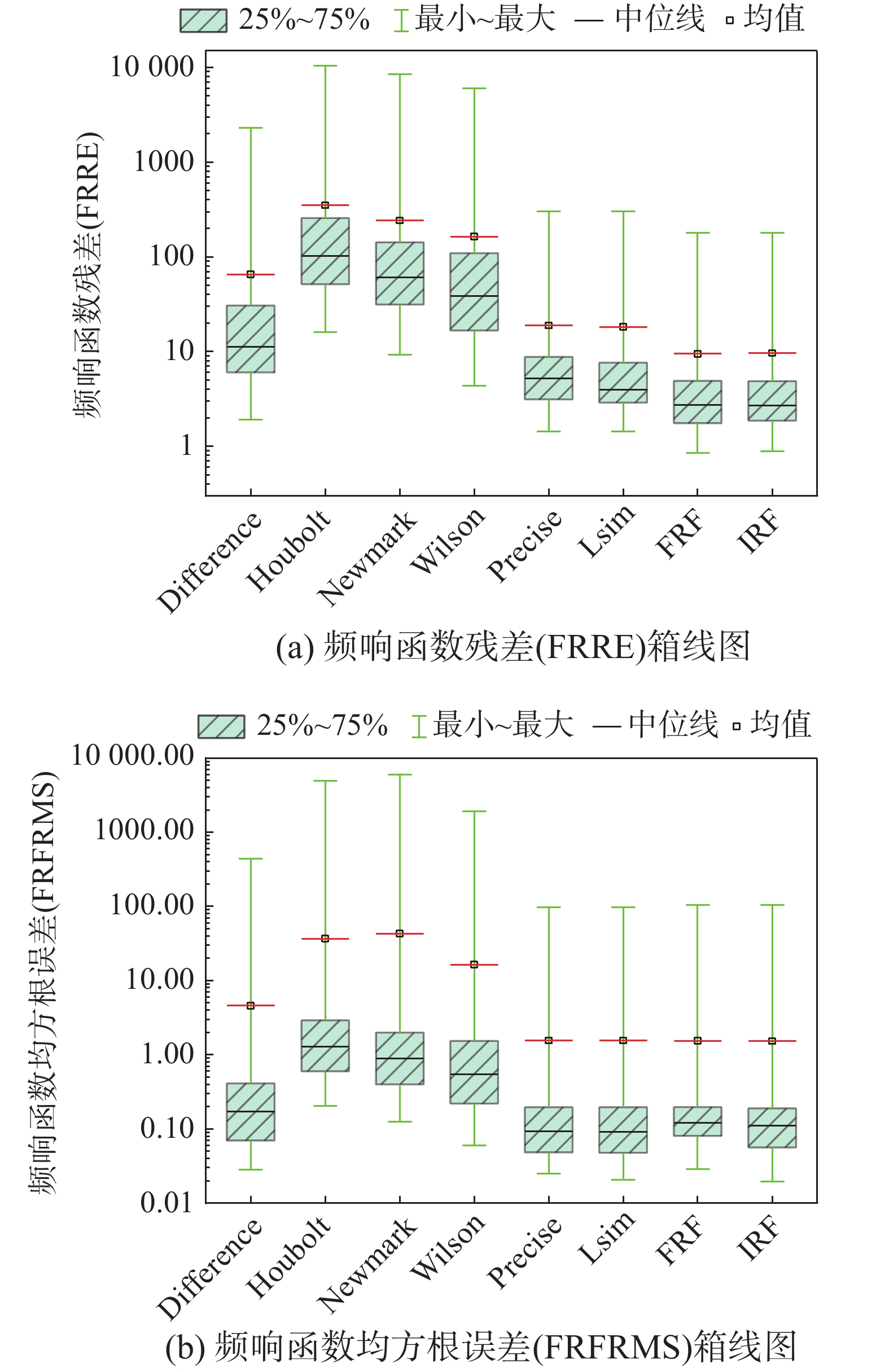
通过频响函数残差(FRRE)和频响函数均方根误差(FRFRMS)来评价两条频响函数曲线的偏差程度，两个参数的值越接近0，则对应的频响函数与理论频响函数的差值越小，反之FRRE与FRFRMS的值越大，说明对应的频响函数曲线与理论频响函数曲线的偏差越大。

如图7所示为频响函数曲线差异性对比图：8种响应计算方法的FRRE和FRFRMS值的中位数均较小，且均值大于75%分位数，说明多数情况下这8种计算方法得到的频响函数曲线与理论频响函数曲线的差值较小，少数情况下FRRE和FRFRMS的值偏高，使得FRRE和FRFRMS的均值大于其75%分位数。相比于其它4种方法，Precise、Lsim函数、FRF和IRF方法的FRRE与FRFRMS值的分布区间更集中，均值和中位数更小；Precise法与Lsim函数方法的FRRE与FRFRMS值分布区间、均值基本一致，Lsim函数方法的FRRE中位数略小与Precise方法；FRF方法与IRF方法FRRE与FRFRMS值分布区间、均值、中位数基本一致。如图7所示，Precise、Lsim函数、FRF和IRF方法FRRE与FRFRMS值残差的中位数、均值以及标准均是均小于其它4种方法；如表7所示，Precise法和Lsim函数方法的FRRE均值约为FRF方法与IRF方法FRRE均值的2倍，Precise法和lsim函数方法的FRRE标准差约为FRF方法与IRF方法FRRE标准差的1.8倍；如表8所示Precise、Lsim函数、FRF和IRF方法FRFRMS值残差的中位数、均值以及标准差基本相同。即Precise法和Lsim函数方法的频响函数与理论频响函数之间的差异基本一致，FRF和IRF方法的频响函数与理论频响函数之间的差异基本一致，FRF和IRF方法的频响函数残差略小于Precise法和Lsim函数方法；Precise、Lsim函数、FRF和IRF方法频响函数与理论频响函数的偏差程度均小于Difference、Houbolt方法、Newmark法和Wilson方法。

图  7  8种响应计算方法频响函数差异性对比图

Figure  7.  Consistency diagram of frequency response function of eight response calculation methods

下载: 全尺寸图片 幻灯片

表  7  频响函数残差统计分析表

Table  7.  Statistical parameter list of FREE

方法	Difference	Houbolt	Newmark	Wilson	Precise	Lsim	FRF	IRF
中位数	11.2500	101.4900	60.5800	38.5400	5.2000	3.9400	2.7200	2.7000
均值	65.3318	349.0170	241.2861	163.7897	18.8428	18.1732	9.4410	9.6313
标准差	200.6700	951.3400	780.5800	504.9600	41.4000	41.5500	22.7500	23.0600

下载: 导出CSV 

| 显示表格

表  8  频响函数均方根误差统计分析表

Table  8.  Statistical parameter list of FRFRMS

方法	Difference	Houbolt	Newmark	Wilson	Precise	Lsim	FRF	IRF
中位数	0.1700	1.2900	0.8900	0.5400	0.0900	0.0900	0.1200	0.1100
均值	4.5682	36.8458	42.8845	16.3704	1.5557	1.5545	1.5310	1.5266
标准差	32.2000	337.1300	398.5200	136.2900	9.1200	9.1300	9.3400	9.4200

下载: 导出CSV 

| 显示表格

综上所述，Precise、Lsim函数、FRF和IRF方法的频响函数与理论频响函数的相似程度接近，且高于Difference、Houbolt方法、Newmark法和Wilson方法；Precise、Lsim函数、FRF和IRF方法的频响函数与理论频响函数的差异程度接近，且小于Difference、Houbolt方法、Newmark法和Wilson方法；Precise、Lsim函数、FRF和IRF方法中后2种方法频响函数的差异程度略小于前2种方法；即8种响应计算方法中，频响函数法(FRF)和脉冲响应函数法(IRF)的计算精度最高；精细积分法(Precise)、状态空间法(Lsim函数方法)的计算精度略低于频响函数法(FRF)和脉冲响应函数法(IRF)。在数值算例的计算过程中发现，状态空间法的计算速度最快，精细积分法(Precise)次之，脉冲响应函数法计算速度最慢；即状态空间法的计算效率最高。因此，基于模态参数计算结构响应的8种方法中状态空间法不仅具有较高的计算精度，还具有较高的计算效率。

1.4   数据库构建的流程

数据库构建有两个核心过程：模态参数取值和结构响应计算。状态空间法是计算结构响应精度和计算效率均较高的方法，因此状态空间法(Lsim函数方法)是结构响应计算的最佳选择。对于集中质量模型，结构响应数据库的构建流程如图8所示。

图  8  结构响应数据库建立流程图

Figure  8.  Structural response database establishment flowchart

下载: 全尺寸图片 幻灯片

2   优化的随机子空间法及其识别精度评价

2.1   奇异熵增量定阶

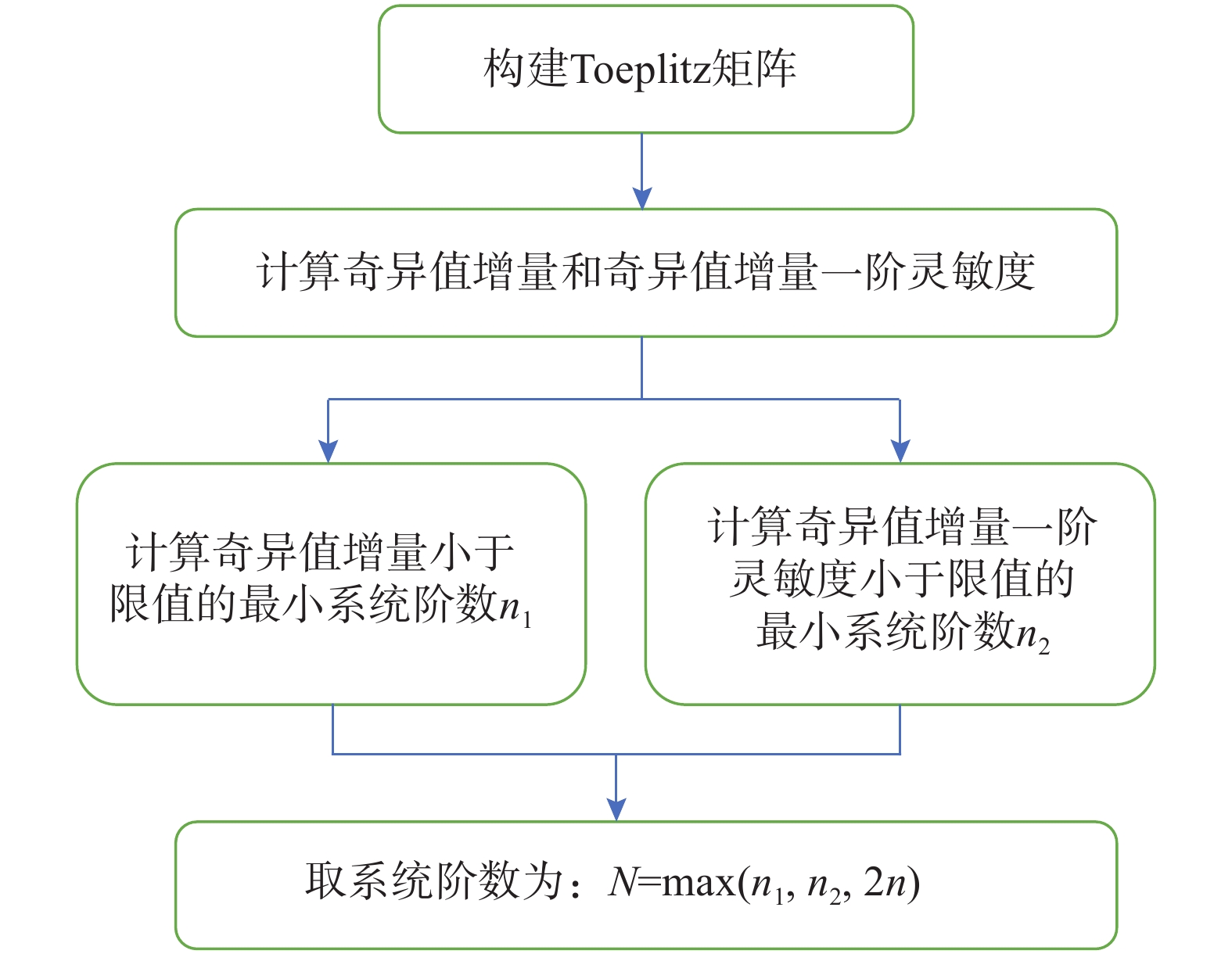
在随机子空间识别时需要确定系统的阶数和Toeplitz矩阵的块数，这两个参数将直接决定随机子空间法识别结果是否会缺失真实模态和虚假模态的占比。经过研究^[37]发现根据奇异熵增量和奇异熵增量一阶灵敏度可以很好地确定系统的阶数。为此设计出图9所示的流程，利用奇异熵增量和奇异熵增量一阶灵敏度确定系统的阶数。

图  9  奇异熵增量定阶流程

Figure  9.  Flow chart of singular entropy increment order determination

下载: 全尺寸图片 幻灯片

图9中：n为结构响应数据中测点的数量；系统阶数N通常取偶数值；Toeplitz矩阵构建时需要确定Toeplitz矩阵的块数，参考刘威^[38]的研究，取Toeplitz矩阵的块数$i = 2\beta \sim 4\beta$，$\beta$为采样频率与结构基频的比值；但在结构模态识别完成之前，结构的基频是未知的，故采用如图10所示流程确定Toeplitz矩阵的块数$i$，图10中f_s为采样频率。

图  10  Toeplitz矩阵块数确定流程图

Figure  10.  Toeplitz matrix block number determination flowchart

下载: 全尺寸图片 幻灯片

2.2   两阶段稳态图虚假模态剔除

现有的稳态图虚假模态剔除方法主要是各类聚类方法，但聚类方法的本质是将“整体”或“整体的绝大部分”按照一定规则分成具有某些相似性的集合。因此，将传统的聚类方法用于稳态图剔除虚假模态、获取稳定轴存在下列风险：

1) 稳态图(或识别结果)中存在虚假模态，且虚假模态的占比是未知的，因此，聚类结果中可能依旧会存在较多虚假模态。

2) 稳态图(或识别结果)中稳定轴(真实模态)的数量与系统阶数、测点数量的关系并不是唯一确定的，即聚类算法中聚类中心的数量也是未知的；错误的聚类中心数量可能导致同一阶模态被聚类为多阶模态、或多阶相似的模态被聚类为同一阶模态。

3) 现有的模态识别方法中通常频率的识别结果精度最高，振型识别精度次之，阻尼比的识别精度最低；随机子空间法亦是如此，阻尼比的识别结果误差较大；现有的稳定图聚类算法中通常将频率、振型和阻尼比都作为聚类的对象，这种做法可能使得阻尼比误差较大的真实模态被剔除或聚类为多阶模态。

分析稳态图中真实模态的特征，发现：

1) 真实模态具有“稳定性”，在稳态图中通常能够形成显著的“稳定轴”。

2) 当两阶模态的频率相互接近时，仅由频率难以区分两阶模态，但振型相关系数(Modal assurance criterion, MAC)能很好地区分两阶模态。

3) 部分真实模态的识别结果中阻尼比离散性较大。

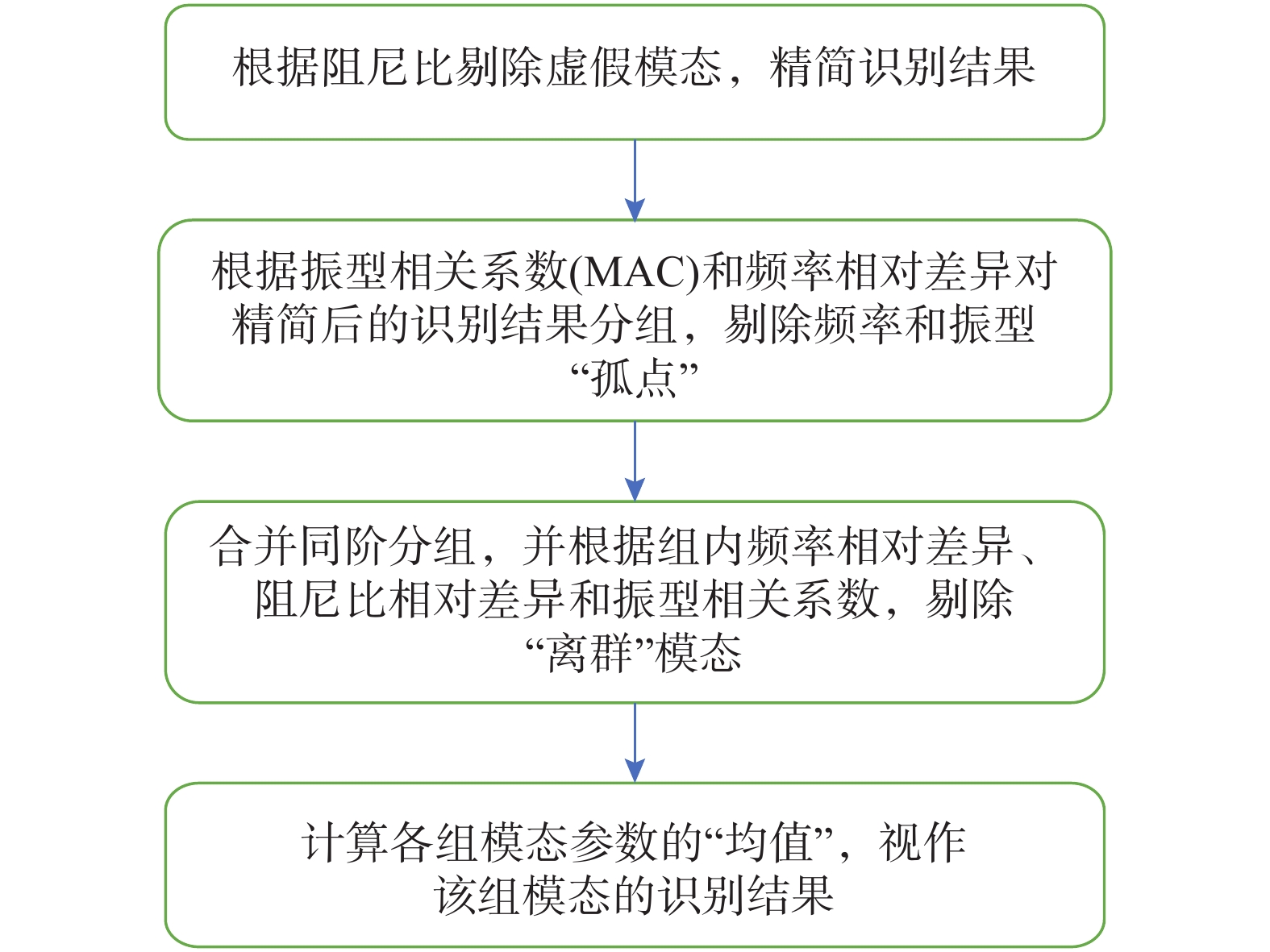
为此针对目前稳态图聚类算法存在的问题和稳态图中真实模态的特征，提出新的稳态图虚假模态剔除方法，其流程如图11所示。

图  11  稳态图两阶段虚假模态剔除流程图

Figure  11.  The flow chart of two-stage spurious mode elimination in steady state diagram

下载: 全尺寸图片 幻灯片

图11中频率和振型“孤点”是指：与其余模态的振型相关系数小于振型相关系数限值或频率相对差异大于频率相对差异限值的模态，在稳定图中的代表该模态的点远离其余的点，故称作“孤点”；“离群”模态是指：在模态分组内，与该组模态“均值”的频率相对差异大于频率相对差异限值、或阻尼比相对差异大于阻尼比相对差异限值或振型相关系数小于振型相关系数限值的模态；模态“均值”在这里是频率均值、阻尼比均值和振型“均值”的统称；频率均值和阻尼比均值即该模态分组频率和阻尼比的平均值；由于振型是向量，存在方向(正负)之分，故振型“均值”并非该组内各振型的均值，而是该组模态中各自由度上振幅绝对值的均值经过振幅方向(正负)调整后的振型。

两阶段稳态图虚假模态剔除方法步骤如下：

1) 根据阻尼比剔除明显不合理的模态，精简识别结果。例如：土楼中阻尼比小于0或阻尼比大于50%的模态显然不合理，可以预先剔除；当然这里的“0”和“50%”只是举例，实际算法中可根据结构的特点做出调整。

2) 根据振型和频率对精简后的数据进行分组。首先，对识别结果中的模态两两之间依次计算振型MAC值，根据MAC值不小于MAC限值为指标将识别结果分组；其次，同样对经过MAC值分组各组内的模态计算两两之间的频率相对差异，以频率相对差异为指标，对识别结果再次分组；此步骤中只有频率和振型均稳定的模态会被保留，频率或振型“孤立”的模态将会被剔除。

3) 合并同阶模态并计算各组的“核心模态”。首先，由于上述“步骤2”中可能因为识别结果离散性较大或MAC限值、频率相对差异限值选取不合理等原因，导致同阶模态被分为两组或多组，故需要将同为一阶模态的不同分组合并，合并方法为：计算各分组频率和振型的“均值”→计算各组频率均值的相对差异和振型均值的MAC矩阵→将振型MAC不小于MAC限值且频率误差不大于频率误差限值的分组视作同阶模态而合并；其次，经过上述步骤后，各分组中可能依旧存在虚假模态或与真实模态误差较大的“离群”识别结果，故需要各分组进一步精简，降低识别结果的误差，具体过程为：计算各分组的频率、振型和阻尼比的“均值”→计算各分组组内模态与对应频率、振型和阻尼比“均值”的频率相对差异向量、振型MAC向量、阻尼比相对差异向量→将频率相对差异或阻尼相对差异大于两者对应误差限值或振型MAC值小于MAC值限值的模态视作虚假模态从各分组中剔除。

4) 上一步中剔除了虚假模态的各组模态便是稳态图剔除虚假模态的结果，其中每一个分组即代表稳态图中的一条稳定轴。计算各分组的频率、振型和阻尼比均值，并将各组的模态参数“均值”视作该组模态的识别结果。

2.3   识别精度评价

基于数据库的模态识别精度评价方法从频率、阻尼比和振型3个方面来评价模态识别的精度，如图12所示，为一个模态识别精度评价算例的评价图示。

图  12  模态识别精度评价示例

Figure  12.  Example of modal identification accuracy evaluation

下载: 全尺寸图片 幻灯片

在共计243个算例中，去除错误的14个算例，将剩余的229个算例，分别计算每个算例每一阶模态的频率相对误差、阻尼比相对误差和振型相关系数以及平均相对误差和振型相关系数平均值。表9所示为识别结果频率的相对误差，其中频率的相对误差最大值为5.55%，各阶频率的平均相对误差最大值为0.3%，频率相对误差的标准差最大值为0.478%。以上数据说明优化的随机子空间法频率的识别相对误差小且误差的离散性也小，优化的随机子空间法频率识别精度较高且识别精度稳定性较好。

表  9  识别结果频率的相对误差统计表

Table  9.  Statistical table of relative errors of frequencies

阶次	1	2	3	4	5
频率相对误差平均值/(%)	0.277	0.300	0.250	0.262	0.209
频率相对误差最小值/(%)	0.002	0.002	0.000	0.001	0.001
频率相对误差最大值/(%)	1.561	5.550	1.579	1.720	1.518
频率相对误差的标准差/(%)	0.288	0.478	0.301	0.285	0.225

下载: 导出CSV 

| 显示表格

表10所示为阻尼比识别结果的相对误差统计表，其中阻尼比的相对误差最大值为93.512%，各阶阻尼比的平均相对误差最大值为15.54%，阻尼比相对误差的标准差最大值也12.353%，这说明优化的随机子空间法阻尼识别相对误差大且误差离散性较大，优化的随机子空间法阻尼比的识别精度低且识别稳定性差。表11所示为振型相关系数统计表，其中振型相关系数的最小值为0.562，各阶振型的平均相关系数均大于0.98，振型平均相关系数的最小值为0.987；振型相关系数的标准差最大值为0.032。上述数据表明：优化的随机子空间法识别结果的振型相关系数与1非常接近且振型相关系数离散性较小，优化的随机子空间法振型识别精度高且振型识别的稳定性较好。

表  10  识别结果阻尼比的相对误差统计表

Table  10.  Statistics of Relative Error of Damping Ratio

阶次	1	2	3	4	5
阻尼比相对误差平均值/(%)	14.277	15.540	11.838	13.927	10.675
阻尼比相对误差最小值/(%)	0.069	0.034	0.055	0.093	0.014
阻尼比相对误差最大值/(%)	78.341	89.918	46.715	42.743	93.512
阻尼比相对误差的标准差/(%)	12.353	12.705	8.558	8.926	11.634

下载: 导出CSV 

| 显示表格

表  11  识别结果振型相关系数统计表

Table  11.  Statistical table of modal correlation coefficient

阶次	1	2	3	4	5
振型相关系数平均值	0.999	0.987	0.992	0.994	0.993
振型相关系数最小值	0.968	0.783	0.652	0.562	0.867
振型相关系数最大值	1.000	1.000	1.000	1.000	1.000
振型相关系数的标准差	0.003	0.025	0.032	0.032	0.018

下载: 导出CSV 

| 显示表格

3   结论

模态识别精度是贯穿模态识别研究全过程的一个关键问题。提出一种基于结构响应数据库确定模态识别方法适用性和识别精度的思路。构建结构响应数据库的核心问题是基于模态参数计算结构响应，整理了4类计算结构响应计算的途径。4类方法计算结构响应不仅需要完整的模态参数，还需要物理参数参与运算，提出一种基于模态参数构建物理参数的方法，实现了模态参数向物理参数的转换。通过数据库建立的算例，对比了4类(中心差分法(Difference)、Houbolt方法、Newmark-β方法、威尔逊θ方法(Wilson)、精细积分法(Precise)、状态空间法、频响函数法(FRF)、脉冲响应函数法(IRF)共8种)基于模态参数计算结构响应方法的精度和计算效率。提出一种优化的随机子空间法，并基于数据方法对优化的随机子空间法进行了模态识别精度评价。得到了以下结论：

(1)单一或少数算例能过获得模态识别的精度估计，但结论存在偶然性且不能完全满足模态识别精度研究的全部场景，因此提出基于结构响应数据库的模态识别精度和适用性的评价方法，有利于模态识别精度评价工作的进一步开展。

(2)数据库方法的关键步骤是建立合适的数据库。数据库的核心数据是算例的结构模态参数理论值和结构响应。对于集中质量模型，提出一种基于模态参数构建结构物理参数的方法，并用数值算例验证了该方法的可行性；通过对比频响函数与理论频响函数的一致性和差异性来评价八种结构响应计算方法的精度；发现频响函数法(FRF)和脉冲响应函数法(IRF)的计算精度最高；精细积分法(Precise)、状态空间法(Lsim函数方法)次之；状态空间法(Lsim函数方法)既能保证计算精度，又能兼顾计算效率，是集中质量模型结构响应计算简单、高效的方法。针对随机子空间法定阶难和虚假模态剔除难的问题，提出一种优化的随机子空间法，并基于数据库对优化的随机子空间法进行了模态识别精度评价；评价结果表明：优化的随机子空间法频率和振型的识别精度高，阻尼比的识别精度较低。通过优化随机子空间法识别精度评价的算例，也验证了基于数据库进行模态参数识别精度进行评价的可行性。