基于模态综合法和模态叠加法的密集模态结构响应重构

邹云峰; 卢玄东; 阳劲松; 周帅; 何旭辉

doi:10.6052/j.issn.1000-4750.2021.08.0671

基于模态综合法和模态叠加法的密集模态结构响应重构

邹云峰^{1, 2,},
卢玄东^1,,
阳劲松^3, ,,
周帅^4,,
何旭辉^{1, 2,}

1.
中南大学土木工程学院，湖南，长沙 410075
2.
轨道交通工程结构防灾减灾湖南省重点实验室，湖南，长沙 410075
3.
中南大学交通运输工程学院，湖南，长沙 410075
4.
中国建筑第五工程局有限公司，湖南，长沙 410004

基金项目: 国家自然科学基金项目(52078504，51925808，U1934209)

详细信息

作者简介:
邹云峰(1984−)，男，湖南邵阳人，副教授，博士，博导，主要从事结构抗风研究(E-mail: yunfengzou@csu.edu.cn)

卢玄东(1997−)，男，广西梧州人，硕士生，主要从事动力响应重构研究(E-mail: 204811120@csu.edu.cn)

周　帅(1986−)，男，湖南宁乡人，高工，博士，主要从事结构施工技术及工程管理研究(E-mail: zhou_shai@hnu.edu.cn)

何旭辉(1975−)，男，贵州遵义人，教授，博士，博导，主要从事桥梁抗风与评估研究(E-mail: xuhuihe@csu.edu.cn)

通讯作者:
阳劲松(1990−)，男，湖南邵阳人，讲师，博士，主要从事健康监测与可靠度评估研究(E-mail: 307767159@qq.com)

中图分类号: TU17；TU973+.2
计量
- 文章访问数: 843
- HTML全文浏览量: 276
- PDF下载量: 174
出版历程
- 收稿日期: 2021-08-27
- 修回日期: 2021-11-17
- 录用日期: 2021-12-09
- 网络出版日期: 2021-12-09
- 刊出日期: 2023-02-28

STRUCTURAL RESPONSE RECONSTRUCTION BASED ON MODE SYNTHESIS METHOD AND MODAL SUPERPOSITION METHOD IN THE PRESENCE OF CLOSELY SPACED MODES

ZOU Yun-feng^{1, 2,},
LU Xuan-dong^1,,
YANG Jing-song^3, ,,
ZHOU Shuai^4,,
HE Xu-hui^{1, 2,}

1.
School of Civil Engineering, Central South University, Changsha, Hu’nan 410075, China
2.
Hunan Provincial Key Laboratory for Disaster Prevention and Mitigation of Rail Transit Engineering Structure, Changsha, Hu’nan 410075, China
3.
School of Traffic and Transportation Engineering, Central South University, Changsha, Hu’nan 410075, China
4.
China Construction Fifth Engineering Division Corp. Ltd., Changsha, Hu’nan 410004, China

摘要

摘要: 提出一种基于模态综合法和模态叠加法的密集模态结构响应重构方法，通过两次坐标变换将全结构缩聚为自由度更少的超单元模型，将超单元模型的模态分为密集模态和剩余模态。通过经验模态分解法分离出已知响应中单阶的剩余模态响应，进而重构出待测位置的剩余模态响应，待测位置的密集模态响应可由模态振型和剩余模态计算得到，通过模态叠加法实现在密集模态下的时域响应重构。进行了数值模拟研究，将待测位置响应的理论值与重构值进行比较以验证该方法的精度和效率，此外还详细研究了主模态数量、子结构划分方式、测量噪声和阻尼对重构结果的影响。结果表明：该文方法通过模型缩聚大大减少了重构的数据量，并且改善了传统EMD方法不能分离频率间隔较小的模态而无法实现响应重构这一不足，无论密集模态存在与否都可适用于结构的应力、应变、位移、加速度等多种动力响应的重构。
- 模态综合法 /
- 模态叠加法 /
- 密集模态 /
- 响应重构 /
- 经验模态分解
Abstract: A structural response reconstruction methodology based on mode synthesis method and modal superposition method in the presence of closely spaced modes is proposed. The whole structure is condensed into a super element model with fewer degrees of freedom through two coordinate transformations, and then the modes of the super element model are divided into closely spaced mode and residual mode. The single order residual mode response of the known response is separated by empirical mode decomposition method, and then the residual mode response of the position to be measured is reconstructed. The closely spaced mode response of the position to be measured can be calculated from the mode shape and the residual mode. The time-domain response reconstruction under the closely spaced mode is realized by mode superposition method. Numerical simulation studies were carried out to verify the accuracy and efficiency of the proposed method by comparing the theoretical response values of the measured position with the reconstructed values. In addition, the influences of the number of main modes, number of substructures, measurement noise and damping on the reconstructed results were studied in detail. The results show that this method greatly reduces the amount of reconstructed data through model condensation and overcomes the deficiency of the traditional EMD method which cannot separate the modes with small frequency interval, and thus cannot realize response reconstruction. Whether there are closely spaced modes or not, it can be applied to the reconstruction of structural stress, strain, displacement, acceleration and other dynamic responses.
- mode synthesis method /
- modal superposition method /
- closely spaced mode /
- response reconstruction /
- empirical mode decomposition

HTML全文

土木工程结构的性能在其使用过程中会随着时间的推移而下降，为了监测结构的健康状况和进行寿命预估，有必要准确获得结构关键区域的系统响应^[1-2]。结构动力响应重构在过去十几年中受到越来越多的关注。然而，鉴于工程结构的几何复杂性及部件多样性，某些位置(例如结构交界面、狭缝等)皆不易安装传感器，实际中并不总是能在期望的位置进行测量^[3-4]。因此，预测关键点的动态响应成为进行结构健康监测的重要组成部分^[5-6]。

目前，响应重构方法主要可分两种：频域方法和时域方法。在频域方法中，RIBEIRO等^[7]首先提出了传递率概念，定义为频域中已知响应函数和其他未知响应函数之间的传递率矩阵，通过传递率可以实现结构任意位置的响应重构；DEVRIENDT等^[8]提出另一个传递率概念，定义为响应谱和单个参考响应谱之间的比值，在响应重构中仅应用于全局传递性；LAW等^[9-11]基于频响函数将上述位移传递率推广至加速度传递率，完成了全模型或子结构上的响应重构。以上的频域方法使用频率响应域中的数据，而且通过逆傅里叶变换来将重构的频域响应转换回时域，会引入额外的计算成本和数值截断误差。在时域方法中，HE等^[12-13]提出一种基于经验模态分解(EMD)的时域响应重构方法，将采集响应分解为由固有模态函数表示的模态响应，然后，利用这些模态响应计算待测位置的模态响应，最后，采用模态叠加法实现时域动态响应重构。为了确保通过EMD得到本征模态函数(IMF)的只包含一个频率成分，还加入了间歇性准则进行频率筛选。该方法在计算成本方面非常有效，并且适用于基于不同类型的传感器测量的动态响应重构，相比于频域方法有着更高的计算效率。

然而，基于EMD的响应重构方法应用于大型土木结构存在一定困难。一方面，该方法需要获取整个结构的全局刚度矩阵与质量矩阵，而大型土木工程结构通常维数较大，在提取刚度矩阵、质量矩阵时需要大量的计算资源和时间；另一方面，带间歇性准则的EMD方法不能有效地分离密集模态，从而难以实现存在密集模态结构的响应的重构。

针对以上两种限制，本文提出一种基于模态综合法和改进模态叠加法的响应重构方法。该方法结合了模态综合法^[14-16]，将结构全模型经过两次坐标变换缩聚为自由度更少的超单元模型，并通过在超单元模型上计算的模态振型进行动态响应重构；当存在密集模态时，在超单元模型的基础上，将结构模态分为密集模态和剩余模态^[17-18]，其中剩余模态的重构通过基于EMD的重构方法实现，密集模态的重构响应可由模态振型和剩余模态计算得到，最后通过模态响应叠加获得待测位置响应。

1 理论推导

1.1 子结构模态综合法

对于一般的土木工程结构而言，可以根据结构的连接特性、实际工程需要等因素划分成多个子结构。在有限元基础上，子结构的动力学运动方程可表示为：

${{\boldsymbol{M}}^s}{{\boldsymbol{\ddot X}}^s}(t) + {{\boldsymbol{C}}^s}{{\boldsymbol{\dot X}}^s}(t) + {{\boldsymbol{K}}^s}{{\boldsymbol{X}}^s}(t) = {{\boldsymbol{f}}^s}(t) + {{\boldsymbol{g}}^s}(t)$

(1)

式中：上标s表示第s个子结构； ${{\boldsymbol{M}}^s}$ 、 ${{\boldsymbol{C}}^s}$ 及 ${{\boldsymbol{K}}^s}$ 分别为子结构的有限元模型的质量矩阵、阻尼矩阵及刚度矩阵； ${{\boldsymbol{X}}^s}(t)$ 、 ${{\boldsymbol{\dot X}}^s}(t)$ 及 ${{\boldsymbol{\ddot X}}^s}(t)$ 分别为自由度位移、速度及加速度； ${{\boldsymbol{f}}^s}(t)$ 为子结构所受外力， ${{\boldsymbol{g}}^s}(t)$ 为子结构的界面力。

根据Craig-Bampton提出的固定界面模态综合法，式(1)中的自由度可分成内部组“i”和边界组“j”，其中，内部组中的自由度不与任何子结构共有，边界组必须包含实际的“边界”，即子结构与子结构之间共有的自由度，也可以将子结构内部任意自由度归到边界组中。将式(1)中的各矩阵的元素按如下形式重新排序：

$\begin{split} & {X}^{s}=\left\{ \begin{array}{c}{X}_{i}^{s}\\ {X}_{j}^{s}\end{array} \right\};{M}^{s}=\left[ \begin{array}{cc}{M}_{ii}^{s}& {M}_{ij}^{s}\\ {M}_{ji}^{s}& {M}_{jj}^{s}\end{array} \right];{C}^{s}=\left[ \begin{array}{cc}{C}_{ii}^{s}& {C}_{ij}^{s}\\ {C}_{ji}^{s}& {C}_{jj}^{s}\end{array} \right];\\& {K}^{s}=\left[ \begin{array}{cc}{K}_{ii}^{s}& {K}_{ij}^{s}\\ {K}_{ji}^{s}& {K}_{jj}^{s}\end{array} \right]\text{；}{f}^{s}=\left\{ \begin{array}{c}{f}_{i}^{s}\\ {f}_{j}^{s}\end{array} \right\};{g}^{s}=\left\{ \begin{array}{c}{g}_{i}^{s}\\ {g}_{j}^{s}\end{array} \right\} \end{split}$

(2)

提取第s个子结构的模态转换矩阵 ${{\boldsymbol{\varPhi }}^s}$ ，该矩阵由两个子集组成，即固定界面选取的主模态集 ${\boldsymbol{\varPhi }}_k^s$ 和全部界面坐标的约束模态集 ${\boldsymbol{\varPhi }}_c^s$ ：

${{\boldsymbol{\varPhi }}^s} = \left[ \begin{matrix} {{\boldsymbol{\varPhi }}_k^s}&{{\boldsymbol{\varPhi }}_c^s} \end{matrix} \right] = \left[ \begin{matrix} {{\boldsymbol{\varPhi }}_{ik}^s}&{{\boldsymbol{\varPhi }}_{ij}^s} \\ {{\boldsymbol{0}}_{jk}^s}&{{\boldsymbol{I}}_{jj}^s} \end{matrix} \right]$

(3)

式中： ${\boldsymbol{\varPhi }}_k^s$ 称为第s个子结构保留的主模态，下标k表示选择保留的主模态数目； ${\boldsymbol{\varPhi }}_{ik}^s$ 是将子结构界面固定后，由公式 $({\boldsymbol{K}}_{ii}^s - {\boldsymbol{\varLambda }}_{ii}^s{\boldsymbol{M}}_{ii}^s){\boldsymbol{\varPhi }}_{ii}^s = {\boldsymbol{0}}$ 求得，其中 ${\boldsymbol{\varPhi }}_{ii}^s$ 和 ${\boldsymbol{\varLambda }}_{ii}^s$ 分别为在刚度矩阵 ${\boldsymbol{K}}_{ii}^s$ 和质量矩阵 ${\boldsymbol{M}}_{ii}^s$ 下求得的特征向量和特征值， ${\boldsymbol{\varPhi }}_{ik}^s$ 是 ${\boldsymbol{\varPhi }}_{ii}^s$ 所取的前 $k$ 列模态， ${\boldsymbol{\varPhi }}_{ij}^s = - {\boldsymbol{K}}_{ii}^{ - 1}{{\boldsymbol{K}}_{ij}}$ ； ${\boldsymbol{I}}_{jj}^s$ 是维度为j的单位矩阵。由此，对模型的各子结构做第一次坐标变换：

$\begin{split} & {{{\boldsymbol{\hat M}}}^s} = {{\boldsymbol{\varPhi }}^s}^{\text{T}}{{\boldsymbol{M}}^s}{{\boldsymbol{\varPhi }}^s};{{\hat {\boldsymbol{C}}}^s} = {{\boldsymbol{\varPhi }}^s}^{\text{T}}{{\boldsymbol{C}}^s}{{\boldsymbol{\varPhi }}^s} \;;\\& {{{\boldsymbol{\hat K}}}^s} = {{\boldsymbol{\varPhi }}^s}^{\text{T}}{{\boldsymbol{K}}^s}{{\boldsymbol{\varPhi }}^s};{{{\boldsymbol{\hat f}}}^s} = {{\boldsymbol{\varPhi }}^s}^{\text{T}}{{\boldsymbol{f}}^s};{{{\boldsymbol{\hat g}}}^s} = {{\boldsymbol{\varPhi }}^s}^{\text{T}}{{\boldsymbol{g}}^s} \end{split}$

(4)

将式(4)代入式(1)，并令 ${{\boldsymbol{X}}^s} = {{\boldsymbol{\varPhi }}^s}{{\boldsymbol{q}}^s}$ ，其中 ${q^s}$ 表示第s个子结构的模态坐标向量，则式(1)可表示为：

${{\boldsymbol{\hat M}}^s}{{\boldsymbol{\ddot q}}^s}(t) + {\hat {\boldsymbol{ C}}^s}{{\boldsymbol{\dot q}}^s}(t) + {{\boldsymbol{\hat K}}^s}{{\boldsymbol{q}}^s}(t) = {{\boldsymbol{\hat f}}^s}(t) + {{\boldsymbol{\hat g}}^s}(t)$

(5)

根据式(3)，模态坐标q和原坐标X之间的关系可具体表示为：

$\left\{ {\begin{matrix} {{\boldsymbol{X}}_i^s} \\ {{\boldsymbol{X}}_j^s} \end{matrix}} \right\} = \left[ {\begin{matrix} {{\boldsymbol{\varPhi }}_{ik}^s}&{{\boldsymbol{\varPhi }}_{ij}^s} \\ {{\boldsymbol{0}}_{jk}^s}&{{\boldsymbol{I}}_{jj}^s} \end{matrix}} \right]\left\{ {\begin{matrix} {{\boldsymbol{q}}_i^s} \\ {{\boldsymbol{q}}_j^s} \end{matrix}} \right\}$

(6)

式中： ${\boldsymbol{q}}_i^s$ 和 ${\boldsymbol{q}}_j^s$ 分别表示第s个子结构的模态坐标向量中的内部组集和边界组集，根据式(6)可以得到如下关系：

${\boldsymbol{X}}_j^s = {\boldsymbol{q}}_j^s$

(7)

即经过第一次坐标变换后，边界组中自由度的模态坐标下的响应与对应的原结构响应相等。

各子结构进行第一次坐标变换之后，整合所有子结构，则整个模型的动力学运动方程可表示为：

$\bar{\boldsymbol{M}} {\boldsymbol{\ddot q}}(t) + \bar {\boldsymbol{C\dot q}}(t) + \bar {\boldsymbol{Kq}}(t) = \bar {\boldsymbol{f}}(t) + \bar {\boldsymbol{g}}(t)$

(8)

其中：

$\begin{split} & \bar {\boldsymbol{M}} = {\text{diag}}({{{\boldsymbol{\hat M}}}^1},\cdots,{{{\boldsymbol{\hat M}}}^s},\cdots,{{{\boldsymbol{\hat M}}}^n}) \;, \\& \bar {\boldsymbol{C}} = {\text{diag}}({{\hat {\boldsymbol{C}}}^1},\cdots,{{\hat {\boldsymbol{C}}}^s},\cdots,{{\hat {\boldsymbol{C}}}^n}) \;, \\& \bar {\boldsymbol{K}} = {\text{diag}}({{{\boldsymbol{\hat K}}}^1},\cdots,{{{\boldsymbol{\hat K}}}^s},\cdots,{{{\boldsymbol{\hat K}}}^n}) \;, \\& {{\boldsymbol{q}}^{\text{T}}} = [ {{{\boldsymbol{q}}^{1{\text{T}}}},\cdots,{{\boldsymbol{q}}^{s{\text{T}}}},\cdots,{{\boldsymbol{q}}^{n{\text{T}}}}} ] \;, \\& {{{\boldsymbol{\bar f}}}^{\text{T}}} = [ {{{{\boldsymbol{\hat f}}}^{1{\text{T}}}},\cdots,{{{\boldsymbol{\hat f}}}^{s{\text{T}}}},\cdots,{{{\boldsymbol{\hat f}}}^{n{\text{T}}}}} ] \;, \\& {{{\boldsymbol{\bar g}}}^{\text{T}}} = [ {{{{\boldsymbol{\hat g}}}^{1{\text{T}}}},\cdots,{{{\boldsymbol{\hat g}}}^{s{\text{T}}}},\cdots,{{{\boldsymbol{\hat g}}}^{n{\text{T}}}}} ] \end{split}$

(9)

由于各个子结构之间存在共有自由度，因此模态坐标q中的元素不是独立的，需要经过第二次坐标变换消除非独立坐标。结合布尔矩阵L可将各子结构耦合成全模型的超单元模型，当各子结构耦合为一个超单元模型之后，界面力为零，即 ${{\boldsymbol{L}}^{\text{T}}}{\boldsymbol{g}}(t) = 0$ ，令 ${\boldsymbol{q}} = {\boldsymbol{Lp}}$ ，其中p表示独立坐标，并代入式(8)，则整个超单元模型的动力学运动方程可表示为：

$\tilde{\boldsymbol{ M}}\ddot {\boldsymbol{p}}(t) + \tilde{\boldsymbol{ C}}\dot {\boldsymbol{p}}(t) + \tilde{\boldsymbol{ K}}{\boldsymbol{p}}(t) = \tilde{\boldsymbol{ f}}(t)$

(10)

式(10)中各矩阵可表示为：

$\tilde{\boldsymbol{ M}} = {{\boldsymbol{L}}^{\text{T}}}{\boldsymbol{\bar ML}};\tilde{\boldsymbol{ C}} = {{\boldsymbol{L}}^{\text{T}}}{{\bar{\boldsymbol CL}}}\;;\tilde{\boldsymbol{ K}} = {{\boldsymbol{L}}^{\text{T}}}{{\bar{\boldsymbol KL}}}\; ;\tilde{\boldsymbol{ f}} = {{\boldsymbol{L}}^{\text{T}}}{{\bar{\boldsymbol f}}}$

(11)

第二次坐标变换只消除耦合模型中的非独立坐标或改变各个坐标的排列顺序，并不会改变元素大小，因此根据式(7)，可以得到以下关系：

${\boldsymbol{X}}_j^s = {\boldsymbol{p}}_j^s$

(12)

式中， ${\boldsymbol{p}}_j^s$ 为超单元模型中第s个子结构的独立坐标向量的边界组集。由此可知，边界组中自由度的超单元模型响应与对应的原结构响应相等，从而可以将实际结构的响应采集自由度和待测自由度加入到边界组中，以便在超单元上进行响应重构。

基于超单元模型的响应重构需要求解模型的超单元模态振型矩阵，如下所示：

$(\tilde{\boldsymbol{ K}} - \tilde{\boldsymbol{ \varLambda}} \tilde {\boldsymbol{M}})\tilde{\boldsymbol{ \varPhi }} = {\boldsymbol{0}}$

(13)

式中： $\tilde{\boldsymbol{ \varLambda }}$ 为整个超单元模型的各阶模态频率矩阵； $\tilde{\boldsymbol{ \varPhi }}$ 为模型的超单元模态振型矩阵，可由式(13)求解。超单元的模态振型矩阵 $\tilde{\boldsymbol{ \varPhi }}$ 具体可表示为：

$\tilde{\boldsymbol{ \varPhi }} = \left[ {\begin{matrix} {{{\tilde \varPhi }_{11}}}& \cdots &{{{\tilde \varPhi }_{1n}}} \\ \vdots & \ddots & \vdots \\ {{{\tilde \varPhi }_{n1}}}& \cdots &{{{\tilde \varPhi }_{nn}}} \end{matrix}} \right]$

(14)

式中， $\tilde{\boldsymbol{ \varPhi }}$ 中每列表示一个模式，每个元素表示每个自由度的位移贡献值。

1.2 基于改进模态叠加法的子结构重构理论

假设结构第w阶和第v阶模态为密集模态，下标a和r分别表示密集模态和剩余模态，下标m和u分别表示响应采集处自由度和待测响应自由度。将响应采集自由度和待测自由度分别置于边界组中，结合式(11)，超单元基础上的已知响应集与未知响应集如下所示：

${{\boldsymbol{X}}_m}(t) = [\begin{matrix} {{{\tilde{\boldsymbol{ \varPhi }}}_{ma}}}&{{{\tilde{\boldsymbol{ \varPhi }}}_{mr}}} \end{matrix}]\left( {\begin{matrix} {{{\boldsymbol{D}}_a}(t)} \\ {{{\boldsymbol{D}}_r}(t)} \end{matrix}} \right)$

(15)

${{\boldsymbol{X}}_u}(t) = [\begin{matrix} {{{\tilde{\boldsymbol{ \varPhi }}}_{ua}}}&{{{\tilde{\boldsymbol{ \varPhi }}}_{ub}}} \end{matrix}]\left( {\begin{matrix} {{{\boldsymbol{D}}_a}(t)} \\ {{{\boldsymbol{D}}_b}(t)} \end{matrix}} \right)$

(16)

式中： $\tilde{\boldsymbol{ \varPhi }}$ 为超单元模型的模态矩阵； ${{\boldsymbol{D}}_a}(t)$ 和 ${{\boldsymbol{D}}_r}(t)$ 分别对应超单元模型模态坐标下密集模态和剩余模态的响应，可表示为如下形式：

${{\boldsymbol{D}}_a}(t) = {[ {{{\boldsymbol{D}}_{a1}}(t)}\;\;{{{\boldsymbol{D}}_{a2}}(t)}\;\; \cdots \;\;{{{\boldsymbol{D}}_{aa}}(t)} ]^{\text{T}}}$

(17)

${{\boldsymbol{D}}_r}(t) = {[ {{{\boldsymbol{D}}_{r1}}(t)}\;\;{{{\boldsymbol{D}}_{r2}}(t)}\;\; \cdots \;\;{{{\boldsymbol{D}}_{rr}}(t)} ]^{\text{T}}}$

(18)

式中：D_a1(t), D_a2(t)··· D_aa(t)为模态坐标中的密集模态响应；D_r1(t), D_r2(t)··· D_rr(t)为模态坐标中的剩余模态响应。由式(17)得模态坐标下的密集模态响应为：

${{\boldsymbol{D}}_a}(t) = \tilde{\boldsymbol{ \varPhi }}_{ma}^ + ({{\boldsymbol{X}}_m}(t) - \tilde{\boldsymbol{ \varPhi }}_{mr}^{}{{\boldsymbol{D}}_r}(t))$

(19)

式中：上标+表示矩阵的广义逆。在这里，已知响应的数目应不小于密集模态的总数。结合式(16)和式(18)，将各个模态组分进行叠加可得未知响应向量：

$\begin{split} {{\boldsymbol{p}}_u}(t) = &\tilde{\boldsymbol{ \varPhi }}_{ua}^{}\tilde{\boldsymbol{ \varPhi }}_{ma}^ + {{\boldsymbol{p}}_m}(t) + \\&\tilde{\boldsymbol{ \varPhi }}_{ub}^{}{{\boldsymbol{D}}_r}(t) - \tilde{\boldsymbol{ \varPhi }}_{ua}^{}\tilde{\boldsymbol{ \varPhi }}_{ma}^ + \tilde{\boldsymbol{ \varPhi }}_{mr}^{}{{\boldsymbol{D}}_r}(t) \end{split}$

(20)

定义如下四个矩阵：

${{\boldsymbol{T}}_{uam}} = \tilde{\boldsymbol{ \varPhi }}_{ua}^{}\tilde{\boldsymbol{ \varPhi }}_{ma}^ +$

(21)

${{\boldsymbol{S}}_{ubr}} = \left[ {\frac{{{{\tilde{\boldsymbol{ \varPhi }}}_{u{r_1}}}}}{{{{\tilde \varPhi }_{b{r_1}}}}}}\;\;{\frac{{{{\tilde{\boldsymbol{ \varPhi }}}_{u{r_2}}}}}{{{{\tilde \varPhi }_{b{r_2}}}}}}\;\; \cdots\;\;{\frac{{{{\tilde{\boldsymbol{ \varPhi }}}_{u{r_r}}}}}{{{{\tilde \varPhi }_{b{r_r}}}}}} \right]$

(22)

${{\boldsymbol{S}}_{mbr}} = \left[ {\frac{{{{\tilde{\boldsymbol{ \varPhi }}}_{m{r_1}}}}}{{{{\tilde \varPhi }_{b{r_1}}}}}}\;\;{\frac{{{{\tilde{\boldsymbol{ \varPhi }}}_{m{r_2}}}}}{{{{\tilde \varPhi }_{b{r_2}}}}}}\;\; \cdots \;\;{\frac{{{{\tilde{\boldsymbol{ \varPhi }}}_{m{r_r}}}}}{{{{\tilde \varPhi }_{b{r_r}}}}}} \right]$

(23)

${\tilde{\boldsymbol{ d}}_{br}}(t) = {[ {{{\tilde{\boldsymbol{ d}}}_{b{r_1}}}(t)}\;\;{{{\tilde{\boldsymbol{ d}}}_{b{r_2}}}(t)}\;\; \cdots \;\;{{{\tilde{\boldsymbol{ d}}}_{b{r_r}}}(t)} ]^{\text{T}}}$

(24)

式中：下标b表示第b自由度(响应采集量中的某个响应自由度)；下标r₁、r₂…r_r表示剩余的r个模态； ${\tilde{\boldsymbol{ d}}_{br}}(t)$ 为第b个自由度的剩余模态响应。式(20)可表示为如下形式：

${{\boldsymbol{X}}_u}(t) = {{\boldsymbol{T}}_{uam}}{{\boldsymbol{X}}_m}(t) + ({{\boldsymbol{S}}_{ubr}} - {{\boldsymbol{T}}_{uam}}{{\boldsymbol{S}}_{mbr}}){\tilde{\boldsymbol{ d}}_{br}}(t)$

(25)

式中： ${\tilde{\boldsymbol{ d}}_{br}}(t)$ 由带有间歇性准则的经验模态分解法求得；矩阵 ${{\boldsymbol{T}}_{uam}}$ 、 ${{\boldsymbol{S}}_{ubr}}$ 和 ${{\boldsymbol{S}}_{mbr}}$ 由式(21)~式(23)求得。若响应不包含密集模态，即密集模态响应集 ${{\boldsymbol{D}}_a}(t)$ 为空集，则式(25)转化为仅有非密集模态的叠加：

${{\boldsymbol{X}}_u}(t) = {{\boldsymbol{S}}_{ubr}}{\tilde{\boldsymbol{ d}}_{br}}(t)$

(26)

若结构的模态中存在密集模态，在响应的傅里叶谱上可能难以辨别其中某一组密集模态具体包含了哪几阶模态，这时候可以选择将该组密集模态可能包含的模态都视为密集模态来计算，并根据式(25)重构。该重构方法适用于应力、应变、位移、加速度等动力响应的重构。

2 数值模拟算例

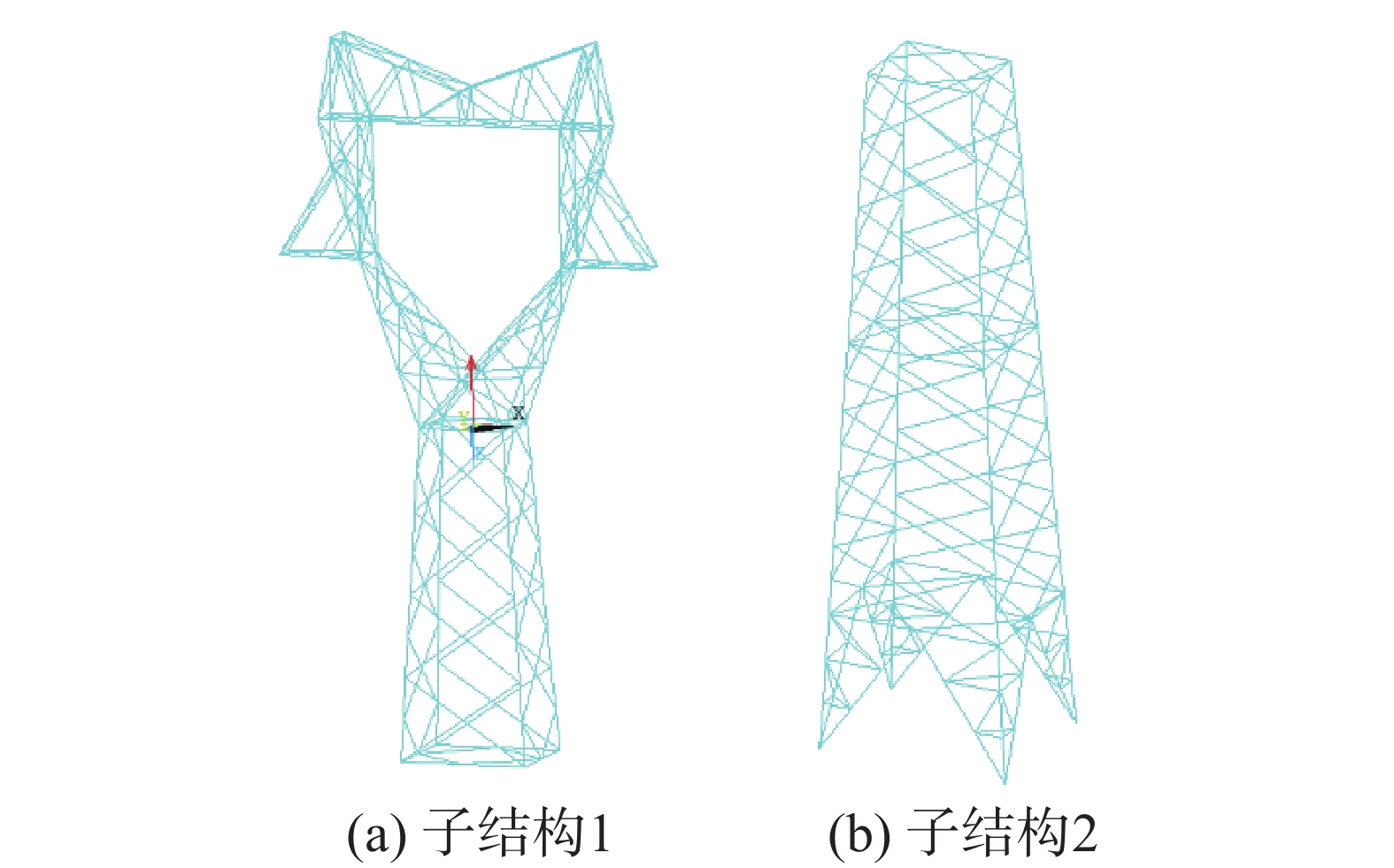
通过输电塔案例验证所提出的响应重构方法对大型结构的适用性。输电塔的有限元模型由ANSYS APDL建立，如图1所示，其中单元类型为beam188，共有3123个单元，2764个节点，16 584个自由度，结构底部通过四个固定约束与地面连结。模型建成后，在ANSYS内提取刚度矩阵和质量矩阵并导入MATLAB中，结构响应的模拟和重构都在MATLAB中实现。

图 1 输电塔模型

Figure 1. The model of power transmission tower

下载: 全尺寸图片幻灯片

为了获取结构响应，假设在结构中设置了6个响应采集点，如图1所示，这些采集点位于离地高度较小的位置，也是在实际中便于安装传感器的位置。此外，响应重构点Loc. R的位置也在图1中标出。将由15阶低通巴特沃斯滤波器过滤的白噪声模拟的随机荷载施加于输电塔的多个节点上，每阶模态阻尼设为1%，采样频率为1 kHz。在超单元模型上根据式(13)计算模态频率矩阵，得出前11阶结构固有频率分别为8.14 Hz、17.89 Hz、36.31 Hz、38.55 Hz、39.38 Hz、45.29 Hz、73.52 Hz、86.41 Hz、87.32 Hz、87.78 Hz和90.40 Hz，图2是响应采集位置Loc. K的响应傅里叶谱。通过对六个响应采集点的响应傅里叶谱进行分析，第11阶模态(频率为90.4 Hz)及其后的模态并没有明显的幅值，为了简化计算，在本案例中仅考虑对响应有较大贡献的前10阶模态。根据超单元模型计算的固有频率值，将第1阶、2阶、6阶、7阶模态视为单阶剩余模态；第3阶~5阶模态和第8阶~10阶模态内的频率间隔很小，很难使用传统的EMD方法对其进行准确的分离，因此将第3阶~5阶模态和第8阶~10阶模态归入密集模态组。

图 2 Loc. K的响应傅里叶谱

Figure 2. Spectrum of the response of Loc. K

下载: 全尺寸图片幻灯片

按照基于模态综合法和模态叠加法的密集模态结构响应重构方法计算Loc. R的动力响应，重构的基本流程如图3所示。图4所示为子结构划分示意图，上半部分结构为子结构1，下半部分结构为子结构2，每个子结构缩聚后均保留20个主模态。本算例中超单元模型的边界组自由度包括子结构1和子结构2的界面自由度，以及输电塔底部多个自由度(包含所有响应采集点)和重构点对应的自由度，压缩后的超单元模型共包含148个自由度，在超单元模型上的重构过程如下：

图 3 重构流程图

Figure 3. Flowchart of the response reconstruction method

下载: 全尺寸图片幻灯片

图 4 子结构划分示意

Figure 4. Division of two substructure

下载: 全尺寸图片幻灯片

1) 由式(13)计算超单元模型的振型 $\tilde{\boldsymbol{ \varPhi }}$ ；

2) 根据式(21)~式(23)计算 ${{\boldsymbol{T}}_{uam}}$ 、 ${{\boldsymbol{S}}_{ubr}}$ 和 ${{\boldsymbol{S}}_{mbr}}$ 。在该案例中，对应于下标m的响应采集位置包括Loc. K、Loc. L、Loc. M、Loc. N、Loc. O、Loc. P；对应于下标m的响应重构位置仅有Loc. R；对应于下标a的密集模态包括第3阶、4阶、5阶、8阶、9阶、10阶模态；对应于下标r的剩余模态包括第1阶、2阶、6阶、7阶模态；

3) 使用EMD方法提取Loc. K的剩余模态响应，由此构建矩阵式(24)中的矩阵 ${\tilde{\boldsymbol{ d}}_{br}}(t)$ 。EMD方法的性能取决于带通滤波器分离不同模式的能力。表1给出了提取剩余模态响应的带通滤波器的频率范围；

表 1 使用EMD方法的每个带通滤波器频率范围

Table 1. Frequency ranges for each band-pass filter using the EMD method

模态	频率/Hz	通带频率	阻带频率
1	8.14	[6~7]	[9~10]
2	17.89	[15~16]	[19~20]
3	45.29	[42~44]	[47~49]
4	73.52	[68~71]	[75~78]

下载: 导出CSV

| 显示表格

4) 根据式(25)重构Loc. R的响应。

重构的理论值与重构值对比如图5所示。为了定量评价重构的精度，定义一种相对误差(RE)用以反映重构值偏离理论值的程度，以及平均绝对误差(MAE)用以评价重构值的平均偏移量，如下所示：

$RE = \frac{{\displaystyle\sum\limits_{t = 1}^n {{{({\boldsymbol{X}}(t) - \bar {\boldsymbol{X}}(t))}^2}} }}{{\displaystyle\sum\limits_{t = 1}^n {{{({\boldsymbol{\bar X}}(t))}^2}} }} \times 100\text{%}$

(27)

${{MAE}}(p) = \frac{1}{n}\sum\limits_{t = 1}^n {\left| {{\boldsymbol{X}}(t) - \bar {\boldsymbol{X}}(t)} \right|} \times 100\text{%}$

(28)

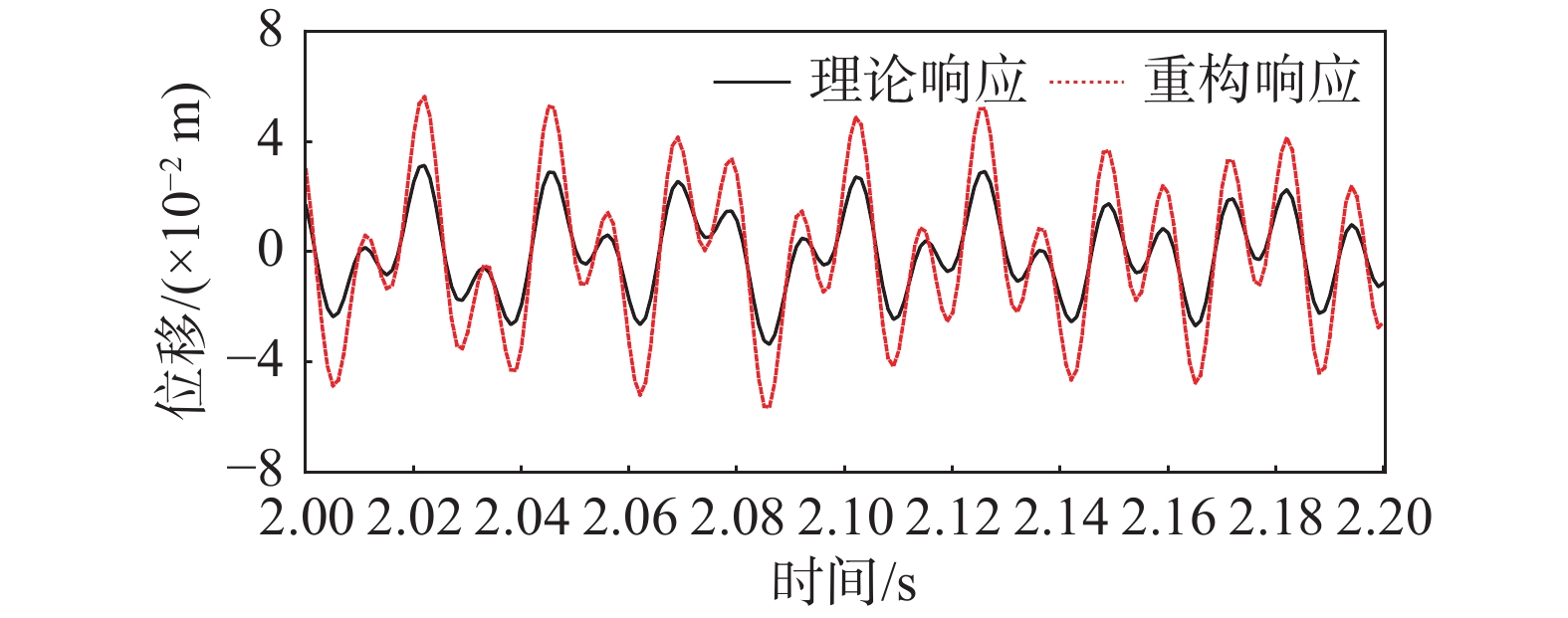
式中：n为时间序列长度； $p(t)$ 为重构值； $\bar p(t)$ 为理论值。图5中重构值和理论值的RE和MAE分别为1.129%和0.103%，重构精度较高。

图 5 理论响应与重构响应

Figure 5. Theoretical response and reconstructed response

下载: 全尺寸图片幻灯片

接下来使用传统的 EMD 方法进行重构，即按照式(26)的重构方法获取待测位置的响应。选取Loc. K的响应重构Loc. R 的响应，表2 给出了每个带通滤波器的频率范围。Loc. R的重构响应和理论响应对比如图6 所示，RE和MAE分别为67.254%和0.815%，重构误差很大，说明在该案例中传统的EMD 方法不能准确实现待测位置响应的重构。

表 2 使用传统EMD方法的每个带通滤波器频率范围

Table 2. Frequency ranges for each band-pass filter using traditional EMD method

模态	频率/Hz	通带频率	阻带频率	模态	频率/Hz	通带频率	阻带频率
1	8.14	[6~7]	[9~10]	6	45.29	[43~44]	[47~49]
2	17.89	[15~16]	[19~20]	7	73.52	[66~69]	[78~81]
3	36.31	[29~32]	[37~38]	8	86.41	[82~84]	[87~88]
4	38.55	[35~37]	[39~40]	9	87.32	[84~86]	[88~90]
5	39.38	[36~38]	[41~42]	10	87.78	[85~87]	[89~92]

下载: 导出CSV

| 显示表格

图 6 理论响应与重构响应(使用传统的EMD方法)

Figure 6. Theoretical response and reconstructed response (using traditional EMD method)

下载: 全尺寸图片幻灯片

此外，大型结构的参数矩阵(刚度矩阵和质量矩阵)存在着大量的数据冗余，即包含很多零元素，在重构全过程中会耗费大量时间和内存。表3给出了原模型和子结构的数据量对比，可以看出，划分为两个子结构之后，参与运算的数据大约减少一半，有效缓解了计算机内存不足和计算时间冗长的问题。

表 3 原模型和超单元模型的运算数据量

Table 3. Calculation data of original model and super-element model

模型	运算矩阵大小	数据总量
原模型	16 584×16 584	550，058，112
超单元模型	9072×9072，7994×7994	292，410，440

下载: 导出CSV

| 显示表格

2.1 主模态数量的影响

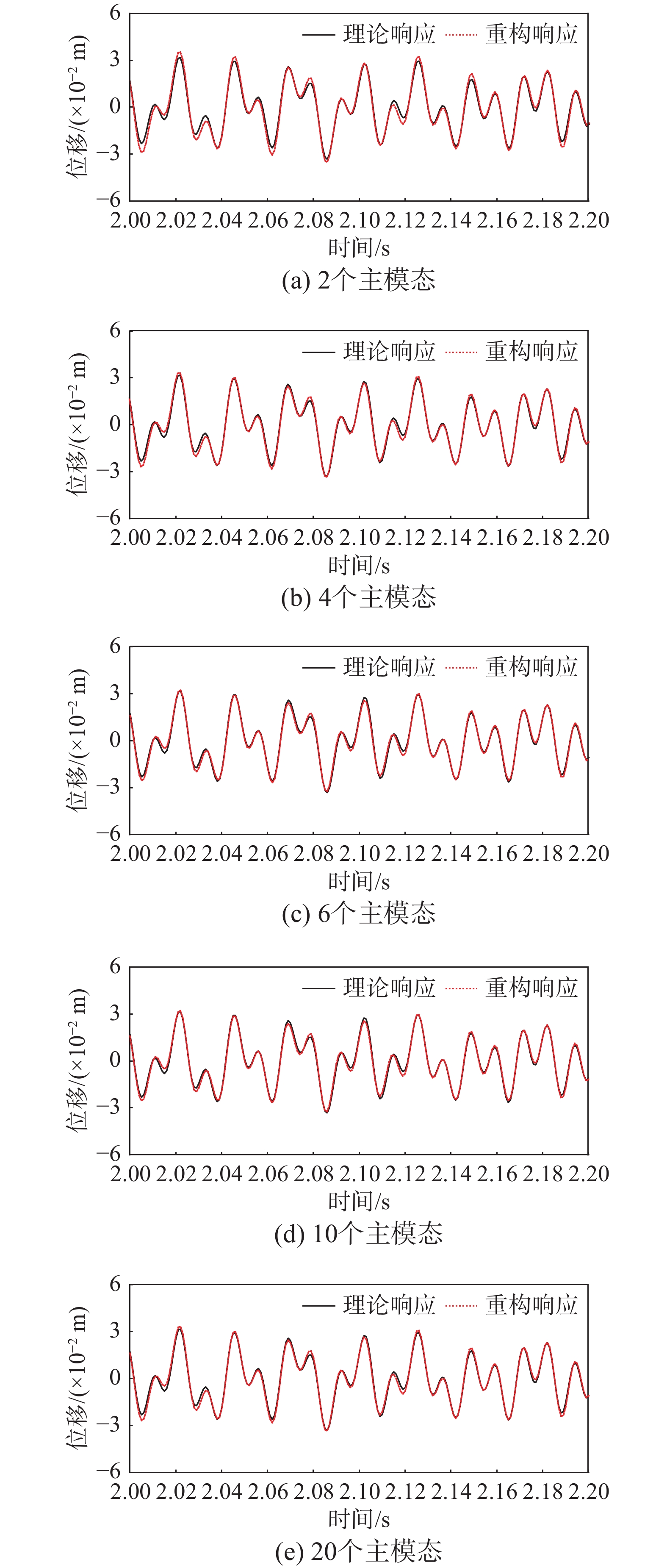
根据式(3)可知，在坐标变换过程中人为选择了保留的主模态数量，该数目通常远小于原结构的自由度数量，以此达到模型缩聚的效果。显然，不同的主模态数量会改变最终超单元模型的振型计算值，从而影响重构结果。为了验证主模态数量对所提出的响应重构方法的影响，对比每个子结构选取的主模态数量分别为2、4、6、10和20时的重构结果。待测位置响应的重构值和理论值对比如图7所示，此外还给出了各主模态数量下的重构精度，如表4所示。

图 7 不同主模态数量下的理论值与重构值

Figure 7. Theoretical value and reconstructed value under different number of main modes

下载: 全尺寸图片幻灯片

表 4 不同主模态数量下的重构精度

Table 4. Reconstruction accuracy under different number of main modes

主模态数量	精度评定指标	数值/(%)
2	RE	2.292
2	MAE	0.149
4	RE	1.333
4	MAE	0.112
6	RE	1.133
6	MAE	0.103
10	RE	1.129
10	MAE	0.103
20	RE	1.129
20	MAE	0.103

下载: 导出CSV

| 显示表格

主模态数量为2时，振型 $\tilde{\boldsymbol{ \varPhi }}$ 的计算不准确，因此导致了重构误差偏大；随着主模态数量增大，重构误差逐渐减小，当主模态数量增加到6，重构结果基本趋于稳定，继续增加主模态数量对结果并无太大影响，这说明保留6阶主模态便可计算出相应点位的比较准确的振型数值。此外，即使保留的主模态数目达到20，超单元模型的自由度数量为148，其相较于原结构的自由度数量而言仍然微乎其微，因此在实际工程中可以考虑保留等同于结构响应贡献较大的模态阶数的主模态数量(例如本案例考虑了响应的前10阶模态，则在坐标变换时保留10阶主模态)，而由于主模态数量对效率几乎没有影响，甚至可以保留更多的主模态以确保重构精度。

2.2 子结构划分方式的影响

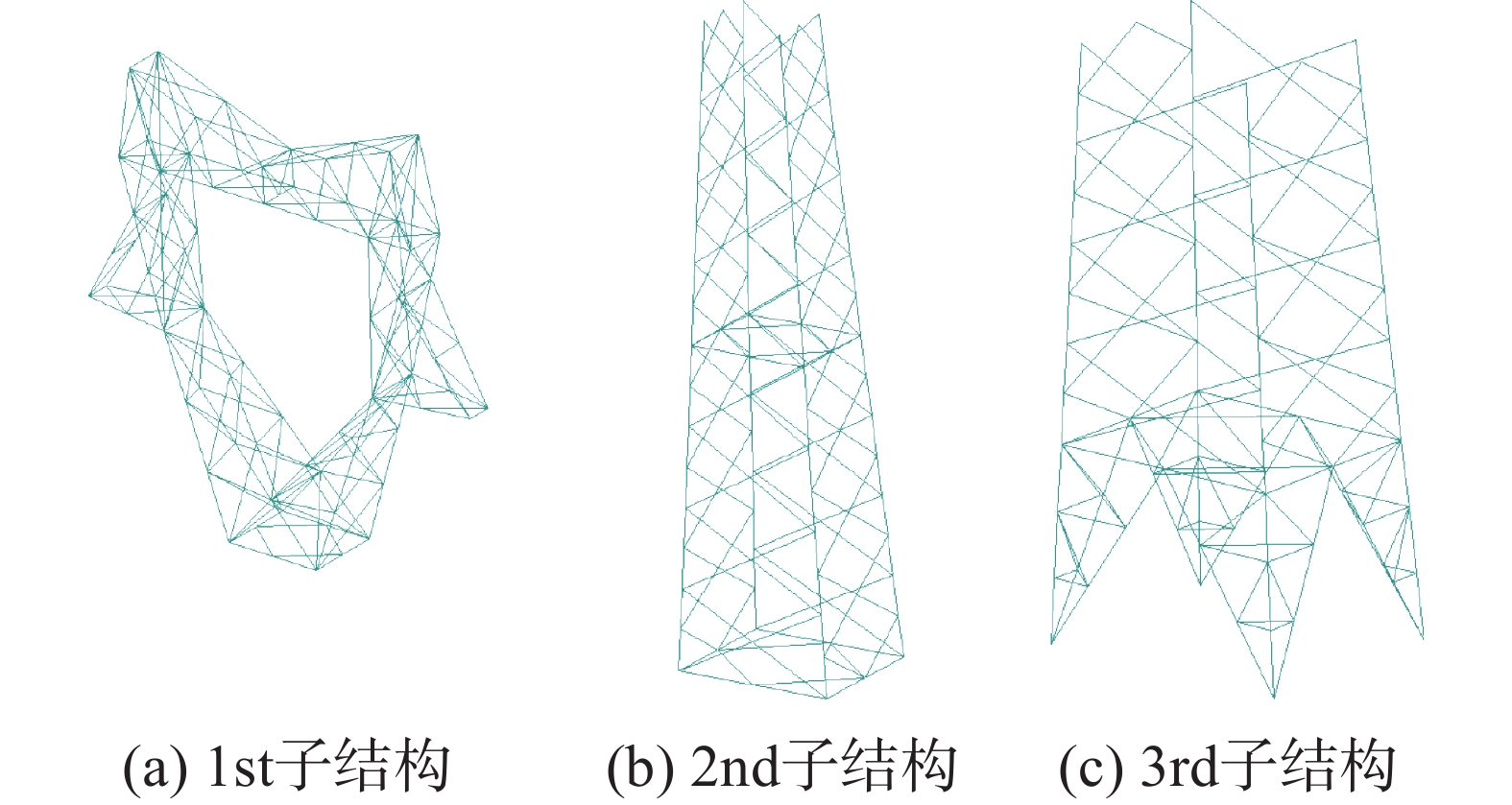
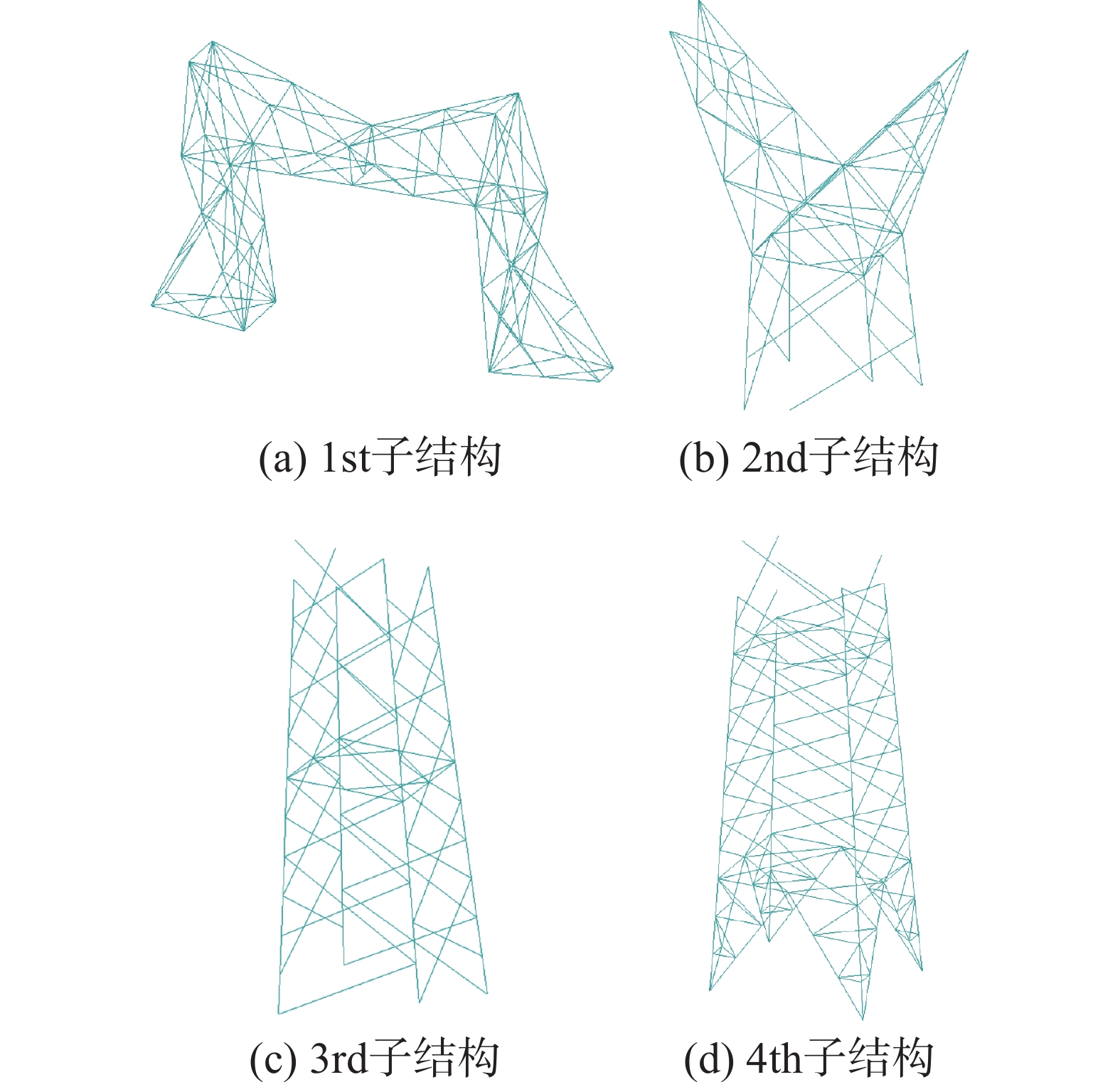
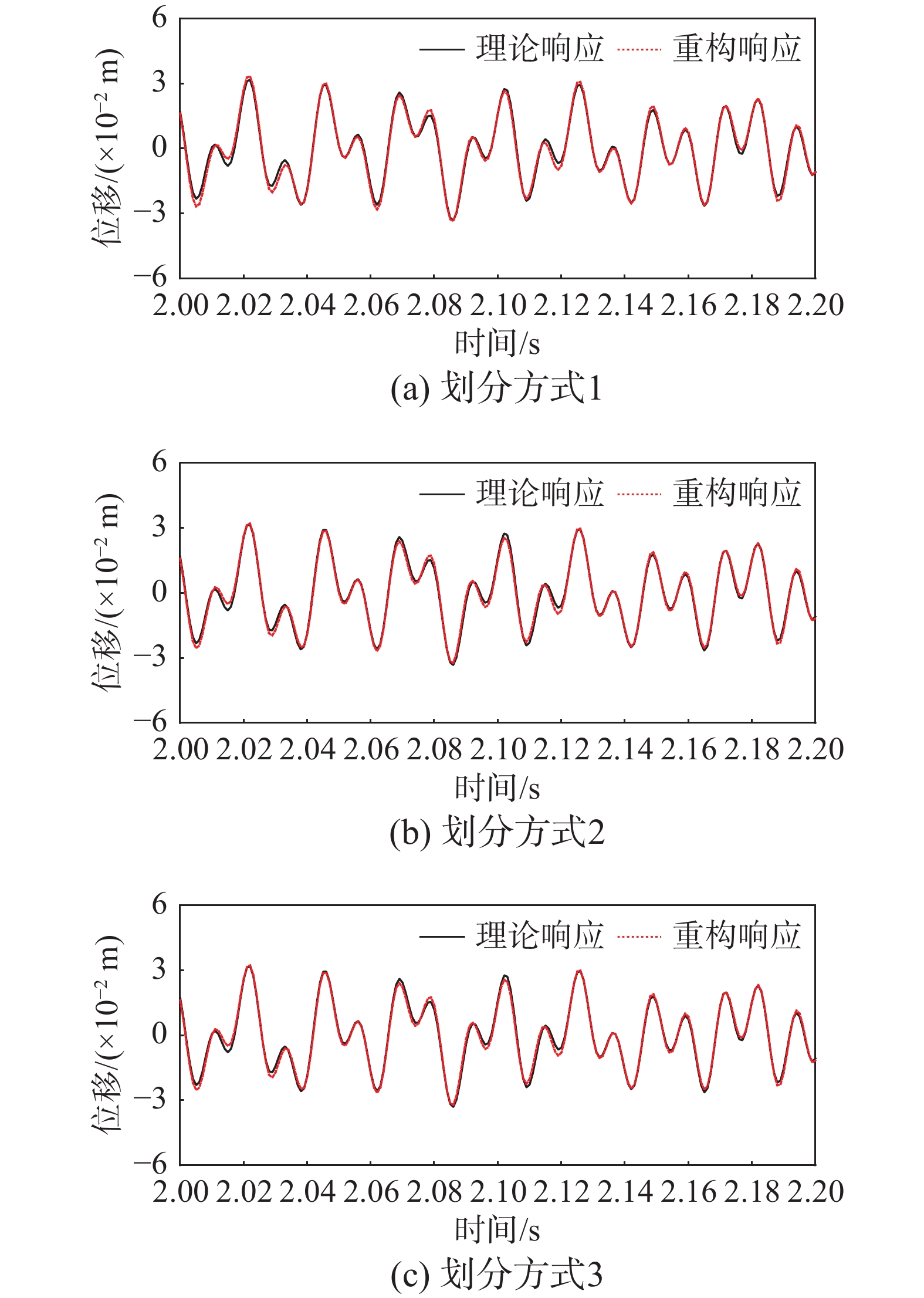
与2.1的讨论类似，不同子结构数量同样会改变振型 $\tilde{\boldsymbol{ \varPhi }}$ 的计算值，从而影响重构结果。比较分析三种不同子结构划分方式对重构的影响，子结构的不同划分方式分别如图8~图10所示，其中，划分方式1、划分方式2和划分方式3分别将结构分为2、3、4个子结构，不同的划分方式下每个子结构在坐标变换后均保留20阶主模态，其余参数和前文相同。图11为各工况下待测位置的理论值和重构值对比图，表5列出了不同子结构数量下的重构精度。从图11和表5可以得知，不同子结构数量对重构的影响很小，仅需根据计算效率考虑子结构数量。

图 8 子结构划分方式1

Figure 8. Substructure division 1

下载: 全尺寸图片幻灯片

图 9 子结构划分方式2

Figure 9. Substructure division 2

下载: 全尺寸图片幻灯片

图 10 子结构划分方式3

Figure 10. Substructure division 3

下载: 全尺寸图片幻灯片

图 11 不同子结构划分方式下的理论值与重构值

Figure 11. Theoretical value and reconstructed value under different substructure division

下载: 全尺寸图片幻灯片

表 5 不同子结构划分方式下的重构精度

Table 5. Reconstruction accuracy under different different substructure division

子结构划分方式	精度评定指标/(%)	数值
划分方式1	RE	1.129
划分方式1	MAE	0.103
划分方式2	RE	1.129
划分方式2	MAE	0.103
划分方式三	RE	1.129
划分方式三	MAE	0.103

下载: 导出CSV

| 显示表格

相对于直接提取原模型的参数矩阵而言，通过分别提取各子结构的参数矩阵再进行耦合的方法，在保证重构精度的前提下，可以减少运算的数据量。表6给出了不同子结构划分下的重构运算数据量对比，可以看出，一定范围内子结构数量越多，运算数据总量越少，对计算效率的提升也越明显。但是随着子结构数量的增大，将需要更多人力设置相应的界面耦合。因此在实际中应综合考虑计算效率和人力投入来划分合适的子结构数量。

表 6 不同子结构划分的重构运算数据量。

Table 6. Calculation data of reconstruction under different substructure division

子结构划分方式	划分方式1	划分方式2	划分方式3
数据总量	192, 060, 608	292, 410, 440	158, 244, 828

下载: 导出CSV

| 显示表格

2.3 噪声等级的影响

现实中响应采集不可避免地存在噪声，为了所提出的响应重构方法在测量噪声环境下的适用性，研究在同一组外部激励下，不同等级的噪声(5%、10%、15%和20%)对重构的影响。测量噪声用高斯脉冲过程来表示，其均方根设置为应变最大均方根的百分比，这里使用噪声等级来表征噪声程度，即添加的噪声是响应最大均方根值等同于噪声等级的高斯过程。重构结果如图12和表7所示，可以看出，重构精度会受到噪声的影响，随着噪声的增大而降低，而且重构响应上的锯齿也趋于明显。

图 12 不同噪声等级下的理论值与重构值

Figure 12. Theoretical value and reconstructed value under different noise level

下载: 全尺寸图片幻灯片

表 7 不同噪声等级下的重构精度

Table 7. Reconstruction accuracy under different noise level

噪声等级/(%)	精度评定指标/(%)	数值
5	RE	1.427
5	MAE	0.116
10	RE	2.047
10	MAE	0.141
15	RE	3.197
15	MAE	0.177
20	RE	4.833
20	MAE	0.218

下载: 导出CSV

| 显示表格

EMD方法本身有着一定的降噪性能，而在本文所提出的重构方法中，仅用EMD提取剩余的单频模态响应，对于密集模态响应则通过已知响应、提取的剩余模态响应和振型矩阵外推至响应重构点，这样一来，已知响应中的噪声将被保留至响应重构点，对重构结果产生影响。因此，对于密集模态成分主导的结构响应，该方法难以在高噪声的情况下重构出准确的结果。对于该案例而言，在不大于15%的噪声下进行重构能得到较为准确的结果。

2.4 阻尼的影响

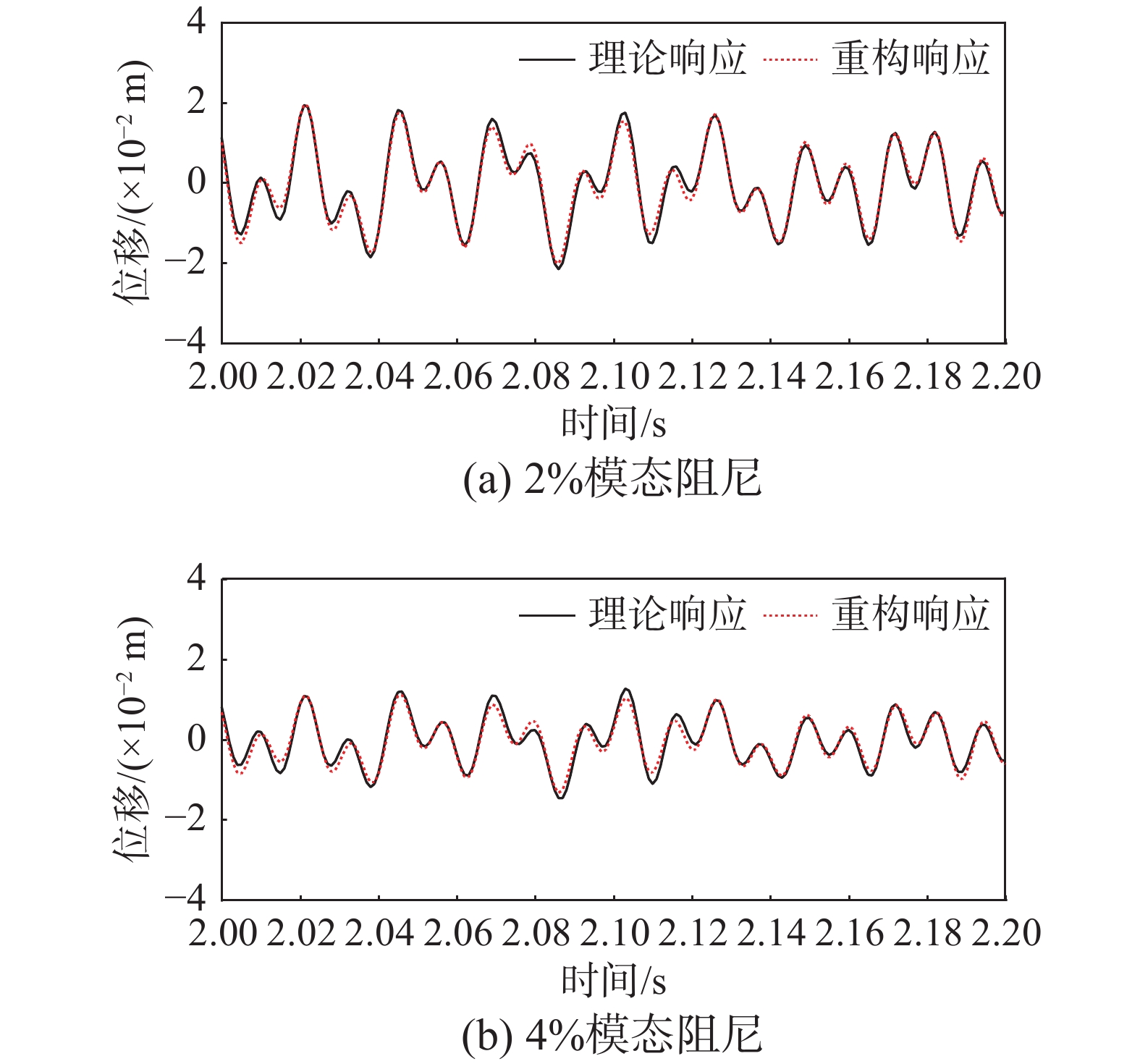
在前文的论述中，该案例采用1%模态阻尼以模拟阻尼效应，而实际工程结构可能存在更高的阻尼，因此接下来讨论不同的阻尼对重构结果的影响。对于同一组外部激励，考虑三种模态阻尼(2%、4%和6%)，不同阻尼下的重构结果如图13和表8所示所示。

下载: 全尺寸图片幻灯片

图 13 不同阻尼下的理论值与重构值

Figure 13. Theoretical value and reconstructed value under different damp

下载: 全尺寸图片幻灯片

表 8 不同阻尼下的重构精度

Table 8. Reconstruction accuracy under different damp

模态阻尼/(%)	精度评定指标/(%)	数值
2	RE	2.702
4	RE	5.374
6	RE	7.945

下载: 导出CSV

| 显示表格

从重构结果可以看出，RE随着阻尼的增大而明显增大，说明在高阻尼下重构精度相对较低。本文所提出的方法将结构响应频率的模态振型和模态响应一一对应实现重构，其基本思想是：结构响应可分解为多个模态响应的叠加，每个模态响应对应着一个固有频率。图14给出了不同阻尼下的Loc. K的响应傅里叶谱，可以看出，随着阻尼的增高，各个模态的能量趋于分散，难以与单一频率相对应，因此高阻尼下重构精度差。对于该输电塔结构而言，应保证重构在模态阻尼不大于4%下的情况下进行。

图 14 不同阻尼下Loc. K的响应傅里叶谱

Figure 14. Spectrum of the response of Loc. K under different damp

下载: 全尺寸图片幻灯片

3 结论

本文提出了一种基于模态综合法和模态叠加法的密集模态结构响应重构方法，以输电塔结构为例开展了响应重构数值计算，探讨了主模态数量、子结构划分方式、噪声等级以及阻尼对重构结果的影响，得到主要结论如下：

(1)该方法结合了模态综合法，通过模型缩聚，参与计算的刚度和质量矩阵数据量大大减少，由此改善了计算机内存不足的问题，从而更加适用于大型结构。

(2)鉴于EMD法难以分离密集模态，本文提出将密集模态视作一个整体，并由剩余模态替代的方法，改善了传统EMD方法不能分离频率间隔较小的模态而无法准确重构未知响应这一不足，且适用于于应力、应变、位移、加速度等各种动力响应的重构。

(3)以输电塔为例的数值计算表明，当主模态数量很小时，重构精度较差，随着主模态数量增加，重构精度趋于稳定，可以考虑保留两倍于结构响应贡献较大的模态阶数的主模态数量；子结构划分方式对该重构精度的影响极小，应综合考虑计算效率和人力投入划分适当的子结构数量。

(4)测量噪声等级越高，重构精度越低，对于密集模态主导且噪声等级较高的情况，难以得到理想的重构结果，作者在今后的研究中也将寻求适合的滤波降噪方法应用于该重构方法；结构阻尼对重构有较大影响，这是因为高阻尼下各个模态的能量趋于分散，难以和单一频率相对应，应保证案例的输电塔结构的重构在模态阻尼不大于4%下的情况下进行。

图 1 输电塔模型

Figure 1. The model of power transmission tower

下载: 全尺寸图片幻灯片

图 2 Loc. K的响应傅里叶谱

Figure 2. Spectrum of the response of Loc. K

下载: 全尺寸图片幻灯片

图 3 重构流程图

Figure 3. Flowchart of the response reconstruction method

下载: 全尺寸图片幻灯片

图 4 子结构划分示意

Figure 4. Division of two substructure

下载: 全尺寸图片幻灯片

图 5 理论响应与重构响应

Figure 5. Theoretical response and reconstructed response

下载: 全尺寸图片幻灯片

图 6 理论响应与重构响应(使用传统的EMD方法)

Figure 6. Theoretical response and reconstructed response (using traditional EMD method)

下载: 全尺寸图片幻灯片

图 7 不同主模态数量下的理论值与重构值

Figure 7. Theoretical value and reconstructed value under different number of main modes

下载: 全尺寸图片幻灯片

图 8 子结构划分方式1

Figure 8. Substructure division 1

下载: 全尺寸图片幻灯片

图 9 子结构划分方式2

Figure 9. Substructure division 2

下载: 全尺寸图片幻灯片

图 10 子结构划分方式3

Figure 10. Substructure division 3

下载: 全尺寸图片幻灯片

图 11 不同子结构划分方式下的理论值与重构值

Figure 11. Theoretical value and reconstructed value under different substructure division

下载: 全尺寸图片幻灯片

图 12 不同噪声等级下的理论值与重构值

Figure 12. Theoretical value and reconstructed value under different noise level

下载: 全尺寸图片幻灯片

图 13 不同阻尼下的理论值与重构值

Figure 13. Theoretical value and reconstructed value under different damp

下载: 全尺寸图片幻灯片

图 14 不同阻尼下Loc. K的响应傅里叶谱

Figure 14. Spectrum of the response of Loc. K under different damp

下载: 全尺寸图片幻灯片

表 1 使用EMD方法的每个带通滤波器频率范围

Table 1 Frequency ranges for each band-pass filter using the EMD method

模态	频率/Hz	通带频率	阻带频率
1	8.14	[6~7]	[9~10]
2	17.89	[15~16]	[19~20]
3	45.29	[42~44]	[47~49]
4	73.52	[68~71]	[75~78]

下载: 导出CSV

表 2 使用传统EMD方法的每个带通滤波器频率范围

Table 2 Frequency ranges for each band-pass filter using traditional EMD method

模态	频率/Hz	通带频率	阻带频率	模态	频率/Hz	通带频率	阻带频率
1	8.14	[6~7]	[9~10]	6	45.29	[43~44]	[47~49]
2	17.89	[15~16]	[19~20]	7	73.52	[66~69]	[78~81]
3	36.31	[29~32]	[37~38]	8	86.41	[82~84]	[87~88]
4	38.55	[35~37]	[39~40]	9	87.32	[84~86]	[88~90]
5	39.38	[36~38]	[41~42]	10	87.78	[85~87]	[89~92]

下载: 导出CSV

表 3 原模型和超单元模型的运算数据量

Table 3 Calculation data of original model and super-element model

模型	运算矩阵大小	数据总量
原模型	16 584×16 584	550，058，112
超单元模型	9072×9072，7994×7994	292，410，440

下载: 导出CSV

表 4 不同主模态数量下的重构精度

Table 4 Reconstruction accuracy under different number of main modes

主模态数量	精度评定指标	数值/(%)
2	RE	2.292
2	MAE	0.149
4	RE	1.333
4	MAE	0.112
6	RE	1.133
6	MAE	0.103
10	RE	1.129
10	MAE	0.103
20	RE	1.129
20	MAE	0.103

下载: 导出CSV

表 5 不同子结构划分方式下的重构精度

Table 5 Reconstruction accuracy under different different substructure division

子结构划分方式	精度评定指标/(%)	数值
划分方式1	RE	1.129
划分方式1	MAE	0.103
划分方式2	RE	1.129
划分方式2	MAE	0.103
划分方式三	RE	1.129
划分方式三	MAE	0.103

下载: 导出CSV

表 6 不同子结构划分的重构运算数据量。

Table 6 Calculation data of reconstruction under different substructure division

子结构划分方式	划分方式1	划分方式2	划分方式3
数据总量	192, 060, 608	292, 410, 440	158, 244, 828

下载: 导出CSV

表 7 不同噪声等级下的重构精度

Table 7 Reconstruction accuracy under different noise level

噪声等级/(%)	精度评定指标/(%)	数值
5	RE	1.427
5	MAE	0.116
10	RE	2.047
10	MAE	0.141
15	RE	3.197
15	MAE	0.177
20	RE	4.833
20	MAE	0.218

下载: 导出CSV

表 8 不同阻尼下的重构精度

Table 8 Reconstruction accuracy under different damp

模态阻尼/(%)	精度评定指标/(%)	数值
2	RE	2.702
4	RE	5.374
6	RE	7.945

下载: 导出CSV

参考文献(18)

[1]	王慧, 王乐, 田润泽. 基于时域响应相关性分析及数据融合的结构损伤检测研究[J]. 工程力学, 2020, 37(9): 30 − 37, 111. doi: 10.6052/j.issn.1000-4750.2019.10.0588 WANG Hui, WANG Le, TIAN Runze. Structural damage detection using correlation functions of time domain vibration responses and data fusion [J]. Engineering Mechanics, 2020, 37(9): 30 − 37, 111. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.10.0588
[2]	任鹏, 周智, 白石, 等. 桁架结构疲劳监测的应变响应估计方法研究[J]. 工程力学, 2018, 35(9): 114 − 125. doi: 10.6052/j.issn.1000-4750.2017.05.0373 REN Peng, ZHOU Zhi, BAI Shi, et al. Research on a strain response estimation method for truss structure fatigue monitoring [J]. Engineering Mechanics, 2018, 35(9): 114 − 125. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.05.0373
[3]	杨振伟, 周广东, 伊廷华, 等. 基于分级免疫萤火虫算法的桥梁振动传感器优化布置研究[J]. 工程力学, 2019, 36(3): 63 − 70. doi: 10.6052/j.issn.1000-4750.2018.01.0075 YANG Zhenwei, ZHOU Guangdong, YI Tinghua, et al. Optimal vibration sensor placement for bridges using gradation-immune firefly algorithm [J]. Engineering Mechanics, 2019, 36(3): 63 − 70. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.01.0075
[4]	ZHANG X H, XU Y L, ZHU S Y, et al. Dual-type sensor placement for multi-scale response reconstruction [J]. Mechatronics, 2014, 24(4): 376 − 384. doi: 10.1016/j.mechatronics.2013.05.007
[5]	李惠, 鲍跃全, 李顺龙, 等. 结构健康监测数据科学与工程[J]. 工程力学, 2015, 32(8): 1 − 7. doi: 10.6052/j.issn.1000-4750.2014.08.ST11 LI Hui, BAO Yuequan, LI Shunlong, et al. Data science and engineering for structural health monitoring [J]. Engineering Mechanics, 2015, 32(8): 1 − 7. (in Chinese) doi: 10.6052/j.issn.1000-4750.2014.08.ST11
[6]	何文朋, 雷家艳. 运营实桥在线监测系统的建立及数据初步分析[J]. 工程力学, 2016, 33(增刊): 234 − 238. doi: 10.6052/j.issn.1000-4750.2015.04.S048 HE Wenpeng, LEI Jiayan. The establishment of online monitoring system for Tianyuan bridge and preliminary analysis of data [J]. Engineering Mechanics, 2016, 33(增刊): 234 − 238. (in Chinese) doi: 10.6052/j.issn.1000-4750.2015.04.S048
[7]	RIBEIRO A M R, SILVA J M M, MAIA N M M. On the generalization of the transmissibility concept [J]. Mechanical Systems and Signal Processing, 2000, 14(1): 29 − 35. doi: 10.1006/mssp.1999.1268
[8]	DEVRIENDT C, GUILLAUME P. The use of transmissibility measurements in output-only modal analysis [J]. Mechanical Systems and Signal Processing, 2007, 21(7): 2689 − 2696. doi: 10.1016/j.ymssp.2007.02.008
[9]	LAW S S, DING Y, LI J. Structural response reconstruction with transmissibility concept in frequency domain [J]. Mechanical Systems and Signal Processing, 2011, 25(3): 952 − 968. doi: 10.1016/j.ymssp.2010.10.001
[10]	LI J, LAW S S, DING Y. Damage detection of a substructure based on response reconstruction in frequency domain [J]. Key Engineering Materials, 2013, 2579(1139): 823 − 830.
[11]	LI J, LAW S S, DING Y. Substructure damage identification based on response reconstruction in frequency domain and model updating [J]. Engineering Structures, 2012, 41: 270 − 284.
[12]	LIU Y M, GUAN X F , HE J J. Structural response reconstruction based on empirical mode decomposition in time domain [J]. Mechanical Systems and Signal Processing, 2012, 28: 348 − 366. doi: 10.1016/j.ymssp.2011.12.010
[13]	HE J, ZHOU Y, GUAN X, et al. Time Domain Strain/Stress Reconstruction Based on Empirical Mode Decomposition: Numerical Study and Experimental Validation [J]. Sensors, 2016, 16(8): 1 − 22. doi: 10.1109/JSEN.2016.2517936
[14]	白斌, 白广忱, 费成巍, 等. 改进的混合界面子结构模态综合法在失谐叶盘结构模态分析中的应用[J]. 工程力学, 2015, 32(4): 178 − 184. doi: 10.6052/j.issn.1000-4750.2013.10.0964 BAI Bin, BAI Guangchen, FEI Chengwei, et al. Application of improved hybrid interface substructure method in the modal analysis of mistuned bladed disk assemblies [J]. Engineering Mechanics, 2015, 32(4): 178 − 184. (in Chinese) doi: 10.6052/j.issn.1000-4750.2013.10.0964
[15]	KRATTIGER D, WU L, ZACHARCZUK M, et al. Interface reduction for Hurty/Craig-Bampton substructure models: Review and improvements [J]. Mechanical Systems and Signal Processing, 2019, 114: 579 − 603. doi: 10.1016/j.ymssp.2018.05.031
[16]	WANG T, HE J C, HOU S, et al. Complex component mode synthesis method using hybrid coordinates for generally damped systems with local nonlinearities [J]. Journal of Sound and Vibration, 2020, 476: 115299. doi: 10.1016/j.jsv.2020.115299
[17]	徐晴晴, 史治宇. 基于改进EMD分解的时变结构密集模态的瞬时参数识别[J]. 机械科学与技术, 2015, 34(8): 1161 − 1165. XU Qingqing, SHI Zhiyu. Identifying parameters of time varying structures with closely spaced modes based on improved emd method [J]. Mechanical Science and Technology, 2015, 34(8): 1161 − 1165. (in Chinese)
[18]	WAN Z M, LI S D, HUANG Q B, et al. Structural response reconstruction based on the modal superposition method in the presence of closely spaced modes [J]. Mechanical Systems and Signal Processing, 2014, 42(1/2): 14 − 30.

施引文献(17)

期刊类型引用(4)

1.	付琪璋. 钢轨焊接区激扰下400 km/h高铁有砟轨道动力响应分析. 铁道标准设计. 2025(01): 36-42+49 . 百度学术
2.	路金涛，彭珍瑞. 自适应窗长改进Sage-Husa卡尔曼滤波的结构响应重构. 计算力学学报. 2025(02): 212-220 . 百度学术
3.	张大伟，殷红，彭珍瑞. 改进Tikhonov正则化的激励修正与结构响应重构. 噪声与振动控制. 2025(03): 21-27+48 . 百度学术
4.	王森，辛涛，王朋松，杨燚，戴传青，滕明利. 减基法在轨道-隧道-土体系统谐响应分析中的应用. 中南大学学报(自然科学版). 2024(03): 1231-1240 . 百度学术

其他类型引用(13)

资源附件(0)

在线预览下载 (5.7MB)

图(15) / 表(8)

计量

文章访问数: 843
HTML全文浏览量: 276
PDF下载量: 174
被引次数: 17

1 理论推导
1.1 子结构模态综合法
1.2 基于改进模态叠加法的子结构重构理论
2 数值模拟算例
2.1 主模态数量的影响
2.2 子结构划分方式的影响
2.3 噪声等级的影响
2.4 阻尼的影响
3 结论

基于模态综合法和模态叠加法的密集模态结构响应重构

通讯作者:
阳劲松(1990−)，男，湖南邵阳人，讲师，博士，主要从事健康监测与可靠度评估研究(E-mail: 307767159@qq.com)

计量

STRUCTURAL RESPONSE RECONSTRUCTION BASED ON MODE SYNTHESIS METHOD AND MODAL SUPERPOSITION METHOD IN THE PRESENCE OF CLOSELY SPACED MODES

1 理论推导

1.1 子结构模态综合法

1.2 基于改进模态叠加法的子结构重构理论

2 数值模拟算例

2.1 主模态数量的影响

2.2 子结构划分方式的影响

2.3 噪声等级的影响

2.4 阻尼的影响

3 结论

期刊类型引用(4)

其他类型引用(13)

计量

目录

1 理论推导

1.1 子结构模态综合法

1.2 基于改进模态叠加法的子结构重构理论

2 数值模拟算例

2.1 主模态数量的影响

2.2 子结构划分方式的影响

2.3 噪声等级的影响

2.4 阻尼的影响

3 结论

HE Xu-hui, xuhuihe@csu.edu.cn

基于模态综合法和模态叠加法的密集模态结构响应重构

通讯作者: 阳劲松(1990−)，男，湖南邵阳人，讲师，博士，主要从事健康监测与可靠度评估研究(E-mail: 307767159@qq.com)

计量

出版历程

STRUCTURAL RESPONSE RECONSTRUCTION BASED ON MODE SYNTHESIS METHOD AND MODAL SUPERPOSITION METHOD IN THE PRESENCE OF CLOSELY SPACED MODES

1 理论推导

1.1 子结构模态综合法

1.2 基于改进模态叠加法的子结构重构理论

2 数值模拟算例

2.1 主模态数量的影响

2.2 子结构划分方式的影响

2.3 噪声等级的影响

2.4 阻尼的影响

3 结论

期刊类型引用(4)

其他类型引用(13)

计量

出版历程

目录

1 理论推导

1.1 子结构模态综合法

1.2 基于改进模态叠加法的子结构重构理论

2 数值模拟算例

2.1 主模态数量的影响

2.2 子结构划分方式的影响

2.3 噪声等级的影响

2.4 阻尼的影响

3 结论

HE Xu-hui, xuhuihe@csu.edu.cn

通讯作者:
阳劲松(1990−)，男，湖南邵阳人，讲师，博士，主要从事健康监测与可靠度评估研究(E-mail: 307767159@qq.com)