功能梯度材料是由两种或两种以上的材料组成的一种复合材料，其成分及相关的材料特性通常在一个方向或者多个方向呈连续平稳变化^[1]。由于其内部材料属性的连续变化，功能梯度材料可以有效避免普通层合材料因内部材料突变所产生的应力集中问题，因此近些年来由功能梯度材料所组成的结构备受关注^[1-5]。近年来结构的振动控制是工程中的热点问题，尤其在航空航天及汽车领域。通常将压电材料作为传感器与致动器粘贴或镶嵌在柔性结构的表面，通过控制电路实现对结构的振动主动控制。因而，包含压电传感器和致动器的智能层合结构的建模、分析以及设计也受到广泛关注^[6]。其中结构的核心层为各向同性材料或层合复合材料的研究文献最为多见，而智能功能梯度层合结构的有限元建模及其振动主动控制的研究则较少^[7-8]。对于包含压电层及功能梯度层的智能层合结构，压电层的力电耦合效应会影响到结构的力学响应。合理的层合板理论对准确且高效地进行层合结构的多场耦合分析十分重要。 MITCHELL和REDDY^[9]提出了一个高效压电层合板分析的杂交板理论，它使用等效单层板理论表征层合板的力学行为，用Layer-wise理论描述其电势场。

一个理想的振动控制方法要以较小的能量和较短的时间实现对结构振动的稳定的控制。基于速度反馈的振动控制方法在压电功能梯度层合结构的振动控制中得到广泛的应用^[10-13]。它通过改变反馈增益的值得到不同大小的控制力实现对功能梯度结构的振动控制。SELIM等^[10]以及YASIN等^[8]研究了常增益负反馈控制的稳定性问题，且SELIM等指出由于压电功能梯度层合结构存在拉弯耦合变形，会使得控制系统变得不稳定，两篇文献均通过改变压电传感器层和致动器层的位置提升系统的稳定性。刘涛等^[13]基于等几何方法同样采用常增益负反馈控制研究了功能梯度板的振动控制问题，引入物理中面的概念避免当传感器与致动器粘贴于功能梯度层表面时由于拉弯耦合效应引起的控制不稳定问题。经典控制方法操作简单但却忽略了控制过程中能量的消耗，所得基于系统输出反馈的控制力往往并非为最优控制力，因而不是最优振动控制。BRUANT等^[7]及HARTI等^[14]基于LQR算法实现功能梯度梁上局部布置压电片时的振动控制，并讨论了压电致动器和传感器的位置对结构振动控制效果的影响。YASIN等^[8]基于Layer-wise理论表述梁内位移场及电势场，提出了一个带内部电学自由度的压电功能梯度梁单元，使用常增益速度反馈控制算法和LQR算法对结构的振动进行控制。结果表明：LQR最优控制比常增益负速度反馈控制所消耗能量更低，且LQR不存在上述稳定性问题。因而，LQR是实现最优主动振动控制的良好选择。

压电功能梯度层合梁具有力-电-热的耦合效应，故对应有限元模型的计算效率对工程问题的求解很重要。现有的力-电-热耦合分析有限元都是采用数值积分^[8,11,14-15]。TIAN等^[16]的工作表明，采用拟协调元法可以得到层合结构的显式单元刚度矩阵，从而避免了数值积分和提高了计算效率。基于弹性力学基本方程以及能量等效原理得出的SHI^[17]改进的三阶剪切变形理论可以精确地考虑横向剪切变形对梁振动高阶频率的影响。

本文采用杂交板理论^[9] 和Hamilton原理推导压电功能梯度层合梁的力-电-热耦合控制方程，其中用SHI^[17]改进的三阶剪切变形理论描述梁的位移场，用Layer-wise理论^[9]分层地描述压电层电势场。然后用假设应变的拟协调元法^[18]推导两节点压电功能梯度层合梁单元的刚度矩阵。由于推导过程中单独假设梁中切应变以及剪切应变梯度，可以有效避免梁单元的剪切自锁。使用所得力-电-热耦合梁单元进行了不同载荷下压电功能梯度层合梁的静力和动力分析，用LQR最优控制算法实现了结构振动的主动控制。所得计算结果与其它梁单元结果及二维有限元解的比对验证了文中所给力-电-热耦合梁单元的准确性。

1   压电功能梯度层合梁单元

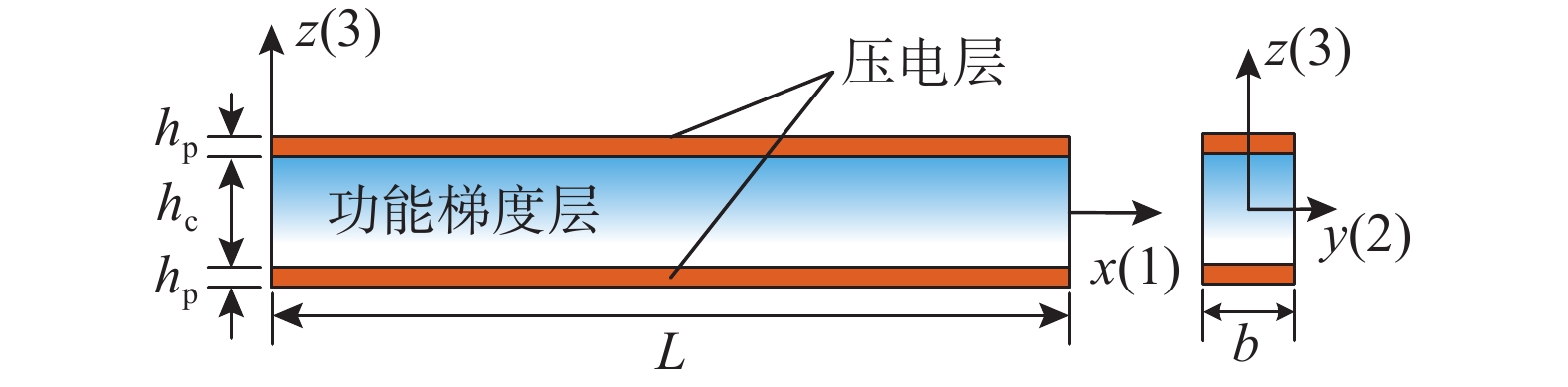
如图1所示为一个压电功能梯度层合梁，梁中间层功能梯度层厚度为h_c，它由两种不同的材料沿梁高度按一定规律梯度分布复合而成。功能梯度上下表面粘贴有等厚度h_p的压电层。假设相邻两层理想粘结且不考虑粘结层影响，并只考虑xoz平面内的荷载。

图  1  压电功能梯度梁示意图

Figure  1.  Geometry of piezoelectric functionally beam

下载: 全尺寸图片 幻灯片

1.1   压电功能梯度梁本构关系

功能梯度层由金属和陶瓷按一定的规律复合而成，其上侧为纯陶瓷，下侧为纯金属。其等效材料参数，如弹性模量、泊松比、热膨胀系数、密度等，沿梁厚度方向呈连续均匀变化。陶瓷体积分数V_c沿厚度方向的分布可表征为^[10]：

其中，N为功能梯度层材料的组分指数，陶瓷体积分数和金属体积分数满足V_c+V_m=1。

研究者提出了许多表征材料性能沿高度梯度变化的细观力学模型，其中最常用的为Voigt模型^[7,10-13,19]和Mori-Tanaka模型^[8,15]。Voigt模型简单易用，可用于预测由常规功能梯度材料组成结构的材料特性和整体响应；而Mori-Tanaka模型更注重相邻内含物之间的相互作用^[8]。由于Voigt模型操作简便，其被多数学者用来预测材料性能的变化。Voigt模型把功能梯度材料的等效材料参数P_f表征为：

式中：P_m为金属材料的材料参数；P_c为陶瓷材料的材料参数。

功能梯度材料最早用于航空航天领域作为隔热涂层，其工作环境通常为高温环境。因此有必要考虑温度对其的影响。功能梯度材料考虑力-热耦合的本构方程为：

其中：

式中，功能梯度材料弹性模量E_f和泊松比μ沿厚度方向的分布，可由式(2)得出。

压电材料考虑力-电-热耦合的三维本构关系为：

其中，σ 和ε 分别为压电材料的应力张量及应变张量，而D和E则分别为其电位移矢量及电场强度矢量；C、e、k分别为弹性矩阵、压电矩阵及介电矩阵；α及p分别为材料的热膨胀系数及热电系数。ΔT=T−T₀，T为材料的温度，T₀为参考温度，在此温度下，物体处于应力自由状态。本文假设温度沿着梁厚度方向线性分布：

式中：T_t、T_b分别为梁上下表面的温度值；h为梁的高度。

对于正交各向异性压电材料，其具有三个相互正交的弹性对称平面，其三维弹性矩阵为：

假设压电材料为正交晶系压电晶体，且沿z方向极化，其三维压电矩阵e、介电矩阵为k：

对图1所示一维梁模型，假设z方向正应力σ₃=0。若其处于平面应力状态，有σ₂=τ₁₂= τ₂₃=0, 以及γ₁₂=γ₂₃=0。并且压电材料只沿着z方向极化，电场分量E₁=E₂=0。将上述已知值代入材料三维本构方程式(5)中得到梁中压电层的力-电-热耦合本构方程：

其中：

1.2   梁内位移场与电势场

对于横向剪切变形不可忽略的层合梁，使用等效单层理论计算其位移场可得到较好结果。而压电层力电耦合效应对结果有一定影响，有必要分层考虑每层压电层的电势分布。若其厚度较厚则需在分层考虑的基础上再次将每层压电层离散为数个子层。本文拟采用此类基于等效单层理论描述层合结构中位移场分布，基于分层理论描述各压电离散层电势场分布的杂交板理论^[9]。

1.2.1   Shi三阶剪切变形理论

采用Shi改进的三阶剪切变形理论^[17]，平面弯曲梁的位移场可写为：

式中：u 和w 分别为梁内的轴向位移及横向位移；u₀和w₀分别为梁中面的轴向位移及挠度；$\bar w$为梁横截面的平均挠度；${\gamma _x}$为梁横截面的剪切变形；h为梁的高度；α=1/4，β=5/3h²。梁横截面的剪切变形${\gamma _x}$为：

式中，${\bar \phi _x}$为梁截面的平均转角。由应变位移关系可得轴向正应变及横向切应变：

式中：e_m为膜应变；e_b为弯曲应变；e_s为剪切应变；e_hs为剪切应变梯度。它们与位移的关系为：

弯曲项对于梁单元的计算精度至关重要，由式(18)中弯曲应变表达式可知，若建立挠度的三次插值，在单元域内会得到沿轴向线性分布的弯曲应变。相比较在单元域内常弯曲应变的梁单元来说，此单元精度更高。

1.2.2   基于Layer-wise理论的电势场

基于Layer-wise理论，本文分层描述梁横截面上压电层的电势的分布。将梁内压电层沿高度离散，假设压电离散层数量为m层，则梁中电势场分布可以表示为^[9]：

式中：${\varphi ^j}$为第j层压电离散层层间接触面的电势分布；L_j(z)则为相应的沿梁高度的插值函数。

若对每一离散层只选取其上下表面电势值作为电势场沿z方向离散的节点，则对于第j层压电层其电势可由此层上下表面电势表示为：

式中，${\varphi ^{j + 1}}$和${\varphi ^j}$分别为第j层压电层上下表面的电势值。而第j压电层的电场为：

式中，${\bar \varphi ^j}$为第j层离散层层间的电势差。

1.3   压电功能梯度梁单元的能量泛函

设压电功能梯度层合梁中压电层数量为m，总铺层数量为n，则考虑力-电-热耦合的单元电热焓为：

式中：下标q为力学量；下标${\text{φ}}$为电学量；下标θ为热学量；Ω_e为单元的体积。从式(22)可以看出，梁的势能主要包括应变能U_qq、压电能$U_{{\text{φ}}{\rm{q}}}$及$U_{{\rm{q}}{\text{φ}}}$、电势能$U_{{\text{φ}}{\text{φ}}}$以及力热耦合能量U_θq、热电耦合能量$U_{{\text{θ}}{\text{φ}} }$。式(22)中应变能部分为：

其中：

功能梯度层中$Q_{11}^j$和$Q_{55}^j$为关于z的函数，对于压电能部分：

其中：

对于电势能部分：

其中：

对于力-热耦合能部分：

其中：

对于电-热耦合能部分：

其中：

1.4   压电功能梯度层合梁单元

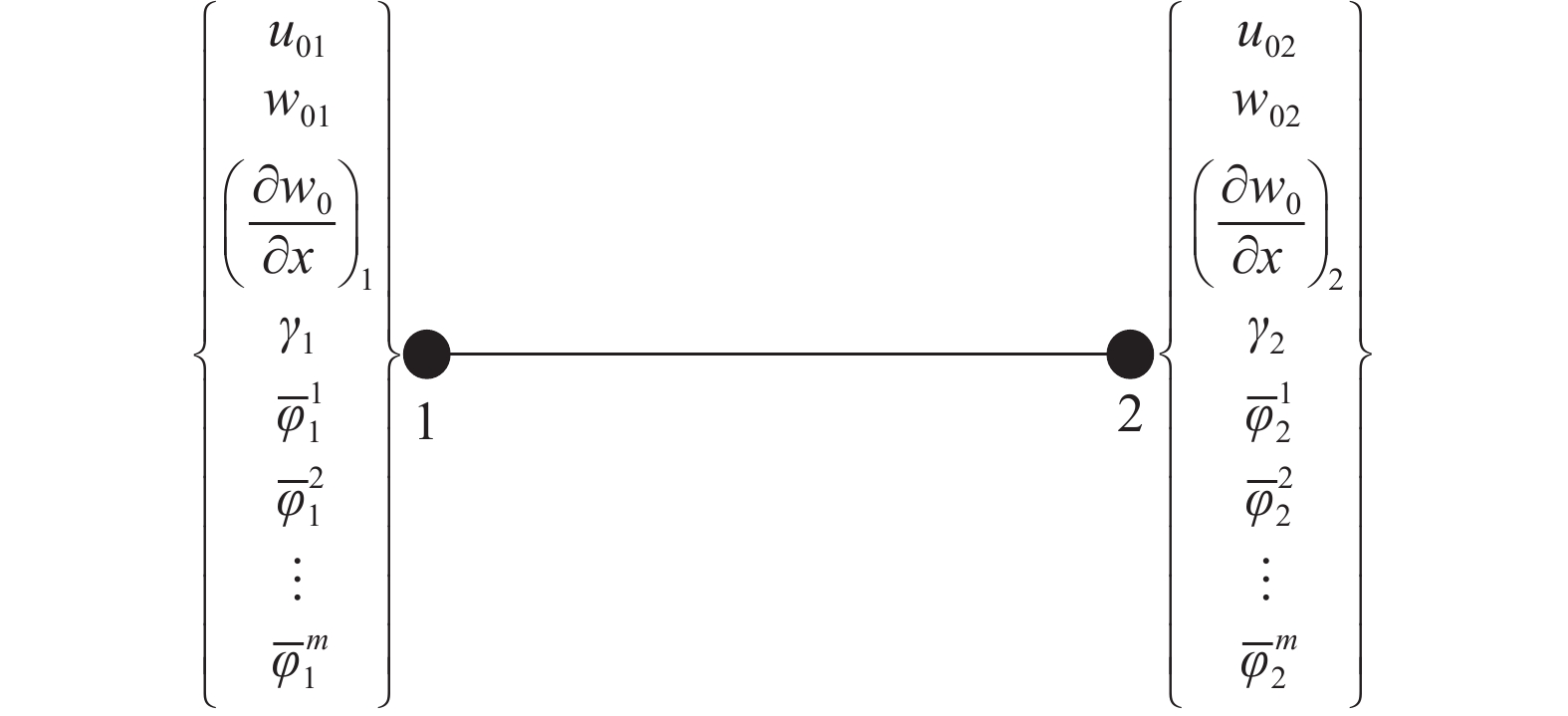
本节将以挠度及横向剪应变作为基本场变量的位移场和以压电层层间电压作为基本未知量的电势场推导一个如图2所示的两节点C¹连续梁单元。单元节点位移及电势向量为：

图  2  两节点压电功能梯度梁单元

Figure  2.  Two-noded piezoelectric functionally graded beam element

下载: 全尺寸图片 幻灯片

1.4.1   基于拟协调元法推导单元应变矩阵

传统以位移为基本未知量的有限元法,单元的应变矩阵基于位移应变关系得出。而以拟协调元法推导单元刚度矩阵则通过直接假设单元的应变场，以弱形式使得协调方程得到满足^[18]。则式(23)单元应变能变为：

式中：${e'_{\rm m}}$、${e'_{\rm b}}$、${e'_{\rm hs}}$及${e'_{\rm s}}$分别为所假设的单元的轴向正应变、弯曲应变、剪切应变梯度及剪切应变；${\boldsymbol{\tilde N}}$、${\boldsymbol{\tilde M}}$、${\boldsymbol{\tilde P}}$和${\boldsymbol{\tilde Q}}$分别为相应应变分量的检验函数。对应于图2中的节点位移参数，单元的弯曲应变${e'_{\rm b}}$可假设沿着轴向线性分布，轴向正应变${e'_{\rm m}}$、横向剪切应变${e'_{\rm s}}$和横向剪切应变梯度${e'_{\rm hs}}$可假设为常数。令式(35)在单元域内逐项满足，并取检验函数为对应应变的插值函数，可得应变矩阵为：

得到各应变分量插值为：

1.4.2   单元刚度矩阵

将式(40)应变插值代入式(23)单元应变能中，可得单元的力学刚度矩阵：

其中：

式中：

式中：A₁₁为拉伸刚度；B₁₁为拉弯耦合刚度；D₁₁为弯曲刚度；E₁₁、F₁₁和H₁₁为与高阶剪切相关的项。

对于第j层压电层，其压电层层间电势差为：

其中，${\boldsymbol{N}}_{\text{φ}} ^j$第j层压电层层间电势插值的形函数矩阵。将式(40)及式(44)代入式(25)所示压电能可得力-电耦合刚度矩阵：

其中：

将式(44)代入式(27)所示电势能可得电学刚度矩阵：

综上所述，单元刚度矩阵为：

1.4.3   单元的一致质量矩阵

由式(15)位移场的表达式对时间求导可以得到速度场的分布：

将之代入到动能表达式可得：

其中：

代入相应的速度场插值，对动能变分可得单元的质量矩阵M_qq：

其中：

式中：${{\boldsymbol M}}_{{u}_{0}}、{\boldsymbol{M}}_{{w}_{0}}$和${{\boldsymbol{M}}_{wx}}$分别为轴向、横向和转动惯量矩阵；${{\boldsymbol{M}}_\gamma }$为高阶剪切变形所引起的质量矩阵；${\boldsymbol{M}}_{uwx}、{\boldsymbol{M}}_{u\gamma }$及${{\boldsymbol{M}}_{wx\gamma }}$分别为不同惯量之间的耦合项；${\boldsymbol{N}}_{{u}_{0}}、{\boldsymbol{N}}_{{w}_{0}}、{\boldsymbol{N}}_{wx}$及${{\boldsymbol{N}}_\gamma }$分别为相应分量的速度场插值。

1.4.4   单元有限元列式

将应变插值代入力-热耦合能式(29)及电-热耦合能式(31)，可得由温度荷载导出的荷载向量${{\boldsymbol{F}}_{{\text{θ}}{\rm{q}} }}$和${{\boldsymbol{F}}_{ {\text{θ}}{\text{φ}}}}$：

若假设梁承受均布荷载f，且第j层压电层上下表面电荷密度为${\boldsymbol{Q}} = {\{ {{Q^{j + 1}}}\;\;{{Q^j}} \}^{\rm T}}$，上下表面电势为${{\bf\textit{φ}}^j} = \{ {{\varphi ^{j + 1}}( {x,{{\textit{z}}_{j + 1}},t} )}\;\;{{\varphi ^j}( {x,{{\textit{z}}_j},t} )} \}$，系统外力及电荷做功为：

将如上所述单元势能U_e、动能T_e和外力功W_e对所有单元求和得到系统整体的势能U、动能T及外力功W代入到Lagrange方程中即可得到系统的运动方程：

求解式(57)可得压电功能梯度梁在力电热耦合荷载作用下有限元方程：

式中：${{\boldsymbol{\bar q}}_{\rm{q}}}$为系统全局节点力向量；${{\boldsymbol{\bar q}}_{\text{φ}} }$为全局节点电学向量。

2   基于LQR的最优振动控制

2.1   动力系统的状态方程

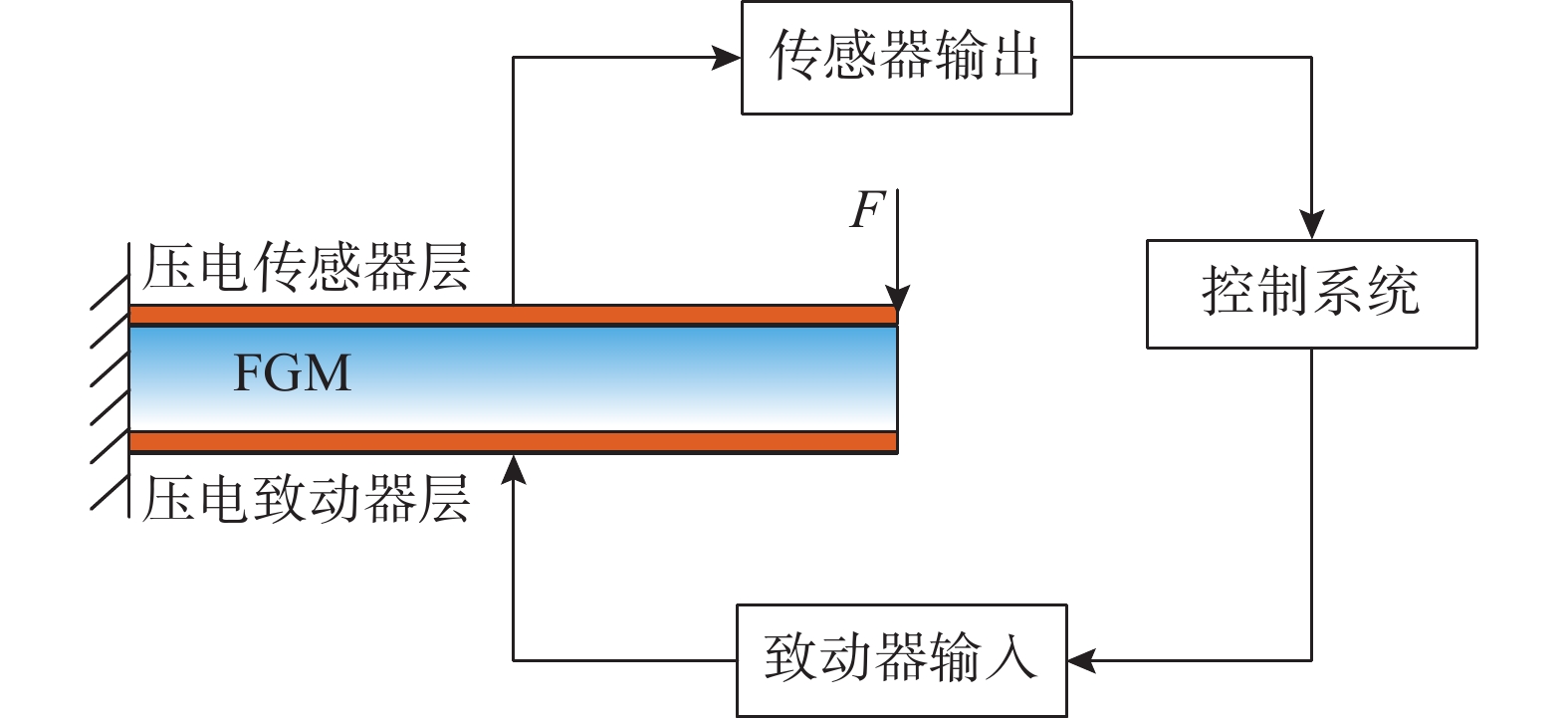
在图3所示振动控制系统中，外加激励下梁产生振动并在压电传感器中产生电压。在接收到动力系统输出电压后，控制系统将反馈信号传入致动器并在其上产生控制电压抑制梁的振动。

图  3  动力系统模型

Figure  3.  Model of the dynamic system

下载: 全尺寸图片 幻灯片

将节点电学自由度分为两部分，压电层传感器电势差${\boldsymbol{q}}_{\text{φ}} ^S$以及压电致动器层电势差${\boldsymbol{q}}_{\text{φ}} ^A$。假设外部温度恒定，则式(58)变为：

由于压电致动器层以及压电传感器层没有共同的电极表面，则$\bar K_{{\text{φ}} {\text{φ}} }^{AS} = \bar K_{{\text{φ}} {\text{φ}} }^{SA} = {\boldsymbol{0}}$。压电传感器用于将信号传入控制系统，因此不考虑压电传感器的逆压电效应，则式(59)中${\bar {\boldsymbol F}}_{\text{φ}} ^S = {\boldsymbol{0}}$。传感器层的电势可由节点力学变量得到：

若考虑系统Rayleigh阻尼可得到压电功能梯度梁强迫振动方程：

其中：

式中，a和b为Rayleigh阻尼系数。

若取动力系统前m_r阶振型在模态空间下求解压电功能梯度梁的动力响应并对其进行振动控制。如式(61)所示强迫振动方程，令外加荷载为零可求其自由振动频率ω_i及模态${\boldsymbol{\phi}}_i$。系统响应可由前m_r阶振型表示为：

其中：Φ为系统振型矩阵；η为系统的模态坐标向量。将式(64)代入式(59)，得到系统在模态坐标描述下运动方程为：

式中，I、Λ和Ω分别为正则化之后的质量矩阵、阻尼矩阵和刚度矩阵。

对动态系统的控制通常在状态空间下描述，本文以模态坐标及其对时间的一阶导数为状态变量，${\boldsymbol{X}}(t) = {\{ {\boldsymbol{\eta }}\;\;{{\boldsymbol{\dot \eta }}} \}^{\rm T}}$，以传感器层电压及其一阶导数为输出变量${\boldsymbol{Y}}(t) = \{ {{\boldsymbol{\bar q}}_{\text{φ}} ^S}\;\;{{\boldsymbol{\dot{ \bar q}}}_{\text{φ}} ^S} \}$可得动力系统的状态空间表达式：

式中：u_q和${\boldsymbol{u}}_{\text{φ}}$为系统的输入变量，分别表示外部施加力向量以及用于控制压电功能梯度梁的振动外部输入电压；A和C为系统的状态矩阵及输出矩阵；B_q和${\boldsymbol{B}}_{\text{φ}}$分别为系统的力学及电学输入矩阵。各变量及矩阵的具体形式为：

2.2   基于LQR的最优振动控制

采用二次型最优控制算法求解最优控制力，系统性能指标泛函为：

式中：Q_x为状态变量的加权矩阵，其为正定或半正定矩阵；R为系统输入变量的加权矩阵，其为对称正定矩阵。

在约束条件式(66)下，可使用拉格朗日乘数矩阵${\boldsymbol{P}}(t)$构造如下的拉格朗日函数^[16]：

将${{\boldsymbol{u}}_{\text{φ}} }(t)$作为自变量对性能指标泛函求变分得到：

求解式(70)可得反馈控制电压${{\boldsymbol{u}}_{\text{φ}} }(t)$：

式中，G_A为最优状态反馈增益矩阵。拉格朗日乘数矩阵P由如下Riccati方程得：

根据现代控制理论，对于无限时间状态调节器P为常数矩阵，则式(72)转化为代数方程。此方程可使用MATLAB控制系统工具箱中lqr函数进行数值求解。将式(71)最优控制力代入原状态方程式(66)之中得到闭环控制系统的状态方程：

3   数值算例

3.1   压电功能梯度层合梁在不同载荷下的静力响应

为了验证文中提出的力-电-热耦合梁单元的计算精度，考虑压电功能梯度层合梁在不同载荷下的静力响应。此算例不仅考虑位移的计算结果，也考虑应力计算结果。主要为如下三种荷载：

荷载1，机械载荷：梁受均布荷载q=−5 kN/m，压电层为闭路边界条件^[15]，即：

荷载2，电场载荷：压电层与功能梯度层接触面接地，梁上下表面施加电压^[15]，即：

荷载3，温度载荷：梁上表面温度为100 ℃，下表面温度为0 ℃，并假设温度为0 ℃材料处于应力自由状态^[19]。

图1所示为一个压电功能梯度层合简支梁，其长L= 250 mm，高度h=5 mm。中间层为由ZrO₂及Al组成的功能梯度层，其高度h_c=4 mm，上表面为纯ZrO₂，下表面为纯Al，中间其材料参数呈梯度变化。本例采用Mori-Tanaka方法^[15]模拟功能梯度层材料的梯度分布。功能梯度层上下表面粘贴有等厚度的PZT-1195N压电薄层。本例所用材料参数为：

Al：E₁=E₂=E₃=70 GPa，μ₁₂=μ₂₃=μ₁₃=0.3，ρ_m=2702 kg/m³；

ZrO₂：E₁=E₂=E₃=200 GPa，μ₁₂=μ₂₃=μ₁₃=0.33，ρ_c=5700 kg/m³；

PZT-1195N：E₁=E₂=E₃=63 GPa，G₁₂=G₂₃=G₁₃=24.2 GPa，μ₁₂=μ₂₃=μ₁₃=0.3，ρ_p=7500 kg/m³，d₃₁= d₃₂=254×10⁻¹² m·V⁻¹，d₃₃=374×10⁻¹² m·V⁻¹，d₁₅=d₂₄=584×10⁻¹² m·V⁻¹，k₁₁=k₂₂=1.53×10⁻⁸ F·m⁻¹，k₃₃=1.5×10⁻⁸ F·m⁻¹。

将梁划分为10个单元。表1为梁在均布荷载及电压作用下梁跨中截面最大位移及最大应力计算结果，图4为在机械载荷和电荷载作用下梯度指数N=0.25时梁中心截面的正应力分布。YASIN等^[15]通过假设电势场沿高度二次分布，并基于本构方程求解得到可描述高阶剪切变形的位移场，提出了一个包含内部电节点的梁单元。其计算结果如表1所示。

表  1  两种荷载下功能梯度简支梁的挠度和正应力计算结果

Table  1.  Central deflection and normal stress of simply supported smart FGM beam under two different loads

梯度 指数N	模型	荷载1			荷载2
		挠度w/mm (0.5L, 0)	正应力σxx /MPa (0.5L, −0.5h)		挠度w/mm (0.5L, 0)	正应力σxx /MPa (0.5L, −0.5h)
0	文献 [15]	−0.18349	4.4811		0.20282	11.881
	本文	−0.18351	4.4663		0.20285	11.910
	Ansys	−0.18349	4.4441		0.20290	11.882
0.25	文献 [15]	−0.22262	5.7942		0.24607	10.670
	本文	−0.22332	5.7970		0.24689	10.683
	Ansys	−0.22453	5.8116		0.24823	10.613
1	文献 [15]	−0.26973	7.3655		0.29814	9.2216
	本文	−0.26950	7.3358		0.29801	9.2615
	Ansys	−0.27006	7.3274		0.29852	9.2096
4	文献 [15]	−0.30483	8.1781		0.33687	8.4753
	本文	−0.30260	8.1074		0.33450	8.5570
	Ansys	−0.30327	8.1348		0.33516	8.5047
∞	文献 [15]	−0.36696	8.9599		0.40552	7.7612
	本文	−0.36702	8.9311		0.40561	7.8208
	Ansys	−0.36696	8.8808		0.40561	7.7637

下载: 导出CSV 

| 显示表格

图  4  两种荷载下梁正应力沿厚度方向变化

Figure  4.  Through-the-thickness variation of σ_x under two different loads

下载: 全尺寸图片 幻灯片

Ansys计算结果为使用软件Ansys平面单元计算所得，采用Plane13单元及Plane182单元分别划分压电层及功能梯度层的网格。并采用等效分层模型描述功能梯度层中材料参数沿高度的分布，即将功能梯度层分为100层子层，每一子层由各向同性材料组成，其材料常数由Mori-Tanaka模型确定。 从表1及图4可以看出使用本文梁单元与YASIN的高阶梁单元及Ansys计算结果基本一致。梁承受均布荷载时随着核心层梯度分布指数增大，在外荷载作用下梁中心截面挠度及最大弯曲正应力逐渐增大。但在电载荷作用下，梁中心截面的挠度逐渐增大，而其弯曲应力却逐渐减小，这表明此压电功能梯度层合梁有很强的力-电耦合效应。

为进一步研究梁的力-电-热耦合效应，本例将考虑如图3所示压电功能梯度层合悬臂梁承受沿梁高度方向线性分布的温度荷载即荷载3。梁的长度为L=200 mm，功能梯度层由Al及ZrO₂复合而成，其厚度为h_c=30 mm。压电层材料为G-1195N厚度为h_p=0.1 mm。本例所用材料参数如下所示：

Al：E =70 GPa，μ=0.3，α₁=23×10⁻⁶；

ZrO₂：E₁=E₂=E₃=151 GPa，μ₁₂=μ₂₃=μ₁₃=0.3；

α₁=10×10⁻⁶；

PZT-1195N: E = 63 GPa，μ = 0.3，d₃₁ = d₃₂ = 254×10⁻¹² m·V⁻¹，k₃₃ = 1.5×10⁻⁸ F·m⁻¹，p₃ = 0.25×10⁻⁴ C·m·⁻²K⁻¹。

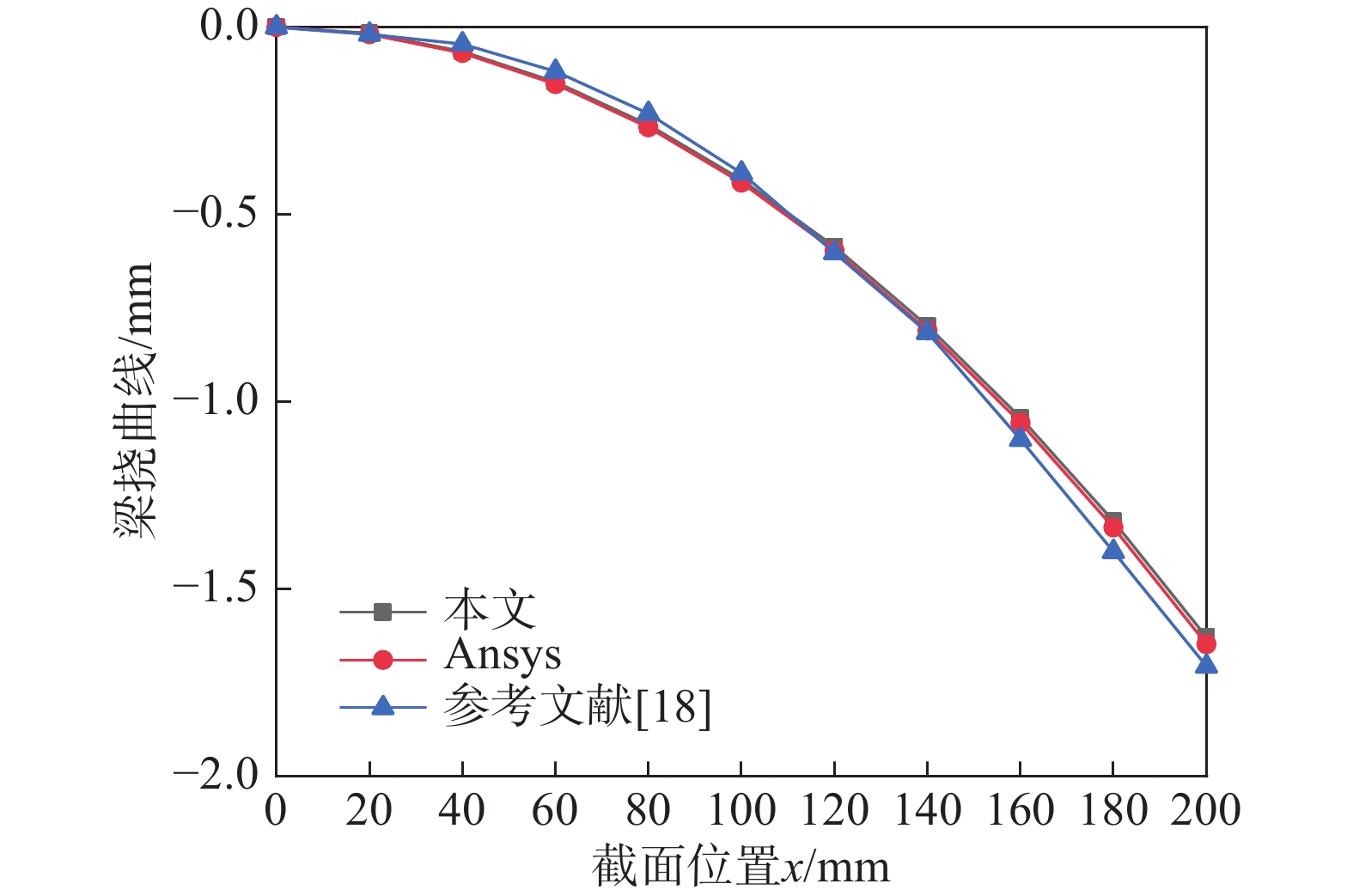
温度荷载作用下，不同组分指数的功能梯度材料梁自由端的最大挠度如表2所示。温度荷载作用下组分指数N=∞ 时梁的挠曲线如图5所示。采用荷载传递法，用Plane55单元划分压电功能梯度梁，计算得到沿厚度方向线性分布的温度场。在相同网格下，使用Plane13单元划分压电层网格，Plane182单元划分功能梯度层网格，施加如前所述温度场得到梁端最大挠度。表2中基于均匀分层模型将功能梯度层分别划分为100及200层，使用Ansys计算温度荷载作用下梁端挠度。使用本文所推导的梁单元计算结果与Ansys计算结果基本一致，与功能梯度层划分为200层时的结果更为接近。图5显示了N=∞ 时梁在温度影响下的挠曲线，其中LIEW等^[19]使用的是一阶剪切变形的板单元并以压电层电压作为节点自由度。从图中结果可以看到，本文的计算结果比文献[19]的解与Ansys解 (200层的计算结果) 吻合的更好。

表  2  温度荷载下梁端挠度

Table  2.  Tip deflections of beam under temperature load

模型	N=0	N=0.5	N=1	N=10	N=15	N=∞
本文	0.7214	0.6866	0.6902	1.149	1.256	1.630
Ansys (100层)	0.7268	0.6905	0.6991	1.236	1.303	1.647
Ansys (200层)	0.7274	0.6905	0.6975	1.176	1.287	1.648

下载: 导出CSV 

| 显示表格

图  5  不同模型给出的温度荷载作用下梁挠曲线 (N=∞)

Figure  5.  Deflection curves of beam under temperature load given by different models (N=∞)

下载: 全尺寸图片 幻灯片

3.2   自由振动分析

如图3所示压电功能梯度悬臂梁，梁的长度为1 m，功能梯度层厚度h_c为0.05 m，由Al及Al₂O₃复合而成。上下压电层厚度h_p为0.001 m，材料为PZT G1195。本例所用材料参数如下：

Al：E₁=E₂=E₃=70 GPa，μ₁₂=μ₂₃=μ₁₃=0.3，ρ_m=2702 kg/m³；

Al₂O₃：E₁=E₂=E₃=380 GPa，μ₁₂=μ₂₃=μ₁₃=0.3；ρ_c=3800 kg/m³；

PZT-1195N：E₁=E₂=E₃=61 GPa，μ₁₂=μ₂₃=μ₁₃=0.3，ρ_p=7750 kg/m³，e₃₁= 6.5 C/m²，e₃₃=23.3 C/m²，e₁₅=17 C/m²，k₁₁=k₂₂=1.53×10⁻⁸ F·m⁻¹，k₃₃=1.5×10⁻⁸ F·m⁻¹。

为准确计算梁的高阶频率，将其划分为20个单元。表3为计算所得压电功能梯度层合梁前五阶无量纲化频率对比。其中Bendine基于Reddy三阶剪切变形理论的位移场以及基于Layer-wise理论描述的线性分布电势场推导得到两节点梁单元^[11]，并利用此单元求解得到梁在不同梯度分布指数下前五阶无量化自由振动频率。表3为梁前五阶自由振动无量纲化频率λ，其中λ的表达式为：

表  3  压电功能梯度梁前五阶无量纲化自由振动频率

Table  3.  The first five non-dimensional frequencies of piezoelectric functionally graded beam

梯度 指数 N	模型	模态
		1	2	3	4	5
0	本文	1.8961	11.773	32.561	58.433	62.809
	文献 [11]	1.9023	11.866	32.981	58.494	63.967
	Ansys	1.9002	11.767	32.348	58.525	61.799
0.5	本文	1.6173	10.053	27.852	52.534	53.886
	文献 [11]	1.6233	10.130	28.175	52.615	54.720
	Ansys	1.6142	10.006	27.546	52.393	52.869
1	本文	1.4664	9.1175	25.270	48.521	49.179
	文献 [11]	1.4725	9.1873	25.548	48.752	49.710
	Ansys	1.4642	9.0757	24.985	47.724	48.860
10	本文	1.2427	7.6852	21.128	35.027	40.461
	文献 [11]	1.2501	7.7788	21.536	35.114	41.568
	Ansys	1.2424	7.6593	20.918	34.987	39.653

下载: 导出CSV 

| 显示表格

表3中的Ansys解为本文采用3.1节同样的单元计算所得自由振动频率。从表中得结果可以看出，使用本文梁单元所算结果与Bendine及Ansys所算结果较为接近，而随着梯度分布指数增大，梁前五阶自由振动频率均增大。相比较Reddy梁理论，Shi梁理论基于三维弹性力学及能量等效原理推导得到位移场中的剪切函数，并且以截面的平均转角为基本场变量可以更好地预测梁的高阶频率，表中梁振动的第五阶频率本文所算结果相比较参考文献[11]的结果更接近Ansys解。

3.3   压电功能梯度层合梁最优振动控制

3.3.1   非对称正交铺设层合梁振动控制

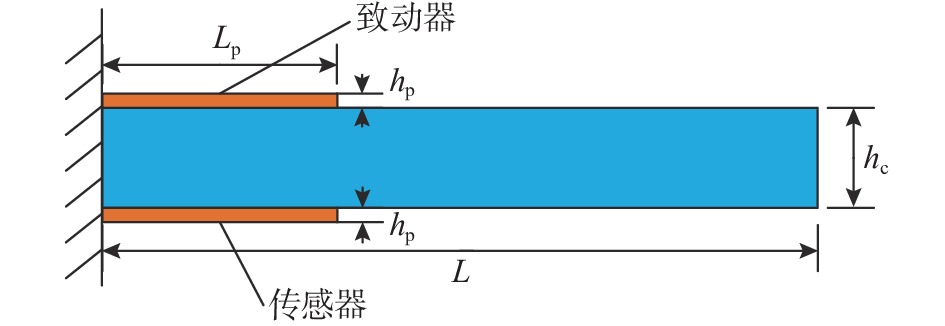
如图6所示为一个非对称正交铺设(0^o/90^o/0^o/90^o)层合悬臂梁^[20]，其固支端处配置有压电传感器及压电致动器，梁总长度L=100 mm，宽度b=10 mm。梁由四层等厚度各向同性层组成，其材料为Gr/Ep，总厚度h_c=2 mm。上下压电层长度均为 L_p=40 mm，其厚度h_p=0.2 mm。压电层由PZT G1195组成，其材料参数如3.1节中所示，本例所用弹性层材料参数为：

Gr/Ep：E₁=150 GPa，E₂=E₃=9 GPa，G₁₂=G₁₃=7.1 GPa，G₂₃=2.5 GPa，μ₁₂=μ₂₃=μ₁₃=0.3，ρ_c=1600 kg/m³；

图  6  带压电片复合材料悬臂梁几何示意图

Figure  6.  Geometry of cantilever composite beam with PZT patches

下载: 全尺寸图片 幻灯片

将梁划分为5个单元，其中压电片划分为2个单元。上层压电层作为致动器，下层压电层作为传感器。在梁端施加大小为1 N方向向下的冲击荷载，作用时间为1 ms。取结构的前6阶模态对其进行控制，设每阶模态所对应阻尼比为0.8%。图7为在冲击荷载作用下梁端挠度及压电致动器层控制电压时间历程。从两图中可以看出，使用LQR算法所求的最优控制力可有效抑制梁的振动。参考文献[20]采用3.1节中YASIN等^[14]所提出压电功能梯度梁单元，此梁单元有一个内部的电学自由度，并且在压电层表面附加等电势条件。另外考虑到测量噪声及观测噪声的影响设计了系统的状态观测器，采用LQR算法中性能泛函为输出变量及控制变量的二次型加权线性组合的输出调节器求解最优控制力。为与参考文献[20]比较，本文同样采用输出调节器并设计了状态观测器求解最优控制力。性能指标中输出变量的权值Q=50 I，而输入变量的权值R=I。从图7中可以看出，使用本文梁单元及YASIN所给出梁单元计算所得未施加控制时梁自由振动曲线基本一致。由于两者采用不同电学自由度，采用本文梁单元所求解的致动器层电压相比较YASIN梁单元所求电压差异明显，且前者更低。而相同权值下施加控制后，两者梁端挠度振动曲线差异较小。

图  7  冲击荷载下反对称正交铺设梁的梁端挠度及压电片控制电压的时间历程

Figure  7.  Tip deflection and control voltage time histories of anti-symmetric cross-ply beam under an impulsive load

下载: 全尺寸图片 幻灯片

3.3.2   压电功能梯度层合梁振动控制

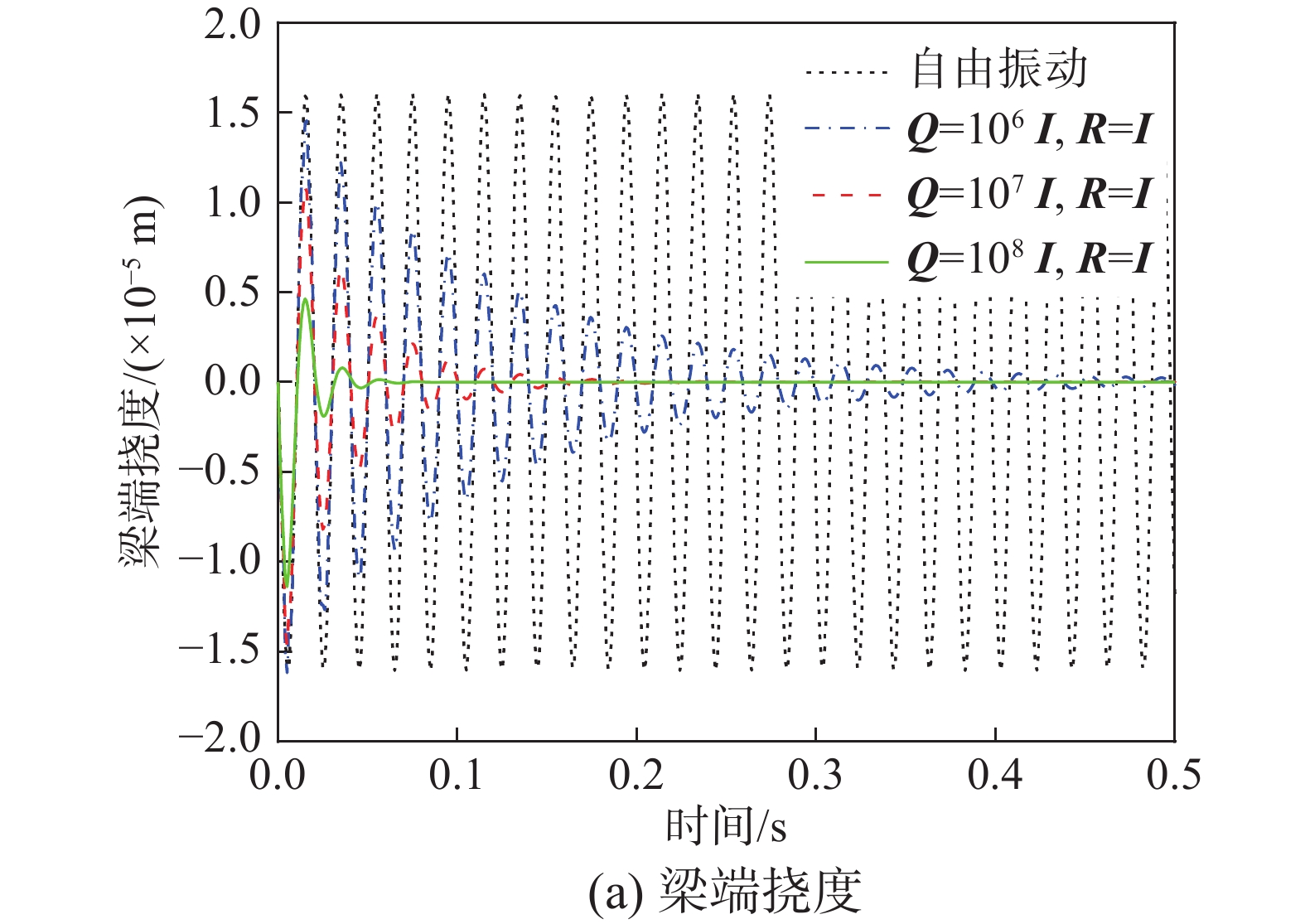
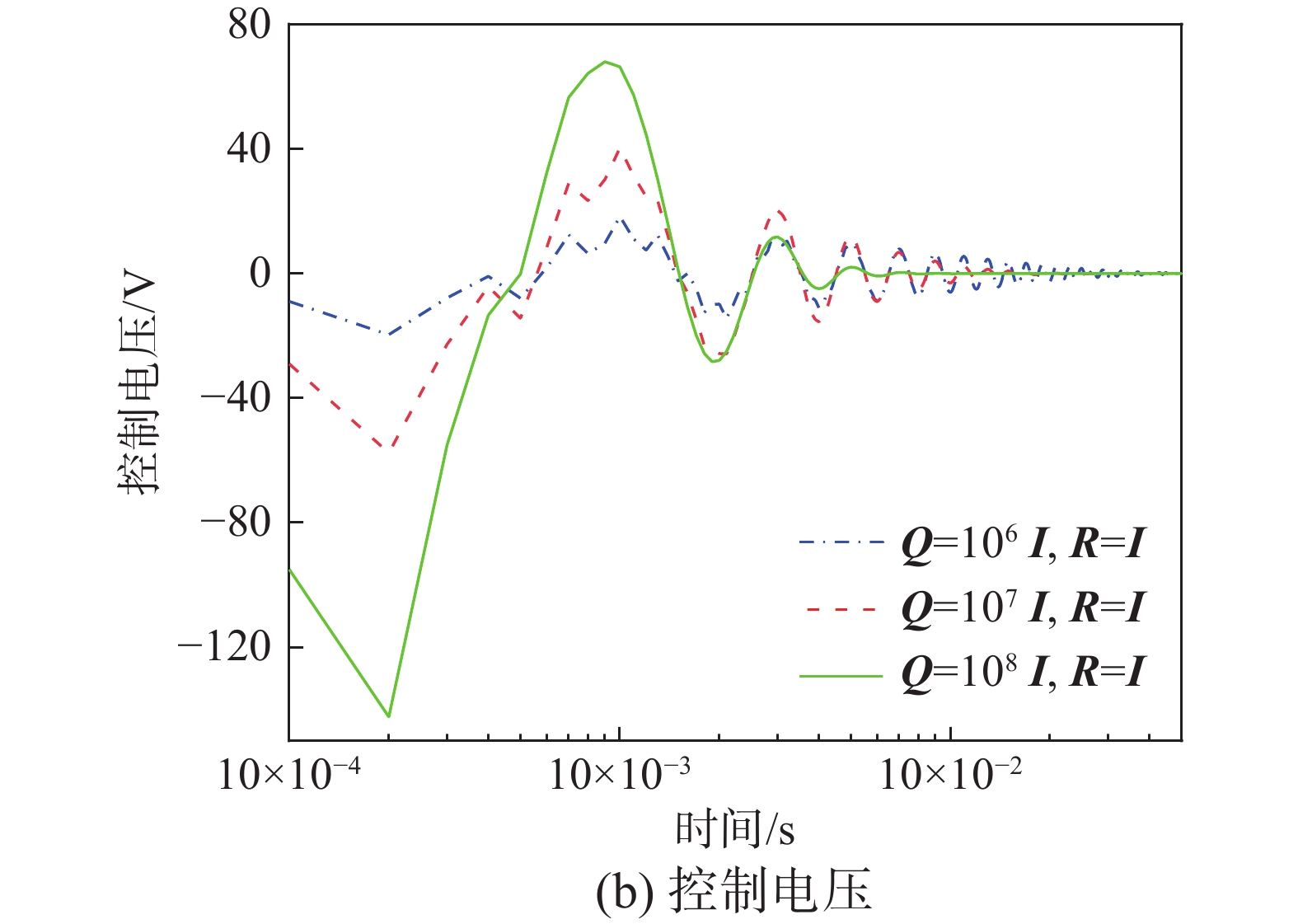
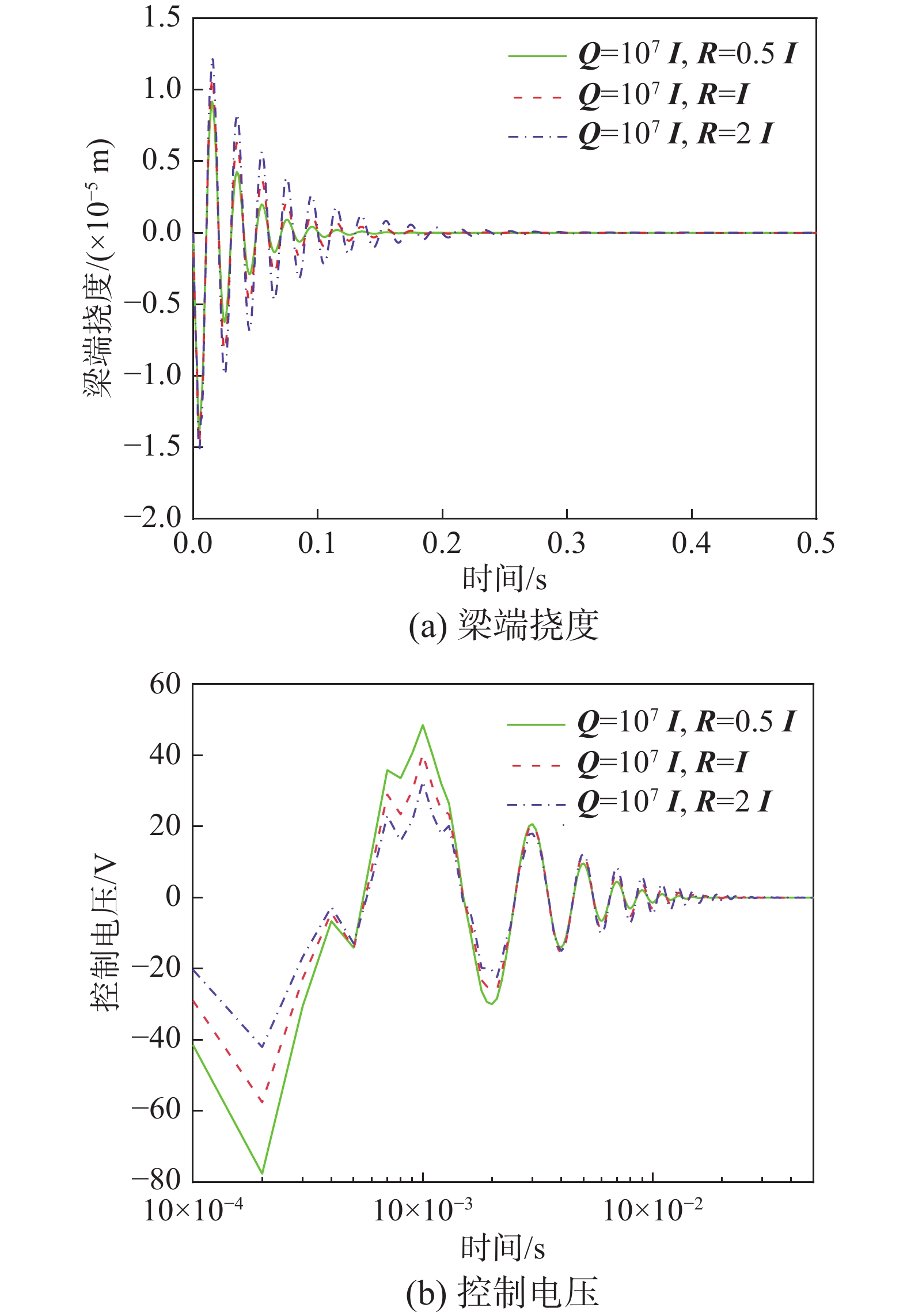
本例将研究性能指标函数中加权矩阵Q以及R的权值大小对结构振动最优控制的影响。仍然采用3.2节中的模型，基于前文所提出的梁单元列式已准确求得梁的自由振动频率如表3所示。现取结构的前五阶频率对其进行振动控制，将梁划分为10个单元，上层压电层作为结构的传感器，下层压电层作为致动器。梁中心功能梯度层梯度分布指数N=10。初始时刻在梁自由端处施加向下的大小为200 N的冲击荷载，作用时间为0.001 s，通过线性二次型最优控制器求得其最优控制电压，将控制电压施加在结构的制动器层上实现对其振动的控制。

图8及图9为在各能量项前加权系数取不同值时梁端的振幅曲线以及施加在第一个单元上的平均电压随时间的变化曲线。表4为不同加权矩阵取值下系统的控制时间及控制电压。从图8、图9以及表4可以看到，固定R的权重，随着Q权重的增大，梁的振动衰减更快，而施加在致动器层的电压更高。而在0.1 s以后在电压变化图中此趋势正好相反，考虑到Q权值大的振幅曲线中振幅已经衰减到一定程度，结构并不需要更大的电压来控制其振动。相反，固定Q的权重，随着R的权重增大，控制电压的幅值越低，振动衰减越慢。

下载: 全尺寸图片 幻灯片

  8  基于不同Q取值下LQR算法的振动控制梁端挠度及控制电压的时间历程

  8.  Tip deflection and control voltage for the optimal vibration control of piezoelectric functionally graded beam using LQR scheme with various weighting matrixes Q

下载: 全尺寸图片 幻灯片

图  9  基于不同R取值下LQR算法的振动控制梁端挠度及控制电压的时间历程

Figure  9.  Tip deflection and control voltage for the optimal vibration control of piezoelectric functionally graded beam using LQR scheme with various weighting matrix R

下载: 全尺寸图片 幻灯片

表  4  Q、R不同取值下梁振动控制时间及最大控制电压比较

Table  4.  The comparison of control time and maximum control voltage with different values of Q and R

Q和R的取值	控制时间/s	最大控制电压/V
Q=106 I，R=I	>0.5	19.61
Q=107 I，R=I	0.249	57.58
Q=108 I，R=I	0.082	142.30
Q=107 I，R=0.5 I	0.188	77.67
Q=107 I，R=2 I	0.367	42.06

下载: 导出CSV 

| 显示表格

4   结论

本文基于杂交板理论推导了一个C¹连续的两节点压电功能梯度层合梁单元，其中以SHI改进的三阶剪切变形理论表示梁内位移场，以Layer-wise理论表示梁内压电层电势场。基于Hamilton变分原理推导得到梁单元的有限元列式，并将此有限元列式用于压电功能梯度层合梁的静力分析及动力分析。通过LQR最优控制算法求得最优控制力实现对压电功能梯度梁的振动最优控制。数值算例结果表明：

(1) 所得压电功能梯度层合梁单元的位移与应力计算结果与Ansys的二维弹性力学单元计算结果一致。但本文使用的梁单元比二维弹性力学模型所使用的单元少很多，表明本文所给梁单元可以准确且高效地描述压电功能梯度层合梁的力-电-热耦合效应。

(2) 压电功能梯度层合梁的频率分析计算结果显示，以截面平均转角为基本场变量的SHI改进三阶剪切变形理论给出比其他三阶剪切变形梁理论更准确的高阶振动频率。

(3) 利用LQR最优控制算法所得最优控制力可有效抑制结构的振动。二次型性能指标泛函中状态变量的权重Q越大，梁的振动衰减越快，控制电压越高。增大输入变量的权重R，梁的振动衰减越慢，控制电压越低。