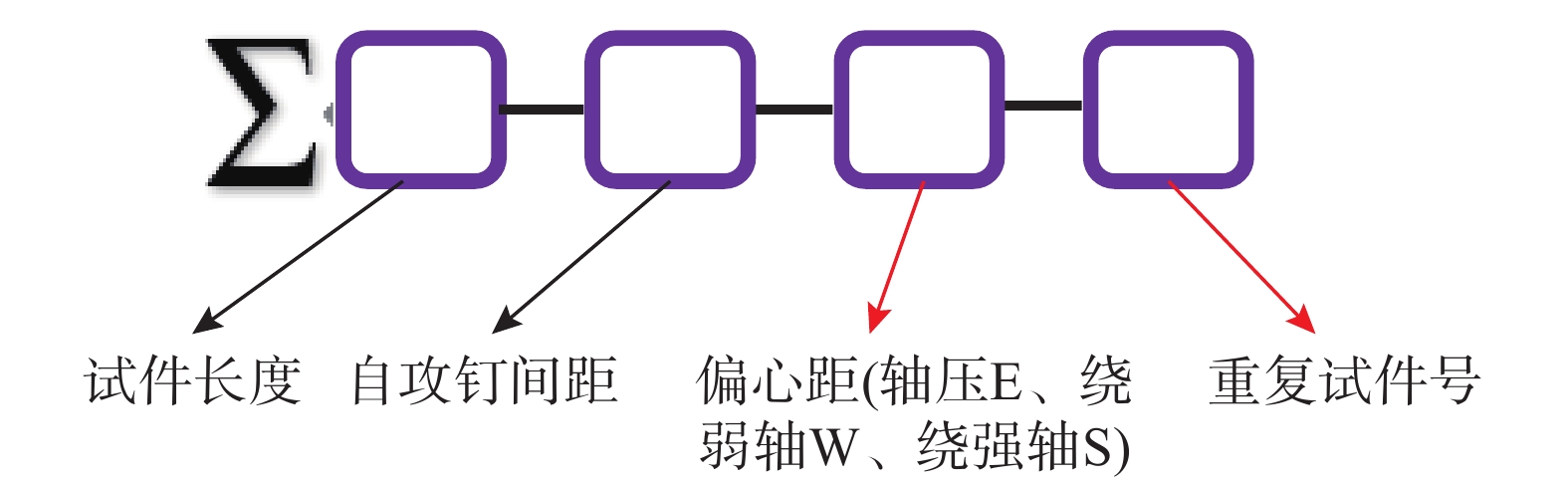
EXPERIMENTAL RESEARCH ON DISTORTIONAL BEHAVIOR OF COLD-FORMED THIN-WALLED Σ-SHAPED STEEL BUILT-UP SECTIONS UNDER ECCENTIRC COMPRESSION
-
摘要: 为研究腹板并合双肢冷弯薄壁Σ型钢拼合钢柱的畸变屈曲性能及其相关作用,并评估现行各国规范计算方法适用性,设计制作了22根构件进行压弯试验。以Σ型加劲、腹板孔位、偏心荷载作用位置、柱长等为主要参数,考察其对试件屈曲行为、破坏特征和极限承载能力的影响。结果表明:试验主要发生畸变屈曲或畸变-整体、畸变-局部相关屈曲,Σ型加劲有效地防止了腹板局部屈曲;腹板开孔不会影响屈曲模式的改变;关于强轴和弱轴的偏压位置及偏心距离对试件畸变屈曲行为有显著影响。采用中美技术标准包括中国规范GB 50018−2002、JGJ/T 421−2018以及北美规范NAS 100−2016计算的承载力结果与试验结果进行了对比分析,结果表明:荷载绕强轴偏心作用时,中美规范计算结果均偏于安全;荷载绕弱轴偏心作用时,GB 50018−2002和NAS 100−2016计算结果偏于安全,而JGJ/T 421−2018计算值较为保守,试验与其比值约为1.64,该文建议腹板双肢并合截面整体协同工作下绕弱轴稳定承载力可按全截面计算。Abstract: To study the distortional buckling and interactive behavior of cold-formed steel composite sections with Σ-shaped web channels, and evaluate the applicability of current Chinese and North American codes, 22 members were designed and fabricated for compression-bending test. The main parameters including Σ-shaped stiffener, opening position, eccentric compression direction with respect to the strong & weak axis and the eccentricity are investigated to obtain the influence of each parameter on buckling behavior, failure mode and ultimate bearing capacity of the specimen. The test results indicate that all the specimens present distortional buckling or interaction buckling involving distortional mode; The stiffened-web can effectively prevent local buckling of the web; The holes in the web have slight effect on buckling mode; The eccentric compression locations with respect to the strong & weak axis have a significant effect on buckling behaviour of the specimen. Comparing the experimental results with the calculated bearing capacity results according to current Chinese and North American specifications, including GB 50018−2002, JGJ/T 421−2018 and NAS 100−2016, it is found that the calculations with respect to the strong axis adopting Chinese and North American specifications are all conservative; When the specimens are under eccentric compression with respect to the weak axis, the calculated results employing GB 50018−2002 and NAS 100−2016 are both conservative, while the ratio of the test results to the calculation results of JGJ/T 421−2018 averages 1.64, which is too conservative. Therefore, it is proposed that the bearing capacity of eccentric compression with respect to the weak axis should be calculated in accordance with the overall built-up cross-section when the two Σ-shaped channels of composite column work well together.
-
冷弯型钢结构因其装配化程度高、施工安装方便等优势近年来得到大量应用和广泛研究,主要进展涉及到结构性能[1]、一体化性能[2]、耐久性能[3]等方面。然而冷弯薄壁型钢构件,其截面腹板宽厚比一般较大,因而局部屈曲问题突出[4],通过对板件弯折而加劲的方式可以提升局部屈曲应力[5]。由于建筑设备管线暗埋在墙体中需要穿越龙骨,需要在龙骨腹板上预留孔洞[6]。将单肢冷弯型钢构件面对面或背对背拼合成双肢构件在构件承载力提升方面具有促进作用,在多层冷弯型钢结构或门窗洞口等承载较大部位应用较多,一系列相关研究是近年的热门课题。在我国规范GB 50018−2002[7]和北美规范NAS 100−2016[8]中给出了针对非加劲和特定加劲类型单肢压弯构件的条款,但Σ形加劲腹板并合压弯构件相关规定尚有欠缺,值得更多关注。
ZHANG等 [9-10]对腹板加劲拼合构件进行轴压试验及有限元参数分析,结果表明:较深的向内腹板加劲和中等向外腹板加劲比其他加劲类型效果更好,提出的直接强度法改进计算式为拼合闭口截面轴压构件的安全设计提供了保障。LIU等[11]考察了拼合截面组成分肢长细比对构件轴压性能的试验,并采用北美规范计算和试验结果分析,认为分肢的细长比应控制在拼合全截面两个主轴细长比较小值的3/4以内。ROY等[12]进行了C型面对面拼合构件轴压试验,基于试验结果采用有限元模拟了从超短柱到细长柱的试验,通过调整多个紧固螺栓的纵向间距,研究发现:螺钉间距翻倍对短柱承载力影响较小,而中长柱承载力降低15%~25%。WANG等[13]对复杂卷边槽形截面双肢拼合柱进行了轴压试验,结果表明:腹板加劲能有效约束孔洞附近的变形且提高承载力。综上所述,国内外学者对冷弯薄壁型钢构件受力性能进行了大量研究,但对于受压构件尚应重视以下内容:1)以往对于冷弯薄壁受压构件的研究主要关注轴压,而关于压弯性能的研究较少[9-13];2)加劲、开孔、拼合是提升承载能力以及改善冷弯型钢构件用途的重要方式[14-17]。因此,这些影响因素应综合考虑,有必要进行相关研究[18]。
对于采用腹板加劲与开孔的冷弯薄壁型钢拼合截面压弯构件,目前需要更多相关试验和设计方法研究[18]。基于此,本文针对四种长细比的Σ型腹板加劲及开洞冷弯薄壁双肢并合工字型试件进行偏压试验,考察其畸变屈曲行为、极限承载力、破坏模式,研究关于强轴、弱轴偏压方向作用下截面畸变行为特征。基于试验结果,采用现行中美规范相关规定进行分析,并评价其设计方法适用条件。
1 试验概况
1.1 试件设计
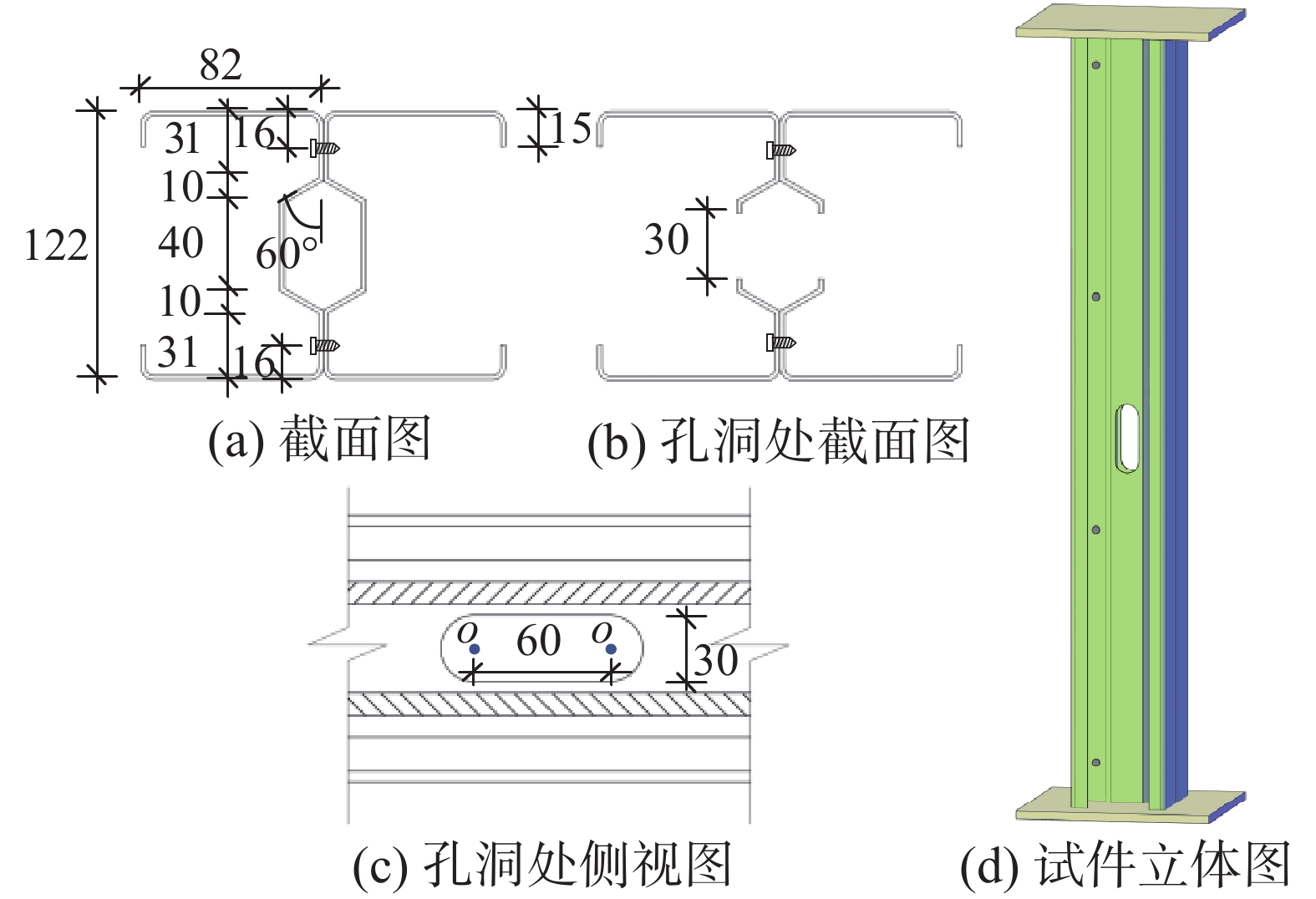
试件为冷弯薄壁Σ型钢腹板并合工字型截面,双肢采用自攻螺钉拼合,钢材等级为Q355,数量共计22个。并合截面尺寸见图1,试件编号见图2所示。设计参数如表1所示,本文对四种长度试件进行了分析,孔洞位于柱长等分点处。为分析自攻螺钉间距对构件的影响,对400 mm长短柱进行轴压试验,考察其轴压受力性能,其余长度试件主要考察压弯性能。
表 1 试验构件设计Table 1. Specimens design压弯长度/mm 自攻钉间距/mm 孔洞位置等分 偏压方向及偏心距/mm 400 300(100、150) − − 1000 300 L/2 S20(40)、W20 1600 300 L/2 S20(40)、W20 2200 300 L/3 S20(40)、W20 注:S为强轴方向;W为弱轴方向。 1.2 材性试验
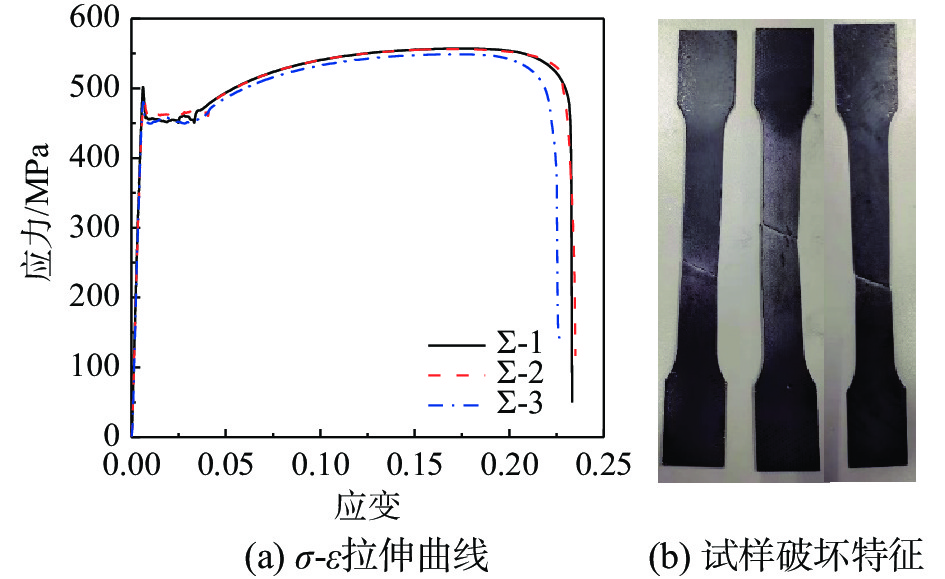
材性试验按照 《金属材料 拉伸试验 第1部分: 室温试验方法》(GB/T 228.1−2010)[19]进行,标准件均从腹板取样,实测屈服强度、抗拉强度、断后伸长率以及弹性模量分别为452 MPa,、549 MPa、26.5%和2.21×105 MPa。材性测试结果见图3。
1.3 试件实际尺寸与初始缺陷
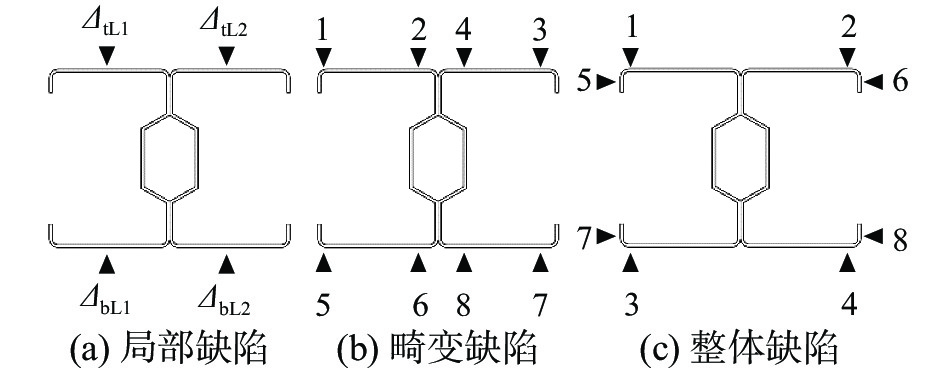
试件实测尺寸和初始几何缺陷代表值见表2所示。本文考虑三种初始几何缺陷,涉及局部(ΔL)、畸变(Δd)及整体弯曲(w
s及ww),其实测位置见图4所示。ΔL反映了翼缘板的平整度(见图4(a)),其测量值取测点标准高度ΔtL1与ΔtL2(或ΔbL1与ΔbL2)的差值,在试件长向间隔50 mm进行,其中下标t和b分别为翼缘两侧;Δd测点见图4(b),其测量值取试件分肢翼缘转角处测量读数之差值,如测点3和测点4的标准高度之差。ws及ww测点见图4(c),取翼缘转角处实测读数差值,s与w分别为绕强轴与绕弱轴方向,编号1~4和5~8为相应四个角部实测读数,ws和ww为对应极差。 表 2 试件实测尺寸及初始缺陷Table 2. Measurements of cross-sections and initial imperfections试件名称 长度L/mm 腹板h/mm 板厚t/mm 翼缘b/mm 卷边d/mm 开孔大小/mm 加劲肋尺寸/mm 螺钉间距/mm Δ L/mm Δd/mm ws/mm ww/mm 圆心距 半径 Σ400-100-E0-1 397.5 117.05 1.92 80.51 14.70 − − 10.0 10.10 0.35 2.48 2.53 1.66 Σ400-100-E0-2 397.2 117.30 2.04 80.75 14.47 − − 9.9 10.00 0.88 2.35 2.61 0.52 Σ400-150-E0 396.9 117.87 1.92 80.33 15.09 − − 9.8 15.21 0.31 2.07 0.56 0.59 Σ400-300-E0 397.9 120.20 1.91 80.83 15.02 − − 9.7 29.95 0.19 0.90 3.30 0.57 Σ1000-300-S20-1 998.3 123.92 2.08 80.71 14.84 60.21 29.8 9.9 30.02 0.49 0.96 1.92 1.51 Σ1000-300-S20-2 997.5 123.86 2.03 80.91 14.73 60.31 29.5 10.1 29.99 0.83 0.93 0.89 0.48 Σ1000-300-S40-1 999.0 121.96 2.08 80.71 14.69 60.00 30.0 9.9 30.09 0.63 0.02 1.21 0.82 Σ1000-300-S40-2 997.5 123.08 2.01 80.98 14.51 60.94 29.0 9.8 30.08 0.44 0.54 3.00 0.48 Σ1000-300-W20-1 998.9 122.94 2.11 81.32 14.58 60.80 29.1 10.1 30.26 0.69 0.47 0.66 0.72 Σ1000-300-W20-2 998.5 124.50 2.06 80.41 14.43 60.80 29.2 10.1 30.06 1.00 1.25 3.39 0.66 Σ1600-300-S20-1 1598.8 126.33 2.00 81.02 15.09 60.76 28.0 10.1 30.06 0.80 2.17 2.35 0.39 Σ1600-300-S20-2 1598.5 127.07 1.89 80.20 14.83 61.90 28.0 10.2 30.04 0.41 2.54 1.45 0.71 Σ1600-300-S40-1 1600.5 125.83 1.93 80.39 14.30 61.03 29.0 9.5 30.10 0.89 1.92 1.16 0.81 Σ1600-300-S40-2 1588.9 125.81 2.10 80.63 14.44 60.02 30.0 10.2 30.08 1.23 1.91 1.15 0.93 Σ1600-300-W20-1 1599.1 125.07 2.01 80.99 15.01 61.33 29.0 9.8 30.01 1.01 1.54 1.18 1.28 Σ1600-300-W20-2 1600.5 125.83 2.05 80.82 14.75 61.10 29.0 9.9 30.04 0.53 1.92 1.68 0.42 Σ2200-300-S20-1 2198.2 128.15 2.04 80.92 14.77 60.00 29.5 10.1 30.03 1.11 3.08 2.04 0.45 Σ2200-300-S20-2 2199.2 127.40 2.07 80.57 14.71 59.60 29.5 10.0 29.99 1.01 2.70 0.70 1.88 Σ2200-300-S40-1 2198.2 128.70 2.02 81.10 15.17 59.50 29.5 10.6 30.11 1.41 3.35 1.08 1.56 Σ2200-300-S40-2 2195.9 123.84 2.07 81.04 14.87 59.53 29.9 10.7 30.00 1.18 0.92 2.14 1.19 Σ2200-300-W20-1 2198.5 127.80 2.06 80.64 15.37 58.00 30.0 10.3 30.10 0.55 2.90 2.31 1.77 Σ2200-300-W20-2 2197.6 125.50 2.02 80.63 14.98 60.36 29.5 9.7 29.56 0.95 1.75 3.15 5.98 注:400 mm短柱试件未开孔;开孔为长圆孔,圆心距为孔洞两个半圆圆心间距离。 1.4 加载装置及测点布置
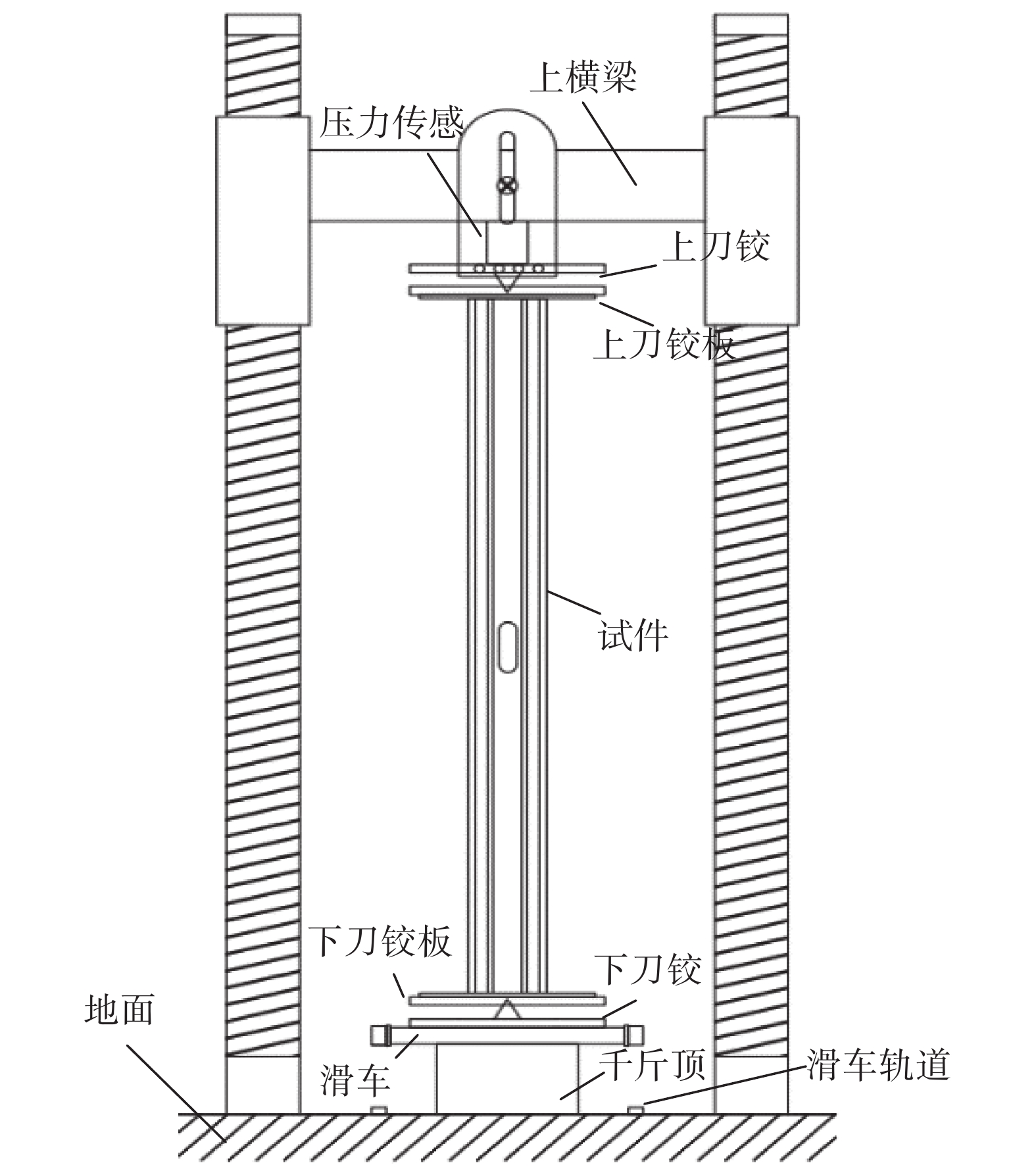
本次试验加载由液压系统顶升底板实现,边界条件为铰接支座。试验装置如图5所示。端部布置的位移计用来记录试件竖向压缩变形情况;沿试件高度方向,截面角部布置的位移计用来记录试件畸变屈曲变形情况。本次试验在腹板、分肢翼缘、截面角部处布置了成对应变片,用以记录构件荷载作用时的截面受力特征。
试验采用逐级加载方式,每级荷载增量取预估试件承载值的5%,分级加载后持荷1 min~2 min;持续加载中如试件发生凸曲变形或加载至预估试件承载值的80%时,加载增值缩半;在荷载趋近极限承载值时,加载过程须缓慢且连续,直至捕捉到极限承载力;当荷载降至峰值的80%~70%时,视为试验结束[20]。
2 试验现象
2.1 短柱轴压试件
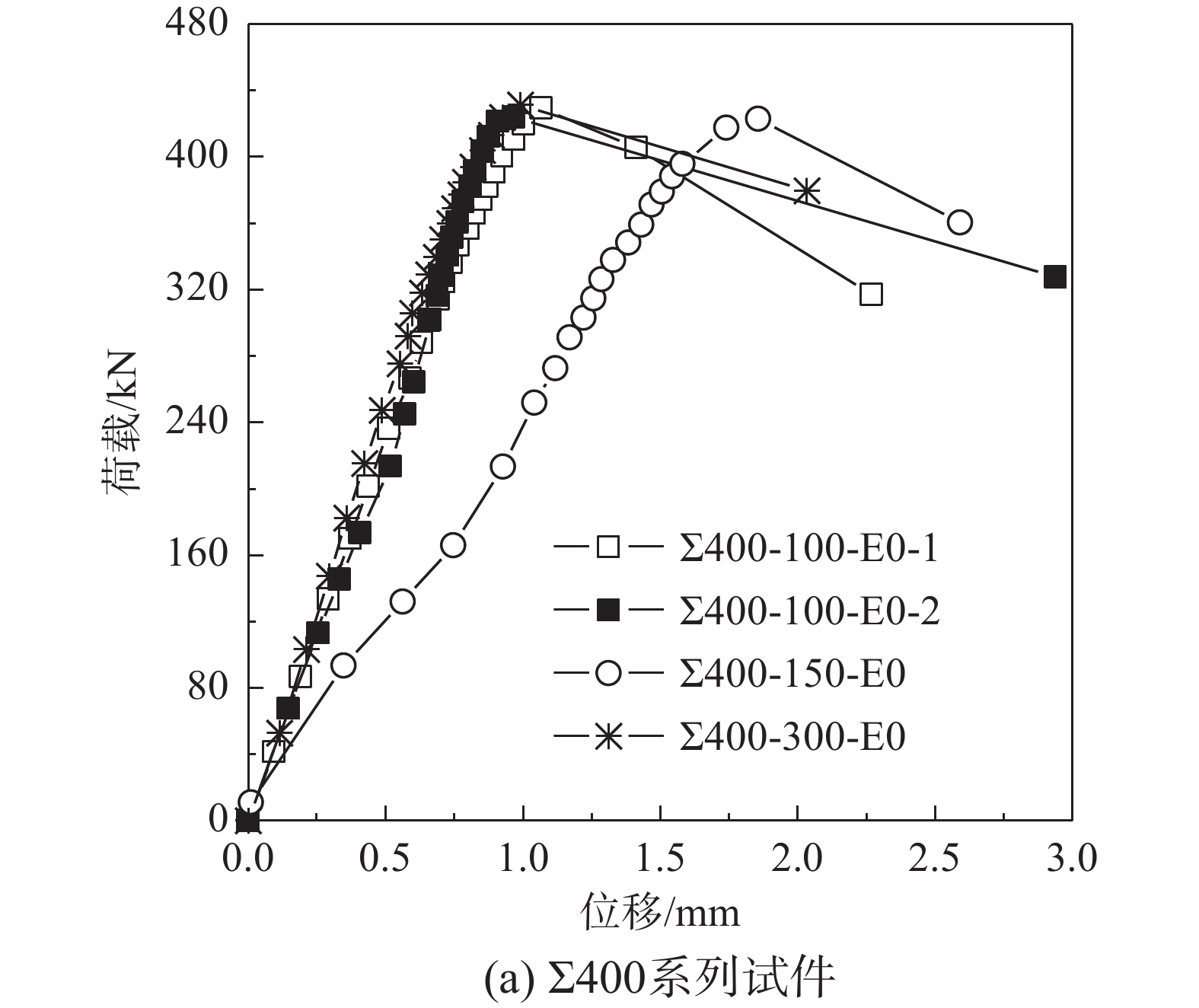
400 mm短柱进行轴压试验,加载过程中试验现象主要如下:随着荷载的增加,试件两侧翼缘呈现出一个畸变屈曲半波变形;当荷载增至顶峰时,试件分肢翼缘屈曲变形量迅速变大;随着荷载的降低,此处翼缘变形过大而致卷边折屈,试件破坏形态见图6(a)所示。
短柱均发生了畸变屈曲或畸变与局部耦合屈曲,破坏形态基本一致。试件一侧翼缘变形较大,而另一侧翼缘及腹板变形较小,表明构件的并合和腹板加劲加强了腹板局部屈曲能力。各试件畸变半波数均为1个,波峰位置临近试件长度中央,半波长约200 mm~300 mm,自攻螺钉间距从100 mm、150 mm、300 mm改变对屈曲模式的影响较小。
从图6(a)可以看出,试件同侧的翼缘板均向外凸曲,此类畸变屈曲变形有使并合的两单肢构件腹板相背离趋势,螺钉间距为300 mm的试件现象较明显,其余试件未发现腹板背离的间隙。由于自攻螺钉的紧固作用,试验加载过程中连接处并合状况较好(见图6(a)~图6(d)),说明当螺钉间距适当时,可以保证拼合构件分肢的协同工作(见图7)。
2.2 中长柱及长柱压弯试件
试件绕强轴偏心受压作用,随着荷载增加,受压一侧翼缘板件呈现凹凸变形。1000 mm和1600 mm试件两侧翼缘呈现的凸曲变形互相对称,变形发展趋势相同,而2200 mm试件两侧翼缘呈现的凸曲变形朝向相反;当荷载增至顶峰时,在翼缘屈曲变形快速增大;随着荷载的降低,试件在翼缘-卷边处发生塑性折曲。1000 mm和1600 mm试件大多在上部发生弯矩作用平面内的破坏,见图6(b)、图6(c),而2200 mm试件多在1/3~1/2长度处发生弯矩作用平面外破坏,见图6(d)。
试件绕弱轴偏心受压作用,当加载到一定荷载值时,两侧翼缘板件呈现明显的畸变屈曲半波,且两侧波形相互对称;当荷载接近极值时,屈曲变形快速增大;当荷载降至极值80%时,试件受压翼缘出现明显鼓曲或折曲,破坏时试件跨中挠度比绕强轴偏压时要大,见图6(b)。从图6中可以看出,受压一侧翼缘变形较大,且未见试件腹板出现明显的折曲,表明腹板Σ型加劲以及并合都对腹板的局部屈曲起到了约束作用。畸变屈曲半波个数随试件长度增加而增多,1000 mm试件2个~3个,1600 mm试件3个,2200 mm试件为3个~5个。试件在孔洞处的变形较小,孔洞对屈曲半波分布无明显规律性,故孔洞的存在对腹板Σ型加劲试件的屈曲模式影响并不明显。
3 试验结果及分析
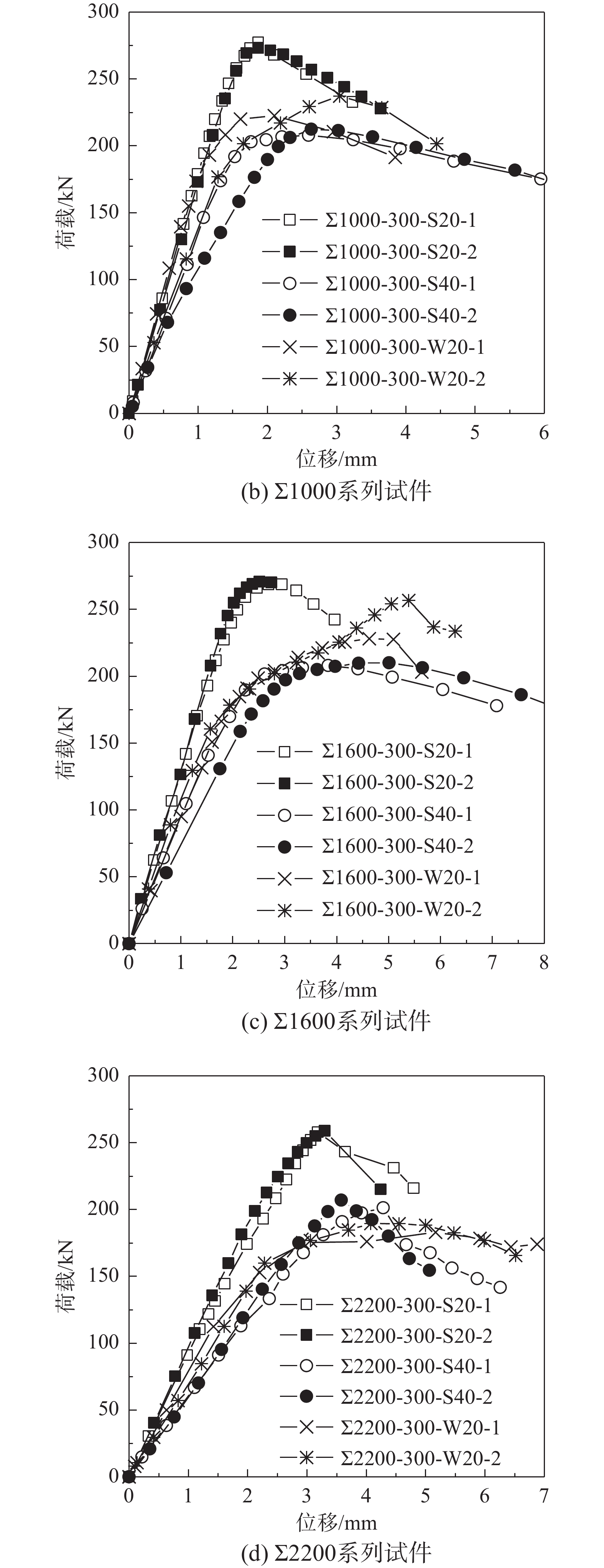
试验的荷载-轴向位移曲线见图8,曲线特征表明,各试件在加载初始阶段为线弹性增长趋势,表明构件刚度几无变化,试件保持弹性受力阶段;趋近极限荷载过程中,曲线为非线性增长,刚度退化;轴向压缩位移在达到极限荷载后开始迅速增大,即告试件破坏。对照试件的结果基本一致,试验可重复可靠。
从图8(a)中看出,改变自攻螺钉间距对承载力影响较小,各试件极限承载力基本接近,除Σ400-300-E0外,400 mm长各试件弹性刚度也基本相同;从图8(b)、图8(c)、图8(d)中看出,在同一偏心轴下,试件极限荷载随着偏心距的增大而显著下降。在荷载绕不同偏心轴且同一偏心距作用下,试件极限荷载随着荷载作用位置由绕强轴改变为绕弱轴而显著降低。当腹板开洞数目一定时,试件极限荷载随着其长度增加而有所下降。绕弱轴压弯的试件具有较为明显的屈曲后强度,如图8(c)中试件Σ1600-300-W20-2屈曲后行为可见。
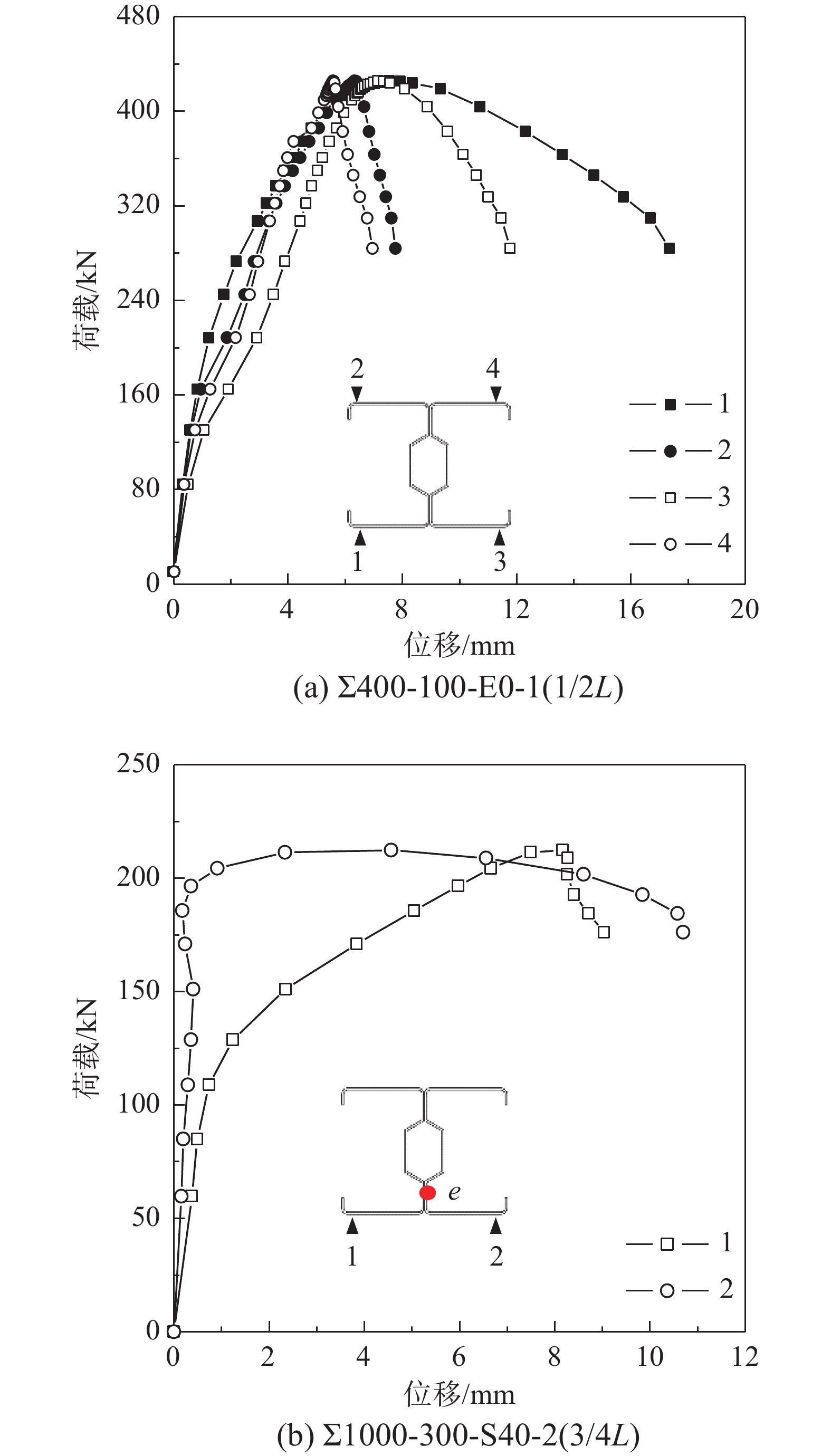
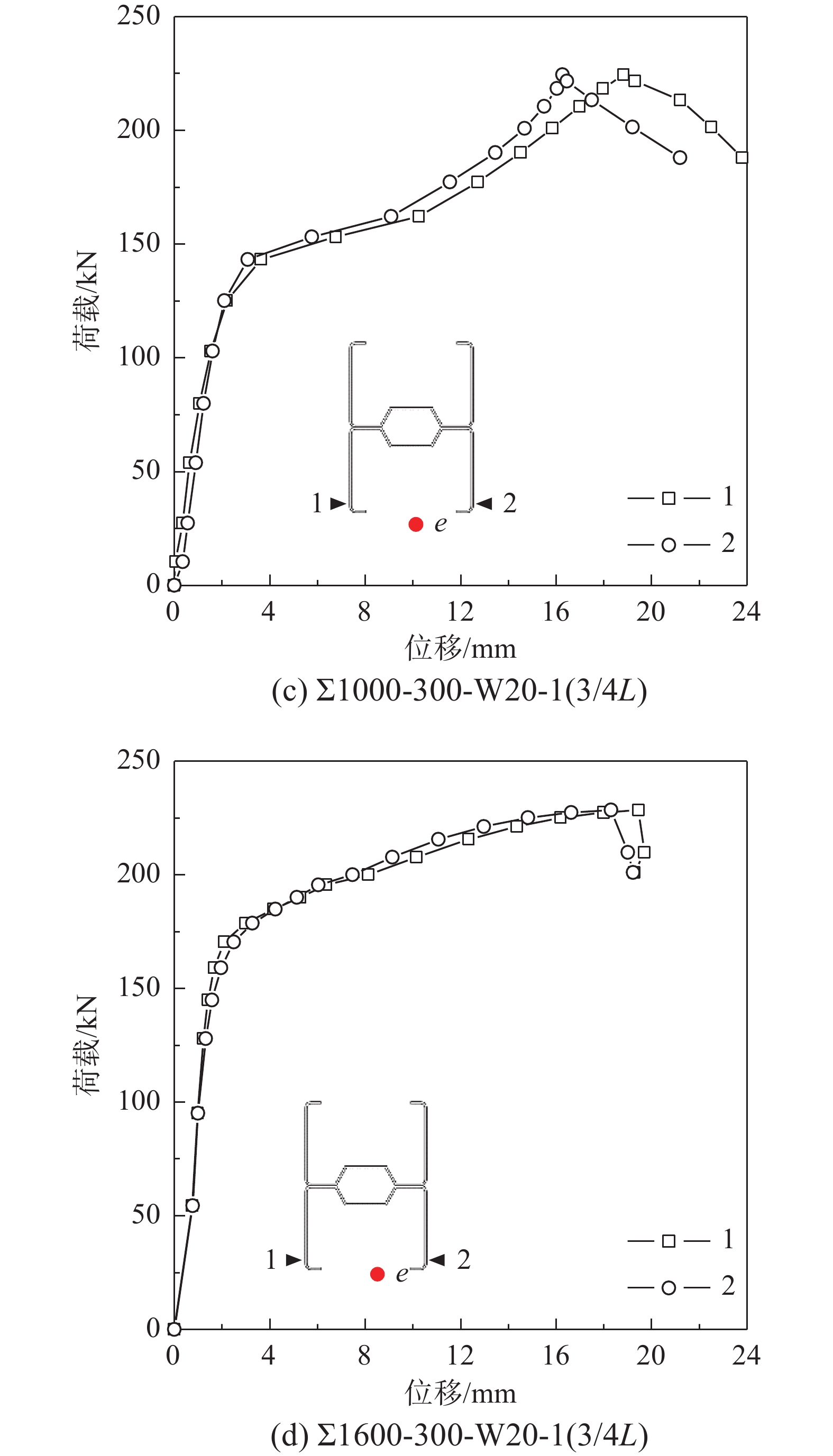
荷载-侧向位移曲线见图9,曲线中测点正负号规则以截面板件平面凸曲为正,凹曲为负,括号内字母表示位移计设置于试件位置。从图9(a)看出,到极限荷载前400 mm短柱截面四个角点的侧向位移增量接近,而荷载下降阶段试件一侧翼缘变形显著。对偏压试件,初始加载阶段侧向位移几无变化或增量较小,当荷载增大到一定值时,测点处的侧向位移明显增大,表明截面发生翼缘畸变屈曲,见图9(b)~图9(d)曲线所示。
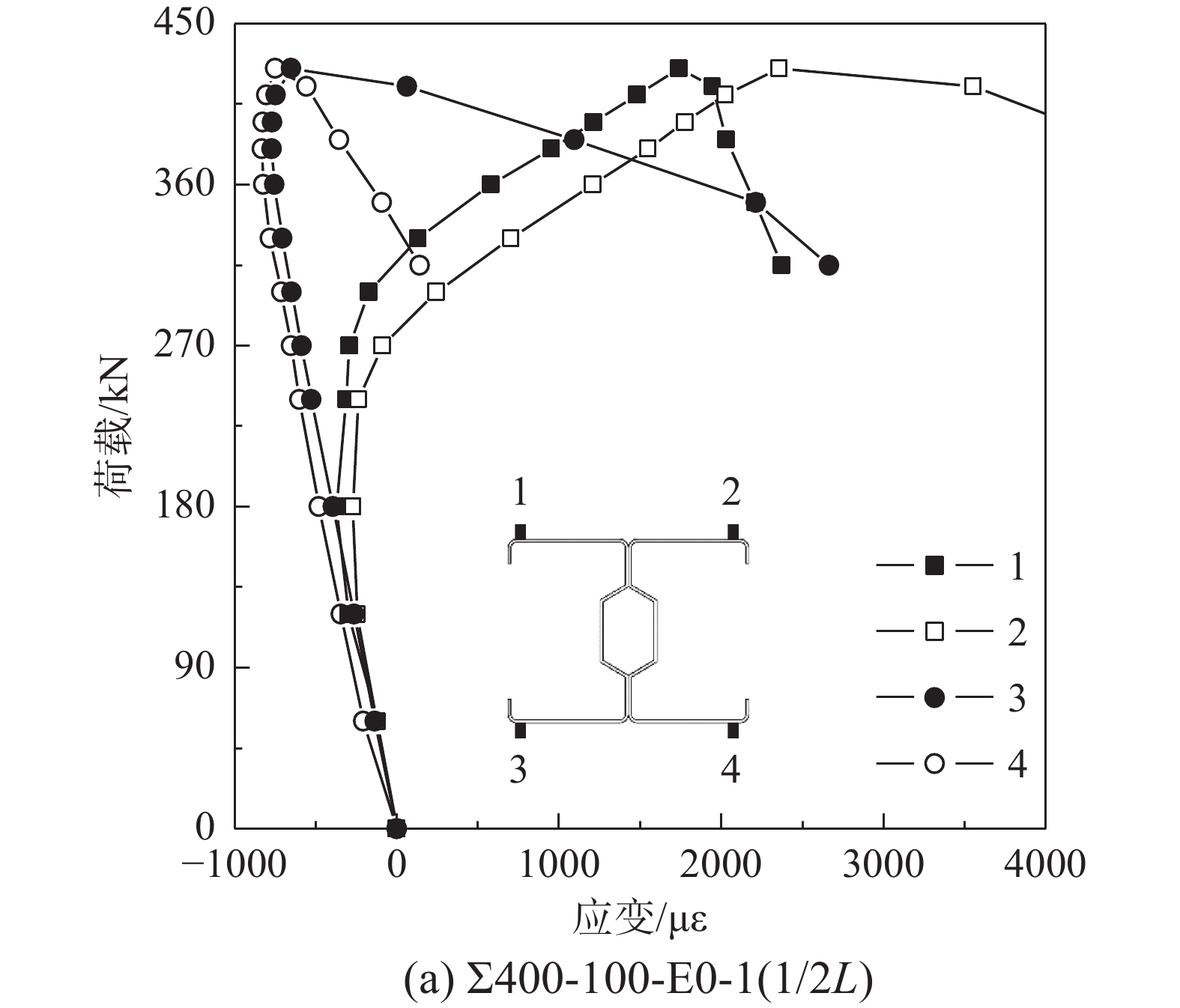
荷载-应变曲线见图10,施加不同荷载试件的应变片数据选取位置略有不同,轴心受压试件取截面角点部位,偏心受压试件取截面受压侧分肢翼缘的中点。从图10曲线观察可得,初始加载阶段试件截面均匀受压,曲线正比例增长是主要特征,截面各点处应变基本相同;在逐渐接近屈曲及极限荷载时,屈曲附近区域的应变速率显著,应变曲线出现分叉现象。当畸变变形严重导致翼缘塑性折曲,同时板件两侧应变反向,表现出局部塑性破坏。如图10(c)中,Σ1000-300-W20-1翼缘板表面成对的1号和3号应变片(4号和6号同)分叉后反向,该试件应变片正好在翼缘板件折曲部位,对比观察图6(b)为畸变屈曲破坏模式,应变信息与试验破坏现象较为一致。
短柱轴压破坏模式及承载力试验结果见表3,中长柱及长柱压弯破坏模式及承载力见表4。表3和表4中结果表明:本次试验中各组试件的屈曲行为、破坏模式、极限承载力都基本一致,承载力差值在5%以内浮动。对短柱轴压承载力进行分析,当螺钉间距从100 mm增到150 mm和300 mm,承载力分别下降1.3%和2.9%。从中长柱及长柱压弯结果表明:偏心距从20 mm增到40 mm,极限承载力降低21%~23%。当试件由绕强轴压弯改变为绕弱轴压弯时,极限承载力会显著下降。对于腹板开孔个数相同的试件,极限承载力随着试件长度的增加而降低。
表 3 短柱试件试验结果与中美规范计算值对比Table 3. Comparison of the test results and the calculation results of Chinese and American standards for short axial compression columns试件名称 A/mm2 L0/mm L/mm 屈曲部位 破坏模式 半波长/mm Pt/kN PGB/kN PJGJ/T/kN PNAS/kN Pt/PGB Pt/PJGJ/T Pt/PNAS Σ400-100-E0-1 1180.7 462 398 1/2L D(1) 200 430 362.3 362.30 453.8 1.19 1.19 0.95 Σ400-100-E0-2 1255.6 461 397 1/2L D(1) 200 425 362.3 362.30 453.8 1.17 1.17 0.94 Σ400-150-E0 1185.5 461 397 1/2L D(1) 240 422 362.3 362.32 453.8 1.16 1.16 0.93 Σ400-300-E0 1191.5 462 398 1/2L D(1) 200 415 362.3 362.32 453.8 1.15 1.15 0.91 注:A为截面积; L0为试件计算长度; L为试件几何长度;Pt为试验值; PGB为GB 50018−2002计算值; PJGJ/T为JGJ/T 421−2018计算值;PNAS为北美NAS 100−2016计算值。 表 4 压弯试件试验结果与中美规范计算值对比Table 4. Comparison of the test results and the calculation results of Chinese and American standards for eccentric compressive columns试件名称 A/mm2 L0/mm L/mm 屈曲部位 破坏模式 半波长/mm Pt/kN PGB/kN PJGJ/T/kN PNAS/kN Pt/PGB Pt/PJGJ/T Pt/PNAS Σ1000-300-S20-1 1310.5 1062 998 3/4L D(2) 400 277 234.1 234.1 263.6 1.18 1.18 1.05 Σ1000-300-S20-2 1279.5 1062 998 3/4L D(2) 400 273 234.1 234.1 263.6 1.17 1.17 1.04 Σ1000-300-S40-1 1301.1 1063 999 3/4L D(2)+L 400 210 190.2 190.2 202.5 1.10 1.10 1.04 Σ1000-300-S40-2 1262.5 1062 998 3/4L D(2) 400 212 190.2 190.2 202.5 1.12 1.12 1.05 Σ1000-300-W20-1 1328.2 1063 999 1/2L D(3)+F 300 224 207.1 145.0 212.7 1.08 1.54 1.05 Σ1000-300-W20-2 1294.4 1063 999 1/2L D(3)+F 300 239 207.1 145.0 212.7 1.16 1.65 1.13 Σ1600-300-S20-1 1274.2 1663 1599 3/4L D(3) 500 269 222.2 222.2 240.6 1.21 1.21 1.12 Σ1600-300-S20-2 1198.8 1662 1599 3/4L D(3)+L 500 271 222.2 222.2 240.6 1.22 1.22 1.13 Σ1600-300-S40-1 1216.7 1665 1601 3/4L D(3) 500 208 178.7 178.7 185.0 1.16 1.16 1.12 Σ1600-300-S40-2 1327.0 1653 1589 3/4L D(3) 500 210 178.7 178.7 185.0 1.18 1.18 1.14 Σ1600-300-W20-1 1275.0 1663 1599 1/2L D(3)+F 500 228 192.4 134.7 195.0 1.19 1.69 1.17 Σ1600-300-W20-2 1300.0 1665 1601 1/2L D(3)+F 500 258 192.4 134.7 195.0 1.34 1.92 1.32 Σ2200-300-S20-1 1304.0 2262 2198 1/2L D(3)+FT 650 260 208.7 208.7 230.2 1.25 1.25 1.13 Σ2200-300-S20-2 1316.0 2263 2199 1/2L D(3)+FT 650 262 208.7 208.7 230.2 1.26 1.26 1.14 Σ2200-300-S40-1 1298.0 2262 2198 1/2L D(3)+FT 650 200 165.6 165.6 176.6 1.21 1.21 1.13 Σ2200-300-S40-2 1307.0 2260 2196 1/2L D(3)+FT 650 209 165.6 165.6 176.6 1.26 1.26 1.18 Σ2200-300-W20-1 1318.0 2263 2199 1/2L D(5)+F 400 192 176.7 123.7 186.4 1.09 1.55 1.03 Σ2200-300-W20-2 1280.0 2262 2198 1/3L D(4)+F 500 183 176.7 123.7 186.4 1.04 1.48 0.98 平均值 1.18 1.34 1.11 标准差 0.073 0.229 0.075 变异系数 0.062 0.171 0.068 注:A为截面积; L0为试件计算长度; L为试件几何长度;Pt为试验值; PGB为GB 50018−2002计算值; PJGJ/T为JGJ/T 421−2018计算值;PNAS为北美NAS 100−2016计算值。 4 试验结果与中美规范计算值对比
有效宽度法和直接强度法是目前冷弯薄壁型钢试件承载力的两种主要计算方法。基于本文试验结果与现行中美规范设计方法计算值对比分析,验证并评估其适用条件。自攻螺钉连接紧固Σ腹板并合效果较好(图7所示),因此采用中美规范计算时,取工字形全截面进行分析。
1)我国规范GB 50018−2002 [7]为有效宽度法,但不涵盖本文的试件截面形式。JGJ 227−2011[21]对截面畸变屈曲的设计方法在附录补充。JGJ/T 421−2018[22]规定,绕强轴稳定计算时可按单肢截面稳定承载力的2倍取值;绕弱轴稳定计算按整体截面承载力的0.7倍取值。采用我国规范计算压弯构件畸变屈曲承载力的具体计算公式如下:
NNA+βmMMA⩽ (1) {N_{\rm{A}}} = {A_{{\rm{od}}}}f (2) {M_{\rm{A}}} = \left(1 - \frac{N}{{N_E'}}\varphi \right){M_{{\rm{od}}}} (3) 式中:βm为等效弯矩系数,按GB 50018−2002相关条文确定; NA为轴压畸变屈曲承载力,取式(2)计算值;MA为考虑轴力影响的受弯畸变屈曲承载力,取式(3)计算值; Aod为截面畸变屈曲有效面积,按JGJ 227−2011相关条文确定;钢材强度设计值f=fy/γR,γR=1.165;Mod为截面受弯畸变屈曲承载力。
2)北美规范NAS 100−2016中压弯构件畸变屈曲直接强度法计算公式如下:
\frac{{\overline P }}{{{P_{\rm{a}}}}} + \frac{{{{\overline M }_x}}}{{{M_{{\rm{a}}x}}}} + \frac{{{{\overline M }_y}}}{{{M_{{\rm{a}}y}}}} \leqslant 1.0 (4) 式中:
\overline P 为轴压力设计值;{\overline M _x} 、{\overline M _y} 分别为绕x、y轴的弯矩设计值,按照北美规范LRFD法计算;Pa为畸变屈曲轴压承载力;Max、May为关于x、y轴的畸变屈曲受弯承载力,按北美规范直接强度法相关公式计算。 4.1 短柱轴压试件承载力计算
表3为短柱轴心受压计算结果,表中D表示畸变屈曲,括号内数值为试件畸变半波数目;Pt试验值;PGB为按规范GB 50018−2002考虑板组约束系数并取工字形全截面计算值;PJGJ/T为按多层规程JGJ/T 421−2018规定方法计算值;PNAS为按北美NAS 100−2016取全截面计算值。
GB 50018−2002计算值偏于安全,其中:(Pt/PGB)max为1.19;(Pt/PGB)min为1.15。试验中,试件在轴压时绕强轴破坏,取PJGJ/T为各单肢构件稳定承载力之和,此时PJGJ/T与PGB相同,偏于安全。北美规范计算值基本可靠,其中:(Pt/PNAS)max为0.95;(Pt/PNAS)min为0.91。
4.2 中长柱及长柱压弯试件计算
表4为偏心荷载作用试件的计算结果,表中字母L、D、T、F分别代表局部、畸变、扭曲、弯曲模式,括号内数字为畸变半波数。表中,Pt/PGB均值为1.18、最大值1.34、最小值1.04;方差和变异系数为0.073、0.062。统计结果表明:GB 50018−2002规范计算值均小于试验结果,偏于安全,且离散性较小。其中,采用JGJ/T 421−2018计算拼合截面畸变屈曲承载力,绕强轴偏压承载力计算时,PJGJ/T等于PGB;而绕弱轴计算时PJGJ/T按0.7PGB取用,此时试验与PJGJ/T计算结果相差大。表中,Pt/PJGJ/T均值为1.34、最大值1.92、最小值1.48;方差和变异系数为34、0.229、0.171。统计结果表明:按JGJ/T 421−2018规定,绕弱轴稳定承载力计算时对拼和截面畸变屈曲承载力不可靠,规定取值偏于保守。因此,当腹板并合Σ型加劲试件的连接能保证各分肢协同整体工作时, JGJ/T 421−2018绕弱轴畸变屈曲稳定承载力计算可不必取0.7倍进行折减,建议取拼合整体截面进行计算。
采用北美NAS 100−2016计算,表中Pt/PNAS均值为1.11、最大值1.38、最小值0.98;方差和变异系数为0.075、0.068。统计结果表明:除个别试件外,北美规范NAS 100−2016 计算值均小于试验结果,偏于安全,离散性也较小。
5 结论
本文以试件柱长、腹板孔位、偏心荷载作用位置等为主要参数,对双肢冷弯薄壁Σ型钢腹板并合钢柱进行压弯性能试验,研究并分析了各参数对试件屈曲行为、破坏特征和最大承载能力的影响。采用现行中美规范计算方法对试验结果进行了分析,主要结论如下。
(1)试件主要发生畸变屈曲、畸变-整体、畸变-局部相关屈曲,试件发生屈曲行为和破坏模式基本不受腹板开孔的影响;畸变屈曲半波分布与孔洞的设置无明显规律性,其波长以及分布个数对试件长度的增加较敏感;自攻螺钉对分肢的紧固作用以及腹板加劲对腹板抗屈曲能力具有显著提升作用;绕强轴和弱轴偏心受压作用下,试件荷载峰值随偏心距的增加而减少;偏压方向由绕强轴转为绕弱轴,试件极限荷载也大幅度减小。
(2)试件在不同荷载偏压方向下的截面破坏特征有较大差别。短柱及中长柱绕强轴压弯试件偏心受压侧两分肢翼缘凸曲变形相互对称且波幅较大,压力作用影响明显;长柱绕强轴压弯试件两侧翼缘呈现的凸曲变形朝向相反,弯矩作用影响较为显著,与受弯构件畸变破坏模式较一致;绕弱轴压弯作用,分肢受压一侧翼缘凸曲变形相互对称且变形明显,而另一分肢以受拉为主、翼缘几无变形。
(3)采用规范GB 50018−2002、JGJ/T 421−2018、NAS 100 − 2016绕强轴压弯承载力计算值表明,试验结果与计算值比值的均值为1.19、1.19、1.11,均偏于安全,其中NAS 100 − 2016的计算值更接近试验结果。绕弱轴压弯承载力计算值表明,试验结果与规范GB 50018−2002、NAS 100 − 2016计算值比值的均值为1.15、1.11,偏于安全;采用规范JGJ/T 421−2018计算绕弱轴压弯承载时取为0.7倍全截面,试验结果与计算值之比的均值为1.64,计算不可靠。因此,当腹板并合Σ形加劲截面试件的双肢能可靠整体协同工作时,计算绕弱轴压弯稳定承载力,不必乘以0.7倍进行折减,建议按拼合整体截面计算。此外,关于绕弱轴压弯承载力计算方法,特别是其他屈曲模式控制时有待进一步试验证实。
-
表 1 试验构件设计
Table 1 Specimens design
压弯长度/mm 自攻钉间距/mm 孔洞位置等分 偏压方向及偏心距/mm 400 300(100、150) − − 1000 300 L/2 S20(40)、W20 1600 300 L/2 S20(40)、W20 2200 300 L/3 S20(40)、W20 注:S为强轴方向;W为弱轴方向。 表 2 试件实测尺寸及初始缺陷
Table 2 Measurements of cross-sections and initial imperfections
试件名称 长度L/mm 腹板h/mm 板厚t/mm 翼缘b/mm 卷边d/mm 开孔大小/mm 加劲肋尺寸/mm 螺钉间距/mm Δ L/mm Δd/mm ws/mm ww/mm 圆心距 半径 Σ400-100-E0-1 397.5 117.05 1.92 80.51 14.70 − − 10.0 10.10 0.35 2.48 2.53 1.66 Σ400-100-E0-2 397.2 117.30 2.04 80.75 14.47 − − 9.9 10.00 0.88 2.35 2.61 0.52 Σ400-150-E0 396.9 117.87 1.92 80.33 15.09 − − 9.8 15.21 0.31 2.07 0.56 0.59 Σ400-300-E0 397.9 120.20 1.91 80.83 15.02 − − 9.7 29.95 0.19 0.90 3.30 0.57 Σ1000-300-S20-1 998.3 123.92 2.08 80.71 14.84 60.21 29.8 9.9 30.02 0.49 0.96 1.92 1.51 Σ1000-300-S20-2 997.5 123.86 2.03 80.91 14.73 60.31 29.5 10.1 29.99 0.83 0.93 0.89 0.48 Σ1000-300-S40-1 999.0 121.96 2.08 80.71 14.69 60.00 30.0 9.9 30.09 0.63 0.02 1.21 0.82 Σ1000-300-S40-2 997.5 123.08 2.01 80.98 14.51 60.94 29.0 9.8 30.08 0.44 0.54 3.00 0.48 Σ1000-300-W20-1 998.9 122.94 2.11 81.32 14.58 60.80 29.1 10.1 30.26 0.69 0.47 0.66 0.72 Σ1000-300-W20-2 998.5 124.50 2.06 80.41 14.43 60.80 29.2 10.1 30.06 1.00 1.25 3.39 0.66 Σ1600-300-S20-1 1598.8 126.33 2.00 81.02 15.09 60.76 28.0 10.1 30.06 0.80 2.17 2.35 0.39 Σ1600-300-S20-2 1598.5 127.07 1.89 80.20 14.83 61.90 28.0 10.2 30.04 0.41 2.54 1.45 0.71 Σ1600-300-S40-1 1600.5 125.83 1.93 80.39 14.30 61.03 29.0 9.5 30.10 0.89 1.92 1.16 0.81 Σ1600-300-S40-2 1588.9 125.81 2.10 80.63 14.44 60.02 30.0 10.2 30.08 1.23 1.91 1.15 0.93 Σ1600-300-W20-1 1599.1 125.07 2.01 80.99 15.01 61.33 29.0 9.8 30.01 1.01 1.54 1.18 1.28 Σ1600-300-W20-2 1600.5 125.83 2.05 80.82 14.75 61.10 29.0 9.9 30.04 0.53 1.92 1.68 0.42 Σ2200-300-S20-1 2198.2 128.15 2.04 80.92 14.77 60.00 29.5 10.1 30.03 1.11 3.08 2.04 0.45 Σ2200-300-S20-2 2199.2 127.40 2.07 80.57 14.71 59.60 29.5 10.0 29.99 1.01 2.70 0.70 1.88 Σ2200-300-S40-1 2198.2 128.70 2.02 81.10 15.17 59.50 29.5 10.6 30.11 1.41 3.35 1.08 1.56 Σ2200-300-S40-2 2195.9 123.84 2.07 81.04 14.87 59.53 29.9 10.7 30.00 1.18 0.92 2.14 1.19 Σ2200-300-W20-1 2198.5 127.80 2.06 80.64 15.37 58.00 30.0 10.3 30.10 0.55 2.90 2.31 1.77 Σ2200-300-W20-2 2197.6 125.50 2.02 80.63 14.98 60.36 29.5 9.7 29.56 0.95 1.75 3.15 5.98 注:400 mm短柱试件未开孔;开孔为长圆孔,圆心距为孔洞两个半圆圆心间距离。 表 3 短柱试件试验结果与中美规范计算值对比
Table 3 Comparison of the test results and the calculation results of Chinese and American standards for short axial compression columns
试件名称 A/mm2 L0/mm L/mm 屈曲部位 破坏模式 半波长/mm Pt/kN PGB/kN PJGJ/T/kN PNAS/kN Pt/PGB Pt/PJGJ/T Pt/PNAS Σ400-100-E0-1 1180.7 462 398 1/2L D(1) 200 430 362.3 362.30 453.8 1.19 1.19 0.95 Σ400-100-E0-2 1255.6 461 397 1/2L D(1) 200 425 362.3 362.30 453.8 1.17 1.17 0.94 Σ400-150-E0 1185.5 461 397 1/2L D(1) 240 422 362.3 362.32 453.8 1.16 1.16 0.93 Σ400-300-E0 1191.5 462 398 1/2L D(1) 200 415 362.3 362.32 453.8 1.15 1.15 0.91 注:A为截面积; L0为试件计算长度; L为试件几何长度;Pt为试验值; PGB为GB 50018−2002计算值; PJGJ/T为JGJ/T 421−2018计算值;PNAS为北美NAS 100−2016计算值。 表 4 压弯试件试验结果与中美规范计算值对比
Table 4 Comparison of the test results and the calculation results of Chinese and American standards for eccentric compressive columns
试件名称 A/mm2 L0/mm L/mm 屈曲部位 破坏模式 半波长/mm Pt/kN PGB/kN PJGJ/T/kN PNAS/kN Pt/PGB Pt/PJGJ/T Pt/PNAS Σ1000-300-S20-1 1310.5 1062 998 3/4L D(2) 400 277 234.1 234.1 263.6 1.18 1.18 1.05 Σ1000-300-S20-2 1279.5 1062 998 3/4L D(2) 400 273 234.1 234.1 263.6 1.17 1.17 1.04 Σ1000-300-S40-1 1301.1 1063 999 3/4L D(2)+L 400 210 190.2 190.2 202.5 1.10 1.10 1.04 Σ1000-300-S40-2 1262.5 1062 998 3/4L D(2) 400 212 190.2 190.2 202.5 1.12 1.12 1.05 Σ1000-300-W20-1 1328.2 1063 999 1/2L D(3)+F 300 224 207.1 145.0 212.7 1.08 1.54 1.05 Σ1000-300-W20-2 1294.4 1063 999 1/2L D(3)+F 300 239 207.1 145.0 212.7 1.16 1.65 1.13 Σ1600-300-S20-1 1274.2 1663 1599 3/4L D(3) 500 269 222.2 222.2 240.6 1.21 1.21 1.12 Σ1600-300-S20-2 1198.8 1662 1599 3/4L D(3)+L 500 271 222.2 222.2 240.6 1.22 1.22 1.13 Σ1600-300-S40-1 1216.7 1665 1601 3/4L D(3) 500 208 178.7 178.7 185.0 1.16 1.16 1.12 Σ1600-300-S40-2 1327.0 1653 1589 3/4L D(3) 500 210 178.7 178.7 185.0 1.18 1.18 1.14 Σ1600-300-W20-1 1275.0 1663 1599 1/2L D(3)+F 500 228 192.4 134.7 195.0 1.19 1.69 1.17 Σ1600-300-W20-2 1300.0 1665 1601 1/2L D(3)+F 500 258 192.4 134.7 195.0 1.34 1.92 1.32 Σ2200-300-S20-1 1304.0 2262 2198 1/2L D(3)+FT 650 260 208.7 208.7 230.2 1.25 1.25 1.13 Σ2200-300-S20-2 1316.0 2263 2199 1/2L D(3)+FT 650 262 208.7 208.7 230.2 1.26 1.26 1.14 Σ2200-300-S40-1 1298.0 2262 2198 1/2L D(3)+FT 650 200 165.6 165.6 176.6 1.21 1.21 1.13 Σ2200-300-S40-2 1307.0 2260 2196 1/2L D(3)+FT 650 209 165.6 165.6 176.6 1.26 1.26 1.18 Σ2200-300-W20-1 1318.0 2263 2199 1/2L D(5)+F 400 192 176.7 123.7 186.4 1.09 1.55 1.03 Σ2200-300-W20-2 1280.0 2262 2198 1/3L D(4)+F 500 183 176.7 123.7 186.4 1.04 1.48 0.98 平均值 1.18 1.34 1.11 标准差 0.073 0.229 0.075 变异系数 0.062 0.171 0.068 注:A为截面积; L0为试件计算长度; L为试件几何长度;Pt为试验值; PGB为GB 50018−2002计算值; PJGJ/T为JGJ/T 421−2018计算值;PNAS为北美NAS 100−2016计算值。 -
[1] 叶露, 王宇航, 石宇, 等. 冷弯薄壁型钢框架-开缝钢板剪力墙力学性能研究[J]. 工程力学, 2020, 37(11): 156 − 166. doi: 10.6052/j.issn.1000-4750.2020.01.0005 YE Lu, WANG Yuhang, SHI Yu, et al. Study on the mechanical properties of cold-formed steel framed shear wall with slits [J]. Engineering Mechanics, 2020, 37(11): 156 − 166. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.01.0005
[2] 吴函恒, 隋璐, 聂少锋, 等. 填充石膏基轻质材料的冷弯型钢复合墙体受剪承载力分析[J]. 工程力学, 2022, 39(4): 177 − 186. doi: 10.6052/j.issn.1000-4750.2021.02.0126 WU Hanheng, SUI Lu, NIE Shaofeng, et al. Study on shear bearing capacity of cold-formed steel composite walls with lightweight gypsum fillings [J]. Engineering Mechanics, 2022, 39(4): 177 − 186. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.02.0126
[3] 徐吉民, 幸坤涛, 高向宇, 等. 锈损冷弯薄壁卷边槽钢短柱受压承载力试验研究[J]. 工程力学, 2021, 38(4): 191 − 199, 210. doi: 10.6052/j.issn.1000-4750.2020.06.0376 XU Jimin, XING Kuntao, GAO Xiangyu, et al. Experimental investigation on compressive bearing capacity of cold-formed thin-walled lipped channel short columns with corrosion [J]. Engineering Mechanics, 2021, 38(4): 191 − 199, 210. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.06.0376
[4] SCHAFER B W. Local, distortional, and Euler buckling of thin-walled columns [J]. Journal of Structural Engineering, 2002, 128(3): 289 − 299. doi: 10.1061/(ASCE)0733-9445(2002)128:3(289)
[5] YOUNG B, CHEN J. Design of cold-formed steel built-up closed sections with intermediate stiffeners [J]. Journal of Structural Engineering, 2008, 134(5): 727 − 737. doi: 10.1061/(ASCE)0733-9445(2008)134:5(727)
[6] MOEN C D. Direct strength design of cold-formed steel members with perforations [D]. Baltimore: Johns Hopkins University, 2008.
[7] GB 50018−2002, 冷弯薄壁型钢结构技术规范 [S]. 北京: 中国标准出版社, 2003. GB 50018−2002, Technical code of cold-formed thin-wall steel structures [S]. Beijing: Standards Press of China, 2003. (in Chinese)
[8] NAS 100−2016, North American specification for the design of cold-formed steel structural members [S]. Washington DC: American Iron and Steel Institute, 2016.
[9] ZHANG J H, YOUNG B. Experimental investigation of cold-formed steel built-up closed section columns with web stiffeners [J]. Journal of Constructional Steel Research, 2018, 147: 380 − 392. doi: 10.1016/j.jcsr.2018.04.008
[10] ZHANG J H, YOUNG B. Finite element analysis and design of cold-formed steel built-up closed section columns with web stiffeners [J]. Thin-Walled Structures, 2018, 131: 223 − 237. doi: 10.1016/j.tws.2018.06.008
[11] LIU J L, LUE D M, LIN C H. Investigation on slenderness ratios of built-up compression members [J]. Journal of Constructional Steel Research, 2009, 65(1): 237 − 248. doi: 10.1016/j.jcsr.2008.02.012
[12] ROY K, MOHAMMADJANI C, LIM J B P. Experimental and numerical investigation into the behaviour of face-to-face built-up cold-formed steel channel sections under compression [J]. Thin-Walled Structures, 2019, 134: 291 − 309. doi: 10.1016/j.tws.2018.09.045
[13] WANG C G, GUO Q L, ZHANG Z N, et al. Experimental and numerical investigation of perforated cold-formed steel built-up I-section columns with web stiffeners and complex edge stiffeners [J]. Advances in Structural Engineering, 2019, 22(10): 2205 − 2221. doi: 10.1177/1369433219836174
[14] KECHIDI S, FRATAMICO D C, SCHAFER B W, et al. Simulation of screw connected built-up cold-formed steel back-to-back lipped channels under axial compression [J]. Engineering Structures, 2020, 206: 110109. doi: 10.1016/j.engstruct.2019.110109
[15] ZHOU T H, LI Y C, REN L J, et al. Research on the elastic buckling of composite webs in cold-formed steel back-to-back built-up columns- Part I: Experimental and numerical investigation [J]. Structures, 2021, 30: 115 − 133. doi: 10.1016/j.istruc.2020.12.059
[16] VY S T, MAHENDRAN M, SIVAPRAKASAM T. Built-up back-to-back cold-formed steel compression members failing by local and distortional buckling [J]. Thin-Walled Structures, 2021, 159: 107224. doi: 10.1016/j.tws.2020.107224
[17] VY S T, MAHENDRAN M. DSM design of fixed-ended slender built-up back-to-back cold-formed steel compression members [J]. Journal of Constructional Steel Research, 2022, 189: 107053. doi: 10.1016/j.jcsr.2021.107053
[18] 何子奇, 杨光, 周绪红, 等. 腹板加劲冷弯薄壁拼合H形钢压弯构件畸变性能试验研究[J]. 建筑结构学报, 2022, 43(10): 237 − 248. HE Ziqi, YANG Guang, ZHOU Xuhong, et al. Experimental investigation on distortional performance of cold-formed steel built-up channel columns with web-stiffeners under eccentric compression [J]. Journal of Building Structures, 2022, 43(10): 237 − 248. (in Chinese)
[19] GB/T 228.1−2010, 金属材料 拉伸试验 第1部分: 室温试验方法 [S]. 北京: 中国标准出版社, 2011. GB/T 228.1−2010, Metallic materials- tensile testing- Part 1: Method of test at room temperature [S]. Beijing: Standards Press of China, 2011. (in Chinese)
[20] 周绪红, 王世纪. 薄壁构件稳定理论及其应用 [M]. 北京: 科学出版社, 2009. ZHOU Xuhong, WANG Shiji. Stability theory and application of thin-walled structure [M]. Beijing: Science Press, 2009. (in Chinese)
[21] JGJ 227−2011, 低层冷弯薄壁型钢房屋建筑技术规程 [S]. 北京: 中国建筑工业出版社, 2011. JGJ 227−2011, Technical specification for low-rise cold-formed thin-walled steel buildings [S]. Beijing: China Building Industry Press, 2011. (in Chinese)
[22] JGJ/T 421−2018, 冷弯薄壁型钢多层住宅技术标准 [S]. 北京: 中国建筑工业出版社, 2018. JGJ/T 421−2018, Technical standard for cold-formed thin-walled light steel multi-storey residential buildings [S]. Beijing: China Building Industry Press, 2018. (in Chinese)
-
期刊类型引用(6)
1. 谢志强,王凯,吴经纬,周大兴,张向东,虞诚,董磊. 锁铆连接冷弯型钢剪力墙受剪性能及其承载力计算方法研究. 工程力学. 2025(05): 228-240 .  本站查看
本站查看
2. 张文福,周呈鑫,邵琰皓. 基于板-梁理论的UHPC-钢三角形薄壁截面组合梁扭转理论及有限元模拟. 苏州科技大学学报(自然科学版). 2025(02): 13-20+37 .  百度学术
百度学术
3. 徐方,袁伟斌. 背对式槽钢组合梁均布荷载下的弯曲应力研究. 四川轻化工大学学报(自然科学版). 2024(02): 93-100 .  百度学术
百度学术
4. 陈明,李恒凯,李补拴,徐立丹,兰涛. 冷弯薄壁型钢T形拼合柱轴压性能研究与承载力计算. 建筑钢结构进展. 2024(07): 14-23 .  百度学术
百度学术
5. 孙军. 新型冷弯薄壁型钢截面设计及横向载荷的性能研究. 工业技术与职业教育. 2023(03): 28-32 .  百度学术
百度学术
6. 姚欣梅,周绪红,李权伦,石宇,管宇,姚斌,王强. 缀板加强冷弯薄壁C形钢受压极限承载力研究. 湖南大学学报(自然科学版). 2023(11): 79-88 .  百度学术
百度学术
其他类型引用(7)



 下载:
下载: