EXPERIMENTAL INVESTIGATION OF PLASMA FLOW CONTROL ON A FLYING WING MODEL BASED ON MICROSECOND PULSED EXCITATION
-
摘要: 为了改善飞翼布局的大迎角气动特性,采用飞翼全模和半模分别在低速和跨声速风洞中开展了微秒脉冲介质阻挡放电等离子体流动控制的试验研究。通过流动显示和测力的试验方法研究了等离子体流动控制的主要作用机制和激励频率与激励电压等对飞翼模型失速特性的影响规律,验证了微秒脉冲介质阻挡放电等离子体流动控制技术从低速到亚声速的有效性,有效的试验最高马赫数Ma达到0.6、雷诺数Re达到3.05×106。试验研究表明:微秒脉冲介质阻挡放电等离子体通过非定常微尺度压缩波扰动的形式作用于翼面流场,通过频率耦合机制减弱模型的前缘分离涡、抑制翼面的流动分离;无量纲频率F+是影响等离子体流动控制效果的重要参数;在低速风洞试验风速V=30 m/s时,无量纲频率F+=0.35~1.06的控制效果较好,可将模型的最大升力系数提高25%以上、失速迎角推迟4°;在跨声速风洞试验马赫数Ma=0.6时,无量纲频率F+=0.22和F+=0.44的控制效果较好,可将模型的最大升力系数分别提高4.72%、4.77%,失速迎角分别推迟2°、1°;激励电压越高激励强度越大、等离子体流动控制效果越好。Abstract: In order to improve the aerodynamic performance of flying wing layout aircrafts at high attack angles , an experimental study of microsecond pulsed dielectric barrier discharge (μs-DBD) plasma flow control was carried out in low-speed and transonic wind tunnels, using both full and half models of a flying wing. Flow visualization and force measurements are deployed to reveal the main mechanisms of plasma flow control and, to analyze the effects of excitation frequency and voltage on the stall characteristics of the flying wing model. The effectiveness of μs-DBD plasma in manipulating low-speed to subsonic flows is successfully verified, with the highest test Mach number and Reynolds number tested being 0.6 and 3.05×106, respectively. Results show that μs-DBD plasma perturbs the model airfoil flow field by unsteady micro-scale compressive wave. These wave perturbations weaken the front separation vortex of the model and suppresses the flow separation by frequency coupling, thus leaving dimensionless frequency as a key parameter which influences the effectiveness of plasma flow control. In a low-speed wind regime (wind speed: 30 m/s), the optimal dimensionless frequency range is 0.35 to 1.06, accompanied by more than 25% in the maximum lift coefficient and 4 degrees postponement in the stall attack angle. As a comparison, in the transonic regime of Mach 0.6, the favorable dimensionless frequency drops to 0.22 and 0.44, with the maximum lift coefficient increased by 4.72% and 4.77%, respectively, and the stall attack angle postponed by 1 and 2 degrees, respectively. Additionally, since the excitation voltage of plasma affects the intensity of the compressive wave perturbation, the higher the excitation voltage is, the better the effect of plasma flow control will be.
-
Keywords:
- fluid mechanics /
- flow control /
- wind tunnel test /
- flow separation /
- plasma /
- flying wing
-
飞翼布局飞行器是一种翼身融合的无尾布局飞行器[1-2],具有气动效率高、结构重量轻、装载空间大、隐身性能好等突出优点[3-5],是未来商用客机、运输机和无人机设计中潜在的最优气动布局方案[6-7]。与三角翼类似,飞翼布局飞行器的升力主要由翼型环量和机翼前缘分离涡两种机制产生[8],由于其机翼前缘一般为钝前缘,前缘分离涡强度远低于战斗机,能够提供的升力有限,且前缘分离涡会诱发翼面出现大面积的流动分离,导致控制舵面失效和飞行器失速等。因此,开展介质阻挡放电(DBD)等离子体流动控制技术抑制翼面流动分离、改善大迎角气动特性的研究,对飞翼布局飞行器的研制具有重要意义[9]。
DBD等离子体是一种新型的主动流动控制技术,能够抑制流动分离、防止附面层转捩、减弱湍流、降低激波干扰等,具有结构简单、重量轻、无运动部件、能耗低、响应快、频带宽、系统兼容性好、流动控制效果显著等突出优点,近年来国内外很多研究机构和学者针对DBD等离子体流动控制技术开展了大量的研究[10]。
KOZLOV等[11]采用DBD等离子体抑制了圆柱体后卡门涡街的脱落,使近场声压级降低14 dB。DENNIS等[12]和VAN等[13-14]在低压涡轮叶片上使用DBD等离子体削弱了叶尖涡、抑制了叶片角区的流动分离,根据雷诺数不同使下游的总压损失减少2%~12%。文献[15-25]在平板、翼型和简化模型上开展了DBD等离子体抑制翼面流动分离的风洞试验研究,研究表明纳秒脉冲(NS-DBD)等离子体与正弦波激励(AS-DBS)等离子体的控制机制不同,不是附面层内的动量输运,而是近璧区边界层内的能量传递和气流快速加热,在Re=1×105附近翼型的最大升力系数可提高25%以上、失速迎角可推迟4°以上,其流动控制效果与基于平均气动弦长(
cA )的无量纲频率(F+=fcA/V ,式中,f为物理激励频率,V为风洞来流风速)有很大关系,研究没有给出其影响的规律性结论。LOPERA等[26]和PETEL等[9]在风洞试验中采用等离子体流动控制技术抑制了1303飞翼模型翼面的流动分离、推迟了模型失速、提升了模型最大升力系数,研究工作验证了等离子体流动控制技术的有效性,但由于试验的风速和雷诺数较低(V=15 m/s、Re=4.3×105),其与飞行器实际工程应用相差较大。KAPAROS等[27]在飞翼模型上进行了等离子体控制前缘涡和抑制流动分离的风洞试验研究,研究指出等离子体是一种高效的流动控制技术,既能抑制飞翼模型的失速,又能使大尺度的涡结构稳定在机身附近,其研究工作基于试验模型平均气动弦长的雷诺数Re为1.4×105。国内李应红等[28-29]、牛中国等[30-32]、刘汝兵等[33-34]、何伟等[35]、ZHAO等[36]、龙玥霄等[37]也相继开展了等离子体抑制模型翼面流动分离的风洞试验研究,验证了等离子体抑制流动分离、推迟模型失速和提高模型最大升力系数的作用,这些研究的试验马赫数Ma低于0.3。
可见,国内外采用等离子体流动控制技术对流动分离控制的研究大多在低速下开展,基于模型平均气动弦长的有效雷诺数在105量级,尚未在亚声速条件下开展改善飞翼模型失速特性的研究,本文的研究将能够弥补这一缺失。
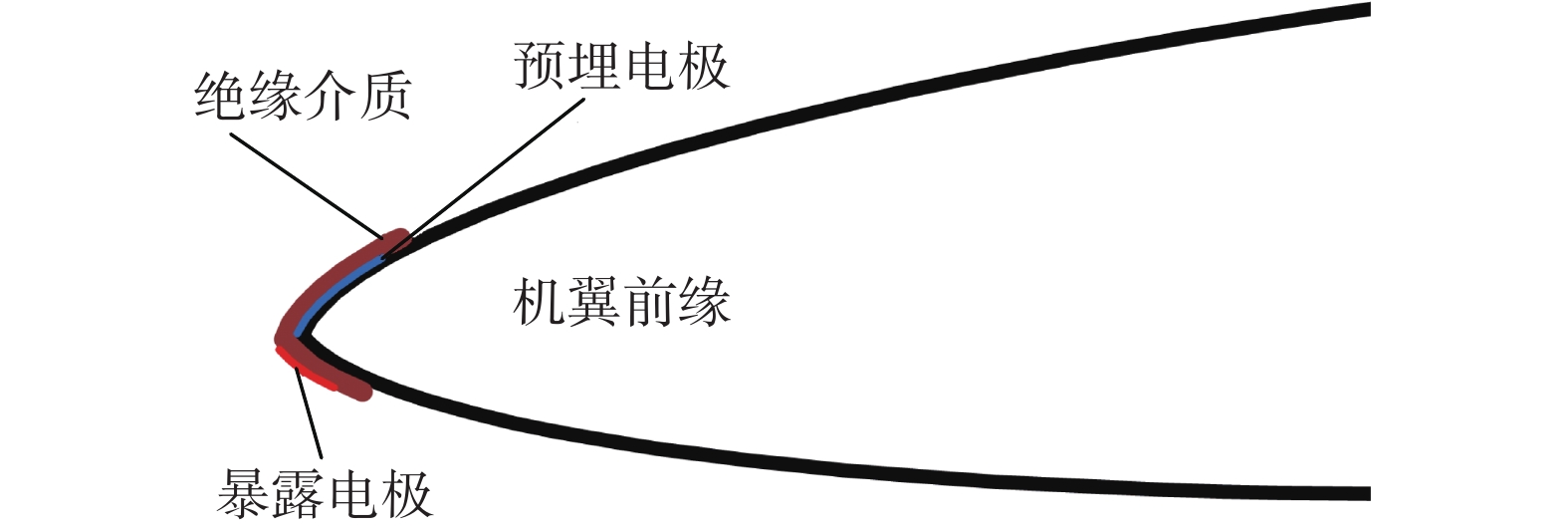
DBD等离子体激励器由暴露电极、预埋电极、绝缘介质和高压激励电源等部分组成,结构原理图如图1所示[37]。在高压电场作用下,暴露电极周围的空气会发生电离,产生等离子体。当高压电场的激励信号为毫秒量级(正弦波半周期或脉冲信号脉冲宽)时,带电粒子在电场力作用下沿电场定向运动,诱导气流产生约为2 m/s~3 m/s沿壁面流动的射流,主要以动量传输的方式实施控制,在低速范围内控制效果较好[10, 17-19];当高压电场的激励信号为纳秒脉冲信号时,在暴露电极附近产生微尺度的压缩波扰动,通过能量传输的方式实施控制[37],HU等[38]将纳秒脉冲激励等离子体的发展分为3个阶段:微秒阶段,对流场的影响表现为压缩波的传播;毫秒阶段,对流场的影响表现为对气体的热扰动;秒阶段,对流场的影响表现为启动涡的诱导阶段,但诱导产生的射流速度非常低。纳秒脉冲等离子体流动控制技术的适用速度范围较广,但同时电磁干扰也相对增强。
微秒脉冲激励与纳秒脉冲激励相比,其脉冲宽度增加、脉冲上升沿和下降沿时间延长,电磁干扰大幅降低[31],更容易实现工程应用。采用微秒脉冲的激励方式既能减小纳秒脉冲等离子体流动控制的电磁干扰,又能在较大速度范围内取得较好的控制效果。本文通过风洞试验研究了微秒脉冲等离子体流动控制的主要作用机制,在低速和亚声速条件下获得了对飞翼模型失速特性的影响规律。
1 实验装置与方法
1.1 低速风洞实验装置与模型
低速风洞试验研究在中国航空工业空气动力研究院FL-5风洞中开展,FL-5风洞是一座开口试验段、单回路、连续式低速风洞。试验段截面为圆形,直径为1.5 m,试验段长1.95 m,空风洞最大风速53 m/s,试验段平均湍流度0.1%。
试验模型为双“W”后缘飞翼模型,模型平均气动弦长0.213 m、参考面积0.157 m2、展弦比5.78。模型为玻璃钢结构,内部金属骨架与天平连接,外部玻璃钢用于粘贴等离子体激励器。天平为内式6分量应变天平,连接模型和风洞半弯刀尾撑支杆。模型在低速风洞中的照片如图2所示。
1.2 跨声速风洞实验装置与模型
等离子体流动控制的亚声速风洞试验研究在中国航空工业空气动力研究院FL-7跨声速风洞中开展,FL-7风洞是一座直流连续式跨声速风洞,入口直接通大气,试验段截面为0.64 m×0.52 m,试验马赫数取0.2~1.5。
试验模型为飞翼半模,气动布局与低速模型相同,模型平均气动弦长0.211 m,半展长0.437 m,参考面积0.066 m2。模型内部为钢骨架,外部敷设玻璃钢。钢骨架与风洞侧壁转盘外的半模天平连接,半模天平为外式5分量应变天平。模型在跨声速风洞中的照片如图3所示。
1.3 等离子体激励器和电源
等离子体激励器采用厚0.1 mm的聚酰亚胺薄膜作为绝缘介质,采用0.02 mm厚的铜箔作为放电电极,预埋电极宽5 mm,暴露电极宽2 mm。等离子体激励器沿展向由机头布置到翼梢,如图2和图3所示,沿弦向布置在机翼前缘,如图4所示。
等离子体电源采用微秒脉冲电源,见图5,其输出波形为正极性脉冲,输出电压幅值0 kV~20 kV连续可调,输出脉冲重复频率1 Hz~1.5 kHz可调,脉冲上升沿10 µs,半高脉宽20 µs,最大输出功率为200 W。等离子体放电参数采用P6015A高压探针和DP04104示波器测量。
1.4 试验方法
1.4.1 测力试验方法
低速风洞和跨声速风洞中测力试验均采用迎角阶梯变化法,使用VXI(VME bus extension for instrumentation)数据采集系统进行天平测力数据采集。试验结束后,根据天平公式和模型参数计算得到气动力系数。低速风洞试验的天平量程和测量误差如表1所示,亚声速风洞试验的天平量程和测量误差如表2所示。
表 1 低速风洞天平量程和相对误差Table 1. Measurement range and relative error of the balance in low speed wind tunnel项目 Y X Z My Mx Mz 天平量程 ±300 ±150 ±100 ±12 ±10 ±12 相对误差/(%) 0.09 0.22 0.30 0.29 0.14 0.11 表 2 亚声速风洞天平量程和相对误差Table 2. Measurement range and relative error of the balance in subsonic wind tunnel项目 Y X My Mx Mz 天平量程 ±5000 ±300 ±84 ±500 ±200 相对误差/(%) 0.06 0.18 0.34 0.08 0.13 测力试验在每一个迎角位置采集600个数据样本,滤波后取平均作为天平测量值,根据天平公式计算出气动力系数,然后对气动力系数进行天平弹性角修正、风洞洞壁干扰修正、风洞轴向静压梯度修正、风洞气流偏角修正和气动力轴系转换等。
1.4.2 PIV试验方法
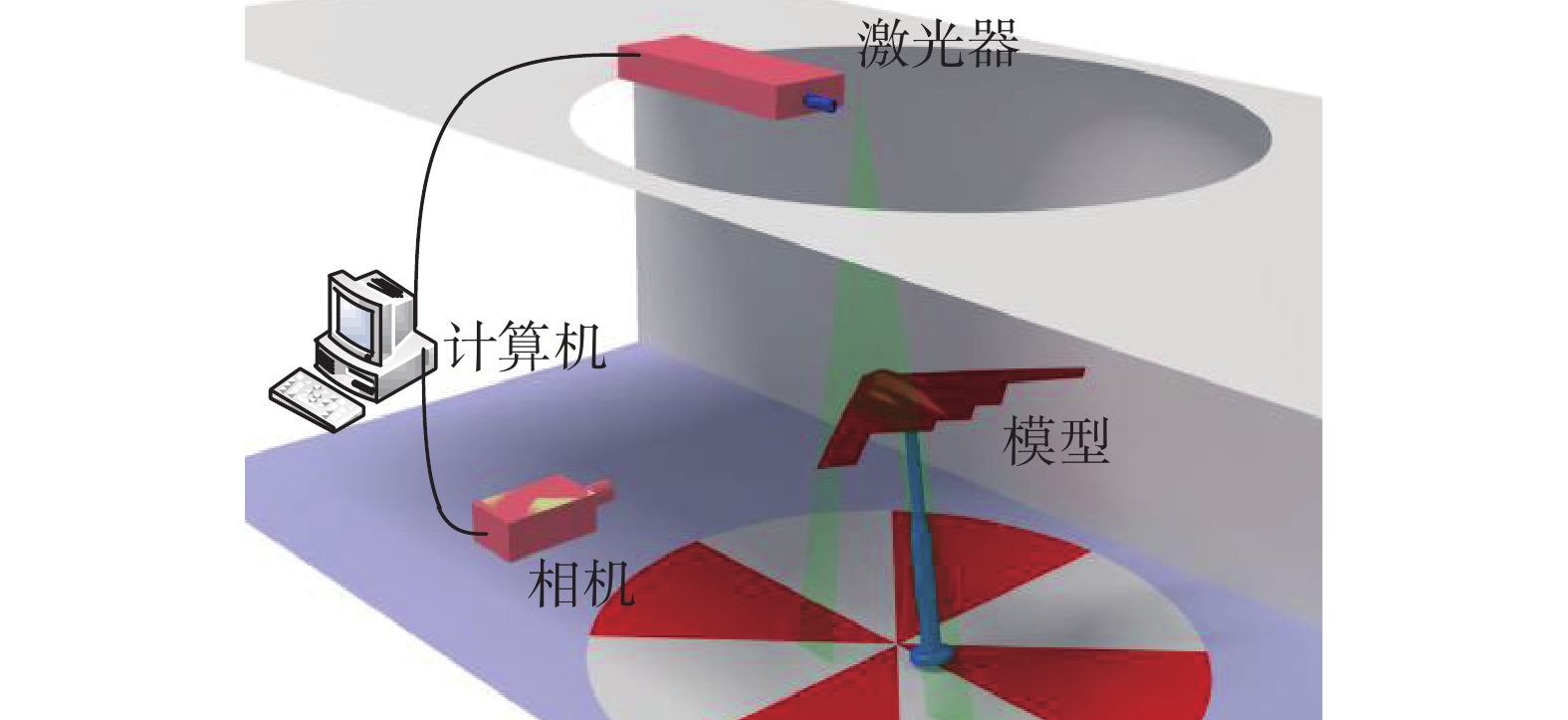
PIV (particle image velocimetry) 试验的激光器为集成式双Nd:YAG激光器,单脉冲能量最大为200 mJ,CCD相机像素为4M(2048 pixel×2048 pixel),灰度分辨率为14 bit,图像采集频率为14 fps(帧/秒)。采用可编程时间控制器PTU实现系统同步,控制信号时间分辨率为0.3 ns。采用Davis 8.3软件进行PIV数据采集与处理。示踪粒子采用压力雾化法产生,粒子介质为橄榄油,粒子直径约2 μm。
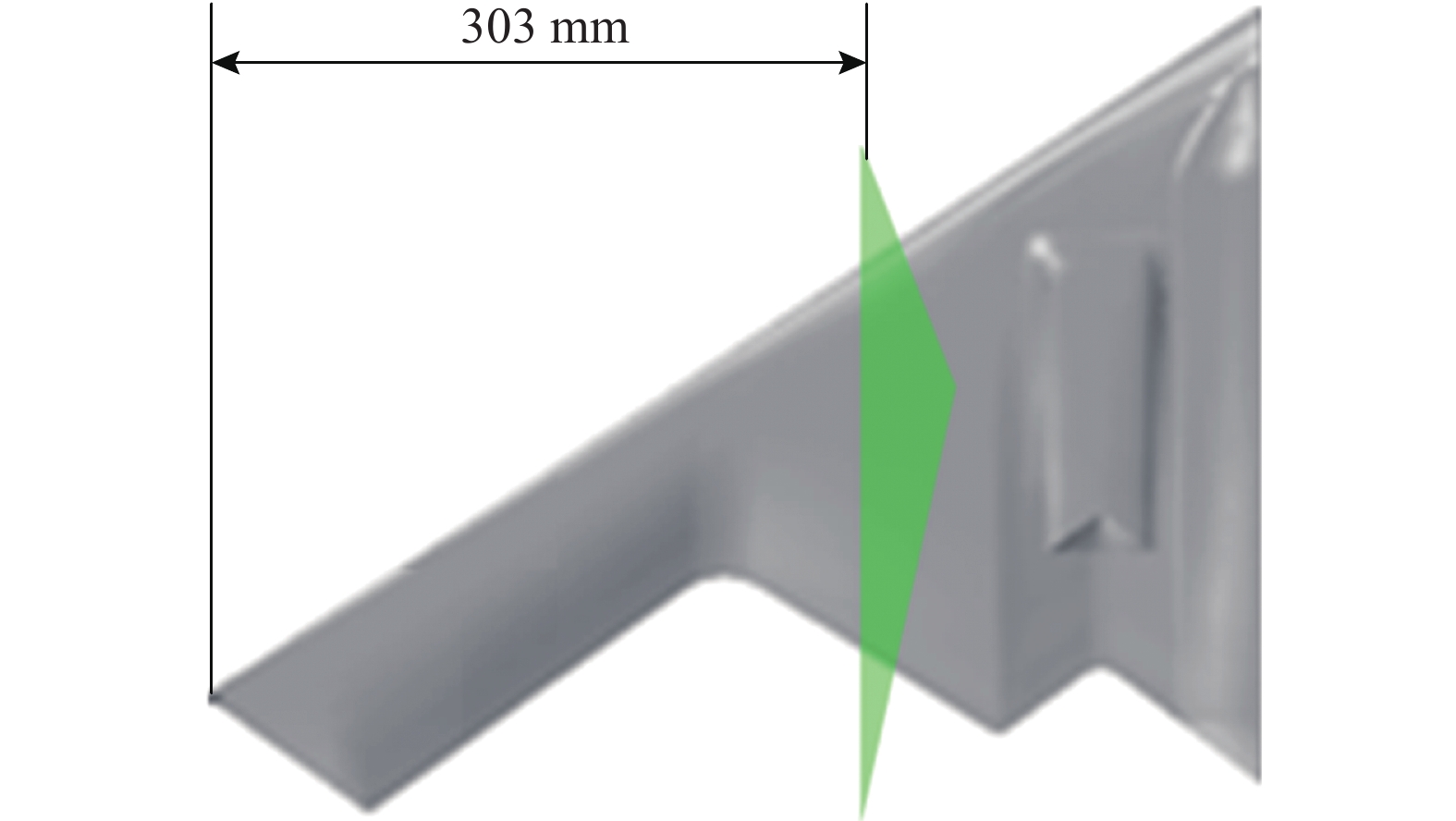
PIV试验主要用于在实验室内测量激励器表面的二维速度矢量场、在FL-5风洞内测量飞翼模型顺气流方向的纵向二维速度矢量场,研究等离子体对静止流场的诱导和对飞翼模型翼面流动分离的抑制。PIV试验一次性采集50组图像,计算后将数据平均得到平均流场,以平均流场作为定常流场进行分析。图6为PIV试验设备在风洞内的布置示意图,激光器安装在风洞上部,激光片光自上而下照射顺气流方向的测量剖面。相机布置在风洞侧面,相机轴线与片光平面垂直,拍摄顺气流方向的粒子图像,PIV测量测量剖面如图7所示,测量剖面距离翼梢303 mm。
1.4.3 纹影试验方法
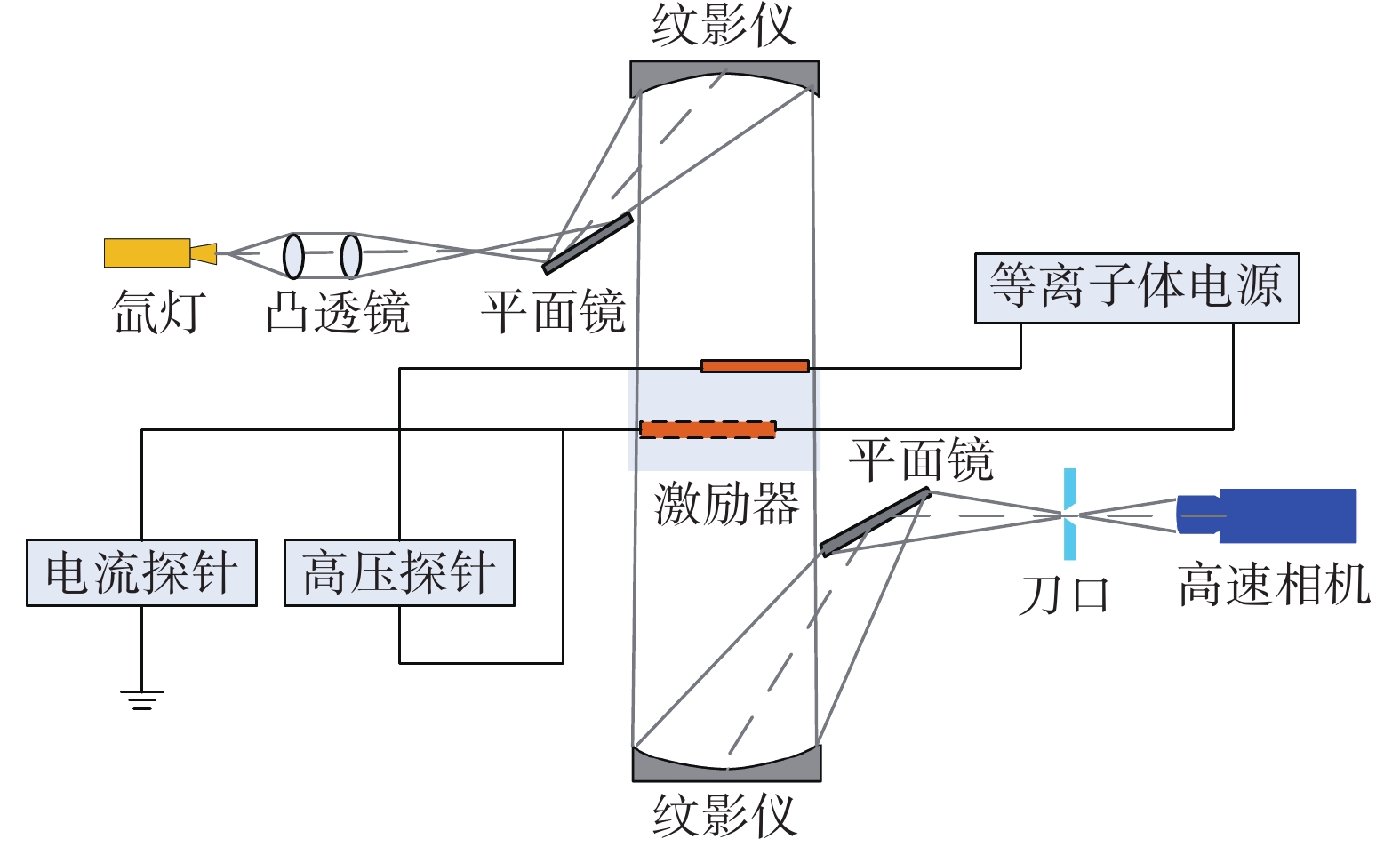
采用高速纹影系统测量等离子体激励器放电时空间流场空气密度的演化过程,高速纹影系统主要包括光源、高速相机、双凹球反射镜、平面镜、刀口等。实验系统光路如图8所示,采用氙灯作为光源,选用高速CCD相机成像,相机在最大分辨率(1280 pixel×800 pixel)下的拍摄帧频为3250 fps,在最小分辨率(128 pixel×8 pixel)下的拍摄帧频为500 000 fps。实验时选取的拍摄分辨率为240×400,帧频为22012 fps,帧间隔为45.43 µs,曝光时间为1 µs。
2 试验结果与讨论
2.1 等离子体激励特性
图9所示为微秒脉冲激励时PIV测量的等离子体激励器表面速度矢量和云图。由图可知,等离子体诱导气流速度最大约为0.07 m/s,显然该速度对模型翼面流场的影响较微弱,这说明动量输运在微秒脉冲等离子体流动控制中起的作用非常小。
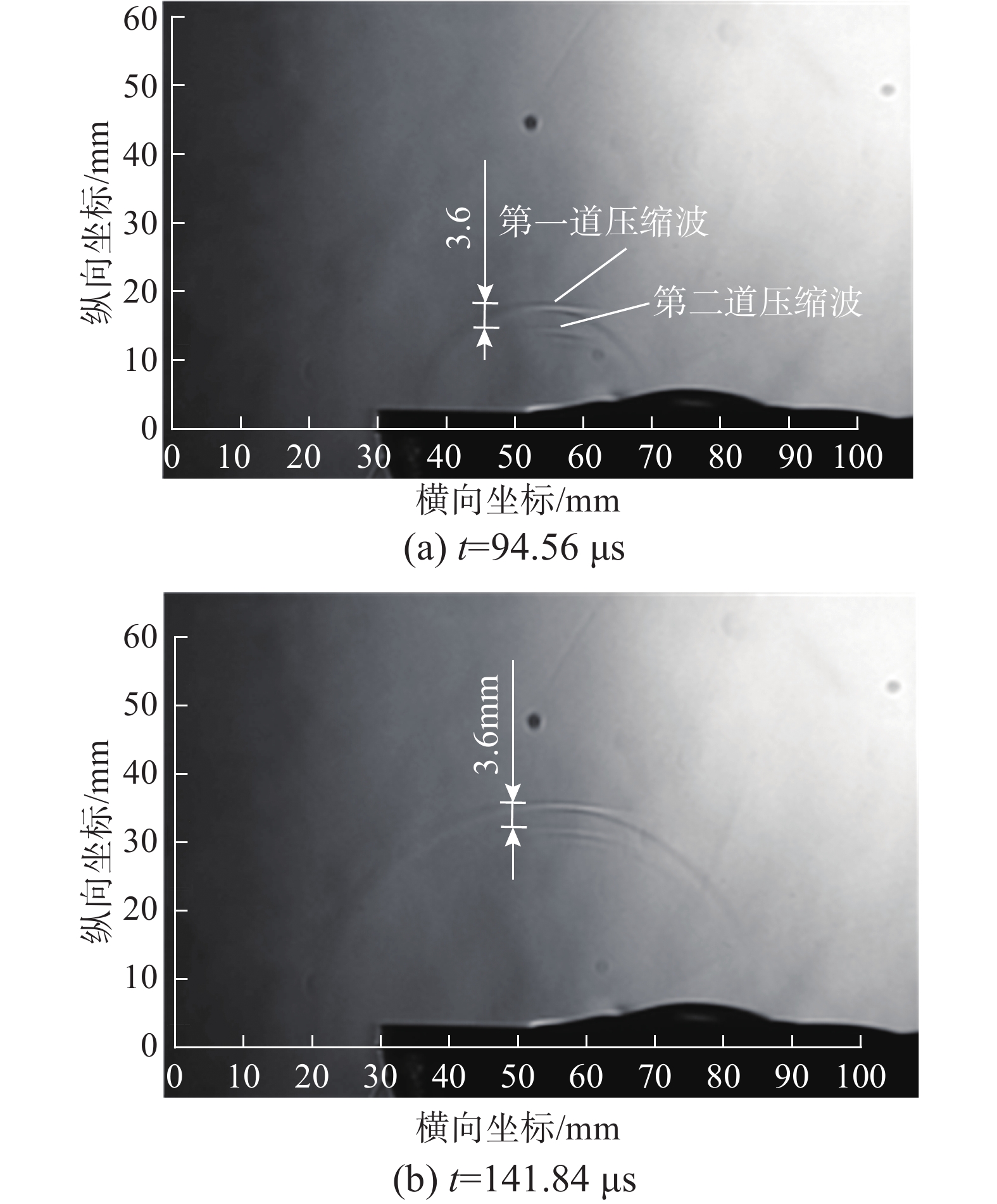
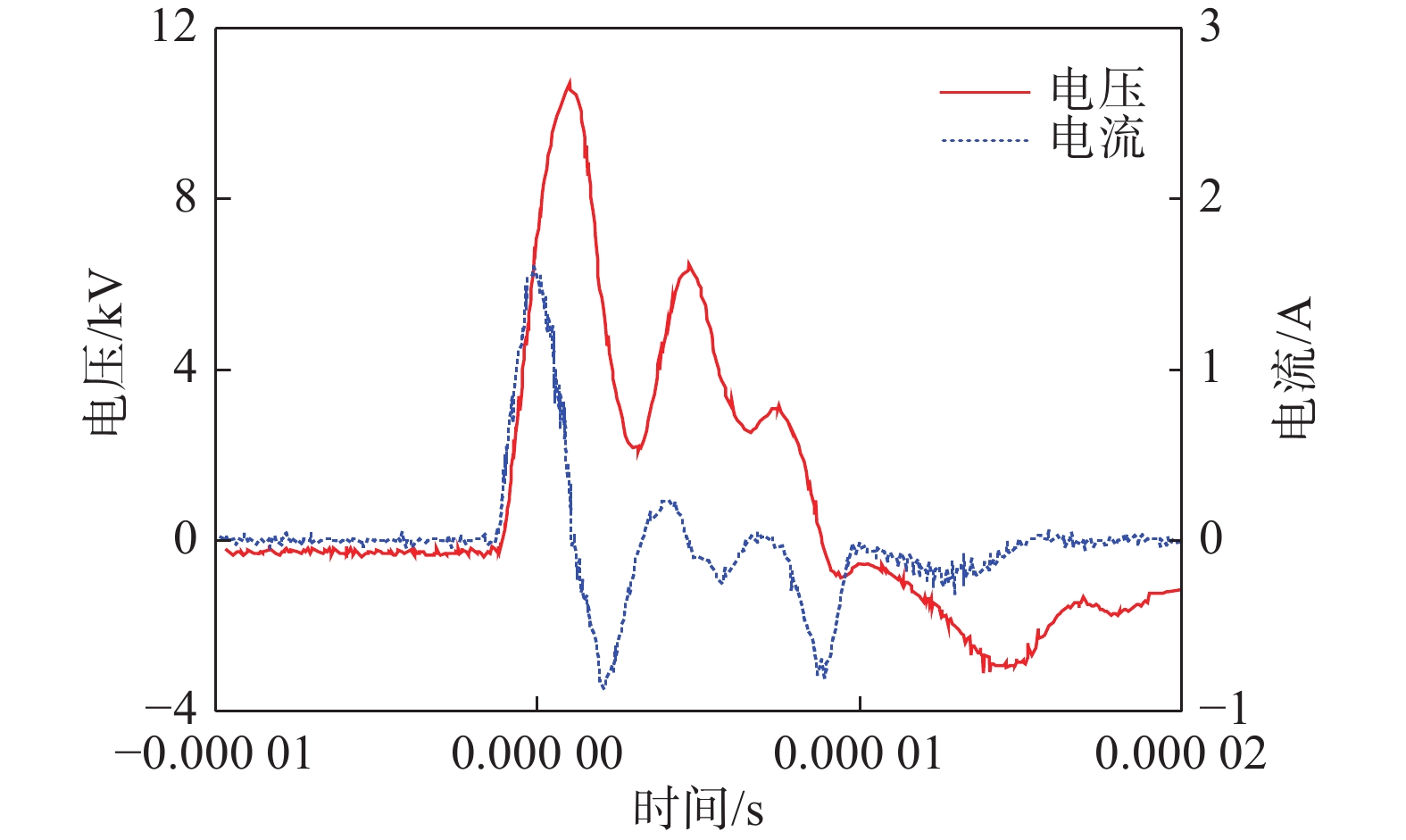
为探索微秒脉冲等离子体流动控制技术的主要作用机制,使用高速纹影测量了等离子体激励器的空间气流密度场。图10所示为连续拍摄的两帧纹影照片,由图可知,等离子体激励器放电后空间流场存在两道压缩波,两道压缩波轮廓随时间不断增大,但两道压缩波的距离保持3.6 mm不变。根据压缩波的传播距离和时间间隔计算出其传播速度约为348 m/s,此时大气温度为29 ℃,气压约为95 kPa,由此计算出当地声速为348.1 m/s,因此该波运动的马赫数Ma为1。纹影图像上之所以出现两道压缩波,是由脉冲放电过程引起的,图11所示为这一试验过程的放电电压和电流波形,由于DBD等离子体放电属于容性放电,当正极性脉冲放电结束后,会进行电容储能并产生负极性脉冲放电现象。根据两道压缩波距离和传播速度可计算出两道激波的放电时间间隔约为10.3 μs,而这一时间正是正极性脉冲和负极性脉冲的相隔时间,这说明使用高速纹影拍摄到的压缩波扰动是合理的。微尺度压缩波主要作用是能量输运,通过微尺度压缩波扰动与流场的耦合实现流动分离控制。
本文采用前面所述的无量纲频率F+研究等离子体激励频率的影响。图12所示为试验风速为20 m/s、模型迎角为18°时PIV试验的速度云图,由图可知,不施加等离子体流动控制时,模型表面存在大面积的流动分离,分离点约在50%当地弦长附近;当U=10 kV、F+=1.06时,等离子体流动控制使分离区的空间尺度大幅减小,形成一个狭长的分离泡结构;当U=10 kV、F+=10.6时,等离子体流动控制对分离区几乎没有影响。可见,等离子体激励频率对流动分离抑制的影响较大。图13所示为对应的涡量云图,由图可知,机翼前缘脱落出一负向涡量,该涡量诱使翼面出现大面积的流动分离区;当施加等离子体的无量纲频率F+=1.06时,该涡量在机翼前缘被打散,相应的翼面流动分离区大幅降低。因此,微秒脉冲等离子体流动控制能够通过微尺度压缩波的频率耦合机制打散前缘分离涡,抑制翼面的流动分离。
2.2 等离子体低速控制特性
图14所示为试验风速V=30 m/s、激励电压U=10 kV时飞翼模型不同激励频率等离子体流动控制的试验曲线。由曲线可知:当迎角
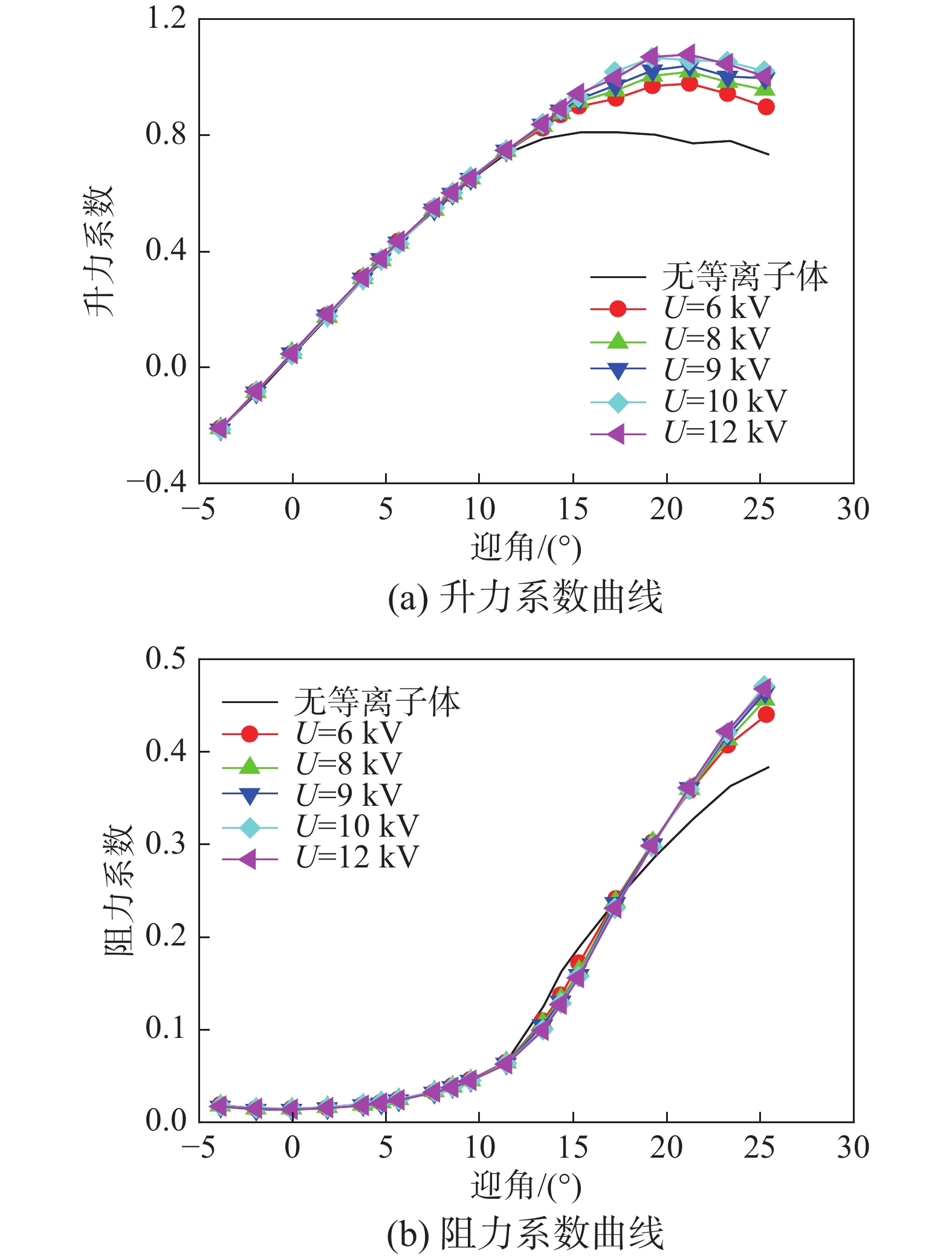
α<12∘ 时,升力系数曲线为线性段,模型翼面流动为附着流动,各条升力系数曲线重合,等离子体流动控制对气动力的影响不大;当迎角α⩾ 时,受前缘负向涡量影响,翼面出现流动分离,升力系数曲线为非线性段,施加等离子体流动控制后非线性升力系数增加、失速迎角推迟,其主要原因是等离子体流动控制打散了前缘涡,延缓了翼面流动分离。等离子体的流动控制效果与频率关系密切,图15为最大升力系数随激励频率的变化曲线,可见,当无量纲频率F+=0.35~1.06时控制效果较好,最大升力系数可提高25%以上,对应的失速迎角可推迟4°;当无量纲频率提高时,等离子体对模型失速特性的改善效果降低。当无量纲频率F+=0.71时,等离子体流动控制效果最好,使模型的最大升力系数提高31%、失速迎角推迟4°。当激励频率一定时,激励电压影响等离子体的扰动强度,图16所示为试验风速V=30 m/s、无量纲激励频率F+=0.71时飞翼模型等离子体流动控制不同激励电压的试验曲线,由曲线可知,在试验的电压范围内,随激励电压的增大等离子体流动控制效果提高,当激励电压升高到一定程度,控制效果的增益逐渐减小,图中U=10 kV时的控制效果和U=12 kV时的控制效果基本一致。在试验中发现,如果采用12 kV的激励电压进行试验,激励器非常容易被击穿,而10 kV的激励电压则能使激励器长期工作。因此,本文选用U=10 kV的激励电压开展研究。
2.3 等离子体控亚声速控制特性
在跨声速风洞马赫数Ma为0.4和0.6时,以模型平均气动弦长为参考长度的雷诺数Re分别为2.03×106和3.05×106。
图17所示为Ma=0.4、激励电压为10 kV时飞翼模型等离子体流动控制不同频率的试验曲线,由曲线可知,与低速试验结果类似,等离子体流动控制能够改善模型的大迎角气动特性,提高模型的最大升力系数和推迟失速;等离子体无量纲频率F+为0.33、0.66和0.99时,飞翼模型的最大升力系数分别提高7.74%、7.22%、3.22%,失速迎角分别推迟8°、6°、6°,无量纲频率F+为0.33和0.66时控制效果较好。图18所示为Ma=0.6、激励电压为10 kV时,飞翼模型等离子体流动控制不同频率的试验曲线,由曲线可知,无量纲频率F+为0.22和0.44时,模型最大升力系数分别提高4.72%、4.77%,失速迎角分别推迟2°、1°。可见,亚声速等离子体流动控制规律与低速存在一定差异,这可能是气流压缩性的影响,其适用的无量纲频率要更低一些。产生这一效果的主要机制和原因还有待进一步的研究。
3 结论
本文采用PIV、高速纹影和测力等试验方法,在低速和亚声速范围内研究了微秒脉冲等离子体对流场和飞翼模型气动特性的影响,主要结论如下:
(1) 微秒脉冲等离子体以非定常微尺度压缩波强扰动的形式作用于流场,该扰动能够减弱或打散飞翼模型前缘的负向涡量、抑制翼面的流动分离、减弱翼面流动分离区。
(2) 无量纲频率 F+是影响等离子体流动控制的重要参数,特定频率 下等离子体与流场的耦合能够有效改善飞翼模型失速特性、提高模型的最大升力系数和失速迎角,激励电压越高控制效果越好。
(3) 本文在低速和亚声速下,验证了等离子体流动控制技术改善飞翼模型失速特性的有效性和普适性,提升了其工程应用价值。但要实现等离子体流动控制技术在飞行器上的应用,还需要解决等离子体与飞行器相结合的气动设计、等离子体设备小型化、等离子体装机适配性等问题,这也是今后研究的重点方向。
-
表 1 低速风洞天平量程和相对误差
Table 1 Measurement range and relative error of the balance in low speed wind tunnel
项目 Y X Z My Mx Mz 天平量程 ±300 ±150 ±100 ±12 ±10 ±12 相对误差/(%) 0.09 0.22 0.30 0.29 0.14 0.11 表 2 亚声速风洞天平量程和相对误差
Table 2 Measurement range and relative error of the balance in subsonic wind tunnel
项目 Y X My Mx Mz 天平量程 ±5000 ±300 ±84 ±500 ±200 相对误差/(%) 0.06 0.18 0.34 0.08 0.13 -
[1] WOOD R M, BAUER S X S. Flying wings/Flying fuselages [C]. Reno: 39th AIAA Aerospace Sciences Meeting & Exhibit, 2001.
[2] LEHMKUEHLER K, WONG K C, VERSTRAETE D. Design and test of a UAV blended wing body configuration [C]. Brisbane: 28th Congress of the International Council of the Aeronautical Sciences, 2012.
[3] PATIL M J, HODGES D H. Flight dynamics of highly flexible flying wings [J]. Journal of Aircraft, 2006, 43(6): 1790 − 1798.
[4] XU X P, ZHOU Z. Active separation control for the flying-wing UAV using synthetic jet [J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(4): 497 − 504.
[5] 张子健, 安国锋, 刘斌. 飞翼飞行器气动伺服弹性耦合动力学特性研究[J]. 工程力学, 2014, 31(11): 231 − 236. doi: 10.6052/j.issn.1000-4750.2013.05.0426 ZHANG Zijian, AN Guofeng, LIU Bin. Investigation of aeroservoelatic dynamic characteristics of elastic flight-wings [J]. Engineering Mechanics, 2014, 31(11): 231 − 236. (in Chinese) doi: 10.6052/j.issn.1000-4750.2013.05.0426
[6] 张庆, 叶正寅. 排式双翼布局低雷诺数气动特性计算研究[J]. 工程力学, 2019, 36(10): 244 − 256. doi: 10.6052/j.issn.1000-4750.2018.09.0514 ZHANG Qing, YE Zhengyin. Computational investigations for aerodynamic characteristic analysis of low renolds number doubly-tandem wing configurations [J]. Engineering Mechanics, 2019, 36(10): 244 − 256. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.09.0514
[7] 安朝, 谢长川, 孟杨, 等. 多体组合式无人机飞行力学稳定性分析及增稳控制研究[J]. 工程力学, 2021, 38(11): 248 − 256. doi: 10.6052/j.issn.1000-4750.2020.11.0820 AN Chao, XIE Changchuan, MENG Yang, et al. Flight dynamics and stable control analyses of multi-body aircraft [J]. Engineering Mechanics, 2021, 38(11): 248 − 256. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.11.0820
[8] NANGIA R K, PALMER M E. Flying wings (Blended Wing Bodies) with AFT- & forward- sweep relating design camber & twist to longitudinal control [C]// Monterey, California: AIAA Atmospheric Flight Mechanics Conference & Exhibit, 2002: AIAA 2002-4616. https://doi.org/10.2514/6.2002-4616
[9] PATEL M P, NG T T, VASUDEVAN S, et al. Plasma actuators for hingeless aerodynamic control of an unmanned air vehicle [J]. Journal of Aircraft, 2007, 44(4): 1264 − 1274. doi: 10.2514/1.25368
[10] WANG J J, CHOI KWING-SO, FENG L H, et al. Recent developments in DBD plasma flow control [J]. Progress in Aerospace Sciences, 2013, 62(4): 52 − 78.
[11] KOZLOV A V, THOMAS F O. Active noise control of bluff-body flows using dielectric barrier discharge plasma actuators [C]// 30th AIAA Aeroacoustics Conference. Miami, Florida, AIAA, 2009. DOI: 10.2514/6.2009-3245
[12] DENNIS K, SUZEN Y B. Simulations of plasma flow control in low-pressure turbines [C]// 46th AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada, AIAA, 2008. DOI: 10.2514/6.2008-543
[13] VAN NESS II D K, CORKE T C, MORRIS S C. Tip clearance flow control in a linear turbine cascade using plasma actuation [C]// 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition. Orlando, Florida, AIAA, 2009. DOI: 10.2514/6.2009-300
[14] VAN NESS II D K, CORKE T C, MORRIS S C. Turbine tip clearance flow control using plasma actuators [C]// 44th AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada, AIAA, 2006. DOI: 10.2514/6.2006-21
[15] LITTLE J, TAKASHIMA K, NISHIHARA M, et al. Separation control with nanosecond-pulse-driven dielectric barrier discharge plasma actuators [J]. AIAA Journal, 2012, 50(50): 350 − 365.
[16] GRUNDMANN S, TROPEA S. Delay of boundary-layer transition using plasma actuators [C]// 46th AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada, AIAA, 2008. DOI: 10.2514/6.2008-1369
[17] ROTH J R, SHERMAN D M, WILKINSON S P. Boundary layer flow control with a one atmosphere uniform glow discharge surface plasma [C]// 36th AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada, AIAA, 1998. DOI: 10.2514/6.1998-328
[18] ROTH J R. Aerodynamic flow acceleration using paraelectric and peristaltic electrohydrodynamic effects of a one atmosphere uniform glow discharge plasma [J]. Physics of Plasmas, 2003, 10(5): 2117 − 2126. doi: 10.1063/1.1564823
[19] SEIFERT A, PACK L G. Oscillatory excitation of unsteady compressible flows over airfoils at flight Reynolds numbers [C]// 37th Aerospace Sciences Meeting and Exhibit. Reno, Nevada, AIAA, 1999. DOI: 10.2514/6.1999-925
[20] POST M L, CORKE T C. Separation control on high angle of attack airfoil using plasma actuators [J]. AIAA Journal, 2012, 42(11): 2177 − 2184.
[21] PATEL M P, SOWLE Z H, CORKE T C, et al. Autonomous sensing and control of wing stall using a smart plasma slat [J]. Journal of Aircraft, 2007, 44(2): 516 − 527. doi: 10.2514/1.24057
[22] ROUPASSOV D V, NIKIPELOV A A, NUDNOVA M M, et al. Flow separation control by plasma actuator with nanosecond pulse-periodic discharge [J]. AIAA Journal, 2009, 47(1): 168 − 185. doi: 10.2514/1.38113
[23] RETHMEL C. Airfoil leading edge flow separation control using nanosecond pulse dbd plasma actuators [D]. USA: Department of Mechanical Engineering, The Ohio State University, 2011.
[24] YADALA S, HEHNER M T, SERPIERI J, et al. Swept-wing transition control using DBD plasma actuators [C]// 2018 Flow Control Conference. Atlanta, Georgia, AIAA, 2018. DOI: 10.2514/6.2018-3215
[25] PESCINI E, FRANCIOSO L, GIORGI M G D, et al. Investigation of a micro dielectric barrier discharge plasma actuator for regional aircraft active flow control [J]. IEEE Transactions on Plasma Science, 2015, 43(10): 3668 − 3680. doi: 10.1109/TPS.2015.2461016
[26] LOPERA J, NG T T, CORKE T C. Aerodynamic control of 1303 UAV using windward surface plasma actuators on a separation ramp [J]. Journal of Aircraft, 2007, 44(44): 1889 − 1895.
[27] KAPAROS P, KOLTSAKIDIS S, PANAGIOTOU P, et al. Experimental investigation of DBD plasma actuators on a BWB aerial vehicle model [C]// 2018 Flow Control Conference. Atlanta, Georgia, AIAA, 2018. DOI: 10.2514/6.2018-4028
[28] ZHAO G, LI Y, HUA L, et al. Flow separation control on swept wing with nanosecond pulse driven DBD plasma actuators [J]. Chinese Journal of Aeronautics, 2015, 28(2): 368 − 376.
[29] 李应红, 梁华, 马清源, 等. 脉冲等离子体气动激励抑制翼型吸力面流动分离的实验[J]. 航空学报, 2008, 30(6): 1429 − 1435. LI Yinghong, LIANG Hua, MA Qingyuan, et al. Experimental investigation on airfoil suction side flow separation by pulse plasma aerodynamic actuation [J]. Acta Aeronauticaet Astronautica Sinica, 2008, 30(6): 1429 − 1435. (in Chinese)
[30] 牛中国, 赵光银, 梁华, 等. 三角翼DBD等离子体流动控制研究进展[J]. 航空学报, 2019, 40(3): 022201. NIU Zhongguo, ZHAO Guanggen, LIANG Hua, et al. A review of vortical flow control over delta wings using DBD plasma actuation [J]. Acta Aeronauticaet Astronautica Sinica, 2019, 40(3): 022201. (in Chinese)
[31] 牛中国, 胡秋琦, 梁华, 等. 飞翼模型微秒脉冲等离子体控制低速风洞试验研究[J]. 推进技术, 2019, 40(12): 2816 − 2826. NIU Zhongguo, HU Qiuqi, LIANG Hua, et al. Study of low speed wind tunnel test using microsecond pulsed plasma actuation on flying wing model [J]. Journal of Propulsion Technology, 2019, 40(12): 2816 − 2826. (in Chinese)
[32] NIU Z, LIU J, LIANG H, et al. Flying wing flow separation control by microsecond pulsed dielectric barrier discharge at high Reynolds number [J]. AIP Advances 9, 2019: 125120. doi: 10.1063/1.5125847
[33] 刘汝兵, 牛中国, 王萌萌, 等. 等离子体射流控制机翼气动力矩的实验研究[J]. 工程力学, 2016, 33(3): 232 − 238. doi: 10.6052/j.issn.1000-4750.2014.07.0631 LIU Rubing, NIU Zhongguo, WANG Mengmeng, et al. Aerodynamic moments control of wing model using plasma jet [J]. Engineering Mechanics, 2016, 33(3): 232 − 238. (in Chinese) doi: 10.6052/j.issn.1000-4750.2014.07.0631
[34] 刘汝兵, 孙伟, 牛中国, 等. 火花放电等离子体射流实验研究[J]. 推进技术, 2015, 36(3): 372 − 377. LIU Rubing, SUN Wei, NIU Zhongguo, et al. Experimental investigation on spark discharge plasma jet [J]. Jounal of Propulsion Technology, 2015, 36(3): 372 − 377. (in Chinese)
[35] 何伟, 牛中国, 潘波, 等. 等离子抑制翼尖涡实验研究[J]. 工程力学, 2013, 30(5): 277 − 281. doi: 10.6052/j.issn.1000-4750.2011.10.0718 HE Wei, NIU Zhongguo, PAN Bo, et al. Study on experiments for suppressing wingtip vortices with plasma [J]. Engineering Mechanics, 2013, 30(5): 277 − 281. (in Chinese) doi: 10.6052/j.issn.1000-4750.2011.10.0718
[36] ZHAO Z, LI J, ZHENG J, et al. Study of shock and induced flow dynamics by nanosecond dielectric-barrier-discharge plasma actuators [J]. AIAA Journal, 2014, 53(5): 1336 − 1348.
[37] 龙玥霄, 刘国政, 孟宣市, 等. 飞翼布局纵向气动特性的等离子体激励控制[J]. 高电压技术, 2018, 44(9): 3049 − 3057. LONG Yuexiao, LIU Guozheng, MENG Xuanshi, et al. Longitudinal aerodynamic control over flying wing using plasma actuators [J]. High Voltage Engineering, 2018, 44(9): 3049 − 3057. (in Chinese)
[38] HU H, LI H, MENG X, et al. Phase-locked schlieren of periodic nanosecond-pulsed DBD actuation in quiescent air [C]// 54th AIAA Aerospace Sciences Meeting. San Diego, California, AIAA, 2016. DOI: 10.2514/6.2016-1696.
-
期刊类型引用(2)
1. 牛中国,刘捷,胡秋琦,梁华. 基于压力反馈的等离子体主动流动控制试验. 航空动力学报. 2024(03): 74-81 .  百度学术
百度学术
2. 郝春阳,董祥瑞,蔡天意,周骛,蔡小舒. 基于多特征提取的合成射流涡流控制机理研究. 工程力学. 2024(11): 225-237 .  本站查看
本站查看
其他类型引用(5)






 下载:
下载: