STRUCTURAL INFLUENCE LINE IDENTIFICATION: INVERSE PROBLEM IDENTIFIABILITY ANALYSIS AND REDUCED-DIMENSION BAYESIAN UNCERTAINTY QUANTIFICATION
-
摘要: 结构影响线识别是移动荷载下既有结构评估的理论基础，其本质上是基于系统输入-输出含噪数据反向对静力系统指定截面的响应函数进行识别。已有研究虽然取得了进展，但它们在以下两个方面存在局限性：缺乏反问题可识别性分析；缺乏不确定性量化。反问题可识别性分析是为了厘清系统识别的参数的解的情况。不确定性量化是基于测量输入-输出含噪数据估计影响线参数的后验概率密度函数。针对上述两个局限性，该文在贝叶斯概率框架的基础上开展关于影响线识别的反问题可识别性分析与贝叶斯不确定性量化。该文进行基于直接参数化的影响线识别，包括系统输入与输出、反问题可识别性分析、参数最优值。经分析得出：一方面，直接参数化无法保证全局模型可识别；另一方面，现有方法即使是全局模型可识别的情况下也无法进行不确定性量化。为保证反问题是全局模型可识别且同时获取参数后验概率密度函数，该文提出基于降维贝叶斯不确定性量化的影响线后验识别，包括系统输入与输出重构、反问题可识别性分析、后验概率密度函数。该文进行模拟数据下新光大桥吊杆拉力影响线识别，与实测及模拟数据下简支梁桥应变影响线识别，验证提出方法的有效性。Abstract: Structural influence line identification is the theoretical basis of evaluation for an existing structure under moving loads, which is essentially to identify the response function of a specified section of a static system based on finite dimensional input-output noisy data. Despite progress in previous researches, there are limitations in two aspects, i.e., lack of identifiability analysis of inverse problem and lack of Uncertainty Quantification (UQ). The identifiability analysis of the inverse problem is to clarify the solution situation of the parameters. UQ is to estimate the posterior probability density function (PDF) of the influence line based on the measured input-output noisy data. For these two limitations, this paper conducts the inverse problem identifiability analysis and Bayesian UQ of influence line identification based on Bayesian probability framework. This paper identifies influence lines based on direct parameterization, including system input and output, inverse problem identifiability analysis and optimal values of parameters. The results show that: direct parameterization cannot guarantee that the model is globally model-identifiable; even if the model is globally model-identifiable, the existing methods can only obtain the optimal values of the parameters. In order to ensure the globally model-identifiable case and to obtain the posterior PDF of the parameters simultaneously, the posterior identification of influence lines based on reduced-dimension Bayesian UQ is proposed, including system input and output reconstruction, inverse problem identifiability analysis and posterior PDF. The effectiveness of the proposed method is verified by identifying the influence lines of the suspender force of the Xinguang Bridge using simulated data, and the influence lines of the strain of a simply supported beam bridge using measured and simulated data.
-
-
![]()
图 2 不同工况的识别影响线后验最优值与后验95%置信区间
Figure 2. Posterior optimal values and 95% confidence intervals of identified influence lines of different cases
![]()
图 3 不同工况下识别影响线的残差绝对值与标准差箱线图
Figure 3. Box plots of absolute values of residuals and standard deviations of identified influence lines of different cases
![]()
图 4 m2-Q20-d80工况下不同参数位置间隔长度的识别影响线的残差绝对值与标准差箱线图
Figure 4. Box plots of absolute values of residuals and standard deviations of identified influence lines by different interval lengths of position of parameter under the case of m2-Q20-D80
![]()
图 5 实测数据和模拟数据下三种方法的识别影响线
Figure 5. Identified influence lines by three different methods using measured and simulated datasets
![]()
图 6 模拟数据下三种方法的识别影响线的残差绝对值与标准差箱线图
Figure 6. Box plots of absolute values of residuals and standard deviations of identified influence lines by three different methods using simulated datasets
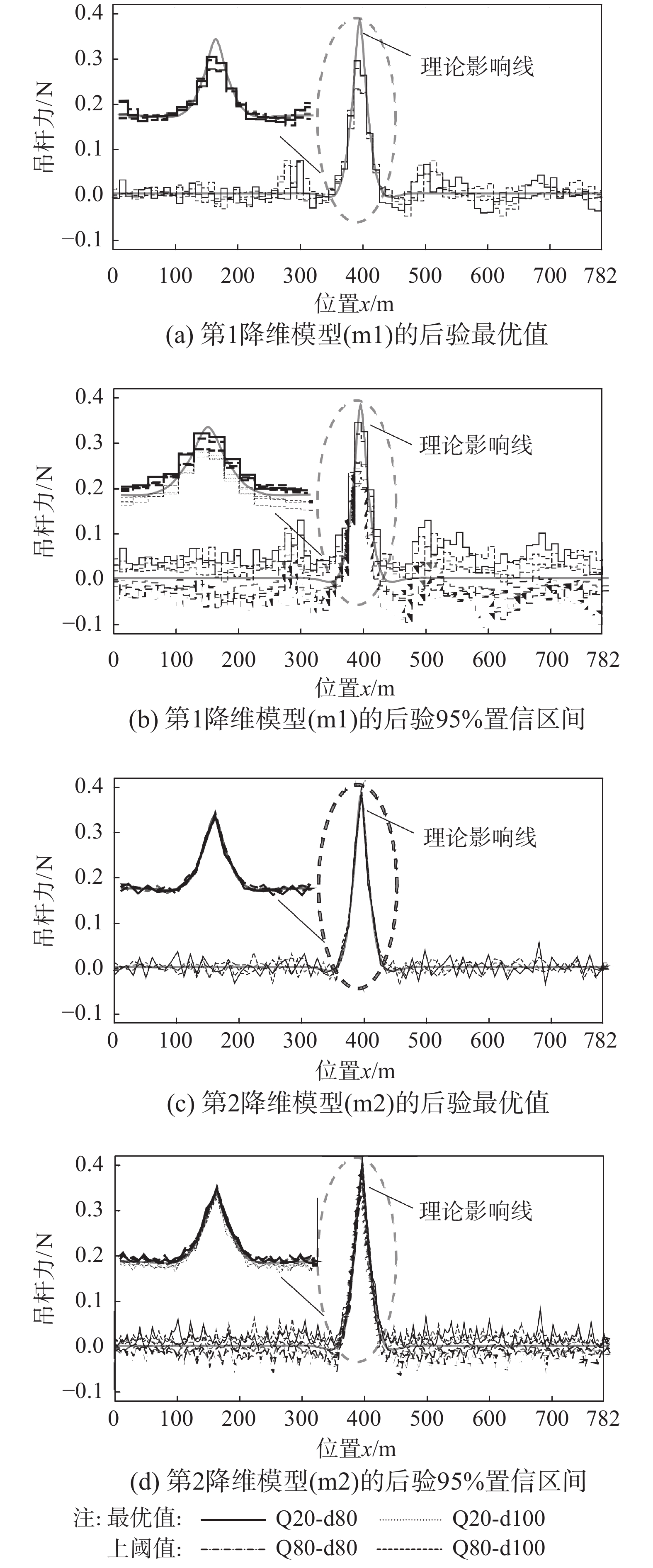
表 1 车辆荷载工况与降维贝叶斯方法参数工况
Table 1 Different cases of vehicle loads and parameters of reduced-dimension Bayesian uncertainty quantification
目的 车辆荷载工况 降维贝叶斯方法参数工况 车队车辆
数工况车间距
工况降维模
型种类影响线参数位置
间隔长度Δx/m检验不同车辆荷载
工况下降维贝叶斯方
法的有效性Q20 d80 m1 10 Q20 d100 m1 10 Q80 d80 m1 10 Q80 d100 m1 10 Q20 d80 m2 10 Q20 d100 m2 10 Q80 d80 m2 10 Q80 d100 m2 10 探索影响线参数位置
间隔长度对降维贝叶斯
方法识别效果的影响Q20 d80 m2 5 Q20 d80 m2 20 Q20 d80 m2 40 Q20 d80 m2 80 
下载: 导出CSV
-
[1] HOZHABROSSADATI S M, SANI A A. Application of green’s functions for constructing influence lines [J]. Journal of Engineering Mechanics, 2016, 142(3): 04015097. doi: 10.1061/(ASCE)EM.1943-7889.0001016
[2] ZHENG X, YANG D H, YI T H, et al. Development of bridge influence line identification methods based on direct measurement data: A comprehensive review and comparison [J]. Engineering Structures, 2019, 198: 109539.
[3] LIU Y S, WANG X Q, ZHOU F X. Study on damage identification of the simply supported beam employ the difference of deflection influence line under symmetrically load [J]. Applied Mechanics and Materials, 2012, 166(169): 1254 − 1257.
[4] CHEN Z W, CAI Q L, ZHU S Y. Damage quantification of beam structures using deflection influence lines [J]. Structural Control and Health Monitoring, 2018, 25(11): 1 − 17.
[5] ZHU S Y, CHEN Z W, CAI Q L, et al. Locate damage in long-span bridges based on stress influence lines and information fusion technique [J]. Advances in Structural Engineering, 2014, 8(17): 1089 − 1102.
[6] ZHOU Y, DI S K, XIANG C S, et al. Damage identification in simply supported bridge based on rotational-angle influence lines method [J]. Transactions of Tianjin University, 2018, 24(6): 587 − 601. doi: 10.1007/s12209-018-0135-9
[7] REN W X, FANG S E, DENG M Y. Response surface-based finite-element-model updating using structural static responses [J]. Journal of Engineering Mechanics, 2011, 137(4): 248 − 257. doi: 10.1061/(ASCE)EM.1943-7889.0000223
[8] LIAO J B, TANG G W, MENG L B, et al. Finite element model updating based on field quasi-static generalized influence line and its bridge engineering application [J]. Procedia Engineering, 2012, 31: 348 − 353. doi: 10.1016/j.proeng.2012.01.1035
[9] XIAO X, XU Y L, ZHU Q. Multiscale modeling and model updating of a cable-stayed bridge. II: model updating using modal frequencies and influence lines [J]. Journal of Bridge Engineering, 2015, 20(10): 04014113. doi: 10.1061/(ASCE)BE.1943-5592.0000723
[10] MOSES F. weight-in-motion system with instrumented bridge [J]. Journal of Transportation Engineering, 1979, 105(3): 233 − 249.
[11] PETERSEN D R, LINK R E, MCNULTY P, et al. Testing of bridge weigh-in-motion system in a sub-arctic climate [J]. Journal of Testing and Evaluation, 2003, 31(6): 497 − 506.
[12] LILJENCRANTZ A, OLOFSSON P, OLOFSSON P. Implementing bridge weigh-in-motion for railway traffic [J]. Computers and Structures, 2006, 85(1/2): 80 − 88.
[13] O'BRIEN E J, QUILLIGAN M J, KAROUMI R. Calculating an influence line from direct measurements [J]. Journal of Bridge Engineering, 2006, 159(1): 31 − 34.
[14] YAMAGUCHI E, KAWAMURA S, MATUSO K, et al. Bridge-Weigh-in-Motion by two-span continuous bridge with skew and heavy-truck flow in Fukuoka area, Japan [J]. Advances in Structural Engineering, 2009, 12(1): 115 − 125. doi: 10.1260/136943309787522614
[15] 王宁波, 任伟新, 何立翔. 基于桥梁动力响应的应变影响线提取[J]. 中南大学学报(自然科学版), 2014, 45(12): 4362 − 4369. WANG Ningbo, REN Weixin, HE Lixiang. Extraction of strain influence line of bridge from dynamic responses [J]. Journal of Central South University (Science and Technology), 2014, 45(12): 4362 − 4369. (in Chinese)
[16] IENG S S. Bridge influence line estimation for bridge weigh-in-motion system [J]. Journal of Computing in Civil Engineering, 2015, 29(1): 1 − 4.
[17] 陈志为, 杨维彪, 程棋锋, 等. 基于正则化与B样条曲线的桥梁影响线识别方法[J]. 中国公路学报, 2019, 32(3): 101 − 108. CHEN Zhiwei, YANG Weibiao, CHENG Qifeng, et al. Bridge influence line identification method based onregularization and b-spline curves [J]. China Journal of Highway and Transport, 2019, 32(3): 101 − 108. (in Chinese)
[18] ZHENG X, YANG D H, YI T H, et al. Bridge influence line identification based on regularized least squares QR decomposition method [J]. Journal of Bridge Engineering, 2019, 24(8): 06019004. doi: 10.1061/(ASCE)BE.1943-5592.0001458
[19] KHUC T, CATBAS F N. Structural identification using computer vision-based bridge health monitoring [J]. Journal of Structural Engineering, 2018, 144(2): 1 − 13.
[20] ZHENG X, YANG D H, YI T H, et al. Bridge influence line identification from structural dynamic responses induced by a high-speed vehicle [J]. Structural Control and Health Monitoring, 2020, 27(7): 1 − 10.
[21] 朱前坤, 陈建邦, 张琼, 等. 基于计算机视觉人行桥挠度影响线非接触式识别[J]. 工程力学, 2021, 38(8): 145 − 153. doi: 10.6052/j.issn.1000-4750.2017.02.0106 ZHU Qiankun, CHEN Jianbang, ZHANG Qiong, et al. A non-contact recognition for deflection influence line of footbridge based on computer vision [J]. Engineering Mechanics, 2021, 38(8): 145 − 153. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.02.0106
[22] ZHOU Y, ZHOU S, HAO G, et al. Bridge influence line identification based on big data and interval analysis with affine arithmetic [J]. Measurement, 2021, 183: 109807.
[23] ZHENG X, YANG D H, YI T H, et al. Bridge influence surface identification method considering the spatial effect of vehicle load [J]. Structural Control and Health Monitoring, 2021, 28(8): 1 − 14.
[24] HUNT V J. Nondestructive evaluation and health monitoring of highway bridges [D]. Cincinnati, Ohio, USA: University of Cincinnati, 2000.
[25] FRØSETH G T, RØNNQUIST A, CANTERO D, et al. Influence line extraction by deconvolution in the frequency domain [J]. Computers and Structures, 2017, 189: 21 − 30. doi: 10.1016/j.compstruc.2017.04.014
[26] YAN W J, YUEN K V. A new probabilistic frequency-domain approach for influence line extraction from static transmissibility measurements under unknown moving loads [J]. Engineering Structures, 2020, 216: 110625. doi: 10.1016/j.engstruct.2020.110625
[27] JAYNES E T. Probability theory: The logic of science [M]. London, UK: Cambridge University Press, 2003.
[28] BECK J L, KATAFYGIOTIS L S. Updating models and their uncertainties. I: Bayesian statistical framework [J]. Journal of Engineering Mechanics, 1998, 124(4): 455 − 461. doi: 10.1061/(ASCE)0733-9399(1998)124:4(455)
[29] BECK J L. Bayesian system identification based on probability logic [J]. Structural Control and Health Monitoring, 2020, 17(7): 825 − 847.
[30] YUEN K V. Bayesian methods for structural dynamics and civil engineering [M]. Hoboken, New Jersey, USA, John Wiley and Sons, 2010.
[31] YUEN K V, KUOK S C. Bayesian methods for updating dynamic models [J]. Applied Mechanics Reviews, 2011, 64(1): 010802. doi: 10.1115/1.4004479
[32] 颜王吉, 曹诗泽, 任伟新. 结构系统识别不确定性分析的Bayes方法及其进[J]. 应用数学和力学, 2017, 38(1): 44 − 59. YAN Wangji, CAO Shize, REN Weixin. Uncertainty quantification for system identification utilizing the Bayesian theory and its recent advances [J]. Applied Mathematics and Mechanics, 2017, 38(1): 44 − 59. (in Chinese)
[33] HUANG Y, SHAO C, WU B, et al. State-of-the-art review on Bayesian inference in structural system identification and damage assessment [J]. Advances in Structural Engineering, 2019, 22(6): 1329 − 1351. doi: 10.1177/1369433218811540
[34] 陈龙, 黄天立. 基于贝叶斯更新和逆高斯过程的在役钢筋混凝土桥梁构件可靠度动态预测方法[J]. 工程力学, 2020, 37(4): 186 − 195. doi: 10.6052/j.issn.1000-4750.2019.05.0273 CHEN Long, HUANG Tianli. Dynamic prediction of reliability of in-service RC bridges using the bayesian updating and inverse gaussian process [J]. Engineering Mechanics, 2020, 37(4): 186 − 195. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.05.0273
[35] ZHANG Y M, WANG H, MAO J X, et al. Probabilistic framework with bayesian optimization for predicting typhoon-induced dynamic responses of a long-span bridge [J]. Journal of Structural Engineering, 2021, 147(1): 04020297. doi: 10.1061/(ASCE)ST.1943-541X.0002881
[36] 秦超, 颜王吉, 孙倩, 等. 基于贝叶斯功率谱变量分离方法的实桥模态参数识别[J]. 工程力学, 2019, 36(10): 212 − 222. doi: 10.6052/j.issn.1000-4750.2018.11.0604 QIN Chao, YAN Wangji, SUN Qian, et al. Operational modal analysis of bridge engineering based on bayesian spectral density approach using a variable separation technique [J]. Engineering Mechanics, 2019, 36(10): 212 − 222. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.11.0604
[37] AU S K, ZHANG F L, NI Y C. Bayesian operational modal analysis: theory, computation, practice [J]. Computers and Structures, 2013, 126: 3 − 14.
[38] 蒋伟, 刘纲. 基于多链差分进化的贝叶斯有限元模型修正方法[J]. 工程力学, 2019, 36(6): 101 − 108. doi: 10.6052/j.issn.1000-4750.2018.04.0229 JIANG Wei, LIU Gang. Bayesian finite element model updating method based on multi-chain differential evolution [J]. Engineering Mechanics, 2019, 36(6): 101 − 108. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.04.0229
[39] YUEN K. V, Mu H Q. Real‐time system identification: an algorithm for simultaneous model class selection and parametric identification [J]. Computer‐Aided Civil and Infrastructure Engineering, 2015, 30(10): 785 − 801. doi: 10.1111/mice.12146
[40] MU H Q, YUEN K V. Modal frequency-environmental condition relation development using long-term structural health monitoring measurement: Uncertainty quantification, sparse feature selection and multivariate prediction [J]. Measurement, 2018, 130: 384 − 397. doi: 10.1016/j.measurement.2018.08.022
[41] MU H Q, HU Q, GUO H Z, et al. Uncertainty quantification of load effects under stochastic traffic flows [J]. International Journal of Structural Stability and Dynamics, 2019, 19(1): 1940009. doi: 10.1142/S0219455419400091
[42] MU H Q, YUEN K V. Ground motion prediction equation development by heterogeneous Bayesian learning [J]. Computer‐Aided Civil and Infrastructure Engineering, 2016, 31(10): 761 − 776. doi: 10.1111/mice.12215
[43] 苏成, 廖威, 袁昆, 等. 桥梁健康监测在线预警指标研究[J]. 桥梁建设, 2015, 45(3): 44 − 50. SU Cheng, LIAO Wei, YUAN Kun, et al. Research of online early warning indices for bridge health monitoring [J]. Bridge Construction, 2015, 45(3): 44 − 50. (in Chinese)
[44] 张喜刚. 公路桥梁汽车荷载标准研究[M]. 北京: 人民交通出版社, 2014. ZHANG Xigang. Research on vehicle load standard of highway bridge [M]. Beijing: China Communications Press, 2014. (in Chinese)
[45] JTG D60−2015, 公路桥涵设计通用规范[S]. 北京: 人民交通出版社, 2015. JTG D60−2015, General specifications for design of highway bridges and culverts [S]. Beijing: China Communications Press, 2015. (in Chinese)
计量
- 文章访问数: 673
- HTML全文浏览量: 156
- PDF下载量: 155
