RESEARCH ON THE SHEAR PERFORMANCE OF SELF-DRILLING SCREW DOUBLE-SIDED SHEAR CONNECTIONS
-
摘要: 该文通过ABAQUS有限元软件对自攻螺钉双面剪切连接抗剪性能进行了研究,通过已有试验结果验证了有限元模型的准确性,基于此模型讨论了钢材强度等级、钢板厚度、螺钉直径以及不同中间钢板厚度对螺钉双面剪切连接的破坏模式和抗剪承载力的影响。结果表明:螺钉双面剪切连接构件的破坏模式可分成3类,分别为:承压破坏、承压-剪切破坏和剪切破坏。螺钉双面剪切连接抗剪承载力随着钢材强度等级和钢板厚度的增加而提高并趋于稳定;随着螺钉直径的增加,螺钉双面剪切连接抗剪承载力呈线性增加;在一定范围增加中间钢板厚度也可显著提高螺钉双面剪切连接抗剪承载力。将数值模拟结果与中美欧规范计算值进行比较分析得出,当钢板发生承压破坏时,中国、欧洲和AISC规范公式计算值偏于保守,AISI规范计算值较接近有限元值;当螺钉发生剪切破坏时,AISI和中欧规范过于保守。AISC规范公式计算值与有限元值吻合较好,因此,当螺钉发生剪切破坏时,使用AISC规范公式计算具有一定参考价值。Abstract: The shear performance of self-drilling screw double-sided shear connections is studied by numerical simulation using the ABAQUS finite element software. The accuracy of the finite element (FE) model is verified through a comparison with the existing test results. Based on this model, the steel strength, the steel plate thickness, the screw diameter and the middle steel plate thickness are discussed on their influences on the failure modes and shear capacity of the screw double-sided shear connections. The results show that the failure modes can be divided into three categories: namely bearing failure, shear-compression failure and shear failure. With the increase of the steel strength grade and the steel plate thickness, the shear capacity of the screw double-sided shear connections continues to increase and gradually stabilizes. With the increase of the screw diameter, the shear capacity of the screw double-sided shear connections increases linearly. Moreover, the shear capacity of the screw double-sided shear connections can also be significantly increased by increasing the middle steel plate thickness in a certain range. The numerical simulation results are compared with the calculated values of the Chinese, American and European standards. The results show that when the bearing failure of the steel plates occurs, the calculated values of the Chinese, European and AISC standards formulas are conservative, and the calculated values of the AISI standard are closer to the FE values. When the shear failure of the screws occurs, the AISI, Chinese and European standards are too conservative. The calculated values of the AISC standard formula are in good agreement with the FE values. Therefore, the calculation of the AISC standard formula is of reference value when the shear failure of the screws occurs.
-
自攻螺钉因其经济性好、施工便利、连接刚度好以及抗剪承载力高等优势,被广泛用于冷弯薄壁(厚度≤6 mm)型钢构件之间的连接。另外,冷弯钢组合墙板的蒙皮效应之所以能正常发挥,除了板自身强度和刚度外,另一个关键因素就是螺钉的可靠连接。因此,随着冷弯薄壁型钢结构的推广应用,螺钉连接性能日益受到重视。潘景龙等[1]根据国内外30余组试件的试验结果拟合得到了螺钉抗剪强度表达式,最后还得出了自攻螺连接在剪、拉共同作用下的强度验算公式。郝际平和石宇等[2-3]通过试验研究了不同板件之间自攻螺钉连接的抗剪性能,分析了板材类型、螺钉端距等对螺钉连接抗剪承载力的影响,并将试验值与中、英、美规范计算值进行对比分析,最后提出钢板-非钢板单颗螺钉连接抗剪承载力设计方法。李元齐等[4]总结分析了螺钉单剪连接的受力机理及破坏模式,并简要介绍了中美欧等规范关于螺钉单剪连接承载力的设计方法。卢林枫等[5]研究了不同参数对螺钉连接抗剪性能的影响,最后给出了考虑螺钉群效应和螺钉间距影响系数的抗剪承载力计算公式。王小平等[6]用ANSYS有限元软件建立了自攻螺钉抗剪连接的7种简化计算模型,并最后总结出适合模拟螺钉抗剪承载力的有限元建模方法。Feng等[7]研究发现螺钉直径、钢板厚度等对螺钉连接抗剪承载力影响较大。石膏板厚度以及当螺钉端距、边距和螺钉间距超过一定值时,上述因素对螺钉抗剪承载力几乎无影响。Roy等[8]和Huynh等[9-10]通过试验研究了螺钉布置形式、螺钉数量及螺钉间距对高强冷弯钢自攻螺钉连接抗剪性能的影响,并开发了模拟螺钉抗剪连接的有限元模型。
然而,上述文献均只针对螺钉单面剪切连接抗剪性能进行了研究,有关螺钉双面剪切连接抗剪性能研究鲜有报导。刘楠等[11]对螺钉连接单面受剪和双面受剪开展了试验研究,分析得到单个螺钉连接较厚钢板的抗剪承载力设计方法。然而,文中没有具体讨论不同参数对螺钉连接双面剪切抗剪承载力的影响,且文中研究的板件厚度均超过2.5 mm,未对厚度小于2.0 mm板件开展研究。另外,采用试验方法研究螺钉剪切性能时,无法较好观察到螺钉及板件的破坏过程,尤其是螺钉在双面剪切连接时,中间板件承压破坏和螺钉剪切破坏过程无法观察。Zhou等[12]对钉子单面剪切和双面剪切连接的抗剪性能进行了单调和循环加载试验,研究表明钉子双剪连接抗剪强度和刚度明显优于钉子单剪连接。
螺钉双面剪切连接更多的应用于夹板剪力墙结构中。夹板剪力墙是一种新型的剪力墙结构,在该墙体系统中,面板被放置在墙体中心,并且墙面板被两侧立柱和上、下导梁夹在中间,立柱相对标准剪力墙中的立柱旋转了90°,螺钉依次穿过立柱-夹板-立柱,螺钉的受力机制从单向剪切受力状态变为双向剪切受力状态,从而使得这种墙体抗剪强度和侧向刚度大幅提升[13-16]。Varoglu等[13-14]和郑维等[15-16]通过足尺的夹板木剪力墙抗侧力试验证实夹板木剪力墙的抗剪强度和抗侧刚度是标准木剪力墙的2倍~3倍。随着冷弯钢结构的快速发展与兴起,冷弯钢结构房屋建筑开始逐渐取代木结构房屋建筑,冷弯钢结构也因此获得研究学者的广泛关注。周绪红等[17]和Brière等[18]通过试验研究了冷弯薄壁型钢-夹板剪力墙的抗震性能,其中龙骨与钢板之间的连接方式为螺钉双面剪切连接,研究发现此类构造墙体的抗剪强度和抗侧刚度是规范给出的标准冷弯钢剪力墙的2倍~4倍。之后,周绪红等[19]对6层足尺冷弯薄壁型钢-钢板剪力墙结构房屋开展了振动台试验,其中帽形截面端柱夹支单层薄钢板剪力墙的螺钉连接方式为典型的螺钉双面剪切连接,研究结果表明该墙体的抗剪承载力及刚度均明显高于传统冷弯薄壁型钢组合墙体,这对发展多高层冷弯薄壁型钢结构房屋建筑体系有重要意义,符合国家绿色发展战略和“人多地少”的基本国情。Yanagi等[20]提出了可用于计算钢板剪力墙抗剪承载力的理论设计公式且计算结果具有良好的可靠性与精确性,其中公式主要形式与螺钉承载力规范设计公式完全一致。目前规范的螺钉抗剪承载力计算公式均只针对螺钉单面剪切连接,基于文献[20]分析可知,采用螺钉单剪承载力规范设计公式计算文献[17]墙体承载力偏于保守。因此上述关于自攻螺钉双面剪切连接抗剪性能的研究仍然不完善,有待对其开展进一步研究。
针对上述研究存在的不足,本文采用ABAQUS有限元软件对螺钉双面剪切连接的破坏模式和抗剪承载力等进行了分析。讨论了钢材强度等级、连接板件厚度、螺钉直径以及不同中间钢板厚度对螺钉双面剪切连接破坏模式和抗剪承载力的影响。最后,将有限元模型得到的螺钉双面剪切连接抗剪承载力与中美欧规范公式计算值进行了比较。
1 有限元模型
1.1 文献[11]试验简况
文献[11]设计的试件尺寸为220 mm×50 mm,钢板厚度为2.5 mm~6.0 mm,且均为Q235级钢。螺钉公称直径分别为4.8 mm、5.5 mm和6.3 mm。螺钉维氏硬度HV=388,换算成极限强度为1250 MPa。试件由连接钢板和螺钉组成,螺钉攻入钢板前,根据规范要求在钢板上钻出预钻小孔,然后通过手提电钻攻入连接板内。连接钢板的力学性能由材性试验获得。试验过程中,通过位移计测量连接板上距螺钉较近的点之间的相对位移作为螺钉连接的相对位移。试验采用了100 kN穿心千斤顶和圆筒形手动液压油泵,试验操作者通过已标定的应变仪读取拉、压传感器的应变值,60 με代表1 kN的拉力或压力,最后换算得到试件的荷载值。因此,施加在试件上的荷载要根据应变仪读数手动控制液压油泵。加载装置对试件施加的荷载即为某时刻试件的荷载。试验时,采用分级加载,加载初期,每级荷载为0.25 kN~0.33 kN,加载中期,每级荷载为0.83 kN~1 kN,加载后期,每级荷载为0.17 kN,直至试件破坏。
1.2 模型建立
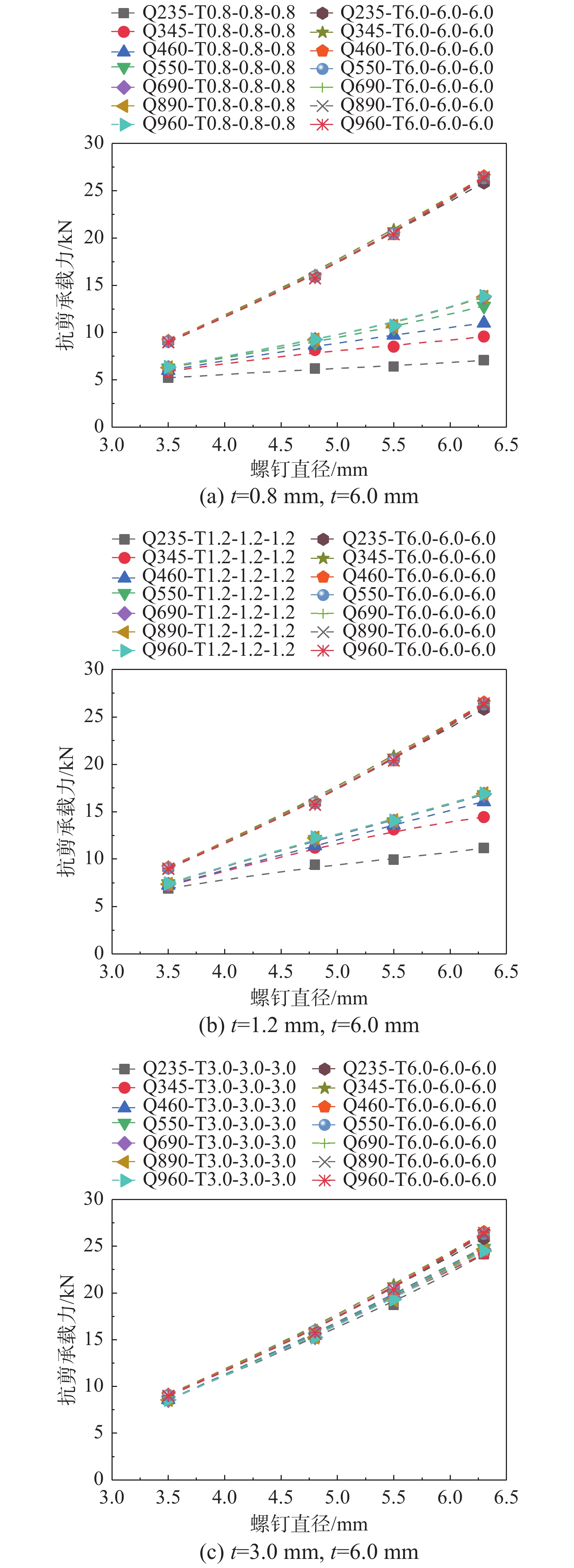
采用ABAQUS有限元软件对自攻螺钉双面剪切连接抗剪性能进行分析。有限元模型(图1)由4部分组成:上钢板、下钢板、中间钢板和自攻螺钉。其中螺钉和垫圈简化成一个实体单元,钉头和钉杆均简化为圆柱体,螺钉直径与螺钉公称直径保持一致[5, 8]。模型部件均采用8节点减缩积分三维实体单元[21]。上、下钢板的左端完全固定,在中间钢板右端耦合点RP-1处施加拉伸位移荷载。为了提高模拟结果的准确性和运行效率,在模型应力集中的位置处将网格细化,而在应力较小的区域网格划分较粗[21-22]。因此,螺钉孔附近钢板的网格尺寸为0.6 mm×0.6 mm,钢板其他部分网格尺寸为2 mm×2 mm,钢板网格的高度由钢板自身的厚度决定,自攻螺钉的网格尺寸为0.4 mm×0.4 mm×0.4 mm。钢板与钢板之间,钢板与自攻螺钉之间定义接触对,接触属性为:法向硬接触;切向可滑动,且滑动摩擦系数为0.3[23]。为了避免螺钉与钢板孔之间复杂的相互作用而导致的收敛问题,且显式求解器可以以更高的效率解决高度不连续的问题,模型采用显式动力学方法进行求解分析。
1.3 模型参数
本文共设计了124组自攻螺钉双面剪切连接模型,研究了不同钢材强度、钢板厚度、螺钉直径,以及上、下钢板厚度和螺钉直径一定时,不同中间钢板厚度对自攻螺钉双面剪切连接抗剪性能的影响。钢板模型尺寸为220 mm×50 mm,与试验构件[11]尺寸一致,钢板厚度分别为0.8 mm、1.2 mm、3.0 mm和6.0 mm。钢材强度等级别为Q235、Q345、Q460、Q550、Q690、Q890和Q960,钢材材料属性见表1[24-26],钢材本构关系采用理想弹塑性模型并考虑材料强化,弹性模量E取206 GPa,第二模量Es=E/100,泊松比ν=0.3[27]。在数值模拟中,应将拉伸试验得到的工程应力σnom和工程应变εnom转化为真实应力σtrue和真实应变εtrue[9]。真实应力和真实应变以及工程应力和工程应变之间的关系可以表示为[28]:σtrue=σnom(1+εnom),εtrue=ln(1+εnom)。另外,ABAQUS中使用的塑性应变εpl可定义为:εpl=ln(1+εnom)−σtrue/E。为了避免发生面板端部和边部发生撕裂破坏,螺钉端距取30 mm,边距取25 mm。螺钉中心孔到板端的距离大于螺钉直径的3倍,满足规范[29-32]规定的螺钉连接最小要求。自攻螺钉直径为3.5 mm、4.8 mm、5.5 mm和6.3 mm。由于自攻螺钉的材料多为合金钢,材质较硬,当达到极限强度时会发生脆性断裂,因此,在ABAQUS有限元软件的材料属性中采用金属柔性损伤准则,断裂应变和应力三轴度的取值参考文献[33]。自攻螺钉弹性模量取206 GPa,泊松比为0.3,极限强度取1250 MPa[11]。考虑到螺钉螺纹造成的应力集中,由文献[34]得到其应力集中系数为1.79,折算后的极限强度取700 MPa。
以Q235-D3.5-T0.8-1.2-0.8为例,构件编号中的各字母及数字的含义分别为:Q235表示连接钢板为Q235钢;D3.5表示自攻螺钉直径为3.5 mm;T0.8-1.2-0.8表示连接钢板的厚度,依次是上钢板的厚度为0.8 mm、中间钢板的厚度为1.2 mm、下钢板厚度为0.8 mm。
1.4 模型验证
本文对采用上述建模方法建立的有限元模型进行计算分析,并与文献[11]的试验结果进行对比分析,以验证有限元模型的有效性和准确性。其中文献[11]连接板选用的是Q235钢材,钢材力学性能由材性试验获得,具体参见文献[11]。
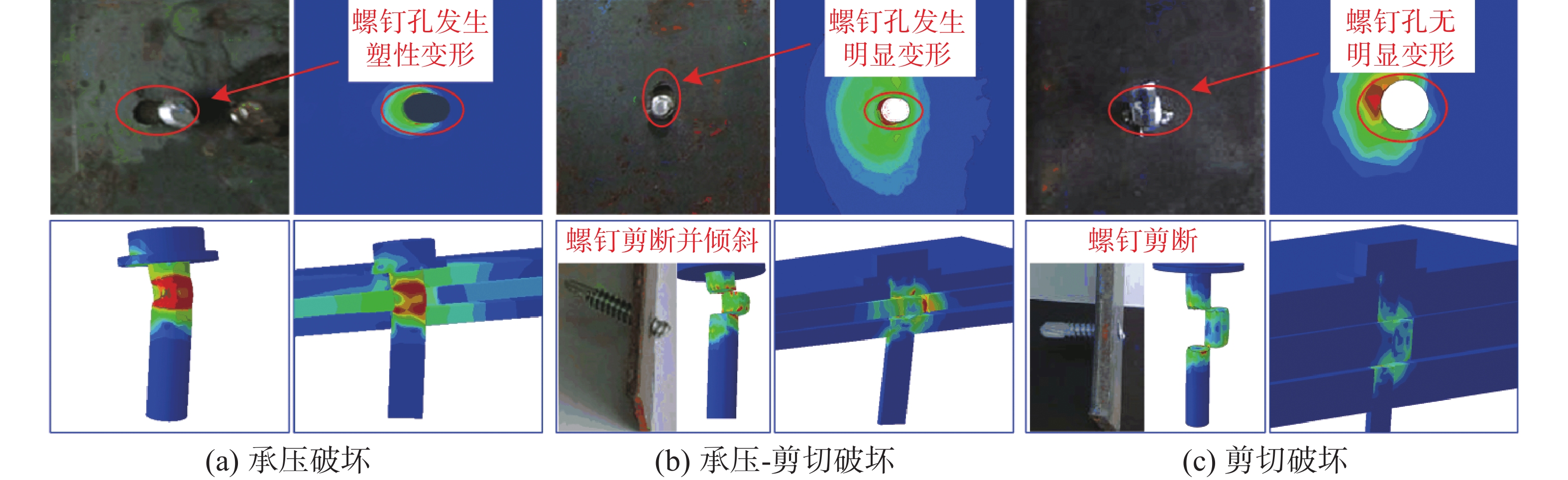
文献[11]中表明,自攻螺钉双面剪切连接试件破坏模式分为3种:连接板孔壁承压破坏,如图2(a)所示;连接件发生承压-剪切破坏,即自攻螺钉剪切断裂且伴随着钢板孔壁附近发生明显变形,如图2(b)所示;螺钉剪切断裂,如图2(c)所示。对比几组典型的不同破坏模式下试件与相对应的有限元模拟的试件,模拟得到的破坏模式与试验破坏模式完全一致。
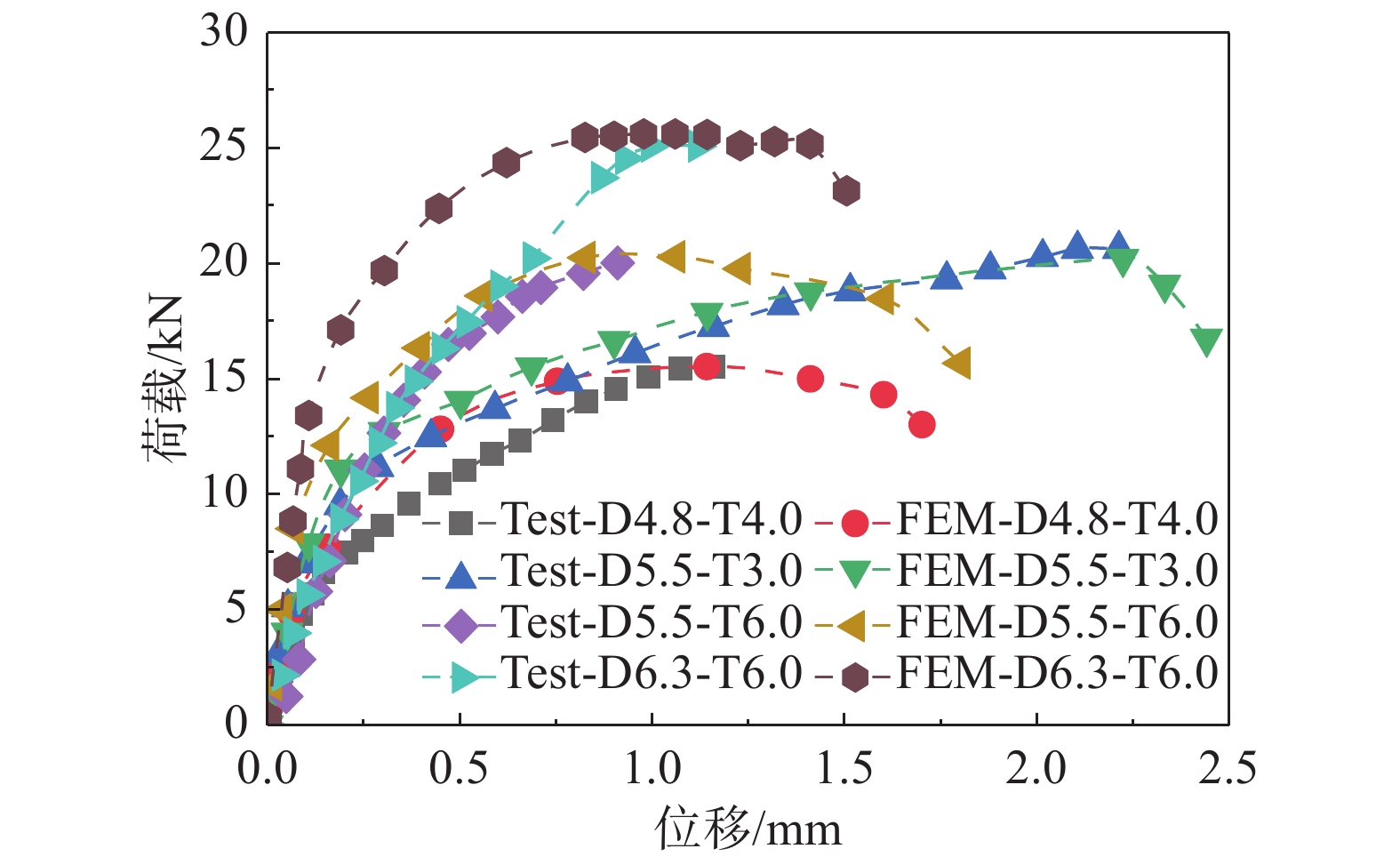
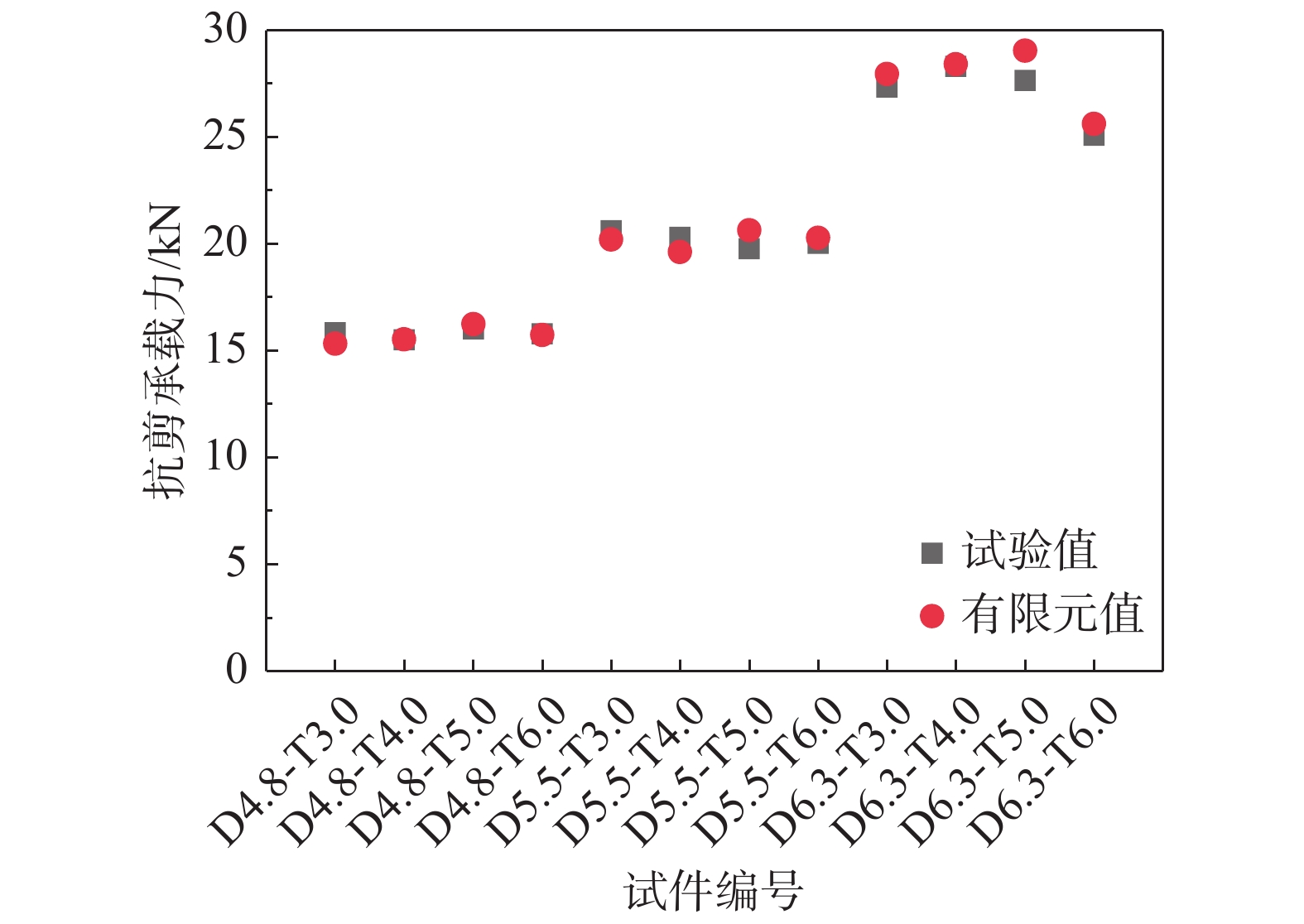
试件的变形包括螺钉孔附件钢板挤压变形、螺钉剪切变形及钢板拉伸变形,为验证模型的荷载位移曲线以及抗剪承载力的准确性,提取RP-1处的荷载和螺钉连接处的位移,并与试验结果进行了比较。另外,为了与文献[11]试件编号统一和方便比较,验证模型编号与试验编号一致。由图3可知,通过有限元模拟获得的自攻螺钉双面剪切连接的载荷-位移曲线与通过试验[11]获得的结果基本吻合。由于缺乏相关的金属损伤参数,使得模型的材料属性设置不完善,且试验测得的位移不仅仅是螺钉孔变形,还包括钢板拉伸变形,因此有限元模拟得到的螺钉节点破坏位移与试验值有一定差异。在试验过程[11]中,观察到螺钉会有初始滑移,且有限元模型输入的钢材弹性模量和屈服应力等与材性试验获得的结果有一定差异以及制作误差等,因此,有限元模拟获得的初始刚度高于试验结果。由图4可知,螺钉双面剪切连接抗剪承载力试验值[11]与有限元值之比的均值为1.01,变异系数仅为2.67%,且有限元模拟得出的螺钉双面剪切抗剪承载力与试验结果基本保持一致,误差控制在±5%以内。
综上所述,该模型可以较准确地反映自攻螺钉双面剪切连接破坏模式和抗剪承载力值。从而证明,模型的建模方法、单元选取、本构模型、材料属性设置、网格划分以及求解方法的准确性,采用该方法建立的有限元模型可用于自攻螺钉双面剪切连接抗剪性能模拟。
2 模型结果分析
2.1 破坏模式
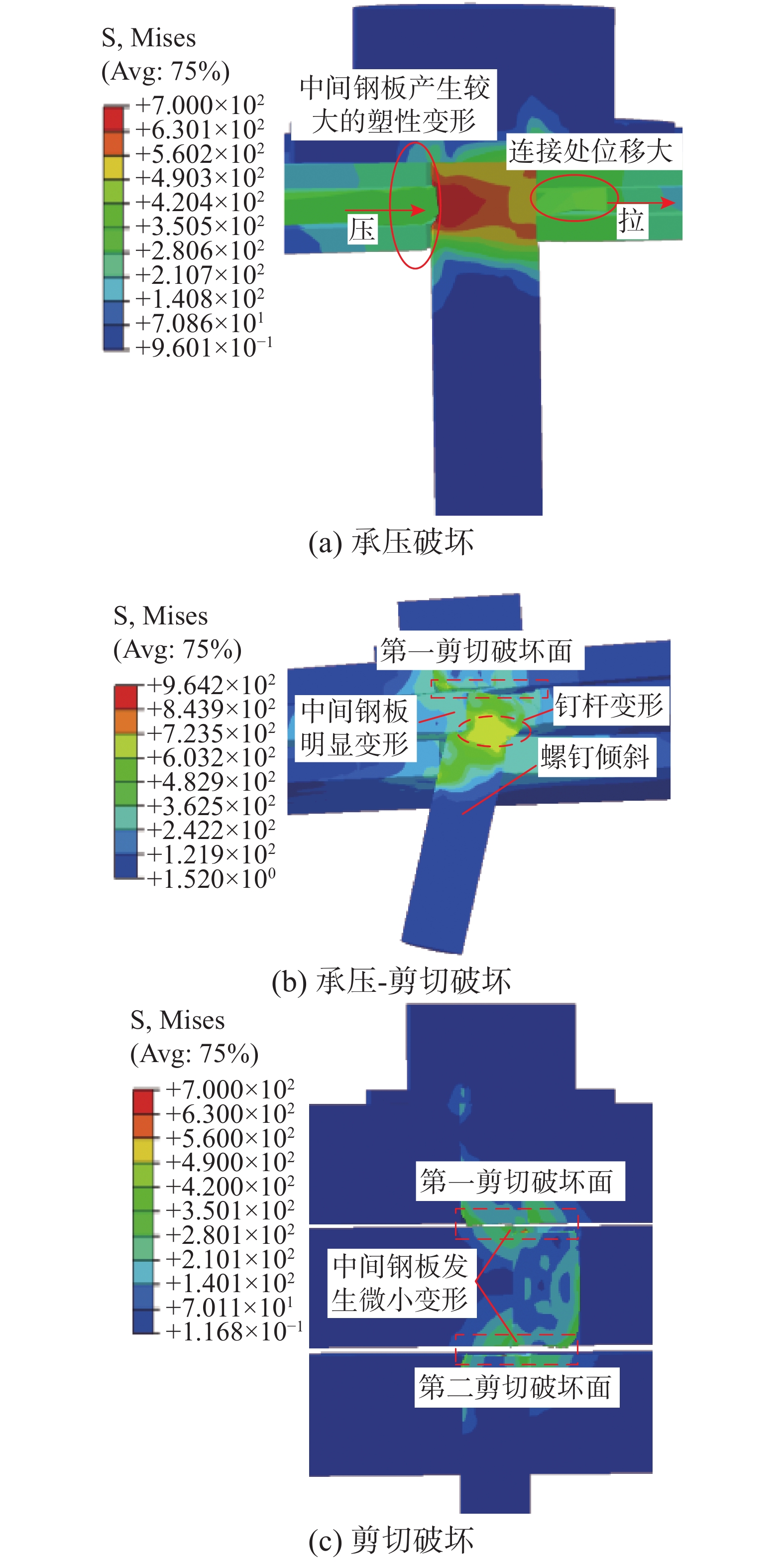
根据ABAQUS有限元模拟结果,本文将自攻螺钉双面剪切连接破坏模式分为3类:螺钉孔附近钢板承压破坏、钢板承压-螺钉剪切破坏和螺钉剪切破坏,如图5所示。
图5(a)为典型承压破坏示意图,螺孔在螺杆的压力作用下,螺钉孔附近中间连接钢板产生了较大的沿厚度方向的塑性变形,上、下连接钢板变形较小且螺钉未被剪断。由于螺钉孔附近中间钢板发生明显的塑性变形,破坏时钢板之间会分离。螺钉连接处发生承压破坏时,峰值荷载较低,但是破坏位移值大,均超过2 mm,有的甚至超过4 mm。这表明,螺钉连接处发生承压破坏时,螺钉孔壁附近产生了较大的塑性变形,破坏前有明显的预兆,属于塑性破坏。此种破坏模式发生在钢板厚度为0.8 mm和1.2 mm的试件中,如Q235-D6.3-T0.8-0.8-0.8。随着钢材强度等级的提高,连接钢板破坏模式基本保持不变,螺钉会产生较大的弯曲变形,但仍未断裂。对于上、下钢板为0.8 mm,中间钢板厚度为0.8 mm~6.0 mm的试件,上、下钢板会产生较大的塑性变形。随着中间钢板厚度的增加,中间钢板塑性变形减小,螺钉弯曲变形增加;对于上、下钢板为6.0 mm,中间钢板厚度为0.8 mm~1.2 mm时,中间钢板会产生较大的塑性变形,上、下钢板无明显塑性变形,当中间钢板厚度达到3 mm时发生剪切破坏。
图5(b)表示连接件发生了钢板承压-螺钉剪切破坏,发生此类破坏时,螺钉只有一个剪切破坏面且破坏面较光滑。剪切破坏面发生在上钢板与中间钢板的交界处,破坏时钉头保持与钢板垂直,钉尾严重倾斜,且中间钢板与下钢板交界处钉杆发生严重变形,中间钢板和下钢板也有明显的塑性变形。承压-剪切破坏与钢材强度等级和螺钉直径以及钢板厚度有关。当钢板厚度为3.0 mm,钢材强度等级小于460 MPa且螺钉直径大于3.5 mm或钢材强度等级为460 MPa且螺钉直径为6.3 mm时,连接件会发生承压-剪切破坏,如Q235-D4.8-T3.0-3.0-3.0。
图5(c)为典型的螺钉剪切破坏示意图。发生此类破坏时,螺钉有2个剪切破坏面且破坏面较光滑。破坏面发生在钢板与钢板连接的交界处,破坏时钉头保持与钢板垂直,钉尾略微倾斜,上、下钢板无明显变形。螺钉连接处的位移较小,抗剪承载力较高,破坏前无明显的预兆,属于脆性破坏。当钢板厚度为3.0 mm且螺钉直径为3.5 mm,或钢材强度等级不小于460 MPa时,连接件会发生螺钉剪切破坏形式,如Q235-D3.5-T3.0-3.0-3.0,Q460-D5.5-T3.0-3.0-3.0;当钢板厚度为6.0 mm时,连接件均发生螺钉剪切破坏,如Q550-D6.3-T6.0-6.0-6.0。
2.2 钢材强度对抗剪承载力的影响
为了直观展示钢材强度等级对螺钉连接处荷载-位移曲线的影响,本小节分别列举了不同钢材强度下螺钉直径为3.5 mm和4.8 mm,连接板件厚度为0.8 mm和3.0 mm试件上螺钉连接处的荷载-位移曲线图。由图6可知,荷载-位移曲线可分为3个阶段:加载初期,螺钉节点处于弹性阶段,荷载随位移呈线性变化;随后,螺钉节点刚度逐渐减小,塑性变形增加,荷载随位移呈非线性增长,此为塑性阶段;最后,螺钉双面剪切连接抗剪承载力达到峰值,螺钉连接处位移和变形继续增加但承载力突然下降,刚度变为负值,此为破坏阶段。此外,由图6(a)可知,当螺钉直径为3.5 mm且连接板厚度为3.0 mm时,增大钢材强度对螺钉节点的弹性阶段几乎没影响,对塑性阶段影响较小;由图6(b)可知,当螺钉直径为4.8 mm且连接板厚度为0.8 mm时,增大钢材强度可延缓螺钉节点进入塑性阶段。分析认为:当钢板厚度较大,破坏模式主要受钢板厚度影响,破坏时螺钉先于连接板进入塑性阶段,因此,增大钢材强度等级对螺钉节点的弹性阶段几乎无影响;当钢板厚度较小,破坏模式主要受钢材强度等级影响,螺钉屈服前后,钢板相继进入塑性阶段,因此,钢材强度等级越大,螺钉节点到达塑性阶段越缓慢。
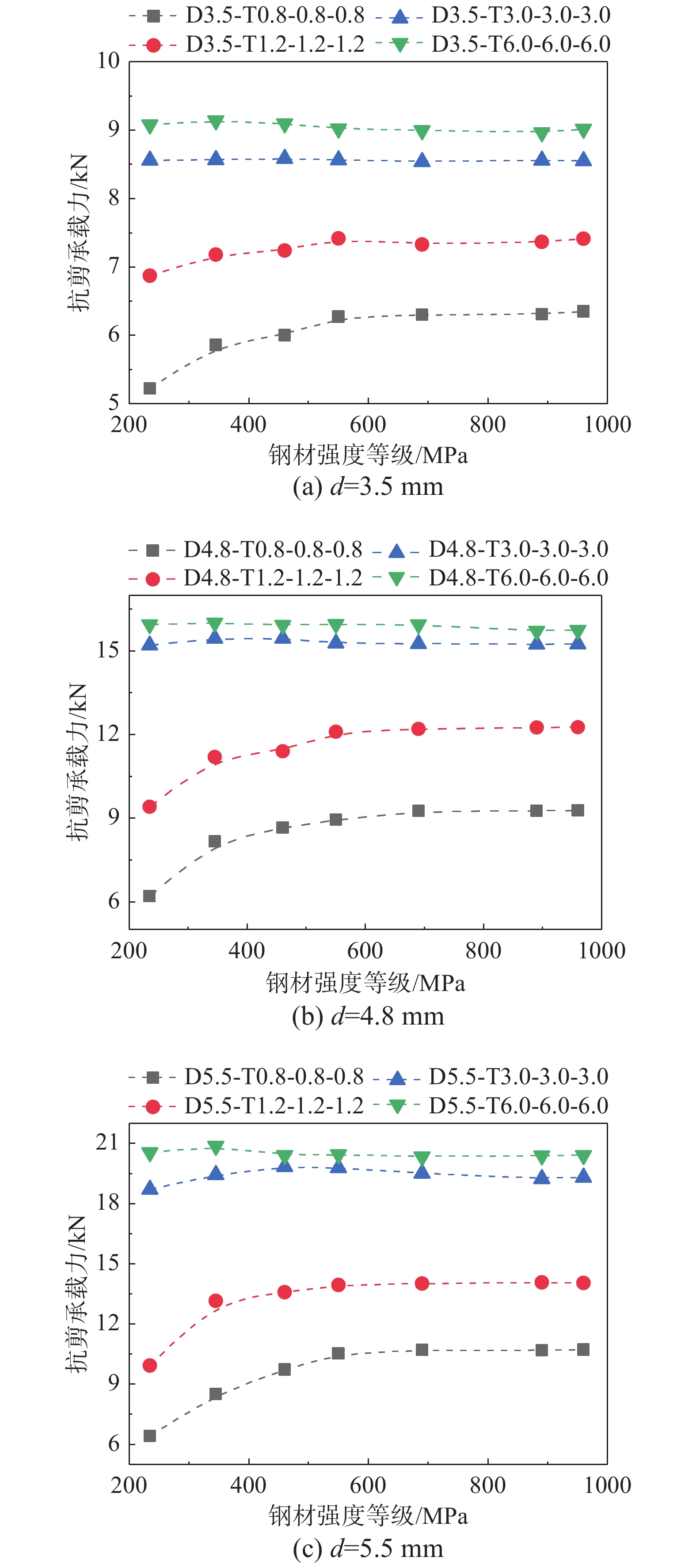
图7给出了相同螺钉直径情况下螺钉双面剪切连接抗剪承载力随钢材强度等级变化的关系曲线。当连接钢板厚度为0.8 mm和1.2 mm且自攻螺钉直径不变时,随着钢材强度等级的提高,螺钉双面剪切连接抗剪承载力不断提高并最后趋于稳定。因为螺钉连接处发生承压破坏时,螺钉双面剪切连接抗剪承载力主要由钢板自身强度控制,但是当钢材强度达到550 MPa时,螺钉会产生较大的塑性变形,但仍未剪断,而承载力开始大幅下降,因此继续提高钢材强度等级对螺钉连接抗剪承载力影响不大。当钢材强度等级由235 MPa增至550 MPa时,螺钉双面剪切连接抗剪承载力最大可提高81.24%。当连接钢板厚度为3.0 mm和6.0 mm时,螺钉连接处均发生螺钉剪切破坏,螺钉双面剪切连接抗剪承载力由自攻螺钉自身强度与直径控制,增加钢材强度等级对螺钉双面剪切连接抗剪承载力几乎没影响,螺钉双面剪切连接抗剪承载力波动范围控制在±6%以内,二者几乎呈水平线性关系。
2.3 钢板厚度对抗剪承载力的影响
图8给出了4组相同钢材强度等级情况下螺钉双面剪切连接抗剪承载力随钢板厚度变化的关系曲线。由图8可知,螺钉双面剪切连接抗剪承载力与连接钢板厚度基本呈二折线关系,螺钉双面剪切连接抗剪承载力随钢板厚度的增加而增加,最后基本保持不变,其中钢板厚度为3.0 mm是图8曲线的折点。当钢板厚度小于3.0 mm且钢材强度等级和螺钉直径保持不变时,螺钉双面剪切连接抗剪承载力随着连接钢板厚度的增加而增加。当钢板厚度从0.8 mm增至3.0 mm时,螺钉双面剪切连接抗剪承载力至少提高35%,最大可提高242%。但是,当钢板厚度达到3.0 mm时,增加钢板厚度对螺钉双面剪切连接抗剪承载力影响不大。这是由于当钢板厚度超过3.0 mm时,螺钉均发生剪切断裂破坏,螺钉双面剪切连接抗剪承载力主要受螺钉的影响。当钢板厚度从3.0 mm增至6.0 mm,螺钉双面剪切连接抗剪承载力最大仅提高10%。因此,从经济性角度分析,钢板厚度取3.0 mm既可保证试件上螺钉连接处具有较高的抗剪承载力,且相比于钢板厚度为6.0 mm的试件可显著降低施工建造成本。
2.4 螺钉直径对抗剪承载力的影响
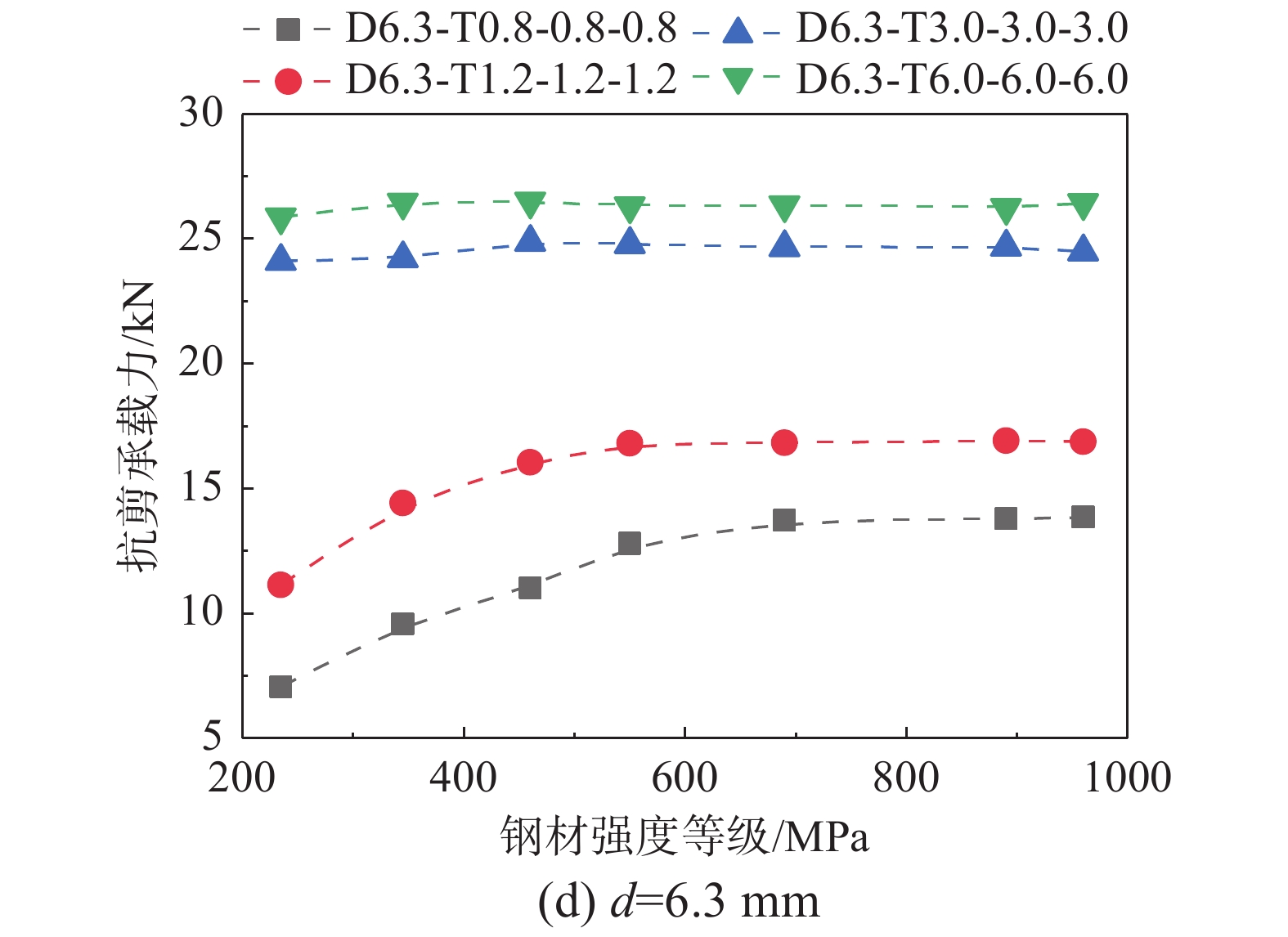
图9给出了螺钉双面剪切连接抗剪承载力随螺钉直径变化的关系图。由图9可知,当钢材强度等级和钢板厚度不变时,螺钉双面剪切连接抗剪承载力随螺钉直径增长几乎呈线性增长。由图9(a)~图9(b)可知,当钢板厚度小于3.0 mm时,螺钉直径对螺钉双面剪切连接抗剪承载力影响较小,且螺钉直径较小时,不同钢材强度等级的螺钉连接抗剪承载力相差不大。随着钢材强度等级的提高,螺钉直径增大对螺钉连接抗剪承载力的增强效果增大,并在钢材强度等级达到550 MPa时趋于稳定。因为,当钢材强度等级增长到一定值时,钢板承压破坏时会伴随着螺钉较大的弯曲变形,但螺钉仍未剪断,而当承载力开始大幅下降,此时再仅提高钢材强度等级无法明显提高螺钉连接抗剪承载力。由图9(c)曲线的斜率可知,对于钢板厚度大于3.0 mm的试件,随着钢材强度等级的提高,螺钉双面剪切连接抗剪承载力会略微增加,这表明提高钢材强度等级对螺钉双面剪切连接抗剪承载力影响不大,这是由于此时螺钉连接处主要发生螺钉剪切破坏,螺钉双面剪切连接抗剪承载力主要取决于螺钉参数,螺钉在受剪过程中出现较大变形直至剪断,因此在相同钢材强度等级下,螺钉直径大小对螺钉连接抗剪承载力影响显著。
2.5 中间钢板厚度对抗剪承载力的影响
为了分析中间钢板厚度对螺钉双面剪切连接抗剪承载力的影响,本文共设计了16组试件,用于分析薄板夹厚板和厚板夹薄板两种情况对螺钉双面剪切连接抗剪承载力的影响,其中钢材强度等级均为Q235,上、下钢板厚度为0.8 mm或6.0 mm,螺钉直径为3.5 mm和6.3 mm。当薄板夹厚板且螺钉直径为3.5 mm时,螺钉连接破坏时上、下两块较薄板发生承压破坏,破坏模式主要受薄板控制。但是,当中间钢板厚度为3.0 mm和6.0 mm时,螺钉连接发生剪切破坏,破坏模式主要受厚板控制。当薄板夹厚板且螺钉直径为6.3 mm时,螺钉连接均发生承压破坏。当厚板夹薄板且中间钢板厚度小于3.0 mm时,螺钉连接发生承压破坏,中间板厚为3.0 mm时发生剪切破坏。图10描述了螺钉双面剪切连接抗剪承载力随中间钢板厚度变化的趋势。由图10可知,当上、下两块钢板厚度一定时,螺钉双面剪切连接抗剪承载力随着中间钢板厚度的增加而增加,且当中间板厚度较小时,抗剪承载力的增长效果较为显著。
在不同螺钉直径下提高中间钢板厚度对螺钉双面剪切连接抗剪承载力的影响也不一样。当螺钉直径为3.5 mm时,增加中间钢板厚度对螺钉双面剪切连接抗剪承载力的提升不明显,当中间钢板厚度由0.8 mm增至6.0 mm时,薄板夹厚板和厚板夹薄板的螺钉双面剪切连接抗剪承载力分别提高了58.2%和60.1%。当螺钉直径为6.3 mm时,增加中间钢板厚度可显著提高螺钉双面剪切连接抗剪承载力,尤其对于上、下钢板厚度为6.0 mm的试件,当中间钢板厚度由0.8 mm增至3.0 mm时,螺钉双面剪切连接抗剪承载力提高了222.8%。但是,当中间钢板厚度由3.0 mm增至6.0 mm时,中间钢板厚度对螺钉双面剪切抗剪承载力影响不大,最大增幅仅有9.2%,此时螺钉连接发生剪切破坏,增大中间钢板厚度对螺钉抗剪承载力影响不大。因此,相比于薄板夹厚板,厚板夹薄板时增加中间钢板厚度对螺钉双面剪切连接抗剪承载力影响更大。此外,当中间连接钢板厚度一定时,增大螺钉直径可显著提高螺钉双面剪切连接抗剪承载力,最大增幅高达184.9%。
3 螺钉连接抗剪承载力理论公式
目前,有关单个自攻螺钉单面剪切连接抗剪承载力设计公式存在于北美规范AISI S100−2007[29]、美国规范AISC 360-16[30]、中国规范GB 50018−2002[31]以及欧洲规范EN 1993-1-3:2006[32]等规范中,具体形式如下。
3.1 螺钉被剪断
北美、中国和欧洲规范规定节点承载力为[22]:
Pn=AnFn (1) 式中:An为螺钉横截面面积;Fn为螺钉抗剪强度。
美国规范AISC360-16规定节点设计抗剪承载力为:
Pn=ϕAnFnv (2) 式中:Fnv=0.45Fu;
ϕ =0.75。3.2 螺钉倾斜伴随钢板承压破坏
3.2.1 北美规范规定
1) t2/t1≤1.0时,单个螺钉连接承载力取式(3)~式(5)计算得到的最小值。
Pn=4.2√t32dFu2 (3) Pn=2.7t1dFu1 (4) Pn=2.7t2dFu2 (5) 式中:d为螺钉直径;t1为与垫圈接触的板件厚度,t2为不与垫圈接触的板件厚度;Fu1为与垫圈接触的板件的抗拉强度,Fu2为不与垫圈接触的板件的抗拉强度。
2) t2/t1≥2.5时,单个螺钉连接承载力取式(6)~式(7)计算得到的最小值。
Pn=2.7t1dFu1 (6) Pn=2.7t2dFu2 (7) 3) 当1.0<t2/t1<2.5时,单个螺钉连接承载力是上述两种情况的线性插值。
3.2.2 中国规范规定
1) t1/t=1.0时,单个螺钉连接承载力按式(8)计算。
Pn=3.7√t3df且Pn⩽ (8) 式中:t为较薄板的厚度;f为被连接钢板的抗拉强度设计值。
2) t1/t≥2.5时,单个螺钉连接承载力按式(9)计算。
{P_{\rm{n}}}{\rm{ = }}2.4tdf (9) 3) 当1.0<t1/t <2.5时,单个螺钉连接承载力是上述两种情况的线性插值。
3.2.3 欧洲规范规定
单个螺钉连接承载力按下式计算:
{P_{\rm{n}}} = \alpha {F_{\rm{u}}}dt (10) 式中:
\begin{split} & {\alpha = 3.2\sqrt {{t_1}/d} \leqslant 2.1, {t_2}/{t_1} = 1.0;}\\& {\alpha = 3.2\sqrt {{t_1}/d} \leqslant 2.1, {t_2}/{t_1} \geqslant 2.5,{t_1} < 1.0\;{\rm{mm}};}\\& {\alpha = 2.1, {t_2}/{t_1} \geqslant 2.5,{t_1} \geqslant 1.0\;{\rm{mm}};} \end{split} 当1.0<t2/t1<2.5时,采用线性插值法求取α。
3.2.4 AISC360-16规范规定
单个螺钉连接承载力设计值按下式计算:
{P_{\rm{n}}} = 2.4\phi {F_{\rm{u}}}dt (11) 其中,
\phi =0.75。4 有限元值与规范值比较
对124组螺钉双面剪切连接抗剪承载力有限元值与规范公式计算值进行了比较,并在表2和表3中列举了28组螺钉双面剪切连接抗剪承载力有限元值与规范公式计算值,其中Pu为数值模拟获得的螺钉双面剪切连接抗剪承载力值,Pn为抗剪承载力设计公式计算值。“AISI”代表北美设计规范AISI S100-2007[29],“AISC”代表美国钢结构设计规范AISC 360-16[30],“GB”表示冷弯薄壁型钢结构技术规范(GB 50018−2002)[31],“EC”表示欧洲规范EN 1993-1-3:2006[32]。由于目前规范的抗剪承载力计算公式均只针对螺钉单面剪切连接,因此本文在计算螺钉双面剪切连接抗剪承载力时,参考螺钉单剪抗剪承载力计算公式和螺栓抗剪承载力计算公式,在规范单剪承载力计算公式基础均乘以系数nv,其中nv=2,表示试件有2个剪切面[31]。另外,试件发生剪切破坏或承压-剪切破坏时,螺钉均发生剪切破坏且两种破坏模式对应的抗剪承载力值相差不大,因此二者均采用相同的计算公式。
表 2 剪切破坏时抗剪承载力有限元值与规范值比较Table 2. Comparison of the FE values and the standard values of the shear capacity under shear failure试件编号 钢材强度等级f/MPa 螺钉直径d/mm 钢板厚度t/mm 有限元值Pu/kN 规范值Pn/kN AISI GB EC AISC Q235-D3.5-T3.0-3.0-3.0 235 3.5 3 8.56 4.33 4.33 4.33 8.11 Q235-D4.8-T3.0-3.0-3.0 235 4.8 3 15.21 8.14 8.14 8.14 15.26 Q550-D5.5-T3.0-3.0-3.0 550 5.5 3 19.78 10.69 10.69 10.69 20.04 Q550-D6.3-T3.0-3.0-3.0 550 6.3 3 24.79 14.02 14.02 14.02 26.29 Q960-D4.8-T3.0-3.0-3.0 960 4.8 3 15.25 8.14 8.14 8.14 15.26 Q960-D5.5-T3.0-3.0-3.0 960 5.5 3 19.31 10.69 10.69 10.69 20.04 Q345-D5.5-T6.0-6.0-6.0 345 5.5 6 20.86 10.69 10.69 10.69 20.04 Q345-D6.3-T6.0-6.0-6.0 345 6.3 6 26.47 14.02 14.02 14.02 26.29 Q460-D3.5-T6.0-6.0-6.0 460 3.5 6 9.10 4.33 4.33 4.33 8.11 Q460-D4.8-T6.0-6.0-6.0 460 4.8 6 15.94 8.14 8.14 8.14 15.26 Q690-D5.5-T6.0-6.0-6.0 690 5.5 6 20.33 10.69 10.69 10.69 20.04 Q690-D6.3-T6.0-6.0-6.0 690 6.3 6 26.35 14.02 14.02 14.02 26.29 Q890-D3.5-T6.0-6.0-6.0 890 3.5 6 8.97 4.33 4.33 4.33 8.11 Q890-D4.8-T6.0-6.0-6.0 890 4.8 6 15.72 8.14 8.14 8.14 15.26 表 3 承压破坏时抗剪承载力有限元值与规范值比较Table 3. Comparison of the FE values and the standard values of the shear capacity under bearing failure试件编号 钢材强度等级f/MPa 螺钉直径d/mm 钢板厚度t/mm 有限元值Pu/kN 规范值Pn/kN AISI GB EC AISC Q235-D3.5-T0.8-0.8-0.8 235 3.5 0.8 5.22 3.43 3.02 2.61 3.07 Q235-D6.3-T1.2-1.2-1.2 235 6.3 1.2 11.14 8.45 7.45 6.44 8.30 Q345-D4.8-T1.2-1.2-1.2 345 4.8 1.2 11.20 10.84 9.55 8.26 9.29 Q345-D5.5-T0.8-0.8-0.8 345 5.5 0.8 8.50 6.32 5.56 4.81 7.10 Q460-D3.5-T1.2-1.2-1.2 460 3.5 1.2 7.24 11.36 10.01 8.66 8.32 Q460-D4.8-T0.8-0.8-0.8 460 4.8 0.8 8.65 7.24 6.38 5.52 7.60 Q550-D5.5-T1.2-1.2-1.2 550 5.5 1.2 13.94 17.35 15.28 13.22 15.92 Q550-D6.3-T0.8-0.8-0.8 550 6.3 0.8 12.79 10.11 8.90 7.70 12.16 Q690-D3.5-T0.8-0.8-0.8 690 3.5 0.8 6.31 8.66 7.63 6.60 7.76 Q690-D6.3-T1.2-1.2-1.2 690 6.3 1.2 16.84 21.34 18.80 16.26 20.96 Q890-D4.8-T0.8-0.8-0.8 890 4.8 0.8 9.25 12.38 10.90 9.43 12.99 Q890-D5.5-T1.2-1.2-1.2 890 5.5 1.2 14.07 24.34 21.44 18.55 22.33 Q960-D3.5-T1.2-1.2-1.2 960 3.5 1.2 7.41 20.24 17.83 15.42 14.82 Q960-D5.5-T0.8-0.8-0.8 960 5.5 0.8 10.72 13.81 12.17 10.53 15.52 由表4可知,当螺钉连接处发生承压破坏时,有限元值分别与AISI、中国、欧洲和AISC规范计算值之比的平均值与变异系数分别为1.00、32%,1.18、52%,1.36、59%,1.06、37%。当螺钉连接处发生剪切破坏时,有限元值分别与AISI、中国和欧洲规范计算值之比的平均值与变异系数均为1.90、5%,与AISC规范之比的平均值与变异系数分别为1.02、5%。由此可以得出:① 当钢板发生承压破坏时,中国、欧洲和AISC规范设计公式偏保守,螺钉双面剪切连接抗剪承载力低估了18%、36%和6%,AISI规范计算值的平均值最接近有限元值。就变异系数而言,欧洲规范最大,中国规范次之,AISC规范较小,ASIS规范最小,但四者的变异系数均超过30%。分析认为影响螺钉连接构件承压破坏时抗剪承载力的因素较多,如螺钉直径、钢板厚度、钢材强度等级等,且各国规范的适用范围不尽相同,因此使得规范计算值比较离散。② 当螺钉发生剪切破坏时,AISI、中国和欧洲规范均过于保守,抗剪承载力低估了90%,变异系数较小,仅为5%。分析认为螺钉连接的方法决定了它的抗剪强度计算方法与螺栓连接有根本区别[1]。螺钉双面剪切连接时,螺钉处于双剪受力状态,使得螺钉双面剪切连接抗剪承载力大约是螺钉单面剪切连接抗剪承载力的2倍,但是二者之间绝不是简单的2倍关系,具体需要通过大量试验数据统计来确认。③ 由图11(a)可知,当钢板发生承压破坏时,虽然中美欧规范较保守,但有限元值与规范值之间的误差高达20%,部分规范计算值偏于不安全,且偏不安全的数据中AISI和AISC规范值居多,中国规范次之,欧洲规范最少。因此分析认为有必要提出能够更准确预测构件发生承压破坏时的螺钉双面剪切连接抗剪承载力设计公式。④ 由表2和图11(b)可知,当螺钉双面剪切连接构件发生螺钉剪切破坏时,AISC规范公式计算值与有限元值吻合较好且变异系数较小,二者之间的误差小于20%,因此螺钉双面剪切连接构件发生螺钉剪切破坏时使用AISC规范公式计算其抗剪承载力具有一定参考价值。
表 4 有限元值与规范值比值统计Table 4. Statistics of ratio of FE values to Standard values破坏模式 试件数量 Pu/Pn AISI GB EC AISC 承压 64组 平均值 1.00 1.18 1.36 1.06 COV/(%) 32 52 59 37 剪切/承压-剪切 60组 平均值 1.90 1.90 1.90 1.02 COV/(%) 5 5 5 5 注:螺钉抗剪强度为225 MPa[11]。 5 结论
本文采用验证后的ABAQUS有限元模型对自攻螺钉双面剪切连接抗剪性能进行研究,讨论了不同钢材强度等级、钢板厚度、螺钉直径及中间钢板厚度对螺钉双面剪切连接破坏模式和抗剪承载力的影响。通过分析讨论得出以下结论:
(1) 螺钉双面剪切连接会发生3种破坏模式:承压破坏、承压-剪切破坏和剪切破坏。其中对于钢板厚度为0.8 mm和1.2 mm的试件,螺钉连接处均发生钢板承压破坏;对于钢板厚度为3.0 mm或6.0 mm的试件,螺钉连接处均会发生螺钉剪切破坏。但螺钉剪切破坏形式与钢材强度等级和螺钉直径以及钢板厚度有关,当钢板厚度为3.0 mm、钢材强度等级小于460 MPa且螺钉直径大于3.5 mm或钢材强度等级为460 MPa且螺钉直径为6.3 mm时,连接件会发生钢板承压-螺钉剪切破坏。当钢板厚度为6.0 mm或钢板厚度为3.0 mm且螺钉直径为3.5 mm或钢材强度等级不小于460 MPa时,连接件会发生螺钉剪切破坏形式。
(2) 对于螺钉双面剪切连接构件,当钢板厚度不超过3.0 mm时,其抗剪承载力会随着钢材强度等级和钢板厚度的增加而增大,并在厚度超过3.0 mm时趋于稳定。此外,增加螺钉直径同样可以提高此类构件的抗剪承载力,且二者呈线性关系,当钢材强度等级在一定范围内提高时,螺钉直径对构件抗剪承载力的影响将逐渐增大。另外,当构件的中间钢板厚度在一定范围增加,也可显著提高其抗剪承载力。
(3) 当钢板发生承压破坏时,中国、欧洲和AISC规范公式计算值偏于保守,AISI规范计算值较接近有限元值,但四者的变异系数均超过30%,且部分规范计算值偏于不安全;当螺钉发生剪切破坏时,AISI和中欧规范过于保守,且误差均超过20%。AISC规范公式计算值与有限元值吻合较好,且变异系数较小,因此,螺钉双面剪切连接构件发生螺钉剪切破坏时,使用AISC规范公式计算具有一定参考价值。
(4) 通过分析比较可知,目前已有规范设计公式不适用于螺钉双面剪切连接构件发生承压破坏时其抗剪承载力设计,有必要提出能够更准确预测构件发生承压破坏时的螺钉双面剪切连接抗剪承载力设计公式。另外,自攻螺钉连接也存在明显的群体效应,因此,后续可针对不同的板厚、螺钉间距、螺钉排列方式以及螺钉数量对螺钉双面剪切连接抗剪性能开展进一步研究。
-
钢材强度
等级屈服强度
fy/MPa极限强度
fu/MPa弹性模量
E/GPa屈服应变
εy极限应变
εuQ235 235 305 206 0.0011 0.0351 Q345 345 448 206 0.0017 0.0517 Q460 460 550 206 0.0022 0.0459 Q550 550 670 206 0.0027 0.0609 Q690 690 770 206 0.0033 0.0422 Q890 890 940 206 0.0043 0.0286 Q960 960 980 206 0.0047 0.0144 表 2 剪切破坏时抗剪承载力有限元值与规范值比较
Table 2 Comparison of the FE values and the standard values of the shear capacity under shear failure
试件编号 钢材强度等级f/MPa 螺钉直径d/mm 钢板厚度t/mm 有限元值Pu/kN 规范值Pn/kN AISI GB EC AISC Q235-D3.5-T3.0-3.0-3.0 235 3.5 3 8.56 4.33 4.33 4.33 8.11 Q235-D4.8-T3.0-3.0-3.0 235 4.8 3 15.21 8.14 8.14 8.14 15.26 Q550-D5.5-T3.0-3.0-3.0 550 5.5 3 19.78 10.69 10.69 10.69 20.04 Q550-D6.3-T3.0-3.0-3.0 550 6.3 3 24.79 14.02 14.02 14.02 26.29 Q960-D4.8-T3.0-3.0-3.0 960 4.8 3 15.25 8.14 8.14 8.14 15.26 Q960-D5.5-T3.0-3.0-3.0 960 5.5 3 19.31 10.69 10.69 10.69 20.04 Q345-D5.5-T6.0-6.0-6.0 345 5.5 6 20.86 10.69 10.69 10.69 20.04 Q345-D6.3-T6.0-6.0-6.0 345 6.3 6 26.47 14.02 14.02 14.02 26.29 Q460-D3.5-T6.0-6.0-6.0 460 3.5 6 9.10 4.33 4.33 4.33 8.11 Q460-D4.8-T6.0-6.0-6.0 460 4.8 6 15.94 8.14 8.14 8.14 15.26 Q690-D5.5-T6.0-6.0-6.0 690 5.5 6 20.33 10.69 10.69 10.69 20.04 Q690-D6.3-T6.0-6.0-6.0 690 6.3 6 26.35 14.02 14.02 14.02 26.29 Q890-D3.5-T6.0-6.0-6.0 890 3.5 6 8.97 4.33 4.33 4.33 8.11 Q890-D4.8-T6.0-6.0-6.0 890 4.8 6 15.72 8.14 8.14 8.14 15.26 表 3 承压破坏时抗剪承载力有限元值与规范值比较
Table 3 Comparison of the FE values and the standard values of the shear capacity under bearing failure
试件编号 钢材强度等级f/MPa 螺钉直径d/mm 钢板厚度t/mm 有限元值Pu/kN 规范值Pn/kN AISI GB EC AISC Q235-D3.5-T0.8-0.8-0.8 235 3.5 0.8 5.22 3.43 3.02 2.61 3.07 Q235-D6.3-T1.2-1.2-1.2 235 6.3 1.2 11.14 8.45 7.45 6.44 8.30 Q345-D4.8-T1.2-1.2-1.2 345 4.8 1.2 11.20 10.84 9.55 8.26 9.29 Q345-D5.5-T0.8-0.8-0.8 345 5.5 0.8 8.50 6.32 5.56 4.81 7.10 Q460-D3.5-T1.2-1.2-1.2 460 3.5 1.2 7.24 11.36 10.01 8.66 8.32 Q460-D4.8-T0.8-0.8-0.8 460 4.8 0.8 8.65 7.24 6.38 5.52 7.60 Q550-D5.5-T1.2-1.2-1.2 550 5.5 1.2 13.94 17.35 15.28 13.22 15.92 Q550-D6.3-T0.8-0.8-0.8 550 6.3 0.8 12.79 10.11 8.90 7.70 12.16 Q690-D3.5-T0.8-0.8-0.8 690 3.5 0.8 6.31 8.66 7.63 6.60 7.76 Q690-D6.3-T1.2-1.2-1.2 690 6.3 1.2 16.84 21.34 18.80 16.26 20.96 Q890-D4.8-T0.8-0.8-0.8 890 4.8 0.8 9.25 12.38 10.90 9.43 12.99 Q890-D5.5-T1.2-1.2-1.2 890 5.5 1.2 14.07 24.34 21.44 18.55 22.33 Q960-D3.5-T1.2-1.2-1.2 960 3.5 1.2 7.41 20.24 17.83 15.42 14.82 Q960-D5.5-T0.8-0.8-0.8 960 5.5 0.8 10.72 13.81 12.17 10.53 15.52 表 4 有限元值与规范值比值统计
Table 4 Statistics of ratio of FE values to Standard values
破坏模式 试件数量 Pu/Pn AISI GB EC AISC 承压 64组 平均值 1.00 1.18 1.36 1.06 COV/(%) 32 52 59 37 剪切/承压-剪切 60组 平均值 1.90 1.90 1.90 1.02 COV/(%) 5 5 5 5 注:螺钉抗剪强度为225 MPa[11]。 -
[1] 潘景龙. 自攻螺钉连接的抗剪性能研究[J]. 哈尔滨建筑大学学报, 1995, 28(6): 41 − 47. Pan Jinglong. A study on the shear behaviour of the self-tapping screw connection [J]. Journal of Harbin University of Architecture and Engineering, 1995, 28(6): 41 − 47. (in Chinese)
[2] 郝际平, 刘斌, 邵大余, 等. 冷弯薄壁型钢结构体系中自攻螺钉连接的抗剪性能试验研究[J]. 西安建筑科技大学学报(自然科学版), 2014, 46(6): 769 − 773. Hao Jiping, Liu Bin, Shao Dayu, et al. Experimental study on shear behavior of screw connections in cold-formed thin-wall steel structures [J]. Journal of Xi’an University of Architecture & Technology (Social Sciences Edition), 2014, 46(6): 769 − 773. (in Chinese)
[3] 石宇, 王身伟, 刘永健. 冷弯薄壁型钢单颗自攻螺钉抗剪连接性能研究[J]. 建筑科学与工程学报, 2014, 31(2): 57 − 64. doi: 10.3969/j.issn.1673-2049.2014.02.011 Shi Yu, Wang Shenwei, Liu Yongjian. Research on the shear behavior of single tapping screw connection in cold-formed thin-walled steel structure [J]. Journal of Architecture and Civil Engineering, 2014, 31(2): 57 − 64. (in Chinese) doi: 10.3969/j.issn.1673-2049.2014.02.011
[4] 李元齐, 潘斯勇. 自攻螺钉连接承载力研究现状[J]. 结构工程师, 2008, 24(6): 154 − 158. doi: 10.3969/j.issn.1005-0159.2008.06.030 Li Yuanqi, Pan Siyong. Research progress on self-drilling screw connection capacity [J]. Structural Engineers, 2008, 24(6): 154 − 158. (in Chinese) doi: 10.3969/j.issn.1005-0159.2008.06.030
[5] 卢林枫, 张亚平, 方文琦, 等. 冷弯薄壁型钢自攻螺钉连接抗剪性能试验研究及数值分析Ⅱ: 数值分析[J]. 中南大学学报(自然科学版), 2013, 44(8): 3493 − 3502. Lu Linfeng, Zhang Yaping, Fang Wenqi, et al. Experimental investigation and numerical analysis on shear-bearing capacity for self-drilling screw connections of cold-formed thin-walled steel Ⅱ: Numerical analysis [J]. Journal of Central South University (Science and Technology), 2013, 44(8): 3493 − 3502. (in Chinese)
[6] 王小平, 房玉松. 自攻螺钉连接抗剪承载力的有限元建模方法[J]. 武汉大学学报(工学版), 2012, 45(1): 75 − 79. Wang Xiaoping, Fang Yusong. Finite element modeling method of anti-shear capacity of self-drilling screw connection [J]. Engineering Journal of Wuhan University, 2012, 45(1): 75 − 79. (in Chinese)
[7] Feng R Q, Cai Q, Ma Y, et al. Shear analysis of self-drilling screw connections of CFS walls with steel sheathing [J]. Journal of Constructional Steel Research, 2020, 167(4): 105842.
[8] Roy K, Lau H H, Ting T C H, et al. Experiments and finite element modelling of screw pattern of self-drilling screw connections for high strength cold-formed steel [J]. Thin Walled Structures, 2019, 145(12): 106393.
[9] Huynh M T, Pham C H, Hancock G J. Experimental behaviour and modelling of screwed connections of high strength sheet steels in shear [J]. Thin-Walled Structures, 2020, 146(1): 106357.
[10] Huynh M T, Pham C H, Hancock G J. Design of screwed connections in cold-formed steels in shear [J]. Thin-Walled Structures, 2020, 154(5): 106817.
[11] 刘楠. 自攻螺钉连接抗剪性能及其设计方法的研究[D]. 黑龙江: 哈尔滨工业大学, 2007. Liu Nan. Research on shear behavior and design method of self-tapping screw connecting [D]. Heilongjiang: Harbin Institute of Technology, 2007. (in Chinese)
[12] Zhou Lina, Chui Yinghei, Ni Chun. Influence of middle member thickness on properties of double-shear nail joints [J]. Journal of Structural Engineering, 2018, 144(8): 04018109. doi: 10.1061/(ASCE)ST.1943-541X.0002126
[13] Varoglu E, Karacabeyli E, Stiemer S F, et al. Midply wood shear wall system: Concept and performance in static and cyclic testing [J]. Journal of Structural Engineering, 2006, 132(9): 1417 − 1425. doi: 10.1061/(ASCE)0733-9445(2006)132:9(1417)
[14] Varoglu E, Karacabeyli E, Stiemer S F, et al. Midply wood shear wall system: Performance in dynamic testing [J]. Journal of Structural Engineering, 2007, 133(7): 1035 − 1042. doi: 10.1061/(ASCE)0733-9445(2007)133:7(1035)
[15] Zheng W, Lu W D, Liu W Q, et al. Lateral loading behavior of glulam frame-midply hybrid lateral systems [J]. Construction and Building Materials, 2019, 220: 53 − 63. doi: 10.1016/j.conbuildmat.2019.05.182
[16] Zheng W, Lu W D, Liu W Q, et al. Experimental investigation of laterally loaded double-shear-nail connections used in midply wood shear walls [J]. Construction and Building Materials, 2015, 101: 761 − 771. doi: 10.1016/j.conbuildmat.2015.10.100
[17] 周绪红, 邹昱瑄, 徐磊, 等. 冷弯薄壁型钢-钢板剪力墙抗震性能试验研究[J]. 建筑结构学报, 2020(5): 65 − 75. Zhou Xuhong, Zou Yuxuan, Xu Lei, et al. Seismic behavior of cold-formed thin-walled steel plate shear wall [J]. Journal of Building Structures, 2020(5): 65 − 75. (in Chinese)
[18] Brière V, Santos V, Colin A. Rogers. Cold-formed steel centre-sheathed (mid-ply) shear walls [J]. Soil Dynamics and Earthquake Engineering, 2018, 114(11): 253 − 266.
[19] 周绪红, 姚欣梅, 石宇, 等. 六层足尺冷弯薄壁型钢钢板剪力墙结构房屋抗震性能振动台试验研究[J]. 土木与环境工程学报(中英文), 2020, 42(4): 203 − 204. Zhou Xuhong, Yao Xinmei, Shi Yu, et al. Shake table tests on seismic performance of six-storey full scale cold-formed steel-steel plate shear wall structure buildings [J]. Journal of Civil and Environmental Engineering, 2020, 42(4): 203 − 204. (in Chinese)
[20] Yanagi N, Yu C. Effective strip method for the design of cold-formed steel framed shear wall with steel sheet sheathing [J]. Journal of Structural Engineering, 2013, 140(4): 04013101.
[21] 曹春利, 孙志娟, 刘继良, 等. 低剪跨比的榫卯连接装配整体式剪力墙受力性能数值分析[J]. 工程力学, 2021, 38(增刊): 110 − 118. doi: 10.6052/j.issn.1000-4750.2020.05.S020 Cao Chunli, Sun Zhijuan, Liu Jiliang, et al. Numerical analysis on mechanical behaviors of assembled monolithic concrete shear walls with mortise-tenon joints and low shear span ratio [J]. Engineering Mechanics, 2021, 38(Suppl): 110 − 118. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.05.S020
[22] 张颖, 王元清, 张俊光, 等. 铝合金网壳结构箱型-工字型盘式节点单肢受力性能有限元分析[J]. 工程力学, 2020, 37(增刊): 130 − 138. doi: 10.6052/j.issn.1000-4750.2019.04.S021 Zhang Ying, Wang Yuanqing, Zhang Junguang, et al. Finite element analysis on mechanical performance of single-limbed box-I section member temcor joints in aluminum alloy spatial reticulated shell structures [J]. Engineering Mechanics, 2020, 37(Suppl): 130 − 138. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.04.S021
[23] 张曼, 韩振林, 孙健, 等. 高温下自攻螺钉搭接连接薄钢板抗剪性能研究[J]. 建筑钢结构进展, 2020(5): 108 − 117. Zhang Man, Han Zhenlin, Sun Jian, et al. Research on the behavior of screwed shear lapped connections of thin steel sheet at elevated temperature [J]. Progress in Steel Building Structures, 2020(5): 108 − 117. (in Chinese)
[24] 石宇, 周绪红, 管宇, 等. 冷弯薄壁型钢屋架受力性能及杆件计算长度研究[J]. 建筑结构学报, 2019, 40(11): 65 − 75. Shi Yu, Zhou Xuhong, Guan Yu, et al. Study on mechanical behavior and effective length of cold-formed thin-walled steel roof truss [J]. Journal of Building Structures, 2019, 40(11): 65 − 75. (in Chinese)
[25] 施刚, 朱希. 高强度结构钢材单调荷载作用下的本构模型研究[J]. 工程力学, 2017, 34(2): 50 − 59. doi: 10.6052/j.issn.1000-4750.2015.09.0799 Shi Gang, Zhu Xi. Study on constitutive model of high-strength structural steel under monotonic loading [J]. Engineering Mechanics, 2017, 34(2): 50 − 59. (in Chinese) doi: 10.6052/j.issn.1000-4750.2015.09.0799
[26] 邓露, 钟玉婷, 杨远亮, 等. 冷弯薄壁型钢受弯构件承载力与延性优化研究[J]. 工程力学, 2021, 38(4): 93 − 101. doi: 10.6052/j.issn.1000-4750.2020.05.0327 Deng Lu, Zhong Yuting, Yang Yuanliang, et al. Optimization on bearing capacity and ductility of cold-formed thin-walled steel flexural member [J]. Engineering Mechanics, 2021, 38(4): 93 − 101. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.05.0327
[27] 蔡健, 巫博璘, 罗翼锋, 等. 新型双层钢板-混凝土组合剪力墙力学性能研究[J]. 工程力学, 2020, 37(10): 134 − 144. doi: 10.6052/j.issn.1000-4750.2019.10.0680 Cai Jian, Wu Bolin, Luo Yifeng, et al. Mechanical behavior research of a new type of double-skin steel-concrete shear wall [J]. Engineering Mechanics, 2020, 37(10): 134 − 144. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.10.0680
[28] Usefi N, Ronagh H, Sharafi P. Numerical modelling and design of hybrid cold-formed steel wall panels [J]. Thin-Walled Structures, 2020, 157(5): 107084.
[29] AISI S100-2007, North American specification for the design of cold-formed steel structural members [S]. Washington, D. C. : American Iron and Steel Institute, 2007.
[30] ANSI/AISC 360-16, Specification for structural steel buildings [S]. American Institute of Steel Construction, 2016.
[31] GB 50018−2002, 冷弯薄壁型钢结构技术规范 [S]. 北京: 中国计划出版社, 2002. GB 50018−2002, Technical code of cold-formed thin-walled steel structures [S]. Beijing: China Planning Press, 2002. (in Chinese)
[32] EN 1993-1-3: 2006, Eurocode 3, Design of steel structures - Part 1-3 General rules – Supplementary rules for cold-formed members and sheeting [S]. Brussels: The European Committee for Standardization, 2006.
[33] Choung J, Shim C-S, Song H-C. Estimation of failure strain of EH36 high strength marine structural steel using average stress triaxiality [J]. Marine Structures, 2012, 29(1): 1 − 21. doi: 10.1016/j.marstruc.2012.08.001
[34] 张雪丽, 张耀春. 基于ANSYS的自攻螺钉波峰连接的抗剪性能有限元分析[J]. 建筑钢结构进展, 2010, 12(2): 23 − 29. Zhang Xueli, Zhang Yaochun. Finite element analysis for shearing resistance of screw connections in crest-fixed profiled steel sheeting [J]. Progress in Steel Building Structures, 2010, 12(2): 23 − 29. (in Chinese)
-
期刊类型引用(3)
1. 陈桂龙,孙新宇. 轻钢建筑屋面板连接件破坏临界风速计算方法研究. 高速铁路技术. 2025(02): 57-61 .  百度学术
百度学术
2. 熊刚,折志伟,李环宇,石宇,刘宜丰,姜雪. 冷弯薄壁型钢-结构防火一体板自攻螺钉连接性能试验研究. 土木与环境工程学报(中英文). 2024(03): 134-143 .  百度学术
百度学术
3. 朱兆一,李晓文,蔡应强,陈清林,彭苗娇,熊云峰. 船体开孔薄板面内剪切屈曲特性研究. 工程力学. 2023(05): 228-235 .  本站查看
本站查看
其他类型引用(4)



 下载:
下载: