DOUBLE NONLINEAR HYPERELASTIC THEORY AND EXPERIMENTAL RESEARCH ON THE LARGE DEFORMATION OF NATURAL RUBBER BEARING IN COMPRESSION AND SHEAR
-
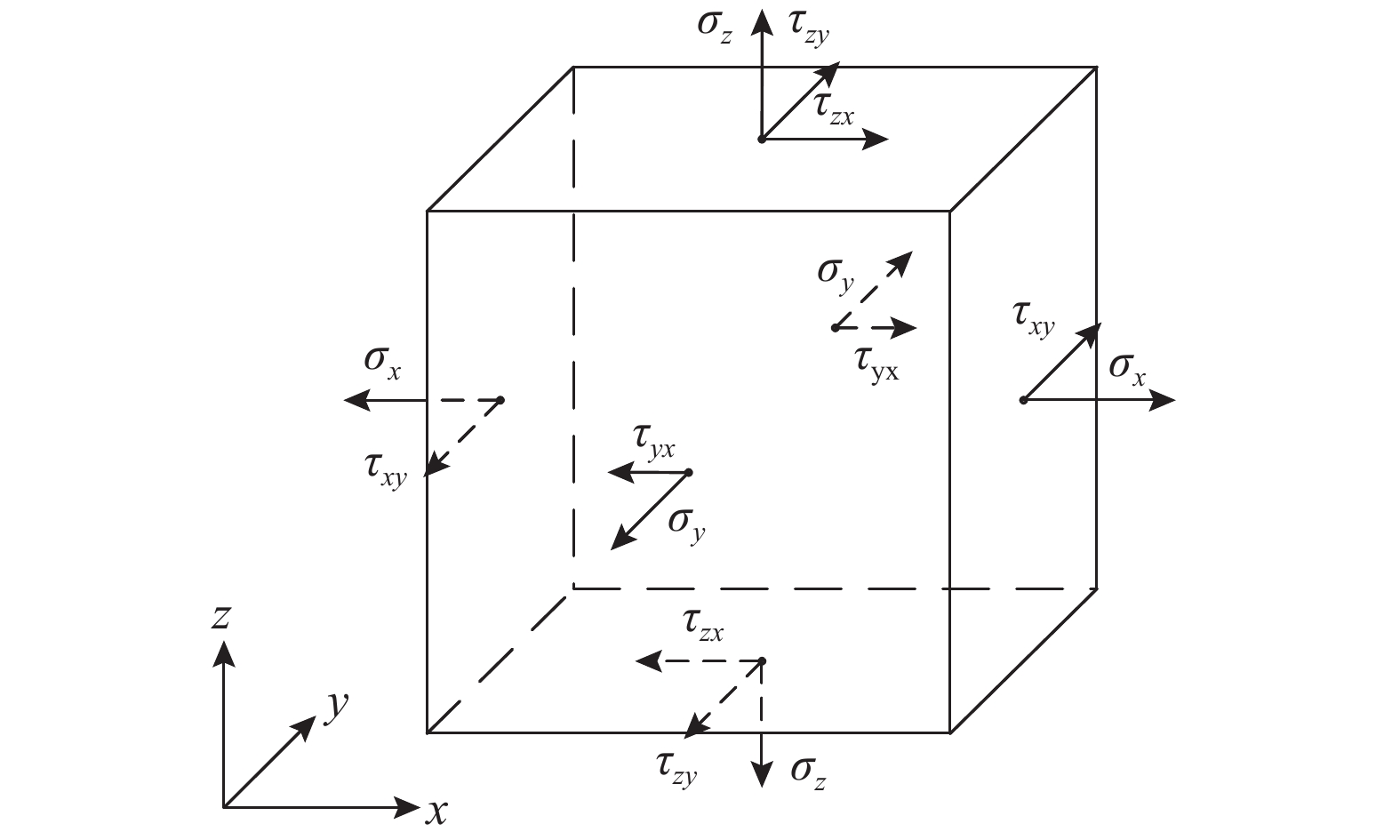
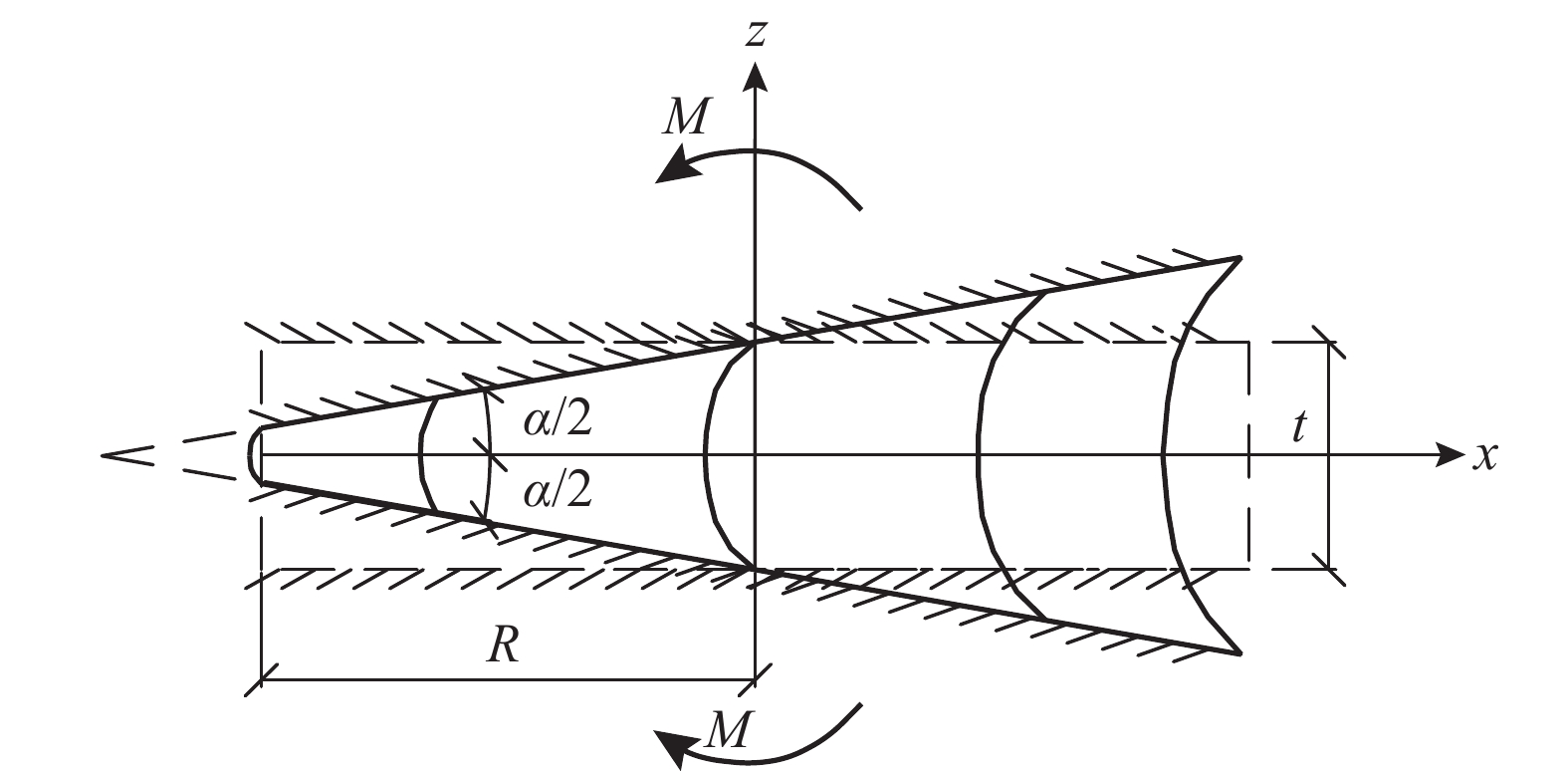
摘要: 基于非线性固体力学已经形成与材料微观结构紧密结合的发展局面，该文从微观上橡胶的超弹性本构方程出发，推导出单层橡胶内任一点的竖向应力满足调和函数，进一步对竖向应力积分得到单层橡胶的单轴等效弹性模量
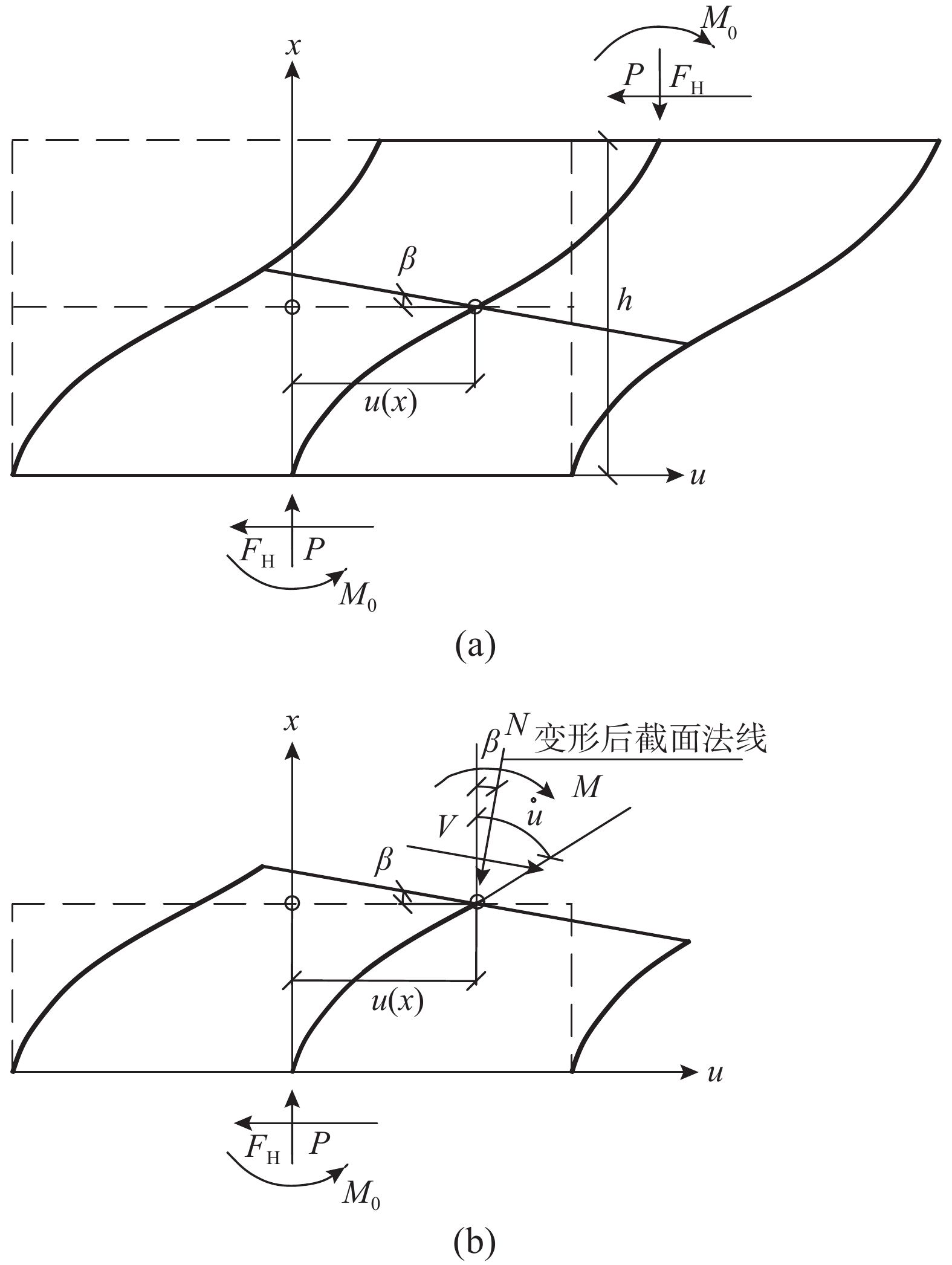
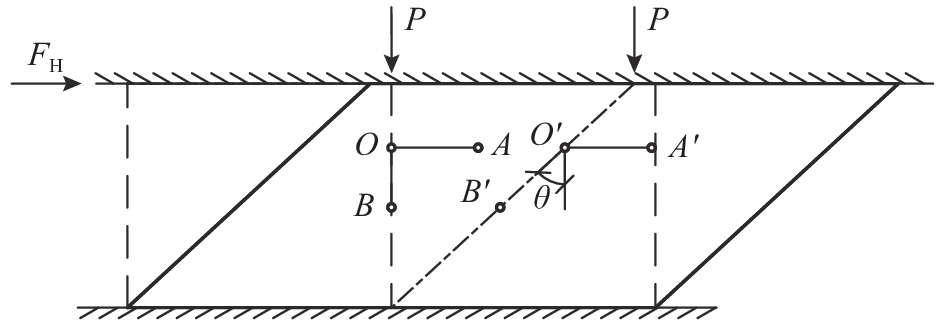
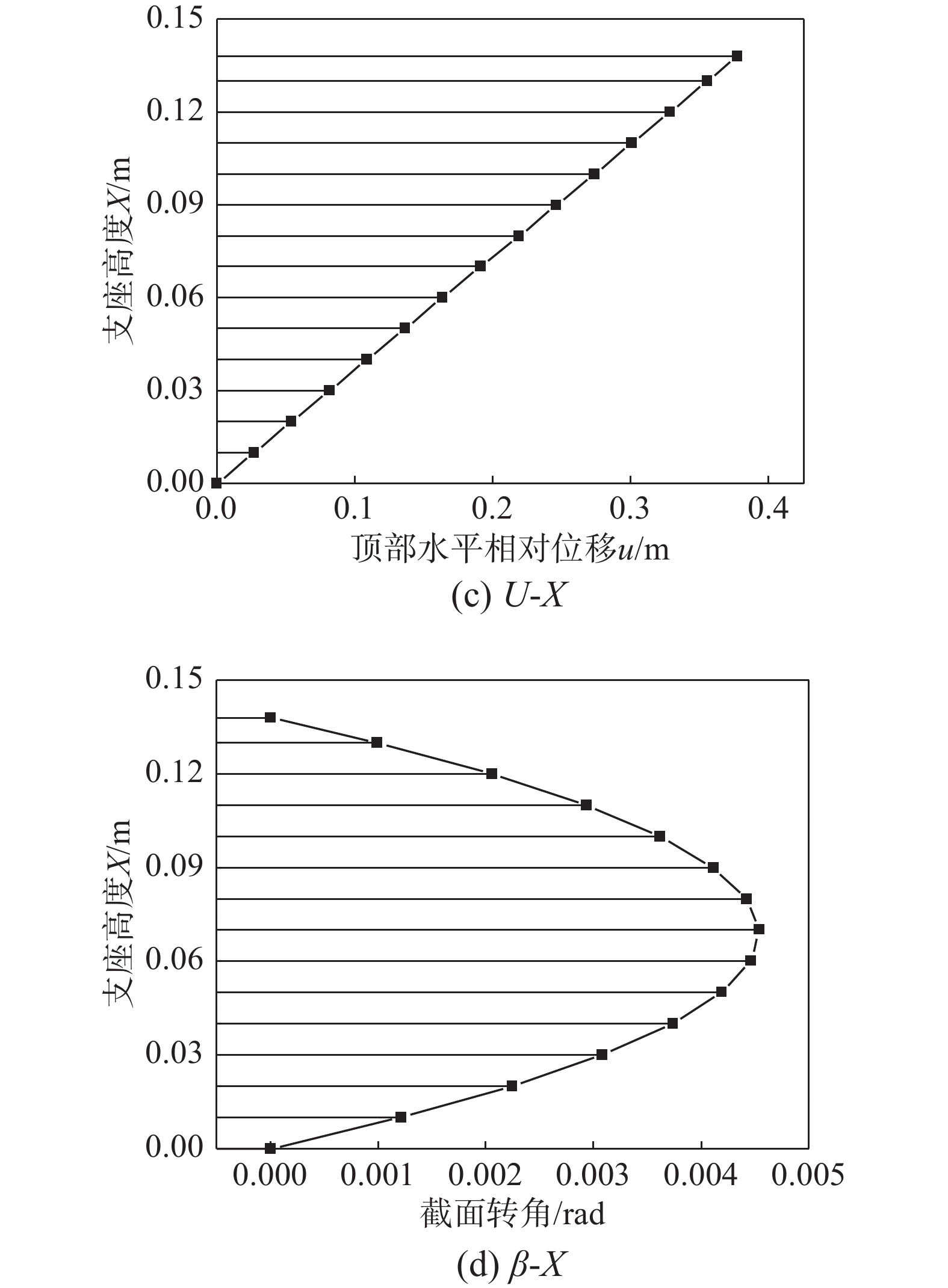
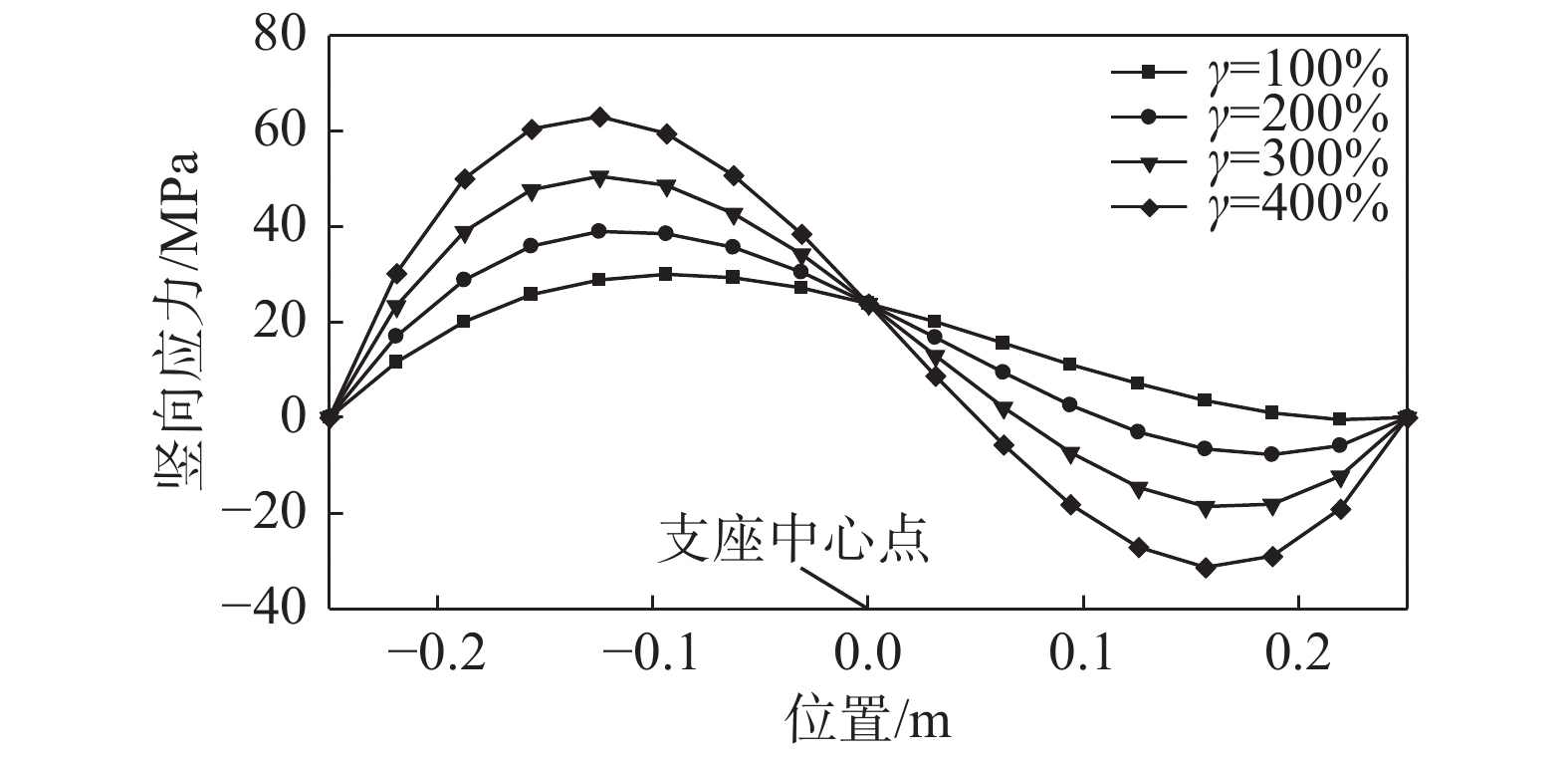
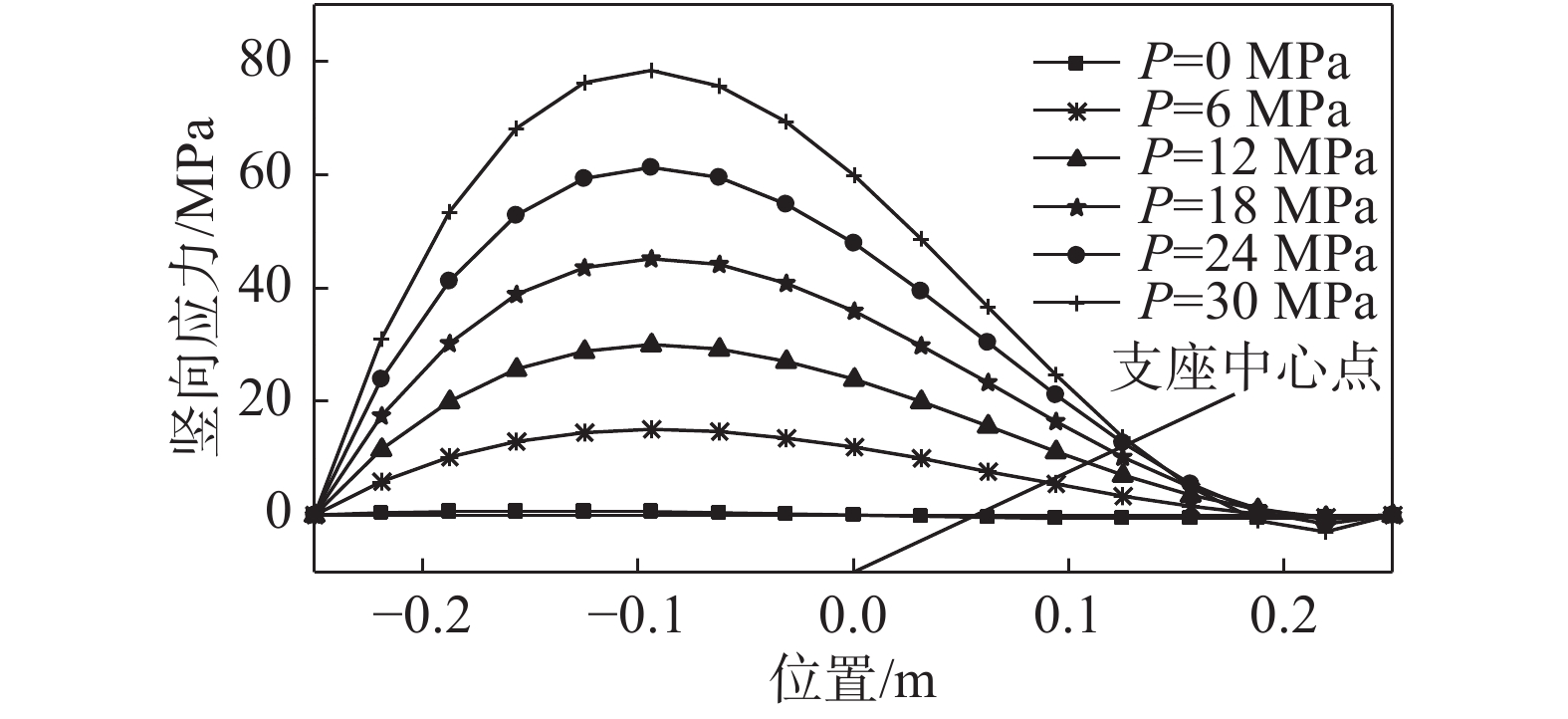
Ec 与纯弯等效弯曲刚度EcIs 。将隔震橡胶支座等效为符合Ec 与EcIs 的均质体，建立橡胶支座在两种外部荷载同时作用下，能宏观反映剪切变形与弯曲程度的偏微分平衡方程，并得到通用解答，解决了橡胶支座竖向与水平两种荷载耦合作用时大剪切变形的几何非线性问题。在此基础上，开展了足尺隔震橡胶支座压剪实验，依据实验剪切模量G 和水平剪应变γ 曲线，得到的支座水平推力FH 和γ 的实验曲线与理论曲线几乎完全重叠，即通过将材料非线性引入以上微分平衡方程，实现了超弹性橡胶支座大剪切变形的双非线性问题。通过以上解答，得到了隔震橡胶支座内力分布规律，对判断支座薄弱部位有明确的指导意义。随后，对隔震橡胶支座比较重要的两个特性(剪应变相关性，轴压力相关性)进行了对比分析，结果表明：随着轴力增大，橡胶支座的P-Δ效应并不明显，而橡胶内应力的变化不可忽视，同时，剪应变越大，压力相关性越强。可以采用该文的理论方法，通过传感器监测到支座内部应力反演支座水平推力与位移，从而实现地震作用时隔震建筑的健康监测。Abstract: Based on the fact that the development of nonlinear solid mechanics has been closely integrated with the material microstructure, it derived the vertical stress satisfying the harmonic function at any point from the super-elastic constitutive equation of the rubber; further, the uniaxial equivalent elastic modulusEc and the pure bending equivalent bending stiffnessEcIs of the single-layer rubber were obtained from the vertical stress integration. The seismic isolation rubber bearing was equivalent to a homogeneous body conforming toEc andEcIs , and the partial differential equilibrium equation macroscopically reflecting the degree of shear and bending deformation of the rubber bearing was established in the simultaneous action of two external load, and its general solution was obtained. The difficulties of the geometrical non-uniformity of large shear deformation of rubber support were solved in the vertical and horizontal loads. On this basis, a full-scale seismic isolation test of rubber bearing for compression and shear experiment was carried out. According to the experimental shear modulusG and horizontal shear strainγ curves, the experimental curves of the horizontal thrustFH andγ of the bearing were obtained. It was almost completely overlapped with the theoretical curve. Therefore by introducing the material nonlinearity into the above differential equilibrium equation, the double nonlinear problem of large shear deformation of the superelastic rubber bearing was solved. Through the above answers, the internal force distribution law of the rubber bearing was obtained, which has a clear guiding significance for judging the weak part of the bearing. Subsequently, the comparative analysis of two more important characteristics (shear strain correlation and axial pressure correlation) of the rubber bearing was carried out, the results showed that as the axial force increased, the P-Δ effect of the rubber bearing was not obvious, but the change of internal stress in the rubber couldn't be ignored, Concurrently, the greater the shear strain was, the stronger the pressure dependence was. The horizontal thrust and displacement of the support can be obtained through the sensor monitoring the internal stress of the support, achieving the health monitoring of the isolated building during the earthquake. -
拉索是大跨度桥梁关键受力构件，具有自重轻、柔度大、阻尼低等特点，在风力作用下极易发生大幅振动，严重时可造成结构损伤累积甚至结构破坏。实际桥梁工程中常出现多根拉索相邻布置的情况，如斜拉桥拉索、悬索桥吊索以及悬索桥主缆等。这类布置方式易引发复杂的气动干扰效应，并导致大幅拉索尾流振动。开展拉索尾流致振及气动减振控制研究，对拉索构件设计以及桥梁安全运营具有重要的现实意义。
拉索多为圆柱外形，其尾流干扰效应本质上属于存在流体介质内的圆柱绕流及弹性振动问题。串列布置形式下的双圆柱有着较强的相互作用[1]。当流体流经上游圆柱之后，在上游圆柱的尾流末端形成一个尾流区，下游圆柱位于尾流区域内，受到上游圆柱的尾流区流场影响，下游圆柱的振动受到抑制或者促进，反过来影响上游圆柱的尾流区域的流态，尾流区域的变化使得上、下游圆柱的振动响应发生相应变化。
圆柱体的二维绕流与雷诺数和圆柱间距有着密切的关系，随着雷诺数从由低到高，会出现许多的流动形态。FARELL[2]研究了亚临界至临界区内流场参数的变化。SCRUTON[3]对不同截面柱体的雷诺数效应进行总结，并指出在不同雷诺数区间下阻力系数的变化规律。ZDRAVKOVICH[4 − 5]通过试验发现，他认为在串列圆柱的绕流中存在一个临界间距，在临界间距前后流态存在明显的区别。WANG等[6]在正弦来流下研究了在临界间距比下三种流动模式的影响参数。李欢等[7]利用测压试验和流动可视化研究了间隙比、间距比及雷诺数对圆角方柱-矩形板系统的气动特性和绕流形态的影响。
在桥梁拉索风致振动领域，李永乐等[8]、胡建华等[9]通过节段气弹模型研究了拉索中心距、风向角等对尾流斜拉索振动的影响。杜晓庆等[10]研究了风攻角、雷诺数和阻尼比等参数对尾流涡激振动和尾流驰振的影响，探讨了尾流驰振的雷诺数效应。李寿英和黄君等[11]首先测得了不同相对坐标下双吊索尾流索的振动响应规律并研究了不同阻尼比下尾流索股运动响应随风速的变化规律，基于上述试验数据DENG等[12]采用有限差分法对所建立的运动方程进行了数值求解，结果与西堠门大桥现场观测的主要特征吻合较好。邵林媛等[13]通过测压手段研究了斜拉索在亚临界至超临界雷诺数范围气动力的变化，重点研究了气动力和压力分布在临界雷诺数区间的演变规律。
气动措施是控制拉索风致振动的高效方法，主要通过改变拉索截面形状或表面特征等方式来改变原有的流场，具有结构简单、成本低、工程实用性强等优点。OWEN等[14]通过改变圆柱的截面形状，发现波浪轴的圆形截面体可以显著抑制旋涡脱落，按螺旋线排列的球状突起同样具有较好的减阻和抑制旋涡脱落的控制效果，且在相对很小的质量阻尼参数下，涡激振动就可以被完全抑制。卢照亮等[15]发现在高雷诺数下表面粗糙度对斜拉索振动起到抑制的效果，并且随着粗糙度的增加，雷诺数效应减小。
然而，目前针对串列拉索尾流致振特性的研究还不充分，串列拉索作为多圆柱体系中最常见的一种布置方式，相较于其他布置形式具有更强的气动干扰作用[16 − 18]，系统的流场更加复杂，旋涡与结构的耦合过程难以分辨。已有的研究中往往采用一个固定拉索后跟随一个弹性支承拉索作为研究对象，以降低分析难度。这种方法本质上是研究上游拉索尾流对下游拉索的影响，属于尾流激振的范畴，但忽略了下游拉索振动对上游索的影响，无法反映实际工程应用中多拉索体系的情况。同样的，国内外学者对串列双索尾流致振的机理做了很多研究，能够在一定程度上解决拉索结构尾流驰振的问题，但围绕串列拉索结构以及超大跨斜拉桥大尺度拉索结构间的尾流干扰效应的研究很少，对其在高雷诺数下的尾流致振动现象认识不够深入，针对雷诺数效应影响下的串列拉索尾流致振的相关研究则更为缺乏，导致研究在工程应用上存在一定局限性。
本文选取串列拉索构件作为研究对象，采用不同缩尺比的模型，开展了亚临界、临界、超临界雷诺数环境下的串列拉索自由振动试验。基于这些试验深入探究了气动干扰效应和尾流振动特征，并研究各种气动措施的振动控制效果，为串列拉索设计与控制措施选取提供参考。
1 试验概况
1.1 风洞实验室
自由振动试验在同济大学 TJ-2风洞与TJ-7风洞试验进行。TJ-2 号边界层风洞，试验段长 15 m、 宽 3 m、高 2.5 m。风洞动力系统由功率 530 kW 的直流电机驱动，空风洞可控风速范围为 1 m/s~68 m/s，湍流度Iu ≤ 0.5%，风速均匀性指标δU/U ≤ 1%，气流竖向和水平偏角均小于0.5°，流场可近似为均匀流。TJ-7号风洞为小型直流吹气式风洞，主要由风机动力段、扩散段、稳定段、收缩段、试验段和出口段组成，试验段截面尺寸宽0.65 m、高1.20 m。TJ-7风洞试验风速范围为1 m/s~15 m/s连续可调，背景湍流强度小于 1%，气流不均匀性及气流不稳定性均<2%。
1.2 节段模型
为系统性研究串列拉索的尾流致振问题，本节通过多种尺度拉索模型的风洞试验对串列圆形拉索尾流致振开展了一系列研究，并重点分析不同雷诺数范围下的振动规律。试验对雷诺数Re、斯托拉哈数St以及斯柯诺顿数Sc等相似比关系进行了准确模拟，并对结构非线性参数进行识别，以尽可能还原实际结构在工程中的风环境。如下给出各个参数的计算公式和物理意义。
(1)斯托拉哈数(Strouhal number)
St=nsDU (1) 式中：ns为物体绕流的旋涡脱落频率；D为横截面特征尺寸；U为流体平均速度，斯托拉哈数作为常用的相似准则，表征了非定常运动的惯性力和来流惯性力之间相对大小。
(2)雷诺数(Reynolds number)
Re=ρDUμ=DUν (2) 式中：ρ为空气密度；μ为空气的动力黏性系数；v为空气的运动黏性系数。惯性力和黏性力是影响流动形态的两个主要参数，它们之间的相对大小决定了流动类型的性质特点，用于区分流动的类型，雷诺数就作为表征流动的惯性力和黏性力之间的比值相似准则，它反映了流体的惯性力和黏性力之间的比例关系，也称黏性参数。
(3)斯柯诺顿数(Scruton number)
Sc=4πmζρD2 (3) 式中：m为拉索单位长度的质量；ζ为结构阻尼比；ρ为空气密度；D为拉索直径。如表达式所示，它表示结构阻尼和结构-流体质量比的综合影响。
模型设计参数如表1所示。整个支架采用钢桁架进行拼装，两侧各设计了8根可供悬吊的吊杆，以便悬挂两根试验模型，并可针对试验所需的风偏角以及模型倾角进行模拟。整个支架可悬挂质量超过200 kg的物体，并能在50 m/s风速下保持静止。
表 1 拉索不同缩尺比模型设计参数Table 1. Design parameters for cylinder with different scale ratio类别 参数 小尺寸模型 中尺寸模型 大尺寸模型 尺寸 直径D/m 0.025 0.100 0.200 长度L/m 0.600 1.500 1.500 等效质量 质量m/(kg/m) 3.3 12.5 53 振动频率 顺风向fx/Hz 2.78 3.50 1.75 横风向fy/Hz 2.78 3.50 1.75 阻尼比 顺风向ξx/(%) 0.1 0.4 0.4 横风向ξy/(%) 0.1 0.4 0.4 无量纲参数 Sc数 52.2 52.2 52.2 Re数 2.33 × 104 3.33 × 105 6.67 × 105 试验材料 铸铁 铸铁 HDPE外护套管 风洞试验中受到实验室风速上限与风洞截面尺寸限制，通常采用降低试验尺度的方式进行试验，这导致了试验雷诺数的减小，可能影响试验结果的准确性。因此，在进行风洞试验时需要考虑试验的雷诺数效应。本文结合TJ-2边界层风洞可实现高风速的特点，采用多种尺寸缩尺模型进行风洞试验研究，小尺寸、中等尺寸与大尺寸节段模型可以实现针对亚临界雷诺数(Re≤2×105)、临界雷诺数(2×105≤Re≤5×105)与超临界雷诺数(5×105≤Re≤4×106)范围的模拟。三种不同缩尺比模型涵盖了阻力平稳段以及下降段，较为完整地模拟了拉索结构的阻力变化效应，重现了与实桥相同的雷诺数环境[19 − 23]，具体如图1所示。
![]()
2 串列拉索自由振动试验
2.1 试验设置和工况安排
图2给出了迎风侧拉索和尾流侧拉索在空间上的相对位置关系，三种比例节段模型分别在TJ-7(图2(a))与TJ-2号(图2(b)、(图2(c)))风洞试验段进行试验。根据风洞试验室的风速范围，为尽可能实现更高雷诺数区间下的试验模拟，分别取14 m/s与50 m/s作为试验的最高风速。同时试验中心距L/D取为2.5~9，覆盖尾流干扰效应的主要发生区域，并实现在成桥状态时最小中心距下的尾流干扰效应模拟。表2给出了模型自由振动试验工况汇总。
表 2 模型自由振动试验工况汇总Table 2. Summary of free vibration testing cases of the model工况设置 模型比例 小尺寸 中等尺寸 大尺寸 振动类型 自由振动 自由振动 自由振动 振动自由度 2 2 2 中心距L/D 3∶1.5∶9 2.5∶0.5∶4.5 2.5∶0.5∶4.5 模型倾角α 0° 20° 20° 试验风速U/(m/s) 1~14，△U=1 1~50，△U=2 1~50，△U=2 模拟雷诺数范围 亚临界 临界 超临界 2.2 试验结果
2.2.1 试验雷诺数效应
三种缩尺比模型在不同雷诺数区间下的风洞试验结果分别由图3~图5给出，图中对振幅和风速进行了无量纲化处理，Arms为模型振幅信号的最大均方根值，U为来流风速单位，f为模型固有频率，D为模型直径。结果表明：在不同尺寸模型风洞试验中下游拉索均出现尾流驰振现象，振动发生在中心距为3D~4.5D范围内。亚临界雷诺数发生尾流驰振的不利间距为4.5D，而临界雷诺数与超临界雷诺数分别为 3D和3.5D。在临界雷诺数区间发生了尾流驰振发散的现象，同时上游拉索也出现大幅驰振，上游与下游拉索最大振幅Arms分别为0.42D和0.85D。然而，在相同的折减风速范围下，亚临界与超临界雷诺数试验中的下游拉索最大振幅Arms仅为临界雷诺数最大振幅Arms的12%和21%。此外，在超临界雷诺数范围内，当中心距较小(L=2.5D)时，观察到下游拉索存在类似涡振锁定区间的限幅振动现象，振幅随风速呈现先增大后减小的变化。
![]()
图 3 亚临界雷诺数拉索位移响应随风速变化关系曲线(小尺寸节段模型)Figure 3. Subcritical Reynolds number cable displacement response versus wind speed relationship (small size sectional model)![]()
图 4 临界雷诺数拉索位移响应随风速变化关系曲线(中等尺寸节段模型)Figure 4. Critical Reynolds number cable displacement response versus wind speed relationship (medium size sectional model)![]()
图 5 超临界雷诺数拉索位移响应随风速变化关系曲线(大尺寸节段模型)Figure 5. Supercritical Reynolds number cable displacement response versus wind speed relationship (large size sectional model)2.2.2 亚临界雷诺数尾流驰振特性
为探究串列拉索在亚临界雷诺数下发生尾流驰振的机理，结合测力试验讨论不同中心距下的下游拉索气动力特性及其对尾流振动的影响。测力天平采样频率为512 Hz，采样时长为120 s。测力试验首先对单拉索的气动阻力系数以及Strouhal 数进行了验证，试验结果与图3中的试验结果保持一致，验证了该试验装置的可靠性。
图6给出了下游拉索平均阻力系数、Strouhal 数以及脉动升力、阻力系数随中心距的变化规律，并与相关学者的研究结果进行了对比验证[24 − 25]。图6(a)表明，平均阻力系数随着中心距L/D的增大而逐渐增大，当中心距L/D由3变为3.5时，增大较为明显。图6(b)表明：Strouhal 数随着中心距的增大呈现先减小后增大的趋势，并在中心距L/D=3时达到最小，为0.142。当中心距L/D由3变为3.5时，Strouhal 数出现显著的增大趋势，由最低值0.142增大到0.183，说明流经上游拉索的尾流与下游拉索表面之间的相互作用变得更加剧烈，产生了更为强烈的旋涡脱落。
拉索尾流中的旋涡脱落是造成拉索振动的主要原因，脉动力系数(均方根升力和阻力系数)直接影响着拉索的振动幅值，图6(c)反应了下游拉索脉动升力系数随中心距的变化情况，脉动升力与Strouhal 数的变化趋势较为接近，脉动升力系数在L/D=3时达到最小值0.245，在L/D=3.5时达到最大值1.178，并随着中心距的进一步增大缓慢减小。试验结果表明，拉索表面的脉动升力系数并非是随着中心距的增大而线性变化的，而是存在一个临界中心距，且在该间距下拉索表面的流场将发生显著性的改变。结合图6(b)结果可以推断，是该间距下更强烈的旋涡脱落导致了下游拉索表面升力的显著变化。图6 (d)表明，下游拉索表面的脉动阻力系数随着中心距增大呈现先增大后减小的规律。
结合上述气动力参数随中心距的变化情况，本文试验结果与前述研究的结果相近，均发现当中心距L/D由3逐渐增大的过程中，下游拉索表面气动力特性发生显著变化，旋涡脱落强度明显增强，气动升力不稳定性加剧。这些因素可能导致下游拉索发生失稳，进而产生图3的试验结果。
2.2.3 临界雷诺数尾流驰振特性
图7展示了临界雷诺数下发生尾流驰振时的振动特性随风速的变化关系。在试验风速范围内，下游拉索共发生了两次振动幅值大幅增加的过程，其中第一次大幅振动发生在由亚临界雷诺数进入临界雷诺数时。通常当雷诺数接近临界点(约2×105)时，分离点的位置在拉索两侧的边缘，此时尾流宽度相当大，超过了拉索体的直径，旋涡的脱落仍是颇有规律的。当雷诺数超过临界点时，流动的分离点突然迁移到后侧，使得尾流变窄同时旋涡的脱落也变得随机而无规律。其中，在2×105~5×105雷诺数范围内，拉索表面上所形成的边界层内发生层流向湍流的过渡。进入该雷诺数范围时，下游拉索振动幅值似乎发生了锁定，保持稳定。
![]()
图 7 临界雷诺数尾流驰振特性随风速变化关系曲线(中等尺寸节段模型)Figure 7. Critical Reynolds number wake galloping characteristics versus wind speed relationship (medium size sectional model)但当Re=2.93×105时，上游拉索横风向产生了较为显著的振动现象，并随着雷诺数的增大而产生更大的振幅，同时下游拉索发生了尾流驰振发散现象。在试验风速范围内，上游与下游拉索始终以结构固有频率fn进行振动，振动频率f0不受振幅的显著增加而改变。上游拉索与下游拉索运动相位差在临界雷诺数范围内波动较小，约为-175°，且当下游拉索出现尾流驰振发散现象时，仍对相位差影响较小。
通常情况下，上游拉索一般不会发生大幅振动的现象。LIN等[26]对倾角为20°的单拉索进行了风偏角效应风洞测力试验，与本文试验模型的倾角保持完全一致。研究发现当β=90°时(对应于本文β=0°)将会出现“阻力危机”效应，同时在临界雷诺数(2×105≤Re≤5×105)与超临界雷诺数范围(Re≥5×105)，阻力系数相较于其它风偏角β均为最大值，并且数值存在极大差异。对于升力系数，在临界雷诺数(Re=2×105~5×105)区间下变化十分剧烈，随雷诺数增大呈现先增大后减小的变化规律，当雷诺数为4×105时达到升力系数的最大值，并随着雷诺数进入超临界范围而趋于稳定。在本文风洞试验中，图4的上游拉索发生大幅振动时对应的雷诺数为3×105，在该雷诺数区间上游拉索将会受到急剧变化的升力作用且上游与下游拉索之间存在复杂的气动干扰关系。由此可推测，可能是两者的共同作用使得上游拉索发生失稳产生大幅振动，并进一步诱发下游拉索发生尾流驰振发散现象。
2.2.4 超临界雷诺数尾流致振特性
图8 给出了超临界雷诺数下尾流致振特性随风速变化关系曲线。在这些工况下尾流致振出现类似涡振现象，振幅发展曲线呈现锁定区间且不随风速的增大而继续增大。起振过程发生在试验雷诺数处于临界雷诺数与超临界雷诺数边界(Re=5×105)，在该雷诺数范围上游与下游拉索在不同程度上都产生了振幅先增大后减小的锁定现象，其中下游结构的振幅锁定区间更为显著，最大振幅达到了0.19D。在振幅锁定区间前、后以及锁定区内，上游与下游拉索始终以结构固有频率发生振动，与临界雷诺数范围下的试验结论一致。但上游与下游拉索间的相位差受到振幅变化带来的影响，相位差由发生大幅振动时的−40°减小到约−20°，表现为随振动幅值的减小而减小，并最终随振幅趋于稳定并保持在−20°。
![]()
图 8 超临界雷诺数尾流致振特性随风速变化关系曲线(大尺寸节段模型)Figure 8. Supercritical Reynolds number wake-induced vibration characteristics versus wind speed relationship (large size sectional model)针对串列圆柱在超临界雷诺数下的尾流干扰效应，Gu[27]对Re=4.52×105的串列圆柱开展了固定状态下的测压风洞试验，试验中心距为L/D =1.1~3.0。该研究中的“过渡间距”正好与图5下游圆柱发生大幅振动时的中心距L/D = 2.5一致，同时该研究中的雷诺数4.52×105也与起振过程雷诺数4.7×105极为接近。结合GU[27]的研究可知，该起振状态中，上游拉索分离出来的剪切层尾部可能直接作用于下游拉索。考虑上述试验结果(图5)，推测当上游拉索分离出来的剪切层尾部直接作用于下游拉索时，易导致下游拉索失稳并发生尾流致振。
3 振动控制试验
通过对串列双拉索的自由振动试验，发现在不同雷诺数试验环境下将可能产生显著的尾流驰振现象，振动幅值随风速的增大而逐渐增大甚至发散，对于桥梁结构安全造成极大隐患。因此，本节基于亚临界雷诺数与超临界雷诺数节段模型自由振动风洞试验，考虑风偏角带来的影响，通过对拉索缠绕螺旋线、增加表面粗糙度的方式减小其最大振幅。表3为小尺寸、大尺寸节段模型自由振动减振试验工况设计。
表 3 振动控制试验工况汇总表Table 3. Summary table of vibration control testing cases工况设置 模型比例 小尺寸 大尺寸 振动类型 自由振动 自由振动 振动自由度 2 2 中心距L/D 4.5 2.5~4.5，△L/D=0.5 减振措施 螺旋线表面粗糙度 双螺旋线检修栏杆 风偏角β 0° 15°和30° 试验风速U/(m/s) 1~14，△U=1 1~50，△U=2 模拟雷诺数范围 亚临界 超临界 3.1 亚临界雷诺数振动控制结果
图9 展示了采用直径为0.08D的螺旋线以2D~7D(△D=1)间距进行缠绕时，下游拉索位移响应随风速变化的曲线(P代表螺旋线间距)，图10则给出采用三种分别为NO.100、NO.240、NO.600粗糙度的砂纸模拟拉索表面粗糙度时下游拉索位移响应结果。在均匀流场中，当螺旋线间距P=2D时，下游拉索的最大振幅为0.4D，出现了较光滑拉索更为显著的尾流驰振现象。不同螺旋线间距对上游拉索振幅无明显影响，对下游拉索振幅影响较大。当螺旋线间距为3D~7D时，下游拉索的最大振幅均小于无螺旋线拉索的最大振幅。随着螺旋线间距的增大，下游拉索的最大振幅逐渐降低，尾流驰振现象消失。螺旋线间距增大到6D和7D时，仍具有较好的减振效果，尾流驰振现象消失，且下游拉索的最大振幅有大幅度的下降。表面粘贴NO.240砂纸的减振效果最明显，由无减振措施的拉索的最大振动幅值0.32D减少到了0.14D。改变表面粗糙度对下游拉索的减振效果显著，且在试验风速范围内均起到显著的减振效果。
![]()
图 9 缠绕螺旋线的下游拉索位移响应与风速关系曲线Figure 9. Relationship between the displacement response of the downstream cable and wind speed with a helical wrapping![]()
图 10 粘贴不同粗糙度砂纸的下游拉索位移响应与风速关系曲线Figure 10. Relationship between the displacement response of the downstream cable with different roughness sandpapers attached and wind speed![]()
图 11 超临界雷诺数下气动措施下位移响应与风速关系曲线(L/D=4.5)Figure 11. Displacement response versus wind speed relationship curve under aerodynamic measures at supercritical Reynolds numbers(L/D=4.5)3.2 超临界雷诺数振动控制结果
依据超临界雷诺数节段模型自由振动试验结果，考虑为上游和下游拉索通过缠绕螺旋线的方式实现针对上游拉索出现的涡振以及下游拉索出现的尾流驰振现象的抑制。试验采用直径为0.03D的螺旋线以4D的间距进行缠绕，其中上游和下游拉索分别按顺时针和逆时针的方式缠绕。
超临界雷诺数节段模型在气动措施下位移响应随风速变化关系曲线如图11所示。TOKOROA等[28]研究发现在间距比4.3D，风偏角为β=15°时振动最为显著，LIU等[29]发现单圆柱涡激振动主要发生在风偏角为15°~30°的情况下。因此，选取拉索中心距4.5D和风偏角β=15°及β=30°作为拉索风致干扰最不利工况。在此工况下，拉索表面缠绕螺旋线可以避免下游拉索发生尾流驰振，在试验风速范围内最大振幅仅为光滑拉索最大振幅的0.14倍。随着风偏角的增大，上游光滑拉索将发生大幅振动，添加螺旋线能降低最大振幅，提高上游拉索的抗风性能。但值得注意的是，螺旋线提高上游拉索抗风性能的同时也造成下游缠绕螺旋线拉索发生更为不利的大幅振动，造成此现象的原因可能是上游拉索常规旋涡脱落受到了抑制，两拉索间气动干扰增加，从而导致了下游拉索表面气动特性发生变化。
4 结论
本文对大跨桥梁的串列拉索索尾流致振及气动减振控制问题进行研究。通过采用不同缩尺比的模型考虑不同雷诺数的影响，进行了串列拉索的自由振动试验。基于这些试验深入探究了气动干扰效应和尾流振动特征，并研究各种气动措施的振动控制效果。对于拉索振动部分的深入分析，将会在后续的工作中通过测压试验或者CFD计算进行机理方面的解释。主要结论如下：
(1)串列拉索的中心距对其振动性能影响显著。在亚临界、临界与超临界雷诺数等不同区间条件下，最大振幅与不利中心距均存在显著差异，不利中心距主要集中在2.5D~4.5D范围内，说明从塔顶鞍座处到散索鞍座处局部出现明显振动。
(2)串列拉索自由振动具有显著的雷诺数效应。亚临界状态下结构振动响应最小；临界状态下结构尾流驰振发散；超临界雷诺数区间上游与下游拉索的相互作用影响显著，下游拉索在多个中心距下发生连续的尾流涡振-驰振现象。
(3)亚临界雷诺数试验中，缠绕螺旋线与添加表面粗糙度不会造成上游拉索振幅的增加；螺旋线间距增大到6D和7D时，具有较好的减振效果；表面粘贴NO.240砂纸使最大振动幅值从0.32D减少到了0.14D。但在超临界雷诺数试验中，缠绕螺旋线存在潜在的尾流致振动风险。
-
![]()
图 7 剪切模量G与剪应变
γ 计算程序框图Figure 7. Block diagram for calculation program of shear modulus G and shear strain
γ ![]()
图 8 隔震橡胶支座压剪
G−γ 实验、理论曲线(P=12 MPa)Figure 8. Compression-shear
G−γ experiment and theoretical curve of vibration isolation rubber bearing (P=12 MPa)![]()
图 9 隔震橡胶支座
FH−γ 理论、实验曲线(P=12 MPa)Figure 9. Compression-shear
FH−γ experiment and theoretical curve of vibration isolation rubber bearing (P=12 MPa)![]()
图 10 沿截面高度内力
M、V 及运动量μ、β 的分布图Figure 10. Distribution diagram of internal force
M、V and movement amountμ、β along the section height![]()
图 11 轴压不变、不同剪应变时橡胶支座竖向应力分布图
注：压为正，拉为负
Figure 11. The vertical stress distribution diagram of the rubber bearing when the axial pressure is constant and the shear strain is different
![]()
图 12 不同轴压，支座顶端水平位移与内力变化图
Figure 12. The horizontal displacement of the top of the support and the internal force change diagram under different axial pressure
![]()
图 13 剪应变100%、不同轴压支座顶部竖向应力变化图
注：压为正，拉为负
Figure 13. The vertical stress change diagram on the top of the support, with 100% shear strain and different axial compression
![]()
图 14 剪应变400%、不同轴压支座顶部竖向应力变化图
Figure 14. The vertical stress change diagram on the top of the support, with 400% shear strain and different axial compression
![]()
图 15 剪应变100%、400%，不同轴压下支座顶部竖应力对比图
注：压为正，拉为负
Figure 15. Comparison of the vertical stress on the top of the support, when the shear strain is 100%, 400%, and different axial compressions
表 1 橡胶支座尺寸
Table 1 Size of rubber bearing
材料 单层厚度t/
mm层数n/
个总厚度/
mm支座半径R/
mm支座总高h/
mm橡胶 5.81 16 93 250 138 钢板 3.00 15 45 
下载: 导出CSV
表 2 等截面不同材料属性对比
Table 2 Comparison of different material properties of equal section
材料参数(刚度) 等效均质体 HRB335钢 C40混凝土 G/(N/mm2) 0.89 8.32×104 1.35×104 Ec/(N/mm2) 2.47×103 2.00×105 3.25×104 A(As)/mm2 2.91×105 1.96×105 1.96×105 I(Is)/mm4 4.55×109 3.07×109 3.07×109 EI(EcIs)/(N·mm2) 1.13×1013 6.14×1014 9.97×1013 GAs/hr(GA/h)
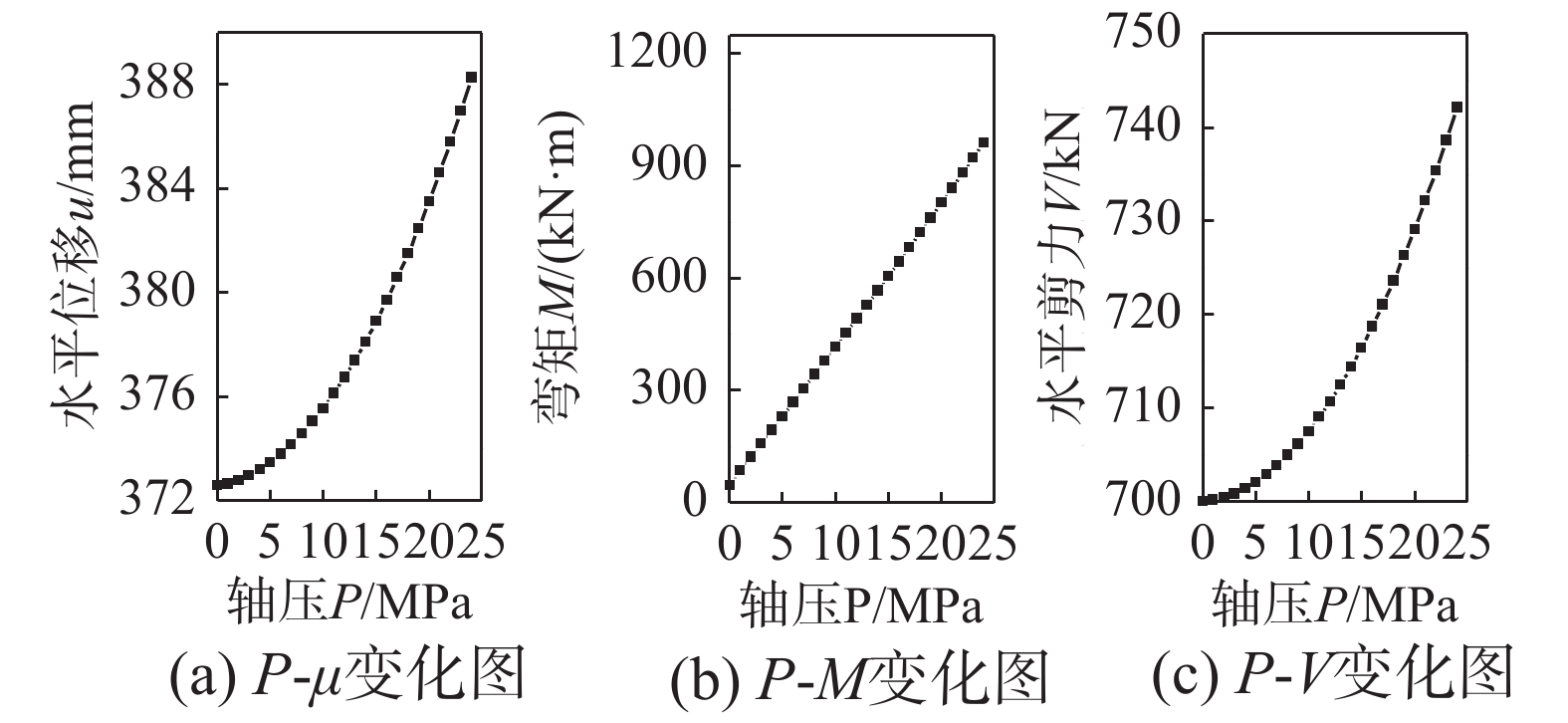
/(N/mm)2.79×103 1.18×108 1.92×107
下载: 导出CSV
表 3 不同轴力下，支座顶部截面内力与水平位移理论值
Table 3 The theoretical values of the internal force and horizontal displacement of the top section of the support, under different axial forces
竖向轴力P/MPa 顶部μ/mm 支座M/(kN·m) 跨中V/kN 0 372.6 48.3 700.0 2 372.8 121.5 700.4 4 373.2 194.9 701.4 6 373.8 268.5 702.9 8 374.6 342.5 705.0 10 375.6 417.0 707.5 12 376.7 492.1 710.7 14 378.1 568.0 714.4 16 379.7 644.7 718.7 18 381.5 722.5 723.6 20 383.5 801.4 729.1 22 385.8 881.5 735.3 24 388.3 963.2 742.2
下载: 导出CSV
表 4 纯剪切内力与位移理论值
Table 4 Theoretical values of internal force and displacement in pure shear
竖向轴力
P/kN水平力
FH/kN顶部水平位移最大值
μmax/mm支座弯矩
M/(kN·m)跨中剪力
V/kN弯曲位移{\mu _{\rm E}} 剪力位移{\mu _{\rm G}} 0 700 2.553×10−3 372.5 48.3 700.0
下载: 导出CSV
-
[1] Anil K Chopra. 结构动力学理论及其在地震工程中的应用[M]. 第四版. 谢礼立, 吕大刚, 等 译. 北京: 高等教育出版社, 2016. Anil K Chopra. Structural dynamics theory and its application in earthquake engineering [M]. 4th ed. Translated by Xie Lili, Lü Dagang, et al. Beijing: Higher Education Press, 2016. (in Chinese)
[2] Haringx J A. On highly compressible helical springs and rubber rods and their application for vibration-free mountings [J]. Philips Research Reports 4, 1949: 49 − 80, 206 − 220.
[3] Kelly J M. Earthquake-resistant design with rubber [M]. Oxford: The Alden Press, 1993.
[4] Chang C H. Modeling of laminated rubber bearings using an analytical stiffness matrix [J]. International Journal Of Solids and Structures, 2002, 39(24): 6055 − 6078. doi: 10.1016/S0020-7683(02)00471-7
[5] Ding L, Zhu H P, Wu L. Analysis of mechanical properties of laminated rubber bearings based on transfer matrix method [J]. Composite Structures, 2017, 159: 390 − 396. doi: 10.1016/j.compstruct.2016.09.074
[6] 周福霖. 工程结构减震控制[M]. 北京: 地震出版社, 1997. Zhou Fulin. Seismic mitigation control of engineering structures [M]. Beijing: Seismological Press, 1997. (in Chinese)
[7] 日本建筑学会, 著. 隔震结构设计[M]. 刘文光, 译. 北京: 地震出版社, 2005. The Architectural Society of Japan. Seismic isolation structure design [M]. Translated by Liu Wenguang. Beijing: Earthquake Press, 2005. (in Chinese)
[8] Takaoka E. Nonlinear mechanical model for laminated rubber bearings subjected to monotonic loading based on Haringx's theory [J]. Journal of Structural and Construction Engineering, 2014, 79(701): 913 − 921. doi: 10.3130/aijs.79.913
[9] 郑哲敏. 非线性连续介质力学[J]. 中国科学院院刊, 1993(4): 283 − 289. Zheng Zhemin. Nonlinear continuum mechanics [J]. Bulletin of the Chinese Academy of Sciences, 1993(4): 283 − 289. (in Chinese)
[10] 黄可智. 非线性连续介质力学[M]. 北京: 清华大学出版社, 1989. Huang Kezhi. Nonlinear continuum mechanics [M]. Beijing: Tsinghua University Press, 1989. (in Chinese)
[11] Lindley Peter Brian. Effect of poisson's ratio on compression modulus [J]. Journal of Strain Analysis, 1968, 3(2): 142 − 145. doi: 10.1243/03093247V032142
[12] Lindley Peter Brian. Engineering design with natural rubber [M]. Great Britain: The Malaysian Rubber Producers Research Association, 1978.
[13] Gent AN. Elastic stability of rubber compression springs [J]. Mechanical Engineering Science, 1964, 6(318): 415 − 430.
[14] 徐芝纶. 弹性力学简明教程[M]. 第三版. 北京: 高等教育出版社, 2002. Xu Zhilun. A concise course of elasticity [M]. 3rd ed. Beijing: Higher Education Press, 2002. (in Chinese)
[15] GB 20688.3−2006, 建筑隔震橡胶支座[S]. 北京: 中国标准出版社, 2007. GB 20688.3−2006, Building vibration isolation rubber bearing [S]. Beijing: China Standard Press, 2007. (in Chinese)
[16] GB/T 20688.1−2007, 隔震橡胶支座试验方法 [S]. 北京: 中国标准出版社, 2007. GB/T 20688.1−2007, Test method for vibration isolation rubber bearings [S]. Beijing: China Standard Press, 2007. (in Chinese)
[17] 朱宏平, 沈文爱, 雷鹰, 等. 结构减隔震控制系统性能监测、评估与提升[J]. 工程力学, 2020, 37(1): 1 − 16. doi: 10.6052/j.issn.1000-4750.2019.05.ST06 Zhu Hongping, Shen Wen'ai, Lei Ying, et al. Performance testing, evaluation and improvement of structural seismic isolation control system [J]. Engineering Mechanics, 2020, 37(1): 1 − 16. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.05.ST06
[18] Makoto ohsaki, Tomoshi Miyamura, Masayuki Kohiyama, et al. Finite-element analysis of laminated rubber bearing of building frame under seismic excitation [J]. Earthquake Engineering and Structural Dynamics, 2015, 44: 1881 − 1898. doi: 10.1002/eqe.2570
[19] 朱宏平, 谭平, 叶昆. 极罕遇地震作用下铅芯橡胶隔震支座基础隔震结构抗震性能研究[J]. 建筑结构学报, 2019, 40(10): 122 − 131. Zhu Hongping, Tan Ping, Ye Kun. Investigation of seismic performance of LRB base-isolated structures subjected to extremely rare earthquakes [J]. Journal of Building Structures, 2019, 40(10): 122 − 131. (in Chinese)
[20] 袁涌, 魏威, 谭平. 一种基于改进超弹性 Zener 模型的高阻尼橡胶隔震支座速度相关性本构模型[J]. 土木工程学报, 2016, 49(3): 73 − 79. Yuan Yong, Wei Wei, Tan Ping. A rate-dependent constitutive model of high damping rubber bearing based on the improved hyperelastic Zener model [J]. China Civil Engineering Journal, 2016, 49(3): 73 − 79. (in Chinese)
[21] 李忠献, 高营, 李宁. 基于RSAPS平台的隔震单元模型[J]. 工程力学, 2016, 33(4): 144 − 149. doi: 10.6052/j.issn.1000-4750.2014.09.0768 Li Zhongxian, Gao Ying, Li Ning. RSAPS-based isolation element model [J]. Engineering Mechanics, 2016, 33(4): 144 − 149. (in Chinese) doi: 10.6052/j.issn.1000-4750.2014.09.0768
[22] 何文福, 许浩, 魏陆顺, 等. 多级性态隔震体系试验研究和结构动力响应分析[J]. 工程力学, 2018, 35(9): 107 − 116. doi: 10.6052/j.issn.1000-4750.2017.05.0370 He Wenfu, Xu Hao, Wei Lushun, el al. Experiment research and dynamic response analysis of high performance multi-level bearing [J]. Engineering Mechanics, 2018, 35(9): 107 − 116. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.05.0370
[23] 朱宏平, 周方圆, 袁涌. 建筑隔震结构研究进展与分析[J]. 工程力学, 2014, 31(3): 1 − 10. doi: 10.6052/j.issn.1000-4750.2013.05.ST05 Zhu Hongping, Zhou Fangyuan, Yuan Yong. Development and analysis of the research on base isolated structures [J]. Engineering Mechanics, 2014, 31(3): 1 − 10. (in Chinese) doi: 10.6052/j.issn.1000-4750.2013.05.ST05
[24] 彭天波, 李翊鸣, 吴意诚. 叠层天然橡胶支座抗震性能的实时混合试验研究[J]. 工程力学, 2018, 35(增刊): 300 − 306. doi: 10.6052/j.issn.1000-4750.2017.05.S058 Peng Tianbo, Li Yiming, Wu Yicheng. Real time hybrid test of seismic performance of laminated nature rubber bearings [J]. Engineering Mechanics, 2018, 35(Suppl): 300 − 306. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.05.S058
计量
- 文章访问数: 467
- HTML全文浏览量: 277
- PDF下载量: 95
