THE INFLUENCE OF BOX GIRDER SURFACE PRESSURE DISTRIBUTION ON FLUTTER STABILITY
-
摘要: 该文建立了箱梁表面压力与颤振导数之间的数学关系,探讨了表面压力的分布特性对箱梁颤振导数和颤振临界风速的影响。结合流固松耦合的计算方法,利用动网格技术模拟了箱梁的风致振动。采用分块分析方法研究了箱梁表面压力的局部特性对颤振导数以及系统振动能量的影响。研究结果表明:箱梁迎风侧风嘴附近的分布压力对模型振动的稳定性产生了不利的影响,而模型尾部的压力则有助于提高系统的颤振临界风速。当迎风侧的分布压力向模型尾部移动时,对箱梁颤振稳定性影响较大的颤振导数则会发生较显著的变化,箱梁的颤振临界风速也随之增加,因此断面迎风侧风嘴附近区域的分布压力对颤振导数和系统振动的稳定性影响最大。另外,迎风侧风嘴附近的区域也是振动系统吸收气动能量的主要部位,而箱梁尾部风嘴附近的区域则消耗系统的振动能量。箱梁表面压力与模型振动最大位移之间的相位差对颤振导数有较大影响,当相位差沿断面呈反对称分布,并使气动阻尼始终为负时,则有利于箱梁颤振的稳定性。Abstract: The relationship between box girder surface pressure and flutter derivatives was established. Based on qualitative and quantitative analyses, the influences of the pressure distribution along box girder on aerodynamic derivatives and flutter critical wind speed were discussed. Combined with fluid-structure loose coupling calculation method, the wind-induced vibration of the box girder was simulated by dynamic grid technique. The effects of pressure local characteristics on box girders’ main flutter derivatives and system vibration energy were investigated by using the block analysis method. The results show that the distribution pressures near the wind fairing on the model windward side are not conducive to box girder flutter stability, but the pressures on the model tail are helpful to improve the flutter critical wind speed. When the distribution pressure on box girder windward side moves to the model tail, the aerodynamic derivatives, which have a great influence on box girder flutter, have great changes, and the box girder flutter critical wind speed also increases. The local characteristics of pressures on the model windward side wind fairing have the greatest influence on flutter derivatives and system vibration stability. The aerodynamic force near the model windward side region transfers energy to the vibration system, while that near the model leeward side consumes system energy. The phase lag between the pressure and the model maximum displacement also has a great influence on flutter derivatives. When the phase lag along the model surface is antisymmetric and the aerodynamic damping force is always negative, it has a beneficial effect on system vibration stability.
-
Keywords:
- flutter derivatives /
- flutter critical wind speed /
- surface pressure /
- phase lag /
- box girders
-
箱梁是目前大跨度桥梁通常采用的截面形式。为提高其颤振临界风速,往往可以通过改变截面的气动外形来实现。但是箱梁的颤振与理想平板类似,多为弯扭耦合的颤振失稳形态,其发生的细观机理尚不够清楚。
SCANLAN等[1]引入航空领域颤振导数的概念,将作用在振动断面上自激力表述为结构运动状态与颤振导数的线性组合,并根据结构动力学方法建立了颤振运动控制方程,形成了完整的桥梁颤振分析理论。后来的研究者多以此为基础,开展了桥梁的颤振性能研究。CHEN[2]提出的宏观机理分析方法可以采用非迭代的手段研究颤振导数对系统颤振性能的影响。MATSUMOTO等[3-4]提出了分步分析方法求解耦合的颤振控制方程,并以此为基础,研究了多种断面的颤振导数和气动阻尼的变化规律。杨詠昕等[5]在Matsumoto研究思路的基础上,导出了二维三自由度耦合颤振分析方法,并用该方法研究了箱梁的颤振机理。丁泉顺等[6]也采用类似方法,探讨了扁平箱梁颤振的发生机理。这些对箱梁颤振机理的研究侧重于分析颤振过程中颤振导数的变化规律。
除此之外,鲜荣等[7]采用风洞节段模型试验研究了风嘴、栏杆、检修轨道以及导流板对箱梁颤振稳定性的影响。金挺等[8]通过对箱梁表面测压数据进行积分的方法研究了箱梁断面的雷诺数效应。任若松等[9]也采用表面测压方法对准流线型桥梁断面的表面压力分布规律进行了研究。赵林[10]通过节段模型测压试验分析了在箱梁颤振过程中,模型表面压力分布特性的变化规律。孟晓亮等[11]通过节段模型测振试验和计算流体力学的方法,分析了不同风嘴角度对箱梁颤振和涡振性能的影响。张伟等[12]利用流场显示技术研究了箱梁断面颤振过程中,模型周围流场的变化情况。这些研究分析了箱梁颤振过程中压力场和流场的变化规律,但是没有阐明模型表面压力分布特性是如何影响箱梁的颤振导数以及颤振稳定性的。ARGENTINI等[13]提出的分布式非定常气动力表达方法则聚焦于表面风压对颤振和抖振的影响。 LI等[14]采用微观机理分析方法,探讨了表面压力与颤振性能的联系,并绘制了气动阻尼的分布图。
从研究现状来看,目前从宏观和细观两个层面上都对箱梁的颤振机理进行了研究,但两个层面之间缺乏联系,很少将体现自激作用的颤振导数与模型表面的分布压力关联起来,因此也就缺乏对箱梁颤振机理深入认识。本文推导了颤振导数与模型表面压力之间的数学关系,研究了分布压力的空间作用位置以及相位分布特性对箱梁颤振导数和颤振临界风速的影响。通过对模型表面进行分区,研究了压力的局部特性对颤振导数和系统振动能量的影响。本项研究加深了对箱梁颤振发生机理的认识,为有效实施箱梁的颤振控制提供理论基础。
1 颤振导数与表面压力的联系
1.1 颤振导数与表面压力的数学关系
在空气中振动的桥梁断面,其运动状态与作用在模型上的自激气动力密切相关,而自激力是模型表面分布压力的合力。因此,为了深入理解箱梁断面颤振发生的本质就需要探讨箱梁颤振过程中模型表面分布压力的变化规律,并建立颤振导数与分布压力之间的数学关系式。
将推导模型表面分布压力与颤振导数之间的联系,通常采用8个颤振导数来描述的气动升力和升力矩[15-17],如式(1)所示:
Ls=12ρU2B×(KH∗1˙hU+KH∗2B˙αU+K2H∗3α+K2H∗4hB) (1) Ms=12ρU2B2×(KA∗1˙hU+KA∗2B˙αU+K2A∗3α+K2A∗4hB) (2) 式中:
Ls 和Ms 分别为作用在桥梁断面上的升力和升力矩;ρ 为空气密度;U 为来流风速;H∗i 、A∗i (i=1,2,⋯,4) 为颤振导数;K=Bω/U 为折减频率;B 为桥面宽度;h 和a 为模型竖向和扭转振动的位移。当仅发生扭转振动时,气动力可简化为:
Lsα=12ρU2B[KH∗2B˙αU+K2H∗3α] (3) Msα=12ρU2B2[KA∗2B˙αU+K2A∗3α] (4) 主梁断面处于颤振临界状态时,其模型的振动可近似认为是等幅的简谐振动,即扭转振动可以采用下列方程形式:
a(t)=a0cos(ωt) (5) 式中,
a0 和ω 为振动频率和振幅。因此,气动力
Lsα 、Msα 可以表达成下列形式:F(t)=Asin(ωt)+Bcos(ωt) (6) 周期性运动的模型,其表面压力
P 可分解为两部分:平均压力成份¯P 和周期性变化的成份⌢P 即:P=¯P+⌢P (7) 对周期性变化的压力
⌢P 沿模型表面积分就可以求出Lsα ,即Lsα=∫ba⌢Pdx 。由于Lsα 能表达成Asin(ωt)+Bcos(ωt) 的形式,因此,压力⌢P 就可以写成如下的形式。⌢P=A0sin(ωt)+B0cos(ωt)=⌢Cpsin(ωt+φ) (8) 式中:
⌢Cp 为压力变化的幅值,⌢Cp=√A20+B20 ;φ 表示了压力变化滞后于模型运动的相位差,φ=arctg(b/a) 。为便于比较,采用压力系数的形式来表述
⌢P :⌢P=⌢Cpsin(ωt+φ)=(1/2)ρU2{C∗psin(ωt+φ)} (9) 式中,
C∗p 为无量纲系数,C∗p=⌢Cp/(1/2)ρU2 。以扭转振动为例,求解如何采用表面压力来描述颤振导数
H∗2、H∗3 、A∗2、A∗3 。当模型仅发生扭转运动时,气动升力和升力矩Lα、Mα 可以表述为:Lα=∫xbxa12ρU2B{−C∗psin(ωt+φα)}dx (10) Mα=∫xbxa12ρU2B2{−C∗psin(ωt+φα)x}dx (11) 式中:
φα 为气动力与模型扭转运动之间的相位差;x 为沿模型宽度方向上的任意一点与模型中心之间的距离。联立式(3)~式(4)、式(10)~式(11),并通过比较系数可以求出
H∗2、H∗3 、A∗2、A∗3 这4个颤振导数:H∗2=U2B2ω2∫xbxaC∗p⋅sinφαdx,H∗3=−U2B2ω2∫xbxaC∗p⋅cosφαdx, A∗2=U2B2ω2∫xbxaC∗p⋅sinφαxdx,A∗3=−U2B2ω2∫xbxaC∗p⋅cosφαxdx (12) 同理,当模型仅做竖向振动时产生的气动升力和升力矩
Lh、Mh 可以表述为:Lh=∫xbxa12ρU2B{−C∗psin(ωt+φh)}dx (13) Mh=∫xbxa12ρU2B2{−C∗psin(ωt+φh)x}dx (14) 式中,
φh 为气动力与竖向运动之间的相位差。类似的,可以求出另外4个颤振导数
H∗1、H∗4 、A∗1、A∗4 的表达式:H∗1=−UBω∫xbxaC∗p⋅sinφhdx,H∗4=−UBω∫xbxaC∗p⋅cosφhdx, A∗1=−UBω∫xbxaC∗p⋅sinφhxdx,A∗4=−UBω∫xbxaC∗p⋅cosφhxdx (15) 需要特别说的是本文在进行上述公式推导时假设桥梁颤振临界状态的振动形式为等幅的简谐振动。其主要是基于以下几点考虑:
1)目前对于桥梁―气流系统线性颤振临界状态的分析通常是认为当处于颤振临界点时,系统的阻尼为零,系统的振动为等幅简谐振动,气流输入到系统的能量刚好等于系统的阻尼耗能。例如:塔科马大桥在坠毁之前就经历的较长时间的扭转振动,较多学者在对该桥的颤振机理进行分析时也大多假设结构的振动为等幅的简谐振动。另外,在采用强迫振动试验确定颤振导数时,也通常是强迫断面做等幅的简谐振动,从而获得作用在断面上的气动力,进而识别颤振导数。因此本文基于现有的方法,仍假设桥梁―气流系统线性颤振临界状态的运动形式为等幅的简谐运动。
2)这一假设仅适用于桥梁发生小幅振动,并且不考虑系统非线性影响因素的条件下。对于线性系统而言,如果系统的振动位移为等幅的简谐振动,那么输入到系统的气动力也应该是简谐振动形 式,气动力与振动位移之间只存在相位差。由于气动力是模型表面压力积分之和,因此如果气动力是按照简谐振动方程的形式发生变化,则模型表面的分布压力也可以近似认为是按照同样的规律发生变化。但是如果强烈的流固耦合作用使得气动力具有较强的非线性时(气动力含有高阶成份),这些假设条件就不再适用了。
1.2 数值实现途径
通过上述的理论分析可知,采用模型表面压力来求解颤振导数的关键是如何获取模型表面压力系数的幅值
C∗p 和相位差φ ,结合数值方法研究具体的实现过程,步骤如下(图1):1)设定振动频率
ω ,振动幅值及来流风速,采用数值方法结合动网格技术模拟结构的强迫振动。2)数值模拟时当结构运动状态达到平稳后,提取模型表面任意一点N个时刻的压力P,设
x 为n 个时刻,y 为与之相对应的压力P ,即:x=[t1,t2,⋯,tn] ,y=[P1,P2,⋯,Pn] 。3)针对模型表面的任意一点,采用函数
y=asin(ωx)+bcos(ωx)+c 来拟合步骤2中提取的N个时刻的压力值P,获得拟合函数的系数a 、b 、c 。4)对模型表面所有网格点采用上述方法求得系数
a 、b 、c 后就可以获得模型表面的压力分布特性。其中模型表面任意一点的压力幅值⌢Cp=√a2+b2 ,压力系数幅值⌢Cp=2√a2+b2/ρU2 ,相位差φ=arcsin(b/√a2+b2) ,¯P=c 。5)获得模型表面上任意点的压力幅值
⌢Cp 和¯P=c 后,就可以分析模型表面的压力分布特性,并确定与颤振导数相对应的压力分布特征。通过上述分析可知,我们可以通过系数
a 、b 、c 计算模型表面任意点的压力幅值⌢Cp 和相位差φ ,然后代入本文推导的颤振导数表达式中,就能得到采用模型表面压力来表述的颤振导数,以此为基础可以分析模型表面压力分布特性对颤振导数的影响。上述建立了颤振导数与模型表面压力之间的联系,为分析模型表面压力分布特性对箱梁颤振稳定性的影响提供了基础。需要说明的是采用表面压力来描述颤振导数时,需要获得压力幅值
C∗p 以及压力与振动位移之间的相位差φ 。这里的相位差定义为箱梁表面压力的峰值与模型振动最大位移之间的相位延迟。2 箱梁断面风致振动的数值模拟
根据上述建立的模型表面压力与颤振导数之间的数学关系,采用计算流体动力学方法(CFD)模拟了箱梁的强迫振动,提取了模型表面不同时刻的压力值,结合本文1.2节中提出的分析方法,研究了分布压力对颤振导数的影响。
箱梁断面以大海带桥的主梁为原型进行了缩尺,其几何尺寸如图2所示。应用商业软件Fluent进行数值模拟计算,计算域的选取如图3所示,计算时壁面附近最小网格尺寸为0.0004 m,计算域采用分块结构化网格。网格数量为15.6万。湍流模型采用基于RANS方法的
k−ωSST 两方程模型,压力速度耦合采用SIMPLE算法,求解器采用分离式。基于流固弱耦合的计算策略和动网格技术分别模拟了箱梁的竖向和扭转强迫振动。结合该模型的颤振风洞试验结果,设置计算风速为20.8 m/s,竖向振幅为1.8 cm,扭转幅值为2.4°,振动频率为6.05 Hz。计算域的上端和下端设为壁面边界条件。计算时间步长取
Δt=0.004s ,每次迭代计算的残差小于10−5 认为计算结果收敛。调整近壁面的第一层网格尺寸,使y+<5 (图4)。3 箱梁表面压力分布特性与颤振导数之间的联系
3.1 模型表面压力分布特点与颤振导数的关系
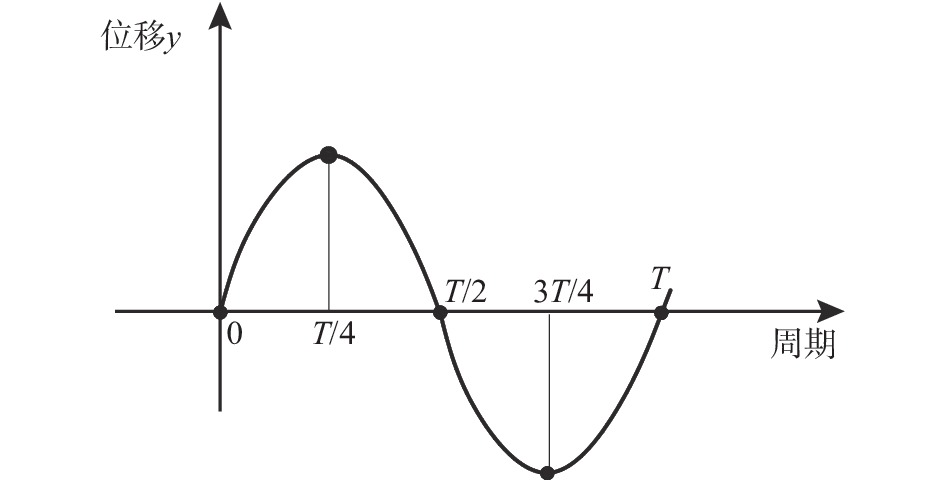
根据1.2节中的方法,研究了箱梁表面压力分布特点与颤振导数之间的关系。模型运动的相位定义如图5所示。为了说明数值拟合的精度,图6给出了模型分别处于平衡位置(T/2时刻),此时模型具有最大速度,以及模型运动到最大位移时(3T/4时刻),模型上下表面压力拟合的残差沿模型宽度方向的分布。从图6可以看出,数值拟合的残差绝大部分在5%以内,只是在个别点处拟合的残差超过了5%,因此拟合的精度满足要求。另外,图7给出了
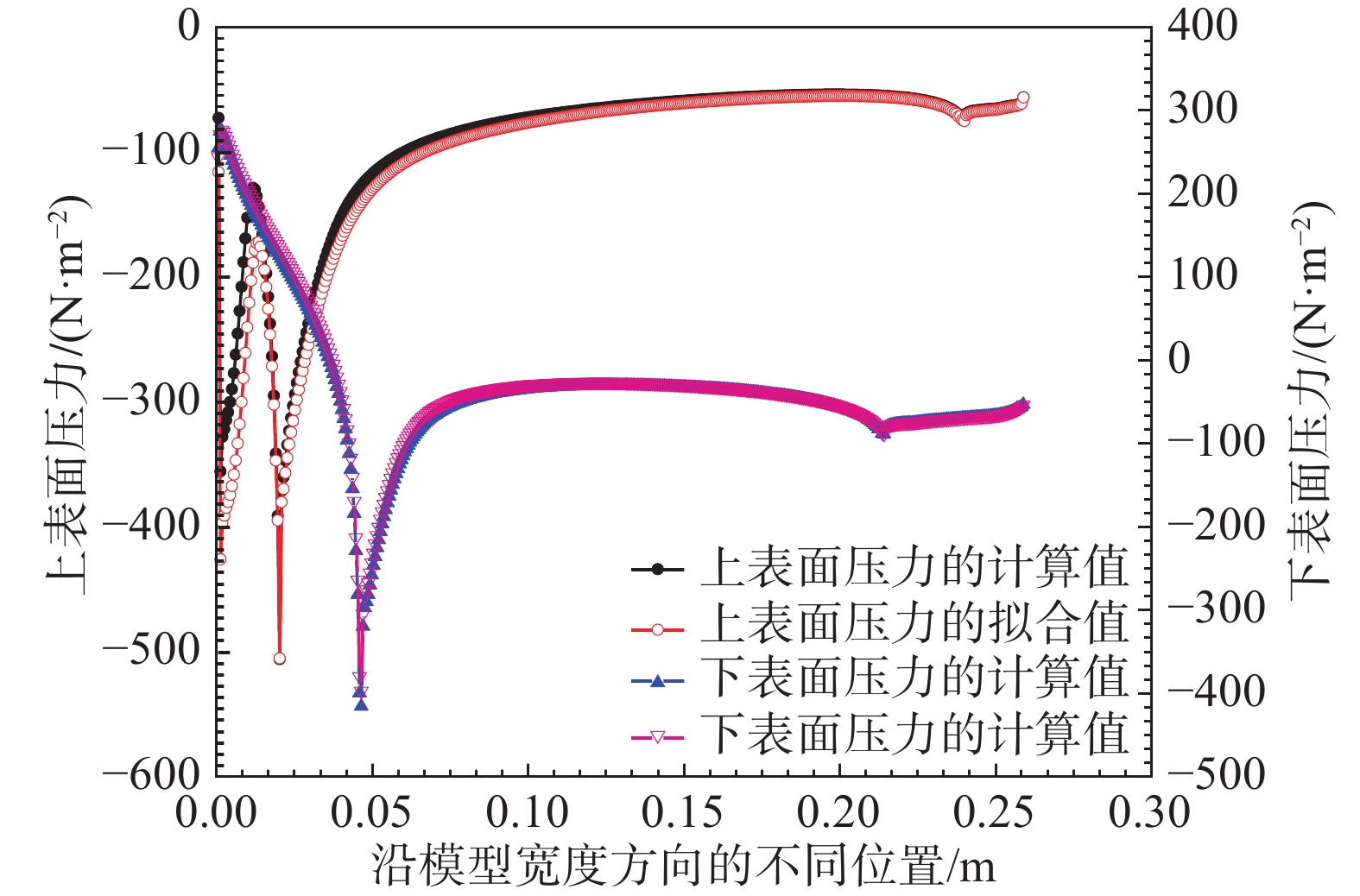
T/2 时刻,模型上下表面压力的计算值与拟合值,从图中可以看出,二者之间吻合较好。上述分析说明了本文方法的有效性。根据CFD计算获得的模型运动状态下的气动力,结合本文1.2节中的方法,计算了拟合系数
c 沿箱梁表面的分布情况,如图8所示。拟合系数c的分布情况代表了箱梁表面平均压力的分布特征。从图8可以看出箱梁迎风侧风嘴附近的平均压力较大,上下表面压力的分布规律类似,但力的作用方向相反。在拟合方程
y=asin(wx)+bcos(wx)+c 中,系数a 、b 与气动导数之间又存在如下的关系(可结合本文1.2节的第4步进行推导):A∗1=−UBω2ρU2∫b0a0axdx,A∗2=U2B2ω22ρU2∫b0a0bxdx, A∗3=−U2B2ω22ρU2∫b0a0axdx,H∗3=−U2B2ω22ρU2∫b0a0adx (16) 由于拟合系数
a 、b 代表了模型表面周期性变化压力的幅值特性,因此结合上述A∗1 、A∗2 、A∗3 、H∗3 的表达式,可以清楚的看到拟合系数a 的分布特点决定了气动导数A∗1 、A∗3 和H∗3 ,而拟合系数b 决定了气动导数A∗2 。图9给出了拟合系数
a 沿模型宽度的分布情况,系数a 在模型迎风侧风嘴所在区域数值较大,而在模型尾部的区域则数值较小,因此,箱梁迎风端的外形对其颤振导数A∗1 、A∗3 、和H∗3 影响很大。图10给出了拟合系数
b 沿模型表面的分布情况,同图9相比,二者的分布规律相似,也是在模型迎风侧风嘴所在区域数值较大,而在箱梁尾部所在区域数值较小。由于系数b 的分布与气动导数A∗2 直接相关联,因此箱梁迎风端的外形对颤振导数A∗2 影响很大,而颤振导数A∗2 对系统振动的稳定起到了非常重要的作用。从已有的研究成果来看,对箱梁断面颤振性能影响较大的气动导数是
A∗1 、H∗3 和A∗2 。由A∗1 和H∗3 构成联合导数A∗1 、H∗3 向振动系统输入能量,而A∗2 则是振动系统的主要耗能因素。本文的研究结果表明对A∗1 、H∗3 和A∗2 产生较大影响的是箱梁迎风侧风嘴所在的区域。通过上述分析得到两点启示:1)由于确定气动导数A∗1 、H∗3 和A∗2 的分布压力特性基本相似, 从而使得影响A∗1 、H∗3 和A∗2 的基本因素也就非常类似,因此,气动力的耦合现象主要是由模型表面压力分布特性所决定;2)当箱梁振动时,模型迎风侧风嘴附近的分布压力明显的大于箱梁尾部的压力,因此箱梁风振过程中,模型表面的主要控制压力会向迎风侧移动,从而对颤振导数A∗1 、H∗3 和A∗2 产生较大的影响,最终会导致模型振动稳定性的丧失。3.2 箱梁表面压力的局部特性对颤振导数的影响
通过3.1节的分析可知在箱梁振动过程中模型表面压力的分布是不均匀的,模型表面的不同区域的分布压力对颤振导数的影响也是不相同,因此模型表面压力的局部特性对箱梁颤振稳定性产生的影响也不尽相同。因此,本节提出通过分块分析的方法来定量研究模型表面压力的局部特性对颤振导数的影响,模型表面分区如图11所示。
根据CFD数值计算结果,提取了箱梁断面在一个振动的周期内模型表面4个分区上下表面压力差随计算时间变化关系,如图12所示。从图12可以看出,在一个振动周期内,位于模型的迎风侧的3区和2区的压力差的变化随时间呈现出较明显的波动性,这与模型的周期性运动相对应。而位于模型背风侧的1区和4区的压力差基本上不随时间发生较大的变化。
结合建立的颤振导数与模型表面压力之间关系,讨论模型表面不同区域的分布压力对颤振导数的贡献。
颤振导数在每个分区的计算表达式为(仅以
A∗1 为例,其它与此类似):A∗1(i)=−UBω2ρU2∫b0(i)a0(i)axdx,i=1,2,⋯,4 (17) 各分区对该导数的贡献
C(i) :C(i)=A∗1(i)4∑i=1A∗1(i) (18) 式中:
A∗1(i) 为气动导数A∗1 在第i 个分区上的数值;a0(i) 和b0(i) 分别为第i 个分区的起点位置和终点位置 。根据式(17)、式(18),计算了箱梁表面4个区域对颤振导数
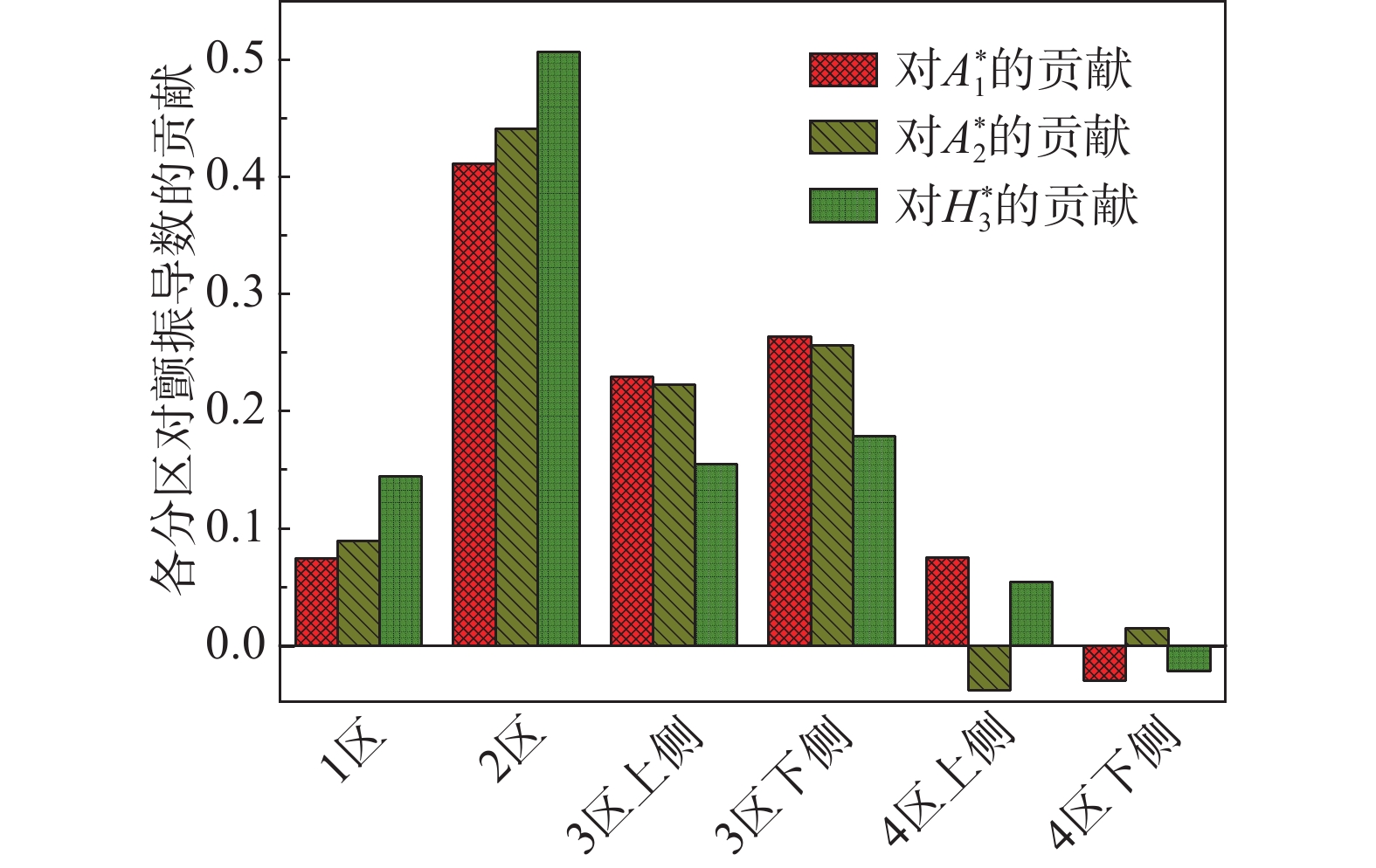
A∗1 、A∗2 、H∗3 的贡献,如图13所示。从图13结果来看,在模型的4个分区中迎风侧风嘴所在的3区下侧面对A∗1 和A∗2 影响最大,2区的影响次之,而4区的影响最小。对H∗3 而言对其影响最大的区域是2区,3区的影响则次之。通过对图13的分析可以看出对箱梁振动稳定性影响较大的颤振导数(如:
A∗1 、A∗2 、H∗3 ),其性质主要由箱梁表面迎风侧风嘴及其附近区域的表面压力特性所决定。这些研究结果为精准的实施风振控制措施提供参考。例如:为提高颤振临界风速,要求增加A∗2 的绝对值,则可以通过优化箱梁风嘴的气动外形(本文中的3区);而减小H∗3 绝对值最有效方法是通过合适的气动措施改变分布压力在箱梁迎风侧附近区域(本文中的2区)的数值。通过计算模型表面不同区域输送给主梁的气动能量来更加清楚的说明模型表面分布压力的局部特性对主梁振动产生的影响。
一个周期内单位面积上的气动力输送给振动系统的非定常平均积累功
w(x,t) 和功率N(t) 的定义为:w(x,t)=1T∫t0+Tt0P(x,t)⋅v(x,t)⋅n(x,t)dt (19) N(t)=∬ (20) 则模型表面上面积为S的区域内,气动力输入的平均累积能量
w(s,t) 为:w(s,t) = \iint_s {w(x,t)}{\rm{d}}s = \frac{1}{T}\int\nolimits_{{t_o}}^{{t_0} + T} {N(t){\rm{d}}t} (21) 式中:
P(x,t) 为结构表面的压力;v(x,t) 为结构运动速度;n(x,t) 为压力与速度之间的夹角。根据式(21)计算了在一个振动周期内箱梁表面的不同区域输送给主梁的气动能量(图14)。迎风侧风嘴所在的3区对模型输入的能量最大,2区次之,相比之下1区输入的气动能量则较小,而位于模型背风侧风嘴处的4区输入给主梁的气动能量会由正变为负,因此有利于系统振动的稳定性。从这一分析结果可以看出迎风侧风嘴附近的分布压力对运动断面输入正能量,而背风侧风嘴附近的分布压力消耗运动断面的能量,因此在模型振动过程中,如果模型表面的主要分布压力向模型迎风侧移动,则气动力输入到系统的正能量逐渐增加,最终会导致模型振动稳定性的丧失。
4 探讨箱梁表面压力分布特性对颤振稳定性的影响
以上分析了箱梁表面压力分布特点与颤振导数的之间联系,以及分布压力的局部特性对颤振导数的影响,以此为基础来研究压力的分布特性是如何对箱梁颤振稳定性产生影响。为了便于说明问题,建立如图15所示的箱梁断面的坐标系,靠近来流风场所在的箱梁区域为迎风侧,而靠近箱梁尾部的区域为背风侧。
4.1 提高箱梁颤振稳定性所需要的压力分布特性
根据现有的研究成果可知,为提高箱梁颤振的临界风速,则要求颤振导数
A_2^* 的绝对值较大,并且数值为负,而A_1^* \times H_3^* \times \cos \varphi 绝对值较小,数值为正。从压力分布的空间位置和相位差两个方面来讨论为满足上述要求所需要的压力分布特性,这里暂不考虑压力幅值的波动,认为C_{\rm{p}}^* 在模型宽度范围内为某一恒定的数值。根据式(12)可知为了使
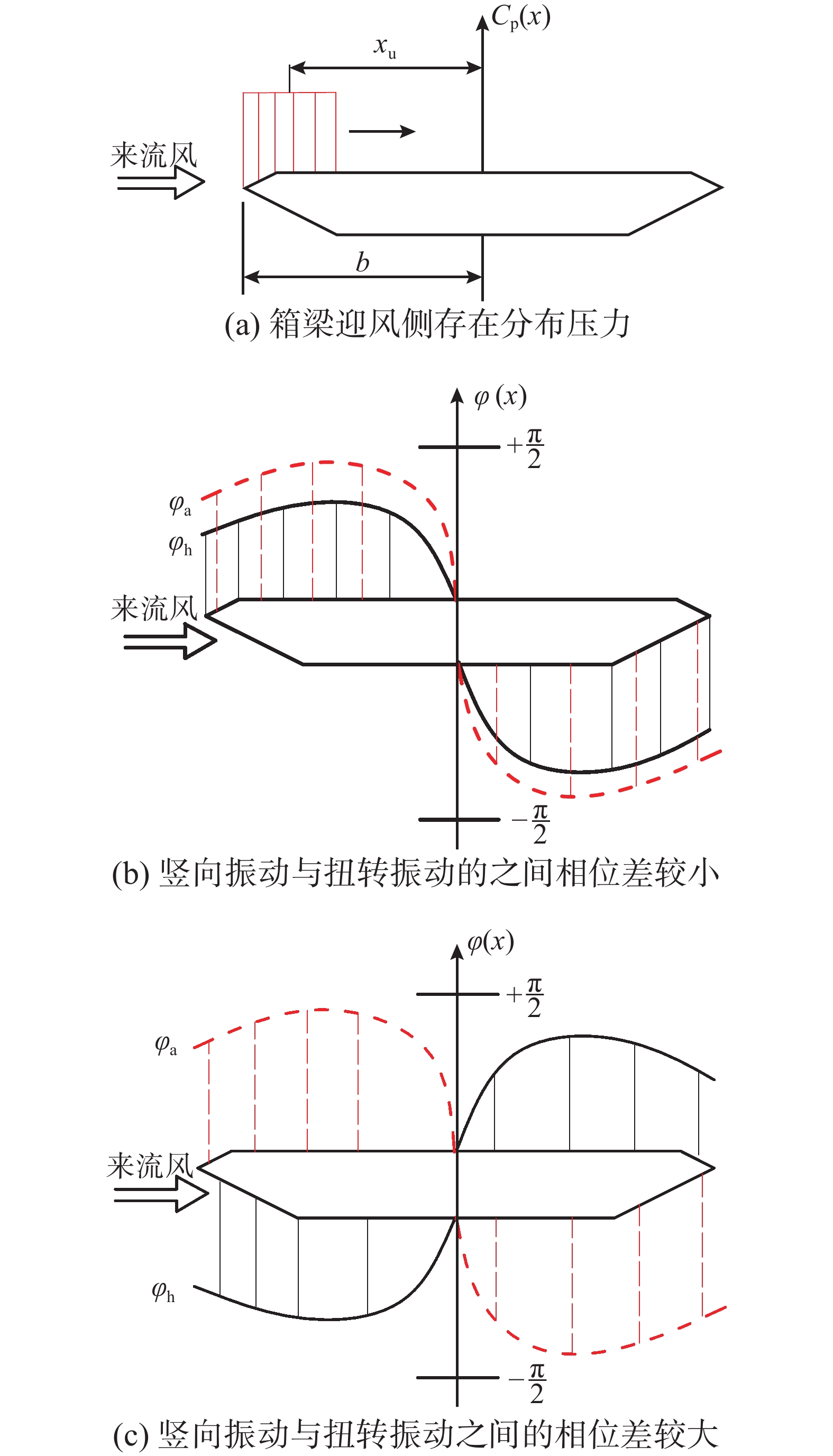
A_2^* 的绝对值较大,则需要压力中心到模型形心之间的距离{x_{\rm{u}}} (图16(a))以及最大压力与模型扭转最大位移之间的相位差{\varphi _{\rm{a}}} ,这两个参数取较大的数值,并且在迎风侧使得0 \leqslant {\varphi _{\rm{a}}} \leqslant {\pi / 2} ,在背风侧{{-\pi } / 2} \leqslant {\varphi _{\rm{a}}} \leqslant 0 ,如图16(b)所示。但是为了减小\left| {A_1^*} \right| \times \left| {H_3^*} \right| \times \left| {\cos \varphi } \right| 的数值则要求减小{x_{\rm{u}}} 的数值,同时增大最大压力与模型竖向运动最大位移之间的相位差{\varphi _{\rm{h}}} ,并且能够使得\varphi = {\varphi _{\rm{a}}} - {\varphi _{\rm{h}}} 的数值也增加,如图16(c)。因此,图16(c)所示的这种{\varphi _{\rm{a}}} 和{\varphi _{\rm{h}}} 呈反对称的相位差分布比图16(b)所示的{\varphi _{\rm{a}}} 、{\varphi _{\rm{h}}} 呈正对称的相位差分布更有利于箱梁颤振的稳定性。4.2 压力分布特性对箱梁颤振临界风速的影响
4.1节初步探讨了为提高箱梁颤振临界风速所需的压力分布规律。结合箱梁模型的具体参数,根据假设的模型表面压力分布,应用本文的式(12)、式(13)计算颤振导数,通过二维耦合颤振分析方法,计算当分布压力处在模型表面不同位置,并且处于不同的相位差分布时箱梁的颤振临界风速。箱梁截面仍然采用如图2,纵向长度0.8 m。模型的基本参数如下:每延米的质量
m = 1.3625\;{\rm{kg/m }} ,每延米的质量惯性矩{I_{\rm m}} = 0.01277\;{\rm{kg}}\cdot{{\rm{m}}^2}/{\rm{m}} ,竖向振动频率{f_{\rm{h}}} = 2.825\;{\rm{Hz}} ,扭转振动频率{f_{\rm{a}}} = 7.452\;{\rm{Hz}} ,竖弯阻比{\xi _{\rm{h}}} = 0.0127 ,扭转阻比{\xi _{\rm{a}}} = 0.047 。首先分析分布压力的空间位置对模型颤振临界风速的影响。假设模型表面压力的分布范围是0.2b,压力的幅值
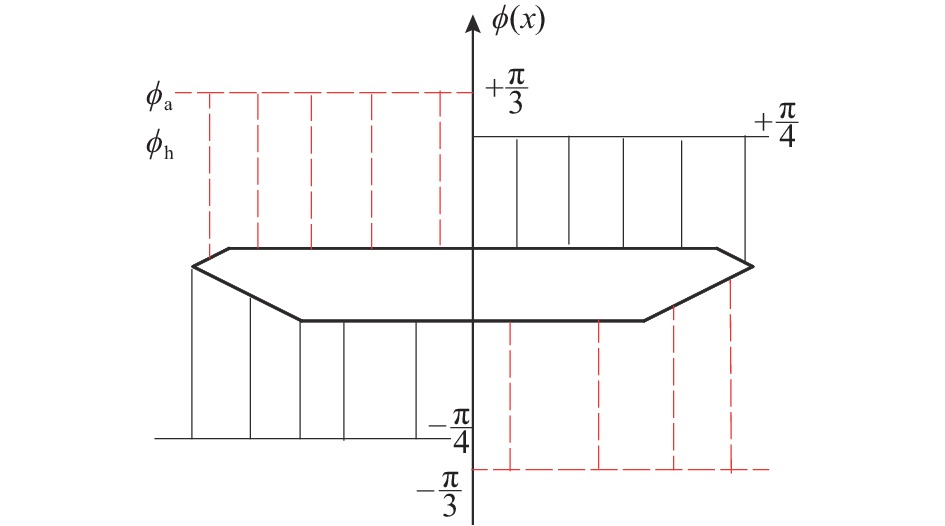
C_{\rm{p}}^* = 10.0 ,压力中心距截面形心的距离{x_{\rm{u}}} 分别为- 0.9b 、- 0.4b 、0.4b 、0.9b (图17(a))。相位差呈对称分布,如图17(b)所示,在靠近迎风侧{\varphi _{\rm{a}}} = \pi /3 、{\varphi _{\rm{h}}} = {\pi / 4} ;而在背风侧{\varphi _{\rm{a}}} = - \pi /3 、{\varphi _{\rm{h}}} = - {\pi / 4} 。根据上述压力分布规律,应用本文推导的颤振导数与分布压力之间的关系,可以计算出上述4种压力分布情况下的颤振导数,应用二维耦合颤振分析,求得了与上述4种压力分布状况相对应的颤振临界风速(图17(c))。从图中可以看出当分布压力位于模型的迎风侧时,箱梁的颤振临界风速最小,数值为16 m/s, 而当分布压力位于模型的背风侧时,箱梁的颤振临界风速最高,数值为36.5 m/s。因此,当箱梁表面峰值压力逐渐向模型尾部移动时,箱梁的颤振临界风速会逐渐提高。这也意味着如果箱梁尾部存在较强的压力作用则有利于箱梁颤振的稳定性。分析相位差的分布对箱梁颤振临界风速的影响,这里进行了两种情况下的计算:第1种情况下,
{x_{\rm{u}}} 分别取为- 0.9b 、- 0.4b 、0.4b 、0.9b ,相位差呈反对称分布,在靠近迎风侧{\varphi _{\rm{a}}} = \pi /3 、{\varphi _{\rm{a}}} = - \pi /4 ;在背风侧{\varphi _{\rm{a}}} = - \pi /3 、{\varphi _{\rm{h}}} = + {\pi / 4} ,如图18所示。通过计算发现在这种相位差分布情况下,上述4种压力分布状况对应的颤振临界风速高达288.8 m/s,也就意味着很难发生颤振失稳。第2种情况下的计算条件为:
- 0.9b \leqslant {x_{{\rm{u}}1}} \leqslant - 0.4b 、0.4b \leqslant {x_{{\rm{u}}2}} \leqslant 0.9b ;相位差{\varphi _{\rm{a}}} 与{\varphi _{\rm{h}}} 分布规律相同,在迎风侧{\pi /6} \leqslant {\varphi _{\rm{a}}} = {\varphi _{\rm{h}}} \leqslant {\pi / 2} ,在背风侧{{-\pi } / {2 \leqslant {{{\varphi _{\rm{a}}} = {\varphi _{\rm{h}}} \leqslant -\pi } / 6}}} 。通过二维耦合颤振分析方法获得箱梁颤振临界风速如图19所示。图19(a)给出了当分布压力位于模型迎风侧时(
- 0.9b \leqslant {x_{{\rm{u}}1}} \leqslant - 0.4b )相位差由{\pi \mathord{\left/ {\vphantom {\pi 6}} \right. } 6} 变化到{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. } 2} 的过程中,箱梁颤振临界风速变化规律。从图19(a)可以看出当迎风侧的分布压力向模型下游移动时,颤振临界风速逐渐增加。而当分布压力空间位置固定时,相位差由{\pi \mathord{\left/ {\vphantom {\pi 6}} \right. } 6} 变化到{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. } 2} 的过程中,箱梁颤振临界风速先增加后减小。图19(b)给出了当分布压力位于模型背风侧时(
0.4b \leqslant {x_{{\rm{u}}2}} \leqslant 0.9b )相位差由-{\pi /2} 变化到-{\pi / 6} 的过程中,箱梁颤振临界风速变化规律。从图19(b)可以看出当模型背风侧的分布压力向模型尾部移动时,箱梁的颤振临界风速增加;而当分布压力空间位置固定时,在相位差由-{\pi /2} 变化到-{\pi / 6} 的过程中,箱梁颤振临界风速风速也不断增加。通过探讨表面分布压力的空间位置和相位差对箱梁颤振临界风速的影响。可以得出一些启示:
1)颤振导数与模型表面压力的空间位置和相位差密切相关。在峰值压力向箱梁尾部移动过程中,颤振导数
A_1^* 和A_2^* 的绝对值会不断减小,但是压力分布的空间位置对颤振导数{{H}}_2^* 和{{H}}_3^* 却没有影响。箱梁迎风侧的分布压力对模型的颤振稳定性起了不利的作用,而当迎风侧分布压力向模型尾部移动时,箱梁的颤振临界风速将会不断的提高。这也说明了如果箱梁尾部存在较强分布压力,则会有利于箱梁颤振的稳定性。2)相位差的分布对所有的颤振导数都产生影响。相位差
{\varphi _{\rm{a}}} 、{\varphi _{\rm{h}}} 呈反对称分布则能够对振动系统的稳定性产生有利作用,提高了系统的颤振临界风速。如果{\varphi _{\rm{a}}} 与{\varphi _{\rm{h}}} 的空间分布规律相同,那么当分布压力位于模型迎风侧时,颤振临界风速随相位差的增加先增大后减小;当分布压力位于模型背风侧时,颤振临界风速随相位差的增加而增大。5 结论
本文建立了箱梁表面压力与颤振导数之间的数学关系式,应用CFD数值模拟方法获得了箱梁振动状态下的表面压力,研究了箱梁表压力与颤振导数的联系,探讨了表面压力分布的空间位置和相位差的分布规律对箱梁颤振稳定性的影响。通过本项研究得出以下几点结论:
(1)对主要颤振导数
A_1^* 、A_2^* 、H_3^* 贡献较大的是箱梁迎风侧风嘴所在的区域,并且决定A_1^* 和H_3^* 的表面压力的分布规律类似。当竖向振动与扭转振动的相位差不断减小时,决定A_1^* 和H_3^* 的表面压力的分布规律也就基本趋于相同,从而使得A_1^* 和H_3^* 的耦合作用更为强烈,因此,气动耦合效应与模型表面压力的分布特性密切相关。(2)箱梁迎风侧风嘴及其附近区域的压力特性决定了箱梁主要颤振导数的性质,这对有效实施风振控制措施具有指导意义,通过合适的气动控制措施改变这些区域的流场特性,则能影响压力在这些区域的分布规律,从而提颤振临界风速。
(3)箱梁表面压力分布的空间位置对箱梁的颤振导数和颤振临界风速都有重要的影响。表面分布压力位于箱梁迎风侧时,则对箱梁的颤振稳定起了不利的作用,而当箱梁尾部存在较强的分布压力时,箱梁的颤振临界风速将会提高。当迎风侧的分布压力向箱梁尾部移动时,颤振导数
A_1^* 和A_2^* 的绝对值会不断减小,而颤振导数{{H}}_2^* 和{{H}}_3^* 不受此影响,箱梁的颤振临界风速会逐渐增加。(4)箱梁表面压力的相位差沿模型宽度的分布特性会对箱梁的所用颤振导数都产生影响。当表面压力与扭转和竖向振动最大位移之间的相位差
{\varphi _{\rm a}} 、{\varphi _{\rm h}} 呈反对称分布时,系统的颤振临界风速较高。而当{\varphi _a} 与{\varphi _h} 的分布特性相同时,箱梁颤振临界风速随相位差的变化规律与模型表面压力所处的空间位置有较大关系。 -
-
[1] SCANLAN R H, JONES N P. Aeroelastic analysis of cable-stayed bridges [J]. Journal of Structural Engineering, 1990, 116(2): 279 − 297. doi: 10.1061/(ASCE)0733-9445(1990)116:2(279)
[2] CHEN X. Improved understanding of bimodal coupled bridge flutter based on closed-form solutions [J]. Journal of Structural Engineering, 2007, 133(1): 22 − 31. doi: 10.1061/(ASCE)0733-9445(2007)133:1(22)
[3] MATSUMOTO M. Flutter classification of bridge girders [M]// Proceeding of the 1st International Symposium on Wind and Structures for the 21st Century. Chcju, Techno-Press, 2000: 39 − 79.
[4] MATSUMOTO M, SHIRATO H, SHIJO R, et al. Flutter stabilization of long span bridges [M]// Proceeding of the 2nd International Symposium on Advances in Wind & Structures. Busan, Teehno-Press, 2002: 257 − 264.
[5] 杨詠昕, 葛耀君, 项海帆. 大跨度桥梁典型断面颤振机理[J]. 同济大学学报(自然科学版), 2006, 34(4): 455 − 460. doi: 10.3321/j.issn:0253-374X.2006.04.006 YANG Yongxin, GE Yaojun, XIANG Haifan. Flutter mechanism of representative sections for long-span bridge [J]. Journal of Tongji University (Natural Science), 2006, 34(4): 455 − 460. (in Chinese) doi: 10.3321/j.issn:0253-374X.2006.04.006
[6] 丁泉顺, 朱乐东. 桥梁主梁断面气动耦合颤振分析与颤振机理研究[J]. 土木工程学报, 2007, 40(34): 69 − 73. DING Quanshun, ZHU Ledong. Aerodynamically coupling flutter analysis and flutter for bridge deck sections [J]. China Civil Engineering Journal, 2007, 40(34): 69 − 73. (in Chinese)
[7] 鲜荣, 廖海黎. 封闭式扁平钢箱梁颤振稳定性气动优化措施风洞试验研究[J]. 世界桥梁, 2008, 40(3): 44 − 47. XIAN Rong, LIAO Haili. Wind tunnel test study of aerodynamic optimization measures for flutter stability of closed flat steel box girder [J]. World Bridges, 2008, 40(3): 44 − 47. (in Chinese)
[8] 金挺, 林志兴. 扁平箱形桥梁断面斯特罗哈数的雷诺数效应研究[J]. 工程力学, 2006, 23(10): 174 − 179. doi: 10.3969/j.issn.1000-4750.2006.10.033 JIN Ting, LIN Zhixing. Reynolds number effects on strouhal number of flat-box girder bridge decks [J]. Engineering Mechanics, 2006, 23(10): 174 − 179. (in Chinese) doi: 10.3969/j.issn.1000-4750.2006.10.033
[9] 任若松, 孙一飞, 郑云飞, 等. 准流线型桥梁表面压力分布研究[J]. 工程力学, 2021, 38(增刊): 184 − 188. doi: 10.6052/j.issn.1000-4750.2020.05.S033 REN Ruosong, SUN Yifei, ZHENG Yunfei, et al. Surface pressure distribution of quasi-streamline bridges. [J]. Engineering Mechanics, 2021, 38(Suppl): 184 − 188. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.05.S033
[10] 赵林. 风场模式数值模拟与大跨桥梁抖振概率评价[D]. 上海: 同济大学, 2003. ZHAO Lin. Numerical simulation of wind field and reliability assessment of buffeting for long-span bridge [D]. Shanghai: Tongji University, 2003. (in Chinese)
[11] 孟晓亮, 郭震山, 丁泉顺, 等. 风嘴角度对封闭和半封闭箱梁涡振及颤振性能的影响[J]. 工程力学, 2011, 28(1): 184 − 188. MENG Xiaoliang, GUO Zhenshan, DING Quanshun, et al. Influence of wind fairing angle on vortex-induced vibration and flutter performances of closed and semi-closed box decks [J]. Engineering Mechanics, 2011, 28(1): 184 − 188. (in Chinese)
[12] 张伟. 基于粒子图像测速技术的桥梁风致振动的细观机理研究[D]. 上海: 同济大学, 2008. ZHANG Wei. Mechanism research of wind induced vibrations of bridges based on particle image velocimetry [D]. Shanghai: Tongji University, 2008. (in Chinese)
[13] ARGENTINI T, ROCCHI D, MUGGIASCA S, et al. Cross-sectional distributions versus integrated coefficients of flutter derivatives and aerodynamic admittances identified with surface pressure measurement [J]. Journal of Wind Engineering & Industrial Aerodynamics, 2012, 104/105/106: 152 − 158. doi: 10.1016/j.jweia.2012.03.009
[14] LI K, LI S P, GE Y J, et al. An investigation into the bimodal flutter details based on flutter derivatives' contribution along the bridge deck's surface [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2019, 192: 1 − 16. doi: 10.1016/j.jweia.2019.06.019
[15] 林阳, 封周权, 华旭刚, 等. 基于自由振动响应识别桥梁断面颤振导数的人工蜂群算法[J]. 工程力学, 2020, 37(2): 192 − 200. doi: 10.6052/j.issn.1000-4750.2019.03.0143 LIN Yang, FENG Zhouquan, HUA Xugang, et al. Artificial bee colony algorithm for flutter derivatives identification of bridge decks using free vibration records. [J]. Engineering Mechanics, 2020, 37(2): 192 − 200. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.03.0143
[16] ANDERSEN M S, OLE JOHANSSON J, BRANDT A. Flutter derivatives from free decay tests of a rectangular B/D=10 section estimated by optimized system identification methods [J]. Engineering Structure, 2018, 156: 284 − 293. doi: 10.1016/j.engstruct.2017.11.059
[17] DING Q S, DONG S H, ZHOU Z Y. Identification of aerodynamic derivatives of bridge decks at high testing wind speed [J]. Canadian Journal of Civil Engineering, 2018, 45(11): 1004 − 1014. doi: 10.1139/cjce-2017-0010
-
期刊类型引用(2)
1. 卢镜宇,杨静宁,张亚民,韦子丰. NiTi形状记忆合金箱型梁非对称弯曲相变分析. 江西科学. 2023(04): 751-754 .  百度学术
百度学术
2. 王红艳,隽文烁. 基于二维流场的方形断面钝体气动性能分析. 齐齐哈尔大学学报(自然科学版). 2023(06): 1-4+10 .  百度学术
百度学术
其他类型引用(0)





















































































 下载:
下载: