在外部加载条件下，脆性材料将产生新的裂纹，而初始裂纹将会进一步发展，最后贯穿并破坏材料。为了研究这类材料中裂纹的演化机理，已有多位学者提出并发展了I型裂纹模型^[1-8]。随着轴向荷载的增大，主裂纹顶部会产生次生裂纹，而次生裂纹将呈现曲线扩展，最终平行于加载方向。

HUANG等^[9]分析了侧限以及应变率效应对于岩石材料动力强度的影响。由于缺乏对材料力学性质退化以及惯性效应的影响，其研究结果不符合实验结果。BHAT等^[10]在前人模型^[4-11]的基础上，引入损伤演化率，扩大了该模型的适用范围，但是该模型没有考虑动力加载时裂纹间的相互作用。

在单轴压缩加载条件下，I型裂纹模型可以表达具有稳定裂纹扩展的非线性应力-应变关系^[5-7]。该模型不能确定材料的压缩强度极限，为了改进这个缺陷，部分学者提出了一些可考虑裂纹相互作用的模型^[12-19]，试件在动力荷载作用下，裂纹间的相互作用强度取决于裂纹的初始尺寸、走向、密度及其空间分布。ASHBY和SAMMIS^[4]通过引入裂纹间的桥连附加内力以考虑裂纹相互作用效应，然而，该方法是一种近似的处理方式。KACHANOV等 ^[12-14]以及FABRIKANT^[15-16]提出了更一般的裂纹间相互作用的处理方法，KACHANOV的方法基于应力叠加原理来求解相互作用函数。根据KACHANOV考虑裂纹间相互作用的方法，ZHENG等^[17]揭示了材料的整体破坏和率效应的机理，但是其研究未考虑裂纹扩展速度对断裂韧性的影响以及弹性模型退化的影响。QI等^[20]考虑裂纹扩展速度、弹性模量退化以及裂纹相互作用等因素，提出了岩石类材料动力加载下的应力-应变本构关系。此模型未考虑裂纹面滑动过程中，滑动速度对裂纹面摩擦系数的影响。研究表明：裂纹面摩擦滑动对裂纹尖端应力强度因子和裂纹发展有重要影响^[21-24]。

本文将考虑裂纹面滑动过程对裂纹面摩擦行为的影响，提出一种考虑裂纹相互作用、裂纹密度以及裂纹面滑动摩擦的裂纹动力扩展模型，用以研究轴向动力加载过程中脆性材料的裂纹扩展和动力行为。

1   轴向加载下岩石的三维动力模型

1.1   惯性效应引起的附加应力

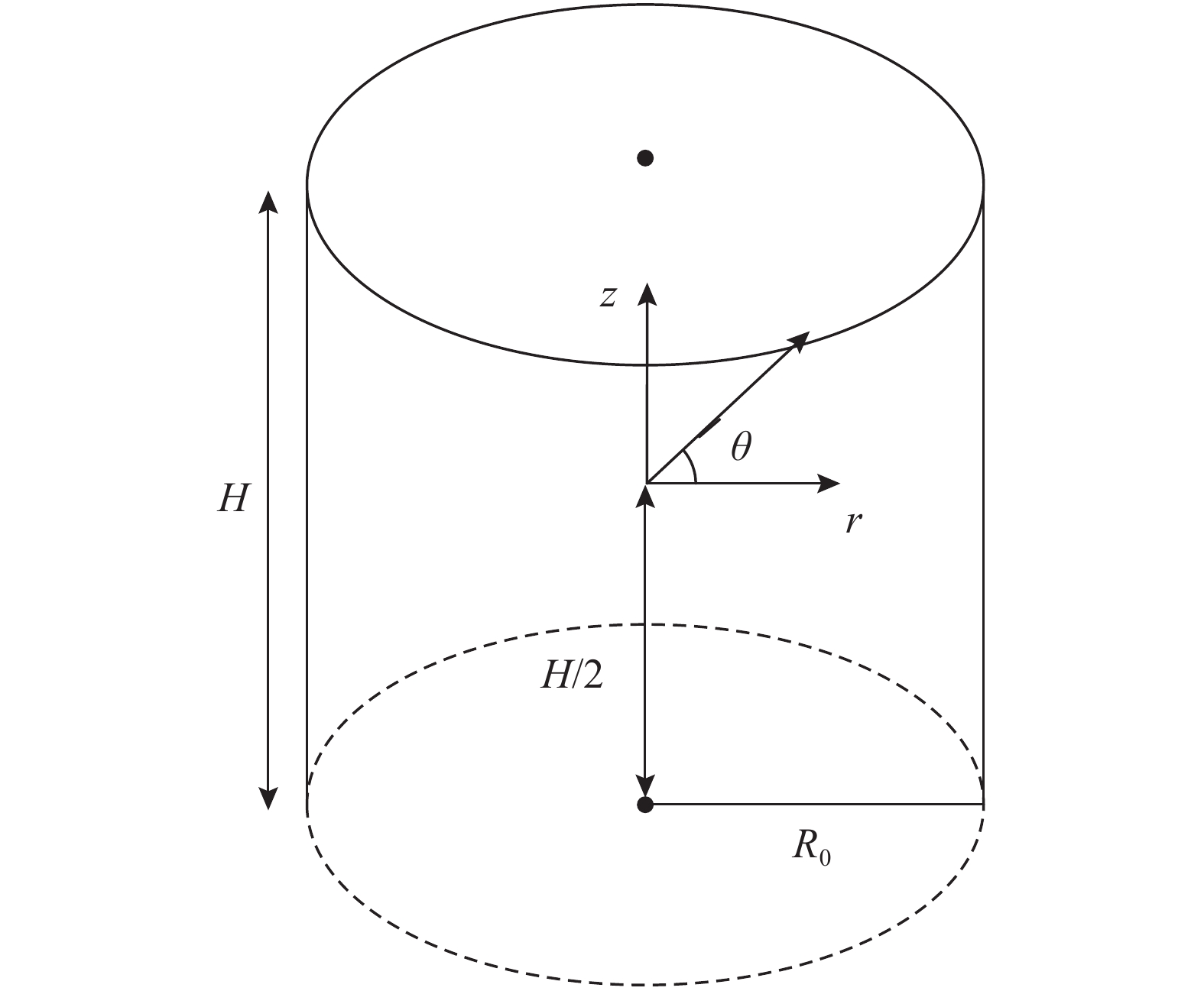
假定圆柱体试件的初始半径为R₀，柱坐标z、r、θ的原点位于z圆柱轴上，z沿着试件轴向，θ与r分别为环向和径向坐标，如图1所示。应力以受压为正，应变以受拉为正。依据FORRESTAL等^[25]的结果，当试件的轴向变形均匀且试件处于动力平衡状态时，由质点加速度所引起的附加应力$\sigma _{{\textit{z}}}^1$、$\sigma _{{r}}^{\text{1}}$和$\sigma _{{\theta }}^{\text{1}}$为：

图  1  圆柱体试件坐标示意图

Figure  1.  Diagram of coordinate axes for cylindrical sample.

下载: 全尺寸图片 幻灯片

试件中应力状态可以表达为：

式中，$\sigma _{{\textit{z}}}^{{0}}{\text{ = }}E\varepsilon _{{\textit{z}}}^{{0}}$ 为单轴压缩条件下的轴向应力。

1.2   轴向加载作用下的裂纹扩展三维模型

假定体积为V的试样中，含有N个币状的初始裂纹，其平均直径为2a。根据ASHBY和SAMMIS^[4]，有效弹性模量可以表达为：

式中：E_eff和E分别为材料的有效弹性模量和弹性模量；D为损伤因子，可由式(4)求解：

式中：l为次生裂纹的长度；$\alpha = \cos \psi$， $\psi$为主裂纹平面与加载方向的夹角；${C_{\text{r}}}$为单位体积内的裂纹数，${C_{\text{r}}} = {N \mathord{\left/ {\vphantom {N V}} \right. } V}$。

根据胡克定理，试件z方向的应变可以表达为：

式中，ν_eff为有效泊松比。假定有效弹性模量与体积模量相等，则有：

根据式(3)、式(5)和式(6)，可得：

试件的轴向应力可表达为：

将式(1)~式(4)代入式(8)，试件的轴向应力-应变关系如下：

式(9)右侧第一项为动力加载项，第二项为应变加速度的贡献。根据式(9)，可研究动力加载过程中，裂纹相互作用、裂纹密度以及裂纹面滑动摩擦行为等不同因素对岩石材料的裂纹扩展、试件受力变形和强度的影响。

1.3   裂纹尖端运动方程

基于BHAT等^[10]的研究，材料的初始动力断裂韧度$K_{{\text{IC}}}^{\text{D}}$可以表达为：

式中：${\dot K_{\text{I}}}$和$K_{{\text{IC}}}^{\text{S}}$分别为加载率和准静力初始断裂韧度；${f_{\text{D}}}( {{{\dot K}_{\text{I}}}} ) = 1 + ( {{{{{\dot K}_{\text{I}}}} \mathord{/ {\vphantom {{{{\dot K}_{\text{I}}}} {K_{{\text{IC}}}^{\text{S}}}}} } {K_{{\text{IC}}}^{\text{S}}}}} ) \cdot 2 \times {10^{ - 5}}$。

初始裂纹启裂后，材料的断裂韧度取决于裂纹扩展速度。动力断裂韧度$K_{{\text{IC}}}^{\text{d}}$可表达为^[10]：

式中：$v$和${v_{\text{m}}}$分别为裂纹的传播速度和分叉速度；${c_{\text{P}}}$为试件的纵波波速。

依据FREUND^[26]的研究结果，当无限体受到不随时间变化的均匀荷载作用时，裂纹尖端动力强度因子可以表达为裂纹瞬时速度$v\left( t \right)$的通用函数乘以此刻裂纹长度$a\left( t \right)$函数的平衡应力强度因子：

式中，${c_{\text{R}}}$为试件的瑞利波速。裂尖运动方程表示为当前的动断裂韧度$K_{{\text{IC}}}^{\text{d}}$等与当前的动应力强度因子$K_{\text{I}}^{\text{d}}$，即：

将式(11)、式(12) 代入式(13)，可得：

通过求解式(14)，可以求得裂纹扩展速度以及裂纹长度。

1.4   裂纹的动力相互作用模型

假定主裂纹和次生裂纹的半径分别为a和l，裂纹中心的间距为2b，如图2所示。依据ASHBY和SAMMIS^[4]的研究，次生裂纹的应力强度因子表达为：

式中：${F_{\text{w}}} = \left( {\tau + \mu \sigma } \right)\pi {a^2}\sin \psi = \left( {{A_1}{\sigma _1} - {A_3}{\sigma _3}} \right){a^2}$为裂纹中间的张开力，平行于${\sigma _3}$方向；${A_1} = \dfrac{{\pi \sqrt \beta }}{{\sqrt 3 }}\cdot [ {{{( {1 + {\mu ^2}} )}^{{1 / 2}}} - \mu } ]$；$\beta = 0.1$；${A_3} = {A_1}\left[ {\dfrac{{{{\left( {1 + {\mu ^2}} \right)}^{{1 / 2}}} + \mu }}{{{{\left( {1 + {\mu ^2}} \right)}^{{1/ 2}}} - \mu }}} \right]$；$\mu$为裂纹面的摩擦系数；${\sigma '_3} = \dfrac{{{F_{\text{w}}}}}{{A - \pi {{\left( {l + \alpha a} \right)}^2}}}$为作用于裂纹间桥连上的附加应力；$\alpha = \cos \psi$；A为裂纹所占的平均面积，$A = {\pi ^{{1 /3}}}{\left( {\dfrac{3}{{4{C_{\text{r}}}}}} \right)^{{2 /3}}}$；C_r为单位体积试件中的裂纹数。

上述模型适用于环绕开展的币状裂纹。根据WANG等^[27]的试验结果，当侧向压力达到轴向压力6%左右，翼裂纹将迅速扩展。而在单轴动力加载时，由于惯性引起的附加侧向压力达到4%~12%。当试件受到强烈冲击荷载作用时，假定试件里的裂纹按照图2(c)扩展，此时裂纹长度$l$应该为$l + \xi a$。根据HORII和NEMAT-NASSER^[5-6]的研究, $\xi = 0.27$。因此，式(15)可表达为：

当不考虑裂纹的相互作用时，即${\sigma '_3} = 0$，应力强度因子可表达为：

不同于ASHBY和SAMMIS^[4]引入裂纹间的桥连附加内应力来近似考虑裂纹间相互作用，LEKESIZ等^[28]基于Kachanov的研究，提出针对I型裂纹的裂纹相互作用计算方法：

式中，$\varphi$为初始裂纹与x轴的夹角。式(18)和式(19)分别适用于正方形和六边形分布的裂纹阵列。通过式(17)可以求得上述式(18)和式(19)中的$K_{\rm{I}}^0$。

图  2  I型裂纹受力状态及单个I型裂纹示意图^[27]

Figure  2.  Stress condition for mode I crack and diagram of one isolated crack^[27]

下载: 全尺寸图片 幻灯片

1.5   裂纹壁摩擦系数与滑移速度的相关性

在研究断层活动以及与摩擦相关的岩石破裂问题时，常采用速度及状态依赖性摩擦本构模型(Rate-and state-frictional law)^[29-31]描述其摩擦行为。次生裂纹受到初始裂纹滑动的驱动，亦可以采用速度及状态依赖性摩擦本构关系进行研究。裂纹摩擦系数可以表达为：

式中：$V$为接触面滑移速度；${V_0}$为参照速度；${\mu _0}$为当滑移速度等于参照速度时的稳态摩擦系数；${a_1}$和${b_1}$分别为材料参数；${D_{\text{c}}}$为特征滑动距离；$\theta$为状态变量。

实验研究结果^[32-33]表明：当滑移速度大于0.1 m/s后，摩擦系数会快速降低，这与速度弱化和非稳态滑移的初动是密切相关的。岩石类别对摩擦系数与滑动速度的依赖性影响不大，可以将滑动分为三个速度区间，如图3所示。

图  3  不同岩石材料摩擦系数与滑移速度相关性^[32-33]

Figure  3.  Dependence of friction coefficient on slip velocity^[32-33]

下载: 全尺寸图片 幻灯片

为了统一这三个速度区间，SPAGNUOLO等^[34]提出一种修正的摩擦定律(Modified friction law, MFL)：

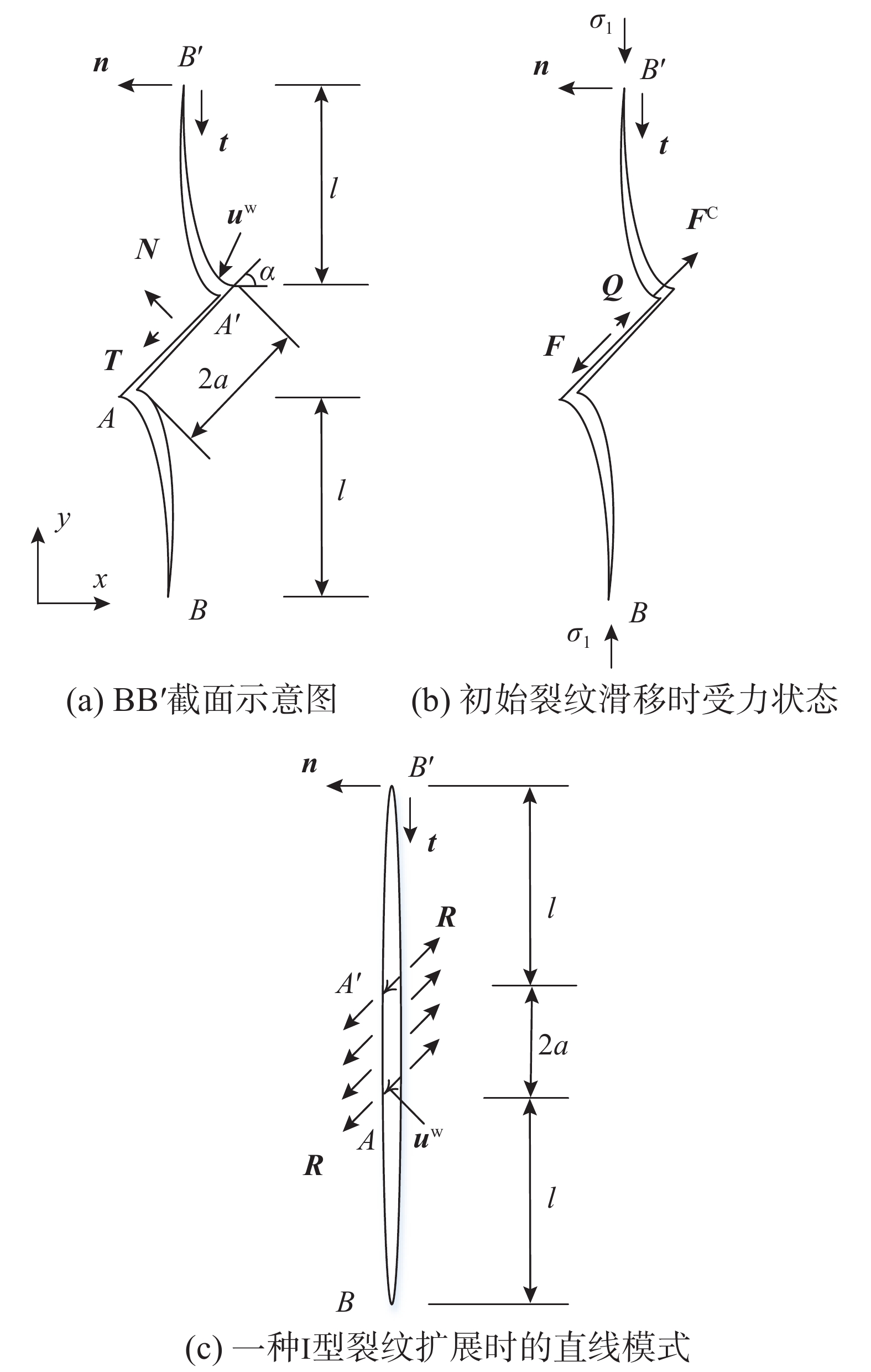
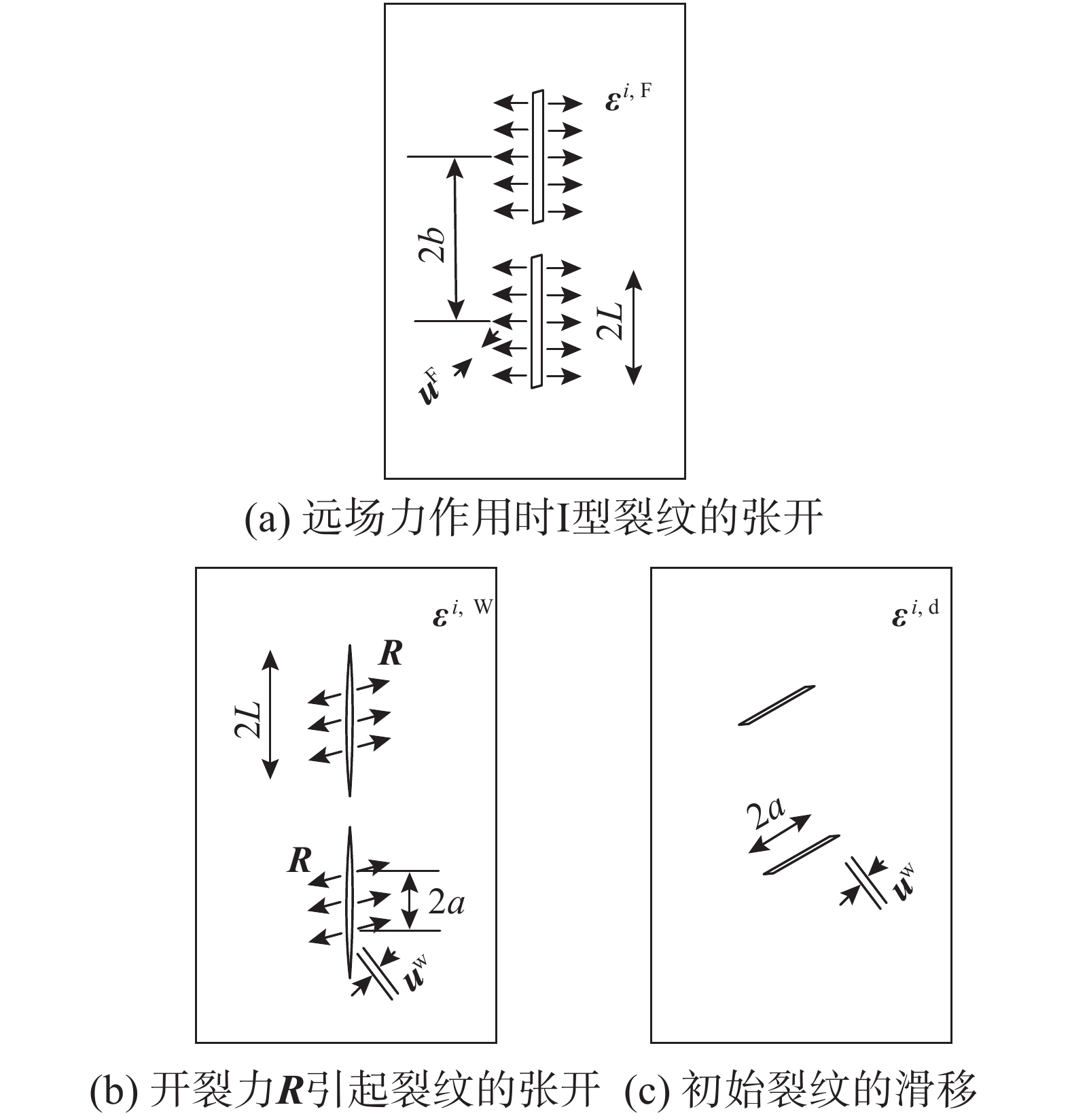
式中，${V_0}$= 1 μm/s以及${\mu _0}\left( {{V_0}} \right) \approx$0.7为速度及状态依赖性摩擦本构中常采用的参数。参数V_c、p和a₂−b₂通过拟合试验数据确定。对于石英岩类a₂−b₂$\approx$−0.013~0.002，V_c =0.016~0.04， p=0.42~0.86；对于碳酸岩类a₂−b₂$\approx$−0.007~0.01，V_c =0.06~0.12，p=0.78~1.07；对于硅酸岩类，a₂−b₂$\approx$0.009~0.035，V_c =0.02~0.035，p=0.44~0.64。

为了确定摩擦对裂纹扩展的影响，需要先求解裂纹面的相对滑移量，进一步可求得相应的摩擦面滑动速度。图4展示了单一I型裂纹的张开。N、n、T以及t分别是单位矢量，其方向如图4所示。AA'为初始裂纹，其长度为2a；次生裂纹长度为l。驱动初始裂纹滑动的力如图4(b)所示，其中：F为驱动力；Q为抵抗力；而F^C为弹性闭合力；R为沿裂纹均匀分布的开裂力。滑动会沿初始裂纹AA′产生相对位移u^W。而裂纹间相互作用会引起I型裂纹上均匀分布的附加荷载，进而引起初始裂纹的相对位移u^F，如图5所示^[35]。

图  4  I型裂纹初始裂纹面滑移时的受力状态^[35]

Figure  4.  Slip over pre-existing crack as a driving mechanism for wing crack growth^[35]

下载: 全尺寸图片 幻灯片

图  5  I型裂纹张开时的相互作用效应^[35]

Figure  5.  Effect of crack interaction on wing crack opening^[35]

下载: 全尺寸图片 幻灯片

因此，初始裂纹面的总相对滑动量可表达为：

在式(25)中：${{{\boldsymbol{F}}}}$为驱动力；${{{\boldsymbol{Q}}}}$为抗力，可以由以下方程求解：

对式(22)所求解的总位移量对时间求导，即可得到初始裂纹面的滑移速度，进而通过式(21)求解裂纹面的动摩擦系数。

2   不同裂纹面摩擦行为对动力加载过程的影响

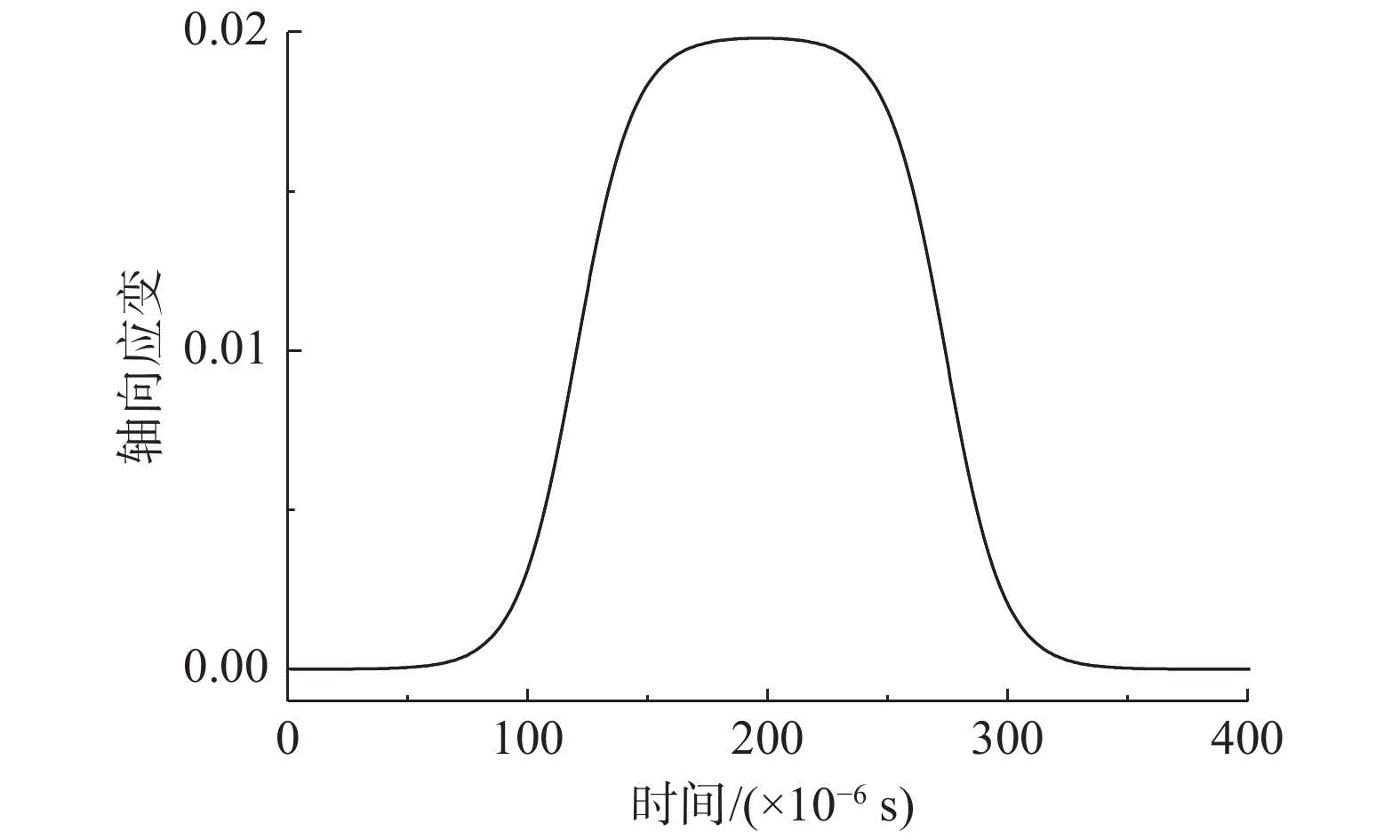
根据ZHANG等^[36]的霍普金森杆试验(SHPB)，试样的半径为37 mm，弹性模量E和泊松比$\nu$分别取17.2 GPa和0.19，初始裂纹长度为3 mm。入射应力脉冲持续时间与撞击杆长相关，可以表达为：

式中：t/μs为时间；${\sigma _{{i}}}$为入射应力脉冲的最大幅值，与撞击速度相关。对于半径37 mm试件的SHPB试验，入射应力脉冲的最大幅值与撞击速度的关系如下：

当撞击速度为15.7 m/s时，入射应力脉冲的最大幅值为128.04 MPa。假设试件的轴向应变值与入射应力脉冲值成正比，即：

根据上述方程及参数，可求得试件的轴向应变、应变率和应变加速度，其结果如图6~图8所示。

图  6  轴向应变随时间的变化

Figure  6.  Axial strain vs time

下载: 全尺寸图片 幻灯片

图  7  轴向应变率随着时间的变化

Figure  7.  Axial strain rate of the specimen vs time

下载: 全尺寸图片 幻灯片

图  8  轴向应变加速度随时间的变化

Figure  8.  Variation of axial strain acceleration of the specimen with time

下载: 全尺寸图片 幻灯片

QI等^[20]研究了在摩擦系数为常数情况下，不同裂纹密度对裂纹的启裂应力、动力加载过程、动强度以及惯性效应的影响。但是实际观测和试验结果表明：裂纹面上的摩擦系数与滑移速度相关，在裂纹面滑动过程中并非常数。下面将采用第1节提出的模型，以ZHANG等^[36]的试验实验数据为参考，采用Matlab进行数值计算，分析动力摩擦过程对动力加载过程中岩石材料行为的影响。

2.1   动摩擦条件下裂纹密度的影响

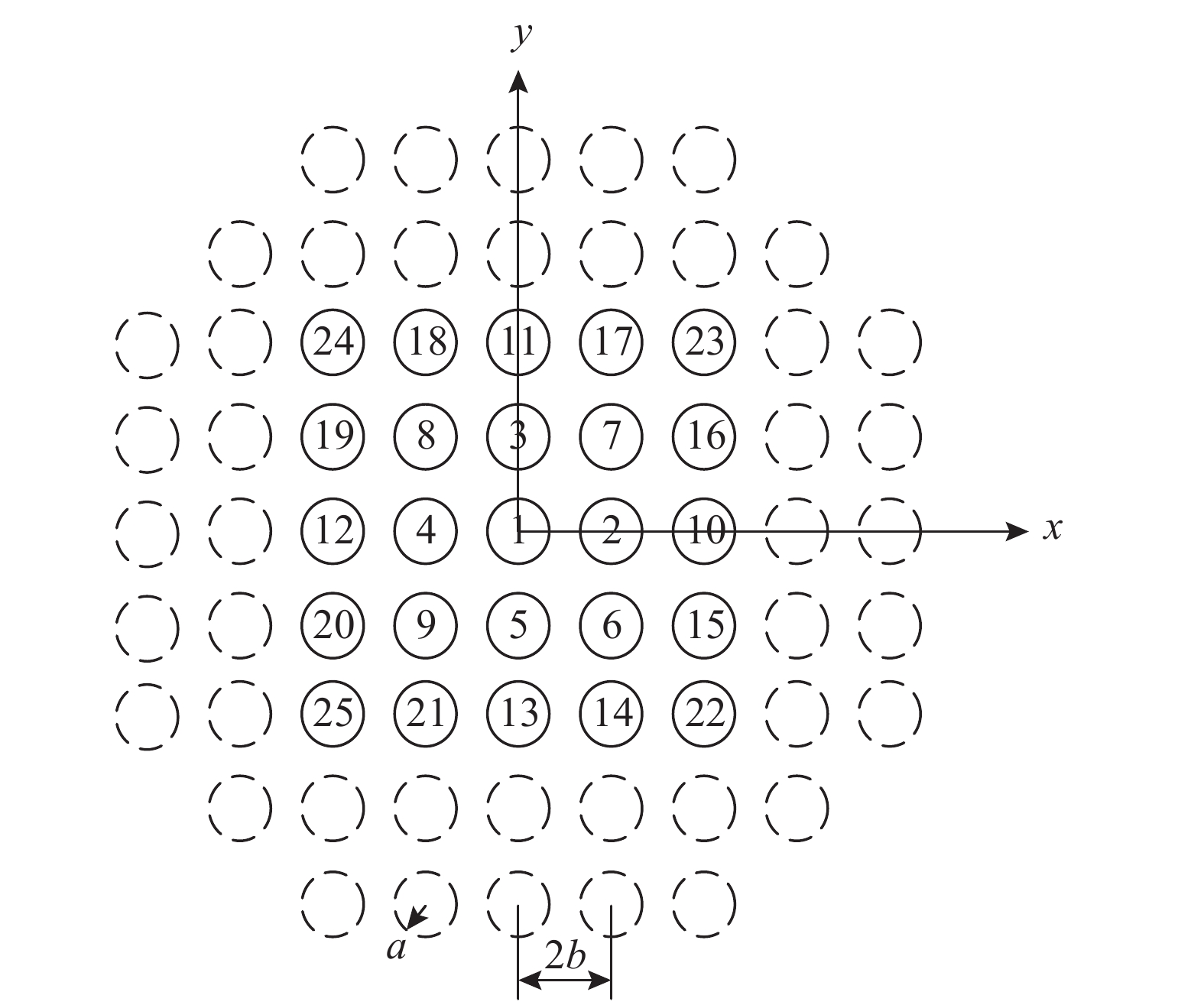
裂纹面上发生相对滑动，其摩擦行为可以采用速度及状态依赖型摩擦本构模型进行研究。本节将采用式(21)描述的摩擦本构模型，以正方形分布的裂纹阵列(如图9所示)为例，考虑裂纹间相互作用，分析不同裂纹密度条件对裂纹启裂应力、动力加载过程、最高强度以及惯性效应的影响。

图  9  正方形分布裂纹阵列示意图^[31]

Figure  9.  Periodic square configuration cracks^[31]

下载: 全尺寸图片 幻灯片

a₂−b₂、p和V_c分别取0.01、0.8以及0.1。${V_0}$= 1 μm/s，${\mu _0}\left( {{V_0}} \right) \approx$0.7。为考虑不同裂纹密度的影响，假定$\lambda = {a \mathord{\left/ {\vphantom {a b}} \right. } b}$分别为0.15、0.30、0.50、0.70、0.8、0.9和0.95。其余主要计算参数如表1所示。联合式(9)和式(18)，可计算不同裂纹密度条件时试件的动力加载过程、破坏强度以及惯性效应的影响等，计算结果如图10~图12和表2所示。在图10中，“S-0.9”代表裂纹密度参数为$\lambda = 0.9$的正方形阵列裂纹结果，文中其他相关表示均遵守这种规则。

表  1  数值计算采用的参数

Table  1.  List of the parameters for the numerical calculations

参数	数值
试件原始半径/mm	37
试件原始高度/mm	42
裂纹初始长度/mm	3
弹性模量E/GPa	17.2
单轴抗压强度/MPa	45
泊松比	0.19
密度/(kg/m)	2179
KI0/(MPa·m1/2)	0.56
${c_{\text{R}}}$/(m/s)	1656
${c_{\rm{P}}}$/(m/s)	2944
${v_{\text{m}}}$/(m/s)	800

下载: 导出CSV 

| 显示表格

图  10  裂纹密度参数为0.9时的裂纹面滑移速度

Figure  10.  Slip velocity vs time for 'S-0.9' cracks

下载: 全尺寸图片 幻灯片

图  11  不同裂纹密度条件下轴向应力随加载时间变化

Figure  11.  Axial stress vs time for different crack concentration

下载: 全尺寸图片 幻灯片

图  12  不同裂纹密度条件下惯性引起附加轴向应力随加载时间变化

Figure  12.  Inertia induced additional axial stress vs time for different crack density

下载: 全尺寸图片 幻灯片

表  2  不同裂纹密度条件下启裂和破坏时刻以及相应的加载应力

Table  2.  The moments of crack growth initiation, sample failure and corresponding loading stresses for different crack density

裂纹 密度	裂纹相互 作用系数	启裂时刻/ (×10−6 s)	启裂时加载 应力/MPa	破坏时刻/ (×10−6 s)	破坏时加载 应力/MPa
0.15	1.0008	64	3.46	124	199.18
0.30	1.0049	63	3.19	113	122.46
0.50	1.0254	62	3.19	99	50.62
0.70	1.0896	62	3.19	92	30.22
0.80	1.1595	61	2.93	88	22.21
0.90	1.2929	60	2.49	91	28.01
0.95	1.4218	59	2.29	88	22.21

下载: 导出CSV 

| 显示表格

从图11和表2可以看出，随着裂纹密度从0.15增大至0.95，裂纹互相作用逐渐增强，相互作用系数从1.0008逐步增长至1.4218。而裂纹的启裂时刻从64×10⁻⁶ s逐步提前至59×10⁻⁶ s，启裂时的加载应力由3.46 MPa降低至2.29 MPa。这个过程中，试件破坏的时刻亦不断提前，破坏时的加载应力从199.18 MPa大幅下降至22.21 MPa。当$\lambda = 0.15$时，裂纹扩展持续了60×10⁻⁶ s；当$\lambda = 0.95$时，裂纹扩展仅持续了29×10⁻⁶ s，为裂纹密度0.15时的一半。由图12可见，惯性效应引起的试件轴向附加应力随裂纹密度的增大而逐渐增大。惯性作用引起的附加轴向应力峰值出现在为裂纹密度0.5的试件中，最大值为1.83 MPa。相对于QI等^[20]摩擦系数为常数的结果，动摩擦过程会促进裂纹发展，并降低试样的强度。

2.2   动强度因子结果对比

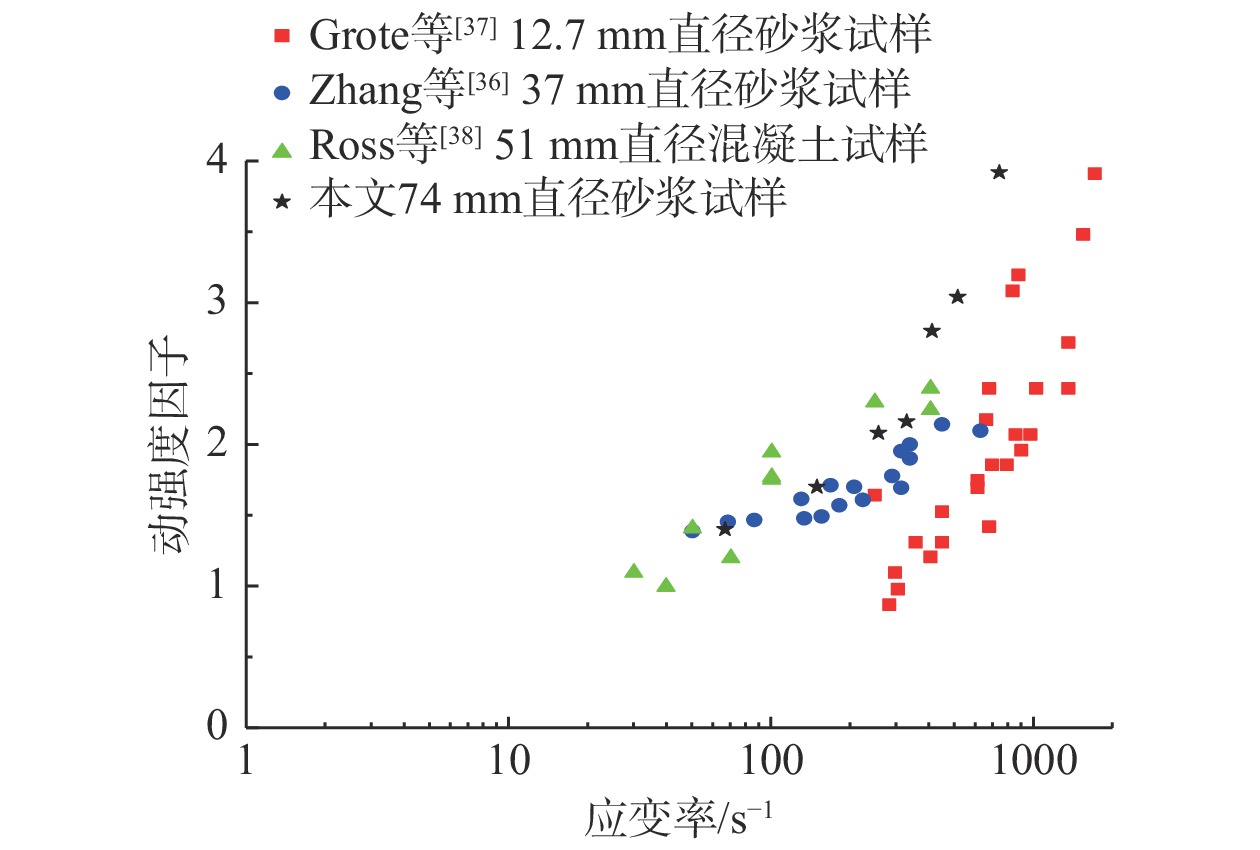
动强度因子(Dynamic increase factor, DIF，为试件破坏时的动强度与精力强度之比)常用于研究应变率效应对岩石材料动力强度的影响。目前，已有众多学者通过实验研究了应变率处于1 s⁻¹~10³ s⁻¹之间时岩石材料的DIF。为验证上述提出的模型，将第2.1节的理论结果与SHPB实验结果^[36-39]对比在图13中。根据ZHENG等^[17]的研究，当材料的受压强度十倍于受拉强度时，裂纹密度参数为0.3。因此，选取了裂纹密度参数为0.3时，采用MFL的理论值，在图13中用黑色星代表。在图13中，动强度因子均随应变增大而增大，表现出明显的应变率效应。同时，在400 s⁻¹~700 s⁻¹应变区间，随着试件直径从12.7 mm增大到74 mm，动强度因子亦呈现增大趋势，表现出明显的动力尺寸效应。

图  13  不同尺寸试样的动强度因子对比

Figure  13.  DIFs of concrete-like materials obtained from this study and SHPB specimens with different diameters

下载: 全尺寸图片 幻灯片

2.3   不同摩擦系数的结果对比

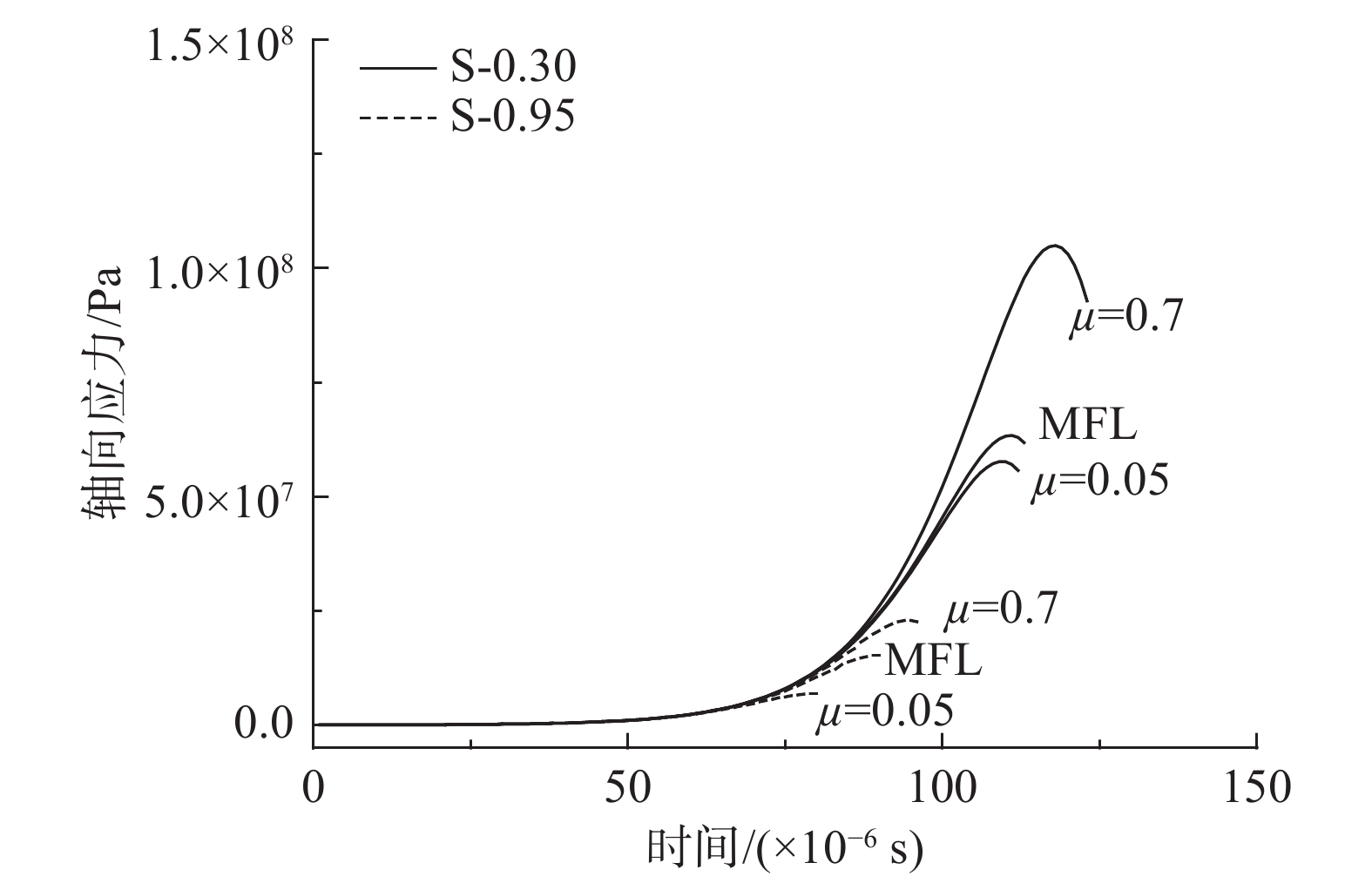
为进一步研究摩擦效应对动强度的影响，将摩擦系数假定为常数，分别取值0.05和0.7。裂纹密度参数λ分别取0.3和0.95，以考虑不同裂纹密度的影响。采用MFL时，裂纹面开始滑动前，摩擦系数假定为0.7。其他参数与第2.1小节保持一致，对比结果如图14所示。

图  14  不同摩擦系数条件下轴向应力随加载时间变化

Figure  14.  Axial stress vs time for different constant friction coefficients for the model of wing crack interaction

下载: 全尺寸图片 幻灯片

随着摩擦系数的增加，轴向应力亦有明显增加，而试件的破坏时间会延迟。相对于摩擦系数为常数0.7的结果，MFL破坏出现得更早(分别为113×10⁻⁶ s和123×10⁻⁶ s)，破坏时试样轴向应力更低(分别为63.8 MPa和91.6 MPa)。这是由于摩擦系数增大后，裂纹面需更高应力克服摩擦进行滑动，进而影响有效模量和试件的强度。此外，当初始裂纹开始滑动后，MFL里的摩擦系数随着速度的增加而降低，促使裂纹增长并降低试件的强度。在地震事件中，尤其是大地震，断层面摩擦滑移产生的热能会引起近1000 ℃的温度增长，导致断层接触面数毫米到数厘米的融化^[40]，断层面的摩擦系数急剧下降。因此，在研究动力加载过程中岩石材料的摩擦行为时，MFL相对于静摩擦系数更为合理，可以考虑接触面滑动引起的摩擦弱化现象。

3   结论

基于岩石类材料的I型裂纹模型，考虑正方形裂纹阵列情况下的裂纹相互作用，采用MFL模型考虑裂纹面的动力摩擦过程，提出了一种考虑裂纹相互作用、裂纹密度以及裂纹面滑动摩擦的脆性材料动力模型。主要结论如下：

(1) 根据此模型和数值计算，定量研究了MFL模型以及常摩擦系数条件下，裂纹密度对裂纹扩展过程、试件受力和破坏的影响。结果表明，随着裂纹密度的增大，裂纹的相互作用增强，试件破坏时的加载应力降低，而惯性效应引起的试件轴向附加应力增大。

(2) 不同裂纹摩擦系数的结果表明，随着摩擦系数的增大，试样轴向应力增加，而破坏时刻会延迟。采用MFL模型计算裂纹的动力摩擦过程时，假定在裂纹滑动前的摩擦系数为0.7。MFL模型结果表明，随着裂纹开始滑动，裂纹面摩擦系数逐渐降低。相对于摩擦系数为常数0.7的结果，其破坏出现得更早(分别为113×10⁻⁶ s和123×10⁻⁶ s)，破坏时试件轴向应力更低(分别为6.38×10⁷ Pa和 9.16×10⁷ Pa)。动力摩擦过程会促进岩石材料中的裂纹发展，并降低材料强度。相对于常数摩擦系数，考虑速度及状态依赖型摩擦模型更为合理。

(3) 本模型计算的动强度因子与其他实验结果对比显示，脆性材料在动力加载过程中表现出明显的应变率效应和动力尺寸效应。本文提出的模型有助于进一步研究动力加载条件下，脆性材料的动力破坏过程。