A DETAILED NUMERICAL ANALYSIS FOR THE PROGRESSIVE COLLAPSE OF CONCRETE FRAME SUBSTRUCTURES STRENGTHENED WITH FRP STRIPS
-
摘要: 外贴FRP布加固是一种有效提高既有建筑抗连续倒塌性能的手段,但现有FRP布加固方式存在降低结构抗震性能、加固施工不便等缺点。该文采用数值模拟方法分析了FRP布加固方式对现浇和装配式混凝土框架子结构抗连续倒塌与抗震性能的影响,并开展了优化方案研究。基于通用有限元软件LS-DYNA建立了FRP布加固混凝土框架子结构的连续倒塌精细数值模型,其中混凝土、钢筋与FRP布分别采用实体、梁与壳单元进行模拟,考虑了FRP布和钢筋的滑移、新旧混凝土界面的粘结失效和机械套筒处的钢筋截面损失。试验验证表明该方法可准确模拟试验试件的破坏模式和承载力发展。分析试验试件的不同粘贴方案结果发现:对现浇混凝土子结构,梁底与梁侧中性轴粘贴纵向FRP布并在梁端塑性铰区粘贴U形横向FRP布后,小变形下的结构倒塌抗力提升有限(最大仅2.6%)、基本不影响结构抗震性能,而对大变形下的结构倒塌抗力提升幅度可达49.5%;对于装配式混凝土子结构,在梁底、梁顶与梁侧底部外贴纵向布并在梁端塑性铰区粘贴U形横向FRP布可将小变形和大变形下的结构抗力最大提升24.2%和48.1%,使得装配式子结构在小变形下受力等同现浇结构,提升了原装配式子结构的抗震性能。对上述最优方案进一步的分析表明:保持FRP布用量不变而将塑性铰区内U形横向FRP布的分布范围和条数增加可提高大变形下的结构倒塌抗力,而不影响小变形下的加固效果。Abstract: Externally bonded FRP strips can effectively improve the progressive collapse-resisting performance of existing structures, but the seismic performance of structures and the ease of construction were not taken into consideration in existing FRP strengthening schemes. Numerical simulation was performed to study the influences of strengthening schemes using FRP strips on the seismic and progressive collapse-resisting behavior of cast-in-site and precast concrete frame substructures, by which the strengthening schemes were consequently optimized. The detailed numerical models of concrete frame substructures strengthened with FRP strips were established using the general finite element (FE) software LS-DYNA, in which the concrete, steel reinforcement and FRP strips were simulated by solid, beam and shell elements, respectively. The bond-slip of steel bars and FRP strips, the bond failure between precast and cast-in-site concrete and the loss of cross-sectional areas of bars at the mechanical sleeves were considered in the numerical models. The numerical models were validated by experimental results, which showed that the failure modes and the strengths of the substructures in the experiment were well captured by the numerical models. The results of the different strengthening schemes suggested that the bonding of the longitudinal FRP strips at the beam bottoms and the neutral axes of beam sides and U-shaped transverse FRP strips in the plastic hinge regions of the beams hardly improved the structural collapse resistances under small deformations for cast-in-site concrete substructures (the maximum percentage increase was only 2.6%). Such a strengthening scheme had almost no effect on the seismic performance of the substructures, while the progressive collapse resistance under large deformations was increased by at most 49.5%. For precast concrete substructures, applying longitudinal FRP strips at the beam tops, beam bottoms and bottoms of the beam sides and U-shaped transverse FRP strips in the plastic hinge regions would improve their maximum resistance under small and large deformations by at most 24.2% and 48.1%, respectively. Under small deformations, their collapse resistance was increased to the same level as cast-in-place ones, which was advantageous for improving the seismic performance of precast concrete substructures. A further analysis of the aforementioned optimal schemes shows that keeping the amount of FRP unchanged and at the same time increasing the covering length and the number of U-shaped transverse FRP strips applied in the plastic hinge regions of the beams could improve the structural collapse resistance under large deformation, while the effect of FRP strengthening on the collapse resistances under small deformation remained unchanged.
-
石砌体结构具有造价低廉,取材方便,耐久性好的特点,在世界各地的历史古迹中有广泛的应用。由于砌筑工艺和灰缝材料的多样性,砌筑技术的差异性,再加上长期受雨水、风化等作用,使得古建筑石砌体结构的力学性能比现代砖砌体结构更加复杂。因此,深入研究古建筑石结构的力学性能,对开展古建筑石结构的健康状态评估和加固修护有重要意义。
近年来,国内外对于石砌体结构的研究主要集中在抗震性能和承载力性能的方面。滕东宇等[1-2]通过对石砌棱柱体试件进行轴压试验,提出受压承载力计算式,并基于分层均质化理论,给出了藏式古建石砌体的各向有效模量。徐秀林等[3]通过对条石砌体试件进行轴压试验,指出在砌体高厚比较低时,在灰缝中增加垫片会使得承载力提高,但随着高厚比的增高,该提高效果会逐渐降低。王兰等[4]通过对石墙灰缝试件进行低周反复试验,发现带有垫片的灰缝在反复碾压作用下,会产生不可忽视的竖向变形,并以摩尔库伦定理为基础,提出了考虑石材粗糙程度的抗剪强度计算式。杨娜和滕东宇[5]通过对泥浆砌筑石墙试件进行双剪试验,指出试件受剪是一个同时发生泥浆变形和界面分离的延性破坏过程,并且分别基于弯剪理论模型和主拉应力破坏-剪摩破坏混合模型,分析了灰缝试件在剪-压复合作用下的强度。高晓鹏等[6]开展了有垫片粗料石砌体墙的低周反复试验研究,发现竖向压应力和模型尺寸是影响失效模式和强度的重要因素。Milosevic等[7-8]以4片毛石砌体墙低周反复试验结果为基础,将荷载-位移曲线、损伤机理、失效模式和性能参数作为校准指标,对材料参数进行修正,建立了非线性毛石墙整体式模型。Vasconcelos等[9-10]通过对U型毛石墙和粗料石墙模型进行面外低周反复试验,对其面外抗震性能进行研究,并建立了整体式模型,进行参数分析,指出材料的弹性模量和抗拉强度是影响面外强度的主要因素。
已有的石砌体研究取得一定成果,但还存在以下问题:1)小型石砌体试件的研究成果很难直接拓展到石墙的性能研究上;2)对于石砌体结构的数值模拟研究较少;3)很少考虑砌块形状、大小和分布的随机性对墙体性能的影响。
一些学者[11-13]发现部分石砌体结构的几何构造存在一定程度随机性:如图1所示,结构具有明显的水平分层,同一层次的砌块处于同一水平线并且砌块高度基本一致,但宽度可能存在差别;此外,不同层次的砌块高度也可能存在差别。Cluni等[11]基于均质化理论,针对几何构造具有一定随机性的砌体,提出了一种计算砌体有效模量的有限尺度测试窗法。一些学者[13-18]基于砌块、灰缝的尺寸和位置的统计数据,提出了能描述砌体结构几何构造的概率统计分布模型。部分学者[11-13]针对几何构造具有一定随机性的砌体结构,将包含构造信息的概率统计分布模型与均质化方法结合,提出了砌体有效模量的计算方法。
本文基于Cluni等[11]的有限尺度测试窗法,提出了一种改进的有效模量计算方法,与文献的试验和数值模拟结果进行了对比,说明所得模量的准确性。分别利用该计算方法和有限尺度测试窗法,对藏式古建石砌体有效模量进行对比分析,并以所得有效模量为基础,建立了整体式模型,与分离式模型进行对比,证明了该模型可以较为合理地复制结构的整体变形,弥补了有限尺度测试窗法不能反映泊松效应的缺点。
1 砌体材料的有效模量计算方法
1.1 有效模量理论
本文的有效模量计算方法与Cluni等[11]的有限尺度测试窗法均以有效模量理论作为基础。复合材料力学中,常用有效模量和有效柔度描述平均应力和平均应力的关系,该关系式如下所示:
¯σij=Ceffij⋅¯εij (1) ¯εij=Seffij⋅¯σij (2) 式中:
¯σij 、¯εij 分别为复合材料的平均应力分量和平均应变分量;Ceffij 、Seffij 分别为复合材料的有效模量分量、有效柔度分量。RVE单元的平均应力分量
¯σij 、平均应变分量¯εij 可由式(3)和式(4)得到:¯σij=1V∫vσijdV (3) ¯εij=1V∫vεijdV (4) 式中:
σij 、εij 分别为RVE单元中任意位置的局部应力、应变分量;V为RVE单元的体积。通常对RVE单元施加两种不同的边界条件,得到
¯σij 、¯εij 。该边界条件如下所示:1)均匀应变边界条件
ui=ε0ijxj (5) 式中:
ui 为边界上任意位置的位移;ε0ij 为应变常量;xj 为边界上任意位置的坐标。2)均匀应力边界条件
{t_i} = \sigma _{ij}^0{{\boldsymbol n}_j} (6) 式中:
{t_i} 为边界上任意位置的点荷载;\sigma _{ij}^0 为应力常量;{\boldsymbol {n}_j} 为边界上任意位置的外法线向量。1.2 砌体材料的正交各向异性本构
考虑许多研究者[19-20]认为正交各向异性本构接近砌体材料的真实性质,假定所求的砌体材料及其RVE单元均满足正交各向异性,其有效模量矩阵如式(7)所示:
{{\boldsymbol{C}}^{{\rm{eff}}}} = \left[ {\begin{array}{*{20}{c}} {C_{11}^{{\rm{eff}}}}&{C_{12}^{{\rm{eff}}}}&{C_{13}^{{\rm{eff}}}}&{}&{}&{} \\ {C_{21}^{{\rm{eff}}}}&{C_{22}^{{\rm{eff}}}}&{C_{23}^{{\rm{eff}}}}&{}&{}&{} \\ {C_{31}^{{\rm{eff}}}}&{C_{32}^{{\rm{eff}}}}&{C_{33}^{{\rm{eff}}}}&{}&{}&{} \\ {}&{}&{}&{C_{44}^{{\rm{eff}}}}&{}&{} \\ {}&{}&{}&{}&{C_{55}^{{\rm{eff}}}}&{} \\ {}&{}&{}&{}&{}&{C_{66}^{{\rm{eff}}}} \end{array}} \right] (7) 式中:
{{\boldsymbol{C}}^{{\rm{eff}}}} 为有效模量矩阵;C_{ij}^{{\rm{eff}}} 为有效模量分量。砌体材料的有效柔度矩阵与工程弹性常数的关系,如式(8)所示:
\begin{split} {{\boldsymbol{S}}^{{\rm{eff}}}} =& \left[ {\begin{array}{*{20}{c}} {S_{11}^{{\rm{eff}}}}&{S_{12}^{{\rm{eff}}}}&{S_{13}^{{\rm{eff}}}}&{}&{}&{} \\ {S_{21}^{{\rm{eff}}}}&{S_{22}^{{\rm{eff}}}}&{S_{23}^{{\rm{eff}}}}&{}&{}&{} \\ {S_{31}^{{\rm{eff}}}}&{S_{32}^{{\rm{eff}}}}&{S_{33}^{{\rm{eff}}}}&{}&{}&{} \\ {}&{}&{}&{S_{44}^{{\rm{eff}}}}&{}&{} \\ {}&{}&{}&{}&{S_{55}^{{\rm{eff}}}}&{} \\ {}&{}&{}&{}&{}&{S_{66}^{{\rm{eff}}}} \end{array}} \right]= \\ & \left[ {\begin{array}{*{20}{c}} {\dfrac{1}{{{E_1}}}}&{\dfrac{{ - {{\nu}_{12}}}}{{{E_2}}}}&{\dfrac{{ - {{\nu}_{13}}}}{{{E_3}}}}&{}&{}&{} \\ {\dfrac{{ - {{\nu}_{21}}}}{{{E_1}}}}&{\dfrac{1}{{{E_2}}}}&{\dfrac{{ - {{\nu}_{23}}}}{{{E_3}}}}&{}&{}&{} \\ {\dfrac{{ - {{\nu}_{31}}}}{{{E_1}}}}&{\dfrac{{ - {{\nu}_{32}}}}{{{E_2}}}}&{\dfrac{1}{{{E_3}}}}&{}&{}&{} \\ {}&{}&{}&{\dfrac{1}{{{G_{12}}}}}&{}&{} \\ {}&{}&{}&{}&{\dfrac{1}{{{G_{13}}}}}&{} \\ {}&{}&{}&{}&{}&{\dfrac{1}{{{G_{23}}}}} \end{array}} \right] \end{split} (8) 式中:
{{\boldsymbol{S}}^{{\rm{eff}}}} 为有效柔度矩阵;S_{ij}^{{\rm{eff}}} 为有效模量分量;{E_i} 、{\nu_{ij}} 、{G_{ij}} 分别为材料的弹性模量、泊松比、剪切模量。根据模量矩阵和柔度矩阵互逆的性质可得式(9):
{{\boldsymbol{C}}^{{\rm{eff}}}} = {( {{{\boldsymbol{S}}^{{\rm{eff}}}}} )^{ - 1}} (9) 1.3 砌体材料的有效模量求解
基于两种边界条件和正交各向异性假定,可对砌体材料的有效模量进行求解。图2为三维情况下RVE单元的边界条件示意图[21]。
将式(7)、式(8)分别代入式(1)、式(2)中,可以看出,正交各向异性材料的压-拉应力和切应力不耦合。因此,当RVE单元处于均匀应力或应变条件时,若受法向荷载,仅产生平均正应力;若受切向荷载时,仅产生平均切应力。
1)法向荷载
当RVE单元的某条边界受到i方向的法向均匀应力或应变时,除受到位移约束和荷载的一对边界以外,其余边界上无法向约束。再考虑到此时仅产生平均正应力,因此RVE单元的平均正应力分量如式(10)所示:
{\overline \sigma _{ii}} \ne 0,\;{\overline \sigma _{jj}}{\rm{ = }}0,\;{\overline \sigma _{kk}}{\rm{ = }}0 (10) 将式(8)、式(10)代入式(2),得到弹性模量和泊松比的求解式,如式(11)、式(12)所示:
{E_i} = \frac{{{{\overline \sigma }_{ii}}}}{{{{\overline \varepsilon }_{ii}}}} (11) {v_{ji}} = - \frac{{{{\overline \varepsilon }_{jj}}}}{{{{\overline \varepsilon }_{ii}}}} (12) 式中:
{\overline \sigma _{ii}} 、{\overline \varepsilon _{ii}} 分别为仅有i方向正应力或应变作用时的i方向平均正应力分量和平均正应变分量;{v_{ji}} 为均质化的泊松比;{\overline \varepsilon _{ii}} 、{\overline \varepsilon _{jj}} 分别为仅有i方向正应力或正应变作用时的i方向和j方向平均正应变分量;下标ii、jj不是哑标,可取11、22、33。2)切向荷载
当RVE单元的某条边界受到ij方向的均匀切应力或切应变时,所施加的位移约束主要提供ij方向的剪切反力,其他方向的应力极小。再考虑到此时仅产生平均切应力,因此RVE单元的平均切应力分量如式(13)所示:
{\overline \sigma _{ij}} \ne 0,\;{\overline \sigma _{ik}}{\rm{ = }}0,\;{\overline \sigma _{jk}}{\rm{ = }}0 (13) 将式(8)、式(13)代入式(2),得到剪切弹性模量的计算式,如式(14)所示:
{G_{ij}} = \frac{{{{\overline \sigma }_{ij}}}}{{{{\overline \varepsilon }_{ij}}}} (14) 式中:
{G_{ij}} 为均质化的剪切模量;{\overline \sigma _{ij}} 、{\overline \varepsilon _{ij}} 分别为ij方向切应力或切应变作用时的平均切应力和切应变分量;下标ij可取12、13、23。利用式(11)、式(12)、式(14)得到均质化的工程弹性常数,并代入式(8)、式(9),即可得到均匀应变边界条件下的Voigt有效模量
C_{ij}^{\rm{V}} 和均匀应力边界条件下的Reuss有效模量C_{ij}^{\rm{R}} 。运用能量极值法[22],可推导出C_{ij}^{\rm{V}} 为真实有效模量的上限,C_{ij}^{\rm{R}} 为真实有效模量的下限。1.4 有效模量的计算步骤
砌体均质化的目的是得到与砌体材料性质相同的材料,则整个砌体可以看成是由多个力学性质相同的RVE单元组成[23]。那么完整砌体结构和RVE单元的力学性能基本是相同的。通常学者们把几何可复制性作为选取砖砌体RVE单元的依据,即通过平移复制RVE单元,可得到整个砌体结构。满足几何可复制性的RVE单元和整体结构的几何构造基本一致,力学性能往往非常接近。但石砌体具有一定几何构造随机性,不能直接按该依据指定RVE单元。Huet[24]指出当RVE单元的尺寸增大到一定程度以后,单元几何构造的统计分布将向完整结构构造的统计分布接近,同时Voigt有效模量
C_{ij}^{\rm{V}} 和Reuss有效模量C_{ij}^{\rm{R}} 将收敛于真实的砌体有效模量。基于该结论,在石砌体上选取多个不同位置、大小的备选RVE单元,衡量该单元的两种有效模量收敛程度。若足够收敛,该备选单元即为合理的RVE单元,同时可由C_{ij}^{\rm{V}} 和C_{ij}^{\rm{R}} 获得真实的砌体有效模量。上述过程的具体步骤如下所述。1) 借鉴Cluni等[11]的有限尺度测试窗法,在砌体墙上选择多个区域,于各区域框选多个尺寸的方框,框内的部分即为备选RVE单元,如图3所示。
2) 建立备选RVE单元线弹性数值模拟模型,按图2所示,对RVE单元施加均匀应变边界条件和均匀应力边界条件,并进行数值模拟。
3) 对数值模拟结果进行后处理,根据式(15)和式(16),计算备选RVE单元的平均应力分量和平均应变分量。
\overline \sigma _{ij}^{} = \frac{{\displaystyle\sum {\sigma _{ij}^{} \cdot v_{}^{}} }}{{\displaystyle\sum {v_{}^{}} }} (15) \overline \varepsilon _{ij}^{} = \frac{{\displaystyle\sum {\varepsilon _{ij}^{} \cdot v_{}^{}} }}{{\displaystyle\sum {v_{}^{}} }} (16) 式中:
\sigma _{ij}^{} 、\varepsilon _{ij} 分别为RVE单元内任意单元的应力、应变分量;v 为RVE单元内任意单元的体积。4) 把平均应力分量和平均应变分量代入式(11)、式(12)、式(14),得到均匀应变边界条件下的Voigt工程弹性常数
E_i^{\rm{V}} 、v_{ij}^{\rm{V}} 、G_{ij}^{\rm{V}} 和均匀应力边界条件下的Reuss工程弹性常数E_i^{\rm{R}} 、v_{ij}^{\rm{R}} 、G_{ij}^{\rm{R}} 。5) 将所得的工程弹性常数代入式(8),即可得到均匀应变边界条件下的Voigt有效柔度矩阵
{{\boldsymbol{S}}^{\rm{V}}} 和均匀应力边界条件下的Reuss有效柔度矩阵{{\boldsymbol{S}}^{\rm{R}}} 。6) 将两种边界条件下的有效柔度矩阵分别代入式(9),即可得到均匀应变边界条件下的有效模量分量
C_{ij}^{\rm{V}} 、均匀应力边界条件下的有效模量分量C_{ij}^{\rm{R}} 。值得注意的是,为满足正交各向异性的假定,对所求得的部分有效柔度进行如下平均计算:
\left\{ \begin{aligned} & {\overline C_{ij}^{\rm{V}}{\rm{ = }}\overline C_{ji}^{\rm{V}}{\rm{ = }}\frac{{C_{ij}^{\rm{V}} + C_{ji}^{\rm{V}}}}{2}} \\ & {\overline C_{ij}^{\rm{R}}{\rm{ = }}\overline C_{ji}^{\rm{R}}{\rm{ = }}\frac{{C_{ij}^{\rm{R}} + C_{ji}^{\rm{R}}}}{2}} \end{aligned}\right. (17) 为了消除组元分布不均匀造成的影响,计算相同尺寸备选RVE单元的Voigt和Reuss有效模量平均值,作为该尺寸备选RVE单元的有效模量计算结果。
7) 根据所得的
C_{ij}^{\rm{V}} 、C_{ij}^{\rm{R}} ,计算砌体材料的有效模量预估值以及衡量两种有效模量收敛程度的指标。① 有效模量预估值
\overline C_{ij}^{} ,通过式(18)计算:\overline C_{ij}^{} = \frac{{C_{ij}^{\rm{V}} + C_{ij}^{\rm{R}}}}{2} (18) ② 有效模量收敛幅值
\delta ,通过式(19)计算:\delta = \frac{{C_{ij}^{\rm{V}} - C_{ij}^{\rm{R}}}}{{\overline C_{ij}^{}}} (19) ③ 考虑有效模量的各个分量的收敛幅值有所差别,通过式(20)计算有效模量的收敛变化率
{v^{(k)}} :{v^{(k)}} = \frac{{{\delta ^{(k)}}}}{{{\delta ^{(1)}}}} (20) 式中:将备选RVE单元的次序按单元的尺寸由小到大进行排列,上角标(k)表示该变量为第k个备选RVE单元的变量;
{\delta ^{(1)}} 、{\delta ^{(k)}} 分别为第1、k个备选RVE单元的收敛幅值;{v^{(k)}} 为第k个备选RVE单元的收敛变化率。8) 通过综合考虑所有模量分量的收敛变化率
{v^{(k)}} ,判断RVE单元的有效模量是否足够收敛;若足够收敛,此时有效模量的预估值\overline C_{ij}^{} 即为砌体结构的有效模量;若不够收敛,说明该尺寸RVE单元的力学性能与完整砌体结构的存在差距,需对更大尺寸的备选RVE单元进行有效模量计算。上述有效模量计算步骤对应的流程图如图4所示。
2 有效模量计算方法的验证
2.1 有限元建模
本文采用有限元软件ABAQUS,建备选RVE单元有限元模型。该模型的单元均采用空间三维六面体线性减缩积分单元(C3D8R),构件之间均采用merge。有限元模型的边界条件如图2所示。
2.2 验证
为验证本文的有效模量计算方法的准确性及适用性,选取Vermeltfoort等[25]和Gumaste等[26]的试验、Drougkas等[27]的数值模拟、Cluni等[11]的有限尺度测试窗法的模型进行验证。
2.2.1 试验和数值模拟的验证
由于具有几何尺寸信息、材料本构和砌体有效模量的石砌体试验非常少,本文选取Vermeltfoort等[25]、Gumaste等[26]的砖砌体试验进行验证,以说明本文方法所得有效模量的有效性。基于原文献的几何参数、材料属性,建立有限元模型。有限尺度测试窗法的研究[21]表明:满足几何可复制性的砖砌体备选RVE单元可作为合理的RVE单元,所得有效模量非常接近。所以,本文对于一类砖砌体只选取一个RVE单元进行计算,几何模型和所选取的RVE单元形式如图5所示。
本文方法所得结果、砖砌体试验结果和数值模拟结果如表1所示,两两相互对比如图6所示。可以看出,本文方法所得竖向有效模量接近试验和数值模拟所得的有效模量,说明了本文方法所得有效模量的有效性。值得注意的是,与数值模拟所得模量的接近程度相对更高,这是由于建模所用本构与实际有差距造成的。
2.2.2 有限尺度测试窗法模型的验证
具有足够建模信息的石砌体结构试验研究很少,因此利用Cluni等[11]的有限尺度测试窗法的模型对模量计算方法进行验证,以说明本文方法适用于几何构造具有一定随机性的石砌体。几何模型和所选取的RVE单元形式如图7所示。
本文所得的结果与Cluni等[11]的结果对比如图8所示,有效模量的收敛变化速率如图9所示。可以看出当RVE单元的边长达到400 mm后,所有模量分量的收敛变化率的变动极小,说明RVE单元的尺寸变化对有效模量收敛的影响极小,此时有效模量的收敛程度已足够高。根据本文的模量计算方法,400 mm和500 mm的RVE单元的有效模量预估值均可作为完整砌体结构的有效模量。该模量与Cluni结果的差距很小,这说明了本文的有效模量计算方法适用于几何构造具有一定随机性的石砌体。
3 藏式古建石墙的有效模量计算
3.1 藏式古建石墙
藏式古建石墙是藏式古建筑中常见的承重结构,该石墙最常见的砌筑工艺如图10所示,通常以花岗岩和天然黄泥分别作为砌块和砂浆,同时具有明显的三叶墙特征:外观上近似于夹心墙,外壳是两片砌块较大且规整的外叶墙,夹心是一片由黄泥、碎石和小石块组成的内叶墙。
此外,藏式古建石砌体墙的砌块规格和形状并不统一:如图11所示,外叶墙上体积较大、形状较为规则的长方体状石块被称为块石。为了填充块石之间的缝隙,相邻块石之间会砌入几块小石块,该石块被称为碎石。块石和碎石所在的水平层被称为块石层。砌筑时为了便于找平,块石层之间会铺筑大量的扁平状石片,该石片被称为片石。片石所在的水平层被称为片石层。
3.2 藏式古建石墙随机模型
对某藏式石砌体古建筑群进行调研,得到大量藏式古建石墙的外叶墙组元尺寸的概率密度函数[28],如表2所示,相应的组元尺寸如图12所示。
表 2 藏式古建石墙各组元概率密度函数表[28]Table 2. The probability density function of each component of Tibetan ancient stone masonry[28]尺寸类型 代表符号 分布类型 均值/cm 标准差/cm 碎石宽度 {B_{\rm{c}}} 正态分布 9.58 2.97 块石宽度 {B_{\rm{b}}} 对数正态分布 3.28 0.28 片石宽度 {B_{\rm{f}}} 2.75 0.29 水平泥浆 {B_{\rm{h}}} 0.71 0.63 块石厚度 {H_{\rm{b}}} 2.50 0.24 片石厚度 {H_{\rm{f}}} 1.21 0.36 竖直泥浆 {H_{\rm{v}}} 0.55 0.35 为了简化随机模型的生成难度,假定砌块均为长方体,处于同一层的块石或片石高度一致。参考某藏式古建筑的常见墙体的尺寸,并以统计所得的尺寸参数的概率密度函数为依据,生成了一个2250 mm×3000 mm×660 mm(长×高×厚)随机墙体模型,如图13所示。由于缺少厚度方向上的组元尺寸数据,参考常见的砌块厚度,设定块石厚150 mm,片石和碎石均厚90 mm,内叶墙厚360 mm。在该墙体模型上,从A、B、C、D四个区域,各选取了边长为200 mm、400 mm、600 mm、800 mm、1000 mm的5个正方形备选RVE单元。
3.3 有限元模型的参数设计
根据试验数据和强度相近材料的性能参数,设定本文的本构模型参数,如表3所示。
3.4 有效模量的对比分析
分别按照本文的方法和Cluni等[11]的有限尺度测试窗法,对藏式古建石墙模型的有效模量进行计算,计算结果如图14、图15所示。通过Voigt有效模量
C_{ij}^{\rm{V}} 、Reuss有效模量C_{ij}^{\rm{R}} 、有效模量预估值\overline C_{ij}^{} 的对比,可以确定有效模量值的变化;通过观察有效模量收敛幅值\delta 、收敛变化率v的变化,可以衡量各个有效模量分量的收敛程度。从图14可以看出,随着备选RVE单元尺寸增大,根据有限尺度测试窗法和本文方法所得的有效模量的变化趋势较为接近,多数有效模量分量在逐渐收敛,并且呈现先快后慢的趋势。通过观察Voigt和Reuss有效模量的变化幅度可以看出:200 mm~400 mm阶段,有效模量的变化幅度往往最大;400 mm~800 mm阶段,有效模量的变化幅度往往较大;800 mm~1000 mm阶段变化幅度往往最小。这是因为随着单元尺寸增大,砌体RVE单元的材料性质逐渐接近完整结构的性质;初始阶段,RVE单元和结构的材料性质差距很大,有效模量的收敛和变化幅度较为明显;当尺寸增大到一定范围以后,二者的材料性质基本一致,有效模量的收敛趋势和变化幅度变得很小。对比有限尺度测试窗法和本文方法所得的有效模量,可以看出,有限尺度测试窗法所得的
{C_{11}} 、{C_{22}} 、{C_{33}} 比本文方法所得的略大,这是由于有限尺度测试窗法假定了泊松比为0造成的。根据本文的模量计算方法,对比图15中各个有效模量分量的收敛变化率,可以看出,在800 mm ~ 1000 mm范围内,除了
{C_{33}} ,其他模量分量的收敛变化率的数值很小并且相邻点间差值很小,说明边长800 mm、1000 mm的RVE单元的Voigt和Reuss有效模量的收敛程度已足够高。那么800 mm、1000 mm的RVE单元有效模量预估值均可作为藏式古建石墙的有效模量。从图14、图15可以看出,两种方法所得的不同模量分量收敛速率的分布规律大致相近。有限尺度测试窗法所得的六个有效模量,按其受RVE单元影响程度,可以分为三组:1)几乎不受影响:
{C_{33}} ;2)受影响较小:{C_{55}} 、{C_{66}} ;3)受影响较大:{C_{11}} 、{C_{22}} 、{C_{44}} 。按本文的方法所得的九个有效模量分量,按其受到RVE单元尺寸的影响程度,可以分为以下三组:1)几乎不受影响:{C_{33}} ;2)受影响较小:{C_{13}} 、{C_{23}} 、{C_{55}} 、{C_{66}} ;3)受影响较大:{C_{11}} 、{C_{22}} 、{C_{44}} 、{C_{12}} 。即RVE单元尺寸对厚度方向的轴向模量几乎没有影响,对其他面外的模量分量影响较小,对面内的模量分量影响较大。这是因为随着备选RVE单元尺寸发生改变,砌体结构平面上的几何构造会随之发生改变,但沿厚度方向上,几何构造的改变很小。4 石砌体结构整体式模型
基于本文方法所得的有效模量,可以建立整体式模型,代替对完整结构的精细化建模,进而大量地减少计算时间和收敛难度。为了证明本文提出的整体式模型的有效性,以藏式古建石墙为例,分别按本文的方法和有限尺度测试窗法建立整体式模型,与传统分离式模型一并进行砌体墙压剪模型的对比分析。
模型几何尺寸均与图13所示的墙体相同。模型边界条件[21]设置如图16所示,墙体底部设置为固结约束,上端放置一块平面尺寸略大于墙体的刚性板(2500 mm×700 mm×150 mm)。该刚性板与墙体之间定义面对面接触,法向行为定义为默认的硬接触,切向行为定义为罚函数,摩擦系数为0.45。首先对刚性板顶部作用0.5 MPa的均匀压应力,然后保持压力不变,再对刚性板的左端中点作用集中荷载10 kN。分离式模型构件之间均采用merge。模型均采用C3D8R单元。分离式模型本构所采用的组元材料的性能参数如表3所示;整体式模型为正交各向异性本构,参数分别为按本文的方法和有限尺度测试窗法所得的1000 mm RVE单元的有效模量预估值。
外、内叶墙的材料性能存在较大差别,导致分离式模型外、内叶墙的响应存在显著差异,因此分别选取外、内叶墙厚度中心处的A-A、B-B两个截面,代表墙体的绝大部分区域;整体式模型材料性质均匀统一,不存在明显的外、内叶墙响应差异,故取其厚度中心的截面进行分析。
图17为分离式模型、基于本文方法和有限尺度测试窗法的整体式模型在压剪荷载作用下的Mises应力云图。从图17(a)可以看出,分离式模型外叶墙的Mises应力分布不均匀,砌块所受应力明显比灰缝所受应力大。在块石层,块石中部区域的应力较小,越靠近边缘,应力越大;与块石相比,碎石所受应力明显较小。在片石层,上下两侧均与块石相邻的片石所受应力较大,与碎石相邻的片石所受应力较小。这说明,模型处于一个刚度分布不均匀的状态:在块石层,块石的刚度比碎石区域的刚度大得多,导致块石承担了大部分的压力,而碎石承担的压力较小。块石和碎石区域的压力传递到片石层,片石层有一定的分散应力作用,使得应力的不均匀程度有明显降低。与外叶墙相比,分离式模型内叶墙的Mises应力较为均匀,所受应力低得多。从图17(b)可以看出,按本文方法所建的整体式模型的大部分区域呈现较为均匀的状态,仅在墙体的底部,受到边界条件的约束,Mises应力相对较小。从图17(c)可以看出,按有限尺度测试窗法所建的整体式模型在墙体中间大部分区域的Mises应力较为均匀,但在左右两侧出现了反对称分布的应力。分离式模型和两种整体式模型的应力分布状态存在显著的差异,这主要由于分离式模型和整体式模型的建模精细程度存在差别导致的,但整体式模型的应力可以看作是分离式模型外叶墙、内叶墙应力综合后所得的结果。将两种整体式模型进行对比,可以看出,有限尺度测试窗法所得的整体式没有考虑泊松比,不能反映更接近实际情况的状态:水平向剪力荷载使墙体左右两侧分别产生了拉、压应力,该应力与墙体顶部所受的均匀压应力叠加,使墙体左右两侧所受的竖向压应力不同。考虑泊松比,此时墙体两侧应产生不同大小的横向应力,所以Mises应力云图应该呈现更接近图17(b)的分布,而并不是如图17(c)一样的简单反对称分布。
图18为分离式和两种整体式模型在压剪作用下的位移云图。对比可以看出,三个模型的位移数值大小较为接近,位移分布近似,说明基于本文方法和有限尺度测试窗法的整体式模型均可以较为合理地复制砌体结构的压剪变形特征。
为了比较各模型的变形数值大小,将各模型的顶部压缩位移
\Delta v 、水平位移\Delta u 进行对比,如表4所示。通过对比可以看出三个模型在关键部位上的变形是很接近的。表 4 墙体顶部压缩位移和水平位移Table 4. Compressive and horizontal displacement on the top of the wall模型形式 顶部压缩位移/mm 顶部水平位移/mm 分离式 1.321 0.153 基于本文方法的整体式 1.294 0.143 基于有限尺度测试窗法的整体式 1.294 0.144 为了说明基于本文方法的整体式模型在模拟侧向变形的优势,将分离式和两种整体式模型在压剪作用下的水平位移进行对比,如图19所示。考虑到水平位移在厚度方向上变化极小,故取厚度方向中线的水平位移为代表值,同时设定向右位移为正。可以看出,分离式模型和基于本文方法的整体式模型的水平位移是极为接近的;而基于有限尺度测试窗法的整体式模型,左侧和右侧的水平位移基本一致,与分离式模型的水平位移相比,具有明显差异。这是因为有限尺度测试窗法忽略了泊松比,将轴向压应力和切应力引起的侧向变形简化为单纯的剪切变形,而本文的方法弥补了该缺陷。基于本文方法的整体式模型可以反映分离式模型的变形状态:墙体在轴压力作用下,向两侧膨胀;在受到水平荷载作用后,墙体出现向右的剪切变形。墙体底部受到固结约束,位移基本为零;墙体中部位移是膨胀变形和剪切变形叠加的结果;墙体顶部受到摩擦力的作用,膨胀变形受到限制,左、右两侧位移的差距与中部的相比有少许的下降。
综合上述内容,证明了基于本文方法的整体式模型可以较为合理地复制砌体结构在宏观层面上的整体变形,并且弥补了有限尺度测试窗法不能反映泊松效应的缺陷。
5 结论
本文基于有限尺度测试窗法,提出了一种改进的有效模量计算方法。分别利用该计算方法和有限尺度测试窗法,对藏式古建石砌体有效模量进行对比分析,并以所得有效模量为基础,建立了整体式模型,与精细化模型进行了应力和变形的对比。主要结论如下:
(1)本文基于代表性体积单元,假定砌体材料为正交各向异性,针对几何构造具有一定随机性的石砌体,提出了一种有效模量计算方法,能得到石砌体的九个有效模量分量。
(2)将本文方法所得的有效模量与有限尺度测试窗法所得的有效模量对比,得知两种方法所得的各有效模量分量数值大小和变化趋势相近,但本文方法弥补了有限尺度测试窗法不能获得泊松比的缺陷。
(3)通过分析RVE单元的尺寸大小对有效模量的影响,得知单元尺寸的增大会使得其组元分布逐渐向完整结构的组元分布接近,导致大部分的Voigt、Reuss有效模量分量呈现先快后慢的收敛趋势。RVE单元尺寸对厚度方向的轴向模量收敛程度几乎没有影响,对其他面外的模量分量影响较小,对面内的模量分量影响较大。
(4)基于本文方法所得有效模量建立了整体式模型,在减少计算时间和收敛难度的同时,可以代替传统的精细化模型,模拟结构的宏观变形。
-
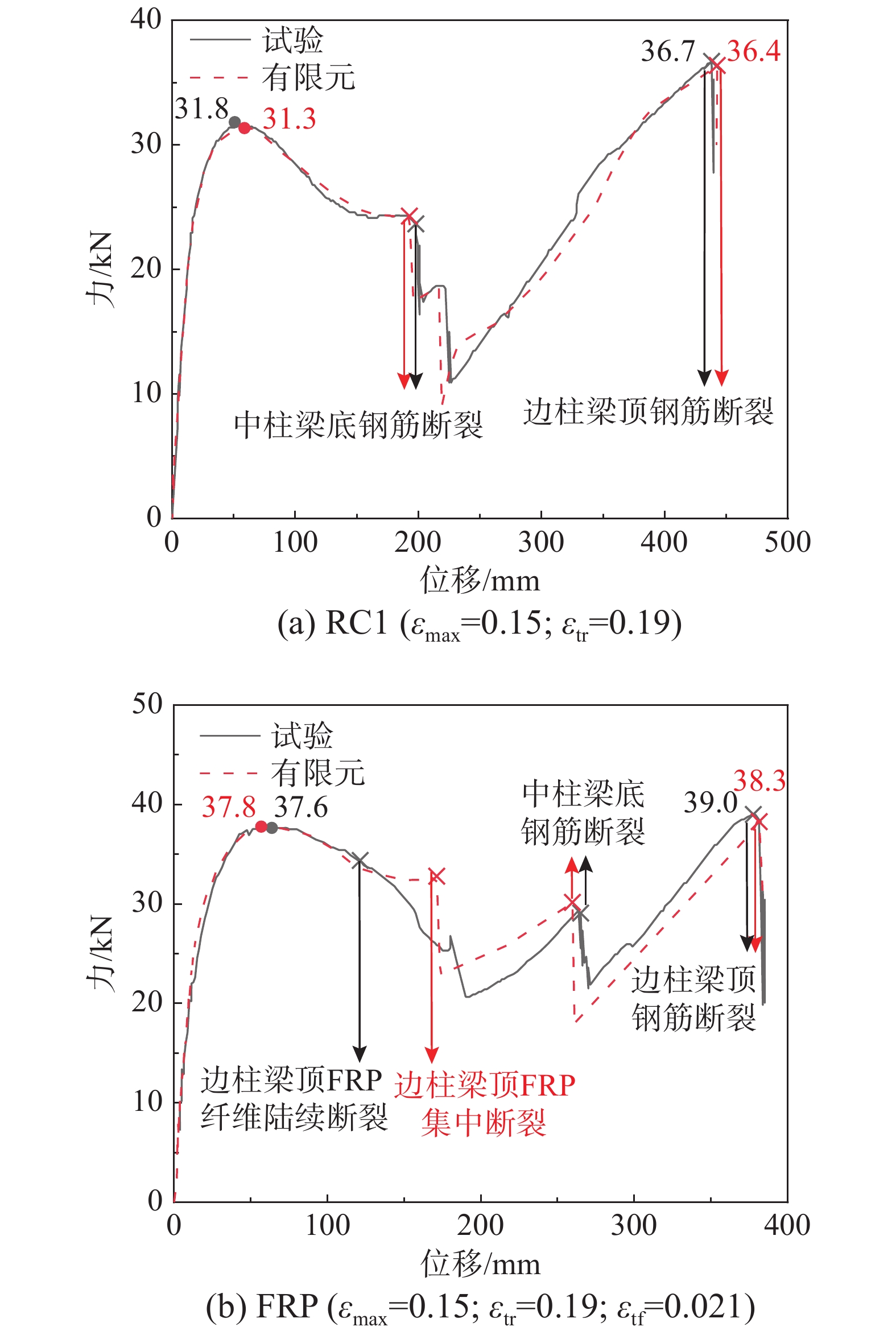
表 1 试件材料信息 (RC1和FRP)
Table 1 Material details of substructures (RC1 and FRP)
混凝土等级 加密区 非加密区 上侧纵筋 下侧纵筋 箍筋 上侧纵筋 下侧纵筋 箍筋 C30 3 
2 

2 
2 

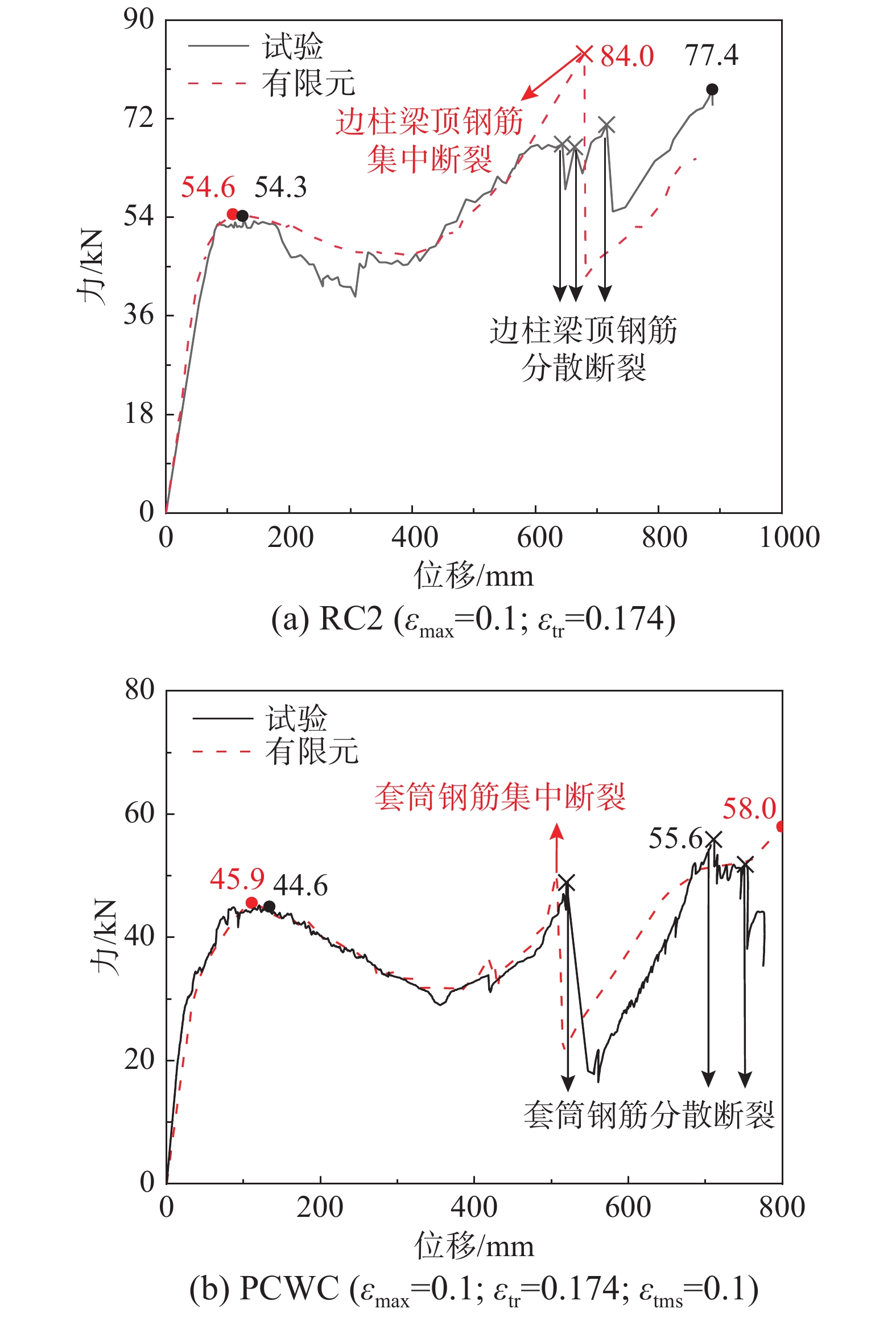
表 2 试件材料信息 (RC2和PCWC)
Table 2 Material details of substructures (RC2 and PCWC)
加密区 非加密区 上侧/下侧纵筋 箍筋 上侧/下侧纵筋 箍筋 3 


2 


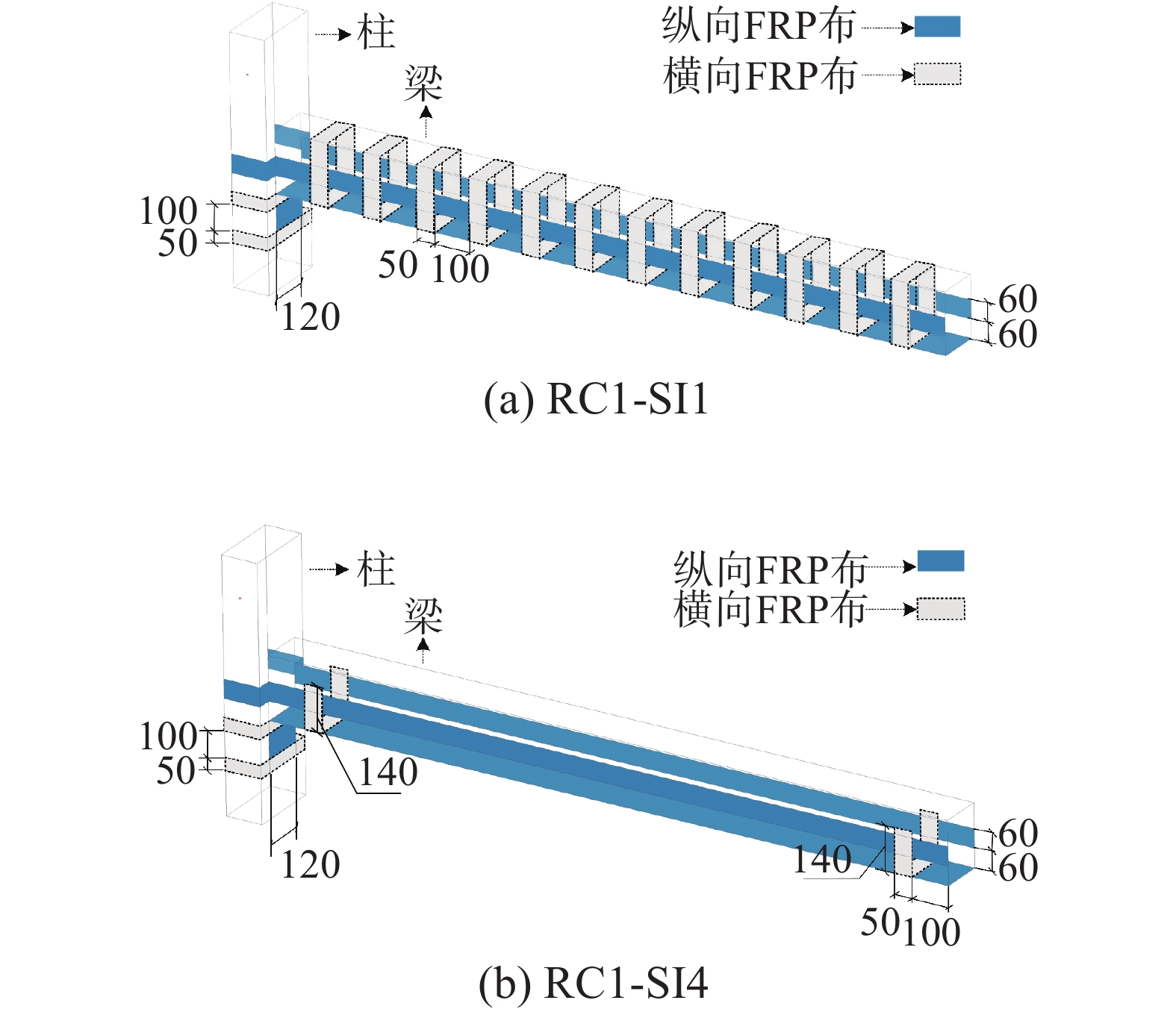
表 3 FRP加固方式(现浇子结构)
Table 3 FRP strengthening methods (RC substructures)
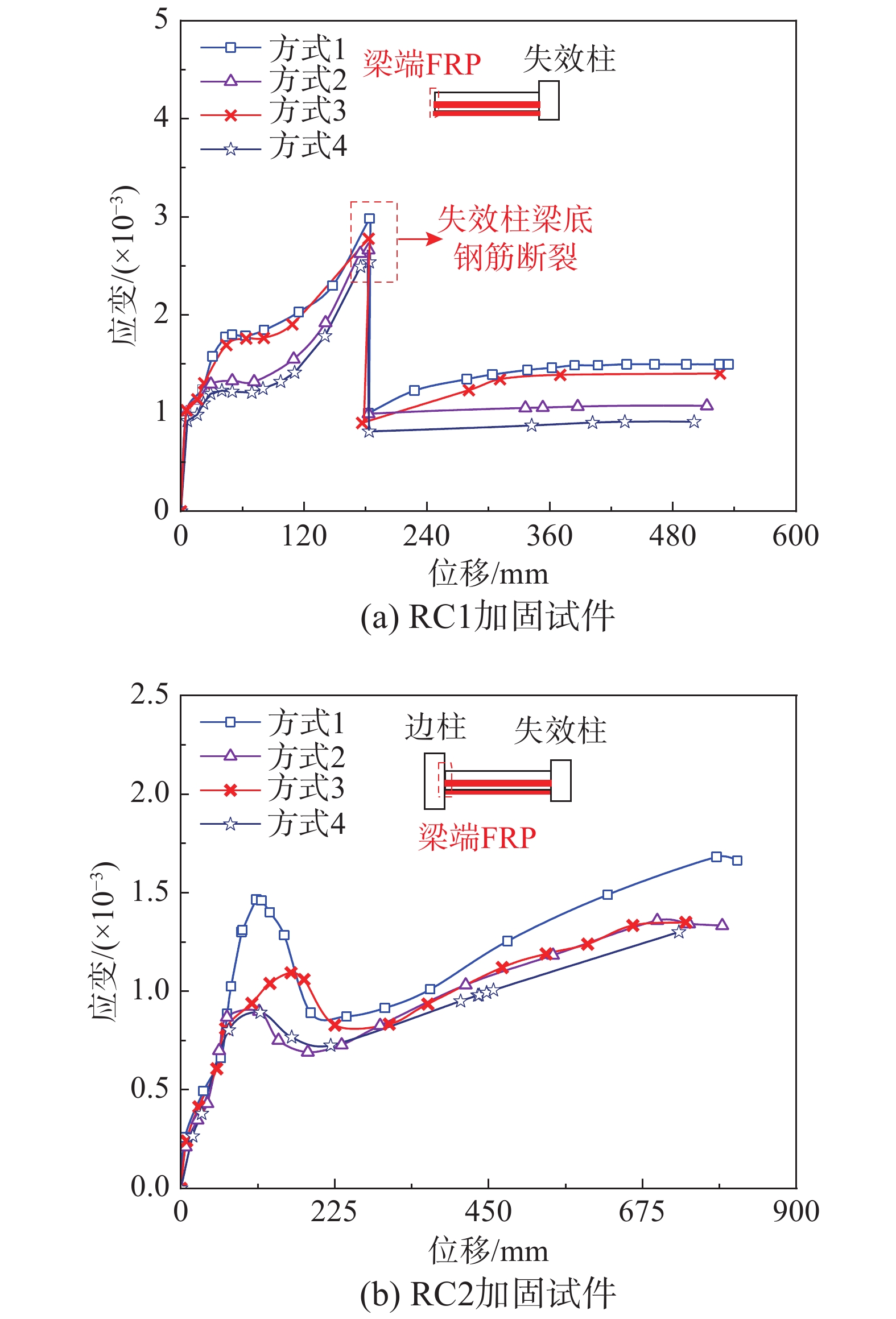
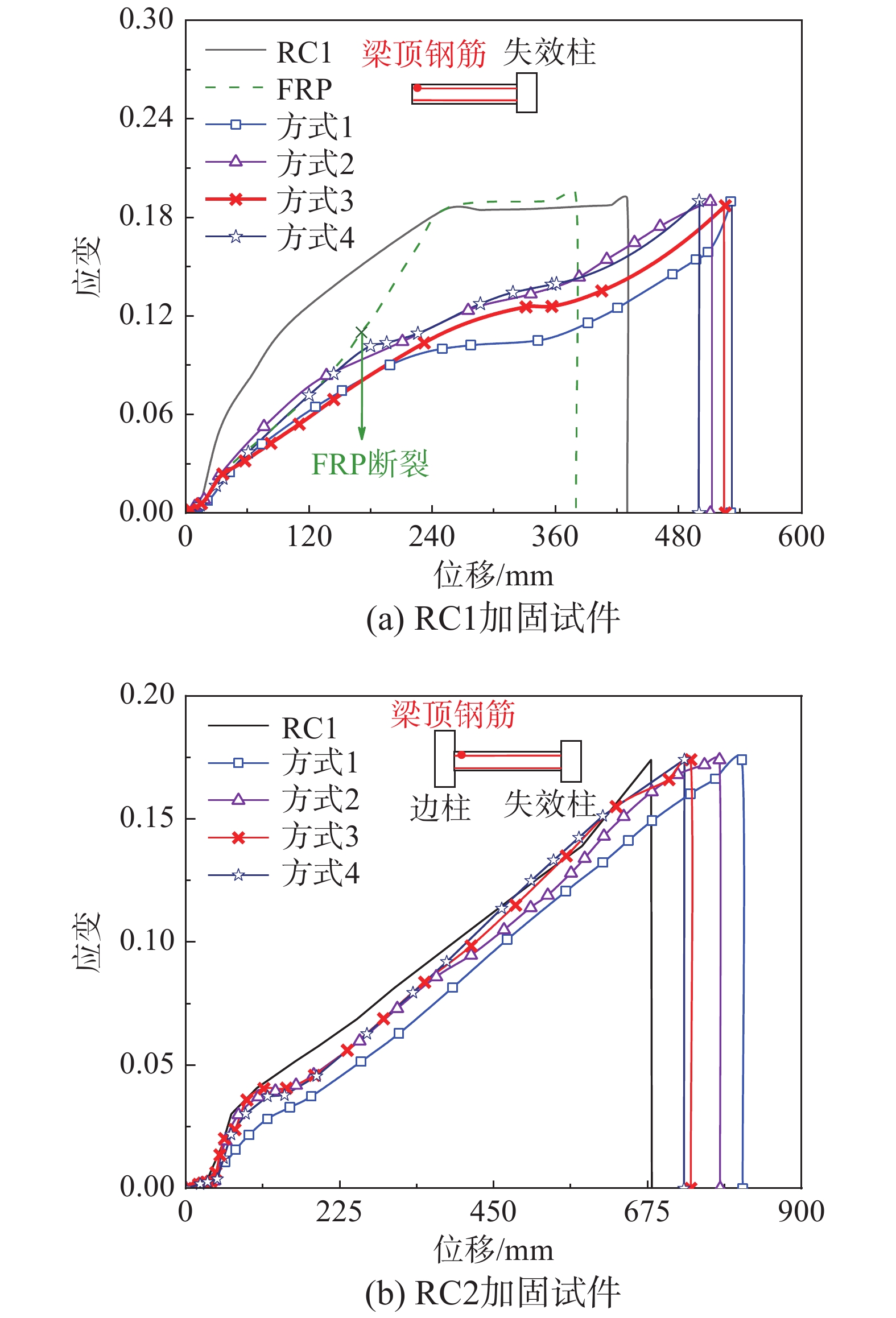
加固方式 纵向FRP布 横向FRP布 方式1 (SI1) 梁底+梁侧中性轴 间隔100 mm,环形封闭 方式2 (SI2) 梁端塑性铰区,环形封闭 方式3 (SI3) 间隔100 mm,U形不封闭 方式4 (SI4) 梁端塑性铰区,U形不封闭 表 4 承载力对比 (现浇子结构)
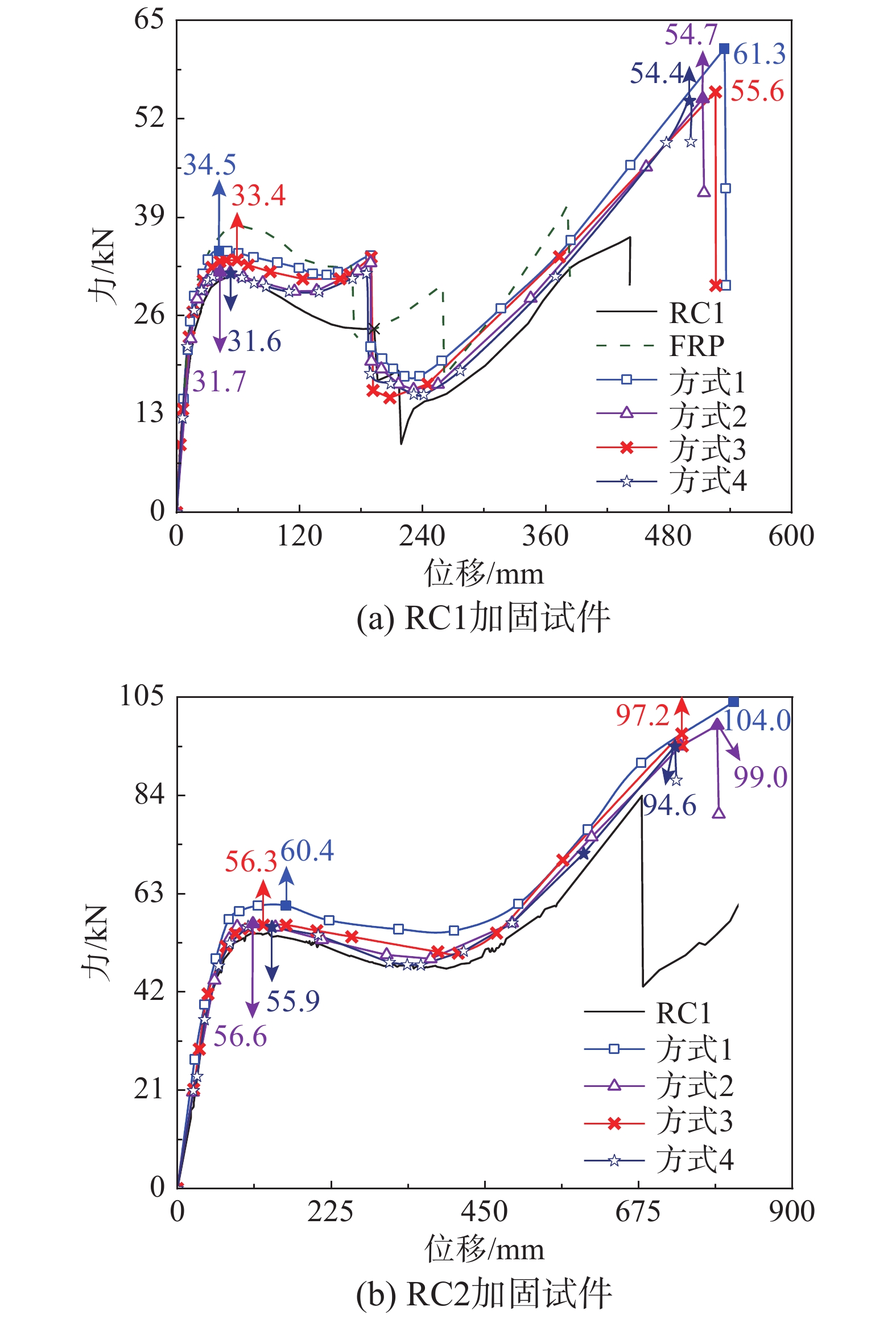
Table 4 Comparison of structural strengths (RC substructures)
试件 小变形 大变形 峰值/kN 提升率/(%) 峰值/kN 提升率/(%) 极限变形/mm FRP 37.8 20.7 38.3 5.2 379.6 RC1-SI1 34.5 10.2 61.3 68.3 534.3 RC1-SI2 31.7 1.3 54.7 50.3 513.1 RC1-SI3 33.4 6.7 55.6 52.7 525.7 RC1-SI4 31.6 0.9 54.4 49.5 500.0 RC2-SI1 60.4 10.8 104.0 23.8 814.0 RC2-SI2 56.6 3.8 99.0 17.9 792.2 RC2-SI3 56.3 3.3 97.2 15.7 738.0 RC2-SI4 55.9 2.6 94.6 12.6 728.1 表 5 FRP承载力贡献 (现浇子结构)
Table 5 Contribution of FRP to structural strengths (RC substructures)
/kN 试件 小变形峰值 大变形峰值 梁侧 梁底 总计 梁侧 梁底 总计 RC1-SI1 1.1 1.3 2.4 9.1 6.7 15.8 RC1-SI2 0.5 0.6 1.1 6.5 8.1 14.6 RC1-SI3 0.5 0.7 1.2 6.8 7.5 14.3 RC1-SI4 0.4 0.5 0.9 5.9 7.8 13.7 RC2-SI1 0.9 4.5 5.4 9.9 9.5 19.4 RC2-SI2 1.0 2.6 3.6 8.0 5.2 13.2 RC2-SI3 0.3 2.9 3.2 8.3 4.6 12.9 RC2-SI4 0.5 0.7 1.2 5.4 6.0 11.4 表 6 FRP加固方式 (装配式子结构)
Table 6 FRP strengthening methods (PC substructure)
加固方式 梁侧纵向FRP布 横向FRP布 方式1 (DI1) 距离梁底100 mm~200 mm 梁端塑性铰区
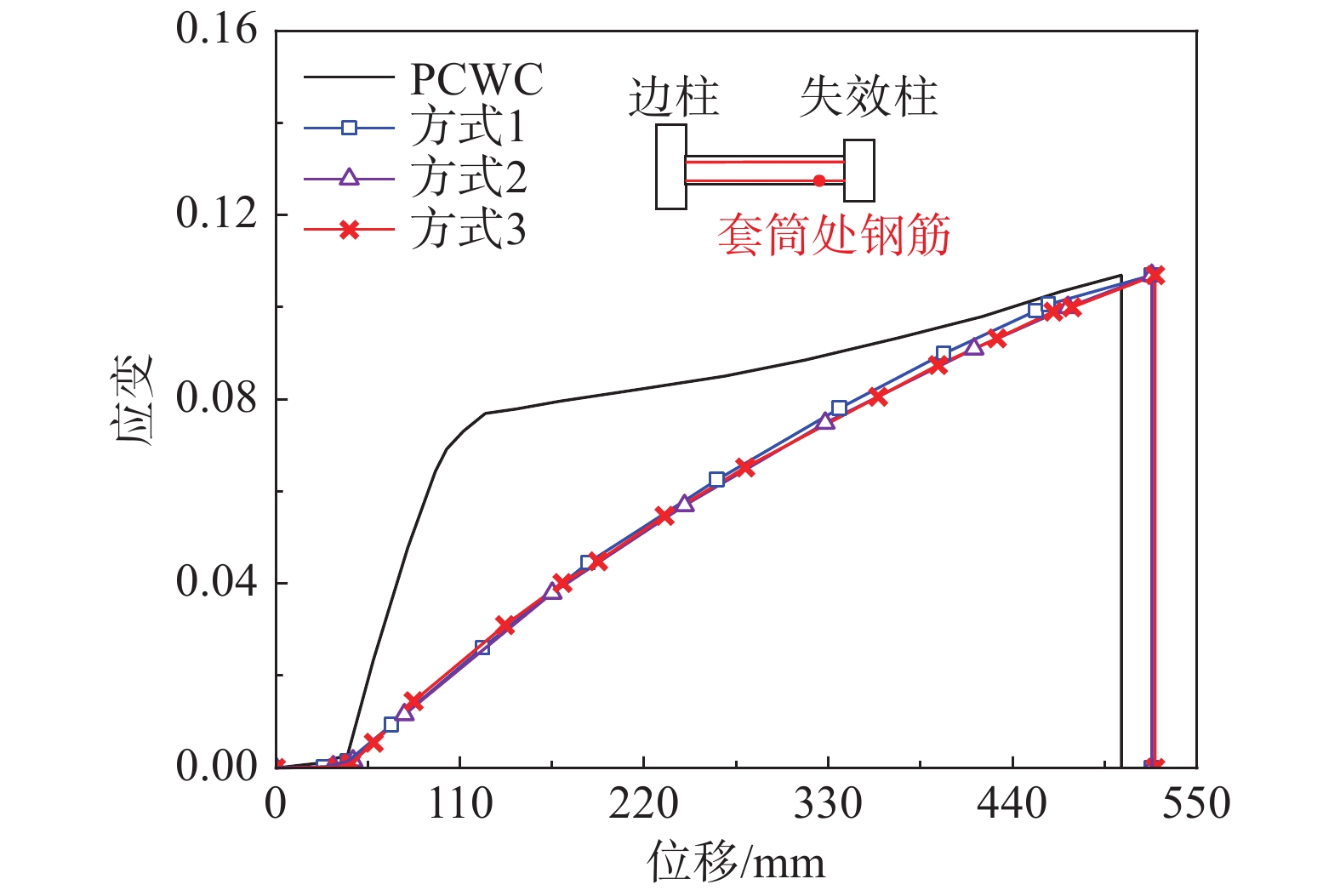
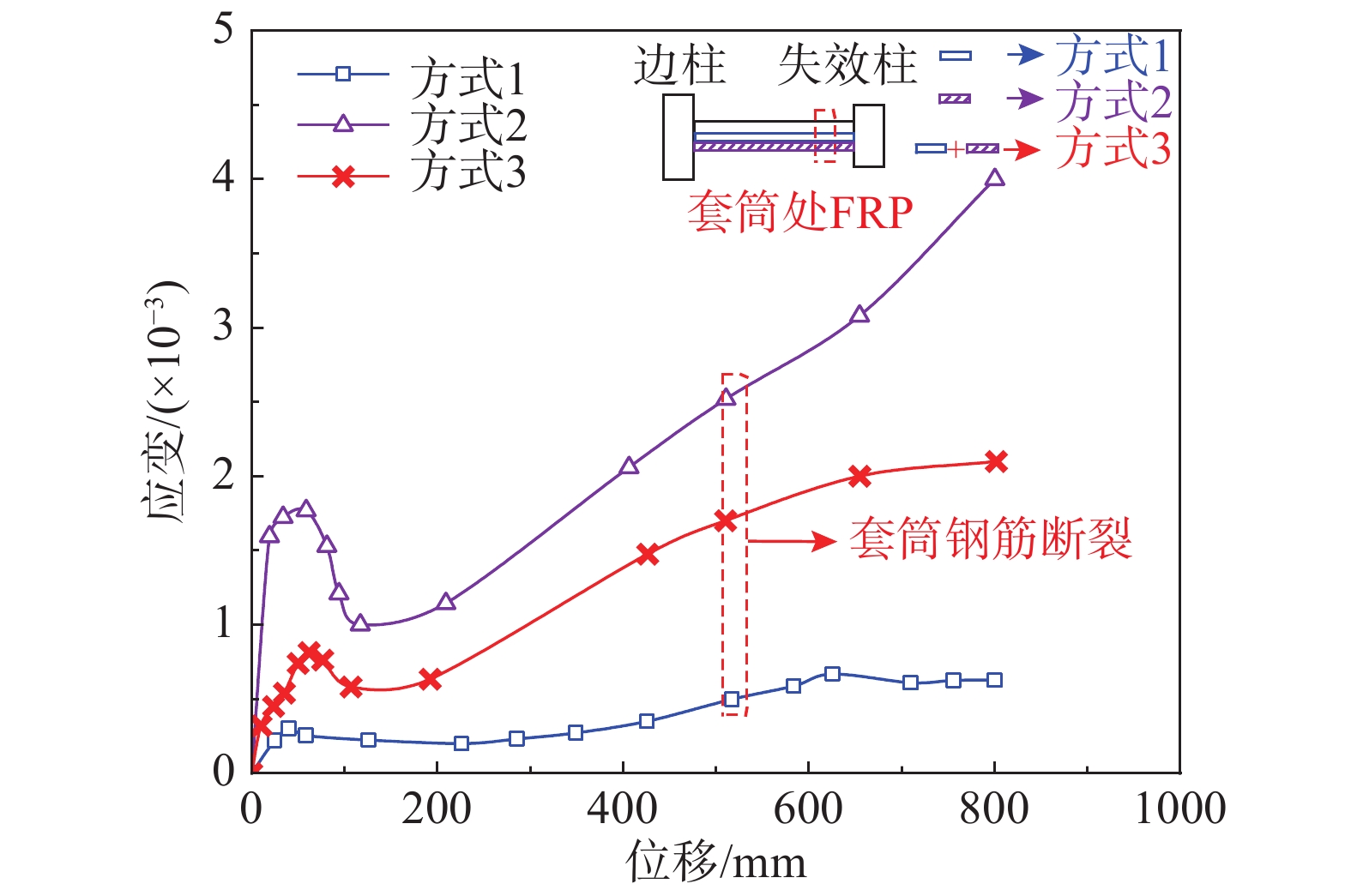
U形不封闭方式2 (DI2) 距离梁底0 mm~100 mm 方式3 (DI3) 距离梁底0 mm~200 mm 表 7 承载力对比 (装配式子结构)
Table 7 Comparisons of structural strengths (PC substructure)
试件 小变形 大变形 峰值/kN 提升率/(%) 峰值/kN 提升率 PCWC 45.9 − 58.0 − RC2 54.6 − 84.0 − PCWC-DI1 49.7 8.3 66.6 5.7 PCWC-DI2 53.8 17.2 83.0 43.1 PCWC-DI3 57.0 24.2 85.9 48.1 表 8 FRP承载力贡献 (装配式子结构)
Table 8 Contribution of FRP to structural strengths (PC substructure)
/kN 试件 小变形峰值 大变形峰值 梁侧 梁顶底 总计 梁侧 梁顶底 总计 PCWC-DI1 0.6 1.5 2.1 0.8 10.1 10.9 PCWC-DI2 4.8 1.1 5.9 8.4 20.1 28.5 PCWC-DI3 9.0 1.5 10.5 8.9 19.8 28.7 表 9 横向U形FRP布参数
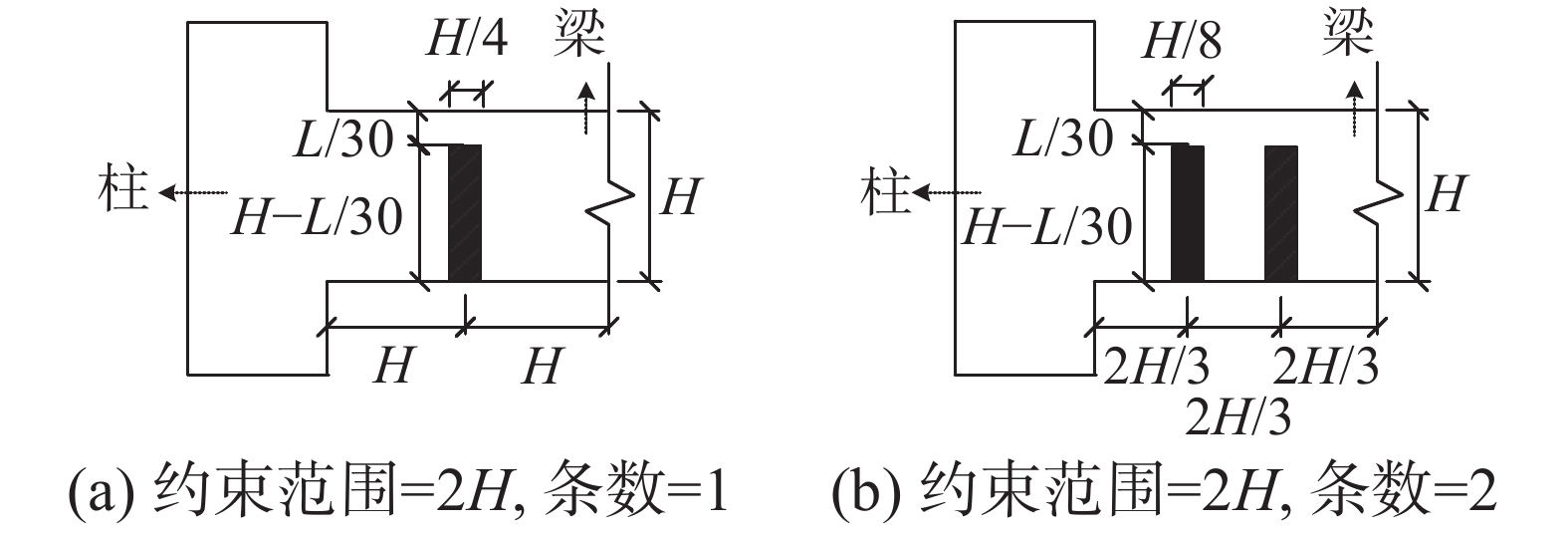
Table 9 Parameters of U-shaped transverse FRP strips
名称 约束范围 条数(宽度) 梁侧长度 H 1(H/4) 取值 5H/4 H−L/30 2H 2(H/8) 注:H与L分别代表梁高与梁跨度。 表 10 承载力对比 (参数优化)
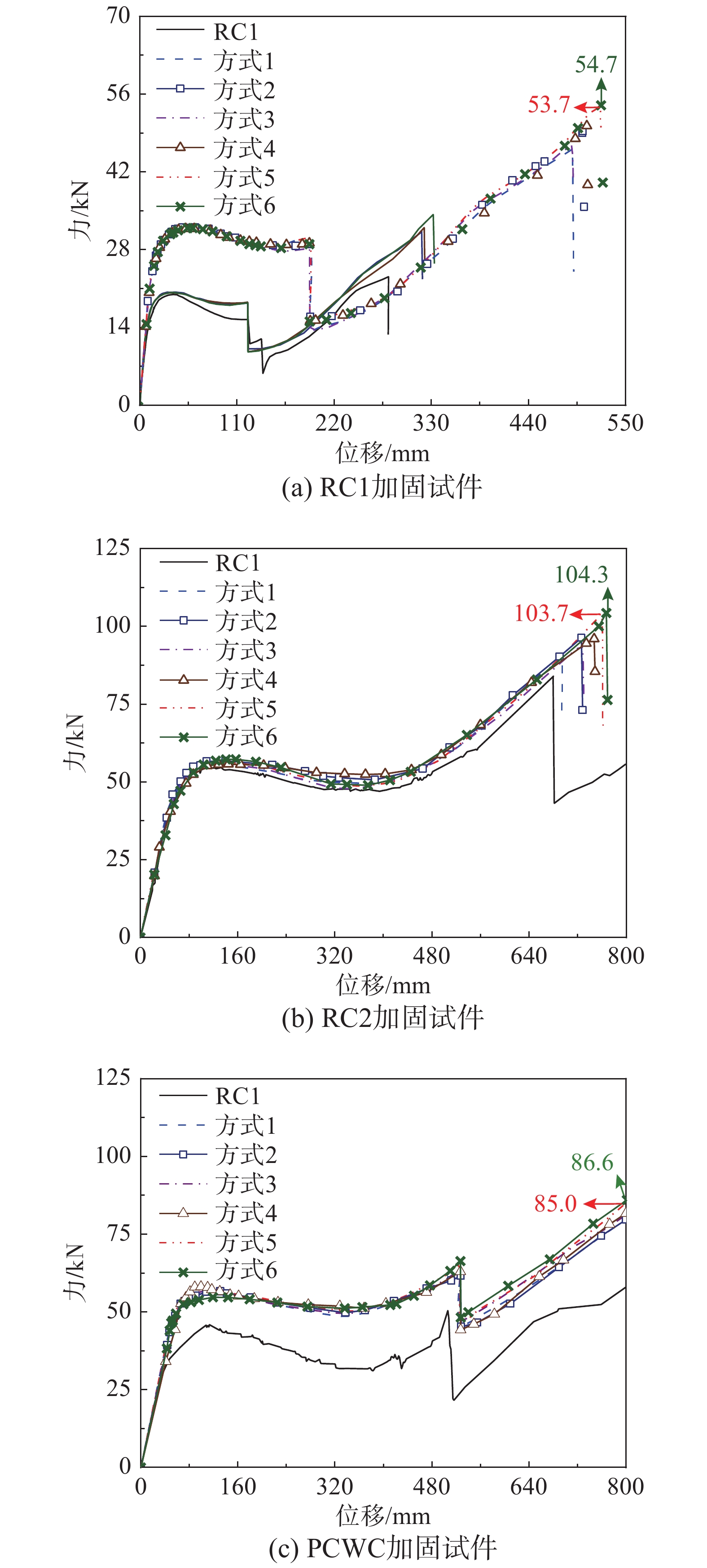
Table 10 Comparison of structural strengths (parameter optimization)
加固方式 RC1 RC2 PCWC 峰值/kN 提升率/(%) 峰值/kN 提升率/(%) 峰值/kN 提升率/(%) 1 (2H2) 54.7 50.3 104.3 24.3 86.6 49.3 2 (2H1) 53.7 47.6 103.7 23.6 85.0 46.6 3 (5/4H2) 50.3 38.2 96.0 14.4 81.7 40.9 4 (5/4H1) 46.8 28.6 94.6 12.8 81.2 40.0 5 (1H2) 49.3 35.4 96.3 14.8 79.6 37.2 6 (1H1) 46.3 27.2 89.0 6.1 79.7 37.4 注:方式简称的第1、2个数字分别代表分布范围与梁高之比、FRP条数。如,2H2代表梁端2倍梁高范围内粘贴2条横向FRP。 表 11 FRP峰值贡献 (参数优化)
Table 11 Contribution of FRP to peak loads (parameter optimization)
/kN 加固方式 RC1 RC2 PCWC 梁侧/底 总计 梁侧/底 总计 梁侧/顶底 总计 2H2 7.3/6.8 14.1 11.1/7.4 18.5 4.9/25.0 29.9 2H1 7.1/5.2 13.3 9.3/7.7 18.0 6.3/22.8 29.1 5/4H2 5.2/4.8 10.0 8.8/7.9 16.7 5.9/22.3 28.2 5/4H1 5.1/3.9 9.0 7.1/3.9 11.0 6.7/20.7 27.4 1H2 5.7/4.0 9.7 7.5/5.0 12.5 4.2/18.6 22.8 1H1 4.6/2.9 7.5 5.3/2.2 7.5 4.7/19.2 23.9 -
[1] ASCE/SEI 7-10, Minimum design loads for buildings and other structures [S]. Reston, Virginia: American Society of Civil Engineers, 2010.
[2] DENG X F, LIANG S L, FU F, et al. Effects of high-strength concrete on progressive collapse resistance of reinforced concrete frame [J]. Journal of Structural Engineering, 2020, 146(6): 04020078. doi: 10.1061/(ASCE)ST.1943-541X.0002628
[3] YOUSEF A M, EL-MANDOUH M A. Dynamic analysis of high-strength concrete frame buildings for progressive collapse [J]. Case Studies in Construction Materials, 2020, 13: e00407. doi: 10.1016/j.cscm.2020.e00407
[4] YU J, TAN K H. Special detailing techniques to improve structural resistance against progressive collapse [J]. Journal of Structural Engineering, 2014, 140(3): 04013077. doi: 10.1061/(ASCE)ST.1943-541X.0000886
[5] LIN K Q, LU X Z, LI Y, et al. Analytical model for multi-hazard resilient prefabricated concrete frame considering earthquake and column removal scenarios [J]. Frontiers in Built Environment, 2018, 4: 73. doi: 10.3389/fbuil.2018.00073
[6] 余洋, 李治, 肖龙山, 等. 边柱失效后预应力拼接连接装配式结构抗连续倒塌机理研究[J]. 工程力学, 2021, 38(4): 159 − 168. doi: 10.6052/j.issn.1000-4750.2020.06.0366 YU Yang, LI Zhi, XIAO Longshan, et al. Load resisting mechanism of precast structure underexterior column failure [J]. Engineering Mechanics, 2021, 38(4): 159 − 168. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.06.0366
[7] QIAN K, HU H N, WENG Y H, et al. Numerical investigation on load transfer mechanism of bonded post-tensioned concrete beam-column substructures against progressive collapse [J]. Advances in Structural Engineering, 2021, 24(8): 1569 − 1582. doi: 10.1177/1369433220981655
[8] LI Z X, LIU H K, SHI Y C, et al. Experimental investigation on progressive collapse performance of prestressed precast concrete frames with dry joints [J]. Engineering Structures, 2021, 246: 113071. doi: 10.1016/j.engstruct.2021.113071
[9] FENG D C, SHI H R, PARISI F, et al. Efficient numerical model for progressive collapse analysis of prestressed concrete frame structures [J]. Engineering Failure Analysis, 2021, 129: 105683. doi: 10.1016/j.engfailanal.2021.105683
[10] QIANG H L, YANG J X, FENG P, et al. Kinked rebar configurations for improving the progressive collapse behaviours of RC frames under middle column removal scenarios [J]. Engineering Structures, 2020, 211: 110425. doi: 10.1016/j.engstruct.2020.110425
[11] LIU T, XIAO Y, YANG J, et al. CFRP strip cable retrofit of RC frame for collapse resistance [J]. Journal of Composites for Construction, 2017, 21(1): 04016067. doi: 10.1061/(ASCE)CC.1943-5614.0000722
[12] PAN J W, WANG X, WU F, et al. Strengthening of precast RC frame to mitigate progressive collapse by externally bonded CFRP sheets anchored with HFRP anchors [J]. Advances in Civil Engineering, 2018, 2018: 8098242.
[13] ORTON S, JIRSA J O, BAYRAK O. Carbon fiber-reinforced polymer for continuity in existing reinforced concrete buildings vulnerable to collapse [J]. ACI Structrual Journal, 2009, 106(5): 608 − 616.
[14] FENG P, QIANG H L, OU X, et al. Progressive collapse resistance of GFRP-strengthened RC beam–slab subassemblages in a corner column–removal scenario [J]. Journal of Composites for Construction, 2019, 23(1): 04018076. doi: 10.1061/(ASCE)CC.1943-5614.0000917
[15] QIAN K, LI B. Strengthening and retrofitting precast concrete buildings to mitigate progressive collapse using externally bonded GFRP strips [J]. Journal of Composites for Construction, 2019, 23(3): 04019018. doi: 10.1061/(ASCE)CC.1943-5614.0000943
[16] QIAN K, LI B. Strengthening and retrofitting of RC flat slabs to mitigate progressive collapse by externally bonded CFRP laminates [J]. Journal of Composites for Construction, 2013, 17(4): 554 − 565. doi: 10.1061/(ASCE)CC.1943-5614.0000352
[17] DoD2016, Design of structures to resist progressive collapse [S]. Washington D. C.: Department of Defense, 2016.
[18] GSA2016, Alternate path analysis & design guidelines for progressive collapse resistance [S]. Washington D. C.: General Services Administration, 2016.
[19] 钱爽, 范存新. 基于GFRP加固的RC梁柱结构抗连续倒塌性能研究[J]. 苏州科技大学学报 (工程技术版), 2019, 32(3): 43 − 50. QIAN Shuang, FAN Cunxin. Study on progressive collapse behavior of GFRP strengthened RC beam-column structures [J]. Journal of Suzhou University of Science and Technology (Engineering and Technology), 2019, 32(3): 43 − 50. (in Chinese)
[20] ELSANADEDY H M, AL-SALLOUM Y A, ALRUBAIDI M A, et al. Upgrading of precast RC beam-column joints using innovative FRP/steel hybrid technique for progressive collapse prevention [J]. Construction and Building Materials, 2021, 268: 121130. doi: 10.1016/j.conbuildmat.2020.121130
[21] LIN K Q, LI Y, LU X Z, et al. Effects of seismic and progressive collapse designs on the vulnerability of RC frame structures [J]. Journal of Performance of Constructed Facilities, 2017, 31(1): 04016079. doi: 10.1061/(ASCE)CF.1943-5509.0000942
[22] YU J, LUO L Z, LI Y. Numerical study of progressive collapse resistance of RC beam-slab substructures under perimeter column removal scenarios [J]. Engineering Structures, 2018, 159: 14 − 27. doi: 10.1016/j.engstruct.2017.12.038
[23] 钱凯, 李治, 翁运昊, 等. 钢筋混凝土梁-板子结构抗连续性倒塌性能研究[J]. 工程力学, 2019, 36(6): 239 − 247. doi: 10.6052/j.issn.1000-4750.2018.05.0297 QIAN Kai, LI Zhi, WENG Yunhao, et al. Behavior of RC beam-slab substructures to resist progressive collapse [J]. Engineering Mechanics, 2019, 36(6): 239 − 247. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.05.0297
[24] WENG Y H, QIAN K, FU F, et al. Numerical investigation on load redistribution capacity of flat slab substructures to resist progressive collapse [J]. Journal of Building Engineering, 2020, 29: 101109. doi: 10.1016/j.jobe.2019.101109
[25] MURRAY Y D, ABU-ODEH A, BLIGH R. Evaluation of LS-DYNA concrete material model 159 [R]. Cambridge, MA: Federal Highway Administration, 2007.
[26] ELSANADEDY H M, AL-SALLOUM Y A, ALMUSALLAM T H, et al. Experimental and numerical study on FRP-upgraded RC beams with large rectangular web openings in shear zones [J]. Construction and Building Materials, 2019, 194: 322 − 343. doi: 10.1016/j.conbuildmat.2018.10.238
[27] 万军. 碳纤维布加固砌体填充墙抗近距离小当量炸药爆炸数值模拟研究[J]. 工程力学, 2020, 37(增刊 1): 82 − 90. doi: 10.6052/j.issn.1000-4750.2019.04.S012 WAN Jun. Numerical simulation of CFRP reinforced concrete masonry wall against small stand-off distance explosive charge [J]. Engineering Mechanics, 2020, 37(Suppl 1): 82 − 90. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.04.S012
[28] CHANG F K, CHANG K Y. A progressive damage model for laminated composites containing stress concentrations [J]. Journal of Composite Materials, 1987, 21(9): 834 − 855. doi: 10.1177/002199838702100904
[29] 陆新征, 冯鹏, 叶列平. FRP布约束混凝土方柱轴心受压性能的有限元分析[J]. 土木工程学报, 2003, 36(2): 46 − 51. doi: 10.3321/j.issn:1000-131X.2003.02.009 LU Xinzheng, FENG Peng, YE Lieping. Behavior of FRP-confined concrete square columns under uniaxial loading [J]. Civil Engineering Journal, 2003, 36(2): 46 − 51. (in Chinese) doi: 10.3321/j.issn:1000-131X.2003.02.009
[30] PHAM A T, TAN K H, YU J. Numerical investigations on static and dynamic responses of reinforced concrete sub-assemblages under progressive collapse [J]. Engineering Structures, 2017, 149: 2 − 20. doi: 10.1016/j.engstruct.2016.07.042
[31] PHAM A T, LIM A S, TAN K H. Investigations of tensile membrane action in beam-slab systems under progressive collapse subject to different loading configurations and boundary conditions [J]. Engineering Structures, 2017, 150: 520 − 536. doi: 10.1016/j.engstruct.2017.07.060
[32] fib, Fib model code for concrete structures [S]. Lausanne, Switzerland: International Federation for Structural Concrete, 2013.
[33] LU X Z, TENG J G, YE L P, et al. Bond-slip models for FRP sheets/plates bonded to concrete [J]. Engineering Structures, 2005, 27(6): 920 − 937. doi: 10.1016/j.engstruct.2005.01.014
[34] 陆新征, 叶列平, 滕锦光, 等. FRP片材与混凝土粘结性能的精细有限元分析[J]. 工程力学, 2006, 23(5): 74 − 82. doi: 10.3969/j.issn.1000-4750.2006.05.014 LU Xinzheng, YE Lieping, TENG Jinguang, et al. Meso-scale finite element analysis of FRP-to-concrete bond behavior [J]. Engineering Mechanics, 2006, 23(5): 74 − 82. (in Chinese) doi: 10.3969/j.issn.1000-4750.2006.05.014
[35] LSTC. LS-DYNA keyword user’s manual volume II material models [R]. Livermore, CA: United States Livemore, 2017.
[36] 钱凯, 李治, 翁运昊, 等. 后浇整体式预制混凝土梁-板子结构抗连续倒塌机理研究[J]. 建筑结构学报, 2021, 42(7): 183 − 193. QIAN Kai, LI Zhi, WENG Yunhao, et al. Load resisting mechanism of precast concrete beam-slab substructures with monolithic joints to mitigate progressive collapse [J]. Journal of Building Structures, 2021, 42(7): 183 − 193. (in Chinese)
[37] JGJ 107−2010, 钢筋机械连接技术规程 [S]. 北京: 中国建筑工业出版社, 2010. JGJ 107−2010, Technical specification for mechanical splicing of steel reinforcing bars [S]. Beijing: China Architecture and Building Press, 2010. (in Chinese)
[38] JGJ 256−2011, 钢筋锚固板应用技术规程[S]. 北京: 中国建筑工业出版社, 2011. JGJ 256−2011, Technical specification for application of headed bars [S]. Beijing: China Architecture and Building Press, 2011. (in Chinese)
[39] 秦卫红, 冯鹏, 施凯捷, 等. 玻璃纤维加固梁柱结构抗连续倒塌性能数值分析[J]. 同济大学学报 (自然科学版), 2014, 42(11): 1647 − 1653. QIN Weihong, FENG Peng, SHI Kaijie, et al. Numerical analysis of progressive collapse behavior of glass fiber reinforced polymer strengthened beam-column structures [J]. Journal of Tongji University (Natural Science), 2014, 42(11): 1647 − 1653. (in Chinese)
[40] 袁鑫杰, 李易, 陆新征, 等. 湿式连接装配式混凝土框架抗连续倒塌静力试验研究[J]. 土木工程学报, 2019, 52(12): 46 − 56. doi: 10.15951/j.tmgcxb.2019.12.005 YUAN Xinjie, LI Yi, LU Xinzheng, et al. Static progressive collapse test on prefabricated concrete frames with wet connections [J]. Civil Engineering Journal, 2019, 52(12): 46 − 56. (in Chinese) doi: 10.15951/j.tmgcxb.2019.12.005
[41] JGJ 1−2014, 装配式混凝土结构技术规程[S]. 北京: 中国建筑工业出版社, 2014. JGJ 1−2014, Technical specifications for prefabricated concrete structures [S]. Beijing: China Architecture and Building Press, 2014. (in Chinese)
[42] GB 50010−2010, 混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2010. GB 50010−2010, Code for design of concrete structures [S]. Beijing: China Architecture & Building Press, 2010. (in Chinese)
-
期刊类型引用(0)
其他类型引用(2)




 下载:
下载: