粘弹性流体法向力作用下的抽油杆柱横向振动仿真

王树强; 董世民; 张洋; 位中达

doi:10.6052/j.issn.1000-4750.2021.06.0487

粘弹性流体法向力作用下的抽油杆柱横向振动仿真

燕山大学机械工程学院，秦皇岛 066004

基金项目: 国家自然科学基金项目(51974276)

详细信息

作者简介:
王树强(1993−)，男，山东滨州人，博士生，主要从事抽油杆柱屈曲和力学研究(E-mail: wangshuqiang1993@163.com)

张　洋(1997−)，男，四川宜宾人，硕士生，主要从事石油机采仿真及抽油杆杆柱力学研究(E-mail: 1936025628@qq.com)

位中达(1995−)，男，河北辛集人，硕士生，主要从事聚合物驱抽油机井杆柱力学研究(E-mail: weizhongda3@163.com)

通讯作者:
董世民(1962−)，男，吉林松原人，教授，博士，博导，主要从事机械采油系统动态仿真与运行优化的研究(E-mail: ysudshm@163.com)

中图分类号: TE933
计量
- 文章访问数: 330
- HTML全文浏览量: 100
- PDF下载量: 58
出版历程
- 收稿日期: 2021-06-27
- 修回日期: 2021-10-27
- 录用日期: 2021-11-04
- 网络出版日期: 2021-11-04
- 刊出日期: 2022-10-31

TRANSVERSE VIBRATION SIMULATION OF SUCKER ROD STRINGS UNDER NORMAL DISTRIBUTED LOAD CAUSED BY VISCO-ELASTIC FLUID

School of Mechanical Engineering, Yanshan University, Qinhuangdao 066004, China

摘要

摘要: 聚合物抽油机井抽油杆柱在粘弹性流体井筒内偏心运动时，抽油杆柱受到交变粘弹性流体法向力的作用。该文指出了交变粘弹性流体法向力是抽油杆柱横向振动的激励。考虑抽油杆柱所受粘弹性流体法向力与抽油杆柱横向振动位移的耦合关系，建立了受粘弹性流体法向力作用的抽油杆柱在油管内横向振动仿真的力学和数学模型。采用有限差分法和Newmark法实现了对抽油杆柱在油管内横向振动的仿真计算。分析了抽油杆柱在初始偏心和粘弹性流体法向力激励下的横向振动规律。仿真结果表明：抽油杆柱的任何初始偏心都会导致在全井范围内发生杆管碰撞现象；抽油杆柱下冲程杆管碰撞更为剧烈，且泵端附近碰撞力最大；由于粘弹性流体法向力的存在，杆柱与油管壁的接触碰撞更加频繁，加剧了杆管偏磨。所建立的粘弹性流体法向力作用下的抽油杆柱横向振动仿真模型对于聚驱井杆管偏磨分析、扶正器的优化配置具有指导作用。
- 采油工程 /
- 抽油杆柱 /
- 横向振动 /
- 粘弹性流体法向力 /
- 碰撞 /
- 仿真模型
Abstract: When sucker rod string (SRS) undergoes an eccentric motion within the wellbore containing visco-elastic fluid for the polymer flooding pumping wells, the SRS is subjected to an alternating normal distributed load caused by visco-elastic fluid. The alternating normal distributed load caused by visco-elastic fluid is the transverse vibration excitation of the SRS. The coupling relationship between the normal distributed load caused by visco-elastic fluid and the lateral vibration displacement of SRS is considered. The mechanical and mathematical models are established for the transverse vibration simulation of SRS in tubing under the normal distributed load caused by visco-elastic fluid. The transverse vibration of the SRS in tubing is simulated through the finite difference method and Newmark method. The transverse vibration law of the SRS is analyzed due to the excitation of the initial eccentric and to the alternating normal distributed load caused by visco-elastic fluid. The simulation results show that any initial eccentricity of SRS will lead to rod tube collision in the whole well. The high frequency collision occurs in the down stroke, and the collision force takes the largest value near the bottom. Owing to the normal distributed load caused by visco-elastic fluid, the collision between rod and tubing wall is more frequent, and the eccentric wear of rod-tubing is aggravated. The transverse vibration simulation model of SRS in tubing under the normal distributed load caused by visco-elastic fluid has a direction effort on the eccentric wear analysis of rod-tubing and optimal allocation of centralizer in the polymer flooding pumping wells.
- oil extraction engineering /
- sucker rod string /
- transverse vibration /
- the normal distributed load caused by visco-elastic fluid /
- collision /
- simulation model

HTML全文

随着油井含水率的升高，聚合物驱油技术大规模应用到了抽油机井中。与水驱井相比，聚驱井产出液含有一定浓度的聚合物，而聚合物溶液具有粘性和弹性双重效应。油井产出液的弹性和杆管环空的偏心导致抽油杆受到一个与其轴线相垂直的法向力，法向力的存在加剧了杆管偏磨^[1-2]，导致了杆断管漏率增加和检泵周期显著下降等诸多问题。杆柱力学的研究是预防杆管偏磨的重要依据^[3-4]，因此研究在粘弹性流体法向力作用下的抽油杆柱在油管内的力学行为具有重要的理论与实际意义。

杆管偏磨现象与抽油杆柱在油管内的弯曲变形有关。国内外专家学者从静力学和动力学两个方面对抽油杆柱在油管内的弯曲变形行为进行了大量研究。董世民等^[5]基于杆管接触弹簧元分析方法，建立了抽油杆柱在油管内弯曲变形规律与接触压力的混合有限元仿真模型。狄勤丰等^[6]以曲率半径法描述井眼轨迹的空间形态，通过有限元法实现了杆柱空间载荷以及变形状态的求解。YUE等^[7]基于能量法建立了井筒中细长杆柱屈曲临界载荷、接触力和摩擦阻力的计算公式。HUANG等^[8]描述了带连接件的管柱在弯曲井筒中的挠曲行为，分析了弯矩和接触力的影响因素。ZHANG等^[9]建立了三维弯曲井中管柱的屈曲模型以及临界屈曲载荷数学模型，并确定了管柱屈曲后与井筒的接触力。以上静力学研究建立了抽油杆柱在油管内的弯曲变形规律，给出了杆管接触力的计算方式。文献[10-17]基于不同的方法，建立了不同激励下抽油杆柱的动力学模型，研究了抽油杆柱在油管内的弯曲变形规律。文献[10-12]考虑井眼初弯曲以及油管对杆柱的约束，建立了抽油杆柱的纵横耦合振动仿真模型。文献[13-14]采用有限元方法建立了抽油杆柱非线性动力学模型，计算出了抽油杆柱在井下的径向变形和侧向力。王宏博等^[15-16]综合考虑弯曲井眼以及交变轴向载荷对于抽油杆柱横向振动的激励，建立了具有初弯曲的抽油杆柱在弯曲井眼内的横向振动仿真模型。SUN等^[17]提出了基于屈曲位移激励下的铅直杆柱在圆筒内的横向振动仿真模型。与抽油杆柱的横向振动问题类似，WANG等^[18-19]应用有限元、能量法与哈密顿原理建立了油管的纵横耦合振动仿真模型，并采用 Newmark 法实现了数值求解。在以上研究中，抽油杆柱横向振动的激励可概括为：1) 抽油杆柱在交变轴向载荷激励下产生横向振动，即交变轴向载荷是抽油杆柱横向振动的激励，交变轴向载荷激励抽油杆柱横向振动的实质是交变轴向载荷导致抽油杆柱横向振动的几何抗弯刚度随时间变化，属于参数激励的非线性振动问题^[20-21]；2) 抽油杆柱与油管的间断接触碰撞对抽油杆柱横向振动的激励；3) 下冲程底部受压段的抽油杆柱屈曲位移对抽油杆柱横向振动的激励。

对于聚合物驱抽油机井，当抽油杆柱在粘弹性流体井筒内偏心运动时，杆柱将受到粘弹性流体法向力的作用。尽管文献[1-2]建立了井筒内抽油杆柱所受粘弹性流体法向力的计算模型，但所建立的计算模型仅适用于偏心距已知的情况，而没有深入研究在实际井筒内如何确定杆柱的偏心距。抽油杆柱所受粘弹性流体法向力不仅和抽油杆柱瞬时轴向运动速度有关，而且和杆柱瞬时弯曲变形有关，从而导致杆柱所受分布横向力随时间变化，并是杆柱横向振动的主动激励力。目前关于粘弹性流体法向力激励的抽油杆柱横向振动研究未见文献报道。本文拟将抽油杆柱所受交变粘弹性流体法向力作为横向振动的激励，考虑抽油杆柱所受粘弹性流体法向力与抽油杆柱横向振动位移的耦合关系，建立粘弹性流体法向力作用下的抽油杆柱横向振动仿真模型，分别以抽油杆柱初始偏心、空间屈曲构型作为初始条件，实现对抽油杆柱在井筒内横向振动规律、杆管接触碰撞随时间变化规律的仿真。

1 抽油杆柱横向振动力学模型

为便于研究，同时突出本文研究重点，做如下假设和简化：

1) 井筒为铅直井筒；

2) 抽油杆柱为均质单级杆；

3) 不考虑杆柱弯曲和扭转对抽油杆柱纵向振动的影响，基于波动方程仿真抽油杆柱的轴向载荷、轴向分布载荷与泵端集中轴向力，为抽油杆柱弯曲振动分析提供环境载荷；

4) 不考虑抽油杆柱纵向振动和扭转振动对横向振动的影响；

5) 将抽油杆柱简化为欧拉梁；

6) 粘弹性流体为各向同性不可压缩流体，在偏心环空中做定常等温层流流动。

1.1 力学模型

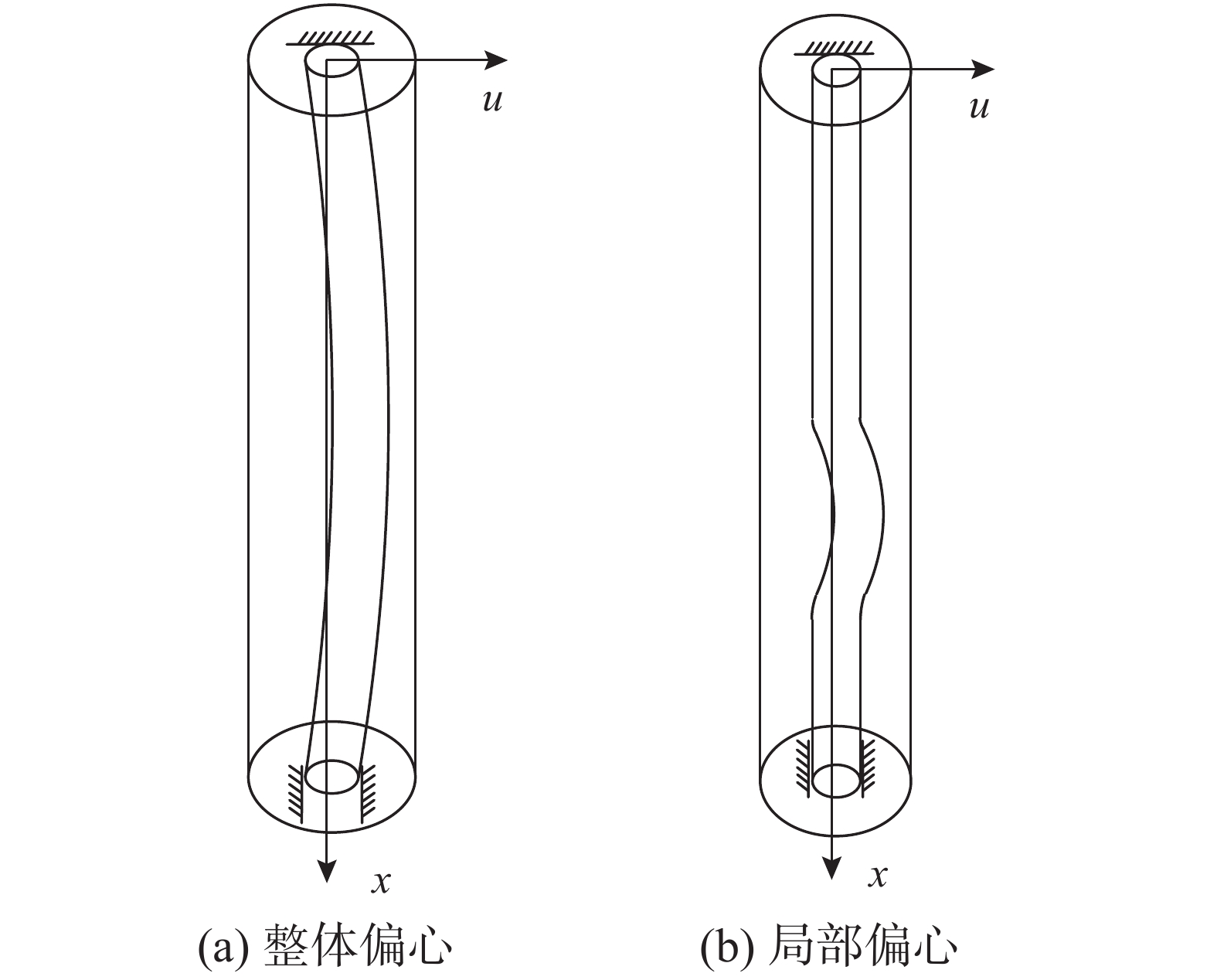
基于上述假设，建立受粘弹性流体法向力作用的抽油杆柱横向振动力学模型，如图1所示。图1(a)为杆柱的横向振动力学模型，图1(b)为杆柱的微元受力图。

图 1 抽油杆柱横向振动力学模型

Figure 1. Mechanical model of SRS transverse vibration

下载: 全尺寸图片幻灯片

图中抽油杆柱顶端的横向位移受到井口约束，简化为固定端；抽油杆柱底端的横向位移受到泵筒约束，简化为可滑动的固定端。以井口作为坐标原点，抽油杆柱轴线上任意一点的位置用井深坐标x表示。任意时刻t抽油杆柱所受环境载荷包括：作用于抽油杆柱底端的交变轴向载荷P(t)，以拉力为正；井深x处单位长度抽油杆柱所受的轴向分布载荷q_x(x,t)；设井深x处抽油杆柱的偏心率为ε(x,t)，单位长度抽油杆柱所受的粘弹性流体法向力为q_r(x,ε,t)；单位长度抽油杆柱所受的液体粘滞阻尼力为f_r(x,t)。

1.2 环境载荷计算模型

1.2.1 泵端集中轴向载荷计算模型

抽油杆柱底端的集中轴向载荷P(t)由柱塞所受液体载荷P_l(t)和柱塞与泵筒之间的液体摩擦载荷P_f(t)两部分组成^[22]：

$P\left( t \right){\text{ = }}{P_{\text{l}}}\left( t \right) + {P_{\text{f}}}\left( t \right)$

(1)

柱塞所受液体载荷由柱塞上、下表面的压差产生，计算公式为：

${P_{\text{l}}}\left( t \right) {\text{ = }}{A_{\text{p}}}\left( {{p_{\text{d}}} - p} \right) - {A_{\text{r}}}{p_{\text{d}}}$

(2)

式中：A_p/m²为抽油泵柱塞横截面积；p_d/Pa为抽油泵的排出压力；p/Pa为泵筒内液体压力；A_r/m²为抽油杆柱的横截面积。

柱塞与泵筒之间的液体摩擦载荷可以通过缝隙理论推导得出：

${P_{\text{f}}}\left( t \right)=\pi {L_{\text{p}}}D\left[ {\frac{{( {{p_{\text{d}}} - p} )\delta }}{{2{L_{\text{p}}}}} - \frac{{{\mu _{\rm{l}}}{v_{\text{p}}}}}{\delta }\frac{1}{{\sqrt {1 - \varepsilon _0^2} }}} \right]$

(3)

式中：L_p/m为抽油泵柱塞的长度；D/m为抽油泵柱塞的直径；δ/m为抽油泵柱塞与泵筒之间的径向间隙；μ_l/(Pa·s)为流过阀隙井液的动力粘度；v_p/(m/s)为抽油泵柱塞的运动速度；ε₀为偏心度，ε₀=e₀/δ；e₀/m为柱塞与泵筒之间的偏心距。

1.2.2 抽油杆柱轴向分布载荷仿真模型

抽油杆柱轴向分布载荷包括：单位长度抽油杆柱自重、液体粘滞摩擦力、杆柱纵向运动的惯性载荷以及杆柱纵向振动的振动载荷。通过波动方程描述抽油杆柱的纵向振动^[22]：

$\left\{ \begin{aligned} & \frac{{{\partial ^2}U}}{{\partial {t^2}}} - {c^2}\frac{{{\partial ^2}U}}{{\partial {x^2}}} + \upsilon \frac{{\partial U}}{{\partial t}} = g \\& U| _{x = 0} = {U^*}\left( t \right) \\& E{A_{\text{r}}}\left.\frac{{\partial U}}{{\partial x}}\right| _{x = L} = P\left( t \right) \end{aligned}\right.$

(4)

式中：U(x,t)/m为抽油杆柱任意截面x在时刻t相对于上死点的位移；c/(m/s)为声音在抽油杆柱中的传播速度；υ/(1/s)为油井液体对抽油杆柱的阻尼系数；g/(m/s²)为重力加速度；U^*(t) /m为悬点在时刻t相对于上死点的位移；E/Pa为杆柱材料的弹性模量。

应用有限差分法求解纵向振动仿真模型可以确定轴向载荷P_x(x,t)以及轴向分布载荷q_x(x,t)：

$\left\{ \begin{gathered} {P_x}\left( {x,t} \right) = E{A_{\text{r}}}\frac{{\partial U}}{{\partial x}} \\ {q_x}\left( {x,t} \right) = E{A_{\text{r}}}\frac{{{\partial ^2}U}}{{\partial {x^2}}} \\ \end{gathered} \right.$

(5)

1.2.3 粘弹性流体法向力计算模型

通过大量实验表明，含聚流体作用在杆柱的法向力主要与偏心度、流速及含聚浓度有关。运用试验结果，得到工程比较适用的法向力计算公式^[23]：

${q_{\text{r}}}\left( {x,\varepsilon ,t} \right) = \left\{ \begin{aligned} & {47.0413{\varepsilon ^{ - 12.3797}}{\eta ^{ - 3.8840}}{v_{\text{f}}}^{8.1153}} \\ & {59.5728{\varepsilon ^{2.2461}}{\eta ^{ - 0.7572}}{v_{\text{f}}^{0.7592}}} \\ & {69.6089{\varepsilon ^{2.4413}}{\eta ^{ - 0.6532}}{v_{\text{f}}^{0.6942}}} \\ & {79.5006{\varepsilon ^{2.7607}}{\eta ^{ - 0.5656}}{v_{\text{f}}^{0.2418}}} \\ & {92.1315{\varepsilon ^{ - 2.2618}}{\eta ^{ - 1.1827}}{v_{\text{f}}^{2.4916}}} \\ & {99.0442{\varepsilon ^{1.5698}}{\eta ^{ - 0.5701}}{v_{\text{f}}^{0.9883}}} \end{aligned} \right.$

(6)

式中：q_r(x,ε,t)/(N/m)为单位长度的法向力；ε为偏心度，ε=e/(R−r)，e/m为偏心距，R/m为油管内半径，r/m为抽油杆半径；η/(mg/L)为聚合物浓度，式中各项分别对应浓度为(0~100)，(100~200)，(200~400)，(400~600)，(600~800)，(800~1000)；v_f/(m/s)为杆液相对运动速度。

2 抽油杆柱横向振动数学模型

2.1 抽油杆柱横向振动方程

设任意时刻t，井深x处抽油杆柱的横向振动位移为u(x,t)和w(x,t)。通过微元受力分析，抽油杆柱微元段在xou平面内的动力平衡方程为：

$\rho {A_{\text{r}}}\frac{{{\partial ^2}u}}{{\partial {t^2}}}{\text{d}}x = - {\text{d}}{Q_u} - {f_{{\text{r}}u}}\left( {x,t} \right){\text{d}}x + {q_{{\text{r}}u}}\left( {x,\varepsilon ,t} \right){\text{d}}x$

(7)

其中：

$\left\{ \begin{gathered} {Q_u} = \frac{{\partial {M_u}}}{{\partial x}} + {F_u}\frac{{\partial u}}{{\partial x}} \\ {\text{d}}{Q_u} = \frac{{\partial {Q_u}}}{{\partial x}}{\text{d}}x \\ F = - P\left( t \right) - \int_x^L {q\left( {x,t} \right)} {\text{d}}x \\ {f_{{\text{r}}u}}\left( {x,t} \right) = \mu \frac{{\partial u}}{{\partial t}} \\ {q_{{\text{r}}u}}\left( {x,\varepsilon ,t} \right){\text{ = }}{q_{\text{r}}}\left( {x,\varepsilon ,t} \right)\frac{u}{{\sqrt {{u^2} + {w^2}} }} \\ \end{gathered} \right.$

(8)

$\varepsilon = \frac{{\sqrt {{u^2} + {w^2}} }}{{R - r}}$

(9)

式中：ρ/(kg/m³)为抽油杆柱材料密度；μ/(N·s/m²)为液体粘滞阻尼系数；I/m⁴为抽油杆柱的抗弯惯性距；q_ru(x,ε,t)、q_rw(x,ε,t)分别为作用在杆柱上的粘弹性流体法向力在u和w方向上的分量。

在线弹性变形假设下，弯矩和挠度的关系可以表示为：

$M = EI\frac{{{\partial ^2}u}}{{\partial {x^2}}}$

(10)

将式(10)代入动力平衡方程式(7)，建立抽油杆柱在xou平面内的横向振动微分方程如下：

$\begin{split}& \rho {A_{\text{r}}}\frac{{{\partial ^2}u}}{{\partial {t^2}}} + \mu \frac{{\partial u}}{{\partial t}} = - EI\frac{{{\partial ^4}u}}{{\partial {x^4}}} + \\& \;\;\frac{\partial }{{\partial x}}\left[ {\left( {P( t ) + \int_x^L {{q_x}\left( {x,t} \right){\text{d}}x} } \right)\frac{{\partial u}}{{\partial x}}} \right] + {q_{{\text{r}}u}}( {x,\varepsilon ,t} ) \end{split}$

(11)

同理，可以得到抽油杆柱在xow平面内的横向振动微分方程：

$\begin{split}& \rho {A_{\text{r}}}\frac{{{\partial ^2}w}}{{\partial {t^2}}} + \mu \frac{{\partial w}}{{\partial t}} = - EI\frac{{{\partial ^4}w}}{{\partial {x^4}}} + \\& \;\;\frac{\partial }{{\partial x}}\left[ {\left( {P( t ) + \int_x^L {{q_x}\left( {x,t} \right){\text{d}}x} } \right)\frac{{\partial w}}{{\partial x}}} \right] + {q_{{\text{r}}w}}( {x,\varepsilon ,t} ) \end{split}$

(12)

其中：

${q_{{\text{r}}w}}\left( {x,\varepsilon ,t} \right){\text{ = }}{q_{\text{r}}}\left( {x,\varepsilon ,t} \right)\frac{w}{{\sqrt {{u^2} + {w^2}} }}$

(13)

2.2 边界条件

抽油杆柱顶端的横向位移和角位移受到井口约束，可以将杆柱的顶端简化为固定约束；抽油杆柱底端的横向位移和角位移受到泵筒约束，可以将杆柱的底端简化为可滑动的固定约束。抽油杆柱两端的边界条件为：

$\left\{ \begin{aligned} & u,w| _{\left( {0,t} \right)} = 0,\;\;\left.\frac{{\partial u,w}}{{\partial x}}\right| {_{\left( {0,t} \right)}} = 0 \\& u,w| _{\left( {L,t} \right)} = 0,\;\;\left.\frac{{\partial u,w}}{{\partial x}}\right| _{\left( {L,t} \right)} = 0 \end{aligned} \right.$

(14)

2.3 初始条件

聚合物抽油机井杆管环空的偏心是产生粘弹性流体法向力的必要条件之一。本文将分别以抽油杆柱的初始偏心和空间屈曲构型作为初始条件激励，研究粘弹性流体法向力激励的抽油杆柱受迫振动。并假设悬点位于下死点。则抽油杆柱横向振动的初始条件可以表示为：

$\left\{ \begin{aligned} & u,w| _{\left( {x,0} \right)} = \varphi ( x )\\& \left.\frac{{\partial u,w}}{{\partial t}}\right| _{\left( {x,0} \right)} = 0 \end{aligned}\right.$

(15)

2.4 杆管碰撞条件

抽油杆柱仿真节点的横向位移超出油管边界时，杆柱与油管发生碰撞，因此杆管碰撞条件可以表示为：

$\sqrt {{u^2} + {w^2}} \geqslant R - r$

(16)

抽油杆柱与油管发生碰撞后相应节点落在油管内壁上，采用t+表示碰撞后，t−表示碰撞前，则抽油杆柱与油管发生碰撞后相应节点的位置：

$\left\{ \begin{gathered} u\left| {_{t + }} \right. = {\kern 1pt} \left( {R - r} \right)\cos {\theta _1} \\ {\kern 1pt} w\left| {_{t + }} \right. = {\kern 1pt} \left( {R - r} \right)\sin {\theta _1}{\kern 1pt} {\kern 1pt} \end{gathered} \right.$

(17)

其中：

${\theta _1} = \left\{ \begin{gathered} \arctan \left| {\frac{w}{u}} \right|,\;\;u \ne 0 \\ \frac{{\text{π }}}{2},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;u = 0 \end{gathered} \right.$

(18)

将节点速度v分解为沿油管内壁法线方向的径向速度v_n和切线方向的切向速度v_τ，γ_i表示碰撞恢复系数，其值取决于碰撞体的材料^[24]，抽油杆柱与油管发生碰撞后相应节点的速度：

$\left\{ \begin{gathered} {v_{\text{n}}}\left| {_{t + }} \right. = - {\gamma _i}v\left| {_{t - }\cos \Delta \theta } \right. \\ {v_{\text{τ }}}\left| {_{t + }} \right. = v\left| {_{t - }\sin \Delta \theta } \right. \\ \end{gathered} \right.$

(19)

其中：

$\Delta \theta = \left| {{\theta _1} - {\theta _2}} \right|$

(20)

${\theta _2} = \left\{ \begin{aligned} & \arctan \left| {\frac{{{v_w}}}{{{v_u}}}} \right|,\;\;\;\;{v_u} \ne 0 \\& \frac{{\text{π }}}{2}{\kern 1pt}, \qquad\qquad \;\;\;{v_u} = 0 \end{aligned} \right.$

(21)

由于碰撞过程中碰撞力的瞬时值是难以确定的，本文采用冲量的改变作为碰撞力的度量。假设在∆t^[25]时间内杆管完成碰撞，由冲量定理可以获得碰撞时间内的碰撞力：

${F_{\text{t}}} = \frac{{\rho {A_{\text{r}}}}}{{\Delta t}}\left( {{v_{\text{n}}}\left| {_{t + }} \right. - {v_{\text{n}}}\left| {_{t - }} \right.} \right)$

(22)

3 横向振动仿真方法

本文采用数值方法求解抽油杆柱轴向载荷计算模型和横向振动仿真模型，通过有限差分法离散空间变量x，通过Newmark-β法离散时间变量t。

将抽油杆柱沿轴线离散成n个单元，各单元具有相同步长∆x。采用中心差分形式处理偏微分方程中位移关于x的各阶导数，并将边界条件进行差分处理。

采用Newmark-β法对时间t进行离散：

$\left\{ \begin{gathered} {{\dot u}_{(t + \Delta t)}} = {{\dot u}_{(t)}} + \left[ {\left( {1 - \alpha } \right){{\ddot u}_{(t)}} + \alpha {{\ddot u}_{(t + \Delta t)}}} \right]\Delta t \\ {\kern 1pt} {u_{(t + \Delta t)}} = {u_{(t)}} + {{\dot u}_{(t)}}\Delta t + \left[ {\left( {\frac{1}{2} - \beta } \right){{\ddot u}_{(t)}} + \beta {{\ddot u}_{(t + \Delta t)}}} \right]\Delta {t^2} \\ \end{gathered} \right.$

(23)

式中：α和β是按积分精度和稳定性要求进行调整的参数。本文取α=0.5，β=0.25，此时仿真精度较高，稳定性好^[26]。

由式(23)可以得到t+∆t的速度和加速度的表达式，即：

$\left\{ \begin{gathered} {{\ddot u}_{\left( {t + \Delta t} \right)}} = {\alpha _0}( {{u_{\left( {t + \Delta t} \right)}} - {u_{\left( t \right)}}} ) - {\alpha _2}{{\dot u}_{\left( t \right)}} - {\alpha _3}{{\ddot u}_{\left( t \right)}} \\ {{\dot u}_{\left( {t + \Delta t} \right)}} = {\alpha _1}( {{u_{\left( {t + \Delta t} \right)}} - {u_{\left( t \right)}}} ) - {\alpha _4}{{\dot u}_{\left( t \right)}} - {\alpha _5}{{\ddot u}_{\left( t \right)}} \\ {\alpha _0} = \frac{1}{{\beta \Delta {t^2}}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _1} = \frac{\alpha }{{\beta \Delta t}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _2} = \frac{1}{{\beta \Delta t}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _3} = \frac{1}{{2\beta }} - 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _4} = \frac{\alpha }{\beta } - 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _5} = \frac{{\Delta t}}{2}\left( {\frac{\alpha }{\beta } - 2} \right) \\ \end{gathered} \right.$

(24)

t+∆t时刻的振动微分方程为：

$M{\ddot u_{\left( {t + \Delta t} \right)}} + C{\dot u_{\left( {t + \Delta t} \right)}} + K{u_{\left( {t + \Delta t} \right)}} = {R_{\left( {t + \Delta t} \right)}}$

(25)

将式(23)、式(24)代入振动微分方程式(25)，得到关于u_(t+∆t)的方程：

$\left\{ \begin{split}& \bar K{u_{\left( {t + \Delta t} \right)}} = {{\bar R}_{\left( {t + \Delta t} \right)}} \\& \bar K = K + {\alpha _0}M + {\alpha _1}C \\& {{\bar R}_{\left( {t + \Delta t} \right)}} = {R_{\left( {t + \Delta t} \right)}} + M\left( {{\alpha _0}{u_{\left( t \right)}} - {\alpha _2}{{\dot u}_{\left( t \right)}} - {\alpha _3}{{\ddot u}_{\left( t \right)}}} \right)+ \\& {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} C\left( {{\alpha _1}{u_{\left( t \right)}} - {\alpha _4}{{\dot u}_{\left( t \right)}} - {\alpha _5}{{\ddot u}_{\left( t \right)}}} \right) \end{split} \right.$

(26)

根据振动微分方程可以确定质量矩阵M、阻尼矩阵C和刚度矩阵K，并由式(26)得到振动微分方程式(25)的离散形式式(27)：

$\left\{ \begin{gathered} G_i^j{\text{ = }}A_{i - 2}^ju_{i - 2}^j + B_{i - 1}^ju_{i - 1}^j + C_i^ju_i^j + D_{i + 1}^ju_{i + 1}^j + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} F_{i + 2}^ju_{i + 2}^j \\ {\kern 1pt} A_{i - 2}^j = F_{i + 2}^j = \frac{{EI}}{{\Delta {x^4}}} \\ B_{i - 1}^j = - \frac{{4EI}}{{\Delta {x^4}}} - \frac{{P\left( t \right) + \int_x^L {q\left( x \right){\rm d}x} }}{{\Delta {x^2}}} - \frac{{q\left( x \right)}}{{2\Delta x}} \\ C_i^j = \frac{{6EI}}{{\Delta {x^4}}} + 2\frac{{P\left( t \right) + \int_x^L {q\left( x \right){\rm d}x} }}{{\Delta {x^2}}}+{\alpha _0}\rho {A_{\text{r}}} + {\alpha _1}\mu \\ D_{i + 1}^j = - \frac{{4EI}}{{\Delta {x^4}}} - \frac{{P\left( t \right) + \int_x^L {q\left( x \right){\rm d}x} }}{{\Delta {x^2}}} + \frac{{q\left( x \right)}}{{2\Delta x}} \\ G_i^j = \rho {A_{\text{r}}}( {{\alpha _0}u_i^{j - 1} + {\alpha _2}\dot u_i^{j - 1} + {\alpha _3}\ddot u_i^{j - 1}} )+ \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mu ( {{\alpha _1}u_i^{j - 1} + {\alpha _4}\dot u_i^{j - 1} + {\alpha _5}\ddot u_i^{j - 1}} )+{q_{{{\rm r}}u}}( {x,\varepsilon ,t} ) \\ \end{gathered} \right.$

(27)

通过求解振动微分方程的离散形式式(27)，可以得到t+∆t时刻的抽油杆柱的横向振动位移，然后，由式(24)可以得到对应节点的速度和加速度。

4 仿真实例与分析

仿真基本参数：抽油杆柱直径为22 mm，抽油杆柱长度为1000 m，抽油杆柱密度为7860 kg/m³，抽油杆柱弹性模量为209 GPa，接箍外径为46 mm，油管内径为62 mm，阻尼系数为0.2 N·s/m²，抽油机冲程为3 m，冲次为6 min⁻¹，油井产出液聚合物浓度为300 mg/L，碰撞恢复系数为0.56，单次碰撞时间为0.03 s。

通过抽油机机构运动分析，可以得到悬点位移规律，并由本文1.2节中抽油杆柱轴向分布载荷仿真模型可以得到杆柱轴向力分布情况，如图2(a)、图2(b)所示。

图 2 悬点位移和杆柱轴向力

Figure 2. Suspension displacement and rod string axial stress

下载: 全尺寸图片幻灯片

下面分别研究抽油杆柱在初始偏心与屈曲构型激励下的横向振动规律。

4.1 抽油杆柱初始偏心激励下的横向振动

杆管环空的偏心是产生粘弹性流体法向力的必要条件之一，偏心度的大小对于粘弹性流体法向力起到决定性的作用。本文通过给定抽油杆柱一个整体偏心和局部偏心，研究初始偏心条件下粘弹性流体法向力激励的抽油杆柱横向振动规律。抽油杆柱偏心示意图如图3所示。式(28)、式(29)分别为抽油杆柱整体偏心初始条件和局部偏心初始条件公式。取偏心度ε分别为0.25、0.50、0.75，开展初始偏心条件下粘弹性流体法向力激励的抽油杆柱横向振动规律仿真。

图 3 抽油杆柱偏心示意图

Figure 3. Eccentric schematic diagram of SRS

下载: 全尺寸图片幻灯片

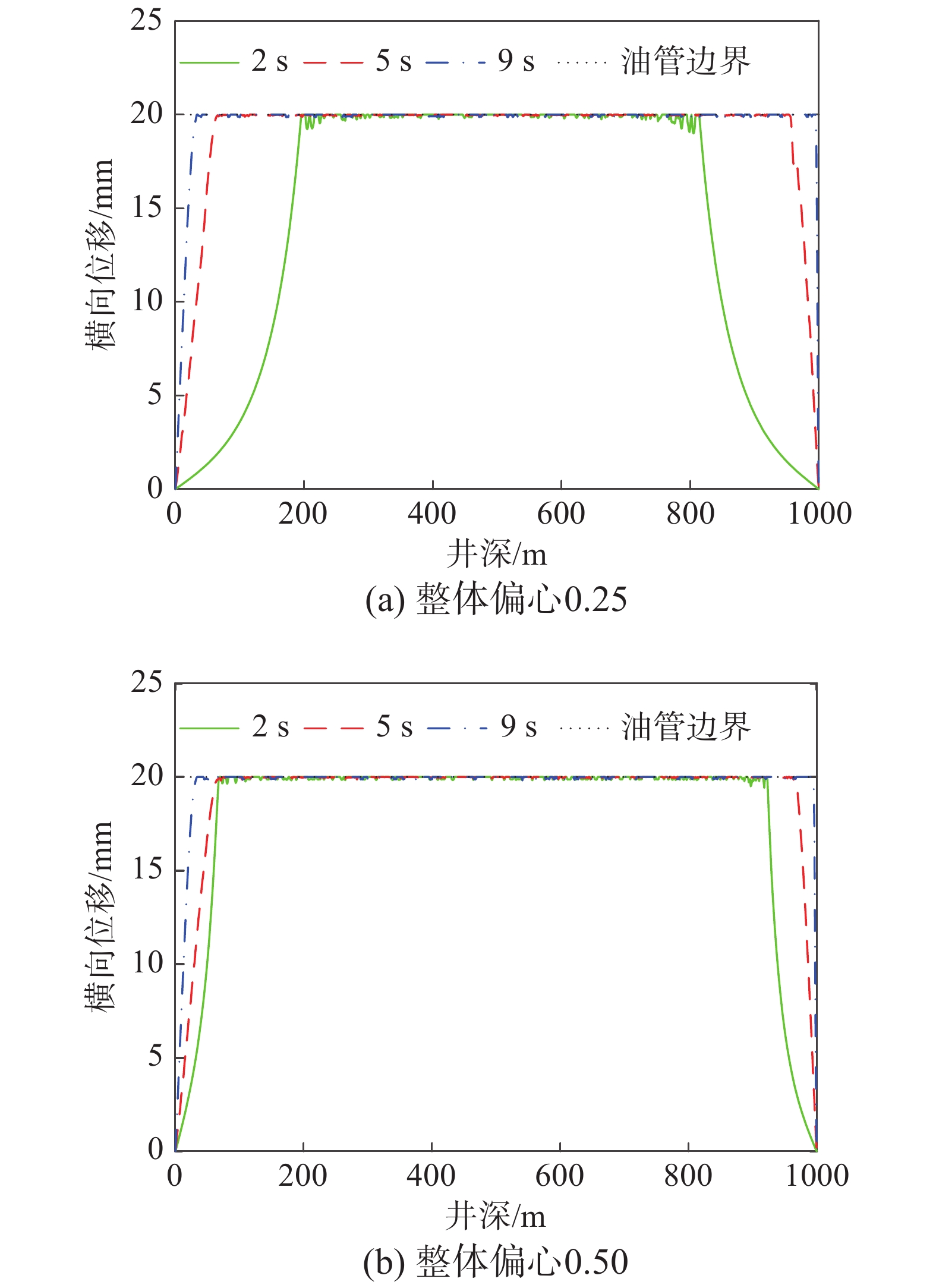
$\varphi \left( x \right) = \varepsilon \left( {R - r} \right)\sin \left( {\frac{{\text{π }}}{L}x} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} 0 \leqslant x \leqslant L$

(28)

$\varphi \left( x \right) = \left\{ \begin{gathered} 0, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \leqslant x < \frac{L}{2} \\ \varepsilon \left( {R - r} \right)\sin \left[ {\frac{{4{\text{π }}}}{L}\left( {x - \frac{L}{2}} \right)} \right],{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{L}{2} \leqslant x \leqslant \frac{{3L}}{4} \\ 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{3L}}{4} < x \leqslant L{\kern 1pt} {\kern 1pt} {\kern 1pt} \end{gathered} \right.$

(29)

图4 和图5分别绘制了不同偏心度条件下杆柱横向位移随井深的变化规律。图中给出了时间为2 s、5 s和9 s时杆柱横向位移随井深的变化曲线。

下载: 全尺寸图片幻灯片

4 整体偏心条件下杆柱横向位移变化曲线

4. Transverse displacement curves under overall eccentricity

下载: 全尺寸图片幻灯片

图 5 局部偏心条件下杆柱横向位移变化曲线

Figure 5. Transverse displacement curves under local eccentricity

下载: 全尺寸图片幻灯片

由图4和图5可以看出：1) 存在偏心的杆柱由局部杆管接触然后缓慢延伸至几乎全井接触；2) 随着杆柱偏心度的增大，杆管接触的发生时间提前；3) 杆柱顶端数十米由于边界条件的限制，不会发生杆管接触；4) 由于粘弹性流体法向力的存在，杆柱与油管的接触点几乎存在于全井范围内。

综上所述，由于粘弹性流体法向力的存在，无论抽油杆柱存在整体偏心还是局部偏心，都会导致杆管偏磨现象几乎在全井范围内都有发生，因此有必要采取全井布置扶正器的策略。

4.2 抽油杆柱初始屈曲构型激励下的横向振动

抽油杆柱在下冲程运行过程中，随着杆柱受压载荷的不断增大，杆柱会产生空间屈曲，同时会受到指向窄间隙侧的法向力，粘弹性流体法向力激励整体杆柱产生横向振动。本节，基于1.2节抽油杆柱轴向载荷计算模型，考虑油管内壁对于杆柱上接箍节点的影响，基于文献[27]中抽油杆柱屈曲构型仿真方法，建立整体抽油杆柱在油管内的屈曲构型，将该屈曲构型作为杆柱横向振动的初始位移条件，研究粘弹性流体法向力作用下的抽油杆柱横向振动规律。整体抽油杆柱空间屈曲构型如图6所示。

图 6 空间屈曲构型

Figure 6. Spatial buckling configuration

下载: 全尺寸图片幻灯片

4.2.1 碰撞力变化规律

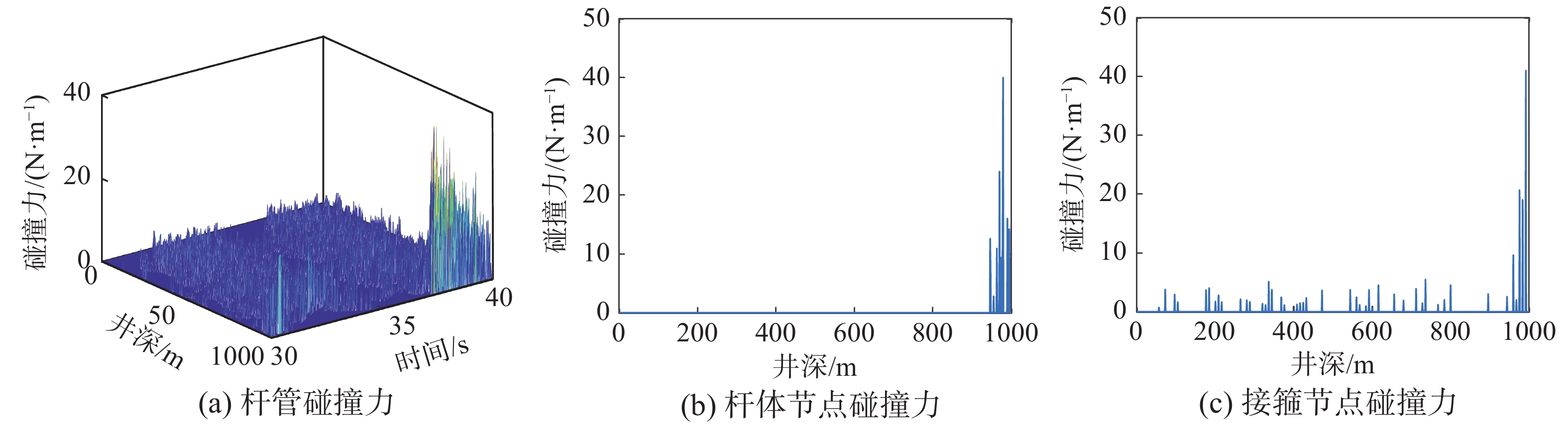
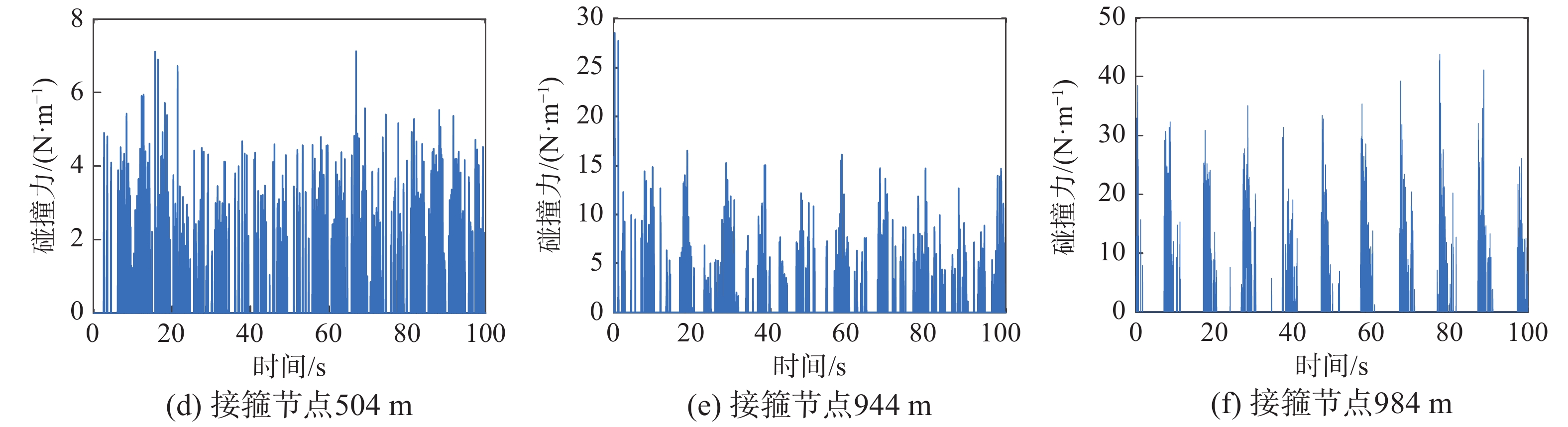
图7(a)绘制了第3个周期内碰撞力随井深和时间的变化规律；图7(b)、图7(c)绘制了37.5 s时不同井深处杆体节点和接箍节点碰撞力的变化规律。由图7可以得到：1) 碰撞力沿全井都有分布，在每个运动周期内，下冲程的杆管碰撞最剧烈，且在泵端附近碰撞力最大；2) 抽油杆柱上冲程同样存在杆管碰撞现象，但碰撞点相对较少，碰撞力也较小；3) 杆体与油管的接触碰撞主要集中在距泵端940 m以下位置，在940 m以上位置杆体与油管几乎无接触；4) 接箍与油管的接触碰撞在全井均有分布，且在泵端附近碰撞最剧烈，随着节点上移，碰撞力减小。

图 7 碰撞力随井深和时间变化规律

Figure 7. The variation of impact force with well depth and time

下载: 全尺寸图片幻灯片

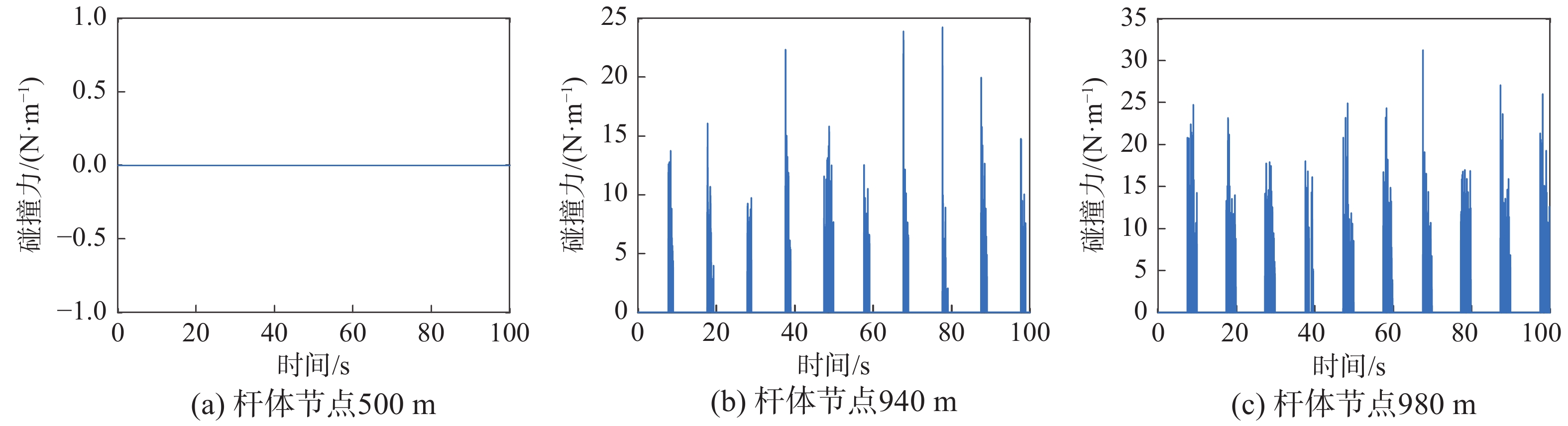
分别对比了不同井深位置处杆柱节点和接箍节点在10个周期内的碰撞力分布规律，如图8所示。由图8 可以看出：1) 杆体与油管壁的接触碰撞主要存在于下冲程，且碰撞力随着井深增大而增大；2) 接箍与油管壁的接触碰撞在接近泵端位置主要集中在下冲程，上冲程碰撞节点较少，且碰撞力较高。随着节点上移，上下冲程内节点碰撞均很密集，且碰撞力随之减小。

下载: 全尺寸图片幻灯片

图 8 节点碰撞力随时间的变化规律

Figure 8. The variation of impact force with time of nodes

下载: 全尺寸图片幻灯片

综上所述，杆管碰撞现象在全井全周期范围内都存在；杆体节点与油管壁的碰撞主要集中在泵端附近，且主要发生在下冲程；接箍节点与油管壁的碰撞沿全井都有分布，且上下冲程均存在密集碰撞现象。因此目前全井均匀布置扶正器的防偏磨措施是不科学的，需要根据杆管接触力优化配置扶正器。

4.2.2 横向振动规律

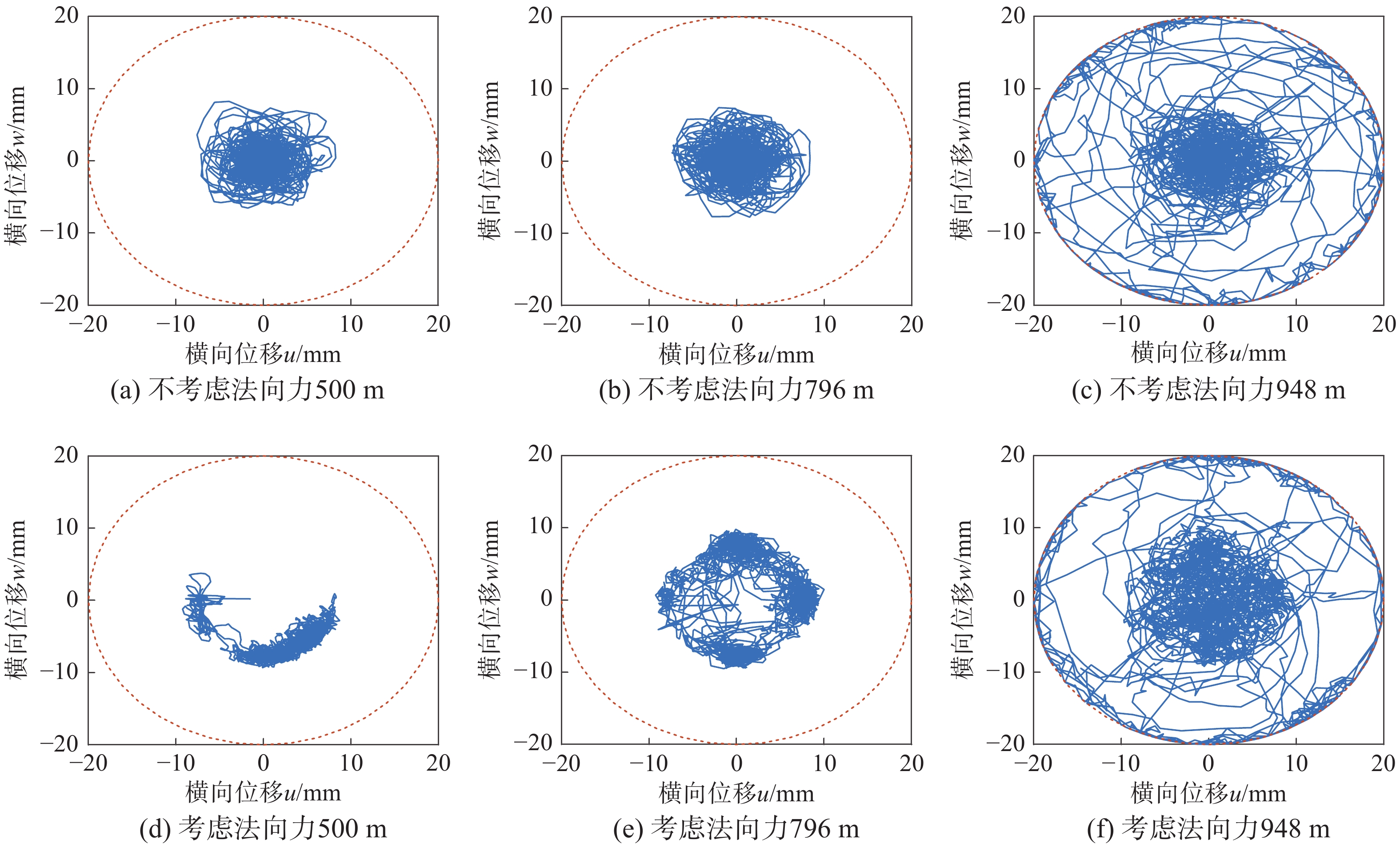
对比了不考虑粘弹性流体法向力和考虑粘弹性流体法向力时抽油杆柱的节点振动情况。图9为杆体节点分别在500 m、796 m和948 m处的横向位移规律曲线，图10为接箍节点分别在504 m、800 m和952 m处的横向位移规律曲线。

图 9 杆柱节点横向位移仿真结果

Figure 9. Simulation results of rod nodes transversal displacement

下载: 全尺寸图片幻灯片

图 10 接箍节点横向位移仿真结果

Figure 10. Simulation results of coupling nodes transversal displacement

下载: 全尺寸图片幻灯片

由图9和图10可知：1) 抽油杆柱在各井深位置处均存在杆管碰撞现象；2) 杆体节点与油管壁的接触碰撞存在于油井底部，而接箍节点在各井深位置均存在与油管壁的接触碰撞；3) 不考虑粘弹性流体法向力时，抽油杆柱的振动主要集中在井眼中心处；4) 由于指向窄间隙侧粘弹性流体法向力的存在，杆柱与油管壁的接触碰撞更加频繁。井深504 m处接箍节点与油管的接触偏向一侧，而800 m处由于抽油杆柱下端屈曲的原因，抽油杆柱与油管在各个方向上均有接触，但相较于不考虑粘弹性流体法向力的情况，碰撞点更加密集，杆管碰撞现象明显加剧。

5 结论

聚驱井中粘弹性流体法向力的存在是加剧杆管偏磨的重要因素，本文基于抽油杆柱粘弹性流体法向力计算模型，考虑抽油杆柱所受粘弹性流体法向力与抽油杆柱横向振动位移的耦合关系，建立了抽油杆柱在油管内的横向振动仿真模型。采用有限差分法和Newmark-β 法综合计算，考虑杆管间的碰撞效应，实现了对粘弹性流体法向力作用的抽油杆柱在油管内的横向振动仿真。通过实例分析得到如下结论：

(1) 杆管碰撞现象存在于全井范围内，其中杆体节点与油管壁的碰撞主要集中在泵端附近，接箍节点与油管壁的碰撞沿全井都有分布。

(2) 下冲程杆管碰撞更为剧烈，且泵端附近碰撞点最为密集，碰撞力最大，随着节点上移，碰撞力减小；上冲程同样存在杆管碰撞现象，碰撞点主要是接箍节点，且碰撞力较小。

(3) 由于指向窄间隙侧粘弹性流体法向力的存在，抽油杆柱与油管壁的接触碰撞更加频繁，加剧了杆管偏磨。

(4) 聚驱井中全井布置扶正器有助于预防杆管偏磨，但目前均匀扶正器配置方法是不科学的，有必要根据杆管接触力优化配置扶正器，本文所建立的粘弹性流体法向力作用下的抽油杆柱横向振动仿真模型对于杆管偏磨分析、扶正器的优化配置具有指导作用。

(5) 本文为直井中的抽油杆柱横向振动规律分析，在弯曲井眼中，受井筒弯曲、接箍与扶正器局部径向支撑以及重力横向分力的综合影响，抽油杆柱发生弯曲变形，并导致杆柱在井筒内处于分布式接触—悬空的偏心状态，因此，抽油杆柱在弯曲井筒内的横向振动规律仿真需要进一步研究。

图 1 抽油杆柱横向振动力学模型

Figure 1. Mechanical model of SRS transverse vibration

下载: 全尺寸图片幻灯片

图 2 悬点位移和杆柱轴向力

Figure 2. Suspension displacement and rod string axial stress

下载: 全尺寸图片幻灯片

图 3 抽油杆柱偏心示意图

Figure 3. Eccentric schematic diagram of SRS

下载: 全尺寸图片幻灯片

下载: 全尺寸图片幻灯片

4 整体偏心条件下杆柱横向位移变化曲线

4. Transverse displacement curves under overall eccentricity

下载: 全尺寸图片幻灯片

图 5 局部偏心条件下杆柱横向位移变化曲线

Figure 5. Transverse displacement curves under local eccentricity

下载: 全尺寸图片幻灯片

图 6 空间屈曲构型

Figure 6. Spatial buckling configuration

下载: 全尺寸图片幻灯片

图 7 碰撞力随井深和时间变化规律

Figure 7. The variation of impact force with well depth and time

下载: 全尺寸图片幻灯片

下载: 全尺寸图片幻灯片

图 8 节点碰撞力随时间的变化规律

Figure 8. The variation of impact force with time of nodes

下载: 全尺寸图片幻灯片

图 9 杆柱节点横向位移仿真结果

Figure 9. Simulation results of rod nodes transversal displacement

下载: 全尺寸图片幻灯片

下载: 全尺寸图片幻灯片

图 10 接箍节点横向位移仿真结果

Figure 10. Simulation results of coupling nodes transversal displacement

下载: 全尺寸图片幻灯片

参考文献(27)

[1]	韩洪升, 王德民, 国丽萍, 等. 黏弹性流体法向应力对抽油杆偏磨的影响机理[J]. 石油学报, 2004, 25(4): 92 − 95. doi: 10.3321/j.issn:0253-2697.2004.04.021 HAN Hongsheng, WANG Demin, GUO Liping, et al. Partial abrasion mechanism of sucker rod caused by normal stress of visco-elastic fluid [J]. Acta Petrolei Sinica, 2004, 25(4): 92 − 95. (in Chinese) doi: 10.3321/j.issn:0253-2697.2004.04.021
[2]	黄善波, 李兆敏. 聚合物驱井内流体作用于抽油杆的侧向力解析[J]. 石油学报, 2009, 30(1): 149 − 153. doi: 10.3321/j.issn:0253-2697.2009.01.031 HUANG Shanbo, LI Zhaomin. Analysis on lateral force of produced fluid acting on the sucker rod in polymer flooding wells [J]. Acta Petrolei Sinica, 2009, 30(1): 149 − 153. (in Chinese) doi: 10.3321/j.issn:0253-2697.2009.01.031
[3]	LI Z F, ZHANG C Y, SONG G M. Research advances and debates on tubular mechanics in oil and gas wells [J]. Journal of Petroleum Science and Engineering, 2017, 151: 194 − 212. doi: 10.1016/j.petrol.2016.10.025
[4]	MORENO G A, GARRIZ A E. Sucker rod string dynamics in deviated wells [J]. Journal of Petroleum Science and Engineering, 2020, 184: 1 − 12.
[5]	董世民, 张万胜, 张红, 等. 定向井有杆抽油系统杆管分布接触压力的研究[J]. 工程力学, 2011, 28(10): 179 − 184. DONG Shimin, ZHANG Wansheng, ZHANG Hong, et al. Research on the distribution contact pressure between sucker rod and tubing string of rod pumping system in directional wells [J]. Engineering Mechanics, 2011, 28(10): 179 − 184. (in Chinese)
[6]	狄勤丰, 王文昌, 胡以宝, 等. 定向井抽油杆柱空间形态的计算方法[J]. 中国石油大学学报(自然科学版), 2011, 35(3): 72 − 75. DI Qinfeng, WANG Wenchang, HU Yibao, et al. Calculation method of sucker rod strings space configuration in directional well [J]. Journal of China University of Petroleum, 2011, 35(3): 72 − 75. (in Chinese)
[7]	YUE Q B, LIU J B, DONG R Z. The research of post-buckling about slender rod string in wellbore based on energy method and experiment [J]. Journal of Petroleum Science and Engineering, 2017, 156: 732 − 739.
[8]	HUANG W J, GAO D L, WEI S L. Local mechanical model of down-hole tubular strings constrained in curved wellbores [J]. Journal of Petroleum Science and Engineering, 2015, 129: 233 − 242. doi: 10.1016/j.petrol.2015.03.017
[9]	ZHANG J T, YIN G F, LI Y F, et al. Buckling configurations of tubular strings constrained in three-dimensional curved wellbores [J]. Journal of Petroleum Science and Engineering, 2020, 195: 1 − 14.
[10]	LUKASIEWICZ S A. D. Dynamic behavior of the sucker rod string in the inclined well [R]. SPE 21665, 1990.
[11]	XU J. A new approach to the analysis of deviated rod-pumped wells [R]. SPE 28697, 1994.
[12]	XU J, DOTY D R, SHAHRAKI A. A comprehensive rod-pumping model and its applications to vertical and deviated wells [R]. SPE 52215, 1999.
[13]	刘合, 王素玲. 用有限元法预测抽油杆柱与油管柱偏磨点位置[J]. 石油学报, 2008, 29(1): 149 − 152. doi: 10.3321/j.issn:0253-2697.2008.01.030 LIU He, WANG Suling. Prediction of abraded points between sucker rod string and tubing by using finite element method [J]. Acta Petrolei Sinica, 2008, 29(1): 149 − 152. (in Chinese) doi: 10.3321/j.issn:0253-2697.2008.01.030
[14]	王文昌, 狄勤丰, 姚建林, 等. 三维定向井抽油杆柱力学特性有限元分析新方法[J]. 石油学报, 2010, 31(6): 1018 − 1023. doi: 10.7623/syxb201006026 WANG Wenchang, DI Qinfeng, YAO Jianlin, et al. A new finite element method in analyzing mechanical properties of sucker rod strings in 3D directional wellbores [J]. Acta Petrolei Sinica, 2010, 31(6): 1018 − 1023. (in Chinese) doi: 10.7623/syxb201006026
[15]	王宏博, 董世民. 轴向往复运动抽油杆柱在弯曲井眼内横向振动的仿真模型[J]. 工程力学, 2020, 37(10): 228 − 237. doi: 10.6052/j.issn.1000-4750.2019.12.0731 WANG Hongbo, DONG Shimin. A model for the transverse vibration simulation of sucker rod strings with axial reciprocating motion in curved wellbores [J]. Engineering Mechanics, 2020, 37(10): 228 − 237. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.12.0731
[16]	WANG H B, DONG S M. Spatial transverse vibration simulation model of axially moving sucker rod string under the excitation of curved borehole [J]. Shock and Vibration, 2020, Article ID 3108718.
[17]	SUN X R, DONG S M, LIU M S. The simulation model of sucker rod string transverse vibration under the space buckling deformation excitation and rod-tubing eccentric wear in vertical wells [J]. Journal of Vibroengineering, 2018, 20(1): 283 − 299. doi: 10.21595/jve.2017.19138
[18]	LIU J, GUO X Q, WANG G R, et al. Bi-nonlinear vibration model of tubing string in oil & gas well and its experimental verification [J]. Applied Mathematical Modelling, 2020, 81: 50 − 69. doi: 10.1016/j.apm.2019.09.057
[19]	GUO X Q, LIU J, WANG G R, et al. Nonlinear flow-induced vibration response characteristics of a tubing string in HPHT oil & gas well [J]. Applied Ocean Research, 2021, 106: 102468.
[20]	杨浩文, 吴斌, 潘天林, 等. Timoshenko梁能量守恒逐步积分算法[J]. 工程力学, 2019, 36(6): 21 − 28. doi: 10.6052/j.issn.1000-4750.2018.01.0033 YANG Haowen, WU Bin, PAN Tianlin, et al. Energy-conserving time integration method for Timoshenko beams [J]. Engineering Mechanics, 2019, 36(6): 21 − 28. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.01.0033
[21]	赵翔, 周扬, 邵永波, 等. 基于Green函数法的Timoshenko曲梁强迫振动分析[J]. 工程力学, 2020, 37(11): 12 − 27. doi: 10.6052/j.issn.1000-4750.2019.11.0708 ZHAO Xiang, ZHOU Yang, SHAO Yongbo, et al. Analytical solutions for forced vibrations of Timoshenko curved beam by means of Green’s functions [J]. Engineering Mechanics, 2020, 37(11): 12 − 27. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.11.0708
[22]	董世民. 抽油机井动态参数计算机仿真与系统优化[M]. 北京: 石油工业出版社, 2003: 156. DONG Shimin. Computer simulation of dynamic parameters of rod pumping system optimization [M]. Beijing: Petroleum Industry Press, 2003: 156. (in Chinese)
[23]	吴奇, 刘合, 师国臣. 聚驱抽油机井杆柱扶正器合理布置新方法[J]. 石油钻采工艺, 2004, 26(3): 52 − 54. doi: 10.3969/j.issn.1000-7393.2004.03.014 WU Qi, LIU He, SHI Guocheng. New and reasonable tubing centralizer arrangement method of polymer flooding artificial lifting well [J]. Oil Drilling & Production Technology, 2004, 26(3): 52 − 54. (in Chinese) doi: 10.3969/j.issn.1000-7393.2004.03.014
[24]	祝效华, 童华, 刘清友, 等. 旋转钻柱与井壁的碰撞摩擦边界问题研究[J]. 中国机械工程, 2007, 18(15): 1833 − 1837. doi: 10.3321/j.issn:1004-132x.2007.15.018 ZHU Xiaohua, TONG Hua, LIU Qingyou, et al. Research on dynamic boundary condition between revolving drill string and borehole wall [J]. China Mechanical Engineering, 2007, 18(15): 1833 − 1837. (in Chinese) doi: 10.3321/j.issn:1004-132x.2007.15.018
[25]	宋晓华, 李伟. 材料特性对转向柱碰撞性能影响的仿真研究[J]. 重庆交通大学学报(自然科学版), 2012, 31(4): 866 − 868. SONG Xiaohua, LI Wei. Crashworthiness numerical simulation of material properties on vehicle steering mast [J]. Journal of Chongqing Jiaotong University (Natural Science), 2012, 31(4): 866 − 868. (in Chinese)
[26]	王海波, 陈伯望, 余志武. 结构动力方程Newmark-β方法递推简化分析[J]. 四川大学学报(工程科学版), 2008, 40(3): 47 − 52. WANG Haibo, CHEN Bowang, YU Zhiwu. A simplified numerical integration format of Newmark-β method for structural dynamic equations [J]. Journal of Sichuan University (Engineering Science Edition), 2008, 40(3): 47 − 52. (in Chinese)
[27]	SUN X R, DONG S M, LI W C, et al. The numerical simulation of entire sucker rod string buckling with couplings in vertical wells [J]. Cluster Computing, 2019, 22: 12283 − 12295. doi: 10.1007/s10586-017-1611-z

施引文献(2)

期刊类型引用(2)

1.	曹晗. 采油螺杆泵抽油杆扶正器安放间距对扭转屈曲的影响分析. 化学工程与装备. 2025(03): 119-121 . 百度学术
2.	李骥. 采油井抽油杆断脱原因及防治对策. 化学工程与装备. 2023(11): 117-119 . 百度学术

其他类型引用(0)

资源附件(0)

图(13)

计量

文章访问数: 330
HTML全文浏览量: 100
PDF下载量: 58
被引次数: 2

1 抽油杆柱横向振动力学模型
1.1 力学模型
1.2 环境载荷计算模型
1.2.1 泵端集中轴向载荷计算模型
1.2.2 抽油杆柱轴向分布载荷仿真模型
1.2.3 粘弹性流体法向力计算模型
2 抽油杆柱横向振动数学模型
2.1 抽油杆柱横向振动方程
2.2 边界条件
2.3 初始条件
2.4 杆管碰撞条件
3 横向振动仿真方法
4 仿真实例与分析
4.1 抽油杆柱初始偏心激励下的横向振动
4.2 抽油杆柱初始屈曲构型激励下的横向振动
4.2.1 碰撞力变化规律
4.2.2 横向振动规律
5 结论

1 抽油杆柱横向振动力学模型
1.1 力学模型
1.2 环境载荷计算模型
1.2.1 泵端集中轴向载荷计算模型
1.2.2 抽油杆柱轴向分布载荷仿真模型
1.2.3 粘弹性流体法向力计算模型
2 抽油杆柱横向振动数学模型
2.1 抽油杆柱横向振动方程
2.2 边界条件
2.3 初始条件
2.4 杆管碰撞条件
3 横向振动仿真方法
4 仿真实例与分析
4.1 抽油杆柱初始偏心激励下的横向振动
4.2 抽油杆柱初始屈曲构型激励下的横向振动
4.2.1 碰撞力变化规律
4.2.2 横向振动规律
5 结论

参考文献(27)

施引文献

资源附件(0)

粘弹性流体法向力作用下的抽油杆柱横向振动仿真

通讯作者: 董世民(1962−)，男，吉林松原人，教授，博士，博导，主要从事机械采油系统动态仿真与运行优化的研究(E-mail: ysudshm@163.com)

计量

出版历程

TRANSVERSE VIBRATION SIMULATION OF SUCKER ROD STRINGS UNDER NORMAL DISTRIBUTED LOAD CAUSED BY VISCO-ELASTIC FLUID

1 抽油杆柱横向振动力学模型

1.1 力学模型

1.2 环境载荷计算模型

1.2.1 泵端集中轴向载荷计算模型

1.2.2 抽油杆柱轴向分布载荷仿真模型

1.2.3 粘弹性流体法向力计算模型

2 抽油杆柱横向振动数学模型

2.1 抽油杆柱横向振动方程

2.2 边界条件

2.3 初始条件

2.4 杆管碰撞条件

3 横向振动仿真方法

4 仿真实例与分析

4.1 抽油杆柱初始偏心激励下的横向振动

4.2 抽油杆柱初始屈曲构型激励下的横向振动

4.2.1 碰撞力变化规律

4.2.2 横向振动规律

5 结论

期刊类型引用(2)

其他类型引用(0)

计量

出版历程

目录

1 抽油杆柱横向振动力学模型

1.1 力学模型

1.2 环境载荷计算模型

1.2.1 泵端集中轴向载荷计算模型

1.2.2 抽油杆柱轴向分布载荷仿真模型

1.2.3 粘弹性流体法向力计算模型

2 抽油杆柱横向振动数学模型

2.1 抽油杆柱横向振动方程

2.2 边界条件

2.3 初始条件

2.4 杆管碰撞条件

3 横向振动仿真方法

4 仿真实例与分析

4.1 抽油杆柱初始偏心激励下的横向振动

4.2 抽油杆柱初始屈曲构型激励下的横向振动

4.2.1 碰撞力变化规律

4.2.2 横向振动规律

5 结论

通讯作者:
董世民(1962−)，男，吉林松原人，教授，博士，博导，主要从事机械采油系统动态仿真与运行优化的研究(E-mail: ysudshm@163.com)