用于光滑/非光滑壳的稳定化新型协同转动4节点四边形壳单元

李忠学; 胡万波

doi:10.6052/j.issn.1000-4750.2019.10.0611

用于光滑/非光滑壳的稳定化新型协同转动4节点四边形壳单元

李忠学^,,
胡万波

浙江大学土木工程系，杭州 310058

基金项目: 国家自然科学基金项目(11672266)

详细信息

作者简介:
胡万波(1995−)，男，浙江宁波人，硕士生，从事有限元理论及应用研究(E-mail: huwanbo@zju.edu.cn)

通讯作者:
李忠学(1970−)，男，河南商城人，副教授，博士，从事有限元理论及应用研究(E-mail: lizx19993@zju.edu.cn)

中图分类号: O302
计量
- 文章访问数: 555
- HTML全文浏览量: 168
- PDF下载量: 56
出版历程
- 收稿日期: 2019-10-18
- 修回日期: 2020-03-03
- 网络出版日期: 2020-05-20
- 刊出日期: 2020-09-06

A STABILIZED FOUR-NODE CO-ROTATIONAL QUADRILATERAL SHELL ELEMENT FOR SMOOTH AND NON-SMOOTH SHELL STRUCTURES

LI Zhong-xue^,,
HU Wan-bo

Department of Civil Engineering Zhejiang University, Hangzhou 310058, China

摘要

摘要: 该文发展了一种适用于光滑壳和非光滑壳的新型协同转动4节点四边形壳单元。在单元中每个节点采用了3个平动自由度和2/3个矢量型转动自由度，每个光滑壳的节点或非光滑壳的非交界节点采用壳中性面法向矢量的2个最小分量作为矢量型转动变量，在非光滑壳中性面交界线上的节点采用3个矢量型转动变量，他们分别是节点定向矢量组中一个定向矢量的较小或最小分量和另一定向矢量的2个最小分量。在非线性增量求解过程中，这些矢量型转动变量可以采用简单的加法将增量累加到原矢量中直接进行更新，且采用了协同转动框架的单元在局部和整体坐标系下得到的切线刚度矩阵都是对称的，结构整体切线刚度矩阵可以采用一维线性存储，可节省大量的计算机存储资源和计算时间。为消除膜闭锁和剪切闭锁的不利影响，采用单点积分方案计算单元内力矢量和切线刚度矩阵，并借鉴Belytschko提出的物理稳定化零能模态控制法来消除可能出现的零能模态。通过对2个光滑壳和2个非光滑壳进行非线性分析，检验了单元的可靠性、计算效率与计算精度。
- 四边形壳单元 /
- 协同转动法 /
- 矢量型转动变量 /
- 单点积分 /
- 闭锁现象 /
- 零能模态 /
- 稳定化方法
Abstract: A four-node co-rotational quadrilateral shell element for smooth and non-smooth shell structures is presented. Each node of the element has three translational degrees of freedom and two or three vectorial rotational degrees of freedom. For the nodes of smooth shells or nodes away from the intersection of non-smooth shells, the two smallest components of the mid-surface normal vector are defined as the nodal rotational variables. For the nodes at intersections of non-smooth shells, two smallest components of one orientation vector, together with one smaller or the smallest component of another nodal orientation vector, are employed as rotational variables. In a nonlinear incremental solution procedure, the vectorial rotational variables are additive and the symmetric tangent stiffness matrices are obtained in both global and local coordinate systems, thus, one-dimensional linear storage scheme can be adopted, saving computer storage and computing time effectively. To alleviate membrane and shear locking phenomena, one-point quadrature is adopted in calculating the element tangent stiffness matrices and the internal force vector, and the physically stabilized method is employed to avoid the occurrence of spurious zero energy modes. The reliability and computational accuracy are verified through two smooth shell problems and two non-smooth shell problems undergoing large displacements and large rotations.
- quadrilateral shell element /
- co-rotational approach /
- vectorial rotational variable /
- one-point quadrature /
- locking phenomenon /
- zero energy mode /
- physical stabilized method

HTML全文

在单元中引入协同转动法，可采用线性单元理论求解几何非线性问题，而且协同转动框架不依赖于特定的某个单元，因此可以利用现有的、性能较好的线性单元作为协同转动单元公式的“核”，建立新的单元公式，使一些原本只能用于解决小位移与小转角问题的单元公式可用于解决大位移、大转角问题^[1-4]。

在进行壳单元有限元分析时，往往会遇到闭锁现象^[5-6]。闭锁现象的实质是单元的假设位移模式无法准确地描述实际位移模式，导致单元刚度偏硬，位移的计算值偏小^[7]。在壳单元有限元计算中，剪切闭锁和膜闭锁的影响较为严重^[8]。对于以受弯为主的单元，当其膜应力很小或接近于零时，采用数值积分将会导致膜闭锁问题，使单元的膜刚度被夸大而使求解失真。对于薄壁梁元或薄板单元、薄壳单元，在采用数值积分计算单元刚度矩阵时，常会由于剪切闭锁而导致单元剪切刚度被夸大，从而使得到的结构变形偏小^[9]。

解决闭锁问题常采用2类方法：一类是通过改变积分方案来消除闭锁，如缩减积分法；另一类是改变应变能表达式，如各种假定应变法^[10-14]。缩减积分法有简单、精度高、计算效率高等优点，但由于使用的积分点少于高斯积分所需的积分点数，在求解过程中，单元刚度矩阵的秩有时会出现缺陷，导致无法捕捉到某些变形模式，从而导致求解失败。

自Zienkiewicz等^[15]首次提出缩减积分法以来，为了控制因缩减积分引起的零能模态，使单元更稳定，Kosloff^[16]、Taylor^[17]、Flanagan^[18]、Liu^[19-20]、王丽等^[21]相继提出了各种改进方法。MacNeal^[22]基于释放多余约束的等参原理，发展了QUAD4单元。Hughes等^[23]在MacNeal^[22]启发下，基于缩减积分法，横向变形采用9节点双二次幂形函数进行插值，转动变量采用4节点双线性形函数插值，构造出一种没有零能模态的新型4节点四边形双线性等参单元。Belytschko和Bindeman^[24]基于稳定性刚度与不完全积分刚度两者最大特征值成比例的思路，提出了稳定性参数的取值方法，选用合理的参数来控制零能模态，又不至于引起闭锁现象。Belytschko和Tsay^[25]通过增广B矩阵并设置稳定性参数实现稳定化过程，提出了扰动零能模态控制法。然而，扰动法也无法完全消除潜在的零能模态，且计算结果容易受稳定性参数的影响。Belytschko和Leviathan^[26]基于Hu-Washizu变分原理，在4节点四边形单元中，利用混合张量插值法来消除剪切闭锁，通过广义应变来控制零能模态，提出了采用物理稳定化零能模态控制法的QPH单元。李忠学等^[27]采用假定应变法构造出稳定应变来消除零能模态，发展了一种适用于光滑壳的新型协同转动9节点四边形单元。

本文发展了一种新型协同转动4节点四边形壳单元，采用矢量型转动变量描述旋转，这些变量在非线性增量求解过程中可以采用简单的加法进行更新，在整体坐标系和局部坐标系下都能得到对称的单元切线刚度矩阵，可提高计算效率和节省存储空间。为消除单元中可能出现的闭锁现象，本文采用了单点积分方案计算内力矢量和单元切线刚度矩阵，并引入Belytschko等^[26]的物理稳定化零能模态控制法，以避免因切线刚度矩阵缺秩而产生的零能模态。新型单元在4种典型算例中均表现出良好的性能。

1 单元的新型协同转动法描述

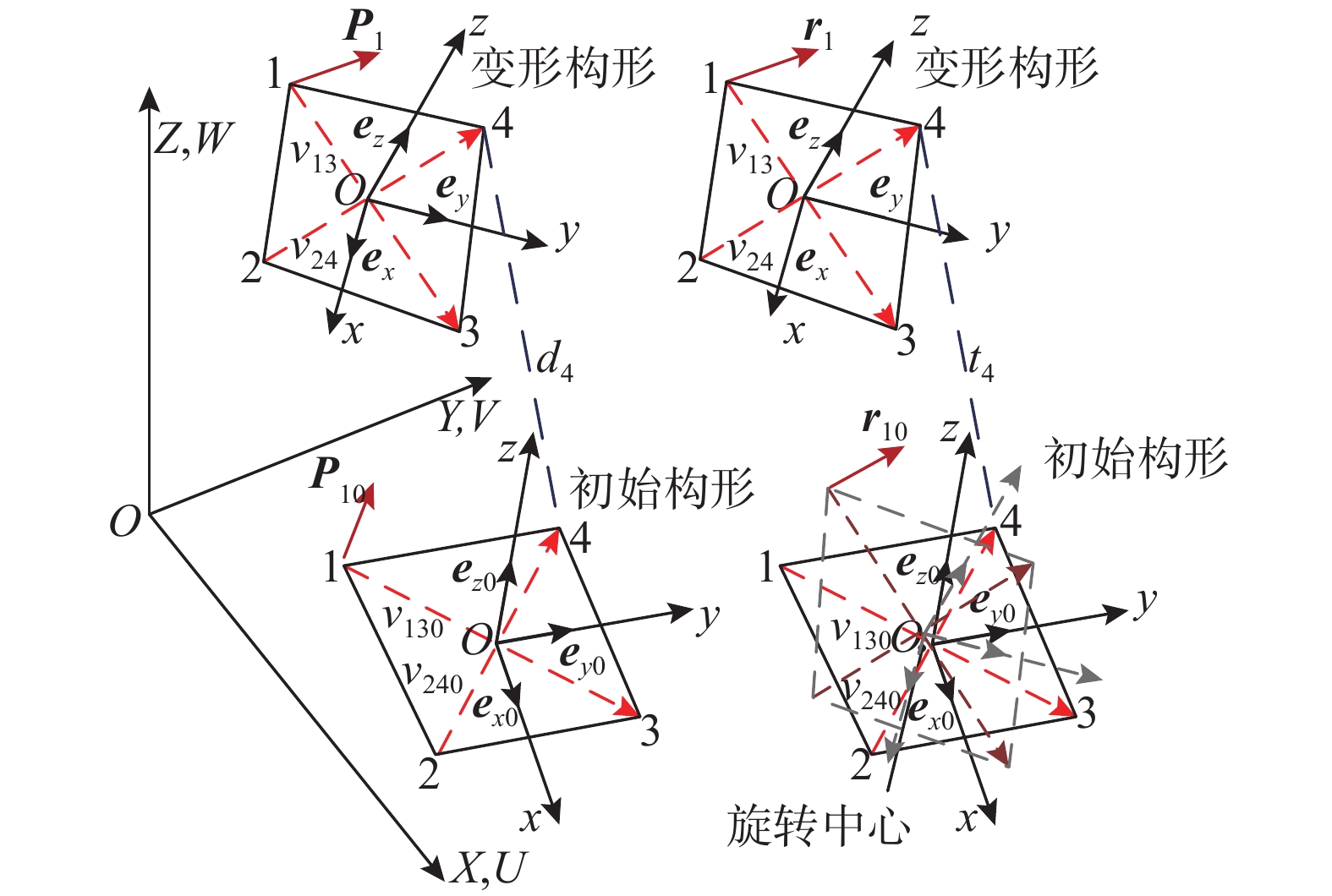
单元协同转动框架如图1所示。初始构形下，四边形两条对角线的方向矢量 ${{{v}}_{130}}$ 和 ${{{v}}_{240}}$ 的定义如下：

图 1 协同转动框架

Figure 1. Description of the co-rotational framework

下载: 全尺寸图片幻灯片

$\left\{ {\begin{aligned} & {{{{v}}_{130}} = {{{X}}_{30}} - {{{X}}_{10}}}\\& {{{{v}}_{240}} = {{{X}}_{40}} - {{{X}}_{20}}} \end{aligned}} \right.$

(1)

其中， ${{{X}}_{i0}}\left( {i = 1,2,3,4} \right)$ 为节点 $i$ 在整体坐标系下的坐标。

将 ${{{v}}_{130}}$ 和 ${{{v}}_{240}}$ 进行规范化，可以得到：

$\left\{ {\begin{aligned} & {{{{e}}_{130}} = \frac{{{{{v}}_{130}}}}{{\left| {{{{v}}_{130}}} \right|}}}\\& {{{{e}}_{240}} = \frac{{{{{v}}_{240}}}}{{\left| {{{{v}}_{240}}} \right|}}} \end{aligned}} \right.$

(2)

初始构形下局部坐标系的方向矢量通过下式计算得到：

$\left\{ {\begin{aligned} & {{{{e}}_{{\rm x}0}} = \frac{{{{{e}}_{130}} - {{{e}}_{240}}}}{{\left| {{{{e}}_{130}} - {{{e}}_{240}}} \right|}}}\\& {{{{e}}_{{\rm y}0}} = \frac{{{{{e}}_{130}} + {{{e}}_{240}}}}{{\left| {{{{e}}_{130}} + {{{e}}_{240}}} \right|}}}\\& {{{{e}}_{{\rm z}0}} = {{{e}}_{{\rm x}0}} \times {{{e}}_{{\rm y}0}}} \end{aligned}} \right.$

(3)

在变形构形下，四边形两条对角线的方向矢量 ${{{v}}_{13}}$ 和 ${{{v}}_{24}}$ 的定义如下：

$\left\{ {\begin{aligned} & {{{{v}}_{13}} = \left( {{{{X}}_{30}} + {{{d}}_3}} \right) - \left( {{{{X}}_{10}} + {{{d}}_1}} \right)}\\& {{{{v}}_{24}} = \left( {{{{X}}_{40}} + {{{d}}_4}} \right) - \left( {{{{X}}_{20}} + {{{d}}_2}} \right)} \end{aligned}} \right.$

(4)

其中， ${{{d}}_i}\left( {i = 1,2,3,4} \right)$ 是节点 $i$ 的平动位移矢量。将 ${{{v}}_{13}}$ 和 ${{{v}}_{24}}$ 进行规范化可以得到：

$\left\{ {\begin{aligned} & {{{{e}}_{13}} = \frac{{{{{v}}_{13}}}}{{\left| {{{{v}}_{13}}} \right|}}}\\& {{{{e}}_{24}} = \frac{{{{{v}}_{24}}}}{{\left| {{{{v}}_{24}}} \right|}}} \end{aligned}} \right.$

(5)

变形构形下的局部坐标系的方向矢量通过下式计算：

$\left\{ {\begin{aligned} & {{{{e}}_{x}} = \frac{{{{{e}}_{13}} - {{{e}}_{24}}}}{{\left| {{{{e}}_{13}} - {{{e}}_{24}}} \right|}}}\\& {{{{e}}_{y}} = \frac{{{{{e}}_{13}} + {{{e}}_{24}}}}{{\left| {{{{e}}_{13}} + {{{e}}_{24}}} \right|}}}\\& {{{{e}}_{\textit{z}}} = {{{e}}_{x}} \times {{{e}}_{y}}} \end{aligned}} \right.$

(6)

局部坐标系下，每个单元拥有20个节点变量：

${{u}}_{\rm L}^{\rm{T}} = \left\langle { {{{t}}_1^{\rm{T}}}\;\;{{{\theta }}_1^{\rm{T}}}\;\;{ {{{t}}_2^{\rm{T}}}\;\;{ {{{\theta }}_2^{\rm{T}}}\;\;{ {{{t}}_3^{\rm{T}}}\;\;{{{\theta }}_3^{\rm{T}}}\;\;{ {{{t}}_4^{\rm{T}}}\;\;{{{\theta }}_4^{\rm{T}}} } } } } } \right\rangle$

(7)

式中： ${{t}}_i^{{{\rm T}}} = \left\langle { {{u_i}}\;\;{{v_i}}\;\;{{w_i}} } \right\rangle$ 为节点 $i$ 的平动位移； ${{\theta }}_i^{\rm{T}} = \left\langle { {{r_{i{x}}}}\;\;{{r_{i{y}}}}} \right\rangle$ 为中面法向矢量 ${{{r}}_i}$ 的子向量； ${r_{i{x}}}$ 和 ${r_{i{y}}}$ 是节点 $i$ 的两个矢量型转动变量。

整体坐标系下，每个单元拥有20或更多个节点变量：

${{u}}_{\rm G}^{\rm{T}} = \left\langle { {{{d}}_1^{\rm{T}}}\;\;{{{n}}_{{\rm g}1}^{\rm{T}}}\;\;{ {{{d}}_2^{\rm{T}}}\;\;{ {{{n}}_{{\rm g}2}^{\rm{T}}}\;\;{ {{{d}}_3^{\rm{T}}}\;\;{{{n}}_{{\rm g}3}^{\rm{T}}}\;\;{ {{{d}}_4^{\rm{T}}}\;\;{{{n}}_{{\rm g}4}^{\rm{T}}} } } } } } \right\rangle$

(8)

式中： ${{d}}_i^{\rm T} = \left\langle { {{U_i}}\;\;{{V_i}}\;\;{{W_i}} } \right\rangle$ 为节点 $i$ 的平动位移；对于光滑壳的节点或非光滑壳的非交界节点， ${{n}}_{{\rm g}i}^{\rm{T}} = \left\langle { {{p_{i{\rm m}}}}\;\;{{p_{i{\rm n}}}} } \right\rangle$ ， ${p_{i{\rm m}}}$ 和 ${p_{i{\rm n}}}$ 为中面法向矢量 ${{{p}}_i}$ 的2个最小分量，它们是节点的2个矢量型转动变量；对于非光滑壳中性面交界线上的节点有 ${{n}}_{{\rm g}i}^{\rm{T}} = \left\langle { {{e_{iy{\rm m}}}}\;\;{{e_{iy{\rm n}}}}\;\;{{e_{i{\textit{z}}{ m}}}} } \right\rangle$ ， ${e_{iy{\rm m}}}$ 、 ${e_{iy{\rm n}}}$ 和 ${e_{i{\textit{z}}{\rm m}}}$ 为节点 $i$ 的3个矢量型转动变量，它们分别是节点定向矢量组中 ${{{e}}_{i{{\textit{z}}}}}$ 的1个较小或最小分量和 ${{{e}}_{i{y}}}$ 的2个最小分量。

局部坐标系下的节点坐标可通过整体坐标系下的节点坐标计算得到：

${{x}}_{i0}^{} = {{{R}}_0}{{{v}}_{i0}}$

(9)

其中：

$\left\{ {\begin{aligned} & { {{x}}_{i0}^{\rm{T}}=\langle \begin{array}{ccc}{x}_{i0}& {y}_{i0}& {{\textit{z}}}_{i0}\end{array}\rangle}\\& {{{{R}}_0} = {\begin{array}{*{20}{c}} [{{{e}}_{x0}}&{{{e}}_{y0}}&{{{e}}_{{\textit{z}}0}} \end{array}}{]^{\rm{T}}}}\\& {{{{v}}_{i0}} = {{{X}}_{i0}} - {{{X}}_{10}}} \end{aligned}} \right.$

(10)

局部坐标系下的节点变量可通过整体坐标系下的节点变量计算得到：

${{{t}}_i} = {{R}}\left( {{{{d}}_i} + {{{v}}_{i0}}} \right) - {{{R}}_0}{{{v}}_{i0}}$

(11)

${{{\theta }}_{i0}} = {{{R}}_{{\rm h}0}}{{{p}}_{i0}}\qquad\qquad\quad$

(12)

对于光滑壳节点或非光滑壳非交界节点有：

${{{\theta }}_i} = {{{R}}_{\rm h}}{{{p}}_i}$

(13)

对于非光滑壳中性面交界线上的节点有：

${{{\theta }}_i} = {{{R}}_{\rm h}}{{R}}_i^{\rm{T}}{{{R}}_{i0}}{{{p}}_{i0}}$

(14)

其中：

$\begin{split} &{{{R}}^{\rm{T}}} = [\begin{array}{*{20}{c}} {{{{e}}_{x}}}&{{{{e}}_{y}}}&{{{{e}}_{{\textit{z}}}}} \end{array}], \;{{R}}_{{\rm h}0}^{\rm{T}} = [\begin{array}{*{20}{c}} {{{{e}}_{{x}0}}}&{{{{e}}_{{y}0}}} \end{array}],\\& {{R}}_{\rm h}^{\rm{T}} = [\begin{array}{*{20}{c}} {{{{e}}_{x}}}&{{{{e}}_{y}}} \end{array}], \;{{R}}_{i0}^{\rm{T}} = [\begin{array}{*{20}{c}} {{{{e}}_{i{x}0}}}&{{{{e}}_{i{y}0}}}&{{{{e}}_{i{\textit{z}}0}}} \end{array}],\\& {{R}}_i^{\rm{T}} = [\begin{array}{*{20}{c}} {{{{e}}_{i{x}}}}&{{{{e}}_{i{y}}}}&{{{{e}}_{i{\textit{z}}}}} \end{array}] \end{split}$

(15)

在初始构形中，每个节点的中面法向矢量可由该点处沿2个自然坐标轴方向的切线矢量的矢量积计算得到：

${{\bar{ p}}_{i0}} = {\left. {\frac{{\partial {{{\bar{ X}}}_0}}}{{\partial \xi }} \times \frac{{\partial {{{\bar{ X}}}_0}}}{{\partial \eta }}} \right|_{\left( {{\xi _i},{\eta _i}} \right)}}\;$

(16)

${{\bar{ X}}_0} = {N_i}{{{X}}_{i0}}, i = 1,2,3,4$

(17)

式中： ${{\bar{ X}}_0} = \left\langle {\begin{array}{*{20}{c}} {{{\bar X}_0}}&{{{\bar Y}_0}}&{{{\bar Z}_0}} \end{array}} \right\rangle$ 为单元中面任意点在整体坐标系下的坐标； ${{{X}}_{i0}} = \left\langle {\begin{array}{*{20}{c}} {{X_{i0}}}&{{Y_{i0}}}&{{Z_{i0}}} \end{array}} \right\rangle$ 为节点 $i$ 在整体坐标系下的坐标； $\left( {{\xi _i},{\eta _i}} \right)$ 为节点 $i$ 的自然坐标。

文中采用了爱因斯坦求和约定，哑标取值范围为 $i = 1,2,3,4$ 。

在光滑壳的节点或非光滑壳的非交界节点处，节点的法向矢量取共享该节点的所有单元在该节点处的法向矢量的平均值：

${{{p}}_{i0}} = \frac{{\sum {\left( {{{{{{\bar{ p}}}_{i0}}} / {\left| {{{{\bar{ p}}}_{i0}}} \right|}}} \right)} }}{{\left| {\sum {\left( {{{{{{\bar{ p}}}_{i0}}} / {\left| {{{{\bar{ p}}}_{i0}}} \right|}}} \right)} } \right|}}$

(18)

单元内任意一点的位移按下式计算：

${{t}} \!=\! \left\{ {\begin{array}{*{20}{c}} u \\ v \\ w \end{array}} \right\} \!=\! {N_i}\left[ {{{{t}}_i} \!+\! \frac{1}{2}\zeta a({{{r}}_i} \!-\! {{{r}}_{i0}})} \right],\;i \!= \!1,2,3,4$

(19)

2 局部坐标系下的单元公式

将应变 ${{\varepsilon }}$ 分解为3部分，即：膜应变 ${{{\varepsilon }}_{\rm m}}$ 、弯曲应变 ${{\textit{z}}_{\rm l}}{\\text{χ}}$ 、出平面的剪切应变 ${{\gamma }}$ 。各应变按下式计算：

${{{\varepsilon }}_{\rm m}}{\rm{ = }}\left\{ {\begin{array}{*{20}{c}} {{\varepsilon _{xx}}} \\ {{\varepsilon _{yy}}} \\ {{\gamma _{xy}}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {{N_{i,x}}{u_i}} \\ {{N_{i,y}}{v_i}} \\ {{N_{i,y}}{u_i} + {N_{i,x}}{v_i}} \end{array}} \right\}\quad\quad\;\;$

(20)

${{\textit{z}}_{\rm l}} = \frac{1}{2}a\zeta \qquad\qquad\qquad\qquad\qquad\qquad\quad$

(21)

${\\text{χ}} = \left\{ {\begin{array}{*{20}{c}} {{N_{i,x}}({r_{ix}} - {r_{ix0}})} \\ {{N_{i,y}}({r_{iy}} - {r_{iy0}})} \\ {{N_{i,y}}({r_{ix}} - {r_{ix0}}) + {N_{i,x}}({r_{iy}} - {r_{iy0}})} \end{array}} \right\}$

(22)

${{\gamma }} = \left\{ {\begin{array}{*{20}{c}} {{\gamma _{xz}}} \\ {{\gamma _{yz}}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {{N_i}({r_{i{x}}} - {r_{i{x}0}}) + {N_{i,x}}{w_i}} \\ {{N_i}({r_{i{y}}} - {r_{i{y}0}}) + {N_{i,y}}{w_i}} \end{array}} \right\}$

(23)

式中， $a$ 为单元厚度。

应变 ${{{\varepsilon }}_{\rm m}}$ 、 ${\\text{χ}}$ 和 ${{\gamma }}$ 对节点变量的1阶偏微分分别是 ${{{B}}_{\rm m}}$ 、 ${{{B}}_{\rm b}}$ 和 ${{{B}}_{\rm s}}$ ：

${{{B}}_{\rm m}} = \left[ { {{{{B}}_{\rm m1}}}\;\;{{0}}\;\;{{{{B}}_{\rm m2}}}\;\;{{0}}\;\;{{{{B}}_{\rm m3}}}\;\;{{0}}\;\;{{{{B}}_{\rm m4}}}\;\;{{0}} } \right]$

(24)

${{{B}}_{\rm b}} = \left[ { { {{0}}\;\;{{{{B}}_{\rm b1}}}\;\;{ {{0}}\;\;{ {{{{B}}_{\rm b2}}}\;\;{{0}} }\;\;{{{{B}}_{\rm b3}}} } }\;\;{{0}}\;\;{{{{B}}_{\rm b4}}} } \right]\;\;$

(25)

${{{B}}_{\rm s}} = \left[ { {{{{B}}_{\rm s1}}}\;\;{{{{B}}_{\rm s2}}}\;\;{{{{B}}_{\rm s3}}}\;\;{{{{B}}_{\rm s4}}} } \right]\quad\quad\quad\quad\quad$

(26)

式中：

$\begin{split}&{{{B}}_{{\rm m}i}} = \left[ {\begin{array}{*{20}{c}} {{N_{i,x}}}&{\rm{0}}&0 \\ {\rm{0}}&{{N_{i,y}}}&0 \\ {{N_{i,y}}}&{{N_{i,x}}}&0 \end{array}} \right]\\& {{{B}}_{{\rm b}i}} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{N_{i,x}}} \\ 0 \\ {{N_{i,y}}} \end{array}}&{\begin{array}{*{20}{c}} 0 \\ {{N_{i,y}}} \\ {{N_{i,x}}} \end{array}} \end{array}} \right]\\& {{{B}}_{{\rm s}i}} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\rm{0}}&{\rm{0}}&{{N_{i,x}}} \end{array}}&{{N_i}}&0 \end{array}} \\ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\rm{0}}&{\rm{0}}&{{N_{i,y}}} \end{array}}&0&{{N_i}} \end{array}} \end{array}} \right]\end{split}$

(27)

局部坐标系下的内力矢量为：

${{f}} = {{{f}}_{\rm ext}} = \int_{V} {( {{{B}}_{\rm m}^{\rm{T}}{{{D}}_{\rm{1}}}{{{\varepsilon }}_{\rm m}} + {\textit{z}}_{\rm l}^2{{B}}_{\rm b}^{\rm{T}}{{{D}}_{\rm{1}}}{\\text{χ}} + {{B}}_{\rm s}^{\rm{T}}{{{D}}_{\rm{2}}}{{\gamma }}} ){{\rm d}V}}$

(28)

局部坐标系下的单元切线刚度矩阵为：

${{{k}}_{\rm{T}}} = \int_{V} {( {{{B}}_{\rm m}^{\rm{T}}{{{D}}_{\rm{1}}}{{{B}}_{\rm m}} + {\textit{z}}_{\rm l}^2{{B}}_{\rm b}^{\rm{T}}{{{D}}_{\rm{1}}}{{{B}}_{\rm b}} + {{B}}_{\rm s}^{\rm{T}}{{{D}}_{\rm{2}}}{{{B}}_{\rm s}}} ){{\rm d}V}}$

(29)

式中：

$\begin{split}& {{{D}}_1} = \dfrac{E}{{1 - {\mu ^2}}}\left[ {\begin{array}{*{20}{c}} 1&\mu &0 \\ \mu &1&0 \\ 0&0 &{\dfrac{{1 - \mu }}{2}} \end{array}} \right]\\& {{{D}}_2} = {k_1}\frac{E}{{2\left( {1 + \mu } \right)}}\left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right], \;{k_1} = \frac{5}{6} \end{split}$

(30)

3 稳定化的单点积分法

为消除新型协同转动四边形壳单元出现的闭锁现象，采用单点积分方案计算单元内力矢量和切线刚度矩阵。引入Bathe等^[28]提出的的混合张量插值应变法来消除剪切闭锁，并借鉴Belyschko等^[26]的物理稳定化方法来控制零能模态。

4节点四边形壳单元的标准等参形函数：

${{N}} = \left\{ {\begin{array}{*{20}{c}} {{N_1}} \\ {{N_2}} \\ {{N_3}} \\ {{N_4}} \end{array}} \right\} = \frac{1}{4}({{s}} + \xi {{{\xi }}_0})({{s}} + \eta {{{\eta }}_0})$

(31)

式中：

$\begin{split}& {{{s}}^{\rm T}} = \left\langle { 1\;\;1\;\;1\;\;1 } \right\rangle,\\& {{{\xi }}_0^{\rm{T}}} = \left\langle { { - 1}\;\;1\;\;1\;\;{ - 1} } \right\rangle,\\& {{{\eta }}_0^{\rm{T}}} = \left\langle {\begin{array}{*{20}{c}} { - 1}&{ - 1}&1&1 \end{array}} \right\rangle {\text{。}} \end{split}$

(32)

形函数对自然坐标系的1阶偏导数为：

${N_{i,\xi }} = \frac{1}{4}({\xi _i} + {h_i}\eta ), \;{N_{i,\eta }} = \frac{1}{4}({\eta _i} + {h_i}\xi )$

(33)

式中：

${h_i}{\rm{ = }}{\xi _i}{\eta _i}$

(34)

雅克比矩阵：

${{J}} = \left[ {\begin{array}{*{20}{c}} {\dfrac{{\partial x}}{{\partial \xi }}}&{\dfrac{{\partial y}}{{\partial \xi }}} \\ {\dfrac{{\partial x}}{{\partial \eta }}}&{\dfrac{{\partial y}}{{\partial \eta }}} \end{array}} \right]{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {\dfrac{1}{4}({\xi _i} + {h_i}\eta ){x_{i0}}}&{\dfrac{1}{4}({\xi _i} + {h_i}\eta ){y_{i0}}} \\ {\dfrac{1}{4}({\eta _i} + {h_i}\xi ){x_{i0}}}&{\dfrac{1}{4}({\eta _i} + {h_i}\xi ){y_{i0}}} \end{array}} \right]$

(35)

得到雅克比矩阵的行列式：

$J = \left| {{J}} \right| = {J_0} + {J_1}\xi + {J_2}\eta$

(36)

式中：

$\left\{ {\begin{aligned} & { {J_0}{\rm{ = }}\dfrac{1}{{16}}[ {({\xi _i}{x_{i0}})({\eta _j}{y_{j0}}) - ({\eta _i}{x_{i0}})({\xi _j}{y_{j0}})} ]}\\& { {J_1}{\rm{ = }}\frac{1}{{16}}[ {({\xi _i}{x_{i0}})({h_j}{y_{j0}}) - ({h_i}{x_{i0}})({\xi _j}{y_{j0}})} ]}\\& {{J_2}{\rm{ = }}\frac{1}{{16}}[ {({h_i}{x_{i0}})({\eta _j}{y_{j0}}) - ({\eta _i}{x_{i0}})({h_j}{y_{j0}})} ]} \end{aligned}} \right.$

(37)

在4节点四边形壳单元中，借鉴Belytschko等^[29]提出的标准等参形函数的等价形式：

${{N}} = {{\Delta }} + x{{{b}}_{x}} + y{{{b}}_{y}} + h{\\text{κ}}$

(38)

式中：

$\begin{split}&{{\Delta }} = \frac{1}{4}[{{s}} - ({s_i}{x_{i0}}){{{b}}_{x}} - ({s_i}{y_{i0}}){{{b}}_{y}}],i = 1,2,3,4,\\& {\\text{κ}} = \frac{1}{4}[{{{h}}_0} - ({h_i}{x_{i0}}){{{b}}_{x}} - ({h_i}{y_{i0}}){{{b}}_{y}}],i = 1,2,3,4,\\& {{b}}_{x}^{\rm{T}} = \frac{1}{{2A}}\left\langle {\begin{array}{*{20}{c}} {{y_{42}}}&{{y_{13}}}&{{y_{24}}}&{{y_{31}}} \end{array}} \right\rangle ,\\& {{b}}_{y}^{\rm{T}} = \frac{1}{{2A}}\left\langle {\begin{array}{*{20}{c}} {{x_{24}}}&{{x_{31}}}&{{x_{42}}}&{{x_{13}}} \end{array}} \right\rangle ,\\& {x_{ij}} = {x_{i0}} - {x_{j0}}, \;{y_{ij}} = {y_{i0}} - {y_{j0}},\\& {{h}}_0^{\rm{T}} = \left\langle {\begin{array}{*{20}{c}} 1&{ - 1}&1&{ - 1} \end{array}} \right\rangle , \;\;A = 4{J_0} \end{split}$

(39)

形函数对局部坐标系的1阶偏导数为：

${N_{i,x}} = {b_{x}}_i + {h_{,x}}{\kappa _i}, \;{N_{i,y}} = {b_{y}}_i + {h_{,y}}{\kappa _i}$

(40)

式中：

$\left\{ {\begin{aligned} & {{h_{,x}} = \frac{1}{{4J}}[({\eta _i}{y_{i0}})\eta - ({\xi _i}{y_{i0}})\xi ]}\\& {{h_{,y}} = \frac{1}{{4J}}[({\xi _i}{x_{i0}})\xi - ({\eta _i}{x_{i0}})\eta ]} \end{aligned}} \right.$

(41)

将式(40)代入 ${{{B}}_{\rm m}}$ 和 ${{{B}}_{\rm b}}$ 的计算式后拆分得到其常量部分 ${{B}}_{\rm m}^{{O}}$ 、 ${{B}}_{\rm b}^{{O}}$ 和非常量部分 ${{B}}_{\rm m}^{{H}}$ 、 ${{B}}_{\rm b}^{{H}}$ ：

${{B}}_{\rm m}^{{O}} = [ { {{{B}}_{\rm m1}^{{O}}}\;\;{{0}}\;\;{{{B}}_{\rm m2}^{{O}}}\;\;{{0}}\;\;{{{B}}_{\rm m3}^{{O}}}\;\;{{0}}\;\;{{{B}}_{\rm m4}^O}\;\;{{0}} } ]$

(42)

${{B}}_{\rm m}^{{H}} = [ { {{{B}}_{\rm m1}^{{H}}}\;\;{{0}}\;\;{{{B}}_{\rm m2}^{{H}}}\;\;{{0}}\;\;{{{B}}_{\rm m3}^{{H}}}\;\;{{0}}\;\;{{{B}}_{\rm m4}^{{H}}}\;\;{{0}} } ]$

(43)

${{B}}_{\rm b}^{{O}} = [ { { {{0}}\;\;{{{B}}_{\rm b1}^{{O}}}\;\;{ {{0}}\;\;{ {{{B}}_{\rm b2}^{{O}}}\;\;{{0}} }\;\;{{{B}}_{\rm b3}^{{O}}} } }\;\;{{0}}\;\;{{{B}}_{\rm b4}^{{O}}} } ]\quad$

(44)

${{B}}_{\rm b}^{{H}} = [ { { {{0}}\;\;{{{B}}_{\rm b1}^{{H}}}\;\;{ {{0}}\;\;{ {{{B}}_{\rm b2}^{{H}}}\;\;{{0}} }\;\;{{{B}}_{\rm b3}^{{H}}} } }\;\;{{0}}\;\;{{{B}}_{\rm b4}^{{H}}} } ]\quad$

(45)

式中：

$\begin{split}& {{B}}_{{\rm m}i}^{{O}}{\rm{ = }}\left[ {{\kern 1pt} \begin{array}{*{20}{c}} {{b_{{x}i}}}&0&0 \\ 0&{{b_{{y}i}}}&0 \\ {{b_{{y}i}}}&{{b_{{x}i}}}&0 \end{array}} \right], \;\;{{B}}_{{\rm m}i}^{{H}}{\rm{ = }}\left[ {{\kern 1pt} \begin{array}{*{20}{c}} {{h_{,x}}{\kappa _i}}&0&0 \\ 0&{{h_{,y}}{\kappa _i}}&0 \\ {{h_{,y}}{\kappa _i}}&{{h_{,x}}{\kappa _i}}&0 \end{array}} \right],\\& {{B}}_{{\rm{b}}i}^{{O}}{\rm{ = }}\left[ {{\kern 1pt} \begin{array}{*{20}{c}} {{b_{{{x}}i}}}&0 \\ 0&{{b_{{{y}}i}}} \\ {{b_{{{y}}i}}}&{{b_{{{x}}i}}} \end{array}} \right], \;{{B}}_{{\rm{b}}i}^{{H}}{\rm{ = }}\left[ {{\kern 1pt} \begin{array}{*{20}{c}} {{h_{,x}}{\kappa _i}}&0 \\ 0&{{h_{,y}}{\kappa _i}} \\ {{h_{,y}}{\kappa _i}}&{{h_{,x}}{\kappa _i}} \end{array}} \right]\qquad\quad\;\;\;(46) \end{split}$

对 ${{B}}_{{\rm m}i}^{{H}}$ 和 ${{{B}}}_{{\rm b}i}^{{O}}$ 进行扩阶和做如下修正：

$\begin{split}& {{B}}_{{\rm{m}}i}^{{H}}{\rm{ = }}\left[ {{\kern 1pt} \begin{array}{*{20}{c}} {{h_{,x}}{\kappa _i}}&0&0&{ - \dfrac{1}{4}{{\textit{z}}_{\kappa} }{h_{,x}}{s_i}}&0\\ 0&{{h_{,y}}{\kappa _i}}&0&0&{ - \dfrac{1}{4}{{\textit{z}}_{\kappa} }{h_{,y}}{s_i}}\\ {{h_{,y}}{\kappa _i}}&{{h_{,x}}{\kappa _i}}&0&{ - \dfrac{1}{4}{{\textit{z}}_{\kappa} }{h_{,y}}{s_i}}&{ - \dfrac{1}{4}{{\textit{z}}_{\kappa} }{h_{,x}}{s_i}} \end{array}} \right],\\ &{{B}}_{{\rm{b}}i}^{{O}}{\rm{ = }}\left[ {{\kern 1pt} \begin{array}{*{20}{c}} {b_{{{x}}i}^{\rm{c}}}&0&0&{{b_{{{x}}i}}}&0\\ 0&{b_{{{y}}i}^{\rm{c}}}&0&0&{{b_{{{y}}i}}}\\ {b_{{{y}}i}^{\rm{c}}}&{b_{{{x}}i}^{\rm{c}}}&0&{{b_{{{y}}i}}}&{{b_{{{x}}i}}} \end{array}} \right]\qquad\qquad\qquad\quad\;\;(47) \end{split}$

式中：

$\begin{split}& {{\textit{z}}_{\kappa} } = {{\textit{z}}_{i0}}{\kappa _i},i = 1,2,3,4,\\& {{b}}_{x}^{\rm c}{\rm{ = }}\frac{{4{{\textit{z}}_{\kappa} }}}{A}{\left\langle {\begin{array}{*{20}{c}} {{b_{y4}}}&{{b_{y3}}}&{{b_{y2}}}&{{b_{y1}}} \end{array}} \right\rangle ^{\rm{T}}},\\& {{b}}_{y}^{\rm c}{\rm{ = }}\frac{{4{{\textit{z}}_{\kappa} }}}{A}{\left\langle {\begin{array}{*{20}{c}} {{b_{x2}}}&{{b_{x1}}}&{{b_{x4}}}&{{b_{x3}}} \end{array}} \right\rangle ^{\rm{T}}} \end{split}$

(48)

自然坐标系下的单元剪切应变^[26]：

$\begin{split} & {\gamma _{\xi \zeta}} \!=\! {J_{11}}\frac{{\partial u}}{{\partial \zeta }}\!{\rm{ + }}\!{J_{12}}\frac{{\partial v}}{{\partial \zeta }}\! +\! {J_{13}}\frac{{\partial w}}{{\partial \zeta }}\! + \!{J_{31}}\frac{{\partial u}}{{\partial \xi }}\! + \!{J_{32}}\frac{{\partial v}}{{\partial \xi }} \!+\! {J_{33}}\frac{{\partial w}}{{\partial \xi }},\\& {\gamma _{\eta\zeta}} \!=\! {J_{21}}\frac{{\partial u}}{{\partial \zeta }}{\rm{ + }}{J_{22}}\frac{{\partial v}}{{\partial \zeta }} \!+ \!{J_{23}}\frac{{\partial w}}{{\partial \zeta }}\! +\! {J_{31}}\frac{{\partial u}}{{\partial \eta }}\! +\! {J_{32}}\frac{{\partial v}}{{\partial \eta }} \!+\! {J_{33}}\frac{{\partial w}}{{\partial \eta }} \end{split}$

(49)

忽略含有 ${J_{13}}$ 、 ${J_{31}}$ 、 ${J_{23}}$ 和 ${J_{32}}$ 的项，且取 ${J_{33}} \cong \dfrac{a}{2}$ 。并将式(19)代入式(49)得到：

$\begin{split}& {\gamma _{\xi \zeta}}{\rm{ = }}\frac{a}{2}[ {{x_{,\xi }}{N_i}({r_{i{x}}} - {r_{i{x}0}}) + {y_{,\xi }}{N_i}({r_{i{y}}} - {r_{i{y}0}}) + {N_{i,\xi }}{w_i}} ],\\& {\gamma _{\eta \zeta}}{\rm{ = }}\frac{a}{2}[ {{x_{,\eta }}{N_i}({r_{i{x}}} - {r_{i{x}0}}) + {y_{,\eta }}{N_i}({r_{i{y}}} - {r_{i{y}0}}) + {N_{i,\eta }}{w_i}} ] \end{split}$

(50)

对应图2插值关联点A、B、C、D处的剪切应变：

$\begin{split} \gamma _{\xi {\text{ζ}}}^{{A}} = &\frac{a}{8}[ {J_{11}^{{A}}(1 + {\eta _i})({r_{i{x}}} - {r_{i{x}0}}) +}\\ &{J_{12}^{{A}}(1 + {\eta _i})({r_{i{y}}} - {r_{i{y}0}}) + ({\xi _i} + {h_i}){w_i}} ],\\ \gamma _{\xi {\text{ζ}}}^{{C}} = &\frac{a}{8}[ {J_{11}^{{C}}(1 - {\eta _i})({r_{i{x}}} - {r_{i{x}0}}) +}\\& { J_{12}^{{C}}(1 - {\eta _i})({r_{i{y}}} - {r_{i{y}0}}) + ({\xi _i} - {h_i}){w_i}} ],\\ \gamma _{\eta{\text{ζ}}}^{{B}} = &\frac{a}{8}[ {J_{21}^{{B}}(1 - {\xi _i})({r_{i{x}}} - {r_{i{x}0}}) + }\\ &{J_{22}^{{B}}(1 - {\xi _i})({r_{i{y}}} - {r_{i{y}0}}) + ({\eta _i} - {h_i}){w_i}}],\\ \gamma _{\eta{\text{ζ}}}^{{D}} =& \frac{a}{8}[ {J_{21}^{{D}}(1 + {\xi _i})({r_{i{x}}} - {r_{i{x}0}}) + }\\ &{J_{22}^{{D}}(1 + {\xi _i})({r_{i{y}}} - {r_{i{y}0}}) + ({\eta _i} + {h_i}){w_i}} ] \end{split}$

(51)

图 2 剪切应变插值关联点分布图

Figure 2. Interpolation points for shear strain

下载: 全尺寸图片幻灯片

通过混合张量插值应变法^[28]得到自然坐标系下的单元剪切应变：

$\begin{split} {\gamma _{\xi\zeta}} = &\frac{1}{2}(1 + \eta )\gamma _{\xi\zeta}^A + \frac{1}{2}(1 - \eta )\gamma _{\xi\zeta}^C = \\ &\frac{a}{{32}}\{ [({\xi _j} + {h_j}{\eta _i}) + ({h_j} + {\xi _j}{\eta _i})\eta ]{x_{j0}}({r_{ix}} - {r_{ix0}}) + \\ & [({\xi _j} + {h_j}{\eta _i}) + ({h_j} + {\xi _j}{\eta _i})\eta ]{y_{j0}}({r_{iy}} - {r_{iy0}}) +\\ & 4({\xi _i} + {h_i}\eta ){w_i}\},\\ {\gamma _{\eta\zeta}} =& \frac{1}{2}(1 + \xi )\gamma _{\eta\zeta}^D + \frac{1}{2}(1 - \xi )\gamma _{\eta\zeta}^B =\\ & \frac{a}{{32}}\{ [({\eta _j} + {h_j}{\xi _i}) + ({h_j} + {\eta _j}{\xi _i})\xi ]{x_{j0}}({r_{ix}} - {r_{ix0}}) + \\ &[({\eta _j} + {h_j}{\xi _i}) + ({h_j} + {\eta _j}{\xi _i})\xi ]{y_{j0}}({r_{iy}} - {r_{iy0}}) + \\ &4({\eta _i} + {h_i}\xi ){w_i}\} \\[-15pt] \end{split}$

(52)

将自然坐标系下的剪切应变转换到局部卡氏坐标系下：

$\begin{split} {\gamma _{xz}} = &\frac{{\partial \xi }}{{\partial x}}\frac{{\partial \xi }}{{\partial {\textit{z}}}}{\gamma _{\xi\xi}} + \frac{{\partial \xi }}{{\partial x}}\frac{{\partial \eta }}{{\partial {\textit{z}}}}{\gamma _{\xi\eta}} + \frac{{\partial \xi }}{{\partial x}}\frac{{\partial \zeta }}{{\partial {\textit{z}}}}{\gamma _{\xi\zeta}} +\\& \frac{{\partial \eta }}{{\partial x}}\frac{{\partial \xi }}{{\partial {\textit{z}}}}{\gamma _{\eta\xi}} + \frac{{\partial \eta }}{{\partial x}}\frac{{\partial \eta }}{{\partial {\textit{z}}}}{\gamma _{\eta\eta}} + \frac{{\partial \eta }}{{\partial x}}\frac{{\partial \zeta }}{{\partial {\textit{z}}}}{\gamma _{\eta\zeta}} + \\& \frac{{\partial \zeta }}{{\partial x}}\frac{{\partial \xi }}{{\partial {\textit{z}}}}{\gamma _{\zeta\xi}} + \frac{{\partial \zeta }}{{\partial x}}\frac{{\partial \eta }}{{\partial {\textit{z}}}}{\gamma _{\zeta\eta}} + \frac{{\partial \zeta }}{{\partial x}}\frac{{\partial \zeta }}{{\partial {\textit{z}}}}{\gamma _{\zeta\zeta}},\\ {\gamma _{\rm yz}} = &\frac{{\partial \xi }}{{\partial y}}\frac{{\partial \xi }}{{\partial {\textit{z}}}}{\gamma _{\xi\xi}} + \frac{{\partial \xi }}{{\partial y}}\frac{{\partial \eta }}{{\partial {\textit{z}}}}{\gamma _{\xi\eta}} + \frac{{\partial \xi }}{{\partial y}}\frac{{\partial \zeta }}{{\partial {\textit{z}}}}{\gamma _{\xi\zeta}} + \\ & \frac{{\partial \eta }}{{\partial y}}\frac{{\partial \xi }}{{\partial {\textit{z}}}}{\gamma _{\eta\xi}} + \frac{{\partial \eta }}{{\partial y}}\frac{{\partial \eta }}{{\partial {\textit{z}}}}{\gamma _{\eta\eta}} + \frac{{\partial \eta }}{{\partial y}}\frac{{\partial \zeta }}{{\partial {\textit{z}}}}{\gamma _{\eta\zeta}} + \\ &\frac{{\partial \zeta }}{{\partial y}}\frac{{\partial \xi }}{{\partial {\textit{z}}}}{\gamma _{\zeta\xi}} + \frac{{\partial \zeta }}{{\partial y}}\frac{{\partial \eta }}{{\partial {\textit{z}}}}{\gamma _{\zeta\eta}} + \frac{{\partial \zeta }}{{\partial y}}\frac{{\partial \zeta }}{{\partial {\textit{z}}}}{\gamma _{\zeta\zeta}} \end{split}$

(53)

并对以下各项作近似处理：

$\frac{{\partial \xi }}{{\partial {\textit{z}}}} \cong 0, \;\;\frac{{\partial \eta }}{{\partial {\textit{z}}}} \cong 0, \;\;\frac{{\partial \zeta }}{{\partial x}} \cong 0, \;\;\frac{{\partial \zeta }}{{\partial y}} \cong 0$

(54)

得到：

$\begin{split} & {\gamma _{xz}} = {\zeta _{,z}}({\xi _{,x}}{\gamma _{\xi\zeta}}{\rm{ + }}{\eta _{,x}}{\gamma _{\eta\zeta}}),\\& {\gamma _{yz}} = {\zeta _{,z}}({\xi _{,y}}{\gamma _{\xi\zeta}}{\rm{ + }}{\eta _{,y}}{\gamma _{\eta\zeta}}) \end{split}$

(55)

对以下各项作近似处理：

$\begin{split} & {\xi _{,x}} \cong {\xi _{,x}}(0,0) = \frac{1}{A}{\eta _i}{y_{i0}},\\[-2pt]& {\eta _{,x}} \cong {\eta _{,x}}(0,0) = - \frac{1}{A}{\xi _i}{y_{i0}},\\[-2pt]& {\xi _{,y}} \cong {\xi _{,y}}(0,0) = - \frac{1}{A}{\eta _i}{x_{i0}},\\[-2pt]& {\eta _{,y}} \cong {\eta _{,y}}(0,0) = \frac{1}{A}{\xi _i}{x_{i0}},\\[-2pt]& {\zeta _{,{\textit{z}}}} \cong \frac{2}{a} \end{split}$

(56)

得到：

$\begin{split} {\gamma _{xz}} =& \frac{1}{{4A}}[{\eta _j}{y_{j0}}({\xi _i} + {h_i}\eta ) - {\xi _j}{y_{j0}}({\eta _i} + {h_i}\xi )]{w_i} +\\[-2pt] & \frac{1}{{16A}}\{ [({\xi _j} + {h_j}{\eta _i}) + ({h_j} + {\xi _j}{\eta _i})\eta ]{\eta _k}{y_{k0}}{x_{j0}} -\\[-2pt] & [({\eta _j} + {h_j}{\xi _i}) + ({h_j} + {\eta _j}{\xi _i})\xi ]{\xi _k}{y_{k0}}{x_{j0}}\} ({r_{ix}} - {r_{ix0}}) + \\[-2pt] &\frac{1}{{16A}}\{ [({\xi _j} + {h_j}{\eta _i}) + ({h_j} + {\xi _j}{\eta _i})\eta ]{\eta _k}{y_{k0}}{y_{j0}} - \\[-2pt] &[({\eta _j} + {h_j}{\xi _i}) + ({h_j} + {\eta _j}{\xi _i})\xi ]{\xi _k}{y_{k0}}{y_{j0}}\} ({r_{iy}} - {r_{iy0}}), \end{split}$

$\begin{split} {\gamma _{yz}} = &\frac{1}{{4A}}[ - {\eta _j}{x_{j0}}({\xi _i} + {h_i}\eta ) + {\xi _j}{x_{j0}}({\eta _i} + {h_i}\xi )]{w_i} + \\[-2pt] & \frac{1}{{16A}}\{ - [({\xi _j} + {h_j}{\eta _i}) + ({h_j} + {\xi _j}{\eta _i})\eta ]{\eta _k}{x_{k0}}{x_{j0}} + \\[-2pt] & [({\eta _j} + {h_j}{\xi _i}) + ({h_j} + {\eta _j}{\xi _i})\xi ]{\xi _k}{x_{k0}}{x_{j0}}\} ({r_{ix}} - {r_{ix0}}) + \\[-2pt] &\frac{1}{{16A}}\{ - [({\xi _j} + {h_j}{\eta _i}) + ({h_j} + {\xi _j}{\eta _i})\eta ]{\eta _k}{x_{k0}}{y_{j0}} + \\[-2pt] &[({\eta _j} + {h_j}{\xi _i}) + ({h_j} + {\eta _j}{\xi _i})\xi ]{\xi _k}{x_{k0}}{y_{j0}}\} ({r_{iy}} - {r_{iy0}}) \end{split}$

(57)

式(57)进一步缩写为：

$\left\{ \begin{array}{l} {\gamma _{x{\textit{z}}}} \\ {\gamma _{y{\textit{z}}}} \\ \end{array} \right\} = {{{B}}_{{\rm s}i}}\left( {\xi ,\eta } \right)\left\{ {\begin{array}{*{20}{c}} {{{{t}}_i}} \\ {{{{\theta }}_i} - {{{\theta }}_{i0}}} \end{array}} \right\}$

(58)

式中：

${{{B}}_{{\rm s}i}}(\xi ,\eta ) = {{B}}_{{\rm s}i}^{\eta} (\eta ) + {{B}}_{{\rm s}i}^{\xi} (\xi )$

(59)

将 ${{B}}_{{\rm s}i}^{\eta}$ 和 ${{B}}_{{\rm s}i}^{\xi}$ 分解成常量部分和非常量部分：

$\begin{split}& {{B}}{_{{\rm s}i}^{\eta O}} = \frac{1}{{16A}}\left[ {\begin{array}{*{20}{c}} 0&0&{4{\eta _j}{y_{j0}}{\xi _i}}&{({\xi _j} + {h_j}{\eta _i}){\eta _k}{y_k}_0{x_{j0}}}&{({\xi _j} + {h_j}{\eta _i}){\eta _k}{y_k}_0{y_{j0}}}\\ 0&0&{ - 4{\eta _j}{x_{j0}}{\xi _i}}&{ - ({\xi _j} + {h_j}{\eta _i}){\eta _k}{x_k}_0{x_{j0}}}&{ - ({\xi _j} + {h_j}{\eta _i}){\eta _k}{x_k}_0{y_{j0}}} \end{array}} \right],\\& {{B}}{_{{\rm s}i}^{\xi O}} = \frac{1}{{16A}}\left[ {\begin{array}{*{20}{c}} 0&0&{ - 4{\xi _j}{y_{j0}}{\eta _i}}&{ - ({\eta _j} + {h_j}{\xi _i}){\xi _k}{y_k}_0{x_{j0}}}&{ - ({\eta _j} + {h_j}{\xi _i}){\xi _k}{y_k}_0{y_{j0}}}\\ 0&0&{4{\xi _j}{x_{j0}}{\eta _i}}&{({\eta _j} + {h_j}{\xi _i}){\xi _k}{x_k}_0{x_{j0}}}&{({\eta _j} + {h_j}{\xi _i}){\xi _k}{x_k}_0{y_{j0}}} \end{array}} \right],\\& {{B}}{_{{\rm s}i}^{\eta H}} = {\eta _i}\eta {{B}}{_{{\rm s}i}^{\eta O}},\\& {{B}}{_{{\rm s}i}^{\xi H}} = {\xi _i}\xi {{B}}{_{{\rm s}i}^{\xi O}},\;\;\;\;i,j,k = 1,2,3,4 \end{split}$

(60)

假定应变可以表示为：

${{\bar{ \varepsilon }}_{\rm m}} = {{\varepsilon }}_{\rm m}^O + {{\varepsilon }}_{\rm m}^H = {{B}}_{{\rm m}i}^O{{{t}}_i} + {{B}}_{{\rm m}i}^H\left\{ \begin{array}{l} \;\;\; {{{t}}_i} \\ {{{\theta }}_i} - {{{\theta }}_{i0}} \end{array} \right\}\qquad$

(61)

${\bar{\\text{χ}}} = {{\\text{χ}}^O} + {{\\text{χ}}^H} = {{B}}_{{\rm b}i}^O\left\{ {\begin{array}{*{20}{c}} {{{{t}}_i}} \\ {{{{\theta }}_i} - {{{\theta }}_{i0}}} \end{array}} \right\} + {{B}}_{{\rm b}i}^H({{{\theta }}_i} - {{{\theta }}_{i0}})$

(62)

$\begin{split} {\bar{ \gamma }} = &{{{\gamma }}^O} + {{{\gamma }}^H} = {\rm{(}}{{B}}{_{{\rm s}i}^{\eta O}} + {{B}}{_{{\rm s}i}^{\xi O}})\left\{ {\begin{array}{*{20}{c}} {{{{t}}_i}} \\ {{{{\theta }}_i} - {{{\theta }}_{i0}}} \end{array}} \right\} + \\ & {\rm{(}}{{B}}{_{{\rm s}i}^{\eta H}} + {{B}}{_{{\rm s}i}^{\xi H}})\left\{ {\begin{array}{*{20}{c}} {{{{t}}_i}} \\ {{{{\theta }}_i} - {{{\theta }}_{i0}}} \end{array}} \right\} \end{split}$

(63)

考虑如下正交条件：

$\begin{split}&\int_{V} {{{({{B}}_{\rm m}^O)}^{\rm{T}}}{{{D}}_{\rm{1}}}{{B}}_{\rm m}^H{{\rm d}V}} = {{0}}, \;\;\int_{V} {{{({{B}}_{\rm b}^O)}^{\rm{T}}}{{{D}}_{\rm{1}}}{{B}}_{\rm b}^H{{\rm d}V}} = {{0}},\\ &\int_{V} {{{{\rm{(}}{{B}}{{_{\rm s}^{\eta H}}})}^{\rm{T}}}{{{D}}_{\rm{2}}}{{B}}{{_{\rm s}^{\xi H}}{\rm d}V}} = {{0}}\qquad\qquad\qquad\qquad\qquad\;\;\;{{ (64) }} \end{split}$

得到切线刚度矩阵：

${{{k}}_{\rm{T}}} = {{{k}}_{\rm{1}}} + {{{k}}_{{\rm{stab}}}}$

(65)

采用单点积分计算得到的单元切线刚度：

$\begin{split} {{{k}}_{\rm{1}}} =& \int_V {[{{({{B}}_{\rm m}^O)}^{\rm{T}}}{{{D}}_{\rm{1}}}{{B}}_{\rm m}^O + {\textit{z}}_{\rm l}^2{{({{B}}_{\rm b}^O)}^{\rm{T}}}{{{D}}_{\rm{1}}}{{B}}_{\rm b}^O} + \\ & {{\rm{(}}{{B}}{_{\rm s}^{\eta O}} + {{B}}{_{\rm s}^{\xi O}})^{\rm{T}}}{{{D}}_{\rm{2}}}{\rm{(}}{{B}}{_{\rm s}^{\eta O}} + {{B}}{_{\rm s}^{\xi O}})]{{\rm d}V} \end{split}$

(66)

引入稳定化的刚度：

$\begin{split} {{{k}}_{{\rm{stab}}}} = &\int_{V} {{{({{B}}_{\rm m}^H)}^{\rm{T}}}{{{D}}_{\rm{1}}}{{B}}_{\rm m}^H{{\rm d}V}} + \int_{V} {{\textit{z}}_{\rm l}^2{{({{B}}_{\rm b}^H)}^{\rm{T}}}{{{D}}_{\rm{1}}}{{B}}_{\rm b}^H} {{\rm d}V} {\rm{ + }}\\[-2pt] & \int_{V} {{{{\rm{(}}{{B}}{{_{\rm s}^{\eta H}}})}^{\rm{T}}}{{{D}}_{\rm{2}}}{{B}}{{_{\rm s}^{\eta H}}}{\rm{dV}}} {\rm{ + }}\int_{V} {{{{\rm{(}}{{B}}{{_{\rm s}^{\xi H}}})}^{\rm{T}}}{{{D}}_{\rm{2}}}{{B}}{{_{\rm s}^{\xi H}}}{{\rm d}V}} + \\[-2pt] & {\rm{ 2}}\int_{V} {{{{\rm{(}}{{B}}{{_{\rm s}^{\eta O}}} + {{B}}{{_{\rm s}^{\xi O}}})}^{\rm{T}}}{{{D}}_{\rm{2}}}{\rm{(}}{{B}}{{_{\rm s}^{\eta H}}} + {{B}}{{_{\rm s}^{\xi H}}}){{\rm d}V}} \qquad\;\;\;\;{{ (67) }} \end{split}$

对 ${{{k}}_{{\rm{stab}}}}$ 计算式的最后一项做如下近似：

$\int_{V} {{{{\rm{(}}{{B}}{{_{\rm s}^{\eta O}}} + {{B}}{{_{\rm s}^{\xi O}}})}^{\rm{T}}}{{{D}}_{\rm{2}}}{\rm{(}}{{B}}{{_{\rm s}^{\eta H}}} + {{B}}{{_{\rm s}^{\xi H}}}){{\rm d}V}} \cong 0$

(68)

易发现只需计算以下3个简单的积分公式即可：

$\begin{split} {H_{xx}} = & \int_{V} {{h_{,x}}{h_{,x}}{{\rm d}V}} {\rm{ = }}\frac{a}{{3A}}[{({\eta _i}{y_{i0}})^2} + {({\xi _i}{y_{i0}})^2}],\\[-2pt] {H_{yy}} =& \int_{V} {{h_{,y}}{h_{,y}}{{\rm d}V}} {\rm{= }} \frac{a}{{3A}}[{({\xi _i}{x_{i0}})^2} + {({\eta _i}{x_{i0}})^2}],\\[-2pt] {H_{xy}} =& \int_{V} {{h_{,x}}{h_{,y}}{{\rm d}V}} {\rm{ = }} \\[-2pt]& - \frac{a}{{3A}}[({\xi _i}{x_{i0}})({\xi _j}{y_{j0}}) + ({\eta _i}{x_{i0}})({\eta _j}{y_{j0}})] \end{split}$

(69)

单点积分下经过稳定化处理的单元内力矢量：

${{f}} = {{{f}}_{\rm ext}} = {{{f}}_{\rm 1pq}} + {{{f}}_{\rm stab}}$

(70)

采用单点积分计算得到的内力矢量：

$\begin{split} {{{f}}_{\rm 1pq}} =& \int_{V} {[{{({{B}}_{\rm m}^O)}^{\rm{T}}}{{{D}}_{\rm{1}}}{{\varepsilon }}_{\rm m}^O + {\textit{z}}_{\rm l}^2{{({{B}}_{\rm b}^O)}^{\rm{T}}}{{{D}}_{\rm{1}}}{{\\text{χ}}^O}} +\\ & {{\rm{(}}{{B}}{_{\rm s}^{\eta O}} + {{B}}{_{\rm s}^{\xi O}})^{\rm{T}}}{{{D}}_{\rm{2}}}{{{\gamma }}^O}]{{\rm d}V} \end{split}$

(71)

引入稳定化的内力矢量：

$\begin{split} {{f}}_{\rm stab}^{} =& {\left\langle {\begin{array}{*{20}{l}} {{{\left\{ {{{f}}_1^H} \right\}}^{\rm{T}}}}&{{{\left\{ {{{f}}_2^H} \right\}}^{\rm{T}}}}&{{{\left\{ {{{f}}_3^H} \right\}}^{\rm{T}}}}&{{{\left\{ {{{f}}_4^H} \right\}}^{\rm{T}}}} \end{array}} \right\rangle ^{\rm{T}}} = \\[-2pt] & \int_{V} {{{({{B}}_{\rm m}^H)}^{\rm{T}}}{{{D}}_1}{{\varepsilon }}_{\rm m}^H{{\rm d}V}} + \int_{V} {{\textit{z}}_{\rm l}^2{{({{B}}_{\rm b}^H)}^{\rm{T}}}{{{D}}_1}{{\\text{χ}}^H}{{\rm d}V}} + \\[-2pt] & \int_{V} {{{({{B}}{{_{\rm s}^{\eta H}}} + {{B}}{{_{\rm s}^{\xi H}}})}^{\rm{T}}}{{{D}}_2}{{{\gamma }}^H}{{\rm d}V}} \quad\quad\quad\qquad\qquad\;\;{{ (72) }} \end{split}$

式中：

${\left\{ {{{f}}_i^H} \right\}^{\rm{T}}}{\rm{ = }}\left\langle { {f_{{\rm u}i}^H}\;\;{f_{{\rm v}i}^H}\;\;{f_{{\rm w}i}^H}\;\;{f_{{r_{x}}i}^H}\;\;{f_{{r_{y}}i}^H} } \right\rangle$

(73)

对广义膜应变 $\varepsilon _{x}^{\rm m}$ 、 $\varepsilon _{y}^{\rm m}$ ，广义弯曲应变 ${\chi _{x}}$ 、 ${\chi _{y}}$ 和广义剪切应变 ${\gamma _\xi }$ 、 ${\gamma _\eta }$ 进行稳定化处理。

膜项：

$\varepsilon _{x}^{\rm m} = {\kappa _i}{u_i} - \frac{1}{4}{{\textit{z}}_{\kappa} }{s_i}({r_{ix}} - {r_{ix0}})\quad\quad\quad\quad$

(74)

$\varepsilon _{y}^{\rm m} = {\kappa _i}{v_i} - \frac{1}{4}{{\textit{z}}_{\kappa} }{s_i}({r_{iy}} - {r_{iy0}})\quad\quad\quad\quad$

(75)

${{\varepsilon }}_{\rm m}^H = {{B}}_{\rm m}^H{{u}}_{\rm L}^{} = \left[ {\begin{array}{*{20}{c}} {{h_{,x}}\varepsilon _{x}^{\rm m}} \\ {{h_{,y}}\varepsilon _{y}^{\rm m}} \\ {{h_{,y}}\varepsilon _{x}^{\rm m} + {h_{,x}}\varepsilon _{y}^{\rm m}} \end{array}} \right]\quad\quad\;\;$

(76)

${{\sigma }}_{\rm m}^H = {{{D}}_1}{{\varepsilon }}_{\rm m}^H = \left[ {\begin{array}{*{20}{c}} {{C_1}{h_{,x}}\varepsilon _{x}^{\rm m} + {C_2}{h_{,y}}\varepsilon _{y}^{\rm m}} \\ {{C_2}{h_{,x}}\varepsilon _{x}^{\rm m} + {C_1}{h_{,y}}\varepsilon _{y}^{\rm m}} \\ {{C_3}({h_{,y}}\varepsilon _x^m + {h_{,x}}\varepsilon _{y}^{\rm m})} \end{array}} \right]$

(77)

式中：

${C_1}{\rm{ = }}\frac{E}{{1 - {\mu ^2}}}, \;\;{C_2}{\rm{ = }}\frac{{\mu E}}{{1 - {\mu ^2}}}, \;\;{C_3}{\rm{ = }}\frac{E}{{2(1 + \mu )}}$

(78)

$\begin{split} {{f}}_{\rm m}^H =& \int_{V} {{{({{B}}_{\rm m}^H)}^{\rm{T}}}{{\sigma }}_{\rm m}^H{{\rm d}V}} {\rm{ = }}\\ & {\left\langle { {{{\left\{ {{{f}}_{\rm m1}^H} \right\}}^{\rm{T}}}}\;\;{{{\left\{ {{{f}}_{\rm m2}^H} \right\}}^{\rm{T}}}}\;\;{{{\left\{ {{{f}}_{\rm m3}^H} \right\}}^{\rm{T}}}}\;\;{{{\left\{ {{{f}}_{\rm m4}^H} \right\}}^{\rm{T}}}} } \right\rangle ^{\rm{T}}} \end{split} \quad\quad$

(79)

式中：

${{f}}_{{\rm m}i}^H{\rm{ = }}\left[ \!\!\!\!{\begin{array}{*{20}{c}} {[{C_1}{H_{xx}}\varepsilon _{x}^{\rm m} + {C_2}{H_{xy}}\varepsilon _{y}^{\rm m} + {C_3}({H_{yy}}\varepsilon _{x}^{\rm m} + {H_{xy}}\varepsilon _{y}^{\rm m})]{\kappa _i}} \\ {[{C_2}{H_{xy}}\varepsilon _{x}^{\rm m} + {C_1}{H_{yy}}\varepsilon _{y}^{\rm m} + {C_3}({H_{xy}}\varepsilon _{x}^{\rm m} + {H_{xx}}\varepsilon _{y}^{\rm m})]{\kappa _i}} \\ 0 \\ { \!- \dfrac{1}{4}{{\textit{z}}_{\kappa} }[\!{C_1}{H_{xx}}\varepsilon _{x}^{\rm m} \!\!+\! \!{C_2}{H_{xy}}\varepsilon _{y}^{\rm m}\!\! +\!\! {C_3}({H_{yy}}\varepsilon _{x}^{\rm m} \!\!+\!\! {H_{xy}}\varepsilon _{y}^{\rm m})\!]{s_i}} \\ { \!- \dfrac{1}{4}{{\textit{z}}_{\kappa} }[\!{C_2}{H_{xy}}\varepsilon _{x}^{\rm m}\!\! +\! \!{C_1}{H_{yy}}\varepsilon _{y}^{\rm m} \!\!+\! \!{C_3}({H_{xy}}\varepsilon _{x}^{\rm m} \!\!+\!\! {H_{xx}}\varepsilon _{y}^{\rm m})\!]{s_i}} \end{array}} \!\!\!\!\!\right]$

(80)

弯曲项：

${\chi _{x}} = {\kappa _i}({r_{ix}} - {r_{ix0}})\quad\qquad\qquad\qquad\qquad\;\;$

(81)

${\chi _{y}} = {\kappa _i}({r_{iy}} - {r_{iy0}})\qquad\qquad\qquad\quad\qquad\;\;$

(82)

$\begin{split} {{\sigma }}_{\rm b}^H{\rm{ = }}&{{{D}}_1}{{\\text{χ}}^H}{\rm{ = }}{{{D}}_1}\left[ {\begin{array}{*{20}{c}} {{h_{,x}}{\chi _{y}}} \\ {{h_{,y}}{\chi _{x}}} \\ {{h_{,y}}{\chi _{y}} + {h_{,x}}{\chi _{x}}} \end{array}} \right]{\rm{ = }}\\&\left[ {\begin{array}{*{20}{c}} {{C_1}{h_{,x}}{\chi _{y}} + {C_2}{h_{,y}}{\chi _{x}}} \\ {{C_2}{h_{,x}}{\chi _{y}} + {C_1}{h_{,y}}{\chi _{x}}} \\ {{C_3}({h_{,y}}{\chi _{y}} + {h_{,x}}{\chi _{x}})} \end{array}} \right]\end{split} \quad\;\;\;\;$

(83)

$\begin{split} \;\;\;\;\;\;\; {{f}}_{\rm b}^H = &\int_{V} {{\textit{z}}_{\rm l}^2{{({{B}}_{\rm b}^H)}^{\rm{T}}}{{\sigma }}_{\rm b}^H{{\rm d}V}} {\rm{ = }} \\ & {\left\langle {\begin{array}{*{20}{l}} {{{\left\{ {{{f}}_{\rm b1}^H} \right\}}^{\rm{T}}}}&{{{\left\{ {{{f}}_{\rm b2}^H} \right\}}^{\rm{T}}}}&{{{\left\{ {{{f}}_{\rm b3}^H} \right\}}^{\rm{T}}}}&{{{\left\{ {{{f}}_{\rm b4}^H} \right\}}^{\rm{T}}}} \end{array}} \right\rangle ^{\rm{T}}} \end{split}$

(84)

式中：

$\begin{split}&{{f}}_{{\rm b}i}^H = \\&\left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \\ {\dfrac{1}{{12}}{a^2}{\kappa _i}[{C_1}{H_{xx}}{\chi _{y}} + {C_2}{H_{xy}}{\chi _{x}} + {C_3}({H_{yy}}{\chi _{y}} + {H_{xy}}{\chi _{x}})]} \\ {\dfrac{1}{{12}}{a^2}{\kappa _i}[{C_2}{H_{xy}}{\chi _{y}} + {C_1}{H_{yy}}{\chi _{x}} + {C_3}({H_{xy}}{\chi _{y}} + {H_{xx}}{\chi _{x}})]} \end{array}} \right]\end{split}$

(85)

剪切项：

$\begin{split} {\gamma _\eta } = & 4{h_i}{w_i} + ({\xi _j}{x_{j0}}{\eta _i} + {h_j}{x_{j0}}{s_i})({r_{ix}} - {r_{ix0}})+ \\ & ({\xi _j}{y_{j0}}{\eta _i} + {h_j}{y_{j0}}{s_i})({r_{iy}} - {r_{iy0}}) \end{split} \quad\;\;$

(86)

$\begin{split} {\gamma _\xi } =& 4{h_i}{w_i} + ({\eta _j}{x_{j0}}{\xi _i} + {h_j}{x_{j0}}{s_i})({r_{ix}} - {r_{ix0}}) + \\ &({\eta _j}{y_{j0}}{\xi _i} + {h_j}{y_{j0}}{s_i})({r_{iy}} - {r_{iy0}}) \end{split} \quad\;\;$

(87)

${{\sigma }}_{\rm s}^H = {{{D}}_2}{{{\gamma }}^H} = \frac{1}{{16A}}{C_4}\left[ {\begin{array}{*{20}{c}} {\eta {\eta _i}{y_{i0}}{\gamma _\eta } - \xi {\xi _i}{y_{i0}}{\gamma _\xi }} \\ { - \eta {\eta _i}{x_{i0}}{\gamma _\eta } + \xi {\xi _i}{x_{i0}}{\gamma _\xi }} \end{array}} \right]$

(88)

$\begin{split} {{f}}_{\rm s}^H = &\int_{V} {{{({{B}}{_{\rm s}^{\eta H}} + {{B}}{_{\rm s}^{\xi H}})}^{\rm{T}}}{{\sigma }}_{\rm s}^H{{\rm d}V}} {\rm{ = }} \\ & {\left\langle { {{{\left\{ {{{f}}_{\rm s1}^H} \right\}}^{\rm{T}}}}\;\;{{{\left\{ {{{f}}_{\rm s2}^H} \right\}}^{\rm{T}}}}\;\;{{{\left\{ {{{f}}_{\rm s3}^H} \right\}}^{\rm{T}}}}\;\;{{{\left\{ {{{f}}_{\rm s4}^H} \right\}}^{\rm{T}}}} } \right\rangle ^{\rm{T}}} \end{split}\quad\quad\quad\quad\;\;$

(89)

式中：

$\begin{split}&{{f}}_{{\rm s}i}^H =\\& \left[ \!\!{\begin{array}{*{20}{c}} 0 \\ 0 \\ {\dfrac{4}{3}{h_i}({C_5}{\gamma _\eta } \!+\! {C_6}{\gamma _\xi })} \\ {\dfrac{1}{3}{C_5}({\xi _j}{x_j}_0{\eta _i} \!+\! {h_j}{x_{j0}}{s_i}){\gamma _\eta }\! +\! \dfrac{1}{3}{C_6}({\eta _j}{x_j}_0{\xi _i} \!+ \!{h_j}{x_{j0}}{s_i}){\gamma _\xi }} \\ {\dfrac{1}{3}{C_5}({\xi _j}{y_j}_0{\eta _i} \!+ \!{h_j}{y_{j0}}{s_i}){\gamma _\eta }\! +\! \dfrac{1}{3}{C_6}({\eta _j}{y_j}_0{\xi _i} \!+\! {h_j}{y_{j0}}{s_i}){\gamma _\xi }} \end{array}} \!\!\right]\end{split}$

(90)

${C_4}{\rm{ = }}\frac{{5E}}{{12\left( {1 + \mu } \right)}}\;\;\qquad\quad\quad\quad\quad\quad\quad\quad\qquad\qquad$

(91)

${C_5} = \frac{a}{{256A}}{C_4}[{({\eta _i}{y_{i0}})^2} + {({\eta _i}{x_{i0}})^2}]\qquad\qquad\qquad$

(92)

${C_6} = \frac{a}{{256A}}{C_4}[{({\xi _i}{y_{i0}})^2} + {({\xi _i}{x_{i0}})^2}]\qquad\qquad\qquad$

(93)

将 ${{f}}_{{\rm m}i}^H$ 、 ${{f}}_{{\rm b}i}^H$ 和 ${{f}}_{{\rm s}i}^H$ 的计算式代入下式：

${{f}}_i^H = {{f}}_{{\rm m}i}^H + {{f}}_{{\rm b}i}^H + {{f}}_{{\rm s}i}^H$

(94)

得到内力矢量中各分量的值为：

$f_{{{\rm u}i}}^H = [{C_1}{H_{xx}}\varepsilon _{x}^{\rm m} + {C_2}{H_{xy}}\varepsilon _{y}^{\rm m} + {C_3}({H_{yy}}\varepsilon _{x}^{\rm m} + {H_{xy}}\varepsilon _{y}^{\rm m})]{\kappa _i},$

$f_{{\rm v}i}^H = [{C_2}{H_{xy}}\varepsilon _{x}^{\rm m} + {C_1}{H_{yy}}\varepsilon _{y}^{\rm m} + {C_3}({H_{xy}}\varepsilon _{x}^{\rm m} + {H_{xx}}\varepsilon _{y}^{\rm m})]{\kappa _i},$

$f_{{\rm w}i}^H = \frac{4}{3}{h_i}({C_5}{\gamma _\eta } + {C_6}{\gamma _\xi }),\qquad\qquad\qquad\qquad\quad\qquad\;\;$

$\begin{split} f_{{r_{x}}i}^H = & - \frac{1}{4}{{\textit{z}}_{\kappa} }[{C_1}{H_{xx}}\varepsilon _{x}^{\rm m} + {C_2}{H_{xy}}\varepsilon _{y}^{\rm m} + \\& {C_3}({H_{yy}}\varepsilon _{x}^{\rm m} + {H_{xy}}\varepsilon _{y}^{\rm m})]{s_i} +\\& \frac{1}{{12}}{a^2}{\kappa _i}[{C_1}{H_{xx}}{\chi _{y}} + {C_2}{H_{xy}}{\chi _{x}} +\\& {C_3}({H_{yy}}{\chi _{y}} + {H_{xy}}{\chi _{x}})] + \\ & \frac{1}{3}{C_5}({\xi _j}{x_j}_0{\eta _i} + {h_j}{x_{j0}}{s_i}){\gamma _\eta } + \\& \frac{1}{3}{C_6}({\eta _j}{x_j}_0{\xi _i} + {h_j}{x_{j0}}{s_i}){\gamma _\xi } , \end{split}$

$\begin{split} f_{{r_{y}}i}^H = & - \frac{1}{4}{{\textit{z}}_{\kappa} }[{C_2}{H_{xy}}\varepsilon _{x}^{\rm m} + {C_1}{H_{yy}}\varepsilon _{y}^{\rm m} + \\ &{C_3}({H_{xy}}\varepsilon _{x}^{\rm m} + {H_{xx}}\varepsilon _{y}^{\rm m})]{s_i} + \\ & \frac{1}{{12}}{a^2}{\kappa _i}[{C_2}{H_{xy}}{\chi _{y}} + {C_1}{H_{yy}}{\chi _{x}} + \\ &{C_3}({H_{xy}}{\chi _{y}} + {H_{xx}}{\chi _{x}})] + \\ & \frac{1}{3}{C_5}({\xi _j}{y_j}_0{\eta _i} + {h_j}{y_{j0}}{s_i}){\gamma _\eta } + \\ &\frac{1}{3}{C_6}({\eta _j}{y_j}_0{\xi _i} + {h_j}{y_{j0}}{s_i}){\gamma _\xi } \end{split}$

(95)

4 整体坐标系下的单元公式

整体坐标系下的单元内力矢量可从局部坐标系下的单元内力矢量计算得到：

${{{f}}_{\rm g}} = {{{T}}^{\rm{T}}}{{f}}$

(96)

其中，T是通过计算局部坐标系下的节点变量对整体坐标系下的节点变量的1阶偏微分得到：

$\begin{split} {{T}} =& \dfrac{{\partial {{{u}}_{\rm L}}}}{{\partial {{u}}_{\rm G}^{\rm{T}}}} = \left[ {\dfrac{{\partial {u_{{\rm L}i}}}}{{\partial {u_{{\rm G}i}}}}} \right] = \\ & \left[ {\begin{array}{*{20}{c}} {\dfrac{{\partial {{{t}}_1}}}{{\partial {{d}}_1^{\rm{T}}}}}&0& \cdots &{\dfrac{{\partial {{{t}}_1}}}{{\partial {{d}}_4^{\rm{T}}}}}&0 \\ {\dfrac{{\partial {{{\theta }}_1}}}{{\partial {{d}}_1^{\rm{T}}}}}&{\dfrac{{\partial {{{\theta }}_1}}}{{\partial {{n}}_{\rm g1}^{\rm{T}}}}}& \cdots &{\dfrac{{\partial {{{\theta }}_1}}}{{\partial {{d}}_4^{\rm{T}}}}}&{\dfrac{{\partial {{{\theta }}_1}}}{{\partial {{n}}_{\rm g4}^{\rm{T}}}}} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ {\dfrac{{\partial {{{t}}_4}}}{{\partial {{d}}_1^{\rm{T}}}}}&0& \cdots &{\dfrac{{\partial {{{t}}_4}}}{{\partial {{d}}_4^{\rm{T}}}}}&0 \\ {\dfrac{{\partial {{{\theta }}_4}}}{{\partial {{d}}_1^{\rm{T}}}}}&{\dfrac{{\partial {{{\theta }}_4}}}{{\partial {{n}}_{\rm g1}^{\rm{T}}}}}& \cdots &{\dfrac{{\partial {{{\theta }}_4}}}{{\partial {{d}}_4^{\rm{T}}}}}&{\dfrac{{\partial {{{\theta }}_4}}}{{\partial {{n}}_{\rm g4}^{\rm{T}}}}} \end{array}} \right] \end{split}$

(97)

整体坐标系下的单元切线刚度矩阵 ${{{k}}_{\rm TG}}$ 按下式计算：

$\begin{split} {{k}}_{\rm TG} = &\frac{{\partial {{{f}}_{\rm g}}}}{{\partial {{u}}_{\rm G}^{\rm{T}}}} = {{{T}}^{\rm{T}}}\frac{{\partial {{f}}}}{{\partial {{u}}_{\rm G}^{\rm{T}}}} + \frac{{\partial {{{T}}^{\rm{T}}}}}{{\partial {{u}}_{\rm G}^{\rm{T}}}}{{f}} = \\ & {{{T}}^{\rm{T}}}\frac{{\partial {{f}}}}{{\partial {{u}}_{\rm L}^{\rm{T}}}}{{T}} + \frac{{\partial {{{T}}^{\rm{T}}}}}{{\partial {{u}}_{\rm G}^{\rm{T}}}}{{f}} = {{{T}}^{\rm{T}}}{{{k}}_{\rm{T}}}{{T}} + \frac{{\partial {{{T}}^{\rm{T}}}}}{{\partial {{u}}_{\rm G}^{\rm{T}}}}{{f}} \end{split}$

(98)

5 算例分析

将引入物理稳定化零能模态控制法的4节点四边形壳单元简记为PO4Q。

5.1 径向受拉的开口圆柱壳

如图3所示的开口圆柱壳，两端自由，几何尺寸为：长度 ${L = }10.35\;{\rm{m}}$ ，半径 ${R {\rm =} }4.953\;{\rm{m}}$ ，厚度 ${a = }0.094\;{\rm{m}}$ ，材料的弹性模量 ${E = }10.5 \;{\rm MPa}$ ，泊松比 ${\rm{\mu = }}0.3125$ 。圆柱壳在中部受一对大小相等、方向相反的径向集中拉力 ${F = }40 \;{\rm{kN}}$ 作用。利用结构和荷载的对称性，取壳的1/8结构进行分析。

图 3 径向受拉圆柱壳

Figure 3. Pull-out of an open cylindrical shell

下载: 全尺寸图片幻灯片

计算荷载作用点的挠度时，分别采用8×16、12×24的单元网格，得到结构的荷载-位移曲线与Jiang 和 Chernuka^[30]采用8×14单元网格的4节点ANS退化壳单元以及Campello等^[31]采用8×16×2单元网格的6节点三角形曲壳单元的计算结果进行比较，如图4所示。可见，当荷载达到 $20 \;{\rm{kN}}$ 左右时，壳体出现了轻微的跳跃屈曲现象，该单元成功跟踪到了这一过程。得到的临界荷载和荷载-位移曲线与其他文献[30−31]中的结果吻合较好。

图 4 径向受拉圆柱壳在加载点处的荷载-位移曲线

Figure 4. Load-displacement curve of cylindrical shell

下载: 全尺寸图片幻灯片

5.2 悬臂梯形板

图5所示的悬臂梯形板，一端固支，另一端受到平面内均布剪切荷载。结构几何尺寸如下：长 ${L = }48\;{\rm{mm}}$ ，高 ${H_1}{\rm{ = }}16\;{\rm{mm}}$ 、 ${H_2}{\rm{ = }}44\;{\rm{mm}}$ 。材料的弹性模量 ${E = }1.0\;{\rm MPa}$ ，泊松比 ${\rm{\mu = }}{1 / 3}$ ，厚度 ${a = }1.0\;{\rm{mm}}$ 。均布荷载 ${p = }{{P} / {{{H}_1}}}$ ，其中， ${P = }\lambda {{P}_{{\rm{ref}}}}$ ， ${{P}_{{\rm{ref}}}}{= 1}\;{\rm N}$ 。

图 5 悬臂梯形板

Figure 5. A cantilever trapezoidal plate

下载: 全尺寸图片幻灯片

图6给出了分别采用8×8、16×16和32×32个PO4Q单元和ANSYS^[32]有限元软件采用8×8、16×16和32×32个shell181单元的计算结果。表1给出了荷载参数为1时采用16×16、32×32个PO4Q单元和shell181单元的计算结果。可见，PO4Q单元略微偏硬，但采用32×32个PO4Q单元与shell181单元的计算结果的相对误差仅5.40%，PO4Q单元的收敛性和计算精度基本令人满意。

图 6 悬臂板在点A处的荷载-位移曲线

Figure 6. Load-displacement curves at tip A of cantilever plate

下载: 全尺寸图片幻灯片

表 1 悬臂板在点A处的位移(λ=1)

Table 1. Displacement at tip A of cantilever plate (λ=1)

单元类型	PO4Q单元		Shell181单元
网格密度	16×16	32×32	16×16	32×32
位移/mm	15.6298	15.8219	16.6642	16.7260
误差/(%)	6.20	5.40	−	−

下载: 导出CSV

| 显示表格

5.3 直角形折板

图7所示的直角形折板，一端完全约束，另一端自由，并施加竖向均布荷载。结构几何尺寸为：长 ${L = }6\;{\rm{m}}$ ，宽 ${B = }3\;{\rm{m}}$ ，厚度 ${a = }0.03\;{\rm{m}}$ 。材料的弹性模量 ${E = }30 \;{\rm MPa}$ ，泊松比 ${\rm{\mu = }}0.0$ 。自由端受均布荷载 ${p = }{{P} / {B}}$ ，其中， ${P = }\lambda {{P}_{{\rm{ref}}}}$ ， ${{P}_{{\rm{ref}}}}{= 3}\;{\rm N}$ 。

图 7 直角形折板

Figure 7. A right-angle cantilever subjected to distributed force

下载: 全尺寸图片幻灯片

为检验单元的收敛性，分别采用3×6×2和6×12×2的PO4Q单元网格对该折板进行分析，自由端的荷载-位移曲线在图8中给出。作为对比，还给出了采用ANSYS^[32]软件中的shell181、shell281以及Li等^[33]采用QUAD9单元的计算结果。可见，采用PO4Q单元网格得到的结果与ANSYS^[32]和Li等^[33]的计算结果吻合较好。

图 8 直角形折板在自由端处的荷载-位移曲线

Figure 8. Load-displacement curves of right-angle cantilever

下载: 全尺寸图片幻灯片

5.4 镰刀形壳

如图9所示的镰刀形壳，结构左端固支，在右侧自由端的中点A处作用一平面内集中荷载。结构的几何尺寸为： ${L = }10\;{\rm{m}}$ ， ${R = 5}\;{\rm{m}}$ ，宽 ${B = 1}\;{\rm{m}}$ ，厚度 ${a = 0}{\rm{.01}}\;{\rm{m}}$ 。材料的弹性模量 ${E = }30\;{\rm MPa}$ ，泊松比 ${\rm{\mu = }}0.3$ 。自由端作用的集中荷载值为： ${P = } \lambda {{P}_{{\rm{ref}}}}$ ， ${{P}_{{\rm{ref}}}}{\rm{ = 0.01}}\;{\rm N}$ 。

图 9 镰刀形壳

Figure 9. A cantilever sickle shell subjected to a lateral tip force

下载: 全尺寸图片幻灯片

分别采用(15+15)×3和(20+20)×4的单元网格计算该镰刀形壳自由边中点的位移。其结果和Chróścielewski等^[34]采用基于合应力的半混合壳单元SEMe9、基于位移-转动的壳单元CAMe9以及标准退化壳单元SELe9得到的结果吻合较好(见图10)。

图 10 自由边中点的荷载-位移曲线

Figure 10. Load-displacement curves of cantilever sickle shell

下载: 全尺寸图片幻灯片

该镰刀形壳在不同荷载作用下的变形如图11所示。

图 11 不同荷载作用下镰刀形壳变形图

Figure 11. Deformed shape of cantilever sickle shell under different levels of tip force

下载: 全尺寸图片幻灯片

6 结论

本文发展了一种适用于解决光滑和非光滑板壳大位移和大转角弹性变形问题的新型协同转动4节点四边形壳单元。单元中采用矢量型转动变量描述旋转，采用单点积分法消除闭锁现象，引入物理稳定化方法消除单点积分引起的零能模态。通过对2个光滑壳和2个非光滑壳的非线性分析，并将结果与参考文献中的单元或ANSYS软件中的单元的计算结果进行对比，表明该单元已有效地减轻了闭锁现象，并消除了零能模态的不利影响，单元的可靠性、计算效率与计算精度是令人满意的。

图 1 协同转动框架

Figure 1. Description of the co-rotational framework

下载: 全尺寸图片幻灯片

图 2 剪切应变插值关联点分布图

Figure 2. Interpolation points for shear strain

下载: 全尺寸图片幻灯片

图 3 径向受拉圆柱壳

Figure 3. Pull-out of an open cylindrical shell

下载: 全尺寸图片幻灯片

图 4 径向受拉圆柱壳在加载点处的荷载-位移曲线

Figure 4. Load-displacement curve of cylindrical shell

下载: 全尺寸图片幻灯片

图 5 悬臂梯形板

Figure 5. A cantilever trapezoidal plate

下载: 全尺寸图片幻灯片

图 6 悬臂板在点A处的荷载-位移曲线

Figure 6. Load-displacement curves at tip A of cantilever plate

下载: 全尺寸图片幻灯片

图 7 直角形折板

Figure 7. A right-angle cantilever subjected to distributed force

下载: 全尺寸图片幻灯片

图 8 直角形折板在自由端处的荷载-位移曲线

Figure 8. Load-displacement curves of right-angle cantilever

下载: 全尺寸图片幻灯片

图 9 镰刀形壳

Figure 9. A cantilever sickle shell subjected to a lateral tip force

下载: 全尺寸图片幻灯片

图 10 自由边中点的荷载-位移曲线

Figure 10. Load-displacement curves of cantilever sickle shell

下载: 全尺寸图片幻灯片

图 11 不同荷载作用下镰刀形壳变形图

Figure 11. Deformed shape of cantilever sickle shell under different levels of tip force

下载: 全尺寸图片幻灯片

表 1 悬臂板在点A处的位移(λ=1)

Table 1 Displacement at tip A of cantilever plate (λ=1)

单元类型 PO4Q单元 Shell181单元

网格密度 16×16 32×32 16×16 32×32
位移/mm 15.6298 15.8219 16.6642 16.7260
误差/(%) 6.20 5.40 − −

下载: 导出CSV

参考文献(34)

[1]	邓继华, 邵旭东. 四边形八节点共旋法平面单元的几何非线性分析[J]. 工程力学, 2011, 28(7): 6 − 12. Deng Jihua, Shao Xudong. Geometrically nonlinear analysis using a quadrilateral 8-node co-rotational plane element [J]. Engineering Mechanics, 2011, 28(7): 6 − 12. (in Chinese)
[2]	邓继华, 邵旭东. 基于共旋坐标法的带刚臂平面梁元非线性分析[J]. 工程力学, 2012, 29(11): 143 − 151. doi: 10.6052/j.issn.1000-4750.2011.03.0123 Deng Jihua, Shao Xudong. Co-rotational formulation for nonlinear analysis of plane beam element with rigid arms [J]. Engineering Mechanics, 2012, 29(11): 143 − 151. (in Chinese) doi: 10.6052/j.issn.1000-4750.2011.03.0123
[3]	Izzuddin B A. An enhanced co-rotational approach for large displacement analysis of plates [J]. International Journal for Numerical Methods in Engineering, 2005, 64(10): 1350 − 1374. doi: 10.1002/nme.1415
[4]	Li Z X, Zheng T. A 4-node co-rotational quadrilateral composite shell element [J]. International Journal of Structural Stability and Dynamics, 2016, 16(9): 1550053. doi: 10.1142/S0219455415500534
[5]	岑松, 尚闫, 周培蕾, 等. 形状自由的高性能有限元方法研究的一些进展[J]. 工程力学, 2017, 34(3): 1 − 13. doi: 10.6052/j.issn.1000-4750.2016.10.0763 Cen Song, Shang Yan, Zhou Peilei, et al. Advances in shape-free finite element methods: a review [J]. Engineering Mechanics, 2017, 34(3): 1 − 13. (in Chinese) doi: 10.6052/j.issn.1000-4750.2016.10.0763
[6]	夏阳, 廖科. 复杂三维曲梁结构的无闭锁等几何分析算法研究[J]. 工程力学, 2018, 35(11): 17 − 25. doi: 10.6052/j.issn.1000-4750.2017.08.0602 Xia Yang, Liao Ke. Locking-free isogeometric analysis of complex three-dimensional beam structures [J]. Engineering Mechanics, 2018, 35(11): 17 − 25. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.08.0602
[7]	陈晓明, 李云贵. 用广义协调方法推导的平面四节点等参单元[J]. 工程力学, 2018, 35(12): 1 − 6. Chen Xiaoming, Li Yungui. A 4-node isoparametric element formulated with generalized conforming conditions [J]. Engineering Mechanics, 2018, 35(12): 1 − 6. (in Chinese)
[8]	龙驭球, 龙志飞, 岑松. 新型有限元论 [M]. 北京: 清华大学出版社, 2004. Long Yuqiu, Long Zhifei, Cen Song. New developments in finite element method [M]. Beijing: Tsinghua University Press, 2004. (in Chinese)
[9]	李忠学. 梁板壳有限单元中的各种闭锁现象及解决方法[J]. 浙江大学学报, 2007, 41(7): 1119 − 1125. Li Zhongxue. Strategies for overcoming locking phenomena in beam and shell finite element formulations [J]. Journal of Zhejiang University (Engineering Science), 2007, 41(7): 1119 − 1125. (in Chinese)
[10]	Li Z X. A co-rotational formulation for 3D beam element using vectorial rotational variables [J]. Computational Mechanics, 2007, 39(3): 309 − 322.
[11]	向宇, 李忠学, 张传杰. 新型协同转动3节点三边形壳单元[J]. 工程力学, 2015, 32(6): 15 − 21. Xiang Yu, Li Zhongxue. Advanced 3-node co-rotational triangular shell element [J]. Engineering Mechanics, 2015, 32(6): 15 − 21. (in Chinese)
[12]	张传杰, 李忠学. 新型协同转动六节点三边形复合材料壳单元[J]. 工程力学, 2015, 32(5): 94 − 101. Zhang Chuanjie, Li Zhongxue. A new 6-node co-rotational triangular composite shell element [J]. Engineering Mechanics, 2015, 32(5): 94 − 101. (in Chinese)
[13]	岑松, 龙志飞. 一种新型厚薄板通用三角形广义协调元[J]. 工程力学, 1998, 15(1): 10 − 22. Cen Song, Long Zhifei. A new triangular generalized conforming element for thin-thick plates [J]. Engineering Mechanics, 1998, 15(1): 10 − 22. (in Chinese)
[14]	Ko Y, Lee P S, Bathe. A new MITC4+ shell element [J]. Computers & Structures, 2017, 182(1): 404 − 418.
[15]	Zienkiewicz O C, Taylor R L. Reduced integration technique in general analysis of plates and shells [J]. International Journal for Numerical Methods in Engineering, 1971, 3(2): 275 − 290. doi: 10.1002/nme.1620030211
[16]	Kosloff D, Frazier. Treatment of hourglass patterns in low order finite element codes [J]. Numerical and Analytical Methods in Geomechanics, 1978, 2(1): 52 − 72.
[17]	Worsak, Kanok-nukulchai. A simple and efficient finite element for general shell analysis[J]. International Journal for Numerical Methods in Engineering, 1979, 14(2): 179-200.
[18]	Flanagan. A uniform strain hexahedron and quadrilateral with orthogonal hourglass control [J]. International Journal for Numerical Methods in Engineering, 1981, 17(5): 679 − 706. doi: 10.1002/nme.1620170504
[19]	Liu W K. Finite element stabilization matrices—a unification approach [J]. Computer Methods in Applied Mechanics and Engineering, 1985, 53(1): 13 − 46. doi: 10.1016/0045-7825(85)90074-X
[20]	Liu W K, Belytschko T. Use of stabilization matrices in non-linear analysis [J]. Engineering Computations, 2016, 2(1): 47 − 55.
[21]	王丽, 龙驭球, 龙志飞. 采用面积坐标方法和形函数谱方法构造四边形薄板元[J]. 工程力学, 2010, 27(8): 1 − 4. Wang Li, Long Yuqiu, Long Zhifei. Quadrilateral thin plate elements formulated by the area coordinate method and the shape function spectrum method [J]. Engineering Mechanics, 2010, 27(8): 1 − 4. (in Chinese)
[22]	Macneal R H. A simple quadrilateral shell element [J]. Computers&Structures, 1978, 8(2): 175 − 183.
[23]	Hughes T J R, Tezduyar T E. Finite Elements Based Upon Mindlin Plate Theory With Particular Reference to the Four-Node Bilinear Isoparametric Element [J]. Journal of Applied Mechanics, 1981, 48(3): 587 − 596. doi: 10.1115/1.3157679
[24]	Belytschko T, Bindeman L P. Assumed strain stabilization of the 4-node quadrilateral with 1-point quadrature for nonlinear problems [J]. Computer Methods in Applied Mechanics & Engineering, 1991, 88(3): 311 − 340.
[25]	Belytschko T, Tsay C S. A stabilization procedure for the quadrilateral plate element with one‐point quadrature [J]. International Journal for Numerical Methods in Engineering, 1983, 19(3): 405 − 419. doi: 10.1002/nme.1620190308
[26]	Belytschko T, Leviathan I. Physical stabilization of the 4-node shell element with one point quadrature [J]. Computer Methods in Applied Mechanics Engineering, 1994, 113(3/4): 321 − 350. doi: 10.1016/0045-7825(94)90052-3
[27]	李忠学, 刘永方, 徐晋. 稳定化的新型协同转动四边形曲壳单元[J]. 工程力学, 2010, 27(9): 27 − 34. Li Zhongxue, Liu Yongfang, Xu Jin. A stabilized co-rotational curved quadrilateral shell element [J]. Engineering Mechanics, 2010, 27(9): 27 − 34. (in Chinese)
[28]	Dvorkin, Bathe. A continuum mechanics based four-node shell element for general non-linear analysis [J]. Engineering Computations, 1984, 1(1): 77 − 88. doi: 10.1108/eb023562
[29]	Belytschko T, Bachrach W E. Efficient implementation of quadrilaterals with high coarse-mesh accuracy [J]. Computer Methods in Applied Mechanics Engineering, 1986, 54(3): 279 − 301. doi: 10.1016/0045-7825(86)90107-6
[30]	Jiang L, Chernuka M W. A simple four-noded corotational shell element for arbitrarily large rotations [J]. Computers Structures, 1994, 53(5): 1123 − 1132. doi: 10.1016/0045-7949(94)90159-7
[31]	Campello E M B, Pimenta P M, Wriggers P. A triangular finite shell element based on a fully nonlinear shell formulation [J]. Computational Mechanics, 2003, 31(6): 505 − 518. doi: 10.1007/s00466-003-0458-8
[32]	ANSYS Release 18.2, User's manual [M]. USA: Ansys Company, 2017.
[33]	Li Z X, Li T Z. A nine-node corotational curved quadrilateral shell element for smooth, folded and multi-shell structures [J]. International Journal for Numerical Methods in Engineering, 2018, 116(8): 570 − 600. doi: 10.1002/nme.5936
[34]	Chróścielewski J, Makowski J, Stumpf H. Finite element analysis of smooth, folded and multi-shell structures [J]. Computer Methods in Applied Mechanics Engineering, 1997, 141(1/2): 1 − 46. doi: 10.1016/S0045-7825(96)01046-8

施引文献(4)

期刊类型引用(3)

1.	邓继华，梁璐祎，谭平，周福霖. 共旋梁单元几何非线性分析的子结构方法. 土木工程学报. 2024(05): 65-75 . 百度学术
2.	邓继华，杨倩，陈历强，谭平，田仲初. 基于CR列式的平面体外预应力梁非线性有限元模型. 湖南大学学报(自然科学版). 2023(03): 62-70 . 百度学术
3.	邓继华，陈历强，田仲初，谭平. 大转动对称平面梁单元共旋列式研究. 长安大学学报(自然科学版). 2023(04): 60-67 . 百度学术

其他类型引用(1)

资源附件(0)

图(11) / 表(1)

计量

文章访问数: 555
HTML全文浏览量: 168
PDF下载量: 56
被引次数: 4

1 单元的新型协同转动法描述
2 局部坐标系下的单元公式
3 稳定化的单点积分法
4 整体坐标系下的单元公式
5 算例分析
5.1 径向受拉的开口圆柱壳
5.2 悬臂梯形板
5.3 直角形折板
5.4 镰刀形壳
6 结论

用于光滑/非光滑壳的稳定化新型协同转动4节点四边形壳单元

作者简介: 胡万波(1995−)，男，浙江宁波人，硕士生，从事有限元理论及应用研究(E-mail: huwanbo@zju.edu.cn)

通讯作者: 李忠学(1970−)，男，河南商城人，副教授，博士，从事有限元理论及应用研究(E-mail: lizx19993@zju.edu.cn)

计量

出版历程

A STABILIZED FOUR-NODE CO-ROTATIONAL QUADRILATERAL SHELL ELEMENT FOR SMOOTH AND NON-SMOOTH SHELL STRUCTURES

1 单元的新型协同转动法描述

2 局部坐标系下的单元公式

3 稳定化的单点积分法

4 整体坐标系下的单元公式

5 算例分析

5.1 径向受拉的开口圆柱壳

5.2 悬臂梯形板

5.3 直角形折板

5.4 镰刀形壳

6 结论

期刊类型引用(3)

其他类型引用(1)

计量

出版历程

目录

1 单元的新型协同转动法描述

2 局部坐标系下的单元公式

3 稳定化的单点积分法

4 整体坐标系下的单元公式

5 算例分析

5.1 径向受拉的开口圆柱壳

5.2 悬臂梯形板

5.3 直角形折板

5.4 镰刀形壳

6 结论

作者简介:
胡万波(1995−)，男，浙江宁波人，硕士生，从事有限元理论及应用研究(E-mail: huwanbo@zju.edu.cn)

通讯作者:
李忠学(1970−)，男，河南商城人，副教授，博士，从事有限元理论及应用研究(E-mail: lizx19993@zju.edu.cn)