过去30年至未来数年，是我国水电工程建设的一个重要发展时期，一批特大型高混凝土坝拟建、正在建设或已建成。这些高混凝土坝工程，除了具有规模宏大、效益显著的特点外，另一重要的共同点是它们均处于我国地震活动频繁的西南地区，一旦这些高坝大库出现溃坝灾变，后果将不堪设想。如何保证这些工程的安全已经成为坝工界研究的重大前沿课题^{[1 − 2]} 。在高混凝土坝的抗震分析中，有限元法(FEM)以其准确、高效的计算框架和易于获得的成熟商用软件，成为学者用来模拟大坝-库水-地基相互作用系统的首选方案。然而，有限元法也有其不足之处^[3] ，其主要采用低阶插值函数，单元连续性差，应力对网格的依赖性强。特别是处理无限域问题时，需要构建局部或全局人工边界条件满足无限远处的辐射阻尼条件^{[4 − 5]} 。因此，有必要寻求更为有效的其他数值计算方法。

另一方面，混凝土坝抗震分析关注的重点一直围绕着所构建的数值模型的精确性。然而，在高混凝土坝抗震分析中存在诸多不确定性，例如，结构的几何尺寸、材料自身的力学参数、荷载的随机性、人为误差等。若忽略这些因素的影响，可能会导致结构响应模拟失真，甚至引发难以估量的后果。综合考虑不确定性因素，使数值分析更符合实际工程，不确定性量化^[6] (UQ)分析成为近年来的热点方向。目前，对于随机分析问题大多基于概率论的框架，这种方法依赖于输入参数的概率描述和物理系统的数值模型的结合。对于不确定性参数的描述，通常使用随机变量或随机场。随后将其导入到模型中进行不确定传播。学者们通常采用摄动法、多项式混沌展开方法、蒙特卡罗模拟等进行不确定传播，最后得到随机输出，用来评估不确定输入对结构响应的影响。

在不确定传播过程中，蒙特卡罗模拟(MCs)^[7] 以其理论简单和操作方便被认为是解决复杂随机问题的有力工具，只需要重复抽样来获得统计特征。然而，为确保其收敛需要大量的样本^[8] ，造成了巨大的计算成本。特别是进行混凝土坝地震分析时，单点响应计算耗时严重，执行大量采样来确保MCs收敛的成本是无法负担的。因此，直接的MCs很少在实际应用中应用，只能与其他算法结合。为了提高MCs的计算效率和适用性，一些学者对传统的MCs方法做了改进。LUO等^[9] 结合了先进的机器学习技术改进了传统的MCs；JOSHUA等^[10] 在GPUs上开发了一套算法，能够进行大规模并行MCs，提高了计算效率；DING等^[11] 使用模型降阶(MOR)算法加速MCs过程，分析结构的高维不确定性。值得注意的是，MOR从本质上降低了物理问题的自由度，在处理大规模问题具有明显的优势。奇异值分解(SVD)是MOR中最著名的方法之一，也称为主成分分析或本征正交分解(POD)。SVD将全阶模型投影到低阶子空间上，得到原始系统的低阶近似。通过SVD得到的与低阶子空间相关的权系数可使用径向基函数(RBF)和Kriging插值来计算。

对于所构建的物理系统的数值模型，工程界中最早是与有限元法相结合，诞生了经典的随机有限元法(SFEM)^[12] ，它也被认为是解决随机偏微分方程的有效方法。实际上，随机有限元法是有限元法的延伸，其精度也离不开经典有限元法。比例边界有限元法(SBFEM)是由 WOLF、SONG 提出的一种半解析的数值计算方法^[13] ，最初用于解决无限域中的波传播问题。经过20多年的发展，SBFEM已应用于有限域问题^[14] 、无限域问题^{[15 − 16]} 、断裂力学^{[17 − 18]} 、波传播^{[19 − 20]}、接触问题^{[21 − 22]}、板壳结构 ^{[23 − 24]} 等领域^[25] 。此外，SBFEM在网格生成方面提供了更大的灵活性，允许构造具有任意节点、边和面数目的多边形单元。SBFEM采用的多边形、多面体单元允许单元尺寸快速过渡，非常适合基于层次树结构的网格生成算法，且不需要额外的技术处理悬挂节点问题。这种网格生成技术非常有利于大坝的建模，即在大坝的重点关注区域，采用小而密的单元尺寸，而非关键区域则采用较大的单元尺寸。该操作能够有效地减少总体的单元数目和所需的计算资源，随着多边形、多面体SBFEM的发展^{[26 − 28]} ，其在网格生成方面展现了巨大的潜力。

本工作构建一种新颖的基于随机比例边界有限元法(SSBFEM)的高混凝土坝地震响应分析不确定量化方法。首先简要介绍了多面体SBFEM的基本公式，并推导了基于SSBFEM的地震分析的MCs方法。随后在商业软件ABAQUS用户自定义单元集成八叉树网格和SSBFEM。并将随机变量引入到模型信息文件，发展SSBFEM，求得MCs所需的结构响应。接着使用SVD模型降阶法对原始系统进行降阶处理，提供原始模型的压缩表达，RBF被用于计算相关系数。通过低阶子空间的线性组合获得新的结构响应，实现基于MCs的快速高混凝土坝地震不确定量化分析。

1   多面体比例边界有限元法的蒙特卡罗模拟

图1给出了三维域中SBFEM的坐标系统。选择一个点O作为比例中心，要求域S的整个边界可视。通过引入比例系数$\eta$和$\zeta$，确定比例系数和单元局部坐标定义的转换关系，并且这种转化关系是唯一的。$\xi$是比例因子，从比例中心指向边界上任意一点。对于有限域，$0 {\leqslant} \xi {\leqslant} 1$，而对于无限域, $1 {\leqslant} \xi {\leqslant} \infty$。设定比例关系之后，可确定比例边界坐标$(\eta ,\xi ,\zeta )$与笛卡尔坐标系之间的关系：

图  1  比例边界有限元法的坐标系统

Figure  1.  Coordinate system of SBFEM

下载: 全尺寸图片 幻灯片

式中：${{\overline x}}$、${{\overline y}}$和${{\overline z}}$为笛卡尔坐标系下面单元的结点坐标向量；${\boldsymbol{N}}(\eta ,\zeta )$为形函数。在$(\eta ,\xi ,\zeta )$点处的位移可以用分段插值来近似：

在位移场${\boldsymbol{u}}(\eta ,\xi ,\zeta )$上运用微分算子L，应变场表示为：

将式(2)代入式(3)，可得应变与结点位移函数之间的关系：

式中，${{\boldsymbol{B}}_1}(\eta ,\zeta )$和${{\boldsymbol{B}}_2}(\eta ,\zeta )$为节点和位移之间的关系。对于线性弹性问题，应力可以表示为：

式中，${{\boldsymbol{D}}_e}$为弹性矩阵。这里，我们将随机变量引入弹性矩阵，以进一步发展随机比例边界有限元法。假定弹性模量$E$为随机参数，根据弹性模量的概率密度函数${f_X}(E)$，生成N个随机样本${E_e}(i = 1,2,\cdots,N)$，进一步获得带有随机参数的弹性矩阵${{\boldsymbol{D}}_e}$：

运用伽辽金法或虚功原理，得到基于位移的三维SBFEM控制方程^[13] ：

其形式上等同于标准的SBFEM方程，不同的是在系数矩阵${\overline {\boldsymbol{E}} _0}$、${\overline {\boldsymbol{E}} _1}$、${\overline {\boldsymbol{E}} _2}$引入了随机变量。其形式为：

式中：$\rho$为密度；$|{\boldsymbol{J}}|$为雅可比矩阵的行列式。

在单元的面上，内部节点力表示为：

式(7)是Euler-Cauchy方程，可解析求解，引入辅助变量X，随后将其转化为一阶偏微分方程：

将式(12)、式(13)代入式(7)得到：

式中，系数矩阵${{\boldsymbol{ {\textit{Z}}}}_{\boldsymbol{p}}}$表示为：

式(14)可以改写为：

式中：${\boldsymbol{\varPsi }}$为特征向量矩阵；${\boldsymbol{\lambda }}$为包含特征值的对角矩阵。那么，${\boldsymbol{X}}(\xi )$的通解可表示：

式中：${\lambda _n} +$和${\lambda _n} -$分别为实部为正、实部为负的特征值对角矩阵；${{\boldsymbol{c}}_1}$和${{\boldsymbol{c}}_2}$为积分常数。对于有限域， 积分常数${{\boldsymbol{c}}_2}$等于零，节点位移与节点力之间的关系可表示为：

令$\xi = 1$(即在边界处)，可得系统的刚度矩阵：

一个多面体单元的质量矩阵表示为：

式中，系数矩阵${\boldsymbol{m}}$的每个元素表示为：

式中，${{\boldsymbol{m}}_0}$的表达式如下：

将计算模型分为近场有限域与无限域，在近场有限域区域利用八叉树单元网格进行建模，通过施加弹簧-阻尼器元件后，将输入的地震动转化为八叉树单元边界节点上的等效节点力荷载。离散的系统方程表示为：

式中：下标b与s分别为人工边界和有限域其他部分的自由度；${\boldsymbol{\ddot u}}$、${\boldsymbol{\dot u}}$、${\boldsymbol{u}}$分别为加速度、速度和位移；$\overline {\boldsymbol{M}}$、${\boldsymbol{\overline C}}$、$\overline {\boldsymbol{K}}$为带有随机变量的质量、阻尼和刚度矩阵；${{\boldsymbol{F}}_{\text{b}}}$为外界无限域对人工边界处的作用力。

通过显式或隐式时程积分，可以求解带有随机变量的式(23)。随后，收集解的信息，并利用统计关系来评估不确定参数对结构响应的影响。用 ${{\boldsymbol{u}}_i}(j)$表示蒙特卡罗模拟第j个样本点上第i个自由度的位移，则样本的期望和方差的估计值为：

值得注意的是，$D[{{\boldsymbol{u}}_i}]$的平方根为标准差，且MCs的收敛速度为$O({N^{ - 1/2}})$。显然，MCs的精度只与样本点的数目有关。本文蒙特卡罗模拟的解可通过商业软件高效获得。为此，开发了一个算法，能够在商业软件集成八叉树网格和SBFEM。图2描述了一个悬臂梁示例，通过编写的算法1在ABAQUS的用户单元上^[29] 进行SBFEM动力分析。算法1首先识别商业软件的网格文件(如.*cas文件)，将网格文件的节点、面进行十六进制转换，并计算每个八叉树单元的面和节点的数量；随后识别并处理悬挂节点，计算每个单元的比例中心；然后该算法对节点的连接进行处理；最后生成ABAQUS可识别的输入文件。

图  2  基于商业软件实施八叉树SBFEM的流程图

Figure  2.  Flowchart of implementing octree SBFEM based on commercial software

下载: 全尺寸图片 幻灯片

2   快速不确定量化分析

2.1   基于奇异值分解(SVD)模型降阶法

获得每个样本点的响应是蒙特卡罗模拟中计算成本最大的运算，尤其在高混凝土坝地震分析中，该过程将更加耗时。这一节，为了提高MCs的计算效率，构建一种基于模型降阶的快速算法，加速传统的MCs过程。对于基于样本的MCs，根据初始m个样本的波动范围，计算该m个随机变量下的响应，并将这些样本点的响应按列排列，构造快照矩阵${\boldsymbol{\varOmega }}$^[7] ：

式中，${\boldsymbol{\varOmega }} \in {R^{n \times m}}$，n为单个输入变量下的响应个数，m为变量${\alpha _m}$的个数。SVD的首要目标是找出快照矩阵之间的内在关系，提取数据的主要特征，以达到降低数据维数，节约储存空间的效果。利用SVD将矩阵${\boldsymbol{\varOmega }}$分解：

式中：$r {\leqslant} \min (m,n)$；${\boldsymbol{U}} \in {R^{n \times n}}$和${\boldsymbol{V}} \in {R^{m \times m}}$分别为矩阵${\boldsymbol{\varOmega }}$的左、右奇异值矩阵；${\boldsymbol{\varSigma }} \in {R^{n \times m}}$为一个对角矩阵；对角元素${\sigma _j}$按从大到小排列；u_j和v_j分别为${\boldsymbol{\varOmega }}{{\boldsymbol{\varOmega }}^{\text{T}}}$和${{\boldsymbol{\varOmega }}^{\text{T}}}{\boldsymbol{\varOmega }}$的特征向量。定义${\varphi _j} = {u_j}$，${y_j}({\alpha _i}) = {\sigma _j}{v_{ij}}$，式(23)可以改写为：

式中：${\varphi _j}$被称为正交基；${y_j}({\alpha _i})$为相应的基底。使用式(28)，系统响应可以通过压缩表达的向量${\varphi _j}$和${y_j}({\alpha _i})$的线性组合来表示，且其规模比初始模型要小得多。

2.2   径向基函数(RBF)近似

式(28)只提供了原始系统的压缩表达，为了实现对任意随机输入变量的系统响应的连续近似，应用径向基函数(RBF)对降阶空间中的基底进行插值：

式中：$\phi$为基函数；$\eta$为其权系数。本文选取高斯核函数作为基函数：

式中：记号$|| \cdot ||$为欧氏范数；系数$\ell$由基函数的宽度决定。与径向基函数相关的权系数$\eta$由样本点插值条件确定，即：

值得注意的是，根据样本点不同，上述方程组是无条件非奇异的。将式(29)代入式(28)，可以改写为：

任何系统响应都可以通过式(32)这种线性组合来近似，无需完整的SSBFEM计算(快照矩阵的形成仍然需要完整的计算)，意味着全阶系统响应可通过快照矩阵来近似获得。图3给出了改进的MCs的流程图。与直接的MCs相比，改进的算法通过ABAQUS实施SBFEM高效地获得高精度初始样本。SVD模型降阶技术提供了原始系统信息的压缩表达。此外，组合RBF对低阶子空间进行插值近似，利用低阶子空间的线性组合快速获得任意变量下的结构响应。总的来说，SVD-RBF提高了计算效率，降低了计算成本，这些优势一定程度上扩展了MCs的适用性。

图  3  基于模型降阶法加速的蒙特卡罗模拟的流程图

Figure  3.  Flowchart of accelerated Monte Carlo simulation based on model order reduction method

下载: 全尺寸图片 幻灯片

3   数值算例

3.1   三维弹性土体模型的动态响应分析

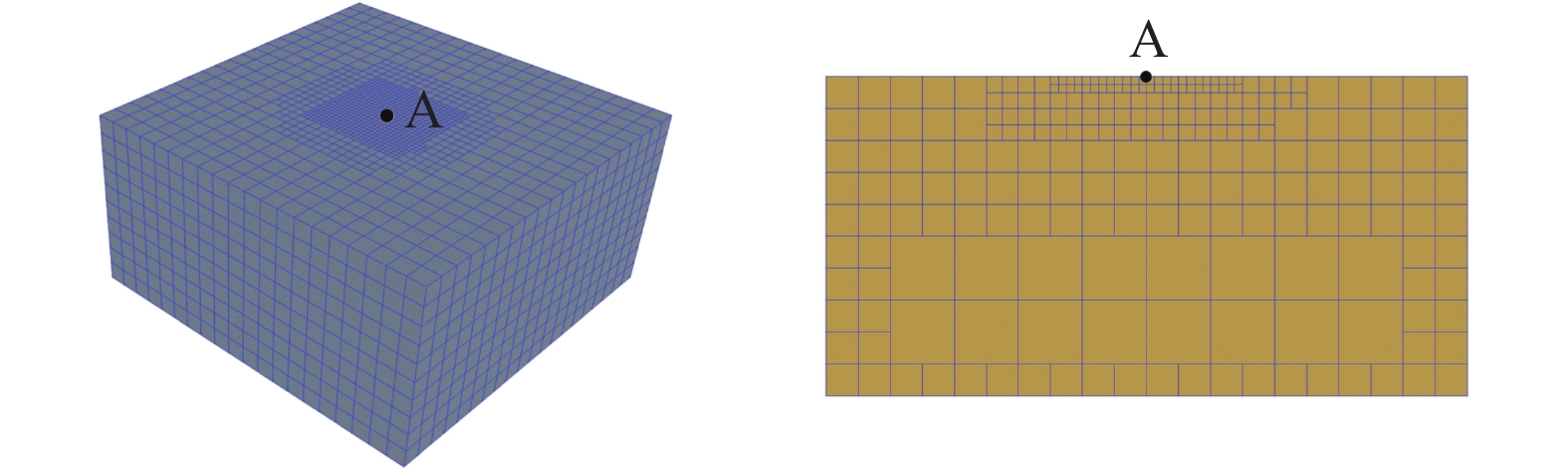
本节考虑一个经典的三维弹性土体模型^[30] ，其受到从底部垂直入射的SV波，验证本文算法的计算精度。如图4所示，该土体计算区域为边长为200 m×200 m×100 m的长方体块，该模型的上方为半空间自由表面，其余边界全部设置黏弹性边界^[31] 。切向边界和法向边界如下：

式中：K_BN和K_BT分别为法向刚度系数和切向刚度系数；C_BN和C_BT分别为法向阻尼系数和切向阻尼系数；r为散射波源到人工边界点的距离；c_s和c_p分别为S波和P波的波速；G为剪切模量和$\rho$介质密度；$\alpha$和$\beta$为无量纲参数，分别为0.8和1.1。分析时间增量步为0.01 s，计算时长2 s。土体介质的力学参数如表1所示。入射波的位移时程曲线如图5所示，其数学表达式如式(30)所示。图6采用八叉树SBFEM划分网格，共划分了5246个节点、7316个单元，还给出了八叉树网格的剖面图。对照组采用有限元法进行计算，离散了67 626个节点、62 500个单元,图4所示。

图  4  土体的有限元网格模型

Figure  4.  Finite element mesh model of soil

下载: 全尺寸图片 幻灯片

表  1  土体材料参数表

Table  1.  Soil of material parameter

弹性模量E/GPa	剪切模量G/GPa	泊松比ν	密度ρ/(kg/m3)	剪切波速cs/(m/s)	压缩波速 cp /(m/s)
24	9.6	0.25	2450	1975.5	3428.6

下载: 导出CSV 

| 显示表格

图  5  入射波时程

Figure  5.  Incident wave time history

下载: 全尺寸图片 幻灯片

图  6  八叉树 SBFEM网格模型

Figure  6.  Mesh model of Octree SBFEM

下载: 全尺寸图片 幻灯片

网格划分完毕后，将SV波作用到土体模型上，验证其动态响应的精度。图7给出了土体模型在该荷载下水平位移的理论解、有限元解和八叉树比例边界有限元解。从图中可以看出，三个解吻合得较好，说明了算法1成功地在ABAQUS上集成了八叉树网格和SBFEM，并且在保证精度的前提下，发挥了八叉树分解显著减少网格数量的优势。

图  7  数值结果的精度对比

Figure  7.  Precision comparison of numerical results

下载: 全尺寸图片 幻灯片

假定土体的弹性模量E为不确定性参数，并服从$\mu$=24 GPa，$\sigma = \mu \times \Upsilon$的正态分布，其中，$\Upsilon$为变异系数(COV)。确定变量的分布之后，随机生成500个样本，通过理论解计算出500个样本下的土体水平位移作为全阶蒙特卡罗模拟的结果。

表2给出了三种不同的变异系数下所选择的初始样本数目。这里，引入系数R²以评估算法的准确性，其计算公式如下：

表  2  不同变异系数条件下SVD-RBF的预测精度

Table  2.  Prediction accuracy of SVD-RBF under different coefficients of variation

变异系数	0.05	0.1	0.2
初始样本点数目	38	83	112
R2	1	1	1

下载: 导出CSV 

| 显示表格

式中：n为样本的个数；y_i为算法得到的第i个水平位移；${\hat y_i}$为第i个水平位移的理论值；${\overline y_i}$为水平位移的理论解的平均值。评价系数R²的值在0~1之间，表示算法解与理论解的偏差，越接近1精度越高。结合表2，可以得出本文算法与理论解之间有着良好的精度。当变异系数增大时，为了保持良好的精度，需要增加初始样本点。

为了更直观地展示本文算法精度，图8对比了不同变异系数下本文的算法解和理论解的结果。可以看到，变异系数控制着变量波动的范围(变异系数越大，数据波动越大)。在各种变异系数下，本文算法与理论解吻合较好。为进一步阐明算法的准确性，表明不确定参数对动态响应的影响，图9给出了不同弹性模量下理论解和SVD-RBF解的峰值水平位移(0.18s)之间的比较(结果保留至6位小数)。可以明显地看出，不确定参数对结构动态响应有一定的影响，SVD-RBF也展现了良好的精度。结合表2，可以得出变异系数越大，数据的波动范围越大，保持算法精度所需的初始样本点也就越多，相应的计算成本也随之增加，所以平衡计算效率与计算精度是值得注意的。

图  8  不同变异系数下观测点A的水平位移理论解(左)和本文算法解(右)的对比

Figure  8.  Comparison between the theoretical solution (left) and the algorithm solution (right) of horizontal displacement at observation point A under different coefficient of variation

下载: 全尺寸图片 幻灯片

图  9  不同弹性模量下0.18s时水平位移的比较

Figure  9.  Comparison of horizontal displacement at 0.18s with different Young’s modulus

下载: 全尺寸图片 幻灯片

在奇异值分解之后，产生了奇异值矩阵${\boldsymbol{\varSigma }}$，其主对角线上的奇异值包含着系统特征。为了节省储存空间，提高计算效率，要对${\boldsymbol{\varSigma }}$矩阵进行合理的截断。讨论了四种不同的截断方案，并进行蒙特卡罗模拟。

方案一：使用SBFEM计算500个随机变量下的水平位移${\boldsymbol{u}}$直接进行MCs，该计算需要重复500次；

方案二：对表2中的原始快照矩阵进行奇异值分解，不对${\boldsymbol{\varSigma }}$矩阵进行截断，再进行MCs；

方案三：对表2中的原始快照矩阵进行奇异值分解，截断${\boldsymbol{\varSigma }}$矩阵，将${\boldsymbol{\varSigma }}$矩阵维数选择为行与列的最小值，再进行蒙特卡罗模拟；

方案四：在方案三的基础上，根据奇异值数值大小，将截断后的${\boldsymbol{\varSigma }}$矩阵维数选择为σ_cat=10⁻¹σ_max。

图10显示了水平位移在不同的变异系数下的期望值和标准差。可以看出，方案二、方案三与方案一的结果基本一致，而方案四则表现出明显的偏差。这种差异是由于在方案四中截断了过多较大的奇异值，从而导致数据失真。综合考虑计算效率、精度以及算法的适用性，后续的例子将奇异值矩阵截断至行与列的最小值。

图  10  不同方案下水平位移的统计特征

Figure  10.  Statistical characteristics of horizontal displacement under different schemes

下载: 全尺寸图片 幻灯片

3.2   黄登混凝土坝地震响应分析

黄登水电站位于云南省兰坪县境内，上游与托巴水电站，下游与大华桥水电站相衔接。选用12号挡水坝段进行数值模拟计算，坝顶高程1625 m，坝基面高程1422 m，坝高 203 m，坝顶宽16 m，正常蓄水位1619 m，坝段厚度为30 m，如图11所示。地基往上下游各延伸1.5倍的坝高，地基深度取为1.5倍的坝高。混凝土弹性模量E_c=25 GPa，密度ρ_c=2400 kg/m³，泊松比ν_c=0.167。地基弹性模量E_r=15 GPa，密度ρ_r=2700 kg/m³，泊松比ν_r=0.24。

图  11  黄登混凝土坝几何模型

Figure  11.  Geometric model of Huangdeng concrete dam

下载: 全尺寸图片 幻灯片

SBFEM通过ABAQUS用户子程序实现，采用八叉树网格共划分了10 451节点、7371单元(图12)。对照组使用ABAQUS进行有限元计算，共划分了72 744节点、60 708单元(图13)。

图  12  八叉树 SBFEM网格模型

Figure  12.  Mesh model of Octree SBFEM

下载: 全尺寸图片 幻灯片

图  13  有限元网格模型

Figure  13.  Mesh model of FEM

下载: 全尺寸图片 幻灯片

从图12可以看出，八叉树网格在大坝和地基的过渡区域进行了细化，同时对重点关注的坝体的网格也进行了细化。虽然FEM也能通过局部加密的手段进行网格细化，但八叉树SBFEM的优势在于能够实现网格的快速过渡，对结构的关键区域进行局部网格细化时，不需要额外的技术处理悬挂节点问题。

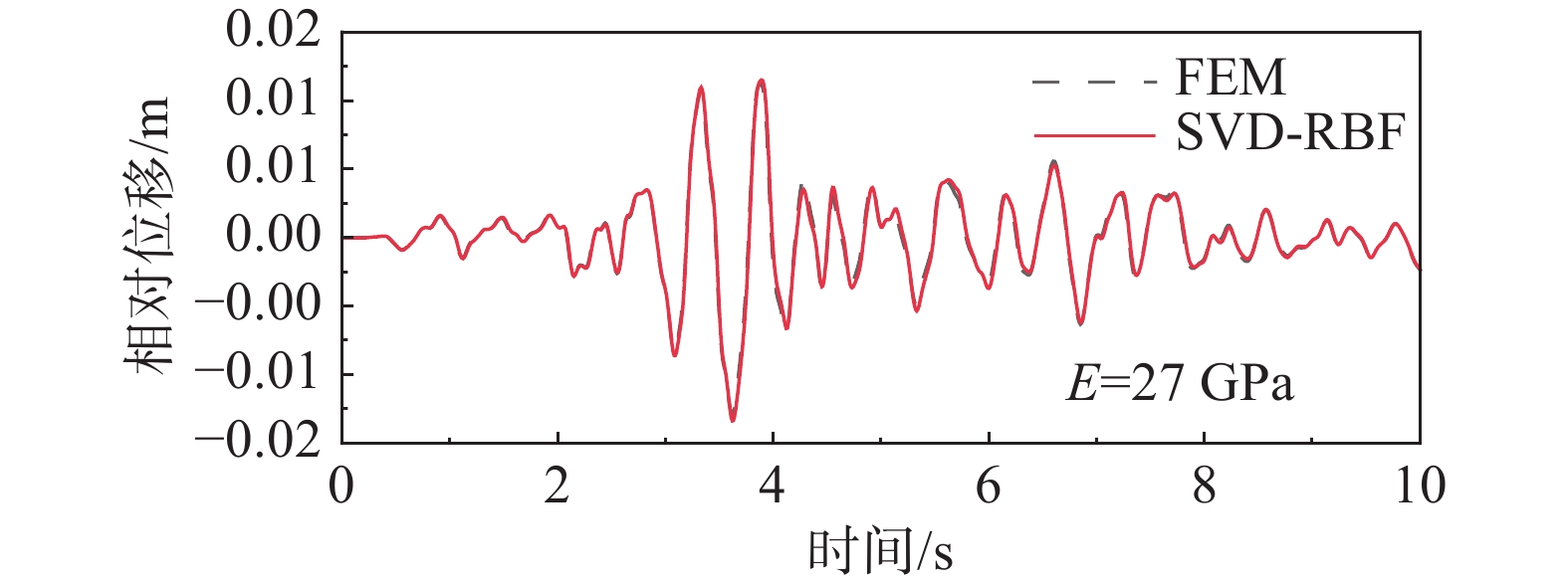
接下来验证通过算法1集成的八叉树SBFEM进行地震分析的准确性。这里考虑了混凝土坝与地基的相互作用。根据《水工建筑物抗震设计标准》(GB51247−2018)^[32] 的要求，将地震荷载的峰值加速度设置为0.40 g，单向人工地震波沿横河向垂直入射，采用黏弹性边界计算等效节点荷载，加速度时程如图14所示。计算采用0.01 s的时间步长，总计算时间为10 s。图15给出了坝顶A点和坝底B点顺河向的相对动力响应，表3对比了两种方法峰值动态响应的相对误差。综合图表结果，可以看出八叉树SBFEM的计算结果与FEM的吻合很好。此外，FEM和八叉树SBFEM的CPU计算时间分别为12 5911 s、8529 s。这些结果显示了八叉树SBFEM能够有效地减少计算自由度数量，提高了计算效率。

将混凝土的弹性模量E_c作为不确定参数，以0.5 GPa为步长，从20 GPa变动到45 GPa，共计51个样本作为MCs的参考解。将这些样本导入转换后的(.*inp)文件中，并选取坝顶A和坝底B两点的顺河向相对位移作为动力响应。图16给出了MCs与SVD-RBF得到的相对位移的统计特征比较。可以看出，SVD-RBF得到的统计特征与MCs的结果基本一致，说明了算法的准确性。值得注意的是，SVD-RBF只使用了17个样本和方案三的截断方案，而直接MCs需要重复计算51次，且没有对数据维数进行降维。为了进一步验证算法的准确性，图17给出了E= 27 GPa时A、B两点相对位移的计算结果，并与有限元结果进行了比较。同样可以看出，本文算法结果与有限元结果吻合得较好。

图  14  人工地震波时程

Figure  14.  Artificial seismic wave time history

下载: 全尺寸图片 幻灯片

图  15  FEM和八叉树SBFEM动力响应对比

Figure  15.  Comparison of dynamic response between FEM and Octree SBFEM

下载: 全尺寸图片 幻灯片

表  3  相对峰值动态响应的对比

Table  3.  Comparison of relative peak dynamic responses

动态响应	FEM	SBFEM	相对误差/(%)
相对峰值位移/m	0.18168	0.18080	0.48
相对峰值速度/(m/s)	0.01227	0.01208	1.55
相对峰值加速度/(m/s2)	3.92637	4.22468	7.60

下载: 导出CSV 

| 显示表格

图  16  相对位移的统计特征的对比

Figure  16.  Comparison of statistical characteristics of relative displacement

下载: 全尺寸图片 幻灯片

图  17  E=27GPa时相对位移的对比

Figure  17.  Comparison of relative displacement when E=27GPa

下载: 全尺寸图片 幻灯片

3.3   旭龙混凝土拱坝地震响应分析

旭龙水电站位于云南省德沁县与四川省德荣县的汇合处。旭龙拱坝^[30] 坝顶高程2308 m，最高高度213 m。拱冠处坝底厚度46.4 m，厚高比0.218。混凝土弹性模量E_c=25 GPa，密度ρ_c=2400 kg/m³，泊松比ν_c=0.167；地基弹性模量E_r=20 GPa，密度ρ_r=2700 kg/m³，泊松比ν_r=0.25。八叉树SBFEM离散了38 380个节点、85 420个单元，如图18；对照组采用有限元模型，离散了147 830个节点、137 293个单元。

假定单向人工地震波沿横河向垂直入射，其加速度时程如图19所示。计算步长设置为0.01s，以大坝的顶点A作为参考点，提取它沿横河向的位移、速度和加速度作为动态响应。图20给出了八叉树SBFEM和FEM的动力响应的结果，表4还给出了坝顶A点峰值动态响应的对比。从图、表结果可以看出，八叉树SBFEM与FEM结果吻合较好。

图  18  八叉树 SBFEM和FEM网格模型

Figure  18.  Mesh model of Octree SBFEM and FEM

下载: 全尺寸图片 幻灯片

图  19  人工地震波时程

Figure  19.  Artificial seismic wave time history

下载: 全尺寸图片 幻灯片

图  20  FEM和八叉树SBFEM关于坝顶A点动力响应的对比

Figure  20.  Comparison of FEM and octree SBFEM for dynamic responses at point A of dam crest

下载: 全尺寸图片 幻灯片

表  4  坝顶A点峰值动态响应的对比

Table  4.  Comparison of peak dynamic responses at point A of dam crest

动态响应	FEM	SBFEM	相对误差/(%)
A点峰值位移/m	0.274 55	0.274 72	0.06
A点峰值速度/(m/s)	0.895 75	0.885 89	1.11
A点峰值加速度/(m/s2)	15.785 94	15.847 27	0.39

下载: 导出CSV 

| 显示表格

假定混凝土的密度ρ_c为不确定参数，以10 kg/m³为步长，从2100 kg/m³变动到2600 kg/m³，共51个样本作为MCs的参考解。图21比较了MCs与SVD-RBF得到的相对位移的统计特征。可以看出，SVD-RBF得到的统计特征与MCs的结果吻合得很好，表明了算法的准确性。SVD-RBF只使用了18个样本和方案三的截断方案，总共耗时45小时。直接MCs重复计算51次，没有对数据维数进行降维，总耗时为125小时。这表明了本文算法在提高计算效率上是有潜力的。同样地，图22还对比了$\rho$= 2500 kg/m³时，A、B两点相对横向位移的本文算法结果和有限元结果。可以看出，本文算法结果与有限元结果基本一致。总的来说，该算法有效地减少了网格数量，提高了直接MCs的计算效率。

图  21  相对位移的统计特征的对比

Figure  21.  Comparison of statistical characteristics of relative displacement

下载: 全尺寸图片 幻灯片

图  22  $\rho$=2500 kg/m³时相对位移的对比

Figure  22.  Comparison of relative displacement when $\rho$=2500 kg/m³

下载: 全尺寸图片 幻灯片

4   结论

本文基于ABAQUS-UEL实施比例边界有限元法的基础上，编写算法在商业软件上集成八叉树网格。并在.*inp文件中引入随机变量，发展SSBFEM，进行高拱坝不确定量化分析。随后，组合模型降阶法和径向基函数，提出一种新颖的高混凝土坝抗震不确定量化分析方法。得到如下结论：

(1)构建了基于随机变量的SSBFEM高混凝土坝地震响应分析方法。该方法利用八叉树网格剖分技术，有效减少了单元数目和计算耗时，同时能够有效地处理不确定参数对高混凝土坝地震响应的影响。与传统的FEM相比，所集成的八叉树SSBFEM在高混凝土坝地震分析中更具优势，且整个操作过程都在商业软件上根据用户需要自动执行，为不确定量化提供了高精度的模型和样本。

(2)提出了一种新颖的基于MCs的高混凝土坝地震响应分析不确定量化方法。采用MCs计算结构响应的统计特征，量化不确定参数对结构响应的影响。利用模型降阶技术改进传统的MCs，提供了原始系统的压缩表达，通过低阶子空间的线性组合快速获得新的结构响应。此外，考虑了不同变异系数对结构响应的影响，并讨论了奇异值矩阵的合理截断。该方法对不同的高混凝土坝模型和较大的变异系数，也展现了良好的精度。