INFLUENCE OF NON-UNIFORMITY OF RAIL DECARBURIZATION LAYER ON WHEEL-RAIL CONTACT BEHAVIOR
-
摘要:
钢轨脱碳层表面到基体的材料力学性能表现出较强的非均匀特性，这些性能的变化对轮轨滚动接触有较大影响。该文采用ANSYS/LS-DYNA建立了可以考虑钢轨脱碳层特性的三维高速轮轨瞬态滚动接触有限元模型，分析了脱碳层对轮轨接触行为的影响规律。通过纳米压痕试验获取脱碳层非均匀材料弹性模量和硬度，从钢轨基体到脱碳层表层，弹性模量和硬度逐渐减小，与钢轨基体相比，脱碳层表层弹性模量和硬度分别降低了10%和34%。计算并对比了脱碳钢轨和未脱碳钢轨的轮轨接触状态，发现钢轨脱碳层对轮轨接触斑大小、黏滑区分布和法向接触应力的影响可以忽略，但对等效应力和应变、摩擦功有较大影响；考虑脱碳层影响后，最大等效应力降低20%，最大等效应变增加115%；虽然脱碳深度只有0.55 mm，但对V-M等效应力的影响深度达3.56 mm。
Abstract:The mechanical properties of the material from the surface of the rail decarburization layer to the substrate exhibit strong non-uniform characteristics, which have a significant impact on the rolling contact between the wheel and the rail. Thusly, a three-dimensional transient rolling contact finite element model of high-speed wheel-rail, which considers the characteristics of the decarburization layer on the steel rail, was established using ANSYS/LS-DYNA, and the influence of the decarburization layer on the wheel-rail contact behavior was analyzed. The non-uniformity of material elastic modulus and hardness of the decarburization layer were obtained through nanoindentation tests. The elastic modulus and hardness gradually decrease from the rail bulk to the surface of the decarburization layer, with the surface elastic modulus and hardness of the decarburization layer decreased by 10% and 34%, compared to the rail bulk. The wheel-rail contact state of the decarburized and non-decarburized steel rail was calculated and compared. It was found that the decarburization layer has a negligible effect on the contact patch size, on the adhesive region distribution and, on the normal contact stress, but has a significant impact on the equivalent stress and strain, as well as the frictional work. After considering the influence of the decarburization layer, the maximum equivalent stress decreased by 20%, and the maximum equivalent strain increased by 115%. Despite the decarburization depth being only 0.55 mm, its impact on the V-M equivalent stress depth reached 3.56 mm.
-
钢轨脱碳层是钢轨在生产过程中表层碳元素被氧化而形成的一层低碳组织，如图1所示。这层组织非常薄，一般不超过0.5 mm，一般不会对轮轨动力学指标造成较大的改变。但碳元素的流失降低了材料表面抵抗变形的能力，改变了表层材料的力学性能，对轮轨界面接触斑内的应力应变产生较大影响。而轮轨接触斑内材料和力学特性正是决定轮轨接触和摩擦磨损性能的关键所在[1 − 3]。因此，钢轨脱碳层会通过改变材料力学性能改变轮轨接触状态，进而影响钢轨磨耗特性，甚至诱发并加速钢轨波磨发展。如GRASSIE[4]在对英国铁路西海岸干线新造钢轨的现场试验中发现，未进行脱碳层处理的在运营20个月就出现了明显的波磨现象，而对脱碳层处理后的钢轨经过50个月的运营仍未发现波磨现象。在我国某高速铁路开通后，也发现了由于脱碳层而导致的钢轨波磨快速发展，最终造成了扣件弹条断裂现象，严重威胁高速铁路运营安全[5 − 6]。
近年来，钢轨脱碳层材料特性及其对钢轨磨耗的影响已经引起了国内外学者的关注，并从试验和理论方面开展了大量的研究。CARROLL等[7]通过双盘对滚试验对脱碳层对钢轨滚动接触疲劳(RCF)展开研究，发现只有当脱碳层的厚度超过某个临界值才会加速RCF裂纹的扩展。ZHAO等[8 − 9]测量了脱碳层的剖面硬度，利用滚-滑磨损实验机研究了干态[8]和湿态[9]下脱碳层对钢轨耐磨性和滚动接触疲劳的影响，揭示了不同脱碳层厚度下的磨损率以及表面和次表面的损伤行为。寇峻瑜等[10]在假设屈服应力与硬度线性相关的基础上，建立了可以考虑钢轨脱碳层的三维滚动接触有限元模型，采用显示有限元方法分析了钢轨脱碳层对轮轨瞬态滚动接触行为的影响，发现钢轨脱碳层加大钢轨表面的塑性变形，对接触应力、黏滑分布和摩擦功造成较大影响。ZHAO等[11]通过引入纳米压痕测试手段，并利用有限元方法再现纳米压痕过程，得到了脱碳层材料弹性模量和硬度的变化规律，并建立了脱碳层非均匀材料本构关系。作者[12]在此基础上，基于可考虑材料性能非均匀性的轮轨滚动接触理论模型，建立了可考虑脱碳层材料特性的波磨发展理论计算模型，再现了脱碳层条件下的波磨发展过程，发现脱碳层弹性模量和硬度的降低均加剧了波磨发展速率，在通过12万次后，考虑脱碳层材料特性后波磨波深增加了9倍多。
现有关于脱碳层的研究[7 − 11]大多数集中在对钢轨脱碳层材料性能、耐磨性、滚动接触疲劳等方面，仅有少数研究者对脱碳层条件下的轮轨接触行为进行研究，尽管作者在以往文献中建立了可考虑脱碳层材料特性的轮轨滚动接触理论模型，但模型中仅考虑了脱碳层材料弹性阶段的性能，且模型为二维模型，无法对脱碳层条件下的轮轨接触行为进行准确刻画。想要准确了解材料性能非均匀分布下的轮轨接触行为，仍需要借助有限元方法[13]。而现有轮轨滚动接触有限元模型，由于没有测量到钢轨脱碳层内部的材料力学性能，在脱碳层材料属性的设置中，其弹性阶段只能采用基体值，塑性阶段只能通过硬度与屈服应力的线性假设进行等效计算[10]，因此应力和应变都无法准确预测，特别是与塑性变形相关行为方面。因此，探明钢轨脱碳层非均匀材料特性及其对轮轨接触行为的影响具有较大的意义。
本文利用纳米压痕试验获取脱碳层非均匀材料特性，并在此基础上借助有限元方法，建立可考虑钢轨脱碳层的高速铁路三维滚动接触有限元模型，计算轮轨接触力、黏滑区划分、V-M等效应力应变和表面摩擦功等结果，分析钢轨脱碳层材料特性对轮轨接触行为的影响。
1 钢轨脱碳层非均匀材料特性
1.1 试样和纳米压痕试验
取CN60钢轨(材料为U17MnG)轨头内材料制成直径为40 mm圆柱体试样。将试样在加热炉重新加热至1200 ℃，保温4 h后自然冷却，得到脱碳深度为0.55 mm的钢轨试样，图1是钢轨脱碳层的微观结构图，上层是钢轨脱碳层区域，下层是未脱碳区域，也称为钢轨基体。
从图1可以看出，钢轨脱碳层非常薄，很难制作成传统拉伸试验所需的试样，无法通过传统测量方法获取钢轨材料非均匀力学性能。此外，脱碳层表面到基体的材料微观组织表现出较强的非均匀性，传统拉伸试验也无法表征这种连续变化的材料力学性能。
采用微纳米压痕技术(或称为深度敏感压痕技术)测量脱碳层的材料应力-应变关系是较为合理的解决方法[14 − 19]。该方法是在微纳米科学中非常成熟的材料性能测量技术，在测量中将探头压入被测材料，在加载和卸载过程中记录载荷和压入深度，利用Oliver-Pharr[20]方法从载荷-深度曲线中得到材料的弹性模量和硬度等信息。
利用TI900纳米压痕仪对距离脱碳层表面不同深度的位置处进行纳米压痕试验，研究脱碳层不同位置处的材料力学性能和本构关系。压头类型为Berkovich压头，采用载荷控制方法，使载荷在5 s内从0均匀加载至6000 μN，并保持2 s，最后再5 s内均匀卸载。选取距离钢轨脱碳层表面0.05 mm、0.15 mm、0.30 mm、0.45 mm、3.00 mm来表征钢轨脱碳层的材料力学性能，其中0.05 mm代替钢轨脱碳层表面的材料，3.00 mm的位置代替钢轨基体。距离表面0.05 mm满足GB 22458−2008规定的压痕点与自由表面或边界之间的距离应大于压痕直径3倍的要求。考虑到纳米压痕尺寸较小，实验结果存在离散性，对每一垂向位置重复了24次实验。
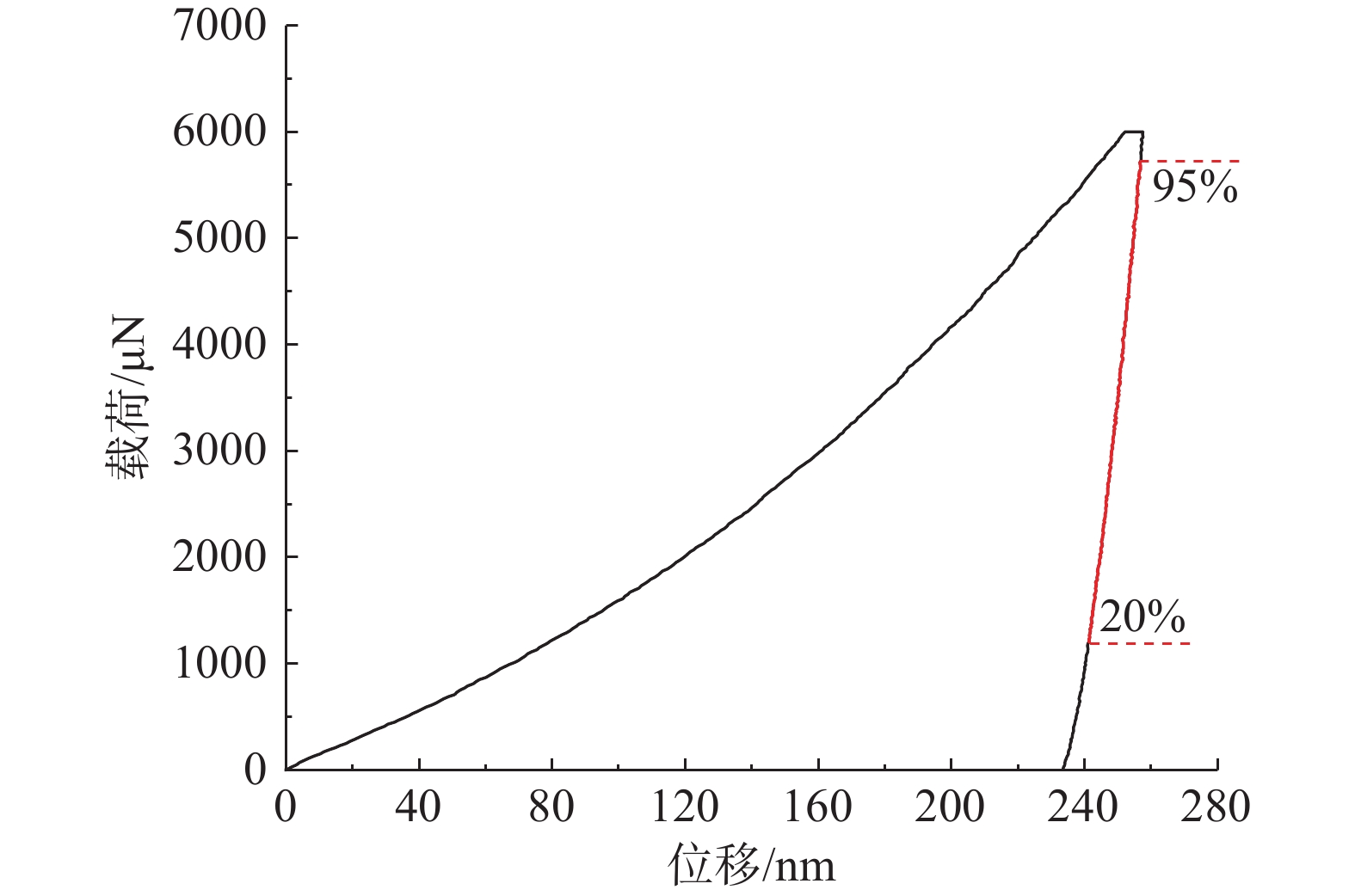
实验过程中，压头被压入试样中，并记录了加载和卸载过程中的深度-位移曲线，如图2所示，弹性模量E和硬度H的计算公式如下：
H=FAc (1) Er=√π2βS√Ac (2) 式中：F为载荷；Ac为接触投影面积；β为与压头几何形状相关的常数，取1.034；S为接触刚度，取20%~95%卸载部分最大载荷处的切线的斜率；Er为约化弹性模量，与弹性模量E的关系如下所示：
1Er=1−ν2E+1−ν2iEi (3) 式中，Ei、νi和E、ν分别为压头和试样的弹性模量和泊松比，其中Berkovich压头的Ei = 1140 GPa，νi = 0.7。
1.2 非均匀材料力学性能
基于Oliver-Pharr[20]方法，根据纳米压痕加载卸载曲线计算发现钢轨基体的弹性模量为231 GPa，较传统拉伸实验得出的206 GPa大了12%。这是因为测试所用压头在磨损之后，尖端形状不规则化，使压头在压入材料的初始阶段与材料之间的相互作用力复杂化，被测材料抵抗变形能力大于理想状态，导致所测弹性模量偏大[21]。研究表明：当接触深度hc<200 nm时，压头尖端曲率半径的影响非常明显；当接触深度hc>500 nm时，该因素的影响才可以忽略。介于本次压痕实验过程中的接触深度在194 mm~244 nm范围内，因此压头磨损对测试结果产生了较大的影响。
考虑到不同垂向位置实验均采用同一压头，因此可以通过修正压头参数来确定最终的弹性模量和硬度。一般情况，采用多项式来计算压头面积函数，理想的玻氏压头只保留C0项。当压头被磨损后，尖端可以近似为曲率半径为R的曲面，压头面积函数可通过增加C1项来进行修正。以钢轨基体测试数据为修正对象，传统拉伸实验得到的弹性模量206 GPa为参考值，联立方程组式(2)~式(4)，确定修正系数C1。
Ac=8∑n=0Cnh12n−1c (4) 最终得到修正后钢轨脱碳层不同垂向位置的弹性模量和硬度的均值与方差，结果显示：从钢轨基体到脱碳层表面，弹性模量和硬度逐渐减小。脱碳层表面弹性模量为185 GPa，硬度为1.90 GPa，较钢轨基体分别降低了10%和34%。
![]()
图 3 脱碳层材料力学性能Figure 3. The mechanical properties of material of rail decarburized layer2 三维滚动接触有限元模型
2.1 有限元模型
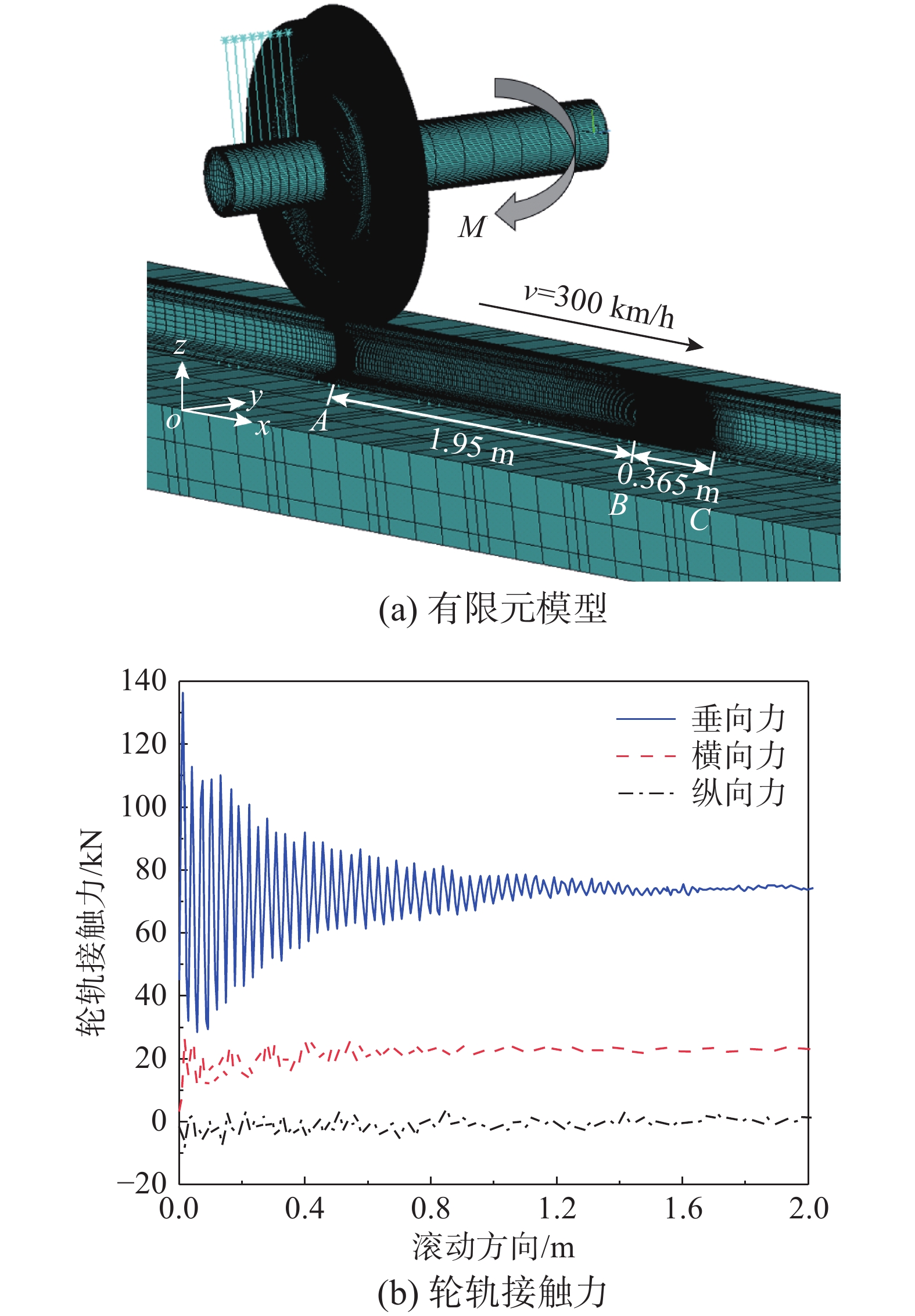
采用ANSYS/LS-DYNA建立了可以考虑钢轨脱碳层特性的三维高速轮轨瞬态滚动接触有限元模型，如图4(a)所示，来模拟中国某高速线路上的车辆-轨道系统。
![]()
图 4 考虑脱碳层的三维轮轨瞬态滚动接触有限元模型Figure 4. The three-dimensional transient rolling contact finite element model considering rail decarburization layer考虑到轮轨系统的对称性，本文只建立了半轮对-半轨道模型。为提高计算效率，将车辆一系悬挂以上的部件简化为质点并通过一系悬挂与车轮相连。轨道为无砟轨道，长15.2 m包含24组扣件，轨道系统中考虑了钢轨、扣件、轨道板和砂浆层，其材料参数如表1所示。此外，考虑到脱碳层主要发生在新线路开通运行初期，故以新轮新轨为例分析脱碳层对轮轨接触行为的影响，同样研究结论也仅适用于新轮新轨工况。模型中，车轮(LMa)和钢轨(CN60)由8节点六面体单元组成，采用罚函数的“面-面”接触算法求解轮轨接触行为。为充分体现脱碳层特性，对轮轨接触区域的网格进行了细化，最小网格尺寸为0.1 mm[22]，模型中共有1458868个节点和1334710个单元。
表 1 材料属性Table 1. Material properties物理量 值 单位 簧上质量 7414 kg 轮对质量 586 kg 一系刚度系数 0.88 MN/m 一系阻尼 4 kN·s/m 车轮弹性模量 206 GPa 车轮泊松比 0.3 − 车轮密度 7790 kg/m3 车轮阻尼常数 1.0×10−4 β/s 轨道板材料弹性模量 34.5 GPa 轨道板泊松比 0.25 − 轨道板密度 2400 kg/m3 橡胶垫刚度系数 22 MN/m 橡胶垫阻尼 200 kN·s/m 钢轨泊松比 0.3 − 钢轨密度 7790 kg/m3 钢轨阻尼常数 1.0×10−4 β/s 砂浆层弹性模量 8 GPa 砂浆层泊松比 0.2 − 砂浆层密度 1600 kg/m3 轨道板接头弹性模量 29.5 GPa 轨道板接头泊松比 0.25 − 轨道板接头密度 2400 kg/m3 在有限元模型中，首先将系统置于初始位置A，并施加重力，利用隐式算法求得静态条件下的位移场；再以得到的位移场为初始状态，设置其他初始条件，并施加载荷，以显示时间积分方法求解车轮以300 km/h从A高速滚向C的瞬态行为。
模型中AB段(动态松弛区)是过渡区，保证在进入BC段(结果区)到达稳态滚动，避免由非完美初始应力场导致的高频振动对结果造成的影响。转矩M施加在车轴上齿轮箱位置以模拟驱动力矩，用牵引系数来衡量，默认取值0.3。模型的边界条件有：砂浆层底部固结，轨道、车辆轴端部以及轨道的对称面施加对称边界条件，一系悬挂、扣件和轨道板只保留垂向自由度。
图4(b)展示了车轮通过无脱碳层钢轨时的轮轨力情况，可以看出在初始时刻，垂向、横向和纵向轮轨力均存在明显波动，如轮轨垂向力的波动范围28 kN~136 kN，波动幅度高达108 kN，是稳定后轮轨垂向力的1.5倍。但随着运行距离的增加，波动幅度逐渐降低，当运行距离达到1.6 m后，波动幅度不足2 kN，仅为稳定后轮轨力的3%。因此，可以认为经过1.6 m后轮轨达到稳态滚动。故在模型中动态松弛区的长度应不小于1.6 m，为此本文将动态松弛区的距离设置为1.95 m。为提高计算效率，仅在结果区BC段(1.95 m<x<2.315 m)设置了钢轨脱碳层。结果区与过渡区通过设置耦合条件和增设“面-面”接触(摩擦系数为100)来削弱两个面之间的错动，保证结果区两端的连续性。
2.2 脱碳层非均匀材料特性模拟
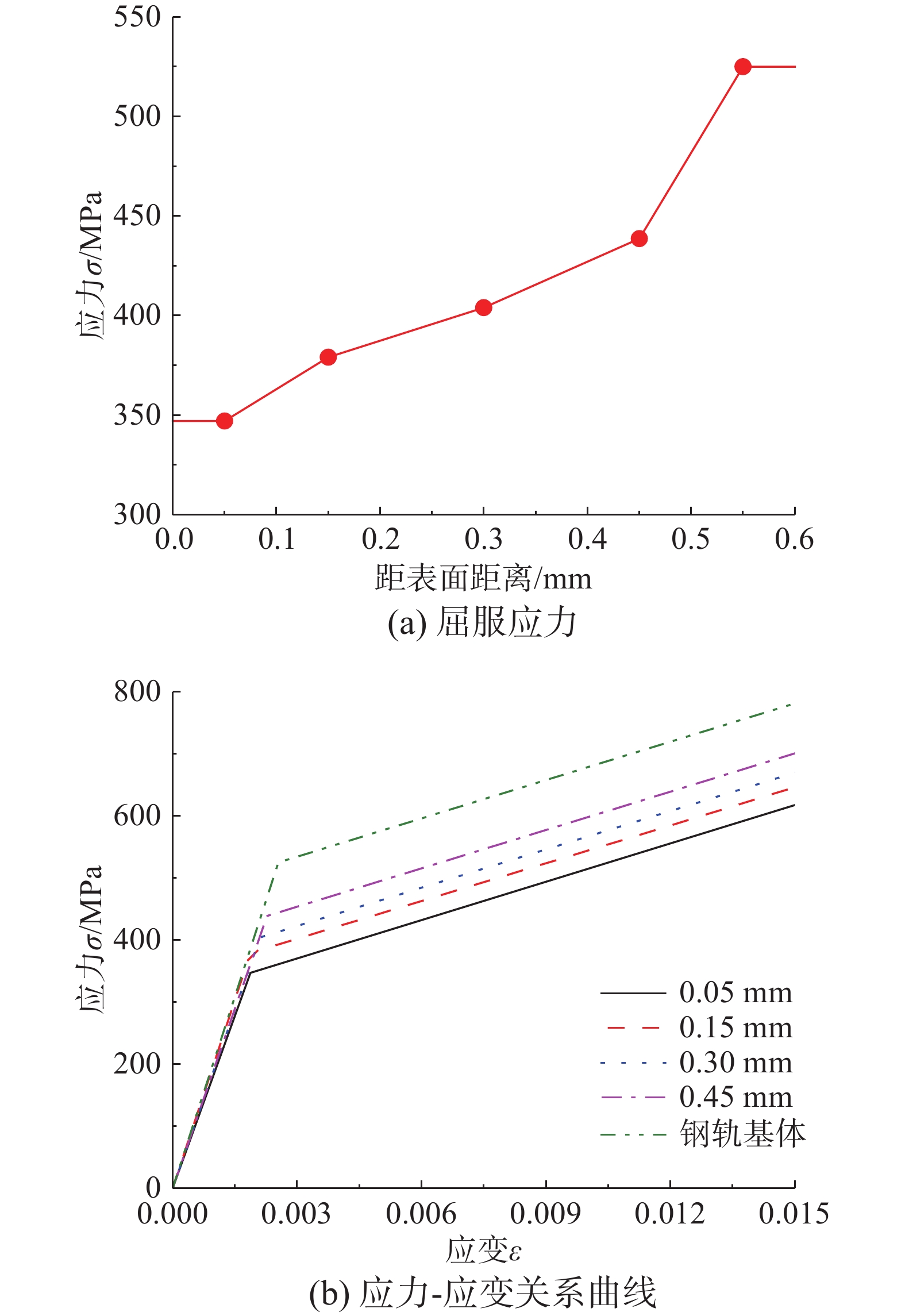
由于纳米压痕试验所采用的压头存在磨损现象，导致作者[11]在前序研究成果中建立的材料本构关系很难直接应用到有限元模型中，故借鉴寇峻瑜等[10]所采用的双线性弹塑性模型进行脱碳层特性表征。假设屈服应力与维氏硬度呈线性关系，并取钢轨基体屈服应力为525 MPa，根据钢轨脱碳层不同垂向位置的硬度值即可得到其当地的屈服应力，如图5(a)所示，图5(b)是钢轨脱碳层不同垂向位置的应力-应变曲线。结果表明：从钢轨基体到脱碳层表面，等效屈服应力和应变逐渐减小；塑性阶段体现出了较大差异，脱碳层表层与基体相差164 MPa。
为分析钢轨脱碳层对轮轨接触行为的影响，本文共设置了2种工况：工况1 (未脱碳钢轨) 不考虑脱碳层特性，从钢轨基体到钢轨表层均设置成基体的弹性模量和应力应变曲线；工况2 (脱碳钢轨) 中钢轨脱碳层不同垂向位置均设置当地的弹性模量和应力-应变曲线，具体参数如表2所示。
表 2 材料属性Table 2. Material properties工况编号 弹性模量/GPa 屈服应力/MPa 工况1 206 525 工况2 185~206 347~525 3 脱碳层对轮轨接触行为的影响
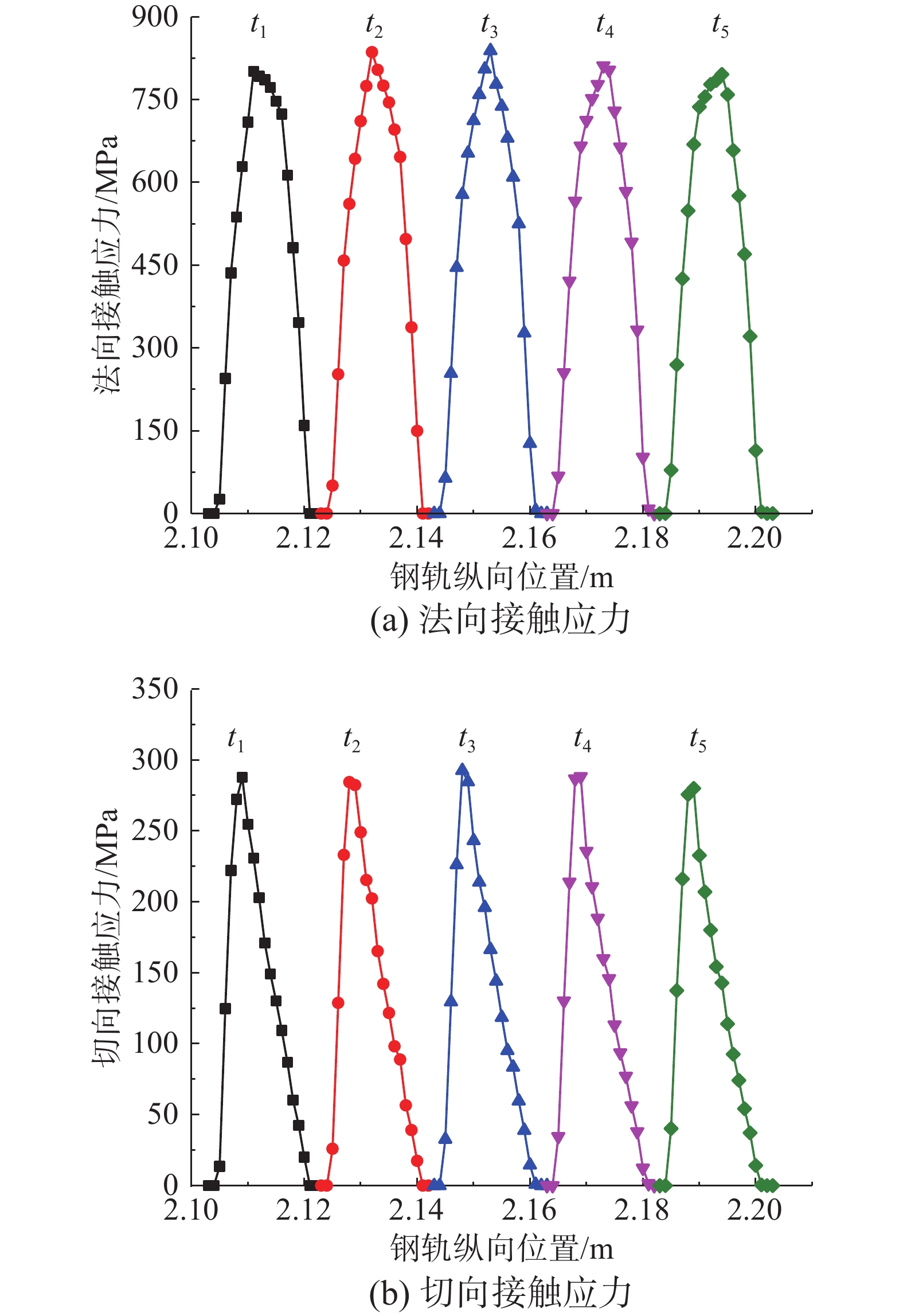
为分析钢轨脱碳层对轮轨接触行为的影响，利用本文建立的可以考虑脱碳层的三维滚动接触有限元模型对车辆以300 km/h高速通过有/无脱碳层钢轨的工况进行了模拟。图6是车轮滚过脱碳钢轨结果区时，瞬态法向和切向接触应力沿纵向路径L(定义经过接触斑内最大接触应力点的钢轨表面纵向路径为L)的分布。
![]()
图 6 轮轨瞬态接触应力纵向路径L的分布Figure 6. Distribution of transient wheel-rail contact stress along longitudinal path L取中间5个连续等间隔时刻t1~t5进行分析，结果表明：在结果区，各时刻的法向、切向接触应力的波动均小于5%，达到稳定状态。表明车轮经过动态松弛区AB段和耦合区后，基本达到了稳态滚动。在无特殊说明情况下，本文都以t3时刻为例进行分析，从接触斑状态、轮轨接触应力、应力应变和摩擦功4个方面分析钢轨脱碳层对轮轨接触行为的影响。
1) 轮轨接触斑
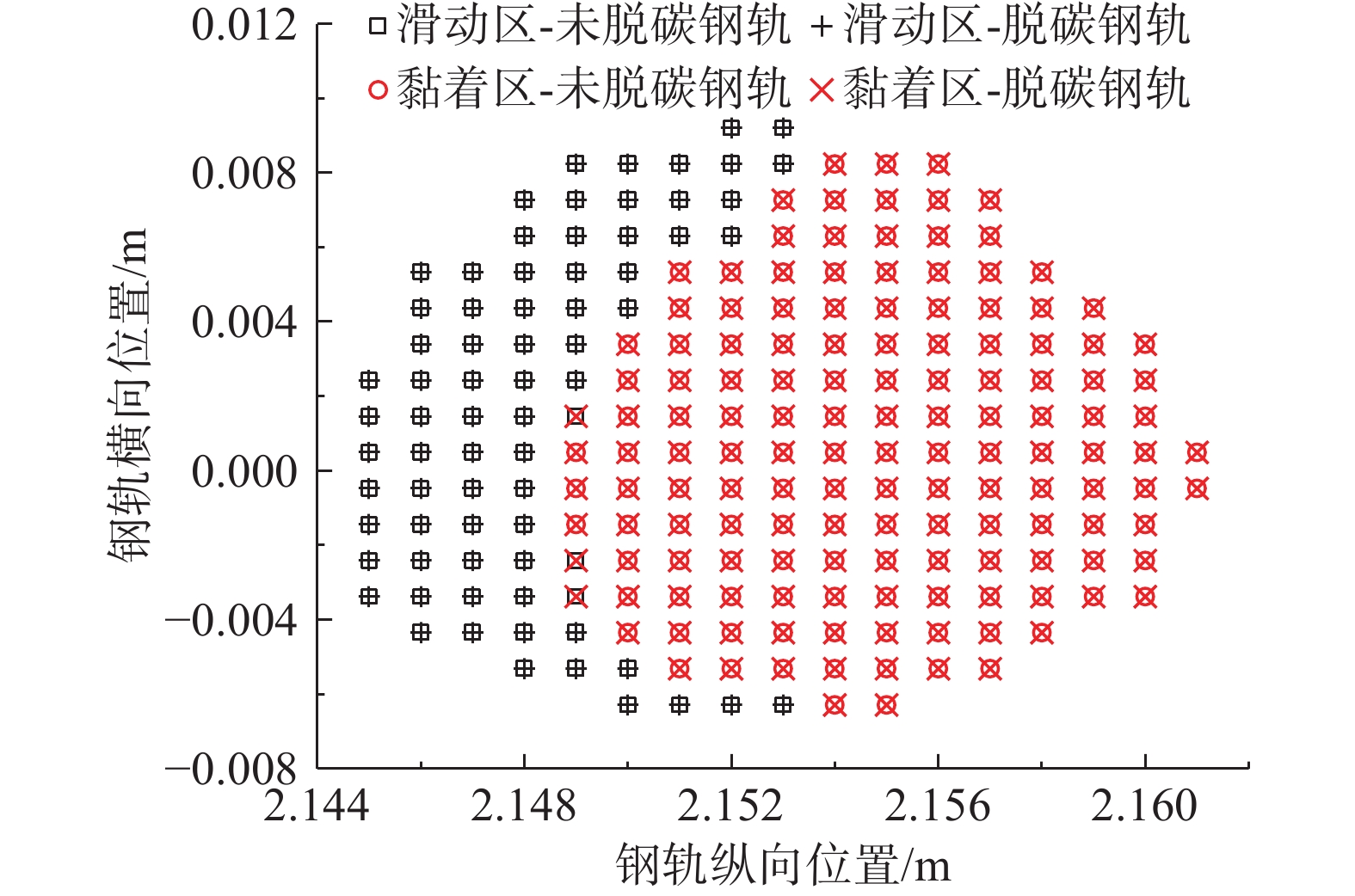
计算得到车轮通过脱碳钢轨和未脱碳钢轨时的轮轨接触斑大小及黏滑区划分，图7是t3时刻轮轨接触状态。结果表明：2种工况计算得到的接触斑形状和面积相同；与不考虑脱碳层结果比，考虑脱碳层后滑动区面积减小了4%，黏着区增加了2%。主要是因为脱碳层较软，在相同的接触应力下会产生更大的塑性变形，进而导致滑动区面积的增加。所以，钢轨脱碳层对轮轨接触斑大小与形状基本无影响，对黏滑区分布有轻微影响。
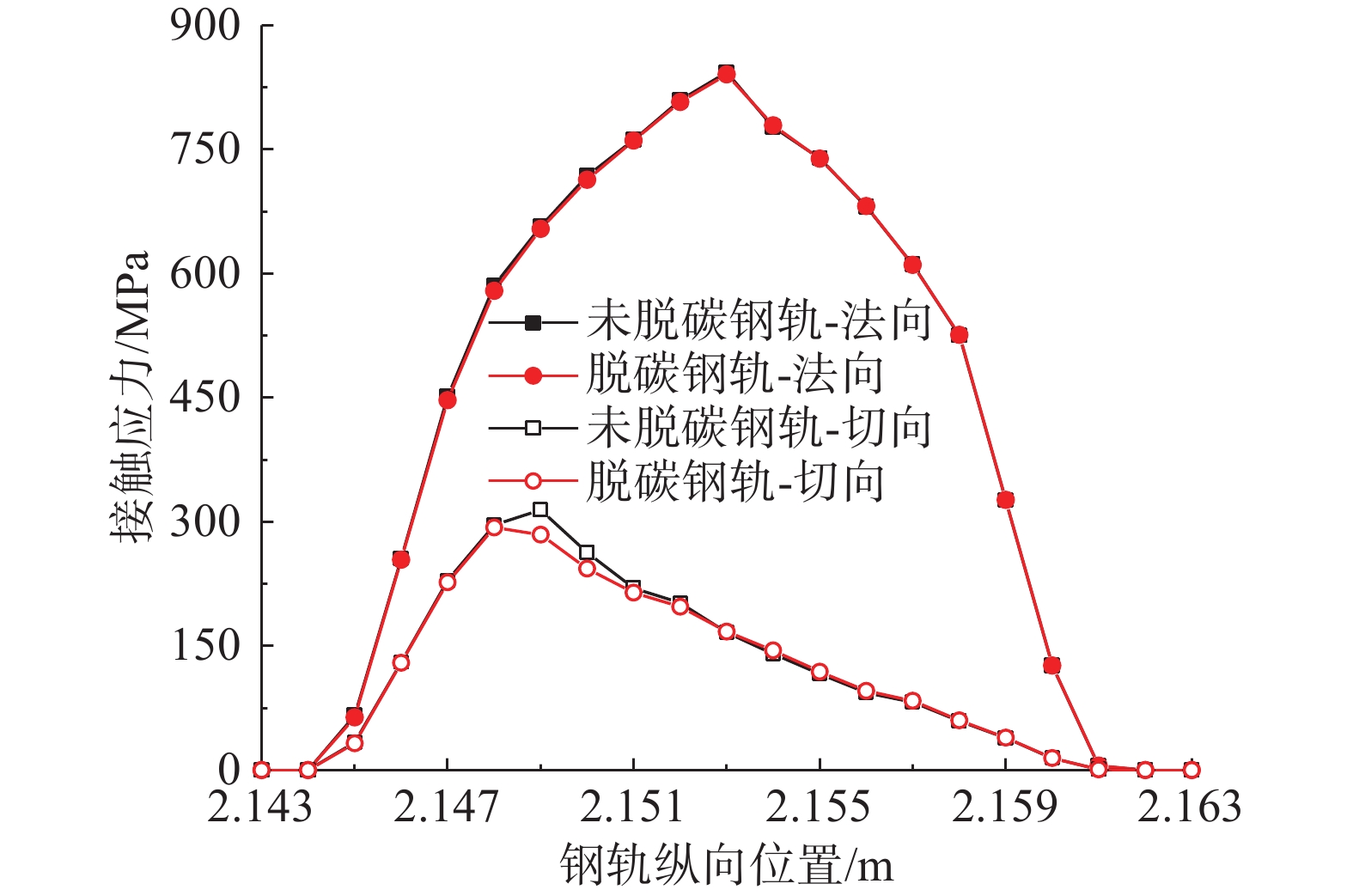
2) 轮轨接触应力
图8是车轮通过脱碳钢轨和未脱碳钢轨时，t3时刻沿路径L轮轨接触应力的对比。考虑脱碳层后最大法向接触应力为839 MPa，较不考虑脱碳层(843 MPa)降低了0.5%；最大切向接触应力为314 MPa，较不考虑脱碳层(292 MPa)降低了7%。脱碳层虽然降低了材料抵抗变形的能力，但是由于其厚度较小，所以对法向接触应力的影响可以忽略；与钢轨基体相比，脱碳层表层硬度和屈服应力降低了34%，大大降低了钢轨表面抵抗塑性变形的能力，所以在相同法向接触力的作用下，其塑性变形更大，因此对切向产生不可忽略的较大。这与接触斑大小和黏滑区划分的规律也是相对应的。
3) V-M等效应力
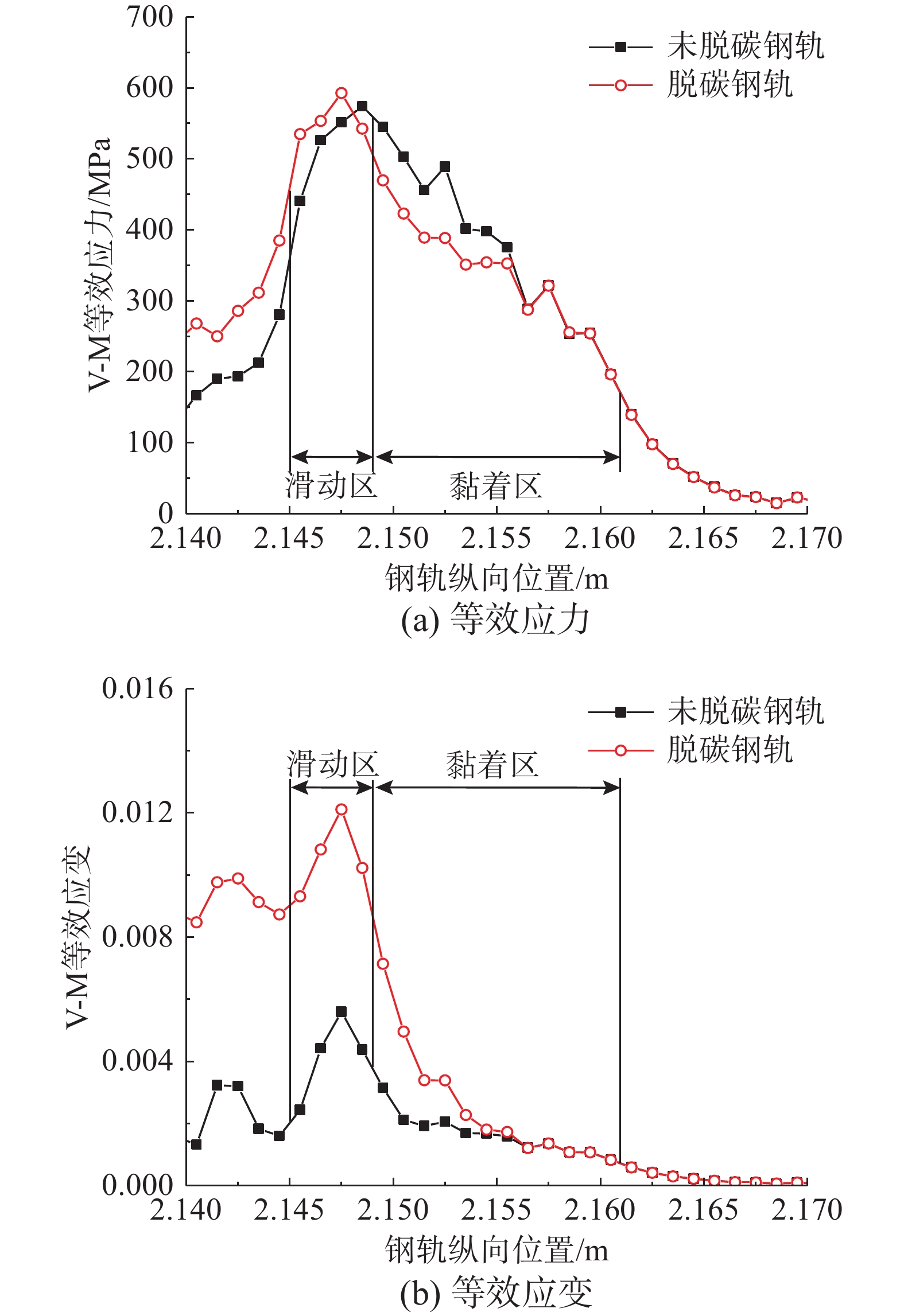
计算了2种工况下，钢轨表层V-M等效应力和应变沿路径L的二维分布，如图9所示，并从以下三个阶段进行分析。
![]()
图 9 钢轨表层V-M等效应力-应变Figure 9. The von mises equivalent stress-strain in rail surface layer第一阶段：脱碳钢轨和未脱碳钢轨均处于弹性阶段，此时V-M等效应力低于350 MPa时。脱碳层虽降低了弹性模量，但降幅较小(仅有10%)，所以呈现出V-M等效应力略有减小和V-M等效应变略有增加，如2.155 < x < 2.165。
第二阶段：脱碳钢轨进入塑性阶段，未脱碳钢轨处于弹性阶段，此时V-M等效应力超过350 MPa。因为弹性阶段比塑性阶段的斜率更大，所以脱碳钢轨等效应力的增长速率变缓，导致与未脱碳钢轨的等效应力的差异逐渐变大，如2.152 < x < 2.155，脱碳钢轨较未脱碳钢轨等效应力最大相差97 MPa，约为20%。
第三阶段：未脱碳钢轨进入塑性阶段，此时V-M等效应力超过500 MPa。由于脱碳钢轨与未脱碳钢轨的等效应力随等效应变的增幅相同，而脱碳钢轨较软，抵抗变形能力较弱，容易产生更大的塑性变形，所以当两者都进入屈服阶段后，脱碳钢轨的等效应变逐渐追上并超过脱碳钢轨；尤其在接触斑后沿部分，脱碳钢轨的等效应力远大于未脱碳钢轨。较不考虑脱碳层相比，考虑脱碳层后最大等效应变增加了115%。
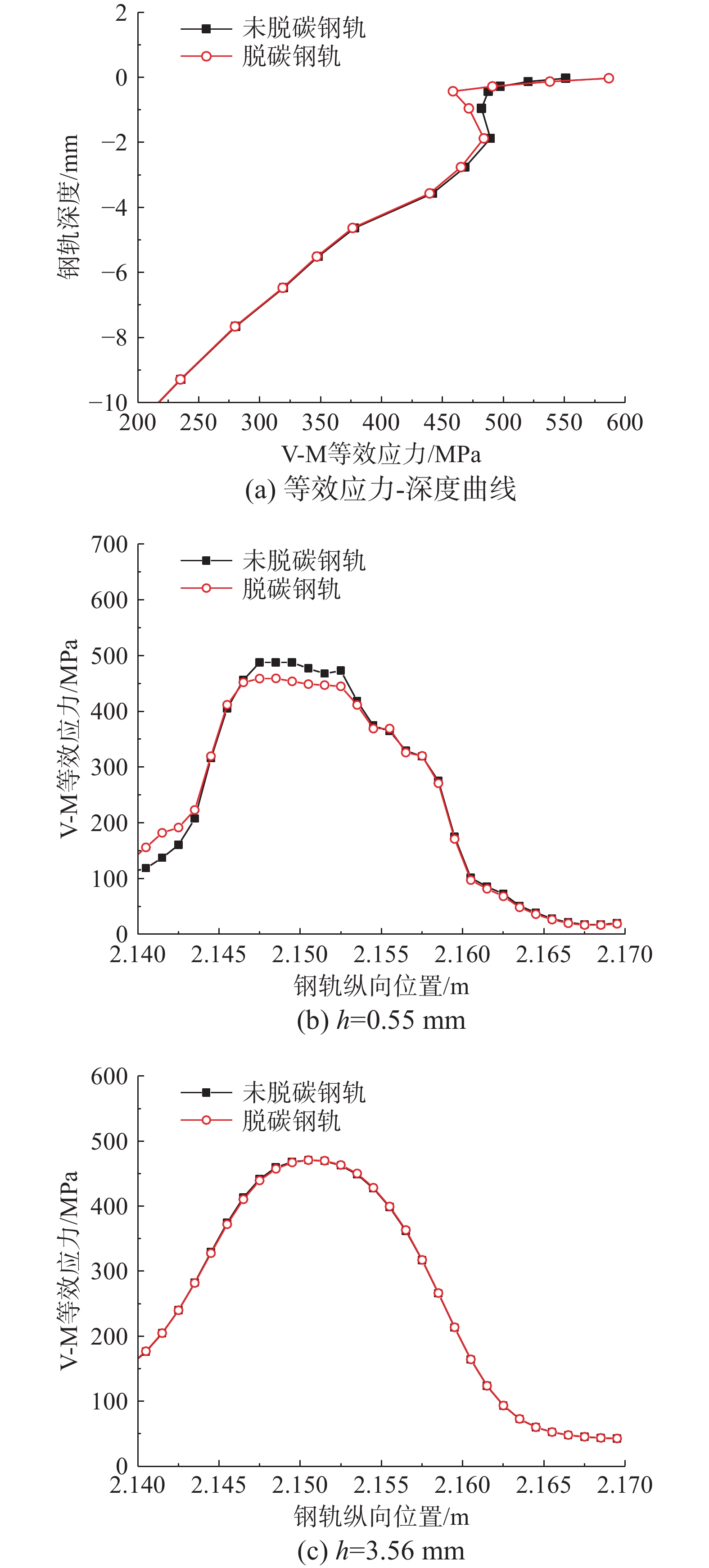
图10(a) 展示了脱碳钢轨和未脱碳钢轨路径L上最大等效应力所在截面的等效应力-深度曲线，结果表明：在脱碳层区域(距离钢轨表面0.55 mm内)，两者在同一深度的等效应力出现明显差异，在钢轨表层，脱碳钢轨的等效应力为587 MPa，较未脱碳钢轨551 MPa大了6.4%；越靠近钢轨基体，两者材料性能差异逐渐缩小，且以弹性变形为主，所以未脱碳钢轨的等效应力逐渐赶上并超越脱碳钢轨；脱碳层最深处两者差异达到最大，此时未脱碳钢轨的等效应力为488 MPa，较未脱碳钢轨459大了5.9%，如图10(b)所示；这与图9所示的等效应力和应变的规律也是吻合的。随后两者的差距开始逐渐缩小，直到距离脱碳层表面3.56 mm时，两者基本重合，如图10(c)所示。虽然脱碳层的深度仅有0.55 mm，但其对等效应力的影响范围达3.56 mm。
![]()
图 10 钢轨次表层V-M等效应力结果Figure 10. The von mises equivalent stress strain in rail subsurface layer钢轨表层及次表层的V-M等效应力和应变可以反映轮轨接触区域钢轨表层及次表层材料的整体应力水平。钢轨出厂时，其对脱碳层厚度的要求为应不大于0.5 mm。但从计算结果来看，尽管脱碳层厚度仅为0.55 mm，但影响程度却高达115%，影响深度也高达3.56 mm。所以，在线路正式运营之前，必须对新钢轨进行去除脱碳层目的的钢轨预打磨，以降低钢轨脱碳层对轮轨接触行为的影响，建议打磨后钢轨脱碳层不超过0.2 mm。
上述结论均是针对直线工况，而对于曲线线路，还会承受较大的横向力，尤其在超高设置不合理工况下，特别是对于小半径曲线，极易出现应力集中现象，这些都将导致轮轨接触会进一步恶化，同时也会扩大脱碳层对轮轨接触行为的影响。
4) 摩擦功
根据车轮滚动过程中在接触斑上的切向力和相对滑动速度可以求解得到摩擦功：
W=∫t0f⋅vdt=n∑i=0fiviΔt (5) 式中：f和v为该点的切向力和相对滑动速度；将t时间分为n份，fi和vi为对应的切向力和相对滑动速度；Δt为时间间隔，Δt = 2.4×10−5 s。
计算得到了钢轨表面沿路径L上材料在车轮滚过结果区所受的摩擦功，脱碳层降低了钢轨表面的摩擦功，降幅为8%。这是因为脱碳层材料较软，抵抗变形能力较小，导致切向力变小，进而降低表面摩擦功。值得注意的是，摩擦功的降低并不意味着材料的磨损率降低。因为材料硬度的降低导致材料抗磨性的降低，而且硬度的降幅为34%，与摩擦功相比，对磨损率的贡献更大。所以脱碳层虽然降低了钢轨表面的摩擦功，但其磨损率却是增加的。
同样，对于磨耗相对严重的曲线线路，尤其对于侧磨严重的小半径曲线，会产生更大的横向、纵向和自旋蠕滑力，导致磨耗进一步加剧。所以，钢轨脱碳层对曲线线路磨耗的影响将会更大。因此，更值得引起现场工作人员的关注，严格控制曲线线路钢轨脱碳层的厚度，包括对曲线换轨后脱碳层深度的控制。
4 结论
对脱碳深度0.55 mm的钢轨脱碳层试样的不同垂向位置进行了纳米压痕实验，利用Oliver-Pharr方法计算得到了脱碳层非均匀弹性模量和硬度。建立了可以考虑脱碳层的三维轮轨瞬态滚动接触有限元模型，分析了脱碳层对轮轨接触行为的影响，主要结论如下：
(1) 从钢轨基体到脱碳层表面，弹性模量和硬度逐渐减小；脱碳深度0.55 mm时，钢轨脱碳层表层弹性模量和硬度分别为185 GPa和1.90 GPa，较钢轨基体分别降低了10%和34%；
(2) 钢轨脱碳层对轮轨接触斑大小、黏滑区划分和法向接触应力的影响可以忽略；降低了轮轨切向接触应力和表层摩擦功，最大降幅分别为9.4%和8%；
(3) 当脱碳钢轨进入塑性阶段，脱碳层对钢轨表层等效应力和应变产生较大影响，最大等效应力降低20%，最大等效应变增加115%；
(4) 钢轨脱碳层对V-M等效应力影响显著，虽然脱碳深度只有0.55 mm，但对V-M等效应力的影响深度达3.56 mm。
(5) 脱碳层材料较软，抵抗变形能力较小，导致表面摩擦功降低，降幅约为8%，但这并不代表轮轨磨损率会因此而降低。
-
![]()
图 3 脱碳层材料力学性能
Figure 3. The mechanical properties of material of rail decarburized layer
![]()
图 4 考虑脱碳层的三维轮轨瞬态滚动接触有限元模型
Figure 4. The three-dimensional transient rolling contact finite element model considering rail decarburization layer
![]()
图 6 轮轨瞬态接触应力纵向路径L的分布
Figure 6. Distribution of transient wheel-rail contact stress along longitudinal path L
![]()
图 9 钢轨表层V-M等效应力-应变
Figure 9. The von mises equivalent stress-strain in rail surface layer
![]()
图 10 钢轨次表层V-M等效应力结果
Figure 10. The von mises equivalent stress strain in rail subsurface layer
表 1 材料属性
Table 1 Material properties
物理量 值 单位 簧上质量 7414 kg 轮对质量 586 kg 一系刚度系数 0.88 MN/m 一系阻尼 4 kN·s/m 车轮弹性模量 206 GPa 车轮泊松比 0.3 − 车轮密度 7790 kg/m3 车轮阻尼常数 1.0×10−4 β/s 轨道板材料弹性模量 34.5 GPa 轨道板泊松比 0.25 − 轨道板密度 2400 kg/m3 橡胶垫刚度系数 22 MN/m 橡胶垫阻尼 200 kN·s/m 钢轨泊松比 0.3 − 钢轨密度 7790 kg/m3 钢轨阻尼常数 1.0×10−4 β/s 砂浆层弹性模量 8 GPa 砂浆层泊松比 0.2 − 砂浆层密度 1600 kg/m3 轨道板接头弹性模量 29.5 GPa 轨道板接头泊松比 0.25 − 轨道板接头密度 2400 kg/m3 
下载: 导出CSV
-
[1] 金学松, 刘启跃. 轮轨摩擦学[M]. 北京: 中国铁道出版社, 2004: 150 − 151. JIN Xuesong, LIU Qiyue. Tribology of wheel and rail [M]. Beijing: China Railway Publishing House, 2004: 150 − 151. (in Chinese)
[2] JOHNSON K L. Contact mechanics [M]. Cambridge: Cambridge University Press, 1992: 287 − 292.
[3] 黎嘉欣, 陶功权, 刘希政, 等. 基于两种轨道线路建模方法的地铁车轮磨耗预测对比分析[J]. 工程力学, 2022, 39(6): 226 − 235. doi: 10.6052/j.issn.1000-4750.2021.02.0117 LI Jiaxin, TAO Gongquan, LIU Xizheng, et al. Comparative analysis of metro wheel wear prediction based on two track modeling methods [J]. Engineering Mechanics, 2022, 39(6): 226 − 235. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.02.0117
[4] GRASSIE S L. Short wavelength rail corrugation: Field trials and measuring technology [J]. Wear, 1996, 191(1/2): 149 − 160.
[5] 谷永磊. 高速铁路无砟轨道钢轨波浪形磨损机理研究[D]. 北京: 北京交通大学, 2017. GU Yonglei. Study on the mechanism of rail corrugation on high-speed railway unballasted track [D]. Beijing: Beijing Jiaotong University, 2017. (in Chinese)
[6] 朱胜阳, 蔡成标, 尹镪, 等. 高速铁路扣件弹条动力学分析[J]. 工程力学, 2013, 30(6): 254 − 258, 287. doi: 10.6052/j.issn.1000-4750.2012.05.0314 ZHU Shengyang, CAI Chengbiao, YIN Qiang, et al. Dynamic analysis of rail fastening clip in high-speed railway [J]. Engineering Mechanics, 2013, 30(6): 254 − 258, 287. (in Chinese) doi: 10.6052/j.issn.1000-4750.2012.05.0314
[7] CARROLL R I, BEYNON J H. Decarburisation and rolling contact fatigue of a rail steel [J]. Wear, 2006, 260(4/5): 523 − 537.
[8] ZHAO X J, GUO J, WANG H Y, et al. Effects of decarburization on the wear resistance and damage mechanisms of rail steels subject to contact fatigue [J]. Wear, 2016, 364/365: 130 − 143. doi: 10.1016/j.wear.2016.07.013
[9] ZHAO X J, WANG H Y, GUO J, et al. The effect of decarburized layer on rolling contact fatigue of rail materials under dry-wet conditions [J]. Engineering Failure Analysis, 2018, 91: 58 − 71. doi: 10.1016/j.engfailanal.2018.04.026
[10] 寇峻瑜, 王衡禹, 赵鑫, 等. 钢轨脱碳层对轮轨瞬态滚动接触行为的影响分析[J]. 机械工程学报, 2018, 54(4): 101 − 108. KOU Junyu, WANG Hengyu, ZHAO Xin, et al. Influence of rail decarburization layer on wheel-rail transient rolling contact behavior [J]. Journal of Mechanical Engineering, 2018, 54(4): 101 − 108. (in Chinese)
[11] ZHAO G T, CHEN S, WU L, et al. Study of constitutive relation of rail decarburized layer [J]. Engineering Failure Analysis, 2021, 130: 105792.
[12] CHEN S, ZHAO G T, LIU S, et al. Effects of decarburized layer's material property on the rail corrugation development [J]. Wear, 2023, 530/531: 205040.
[13] 温泽峰. 钢轨波浪形磨损研究[D]. 成都: 西南交通大学, 2006. WEN Zefeng. Study on rail corrugation [D]. Chengdu: Southwest Jiaotong University, 2006. (in Chinese)
[14] 马亚鑫, 高怡斐, 曾雨吟, 等. 利用纳米压痕表征高铁车轮微观相的力学性能[J]. 材料导报, 2015, 29(6): 102 − 106. doi: 10.11896/j.issn.1005-023X.2015.06.022 MA Yaxin, GAO Yifei, ZENG Yuyin, et al. Characterizing mechanical properties of micro-phases in high-speed railway wheel steel by nano-indentation [J]. Materials Review, 2015, 29(6): 102 − 106. (in Chinese) doi: 10.11896/j.issn.1005-023X.2015.06.022
[15] 秦飞, 项敏, 武伟. 纳米压痕法确定tsv-cu的应力-应变关系[J]. 金属学报, 2014, 50(6): 722 − 726. QIN Fei, XIANG Min, WU Wei. The stress-strain relationship of tsv-cu determined by nanoindentation [J]. Acta Metallurgica Sinica, 2014, 50(6): 722 − 726. (in Chinese)
[16] LEE J, LEE C, KIM B. Reverse analysis of nano-indentation using different representative strains and residual indentation profiles [J]. Materials & Design, 2009, 30(9): 3395 − 3404.
[17] DAO M, CHOLLACOOP N, VAN VLIET K J, et al. Computational modeling of the forward and reverse problems in instrumented sharp indentation [J]. Acta Materialia, 2001, 49(19): 3899 − 3918. doi: 10.1016/S1359-6454(01)00295-6
[18] 刘帅, 陈帅, 林川淇, 等. 多边形磨耗车轮表层材料的力学性能研究[J]. 工程力学, 2023, doi: 10.6052/j.issn.1000-4750.2023.02.0112. LIU Shuai, CHEN Shuai, LIN Chuanqi, et al. Mechanical properties of surface material on polygonal wheels [J]. Engineering Mechanics, 2023, doi: 10.6052/j.issn.1000-4750.2023.02.0112. (in Chinese)
[19] 罗素蓉, 承少坤, 肖建庄, 等. 纳米改性再生骨料混凝土单轴受压疲劳性能[J]. 工程力学, 2021, 38(10): 134 − 144. doi: 10.6052/j.issn.1000-4750.2020.09.0700 LUO Surong, CHENG Shaokun, XIAO Jianzhuang, et al. Fatigue behavior of nano-modified recycled aggregate concrete under uniaxial compression [J]. Engineering Mechanics, 2021, 38(10): 134 − 144. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.09.0700
[20] OLIVER W C, PHARR G M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments [J]. Journal of Materials Research, 1992, 7(6): 1564 − 1583.
[21] 刘美华, 李鸿琦, 王静, 等. 纳米压痕测量精度的影响因素[J]. 机械工程材料, 2008, 32(8): 4 − 7, 73. LIU Meihua, LI Hongqi, WANG Jing, et al. Influencing factors of nano-indentation test precision [J]. Materials for Mechanical Engineering, 2008, 32(8): 4 − 7, 73. (in Chinese)
[22] 赵鑫, 温泽峰, 王衡禹, 等. 三维高速轮轨瞬态滚动接触有限元模型及其应用[J]. 机械工程学报, 2013, 49(18): 1 − 7. doi: 10.3901/JME.2013.18.001 ZHAO Xin, WEN Zefeng, WANG Hengyu, et al. 3D transient finite element model for high-speed wheel-rail rolling contact and its application [J]. Journal of Mechanical Engineering, 2013, 49(18): 1 − 7. (in Chinese) doi: 10.3901/JME.2013.18.001
计量
- 文章访问数: 26
- HTML全文浏览量: 2
- PDF下载量: 7
