STUDY ON PREDICTIVE MODEL FOR EFFECTIVE STIFFNESS OF RC RECTANGULAR HOLLOW PIERS USING INTERPRETABLE ENSEMBLE MACHINE LEARNING
-
摘要:
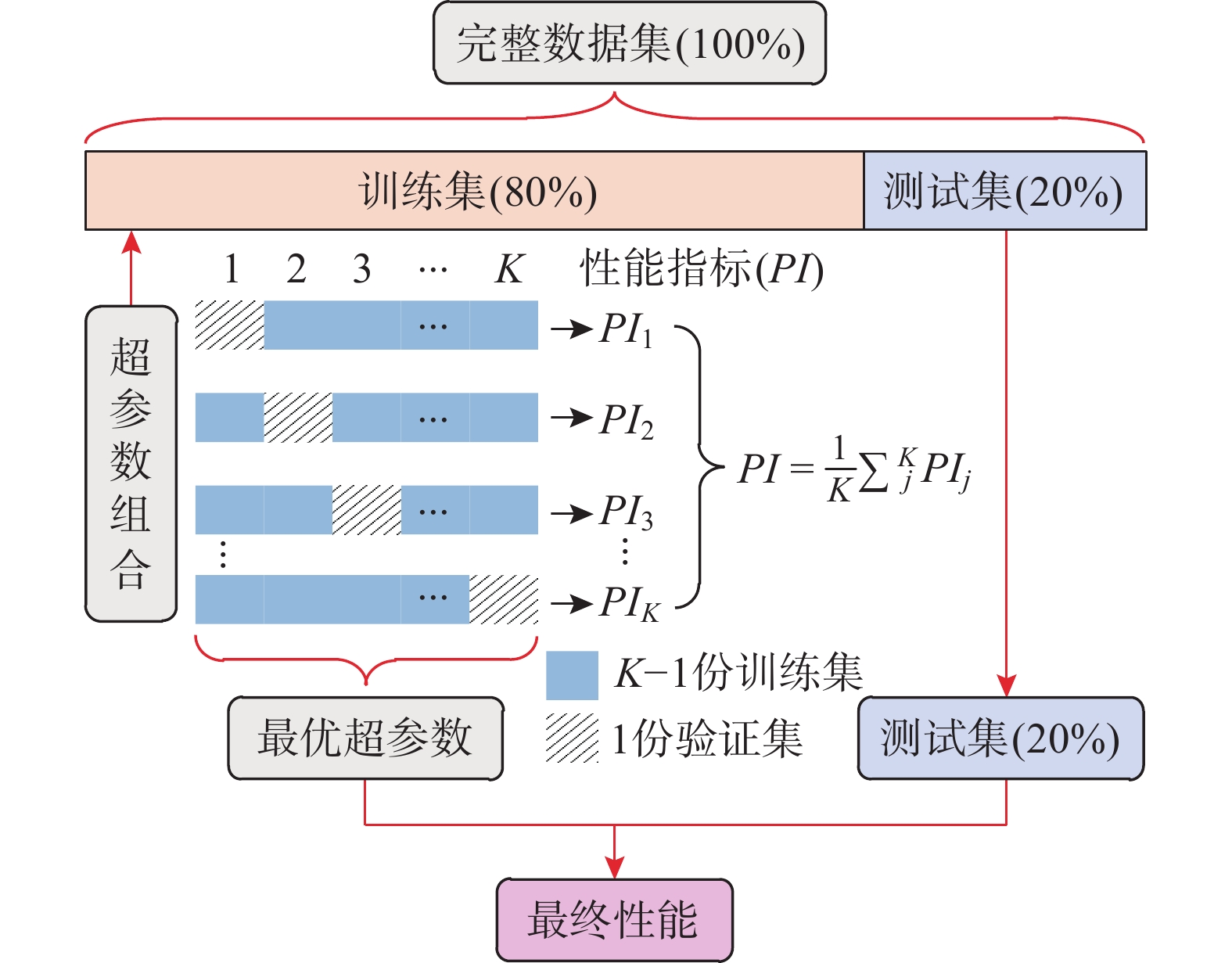
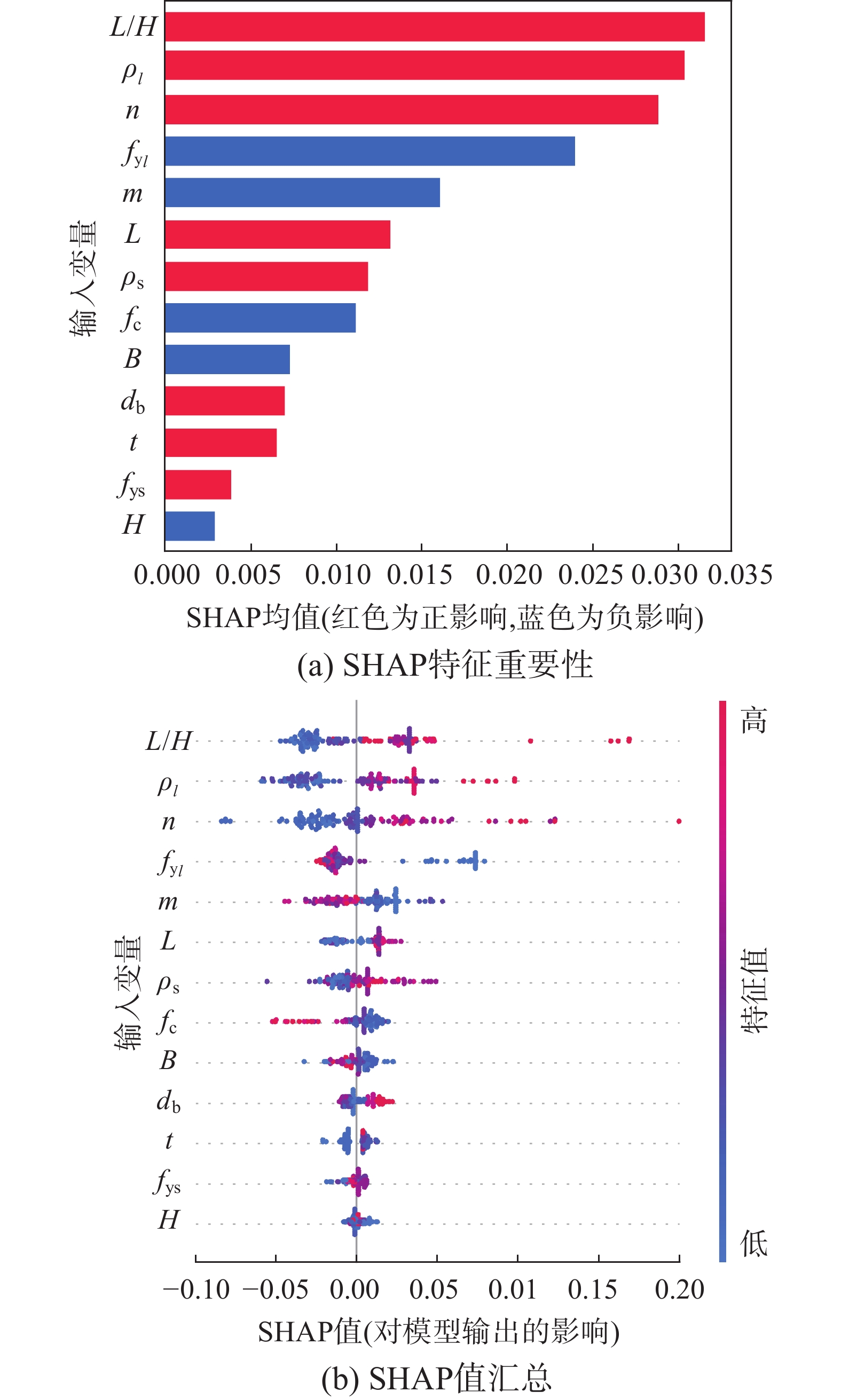
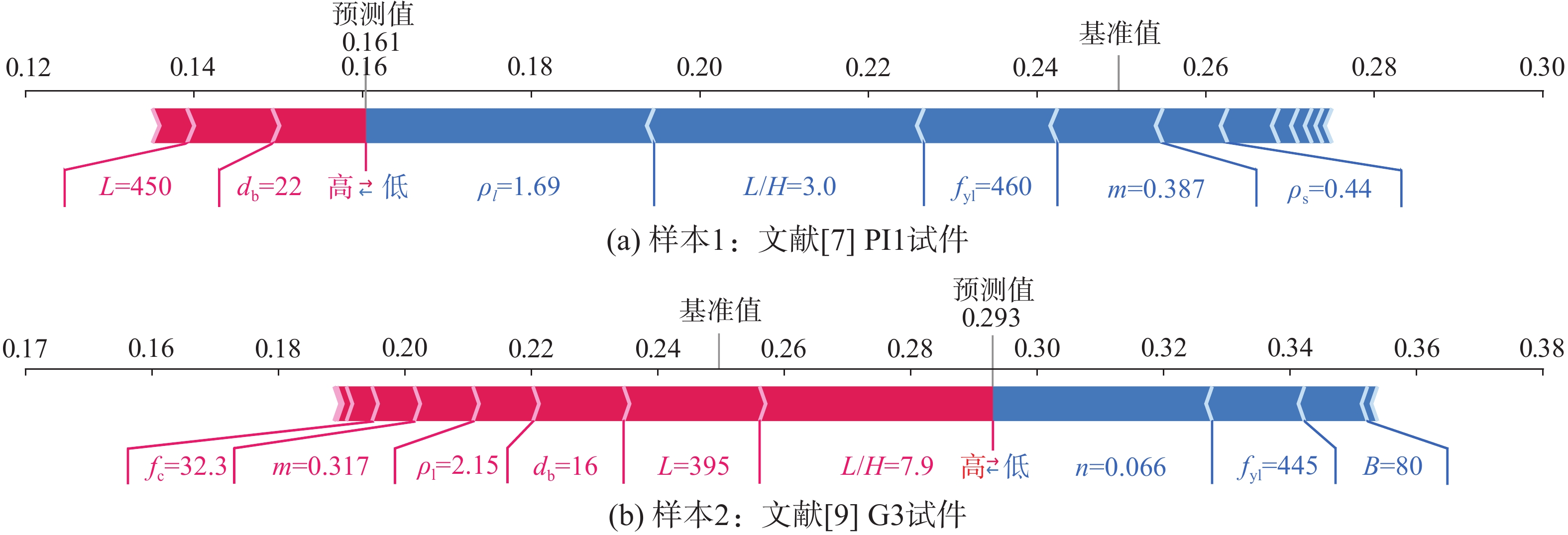
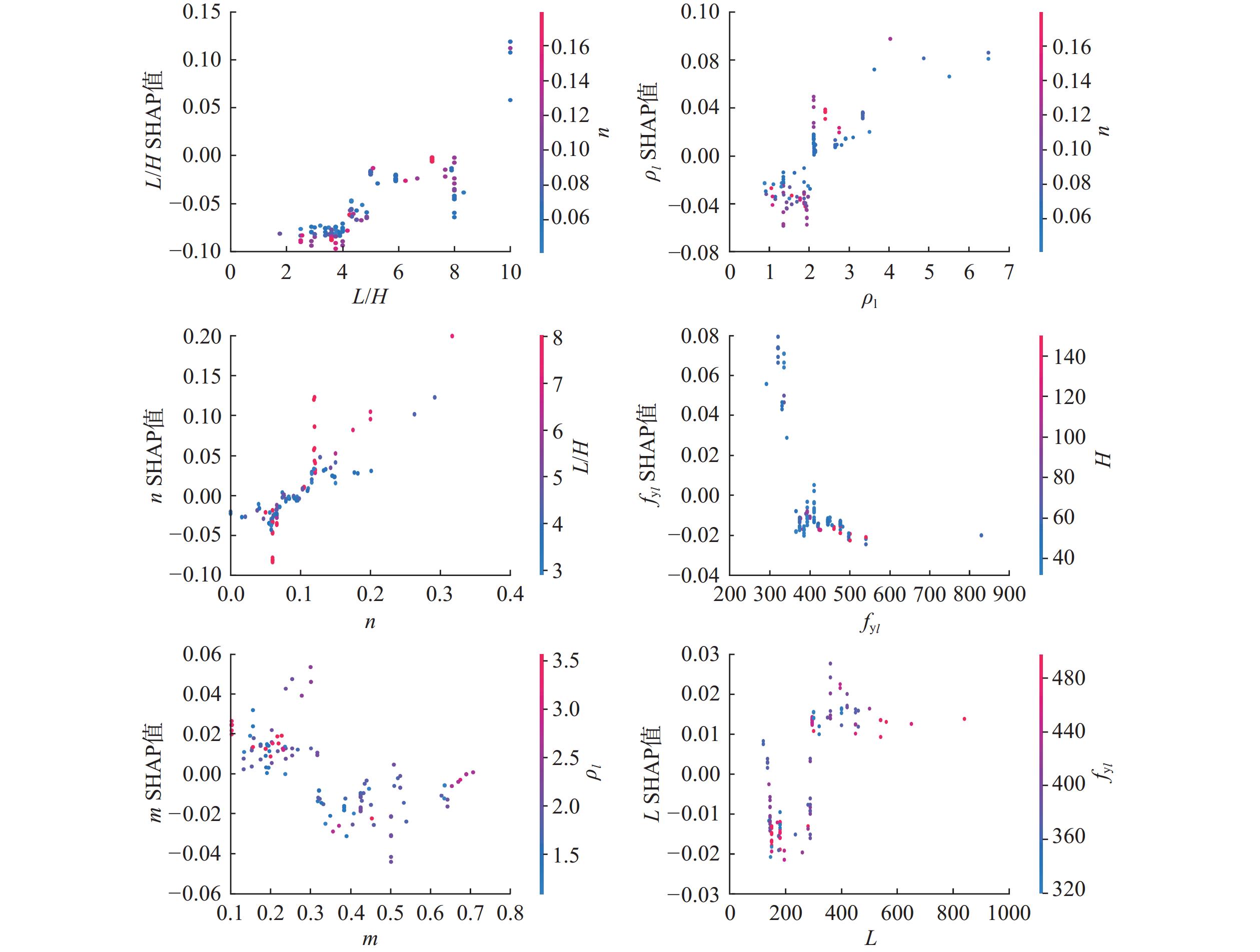
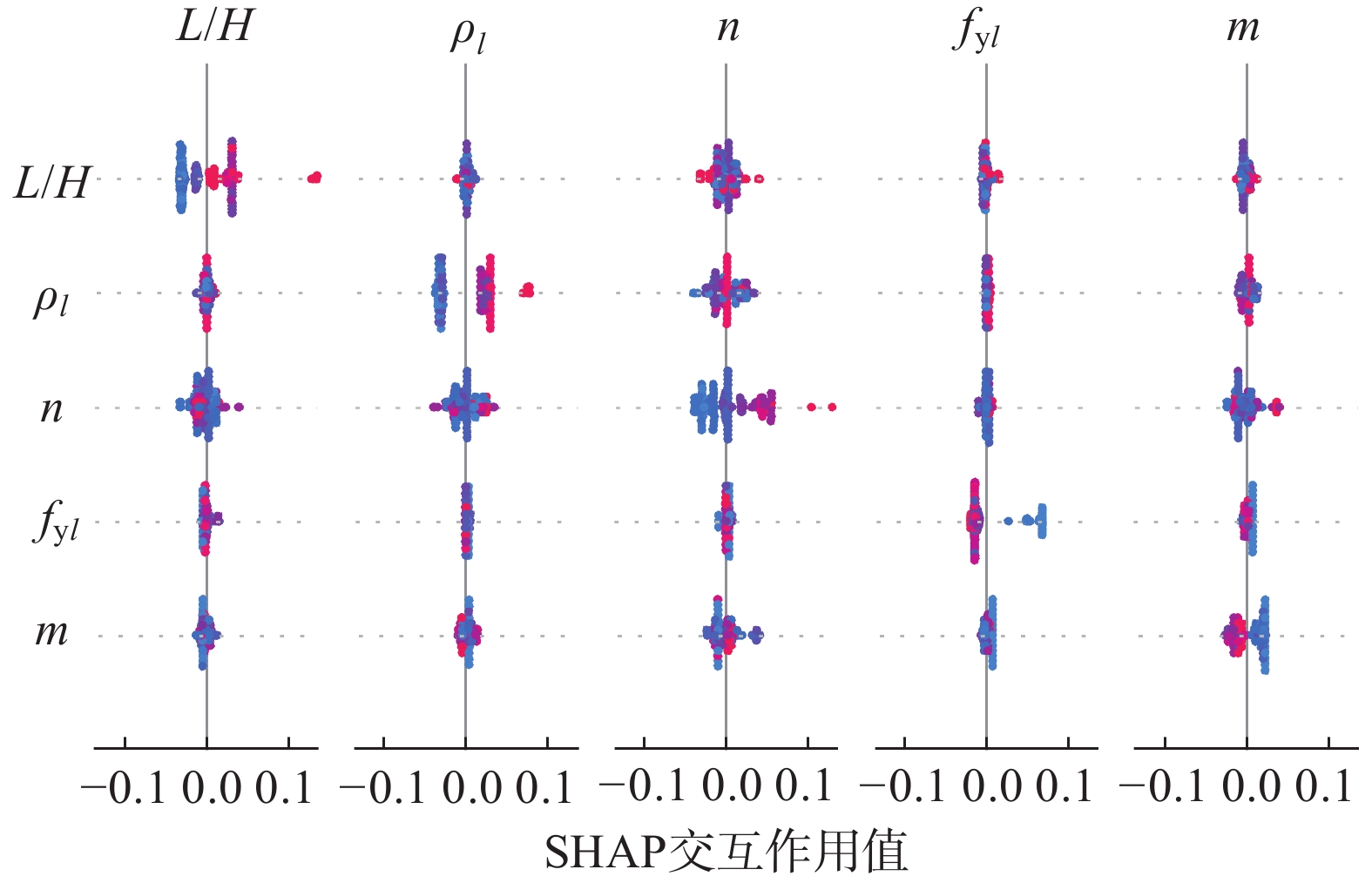
为获得较准确的钢筋混凝土矩形空心墩有效刚度预测模型，建立了包含131个弯曲破坏为主的矩形空心墩有效刚度数据集，分析了既有有效刚度模型对矩形空心墩的适用性；以13个特征作为输入参数，构建了支持向量机回归(SVR)、随机森林回归(RFR)、极端随机树回归(ERTR)、梯度提升树回归(GBTR)、极端梯度提升树回归(XGBR)及投票集成回归(VOTR)等6个有效刚度机器学习模型；对既有模型、机器学习模型的预测性能进行评估与比较；并采用SHAP 方法对XGBR模型进行解释。研究表明：除王震、韦旺模型外，既有公式在平均意义上严重高估了矩形空心墩的有效刚度，且各模型的变异系数较大；与既有模型相比，机器学习算法具有很大的优越性，即使预测性能最低的SVR模型也比所有既有模型的预测精度高；在单次集成器学习模型中，XGBR模型的预测性能较好，该文提出的二次集成VOTR模型的预测性能较XGBR有进一步提高，具有更高的预测精度，其在完整数据集上的均方根误差(RMSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)及决定系数(R2)分别为1.3%、0.7%、3.4%和0.990，预测值与试验值之比的均值和变异系数分别为1.01和0.07，给出了最稳定、安全和准确的预测结果，远优于既有模型；SHAP 方法可以从全局层面和个体水平对模型预测结果作出解释，对于XGBR模型，按重要性排序的前5个特征依次为剪跨比L/H、纵筋率ρl、轴压比n、纵筋屈服强度fyl及材料几何参数m(即fyldb /L√fc)，有助于有效刚度解析模型的改进。
Abstract:To obtain an accurate prediction model for the effective stiffness of RC rectangular hollow piers, established a dataset containing 131 samples with bending failure as the main failure mode. The applicability of existing effective stiffness models to rectangular hollow piers was analyzed. Six machine learning models for predicting effective stiffness were constructed, including support vector regression (SVR), random forest regression (RFR), extreme random tree regression (ERTR), gradient boosting tree regression (GBTR), extreme gradient boosting tree regression (XGBR), and voting ensemble regression (VOTR). These models were trained by using 13 features as input parameters. The prediction performance of existing models and of machine learning models was evaluated by using 131 samples. And the SHAP method was used to explain the XGBR model. The research showed that: except for Wang’s and Wei’s models, existing formulas significantly overestimated the effective stiffness of rectangular hollow piers on mean value of statistical meaning, and the coefficients of variation of each model were relatively large. Compared with existing models, machine learning algorithms had great advantages, and even the SVR model with the lowest prediction performance had higher prediction accuracy than all existing models. Among single-ensemble learning models, the XGBR model had the best prediction performance. The proposed double-ensemble VOTR model further improved the prediction performance and had the highest prediction accuracy. The root-mean square error (RMSE), mean absolute error (MAE), mean absolute percentage error (MAPE), and coefficient of determination (R2) of VOTR model on the complete data set were 1.3%, 0.7%, 3.4%, and 0.990, respectively; and the average and coefficient of variation of the ratio of predicted value to test value were 1.01 and 0.07, respectively. The VOTR model obtained the most stable, safe, and accurate prediction results, which was far superior to existing models. The SHAP method can explain the model prediction results from both the global and individual levels. For XGBR model, the top five features in the importance order were shear span ratio L/H, longitudinal reinforcement ratio ρl, axial compression ratio n, longitudinal reinforcement yield strength fyl, and material geometric parameter m (i.e. fyldb/L√fc), which were helpful for improving the physical analysis model of effective stiffness of RC rectangular hollow piers.
-
基坑工程采用反压土支护具有良好的经济效益，同时更有利于大面积基坑开挖，因而在实际工程中得到了越来越多的应用。但是目前反压土支护尚没有设计规范，设计人员往往只能借鉴已有经验来设计。国内外学者进行了一些理论和数值模拟研究[1 − 4]，笔者也提出了一种基于极限平衡理论的简化计算方法[5]，但是这些研究都是针对比较简单的工况，通常是单级反压土支护悬壁挡墙。北京城市副中心站综合交通枢纽Ⅴ区基坑是深大基坑，采用两级反压土支护，开挖工序复杂，环境保护要求高，本文通过三维数值模拟对该基坑两级反压土支护效果进行分析，采用能反映土体小应变刚度特性的小应变硬化模型(HSs, Hardening strain model with small strain)并确定适用于北京地区土层的相应参数，并将HSs模型的计算结果与工程设计中常用的摩尔-库伦模型的计算结果进行对比。
1 工程概况
1.1 项目及基坑概况
北京城市副中心站综合交通枢纽位于北京城市副中心核心区，是亚洲最大的地下综合交通枢纽，包含京唐城际和城际铁路联络线两条铁路。城际车站区域东西长度为1800 m，宽为195 m，东咽喉及站台区基坑深度约为33 m，西咽喉区自东向西逐渐加深，盾构井处最大深度为48 m。基坑分三期施工，划分了六个区(图1)，一期施工Ⅰ、Ⅲ、Ⅴ区基坑，其中Ⅴ区基坑宽度大、范围广、深度深，施工工序复杂，该基坑北部采用两级反压土支护，且基坑北侧约40 m处是既有京哈铁路线，因此对该区段基坑施工的变形预测为设计的重难点。
1.2 工程地质
根据地勘报告，场地土质条件以砂土、粉质黏土为主，夹杂有粉土层，从上到下具体土层划分为：①素填土；②黏质粉土-砂质粉土；③细砂-中砂；④细砂-中砂；⑤细砂-中砂；⑥1重粉质黏土-粉质黏土；⑥细砂-中砂；⑦粉质黏土-重粉质黏土；⑦1黏质粉土-砂质粉土；⑧细砂-中砂；⑨1粉质黏土-重粉质黏土；⑨细砂-中砂；⑩粉质黏土-重粉质黏土；⑪细砂-中砂；⑫1重粉质黏土-粉质黏土；⑫细砂-中砂；⑬粉质黏土-重粉质黏土；⑬1细砂-中砂；⑭粉质黏土-重粉质黏土；⑭1中砂-细砂。基坑所在地层整体为高水位的富水砂层，各土层厚度及参数将结合后面有限元参数取值给出。另外，根据地勘报告，地下水水位约为地表以下10 m处。
1.3 支护方案与施工工序
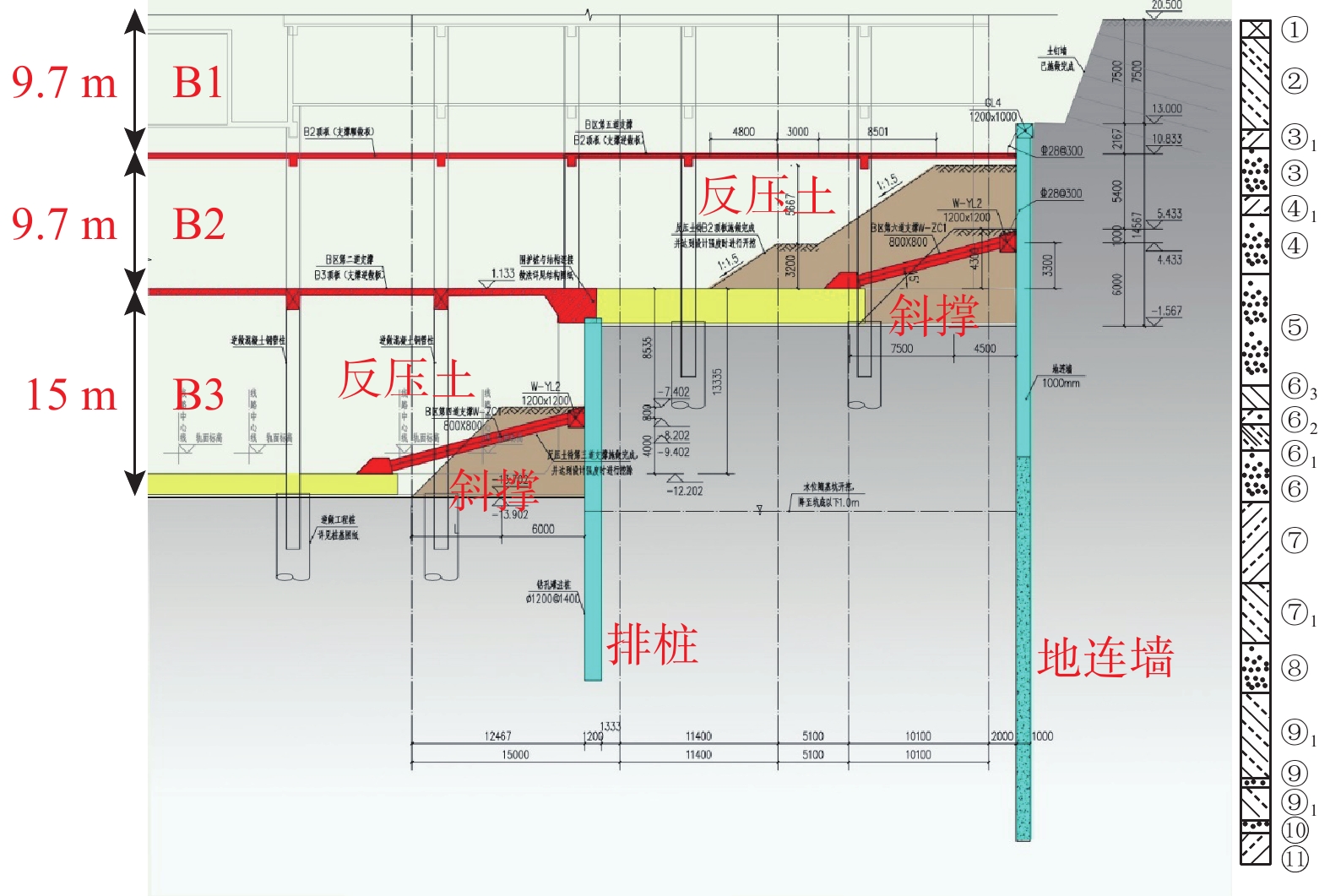
分析断面剖面如图2，一共分为三层，其中B1层是进站层，B2层是候车层，B3层是站台层，其层高分别为9.7 m、9.7 m、15 m，基坑总深度34.4 m。该断面位于Ⅴ区北部，北侧为京哈铁路，因此需要严格控制基坑外侧土体的变形。
由于该基坑宽度接近200 m，如果采用多道钢筋混凝土水平内支撑，则经济性不合理，也不利于大面积挖土作业。另外，由于地下水位较高，该基坑B2、B3层深度范围内地层以饱和砂层为主，如采用预应力锚杆支护需要对坑外进行降水，但降水会引起附近地层较大沉降。
因此，该断面B1层采用放坡开挖，土钉墙支护；B2层采用盆式开挖，中部顺作，外围预留反压土支护地连墙，待中部结构施作后，外围反压土部位的结构采用逆作施工；B3层由于层高达15 m，先施作B3层顶板，对排桩围护结构提供顶部支撑，然后采取逆作施工，并预留反压土支护排桩。B2层反压土高度为8.9 m，顶部宽度为5.4 m，底部宽度为22.1 m，坡度为1∶1.5，中部平台段距底部高3.2 m。B3层反压土高度为6.5 m，顶部宽度为6 m，底部宽度为12.5 m。
该断面支护结构尺寸如表1所示，具体施工工序如下：
Phase 1：分五步开挖B1层，每步开挖1.5 m，随开挖逐步施作土钉墙；
Phase 2：施作地连墙、钻孔灌注桩、立柱、工程桩等构件；
Phase 3：预留反压土开挖B2层，坑内水位随开挖降低到坑底以下1 m；
Phase 4：施作B3层顶板；
Phase 5：预留反压土开挖B3层，坑内水位随开挖降低到坑底以下1 m；
Phase 6：B3层反压土开槽，便于施作斜撑；
Phase 7：施作B3层部分底板及斜撑；
Phase 8：开挖B3层反压土；
Phase 9：施作B3层剩余底板及支撑下侧墙；
Phase 10：拆除B3层斜撑；
Phase 11：施作B3层侧墙；
Phase 12：施作B2层结构柱和顶板；
Phase 13：开挖部分B2层反压土；
Phase 14：B2层反压土开槽，便于施作斜撑；
Phase 15：施作B2层边跨部分底板及斜撑；
Phase 16：开挖B2层剩余反压土；
Phase 17：施作B2层边跨剩余底板及支撑下侧墙；
Phase 18：拆除B2层斜撑；
Phase 19：施作B2层侧墙。
表 1 支护结构尺寸Table 1. Sizes of supporting structures支护结构 尺寸 地连墙 厚度1 m 排桩 直径1.2 m、间距1.4 m 立柱 直径1 m、间距10 m 工程桩 直径2 m、间距10 m B3层顶板 厚度0.6 m B3层底板 厚度1.5 m B3层侧墙 厚度1.9 m B2层顶板 厚度0.3 m B2层边跨底板 厚度2.7 m B2层侧墙 厚度2 m 斜撑 截面0.8 m×0.8 m、间距4.5 m 2 有限元分析
2.1 数值模型及施工工序模拟
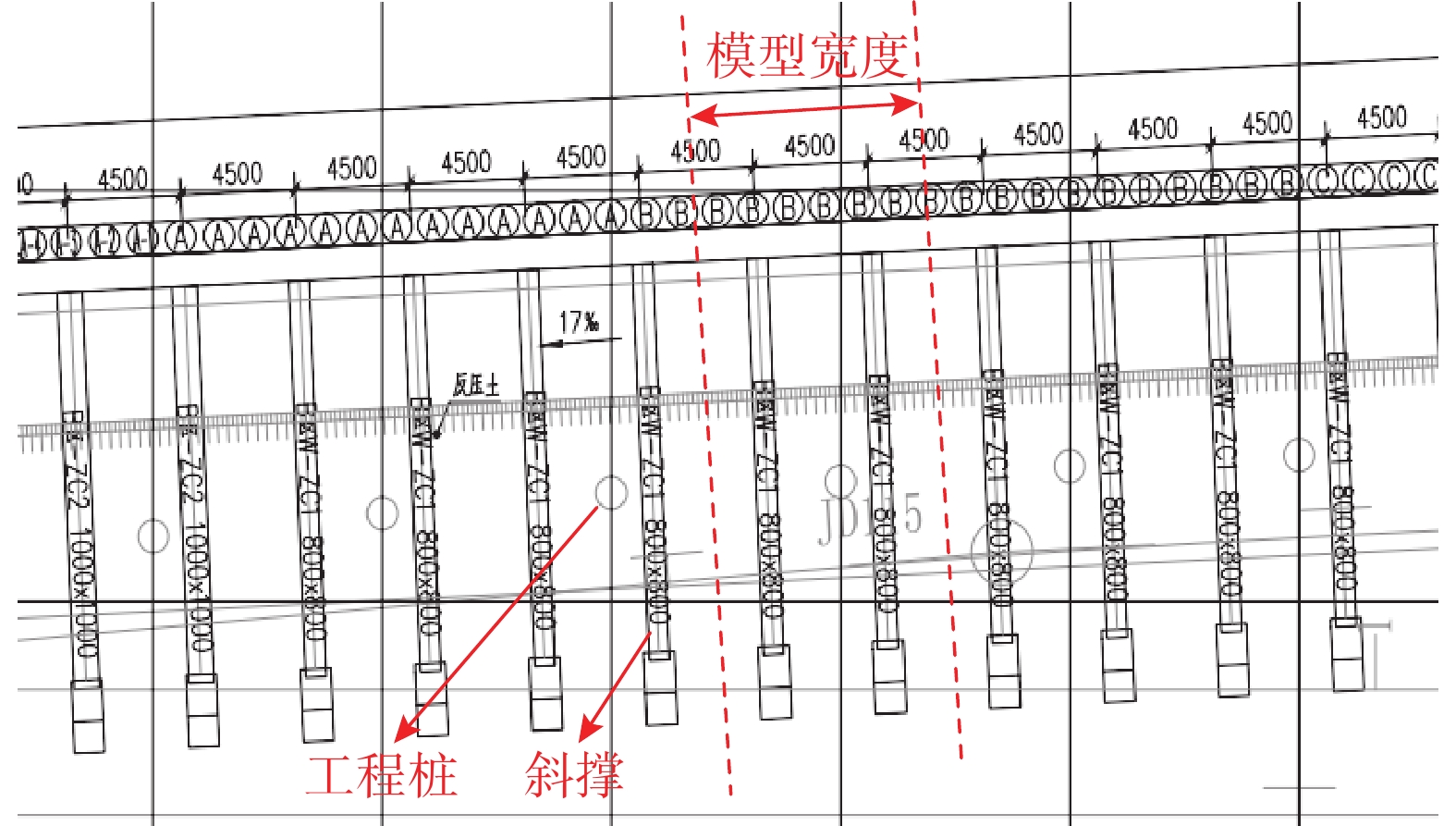
为了建立能够模拟基坑全施工过程的数值模型，采用大型岩土有限元软件Plaxis 3D进行数值模拟[6]。一方面，二维模型将土钉与工程桩等模拟为一片板，不能真实反映土钉间和桩间土体的变形[7]。另一方面，如果对整个Ⅴ区基坑进行建模将导致庞大的计算量，效率很低。Ⅴ区基坑典型支护布置如图3，斜撑间距4.5 m，工程桩间距9 m，刚好成倍数关系。利用对称性，采取宽度方向切片形式，以桩间距为厚度进行建模。该局部三维模型[7]既能考虑土钉、工程桩等结构的三维效应，又节省了计算资源。另外，根据ZDRAVKOVIC等[8]的研究，当矩形基坑长宽比大于4时，长边中点按平面应变来考虑的误差小于10%，而本文所研究的Ⅴ区基坑长度为640 m，远大于基坑深度，且基坑宽度为120 m~190 m，长宽比为5.3~3.4，三维空间效应较弱，因此取局部三维模型计算是合理的。
建立的3D数值模型如图4，模型大小为200 m×100 m×9 m。所建模型宽度方向包括一根工程桩、两个斜撑、六根土钉，桩、柱位置均处于模型中部。其中工程桩采用实体单元模拟，斜撑、结构柱采用梁单元模拟，地连墙、排桩、结构顶板、土钉墙墙面采用板单元模拟，土钉采用嵌入式梁单元模拟。考虑到工程的实际情况，所有构件均采用弹性模型，土钉的弹性模量为50 GPa，其他结构构件均为30 GPa。根据地勘报告，共划分了20个土层。根据前文所述施工工序，数值模型共划分了19个大的计算阶段，如图5，涉及开挖的计算阶段分多步完成。基坑内部水位随开挖降到坑底以下1 m，地连墙外侧水位不变。部分数值模型的详图见图6。
2.2 本构模型及参数取值
由于基坑北侧约40 m处是京哈铁路，因此在设计阶段非常关心基坑施工引起的周边地表沉降，这就需要合理模拟土的变形特性。基坑周边大部分土体处于小应变区间(约10−5~10−3)[9 − 10]，目前的研究表明土体在小应变情况下具有很高的刚度，而且表现为高度非线性[11]，为了合理分析土体变形需要考虑小应变刚度特性[12]。另外土体卸载过程中表现出比加载时要高得多的刚度[13 − 14]，而基坑开挖时坑底土就处于卸载状态，需要考虑加卸载刚度的不同[15]。小应变硬化模型(HSs)[16]能够同时考虑这两种特性，并且能考虑模量与应力水平的关系，已经在国内外许多工程中得到了成功应用[17 − 21]，因此本文采用该模型作为土体本构。
HSs模型包含13个参数，其中部分参数有较成熟的取值方法。强度参数c′、φ′参考地勘报告取值。对于砂土，粘聚力c′考虑湿砂取小值3 kPa。剪胀角ψ表示土体在剪切屈服条件下塑性体应变与塑性剪应变的比值，通常对于粘土可取ψ=0∘；对于砂土[22]和粉土，可取ψ=φ′−0∘；若φ′<30∘，则取ψ=0∘。破坏比Rf表示土体剪切破坏时偏应力与应力应变曲线渐进值的比，一般可取0.8~0.9，计算中取0.9。加卸载泊松比νur表示三轴排水加卸载试验中侧向应变与轴向应变的比值，表征弹性变形行为，根据Plaxis手册的建议取0.2。Knc0表示正常固结土体的侧压力系数，按经验取值Knc0=1−sinφ′。参考应力pref取常见的100 kPa。
刚度参数Erefoed表示标准固结试验中轴向应力为参考应力(100 kPa)时的切线模量。地勘报告给出了固结试验中轴向荷载从0~100 kPa和0~200 kPa的平均压缩模量Es0-1和Es0-2，根据这两个值可以计算出Es1-2，理论上来说该值略大于Erefoed，但考虑取土扰动可近似取Erefoed=Es1-2[23]。刚度参数Eref50、Erefur无法直接从地勘报告中得到，但是可以根据类似土体的试验数据得到与Es1-2的比例关系。王浩然[24]统计了13个工程案例数据，建议砂土按照Erefur=4Es1-2、Eref50=Es1-2来取值；根据李亚玲等[25]对北京地区粉土的试验结果，粉土按照Erefur=6Es1-2、Eref50=2Es1-2来取值；根据周恩平[26]对北京地区粉质黏土的试验结果，粉质黏土按照Erefur=5Es1-2、Eref50=Es1-2来取值。刚度应力水平指数m根据上述试验结果对于粉土取0.6，对于粉质黏土取0.8，对于砂土取0.5。
Gref0表示围压为参考应力条件下土体的小应变剪切模量，根据地勘报告中给出的剪切波波速用公式G0=ρV2s计算G0，再根据应力水平换算Gref0。γ0.7表示小应变割线剪切模量衰减到初始70%时对应的剪应变，根据顾晓强等[27]的总结，对于砂土取4×10−4，对于粉土取3.5×10−4，对于粉质黏土取3×10−4。
同时，根据附近深基坑开挖的监测数据，采用基于卷积神经网络的深度学习方法对主要土体参数进行了反分析 [28]，并对上述取值进行了验证。HSs模型参数取值方法见表2，有限元模型包含的20个土层参数取值见表3。
表 2 HSs模型参数取值Table 2. Parameters for HSs model参数 取值 c′ 砂土：考虑湿砂取小值3 kPa
粉土与粉质粘土：根据地勘报告测孔压CU试验取值φ′ 砂土：根据地勘报告休止角取值
粉土与粉质粘土：根据地勘报告测孔压CU试验取值Rf 0.9 νur 0.2 Knc0 1−sinφ′ ψ ψ=φ′−30∘，若φ′<30∘，则取ψ=0∘ pref 100 kPa Erefoed 地勘报告给出了Es1-2，考虑取土扰动取Erefoed=Es1-2 Eref50 砂土：Eref50=Es1-2
粉土：Eref50=2Es1-2
粉质黏土：Eref50=Es1-2Erefur 砂土：Erefur=4Es1-2
粉土：Erefur=6Es1-2
粉质黏土：Erefur=5Es1-2m 砂土：0.5
粉土：0.6
粉质黏土：0.8Gref0 根据剪切波波速用公式G0=ρV2s计算G0，再根据应力水平换算成Gref0 γ0.7 砂土：4×10−4
粉土：3.5×10−4
粉质黏土：3×10−4表 3 各土层HSs模型参数取值Table 3. Parameters of each soil layer for HSs model土层编号 土性 厚度/m γ/(kN/m3) c′/kPa φ′/(°) m γ0.7 Erefoed/MPa Eref50/MPa Erefur/MPa Gref0/MPa ① 素填土 1.5 19.0 15.0 23.0 0.8 3.0×10−4 7.7 7.7 38.4 106.8 ② 黏质粉土-砂质粉土 6.0 19.4 10.0 30.0 0.6 3.5×10−4 9.2 18.5 55.4 120.4 ③ 细砂-中砂 6.0 19.5 3.0 32.0 0.5 4.0×10−4 30.0 30.0 120.0 143.5 ④ 细砂-中砂 5.9 20.0 3.0 32.0 0.5 4.0×10−4 32.5 32.5 130.0 157.9 ⑤ 细砂-中砂 10.1 20.5 3.0 32.0 0.5 4.0×10−4 35.0 35.0 140.0 200.9 ⑥1 重粉质黏土-粉质黏土 2.3 19.4 20.0 22.5 0.8 3.0×10−4 14.6 14.6 72.9 239.2 ⑥ 细砂-中砂 3.7 20.1 3.0 34.0 0.5 4.0×10−4 37.5 37.5 150.0 256.8 ⑦ 粉质黏土-重粉质黏土 4.0 19.8 19.6 23.5 0.8 3.0×10−4 18.2 18.2 91.2 263.4 ⑦1 黏质粉土-砂质粉土 5.0 20.6 8.0 35.5 0.6 3.5×10−4 29.4 58.8 176.3 264.5 ⑧ 细砂-中砂 6.0 20.3 3.0 35.0 0.5 4.0×10−4 40.0 40.0 160.0 277.3 ⑨1 粉质黏土-重粉质黏土 4.0 19.9 14.0 24.0 0.8 3.0×10−4 20.8 20.8 104.2 232.3 ⑨ 细砂-中砂 2.0 20.3 3.0 36.0 0.5 4.0×10−4 42.5 42.5 170.0 217.0 ⑩ 粉质黏土-重粉质黏土 4.0 20.1 15.2 24.0 0.8 3.0×10−4 23.6 23.6 118.0 169.2 ⑪ 细砂-中砂 13.0 20.5 3.0 36.0 0.5 4.0×10−4 45.0 45.0 180.0 245.8 ⑫1 重粉质黏土-粉质黏土 2.0 19.9 14.2 24.0 0.8 3.0×10−4 24.0 24.0 120.2 179.3 ⑫ 细砂-中砂 9.0 20.5 3.0 36.0 0.5 4.0×10−4 47.5 47.5 190.0 266.4 ⑬ 粉质黏土-重粉质黏土 4.0 20.3 13.7 24.0 0.8 3.0×10−4 28.8 28.8 143.9 217.9 ⑬1 细砂-中砂 5.0 20.5 3.0 38.0 0.5 4.0×10−4 50.0 50.0 200.0 239.6 ⑭ 粉质黏土-重粉质黏土 4.0 20.1 15.0 24.0 0.8 3.0×10−4 30.4 30.4 152.2 217.6 ⑭1 中砂-细砂 2.5 20.5 3.0 38.0 0.5 4.0×10−4 52.5 52.5 210.0 271.9 2.3 数值计算结果及分析
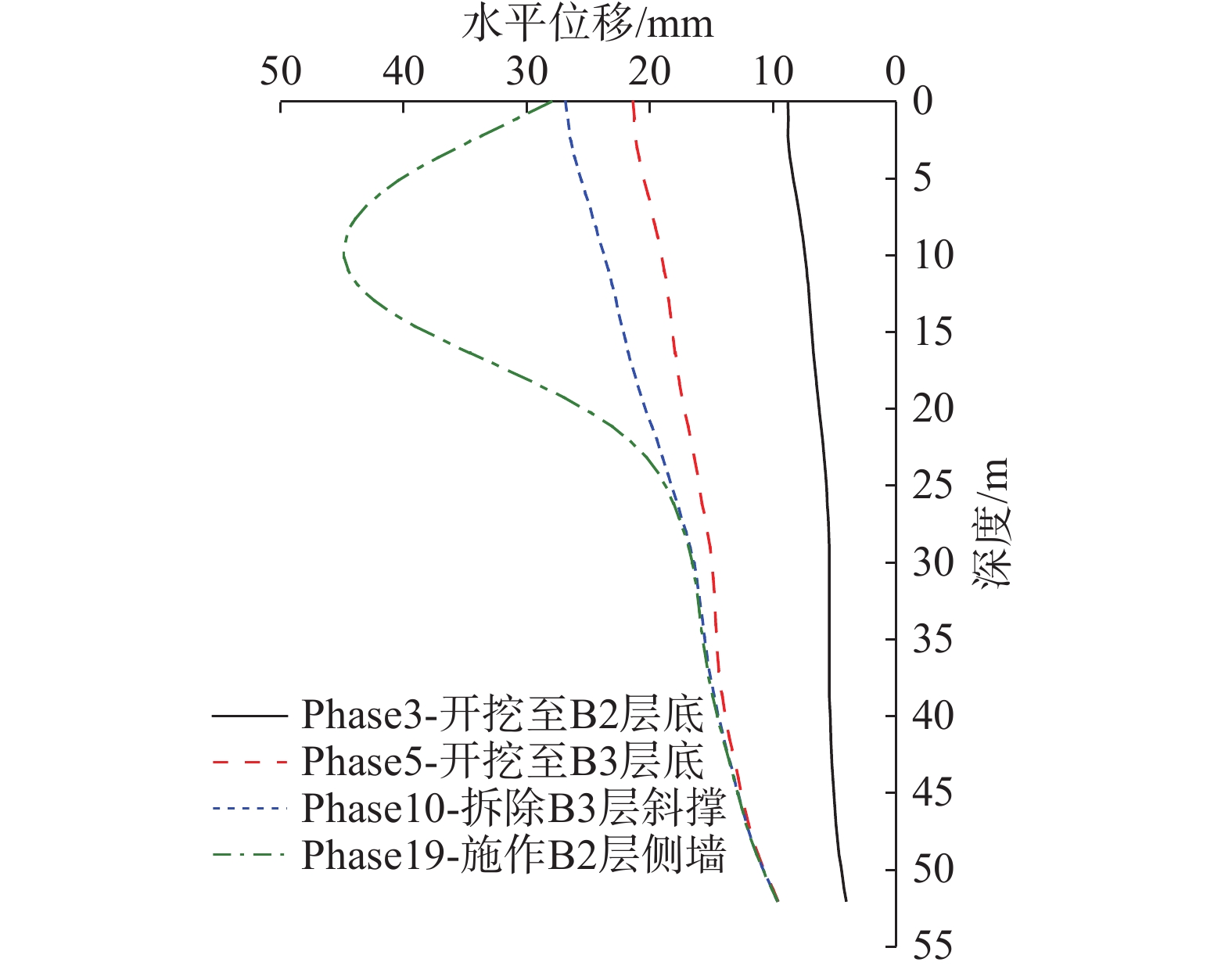
挡土墙侧移计算结果如图7所示，随着开挖的进行侧移逐渐发展，未施作B2层顶板前，挡土墙侧移模式为顶部侧移最大，施作B2层顶板后，挡土墙侧移模式为中上部侧移最大。最终阶段Phase 19的最大侧移发生在B2层中下部，为44.8 mm。该基坑环境保护等级为一级，要求围护结构水平侧移小于0.15％H，本断面基坑深度H=34.4 m，因此限值为51.6 mm，满足要求。
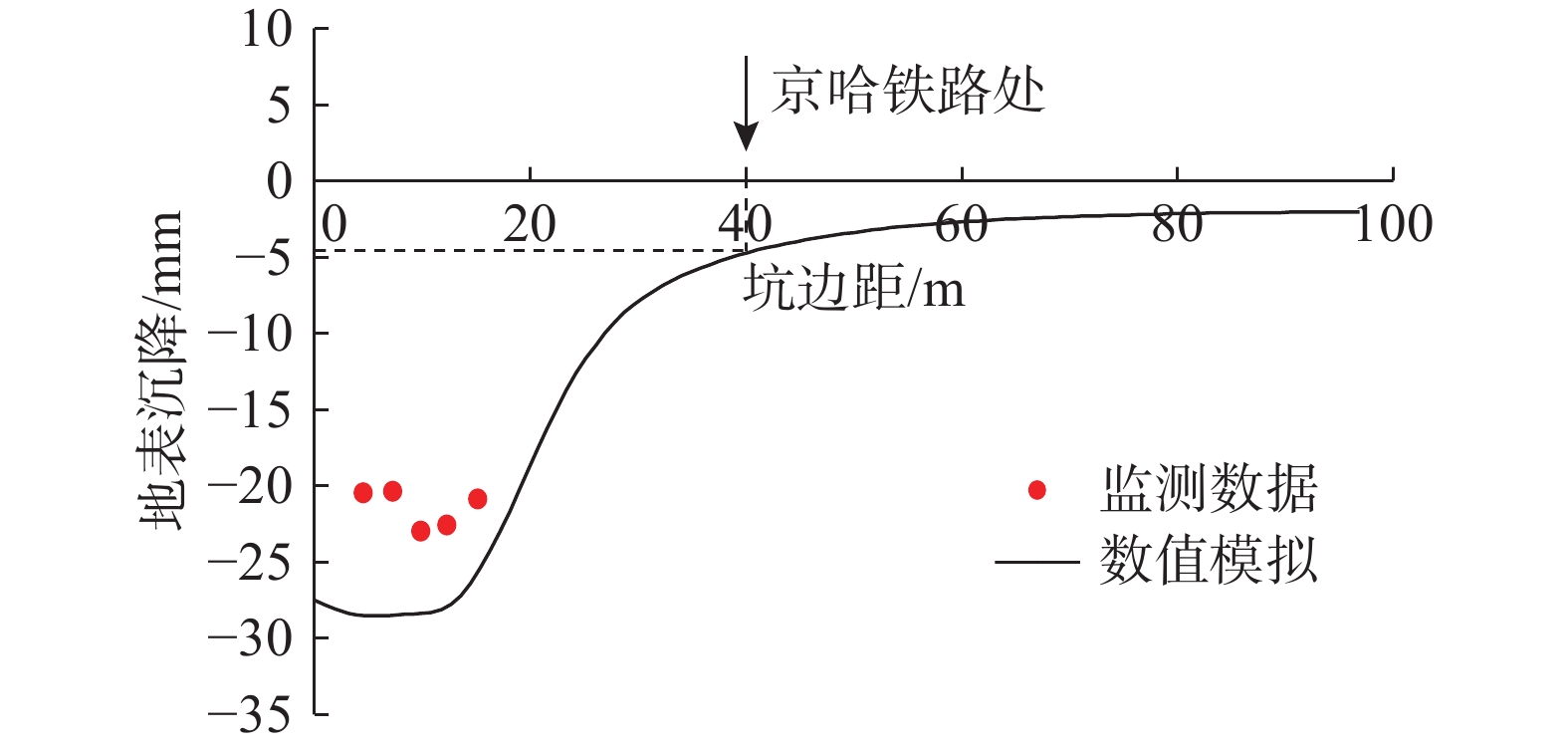
最终阶段的基坑周边地表沉降计算结果如图8所示，沉降槽显示靠近基坑的一段沉降较大，向远处逐渐减小，与工程经验较吻合。本工程要求地表最大沉降小于0.2%H且不超过30 mm，因此限值为30 mm。计算地表最大沉降为28.6 mm，满足要求。距离基坑边越40 m的京哈铁路处沉降的计算结果约为5 mm，也满足要求。
Ⅴ区基坑已于2023年4月完成施工，基坑外地表沉降监测数据为图8中红点所示，最大沉降约为23 mm，与有限元预测结果接近，京哈线列车也在整个基坑施工期间正常运行，表明上述预测分析是较为符合实际的。需指出的是，本文数值模拟工作的开展时间是在基坑进行B2层开挖时(即图5中Phase 3)，所做变形预测是事前预测。
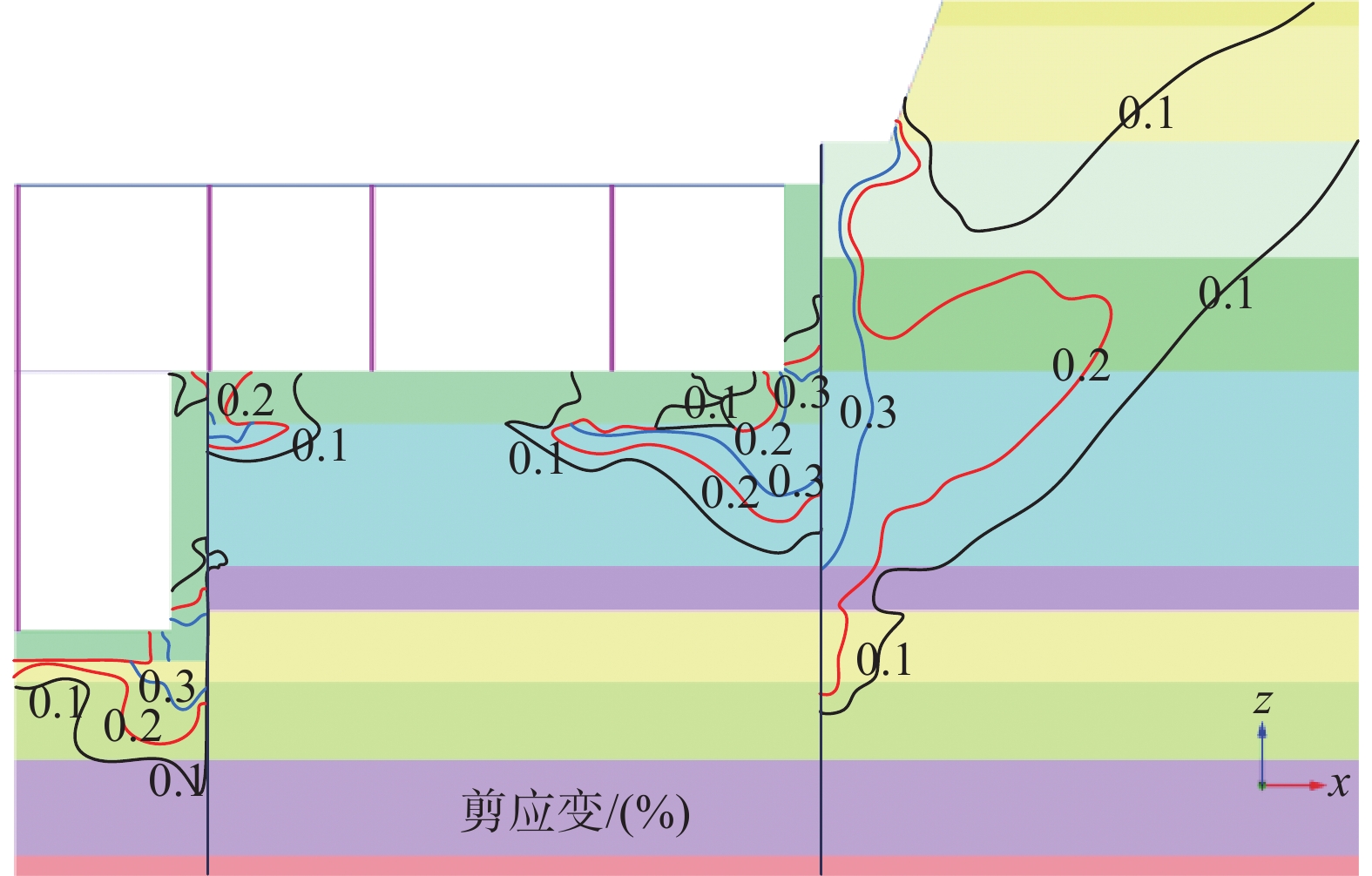
对有限元计算结果进行进一步分析，发现基坑附近土体的剪应变呈现高度不均匀的状态，如图9所示，而且绝大部分区域的剪应变小于0.3%，处于小应变范围，因此数值模拟中非常有必要考虑土体小应变刚度的影响。
反压土开槽示意图如图6b所示，考虑到反压土自身的稳定性，开槽尺寸不能过大，但也要满足斜撑施工的需要。因此对每个斜撑开宽度4.5 m，高度3 m的槽，总开槽体积约占反压土体积的16%。反压土开槽引起的支护结构侧移增量如图10、图11所示。B3层反压土开槽同时引起了地连墙和围护桩的变形，最大侧移发生在B3层中部，约为1.4 mm。B2层反压土开槽仅引起地连墙的侧移，最大侧移发生在B2层中部，约为1.6 mm。这一现象说明两级反压土支护时下部反压土的影响范围更广，而上部反压土几乎不会对下部结构产生影响。上述反压土开槽的影响也从反面说明反压土对控制支护结构水平位移有显著作用。
3 HSs模型与MC模型的对比
基坑设计通常会采用摩尔-库伦模型(MC模型)作为土体本构，因其简单实用、参数易于确定[29 − 30]。但是MC模型无法考虑土体卸载刚度、小应变刚度以及应力历史等的影响。下面以前述有限元模型为基础对比HSs模型与MC模型在深基坑工程中的应用。
3.1 MC模型刚度参数取值
MC模型的刚度参数包括弹性模量和泊松比，泊松比取经验值0.2。MC模型的弹性模量可根据HSs模型的割线模量E50来计算，E50的计算公式如下：
E50=Eref50(c′⋅cotφ′−σ′3c′⋅cotφ′+pref)m (1) 式中，σ′3为土体初始水平有效应力。
方法1：有限元模型共包含20个土层，对每层土计算其中部深度的有效应力σ′3，代入式(1)即可得到E50，从而得到MC模型的弹性模量；
方法2：由于方法1未考虑坑底土体的卸载模量，计算得到的变形会偏大，因此对于基坑底部标高以下的土体，其弹性模量根据HSs模型中加卸载模量Eur来计算[14]，Eur的计算公式如式(2)：
Eur=Erefur(c′⋅cotφ′−σ′3c′⋅cotφ′+pref)m (2) 方法3：如果再考虑挡土墙后土体也处于侧向卸载状态，对所有土层的弹性模量均采用Eur来计算。
下面对比MC模型三种取值方法与HSs模型的计算结果。
3.2 计算结果对比
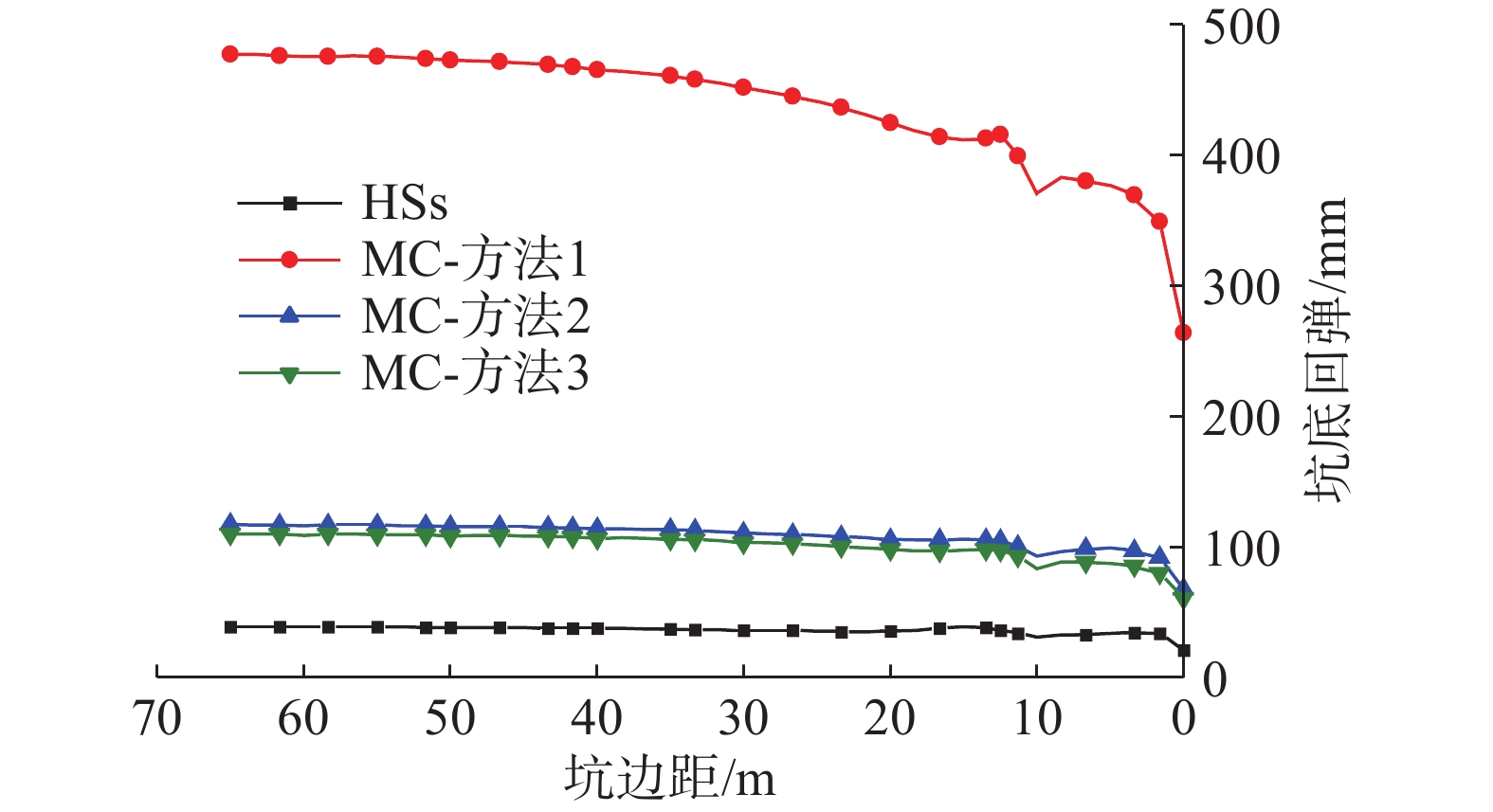
图12为最终坑底回弹的对比，MC模型方法1的回弹量最高，最大回弹达到477 mm，明显不符合实际情况，这是因为其没有考虑土体卸载时刚度更大的特性。特别是对于开挖深度和面积都很大的深大基坑，开挖卸掉的土体重量很大，MC模型导致的回弹偏差就尤为显著。考虑了土体卸载刚度的方法2和方法3所得的坑底回弹十分接近，仅为方法1的23%，但是相比HSs模型仍偏大，这是因为其没有考虑土体小应变刚度的影响。
![]()
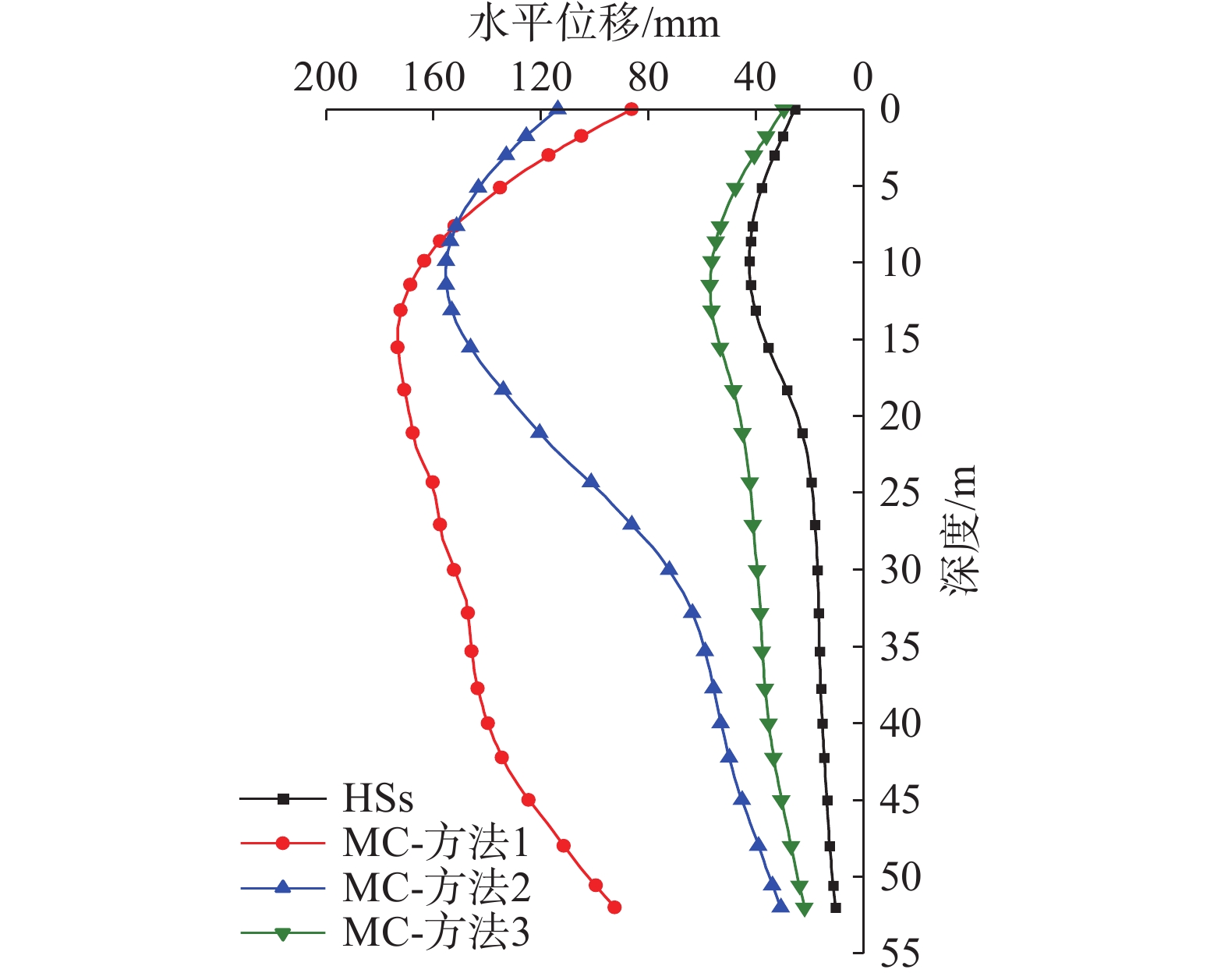
图 12 HSs与MC模型的坑底回弹对比Figure 12. Comparison of excavation rebound between HSs model and MC models图13为挡土墙侧移的对比，MC模型方法1的侧移依然最大，但是方法3的侧移比方法2要小很多，尤其是地连墙中上部。这是因为方法3提高了挡土墙上部坑后土的刚度，能够在一定程度上考虑小应变情况下高模量的特性。
![]()
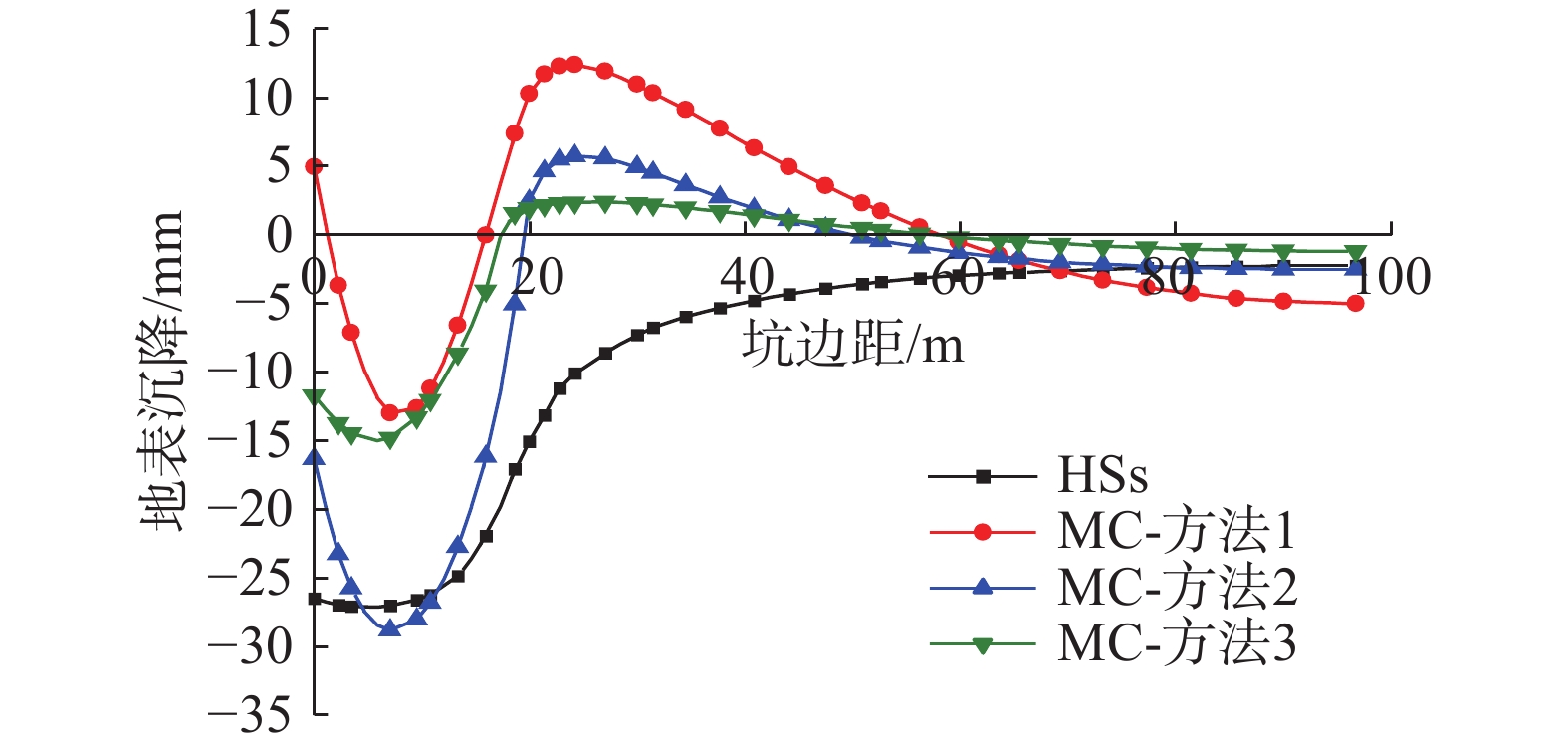
图 13 HSs与MC模型的挡土墙侧移对比Figure 13. Comparison of horizontal displacement of retaining wall between HSs model and MC models图14为基坑周边地表沉降，MC模型的三种方法均出现了隆起的现象，与实际情况不符[31]，而HSs模型的沉降曲线比较符合实际。这一现象也表明尽管MC模型能通过人为增加土体刚度来使得计算出的变形与HSs模型更接近，但是由于采用了单一的刚度参数，对变形的预测不符合实际情况。
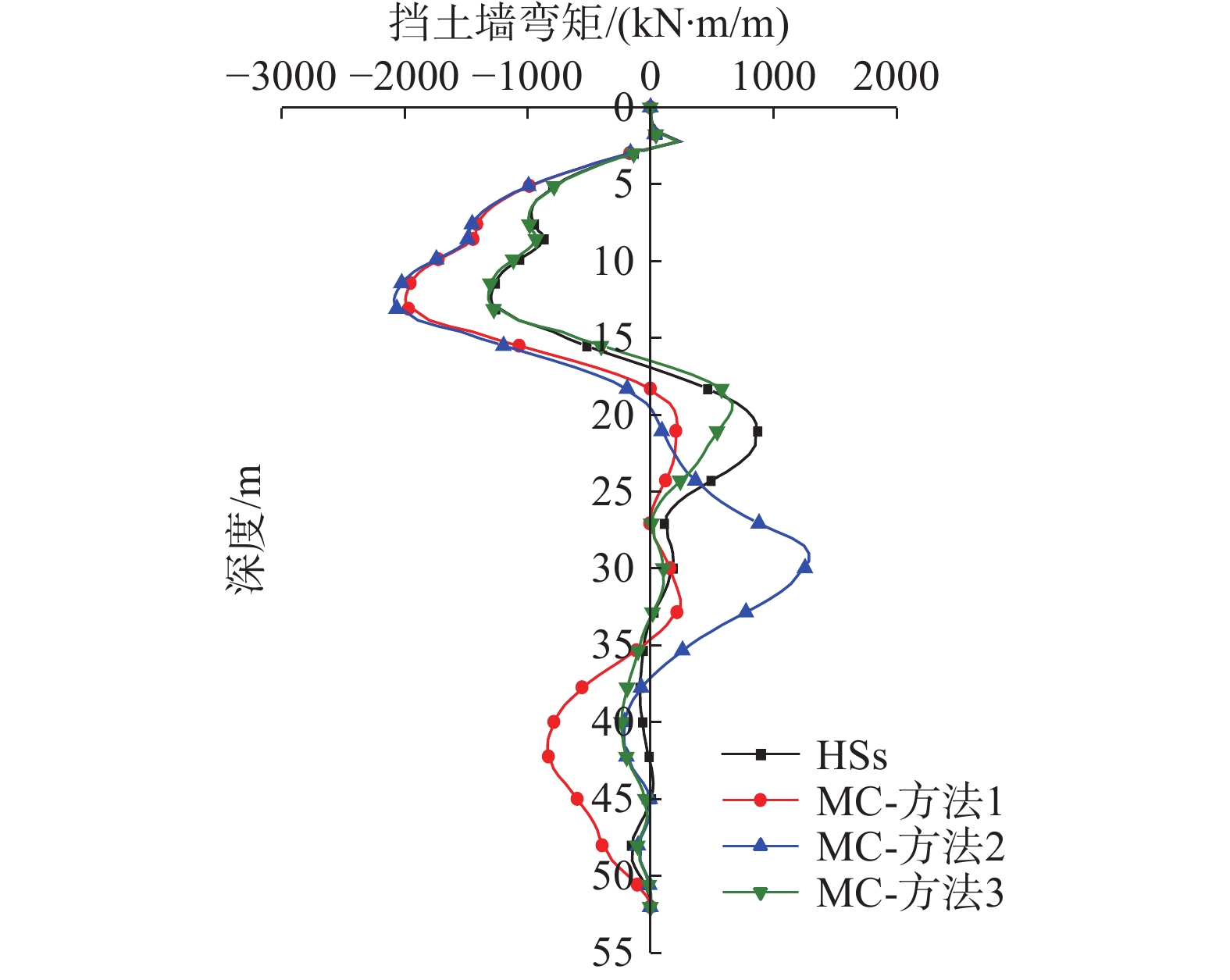
图15为应用MC模型与HSs模型所得挡土墙弯矩的对比，相比变形的较大差别，挡土墙弯矩的差别要小得多，尤其是MC模型的方法3，最大弯矩与HSs模型基本相同。这一现象也说明利用MC模型的计算结果对支护构件进行配筋设计有一定的合理性。
![]()
图 14 HSs与MC模型的挡土墙后地表沉降对比Figure 14. Comparison of settlement for ground surface behind retaining wall between HSs model and MC models![]()
图 15 HSs与MC模型的挡土墙弯矩对比Figure 15. Comparison of bending moments of retaining wall between HSs model and MC models4 结论
本文基于三维有限元模型对开挖深度34.4 m、采用两级反压土支护的北京城市副中心项目基坑工程Ⅴ区基坑进行数值分析，同时考虑土体采用HSs模型与MC模型的对比，所得结论如下：
(1)利用HSs模型进行数值模拟，并基于相关试验结果确定了适用于北京地区土层的模型参数，计算结果表明该采用反压土支护的体系能够满足设计要求。坑外地表最大沉降预测值为28.6 mm，与监测数据吻合较好，说明数值模型能够合理预测真实情况。反压土开槽约16%的体积引起了支护结构约1.5 mm的变形，说明反压土支护效果显著。
(2)有限元计算结果表明，即便是三十多米的深基坑周围绝大部分土体的剪应变也小于0.3%，处于小应变区间。因此要想合理预测深基坑的变形，有必要考虑土体的小应变刚度特性。通常的地勘报告无法获得全部的HSs模型参数，本文基于北京地区土体的相关试验结果给出了该基坑所在区域典型土体参数取值。但是目前的北京地区土体室内试验数据较少，更多针对北京地区典型土体的室内试验以及工程实测数据有助于完善HSs模型参数取值。
(3)三维有限元模拟中采用能反映土体小应变刚度特性及加卸载模量差异的HSs模型，能够较好预测深基坑变形。MC模型由于采用单一模量，即使人为提高模量，也不能得到合理的变形预测结果，但是对于支护构件内力的计算结果与HSs模型比较接近，仍有一定的价值。
-
![]()
图 7 有效刚度既有模型预测值与试验值对比图
Figure 7. Predicted versus experimental effective stiffness based on existing models
![]()
图 8 机器学习模型预测值与试验值对比图
Figure 8. Predicted versus experimental effective stiffness based on machine learning models
![]()
图 9 有效刚度预测值与试验值之比的频数分布直方图
Figure 9. Histogram of predicted to experimental effective stiffness ratio
![]()
图 11 基于SHAP方法的XGBR模型全局解释
Figure 11. Global interpretations of XGBR model by SHAP approach
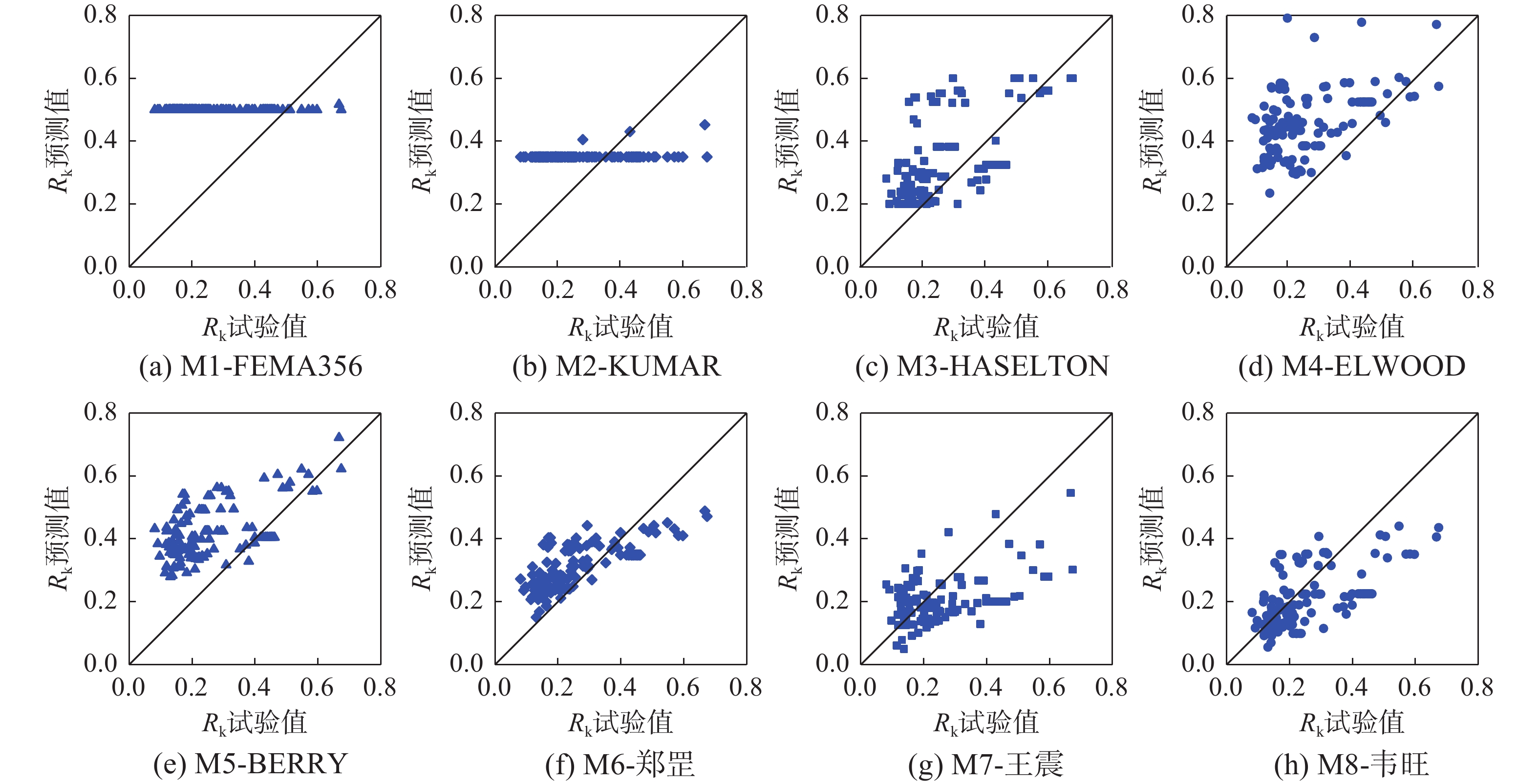
表 1 既有有效刚度计算模型
Table 1 Computational models of effective stiffness
编号 模型来源 计算模型 截面类型 结构类型 考虑因素 M1 FEMA356 [11] Rk = 0.5，n﹤0.3；0.7，n﹥0.5；0.3≤n≤0.5，线性内插 实心 建筑 n M2 KUMAR等 [10] Rk = 0.175+0.875n；且0.35≤ Rk ≤0.7 矩形实心 建筑 n M3 HASELTON等[1] Rk = −0.07+0.59n+0.07γ；且0.2≤ Rk ≤0.6 矩形实心 建筑、桥梁 n、γ M4 ELWOOD等[2] Rk = (0.45+2.5n)/[1+110 (db /H)/γ]；且0.2≤ Rk ≤1.0 实心 建筑、桥梁 n、γ、db、H M5 BERRY等 [3] Rk = 0.15+1.0n+0.035γ+0.10ρl ≤1.0 圆形实心 桥梁 n、γ、ρl M6 郑罡等[12] Rk = 0.072+0.485n+3.041ρl+0.029γ−0.064m ≤1.0 实心 桥梁 n、γ、ρl、m M7 王震等[13] Rk = 0.04+1.4n+0.65ρl+(1−0.5α2)γ/100−0.07m ≤1.0 矩形空心 桥梁 n、γ、ρl、m、α M8 韦旺等[14] Rk = 0.467n+0.04γ−0.1m ≤1.0 矩形空心 桥梁 n、γ、m 注：n为轴压比；γ为剪跨比；db为纵筋直径；H为截面高度；ρl为纵筋率；m为材料几何参数(m= fyldb/L√fc)；fyl 为纵筋屈服强度；fc为混凝土抗压强度；L为墩高；α为截面加载方向空心段高度与截面高度H之比。 
下载: 导出CSV
表 2 RC矩形空心墩参数统计
Table 2 Statistics of parameters for RC rectangular hollow piers
统计参数/单位 B/cm H/cm t/cm L/cm L/H fc/MPa db/mm fyl/MPa ρl/(%) fys/MPa ρs/(%) n m Rk 最大值 150.00 160.00 30.00 840.00 10.00 102.00 22.00 829.00 6.49 700.00 2.62 0.32 0.71 0.67 最小值 24.00 24.00 6.00 120.00 1.80 19.80 6.00 291.00 0.88 220.00 0.03 0.00 0.10 0.08 中位数 50.00 50.00 12.00 288.00 4.40 32.40 10.00 400.00 2.11 389.00 1.08 0.08 0.32 0.22 均值 61.00 58.90 12.40 275.00 5.00 36.90 11.00 409.00 2.25 395.00 0.97 0.09 0.33 0.26 变异系数 0.41 0.54 0.37 0.47 0.38 0.35 0.32 0.17 0.43 0.19 0.51 0.53 0.51 0.51
下载: 导出CSV
表 3 各模型超参数优化结果
Table 3 Optimization results of hyperparameters
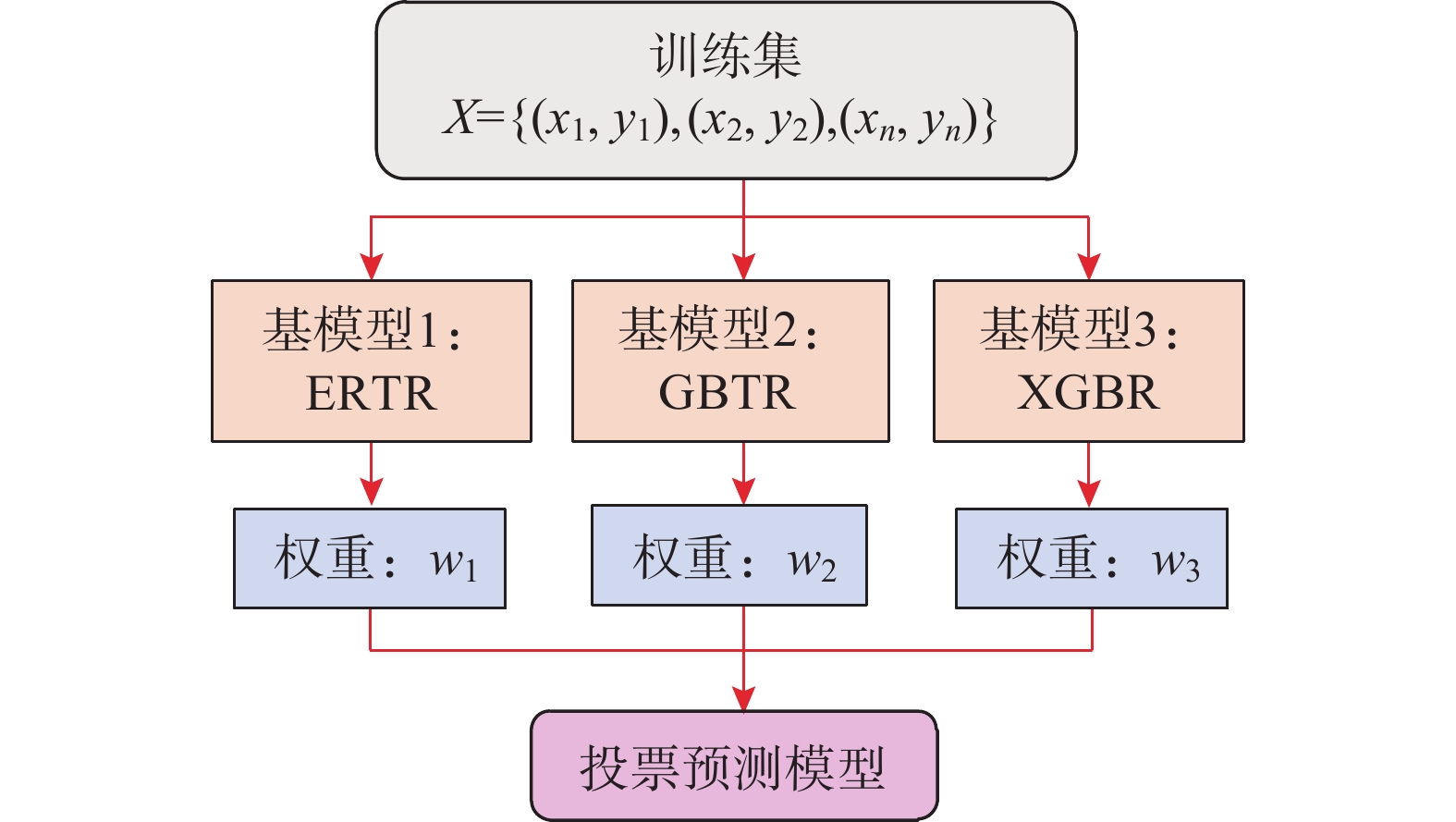
模型 超参数优化值 SVR kernel='rbf'， C=1.5， epsilon=0.024， gamma='auto'; RFR n_estimators=265， max_depth=14， min_samples_leaf=1， min_samples_split=2， max_features=8; ERTR n_estimators=100， max_depth=15， max_leaf_nodes=42，
min_samples_split=2， max_features=9;GBTR n_estimators=355， learning_rate=0.14， max_depth=3， subsample=1， min_samples_split=2， max_features=4; XGBR n_estimators=500， max_depth=3， learning_rate=0.15， subsample=0.62， min_child_weight=1， reg_lambda=1， colsample_bytree=0.77， colsample_bynode=1; VOTR w1=0.1(ERTR模型权重)， w2=0.1(GBTR模型权重)， w3=0.8(XGBR模型权重)
下载: 导出CSV
表 4 有效刚度预测值与试验值之比的统计结果
Table 4 Statistics for ratio of calculated to measured effective stiffness for each models
统计
参数FEMA356[11]
M1KUMAR等[10]
M2HASELTON等[1]
M3ELWOOD等[2]
M4BERRY等[3]
M5郑罡等[12]
M6王震等[13]
M7韦旺等[14]
M8本文VOTR
M9最大值 6.17 4.32 3.46 5.86 5.33 3.36 3.15 2.12 1.34 最小值 0.74 0.52 0.64 0.85 0.86 0.69 0.34 0.37 0.82 中位数 2.33 1.63 1.36 2.00 1.83 1.30 0.79 0.80 1.00 均值 2.41 1.69 1.48 2.13 1.94 1.39 0.93 0.91 1.01 变异系数 0.45 0.44 0.43 0.44 0.41 0.36 0.52 0.44 0.07
下载: 导出CSV
表 5 机器学习模型性能评估
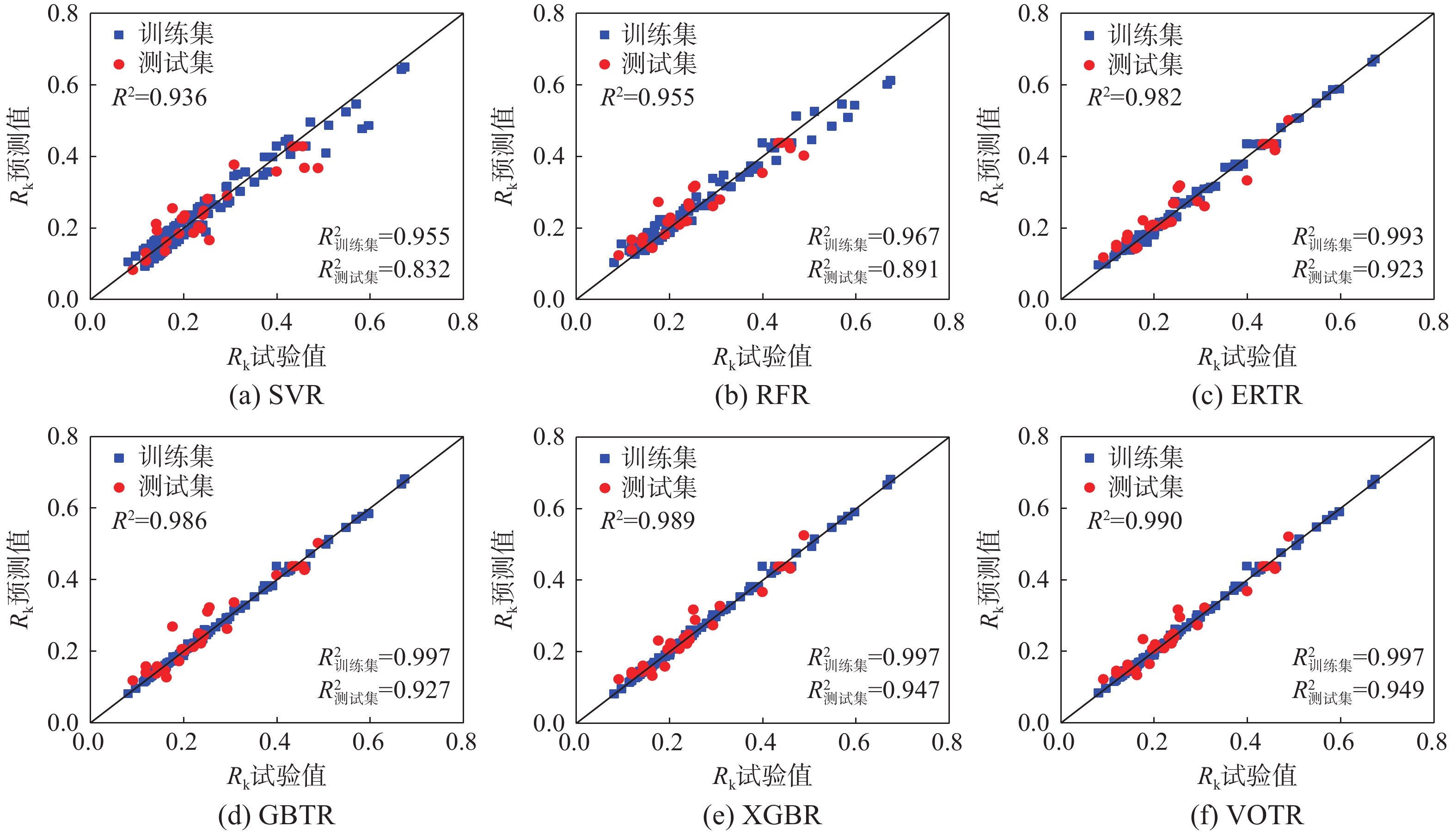
Table 5 Performance measures for ML models
机器
学习模型训练集 测试集 RMSE/
(%)MAE/
(%)MAPE/
(%)RMSE/
(%)MAE/
(%)MAPE/
(%)SVR 2.87 2.39 10.70 4.71 3.51 14.97 RFR 2.44 1.80 8.01 3.80 3.03 14.41 ERTR 1.11 0.86 4.18 3.19 2.65 12.74 GBTR 0.65 0.38 1.54 3.10 2.22 11.27 XGBR 0.65 0.36 1.43 2.62 2.14 10.49 VOTR 0.65 0.34 1.28 2.60 2.10 10.43
下载: 导出CSV
表 6 既有模型与VOTR模型性能
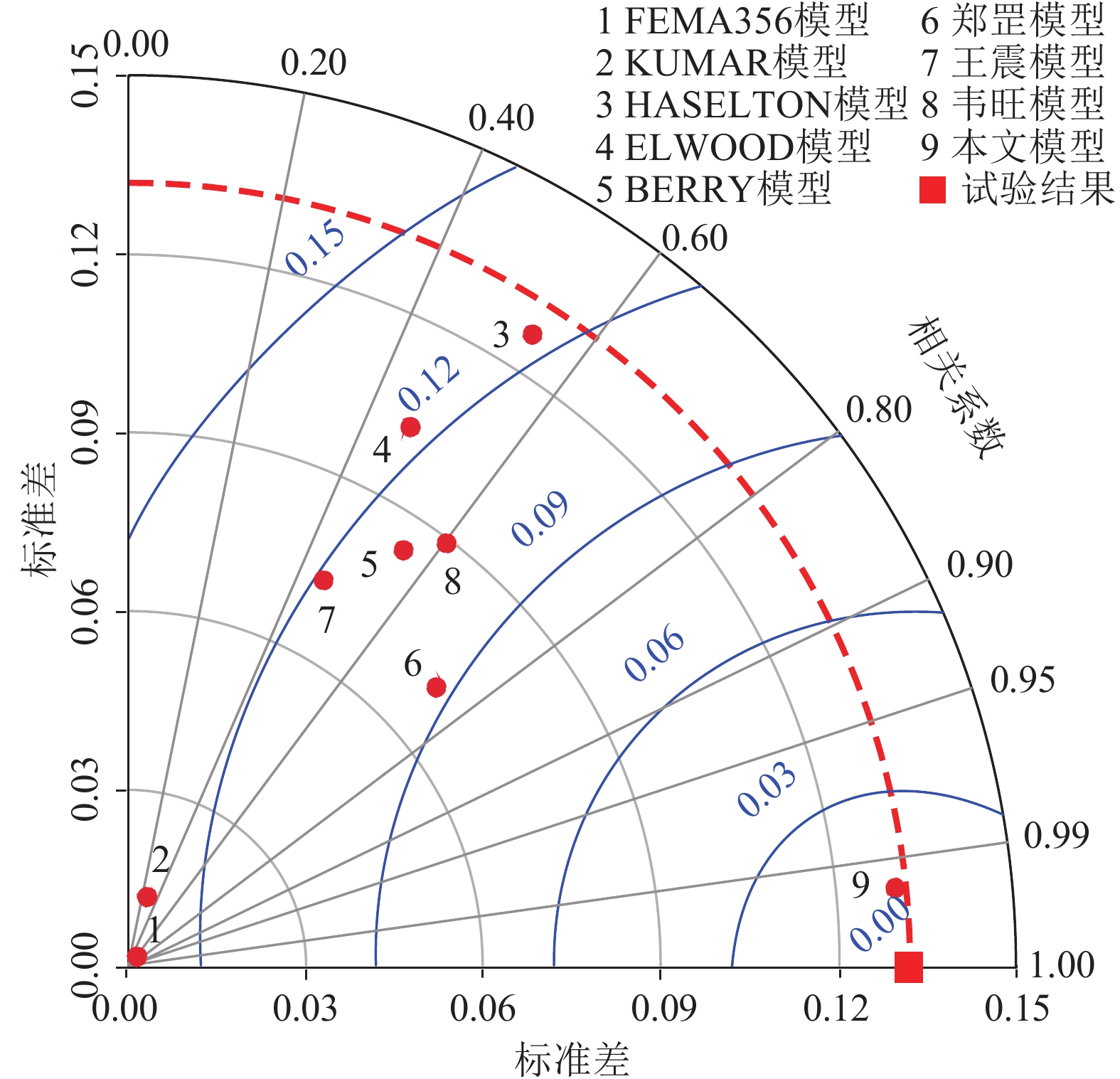
Table 6 Performance for existing models and VOTR
预测
模型评估指标 泰勒图参数 RMSE/
(%)MAE/
(%)MAPE/
(%)CRMSE /
(%)STDE
-R
-M1 27.4 25.1 142.4 13.1 0.001 0.271 M2 15.9 14.5 79.3 12.9 0.012 0.267 M3 14.5 11.6 57.5 12.4 0.127 0.542 M4 23.5 20.4 113.6 12.3 0.103 0.468 M5 19.4 17.0 96.0 11.0 0.085 0.555 M6 10.5 9.0 46.7 9.3 0.071 0.741 M7 13.1 10.4 40.1 11.9 0.074 0.448 M8 11.6 9.1 34.3 10.6 0.090 0.603 M9 1.3 0.7 3.4 1.3 0.131 0.995
下载: 导出CSV
-
[1] HASELTON C B, LIEL A B, LANGE S T, et al. Beam-column element model calibrated for predicting flexural response leading to global collapse of RC frame buildings [R]. Berkeley: Pacific Earthquake Engineering Research Center, 2008.
[2] ELWOOD K J, EBERHARD M O. Effective stiffness of reinforced concrete columns [J]. ACI Structural Journal, 2009, 106(4): 476 − 484.
[3] BERRY M P, LEHMAN D E, LOWES L N. Lumped-plasticity models for performance simulation of bridge columns [J]. ACI Structural Journal, 2008, 105(3): 270 − 279.
[4] JTG/T 2231-01−2020, 公路桥梁抗震设计规范[S]. 北京: 人民交通出版社, 2020. JTG/T 2231-01−2020, Specifications for seismic design of highway bridges [S]. Beijing: China Communications Press, 2020. (in Chinese)
[5] PRIESTLEY M J N, CALVI G M, KOWALSKY M J. Displacement-based seismic design of structures [M]. Pavia: IUSS Press, 2007: 133 − 165.
[6] MANDER J B, PRIESTLEY M J N, PARK R. Behaviour of ductile hollow reinforced concrete columns [J]. Bulletin of the New Zealand Society for Earthquake Engineering, 1983, 16(4): 273 − 290. doi: 10.5459/bnzsee.16.4.273-290
[7] YEH Y K, MO Y L, YANG C Y. Full-scale tests on rectangular hollow bridge piers [J]. Materials and Structures, 2002, 35(246): 117 − 125. doi: 10.1617/13699
[8] KIM T H, LEE J H, SHIN H M. Performance assessment of hollow RC bridge columns with triangular reinforcement details [J]. Magazine of Concrete Research, 2014, 66(16): 809 − 824. doi: 10.1680/macr.13.00257
[9] 邵长江, 漆启明, 韦旺, 等. 矩形混凝土空心墩延性抗震性能试验研究[J]. 西南交通大学学报, 2022, 57(1): 129 − 138, 157. doi: 10.3969/j.issn.0258-2724.20200092 SHAO Changjiang, QI Qiming, WEI Wang, et al. Experimental study on ductile seismic performance of rectangular hollow concrete columns [J]. Journal of Southwest Jiaotong University, 2022, 57(1): 129 − 138, 157. (in Chinese) doi: 10.3969/j.issn.0258-2724.20200092
[10] KUMAR R, SINGH Y. Stiffness of reinforced concrete frame members for seismic analysis [J]. ACI Structural Journal, 2010, 107(5): 607 − 615.
[11] FEMA 356, Prestandard and commentary for the seismic rehabilitation of buildings [S]. Washington, D.C.: Federal Emergency Management Agency, 2000.
[12] 郑罡, 李贵乾. 钢筋混凝土桥墩有效刚度[J]. 土木工程学报, 2013, 46(6): 44 − 52. ZHENG Gang, LI Guiqian. Effective stiffness of reinforced concrete bridge piers [J]. China Civil Engineering Journal, 2013, 46(6): 44 − 52. (in Chinese)
[13] 王震, 王景全, 修洪亮, 等. 矩形空心墩等效塑性铰模型[J]. 中国公路学报, 2019, 32(1): 76 − 86. doi: 10.3969/j.issn.1001-7372.2019.01.009 WANG Zhen, WANG Jingquan, XIU Hongliang, et al. Equivalent plastic hinge model of rectangular hollow piers [J]. China Journal of Highway and Transport, 2019, 32(1): 76 − 86. (in Chinese) doi: 10.3969/j.issn.1001-7372.2019.01.009
[14] 韦旺, 邵长江, 肖正豪, 等. 钢筋混凝土空心墩有效刚度试验研究[J]. 土木工程学报, 2019, 52(10): 101 − 110. WEI Wang, SHAO Changjiang, XIAO Zhenghao, et al. Experimental study on effective stiffness of reinforced concrete hollow piers [J]. China Civil Engineering Journal, 2019, 52(10): 101 − 110. (in Chinese)
[15] 孙治国, 王东升, 李宏男, 等. 钢筋混凝土空心桥墩应用及抗震性能研究综述[J]. 交通运输工程学报, 2013, 13(3): 22 − 32. doi: 10.3969/j.issn.1671-1637.2013.03.004 SUN Zhiguo, WANG Dongsheng, LI Hongnan, et al. Application of RC hollow bridge pier and review of seismic behavior research [J]. Journal of Traffic and Transportation Engineering, 2013, 13(3): 22 − 32. (in Chinese) doi: 10.3969/j.issn.1671-1637.2013.03.004
[16] TRUNG N T, SHAHGOLI A F, ZANDI Y, et al. Moment-rotation prediction of precast beam-to-column connections using extreme learning machine [J]. Structural Engineering and Mechanics, 2019, 70(5): 639 − 647.
[17] CHAHNASIR E S, ZANDI Y, SHARIATI M, et al. Application of support vector machine with firefly algorithm for investigation of the factors affecting the shear strength of angle shear connectors [J]. Smart Structures and Systems, 2018, 22(4): 413 − 424.
[18] THAI H T. Machine learning for structural engineering: A state-of-the-art review [J]. Structures, 2022, 38: 448 − 491. doi: 10.1016/j.istruc.2022.02.003
[19] 李启明, 喻泽成, 余波, 等. 钢筋混凝土柱地震破坏模式判别的两阶段支持向量机方法[J]. 工程力学, 2022, 39(2): 148 − 158. doi: 10.6052/j.issn.1000-4750.2020.12.0937 LI Qiming, YU Zecheng, YU Bo, et al. Two-stage support vector machine method for failure mode classification of reinforced concrete columns [J]. Engineering Mechanics, 2022, 39(2): 148 − 158. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.12.0937
[20] DAS S, CHOUDHURY S. Influence of effective stiffness on the performance of RC frame buildings designed using displacement-based method and evaluation of column effective stiffness using ANN [J]. Engineering Structures, 2019, 197: 109354. doi: 10.1016/j.engstruct.2019.109354
[21] WANG Z, LIU T X, LONG Z L, et al. A machine-learning-based model for predicting the effective stiffness of precast concrete columns [J]. Engineering Structures, 2022, 260: 114224. doi: 10.1016/j.engstruct.2022.114224
[22] 张书颖, 陈适之, 韩万水, 等. 基于集成学习的FRP加固混凝土梁抗弯承载力预测研究[J]. 工程力学, 2022, 39(8): 245 − 256. doi: 10.6052/j.issn.1000-4750.2021.06.0422 ZHANG Shuying, CHEN Shizhi, HAN Wanshui, et al. Study on prediction of FRP strengthened reinforced concrete beam’s moment bearing capacity based on ensemble learning algorithm [J]. Engineering Mechanics, 2022, 39(8): 245 − 256. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.06.0422
[23] 陈隽, 宋颖豪, 王泽涛. 建筑基本周期多因素机器学习预测模型[J]. 工程力学, 2024, 41(2): 171 − 179. doi: 10.6052/j.issn.1000-4750.2022.03.0274 CHEN Jun, SONG Yinghao, WANG Zetao. Multi-factor machine learning prediction model for the natural period of buildings [J]. Engineering Mechanics, 2024, 41(2): 171 − 179. (in Chinese) doi: 10.6052/j.issn.1000-4750.2022.03.0274
[24] TRAN V L, LEE T H, NGUYEN D D, et al. Failure mode identification and shear strength prediction of rectangular hollow RC columns using novel hybrid machine learning models [J]. Buildings, 2023, 13(12): 2914. doi: 10.3390/buildings13122914
[25] NGUYEN X B, TRAN V L, PHAN H T, et al. Predicting shear capacity of rectangular hollow RC columns using neural networks [J]. Asian Journal of Civil Engineering, 2024, 25(3): 2509 − 2520. doi: 10.1007/s42107-023-00924-7
[26] PARK R. Evaluation of ductility of structures and structural assemblages from laboratory testing [J]. Bulletin of the New Zealand Society for Earthquake Engineering, 1989, 22(3): 155 − 166. doi: 10.5459/bnzsee.22.3.155-166
[27] PRIESTLEY M J N, SEIBLE F, CALVI G M. Seismic design and retrofit of bridges [M]. New York: John Wiley & Sons, 1996: 266 − 267.
[28] HASTIE T, TIBSHIRANI R, FRIEDMAN J. The elements of statistical learning [M]. New York: Springer, 2001.
[29] 宋晓东. 桥梁高墩延性抗震性能的理论与试验研究[D]. 上海: 同济大学, 2004. SONG Xiaodong. Theoretical and experimental research on ductile seismic performance of high bridge columns [D]. Shanghai: Tongji University, 2004. (in Chinese)
[30] 崔海琴, 贺拴海, 宋一凡. 空心矩形薄壁墩延性抗震性能试验[J]. 公路交通科技, 2010, 27(6): 58 − 63. doi: 10.3969/j.issn.1002-0268.2010.06.011 CUI Haiqin, HE Shuanhai, SONG Yifan. Experimental study on antiseismic ductility of hollow rectangular thin-walled pier [J]. Journal of Highway and Transportation Research and Development, 2010, 27(6): 58 − 63. (in Chinese) doi: 10.3969/j.issn.1002-0268.2010.06.011
[31] 杜修力, 陈明琦, 韩强. 钢筋混凝土空心桥墩抗震性能试验研究[J]. 振动与冲击, 2011, 30(11): 254 − 259. DU Xiuli, CHEN Mingqi, HAN Qiang. Experimental evaluation of seismic performance of reinforced concrete hollow bridge columns [J]. Journal of Vibration and Shock, 2011, 30(11): 254 − 259. (in Chinese)
[32] 王飞. 混凝土箱型结构的抗震性能研究[D]. 长沙: 湖南大学, 2012. WANG Fei. Study on seismic performance of concrete box structures [D]. Changsha: Hunan University, 2012. (in Chinese)
[33] 董振华, 韩强, 杜修力. 碳纤维增强复合材料约束矩形空心墩抗震性能试验研究[J]. 工业建筑, 2013, 43(6): 27 − 31. DONG Zhenhua, HAN Qiang, DU Xiuli. Experimental study on seismic performance of CFRP confined bridge pier with rectangular hollow cross section [J]. Industrial Construction, 2013, 43(6): 27 − 31. (in Chinese)
[34] 罗征, 李建中. 低周往复荷载下空心矩形墩抗震性能试验研究[J]. 振动与冲击, 2013, 32(8): 183 − 188. doi: 10.3969/j.issn.1000-3835.2013.08.032 LUO Zheng, LI Jianzhong. Tests for a seismic performance of rectangular hollow thin-walled bridge columns under low-cycle reversed loading [J]. Journal of Vibration and Shock, 2013, 32(8): 183 − 188. (in Chinese) doi: 10.3969/j.issn.1000-3835.2013.08.032
[35] HAN Q, DU X L, ZHOU Y H, et al. Experimental study of hollow rectangular bridge column performance under vertical and cyclically bilateral loads [J]. Earthquake Engineering and Engineering Vibration, 2013, 12(3): 433 − 445. doi: 10.1007/s11803-013-0184-y
[36] 韩强, 周雨龙, 杜修力. 钢筋混凝土矩形空心桥墩抗震性能[J]. 工程力学, 2015, 32(3): 28 − 40. doi: 10.6052/j.issn.1000-4750.2013.11.1020 HAN Qiang, ZHOU Yulong, DU Xiuli. Seismic performance of reinforced concrete rectangular hollow bridge columns [J]. Engineering Mechanics, 2015, 32(3): 28 − 40. (in Chinese) doi: 10.6052/j.issn.1000-4750.2013.11.1020
[37] 王军文, 张伟光, 艾庆华. PC与RC空心墩抗震性能试验对比[J]. 中国公路学报, 2015, 28(4): 76 − 85. doi: 10.3969/j.issn.1001-7372.2015.04.010 WANG Junwen, ZHANG Weiguang, AI Qinghua. Comparative experiment on seismic performance of PC and RC hollow piers [J]. China Journal of Highway and Transport, 2015, 28(4): 76 − 85. (in Chinese) doi: 10.3969/j.issn.1001-7372.2015.04.010
[38] 田明丞, 徐锋, 王曙光, 等. 高轴压作用下矩形RC空心柱抗剪承载力[J]. 土木工程与管理学报, 2018, 35(3): 157 − 166. TIAN Mingcheng, XU Feng, WANG Shuguang, et al. Shear capacity of rectangular RC hollow column under high axial compression [J]. Journal of Civil Engineering and Management, 2018, 35(3): 157 − 166. (in Chinese)
[39] 西海健二, 沖本真之, 川端規之, 等. 鋼製エレメントを用いた合成構造中空断面橋脚における実験的研究[J]. 鋼構造論文集, 1993, 3(9): 57 − 66. NISHIUMI K, OKIMOTO M, KAWABATA N, et al. An experimental study on hollow section bridge pier with the use of steel-frame-elements [J]. Steel Construction Engineering, 1993, 3(9): 57 − 66. (in Japanese
[40] TAKAHASHI Y, IEMURA H. Inelastic seismic performance of RC tall piers with hollow section [C]// Proceedings of the 12th World Conference on Earthquake Engineering. Auckland: New Zealand Society for Earthquake Engineering, 2000: 1953 − 1961.
[41] 東邦和, 福井次郎, 橋本万多良,等.スパイラル筋を用いたSRC橋脚構造の耐震性能[C]//第2回地震時保有耐力法に基づく橋梁の耐震設計. 東京: 日本地震工程协会, 1998: 193 − 196. AZUMA K, FUKUI J, HASHIMOTO M, et al. Seismic performance of SRC pier using spiral reinforcement [C]// Proceedings of the 2th Symposium on Ductility Design Method for Bridges. Tokyo: JEES, 1998: 193 − 196. (in Japanese
[42] 増川淳二, 天野玲子, 須田久美子, 等. 高强度鉄筋を用いたRC橋脚部材の開発[J]. コンクリート工学論文集, 1998, 9(1): 123 − 132. MASUKAWA J, AMANO R, SUDA K, et al. Development of RC high pier using high strength reinforcing bars [J]. Concrete Research and Technology, 1998, 9(1): 123 − 132. (in Japanese
[43] 湯川保之, 緒方辰男, 須田久美子, 等. 中空断面鉄筋コンクリート高橋脚の耐震性能[J]. 土木学会論文集, 1999, V-42(613): 103 − 120. YUKAWA Y, OGATA T, SUDA K, et al. Seismic performance of reinforced concrete high pier with hollow section [J]. Doboku Gakkai Ronbunshu, 1999, V-42(613): 103 − 120. (in Japanese
[44] 宇根寛, 川島一彦, 堺淳一. 軸カ変動を受けるRCアーチリブの正負交番載荷実験[C]//第4回地震時保有耐力法に基づく橋梁の耐震設計. 東京: 日本地震工程协会, 2000: 225 − 230. HIROSHI U, KAWASHIMA K, SAKAI J. Seismic performance of reinforced concrete arch rib with hollow section under varying axial loads [C]// Proceedings of the 4th Symposium on Ductility Design Method for Bridges. Tokyo: JEES, 2000: 225 − 230. (in Japanese
[45] 劔持安伸, 川島一彦. 部分拘束を加えた中空断面RC橋脚の耐震性 に関する実験的研究[J]. 土木学会論文集, 2001, I-56(682): 57 − 69. KENMOTSU Y, KAWASHIMA K. Seismic performance of hollow reinforced concrete columns with densely confined zones [J]. Doboku Gakkai Ronbunshu, 2001, I-56(682): 57 − 69. (in Japanese
[46] 永峰雅史, 島弘, 中井将博. 中空プレキャスト橋脚の耐震性能に関する実験[C]//第10回四国支部技術研究発表会講演概要集.東京: 日本土木协会, 2004: 328 − 329. MASASHI N, HIROSHI S, MASAHIRO N. Experimental study on seismic performance of precast hollow Pier [C]// Proceedings of the 10th Annual Conference of the Four-Country Branches of Japan Society of Civil Engineers. Tokyo: JSCE, 2004: 328 − 329. (in Japanese
[47] 篠原聖二, 末崎将司, 堺淳一, 等. 中空断面RC橋脚の断面条件が地震時破壤特性と变形能に及ぼす影響の実験的評価[C] // 第18回地震時保有耐力法に基づく橋梁の耐震設計. 東京: 日本地震工程协会, 2015: 7 − 14. SHINOHARA M, SUEZAKI M, SAKAI J, et al. Evaluation of failure characteristics and ductility of reinforced concrete column with hollow section [C]// Proceedings of the 18th Symposium on Ductility Design Method for Bridges. Tokyo: JEES, 2015: 7 − 14. (in Japanese
[48] 高原良太, 青木圭一. RC中空断面橋脚の耐震性能に関する実験的検討[C] //土木学会第70回年次学術講演会. 東京: 日本土木协会, 2015: 235 − 236. RYOTA T, KEIICHI A. Experimental study on seismic performance of RC hollow section piers [C]// Proceedings of the 70th Annual Conference of the Japan Society of Civil Engineers. Tokyo: JSCE, 2015: 235 − 236. (in Japanese
[49] MO Y L, JENG C H, PERNG S F. Seismic shear behavior of rectangular hollow bridge columns [J]. Structural Engineering and Mechanics, 2001, 12(4): 429 − 448. doi: 10.12989/sem.2001.12.4.429
[50] YEH Y K, MO Y L, YANG C Y. Seismic performance of rectangular hollow bridge columns [J]. Journal of Structural Engineering, 2002, 128(1): 60 − 68. doi: 10.1061/(ASCE)0733-9445(2002)128:1(60)
[51] 김재관, 김익현, 임현우, 등. 수평 반복하중을 받는 비내진상세 RC 중공구형교각의 거동특성[J]. 한국콘크리트학회 논문집, 2003, 15(2): 263 − 272. 김재관, 김익현, 임현우, 등. 수평 반복하중을 받는 비내진상세 RC 중공구형교각의 거동특성[J]. 한국콘크리트학회 논문집, 2003, 15(2): 263 − 272. KIM J K, KIM J H, LIM H W, et al. Behavior of hollow rectangular RC piers without seismic detailing subjected to cyclic lateral load [J]. Journal of the Korea Concrete Institute, 2003, 15(2): 263 − 272. (in Korean
[52] 김 익 현, 이종석, 이 윤 복, 등. 50%주철근 겹침이음을 갖는 중실 및 중공 사각단면 교각의 거동특성[J]. 한국지진공학회 논문집, 2003, 7(5): 25 − 35. 김 익 현, 이종석, 이 윤 복, 등. 50%주철근 겹침이음을 갖는 중실 및 중공 사각단면 교각의 거동특성[J]. 한국지진공학회 논문집, 2003, 7(5): 25 − 35. KIM I H, LEE J S, RHIE Y B, et al. Behavior of Solid and hollow rectangular RC piers with 50% of lap-spliced longitudinal bars [J]. Journal of the Earthquake Engineering Society of Korea, 2003, 7(5): 25 − 35. (in Korean
[53] 고 성 현. 나선철근으로 횡구속된 정사각형 RC 기둥의내진성능[J]. 한국구조물진단유지관리공학회 논문집, 2012, 16(5): 88 − 97. 고 성 현. 나선철근으로 횡구속된 정사각형 RC 기둥의내진성능[J]. 한국구조물진단유지관리공학회 논문집, 2012, 16(5): 88 − 97. KO S H. Seismic performance of square RC column confined with spirals [J]. Journal of the Korea Institute for Structural Maintenance and Inspection, 2012, 16(5): 88 − 97. (in Korean
[54] ZHANG Y Y, HARRIES K A, YUAN W C. Experimental and numerical investigation of the seismic performance of hollow rectangular bridge piers constructed with and without steel fiber reinforced concrete [J]. Engineering Structures, 2013, 48: 255 − 265. doi: 10.1016/j.engstruct.2012.09.040
[55] WANG Z Q, GE J P, WEI H Y. Seismic performance of precast hollow bridge piers with different construction details [J]. Frontiers of Structural and Civil Engineering, 2014, 8(4): 399 − 413. doi: 10.1007/s11709-014-0273-7
[56] PRADO N I, AGUILAR G, LÓPEZ O, et al. Arrangement of transverse reinforcement in hollow piers subjected to lateral load [J]. ACI Structural Journal, 2016, 113(4): 723 − 733.
[57] CASSESE P, RICCI P, VERDERAME G M. Experimental study on the seismic performance of existing reinforced concrete bridge piers with hollow rectangular section [J]. Engineering Structures, 2017, 144: 88 − 106. doi: 10.1016/j.engstruct.2017.04.047
[58] PINTO A V, VERZELETTI G, NEGRO P. Cyclic testing of a squat bridge-pier [R]. Brussels: European Communities, 1995.
[59] PINTO A V, VERZELETTI G, MAGONETTE G, et al. Pseudo-dynamic testing of large-scale R/C bridges in ELSA [R].Brussels: European Communities, 1996.
[60] 韦建刚, 罗霞, 欧智菁, 等. 圆高强钢管超高性能混凝土短柱轴压性能试验研究[J]. 建筑结构学报, 2020, 41(11): 16 − 28. WEI Jiangang, LUO Xia, OU Zhijing, et al. Experimental study on axial compressive behavior of circular UHPC filled high-strength steel tube short columns [J]. Journal of Building Structures, 2020, 41(11): 16 − 28. (in Chinese)
[61] MANSUR M A, ISLAM M M. Interpretation of concrete strength for nonstandard specimens [J]. Journal of Materials in Civil Engineering, 2002, 14(2): 151 − 155. doi: 10.1061/(ASCE)0899-1561(2002)14:2(151)
[62] TUV E. Ensemble learning [M]// GUYON I, NIKRAVESH M, GUNN S, et al. Feature Extraction. Berlin Heidelberg: Springer, 2006: 187 − 204.
[63] BREIMAN L. Bagging predictors [J]. Machine Learning, 1996, 24(2): 123 − 140.
[64] FREUND Y, SCHAPIRE R E. A decision-theoretic generalization of on-line learning and an application to boosting [J]. Journal of Computer and System Sciences, 1997, 55(1): 119 − 139. doi: 10.1006/jcss.1997.1504
[65] PEDREGOSA F, VAROQUAUX G, GRAMFORT A, et al. Scikit-learn: Machine learning in python [J]. Journal of Machine Learning Research, 2011, 12: 2825 − 2830.
[66] FAWAGREH K, GABER M M, ELYAN E. Random forests: From early developments to recent advancements [J]. Systems Science & Control Engineering, 2014, 2(1): 602 − 609.
[67] SVETNIK V, LIAW A, TONG C, et al. Random forest: A classification and regression tool for compound classification and QSAR modeling [J]. Journal of Chemical Information and Computer Sciences, 2003, 43(6): 1947 − 1958. doi: 10.1021/ci034160g
[68] GEURTS P, ERNST D, WEHENKEL L. Extremely randomized trees [J]. Machine Learning, 2006, 63(1): 3 − 42. doi: 10.1007/s10994-006-6226-1
[69] GENTLE J, HÄRDLE W K, MORI Y. Handbook of computational statistics [M]. 2nd ed. Berlin: Springer, 2012: 985 − 1022.
[70] FRIEDMAN J H. Greedy function approximation: A gradient boosting machine [J]. The Annals of Statistics, 2001, 29(5): 1189 − 1232. doi: 10.1214/aos/1013203450
[71] CHEN T Q, GUESTRIN C. XGBoost: A scalable tree boosting system [C]// Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Francisco: American Computer Society, 2016: 785 − 794.
[72] CHEN S Z, ZHANG S Y, HAN W S, et al. Ensemble learning based approach for FRP-concrete bond strength prediction [J]. Construction and Building Materials, 2021, 302: 124230. doi: 10.1016/j.conbuildmat.2021.124230
[73] DRUCKER H, BURGES C J C, KAUFMAN L, et al. Support vector regression machines [C]// Proceedings of the 9th International Conference on Neural Information Processing Systems. Denver: MIT Press, 1996: 155 − 161.
[74] TAYLOR K E. Summarizing multiple aspects of model performance in a single diagram [J]. Journal of Geophysical Research: Atmospheres, 2001, 106(7): 7183 − 7192.
[75] LUNDBERG S M, LEE S I. A unified approach to interpreting model predictions [C]// Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc. , 2017: 4765 − 4774.
[76] LUNDBERG S M, ERION G, CHEN H, et al. From local explanations to global understanding with explainable AI for trees [J]. Nature Machine Intelligence, 2020, 2(1): 56 − 67. doi: 10.1038/s42256-019-0138-9
-
期刊类型引用(9)
1. 冯晓东，冯达，赵文雁，陈耀，郑亦汶. 基于节点松弛法的张拉整体结构力学性能分析. 工程力学. 2025(03): 100-112 . 
本站查看
2. 朱忠义，白光波，周忠发. 索结构找力的扩展广义平衡矩阵奇异值分解法. 建筑结构学报. 2023(04): 118-128 . 百度学术
3. 汪仁才. 混凝土结构强度现场检测方法原理与应用分析. 安徽建筑. 2023(06): 150-152 . 百度学术
4. 吴浩，范重，刘涛，杨开，张爱林，张艳霞. 大高差轮辐结构研究与应用. 工程力学. 2022(S1): 272-285 . 本站查看
5. 赵曦，罗超逸，张艳霞，王庆博. 半球形滑动式索撑节点性能分析. 工业建筑. 2022(08): 132-139 . 百度学术
6. 李军伟，徐飞，王兵，高阳. 混凝土不同骨料粒径对声发射检测的影响. 山东大学学报(工学版). 2021(05): 84-90 . 百度学术
7. 秦卫红，王书良，惠卓，解鹏，李云杰. 索穹顶主动索的张拉影响系数. 工业建筑. 2021(10): 1-8 . 百度学术
8. 鲁建，薛素铎，李雄彦，刘人杰. 索桁张拉结构形状设计及找力分析. 东南大学学报(自然科学版). 2020(02): 244-250 . 百度学术
9. 冯远，王立维，张彦，邱添，杨文，向新岸，刘翔，廖姝莹. 成都凤凰山专业足球场结构设计. 建筑结构. 2020(19): 15-21+14 . 百度学术
其他类型引用(8)
计量
- 文章访问数: 30
- HTML全文浏览量: 3
- PDF下载量: 15
- 被引次数: 17
