STRUCTURAL RELIABILITY ANALYSIS METHOD BASED ON KEY REGION-SAMPLING AND DEEP NEURAL NETWORK-SURROGATE MODEL
-
摘要:
提出了一种自适应重点区域采样方法,通过建立深度神经网络代理模型,对结构可靠性进行评估。该自适应重点区域采样方法结合距离信息和概率分布信息,既可考虑极限状态面附近样本对结构可靠度具有较大影响,又可考虑样本空间全局概率分布规律,从而协调局部搜索和全局探索的均衡。为了避免采样点聚集导致的采样效率降低,提出了一种剔除候选点规则。针对深度神经网络代理模型的特征,初始化采取均匀拉丁超立方实验设计,并给出可考虑深度神经网络预测结果有波动性的收敛准则,保证所提出算法收敛的鲁棒性。通过三个数值算例,验证该文方法在精度和效率方面均有较明显的优势。
Abstract:An adaptive key region sampling method is proposed for evaluating structural reliability by establishing a deep neural network surrogate model. This adaptive key region sampling method combines distance information and probability distribution information, allowing for the consideration of the significant impact of samples near the limit state surface, as well as the influence of sampling points following the global probability distribution, striking a balance between local exploration and global exploitation. To avoid the reduction in sampling efficiency due to the clustering of sampling points, a candidate point removal rule is proposed. Considering the characteristics of deep neural network surrogate model, a uniform Latin hypercube sampling experimental design is adopted for initialization, along with convergence criteria that take into account the fluctuation characteristics of deep neural network predictions, ensuring the robustness of the proposed algorithm's convergence. Validation through three numerical examples demonstrates that the method presented in this paper exhibits significant advantages in terms of accuracy and efficiency.
-
在工程实践中结构的安全性被许多不确定性因素影响,如结构的内在性质(材料强度、几何尺寸)和外在环境(风、地震),因而准确、高效的可靠度评估有重要的现实意义。已知可靠度计算方法中,近似算法(FORM[1 − 2]、SORM[2])高效但只适用于弱非线性的问题,蒙特卡洛模拟法(MCS)虽准确但需大量模拟,只适于功能函数计算消耗小的问题。
为了提高计算效率和精度,基于自适应采样的代理模型方法被提出,它通过使用少数已知样本去拟合一个模型,用于预测结构响应和进行可靠性分析。目前,不同代理模型,如:响应面模型[3]、Kriging模型[4]、支持向量机[5]、神经网络模型[2],以及集成代理模型[6 − 7]等,已被用于结构可靠性分析中。基于代理模型的自适应采样利用已知样本点和当前代理模型的特征选择下一个采样点,并通过迭代不断提高代理模型计算准确度。
自适应采样过程主要基于代理模型的预测均值和偏差,如:AK-MCS法[4]提出的基于U学习函数和EFF学习函数的自适应采样是两种典型算法。EFF函数是基于全局优化提出的,U学习函数更加关注失效边界的预测而具有更高的效率。随后,许多学者从不同的角度提出了很多改进的学习函数,来实现效率和准确性的均衡。LYU等[8]提出了H函数,从信息熵的角度计算预测点的不确定性。SUM等[9]提出的最小改进函数(LIF),同时考虑了Kriging模型统计信息和联合概率密度函数。
随着人工智能的崛起,人们对神经网络的研究逐渐深入,常将隐藏层超过两层的神经网络称为深度神经网路(DNN)。DNN相较于传统神经网络的优势[10]:1)对相同规模的神经元,更深的网络相比更宽的网络更容易训练;2)同样参数下的DNN比一般网络有更强的学习能力和泛化能力。且越来越多的新技术涌现,模型的训练难度不断降低、准确性不断提高。DNN模型也被结构可靠度关注,如:BAO等[11]和XIANG等[12]分别提出基于DNN的自适应子集搜索和权重自适应采样的可靠度评估方法。LIEU等[13]创新性地将基于DNN的可靠度评估分为全局预测和局部预测两个部分,效率较低。而DNN与可靠性评估的结合尚处于起步阶段,性能等各方面还有待提高。
本文提出一种基于DNN代理模型的可靠性评估方法,包括一种自适应重点区域采样方法,集合均匀拉丁超立方(LHS)抽样的初始实验设计和基于误差的收敛准则,通过三个案例的验证,说明所提出方法的准确性和效率优势。
1 基本理论
1.1 蒙特卡洛模拟
可靠度问题中的功能函数可写为:
Z=g(X)=g(x1,x2,⋯,xn) (1) 式中,X为影响结构功能的n个随机变量(x1, x2, ···, xn)。结构功能函数出现小于等于0的概率称为结构的失效概率,用Pf表示如下:
Pf=∫g(X)⩽ (2) 式中,f(X)为关于变量X的联合概率密度函数,式(2)通常计算困难,常采用蒙特卡洛模拟(Monte Carlo Simulation,MCS)计算失效概率,公式可以表示如下:
P_{\mathrm{f}}^{\text{MCS}}\approx\frac{1}{N^{\text{MCS}}}\sum\limits_{i=1}^{N^{\text{MCS}}}I\left(X\right) (3) 式中:NMCS为蒙特卡洛样本数量;I(X)为MCS方法的指示函数,可以写成:
I\left( X \right) = \left\{ \begin{aligned} & 1,&& g\left( X \right) {\leqslant} 0 \\ & 0,&&{{\text{others}}} \end{aligned} \right. (4) 为了评估蒙特卡洛模拟的准确性,工程上使用变异系数(Cov)来表征,变异系数通常要求小于0.05[4]。如果不满足要求,需要增大NMCS。
{\rm Cov}=\sqrt{\frac{1-P_{\mathrm{f}}^{\text{MCS}}}{N^{\text{MCS}}\cdot P_{\mathrm{f}}^{\text{MCS}}}}\leqslant0.05 (5) 1.2 深度神经网络代理模型
最简单的N层神经网络可以用图1表示,包含1个输入层、N−1个隐藏层和1个输出层。
每层之间的网络节点通过关系可以用下面公式表示:
H_i^{\left( l \right)} = \varphi \left( {\sum\limits_{j = 1}^n {w_{ij}^{\left( l \right)}} H_j^{\left( {l - 1} \right)} + b_i^{\left( l \right)}} \right) (6) 式中: H_{i}^{(l)} 为第l层的第i个神经元的输出; w_{ij}^{(l)} 为第l层的第i个神经元的第j个输入的权重; b_{i}^{(l)} 为偏置;n为(l−1)层神经元的个数;φ(·)为激活函数,常采用修正线性单元(Rectified linear unit,ReLU),能够避免梯度爆炸和梯度消失。它的表达式:
\varphi (x) = \left\{ \begin{aligned} & x,&&{x {\geqslant} 0} \\ & 0,&&{x < 0} \end{aligned}\right. (7) 在可靠度问题中,使用神经网络的目的是利用少量的数据去拟合结构功能函数的响应关系,应该使用回归问题的损失函数(loss)作为神经网络的优化目标,即:
{\rm loss} = \frac{1}{m}\sum\limits_{i = 0}^m {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} (8) 式中:yi为真实值; \hat{y}_{i} 为神经网络预测值;m为训练样本数。
通常使用梯度下降法训练神经网络,批量梯度下降、随机梯度下降(SGD)和小批量梯度下降是最常见的三种形式。本文采用了小批量梯度下降法,批量大小的设置对训练有一定的影响,通常采用8、16、32,本文算例均采用min(ns, 32)为批量,ns是已经采样点的个数。为了优化算法效率,有从优化方向和步长改进的算法,如:带动量的随机梯度下降、基于均方根传播算法(RMSProp)、自适应矩估计算法(Adam)等。Adam算法[14]收敛效率高且鲁棒性好,可表示为:
{m_t} \leftarrow {\beta _1} \cdot {m_{t - 1}} + \left( {1 - {\beta _1}} \right) \cdot {g_t} (9) {v_t} \leftarrow {\beta _2} \cdot {v_{t - 1}} + \left( {1 - {\beta _2}} \right) \cdot g_t^2 (10) {\theta }_{t}\leftarrow {\theta }_{t-1}-\alpha \cdot {m}_{t}/(\sqrt{{v}_{t}}+\varepsilon ) (11) 式中:gt为神经网络的梯度;θt为神经网络的参数;t为训练步数;β1和β2分别为一阶、二阶动量衰减系数,本文取0.9和0.99,ε是数值稳定量,取10−8。由于Adam算法对于初始学习率不敏感,本文算例初始学习率均为0.001。
为了防止在神经网络的训练中出现过拟合现象,提高模型的泛化能力,本文采用了L2正则化方法,正则化后损失函数为:
{\rm loss}' = {\rm loss} + \lambda \frac{1}{2}{\left\| \theta \right\|_2} (12) 式中:θ为神经网络的权重参数,不包括偏置b;λ为L2正则化因子,本文取10−4。
2 自适应采样方法
基于代理模型的可靠性分析中,自适应采样方法的构建是重点。本节详细阐述所提出方法,并在2.6节介绍了整个算法流程。
2.1 初始实验设计
对于初始样本的生成,最经典的AK-MCS[4]算法使用的是服从随机变量的概率分布的拉丁超立方(LHS)采样,该做法有一个很明显的缺点:采样点多生成在概率密度较大的区域,不能体现全部样本的响应情况。对于可靠度问题,失效边界一般分布于概率分布较低的区域,使用服从概率分布的随机采样会导致初始采样采不到失效点,从而降低后续的自适应采样的效率。
本文建议使用整个样本空间的均匀采样提高初始采样效率。对于整个样本空间的估计,可以采用3σ原则:对于正态分布的样本,μ是均值,σ是标准差,在(μ−3σ, μ+3σ)区间内已经包含了99.73%的样本空间,即:
P\left( {\left| {x - \mu } \right| > 3\sigma } \right) {\leqslant} 0.003 (13) 对于其他分布的样本,可以采取类似的方法确定出整个样本空间。如果已知可靠性问题的失效概率特别低,可以考虑用5σ来确定样本空间。确定好样本空间后,假定其服从均匀分布,采用LHS进行采样。图2是经典四边界问题(问题阐述见3.1节)初始采样方法的对比,可见本文提出的方法更容易采样到整个样本空间。
2.2 数据标准化
对于不同的可靠性问题,蒙特卡洛样本池(候选样本)SMCS可能存在不同的范围,为了使算法具有通用性,在进行DNN拟合和自适应采样参数计算前,必须进行数据标准化处理。具体处理公式如下:
S_{\text{nor}}=\frac{S_{\text{MCS}}-\mu_{\mathrm{s}}}{\sigma_{\mathrm{s}}} (14) 式中:μs和σs为SMCS样本的均值和标准差;Snor为标准化后的样本。
2.4 自适应重点区域采样法
XIAO等[15]提出一种基于距离的采样方法,将其应用于BP神经网络。这种采样方法只依赖于各个采样点的欧氏距离,因此适用于各种代理模型,其形式可以表示为:
\psi_{\mathrm{d}}^j=\frac{\left|\tilde{g}\left(X_{\mathrm{c}}^j\right)\right|}{d_{\mathbf{p}\min}^j}\text{ }\;,\quad j=1,2,\cdots,n_{\mathrm{c}} (15) 式中:\tilde g 为代理模型; X_{\mathrm{c}}^j 为第j个候选样本点; \tilde{g}(X_{\mathrm{c}}^j) 为代理模型的预测值;nc表示候选样点的个数; d_{\bf{p} \min }^{j} 为第j个候选样本点与已经存在采样点的最小欧式距离。每次选取 \psi_{\mathrm{d}}^j 最小值的点为下一采样点。
XIAO等[15]所提方法一定程度上的做到了全局搜索和局部探索的均衡。但没有考虑概率分布的影响。对 \psi_{\mathrm{d}}数值接近的几个候选点,应优先考虑概率密度较大区域处的点作为下一个采样点。如图3所示,候选点1和点2的 \psi_{\mathrm{d}}很接近,但是候选点2处的概率密度明显大于点1,说明候选点2对模型的可靠度影响更大,应优先考虑。
为了考虑上述概率密度信息,首先提出重点区域的概念:对候选样本点Xc的 \psi_{\mathrm{d}}值较小且概率密度相对较大时,表明该点靠近极限状态面且其附近采样点相对较多,对结构可靠性评估影响相对较大,是采样的重点区域。重点区域自适应采样公式表示如下:
X_\text{s}=\arg \max _{X_\text{c} \in S_{\mathrm{MCS}}} f\left(X_\text{c} \mid \psi_\text{d}\left(X_\text{c}\right)-\psi_{\text {d, min }} {\leqslant} \psi_{\text {d, min }}\right) (16) 式中, \psi_{\mathrm{d},\min}=\min(\psi_{\mathrm{d}}^j) 。即,计算所有候选点的 \psi_{\mathrm{d}}^j ,记其中最小值为ψd,min;在满足限定条件ψd(Xc)−ψd, min ≤ ψd, min中的候选点中选出概率密度f(Xc)最大的点为采样点。本文限定不等式表示的选点范围取为1倍ψd,min,这一取值受功能函数特征等的影响尚有待进一步探讨。通常情况下,ψd越小,该点的功能函数越接近0,该点对可靠度评估越重要。概率密度f(Xc)的计算可使用UQLab工具箱[16]计算。
2.5 候选点剔除原则
\psi_\mathrm{d} 学习函数的形式,与自适应Kriging蒙特卡洛方法(AK-MCS)的U函数形式接近。其缺点在于:在局部探索时,它容易过分探索某个区域,导致采样点在某一区域聚集[17 − 18](多聚集在功能函数接近0的区域),降低采样效率。
为了防止采样点的聚集,提出了一种候选点剔除规则:选出第j个备选采样点Xs,j后,如果其响应值g(Xs,j)≤Δ,则点Xs,j距已有采样点0.5倍最小距离以内的候选样本点需从总的候选样本中删除,Xs,j附近的候选点不被选为后续的采样点,从而提高局部的探索效率。本文根据算例不同,建议Δ取0.01~0.1,根据问题的响应幅值取用。
2.6 基于误差的收敛准则
根据神经网络代理模型的特点,本文提出两种基于失效概率相对误差的收敛准则。
1)收敛准则一
相邻两次迭代相对误差小于限定最大误差,即:
\left\{ \begin{aligned} & {{\varepsilon _j} = {{| {\hat P_\text{f}^{( j )} - \hat P_\text{f}^{( {j - 1} )}} |} / {\hat P_\text{f}^{( j )}}} {\leqslant} {\varepsilon _r}} \\ & {{\varepsilon _{j - 1}} = {{| {\hat P_\text{f}^{( {j - 1} )} - \hat P_\text{f}^{( {j - 2} )}} |} / {\hat P_\text{f}^{( {j - 1} )}}} {\leqslant} {\varepsilon _\text{r}}} \end{aligned}\right. (17) 2)收敛准则二
相邻三次迭代平均误差小于限定最大误差,即:
\left\{ \begin{aligned} & {\hat P_\text{f,mean}^{( j )} = {{( {\hat P_\text{f}^{( {j - 2} )} + \hat P_\text{f}^{( {j - 1} )} + \hat P_\text{f}^{( j )}} )} / 3}} \\& {{\varepsilon _j} = {{| {\hat P_\text{f,mean}^{( j )} - \hat P_\text{f}^{( j )}} |} / {\hat P_\text{f,mean}^{( j )}}} {\leqslant} {\varepsilon _\text{r}}} \\& {{\varepsilon _{j - 1}} = {{| {\hat P_\text{f,mean}^{( j )} - \hat P_\text{f}^{( {j - 1} )}} |} / {\hat P_\text{f,mean}^{( j )}}} {\leqslant} {\varepsilon _\text{r}}} \\& {{\varepsilon _{j - 2}} = {{| {\hat P_\text{f,mean}^{( j )} - \hat P_\text{f}^{( {j - 2} )}} |} / {\hat P_\text{f,mean}^{( j )}}} {\leqslant} {\varepsilon _\text{r}}} \end{aligned}\right. (18) 式中: \hat{P}_{\mathrm{f}}^{(j)} 为第j次迭代得到的失效概率;εr为限定最大误差,建议取0.01~0.02。经第3节案例验证,这两个规则都有很好的适用性。
2.7 计算流程图
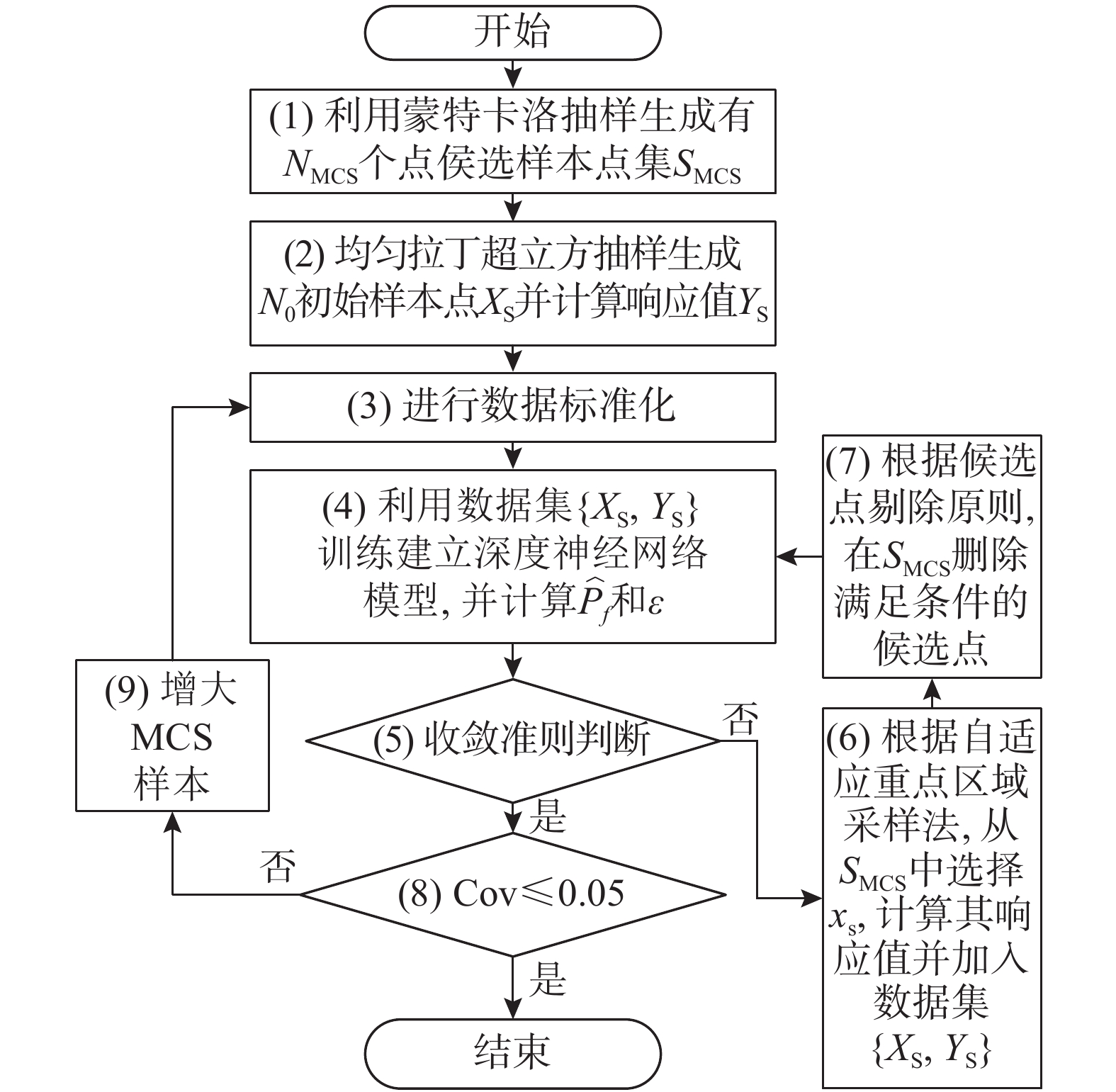
重点区域采样的自适应算法流程图见图4:
1) 通过经验确定蒙特卡洛样本池大小为NMCS,使用UQLab工具箱[16]抽样出候选样本点SMCS;
2) 根据2.1节的3σ(或5σ)原则确定总体样本空间并通过均匀拉丁超立方获取N0个初始样本Xs,并计算对应响应值Ys;
3) 根据式(14)进行数据标准化;
4) 使用数据集{Xs, Ys}训练深度神经网络代理模型并预测候选样本的响应,根据式(3)和式(4)计算失效概率 \hat{P}_{\mathrm{f}} ,根据式(17)和式(18)计算相对误差ε;
5)根据基于误差的收敛准则判断代理模型的收敛性;
6)使用自适应重点区域采样法从SMCS选出xs,计算其功能函数的响应值并加入数据集{Xs, Ys}。
7)根据候选点剔除原则,在SMCS中删除满足条件的候选点;
8)计算Cov;
9)增大蒙特卡洛样本池。
3 测试案例
本章使用3个经典案例验证本文算法的高效性,将绝对误差作为准确性评判标准。绝对误差将MCS方法计算所得的失效概率 P_{\mathrm{f}}^{\text{MCS}} 作为真解,表达式如下:
{\varepsilon _{\rm a}} = \frac{{\left| {P_{\rm f}^{{\text{MCS}}} - {{\hat P}_{\rm f}}} \right|}}{{P_{\rm f}^{{\text{MCS}}}}} (19) 3.1 算例1:四边界串联系统
四边界串联系统[4, 7, 9, 12 − 13, 18 − 19]的功能函数如下:
g\left( {{x_1},{x_2},k} \right) = \min \left\{ \begin{aligned} & {3 + 0.1{{\left( {{x_1} - {x_2}} \right)}^2} - {{\left( {{x_1} + {x_2}} \right)} / {\sqrt 2 }}} \\& {3 + 0.1{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{x_1} + {x_2}} \right)} / {\sqrt 2 }}} \\& {{x_1} - {x_2} + {k / {\sqrt 2 }}} \\& {{x_2} - {x_1} + {k / {\sqrt 2 }}} \end{aligned} \right. (20) 式中,x1、x2均为标准正态分布且相互独立。根据k值不同(6和7),分两种工况。部分超参数设置见表1。
表 1 算例1超参数设置Table 1. Hyperparameter values for Case 1类别 参数 取值 自适应采样 \Delta 0.1 N_{\mathrm{MCS}} {10}^{6} {N}_{0} 12 深度神经网络 神经网络结构 2-8-16-8-1 最大训练次数 800 算例1的结果见表2和表3,可以看出本文方法与MCS结果吻合,误差小。对于k=6工况,与基于U函数和EFF函数的Kriging方法[4]相比,模型调用次数减少了142.3%和138.5%,与XIAO等[15]的BP神经网络相比,性能有些许提升。对于其他基于深度神经网络的方法,比XIANG等[12]和LIEU等[13]的方法,分别减少53.8%和155.8%。对于k=7的工况,可以得到相似的结论。
表 2 算例1(k=6)可靠性计算结果Table 2. Reliability results for Case 1 (k=6)停止准则 方法 模型调用
次数失效概率
(×10−3)MCS
(×10−3)绝对误差/
(%)− AK-MCS-U[4] 126 4.416 4.416 − − AK-MCS-EFF[4] 124 4.412 4.416 0.090 − XIAO[15] 52.4 4.443 4.424 0.224 − XIANG[12] 80 4.414 4.42 0.14 − LIEU[13] 133 4.409 4.428 0.429 \varepsilon_{\mathrm{r},1}=0.02 本文 12+40 4.441 4.43 0.248 \varepsilon_{\mathrm{r},1}=0.01 12+40 4.441 4.43 0.248 \varepsilon_{\mathrm{r},2}=0.02 12+32 4.329 4.43 2.280 \varepsilon_{\mathrm{r},2}=0.01 12+40 4.441 4.43 0.248 注:εr,1为收敛准则1;εr,2为收敛准则2。下同。 表 3 算例1(k=7)可靠性计算结果Table 3. Reliability results for Case 1 (k=7)停止准则 方法 模型调用
次数失效概率
(×10−3)MCS
(×10−3)绝对误差/
(%)− AK-MCS-U[4] 96 2.233 2.233 − − AK-MCS-EFF[4] 101 2.232 2.233 0.045 − XIANG[12] 70 2.192 2.188 0.180 \varepsilon_{\mathrm{r},1}=0.02 本文 12+25 2.160 2.154 0.279 \varepsilon_{\mathrm{r},1}=0.01 12+38 2.080 2.154 3.435 \varepsilon_{\mathrm{r},2}=0.02 12+25 2.160 2.154 0.279 \varepsilon_{\mathrm{r},2}=0.01 12+25 2.160 2.154 0.279 图5为失效概率的收敛曲线。初始时,由于采样较少导致代理模型误差较大,因而预测的失效概率误差大且不稳定。随着采样点的增多,代理模型对失效边界的拟合越来越好,最终得到稳定且精确的失效概率。但在k=6工况的第(12+23)个点训练中,模型拟合效果不佳,有较大失效概率的误差,但是随着迭代的进行,失效概率还是逐渐收敛,说明该算法鲁棒性较好。
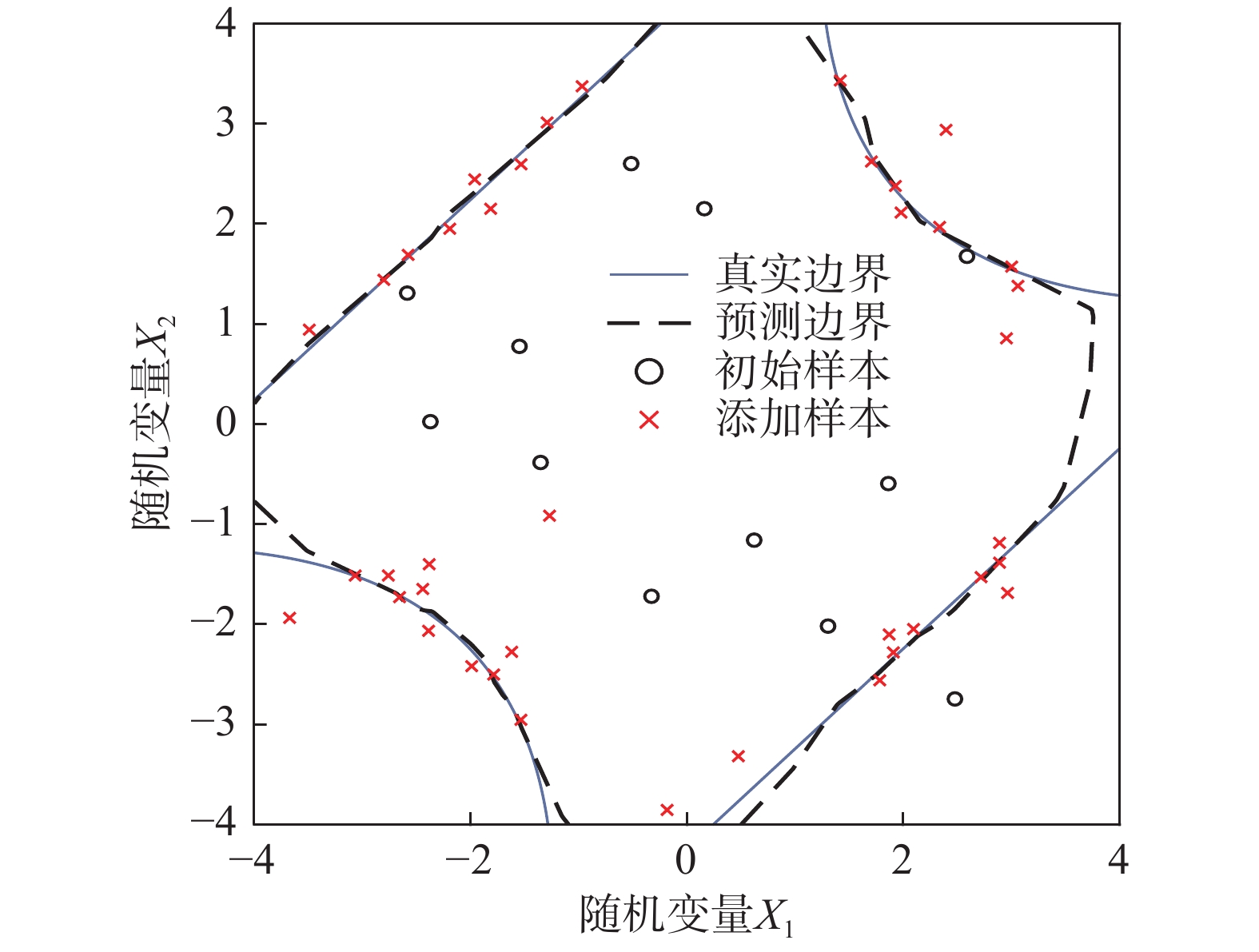
图6展示了算例1(k=6)采样点分布,可以看出基本上所有的采样点均在失效边界附近,证明了该采样规则的有效性。对于失效边界的预测,在绝大多数区域的预测效果很好,但是对于概率分布较低的区域,预测误差较大。结合最终预测结果来看,这个误差没有对结果造成很大的影响。
图7、图8分别展示了算例1(k=6)收敛准则一和二的计算过程,注意y轴使用的是对数坐标。对于收敛准则一,需要相邻两次相对误差均低于限定最大误差εr即可以判断收敛。对于不同的εr建议值,本算例结果相同。对于收敛准则二,对于不同的εr建议值,结果不同。较宽松的收敛准则,收敛越早,但是其预测的准确度也较低。横向对比图7和图8,展示出二者的趋同性,即准则一的误差小,准则二的误差也小。部分Kriging代理模型[18 − 19]采用一次相对误差进行判断,从图7可以看出对于DNN代理模型不适用,可能过早判断收敛。由于DNN代理模型的拟合可能会受到噪音数据的影响,表现出波动性,多次连续相对误差判断收敛比较准确。
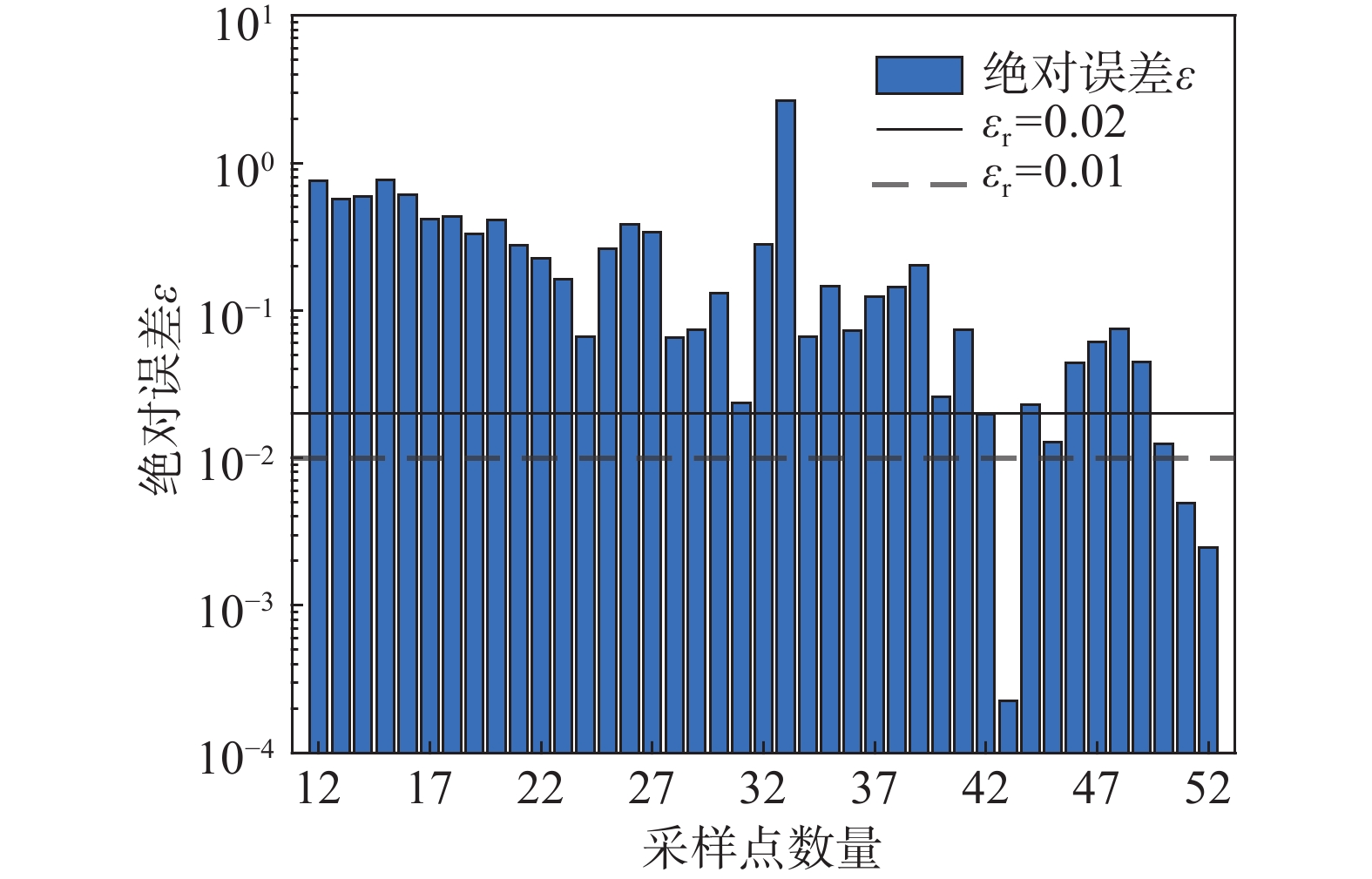
图9表示的是预测失效概率与MSC结果的绝对误差值。可以看出随着采样的进行,绝对误差在不断地递减,再次表明本算法的有效性。结合图7和图8的收敛计算,可以看出本文建议的收敛准则效果做到了效率与准确度的统一。
3.2 算例2:强非线性振动系统
本算例[4, 7, 8, 12 − 13, 15, 18 − 19]是一个工程应用中的可靠度问题,图10的单自由度振动系统的功能函数可以表示为:
\begin{split} & g\left( {m,{c_1},{c_2},r,{F_1},{t_1}} \right) = 3r - \left| {\frac{{2{F_1}}}{{m\omega _0^2}}\sin \left( {\frac{{{\omega _0}{t_1}}}{2}} \right)} \right|\;,\\& {\omega _0} = \sqrt {\frac{{\left( {{c_1} + {c_2}} \right)}}{m}} \end{split} (21) 该问题各随机变量信息见表4,它们相互独立。对于该问题部分超参数设置见表5。
表 4 算例2的随机变量信息Table 4. Random variable information of Case 2变量 参数分布 均值 标准差 m 正态分布 1.0 0.05 {C}_{1} 1.0 0.10 {C}_{2} 0.1 0.01 r 0.5 0.05 {F}_{1} 1.0 0.20 {t}_{1} 1.0 0.20 表 5 算例2超参数设置Table 5. Hyperparameter settings of Case 2类别 参数 取值 自适应采样 \Delta 0.01 N\mathrm{_{MCS}} {7\times 10}^{4} {N}_{0} 12 深度神经网络 神经网络结构 6-8-8-4-1 最大训练次数 3000 计算结果如表6所示。除了XIANG等[12]的方法以外,DNN模型的调用次数高于Kriging[4]代理模型。本文提出的方法比XIAO等[15]方法模型调用次数减少70.93%,显示了本文方法的高效性,但是较基于DNN的XIANG等[12]的方法效率略低。
表 6 算例2可靠性计算结果Table 6. Reliability results of Case 2停止准则 方法 模型调用
次数失效概率/
(×10−2)MCS/
(×10−2)绝对误差/
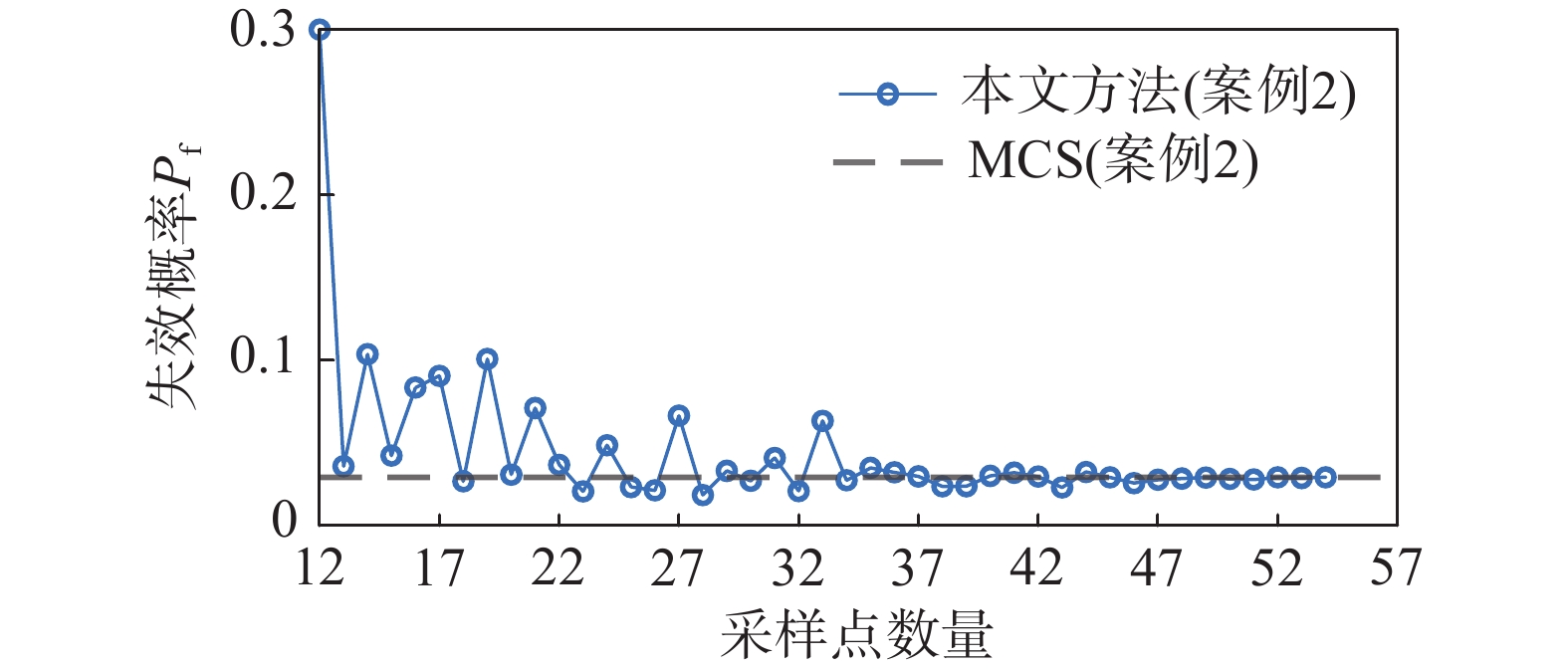
(%)− AK-MCS-U[4] 58 2.834 2.834 0 − AK-MCS-EFF[4] 45 2.851 2.834 0.600 − XIAO[15] 92.3 2.840 2.860 0.699 − XIANG[12] 35 2.849 2.836 0.450 − LIEU[13] 77 2.829 2.841 0.422 εr,1=0.02 本文 12+42 2.921 2.919 0.098 εr,1=0.01 12+69 2.914 2.919 0.147 εr,2=0.02 12+38 2.819 2.919 3.426 εr,2=0.01 12+42 2.921 2.919 0.098 从图11的收敛曲线可以看出,前期的预测波动比较大,猜测可能是被选中的采样点对可靠度评估不起作用,甚至还会产生反作用,即该点远离极限状态面。对照图12的采样点实际响应值查看发现猜想正确。随着自适应采样的进行,预测失效概率波动在不断减小,直至满足收敛准则。
3.3 算例3:屋面桁架系统
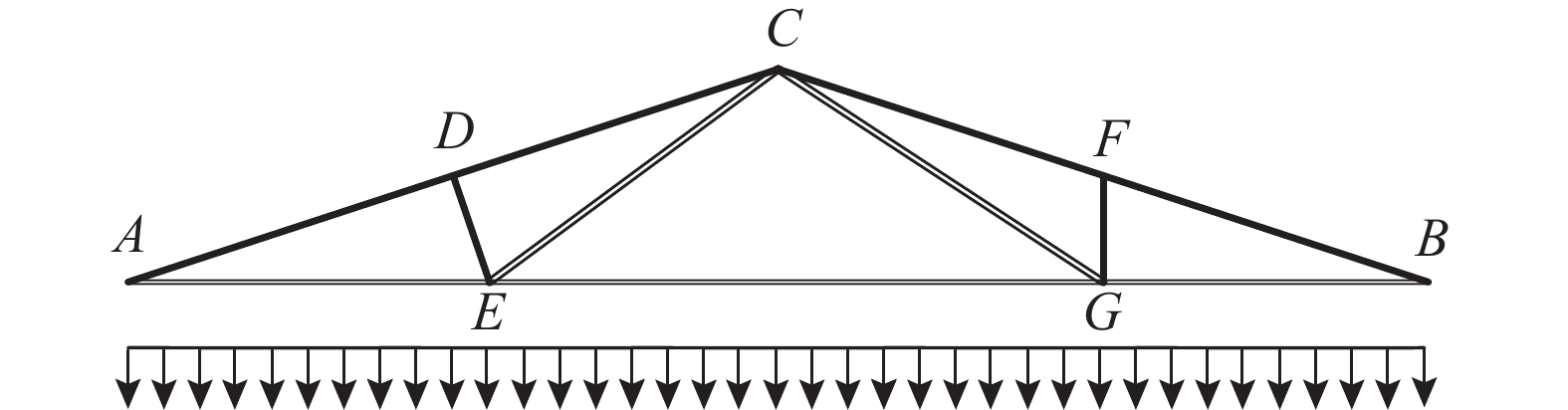
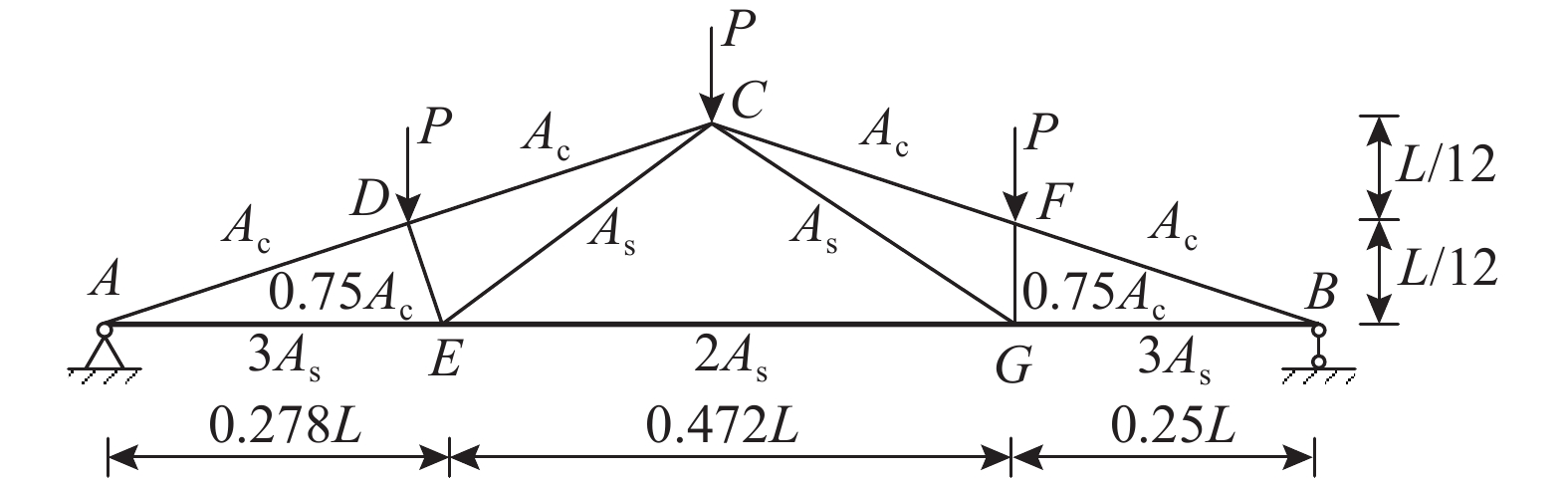
屋面桁架是结构工程最常用的承重体系,如图13所示屋面桁架结构,其下弦和拉杆的材料为钢材,上弦杆和压杆的材料是钢筋混凝土,受到均匀分布的载荷q。经过结构简化见图14,将均布荷载转化为集中力P=qL/4施加在C、D、F三个节点上。
可以计算节点C的位移为:
{\Delta _C} = \frac{{q{l^2}}}{2}\left( {\frac{{3.81}}{{{A_{\mathrm{c}}}{E_{\mathrm{c}}}}} + \frac{{1.13}}{{{A_{\mathrm{s}}}{E_{\mathrm{s}}}}}} \right) (22) 式中,Ac、Ec、As和Es分别为混凝土、钢材的截面积和弹性模量。为了考虑结构的安全性和适用性,假定ΔC≤0.03 m,功能函数表示如下:
g\left( x \right) = 0.03 - {\Delta _C} (23) 该算例[18, 20]的随机变量相互独立(见表7),超参数除了NMCS=106外,其余与算例2相同。
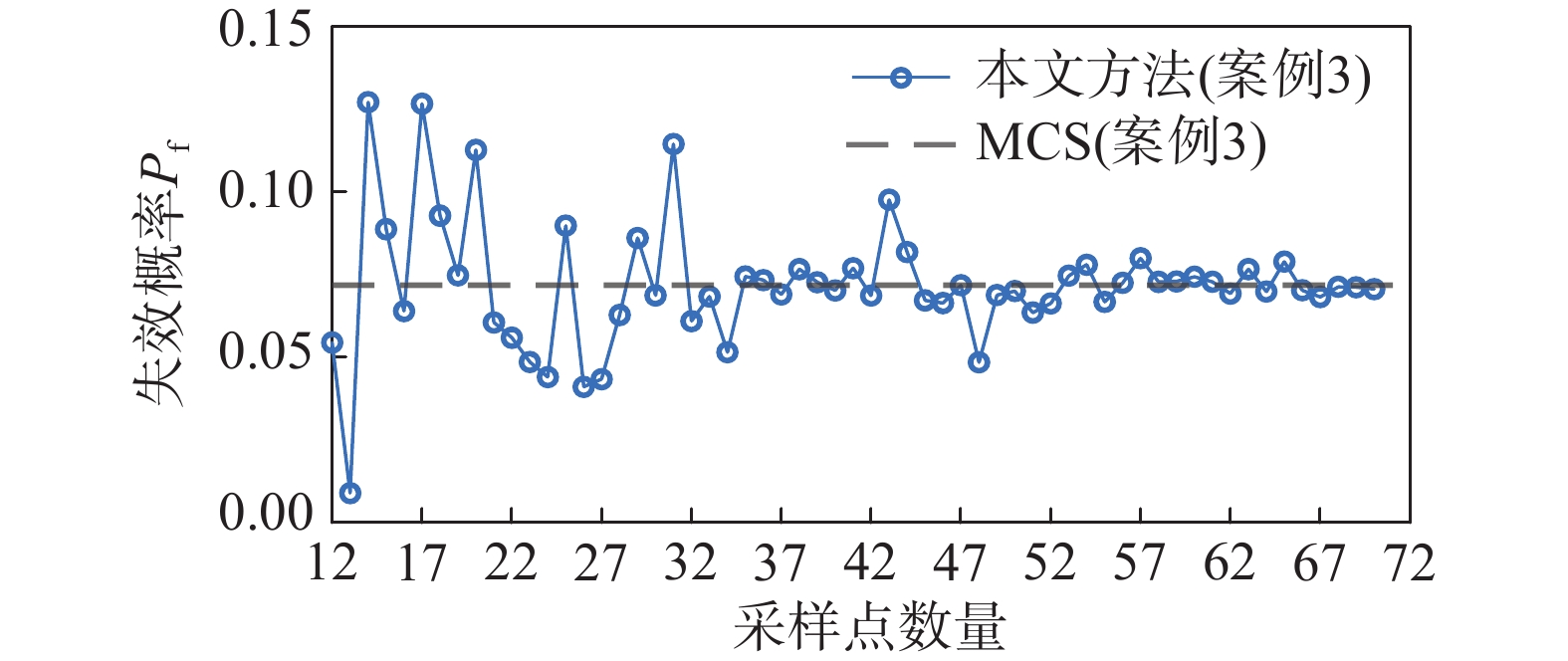
表 7 算例3的随机变量信息Table 7. Random variable information for Case 3变量 参数分布 均值 标准差 q/(N/m) 正态分布 20000 2000 l/m 13.5 0.5 As/m2 9.82×10−4 6×10−5 Ac/m2 0.04 0.008 Es/(N/m2) 1.2×1011 1.2×1010 Ec/(N/m2) 3×1010 3×109 算例3的结果见表8。可见该算例采用本文算法的误差相比于算例1、算例2略有增大(达1.6%)。AK-MCS-EFF方法[4, 18]由于收敛准则设置不当而提前收敛,导致误差较大;从 图15 可以看出本文提出的收敛准则没有出现类似的问题。对比AK-MCS-U算法[4, 18],本文算法减少了122.86%模型调用,效率较高。
表 8 算例3可靠性计算结果Table 8. Reliability results for Case 3停止准则 方法 模型调用
次数失效概率/
(×10−2)MCS/
(×10−2)绝对误差/
(%)− AK-MCS-U[18] 156 7.19 7.18 0.100 − AK-MCS-EFF[18] 57.54 8.17 7.18 16.210 εr,1=0.02 本文 12+48 7.435 7.179 3.572 εr,1=0.01 12+58 7.061 7.179 1.640 εr,2=0.02 12+48 7.435 7.179 3.572 εr,2=0.01 12+58 7.061 7.179 1.640 4 结论
本文提出一种基于深度神经网络(DNN)代理模型的自适应重点区域采样的可靠性评估方法。该算法在距离采样基础上考虑了全局概率分布的影响,提出了自适应重点区域采样策略,做到了全局探索和局部采样的均衡,提高了采样效率。对于距离学习函数的缺陷——采样点聚集,本文也提出一种剔除候选点的改进方式。针对深度神经网络代理模型,给出了不同于Kriging代理模型的初始实验设计和收敛准则,经过三个算例验证得到如下结论:
(1)相对于距离采样,本文算法的效率有较大的提升,对于算例2的功能函数调用次数降低了64.8%。对比其他深度神经网络代理模型算法,本文算法在效率和精度有优势。
(2)提出两种收敛准则具有较好的适用性,对于演算的问题和工况的失效概率计算误差满足需求。本文建议同时使用二个收敛准则进行判断,提升预测结果的准确性。
(3)针对低维度问题展示了DNN代理模型优越的拟合功能,但是算例2也出现DNN模型不如Kriging模型[4](但相差不大)的工况。可能原因是某些采样点的实际响应值过大,对模型可靠度评估贡献小,对此,考虑在后续研究中进一步优化。
说明:本文所提算法是基于代理模型的可靠性评估方法的有益补充,其中DNN模型可依据问题的复杂程度,提供不同的网络或深度优化后的拟合结果。因此,本文误差来源于算法本身对抽样的不确定性和DNN拟合的精度二方面。由于这两者相互结合、互相影响目前尚难于区别分析,后续研究将进一步开展相关探索。
-
表 1 算例1超参数设置
Table 1 Hyperparameter values for Case 1
类别 参数 取值 自适应采样 \Delta 0.1 N_{\mathrm{MCS}} {10}^{6} {N}_{0} 12 深度神经网络 神经网络结构 2-8-16-8-1 最大训练次数 800 表 2 算例1(k=6)可靠性计算结果
Table 2 Reliability results for Case 1 (k=6)
停止准则 方法 模型调用
次数失效概率
(×10−3)MCS
(×10−3)绝对误差/
(%)− AK-MCS-U[4] 126 4.416 4.416 − − AK-MCS-EFF[4] 124 4.412 4.416 0.090 − XIAO[15] 52.4 4.443 4.424 0.224 − XIANG[12] 80 4.414 4.42 0.14 − LIEU[13] 133 4.409 4.428 0.429 \varepsilon_{\mathrm{r},1}=0.02 本文 12+40 4.441 4.43 0.248 \varepsilon_{\mathrm{r},1}=0.01 12+40 4.441 4.43 0.248 \varepsilon_{\mathrm{r},2}=0.02 12+32 4.329 4.43 2.280 \varepsilon_{\mathrm{r},2}=0.01 12+40 4.441 4.43 0.248 注:εr,1为收敛准则1;εr,2为收敛准则2。下同。 表 3 算例1(k=7)可靠性计算结果
Table 3 Reliability results for Case 1 (k=7)
停止准则 方法 模型调用
次数失效概率
(×10−3)MCS
(×10−3)绝对误差/
(%)− AK-MCS-U[4] 96 2.233 2.233 − − AK-MCS-EFF[4] 101 2.232 2.233 0.045 − XIANG[12] 70 2.192 2.188 0.180 \varepsilon_{\mathrm{r},1}=0.02 本文 12+25 2.160 2.154 0.279 \varepsilon_{\mathrm{r},1}=0.01 12+38 2.080 2.154 3.435 \varepsilon_{\mathrm{r},2}=0.02 12+25 2.160 2.154 0.279 \varepsilon_{\mathrm{r},2}=0.01 12+25 2.160 2.154 0.279 表 4 算例2的随机变量信息
Table 4 Random variable information of Case 2
变量 参数分布 均值 标准差 m 正态分布 1.0 0.05 {C}_{1} 1.0 0.10 {C}_{2} 0.1 0.01 r 0.5 0.05 {F}_{1} 1.0 0.20 {t}_{1} 1.0 0.20 表 5 算例2超参数设置
Table 5 Hyperparameter settings of Case 2
类别 参数 取值 自适应采样 \Delta 0.01 N\mathrm{_{MCS}} {7\times 10}^{4} {N}_{0} 12 深度神经网络 神经网络结构 6-8-8-4-1 最大训练次数 3000 表 6 算例2可靠性计算结果
Table 6 Reliability results of Case 2
停止准则 方法 模型调用
次数失效概率/
(×10−2)MCS/
(×10−2)绝对误差/
(%)− AK-MCS-U[4] 58 2.834 2.834 0 − AK-MCS-EFF[4] 45 2.851 2.834 0.600 − XIAO[15] 92.3 2.840 2.860 0.699 − XIANG[12] 35 2.849 2.836 0.450 − LIEU[13] 77 2.829 2.841 0.422 εr,1=0.02 本文 12+42 2.921 2.919 0.098 εr,1=0.01 12+69 2.914 2.919 0.147 εr,2=0.02 12+38 2.819 2.919 3.426 εr,2=0.01 12+42 2.921 2.919 0.098 表 7 算例3的随机变量信息
Table 7 Random variable information for Case 3
变量 参数分布 均值 标准差 q/(N/m) 正态分布 20000 2000 l/m 13.5 0.5 As/m2 9.82×10−4 6×10−5 Ac/m2 0.04 0.008 Es/(N/m2) 1.2×1011 1.2×1010 Ec/(N/m2) 3×1010 3×109 表 8 算例3可靠性计算结果
Table 8 Reliability results for Case 3
停止准则 方法 模型调用
次数失效概率/
(×10−2)MCS/
(×10−2)绝对误差/
(%)− AK-MCS-U[18] 156 7.19 7.18 0.100 − AK-MCS-EFF[18] 57.54 8.17 7.18 16.210 εr,1=0.02 本文 12+48 7.435 7.179 3.572 εr,1=0.01 12+58 7.061 7.179 1.640 εr,2=0.02 12+48 7.435 7.179 3.572 εr,2=0.01 12+58 7.061 7.179 1.640 -
[1] 刘丞, 范文亮, 余书君, 等. 基于主动学习Kriging模型的改进一次可靠度方法[J]. 工程力学, 2024, 41(2): 35 − 42. doi: 10.6052/j.issn.1000-4750.2022.03.0204 LIU Cheng, FAN Wenliang, YU Shujun, et al. Improved first order reliability method based on adaptive Kriging model [J]. Engineering Mechanics, 2024, 41(2): 35 − 42. (in Chinese) doi: 10.6052/j.issn.1000-4750.2022.03.0204
[2] 范文亮, 刘丞, 李正良. 基于HLRF法与修正对称秩1方法的改进可靠度方法[J]. 工程力学, 2022, 39(9): 1 − 9. doi: 10.6052/j.issn.1000-4750.2021.05.0379 FAN Wenliang, LIU Cheng, LI Zhengliang. Improved reliability method based on HLRF and modified symmetric rank 1 method [J]. Engineering Mechanics, 2022, 39(9): 1 − 9. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.05.0379
[3] 张中昊, 段皓鹏, 于艳春, 等. 张弦双向网格型单层柱面网壳稳定性及可靠度分析[J]. 工程力学, 2022, 39(10): 161 − 172. doi: 10.6052/j.issn.1000-4750.2021.06.0438 ZHANG Zhonghao, DUAN Haopeng, YU Yanchun, et al. Stability and reliability analysis of tension-string bidirectional lattice monolayer cylindrical reticulated shells [J]. Engineering Mechanics, 2022, 39(10): 161 − 172. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.06.0438
[4] ECHARD B, GAYTON N, LEMAIRE M. AK-MCS: An active learning reliability method combining Kriging and Monte Carlo Simulation [J]. Structural Safety, 2011, 33(2): 145 − 154. doi: 10.1016/j.strusafe.2011.01.002
[5] 吕大刚, 李功博, 宋彦. 基于MLS-SVM的结构整体可靠度与全局灵敏度分析[J]. 工程力学, 2022, 39(增刊): 92 − 100. doi: 10.6052/j.issn.1000-4750.2021.05.S015 LYU Dagang, LI Gongbo, SONG Yan. Analysis of global reliability and sensitivity of structures based on MLS-SVM [J]. Engineering Mechanics, 2022, 39(Suppl): 92 − 100. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.05.S015
[6] 林光伟, 张熠. 不同结构复杂度下结合集成学习的模型修正方法[J]. 工程力学, 2022, 39(增刊): 153 − 157. doi: 10.6052/j.issn.1000-4750.2021.05.S030 LIN Guangwei, ZHANG Yi. Efficient model updating approaches integrating ensemble learning methods for different structural complexity [J]. Engineering Mechanics, 2022, 39(Suppl): 153 − 157. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.05.S030
[7] 李宁, 潘慧雨, 李忠献. 一种基于自适应集成学习代理模型的结构可靠性分析方法[J]. 工程力学, 2023, 40(3): 27 − 35. doi: 10.6052/j.issn.1000-4750.2021.09.0708 LI Ning, PAN Huiyu, LI Zhongxian. Structural reliability analysis method based on adaptive ensemble learning-surrogate model [J]. Engineering Mechanics, 2023, 40(3): 27 − 35. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.09.0708
[8] LV Z Y, LU Z Z, WANG P. A new learning function for Kriging and its applications to solve reliability problems in engineering [J]. Computers & Mathematics with Applications, 2015, 70(5): 1182 − 1197.
[9] SUN Z L, WANG J, LI R, et al. LIF: A new Kriging based learning function and its application to structural reliability analysis [J]. Reliability Engineering & System Safety, 2017, 157: 152 − 165.
[10] 屈丹, 张文林, 杨绪魁. 实用深度学习基础[M]. 北京: 清华大学出版社, 2022: 91 − 92. QU Dan, ZHANG Wenlin, YANG Xukui. Fundamentals of deep learning with applications [M]. Beijing: Tsinghua University Press, 2022: 91 − 92. (in Chinese)
[11] BAO Y Q, XIANG Z L, LI H. Adaptive subset searching-based deep neural network method for structural reliability analysis [J]. Reliability Engineering & System Safety, 2021, 213: 107778.
[12] XIANG Z L, CHEN J H, BAO Y Q, et al. An active learning method combining deep neural network and weighted sampling for structural reliability analysis [J]. Mechanical Systems and Signal Processing, 2020, 140: 106684. doi: 10.1016/j.ymssp.2020.106684
[13] LIEU Q X, NGUYEN K T, DANG K D, et al. An adaptive surrogate model to structural reliability analysis using deep neural network [J]. Expert Systems with Applications, 2022, 189: 116104. doi: 10.1016/j.eswa.2021.116104
[14] KINGMA D, Ba J. Adam: A Method for Stochastic Optimization [Z]. Computer Science, 2014. DOI: 10.48550/arXiv.1412.6980.
[15] XIAO N C, ZUO M J, ZHOU C N. A new adaptive sequential sampling method to construct surrogate models for efficient reliability analysis [J]. Reliability Engineering & System Safety, 2018, 169: 330 − 338.
[16] MARELLI S, SUDRET B. UQLab: A framework for uncertainty quantification in Matlab [M]// BEER M, AU S K, HALL J W. Vulnerability, Uncertainty, and Risk: Quantification, Mitigation, and Management. Liverpool: American Society of Civil Engineers, 2014: 2554 − 2563.
[17] YU G Q, CHEN C, HOU H T, et al. Integrating adaptive Kriging with expansion optimal linear estimation into real-time hybrid simulation for time-variant experimental analysis of structures with deterioration [J]. Journal of Building Engineering, 2023, 64: 105658. doi: 10.1016/j.jobe.2022.105658
[18] YI J X, ZHOU Q, CHENG Y S, et al. Efficient adaptive Kriging-based reliability analysis combining new learning function and error-based stopping criterion [J]. Structural and Multidisciplinary Optimization, 2020, 62(5): 2517 − 2536. doi: 10.1007/s00158-020-02622-3
[19] WANG Z Y, SHAFIEEZADEH A. ESC: An efficient error-based stopping criterion for Kriging-based reliability analysis methods [J]. Structural and Multidisciplinary Optimization, 2019, 59(5): 1621 − 1637. doi: 10.1007/s00158-018-2150-9
[20] 吕震宙, 宋述芳, 李璐祎, 等. 结构/机构可靠性设计基础[M]. 西安: 西北工业大学出版社, 2019: 200 − 215. LYU Zhenzhou, SONG Shufang, LI Luyi, et al. Fundamental of structure and mechanism reliability design [M]. Xi'an: Northwestern Polytechnical University Press Co. Ltd. , 2019: 200 − 215. (in Chinese)




 下载:
下载: