大跨空间网壳结构具有良好的受力性能和优美的空间造型，在各类大型场馆和公共建筑领域得到广泛应用，此类结构的破坏或倒塌会带来严重的社会影响和人员伤亡，因此有必要对空间网壳结构进行基于性能的抗震设计。作为基于性能的地震工程研究的核心内容，地震易损性分析强调在不同强度地震作用下结构发生极限状态破坏的概率^{[1 − 2]}，广泛适用于各类结构的抗震性能评估。

目前，国内外众多学者对结构地震易损性理论开展了大量的研究，其中VAMVATSIKOS等^[3]提出的增量动力分析方法，建立了地震强度与结构地震需求之间的关系；LUCO等^[4]研究了地震动记录数量对地震动不确定性的影响，给出易损性分析所需的地震动数量；于晓辉等^[5]考虑地震动不确定性和结构不确定性对结构抗震能力的影响，针对钢筋混凝土框架结构进行地震易损性分析和地震风险评估；韩建平等^[6]讨论了不同地震持时对建筑结构抗震性能的影响；杜文风等^[7]提出基于变形和耗能的单层球面网壳双参数损伤模型，华文等^[8]对双参数损伤模型进一步修正，明确了各参数的物理意义；聂桂波等^[9]提出了基于多项特征响应和变形能量的网壳结构地震损伤模型，并据此对结构的性能水准进行量化和分级；钟杰等^[10]考虑近场和远场地震动对网壳结构的影响，认为近场速度脉冲型地震动造成的损伤更为严重；于志伟等^[11]结合模糊数学理论提出铝合金网壳结构两种强震失效模式的判别依据，并通过大量参数分析对结构的不同损伤状态进行划分。

在基于性能的抗震分析中，需要合理划分网壳结构的性能状态并建立对应的性能指标，已有的大多数研究采用确定性失效准则，即不同性能状态的边界为定值，当结构地震需求参数超过极限值时则代表进入新的性能状态，但在实际工程中不同破坏等级的边界是一个模糊的区间^[12]。此外，对于空间网壳结构难以仅采用位移或能量等单一指标来准确描述结构整体的损伤状态，且不同地震需求参数之间存在一定的相关性，如何准确描述其相关性是结构多维联合地震易损性分析的关键。Copula函数是处理变量间相关性的高效方法，不仅能够表达变量间复杂的非线性相关关系，而且其边缘分布函数的形式也不受限制^[13]。王秀振等^[14]针对框架结构提出考虑楼层相关性的地震易损性分析方法，并验证了该方法的有效性。

本文针对大跨空间网壳结构，通过对结构的增量动力分析结果进行统计分析，建立基于结构最大节点位移和应变能的结构地震需求模型，并将模糊失效准则与概率地震风险分析理论相结合，通过隶属函数将结构的极限状态边界模糊化，构建基于模糊失效准则的网壳结构地震易损性函数，然后采用Copula函数考虑不同需求参数之间的相关性，并利用核密度估计和欧式距离法，建立由位移和应变能两个地震需求联合的最优概率分布函数，进一步对单层球面网壳结构进行模糊失效准则下多维联合的地震易损性分析。

1   虑模糊失效准则与多维联合的结构地震易损性分析理论与方法

1.1   考虑模糊失效准则的结构地震易损性分析

结构的地震易损性是指在某一地震动强度下，结构超越某一性能极限状态的条件概率，其从宏观层面描述了地震动强度与结构破坏程度之间的关系^[15]，地震易损性解析函数可用下式表示：

式中：D为结构的地震需求；${C_i}$为结构不同破坏等级下性能水准的极限值；IM为地震动强度参数；$f(D)$为结构地震需求的概率密度函数，一般认为结构地震需求参数符合对数正态分布，将式(1)进行对数变换，可写为：

式中：$\phi (\cdot)$为标准正态分布函数；${m_{D{\text{|}}{\rm IM} = x}}$为结构地震需求中位值，如式(3)所示，通过对结构的非线性时程分析结果进行对数线性回归，可得到参数${\beta _{\mathrm{a}}}$、${\beta _{\mathrm{b}}}$；${\beta _{D{\text{|}}{\rm IM} = x}}$为地震需求的对数标准差，由式(4)计算可得，其中${D_i}$为第i条地震动下的结构地震需求，N为地震动数量；

网壳结构在地震作用下损伤状态的变化实际上是一个逐渐过渡的过程，可采用模糊集的方法考虑结构破坏等级界限值的模糊性^[16]。将结构的地震破坏等级假设为模糊事件，在结构地震易损性分析中采用模糊-概率积分方法计算结构的模糊失效概率，结合式(2)，考虑模糊失效准则的结构地震易损性$P^{\prime }$可表示为：

式中：${\mu _{{_i}}}(D)$为发生第$i$等级破坏时结构性能水准划分指标的隶属函数^{[17 − 19]}，其中模糊区间采用工程中常用的扩增系数法确定，将模糊区间上下界${C_i}(1 + \lambda )$、${C_i}(1 - \lambda )$代入式(5)可得：

在给定地震强度${\rm IM} = x$下，网壳结构考虑破坏等级划分的模糊性时，第$i$个破坏等级下的易损性可进一步表示为：

1.2   考虑多维联合的结构地震易损性分析方法

多维联合地震易损性分析的实质是在地震作用下结构多个地震需求参数超过某一量值的概率，此时联合地震需求模型等同于一个串联系统，系统中任一性能指标失效均会导致结构失效，结构多维联合易损性可表示为：

式中：m为地震需求参数的数量；$P^\prime _i({\rm IM})$为基于单一失效准则的结构模糊地震易损性。

由于结构不同地震需求间具有相关性，多维联合的结构地震易损性难以由单个性能指标的易损性通过简单叠加得到，为此引入多元Copula函数来考虑多维地震需求之间的相关性，描述多维失效准则的联合概率密度特征，于是式(8)可表示为^[20]：

式中：C为Copula函数；θ为其相关参数；$C({P_1},{P_2}, \cdot \cdot \cdot ,{P_m};\theta )$为m个失效准则同时发生时结构的模糊地震易损性。

2   基于Copula函数的多维地震需求参数的相关性分析

2.1   多元Copula函数的基本理论

Copula函数能够将不同变量间的相关结构和边缘分布函数进行分离，用边缘分布函数对联合分布函数进行显式表达，简化联合分布函数的求解。根据Sklar定理可知，若S维边缘分布函数${F_i}{\text{ (}}{x_i}{\text{) }}(i = 1,2,\cdots ,S)$连续，则存在一个Copula函数C使得联合分布函数$F({x_1},{x_2},\cdots ,{x_S})$满足^[16]：

Copula函数的形式多样，能够描述变量之间各种的复杂相关结构，具有广泛的适用性。以结构的节点位移和应变能作为地震需求参数，选择二维Copula函数考虑两者的相关性，于是结构的多维联合地震易损性可表示为：

式中，$P^{\prime }_1$、$P^{\prime }_2$为结构基于位移和能量失效准则下的模糊地震易损性。

2.2   Copula函数的相关参数估计

Copula函数的相关参数可通过地震需求样本值估计获得，FERMANIAN等 ^[21]提出将核密度估计方法应用于函数的参数估中，利用各变量的非参数核密度估计对应的分布函数代替其边缘分布函数，如式(12)~式(13)所示，利用不同结构地震需求参数的边缘分布函数对Copula函数进行光滑可微的估计。

式中：T为样本数量；$\{ {{x_{i}^{(t)}}} \}_{t = 1}^{\rm T}$为地震需求参数的样本值；h为窗宽；$K( \cdot )$为核函数；${\hat F_i}({x_i})$为变量的边缘分布函数。

2.3   Copula函数的优选

Copula函数的类型众多，需对其进行拟合优度检验，选取最优Copula函数。欧式距离判别法是用各Copula函数与样本经验Copula函数的欧式距离作对比，获得的平方欧式距离越小，则表示拟合度越好，所选的函数越优^[13]。平方欧式距离可根据式(14)计算获得：

式中：$C( \cdot )$为备选二元Copula函数；$\hat C( \cdot )$为经验Copula函数；F(x)和G(y)分别为二维变量(x,y)的经验分布函数；${I}_{[·]}$为示性函数，当$F({x_i}) {\leqslant} u$时取1，否则取0。

3   考虑模糊失效准则的网壳结构多维联合地震易损性分析过程与实现

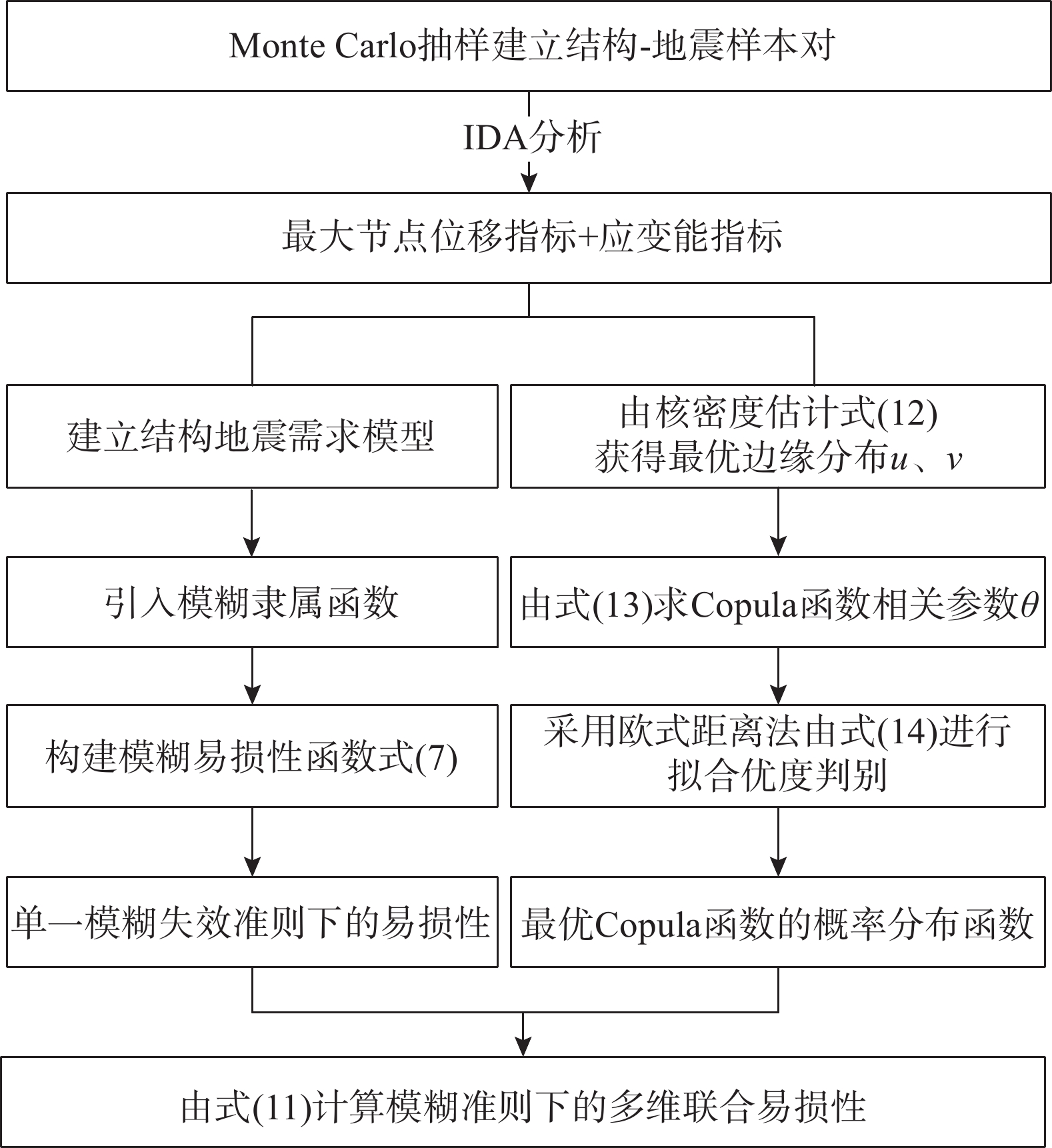
基于模糊失效准则对单层球面网壳结构进行多维联合地震易损性分析，其基本步骤如图1所示。

图  1  考虑模糊失效准则的网壳结构多维联合地震易损性分析流程图

Figure  1.  Flow chart of multi-dimensional joint seismic fragility analysis of reticulated shell structure considering fuzzy failure criterion

下载: 全尺寸图片 幻灯片

步骤1：计算考虑模糊失效准则的结构失效概率。

建立一定数量的地震动-结构样本对并进行增量动力分析(IDA)，获取以结构最大节点位移、应变能为参数的地震需求样本值，通过引入隶属函数考虑结构性能水准界限的模糊性，由式(7)分别计算模糊失效准则下结构基于最大节点位移和应变能指标的地震易损性。

步骤2：进行结构不同地震需求间的相关性分析。

根据结构最大节点位移和应变能的地震需求参数样本值，采用核密度估计方法由式(12)确定各需求的边缘分布函数，由式(13)对备选Copula函数的相关参数进行估计，在此基础上根据式(14)利用平方欧式距离法进行拟合优度检验，选择合适的二元Copula函数描述结构不同地震需求之间的相关结构。

步骤3：进行考虑模糊失效准则的结构多维联合地震易损性分析。

基于结构最大节点位移和应变能指标的地震易损性和最优二元Copula函数，由式(11)计算结构串联体系的地震易损性，获得考虑模糊失效准则的结构多维联合地震易损性曲线。

4   基于模糊失效准的单层球面网壳多维联合地震易损性分析

4.1   网壳结构性能状态划分与量化

在地震作用下结构的损伤程度通常分为4个等级^[22]，为对损伤状态下结构的性能进行准确评估，本文从结构位移和能量两个角度定义结构的损伤等级，位移角度以结构的最大节点位移作为结构性能水准指标，能量角度将地震作用下的结构应变能与结构倒塌应变能极限的比值定义为结构损伤指数，即：

式中：E_c为某一地震强度下的结构应变能需求峰值，包含结构的弹性应变能E_e与塑性耗能E_p；E_s为结构倒塌应变能，随地震加速度峰值的不断增大，当外力做功与结构动能、结构阻尼耗能及结构应变能不再保持平衡时^[23]，可认为该时刻的结构应变能为倒塌临界应变能E_ccr，E_s取不同地震波样本对应的结构倒塌临界应变能的平均值，即：

式中：$n$为选取的地震波样本个数；${E_{{\mathrm{ccr}}i}}$为第i条地震波下的结构倒塌临界应变能。

通过计算不同跨度、矢跨比、荷载和杆件尺寸的球面网壳结构得到以位移和能量为指标的网壳结构性能状态量化指标如表1所示。采用位移限值的结构破坏状态判别结果基本上与单层球面网壳结构振动台试验结果^[24]相符合。

表  1  结构性能状态量化指标^{[7 − 9, 25 − 27]}

Table  1.  Quantitative indicators of the state of structural performance

破坏状态	结构响应	震后措施	位移限值$\delta$	能量限值DE
基本完好	杆件无屈服情况	无需修缮	［0，L/800］	0~0.05
轻微损坏	少量杆件屈服，塑形发展程度较轻	无需或稍加修缮	［L/800，L/300］	0.05~0.2
中等损坏	杆件出现屈服情况较多；塑形发展逐渐加深	需修理并适当加固	［L/300，L/160］	0.2~0.5
严重损坏	大量杆件进入塑形工作阶段，结构刚度明显降低	需维修排险，局部拆除	［L/160，L/100］	0.5~1.0
倒塌破坏	结构整体倒塌，失去承载能力	需要拆除	≥L/100	≥1
注：L为结构的跨度。

下载: 导出CSV 

| 显示表格

4.2   地震波的选取与结构分析模型

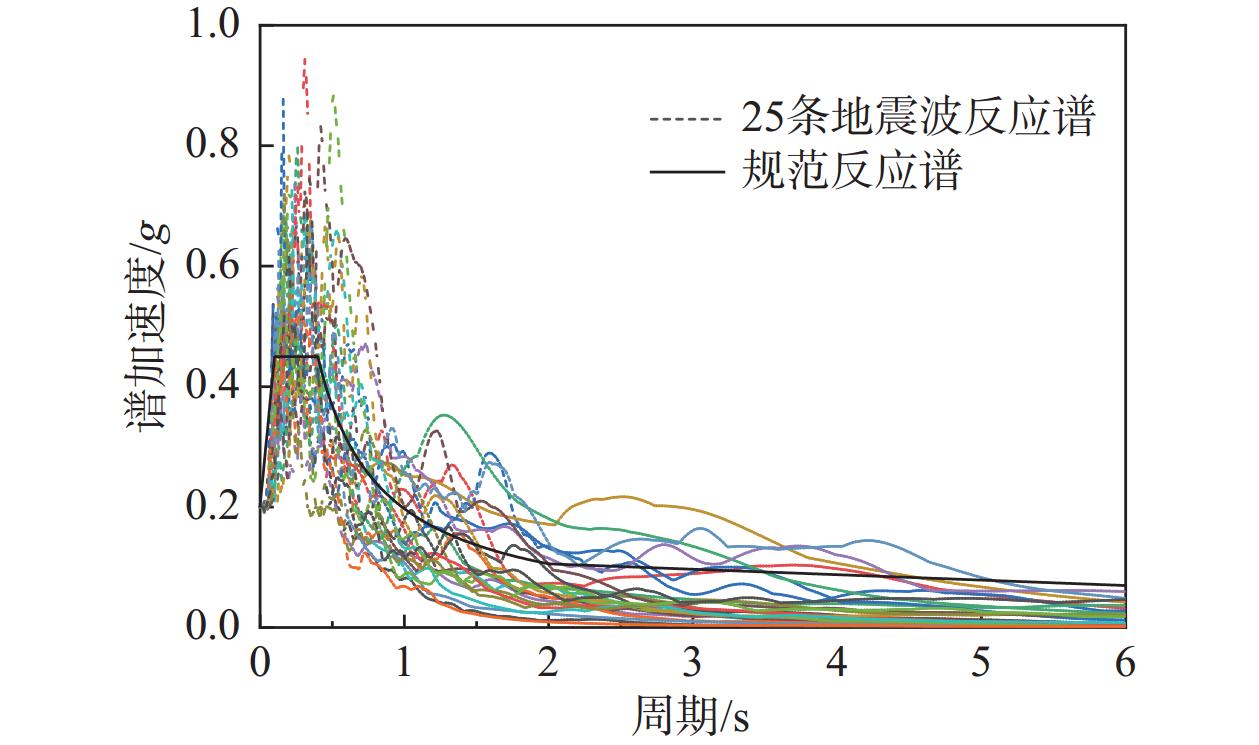
选取25条震级在5.5级以上、震中距大于20 km的远场地震动记录，地震波X向反应谱曲线和规范反应谱曲线如图2所示。以PGA作为地震动强度指标，采用三向地震动输入方式，各地震波三向的峰值加速度比值为X∶Y∶Z=1∶0.85∶0.6，地震波持续时间为30 s。

图  2  地震动反应谱曲线

Figure  2.  The response spectrum curves of ground motion

下载: 全尺寸图片 幻灯片

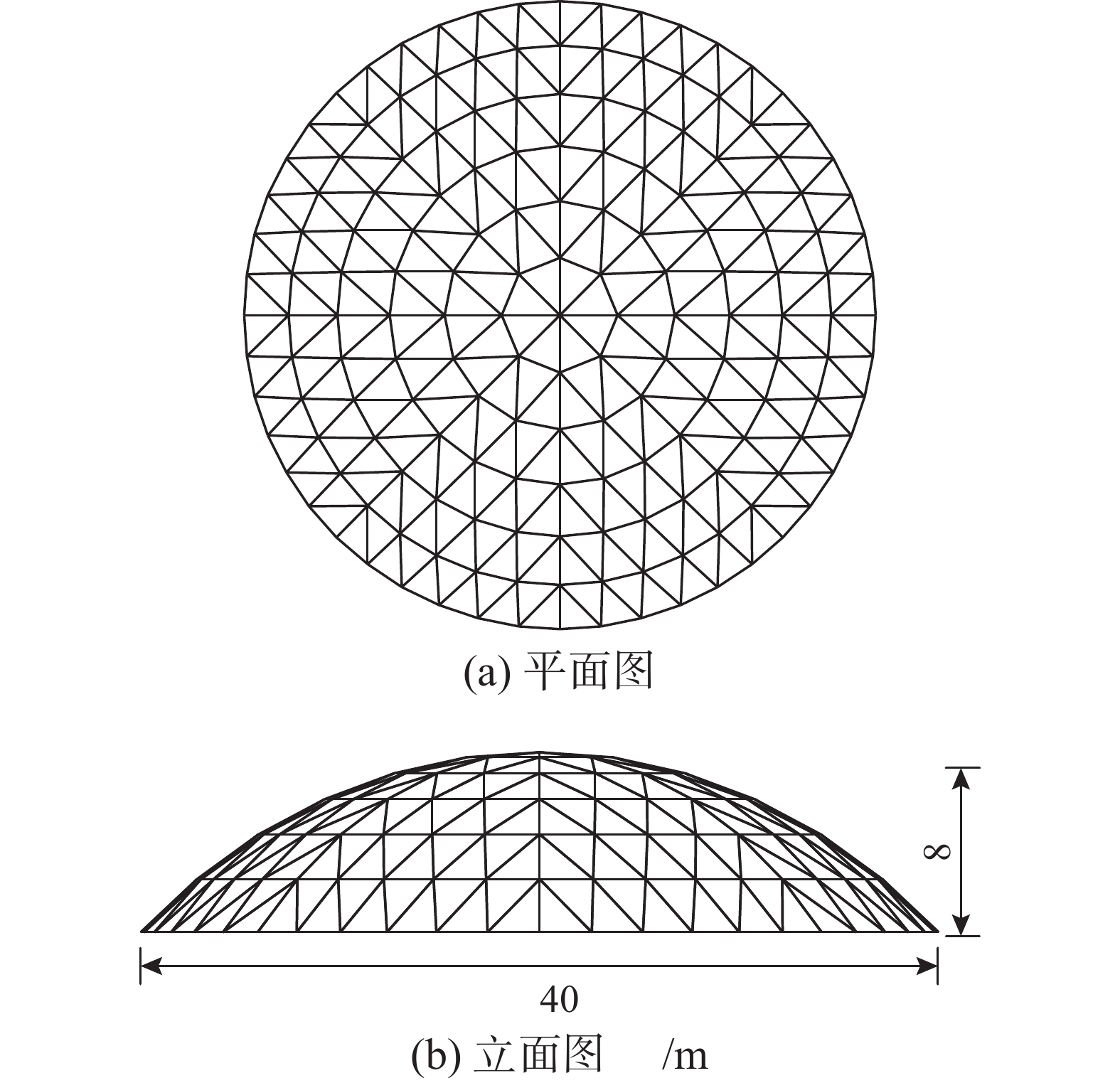
一Kewitt-8型单层球面网壳如图3所示，跨度为40.0 m，矢跨比为1/5，节点为刚性连接，支座采用周边节点固定的三向铰支座，采用Q355钢材，杆件钢管型号为Φ140.0 mm×5.0 mm，节点自重以杆件自重的25%计算，恒荷载以及活荷载等效为节点荷载施加于结构上，采用1.3恒荷载+0.5活荷载的荷载组合方式加入到结构节点上。考虑结构双重非线性的影响，采用Rayleigh阻尼，阻尼比取0.02。

图  3  一K8N6型单层球面网壳结构

Figure  3.  A K8N6 single-layer spherical reticulated shell structure

下载: 全尺寸图片 幻灯片

考虑5个不确定性影响显著的结构参数^[28]，各参数之间相互独立，其随机概率分布模型如表2所示。根据结构中随机变量的概率分布特征，通过Monte Carlo抽样获得25组结构-地震动样本，基于增量动力分析的结果，得到以结构最大节点位移和应变能为参数的结构地震需求模型如图4所示。

表  2  结构建模随机参数

Table  2.  The random parameters of structural modeling

随机变量(单位)	均值	变异系数	概率分布模型
恒荷DL/(kg/m2)	143.48	0.072	正态分布
活荷LL/(kg/m2)	28.02	0.229	极值I型分布
钢材屈服强度fy/MPa	358.85	0.066	对数正态分布
弹性模量E/MPa	2.06×105	0.031	对数正态分布
结构粘滞阻尼ξ	0.02	0.421	正态分布

下载: 导出CSV 

| 显示表格

图  4  结构概率地震需求模型

Figure  4.  The model of structural probabilistic seismic demand

下载: 全尺寸图片 幻灯片

4.3   单个性能指标下的结构地震易损性分析

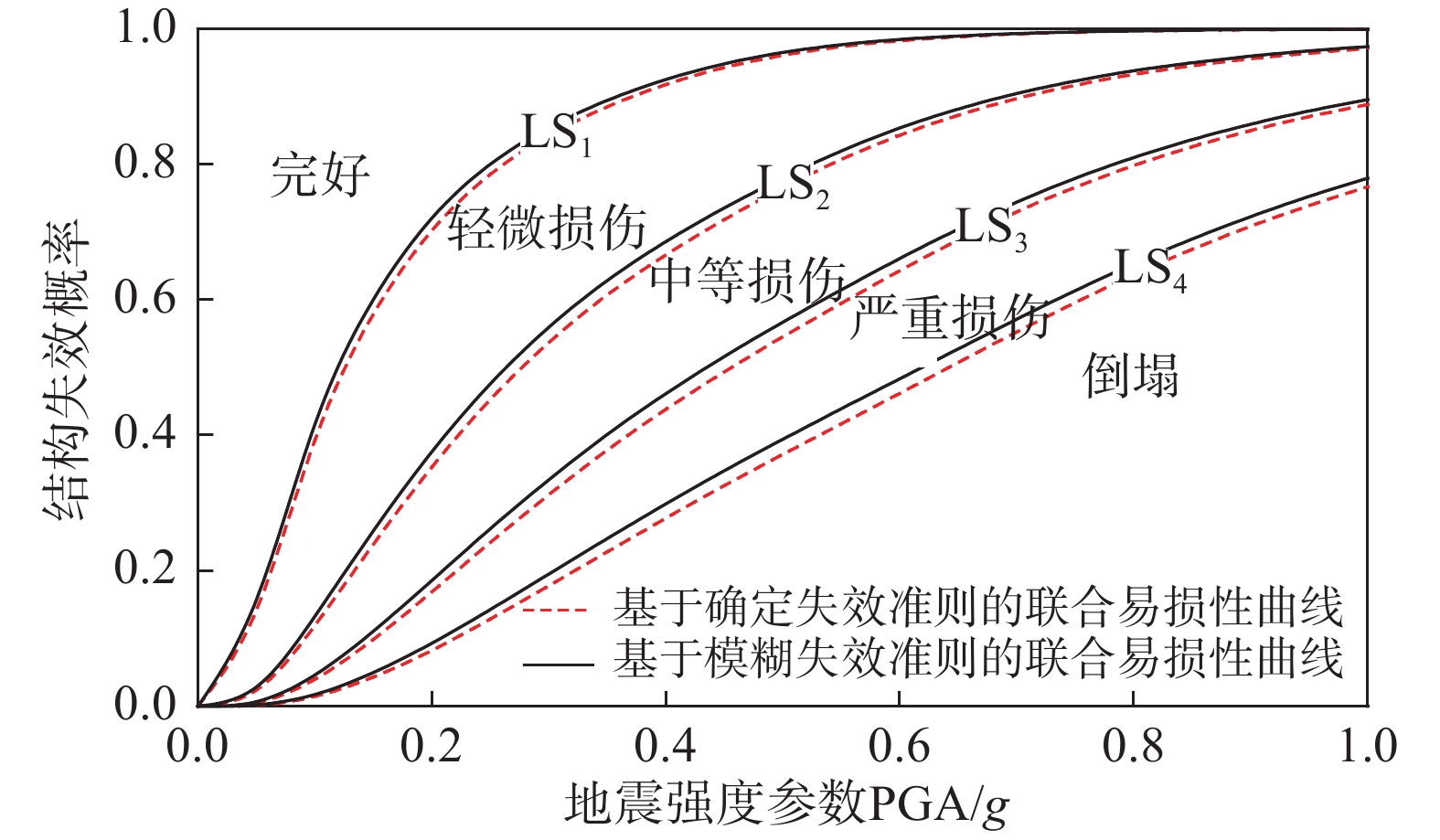
网壳结构的地震易损性是基于传统可靠度理论，结构的可靠隶属度在地震作用下会随着结构需求增大而变小，在利用隶属函数描述结构在区间范围内的可靠隶属度时，可以选择偏小型正态隶属函数来考虑结构地震需求参数的模糊隶属情况。采用扩增系数来确定模糊区间，工程中扩增系数通常为许用值的0.05倍~0.3倍^[29]，取模糊隶属度λ为0.3。根据式(2)、式(7)和表1的性能水准量化指标分别计算得到结构基于确定性失效准则和模糊性失效准则的地震易损性曲线如图5所示。

图  5  基于单个性能指标的结构地震易损性曲线

Figure  5.  Seismic fragility curves of the structure obtained with single performance index

下载: 全尺寸图片 幻灯片

由图5可知，不同性能指标获得的结构地震易损性曲线变化趋势大致相同，但结构失效概率的差异较大。以地震峰值加速度500 gal为例，以位移指标划分破坏等级时，发生轻微破坏、中等损伤、严重损伤和倒塌破坏的概率分别为：94%、75%、54%、37%；而以应变能指标划分破坏等级时，发生轻微破坏、中等损伤、严重损伤和倒塌破坏的概率分别为：95%、74%、50%、32%。可以看出当采用单一性能指标时，获得的结构失效概率有所差别，难以准确评估结构的地震风险。因此需将各性能指标进行联合分析，以获得更加准确的地震风险值。此外，考虑破坏准则模糊性后，结构失效概率较不考虑时有所增加，提高了结构地震风险值。

4.4   考虑地震需求相关性的结构地震易损性分析

根据增量动力分析结果，对各破坏状态下的结构样本值进行非参数核密度估计，由式(12)可知核函数的选择是影响核密度估计优劣的主要因素，本文选用平滑性较好的Gaussian核函数，得到结构基于最大节点位移和应变能作为地震需求参数的边缘分布函数，并绘制出如图6所示的二元频率直方图，可知该频率直方图描述的数据类型在同时趋近0(下尾)或者1(上尾)时比较集中，且存在较强的正相关性，据此选择四种具有类似特征的Copula函数作为备选函数，并由式(12)利用极大似然法对备选Copula函数进行参数估计。

图  6  二维频率直方图

Figure  6.  The histogram of two-dimensional frequency

下载: 全尺寸图片 幻灯片

根据地震需求参数的边缘分布函数，由式(14)可计算得到各Copula函数的平方欧式距离，如表3所示。在各破坏状态下二元frank函数的平方欧式距离最小，因此二元frank函数是描述地震需求参数位移与应变能之间相关性的最优函数。

表  3  二元copula函数的参数比较

Table  3.  Parameter comparison of binary copula functions

Copula函数类型	相关参数	平方欧式距离
t-copula	0.98	0.292
Gaussian	0.97	0.279
Frank	45.54	0.245
Gumbel	6.89	0.302

下载: 导出CSV 

| 显示表格

将由式(13)估计的相关参数值代入二元frank的概率分布函数式(18)中，即可得到这两个地震需求参数之间的相关结构。将分别基于位移指标和能量指标的结构地震易损性代入式(11)，即可得到考虑结构多维地震需求相关性影响的结构联合易损性。结构考虑确定失效准则与模糊失效准则的多维联合地震易损性曲线如图7所示，从图中可以看出，以位移和应变能作为地震需求，考虑两者相关性后，基于确定失效准则的结构地震易损性与基于模糊失效准则的易损性曲线具有相同的变化趋势，两者相互接近，但基于模糊失效准则的结构地震易损性曲线对应的结构失效概率高于基于确定失效准则结构的失效概率。

式中：变量$u,v \in [0,1]$；$\theta$为frank函数的相关参数。

图  7  结构多维联合地震易损性曲线

Figure  7.  Multi-dimensional joint seismic fragility curves of the structure

下载: 全尺寸图片 幻灯片

为了量化分析失效准则模糊性对结构多维联合地震易损性分析结果的影响，采用模糊性影响系数来定量评价影响差异程度^[30]，如下式所示：

式中：$\tau$为模糊影响系数；G为易损性分析中地震动强度的上限值；F'(IM)为失效准则模糊条件下的地震易损性函数；F(IM)为考虑确定失效准则时的地震易损性函数。

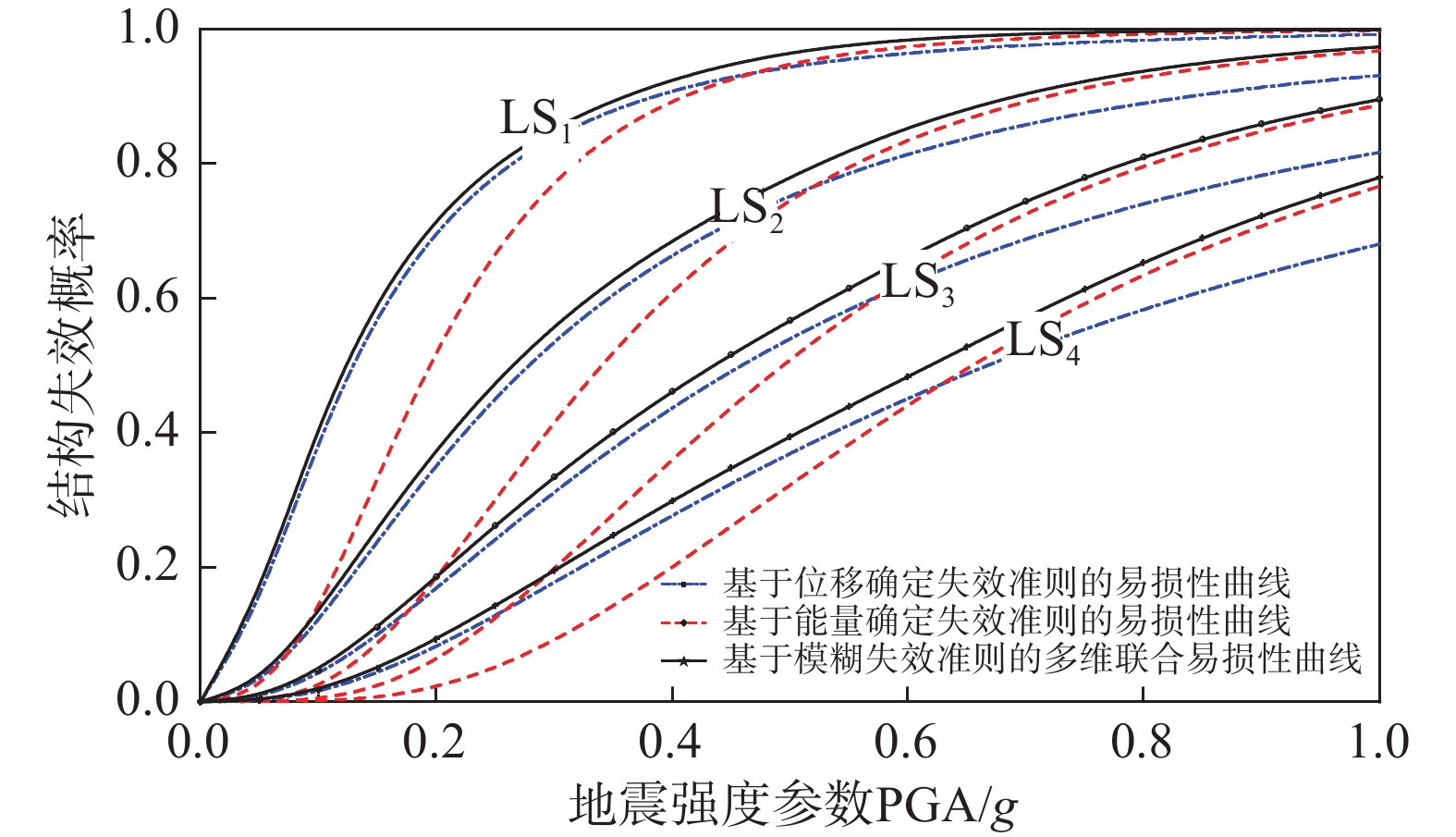
不同结构破坏等级下的模糊性影响系数如表4所示，考虑破坏准则模糊性得到的结构多维联合地震易损性与不考虑破坏准则模糊性的结果之间存在较大的差异性。在同一破坏等级下，随着地震强度的增加，模糊影响系数呈现先增大后减少的趋势；在同一地震强度下，差异性随着破坏等级的提高而增大，破坏等级为LS₄时模糊影响系数达到最大，其值为3.96%。因此，在实际计算时应根据实际情况选择合适的隶属函数来考虑失效准则的模糊性。

表  4  不同破坏等级下的模糊影响系数

Table  4.  Ambiguity influence coefficient at different failure levels

破坏等级	LS1	LS2	LS3	LS4
模糊影响系数$\tau$/(%)	0.86	1.83	2.88	3.96

下载: 导出CSV 

| 显示表格

以位移、能量为地震需求参数，将基于确定性失效准则的结构地震易损性曲线和考虑失效准则模糊性的多维联合易损性曲线分别绘于图8中，可以看出考虑模糊失效准则的结构多维联合地震易损性曲线对应的失效概率在不同性能水准下明显高于基于位移和能量的易损性曲线所对应的结构失效概率。仅采用位移或能量作为性能指标时难以准确衡量结构的地震风险，在地震动强度PGA较小时，基于能量指标所得的结构失效概率低于基于位移指标所得的结构失效概率，而随地震动强度的逐渐提高，基于能量指标的结构失效概率会略高于基于位移指标的结构失效概率。考虑模糊失效准则的多维联合易损性分析可以结合两者的优势，更能准确反映结构在不同破坏等级下的失效概率，更加真实地反映结构的地震风险，该方法一定程度上提高了结构的地震风险值，从而有利于提高结构的安全性。

图  8  结构三种地震易损性曲线对比

Figure  8.  Comparison of three seismic fragility curves of the structure

下载: 全尺寸图片 幻灯片

5   结论

本文考虑位移和应变能地震需求之间的相关性，对单层球面网壳结构进行了基于模糊失效准则的多维联合地震易损性分析，主要有以下结论：

(1) 基于模糊-概率积分理论，推导了失效准则模糊条件下的地震易损性解析函数，所得的结构失效概率高于不考虑模糊准则的计算结果，可以更加准确地衡量结构在地震作用下的失效风险，在计算过程需要根据实际情况选择合适的隶属函数来考虑失效准则的模糊性。

(2) 基于核密度估计和最小欧式距离选择的最优frank copula函数，可以准确描述结构最大节点位移与应变能等地震需求参数间的相关性，形成了有效的单层球面网壳结构多维联合地震易损性分析方法，考虑相关性后结构在不同性能水准下的失效概率明显高于采用单参数地震需求下的结构失效概率。

(3) 基于模糊失效准则的多维联合易损性分析，考虑了破坏等级界限的模糊性，综合了位移、能量两种地震需求参数的优势，能更加准确地预测结构在不同破坏等级下的失效概率，一定程度上提高了结构的地震风险值，有利于提高网壳结构安全性。