强震将导致钢筋混凝土结构发生较严重的破坏。另外，强震发生后通常会出现多次余震，对主震作用后已产生一定程度损伤的结构造成进一步的破坏和生命财产损失^{[1 − 10]}。系统而全面地考虑主震-余震序列作用是精准预测、评估结构抗震性能并对其进行性能提升的必要前提。

地震动具有多维随机特性和非平稳性^[11]，主震和余震作用在结构上的主方向也具有随机性。对于框架柱等截面较对称的构件，其两水平向的刚度较接近，即便主震和余震的主方向有所差异，其抗震能力及损伤模式也不因主方向的改变而发生显著变化。与之不同的是，剪力墙面内和面外的抗侧刚度差距明显，两向的承载能力和延性也不均衡，若余震的主方向与主震的不同，则墙体的损伤模式将显著不同且损伤程度将加剧，在多维主震-余震序列地震作用下很可能出现墙体发生严重破坏甚至失效的现象。这一问题及震害现象已在新西兰基督城地震中被暴露和重视：该地区的Grand Chancellor 酒店在遭受2010年的地震侵袭时，没有出现严重的损坏，但在2011年的6.2级余震发生时部分剪力墙出现突发面外明显变形和剪切破坏。震后调查表明^[12]：该结构为单向少墙的框架剪力墙体系，东西向剪力墙数量明显少于南北向，发生破坏的剪力墙边缘约束构造不合理，配筋率过低。此外，台站记录表明：受地震主方向变化的影响，2010年地震中的结构水平变形主要沿南北方向(剪力墙面内方向)，而2011年地震中结构的水平变形主要为东西方向(剪力墙面外方向)，剪力墙遭受了不同主方向的地震作用。相关研究人员针对这一的破坏现象开展了深入研究，NIROOMANDI等^{[13 − 14]}针对矩形剪力墙，通过试验及数值模拟的手段研究了此类失效模式的发生机制、触发该失效模式的关键参数，但并未开展剪力墙的两个主轴方向依次遭受不同方向地震作用时抗震性能的研究。

为明晰剪力墙在遭受不同方向、不同受力顺序时抗震性能和损伤模式的异同，本文设计了2个剪力墙试件，先分别让其承受面内、外方向的低周往复加载，加载完毕后再进行面内-外、面外-内的低周往复加载。通过对比宏观试验破坏现象、滞回曲线、骨架曲线、刚度退化曲线、延性、钢筋应变及变形等性能指标比较各试件抗震性能的异同，并利用改进Park-Ang模型及弹塑性耗能差率模型进行损伤评估。同时，利用有限元软件进行数值模拟，在标定试验结果的基础上设计了2个框架剪力墙结构，对其进行单一地震、主余震序列不同输入方向下的时程分析，基于最大层间位移角及构件转角完成剪力墙面内和面外方向的损伤评估，探究了结构体系抗震性能的异同。

1   试验概况

1.1   试件设计

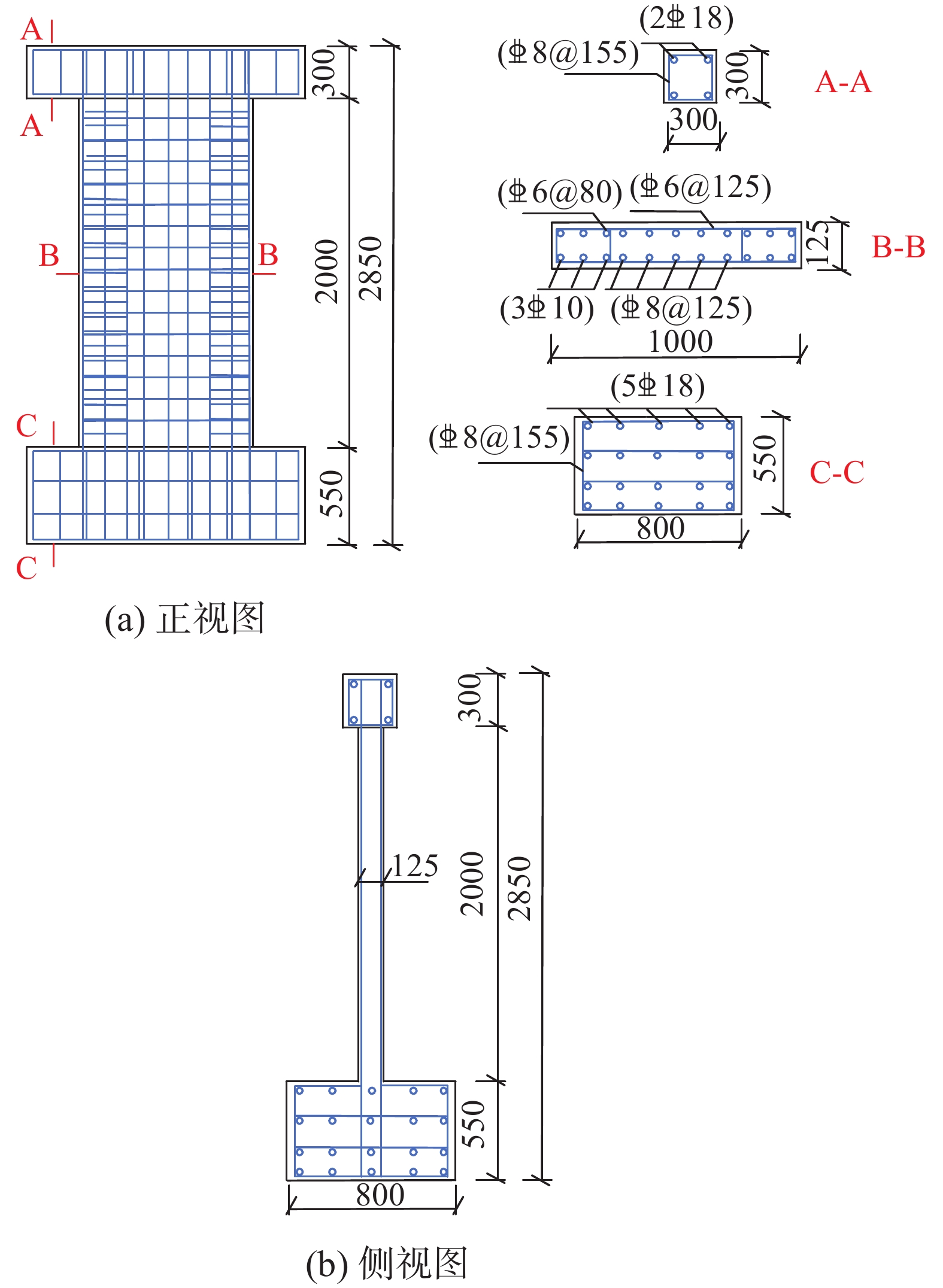
为了研究和比较剪力墙在依次遭受面内或面外作用后各方向抗震性能的异同及相互影响，本文依据《建筑抗震设计规范》^[15]和《混凝土结构设计规范》^[16]设计了依次承受面内-外、面外-内荷载作用的剪力墙试件并进行低周往复加载试验。2片剪力墙试件的配筋相同，尺寸均为2000 mm×1000 mm×125 mm。加载梁尺寸为300 mm×1600 mm×300 mm，地梁尺寸为550 mm×1600 mm×800 mm，试件尺寸及剪力墙、加载梁及地梁的配筋图参见图1。

图  1  试件尺寸及配筋图 　/mm

Figure  1.  Dimensions and reinforcement drawing of specimen

下载: 全尺寸图片 幻灯片

1.2   材料力学性能

剪力墙采用C30商品混凝土浇筑，每片剪力墙取3块立方体试块进行材料强度试验。混凝土立方体试块(150 mm×150 mm×150 mm)28 d实测抗压强度值为32.0 N/mm²。

1.3   加载制度及测点布置

两个试件的加载装置及加载现场如图2所示，试件1为依次承受面内和面外荷载的试件，面内加载时编号为SW1-1，面内-外加载时编号为SW1-2；试件2为依次承受面外和面内荷载的试件，面外加载时编号为SW2-1，面外-内加载时编号为SW2-2。

图  2  加载装置图

Figure  2.  Multidimensional loading device diagram

下载: 全尺寸图片 幻灯片

在剪力墙的底部(L/R-1)、端部(L/R-2)布设混凝土应变片，在中间部位布置混凝土应变花(L/R-H)，内外共12个测点，见图3(a)。在剪力墙的左侧(L)、中部(M)及右侧(R)各选取一根纵筋作为典型钢筋，在其下部、中部及上部分别布设2个、4个及2个测点，见图3(b)。

地震作用下构件的总水平变形主要包括剪切变形、弯曲变形和滑移变形，且不同破坏模式下各变形分量的占比有所区别。剪力墙在面内、面外加载方向下的破坏模式不同，因此位移计的布设也不同，具体情况见图3(c)、图3(d)。面内加载时，主要监测该方向的位移及剪切变形；面外加载时，主要监测该方向的位移及弯曲变形。SW1-1、SW2-2分别布设了8个位移计，编号分别为L1~L8，对应测量值为δ₁~δ₈。其中，L1测量剪力墙总水平变形，L2~L4分别测量剪力墙上、中、下三处的变形，L5测量基底变形，L6测量弯曲变形，L7、L8测量剪切变形。SW1-2、SW2-1分别布设了7个位移计，前6个位移计测量内容同SW1-1、SW2-2，L7测量弯曲变形。

图  3  应变片及位移计布设图

Figure  3.  Layout of strain gauge and displacement gauge

下载: 全尺寸图片 幻灯片

试验设计轴压比为0.20，即在剪力墙加载梁顶端施加492 kN的轴力。面内加载时，采用荷载-位移控制，即试件未到达屈服状态时，采用荷载控制。在加载过程中，宜将钢筋应变是否达到屈服状态作为判定试件屈服的依据，并将该时刻对应的荷载和位移作为屈服荷载、屈服位移。此时，以屈服位移为基准进行位移控制。因剪力墙面外方向的承载力明显低于面内方向的承载力，在面外方向加载时，用荷载控制难度较大。因此，直接采用位移控制，以钢筋屈服时刻对应的位移作为屈服位移进行控制。当试件进行二次加载时，为保证相同方向受力的试件在两次加载中保持一致的受力模式。因此，二次面内、面外加载制度同首次加载制度一致，具体加载信息见表1、图4。

表  1  水平加载等级

Table  1.  Horizontal loading level

加载等级	面内加载数值	面外加载数值/mm
工况1	40 kN	10
工况2	80 kN	20
工况3	120 kN	30
工况4	8 mm	40
工况5	16 mm	50
工况6	24 mm	60
工况7	32 mm	−
工况8	40 mm	−
工况9	48 mm	−

下载: 导出CSV 

| 显示表格

图  4  水平加载制度

Figure  4.  Horizontal loading regime

下载: 全尺寸图片 幻灯片

2   试验结果及分析

2.1   试验宏观现象

SW1-1在面内加载状态下，荷载控制阶段，墙体表面无可直接观察到的裂缝出现。加载至8 mm时，距墙体底部0 mm~20 mm高度处开始出现明显的斜裂缝，主要集中在墙体底角部左侧，钢筋达到屈服。加载至16 mm时，距墙体底部0 mm~800 mm高度处出现大量斜裂缝，右侧居多。加载至24 mm时，混凝土内部发出声响，且距墙体底部0 mm~10 mm高度处有混凝土轻微脱落。底部斜裂缝持续出现，逐渐变宽并形成交叉，并沿墙高由底部向中部蔓延至距墙体底部1400 mm高度处。加载至32 mm时，距墙体底部0 mm~10 mm高度处两侧有大块混凝土脱落，钢筋外露；中部斜裂缝明显增多。加载至40 mm时，距墙体底部0 mm~20 mm高度范围内混凝土大面积脱落，钢筋外露且已屈曲，斜裂缝持续增多。加载至48 mm时，距墙体底部0 mm~20 mm高度范围内两侧混凝土压溃，钢筋屈曲严重，参见图5(a)。斜裂缝主要集中在墙体底部及中部，表明剪力墙在面内加载下主要发生弯剪破坏，参见图6(a)。

图  5  试件宏观破坏

Figure  5.  Macroscopic failure diagram of specimen

下载: 全尺寸图片 幻灯片

SW1-2在面内-外加载状态下，加载至10 mm时，在原混凝土脱落位置附近(距墙体底部0 mm~20 mm高度范围)出现细小的水平裂缝(原有裂缝为黑色，新增裂缝为红色)。加载至20 mm~30 mm时，持续有短小裂缝出现，并向上部延伸至距墙体底部30 mm、40 mm高度处；混凝土脱落位置破坏范围变大，蔓延至距墙体底部40 mm高度处。加载至40 mm时，原脱落位置破坏范围明显变大，蔓延至距墙体底部50 mm高度处，水平裂缝持续出现。加载至50 mm时，墙体中部开始出现水平裂缝，蔓延至距墙体底部600 mm高度处。与原有交叉斜裂缝相比，新增裂缝出现数量较少，主要集中出现在原破坏区域及墙体中部，且均为短小的水平裂缝。因剪力墙面外变形严重，无法继续加载。同SW2-1相比，钢筋屈曲现象更显著，剪力墙距底部200 mm处发生明显的面外变形，参见图5(b)、图5(e)、图6(b)。由此可知：经受面内加载的剪力墙在承受面外加载之后，原有损伤和破坏加剧，尤其是面外变形的幅度加大。

SW2-1在面外加载状态下，加载至10 mm时，距墙体底部0 mm~800 mm高度范围出现多条水平裂缝。加载至20 mm~30 mm时，水平裂缝持续出现、延伸，沿墙高蔓延至距墙体底部1200 mm高度处。加载至40 mm~50 mm时，出现较长的水平裂缝，沿高度方向由墙体中部向上部蔓延至距墙体底部1800 mm高度处，墙体表面距墙体底部10 mm高度处有混凝土轻微脱落。加载至60 mm时，剪力墙距离墙体底部600 mm处发生面外变形，变形偏离原中心线位置，但未有大块混凝土脱落等明显的破坏现象，参见图5(c)、图5(e)。墙身遍布水平裂缝，表明剪力墙在面外加载下主要发生弯曲变形和破坏，参见图6(c)。

SW2-2在面外-内加载状态下，荷载控制阶段，墙体表面无可直接观察到的裂缝出现。加载至8 mm时，距墙体底部0 mm~600 mm高度范围内出现多条较为短小的水平裂缝(原有裂缝为黑色，新增裂缝为红色)。加载至16 mm时，裂缝沿墙高蔓延至距墙体底部800 mm高度处，且在距墙体底部0 mm~600 mm高度范围内出现较大的斜裂缝，新增少量水平裂缝，裂缝延伸；距墙体底部10 mm高度处，左侧混凝土轻微脱落。加载至24 mm时，裂缝沿墙高蔓延至距墙体底部1000 mm高度处，且有大量斜裂缝出现；距墙体底部10 mm高度处，左侧混凝土脱落明显。加载至32 mm时，原有裂缝延伸至距墙体底部1200 mm高度处，且裂缝变长变宽；左侧混凝土脱落明显破坏范围扩大至距墙体底部20 mm高度处，右侧混凝土距墙体底部10 mm高度处开始脱落。加载至40 mm时，斜裂缝持续出现，沿高度蔓延至距墙体底部1400 mm高度处；两侧混凝土大量大块脱落，左侧混凝土脱落范围扩大至距墙体底部50 mm高度处，右侧混凝土脱落范围扩大至距墙体底部40 mm高度处，两侧钢筋裸露、屈曲。加载至48 mm时，裂缝变化不明显，混凝土底部两侧进一步压溃，破坏范围蔓延至距墙体底60 mm、50 mm高度处，两侧钢筋严重屈曲，参见图5(d)、图6(d)。与原有水平裂缝相比，新增裂缝主要为交叉斜裂缝，主要集中在墙体中部、底部，且两底角处混凝土出现严重破坏。由此可知，经受面外加载后的剪力墙若再承受面内加载，其破坏程度与仅受面内加载时相当。

图  6  试件裂缝发展

Figure  6.  Crack development of specimen

下载: 全尺寸图片 幻灯片

综上所述，当剪力墙一向受损后，若在另一向再次遭受荷载，受原有损伤尤其是对面外方向性能的影响将较为明显。在剪力墙承受面内-外受力模式下，虽然二次面外破坏时新增裂缝较为短小，但其无法承载较大的变形作用，基本丧失抗震能力。未损结构SW2-1在距离底部600 mm处发生面外偏离，而受损结构SW1-2则仅在距离底部200 mm处就发生偏离，极易发生面外变形，甚至倒塌。

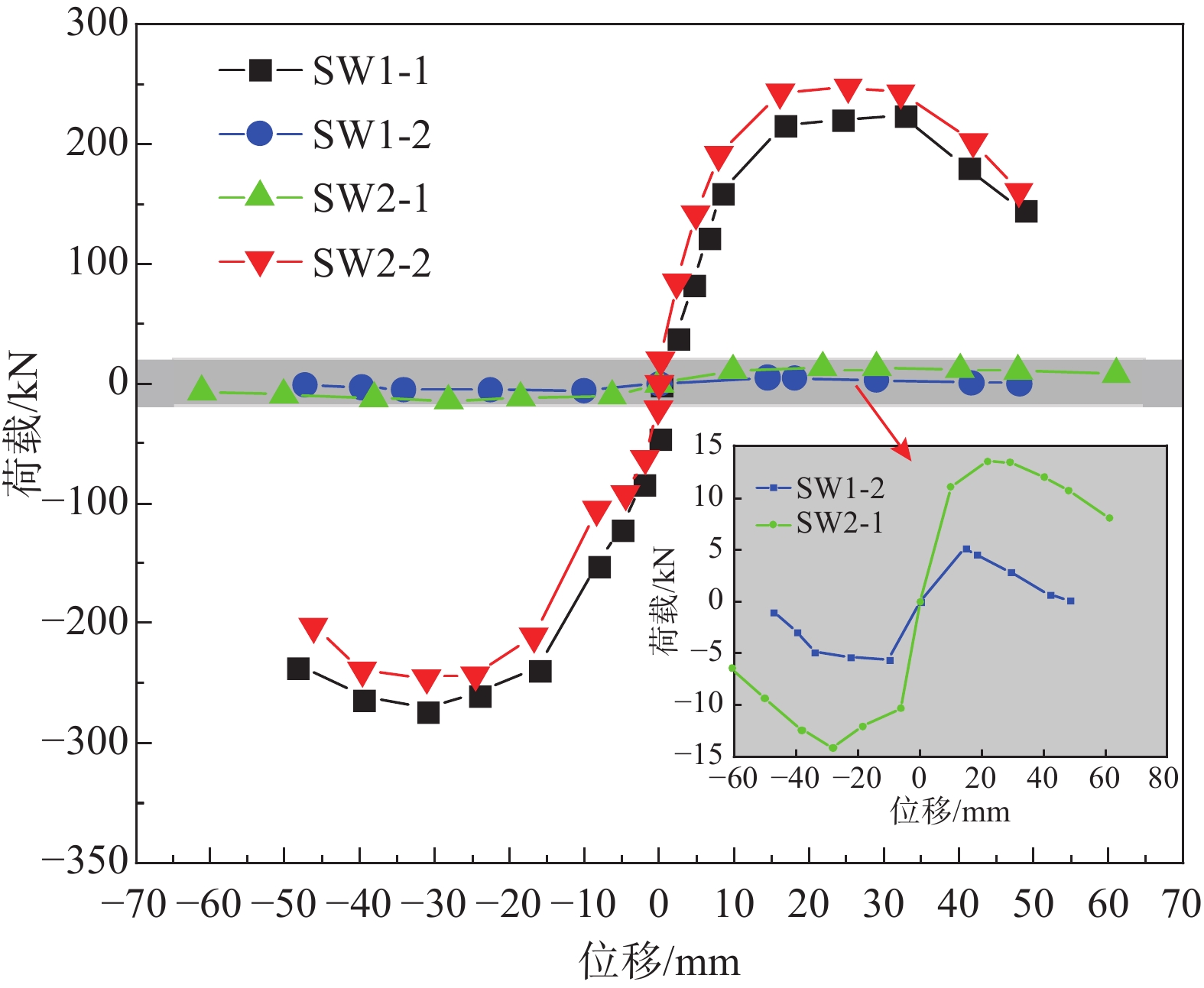
2.2   滞回曲线分析

试件滞回曲线如图7所示，可以看出：SW1-1和SW2-2的滞回曲线基本相同，而SW1-2和SW2-1的滞回曲线有明显差异。说明依次经历面内-外加载及面外-内加载对剪力墙面内、外两方向抗震性能造成的二次影响不同。当剪力墙面内加载完毕之后，剪力墙上有一定的损伤，若再次遭受面外作用，墙体面外方向承载力急剧下降，且后期基本丧失承载力。滞回曲线呈现负刚度发展趋势，滞回环主要集中在二、四象限。在剪力墙面外加载完毕之后，剪力墙无明显损伤，再次遭受面内作用时，面内方向承载能力几乎不受面外加载的影响，与仅承受面内加载剪力墙的滞回特性一致。

图  7  滞回曲线对比图

Figure  7.  Comparison of of hysteresis

下载: 全尺寸图片 幻灯片

2.3   骨架曲线分析

骨架曲线取每级加载的第一圈进行分析，参见图8。可从看出：SW1-1和SW2-2的承载力相当，两者基本接近。SW1-2和SW2-1的承载力有明显差异，且SW1-2承载力下降明显，后期趋近于0。由此可知，剪力墙在遭受二次变向加载时，其各方向上的承载力变化与对仅承受单次加载有所不同。其面内方向的承载力几乎不会受前次面外方向加载的影响，与单次加载时承载力基本接近；但其面外方向的承载力受其前次面内方向加载影响较大，与单次加载时承载力相差较大，最终几乎丧失承载能力。

图  8  骨架曲线对比图

Figure  8.  Comparison of skeleton curves

下载: 全尺寸图片 幻灯片

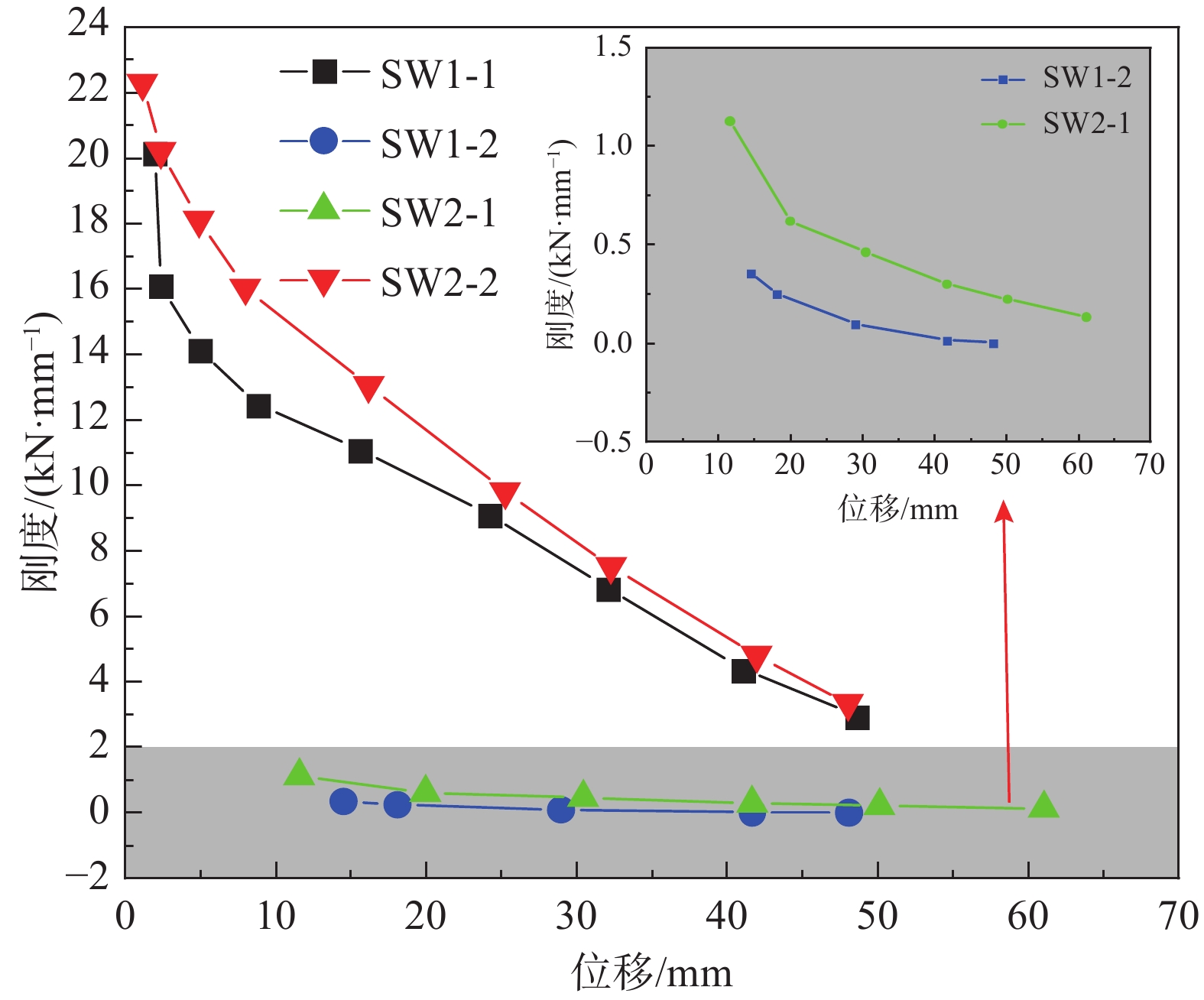
2.4   刚度退化曲线分析

各试件割线刚度随位移的退化曲线如图9所示。可以看出：试件前期刚度退化速度较快，后期刚度退化速度较慢，SW1-1和SW2-2刚度退化趋势一致，SW1-2的初始刚度明显低于SW2-1。

图  9  刚度退化曲线

Figure  9.  Comparison of stiffness degradation curves

下载: 全尺寸图片 幻灯片

2.5   延性分析

试件正向加载的特征点及延性系数见表2，可以看出：SW1-1和SW2-2的延性系数基本接近，各特征点的数值也较相似，表明面内延性几乎不受面外加载的影响，均较为良好。而SW2-1和SW1-2的延性系数相差较大，SW1-2各特征点对应的荷载值明显偏低，说明面外延性性能受面内加载影响严重，导致急剧下降。

表  2  试件特征点及延性系数

Table  2.  Specimen feature points and ductility coefficient

试件编号	开裂位移/mm	开裂荷载/kN	屈服位移/mm	屈服荷载/kN	峰值位移/mm	峰值荷载/kN	极限位移/mm	极限荷载/kN	延性系数
SW1-1	2.56	55.88	8.09	154.6	32.47	223.58	35.55	190.04	4.39
SW1-2	−	−	12.59	4.90	13.77	5.09	48.01	0.15	1.53
SW2-1	1.26	4.63	10.86	11.42	22.87	13.58	45.57	11.54	4.20
SW2-2	−	−	7.95	191.13	31.09	245.96	48.02	160.49	3.97

下载: 导出CSV 

| 显示表格

2.6   应变分析

因二次加载造成混凝土应变片及部分钢筋应变片失效，仅对完好的钢筋应变数据进行对比分析，见图10。由结果可知，SW1-1左侧的钢筋微应变发展趋势同SW2-2，且SW2-2底部钢筋应变要高于SW1-1底部钢筋应变，中部和顶部要低于SW2-2的钢筋应变，这说明当剪力墙经历面外加载之后，再次经历面内加载，底部钢筋受到的混凝土约束较轻，相较其他位置的钢筋有更大的活动空间。两试件中部钢筋应变的数值和发展趋势类似，且数值低于左侧，说明面内加载对剪力墙两侧影响较大。SW1-2左侧仅顶部钢筋有效，与SW2-1相比无明显差异。SW1-2中间位置中部钢筋应变片失效，底部和顶部应变波动范围无明显差异。

图  10  钢筋应变曲线

Figure  10.  Reinforcement strain curves

下载: 全尺寸图片 幻灯片

2.7   损伤评估

地震损伤模型可以定量描述结构或构件的震损程度，量化结构损伤后的性能指标。本文采用改进Park-Ang模型^[17]和弹塑性耗能差率模型^[18]对试件的损伤进行评估。相较于经典模型，改进Park-Ang模型在计算式中增加了与试件轴压比、配筋率及剪跨比相关的组合系数，修正了上下限不收敛的问题，使得大多计算结果不会超过阈值1.0，见式(1)。

式中：β为反应残余能力耗散比的组合系数，即$\beta=\left(F_{{\mathrm{y}}}\left(\delta_{{\mathrm{u}}}-\delta_{ {\mathrm{m}}}\right)\right) /\left(\displaystyle\int {\mathrm{d}} E-F_{{\mathrm{y}}}(\delta_{ {\mathrm{m}}}-\delta_{{\mathrm{y}}})\right)$；δ_m为最大位移；δ_y屈服位移；δ_u极限位移；F_y为屈服强度；dE为塑性耗能增量。

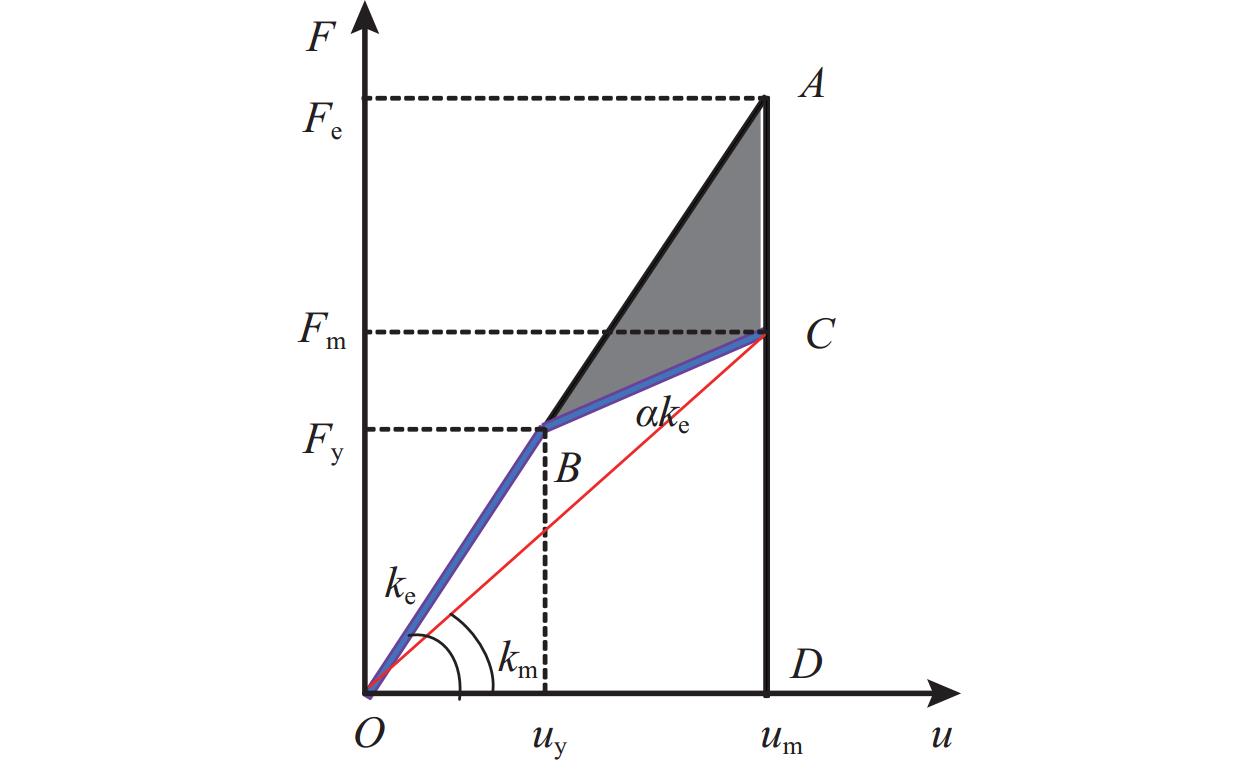
弹塑性耗能差率模型认为损伤指数为体系弹塑性变形能和理想弹性变形能的差值(弹塑性耗能差)与理想弹性变形能的比率。对于如图11所示的理想弹塑性单自由度体系，设其弹性阶段的刚度为k_e，后屈服刚度系数为α，屈服力和屈服位移分别为F_y和u_y。当结构处于弹塑性状态时，在位移u_m处的力和位移分别为F_m和u_m，此时延性为μ_m=u_m/u_y，相应的周期为T_m。面积S_OBCD为结构位移为u_m时实际产生的弹塑性变形能E_F，面积S_OAD为相应的结构理想弹性变形能E_E，面积S_ABC为上述二者之差，即弹塑性耗能差，见式(2)。在此基础上，可推导出拟静力作用下的耗能差率损伤模型，见式(3)。

式中：F_Fi和F_Ei分别为第i步骤时弹塑性状态下和理想弹性状态下的基底剪力；u_Fi和u_Ei分别为第i步骤时弹塑性状态下和理想弹性状态下的顶部位移。

改进Park-Ang模型和弹塑性耗能差率模型对试件的损伤评估结果参见图12。损伤指数演变趋势表明：面内加载之后再次对面外加载所造成的破坏程度远大面外单独加载；面外加载完毕后对面内的影响较小，损伤程度同单独面外加载一致。当剪力墙达到弹塑性层间位移角限值(20 mm)时，由改进Park-Ang模型计算的面内、外损伤指数均小于0.12，这与实际损伤情形明显不符。而由弹塑性耗能差率计算的面内损伤指数在0.8左右、面外损伤指数在0.5左右，能更准确地反映试件的损伤状态。另外，此时面内、外损伤程度较为接近，进一步表明剪力墙面外破坏及损伤不容忽视。

图  11  理想弹塑性体系耗能示意图

Figure  11.  Energy dissipation of ideal elastic-plastic system

下载: 全尺寸图片 幻灯片

图  12  损伤指数曲线

Figure  12.  Comparison of damage index curves

下载: 全尺寸图片 幻灯片

通过对上述性能参数的对比和分析，参见表2和表3，可以认为：剪力墙在经受面内加载、面外-内加载时，面内抗震性能相差不大，但经受面外加载、面内-外加载时，面外抗震性能相差明显。所以，当结构发生破坏时，要及时其进行修复，为确保修复后的结构能在任意方向的地震作用下发挥作用，也要提高其面外方向的抗震性能。

表  3  各试件性能特征对比

Table  3.  Comparison of performance characteristics of specimens

试件 编号	加载方式	裂缝分布	初始刚度/ (kN/mm)	损伤指数(20 mm处)
				改进Park-Ang模型	弹塑性耗能差率模型
SW1-1	面内	斜向交叉裂缝，集中在中下部。	20.15	0.1011	0.8213
SW1-2	面内-面外	新增水平裂缝，集中在中下部。	0.36	0.0017	0.5364
SW2-1	面外	水平裂缝，遍布墙身。	1.13	0.0007	0.4064
SW2-2	面外-面内	新增斜向交叉裂缝，集中在中下部。	22.29	0.1121	0.8350

下载: 导出CSV 

| 显示表格

3   试件有限元模拟

3.1   模型标定

本文采用OpenSEES软件进行试件的非线性性能模拟分析，采用非线性梁柱单元(nonlinearBeamColumn)模拟剪力墙，模拟所得滞回曲线与试验结果的对比参见图7。可见SW1-1、SW2-1及SW2-2的模拟结果与试验结果较接近，因SW1-2破坏严重，混凝土对钢筋的约束减弱，钢筋滑移作用显著，因而模拟的滞回环形状与试验结果相比存在一定差异，但其承载力数值基本吻合。总体而言，在此精度基础上进行结构体系的弹塑性时程分析是适宜的。

3.2   时程分析

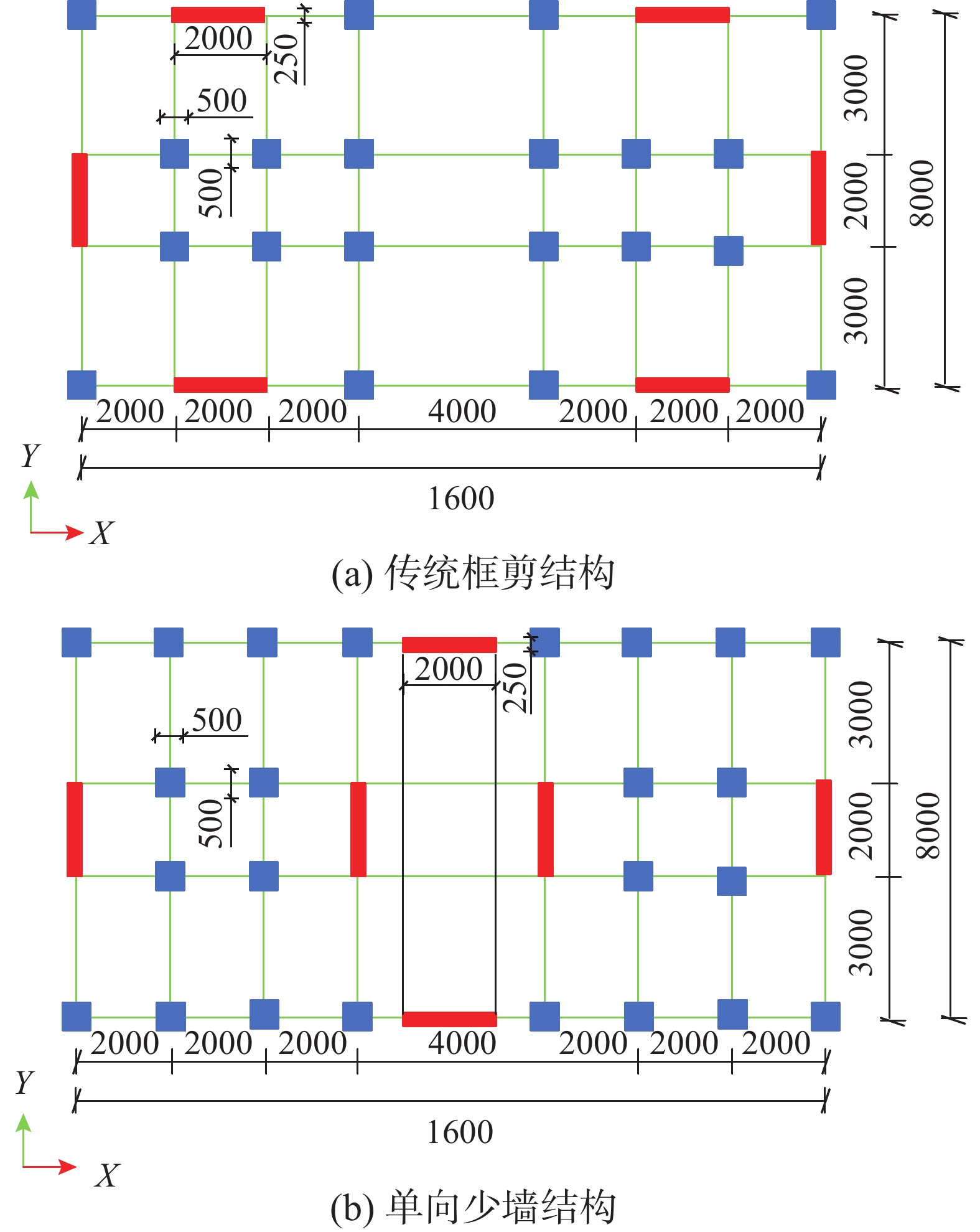
为了研究结构体系抗震性能，设计了2个13层的框架剪力墙结构体系模型^{[15 − 16]}，其中一个为传统框剪结构，在结构外围布设剪力墙，沿长轴方向布设4片、沿短轴方向布设2片。另一个参考新西兰Grand Chancellor 酒店的平面布局^[13]设计为单向少墙结构，沿长轴方向布设2片、沿短轴方向布设4片，见图13。结构层高4000 mm，混凝土强度等级为C35，钢筋均采用HRB400级热轧钢筋。墙厚250 mm，楼板厚200 mm，其余参数见表4。恒载标准值为3 kN/m²、活载标准值为2 kN/m²。抗震设防烈度为7度，设计基本地震加速度为0.15 g，地震分组为第一组，场地类别为Ⅱ类，抗震等级为三级。

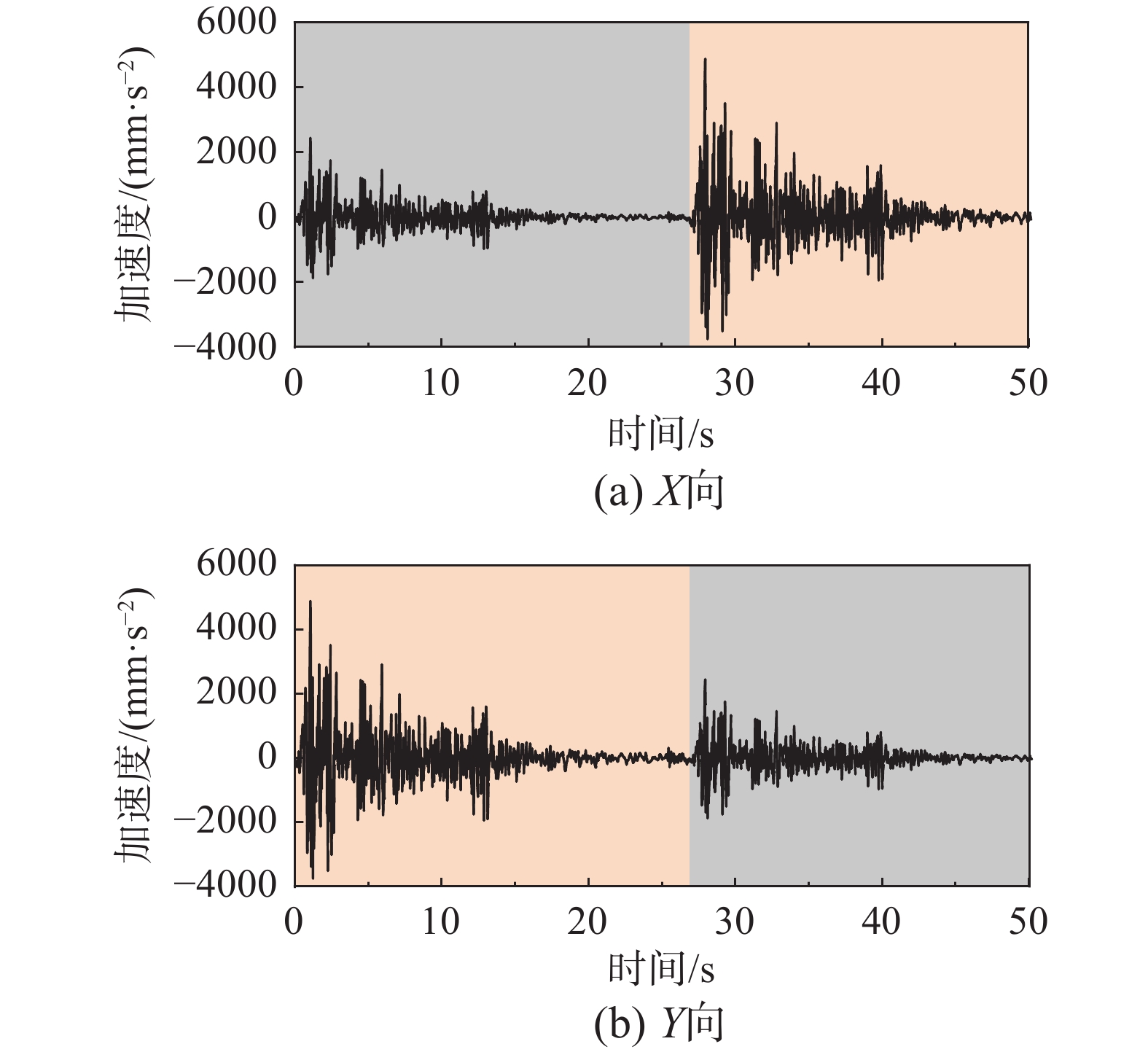
为了模拟剪力墙在面内、外方向依次遭受地震作用，即考虑不同的主余震序列输入方向的影响，以El Centro波、Taft波和Kobe波为依据构造主余震序列地震波进行时程分析，本文采用不同幅值组合的同一条地震波作为主余震序列^{[19 − 20]}。此外，也考虑对结构体系进行单一主震作用下(双向输入)的时程分析。根据Center for Engineering Strong Motion Data(CESMD)公布的数据，可知2011年新西兰M_w6.1级地震中台站监测到最高峰值地面加速度(peak ground acceleration，PGA)达0.5 g，因而将单一主震作用的PGA设为0.5 g，主余震序列PGA为0.5 g+0.25 g，参见图14。

图  13  结构平面尺寸图 　/mm

Figure  13.  Structural plane size

下载: 全尺寸图片 幻灯片

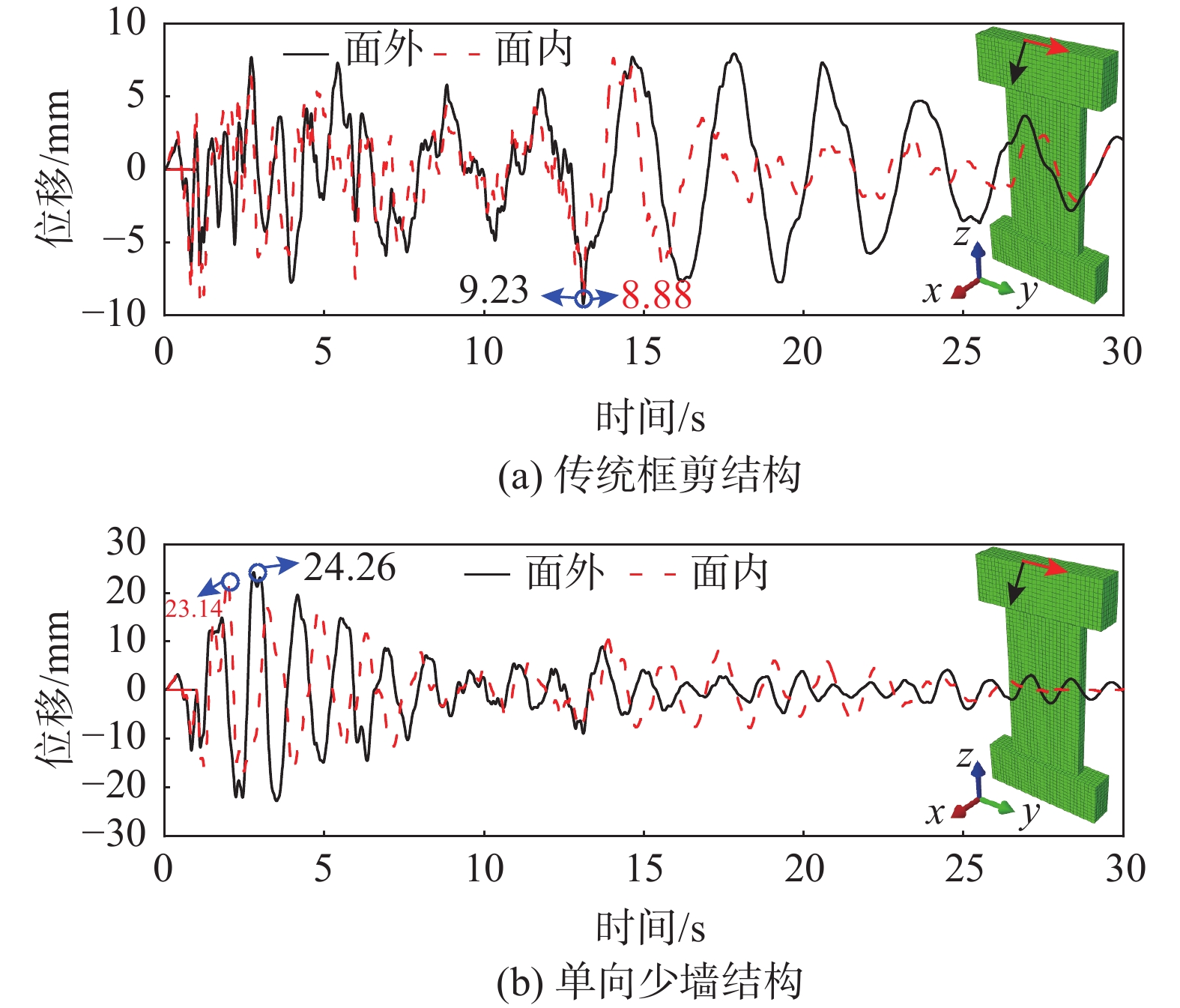
选取关于El Centro波的单一主震作用及不同输入方向主余震序列地震作用下的结构底层沿Y向布设的剪力墙位移时程曲线进行分析，参见图15及图16。由结果可知，传统结构中的剪力墙在遭受面内-面外方向主余震作用后，面内、外方向的两次位移相差不大。而单向少墙结构中面内、外方向的两次位移相差明显。下文对单向少墙结构在3组单一地震、不同输入方向下主余震序列下的损伤情况进行评估。

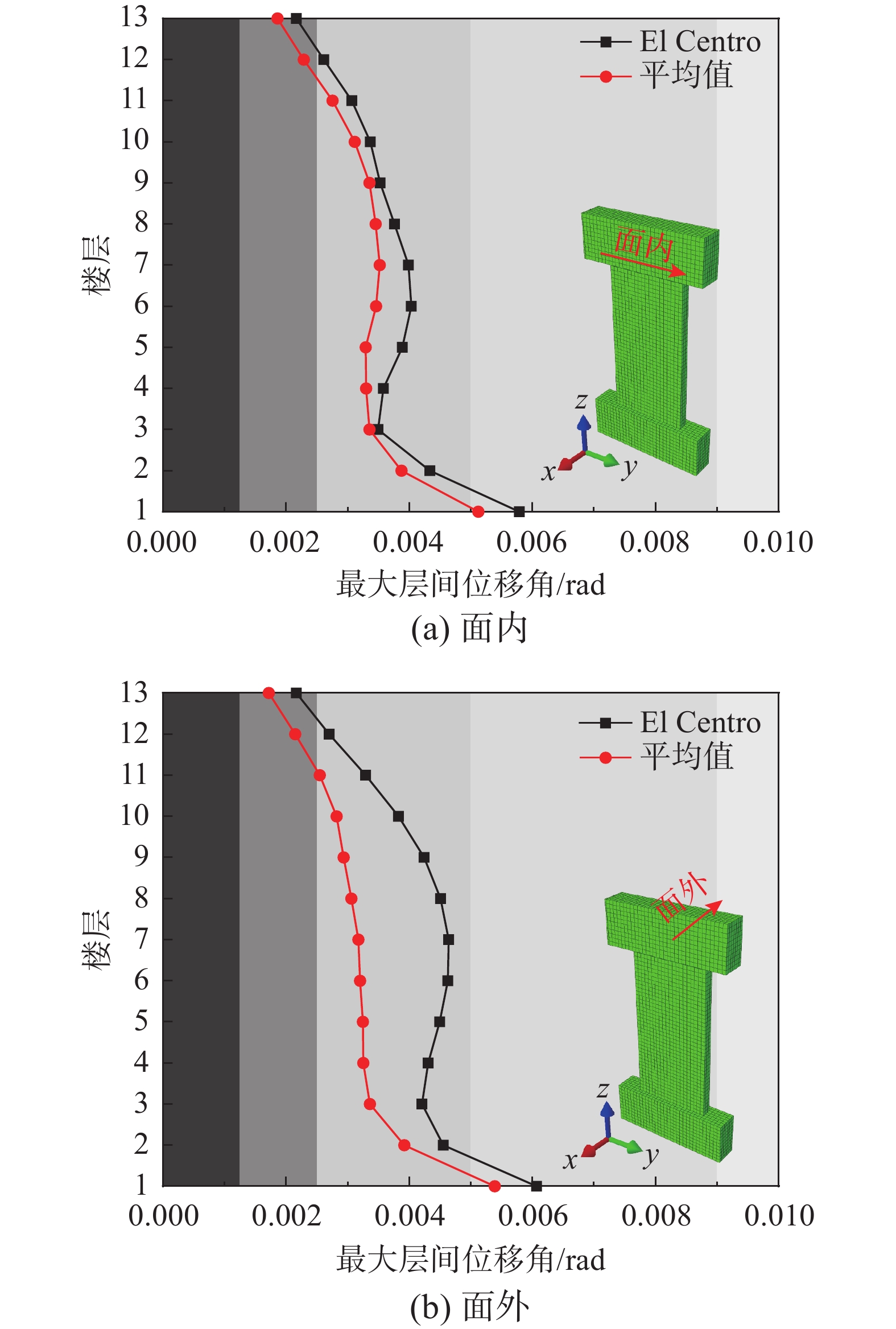
表  4  结构截面尺寸及配筋

Table  4.  Structure section size and reinforcement

构件	截面尺寸/mm	配筋
剪力墙	2000×250	6Φ18+5Φ16
柱	500×500	4Φ22
梁	300×600	2Φ25+2Φ22

下载: 导出CSV 

| 显示表格

图  14  不同输入方向的主余震序列地震波

Figure  14.  Main-aftershock sequence seismic waves in different input directions

下载: 全尺寸图片 幻灯片

图  15  单一主震下位移时程对比

Figure  15.  Comparison of displacement time history under single earthquake

下载: 全尺寸图片 幻灯片

根据《建筑抗震设计规范》^[15]的规定，以最大层间位移角范围作为损伤判断依据对剪力墙进行多级评估，参见表5。损伤评估结果见图17及图18。

图  16  不同输入方向下主余震序列位移时程对比

Figure  16.  Comparison of displacement time histories of main aftershock sequences in different principal directions

下载: 全尺寸图片 幻灯片

表  5  不同破坏等级下层间位移角范围

Table  5.  Range of maximum interlayer drift under different damage levels

破坏程度	基本完好	轻微破坏	中等破坏	严重破坏	倒塌
范围	[0, Δue]	[1.5Δue, 2Δue]	[3Δue, 4Δue]	[4Δue, 0.9Δup]	[Δup, 1]
注：[Δue]=1/800为弹性层间最大位移；[Δup]=1/100为弹塑性层间最大位移。在图17、图18中以不同的渐变颜色表示不同的损伤程度，颜色由深至浅依次为：基本完好、轻微破坏、中等破坏、严重破坏、倒塌。

下载: 导出CSV 

| 显示表格

图  17  单一地震下最大层间位移角及损伤判定

Figure  17.  Maximum drift and damage under single earthquake

下载: 全尺寸图片 幻灯片

图  18  不同输入方向下主余震序列下最大层间位移角及损伤判定

Figure  18.  Maximum drift and damage under main-aftershock with different principal directions

下载: 全尺寸图片 幻灯片

由图17可知，在单一主震作用下，剪力墙面内、外均处于中等破坏和严重破坏状态，且面内破坏程度稍微小于面外破坏程度。由图18可知，在主余震序列下，剪力墙面内、外方向依次成为主要受力方向。在主震作用下，剪力墙主要受面内地震力作用，各楼层剪力墙面内方向处于中等破坏或严重破坏状态，底层剪力墙的损伤最为严重。在余震作用下，剪力墙主要受面外地震力作用，各楼层剪力墙面外方向处于中等破坏和严重破坏状态，在El Centro波下，底层的剪力墙甚至接近倒塌状态。与单一主震作用下的结果相比，在不同主方向的主余震序列下，剪力墙面内、外的层间位移角均较大，损伤也更严重。

该破坏模式在构件层次与本文试验的破坏模式基本一致，当结构体系中的剪力墙面内方向的层间位移角达到限值1/100时，破坏程度较为严重。该状态可对应试件加载至20 mm时的情况，此时试件裂缝增多，混凝土明显脱落，承载力达到最大值；当面外方向达到该限值时，底层剪力墙处于倒塌状态。此状态下试件的破坏程度加剧，底部面外变形严重，承载力急剧下降，已有明显的倒塌趋势。在结构体系层次与新西兰地震^[13]中剪力墙在两次不同输入方向的地震中破坏模式基本一致，即面内方向作为主要抗震方向时，剪力墙破坏程度较轻，当面外方向在余震作用下成为主要抗震方向时，剪力墙破坏严重，甚至达到倒塌状态。

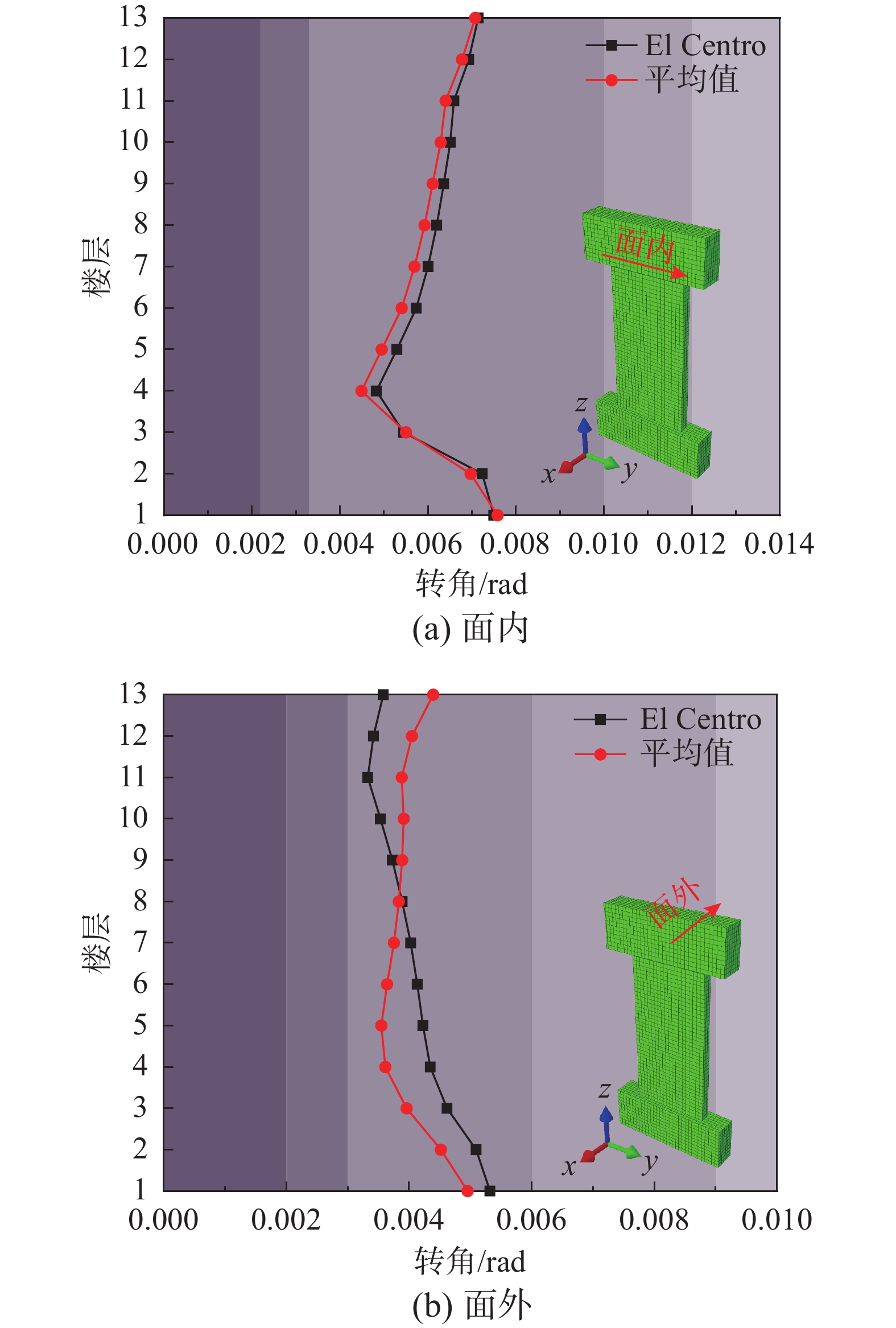
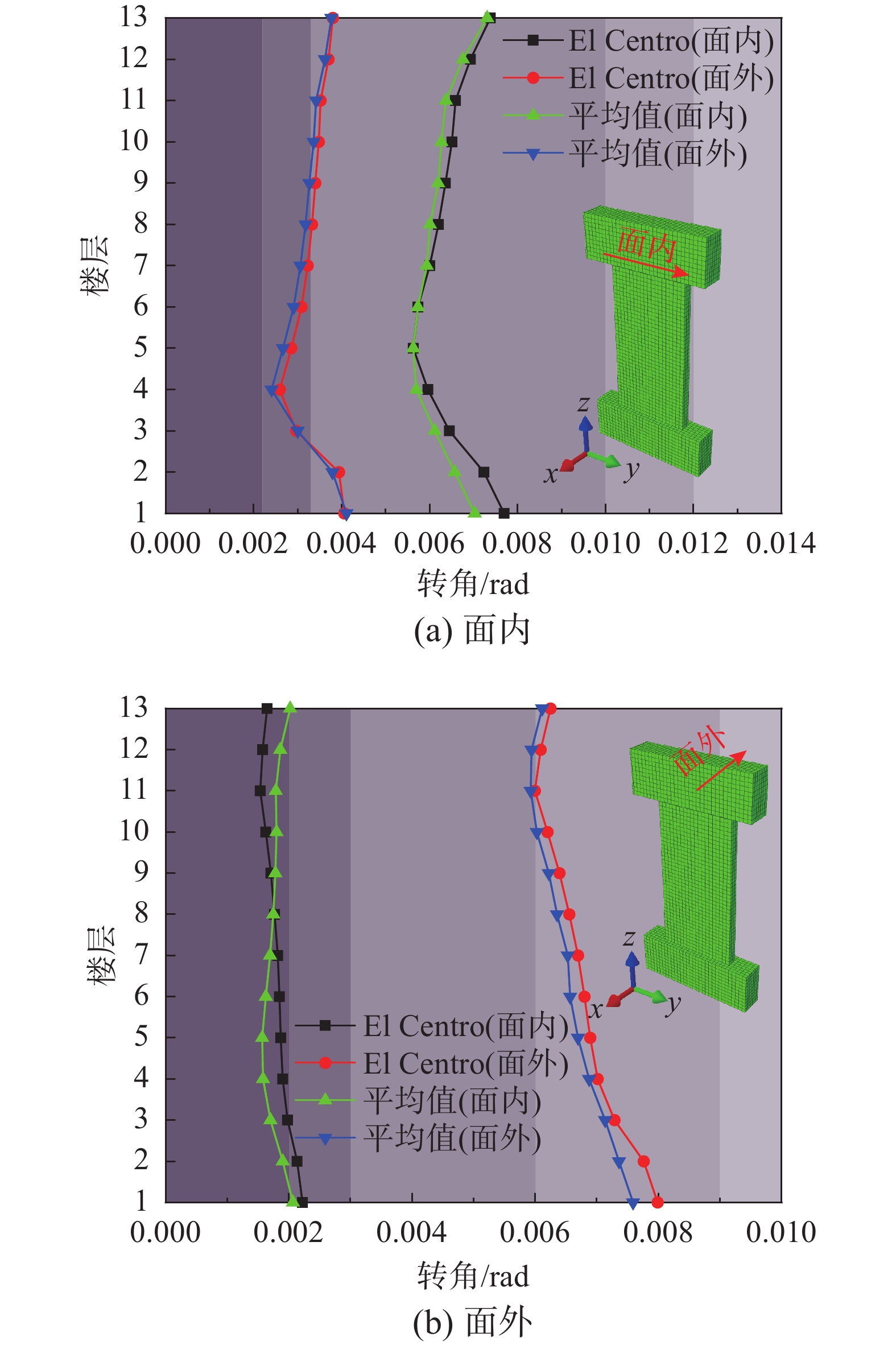
以最大层间位移角作为指标，无法分别对剪力墙构件的面内、外破坏情况分别进行精细评估。因此，根据《建筑抗震韧性评价标准》^[21]对构件转角评估取值的建议方法，结合对本次试验模拟得到的弯矩-曲率曲线，本文提出基于转角的损伤评价指标，面内、外剪力墙破坏等级划分见表6，损伤评估结果见图19及图20。

表  6  不同破坏等级下剪力墙转角限值

Table  6.  Limit values of rotation under different damage levels of shear walls

破坏程度	基本完好	轻微破坏	中等破坏	严重破坏	倒塌
面内	[0, 0.22%）	[0.22%,0.33%）	[0.33%,1%）	[1%,1.2%）	[1.2%,1]
面外	[0, 0.2%）	[0.2%,0.3%）	[0.3%,0.6%）	[0.6%,0.9%）	[0.9%,1]
注：在图19、图20中以不同的渐变颜色表示不同的损伤程度，颜色由深至浅依次为：基本完好、轻微破坏、中等破坏、严重破坏、倒塌。

下载: 导出CSV 

| 显示表格

由图19可知，在单一主震作用下，剪力墙面内、外均处于中等破坏。

图  19  单一主震下转角及损伤判定

Figure  19.  Rotation and damage under single earthquake

下载: 全尺寸图片 幻灯片

图  20  不同输入方向下主余震序列下转角及损伤判定

Figure  20.  Rotation and damage under main-aftershock sequence with different principal directions

下载: 全尺寸图片 幻灯片

由图20可知，在主震作用下，各楼层剪力墙面内方向处于中等破坏状态。在余震作用下，各楼层剪力墙面外方向则基本处于严重破坏状态。主余震序列作用下的损伤程度高于单一主震作用。由此可见，剪力墙面外方向在遭受不同方向的主余震序列地震作用下，最终会发生严重破坏。

综上所述，以最大层间位移角及转角作为损伤评价指标的结果均表明：当剪力墙受到不同主方向的主余震作用时，剪力墙面内、外的损伤状态会随输入的地震作用的方向改变而变化，剪力墙在主要受力轴向的损伤程度更严重，且高于单一主震作用。传统的剪力墙抗震设计通常忽视剪力墙面外的损伤行为，也不考虑主余震序列作用，特别是主余震沿不同方向输入结构的情况。上述简化抗震验算思路和方法与实际情况脱节，尤其对于结构中部分剪力墙在主震下沿面内方向受损后，其沿面外方向再次遭受余震作用的情况，极易发生超出预期的破坏模式。因此，亟需重视剪力墙面外方向的抗震性能，并对结构体系在主余震序列不同输入方向下的抗震性能加以研究及剖析。

4   结论

为研究剪力墙结构在不同方向不同受力顺序状态下抗震性能，通过对2片剪力墙进行低周往复加载试验并结合结构体系的时程分析，得到以下结论：

(1)通过低周往复加载试验可知：剪力墙面内、外的抗震性能存在一定的差异，面外承载力及刚度仅为面内方向的1/20~1/10。且当剪力墙的面内、外方向依次遭受地震作用时，各向对另一向的二次损伤影响程度不同，在经受面内加载、面外-内加载时，面内抗震性能相差不大，但经受面外加载、面内-外加载时，面外抗震性能相差明显。考虑实际情况，应对剪力墙面外方向抗震性能加以重视。

(2)通过结构体系非线性时程分析可知：传统框架剪力墙结构、单向少墙结构的地震响应不同，单向少墙结构容易发生较大的变形，且单向少墙结构在主余震序列地震作用下的损伤程度大于在单一地震作用的损伤程度，文中算例能较真实地再现实际震害中剪力墙面外破坏的典型现象。

(3)对结构进行设计时，除对结构进行单一主震作用下的抗震性能验算之外，还应对结构在不同输入方向下主余震序列地震的抗震性能进行考虑及重视。

(4)在构件层次，利用弹塑性耗能差率对结构进行损伤评估，相较其他损伤评估模型具有区分度显著、阈值范围更合理、适用性强的特点，能更加真实清晰地反映试件的实际损伤。

(5)在结构体系层次，利用最大层间位移角及本文提出的依据面内、外方向的转角对结构体系的损伤进行识别具有一定的准确性，可在实际应用中进行推广。