作为软土地基常见的处理方法之一，排水固结法以造价低廉的优势在实际中被广泛采用，但也必须看到排水固结法处理后的地基其承载力提高幅度有限。为弥补这一不足，实际工程中广泛采用复合地基技术，如砂桩、碎石桩、水泥土搅拌桩及CFG桩等。

马来西亚穆尔平原某路堤在修建过程中，成功引入挤密砂桩法进行地基处理并且取得了较好的地基加固效果^[1]。散体材料桩复合地基在外荷载作用下主要呈现鼓胀破坏的特征，这导致其承载力主要取决于桩周土体的强度^[2]。散体材料桩体提供的竖向排水通道能加速土体的固结，而桩周土体强度的提高又与土体固结息息相关，故研究散体材料桩复合地基固结理论具有重要的理论和实际意义。

散体材料桩复合地基固结理论源于经典的竖井地基固结理论^[3-5]。YOSHIKUNI最早在砂井地基固结理论基础上考虑桩体的应力集中以突显桩体效应^[6]，开启了碎石桩复合地基固结理论研究的篇章。此后，考虑打设桩体引发的不同涂抹效应^[7]、土体固结过程中的非线性特性^[8-9]、实际中不同形式荷载作用下的碎石桩复合地基固结理论应运而生^[10-11]。在此基础上，考虑到高置换率碎石桩桩径较大导致桩体内径向渗流不容忽视，后续建立了更严密的基于等应变假定的碎石桩复合地基固结理论^[12]。

鉴于单一桩型复合地基的不足，近年来多元复合地基在实际中的应用愈来愈广泛，由此复合地基规范中也新增了多元复合地基的相关说明^[13]。近几年多元复合地基的固结计算方法也逐渐取得一些进展，如：不透水桩与竖井相结合的复合地基固结计算^[14-15]等。

目前多元复合地基固结模型大多仅有一种竖向排水体^[16-18]，近年来，新兴了在碎石桩复合地基的桩体间打设塑料排水板或者增设竖井的地基处理方法^[19]。这种地基处理方法：一方面通过在桩间增设竖井以进一步加速土体的固结速率，从而使碎石桩复合地基的承载力得到早期增强；另一方面，与传统加密排水板的单一排水固结法相比，散体材料桩桩体使复合地基最终承载力得到有效增强。必须指出的是，这种地基处理方法与传统单一碎石桩复合地基或竖井地基相比，其桩间土的固结在径向同时向两侧排水体发生渗流。但遗憾的是，对于这种在径向同时向两侧发生渗流的桩间土固结问题目前还鲜有报道，并且关于多元复合地基固结理论的研究还仅局限于单一排水体。

以存在两种竖向排水体的多元复合地基固结问题为研究对象，基于桩间土发生竖向渗流及径向双向渗流的事实，考虑桩体和竖井的涂抹作用，建立桩间土固结模型并给出模型的理论解析解，利用该解析解对组合型复合地基固结性状开展分析，以提供该类问题固结计算的理论和设计依据。

1   选取计算单元

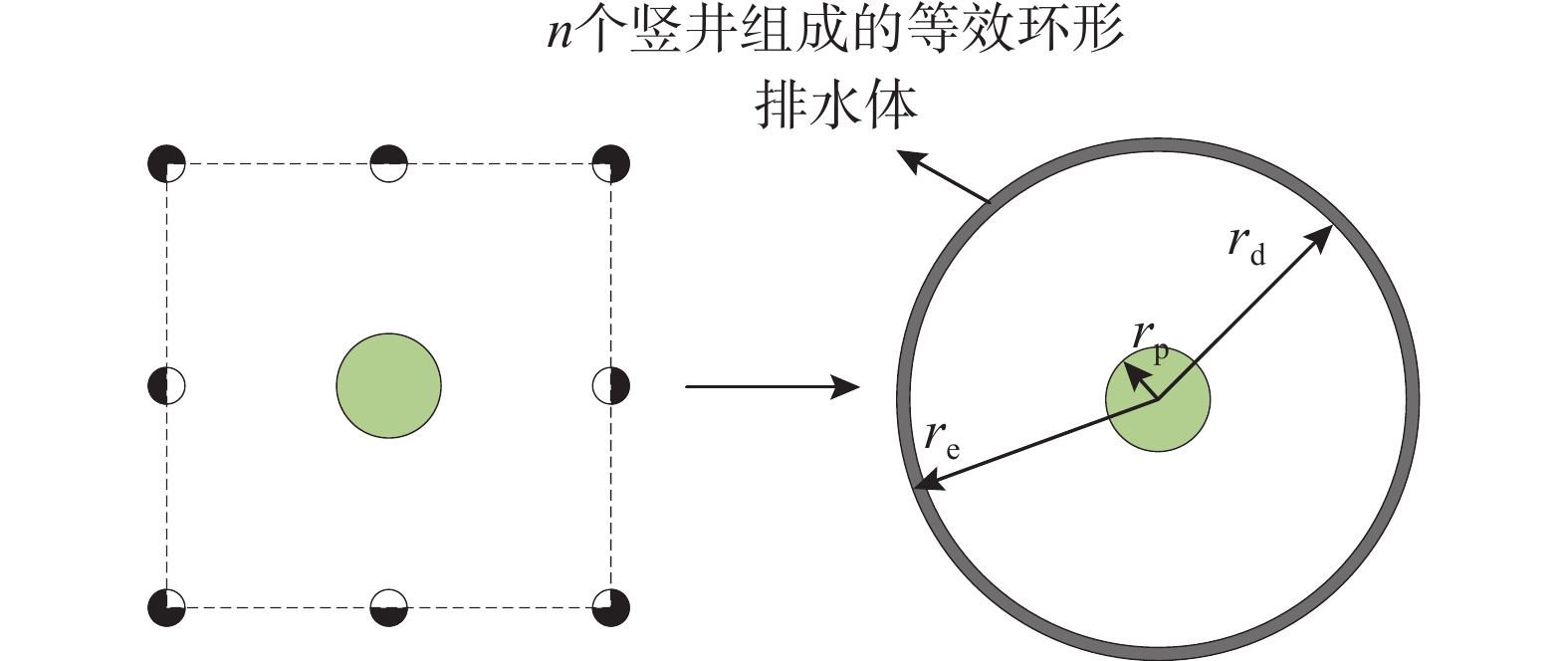
碎石桩-竖井复合地基无疑应以桩体为中心，竖井布置于桩体周围，常见的布置方法有以下几种：1)三角形布置；2)紧密型三角形布置；3)正方形布置；4)紧密型正方形布置。现以紧密型正方形布置为例，如图1所示。碎石桩周围增设8个竖井，其中边角处的4个竖井面积被4个碎石桩影响区平分。另外4个竖井面积被2个碎石桩影响区平分，故每个碎石桩影响区内竖井的数量为n=3。同理，当以三角形布置或者正方形布置时，n=1；当以紧密型三角形布置时，n=2。如果桩间距为l，利用面积等效原则将碎石桩影响区转化为半径为${r_{\text{e}}}$的圆形区域，得到正方形布桩时${r_{\text{e}}} = 0.564l$，三角形布桩时${r_{\text{e}}} = 0.525l$。

图  1  竖井-碎石桩复合地基平面布置

Figure  1.  Plane layout of composite foundation with vertical drains and stone columns

下载: 全尺寸图片 幻灯片

为考虑布置于桩周竖井的排水能力，根据已有研究可将桩周竖井按面积等效原则转化为具有一定透水能力的环形排水体^[20]。如图2所示，桩体中心到排水体内边界的距离${r_{\text{d}}} = \sqrt {{r_{\text{e}}^2 }- n{r_{\text{w}}^2}}$，其中，${r_{\text{w}}}$为竖井的等效半径(以常见的排水板尺寸100 mm×4 mm为例，相应的${r_{\text{w}}} = 0.033\;{\text{m}}$，此时等效圆环的厚度为0.002 m)。在此条件下，将碎石桩体、桩间土体及外侧排水圆环作为计算单元，具体见图3。

图  2  计算单元平面示意图

Figure  2.  Plan diagram of the calculation unit

下载: 全尺寸图片 幻灯片

图  3  计算单元空间简图

Figure  3.  Space diagram of the calculation unit

下载: 全尺寸图片 幻灯片

2   控制方程推导

图3为计算单元的空间简图。与以往单一竖井或碎石桩固结模型所不同，该固结模型中存在两种竖向排水体。如图3所示，碎石桩打穿整个软土层，其厚度或者桩长为H；桩体半径为${r_{\text{p}}}$；桩体引起的涂抹区半径为${r_{{\text{s}}1}}$；竖井引起的涂抹区半径为${r_{{\text{s2}}}}$。

为方便研究上述的固结模型，做如下假定：

1)外荷载瞬时施加，在地基中引起的附加应力沿深度保持不变。当外荷载面积与土层厚度相比较大时，地基土中的附加应力沿深度变化很小。同时，荷载变化对模型求解及性状影响甚微，作为理论初探，选取瞬时加载作为研究对象。

2)对于竖井—碎石桩复合地基而言，等应变条件是适用的，即同一深度处桩体、土体及竖井的竖向变形相等，由该假定可知桩体及竖井内任一深度处平均超静孔压沿径向不变。

3)忽略桩体和竖井内的径向渗流，考虑桩周土体内的径竖向组合渗流，且径竖向渗流均遵从达西定律。

4)竖井除渗透系数与桩周土体不同外，其余如压缩等特性均与桩周土体相同。

5)某深度处从桩周土体流入碎石桩桩体的流量等于该深度处桩体向上流出的流量，从桩周土体流入竖井的流量等于该深度处竖井向上流出的流量。

土中孔隙水在径向发生双向渗流，规定渗流方向与坐标轴r轴方向一致时为正，即水流流向竖井的方向为正，水流流向桩体的方向为负。孔隙水的竖向渗流方向以向上为正，即与坐标轴z轴方向相反时为正。根据基本假定5)获得桩体与桩周土体间的渗流连续方程为：

式中：${k_{\text{r}}}(r)$和${k_{\text{p}}}$分别为桩周土体水平向渗透系数和桩体竖向渗透系数；${\gamma _{\text{w}}}$为水的重度；${u_{\text{s}}}$为土体中任一点的超静孔压；${\overline u_{\text{p}}}$为桩体中任一深度处的平均超静孔压，${k_{\text{r}}}(r)$的表达式为：

式中：${k_{\text{h}}}$为土体未扰动区水平向渗透系数；$f(r)$为用以描述涂抹效应的关于r的函数，其表达式为：

式中：${\alpha _1} = {k_{{\text{s}}1}}/{k_{\text{h}}} \in \left( {0,1} \right)$；${\alpha _2} = {k_{{\text{s2}}}}/{k_{\text{h}}} \in \left( {0,1} \right)$；${r_{{\text{s}}1}} = {s_1}{r_{\text{p}}}$；${r_{{\text{s}}2}} = \sqrt {{r_{\text{d}}^2} - n({r_{\text{s}}^2} - {r_{\text{w}}^2})}$；${k_{{\text{s}}1}}$和${k_{{\text{s2}}}}$分别为碎石桩桩体扰动区内土体的水平渗透系数和竖井扰动区内土体的水平渗透系数；${r_{\text{s}}} = {s_2}{r_{\text{w}}}$，为一个竖井周围土体扰动区半径。其中：${s_1}$为桩周土体的涂抹比；${s_2}$为井周土体的涂抹比。同时，竖井与桩周土体间的渗流连续方程为：

式中：${k_{\text{w}}}$为竖井的竖向渗透系数；${\overline u_{\text{w}}}$为竖井中任一深度处的平均超静孔压。

外部荷载$\sigma$由桩体、桩周土体和竖井共同承担，其平衡方程为：

式中：${\overline \sigma _{\text{s}}}$为桩周土体分担的平均总应力；${\overline \sigma _{\text{p}}}$为桩体分担的平均总应力；${\overline \sigma _{\text{w}}}$为竖井分担的平均总应力。

荷载在复合地基中引起的总平均超静孔压$\overline u$与桩体内平均超静孔压${\overline u_{\text{p}}}$、桩周土体内平均超静孔压${\overline u_{\text{s}}}$及竖井内平均超静孔压${\overline u_{\text{w}}}$间的关系为：

式中：${m_1} = {r_{\text{p}}^2}/{r_{\text{e}}^2}$；${m_2} = {r_{\text{d}}^2}/{r_{\text{e}}^2}$；$\overline u$为任一深度处复合地基内总平均超静孔压；${\overline u_{\text{s}}}$为任一深度处土体内平均超静孔压，其可通过如下积分关系式获得：

由等应变假定及基本假定4)可知：

式中：${E_{\text{s}}}$为土体压缩模量；${E_{\text{p}}}$为桩体压缩模量；${E_{{\text{sp}}}}$为复合地基的复合压缩模量，其可通过土体压缩模量和桩体压缩模量计算如下：

桩周土体的超静孔隙水压力分别在桩体处和竖井处对应的连续条件为：

参考WANG和JIAO^[21]的研究，考虑径竖向渗流下的桩周土体固结控制微分方程为：

式中，${k_{\text{v}}}$为土体的竖向渗透系数。将式(12)两边关于r积分并整理得：

式中：$W = \dfrac{{{k_{\text{v}}}}}{{{\gamma _{\text{w}}}}}\dfrac{{{\partial ^2}{{\overline u}_{\text{s}}}}}{{\partial {{\textit{z}}^2}}} + \dfrac{{\partial {\varepsilon _{\text{v}}}}}{{\partial t}}$；${c_1}$为积分常数。

将式(13)两边关于r在$\left( {{r_{\text{p}}},r} \right)$上再次进行积分并利用边界条件(10)整理得：

式中：${A_0}(r) = \displaystyle\int_{{r_{\text{p}}}}^r {\dfrac{1}{{\xi f\left( \xi \right)}}} {\text{d}}\xi$；${B_0}(r) = \displaystyle\int_{{r_{\text{p}}}}^r {\dfrac{\xi }{{f\left( \xi \right)}}} {\text{d}}\xi$；$\xi$为积分变量。式(14)满足边界条件式(11)可确定积分常数${c_1}$的表达式：

将式(15)代入式(14)可得：

将式(16)代入式(7)可得任一深度处土体内平均超静孔压为：

式中：${A_1} = \displaystyle\int_{{r_{\text{p}}}}^{{r_{\text{d}}}} {r{A_0}\left( r \right)} {\text{d}r}$；${B_1} = \displaystyle\int_{{r_{\text{p}}}}^{{r_{\text{d}}}} {r{B_0}\left( r \right)} {\text{d}r}$。将式(17)与式(6)联立消去${\overline u_{\text{s}}}$得到：

式中：

联立式(1)、式(4)、式(13)及式(15)可得：

式(8)两侧对t求偏导，可得到：

式(6)两边关于z求二阶偏导得：

联立式(9)、式(18)、式(19)、式(20)和式(22)得到：

式中：$C = \dfrac{{{\gamma _{\text{w}}}A}}{B}\left[ {\dfrac{{{m_{\text{1}}} - \dfrac{{{B_0}({r_{\text{d}}})}}{{{r_{\text{e}}^2}{A_0}({r_{\text{d}}})}}}}{{{k_{\text{p}}}}} + \dfrac{{{m_{2}} - {m_{\text{1}}}}}{{{k_{\text{v}}}}} + \dfrac{{\dfrac{{{B_0}({r_{\text{d}}})}}{{{r_{\text{e}}^2}{A_0}({r_{\text{d}}})}} - {m_2}}}{{{k_{\text{w}}}}}} \right]$；$D = 2\dfrac{{{k_{\text{h}}}}}{{{k_{\text{p}}}}}\dfrac{1}{{{r_{\text{e}}^2}{A_0}({r_{\text{d}}})}} - 2\dfrac{{{k_{\text{h}}}}}{{{k_{\text{w}}}}}\dfrac{1}{{{r_{\text{e}}^2}{A_0}({r_{\text{d}}})}} - \dfrac{C}{A}$；$Y = {{{E_{\text{p}}}} / {{E_{\text{s}}}}}$为桩土模量比；${c_{\text{h}}} = {{{E_{\text{s}}}{k_{\text{h}}}} / {{\gamma _{\text{w}}}}}$为土体径向固结系数。

式(23)两边对z再次求二阶偏导可得：

联立式(19)、式(20)、式(23)和式(24)解出${\overline{u}}_{\text{p}}、{\overline{u}}_{\text{w}}$：

式中：

式(18)、式(19)、式(25)、式(26)联立可得：

式中：

式(27)即为本模型的固结控制微分方程。复合地基中总的平均超静孔压$\overline u$需满足的边界条件和初始条件分别为：

3   固结模型求解及解的讨论

3.1   固结模型的解析解

固结模型的控制微分方程式(27)为6阶偏微分方程，很难直接获得该方程的解析解。参考太沙基一维固结模型解析解、竖井地基径向固结解析解^[22]以及径竖向渗流下碎石桩复合地基固结解析解^[23]的级数表达形式以及边界条件式(28)，设置平均超静孔压$\overline u$解析解的级数表达式为：

式中：${A_{\text{m}}}$、$\lambda _{\text{m}}$及${\beta _{\text{m}}}$为待定系数。根据边界条件式(29)可确定系数$\lambda _{\text{m}} = M/H$；$M = (2m - 1)\pi /2$；$m = 1,2,3 \cdot \cdot \cdot$ 。根据初始条件式(30)，并利用三角函数的正交性，可确定参数${A_{\text{m}}} = 2\sigma /M$。将$\lambda _{\text{m}}$及${A_{\text{m}}}$代入式(31)，复合地基总平均超静孔压$\overline u$为：

将式(32)代入控制微分方程式(27)，可确定待定参数${\beta _{\text{m}}}$的表达式为：

在此基础上，利用式(25)和式(26)获桩体内超静孔压${\overline u_{\text{p}}}$及竖井内超静孔压${\overline u_{\text{w}}}$的解答为：

由式(6)可得到${\overline u_{\text{s}}}$的通式：

此时根据土层平均固结的定义，组合型复合地基桩周土体的平均固结度$U(t)$为：

根据弹性力学理论，本文复合地基沉降值${S_{\text{t}}}$可表示为：

3.2   解的退化讨论

3.2.1   退化为碎石桩复合地基固结解析解

当${r_{\text{d}}} \to {r_{\text{e}}}$，${k_{\text{w}}} \to 0$时，外围竖井的等效排水体转化为不透水边界，土中孔隙水径向仅发生向桩体方向的单向渗流，此时${\beta _{\text{m}}}$退化为：

令${n_1^2 }= {1 /{{m_1}}}$，${c_{\text{v}}} = {{{E_{\text{s}}}{k_{\text{v}}}} / {{\gamma _{\text{w}}}}}$，${F_{{\text{c}}1}} = {{2({A_1}{r_{\text{e}}^2} - {B_1})} / {[ {{r_{\text{e}}^2}{r_{\text{p}}^2}({1 / {{m_1}}} - 1)} ]}}$，式(39)可表示为：

式(40)与卢萌盟^[24]瞬时荷载作用下扰动区水平渗透系数不变的解答完全一致，说明本文解答可退化为单一碎石桩复合地基固结解答。

3.2.2   退化为竖井地基径向固结解析解

当${k_{\text{v}}} = 0$，$Y = 1$时，式(40)可进一步退化为：

令${F_{{\text{c2}}}} = \dfrac{{\left( {n_1^2 - 1} \right)}}{{n_1^2}}{F_{{\text{c}}1}}$，${d_{\text{p}}} = 2{r_{\text{p}}}$，${G_1} = \dfrac{{{k_{\text{h}}}}}{{{k_{\text{p}}}}}{\left( {\dfrac{H}{{{d_{\text{p}}}}}} \right)^2}$，式(41)可转化为：

式(42)与谢康和等^[22]给出的砂井地基径向固结解解析解完全一致，说明本文解亦可完全退化为单一竖井地基的固结解析解。

4   固结性状分析

本节将研究各因素对平均固结速率、孔压消散速率及桩土应力比的影响。算例分析中参数按表1选取，控制变量取值分别在图中单独列出。

表  1  初始参数取值

Table  1.  Details of initial parameters

参数	值		参数	值
总应力$\sigma {\rm /kPa}$	200		无量纲地基厚度H/re	10
地基厚度H/m	10		无量纲碎石桩影响区半径re/rp	2
软土径向渗透系数kh/(m/s)	10−8		无量纲碎石桩压缩模量Ep/Es	4
软土竖向渗透系数kv/(m/s)	0.5×10−8		无量纲竖井渗透系数kw/kh	104
软土压缩模量Es/kPa	2000		无量纲碎石桩渗透系数kp/kh	103
桩周土体涂抹比s1	1.5		无量纲桩周涂抹区渗透系数a1	0.5
井周土体涂抹比s2	1.5		无量纲井周涂抹区渗透系数a2	0.5
无量纲深度z/H	0.5		等效竖井数量n	3

下载: 导出CSV 

| 显示表格

4.1   孔压分析

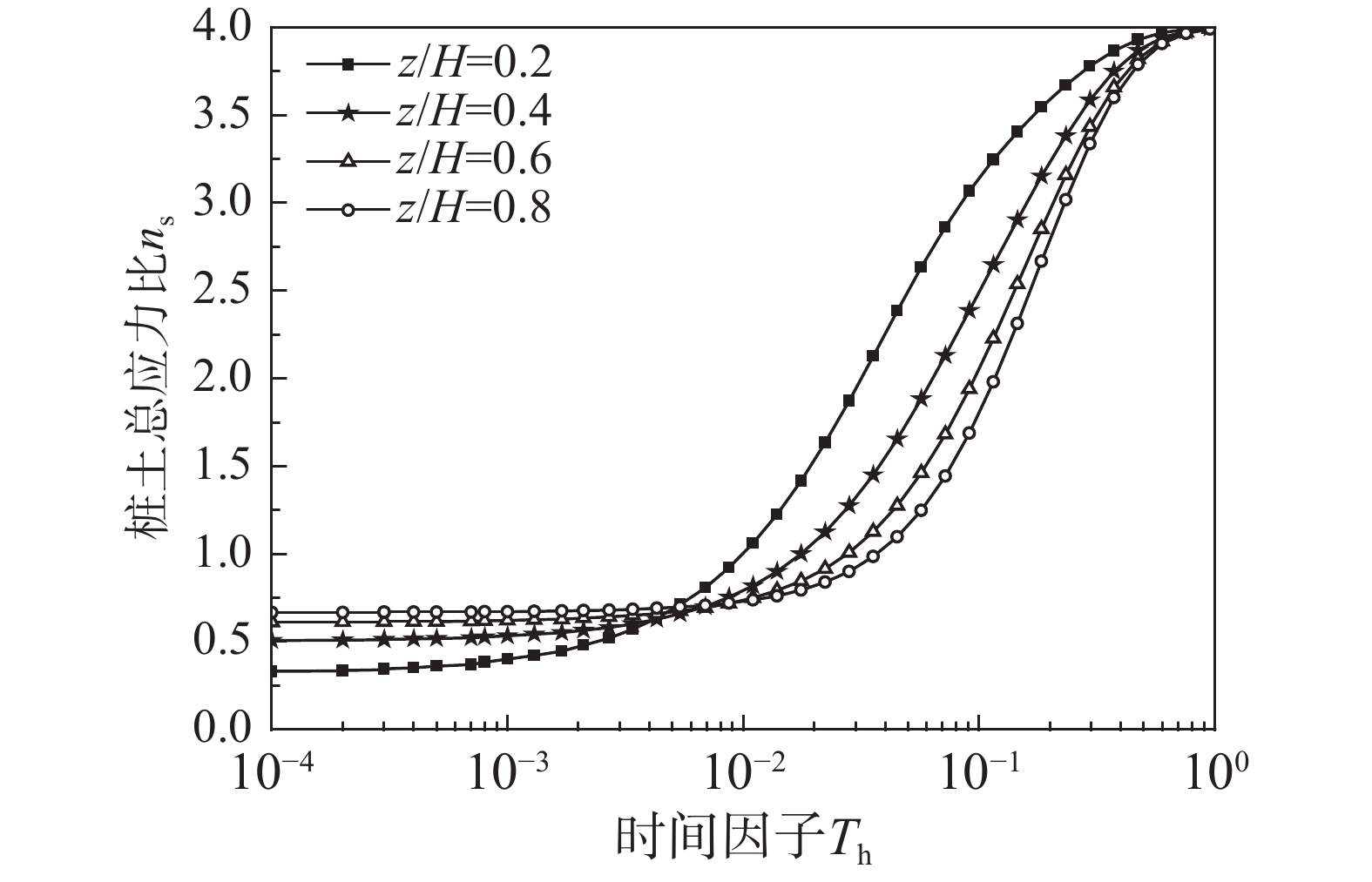
定义时间因子${T_{\text{h}}}$表达式为${T_{\text{h}}} = {{{c_{\text{h}}}t} /{\left( {4{r_{\text{e}}^2}} \right)}}$。图4为不同位置处超静孔压随时间的变化云图。可发现：固结初期，土体内超静孔压与总平均超静孔压基本保持一致且值较大，桩体内孔压与竖井内孔压随深度增加不断增大，而土体内孔压与总平均超静孔压超过某深度后不再明显变化。主要归结为固结初期土体未发生变形而桩体内部分孔压发生消散，此时土体不排水压缩模量远大于桩体的不排水压缩模量^[25-26]，故土体分担了大部分由外荷载引发的附加应力，但复合地基内总平均超静孔压仍等于外荷载引起的附加应力。桩体孔压消散仅在靠近顶部位置，深部则未发生消散，同时周围土体内孔隙水发生径向渗流，故桩体孔压会随着深度增加而增大。相比而言，土体固结速率较慢，故桩周土体的孔压随深度变化不够明显。为进一步说明这一性状，图5列出了不同深度处桩土总应力比值随时间发展的过程曲线。

图  4  超静孔隙水压力随深度和时间消散过程

Figure  4.  The dissipation of excess pore water pressure with time and depth

下载: 全尺寸图片 幻灯片

图  5  不同深度处${n_{\text{s}}}$随时间变化曲线

Figure  5.  The variation of n_s with time under different depths

下载: 全尺寸图片 幻灯片

定义${n_{\text{s}}} = {{{{\overline \sigma }_{\text{p}}}} / {{{\overline \sigma }_{\text{s}}}}}$为桩土总应力比，固结初期，桩土总应力比随着深度增加而增大，因为桩体内超静孔压随深度不断增大，而土体内超静孔压随深度基本不变；随着桩周土体的不断固结，顶部桩体和桩周土体均发生大幅度下降，浅部处桩土应力比趋近于桩土模量比；但由于深度土体尚未发生固结，故桩土应力比随深度增加而减小。当桩周土体固结完成后，深度不同处的桩土应力比n_s均等于桩土模量比，故曲线逐渐趋近于相同值。

4.2   固结度分析

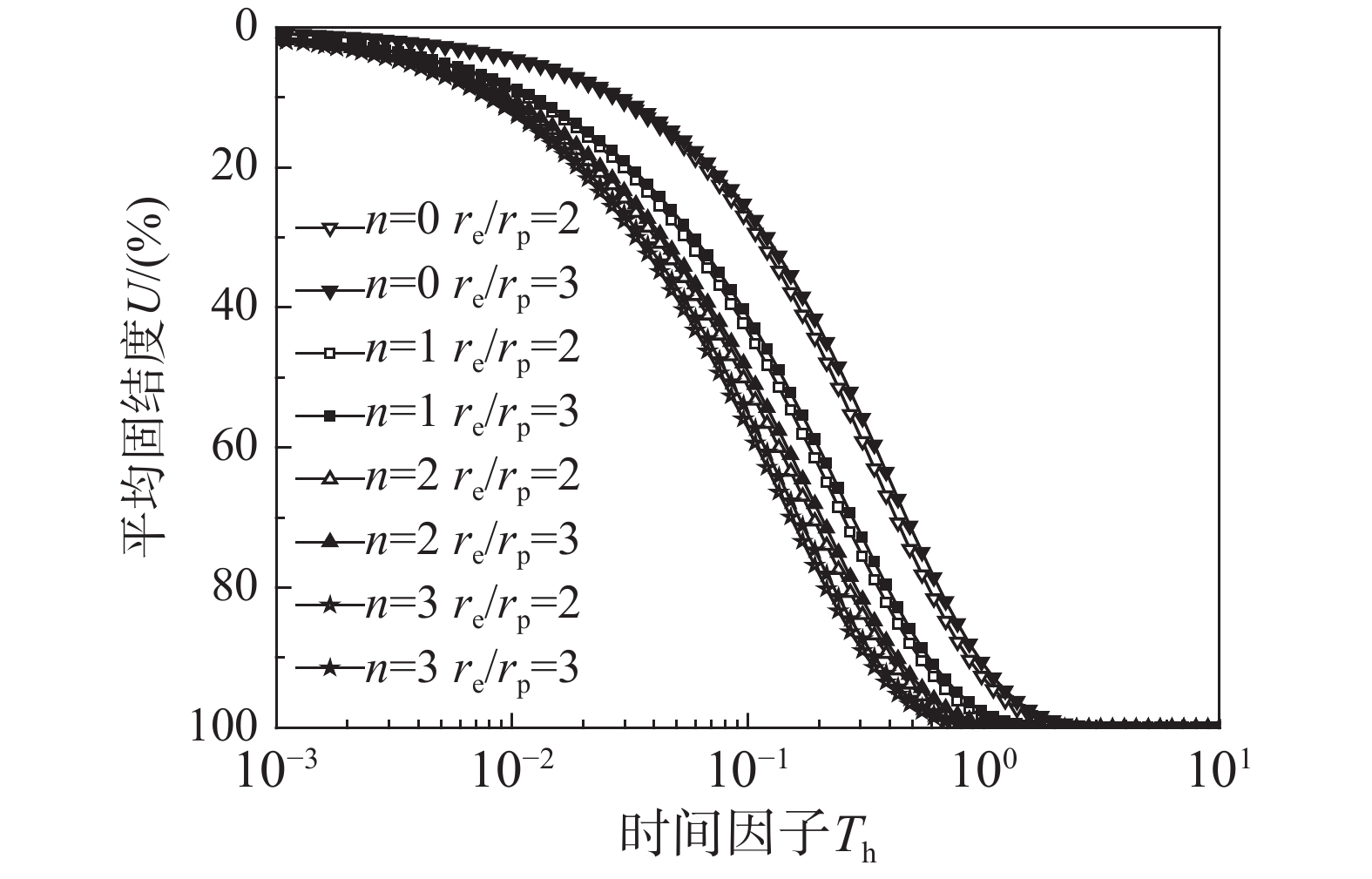
定义${r_{\text{e}}}/{r_{\text{p}}}$为井径比。图6示出了复合地基平均固结度U在桩周布置不同竖井和不同井径比间的差异。可发现如果一味地通过减小井径比从而提高桩间土固结速率，其效果并不明显。而在桩周打设竖井可使土体的固结速率提升明显，且随着桩周竖井布置数量的增加，固结速率的提升幅度会愈加明显。故在满足地基承载力要求时，考虑到经济因素及提升地基固结速率的效果，可在桩周打设竖井来代替减小复合地基的井径比。

图  6  竖井数量n与${r_{\text{e}}}/{r_{\text{p}}}$对固结速率的影响

Figure  6.  Influences of the number of vertical drains n and ${r_{\text{e}}}/{r_{\text{p}}}$ on the rate of consolidation

下载: 全尺寸图片 幻灯片

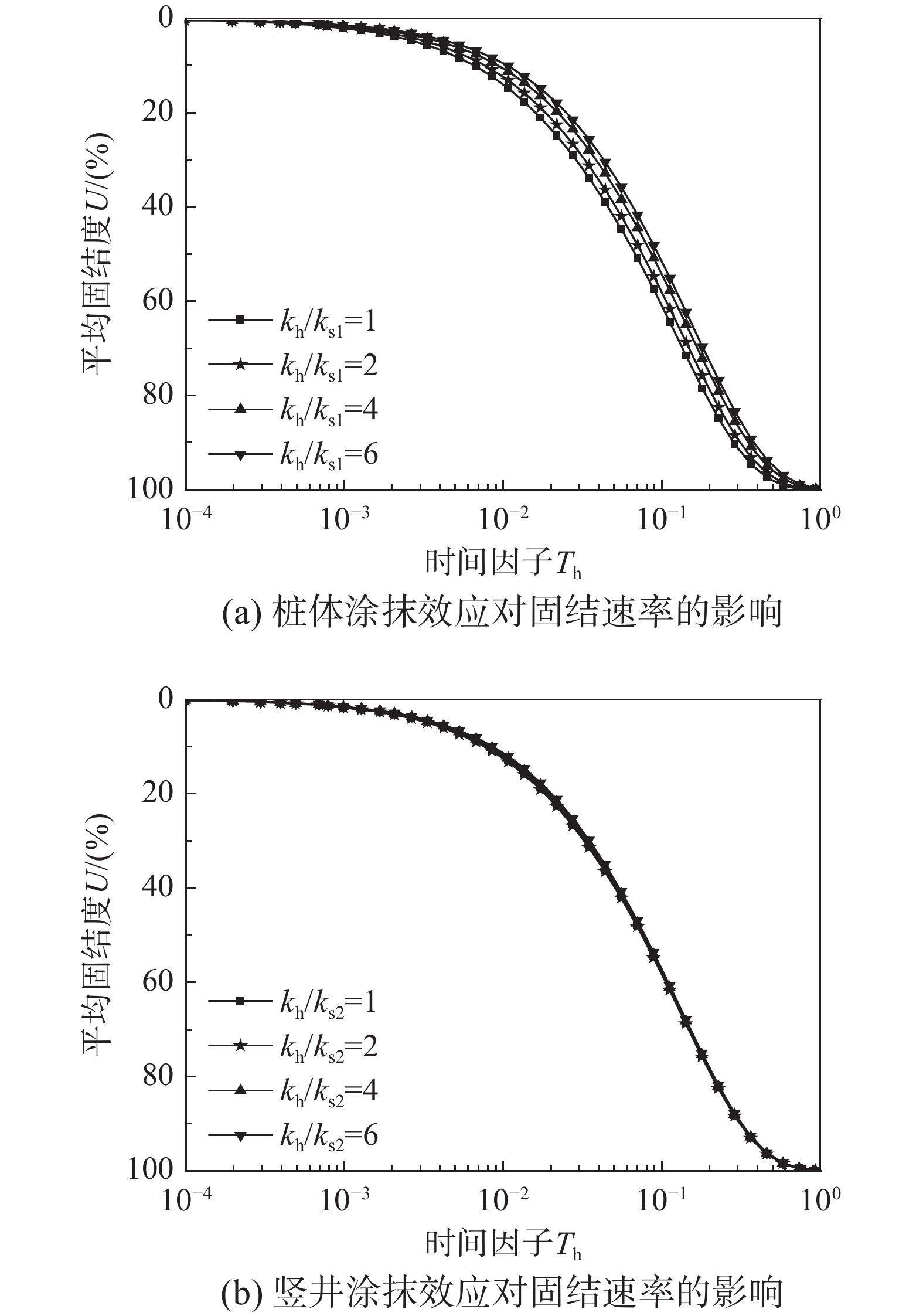
从图7(a)可以看到，当改变${k_{\text{h}}}/{k_{{\text{s1}}}}$的取值时，固结速率有着明显的变化，${k_{\text{h}}}/{k_{{\text{s1}}}}$的取值越大，即桩体涂抹效应越强，涂抹区土体受扰动程度越大，固结速率越慢。因此，在做固结分析时需要考虑打设桩体时对土体带来的扰动。但图7(b)中不同${k_{\text{h}}}/{k_{{\text{s2}}}}$值下的土体固结曲线基本重合，说明${k_{\text{h}}}/{k_{{\text{s2}}}}$对土体固结速率基本无影响，原因是等效环形排水体的面积相对于影响区面积来说非常小，由其引发的涂抹区面积也较小，故打设竖井对土体诱发的扰动对固结速率的影响在该工况下可以忽略。

图  7  涂抹效应对固结速率的影响

Figure  7.  Influences of smear effect on the rate of consolidation

下载: 全尺寸图片 幻灯片

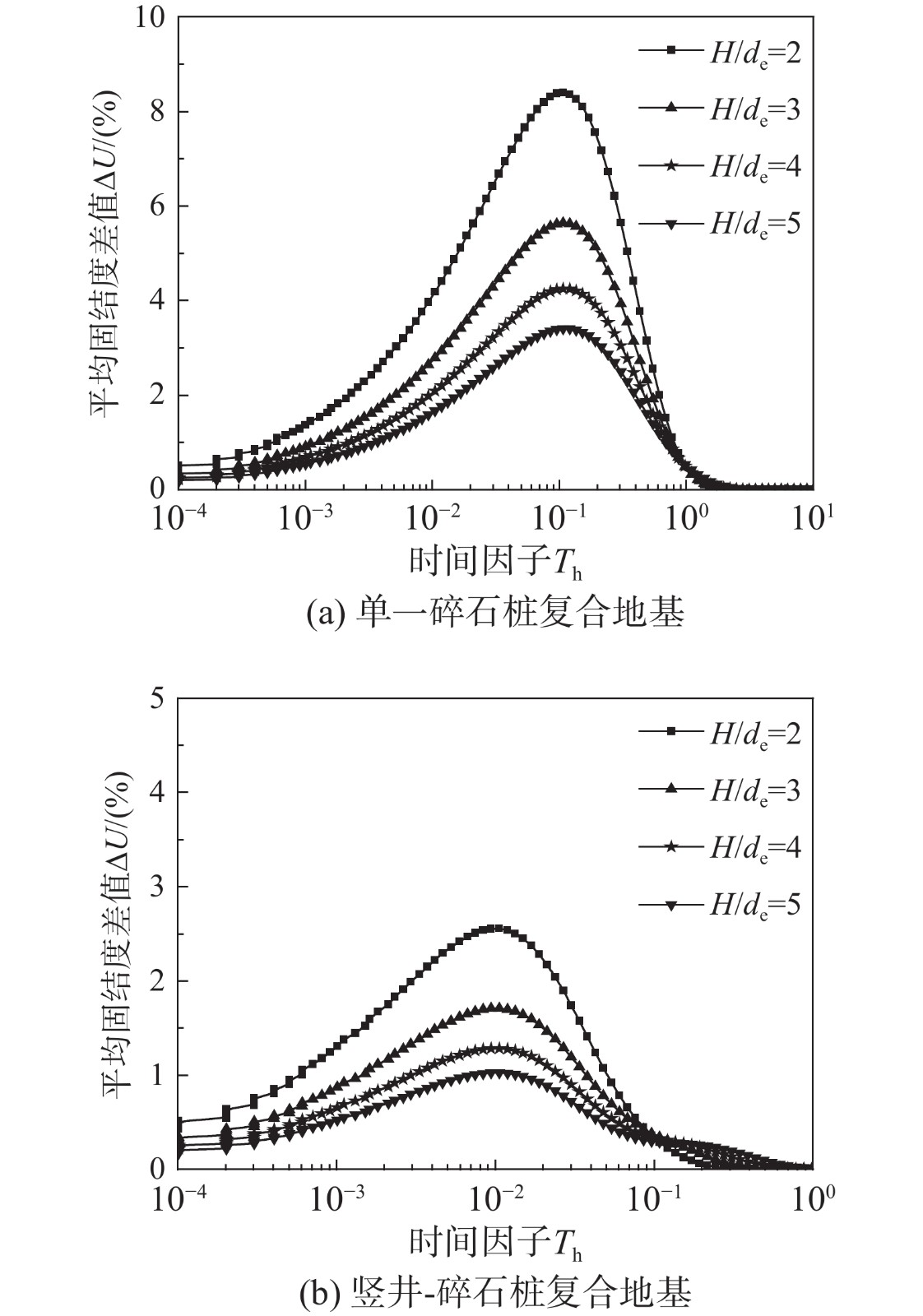
定义$H/{d_{\text{e}}}$为长径比。图8纵坐标为考虑土体内竖向渗流与不考虑土体内竖向渗流间固结度的差值$\Delta U$。无论是仅设置碎石桩的复合地基还是竖井-碎石桩组合型复合地基，两者间的差值都随着长径比值的增大而减小。对仅设置碎石桩的复合地基而言，只有当长径比超过4时，忽略土中竖向渗流引起的固结度差值才会控制在5%以内，即认为此时可以忽略竖向渗流对固结速率带来的影响。而对竖井-碎石桩组合型复合地基而言，即使长径比值为2，忽略竖向渗流引发的固结度偏差均小于5%。造成以上结果的原因是，组合型复合地基中存在两种排水体，孔隙水发生双向渗流，相应地如果忽略土体中的竖向渗流引发的误差会明显降低，故对竖井-碎石桩组合型复合地基而言，土中的竖向渗流对土体的固结作用可以忽略。

图  8  不同$H/{d_{\text{e}}}$下竖向渗流对复合地基固结的影响

Figure  8.  Influences of vertical flow on the consolidation of composite foundation under different $H/{d_{\text{e}}}$

下载: 全尺寸图片 幻灯片

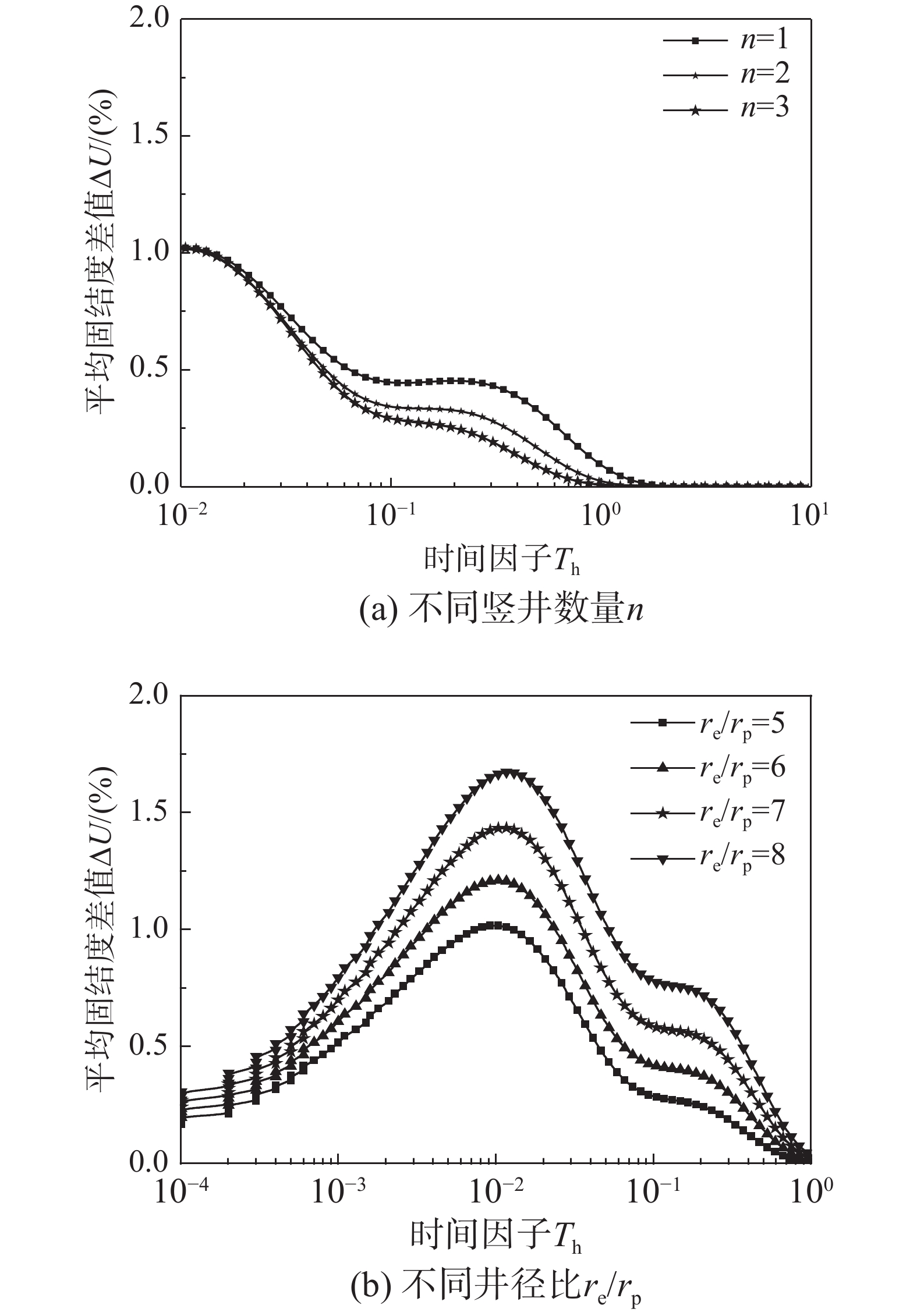
定义${{{r_{\text{e}}}} \mathord{\left/ {\vphantom {{{r_{\text{e}}}} {{r_{\text{p}}}}}} \right. } {{r_{\text{p}}}}}$为井径比。为进一步分析井径比及竖井布置数量对是否忽略竖向渗流的影响，图9(a)给出布设不同数量竖井时考虑土体竖向渗流和忽略竖向渗流间固结度差值随时间发展曲线。可发现布设的竖井数量增加后，竖向渗流对固结速率的影响会越来越小，且两者间的固结度偏差不超过1%。该性状进一步说明土中孔隙水主要发生径向渗流，对于竖向渗流时可忽略。图9(b)不同井径比下考虑竖向渗流和忽略竖向渗流间固结度偏差，可看出随着井径比的增大，考虑与忽略竖向渗流的复合地基固结度差值会增大，原因在于井径比增大时，土中孔隙水的径向排出路径增长，此时会有更多的水流通过竖向排出。但需指出的是，此时两者间的差别仍然不超过2%。综上所述，对于一般的软土层采用竖井-碎石桩复合地基开展地基处理，不论是改变竖井数量，还是改变井径比及长径比的大小，考虑与忽略竖向渗流间固结度的差值都小于5%。故对竖井-碎石桩复合地基而言，其固结计算时可完全忽略土中竖向渗流的影响。

图  9  不同竖井数量及井径比下竖向渗流对固结的影响Fig.9 Influences of vertical flow on the consolidation under different number of vertical drains n and ${{{r_{\text{e}}}}/ {{r_{\text{p}}}}}$

下载: 全尺寸图片 幻灯片

5   工程应用

本文选取马来西亚的一处路堤作为研究对象，将计算结果与实际沉降资料及有限元数值模拟结果对比验证本文解答的可行性。该路堤采用碎石桩对地基进行改良。碎石桩采用正方形布置，其桩间距为2.4 m，桩长为6 m。外部荷载在9 d内施加至36 kPa并保持不变，可等效为瞬时施加。令本文计算模型中竖井的竖向渗透系数k_w等效于土体的竖向渗透系数k_v，从而模拟该工况。土体及桩体各参数由文献[27-28]提供，详见表2。

表  2  工程参数取值

Table  2.  Values of engineering parameters

参数	值		参数	值
总应力$\sigma {\rm /kPa}$	36		碎石桩影响区半径re/m	1.356
地基厚度H/m	6		无量纲碎石桩影响区 半径re/rp	3.39
软土径向渗透 系数kh/(m/s)	3.47×10−9		软土压缩模量Es/kPa	1481
软土竖向渗透 系数kv/(m/s)	1.16×10−9		无量纲碎石桩压缩 模量Ep/Es	10
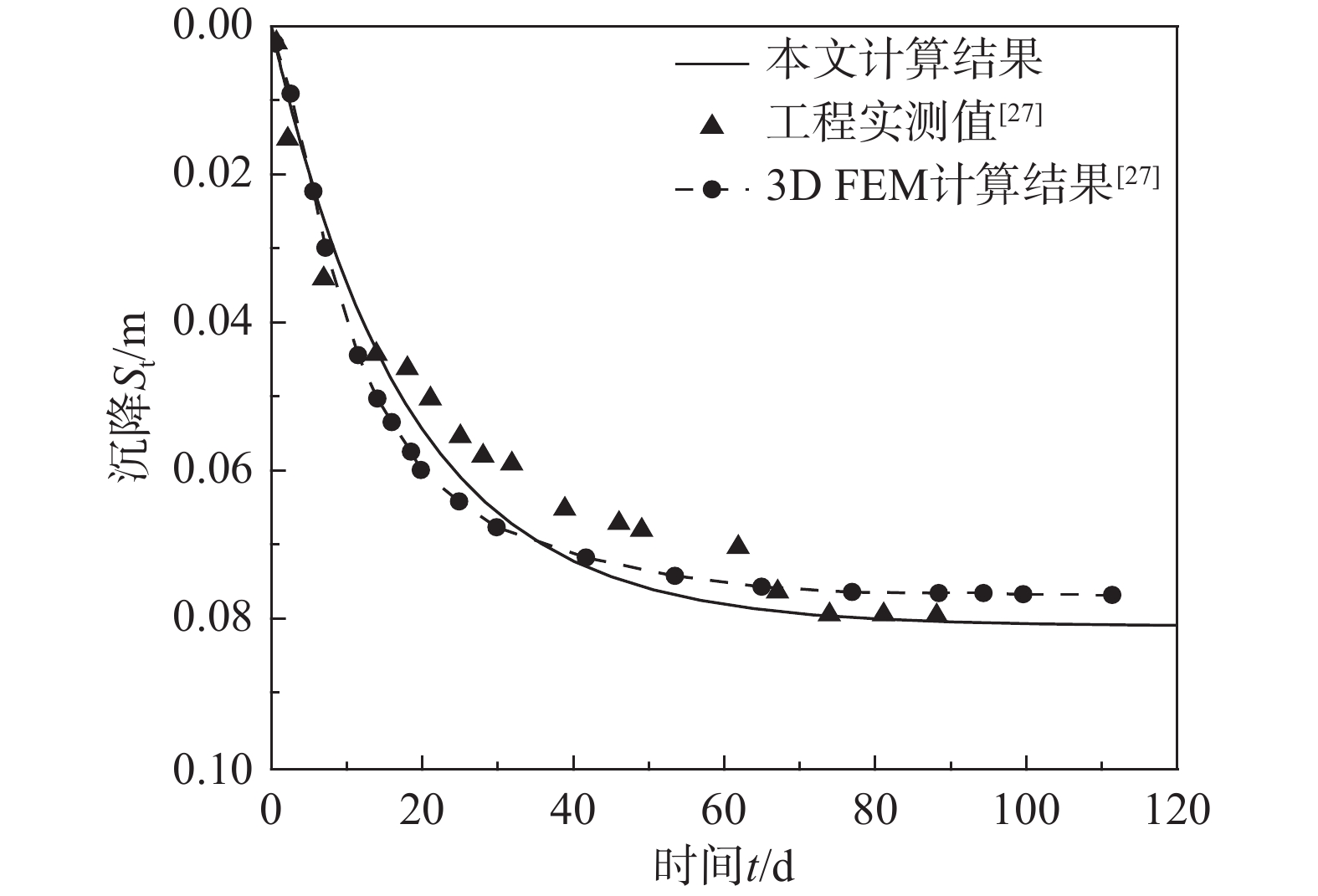
碎石桩渗透 系数kp/(m/s)	1.16×10−4		无量纲桩周涂抹区渗透 系数a1	0.1
桩周土体涂抹比s1	1.15		−	−

下载: 导出CSV 

| 显示表格

从图10可以看出，在固结中期本文预测值高于工程实测值与有限元计算结果。其主要原因为本文未考虑土体及桩体在固结过程中的几何非线性及材料非线性特性，桩体的桩阻随时间与空间的变化以及孔隙水在渗流过程中未完全满足达西定律的事实。在固结前期，本文计算结果与有限元数值计算结果相吻合；在固结后期，本文计算结果与工程实测值结果相吻合。虽然整条固结曲线未能完全对应，但整体能够较好预测实际沉降发展趋势，且计算误差相较于有限元计算结果明显偏小，证明本模型可应用于实际工程中固结度计算与沉降预测。

图  10  本文结果与工程实测值及有限元对比分析

Figure  10.  Comparison of results among the proposal solution, the field data and 3D FEM

下载: 全尺寸图片 幻灯片

6   结论

本文针对竖井-碎石桩复合地基的变形和渗流特性，建立了考虑径竖向渗流的固结模型并获得其解析解，获得如下主要结论：

(1)单一碎石桩复合地基固结解和竖井地基固结解均是所建立的固结模型解析解的特例。

(2)当满足地基承载力要求的情况下，在碎石桩周围打设竖井可有效提高固结速率。竖井和桩体的布置方式可以根据实际情况选择。

(3)打设桩体对周围土体造成的涂抹效应对土体固结速率有明显影响，但竖井引发的涂抹效应对土体固结几乎无影响。

(4)在不同长径比，井径比或者竖井数量下，将考虑土体内竖向渗流与忽略竖向渗流的情况做对比，发现竖向渗流对竖井-碎石桩组合复合地基固结度的影响不超过5%，故可以忽略竖向渗流对固结的影响。