混凝土结构在服役期间可能遭受车、船和落石等冲击荷载作用，纤维增强复合材料(fiber reinforced polymer, FRP)因其轻质高强、施工便捷和耐腐蚀等优异性能被广泛应用于混凝土结构的抗冲击加固改造中^[1-4]。因此，FRP-混凝土界面粘结性能的研究对于冲击荷载作用下FRP外贴加固混凝土结构的评估与设计具有重要的研究价值。已有学者在FRP-混凝土界面的静态粘结滑移性能方面开展了全面深入的试验^[5-7]和数值仿真^[8-9]研究工作，提出了相应的静态粘结滑移模型^[10-12]。本文主要关注FRP-混凝土界面的动态剪切性能。

试验研究方面：YUAN等^[13-17]基于Instron高速拉伸机开展了加载速率在8.33×10⁻⁶ m·s⁻¹~8 m·s⁻¹范围内的碳纤维增强复合材料(carbon fiber reinforced polymer, CFRP)和玄武岩纤维增强复合材料(basalt fiber reinforced polymer, BFRP)与普通和钢纤维增强混凝土界面的动态单剪试验，对应的FRP应变率为2.5×10⁻⁵ s⁻¹~1.7×10² s⁻¹，分析了混凝土强度、钢纤维体积分数和粗骨料粒径等因素对界面动态剪切性能的影响，并拟合得到考虑上述影响因素的界面动态剪切滑移模型。LI等^[18]基于改进的分离式霍普金森压杆开展了动态单剪试验(滑移率为4×10⁻⁶ m·s⁻¹~2 m·s⁻¹)，分析了CFRP粘结宽度、长度和混凝土强度对界面动态剪切性能的影响，得出：混凝土强度增大使界面剪切性能的应变率敏感性降低；粘结宽度减小使其承载能力降低，破坏模式由CFRP与混凝土剥离转变为CFRP断裂。LI等^[19]基于高速拉伸机开展了加载速率在1.67×10⁻⁵ m·s⁻¹~10 m·s⁻¹范围内的单剪试验，对应的FRP应变率为1.2×10⁻⁵ s⁻¹~78.56 s⁻¹，结果表明：界面粘结强度、峰值剪应力和峰值滑移量均随应变率的提高而增大，FRP的有效粘结长度对应变率不敏感。

界面动态剪切滑移模型方面：LI等^[18]基于FRP-混凝土界面的动态单剪试验结果和LU等^[11]建立的双线性准静态界面剪切滑移模型，通过拟合试验数据，引入界面峰值剪应力和断裂能的动态增强因子(dynamic increasing factor, DIF)，建立了界面的动态剪切滑移模型。LI等^[19]基于开展的动态单剪试验，回归分析得到了适用于应变率为5×10⁻⁵ s⁻¹~90 s⁻¹的界面粘结强度、峰值剪应力和峰值滑移量的DIF经验公式。李晓琴等^[20]基于系列FRP-混凝土动态单剪试验的数值模拟结果，引入了界面峰值剪应力和断裂能的DIF，对LU等^[11]提出的准静态双线性界面剪切滑移模型进行了改进，提出了适用于滑移率在10⁻⁴ mm·s⁻¹~10⁰ mm·s⁻¹范围内的FRP-混凝土界面动态剪切滑移模型。LI等^[21]基于商用有限元软件LS-DYNA编写了FRP-混凝土界面动态粘结滑移模型用户自定义程序，对单剪试验、三点弯曲试验和FRP加固钢筋混凝土梁的动态加载试验开展了数值模拟分析和试验对比验证。

数值仿真研究方面：表征FRP-混凝土界面的方式有共节点^[22]、tiebreak接触^[23-24]、cohesive接触^[25]和cohesive单元^[26]。YUAN等^[25]利用LS-DYNA建立了FRP-混凝土界面动态单剪试验的3D有限元模型，利用tiebreak接触描述界面并得到试验^[17]结果的验证。CAGGIANO等^[27]采用零厚度cohesive单元建立了FRP-混凝土单剪试件的有限元模型，基于修正的经典过应力粘塑性方法考虑界面粘结性能的应变率效应，并试验验证了加载速率在0.007 mm·s⁻¹~70 mm·s⁻¹范围内零厚度cohesive单元表征界面的准确性。肖云逸和章子华^[28]利用ABAQUS开展了加载速率在0.2 kN·s⁻¹~200 kN·s⁻¹范围内的FRP-混凝土动态单剪试验的数值模拟，对应的应变率范围为1.5×10⁻³ s⁻¹~10⁻¹ s⁻¹，界面采用零厚度cohesive单元并得到试验^[26]验证。

综上，目前针对高加载速率下FRP-混凝土界面动态剪切滑移模型和剪切剥离的数值模拟研究工作相对较少，FRP-混凝土界面的数值表征方法尚不统一，且界面动态剪切滑移模型的准确性和适用性有待进一步验证。本文针对FRP-混凝土界面的动态剪切滑移关系开展理论模型和数值模拟工作。首先基于4组FRP-混凝土动态单剪试验数据和LS-DYNA中*MAT_COHESIVE_MIXED_ MODE_ELASTOPLASTIC_RATE材料模型，建立了耦合应变率效应的界面动态剪切滑移模型；然后，基于上述模型，对另外3组FRP-混凝土动态单剪试验进行了数值模拟，通过对比界面剪切滑移关系、荷载-位移曲线和FRP应变时程，检验建立模型和参数计算方法的适用性；最后应用上述模型对FRP加固RC板和梁的落锤冲击试验进行了数值模拟分析，评估了常用的FRP-混凝土界面表征方法(共节点、tiebreak和cohesive)的适用性。本文工作可为冲击荷载作用下FRP外贴加固混凝土结构的评估与设计提供参考。

1   动态剪切滑移模型

本节基于YUAN等^[13-15]和LI等^[19]开展的FRP-混凝土界面动态单剪试验，对商用有限元分析程序ANSYS/LS-DYNA R11中*MAT_COHESIVE_MIXED_MODE_ELASTOPLASTIC_RATE(*MAT_240)材料模型参数进行标定，建立了耦合应变率效应的界面动态剪切滑移模型。

1.1   模型建立

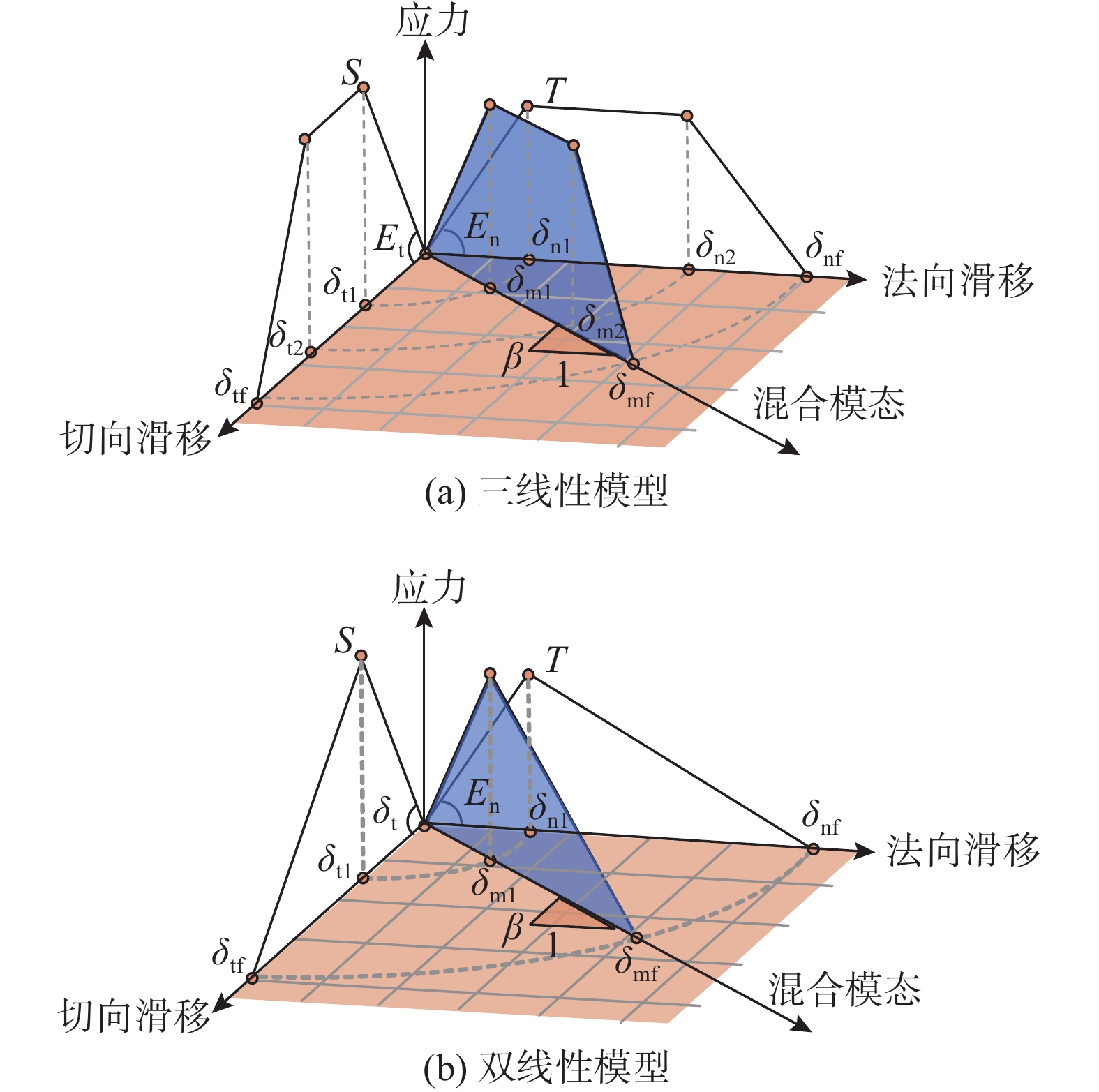
ANSYS/LS-DYNA中可用于描述FRP-混凝土界面的材料模型有：*MAT_138、*MAT_184、*MAT_185、*MAT_186、*MAT_240和*MAT_279，其中仅*MAT_240能够考虑应变率效应，其本构模型可表示为三线性牵引-分离关系，由线弹性上升段，平台段以及线性下降段组成，如图1(a)所示。图中：S和T、E_t和E_n、${\delta _{{\rm{t1}}}}$和${\delta _{{\rm{n1}}}}$、${\delta _{{\rm{t}}2}}$和${\delta _{{\rm{n}}2}}$、${\delta _{{\rm{tf}}}}$和${\delta _{{\rm{nf}}}}$分别为界面的剪切和法向拉伸的强度、刚度、屈服滑移量、失效起始滑移量和失效滑移量。G_p和G_c分别为平台段覆盖的面积和曲线包裹的总面积，即界面变形塑性阶段的断裂能和界面总断裂能。该模型可退化为双线性模型，即：${\delta _{{\rm{t}}1}} = {\delta _{{\rm{t}}2}}$和${\delta _{{\rm{n}}1}} = {\delta _{{\rm{n}}2}}$，分别代表界面的剪切和拉伸峰值滑移量，如图1(b)所示。

图  1  界面牵引-分离关系

Figure  1.  Traction-separation relationships of the interface

下载: 全尺寸图片 幻灯片

*MAT_240材料模型通过考虑界面峰值剪应力和断裂能的应变率效应来表征动态剪切滑移关系，其耦合应变率效应的界面峰值剪应力S和界面断裂能G_2C表达式分别为：

式中：$\dot \varepsilon$为应变率；S和S₀分别为当前和准静态界面峰值剪应力；${\dot \varepsilon _{\rm{S}}}$为界面峰值剪应力的转换应变率；G_2C和G_{2C_0}分别为当前和准静态界面断裂能；G_{2C_INF}为界面断裂能的上限值；S₁和${\dot \varepsilon _{\rm{G}}}$为拟合参数。其中，S₀和G_{2C_0}由FRP-混凝土界面准静态剪切试验确定，S₁、${\dot \varepsilon _{\rm{S}}}$、G_{2C_INF}和${\dot \varepsilon _{\rm{G}}}$通过试验数据拟合确定。以S₀和G_{2C_0}为基准对式(1)和式(2)进行归一化处理，为：

式中，DIF_S和DIF_G分别为界面峰值剪应力和断裂能的动态增强因子，即分别为动态和准静态界面峰值剪应力之比，以及动态和准静态界面断裂能之比。

1.2   模型参数确定

基于YUAN等^[13-15]和LI等^[19]开展的FRP-混凝土界面动态单剪试验，对式(3)和式(4)进行拟合，拟合结果如图2、式(5)和式(6)所示。

图  2  界面峰值剪应力和断裂能的DIF

Figure  2.  DIF of interfacial bonding strength and facture energy

下载: 全尺寸图片 幻灯片

考虑应变率效应的界面峰值剪应力DIF计算公式：

考虑应变率效应的界面断裂能DIF计算公式：

式中，S₀和G_{2C_0}直接采用准静态相关试验的数据，当试验数据缺乏时可按照LU等^[11]双线性模型确定，如下式所示：

式中：S和S₀分别为界面当前剪应力和峰值剪应力；s、s₀和s_f分别为界面当前滑移量、峰值滑移量和界面失效滑移量；f_t为混凝土抗拉强度；${\beta _{\rm{w}}}$为粘结宽度系数；G_{2C_0}为界面断裂能；b_f和b_c分别为FRP和混凝土试件的宽度。

2   模型验证

本节进一步基于LS-DYNA对LI等^[18]和YUAN等^[16-17]开展的另外3组FRP-混凝土动态单剪试验开展数值模拟，通过对比试验和模拟预测结果，验证建立的FRP-混凝土界面动态剪切滑移模型的适用性。

2.1   试验简介

图3为LI等^[18]和YUAN等^[16-17]的动态单剪试件示意图，a、b和h分别表示混凝土试块的长、宽和高，b_f和L为FRP的粘结宽度和长度，具体试验参数见表1所示。试验^[16-17]中沿FRP表面中心线等间距粘贴六个应变片(P1~P6，间距为30 mm)，P1位于粘结和未粘结区域的边界，P6位于FRP自由端附近，如图3(b)所示。

图  3  单剪试件示意图和有限元模型　/mm

Figure  3.  Diagram of single shear specimen and finite element model

下载: 全尺寸图片 幻灯片

表  1  试验参数

Table  1.  Parameters of tests

试验	长×宽×高 a×b×h/ mm	FRP 粘贴 宽度 bf/ mm	FRP 粘贴 长度 L/ mm	混凝土 单轴抗压 强度/MPa	加载速率/ (mm·s−1)
LI等[18]	190×100×100	33	150	32	0.8/8/80
YUAN等[16]	300×150×150	40	200	22.40/30.14/42.34	1000/8000
YUAN等[17]	300×150×150	40	200	30.14	1000/3000/5000/8000

下载: 导出CSV 

| 显示表格

2.2   有限元模型

利用LS-DYNA建立了表1试验的3D有限元模型，YUAN等^[16-17]试验的有限元模型如图3(b)~图3(c)所示。混凝土采用*MAT_272 (Riedel-Hiermaier-Thoma模型，即RHT模型)^[29]，该模型嵌入了与压力相关的弹性极限面、失效面方程和残余强度面方程，主要用于描述混凝土在冲击荷载作用下初始屈服强度、失效强度及残余强度的变化规律。FRP采用*MAT_54材料模型，具体取值见表2。以LI等^[18]的单剪试件编号为例，32 MPa-0.8 mm·s⁻¹表示试件的混凝土强度为32 MPa，加载速率为0.8 mm·s⁻¹。混凝土采用8节点缩减积分实体单元，FRP采用4节点壳单元，界面采用8节点零厚度cohesive单元，界面模型参数取值如表3所示。对混凝土的前后表面施加固定边界条件，对CFRP面外z方向施加位移约束，采用位移加载方法对CFRP加载，如图3(c)所示。

表  2  单剪试验中FRPs材料参数

Table  2.  Material parameters of FRPs in single shear tests

试验	密度/ (kg·m−3)	泊松比	抗拉强度/ MPa	弹性模量/ GPa	失效 应变	厚度/ mm
LI等[18]	1600	0.1	750	82.7	0.009	0.50
YUAN等[16]	1600	0.1	1333	72.0	0.019	0.12
YUAN等[17]	1600	0.1	1333	73.0	0.0188	0.12

下载: 导出CSV 

| 显示表格

以单剪试件32 MPa-0.8 mm·s⁻¹为例，对数值模拟中单元尺寸进行敏感性分析。模型各部分(混凝土、FRP和粘结界面)的单元尺寸相同，分别为2 mm、2.5 mm、3 mm、4 mm、5 mm、7 mm和10 mm，计算得到的荷载-位移曲线如图4所示。

表  3  单剪试验中界面模型参数

Table  3.  Parameters of the interfacial model in single shear tests

试验	试件编号	准静态界面断裂能 G2C0/(N·mm−1)	界面断裂能上限值 G2C_INF/(N·mm−1)	拟合参数 ${\dot \varepsilon _{\rm{G}}}$/s−1	准静态界面峰值 剪应力S0/MPa	拟合参数 S1/MPa	界面峰值剪应力的 转换应变率${\dot \varepsilon _{\rm{S}}}$/s−1	塑性断裂能 比值FG2
LI等[18]	32 MPa-0.8/8/80 mm·s−1	0.750	2.303	35.777	5.097	4.520	10.786	0.001
YUAN等[16]	22 MPa-1/8 m·s−1	0.570	1.750	35.777	1.765	1.565	10.768	0.001
	30 MPa-1/8 m·s−1	0.945	2.901	35.777	3.130	2.776	10.768	0.001
	42 MPa-1/8 m·s−1	1.050	3.224	35.777	4.830	4.283	10.768	0.001
YUAN等[17]	30 MPa-1/3/5/8 m·s−1	0.795	2.441	35.777	2.155	1.911	10.768	0.001

下载: 导出CSV 

| 显示表格

图  4  网格敏感性分析

Figure  4.  Mesh sensitivity analyses

下载: 全尺寸图片 幻灯片

结果表明：随着网格尺寸的减小，第一个峰值荷载趋近于7.5 kN，当网格尺寸小于3 mm后结果趋于收敛。综合考虑计算效率和精度，采用2.5 mm作为模型粘结区域混凝土、CFRP和界面单元的网格尺寸，混凝土沿z方向网格尺寸为10 mm，如图3(b)所示。

2.3   结果对比

图5(a)~图5(c)分别对比了LI等^[18]和YUAN等^[17]的试验荷载-位移曲线和数值模拟结果，其中荷载和位移均基于FRP应变数据计算得出。可以看出：试验和模拟的荷载-位移曲线形状基本相似，初始斜率吻合较好，模拟预测的极限荷载与试验结果相比，误差均低于6.29%。从图5(c)中可以看出30 MPa-3 m·s⁻¹和30 MPa-8 m·s⁻¹试验和数值模拟曲线有较明显差异。主要原因在于试验中FRP剥离通常发生在混凝土层中，混凝土材料的非均质性导致剥离发生位置随机，进一步导致强动载下剥离过程中FRP的应变抖动；在数值模拟中，通常假设剥离破坏发生在粘结界面中(MAT_240)，无法反映出上述应变的抖动现象。

图  5  试验与模拟的荷载-位移曲线对比

Figure  5.  Comparisons of test and simulated load-displacement curves

下载: 全尺寸图片 幻灯片

图6(a)~图6(c)分别对比了试验与数值模拟得到的界面剪应力-滑移曲线。可以看出：曲线形状基本相似，可分为线性上升段和软化段，且上升段斜率吻合较好。模拟得到的界面峰值剪应力与LI等^[18]试验结果相比，最大偏差为10.9%；与YUAN等^[16]试验结果相比，偏差均不超过3.90%。此外，模拟得到的界面断裂能(曲线包围的面积)与上述两组试验结果的最大误差分别为5.12%和4.9%。

图  6  试验与模拟界面粘结剪应力-滑移曲线对比

Figure  6.  Comparisons of test and simulated interfacial bond stress-slip curves

下载: 全尺寸图片 幻灯片

以YUAN等^[17]试验中30 MPa-5 m·s⁻¹试件为例，图7给出了不同加载时刻的界面损伤和FRP应变云图，其中A~D各时刻对应的荷载-位移状态已标注在图5(b)中。可以看出，加载到A时刻，即约50%极限荷载时，界面单元未出现损伤，FRP未发生剥离，其应变集中于加载端；到B时刻后，即达到约88%的极限荷载后，FRP剥离从加载端向自由端扩展，界面单元损伤和FRP应变也由加载端向自由端发展；从B~C时刻，荷载缓慢增加到极限荷载，界面单元损伤和FRP剥离扩展到粘结区域的中间位置；继续加载到D时刻，荷载基本保持恒定，界面单元完全损伤，FRP与混凝土完全剥离。

图  7  界面损伤和FRP应变云图

Figure  7.  Contours of interfacial damage and FRP strain

下载: 全尺寸图片 幻灯片

图8对比了FRP应变时程的两组试验数据^[16-17]和数值模拟结果。可以看出，试验与模拟得到的FRP应变时程曲线吻合较好，极限FRP应变值的最大误差为12.02%。

从图5、图6和图8的对比可以看出，数值仿真结果与FRP-混凝土动态单剪试验数据吻合较好，从而验证了本文建立的耦合应变率效应的界面动态剪切滑移模型的适用性。

图  8  试验与模拟FRP应变时程曲线对比

Figure  8.  Comparisons of test and simulated FRP strain-time histories

下载: 全尺寸图片 幻灯片

3   模型应用

本节基于提出的界面动态剪切滑移模型，以及常用的FRP-混凝土界面表征方法(共节点、tiebreak接触和cohesive接触)，对FRP布加固RC板^[30]和梁^[31]的落锤冲击试验进行了数值模拟分析，进一步验证提出的界面动态剪切滑移模型描述FRP加固混凝土构件界面的适用性，并对比了四种不同的界面表征方法的计算精度和效率。

3.1   FRP-RC板落锤冲击试验^[30]

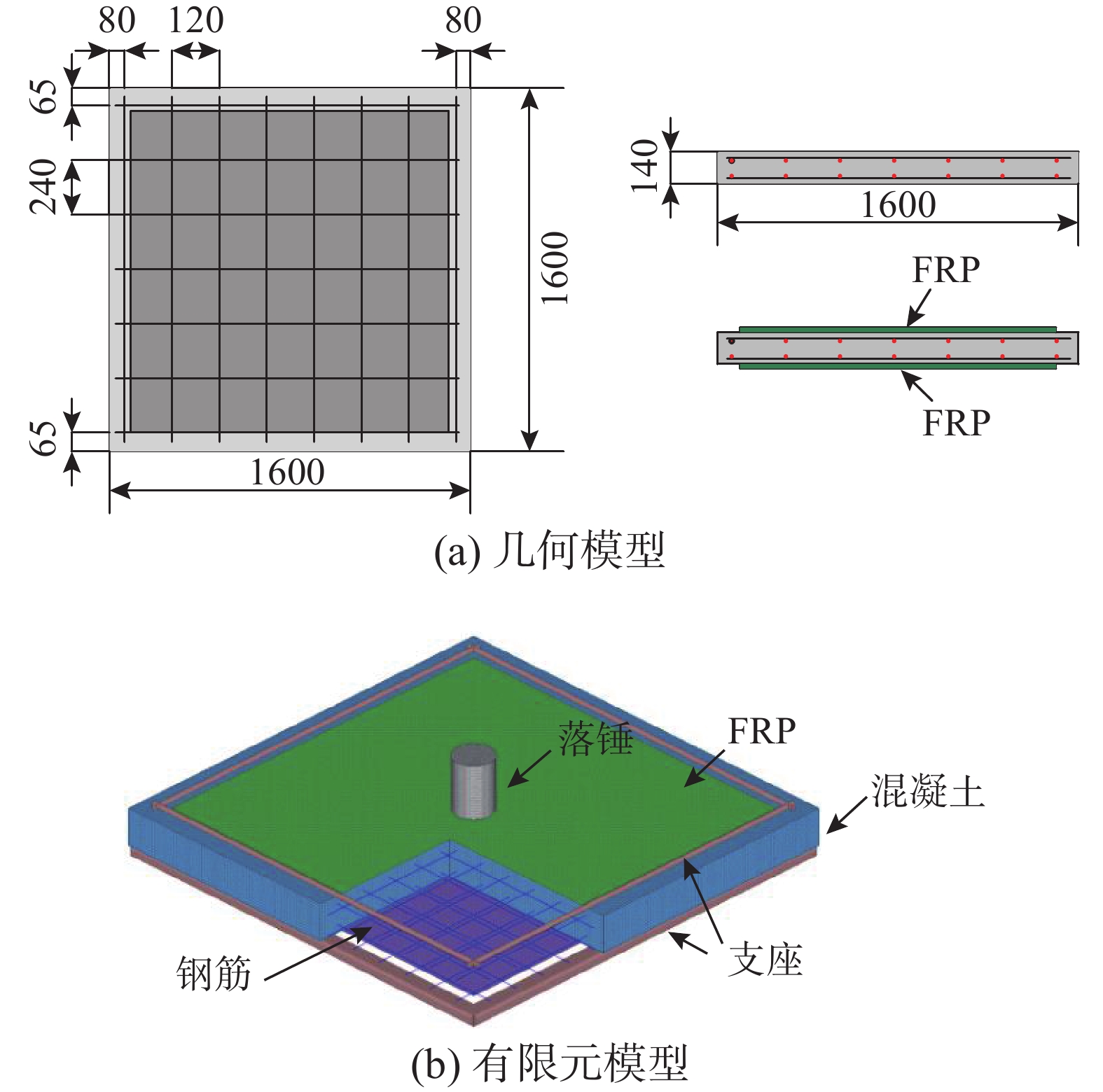
YOO等^[30]试验研究了FRP布加固四边简支RC双向板的抗低速冲击性能，本文选取NC-NF(未加固RC板)和NC-F(双面粘贴FRP布加固的RC板)试验进行数值分析。RC板的长度、宽度和厚度分别为1600 mm、1600 mm和140 mm，采用双层双向配筋，钢筋直径均为13 mm，钢筋的间距分别为240 mm和210 mm，如图9(a)所示。混凝土抗压强度为40 MPa，钢筋的屈服强度为400 MPa，CFRP的抗拉强度为4900 MPa，弹性模量为230 GPa，极限应变为2.1%，厚度为0.34 mm。模型所有部件的网格尺寸均为10 mm，混凝土采用8节点缩减积分实体单元，FRP采用4节点壳单元，界面采用8节点cohesive单元，钢筋采用梁单元，NC-F试件的有限元模型如图9(b)所示。四边约束支座简化为刚体，初始边界条件为完全固定。

图  9  NC-F模型　/mm

Figure  9.  NC-F model

下载: 全尺寸图片 幻灯片

基于LS-DYNA建立了不同FRP-混凝土界面表征方法的四种有限元模型，分别为：考虑界面动态剪切滑移关系的MAT_240模型、共节点模型、采用*CONTACT_TIEBREAK_SURFACE_TO_SURFACE接触的tiebreak接触模型和采用*CONTACT_AUTOMATIC_SURFACE_TO_SURFACE_TIEBREAK OPTION=9接触的cohesive接触模型。混凝土均采用RHT模型，钢筋采用*MAT_3材料模型，失效应变为0.2，CFRP采用MAT_54材料模型，具体参数见表4。MAT_240模型、tiebreak接触模型和cohesive接触模型的具体参数取值见表5，其中tiebreak接触模型仅考虑极限剪切应力，而cohesive接触模型参数与MAT_240模型参数基本相同，其区别仅在于不考虑应变率效应，“—”表示模型无需该参数。需要指出的是，考虑到FRP-混凝土界面法向拉伸数据缺乏且试验中均未观察到法向剥离的现象，有限元模型中未考虑FRP-混凝土界面的法向失效。

表  4  RC板落锤冲击试验中FRP材料参数

Table  4.  Material parameters of FRP of drop weight impact tests on RC slabs

密度/(kg·m−3)	泊松比	抗拉强度/MPa	弹性模量/GPa	失效应变	厚度/mm
1600	0.1	4900	230	0.021	0.34

下载: 导出CSV 

| 显示表格

表  5  RC板落锤冲击试验中界面模型参数

Table  5.  Parameters of the interfacial model of drop weight impact tests on RC slabs

模型类别	准静态界面断裂能 G2C_0/(N·mm−1)	界面断裂能上限值 G2C_INF/(N·mm−1)	拟合参数 ${\dot \varepsilon _{\rm{G}}}$/s−1	准静态界面峰值 剪应力S0/MPa	拟合参数 S1/MPa	界面峰值剪应力的 转换应变率${\dot \varepsilon _{\rm{S}}}$/s−1	塑性断裂能 比值FG2
MAT_240	0.340	1.043	35.777	3.929	3.484	10.768	0.001
tiebreak接触模型	—	—	—	3.929	—	—	—
cohesive接触模型	0.340	—	—	3.929	—	—	—

下载: 导出CSV 

| 显示表格

图10(a)给出了试验和模拟的NC-NF板底面损伤结果，试验中板底出现大量由中心向边缘扩散的辐射状裂纹，且在中心区域存在环向裂纹，板底中心损伤较为严重；从数值模拟损伤云图可以看出，板底部中心损伤严重，且存在大量由板中心向边缘扩展的辐射状损伤条带，破坏模式与试验现象较为吻合。其中数值模拟结果未出现延伸至角部的斜向裂纹，其主要原因在于数值模拟中对试验边界条件进行了一定程度的简化。图10(b)进一步给出了试验和模拟的NC-NF板底中心挠度结果，试验和模拟得的板底最大挠度分别为23.41 mm和20.67 mm，相对误差为11.7%；残余挠度分别为7.75 mm和8.24 mm，相对误差为6.32%，模拟与试验结果吻合较好，验证了未加固RC板有限元模型的准确性。

图  10  NC-NF试验与模拟结果对比

Figure  10.  Comparisons of test and simulation results for NC-NF

下载: 全尺寸图片 幻灯片

基于验证的未加固RC板有限元模型，进一步开展FRP加固RC板的落锤冲击试验的数值仿真分析。图11(a)为NC-F板的试验跨中挠度和四种模型模拟结果的对比，图11(b)~图11(e)分别为四种模型模拟和试验的支座反力时程曲线对比图。由图11(a)对比可以看出，MAT_240模型的最大挠度和残余挠度与试验结果吻合较好，最大挠度偏差仅为2.72%，残余挠度偏差为14.95%；共节点模型由于假定FRP与混凝土之间为完美粘结，高估了二者之间的粘结强度，导致最大挠度和残余挠度相较于试验结果偏小，误差分别达33.49%和48.45%；由于tiebreak接触和cohesive接触模型都不能考虑界面动态力学性能，所得最大挠度和残余挠度均大于MAT_240模型结果，其最大挠度与试验结果误差分别为2.66%和4.34%，相应残余挠度误差分别为26.88%和34.69%。图11(b)~图11(e)可以看出，相较于其他三种界面模型，MAT_240模型得到的支座反力时程曲线与试验吻合最好，其第一个峰值反力相对误差为13.79%。相应的共节点、tiebreak接触和cohesive接触模型的支座反力峰值误差分别为36.05%、5.84%和7.19%。tiebreak和cohesive接触模型得到的接触力抖动更明显，其主要原因可能是接触的强非线性和模型的不连续性。综合对比最大挠度、残余挠度和支座反力等，MAT_240模型结果与试验吻合最好。

图  11  NC-F试验与模拟结果对比

Figure  11.  Comparisons of test and simulation results for NC-F

下载: 全尺寸图片 幻灯片

此外，基于CPU型号为Intel Core i7-8700@3.2 GHz的计算平台，MAT_240、共节点、tiebreak接触和cohesive接触模型的计算时长分别为55 min、42 min、74 min和97 min，MAT_240模型的计算效率略低于共节点模型，高于tiebreak接触和cohesive接触模型。进一步需要指出的是，tiebreak接触算法不能考虑接触界面的损伤软化，而cohesive接触算法考虑了接触界面的损伤软化，因此前者计算效率高于后者。

3.2   FRP-RC梁落锤冲击试验^[31]

KISHI等^[31]对FRP布加固的RC梁开展了一系列落锤低速冲击试验。选取NI-H2.5(未加固的RC梁，落锤冲击高度2.5 m)和CI-H2、CI-H2.5、CI-H3(梁底部粘贴CFRP布，落锤冲击高度分别为2 m、2.5 m和3 m)试验进行数值模拟。图12(a)~图12(b)分别给出了CI-H试件的几何模型和有限元模型。梁的净跨度为3400 mm，宽200 mm，高250 mm，梁上部和下部别配置两根直径为19 mm的纵筋，箍筋直径为10 mm间距为100 mm。NI-H2.5和CI-H试件的混凝土抗压强度分别为32 MPa和33 MPa，CFRP抗拉强度为3400 MPa，弹性模量为245 GPa，极限应变为1.39%，厚度为0.33 mm，NI-H2.5和CI-H模型中钢筋的屈服强度分别取382 MPa和403 MPa，失效应变均为0.2。混凝土、钢筋和CFRP材料模型和网格尺寸与4.1节相同，模型和界面参数分别见表6和表7所示。

图  12  CI-H模型　/mm

Figure  12.  CI-H model

下载: 全尺寸图片 幻灯片

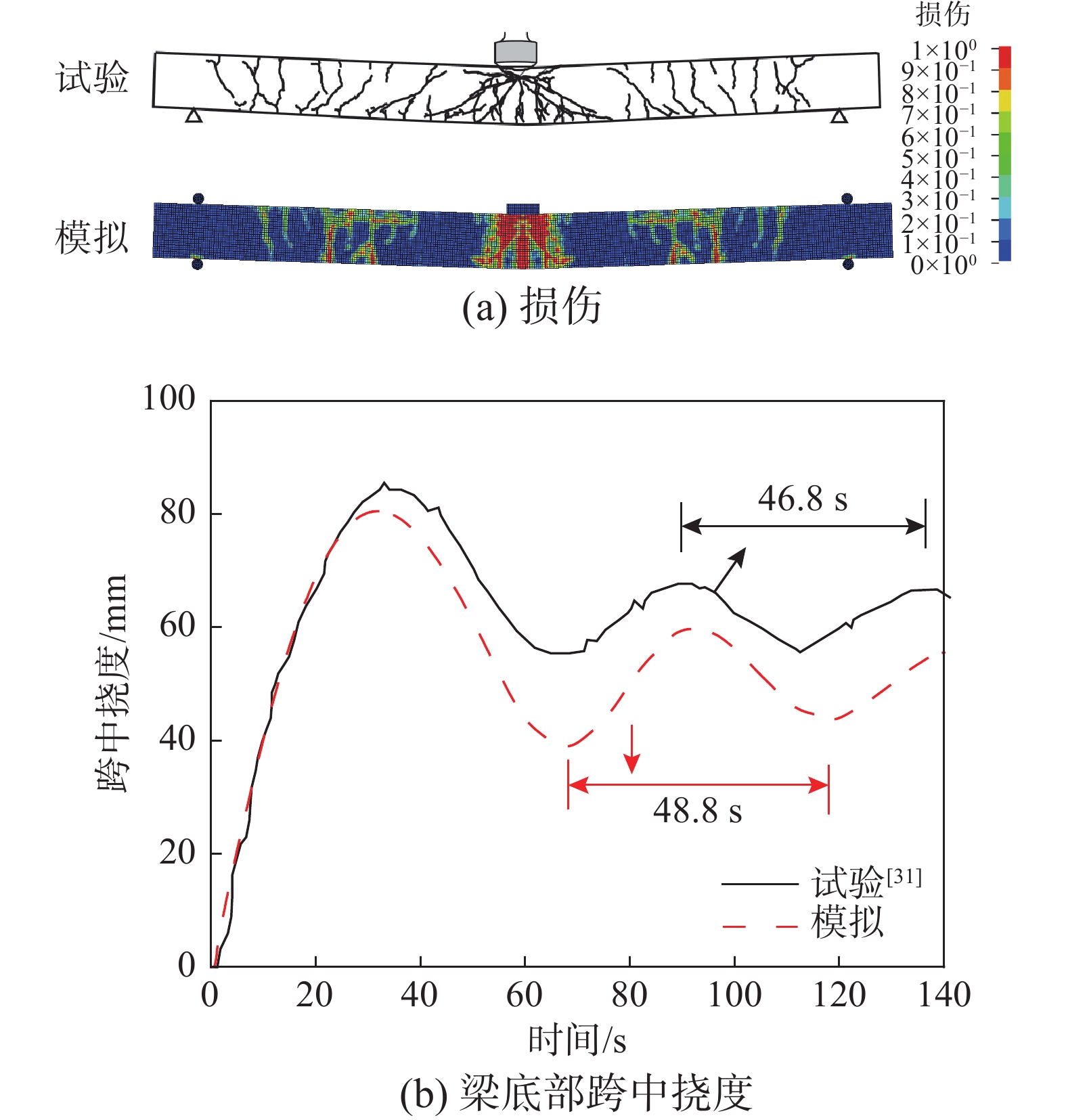
图13(a)给出了试验和模拟的NI-H2.5梁损伤结果，试验中梁出现跨中竖向弯曲裂缝和剪切斜裂缝，支座附近出现从梁上部向下部扩展的竖向裂缝；数值模拟的梁跨中损伤明显，由上向下部发展的裂纹分布于梁1/4跨处，可以看出模拟中板底部损伤与试验结果吻合较好。图13(b)给出了NI-H2.5梁的试验和数值模拟跨中挠度时程，可以看出，试验和模拟得到的最大挠度分别为85.6 mm和80.5 mm，误差为5.96%；振动周期分别为46.8 s和48.8 s，相对误差为4.27%，数值模拟结果与试验结果吻合较好，验证了未加固RC梁有限元模型的准确性。

表  6  RC梁落锤冲击试验中FRP材料参数

Table  6.  Material parameters of FRP of drop weight impact tests on RC beams

密度/(kg·m−3)	泊松比	抗拉强度/MPa	弹性模量/GPa	失效应变	厚度/mm
1600	0.1	3400	245	0.0139	0.33

下载: 导出CSV 

| 显示表格

表  7  RC梁落锤冲击试验中界面模型参数

Table  7.  Parameters of the interfacial model of drop weight impact tests on RC beams

模型类别	准静态界面断裂能 G2C_0/(N·mm−1)	界面断裂能上限值 G2C_INF/(N·mm−1)	拟合参数 ${\dot \varepsilon _{\rm{G}}}$/s−1	准静态界面峰值 剪应力S0/MPa	拟合参数 S1/MPa	界面峰值剪应力的 转换应变率${\dot \varepsilon _{\rm{S}}}$/s−1	塑性断裂能 比值FG2
MAT_240	0.267	0.819	35.777	3.180	3.484	10.768	0.001
tiebreak接触模型	—	—	—	3.180	—	—	—
cohesive接触模型	0.267	—	—	3.180	—	—	—

下载: 导出CSV 

| 显示表格

图  13  NI-H2.5试验与模拟结果对比

Figure  13.  Comparisons of test and simulation results for NI-H2.5

下载: 全尺寸图片 幻灯片

进一步开展FRP加固RC梁的落锤冲击试验的数值仿真分析。图14(a)~图14(c)分别为三种冲击速度下CI-H梁的试验和模拟跨中挠度对比图，图14(d)~图14(f)对比了相应的冲击力时程。以CI-H2.5为例，MAT_240模型的最大挠度误差为2.95%，冲击力峰值误差为10.12%；共节点模型同样由于完美粘结的假定高估了二者之间的粘结强度，导致最大挠度和残余挠度较试验结果偏小，最大挠度和冲击力峰值误差分别达2.07%和10.98%。此外，由于tiebreak接触和cohesive接触模型均不能考虑界面力学性能的应变率增强效应，预测的最大挠度和残余挠度较试验结果偏大，其最大挠度误差分别为3.58%和4.96%，冲击力峰值误差分别达8.04%和10.51%。从图14(a)~图14(c)中可进一步得出，梁挠度时程曲线的初始斜率基本相同，表明采用不同界面模型对梁抗弯刚度的影响不大。挠度产生偏差的主要原因为不同界面模型采用的剪切滑移关系不同。通过上述对比进一步表明建立的FRP-混凝土界面动态剪切滑移模型适用于FRP加固RC梁的抗冲击数值模拟分析。此外，基于同样的计算平台，以CI-H2为例，上述MAT_240、共节点、tiebreak接触和cohesive接触模型的计算时长分别为238 min、234 min、255 min和325 min，得出MAT_240模型的计算效率略低于共节点模型，高于tiebreak接触和cohesive接触模型。

图  14  CI-H系列试验模拟与试验结果对比

Figure  14.  Comparisons of simulation and test results of CI-H tests

下载: 全尺寸图片 幻灯片

4   结论

针对FRP-混凝土界面的动态剪切滑移关系，本文开展了理论分析和数值仿真工作，主要工作和结论如下：

(1)通过对FRP-混凝土动态剪切试验数据进行分析，基于*MAT_COHESIVE_MIXED_ MODE_ELASTOPLASTIC_RATE材料模型，建立了FRP-混凝土界面动态剪切滑移模型，给出了应变率效应参数的计算方法。

(2)基于建立的界面动态剪切滑移模型，对FRP-混凝土动态单剪试验进行了数值模拟，通过对比界面粘结滑移关系、荷载-位移曲线和FRP应变时程曲线，验证了建立的FRP-混凝土界面动态剪切滑移模型、参数计算和数值模拟方法的适用性。

(3)进一步开展了FRP加固RC板和梁落锤冲击试验的数值模拟，与常用的FRP-混凝土界面表征方法(共节点、tiebreak接触和cohesive接触)进行了对比。结果表明：共节点建模方法预测的板和梁跨中挠度偏小；tiebreak和cohesive接触未考虑界面的应变率效应，跨中挠度偏大。提出的界面动态剪切滑移模型结果与试验数据吻合较好，且计算效率与共节点模型相比无明显降低。