RESEARCH ON HYDRODYNAMIC PERFORMANCE OF INTEGRATED SYSTEM OF PERMEABLE BREAKWATER AND OSCILLATING WATER COLUMN WAVE ENERGY DEVICE
-
摘要:
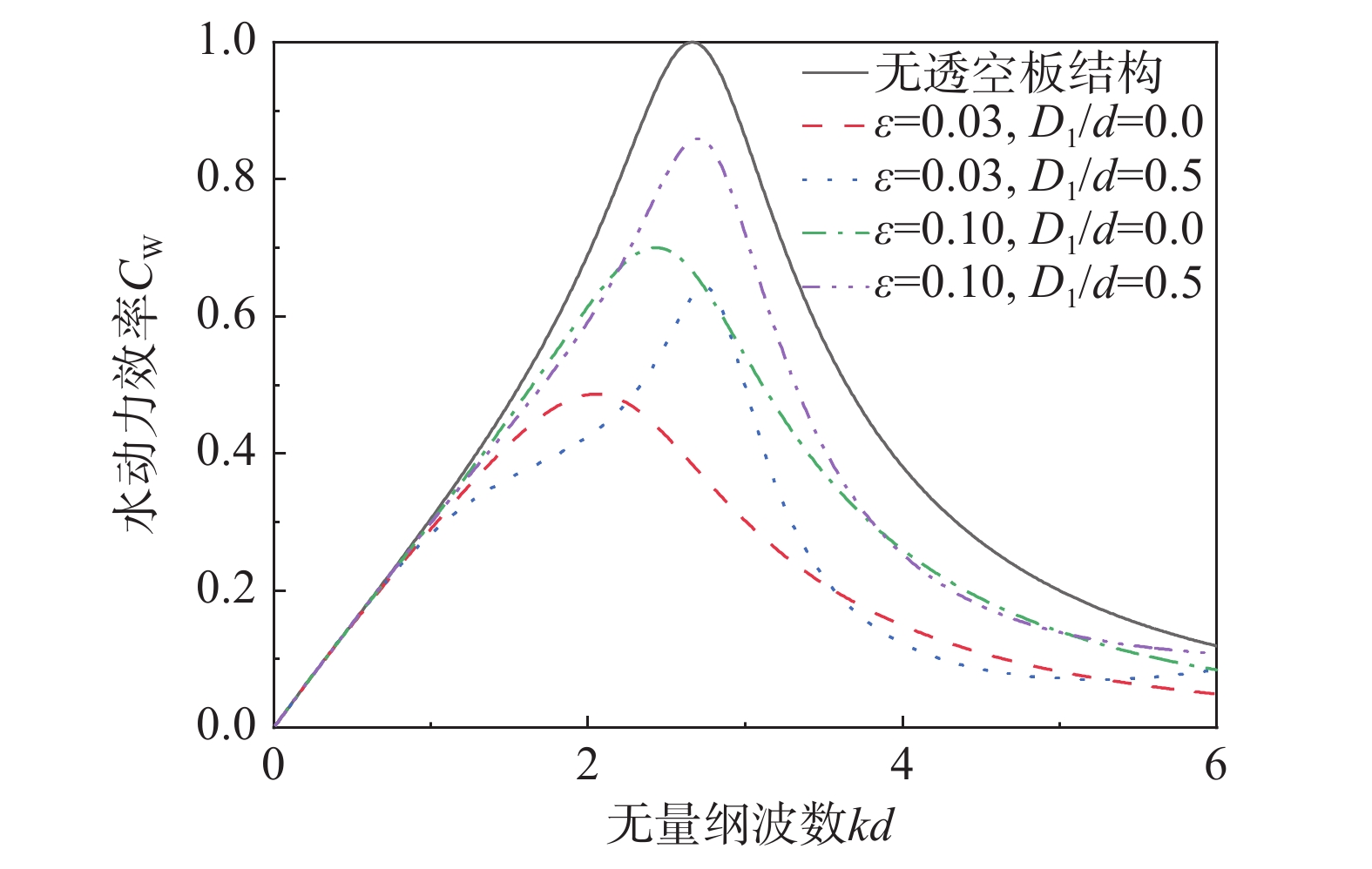
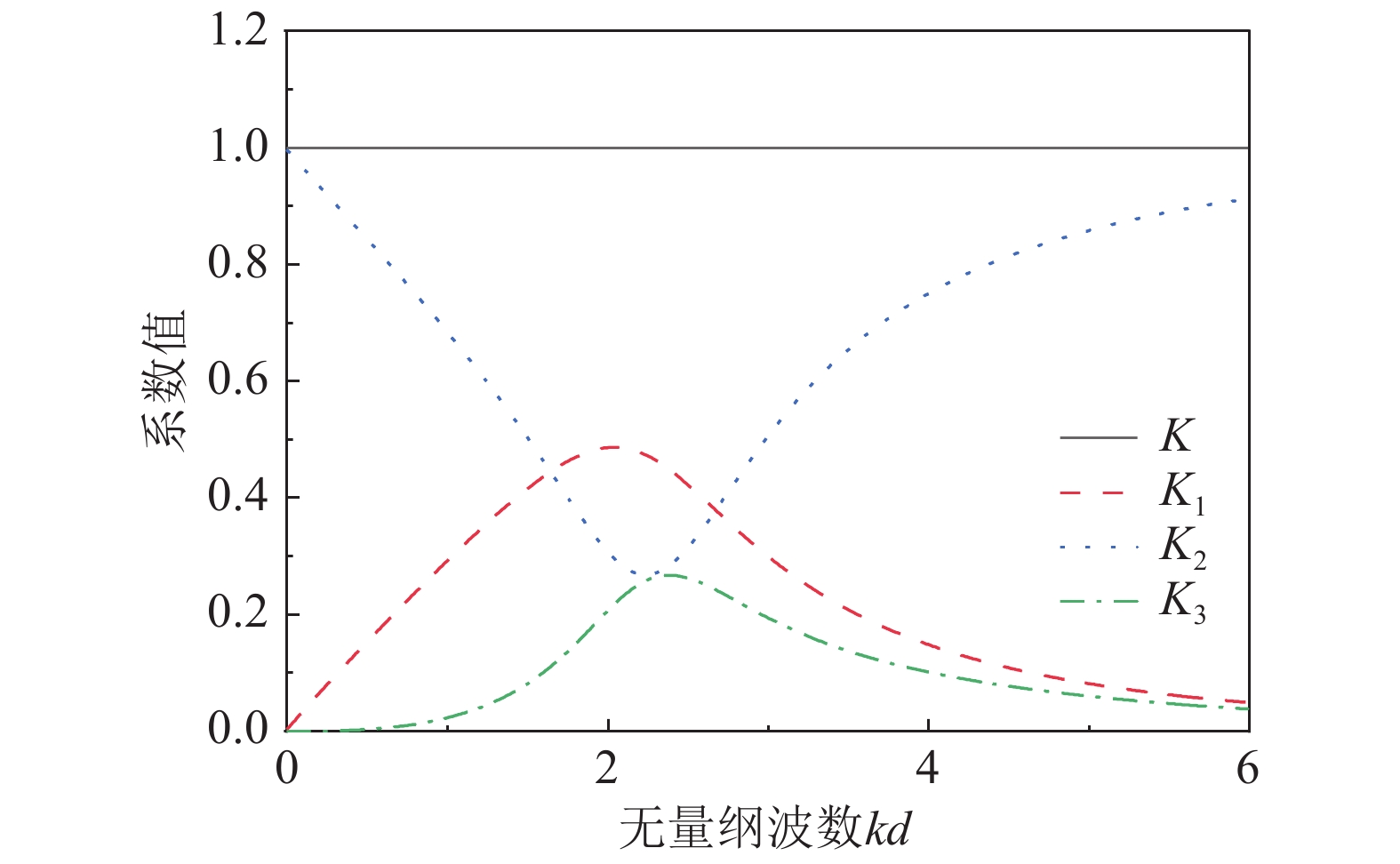
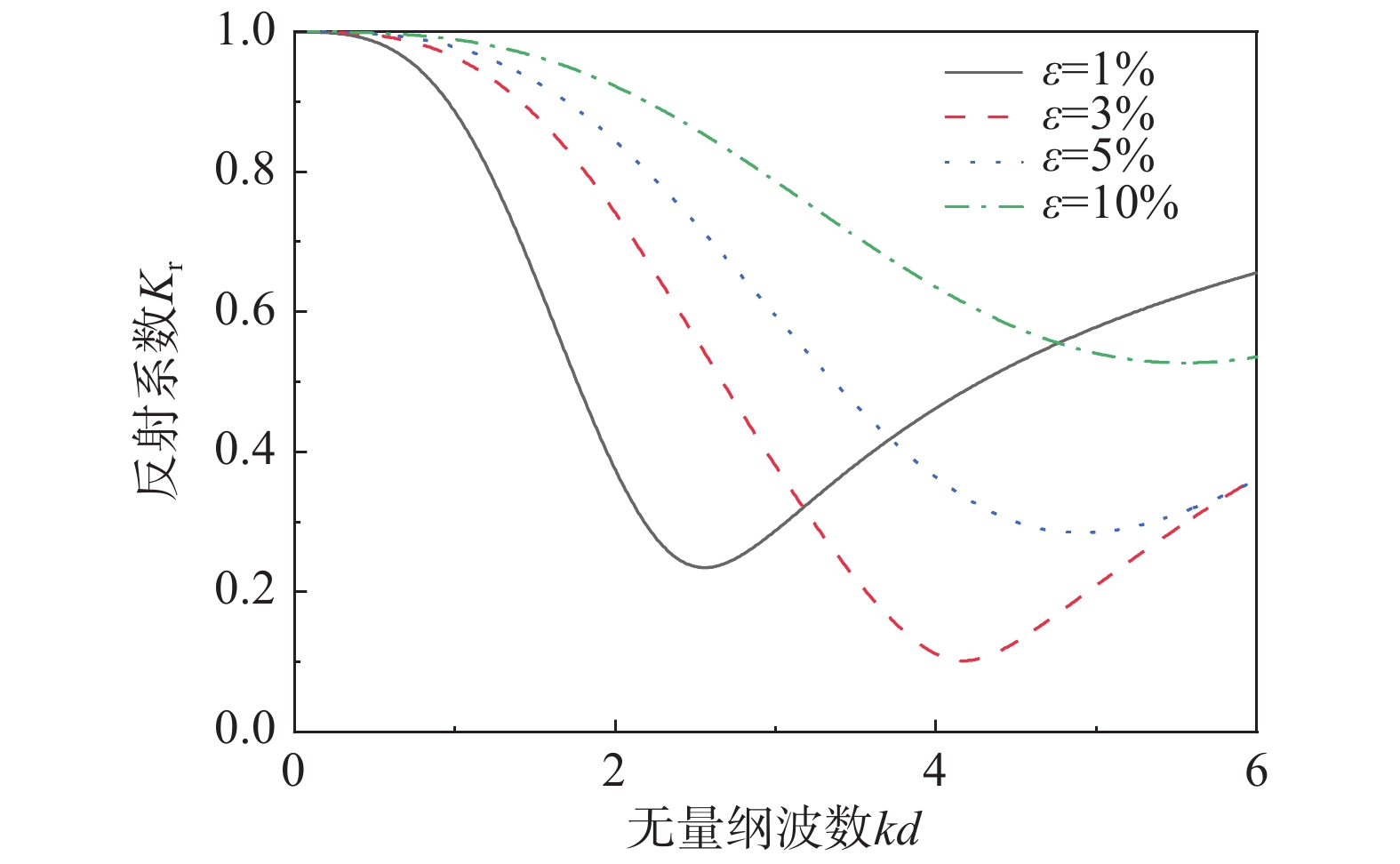
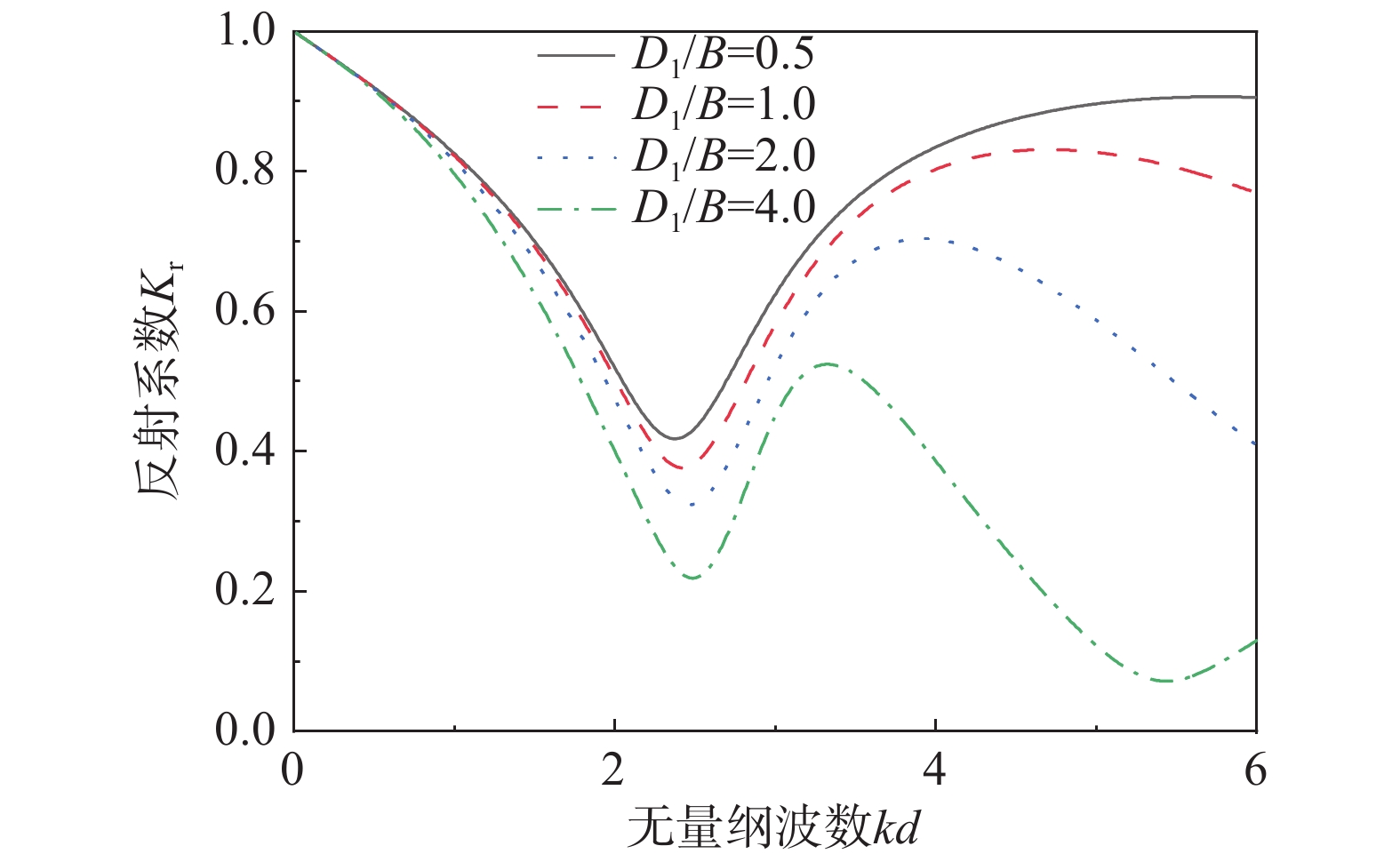
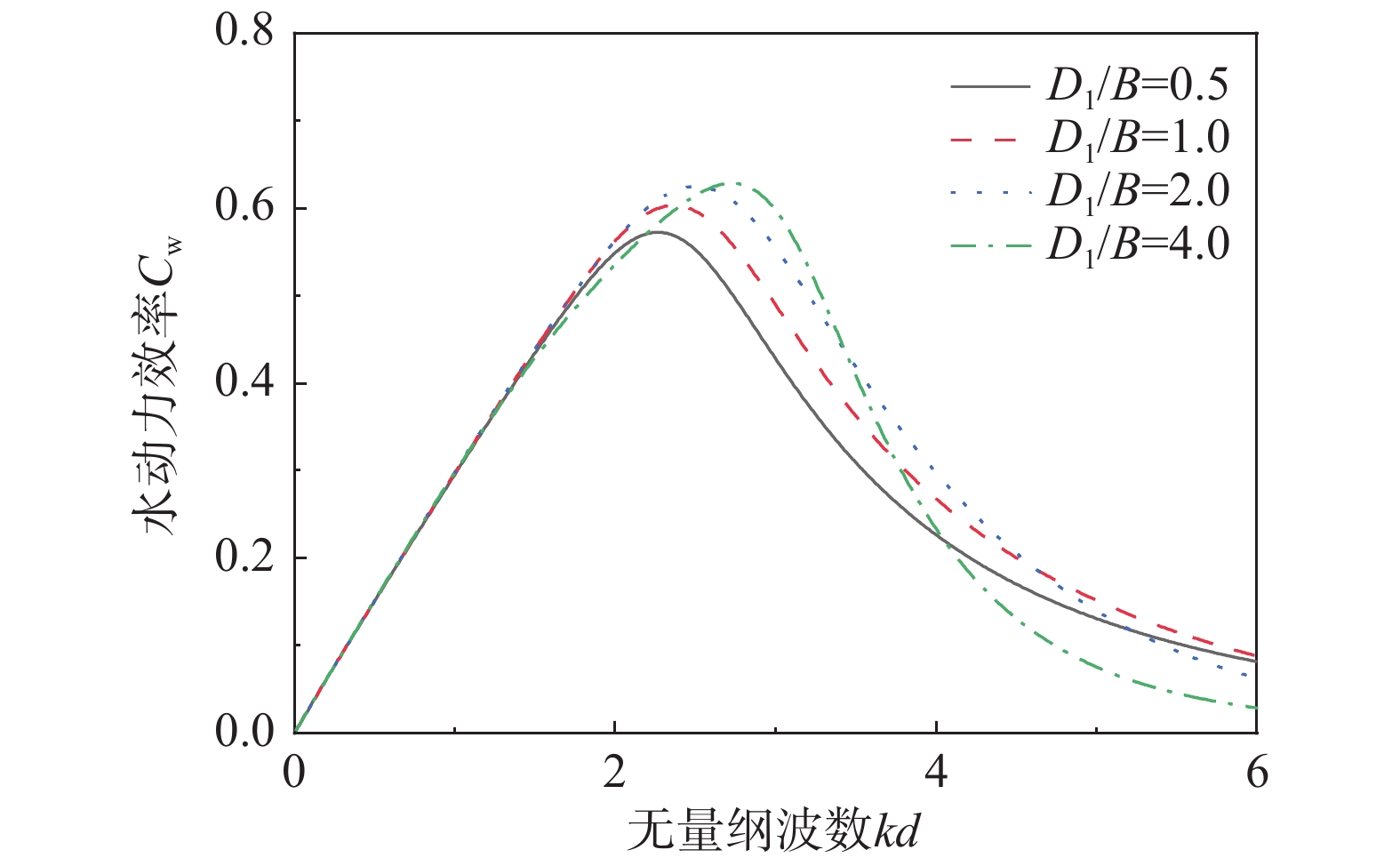
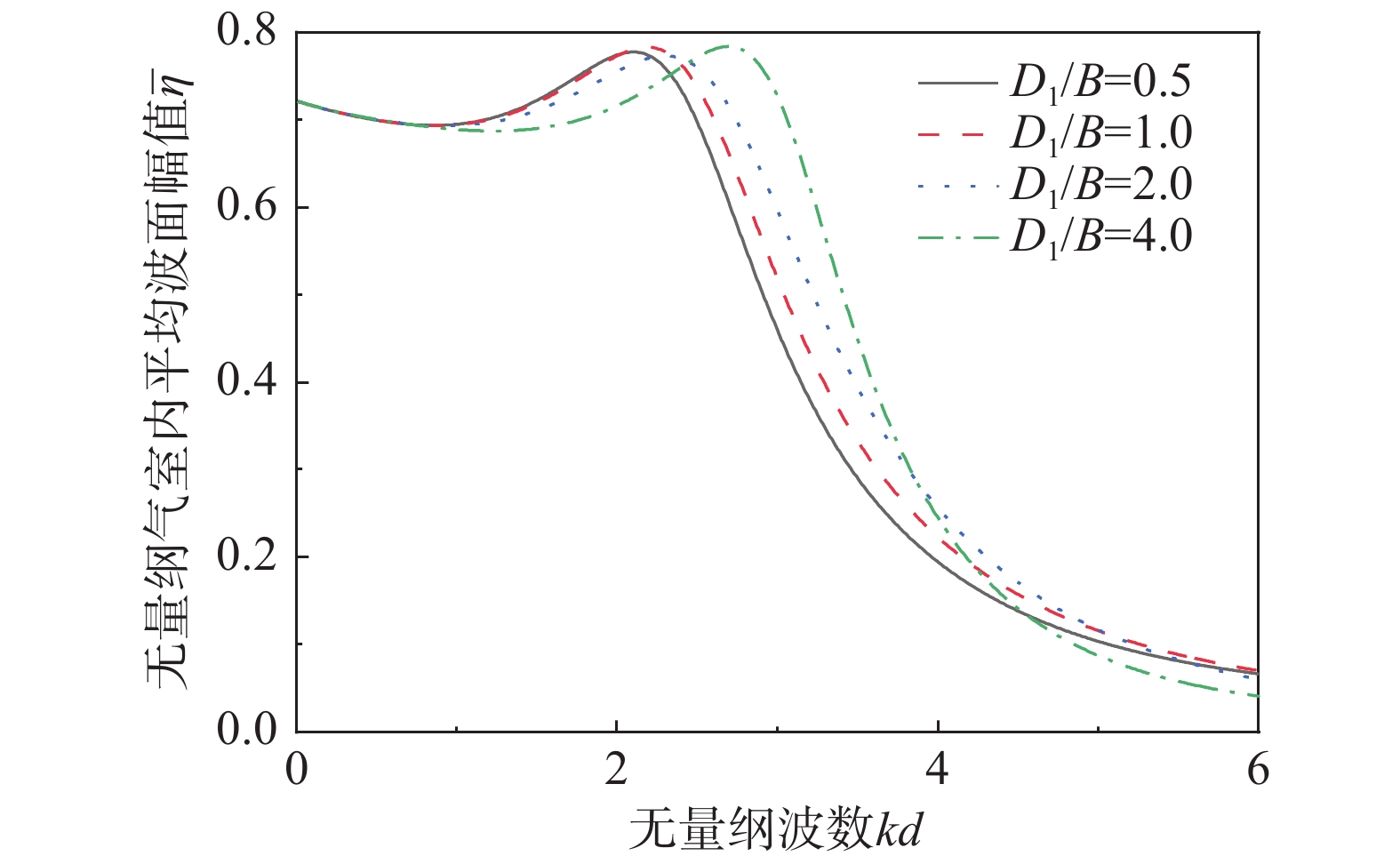
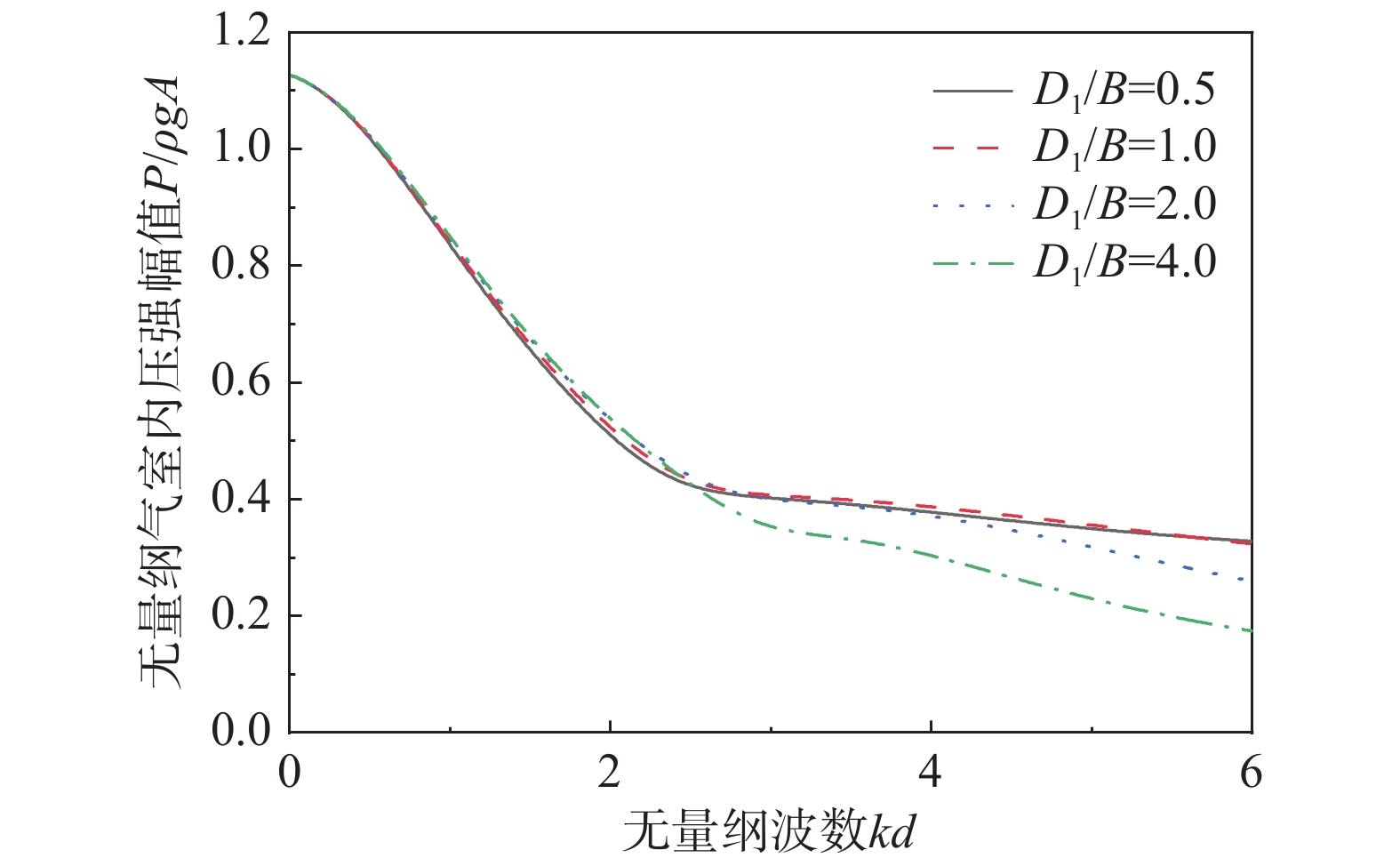
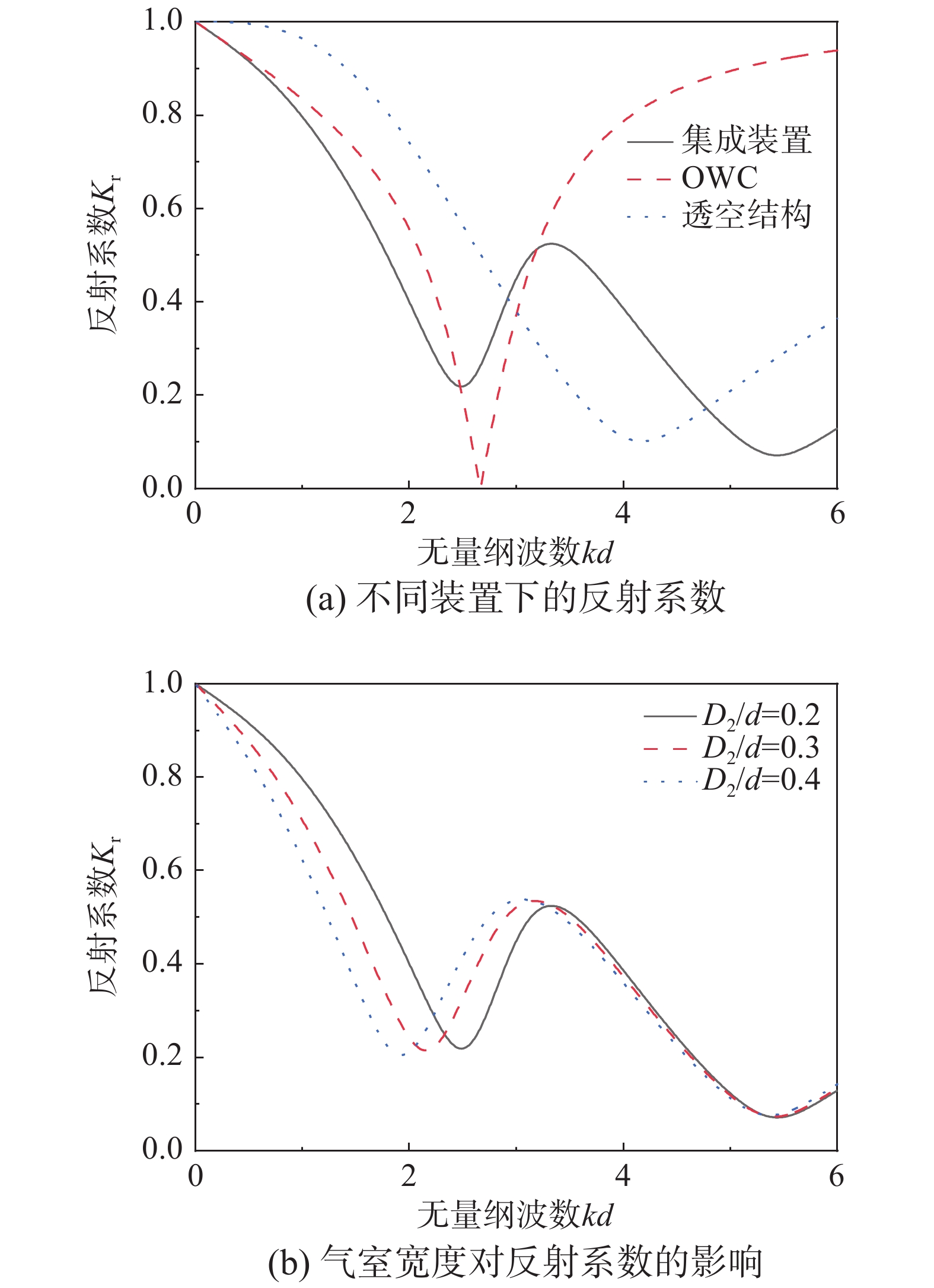
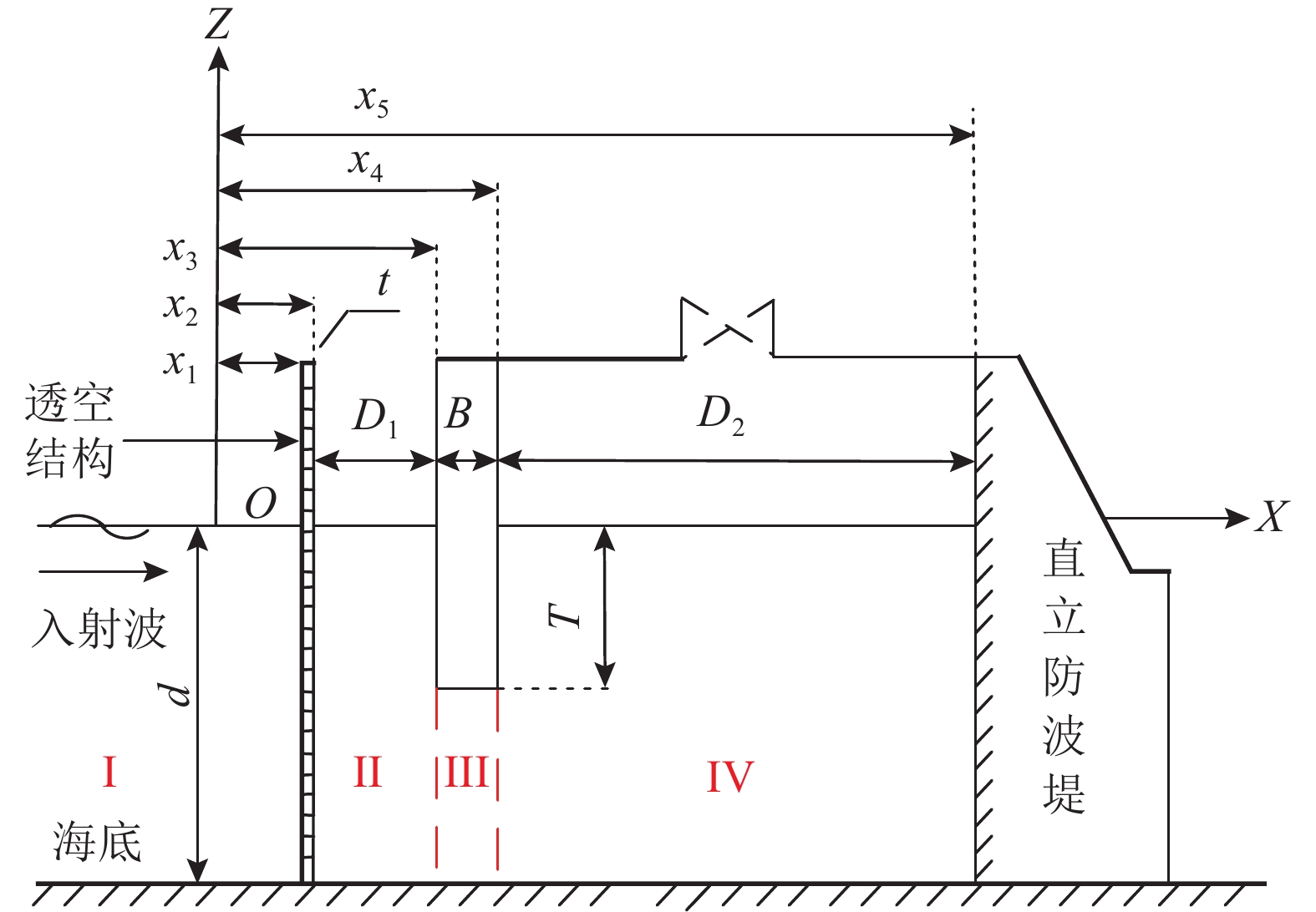
开发和利用可再生能源是解决能源危机的重要途径。波浪能作为一种可再生能源引起了世界各国的关注，其中振荡水柱(Oscillating Water Column, OWC)式波能装置是一种应用最广泛的波浪能转换技术。关于OWC的研究多集中于如何提高能量转换效率，但是由于海况的复杂性，装置面临很大的生存压力，提高装置的生存能力变得愈加重要。透空式防波堤形式已经有很多应用，它对高频短波消浪效果很好，对低频长波则较差，而振荡水柱波能装置对长波吸收能力较强。该研究将透空式防波堤和OWC装置有效结合起来，基于线性势流理论，运用分离变量法和特征函数匹配法建立了解析模型，研究了单独透空式防波堤形式下，不同开孔率对反射系数的影响；之后研究了集成系统下透空结构与OWC装置距离对反射系数、水动力效率等的影响，并与单独透空式防波堤和单独OWC装置对比，说明集成装置消浪的优越性。
Abstract:The development and utilization of renewable energy is an important way to deal with the growing energy crisis. As one form of renewable energy, wave energy has attracted the attention of many countries all over the world. The oscillating water column (OWC) wave energy device is one of the most widely used wave energy conversion technologies. Most of the previous research on OWC focuses on how to improve its energy conversion efficiency. However, the survivability of the device faces great challenges due to the complexity of sea conditions. Thus, it is important to improve the survivability of the device. The permeable breakwater has been widely implemented. It exhibits good performance in dissipating high-frequency short waves, but a poor performance in dissipating low-frequency long waves. The oscillating water column wave energy device has a strong ability to absorb long waves. In this study, the permeable breakwater and the OWC device were effectively combined. Based on the linear potential flow theory, an analytical model has been established by using the separation of variables method and the eigenfunction expansion matching method. The effect of porosity of a solitary permeable breakwater on the reflection coefficient was studied. Then, the effect of the distance between the permeable structure and the OWC device on the reflection coefficient and the hydrodynamic efficiency was studied. Compared with the solitary permeable breakwater and solitary OWC device, the integrated system exhibited superiority in terms of wave elimination.
-
-
![]()
图 2 开孔率与透空板和前墙距离对水动力效率的影响
Figure 2. Effect of porosity and distance between porous plate and front wall on power extraction efficiency
![]()
图 3 不同系数 K、K1、K2和K3随kd的变化
Figure 3. Variations of different coefficients K, K1, K2 and K3 with kd
![]()
图 4 本文水动力效率结果与实验数据的对比
Figure 4. Comparisons of power extraction efficiency between the present results and the experimental data
![]()
图 6 透空板与前墙距离对反射系数的影响
Figure 6. Effect of distance between porous plate and OWC front wall on reflection coefficient
![]()
图 7 透空板与前墙距离对水动力效率的影响
Figure 7. Effect of distance between porous plate and front wall on power extraction efficiency
![]()
图 8 透空板与集成装置距离对气室内平均波面幅值的影响
Figure 8. Effect of distance between porous plate and front wall on average wave surface amplitude in air chamber
![]()
图 9 透空板与前墙距离对气室内压强幅值的影响
Figure 9. Effect of distance between porous plate and front wall on pressure amplitude in air chamber
-
[1] BORTHWICK A G L. Marine renewable energy seascape [J]. Engineering, 2016, 2(1): 69 − 78. doi: 10.1016/J.ENG.2016.01.011
[2] GUNN K, STOCK-WILLIAMS C. Quantifying the global wave power resource [J]. Renewable Energy, 2012, 44: 296 − 304. doi: 10.1016/j.renene.2012.01.101
[3] WANG C, MA T, ZHANG Y L. Semi-analytical study on an integrated-system with separated heaving OWC and breakwater: Structure size optimization and gap resonance utilization [J]. Ocean Engineering, 2022, 245: 110319. doi: 10.1016/j.oceaneng.2021.110319
[4] CHENG Y, DU W M, DAI S S, et al. Hydrodynamic characteristics of a hybrid oscillating water column-oscillating buoy wave energy converter integrated into a π-type floating breakwater [J]. Renewable and Sustainable Energy Reviews, 2022, 161: 112299. doi: 10.1016/j.rser.2022.112299
[5] ZHOU Y, ZHANG C W, NING D Z. Hydrodynamic investigation of a concentric cylindrical OWC wave energy converter [J]. Energies, 2018, 11(4): 11040985. doi: 10.3390/en11040985
[6] NING D Z, ZHOU Y, ZHANG C W. Hydrodynamic modeling of a novel dual-chamber OWC wave energy converter [J]. Applied Ocean Research, 2018, 78: 180 − 191. doi: 10.1016/j.apor.2018.06.016
[7] NING D Z, WANG R Q, CHEN L F, et al. Experimental investigation of a land-based dual-chamber OWC wave energy converter [J]. Renewable and Sustainable Energy Reviews, 2019, 105: 48 − 60. doi: 10.1016/j.rser.2019.01.043
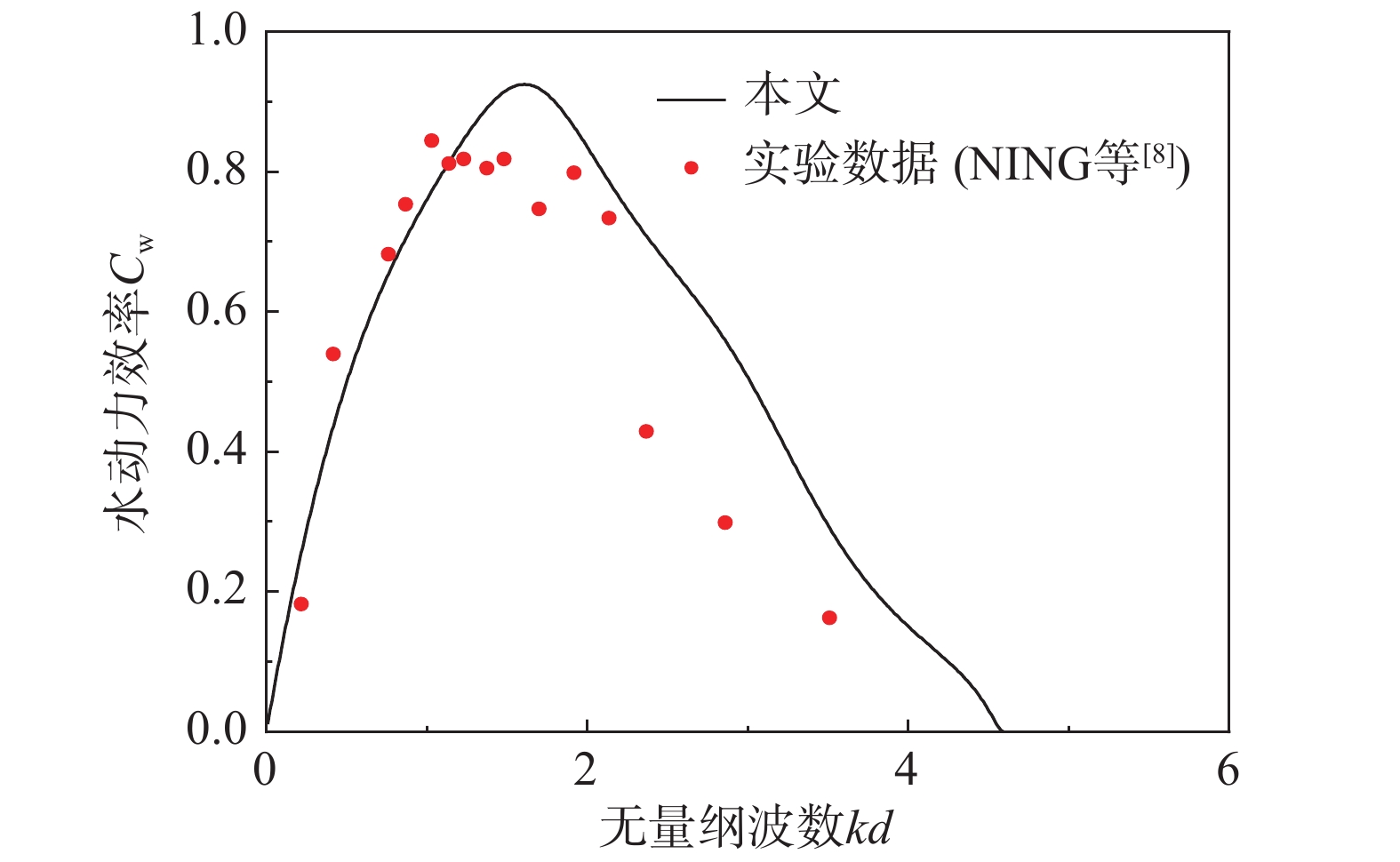
[8] NING D Z, WANG R Q, ZOU Q P, et al. An experimental investigation of hydrodynamics of a fixed OWC wave energy converter [J]. Applied Energy, 2016, 168: 636 − 648. doi: 10.1016/j.apenergy.2016.01.107
[9] 王荣泉, 宁德志, MAYON R. 双气室振荡水柱波能装置水动力特性研究[J]. 水动力学研究与进展, 2020, 35(1): 37 − 41. WANG Rongquan, NING Dezhi, MAYON R. Hydrodynamic investigation on the dual-chamber OWC wave energy converter [J]. Chinese Journal of Hydrodynamics, 2020, 35(1): 37 − 41. (in Chinese)
[10] 韩新宇, 罗鑫, 董胜. 复式防波堤断面尺度对波浪爬高的影响研究[J]. 工程力学, 2019, 36(增刊 1): 261 − 267. doi: 10.6052/j.issn.1000-4750.2018.05.S051 HAN Xinyu, LUO Xin, DONG Sheng. Research on the effect of dounle-slope breakwater section dimensions on wave runup [J]. Engineering Mechanics, 2019, 36(Suppl 1): 261 − 267. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.05.S051
[11] 任家崟, 韩新宇, 董胜. 防波堤帷幕尺度对波浪力和消浪性能的影响研究[J]. 工程力学, 2023, 40(5): 245 − 256. doi: 10.6052/j.issn.1000-4750.2021.10.0822 REN Jiayin, HAN Xinyu, DONG Sheng. Research on the influence of different scales of curtain breakwater on wave force and wave elimnation [J]. Engineering Mechanics, 2023, 40(5): 245 − 256. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.10.0822
[12] YU X P, CHWANG A T. Water waves above submerged porous plate [J]. Journal of Engineering Mechanics, 1994, 120(6): 1270 − 1282. doi: 10.1061/(ASCE)0733-9399(1994)120:6(1270)
[13] LEE M M, CHWANG A T. Scattering and radiation of water waves by permeable barriers [J]. Physics of Fluids, 2000, 12(1): 54 − 65. doi: 10.1063/1.870284
[14] SAHOO T, LEE M M, CHWANG A T. Trapping and generation of waves by vertical porous structures [J]. Journal of Engineering Mechanics, 2000, 126(10): 1074 − 1082. doi: 10.1061/(ASCE)0733-9399(2000)126:10(1074)
[15] NING D Z, ZHAO X L, TENG B, et al. Wave diffraction from a truncated cylinder with an upper porous sidewall and an inner column [J]. Ocean Engineering, 2017, 130: 471 − 481. doi: 10.1016/j.oceaneng.2016.11.043
[16] GENG B L, WANG R Q, NING D Z. The wave absorption efficiency of multi-layer vertical perforated thin plates [J]. Journal of Hydrodynamics, 2018, 30(5): 898 − 907. doi: 10.1007/s42241-018-0103-9
[17] QIAO D S, FENG C L, YAN J, et al. Numerical simulation and experimental analysis of wave interaction with a porous plate [J]. Ocean Engineering, 2020, 218: 108106. doi: 10.1016/j.oceaneng.2020.108106
[18] 赵玄烈, 宁德志, 康海贵, 等. 波浪作用下上部带有透空结构的圆筒垂向水动力特性的解析研究[J]. 工程力学, 2017, 34(12): 239 − 247. doi: 10.6052/j.issn.1000-4750.2016.08.0643 ZHAO Xuanlie, NING Dezhi, KANG Haigui, et al. Analytical study on the vertical hydrodynamics of a truncated cylinder with upper porous wall and inner column [J]. Engineering Mechanics, 2017, 34(12): 239 − 247. (in Chinese) doi: 10.6052/j.issn.1000-4750.2016.08.0643
[19] 李玉成, 滕斌. 波浪对海上建筑物的作用[M]. 3版. 北京: 海洋出版社, 2015: 50 − 85. LI Yucheng, TENG Bin. Wave action on maritime structures [M]. 3rd ed. Beijing: China Ocean Press, 2015: 50 − 85. (in Chinese)
[20] MARTINS-RIVAS H, MEI C C. Wave power extraction from an oscillating water column along a straight coast [J]. Ocean Engineering, 2009, 36(6/7): 426 − 433.
下载:
计量
- 文章访问数: 220
- HTML全文浏览量: 61
- PDF下载量: 55
