TRUNCATED CONE FLAT INDENTATION METHOD FOR PREDICTING MECHANICAL PROPERTIES OF METALLIC MATERIALS
-
摘要:
相比锥形、球形压入，平面压入具有稳定的接触区域及明显的线弹性阶段，有利于更稳定地实现材料弹塑性参数的一体化表征。然而，目前金属材料的圆柱平面压入方法仍存在接触刚度偏大、压头变形损耗较高等不足，故有必要发展一种接触刚度更小、预测精度更高的力学性能测试方法。该文采用含60°锥角的圆台形平压头，通过有限元分析证明了其相比圆柱形平压头具有对钝化的弱敏感性。基于能量等效理论，建立了关联压头端部直径、压入功、压入深度和弹塑性参数的圆台形平面压入(Truncated Cone Flat Indentation, TCFI)理论模型，通过较大参数范围的有限元计算和5种金属材料的圆台形平面压入试验、拉伸试验验证了该模型的准确性。
Abstract:Compared with conical and spherical indentation, flat indentation has a stable contact area and an obvious linear elastic stage, which are beneficial to realize the integrated characterization of material elastic-plastic parameters more stably. However, the current flat indentation testing methods of metal materials still have some shortcomings, such as large contact stiffness and high deformation loss of indenter. Therefore, it is necessary to develop a mechanical property testing method with smaller contact stiffness and higher prediction accuracy. A truncated cone flat indenter with a cone angle of 60° was thusly used, and the finite element analysis proved that it has a weak sensitivity to tip rounding compared with cylindrical flat indenter. Based on the equivalent energy principle, a theoretical model of truncated cone flat indentation (TCFI) was established, which is associated with the diameter of the indenter, indentation work, depth, and the elastic-plastic parameters of materials. A testing method for mechanical properties of materials based on the model was proposed, and the accuracy of the method was verified by the finite element calculation in a wide range of parameters and by the indentation test and tensile test of 5 metallic materials.
-
材料力学测试是通过采集材料变形、破坏等特性信息来获取其力学性能的过程，是保障和维护工程、产品等质量安全的有效手段，也是研究和发展新材料及与其密切相关的新技术、新工艺、新产品的基础技术[1]。一般地，材料的弹塑性力学性能采用传统单轴拉伸方法进行评估。然而，随着小尺度构件、焊接结构及服役结构力学性能测试需求的日益增长，传统拉伸等方法受构件尺度限制，难以取样并有效地开展试验[2]。压入方法因其微损、原位、微区且制备简单等优点，快速发展并成为材料力学性能测试的热点。
传统压入测试仅用于测量材料的硬度[3-4]，直到1992年，OLIVER和PHARR[5]开发出可连续测量压入载荷和压入深度的仪器化压入技术，并提出确定材料弹性模量的经典方法：Oliver-Pharr法，至此基于各种不同几何形状压头的压入方法不断发展并开始应用于材料力学性能的测试。目前，球形压入和锥形压入的材料拉伸性能测试方法已得到较多应用[6-10]，而平面压入多应用于材料蠕变性能的获取[11]，基于平面压入的拉伸性能测试方法有待进一步研究。
平压头即压头端部为平面的一类压头，如圆柱形、圆台形、棱台形压头，相比球形压头、锥形压头，平压头具有一些独特的优势。一方面，相比同尺度的球形、锥形压头，平压头压入材料时接触面内的晶粒最多，其测试结果更稳定，不易受显著影响微/纳米压入测试的因素干扰[12]。另外，平面压入弹塑性材料的载荷-深度曲线具有明显的线性阶段及屈服点[13]，可以更容易、更准确地与拉伸特性建立联系。目前，通过平面压入获取材料拉伸性能的手段大多基于1955年SHIELD[14]基于滑移线理论提出的压入平均接触应力pm与屈服应力σy的关系式：
pm=Cσy (1) 式中：C为约束因子。SHIELD仅给出了刚塑性材料满足Tresca屈服准则时C的精确解为2.875，对于更具代表性的von Mises屈服准则[15]，C取3.285。然而所有金属工程材料都表现出弹塑性应变硬化而非刚塑性，因此在不同的研究中约束因子的取法不尽相同。RICCARDI等[12]基于恒定的约束因子C=3，确定了包括纯金属、钢和耐火合金几种材料的屈服应力；LU等[16]通过有限元分析了铝合金和耐冲击聚苯乙烯(HIPS)在平压头压入下pm与σy的关系，确定了两种材料不同的约束因子(铝合金为3，HIPS为2.6)；此外，SCIBETTA等[17]提出C有关硬化指数n的近似关系；BRUTTI[18]考虑材料在纯弹性和纯塑性的两个极限状态，建立了C关于材料塑性应变εP和泊松比ν的关系式，预测结果较好，然而该模型包含了174个参数，较为复杂；HU等[19-20]基于空腔模型[21]推导出约束因子与空腔半径的关系，然而此半径难以通过试验获得，约束因子C仍需通过试验标定。总之，这些方法大多仅能对材料的屈服强度σy进行估算，无法预测材料的硬化规律，且约束因子C的取值缺少统一的表述，普适性不足。有必要开发一种简单、准确的平面压入测试方法对材料拉伸性能进行预测。
目前圆台形平面压头已在材料硬度表征中逐渐得到应用，典型的是常用于铝合金、铜合金等金属材料的韦氏硬度测试方法[22]，采用锥角60°的圆台形平面压头，在一定的试验力作用下将压头压入材料，用压入的深度表示材料的硬度。基于这种压头的材料硬度测试手段已较为成熟，但利用此类压头获取金属材料的弹塑性力学性能的研究却很少。此外，随着锥角减小(如低于50°)，摩擦对载荷-深度曲线影响增加；而当锥角增大时，钝形压头载荷偏高，易造成过度的压头自身变形影响测试精度等。因此，本文采用含60°锥角的圆台形平压头，通过有限元分析证明了弹塑性压入载荷-深度响应对压头钝化的敏感性远小于目前大量使用的圆柱形平压头，因此可降低压头对加工精度的要求，延长压头使用寿命，提高测试结果的准确性。基于能量等效理论[23-25]，将压入形变能表示为积分中值点应变能密度与有效变形域体积的乘积，对积分中值点应变和有效变形域体积进行合理假设，建立了关联压头直径、压入功、压入深度和材料弹塑性参量的理论模型，经过若干次有限元计算确定了适用于铝合金、铜合金、钛合金、碳钢等在内大部分金属材料的模型参数，提出了圆台形平面压入获取金属材料拉伸性能的测试方法，并通过较大参数范围的有限元计算以及5种金属材料的压入试验、拉伸试验验证了该方法的可行性。
1 圆台形平面压入方法
1.1 理论模型
目前，在大量金属材料力学性能的表征研究中，通常采用式(2)所示线弹-幂硬化本构方程(Hollomon幂律模型)来描述材料的应力-应变关系：
σ={Eε,σ⩽ (2) 式中：σ为应力；ε为应变。该模型可由三个弹塑性参数描述：弹性模量E、屈服应力σy、硬化指数n。若能准确地获取上述参数，即可实现对材料单轴应力-应变关系等的预测。
对于各向同性、均匀连续弹塑性金属材料的圆台形平面压入，在连续的变形域中必然存在积分中值点M (xM, yM, zM)，使得该点的材料代表性体积单元(Representative Volume Element, RVE)的应变能密度uM与有效变形域Ω的体积V的乘积等于圆台形平面压入载荷作用下的形变能U。根据积分中值定理：
U = {u_M}\,V (3) 根据von Mises等效原理，处于复杂应力状态的M点材料RVE的应变能密度可等效转化为简单应力状态(单轴应力状态)下RVE的能量密度，即：
{u_M} = \int_0^{{\varepsilon _{ij\left| M \right.}}} {{\sigma _{ij\left| M \right.}}} {\text{d}}{\varepsilon _{ij}} = \int_0^{{\varepsilon _{{\text{eq}}\left| M \right.}}} {{\sigma _{{\text{eq}}\left| M \right.}}} {\text{d}}{\varepsilon _{{\text{eq}}}} (4) 式中，σij|M、εij|M以及σeq|M、εeq|M分别为中值点M处复杂应力状态下以及等效单轴应力状态下的应力和应变。将式(2)所示Hollomon模型代入式(4)进行积分可得M点应变能密度：
{u_M}{\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} \frac{{{E^n}\sigma _{\text{y}}^{1 - n}}}{{1 + n}}\left( {\varepsilon _{{{\rm{eq}}}\left| M \right.}^{1 + n} - \frac{{1 - n}}{2}\varepsilon _{\text{y}}^{1 + n}} \right) (5) 考虑到圆台形平面压入条件下压头附近材料处于高度应力集中状态，应变远大于屈服应变εy，则式(5)中\varepsilon _{\text{y}}^{1 + n} 相比\varepsilon _{{{\rm{eq}}}\left| M \right.}^{1 + n} 足够小，可以忽略，由此结合式(3)和式(5)可得材料形变能U为：
U{\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} \frac{{{E^n}\sigma _{\rm{y}}^{1 - n}V}}{{1 + n}}\varepsilon _{{{\rm{eq}}}\left| M \right.}^{1 + n} (6) 对于幂律硬化材料，根据有限元分析，圆台形平面压入的压入功-深度关系也是符合幂律的，因此可假设：
\left\{ \begin{gathered} \frac{V}{{{V^*}}} = {k_1}{\left(\frac{h}{{{h^*}}}\right)^{{k_2}}} \\ {\varepsilon _{{\text{eq}}}} = {k_3}{\left(\frac{h}{{{h^*}}}\right)^{{k_4}}} \\ \end{gathered} \right. (7) 式中：h*为特征深度；V*为特征体积，旨在对不同端部直径D的圆台形平面压入功-深度关系进行归一化处理，可取h*=D、V*=D3。k1、k2是与有效变形域体积V相关的有效体积系数和有效体积指数，k3、k4是与等效应变εeq相关的为有效应变系数和有效应变指数，k1~k4可通过少量工况的有限元分析确定，其值如表1所示。
表 1 TCFI模型参数标定值Table 1. Calibration values of TCFI’s model parameters参数 k1 k2 k3 k4 标定值 17.9271 0.6300 0.2941 0.6924 在准静态加载条件下，不考虑其他形式的能量耗散时，压入载荷F作用下材料形变能U等于压入功W，即：
W = U = \int_0^h {Fdh} (8) 将式(7)代入式(6)中，联立式(8)可得压入功W：
W{\kern 1pt} = {\kern 1pt} {\kern 1pt} \frac{{{k_1}k_3^{1 + n}{E^n}\sigma _{{\rm{y}}}^{1 - n}{D^3}}}{{1 + n}}{\left( {\frac{h}{D}} \right)^{{k_4}n + {k_4} + {k_2}}} (9) 引入特征能量W*，压入指数m，可将式(9)简化为能够直观描述联系材料力学参数的无量纲压入功-深度幂律模型：
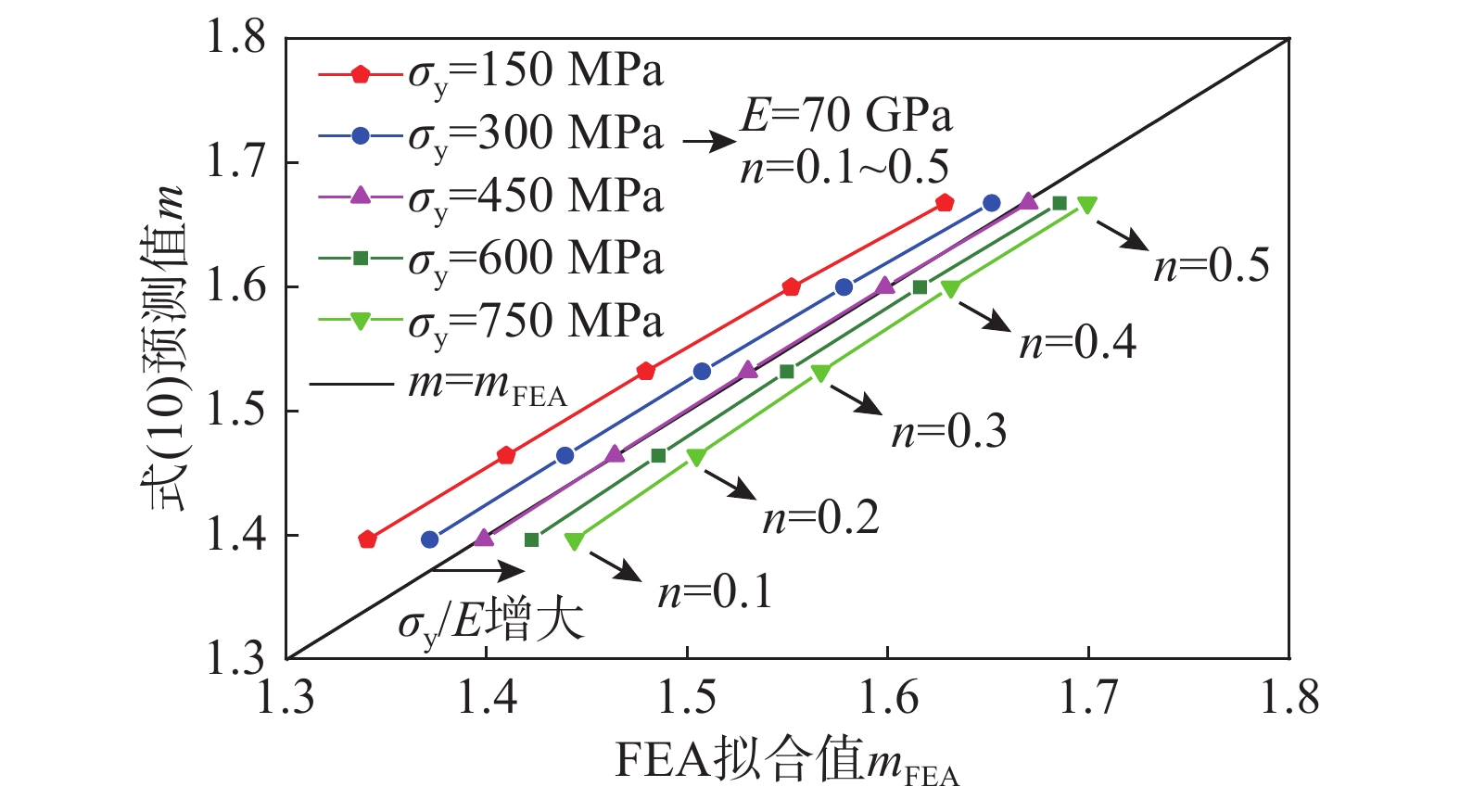
\left\{ \begin{aligned} & W / {W^*} = {\left( {h / D} \right)^m} \\& {W^*} = {k_1}k_3^{1 + n}{E^n}\sigma _{\text{y}}^{1 - n}{D^3} / \left( {1 + n} \right) \\& m = \left( {1 + n} \right){k_4} + {k_2} \end{aligned} \right. (10) 由于在式(5)中，考虑εy对中值点M等效应变较小而在应变能密度积分作了忽略处理，结果导致压入指数m的正向预测结果与FEA计算结果随着σy/E变化存在一定程度的分散性，如图1所示。
![]()
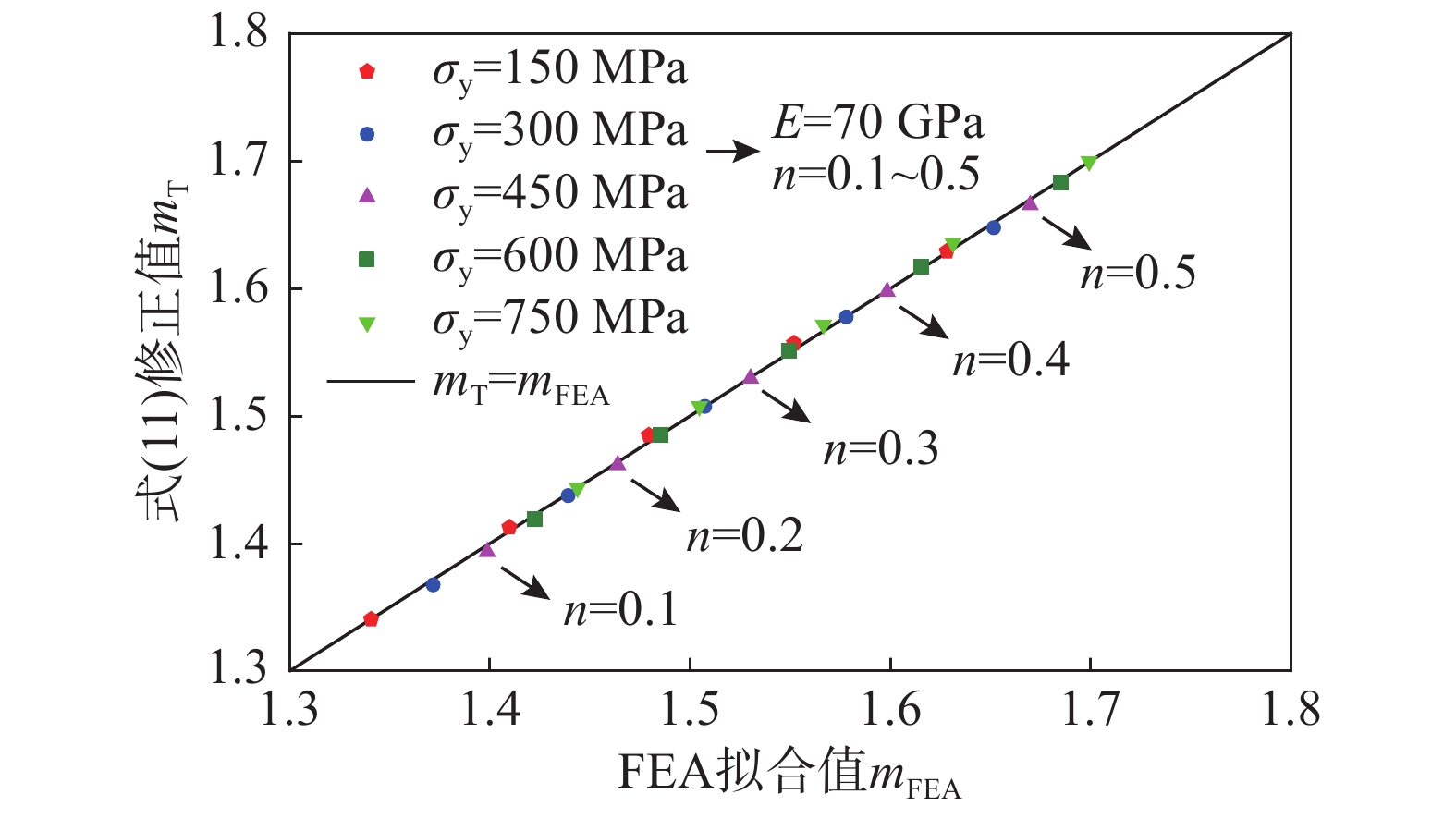
图 1 压入指数预测值与FEA拟合值比较Figure 1. Comparisons of loading index between predicted value and FEA input values由图1可见mFEA-m呈线性关系，因此以σy/E作为自变量确定了式(11)的线性修正函数对式(10)中预测的m进行修正，修正后结果如图2所示：
{m_{{\text{T}}{\kern 1pt} }}\, = {\kern 1pt} \,{\alpha _1}{\kern 1pt} {\text{e}}{{\kern 1pt} ^{{\alpha _2}\left( {{\kern 1pt} {\sigma _{\text{y}}}/E} \right)}}\left( {m{\kern 1pt} - {\kern 1pt} {\alpha _3}{\kern 1pt} } \right){\kern 1pt} + {\kern 1pt} {\alpha _3} (11) 式中：mT为修正后的压入指数，可表示有限元计算或试验得到的压入指数实际值；e为自然底数；α1~α3为模型修正系数，其值列于表2，使用时依据待测材料的弹性模量进行选取。
将式(11)中修正后的mT替换m代入式(10)中，即为关联压头直径、压入功、压入深度和材料弹塑性参数的圆台形平面压入(Truncated Cone Flat Indentation, TCFI)理论模型。
![]()
图 2 压入指数修正值与FEA拟合值比较Figure 2. Comparisons of loading index between correction values and FEA input values表 2 TCFI修正系数标定值Table 2. Calibration values of TCFI’s correction parameters材料类型 α1 α2 α3 轻质合金(E∈50 GPa~120 GPa) 1.103 −16.720 2.117 钢材(E∈120 GPa~220 GPa) −19.166 2.356 1.2 模型参数的确定方法
采用ANSYS18.0商业有限元分析软件，根据圆台形平面压入的几何特性，设计了如图3所示的二维轴对称有限元模型。压头端部直径D=0.1 mm，锥角θ=60°，压头材质为金刚石，不考虑压头变形。假设被压材料连续均匀、各向同性，遵循von Mises屈服准则，且满足Hollomon模型，其弹性模量设置为70 GPa和200 GPa，屈服强度σy分别为150 MPa~750 MPa，步长为150 MPa，硬化指数n分别为0.1~0.5，步长为0.1，考虑到常见金属材料泊松比v的差异较小且对压入曲线影响微弱，因此所有模型中v统一取0.3。被压试样为直径1.5 mm，高1 mm的圆柱体，采用Plane182单元，共由7195个节点和7046个单元组成。压头与试样接触区域网格相对密集，压头端部边缘处试样的网格被细化至0.6 μm，远离试样与压头接触区域的网格较为稀疏，以节约计算成本。压头与被测材料之间为面-面接触，压头外轮廓采用Targe169单元，被压材料接触面采用Contact172单元。在材料底部施加竖直方向约束，左侧施加轴对称水平方向约束，模拟时采用最大压入深度为30 μm的位移载荷，远小于被压试样尺寸。模型的分析结果满足远场无关性、网格收敛性的要求。
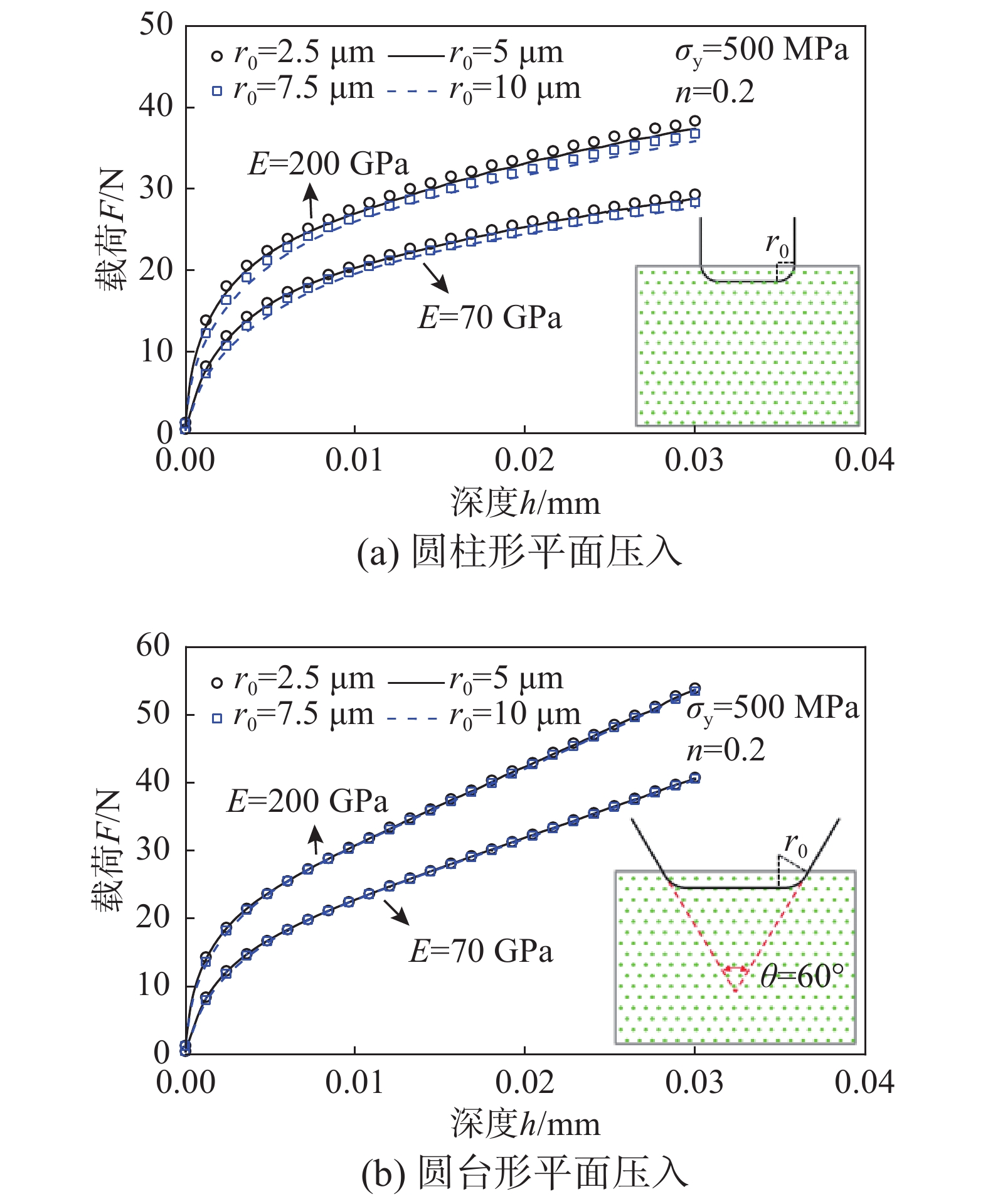
压头由于加工缺陷和使用磨损导致压头不可避免地存在钝化现象。在有限元建模中考虑这一因素，即在压头边缘建立如图3所示圆角，一方面可让模型更接近真实情况，另一方面还可以避免由于尖锐边缘的应力集中造成有限元计算的不收敛，节约计算成本。同时为证明圆台形平面压入对压头钝化的弱敏感性，分析了压头钝化分别对圆柱形平面压入和圆台形平面压入结果的影响，如图4所示。从不同的钝化半径r0的有限元计算结果可见，相比圆柱形平面压入，压头钝化仅在压入深度较浅时对圆台形平面压入载荷-深度(F-h)曲线存在十分微小的影响，随着压入深度的增大，钝化的影响逐渐减小至可忽略不计。综合考虑有限元计算结果准确性和计算效率，钝化半径r0取D/20(=5 μm)。
由于压入行为与压入过程的应力场紧密相关，对比了不同r0圆台形平面压入和圆柱形平面压入相同材料(E=70 GPa, σy=500 MPa, n=0.2)在相同压入深度下(h=25 μm)提取的von Mises应力云图和应变能U，如图5所示。可见，在r0从2.5 μm变化至10 μm的过程中，压头下方核心区逐渐扩大，应力集中效应逐渐减弱，圆柱形平面压入的最大应力减小了7.99 %、圆台形平面压入减小6.58 %；另外，圆柱形平面压入U减小了5.77 %，而圆台形平面压入U仅减小0.82 %，可见，相比圆柱形平面压入，圆台形平面压入的应变能U对r0的敏感性小得多。根据功能原理，体现在压入载荷-变形行为上即为F-h曲线对压头钝化的弱敏感性。
![]()
图 5 压头钝化对von Mises应力云图的影响Figure 5. Influence of tip rounding on the von Mises stress contour plots固定材料的弹性模量E=70 GPa或200 GPa，屈服强度σy=450 MPa，变化硬化指数n由0.1~0.5，对FEA结果的载荷-深度曲线积分可得到压入功-深度曲线，采用幂函数拟合压入功-深度曲线可得不同硬化指数n下特征能量W*和压入指数m，结合式(9)可得TCFI模型参数k1~k4。进一步地，通过变化材料屈服强度从150 MPa~750 MPa，分析仅由模型参数k1~k4代入式(10)中预测所得压入功-深度曲线与FEA结果的偏差，确定了考虑材料屈服的修正公式(11)和模型修正系数α1~α3。
1.3 拉伸性能预测方法
图6(a)为圆台形平面压入弹塑性材料的加卸载曲线示意图，基于Oliver-Pharr法[5]，材料弹性模量E可通过压入加卸载F-h曲线中的卸载部分信息获得，具体过程本文不作赘述。图6(b)为图6(a)加载段F-h曲线积分所得的W-h/D曲线，采用幂函数对该曲线进行拟合可获得实际压入指数mT及特征能量W*。
![]()
图 6 圆台形平面压入加卸载曲线示意图Figure 6. Schematic diagram of loading and unloading curve of truncated cone flat indentation由式(10)可得材料塑性参数σy、n关于特征能量W*和未修正压入指数m的表达式：
\left\{ \begin{gathered} {\sigma _{\text{y}}}{\kern 1pt} = {\left[ {\frac{{(1{\kern 1pt} + {\kern 1pt} n)\,{W^*}}}{{{k_1}k_3^{1 + n}{E^n}{D^3}}}} \right]^{\frac{1}{{1 - n}}}} \\ n = \frac{{m\, - {\kern 1pt} {k_2}{\kern 1pt} - {\kern 1pt} {k_4}{\kern 1pt} }}{{{k_4}}} \\ \end{gathered} \right. (12) 结合式(12)和修正公式(11)可建立预测材料屈服应力σy和硬化指数n的迭代方法，其具体过程如下：
(Ⅰ) 对屈服应力赋值σy=σyi (i=1,2,3\cdots ；σy1可取100 MPa)，将σy/E和mT代入式(11)中，可得压入指数m值；
(Ⅱ) 将特征能量W*和压入指数m代入式(12)，得到更新后的屈服应力σyi+1和硬化指数n；
(Ⅲ) 计算σyi+1与σyi的相对误差，若 |σyi+1−σyi|/σyi ≤0.5%，输出屈服应力σyi+1和硬化指数n；否则，令σy=σyi+1，返回步骤(Ⅰ)继续进行循环计算。
得到屈服应力σy和硬化指数n后，可进一步利用式(13)对材料抗拉强度σb进行预测[26]：
{\sigma _{\text{b}}} = {E^n}\sigma _{\text{y}}^{1 - n}{\left( {\frac{n}{{\text{e}}}} \right)^n} (13) 2 TCFI数值验证
2.1 正向预测：压入功-深度关系验证
圆台形平面压入(TCFI)的正向预测是指：已知材料弹塑性力学参数(E、σy、n)，利用TCFI模型预测得到W-h曲线。为验证TCFI的准确性，对不同参数材料压入功-深度曲线的FEA计算结果和TCFI正向预测结果进行了对比。材料弹性模量E对应表2中材料类型划分为两个区间，轻质合金类：70 GPa、90 GPa、120 GPa和钢材类：150 GPa、180 GPa、200 GPa；屈服应力σy取200 MPa、400 MPa、800 MPa；硬化指数n为0.05、0.20、0.40，涵盖了除铝合金、铜合金、钛合金、钢材等在内大部分金属材料，对于镁合金等常展现出较强各向异性的材料[27]，不符合能量等效理论的基本假设，在此不予考虑。将两种方式得到的曲线进行对比，TCFI正向预测结果与FEA结果吻合良好，如图7所示。
![]()
图 7 TCFI正向预测与FEA结果的W-h曲线的对比Figure 7. Comparisons of indentation W-h curves between TCFI forward predictions and FEA results2.2 反向预测：应力-应变关系验证
圆台形平面压入(TCFI)的反向预测是指：通过试验或有限元计算得到加载段的F-h曲线，对该曲线积分可得W-h曲线，利用1.3中迭代方法预测得材料的塑性参数，进而获得材料的应力-应变(σ-ε)关系。通过有限元计算，获得了包括正向预测中轻质合金材料及钢材在内，屈服应力σy为200 MPa、400 MPa、600 MPa、800 MPa，硬化指数n为0.05、0.1、0.2、0.3、0.4范围内材料的W-h曲线，然后选取压入深度在10 μm~25 μm(1/10D~1/4D)范围内的曲线，通过TCFI反向预测得到材料的σ-ε曲线。将反向预测结果与有限元模型中输入参数对应的应力-应变(σ-ε)曲线进行对比，如图8所示。
为便于评价σ-ε曲线结果的预测精度，增加曲线拟合优度G作为评估指标。选取预测结果中应变区间为Δε的σ-ε曲线(Δε∈[εy , εmax ])，将其分成κ段(κ ≥ 20)，定义表征离散度的拟合优度G如下：
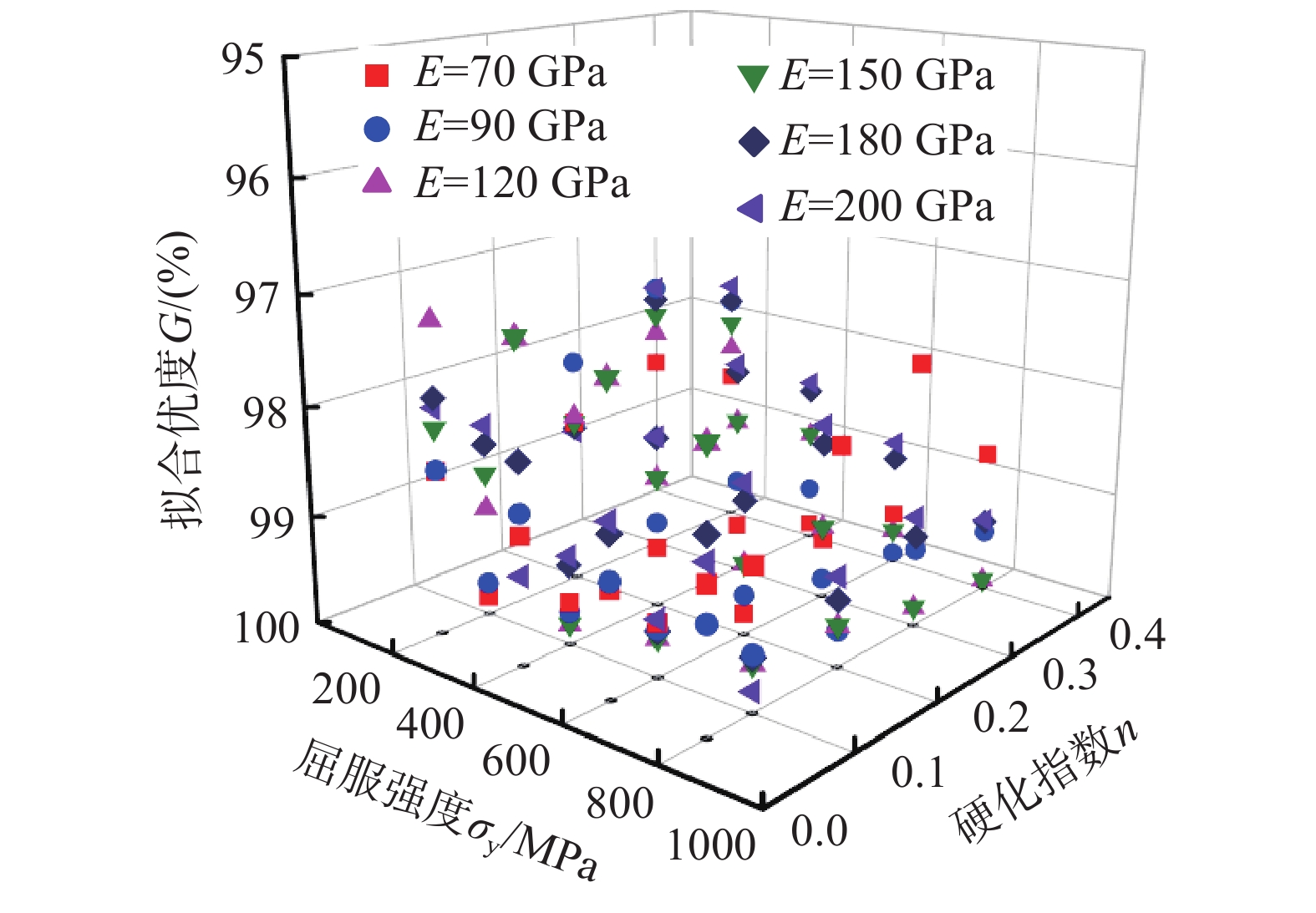
G = 1 - \sqrt {\sum\limits_{i = 1}^\kappa {{{\left( {{\sigma _i} - {\sigma _{i{\text{\_Ref}}}}} \right)}^2}} \Bigg/\sum\limits_{i = 1}^\kappa {\sigma _i^2} } (14) 式中，σi和σi-Ref分别为ε=εi时对应σ的TCFI预测值和参照值，参照曲线为有限元输入值或拉伸试验结果对应的σ-ε曲线，G越接近100%，则说明二者相似度越高。图9描述了TCFI反向预测结果与有限元输入值对应σ-ε曲线的拟合优度，G均在97%以上，预测结果与输入σ-ε曲线吻合较好，证明了TCFI反向预测的准确性。
![]()
图 8 TCFI反向预测与FEA输入值的σ-ε曲线对比Figure 8. Comparisons of σ-ε curves between TCFI reverse predictions and FEA input values![]()
图 9 TCFI预测与FEA输入值σ-ε曲线的拟合优度Figure 9. Goodness of fit of σ-ε curves between TCFI reverse predictions and FEA input values2.3 考虑压头钝化对预测的影响
为分析压头钝化对TCFI预测结果的影响，固定材料的Hollomon模型参数，利用有限元计算出不同钝化半径圆台形平面压入的F-h曲线，积分得到W-h曲线，与相同模型参数的TCFI正向预测结果进行对比，如图10(a)所示，二者吻合较好。基于有限元结果的W-h曲线，利用TCFI反向预测其σ-ε曲线，对比反向预测结果与FEA输入参数对应的σ-ε曲线，如图10(b)所示，可见TCFI预测结果具有对压头钝化的弱敏感性。因此，在正常使用条件下，利用此方法预测材料拉伸性能可在较大范围内忽略压头钝化产生的影响。
![]()
图 10 压头钝化对TCFI正反向预测结果的影响Figure 10. Influence of tip rounding on forward and reverse prediction results of TCFI3 试验验证
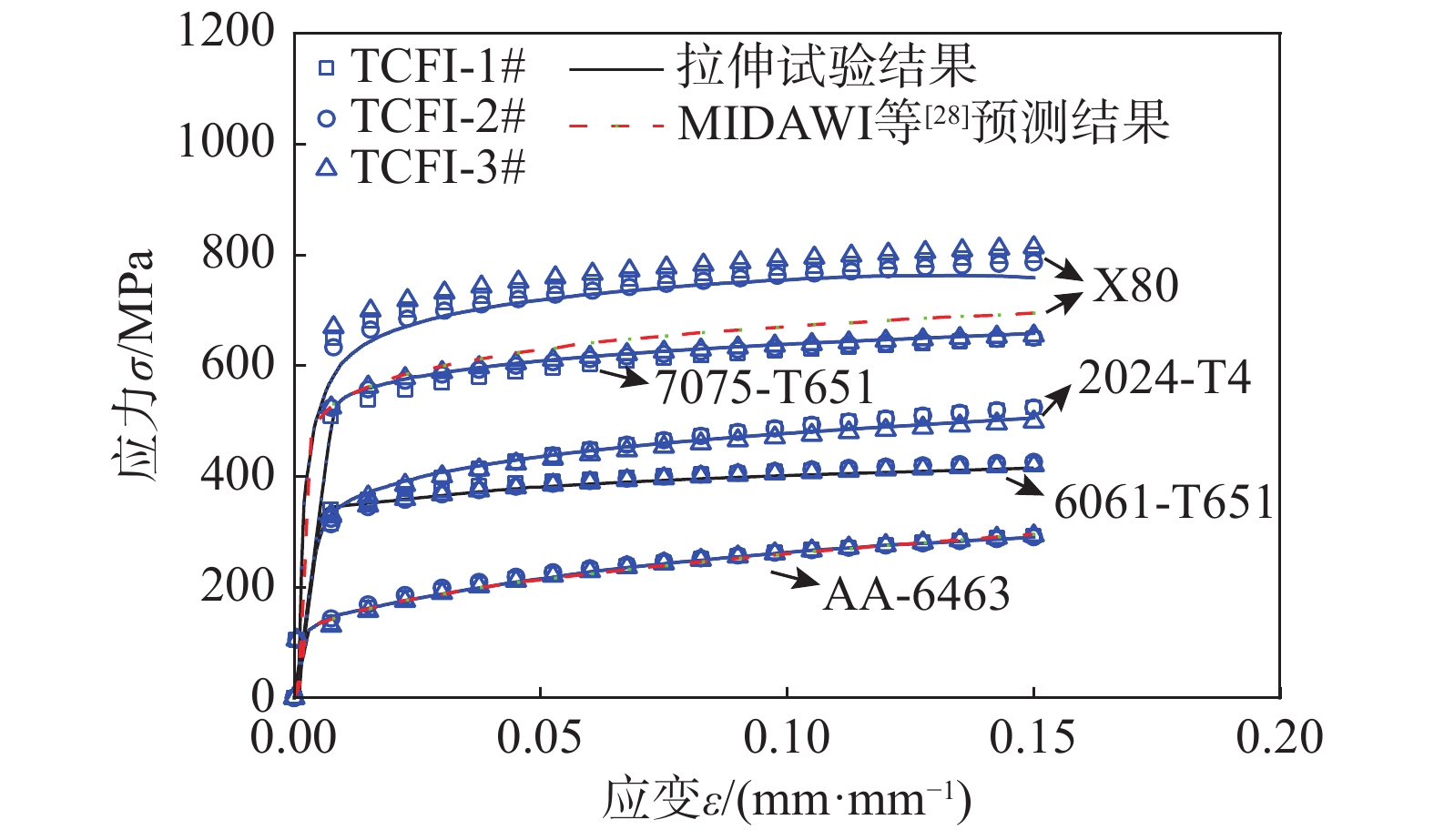
采用MTS AcumenTM的12 kN电动力伺服材料试验机，结合端部直径D=0.4 mm，锥角θ为60°的圆台形平面压头进行压入试验，对6061-T651、2024-T4、7075-T651三种金属进行单轴拉伸和压入试验。压入试样尺寸为直径15 mm，高10 mm的圆柱体，为消除表面粗糙度对测试结果的影响，对表面进行了打磨和抛光处理。最大压入深度设置为0.12 mm，加载速率为1 μm/s，实时深度通过应变引伸计精确测量，每种材料试样进行三次压入试验。同时还引用了MIDAWI等[28]不同端部直径圆台形平面压入(D=0.1 mm，θ=60°)试验数据，其压入材料为AA-6463及X80管线钢。试验结果如图11所示。
用幂函数拟合图12中W-h/D曲线可获得各曲线的W*和mT，基于TCFI模型可反向预测得到材料拉伸性能参数，σ-ε曲线结果如图13所示。
![]()
图 13 TCFI预测σ-ε曲线与拉伸试验结果对比Figure 13. Comparisons of σ-ε curves between TCFI predictions and and those from uniaxial tension表3为不同材料σ-ε曲线、抗拉强度σb的预测结果与拉伸试验结果的量化对比。可见，TCFI预测σ-ε曲线与拉伸试验结果曲线的拟合优度G均大于95%，抗拉强度相对误差小于6%(σb取3次压入TCFI预测结果的平均值)，测试结果稳定、可靠，满足工程应用要求，说明了TCFI模型可有效运用于金属材料拉伸性能的预测。
表 3 5种金属材料的压入试验和拉伸试验结果对比Table 3. Comparisons between indentation and uniaxial tensile results of 5 metallic materials材料 预测σ-ε曲线与试验曲线的拟合
优度G/(%)抗拉强度σb/
MPa相对
误差/
(%)TCFI-1# TCFI-2# TCFI-3# MIDAWI[28] TCFI预
测结果拉伸试
验结果2024-T4 97.46 97.65 98.29 − 445.02 440.40 1.05 6061-T651 97.91 98.26 98.78 − 370.71 359.00 3.26 7075-T651 97.53 99.16 99.53 − 575.45 607.08 5.21 AA-6463 99.03 98.50 99.48 98.86 259.19 253.38 2.29 X80 96.77 98.40 95.05 87.59 706.60 687.69 2.75 4 结论
本文从平面压入金属材料的压入功-深度曲线与材料弹塑性参量的关系着手，提出了一种获取金属材料拉伸性能的圆台形平面压入方法，并结合有限元数值仿真及相关试验数据对该方法进行了对比验证，结论如下：
(1) 本文基于能量等效理论，提出了关联压头直径、压入功、压入深度和材料弹塑性参量的圆台形平面压入TCFI模型，该模型仅包含7个参数，公式简单，预测效果良好。
(2) 结合Hollomon模型参数化的大量有限元分析，用涵盖较大范围金属材料的计算结果验证了TCFI模型的适用性和可靠性。
(3) 对比不同钝化半径圆台形平面压入的TCFI正反向预测结果，结果表明该测试方法具有对压头钝化的弱敏感性，可在平面压入测试结果稳定性较好的基础上，大大降低压头钝化对测试结果准确性的不利影响。
(4) 基于TCFI模型对5种金属材料的应力-应变关系及抗拉强度进行了反向预测，预测结果与拉伸试验结果一致性较好。对于拉伸试验难以取样的焊接结构、服役结构，此方法具有特别的优势，且有望进一步通过合适的力学模型实现薄膜和涂层等小尺度材料的力学性能表征。
-
![]()
图 1 压入指数预测值与FEA拟合值比较
Figure 1. Comparisons of loading index between predicted value and FEA input values
![]()
图 2 压入指数修正值与FEA拟合值比较
Figure 2. Comparisons of loading index between correction values and FEA input values
![]()
图 5 压头钝化对von Mises应力云图的影响
Figure 5. Influence of tip rounding on the von Mises stress contour plots
![]()
图 6 圆台形平面压入加卸载曲线示意图
Figure 6. Schematic diagram of loading and unloading curve of truncated cone flat indentation
![]()
图 7 TCFI正向预测与FEA结果的W-h曲线的对比
Figure 7. Comparisons of indentation W-h curves between TCFI forward predictions and FEA results
![]()
图 8 TCFI反向预测与FEA输入值的σ-ε曲线对比
Figure 8. Comparisons of σ-ε curves between TCFI reverse predictions and FEA input values
![]()
图 9 TCFI预测与FEA输入值σ-ε曲线的拟合优度
Figure 9. Goodness of fit of σ-ε curves between TCFI reverse predictions and FEA input values
![]()
图 10 压头钝化对TCFI正反向预测结果的影响
Figure 10. Influence of tip rounding on forward and reverse prediction results of TCFI
![]()
图 13 TCFI预测σ-ε曲线与拉伸试验结果对比
Figure 13. Comparisons of σ-ε curves between TCFI predictions and and those from uniaxial tension
表 1 TCFI模型参数标定值
Table 1 Calibration values of TCFI’s model parameters
参数 k1 k2 k3 k4 标定值 17.9271 0.6300 0.2941 0.6924 
下载: 导出CSV
表 2 TCFI修正系数标定值
Table 2 Calibration values of TCFI’s correction parameters
材料类型 α1 α2 α3 轻质合金(E∈50 GPa~120 GPa) 1.103 −16.720 2.117 钢材(E∈120 GPa~220 GPa) −19.166 2.356
下载: 导出CSV
表 3 5种金属材料的压入试验和拉伸试验结果对比
Table 3 Comparisons between indentation and uniaxial tensile results of 5 metallic materials
材料 预测σ-ε曲线与试验曲线的拟合
优度G/(%)抗拉强度σb/
MPa相对
误差/
(%)TCFI-1# TCFI-2# TCFI-3# MIDAWI[28] TCFI预
测结果拉伸试
验结果2024-T4 97.46 97.65 98.29 − 445.02 440.40 1.05 6061-T651 97.91 98.26 98.78 − 370.71 359.00 3.26 7075-T651 97.53 99.16 99.53 − 575.45 607.08 5.21 AA-6463 99.03 98.50 99.48 98.86 259.19 253.38 2.29 X80 96.77 98.40 95.05 87.59 706.60 687.69 2.75
下载: 导出CSV
-
[1] 张泰华. 微/纳米力学测试技术——仪器化压入的测量、分析、应用及其标准化[M]. 北京: 科学出版社, 2013: 1 − 3. ZHANG Taihua. Micro/nano mechanical testing techniques: Measurement, analysis, application and standardization of instrumented indentation [M]. Beijing: Science Press, 2013: 1 − 3. (in Chinese)
[2] 管德清, 丁湘泽, 潘嫣然. 考虑残余应力影响的焊接结构疲劳总寿命预测方法[J]. 长沙理工大学学报(自然科学版), 2020, 17(3): 15 − 21. GUAN Deqing, DING Xiangze, PAN Yanran. A method for predicting the total fatigue life of welded joints considering residual stress [J]. Journal of Changsha University of Science & Technology (Natural Science), 2020, 17(3): 15 − 21. (in Chinese)
[3] ARUNKUMAR S. A review of indentation theory [J]. Materials Today: Proceedings, 2018, 5(11): 23664 − 23673. doi: 10.1016/j.matpr.2018.10.156
[4] 张志杰, 郑鹏飞, 陈辉, 等. 基于能量等效原理的金属材料硬度预测方法[J]. 工程力学, 2021, 38(3): 17 − 26. doi: 10.6052/j.issn.1000-4750.2020.04.0249 ZHANG Zhijie, ZHENG Pengfei, CHEN Hui, et al. The method for hardness prediction of metal materials based on energy equivalence principle [J]. Engineering Mechanics, 2021, 38(3): 17 − 26. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.04.0249
[5] OLIVER W C, PHARR G M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments [J]. Journal of Materials Research, 1992, 7(6): 1564 − 1583. doi: 10.1557/JMR.1992.1564
[6] 姚博, 蔡力勋, 包陈. 基于70.3°圆锥形压头的材料压入测试方法研究[J]. 工程力学, 2013, 30(6): 30 − 35. doi: 10.6052/j.issn.1000-4750.2012.02.0096 YAO Bo, CAI Lixun, BAO Chen. The research of indentation test method based on cone indenter of 70.3 degrees [J]. Engineering Mechanics, 2013, 30(6): 30 − 35. (in Chinese) doi: 10.6052/j.issn.1000-4750.2012.02.0096
[7] AMMAR H R, HAGGAG F M, ALABOODI A S, et al. Nondestructive measurements of flow properties of nanocrystalline Al-Cu-Ti alloy using automated ball indentation (ABI) technique [J]. Materials Science and Engineering: A, 2018, 729: 477 − 486. doi: 10.1016/j.msea.2018.05.089
[8] LU L, DAO M, KUMAR P, et al. Extraction of mechanical properties of materials through deep learning from instrumented indentation [J]. Proceedings of the National Academy of Sciences of the United States of America, 2020, 117(13): 7052 − 7062. doi: 10.1073/pnas.1922210117
[9] 陈辉, 蔡力勋, 彭晖. 预测铝合金单轴力学性能的复合型双锥压入法[J]. 机械工程学报, 2021, 57(20): 79 − 88. doi: 10.3901/JME.2021.20.079 CHEN Hui, CAI Lixun, PENG Hui. Composite dual-conical indentation method for predicting the uniaxial mechanical properties of aluminum alloys [J]. Journal of Mechanical Engineering, 2021, 57(20): 79 − 88. (in Chinese) doi: 10.3901/JME.2021.20.079
[10] 张思宇, 蔡力勋, 司淑倩, 等. 弹塑性比例叠加的锥压入半解析模型与试验方法[J]. 工程力学, 2023, 40(2): 232 − 246. doi: 10.6052/j.issn.1000-4750.2021.09.0684 ZHANG Siyu, CAI Lixun, SI Shuqian, et al. Semi-analytical model and test method of cone indentation based on elastoplastic proportional superposition [J]. Engineering Mechanics, 2023, 40(2): 232 − 246. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.09.0684
[11] 岳珠峰, 赵彬, 许宝星, 等. 平头压痕测试技术及其应用[M]. 北京: 科学出版社, 2010: 49 − 80. YUE Zhufeng, ZHAO Bin, XU Baoxing, et al. Flat indentation testing technology and its application [M]. Beijing: Science Press, 2010: 49 − 80. (in Chinese)
[12] RICCARDI B, MONTANARI R. Indentation of metals by a flat-ended cylindrical punch [J]. Materials Science and Engineering: A, 2004, 381(1/2): 281 − 291.
[13] WRIGHT S C, HUANG Y, FLECK N A. Deep penetration of polycarbonate by a cylindrical punch [J]. Mechanics of Materials, 1992, 13(4): 277 − 284. doi: 10.1016/0167-6636(92)90020-E
[14] SHIELD R T. On the plastic flow of metals under conditions of axial symmetry [J]. Proceedings of the Royal Society A: Mathematical, and Physical Sciences, 1955, 233(1193): 267 − 287.
[15] MILLER A G. Review of limit loads of structures containing defects [J]. International Journal of Pressure Vessels and Piping, 1988, 32(1/2/3/4): 197 − 327.
[16] LU Y C, KURAPATI S N V R K, YANG F Q. Finite element analysis of cylindrical indentation for determining plastic properties of materials in small volumes [J]. Journal of Physics D: Applied Physics, 2008, 41(11): 115415. doi: 10.1088/0022-3727/41/11/115415
[17] SCIBETTA M, LUCON E, CHAOUADI R, et al. Instrumented hardness testing using a flat punch [J]. International Journal of Pressure Vessels and Piping, 2003, 80(6): 345 − 349. doi: 10.1016/S0308-0161(03)00077-2
[18] BRUTTI C. A theoretical model for elastic-perfectly plastic flat cylindrical punch indentation [J]. Mechanics of Materials, 2021, 155: 103770. doi: 10.1016/j.mechmat.2021.103770
[19] HU Z, LYNNE K J, MARKONDAPATNAIKUNI S P, et al. Material elastic-plastic property characterization by nanoindentation testing coupled with computer modeling [J]. Materials Science and Engineering:A, 2013, 587: 268 − 282. doi: 10.1016/j.msea.2013.08.071
[20] HU Z, LYNNE K, DELFANIAN F. Characterization of materials’ elasticity and yield strength through micro-/nano-indentation testing with a cylindrical flat-tip indenter [J]. Journal of Materials Research, 2015, 30(4): 578 − 591. doi: 10.1557/jmr.2015.4
[21] JOHNSON K L. The correlation of indentation experiments [J]. Journal of the Mechanics and Physics of Solids, 1970, 18(2): 115 − 126. doi: 10.1016/0022-5096(70)90029-3
[22] GB/T 32660.1-2016, 金属材料 韦氏硬度试验 第1部分: 试验方法[S]. 北京: 中国标准出版社, 2017. GB/T 32660.1-2016, Metallic materials—Webster hardness test—Part 1: Test method [S]. Beijing: Standards Press of China, 2017. (in Chinese)
[23] CHEN H, CAI L X. Theoretical model for predicting uniaxial stress-strain relation by dual conical indentation based on equivalent energy principle [J]. Acta Materialia, 2016, 121: 181 − 189. doi: 10.1016/j.actamat.2016.09.008
[24] CHEN H, CAI L X. Unified elastoplastic model based on a strain energy equivalence principle [J]. Applied Mathematical Modelling, 2017, 52: 664 − 671. doi: 10.1016/j.apm.2017.07.042
[25] 彭云强, 蔡力勋, 韦利明. 基于等效能量原理的延性材料J(δ)阻力曲线测试新方法研究[J]. 工程力学, 2020, 37(10): 7 − 16. doi: 10.6052/j.issn.1000-4750.2019.11.0706 PENG Yunqiang, CAI Lixun, WEI Liming. The research of new testing method for obtaining the J(δ) resistance curves of ductile materials based on equivalent energy principle [J]. Engineering Mechanics, 2020, 37(10): 7 − 16. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.11.0706
[26] 郑学斌, 尚鹏举. 应变硬化指数与屈服强度和抗拉强度关系的研究[J]. 机械工程师, 2017(5): 102 − 105. doi: 10.3969/j.issn.1002-2333.2017.05.042 ZHENG Xuebin, SHANG Pengju. Study on influence of strain hardening exponent on yield strength and tensile strength [J]. Mechanical Engineer, 2017(5): 102 − 105. (in Chinese) doi: 10.3969/j.issn.1002-2333.2017.05.042
[27] 邱玮, 周兵, 黄伟颖, 等. 织构对挤压态AZ80和AZ31镁合金力学性能及各向异性的影响[J]. 长沙理工大学学报(自然科学版), 2021, 18(4): 108 − 117. QIU Wei, ZHOU Bing, HUANG Weiying, et al. Effect of texture on mechanical properties and anisotropy of extruded AZ80 and AZ31 Mg alloys [J]. Journal of Changsha University of Science and Technology (Natural Science), 2021, 18(4): 108 − 117. (in Chinese)
[28] MIDAWI A R H, SIMHA C H M, GESING M A, et al. Elastic-plastic property evaluation using a nearly flat instrumented indenter [J]. International Journal of Solids and Structures, 2017, 104/105: 81 − 91. doi: 10.1016/j.ijsolstr.2016.09.036
-
期刊类型引用(1)
1. 高航舵，胡志强，尹昭，林皋. 基于B可微方程组的弹塑性动力接触问题的研究. 工程力学. 2025(02): 24-32 . 
本站查看
其他类型引用(0)
计量
- 文章访问数: 123
- HTML全文浏览量: 50
- PDF下载量: 32
- 被引次数: 1
