NUMERICAL STUDY ON THE POST-IMPACT MECHANICAL PROPERTIES OF CONCRETE-FILLED HIGH-STRENGTH STEEL TUBES
-
摘要: 为分析高强钢管混凝土撞击后力学性能，该文建立了高强钢管混凝土在低速侧向撞击下以及轴压剩余承载力数值模型，模型考虑了高强钢和混凝土的材料应变率效应等以及动力-静力加载工况之间的结果衔接。使用现有高强钢管混凝土低速侧向撞击和静力加载试验结果对所建立模型的合理性进行了验证。采用建立的有限元模型，对高强钢管混凝土低速侧向撞击和静力侧向加载后的破坏形态、局部损伤和跨中挠度对于其轴压剩余承载力的影响规律进行了对比分析，理清了影响其轴压剩余承载力的关键因素，并发展了相应的简化计算模型。Abstract: To analyze the post-impact mechanical properties of concrete-filled high-strength steel tubes, a numerical model for the residual axial compression resistance of concrete-filled high-strength steel tubes under low-speed lateral impact and axial compression is established in this paper. The model takes into account the material strain rate effects of high-strength steel and concrete, as well as the transfer of results between the dynamic and static analysis procedures. The feasibility of the model is verified using the existing low-speed lateral impact and static loading test results of concrete-filled high-strength steel tubes. The established finite element model is used to compare and analyze the influence of failure mode, local damage and mid-span deflection of post-impact concrete-filled high-strength steel tubes after lateral impact and static lateral loading on its residual axial compressive resistance, elaborating the key factors affecting its residual axial compression resistance. A simplified calculation model for the residual axial compression resistance is established based on the analysis.
-
钢管混凝土因其承载力高，延性好，在工程中有着广泛的应用[1]。近年来，随着高强材料的研究与应用，高强钢管混凝土也开始应用于工程中。以往，对钢管混凝土的抗撞击性能已经有较多试验、数值和理论研究，结果显示由于核心混凝土对钢管的支撑作用和钢管对混凝土的约束保护，钢管混凝土有着良好的抗撞击性能[2]。值得注意的是，现有研究主要集中在普通钢管混凝土的抗撞击性能，而对高强钢管混凝土撞击下及其撞击后的力学性能的研究较少。仅YANG等[3]对高强钢管混凝土撞击下的力学性能开展了试验和理论研究。
理清高强钢管混凝土撞击后的力学性能对进行撞击灾后结构损伤评估和确定修复加固方法具有重要意义，为此本文基于数值模拟对高强钢管混凝土撞击后剩余承载力展开了分析，利用ABAQUS建立了高强钢管混凝土侧向撞击下及撞击后的轴压剩余静力承载力计算模型。基于对高强钢管混凝土撞击加载构件和静力侧向加载对比构件的破坏形态的对比分析，明晰了其轴压剩余承载力的变化规律，并提出了简化计算方法。
1 有限元模型的建立
考虑到撞击为瞬时、大变形动力过程，为进行高强钢管混凝土撞击后力学性能分析，首先基于ABAQUS/Explicit建立了其在侧向撞击下的有限元模型，模拟其遭受落锤撞击过程。之后将撞击后的结构变形和应力状态等作为初始状态导入ABAQUS/Standard中进行轴向静力加载，计算其撞击后的轴压剩余承载力。同时，为分析撞击作用机理，在ABAQUS/Standard中建立了相同构件的静力加载对比模型，通过施加侧向位移使构件产生与撞击作用相同的跨中挠度，之后计算其轴压剩余承载力，并与撞击后剩余承载力进行对比。
1.1 材料本构模型
高强钢本构采用双线性模型，强化段模量取0.01Es，Es为钢材的弹性模量[1]。在低速撞击过程中，材料应变率较低，因此采用Cowper-Symonds模型计算钢材在动态加载下的屈服强度，如式(1)所示。
σdσs=1+(˙εD)1/p (1) 式中：σd为动态应力；σs为静态应力；
˙ε 为应变率；对于高强钢参数D取18404 s−1；参数p取2.38[4]。混凝土采用塑性损伤模型，混凝土单轴受压应力-应变曲线和受拉应力-应变曲线使用文献[1]中的模型，该模型考虑了钢管对于混凝土的约束作用。对于混凝土的受压应变率效应模型，使用CEB规范对混凝土撞击拟合得到的公式，混凝土受拉应变率效应模型，采用文献[5]中根据试验数据拟合得到的公式进行计算。
1.2 接触条件、边界及网格划分等
钢管采用四节点减缩积分格式的壳单元模拟，混凝土和垫块采用八节点减缩积分三维实体单元模拟，落锤采用四节点三维刚体壳单元模拟。侧向撞击和侧向静力加载对比构件网格划分及边界条件如图1所示。
界面之间采用“通用接触”定义，其中钢管与混凝土法向接触为硬接触，切向库仑摩擦系数0.6。钢管和落锤、钢管和垫块之间法向接触为硬接触，切向摩擦系数取0[6]。
![]()
图 1 撞击和静力加载构件网格划分及边界示意图Figure 1. Schematic diagram of grid division and boundary of impact and static loading components1.3 模型验证
为验证有限元模型准确性，对文献[3]中的高强钢管混凝土落锤撞击试验进行了模拟，撞击力和跨中挠度对比如图2所示，可以看出撞击模型精度良好。同样采用文献[7]中静力试验数据对该模型的静力加载部分进行验证，侧向力(P)-跨中(Δ)挠度曲线对比如图3所示，同样可以看出静力模型精度良好。
![]()
图 2 撞击力(F)及跨中挠度(Δ)时程曲线对比图Figure 2. Impact force (F) and mid span deflection (Δ) time history curve comparison chart![]()
图 3 侧向力(P)-跨中挠度(Δ)曲线对比图Figure 3. Lateral force (P)-midspan deflection (Δ) curve comparison chart2 撞击后剩余承载力及影响因素分析
基于以上验证的有限元模型，分别建立高强钢管混凝土侧向撞击模型和侧向静力加载对比模型，并计算其剩余承载力。为了量化剩余承载力指标，定义剩余承载力折减系数nd=Nr/Nu，其中：Nr为轴压剩余承载力；Nu为原始完好构件轴压承载力。典型算例具体参数如表1所示，其中位移加载是施加与侧向撞击造成的相同的跨中残余挠度。
表 1 算例参数Table 1. Example parameters试件编号 fy/
MPafcu/
MPaD×ts/
(mm×mm)L/
mm加载方式 落锤质量
m/kg落锤速度
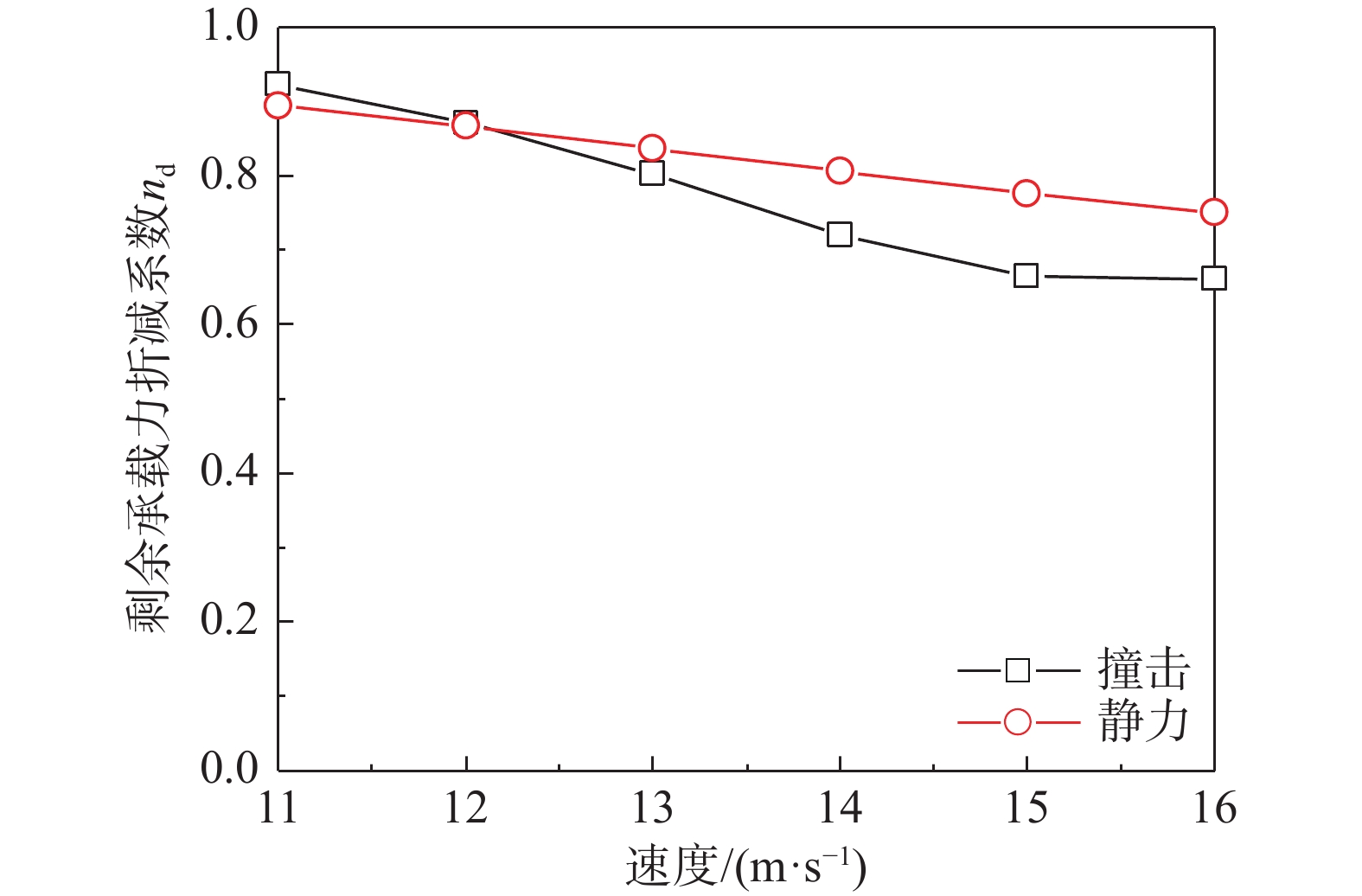
v/(m·s−1)Impact-1 720 60 203×4 2000 撞击加载 465 10~16 Static-1 720 60 203×4 2000 位移加载 − − 注：fy为钢管屈服强度；fcu为混凝土立方体抗压强度；D为截面直径；ts为钢管壁厚；L为试件长度；m为落锤质量；v为落锤速度。 如图4所示为不同撞击速度下构件和静力作用对比件的剩余承载力系数变化对比，在撞击速度较小(10 m/s~12 m/s)时，撞击作用下nd平均值为0.90，静力作用下nd平均值为0.89，nd值几乎相同；而在撞击速度较大(13 m/s~16 m/s)时，撞击作用下nd平均值为0.71，静力作用下nd平均值为0.79，撞击作用下的nd相较静力作用低了10%。
可以看出，撞击速度较大时，在产生相同的残余挠度的前提下，撞击会造成轴压剩余承载力的更大幅度降低。可能影响以上撞击后高强钢管混凝土剩余承载力的因素包括：破坏形态，即弯曲破坏或剪切破坏；局部损伤，即撞击部位局部严重损伤导致的截面承载能力削弱；跨中挠度，即由二阶效应带来的轴压承载力降低。为分析以上各种因素的影响，对算例进行进一步分析。
2.1 破坏形态分析
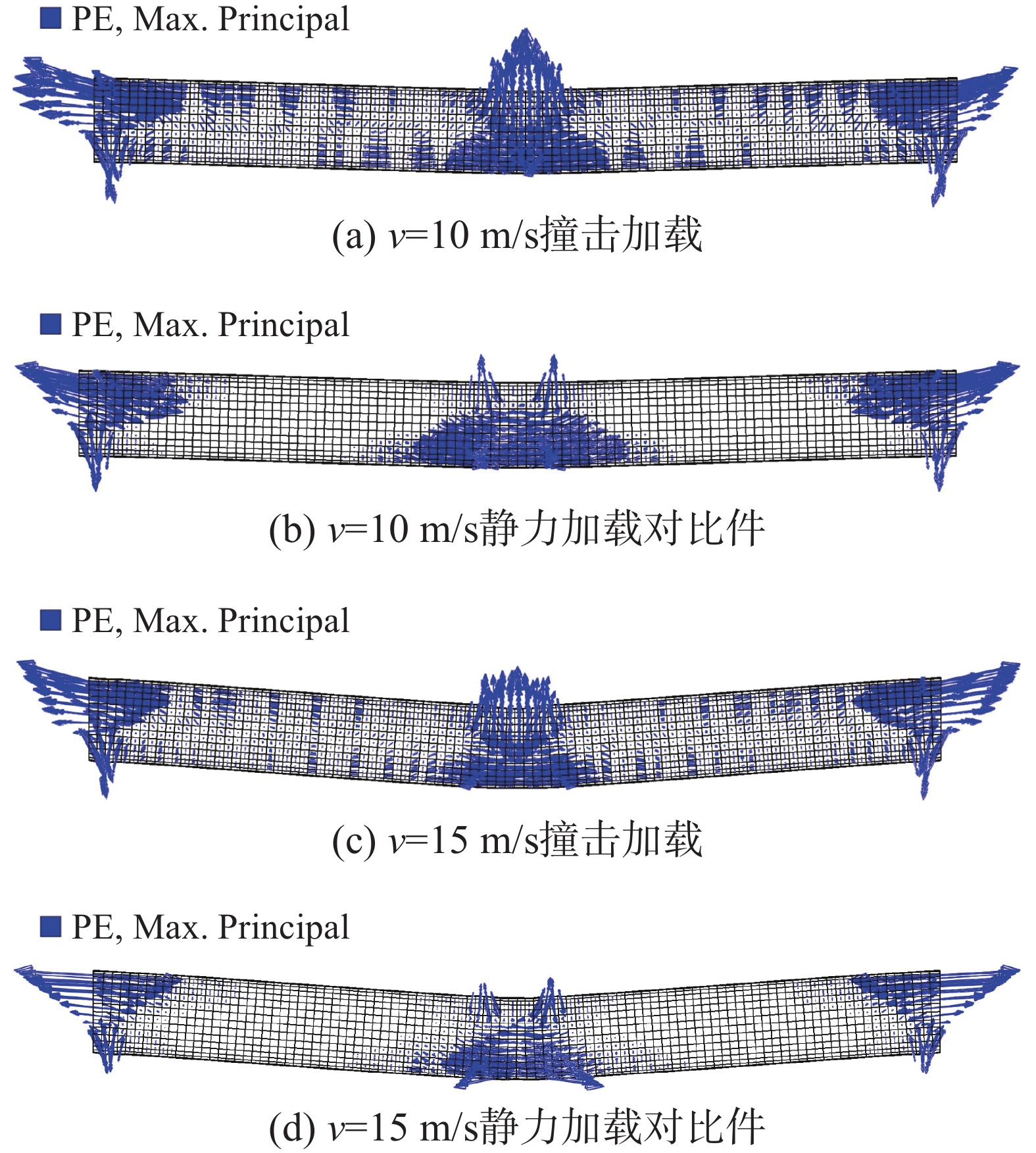
对钢筋混凝土构件来说，在侧向撞击作用下其破坏模式往往为弯剪破坏或者剪切破坏[8]，而由于钢管混凝土有着良好的抗剪能力[9-10]，在撞击作用下一般呈现弯曲破坏[1]。如图5所示为核心混凝土的最大主塑性应变图，垂直于最大主塑性应变方向为混凝土裂缝扩展方向。可以看出，不同加载方式下裂缝均分布于跨中底部混凝土受拉区以及两端固定约束部分，裂缝分布符合弯曲破坏模式。随着撞击速度的增加，混凝土开裂裂缝分布位置基本不变，整体弯曲变形更明显，剪切破坏不显著。
![]()
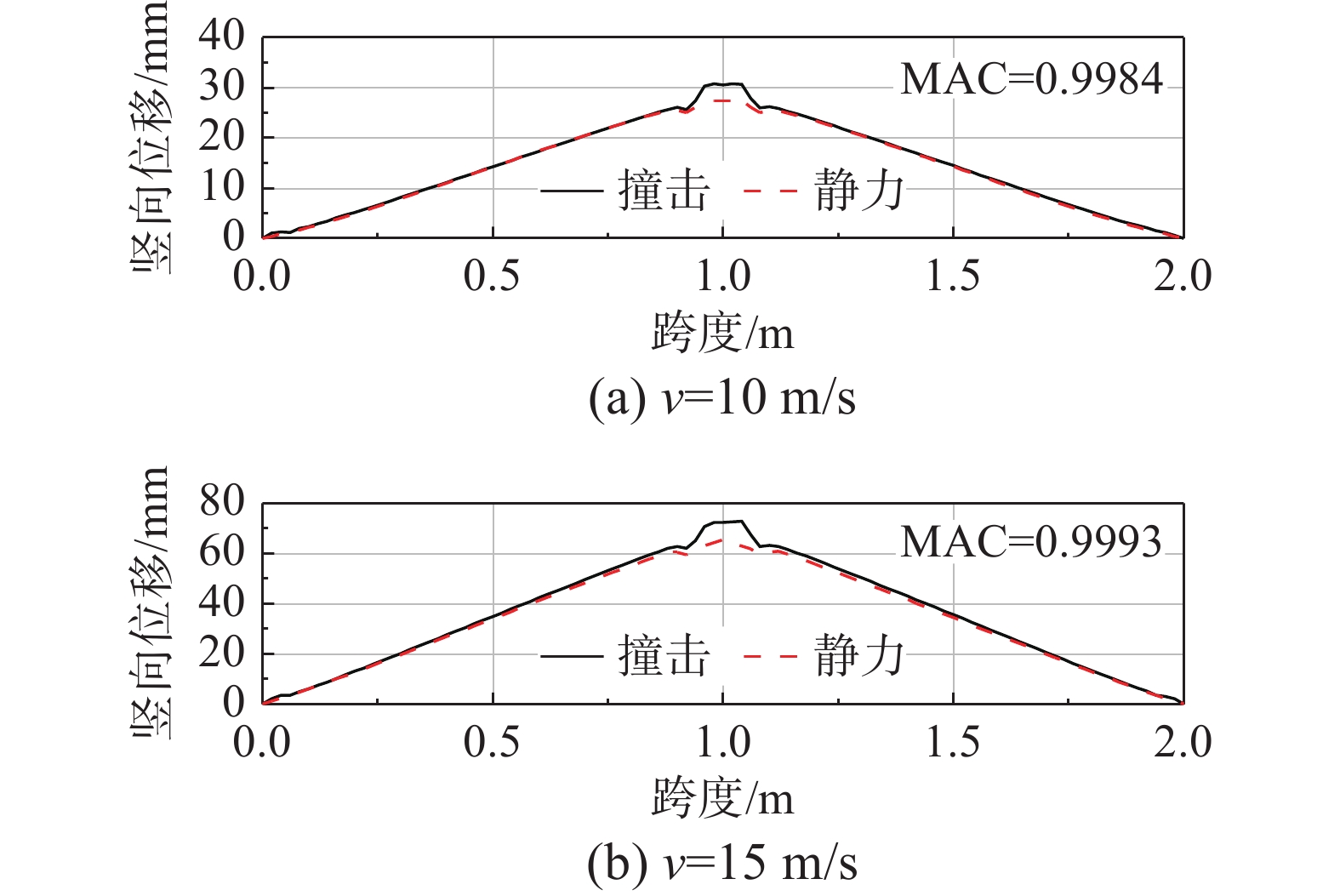
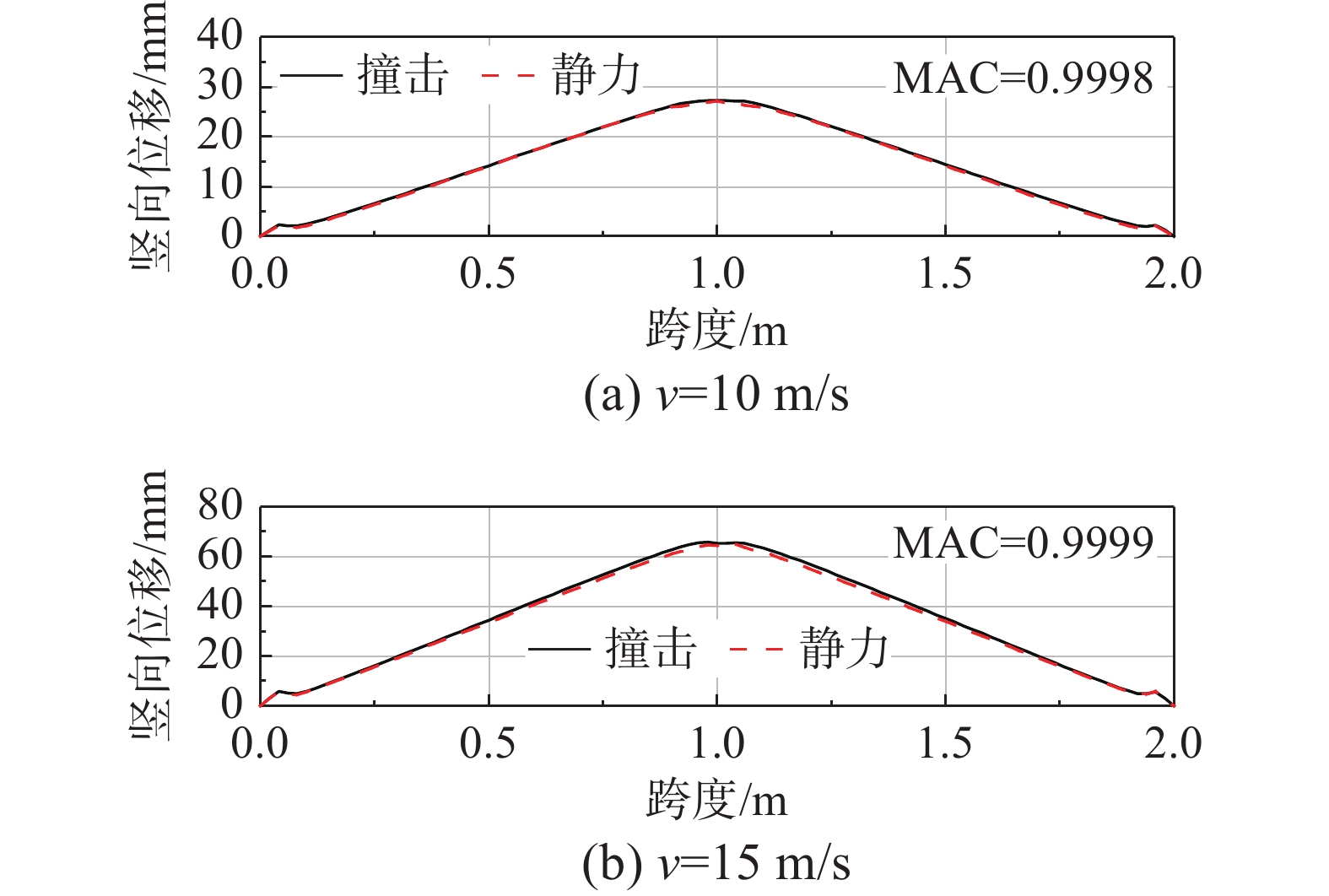
图 5 不同加载方式下核心混凝土最大主塑性应变图Figure 5. Maximum principal plastic strain diagram of core concrete under different load为判断侧向撞击作用和静力加载作用下构件的弯曲变形差异，输出外钢管顶部和底部位移曲线，使用文献[11]中所提供的公式衡量不同加载方式下位移曲线叠合程度。如式(2)所示，其中
ϕ i和ϕ s分别为侧向撞击作用下和静力加载作用下代表竖向位移的两列向量。如图6和图7所示，对于不同撞击速度下的撞击作用和加载至相同位移下的静力作用，计算得到的MAC值均接近于1，表明这两种不同加载方式下钢管混凝土构件弯曲破坏形态一致，因此在本文建立的模型参数范围内，整体破坏形态对于不同加载方式下剩余承载力影响并不显著。
MAC=|{ϕi}T{ϕs}|2|{ϕi}T{ϕi}||{ϕs}T{ϕs}| (2) 2.2 局部损伤分析
由图5可以看出，撞击作用和静力作用最大的区别在于顶部的局部变形，这是由于在侧向撞击作用下，构件与落锤直接接触区域受到撞击力产生局部凹陷，在跨中产生塑性变形[12]。以钢管底部跨中位移Δ作为整体位移，计算得到顶部凹陷位移δ来代表构件的局部损伤程度，如图8所示，随着撞击速度逐渐增大，构件顶部的局部凹陷位移逐渐增大。在相同整体位移下，撞击加载的平均凹陷位移为5.31mm，而静力加载的平均凹陷位移仅为0.47 mm，说明撞击作用相较于静力作用会造成显著的局部变形。
如图9(a)所示，对于撞击作用，剩余承载力折减系数nd随着局部凹陷位移δ的增大而减小，与图4中nd和速度的相关趋势基本一致。如图9(b)所示，对于静力作用，nd与局部凹陷位移δ并没有明显的关联性。这是因为对于撞击作用，随着加载速度的增大，局部凹陷位移也随之增大，构件在跨中形成薄弱部位，导致剩余承载力降低。对于静力作用，局部变形随着加载位移的增大变化不明显，因此对剩余承载力影响不明显。可见局部损伤是影响撞击作用和静力作用剩余承载力的一个显著因素。
![]()
图 9 不同加载方式下nd与局部凹陷位移关系Figure 9. Relationship between nd and local sag displacement under different load2.3 跨中挠度分析
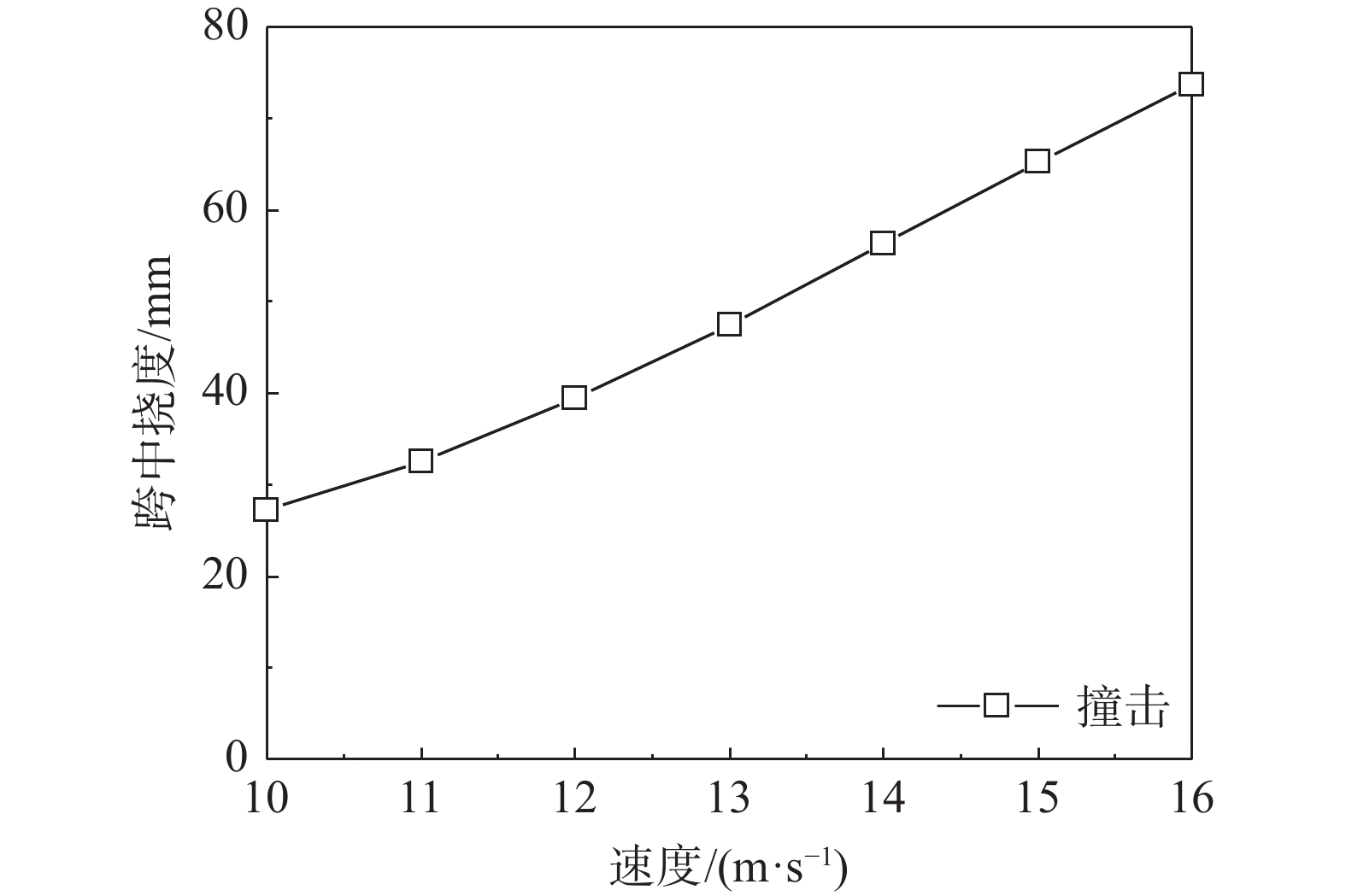
如图10所示，随着撞击速度的增加，构件的跨中挠度Δ0逐渐增大。如图11所示，撞击加载和静力加载作用下，构件剩余承载力折减系数nd随着跨中挠度Δ0的增大而减小。在构件跨中挠度Δ0较小时，撞击加载后的nd与静力加载后的nd基本相同；在构件跨中挠度Δ0较大时，撞击加载后的nd则会小于静力加载后的nd。
在侧向加载后的轴压过程中，由于二阶效应的影响，轴力和挠度会产生附加弯矩MΔ0导致剩余承载力的降低。如图12所示，在轴压过程中，由于两种加载方式下构件初始跨中挠度Δ0相同，因此初始跨中挠度与轴力带来的附加弯矩MΔ0一致，对于不同加载方式下的剩余承载力削弱程度一致。而在初始跨中挠度较大时，此时撞击也会造成的较大局部损伤，进一步削弱剩余承载力，出现撞击加载后剩余承载力小于静力加载后的剩余承载力的现象。
2.4 简化计算公式
基于以上影响因素分析，对于静力加载构件，剩余承载力折减系数nd与跨中挠度Δ0有很强的相关性，拟合得到静力作用下剩余承载力折减系数nd= −0.0034Δ0+1。对于撞击加载构件，剩余承载力折减系数nd与跨中挠度Δ0和局部损伤都呈负相关，拟合得到撞击作用剩余承载力折减系数nd= −0.004Δ0+1。简化公式可用于撞击后高强钢管混凝土轴压剩余承载力的简化计算。
![]()
图 12 轴压过程附加弯矩示意图Figure 12. Schematic diagram of additional bending moment during axial compression3 结论
本文通过数值模拟，对高强钢管混凝土构件在低速侧向撞击后的力学性能，包括轴压剩余承载力进行了分析，初步得到如下结论：
(1) 由于高强钢管混凝土有着良好的延性和抗剪能力，在撞击作用和静力作用下，构件整体破坏形态一致，均为弯曲变形。整体破坏形态对于撞击作用和静力作用后轴压剩余承载力影响较小。
(2) 局部损伤是撞击作用和静力作用后剩余承载力存在差异的主要影响因素。撞击作用下的局部损伤会随着撞击速度增大而增大，而静力作用下局部损伤随着加载位移的增大变化很小，导致速度较大时撞击后轴压剩余承载力低于静力作用后轴压剩余承载力，而在速度较小时轴压剩余承载力基本相同。
(3) 跨中挠度对于撞击作用和静力作用后高强钢管混凝土轴压剩余承载力的影响规律基本相同。相同的跨中挠度下，在撞击加载和静力加载后的轴压加载过程中，由于二阶效应产生的附加弯矩基本相等，对轴压剩余承载力影响基本相同。
(4) 基于数据拟合得到了撞击后高强钢管混凝土轴压剩余承载力简化计算公式。
-
![]()
图 1 撞击和静力加载构件网格划分及边界示意图
Figure 1. Schematic diagram of grid division and boundary of impact and static loading components
![]()
图 2 撞击力(F)及跨中挠度(Δ)时程曲线对比图
Figure 2. Impact force (F) and mid span deflection (Δ) time history curve comparison chart
![]()
图 3 侧向力(P)-跨中挠度(Δ)曲线对比图
Figure 3. Lateral force (P)-midspan deflection (Δ) curve comparison chart
![]()
图 5 不同加载方式下核心混凝土最大主塑性应变图
Figure 5. Maximum principal plastic strain diagram of core concrete under different load
![]()
图 9 不同加载方式下nd与局部凹陷位移关系
Figure 9. Relationship between nd and local sag displacement under different load
![]()
图 12 轴压过程附加弯矩示意图
Figure 12. Schematic diagram of additional bending moment during axial compression
表 1 算例参数
Table 1 Example parameters
试件编号 fy/
MPafcu/
MPaD×ts/
(mm×mm)L/
mm加载方式 落锤质量
m/kg落锤速度
v/(m·s−1)Impact-1 720 60 203×4 2000 撞击加载 465 10~16 Static-1 720 60 203×4 2000 位移加载 − − 注：fy为钢管屈服强度；fcu为混凝土立方体抗压强度；D为截面直径；ts为钢管壁厚；L为试件长度；m为落锤质量；v为落锤速度。 
下载: 导出CSV
-
[1] 韩林海. 钢管混凝土结构—理论与实践[M]. 3版. 北京: 科学出版社, 2016. HAN Linhai. Concrete filled steel tubular structures—theory and practice [M]. 3rd ed. Beijing: Science Press, 2016. (in Chinese)
[2] HAN Linhai, HOU Chuanchuan, ZHAO Xiaoling, et al. Behaviour of high-strength concrete filled steel tubes under transverse impact loading [J]. Journal of Constructional Steel Research, 2014, 92: 25 − 39. doi: 10.1016/j.jcsr.2013.09.003
[3] YANG Xiaoqiang, YANG Hua, ZHANG Sumei. Transverse impact behavior of high-strength concrete filled normal-/high-strength square steel tube columns [J]. International Journal of Impact Engineering, 2020, 139: 103512. doi: 10.1016/j.ijimpeng.2020.103512
[4] YANG Xiaoqiang, YANG Hua, ZHANG Sumei. Rate-dependent constitutive models of S690 high-strength structural steel [J]. Construction and Building Materials, 2019, 198: 597 − 607. doi: 10.1016/j.conbuildmat.2018.11.285
[5] MALVAR L J, ROSS C A. Review of strain rate effects for concrete in tension [J]. ACI Materials Journal, 1998, 95(6): 735 − 739.
[6] 安国青, 赵晖, 王蕊, 等. 外包不锈钢圆中空夹层钢管混凝土柱抗撞计算方法研究[J]. 工程力学, 2021, 38(6): 227 − 236. doi: 10.6052/j.issn.1000-4750.2020.11.0823 AN Guoqing, ZHAO Hui, WANG Rui, et al. Calculation method for impact resistance of circular concrete-filled double-skin tubular columns with external stainless steel tube [J]. Engineering Mechanics, 2021, 38(6): 227 − 236. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.11.0823
[7] 尚柯. 基于Q550以上钢材的高强方钢管高强混凝土纯弯构件力学性能研究[D]. 沈阳: 沈阳建筑大学, 2020. SHANG Ke. Research on mechanical behavior of high strength concrete filled high strength square steel tube based on Q550 under pure bending [D]. Shenyang: Shenyang Jianzhu University, 2020. (in Chinese)
[8] 赵武超, 钱江. 侧向冲击荷载下钢筋混凝土墩柱的性能[J]. 工程科学学报, 2019, 41(3): 408 − 415. ZHAO Wuchao, QIAN Jiang. Performance of reinforced concrete pier columns subjected to lateral impact [J]. Chinese Journal of Engineering, 2019, 41(3): 408 − 415. (in Chinese)
[9] HAN Linhai, TAO Zhong, YAO Guohuang. Behaviour of concrete-filled steel tubular members subjected to shear and constant axial compression [J]. Thin-Walled Structures, 2008, 46(7/8/9): 765 − 780.
[10] LEHMAN D, ROEDER C, HEID A, et al. Shear response of concrete filled tubes part 1: Experiments [J]. Journal of Constructional Steel Research, 2018, 150: 528 − 540. doi: 10.1016/j.jcsr.2018.08.027
[11] HOU Chuanchuan, HAN Linhai, LIANG Zhanshuo, et al. Performance of concrete-encased CFST subjected to low-velocity impact: Shear resistance analysis [J]. International Journal of Impact Engineering, 2021, 150: 103798. doi: 10.1016/j.ijimpeng.2020.103798
[12] 纪孙航, 王文达, 鲜威. CFRP加固火灾作用后圆钢管混凝土构件的侧向撞击性能研究[J]. 工程力学, 2021, 38(8): 178 − 191. doi: 10.6052/j.issn.1000-4750.2020.08.0586 JI Sunhang, WANG Wenda, XIAN Wei. Lateral impact behavior of CFRP-reinforced circular concrete-filled steel tubular members after exposure to fire [J]. Engineering Mechanics, 2021, 38(8): 178 − 191. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.08.0586
-
期刊类型引用(1)
1. 王刚，包延红. 侧向撞击荷载作用下方套方形钢管混凝土叠合柱动力响应的数值研究. 青海大学学报. 2023(06): 32-40 . 
百度学术
其他类型引用(4)
计量
- 文章访问数: 190
- HTML全文浏览量: 40
- PDF下载量: 53
- 被引次数: 5
