现场动力测试提供了一种获取振动信号的途径，已经被广泛应用于土木工程领域^[1]。在桥梁结构健康监测中，一般通过测得的动力响应反向识别结构模态参数(如频率、阻尼比和振型等)。由于难以获得完备的结构输入荷载信息和具有高信噪比的结构响应信息，识别的模态参数具有较大的不确定性(结果的离散性和较差的可重复性)。例如，识别的同一结构的阻尼比在不同测量数据集中表现出很大变异性^[2]，外界温度、拾振器位置以及建模误差等都可能引入误差^[3-5]。这种不确定性往往会掩盖潜在的结构损伤，给结构损伤识别和状态评估带来极大困难。振动测试中的不确定性无法避免，如何计算、理解、评价模态识别的不确定性，以及进一步采取措施优化振动测试方案以降低识别不确定性，对于提高桥梁结构损伤识别和状态评估的准确性和鲁棒性具有极大必要性和现实意义。

国内外研究者针对桥梁结构振动测试方面的研究已持续数十年，新的数据处理方法和测试工具不断涌现，然而大多聚焦于不确定性的定量计算。例如韩建平等^[6]和秦超等^[7]通过贝叶斯理论量化了环境激振下模态参数识别的不确定性。着眼于理解结构动力测试中不确定性产生的机理和影响要素，“不确定性定律”的概念被提出^[8]，即假定结构的动力响应近似满足线性时不变、经典阻尼的结构运动方程，求得长数据和小阻尼比条件下，模态参数估计值变异系数(标准差除以均值)的渐近解析表达式。近年来，针对环境激振测试，区教授团队先后发展了稀疏模态^[9]和密集模态^[10]下的不确定性定律，揭示了识别不确定性形成的内在机理。

在桥梁结构现场动力测试中，由于引入人为激振(如起振机激振、行车激振、跳车激振等)，测试数据的信噪比得以提高，进而可以有效降低模态参数识别不确定性。尽管成本相对较高，激振方法在桥梁荷载实验中仍得到有益发展，并在实桥动力测试中展示出良好应用前景，例如湖南大学的华旭刚教授提出连续跳车激振^[11]，通过增加桥梁振动幅值以提高自由振动下结构响应的信噪比，从而增加阻尼识别的可靠性。激振测试方案与模态识别精度相互影响，但如今仍缺乏对两者动力学互馈本质的理解，模态参数识别不确定性难以直接指导激振测试方案优化，导致激振测试的盲目性和模态识别的被动性。为此，本文提出了单点激振条件下模态参数识别的渐近不确定性并结合现场激振测试进行验证，旨在解构激振测试方案与模态参数识别不确定性影响要素的直接关系，为以降低识别不确定性为目标的激振测试方案优化提供科学依据。

1   贝叶斯FFT模态识别

基于线性时不变系统和经典阻尼假定，并假设在关心频带内只有一阶模态，实测结构加速度响应的频域信号可表示为：

式中：${\timesibfont\bf{\text{φ}}}$为测量点处的振型向量；${{\boldsymbol{\varepsilon}} _k}$为测量误差，假定其满足零均值，协方差为${S_e}{\boldsymbol{I}}$的复高斯分布(${S_{\rm{e}}}$为测量误差的功率谱密度，${\boldsymbol{I}}$为单位阵)；${\ddot {{\eta}} _k }$为结构模态加速度响应，在单点激振条件下的${\ddot {{\eta}} _k }$满足：

式中：$m$为激振器质量；$M$为结构模态质量；${\boldsymbol{ l}}$为一个无量纲的荷载分配系数，表示输入荷载与测量自由度的关联；${u_k}$为激振质量块加速度的傅里叶变换；${h_k}$为该模态频响函数，表示为：

式中：$f$/Hz为该模态的固有频率；${f_k} = k/N\varDelta t$，其中$N$和$\varDelta t$分别为采样样本数和采样间隔；${\rm{i }}$为虚数单位。将式(2)代入式(1)中可得：

需要指出的是，在式(4)中振型向量${\timesibfont\bf{\text{φ}}}$可以任意归一化，为使其可辨识，定义${\timesibfont\bf{\text{φ}} ^{\rm{T}}}{\boldsymbol{l }}= 1$，同时定义质量比修正振型${\timesibfont\bf{\text{φ}}}_r = (m/M){\bf\textit{φ}}$，从而定义待识别模态参数的集合${\boldsymbol{ \theta }} = \{ f,\varsigma , {\timesibfont\bf{\text{φ}}}_r ,{S_e}\}$。

基于复高斯分布噪声假定，在选定的频带内，${\hat {\boldsymbol{F}}_k}$满足独立复高斯分布^[8]，其均值为${h_k}{u_k} {\timesibfont\bf{\text{φ}}}_r$，协方差矩阵为${S_e}{\boldsymbol{I}}$。假定均匀分布的先验信息，根据贝叶斯定理，模态参数集${\boldsymbol{\theta}}$的后验概率密度函数可表示为：

其中：

是负对数似然函数。模态参数的极大后验估计通过求解式(6)所示的负对数似然函数的最小值确定。当使用高斯分布逼近后验分布时，协方差矩阵等于负对数似然函数Hessian(二阶偏导)矩阵在极大后验处的逆矩阵，具体算法可参见文献[12]。

2   渐近不确定性

快速贝叶斯FFT模态识别算法^[12]通过给出特定数据下的后验协方差来量化识别的模态参数的不确定性，但无法解释不确定性的形成机理和影响要素。例如，该结果无法解释激振器和拾振器的位置如何影响模态参数的识别不确定性。模态参数识别渐近不确定性则不依赖于特定的数据和算法，给出了不确定性的解析表达式，揭示了识别不确定性形成的内在机理。

假设在关心频带内只有一阶模态，相关模态参数$\theta = \{ f,\varsigma ,{{\bf\textit{φ}} _r},{S_e}\}$的定义与本文第1节一致。在单点激振条件下，激振质量块的加速度为$u(t)$，其与被测结构的模态质量比为$r = m/M$。用于模态识别的频带为$f(1 \pm \kappa \varsigma )$，其中$\kappa$是无量纲的带宽因子($\kappa = 1$对应半功率带宽)。假设测试时长为${T_d}$，则选取频带内的FFT点数为${N_f} = 2\kappa \varsigma {N_c}$，其中有效数据长度${N_{\rm{c}}} = {T_d}f$表征测试时长对应的振动周期数。基于以上定义，在长数据${N_f} \gg 1$和小阻尼比$\varsigma \ll 1$的假设下，模态参数变异系数的平方近似等于表1给出的解析表达式。

表  1  模态参数识别渐近不确定性核心结果

Table  1.  Key results of asymptotic identification uncertainty of modal parameters

模态参数$x$	模态参数变异系数的平方	数据长度因子${B_x}$	输入荷载因子${b_x}$
$f$	${\delta _f^2}\sim \dfrac{\varsigma }{ {2\pi {N_c}{B_f} } }\left(\dfrac{ { {b_f} } }{\gamma }\right)$	$\dfrac{2}{\pi }\left({\arctan }\kappa - \dfrac{\kappa }{{{\kappa ^2} + 1}}\right)$	$\dfrac{{2\left({\arctan}\kappa - \dfrac{\kappa }{{{\kappa ^2} + 1}}\right)}}{{\left({\arctan}\kappa + \dfrac{\kappa }{{{\kappa ^2} + 1}}\right)}}$
$\varsigma$	${\delta _\varsigma ^2}\sim \dfrac{1}{ {2\pi \varsigma {N_c}{B_\varsigma } } }\left(\dfrac{ { {b_\varsigma } } }{\gamma }\right)$	$\dfrac{2}{\pi }\left[{\arctan }\kappa + \dfrac{\kappa }{{{\kappa ^2} + 1}} - \dfrac{{2{{\left({\arctan}\kappa \right)^2}}}}{\kappa }\right]$	$\dfrac{{4{\arctan}\kappa \left[{\arctan}\kappa + \dfrac{\kappa }{{{\kappa ^2} + 1}} - \dfrac{{2{{\left({\arctan}\kappa \right)^2}}}}{\kappa }\right]}}{{\left({\arctan}\kappa + \dfrac{\kappa }{{{\kappa ^2} + 1}}\right)\left({\arctan}\kappa - \dfrac{\kappa }{{{\kappa ^2} + 1}}\right)}}$
$\overline {\bf\textit{φ}}$	${\delta _{\overline {\bf\textit{φ} } } ^2}\sim \dfrac{ {n - 1} }{ {2\pi \varsigma {N_c}{B_{\overline {\bf\textit{φ} } } } } }\left(\dfrac{ { {b_{\overline {\bf\textit{φ} } } } } }{\gamma }\right)$	$\dfrac{2}{\pi }{\arctan }\kappa$	$1$
注：$\overline {\bf\textit{φ} } = {\left\| { { {\bf\textit{φ} } _r} } \right\|^{ - 1} }{ {\bf\textit{φ} } _r}$为归一化后的振型；$\gamma = {S_u}{\left\| { { {\bf\textit{φ} } _r} } \right\|^2}/4{S_{{e} } }{\varsigma ^2}$为模态信噪比，其中${S_{{u} } } = {N_{f }^{ - 1} }\displaystyle\sum\nolimits_{ {N_f } } { { {\left| { {u_k } } \right|^2} } }$为激振质量块的加速度功率谱密度，假定其在选取频带内是常量；振型的变异系数定义为振型协方差矩阵特征值之和的平方根。

下载: 导出CSV 

| 显示表格

表1中解析表达式的推导主要利用长数据渐近性、小阻尼渐近性和渐近解耦性。长数据渐近性是指，在长数据条件下，即选取频带内包含测量数据FFT点数${N_f} \gg 1$，Hessian矩阵渐近收敛于Fisher信息阵，从而把Hessian矩阵的计算问题(二阶偏导)转换为Fisher信息阵的求解(一阶偏导)^[13]。对于均值为${{\bf\textit{μ}} _k}$、协方差矩阵为${\boldsymbol{C}}$的复高斯分布，其模态参数${\boldsymbol{\theta}}$的Fisher信息阵$J({\boldsymbol{\theta }})$具有以下形式：

小阻尼渐近性是指将式(7)的求和运算转化为积分运算，并只保留关于阻尼比的一阶项，从而获得简化的Fisher信息阵。渐近解耦性是指忽略Fisher信息阵相对较小的非对角元，进而解析求得Fisher信息阵的逆矩阵。最后，这一逆矩阵的对角元除以对应模态参数极大后验估计的平方即给出表1中模态参数变异系数的平方形式。为节省篇幅，本文忽略具体的推导过程，在第3节中以实验形式验证结果的正确性。

3   实验验证

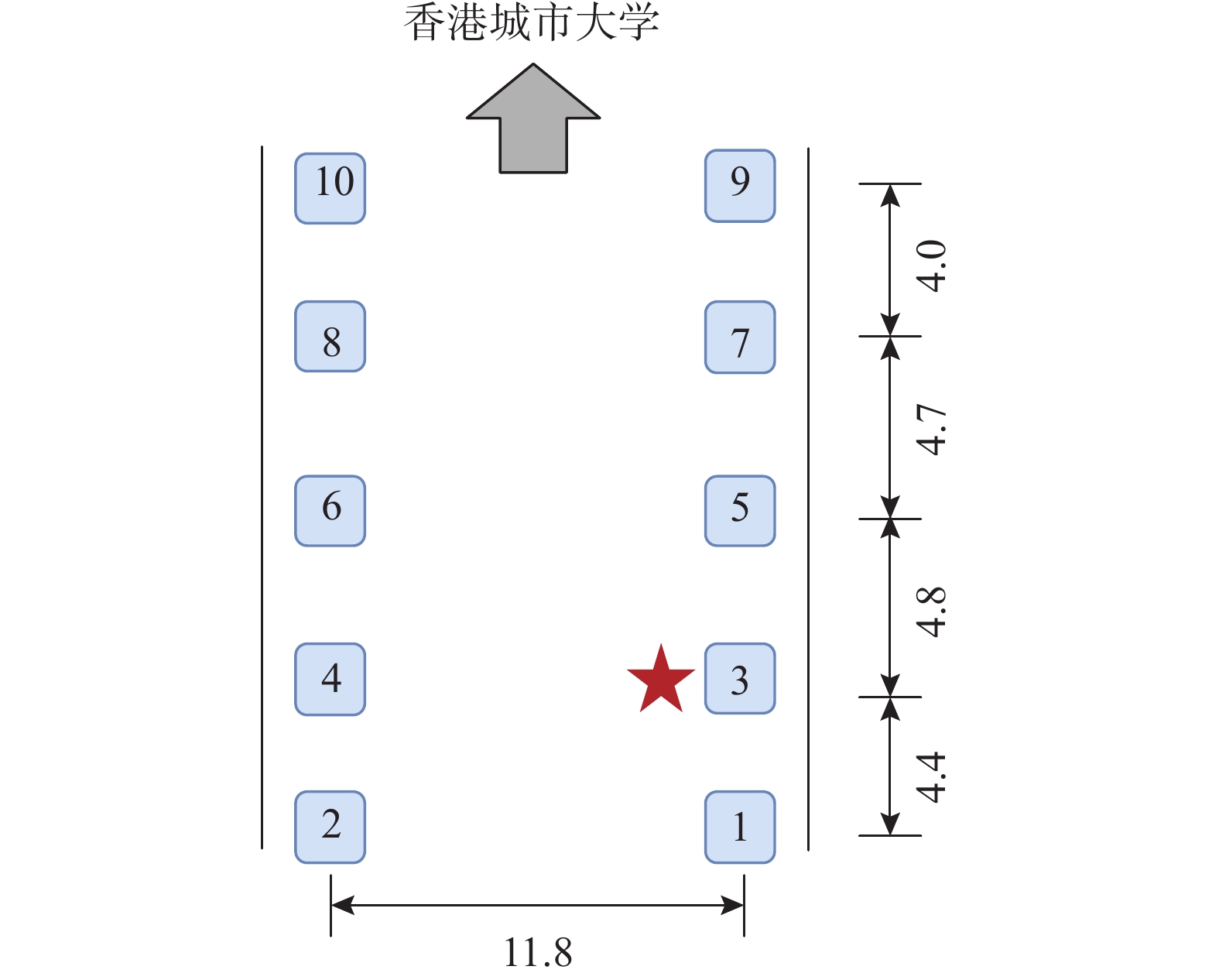
为验证所提出的模态参数识别渐近不确定性，本研究选取香港城市大学入口处的一座混凝土人行桥进行多次激振测试，试验布置方案如图1所示。在试验过程中，将一个激振质量为13.2 kg的电磁振动器(图1中五角星)作为激振设备，使其产生宽频伪随机信号。通过改变激振器的输入电压(1.1 V、1.5 V、1.9 V)实现不同的工况设置，并在不同输入电压下各重复10次激振测试。单次测试时长为60 s，包括激振器开启前和关闭后各10 s。本实验选用10个加速度计(图1中带数字的方框)分别测量相应测点处的竖向加速度响应，采样频率为2048 Hz，获取的数据在分析时则降采样到128 Hz。此外，在激振质量块上安装了相同规格的拾振器，用于记录其加速度时程。

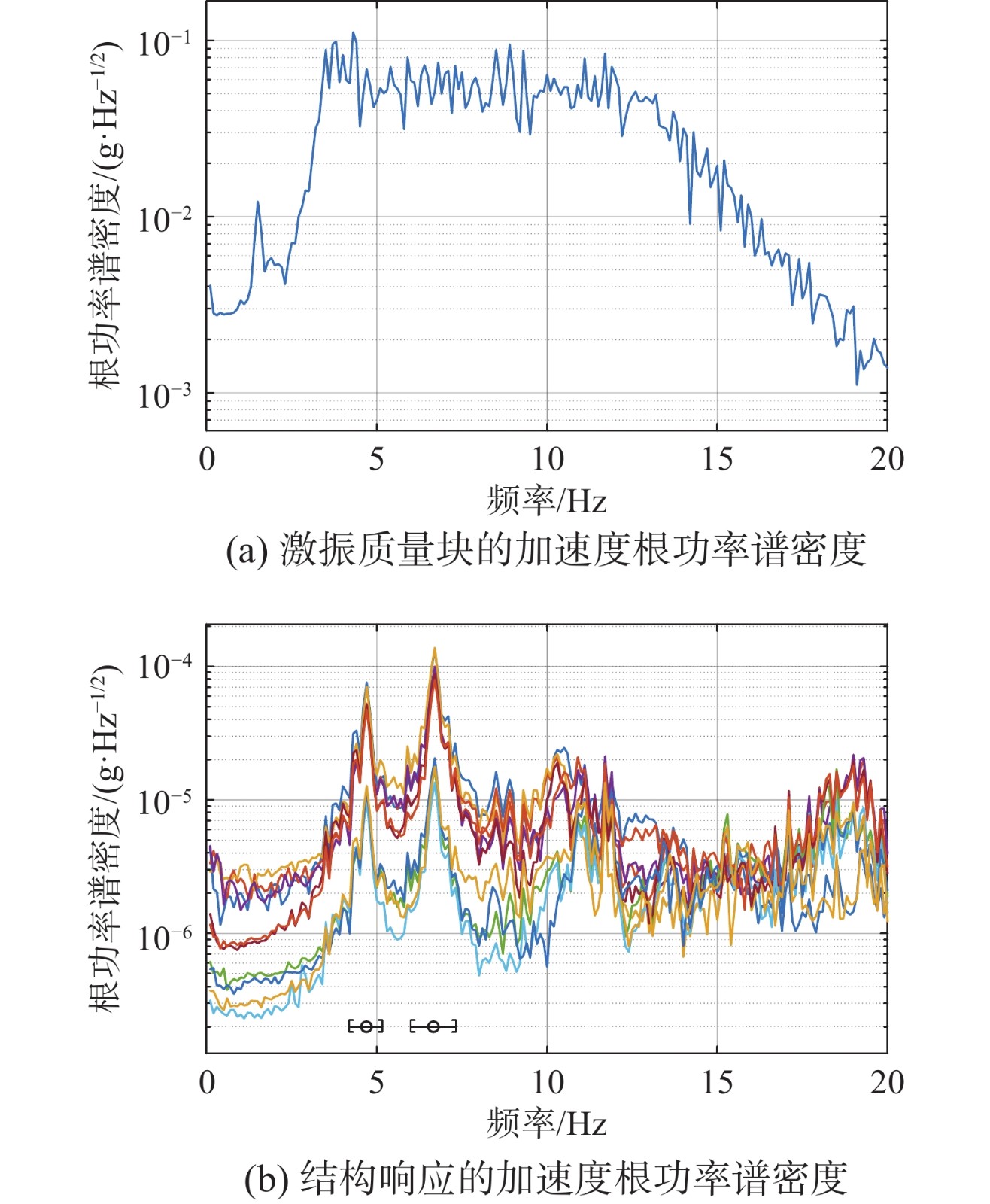
图2(a)是输入电压为1.9 V时激振质量块的典型加速度根功率谱密度，其在4 Hz~12 Hz内具有较为平坦的分布。相应结构响应的功率谱密度如图2(b)所示，通过其峰值可以发现在4 Hz~7 Hz内有两阶明显模态，在图中以空心圆圈表示。本文采用快速贝叶斯FFT模态识别算法^[12]在单点激振条件下识别这两阶模态。识别结果如图3所示，分别对应第一阶竖弯和第一阶扭转模态。

图  1  现场测试方案示意图　/m

Figure  1.  Schematic plot of test configuration

下载: 全尺寸图片 幻灯片

图  2  测得的输入和输出的根功率谱密度

(括号：选取的频带；圆圈：初始频率值)

Figure  2.  Root PSD of measured input and output

下载: 全尺寸图片 幻灯片

图  3  模态识别结果

Figure  3.  Results of modal identification

下载: 全尺寸图片 幻灯片

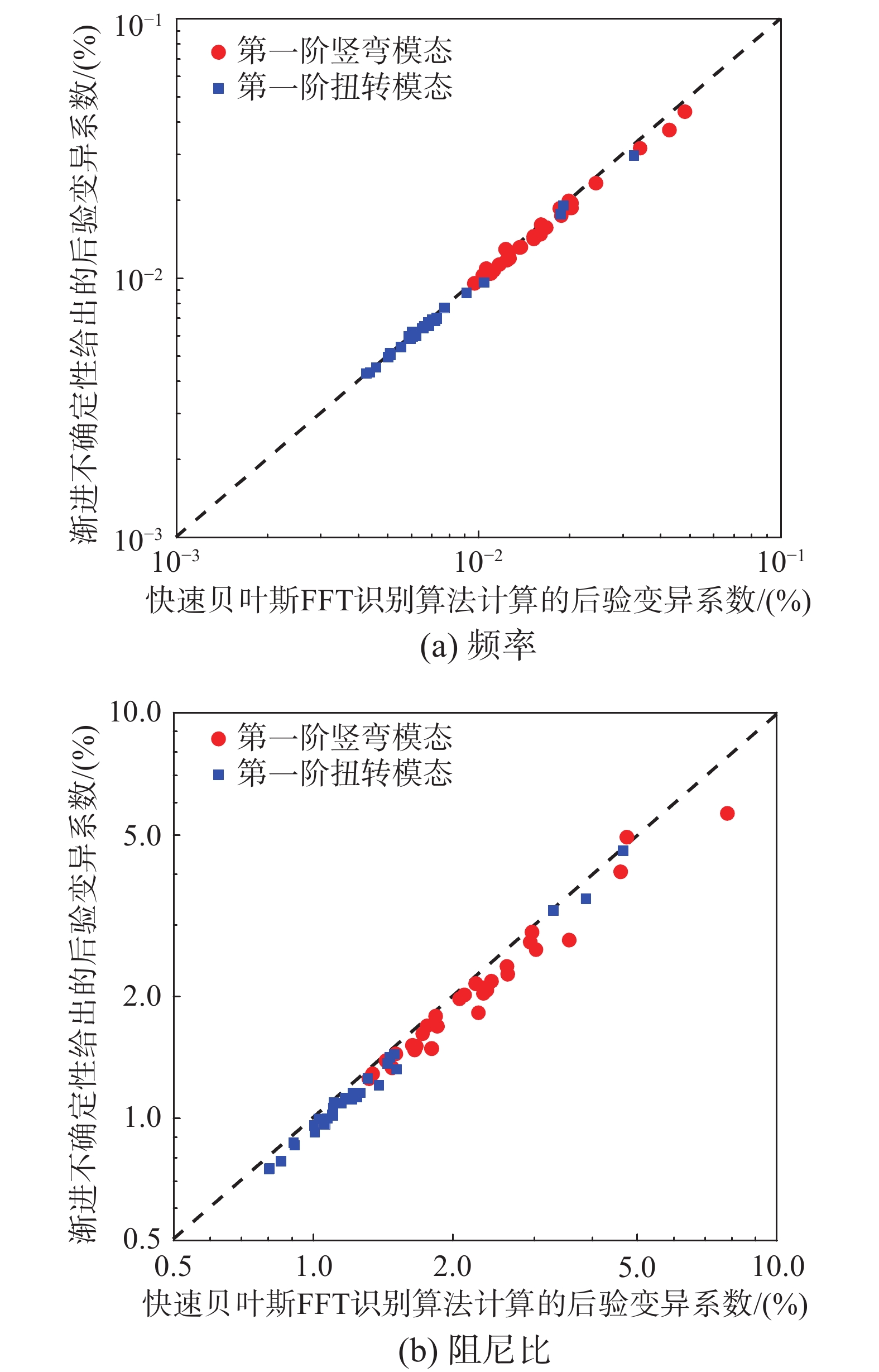
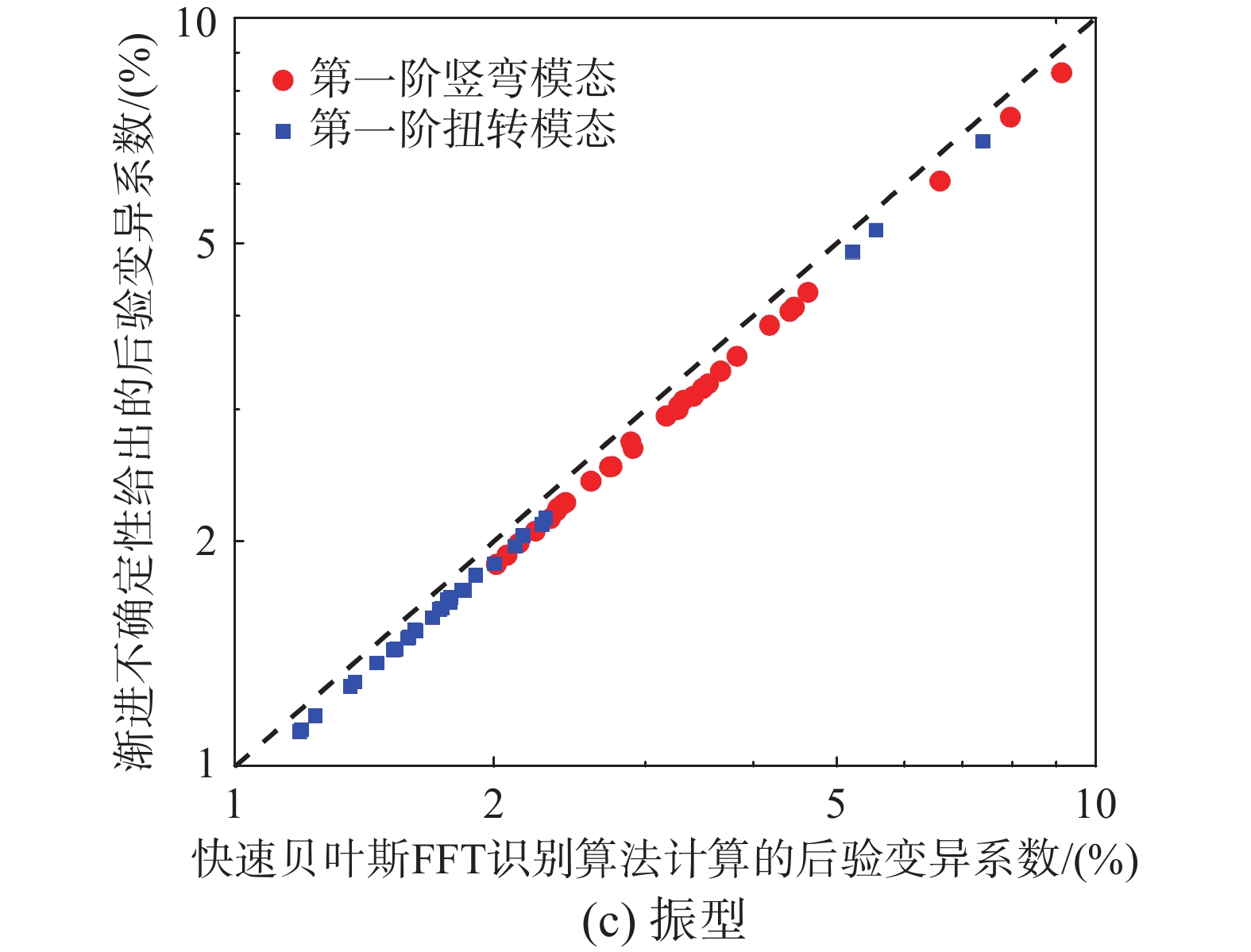
本文将基于渐近不确定性的模态参数后验变异系数与快速贝叶斯FFT模态识别算法给出的结果进行对比分析，如图4所示。图4中圆圈和方框分别表示第一阶竖弯和第一阶扭转模态的结果，中间的虚线表示两者计算结果完全一致。可以看出，所有散点均分布在虚线附近，说明本文所提出的渐近不确定性可较为准确地捕捉到影响模态参数识别不确定性的关键因素。就频率而言，其估计值的后验变异系数小(<1%)，说明其在现场动力测试中识别精度高。在运营模态分析中，阻尼比是极难被准确识别的模态参数，其不确定性常常超过50%。相比之下，当输入荷载已知时，阻尼比的后验变异系数明显降低，本文测得结果均低于10%。振型的后验变异系数与阻尼比类似，介于1%~10%之间。

下载: 全尺寸图片 幻灯片

  4  贝叶斯模态识别算法和渐近不确定性给出的模态参数后验变异系数

  4.  Posterior c.o.v. of modal parameters calculated by Bayesian modal identification and asymptotic uncertainty

下载: 全尺寸图片 幻灯片

4   结论

针对单点激振下模态参数识别的不确定性分析，本文基于长数据和小阻尼比假设提出模态参数识别渐近不确定性，并通过现场激振测试验证其正确性，可得到以下结论：

(1) 本文推求的模态参数识别渐近不确定性准确捕捉到频率、阻尼比和振型的后验不确定性，进而解构了模态参数识别不确定性的形成机理和影响要素。

(2) 在模态参数识别渐近不确定性中，频率变异系数的平方正比于阻尼比，而阻尼比和振型变异系数的平方则反比于阻尼比，解释了阻尼比和振型难以准确识别的原因。

模态参数识别渐近不确定性以解析表达式的给出，可用于指导结构激振测试实践，通过优化试验方案降低模态参数识别不确定性。