近年来，斜拉桥采用钢锚箱组合索塔锚固结构的应用逐渐增多。利用钢锚箱承担斜拉索水平分量的平衡部分，而不平衡水平索力由钢锚箱与混凝土塔壁共同分担，竖向索力则主要由混凝土塔壁承担并向塔柱下部传递至基础^[1-2]。为此，钢锚箱锚固方案可以较好地发挥钢与混凝土材料的各自优势，从而提高索塔锚固区的承载性能。

依据钢锚箱与混凝土塔壁的相对位置，该锚固方案主要分为内置型和外露型两种形式。1987年建成的比利时Ben-Ahin桥首次在混凝土索塔内置钢锚箱以锚固斜拉索^[3]，1995年建成的法国Normandie桥改进了钢锚箱构造以适应斜拉索空间双索面布置^[4]。国内的苏通长江大桥^[5]、杭州湾跨海大桥^[6]分别采用了内置型与外露型钢锚箱索塔锚固结构，显示了很好的应用前景。大跨径斜拉桥索塔锚固区的钢锚箱与混凝土塔壁形成框架结构，受力明确且承载力较高。

为了营造现代城市建筑景观，部分中小跨径桥梁也采用混凝土斜拉桥的结构形式。相比大跨径斜拉桥，城市斜拉桥的索塔截面相对较小，采用钢锚箱组合索塔锚固结构，可以满足斜拉索张拉所需索塔内腔空间，同时抵抗因桥面较宽而增大的斜拉索力。为进一步减小索塔结构尺寸，避免粗笨的索塔截面造成桥梁外形比例不协调，选用外露型钢锚箱索塔锚固结构，并使钢锚箱侧板与混凝土塔壁密贴。索塔锚固区在索力作用下将处于偏心拉压受力状态，同时预应力也将对锚固区受力机理产生较大影响。

既有研究采用模型试验、数值模拟和理论解析等手段，探讨钢锚箱组合索塔锚固结构的承载性能、变形性能和传力机理等。因钢与混凝土结合部刚度变化大，传力机理较为复杂，通常采用平面框架模型进行设计计算。钢锚箱与混凝土塔壁的协同受力状态较为复杂，已有研究很少考虑钢锚箱壁板与混凝土塔壁间相对滑移，对结合部连接件作用机理研究不足^[7-11]。特别是中小跨径斜拉桥采用的外露型钢锚箱，其钢侧板与混凝土塔壁密贴，已不适合采用框架模式进行受力分析。

为此，本文以一座独塔双索面混凝土斜拉桥为依托工程背景，基于弹性介质层法^[10]，考虑钢锚箱侧壁板与混凝土塔壁间的部分连接与滑移效应，推导了外露型钢锚箱索塔锚固结构的结合面相对滑移解析公式；计算其钢与混凝土构件的水平受力分配关系，并与锚固区节段模型试验结果对照以验证理论推导的合理性；进一步通过参数化分析探讨钢锚箱侧壁板厚度、混凝土塔壁厚度、结合面传力长度、连接件抗剪刚度与顺桥向预应力作用对锚固区水平传力机理的影响。

1   外露型钢锚箱索塔锚固区构造

本研究的工程背景是一座主跨123 m的独塔双索面城市斜拉桥^[9]。索塔上塔柱10对斜拉索的索力较大，最大设计索力达到7040 kN，采用外露型钢锚箱进行塔端锚固，受力状态较为复杂。相比大跨斜拉桥组合索塔锚固区的平面布置接近框架受力，该桥锚固区混凝土与外露型钢锚箱因侧面密贴而更接近组合柱的轴向受力。相比组合柱在结合部连续布置连接件，该桥锚固区混凝土与外露型钢锚箱仅在两端锚头附近局部布置连接件，难以直接应用连续弹性介质层法分析其受力。

图1为外露型钢锚箱组合索塔锚固区的典型节段构造，主要包括中间的钢锚箱、两侧的混凝土塔壁、预应力筋及钢混结合部的连接件。钢锚箱为矩形结构，由侧板、端板、锚垫板、承压板、支承板和加劲板等组成。内侧混凝土塔壁为等厚度的矩形截面，而外侧塔壁为变厚度的五边形截面。钢锚箱通过侧板两端的圆柱头焊钉连接件与混凝土塔壁连接。

图  1  外露型钢锚箱索塔锚固区构造^[9]　/mm

Figure  1.  Cable-tower anchorage with exposed steel anchor box^[9]

下载: 全尺寸图片 幻灯片

外露型钢锚箱索塔锚固结构在索力作用下，其横断面偏心受拉而局部发生弯曲变形，使得钢锚箱与混凝土塔壁结合部的焊钉承受拉拔力作用，从而影响剪力传递的效果。为此，在索塔锚固区设置“井”字型预应力筋，顺桥向预应力筋采用钢绞线，横桥向预应力筋采用精轧螺纹钢，从而抵抗斜拉索的水平索力。横桥向预应力可限制混凝土塔壁与钢锚箱因局部弯曲而发生剥离，故顺桥向预应力的作用近似为轴向荷载。

2   组合索塔锚固区水平传力模型

2.1   基本假设

选取外露型钢锚箱组合索塔锚固区的典型节段，分析各构件沿顺桥向的水平受力机理。主要考虑的荷载为斜拉索力的水平分量和顺桥向预应力，以轴力的形式分别作用在钢锚箱侧壁板和混凝土塔壁上，并通过连接件剪力在两种构件之间传递和重新分配。同时，考虑到钢锚箱侧壁板的板厚相对于混凝土塔壁的厚度很小，对塔壁截面抗弯刚度的贡献可以忽略。为此，在分析外露型钢锚箱与塔壁相互作用时，采用以下假设条件：

1)钢锚箱侧壁板、塔壁应变各符合平截面；

2)轴向小变形，忽略弯曲和剪切变形；

3)连接件沿顺桥向剪力与相对滑移成正比；

4)忽略钢锚箱侧壁板与塔壁间粘结摩擦。

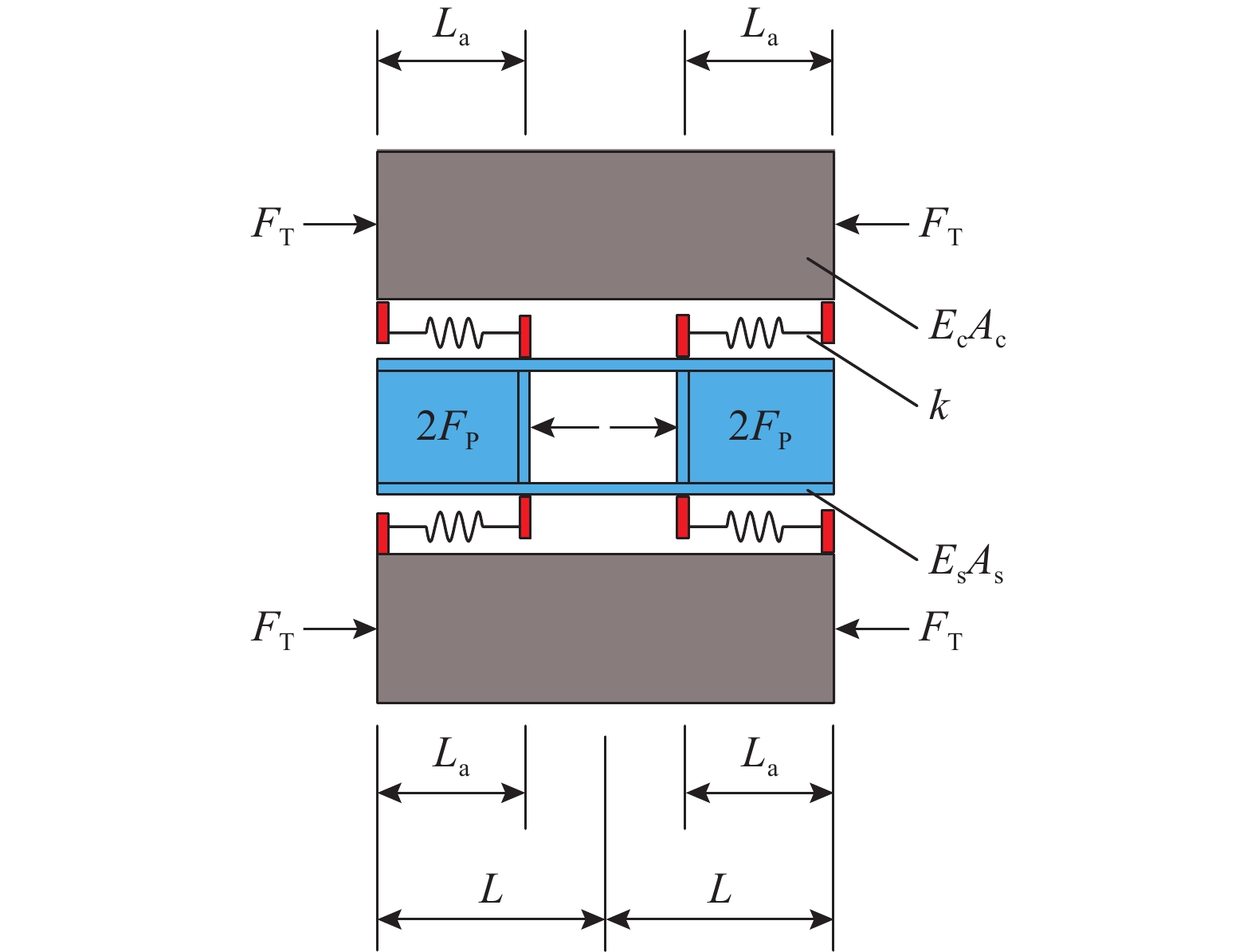
图2所示为外露型钢锚箱-塔壁水平作用计算模型。由于各钢锚箱节段沿顺桥向受力主要由节段内的钢侧壁板与混凝土塔壁承担，可截取其中一个典型钢锚箱节段作为研究对象。设其顺桥向长度为2L，锚头水平传力长度为L_a，连接件布置范围与锚头相同。将节段内水平索力2F_P等效为均布荷载p作用于L_a范围内；将顺桥向预应力作用2F_T等效为集中力作用于混凝土塔壁的端面。钢侧壁板、混凝土塔壁的弹性模量及截面积分别为E_s、E_c及A_s、A_c。设钢锚箱锚头一侧的连接件行数为n，顺桥向间距为d，单个连接件抗剪刚度为k_s，由推出式模型试验测得的剪力-滑移曲线确定^[12-13]。可将每个离散的连接件作用等效为沿d连续均匀分布的抗剪滑移层，则单位长度抗剪刚度为k=nk_s/d。除锚头外区域的滑移层抗剪刚度为k=0。

图  2  外露型钢锚箱-塔壁水平作用计算模型

Figure  2.  Horizontal load transfer model of exposed steel anchor box and concrete tower

下载: 全尺寸图片 幻灯片

2.2   无连接有滑移段传力解析

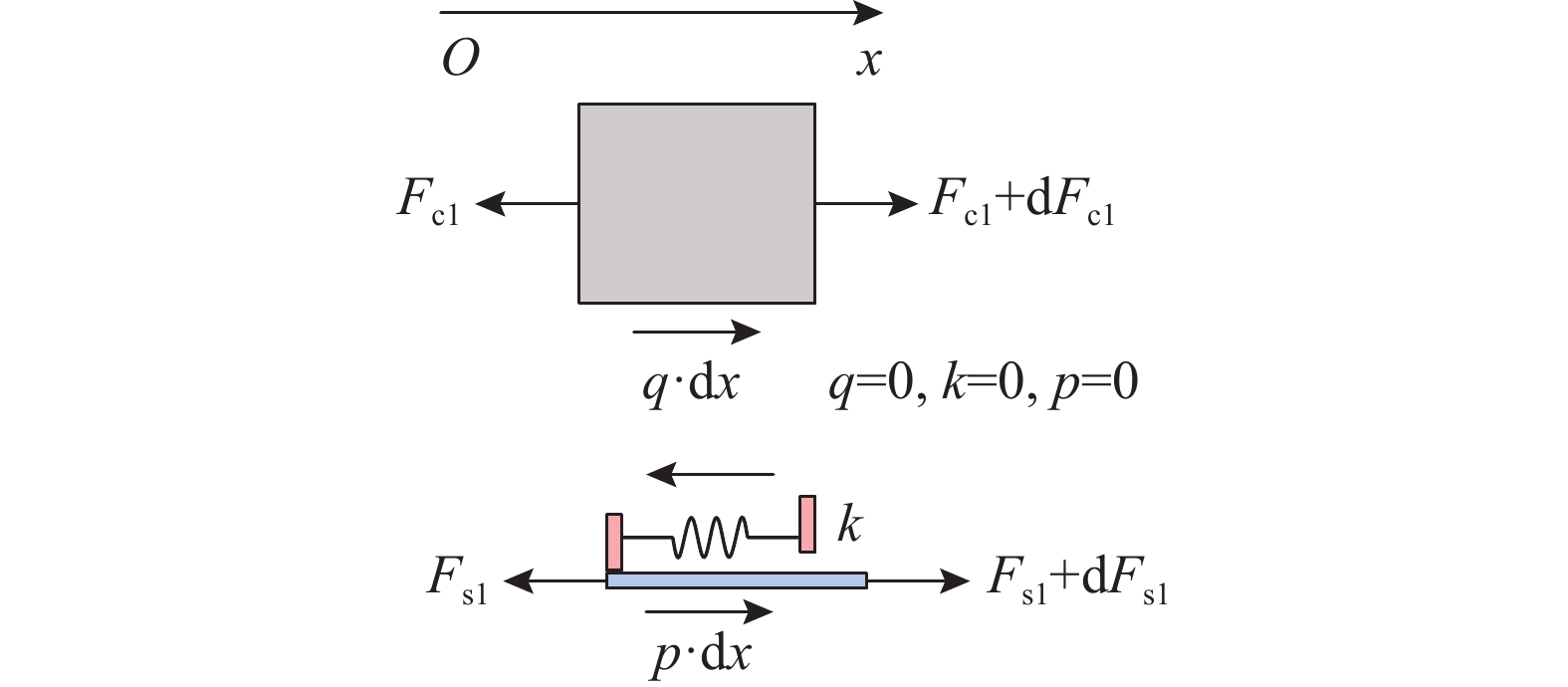
图3所示为外露型钢锚箱侧壁板-塔壁微段计算模型。以钢锚箱节段顺桥向轴线的中点为原点，沿顺桥向指向外侧为x轴正向，建立一维直角坐标系，并截取坐标x处、长度为dx的钢锚箱侧壁板-塔壁微段。钢侧壁板中段2(L−L_a)范围内为无索力荷载、无抗剪连接的区域；两端钢锚头长度均为L_a，直接作用水平索力，而且设置了连接件用于传力；顺桥向最外端，预应力筋锚固于塔壁端部。

图  3  无连接微段计算模型

Figure  3.  Infinitesimal element model without connection

下载: 全尺寸图片 幻灯片

第一区间为无连接有滑移段，则钢壁板微段上仅作用轴力F_s1与F_s1+dF_s1，混凝土塔壁微段上仅作用轴力F_c1与F_c1+dF_c1。

取钢壁板与混凝土塔壁受拉为正，依据微段沿顺桥向的内力平衡条件得：

考虑钢壁板及混凝土塔壁均为线弹性材料，沿轴向发生小变形，且应变分别满足平截面假定：

该区间内无连接件，钢混界面剪力流q显然为0。同时，顺桥向滑移s₁即钢锚箱壁板与混凝土塔壁顺桥向变形的差值，由变形协调条件得：

将式(3)和式(4)代入式(5)，再对两侧求x的一阶导数得：

将式(1)和式(2)代入式(6)，得到以钢混界面滑移s₁表示的变形协调微分方程：

式(7)为钢混界面滑移s₁关于顺桥向坐标x的常系数一元二次微分方程，其通解为：

2.3   有连接有滑移段传力解析

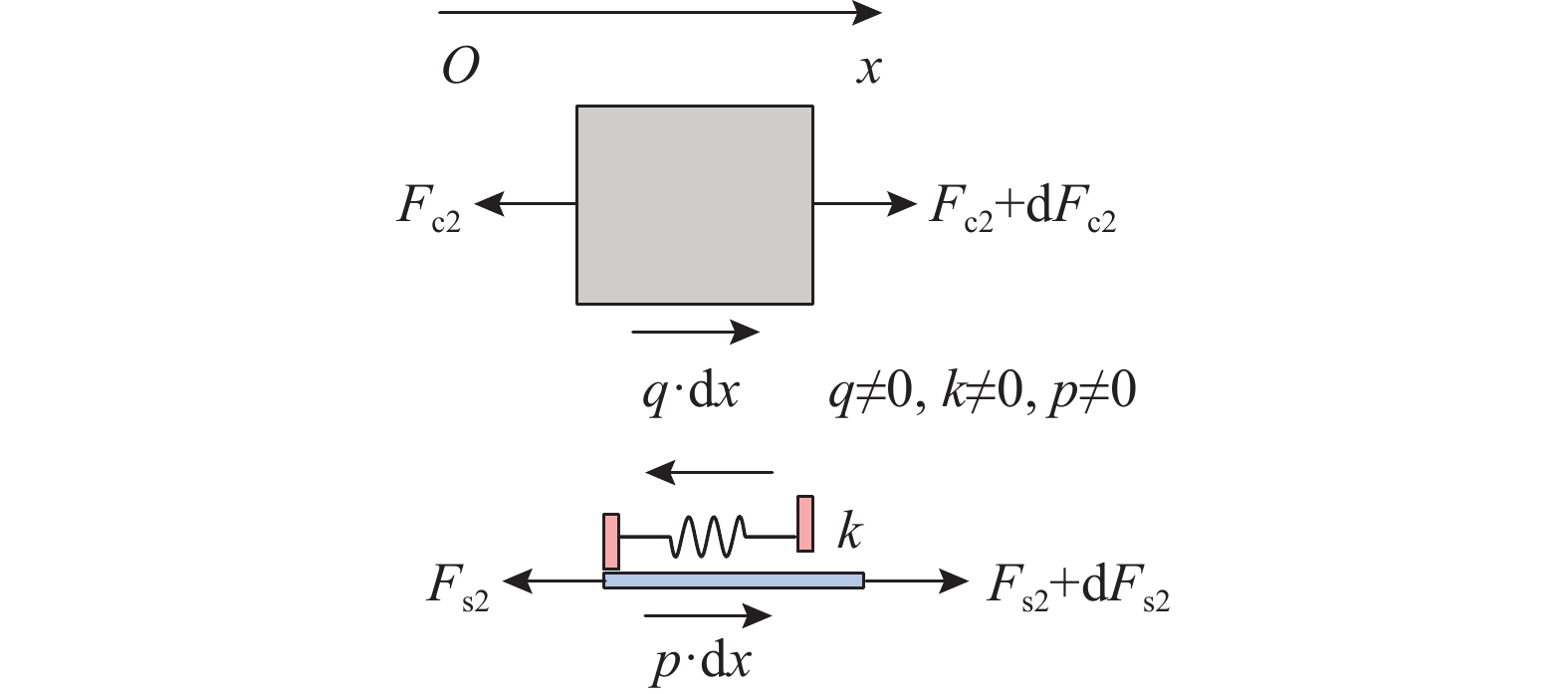
如图4所示，第二区间为有连接有滑移段，则钢壁板微段上作用单位长度水平索力p=F_P/L_a、连接件顺桥向剪力流q及轴力F_s2与F_s2+dF_s2，同时混凝土塔壁微段上作用轴力F_c2与F_c2+dF_c2。

图  4  有连接微段计算模型

Figure  4.  Infinitesimal element model with connection

下载: 全尺寸图片 幻灯片

取钢壁板与混凝土塔壁受拉为正，依据微段沿顺桥向的内力平衡条件得：

考虑钢壁板及混凝土塔壁均为线弹性材料，沿轴向发生小变形，且应变分别满足平截面假定：

由钢混界面连接件剪力与相对滑移成正比得钢混界面的单位间距内连接件剪力流为：

钢混界面的顺桥向滑移s₂即钢锚箱壁板与混凝土塔壁顺桥向变形的差值，由变形协调条件得：

将式(11)和式(12)代入式(14)，再对两侧求x的一阶导数得：

将式(9)和式(10)代入式(15)，并移项整理得：

设$\beta = \displaystyle\sqrt {\frac{k}{{{E_{\text{s}}}{A_{\text{s}}}}} + \frac{k}{{{E_{\text{c}}}{A_{\text{c}}}}}}$，则式(16)简化为以钢混界面滑移s₂表示的变形协调微分方程：

式(17)为钢混界面滑移s₂关于顺桥向坐标x的常系数一元二次微分方程，其通解为：

2.4   利用边界与连续条件求解

由对称性可知，沿顺桥向轴线的中点处，钢锚箱侧壁板与混凝土塔壁的轴向变形均为0，故此处的钢混界面滑移为0，即边界条件为：

在无连接、有连接的交界点，钢锚箱侧壁板与混凝土塔壁的轴向位移与应变分别是连续的，则钢混界面滑移及其一阶导数均连续，由连续条件得：

混凝土塔壁端部直接承受顺桥向预应力作用，再逐步传递至钢侧壁由组合截面共同承担。设预应力效应沿塔截面均匀分布，则边界条件为：

将式(19)~式(22)代入通解式(8)和式(18)，并设${L_{\text{b}}} = \left[ {1 + \beta (L - {L_{\text{a}}})} \right]{{\text{e}}^{2\beta {L_{\text{a}}}}} + \left[ {1 - \beta (L - {L_{\text{a}}})} \right]$，解得常系数C₁~C₄：

将常系数式(23)~式(26)代入通解式(8)和式(18)，可整理得钢锚箱侧壁板与混凝土塔壁相对滑移s₁和s₂的理论计算式：

将式(27)与式(28)合并得，钢锚箱侧壁板与混凝土塔壁相对滑移s的分段函数计算式：

将式(29)代入式(13)得，钢混界面的单位间距内连接件剪力流q为：

依据式(1)、式(2)、式(9)和式(10)积分得，钢锚箱壁板与混凝土塔壁的顺桥向轴力分别为：

3   水平传力模型的算例与验证

图5为本研究工程背景实桥的1∶2缩尺模型试件，选取自实桥最大设计索力为7040 kN的索塔锚固区节段^[9]。缩尺原则为应力等效。考虑实桥节段高度1800 mm缩尺后为900 mm，同时混凝土的上下端均超出钢结构50 mm以减小边界影响，故取模型试件的混凝土塔壁高度为1000 mm。实桥外侧塔壁采用五边形截面仅为景观需求，模型试件将其简化为与内侧塔壁对称的矩形，缩尺后单侧塔壁的尺寸为1860 mm × 450 mm × 1000 mm。节段模型中的钢结构板件均按比例缩尺制作。实桥钢锚箱双侧板两端的钢混结合部采用圆柱头焊钉，单侧一端布置12行6列，规格为ϕ25×200，水平和竖向间距分别为100 mm和150 mm。模型试件依据刚度等效，单侧一端布置12行4列的ϕ16×120焊钉连接件，水平和竖向间距均为75 mm。混凝土塔壁沿横向和纵向分别锚固4根、6根精轧螺纹预应力筋，模拟实桥锚固区横桥向和顺桥向预应力作用。由模型试件参数得：L_a=300 mm，k_s=292.4 kN/mm，E_s=205 GPa，E_c=37.3 GPa，A_s=1.08×10⁴ mm²，A_c=4.50×10⁵ mm²。

图  5  外露型钢锚箱索塔锚固区节段模型　/mm

Figure  5.  Segment model of cable-tower anchorage with exposed steel anchor box

下载: 全尺寸图片 幻灯片

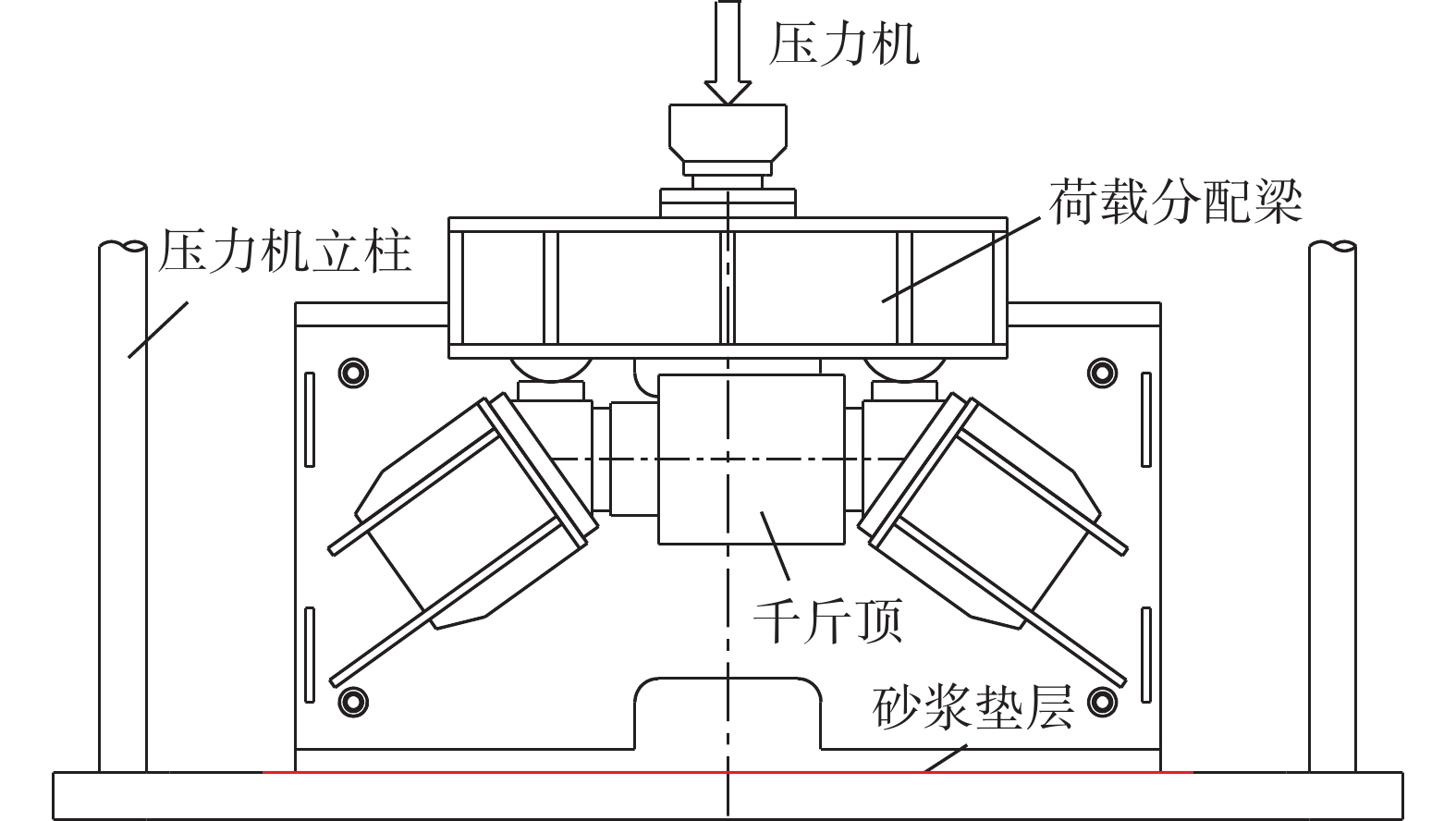
图6所示为外露型钢锚箱索塔锚固区节段模型试验的加载方案。将斜拉索力正交分解，通过压力机施加竖向索力，利用千斤顶施加水平索力。如表1所示，共比较3个工况的试验与计算结果。工况1：横桥向及顺桥向预应力钢筋全部张拉至设计值，未施加索力荷载；工况2：保持横桥向及顺桥向预应力，施加1.0P索力荷载；工况3：保持横桥向预应力，释放顺桥向预应力，重新施加1.0P索力荷载。其中，计算结果考虑按平截面假设及按计算式(31)~式(32)两种情况，分别与外露型钢锚箱索塔锚固区节段模型试验结果进行比较分析。通过在钢混结合部设置位移计，测试钢锚箱与混凝土塔壁的相对滑移与剥离位移。在钢锚箱侧板外侧的焊钉连接件间设置应变花，测得钢侧板截面轴力分布，并逐层求差值得到焊钉连接件的剪力。

图  6  锚固区节段模型加载方案

Figure  6.  Loading of segment model of cable-tower anchorage

下载: 全尺寸图片 幻灯片

表  1  试验与计算结果比较

Table  1.  Comparison of tested and calculated results

工况	横桥向 预应力/kN	顺桥向 预应力/kN	竖向 索力/kN	水平 索力/kN	钢侧板正应力						混凝土塔壁正应力
					试验值/ MPa	平截面/ MPa	计算式/ MPa	(平截面/ 试验值)/(%)	(计算式/ 试验值)/(%)		试验值/ MPa	平截面/ MPa	计算式/ MPa	(平截面/ 试验值)/(%)	(计算式/ 试验值)/(%)
1	120	378	0	0	−19.8	−12.20	−10.80	62	55		−1.89	−2.23	−2.26	118	120
2	120	378	1010	1442	21.6	−4.46	6.55	−21	30		−1.26	−0.81	−1.07	64	85
3	120	0	1010	1442	35.0	7.78	17.40	22	50		0.83	1.42	1.18	171	142

下载: 导出CSV 

| 显示表格

3.1   结合面滑移与连接件受力

图7所示为3种工况下钢锚箱侧壁板与混凝土塔壁间结合面的相对滑移。在顺桥向预应力、水平索力单独作用，以及两者同时作用的情况下，钢混结合面的相对滑移均随着与索塔对称轴距离的增加而增大，并在顺桥向的端部达到最大值。其中顺桥向预应力、水平索力引起的最大相对滑移分别为0.015 mm、0.040 mm，两者同时作用时的最大相对滑移为0.055 mm。

图  7  钢混结合面滑移

Figure  7.  Slip of steel-concrete interface

下载: 全尺寸图片 幻灯片

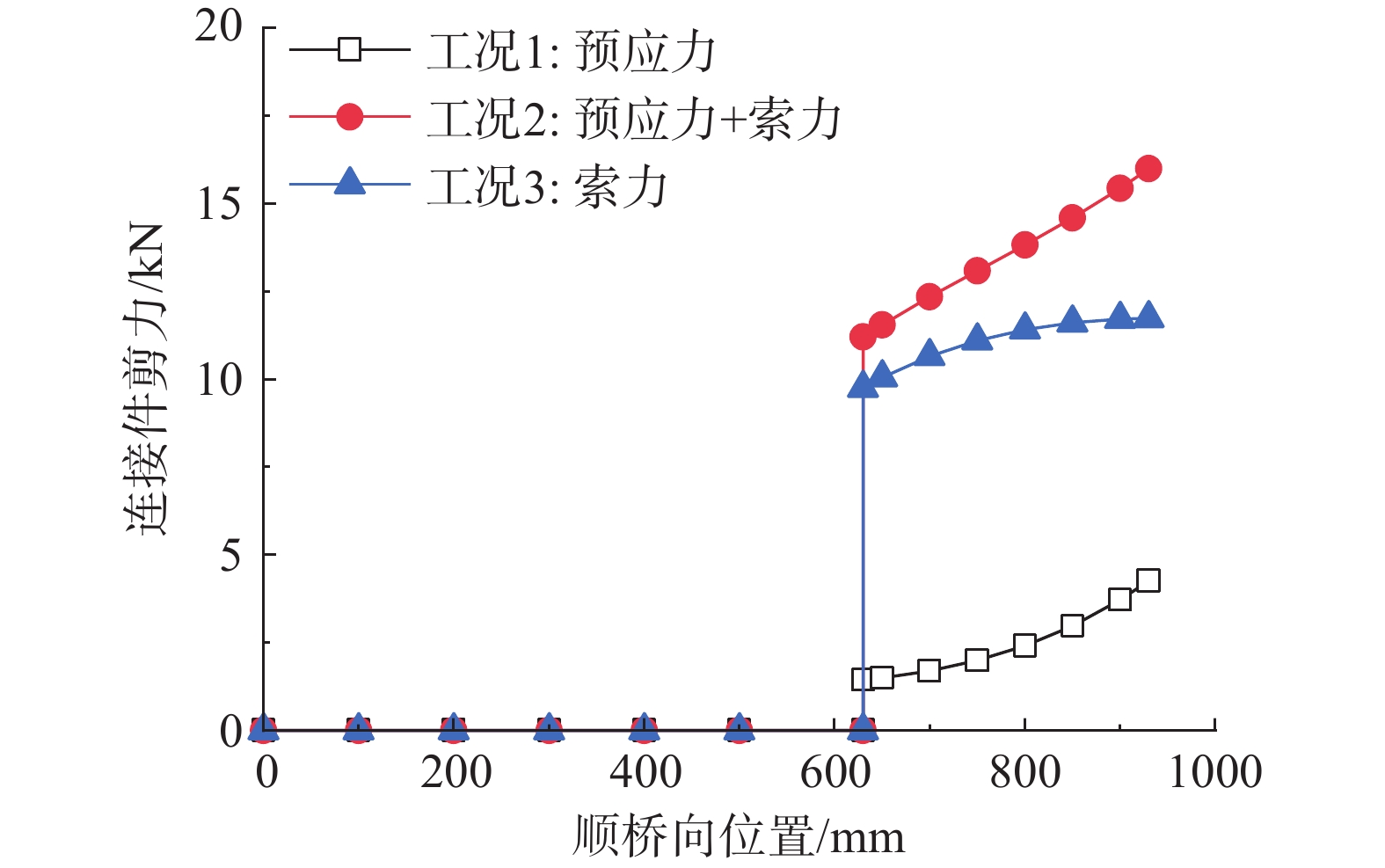
图8所示为钢混结合面焊钉连接件的顺桥向剪力。靠近索塔对称轴的区域未布置连接件，钢锚箱侧壁板与混凝土塔壁可发生相对滑移而不传递水平力。顺桥向的端部附近即钢锚头区域布置了焊钉连接件，其顺桥向剪力随着与索塔对称轴距离的增加而增大。其中顺桥向预应力、水平索力引起的最大连接件剪力分别为4.26 kN、11.73 kN，两者同时作用时的最大连接件剪力为15.99 kN。

图  8  焊钉连接件剪力

Figure  8.  Shear force of stud connector

下载: 全尺寸图片 幻灯片

3.2   钢侧板与塔壁的轴力分配

图9所示为3种工况下钢锚箱侧壁板与混凝土塔壁的截面轴力分配关系。由于顺桥向端部焊钉连接件的传力作用，钢锚箱侧壁板与混凝土塔壁的轴力在顺桥向端部变化明显，而在靠近索塔对称轴的区域趋于平稳。

图  9  钢侧板与塔壁的轴力分配

Figure  9.  Distribution of axial forces between steel side plate and tower wall

下载: 全尺寸图片 幻灯片

顺桥向预应力作用在端部全部由混凝土塔壁承担，然后逐渐传递至钢锚箱侧壁板。钢壁板、塔壁在索塔对称轴位置受到轴向压力−116.80 kN、−1017.20 kN，全截面合力为−1134 kN，钢混构件轴力分配比例分别为10%、90%。

水平索力作用在靠近索塔对称轴的区域由钢锚箱侧壁板与混凝土塔壁共同承担，在顺桥向的端部逐渐减小至0。钢壁板、塔壁在索塔对称轴位置分别受到轴向拉力187.55 kN、533.45 kN，全截面合力为721 kN，钢混构件的轴力分配比例分别为26%、74%。

在顺桥向预应力与水平索力共同作用下，钢锚箱侧壁板在锚头附近局部受压而总体受拉，混凝土塔壁则全部处于受压状态。在索塔对称轴位置，钢壁板截面受到拉力70.75 kN，塔壁截面受到压力−483.75 kN，全截面合力为轴向压力−413 kN。

3.3   钢侧板与塔壁的应力状态

图10所示为3种工况下钢锚箱侧壁板与混凝土塔壁的顺桥向正应力。由于顺桥向端部焊钉连接件的传力作用，钢锚箱侧壁板与混凝土塔壁的应力在顺桥向端部变化明显，而在靠近索塔对称轴的区域趋于平稳。在顺桥向预应力、水平索力单独作用，以及两者同时作用的情况下，钢锚箱侧壁板的正应力在顺桥向端部均为0，而在索塔对称轴位置分别为−10.81 MPa、17.37 MPa和6.55 MPa。同时，混凝土塔壁正应力在顺桥向端部为−2.52 MPa、0 MPa和−2.52 MPa，而在索塔对称轴位置分别为−2.26 MPa、1.19 MPa和−1.07 MPa。

图  10  钢侧板与塔壁的正应力

Figure  10.  Normal stresses of steel side plate and tower wall

下载: 全尺寸图片 幻灯片

3.4   理论计算式的实验验证

由表1可知，依据平截面假定直接按截面刚度分配水平索力与顺桥向预应力荷载，计算得到的钢侧板正应力、混凝土塔壁正应力与试验值^[9]存在较大差异。顺桥向预应力与水平索力同时作用时，钢侧板正应力的平截面计算值与试验值出现符号相反的情况，这对于分析外露型钢锚箱组合索塔锚固区的水平传力机理将产生较大干扰。其原因主要是钢锚箱侧壁板与混凝土塔壁间仅在靠近端部的部分区域设置连接件，而平截面假定更接近于钢混结合面全部设置连接件的情况。

相比平截面假定计算值，按计算式(31)~式(32)的计算结果与试验结果吻合更好，钢侧板正应力、混凝土塔壁正应力与试验值的正负号相符，即构件受拉或受压的状态保持一致，能够更准确地把握钢锚箱与混凝土塔壁的水平受力机理。其中，钢侧板正应力相比试验值较小，这可能是由于钢锚箱的锚头实际上为斜向受力，钢侧板的应力流分布较不均匀。混凝土塔壁正应力计算值与试验值吻合较好，这表明计算式(31)~式(32)能够较合理地反映混凝土塔壁在水平索力、顺桥向预应力荷载共同作用下的受力状态。

4   水平传力机理的参数化分析

4.1   钢锚箱侧壁板厚度的影响

图11所示为钢锚箱侧壁板厚度对锚固区水平传力机理的影响。随着钢锚箱侧壁板厚度由6 mm增加至30 mm，焊钉连接件顺桥向剪力由16.43 kN变化为15.49 kN，减小6%；钢侧壁板正应力由8.35 MPa变化为5.51 MPa，减小34%；混凝土塔壁正应力由−0.98 MPa变化为−1.14 MPa，绝对值增大16%。

图  11  钢锚箱侧壁板厚度的影响

Figure  11.  Influence of side plate thickness of steel anchor box

下载: 全尺寸图片 幻灯片

这主要因为钢锚箱侧壁板厚度越大，其分担的斜拉索水平分力就越大，而传递至混凝土塔壁的斜拉索水平分力就相应减小，故钢混结合面焊钉连接件顺桥向剪力减小。钢侧壁板的受力面积随厚度增加而增大，故钢侧壁板正应力减小。混凝土塔壁所受斜拉索水平分力减少，则顺桥向预应力作用更显著，故塔壁压应力绝对值增大。

4.2   混凝土塔壁厚度的影响

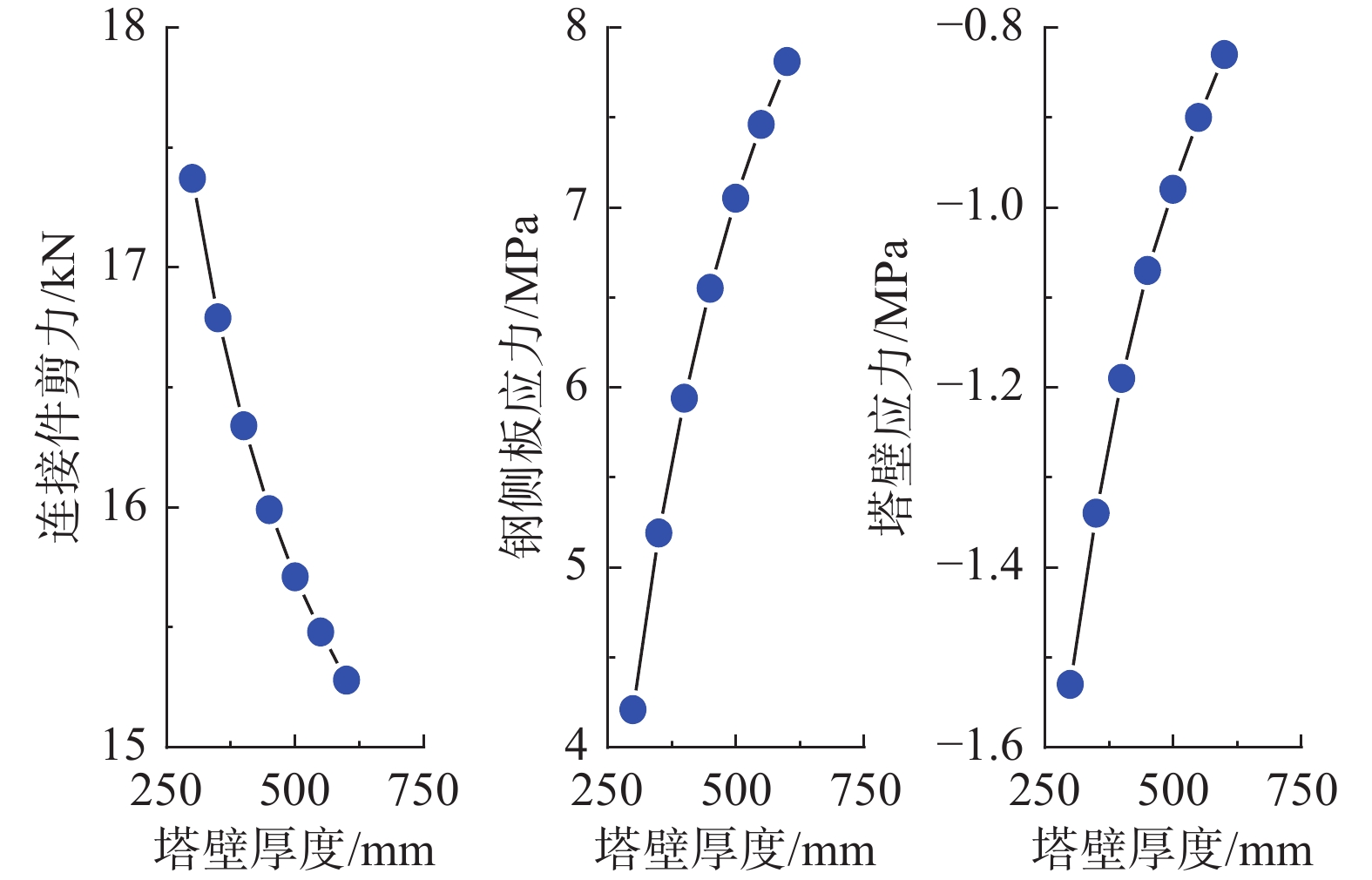
图12所示为混凝土塔壁厚度对锚固区水平传力机理的影响。随着混凝土塔壁厚度由300 mm增加至600 mm，焊钉连接件顺桥向剪力由17.37 kN变化为15.28 kN，减小12%；钢侧壁板正应力由4.21 MPa变化为7.81 MPa，增大86%；混凝土塔壁正应力由−1.53 MPa变化为−0.83 MPa，绝对值减小46%。

图  12  混凝土塔壁厚度的影响

Figure  12.  Influence of thickness of concrete tower wall

下载: 全尺寸图片 幻灯片

这主要因为混凝土塔壁厚度越大，其分担的顺桥向预应力就越大，而传递至钢锚箱侧壁板的预应力相应减小，故钢混结合面焊钉连接件顺桥向剪力减小，同时钢侧壁板正应力减小。混凝土塔壁的受力面积随厚度增加而增大，故塔壁压应力的绝对值增大。

4.3   结合面传力长度的影响

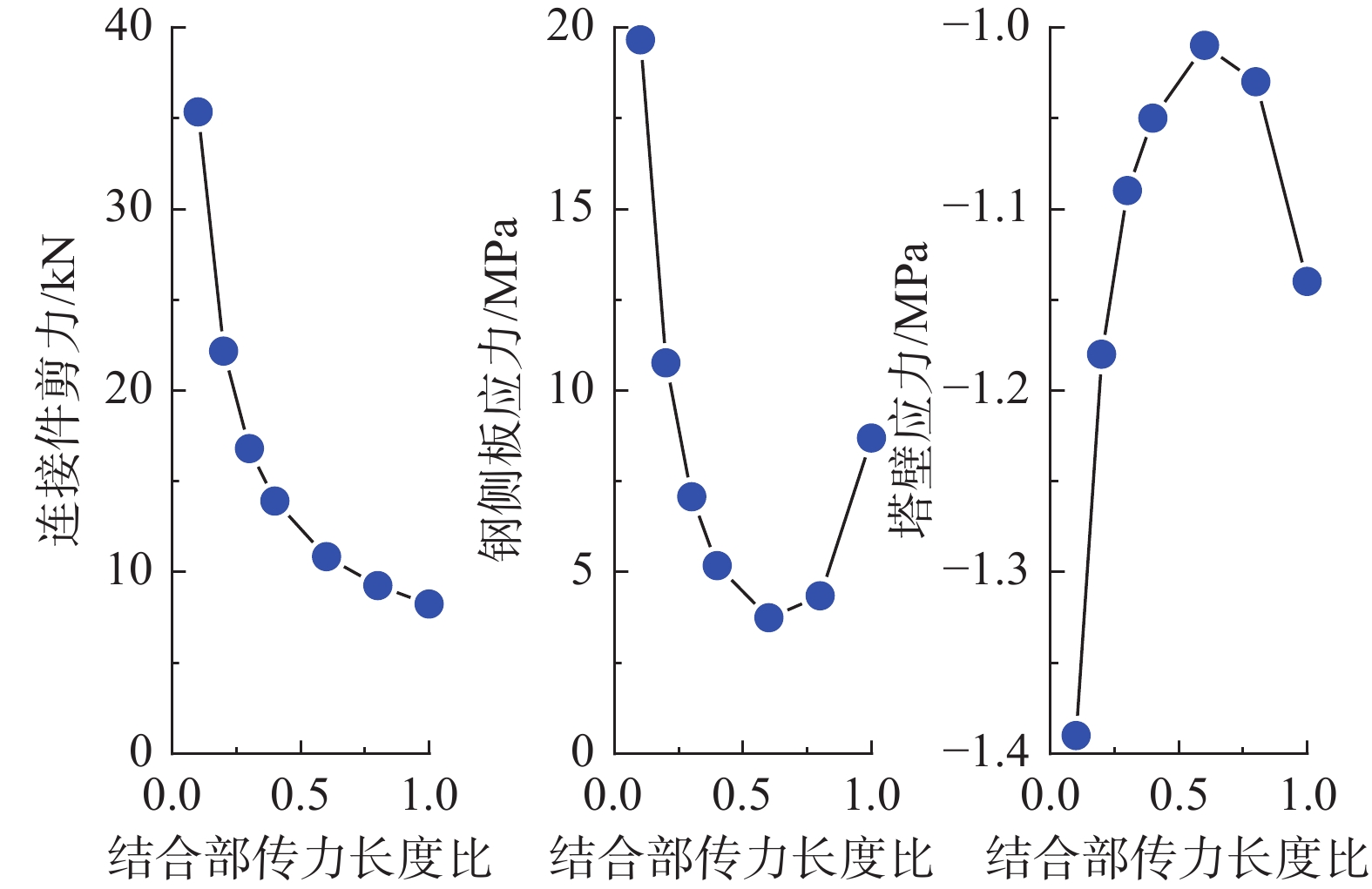
图13所示为钢锚箱与混凝土塔壁结合面传力长度对锚固区水平传力机理的影响。随着结合面长度与钢锚箱半长比值由0.1增加至1.0，焊钉连接件顺桥向剪力由35.34 kN变化为8.23 kN，减小77%；钢侧壁板正应力由19.66 MPa先减小至3.74 MPa再增大至8.69 MPa，即减小比例最多为81%、最后为56%；混凝土塔壁正应力由−1.39 MPa先变化至−1.01 MPa后变化为−1.14 MPa，绝对值减小比例最多27%、最后为18%。

图  13  结合面传力长度的影响

Figure  13.  Influence of transmission length of interface

下载: 全尺寸图片 幻灯片

这主要因为钢混结合面传力长度越大，单位长度上布置的焊钉连接件越多，故钢混结合面焊钉连接件的顺桥向剪力减小。斜拉索水平分力通过钢混结合面传递至混凝土塔壁，同时顺桥向预应力也通过钢混结合面传递至钢锚箱侧壁板，两者作用此消彼长，导致钢侧壁板正应力先减小再增大，同时混凝土塔壁正应力的绝对值先减小后增大。

4.4   连接件抗剪刚度的影响

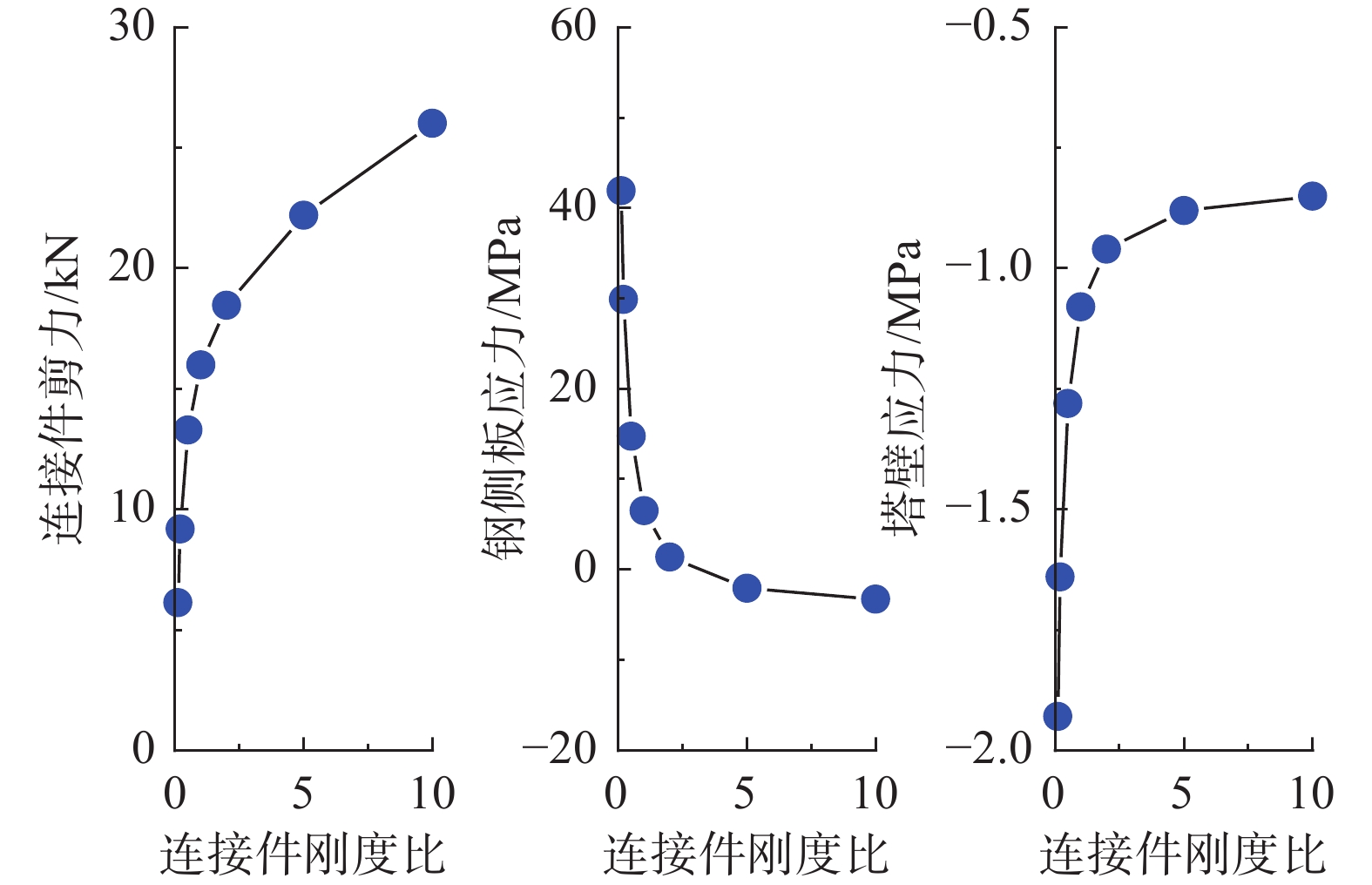
图14所示为钢混结合面焊钉连接件抗剪刚度对锚固区水平传力机理的影响。取第3节中算例采用的ϕ16×120焊钉连接件抗剪刚度为1倍，当连接件抗剪刚度比由0.1增加至10，焊钉连接件顺桥向剪力由6.13 kN变化为26.02 kN，增大324%；钢侧壁板正应力由41.93 MPa先减小至0再反向增大至−3.26 MPa，即绝对值减小92%；混凝土塔壁正应力由−1.93 MPa变化至−0.85 MPa，绝对值减小56%。

图  14  连接件抗剪刚度的影响

Figure  14.  Influence of shear stiffness of connector

下载: 全尺寸图片 幻灯片

这主要因为钢混结合面焊钉连接件抗剪刚度越大，单位长度上传递的剪力流越多，故焊钉连接件顺桥向剪力增大。斜拉索水平分力通过钢混结合面传递至混凝土塔壁，同时顺桥向预应力也通过钢混结合面传递至钢锚箱侧壁板，两者作用此消彼长导致钢侧壁板正应力绝对值先减小再增大，同时混凝土塔壁正应力绝对值减小。

4.5   顺桥向预应力的影响

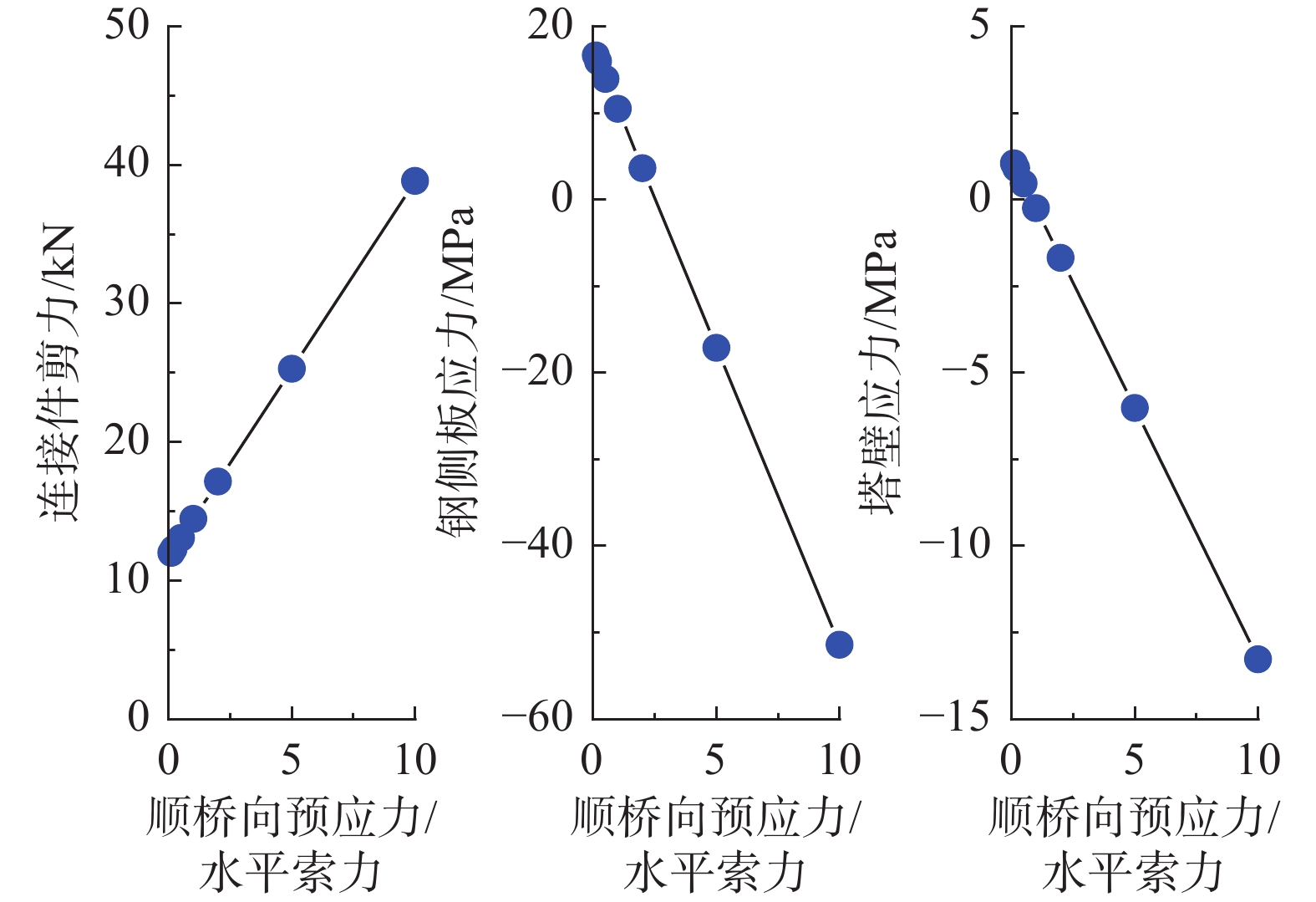
图15所示为顺桥向预应力对锚固区水平传力机理的影响。随着顺桥向预应力与斜拉索水平分力的比值由0.1增加至10，焊钉连接件顺桥向剪力由12.00 kN变化为38.84 kN，增大224%；钢侧壁板正应力由16.64 MPa先减小至0再反向增大至−51.4 MPa，绝对值增大209%；混凝土塔壁正应力由1.04 MPa减小至0 MPa再反向增大至−13.27 MPa，绝对值增大1176%。

图  15  顺桥向预应力的影响

Figure  15.  Influence of longitudinal prestress of bridge

下载: 全尺寸图片 幻灯片

这主要因为顺桥向预应力通过钢混结合面传递至钢锚箱侧壁板，故钢混结合面焊钉连接件顺桥向剪力增大，同时钢锚箱侧壁板、混凝土塔壁的拉应力逐渐减小直至转为受压状态。

5   结论

本文对斜拉桥外露型钢锚箱组合索塔锚固区水平传力机理进行理论解析，得到以下主要结论：

(1) 基于弹性介质层法，考虑钢与混凝土间的局部连接和滑移效应，推导了钢锚箱壁板-混凝土塔壁结合面滑移的理论计算式，进而得到连接件剪力流、钢与混凝土构件轴力等计算方法，并通过与外露型钢锚箱索塔锚固区节段模型试验结果比较得到验证。

(2) 基于外露型钢锚箱索塔锚固区节段模型试件参数，利用理论计算式分析得到顺桥向预应力、水平索力和两者同时作用时的最大相对滑移分别为0.015 mm、0.040 mm和0.055 mm，焊钉连接件剪力分别为4.26 kN、11.73 kN和15.99 kN。

(3) 钢锚箱侧壁板与混凝土塔壁承担轴向力的比例，对于顺桥向预应力是10%和90%，对于水平索力是26%和74%。在顺桥向预应力与水平索力共同作用下，索塔对称轴的钢壁板受拉力70.75 kN，塔壁受压力−483.75 kN，全截面合力为轴向压力−413 kN。

(4) 顺桥向预应力、水平索力和两者同时作用时，钢锚箱侧壁板的正应力在顺桥向端部均为0 MPa，而在索塔对称轴位置分别为−10.81 MPa、17.37 MPa和6.55 MPa。混凝土塔壁正应力在顺桥向端部为−2.52 MPa、0 MPa和−2.52 MPa，而在索塔对称轴位置分别为−2.26 MPa、1.19 MPa和−1.07 MPa。

(5) 依据组合索塔锚固区水平传力机理的参数化分析，焊钉连接件剪力随着钢锚箱侧壁板厚度、混凝土塔壁厚度、结合面传力长度的增加而减小，随着连接件抗剪刚度、顺桥向预应力作用的增加而增大。

本文结果基于混凝土塔壁与外露型钢锚箱侧面密贴连接得到，适用于具有类似构造形式的组合结构。