风力机叶片的气动性能主要是由翼型气动性能决定的，因此，如何精确地预测风力机翼型的气动性能，是目前设计优良的风力机叶片需要解决的一个关键问题，对于风电结构发展具有重要的意义。而翼型的气动性能不仅与翼型本身几何特性有关，还受到雷诺数、来流湍流强度、翼型表面粗糙度等诸多因素的影响，这些影响因素之间互相关联、互相制约。

LIN和PAULEY^[1]、COUNSIL和BOULAMA^[2]对雷诺数低于5×10⁵的许多翼型流动开展了大量数值计算与风洞实验研究，并发展了Eppler387等低雷诺数翼型^[1-2]。MUELLER和BATIL^[3]在低湍流度(I_u≤0.1%)以及不同低雷诺数条件下测量了不同对称翼型气动性能随攻角的变化。SELIG和MCGRANAHAN^[4]对含E387的一系列低雷诺数翼型在伊利诺伊大学香槟分校(UIUC)风洞进行了湍流度0.2%以下的试验研究；KOJIMA等^[5]采用LES方法数值模拟了Re=23 000时不同厚度翼型层流的分离效应，显示低雷诺数下翼型厚度对流动分离点以及分离泡形态、尺寸等有重要的影响。国内学者的研究中，高超等^[6]发现大厚度的NACA翼型在大攻角时能保持较高升阻比。白存儒等^[7]发现湍流度增大会导致翼型NACA 0012的转捩位置后移。李韶武等^[8]、王庶和米建春^[9]采用试验和数值模拟相结合的方法得到湍流度对剪切边界层影响较大，高湍流度对翼型表面流动的影响效果与雷诺数影响相似。唐新姿等^[10-12]以NACA 0012和NREL S809为研究对象，量化了随机湍流不确定性对翼型气动性能的影响，提出了一种在气动优化中耦合层流分离预测的高湍流度、低雷诺数小型风力机翼型优化策略。

本文以大型风力机专用翼型NREL S810为研究对象，通过风洞试验方法分析了高、低不同雷诺数下，湍流度对翼型气动性能的影响特性，得到了雷诺数和湍流度综合影响下翼型的气动荷载，为精确地预测风力机翼型的气动性能提供依据。

1   试验方法

1.1   风洞试验及试验模型

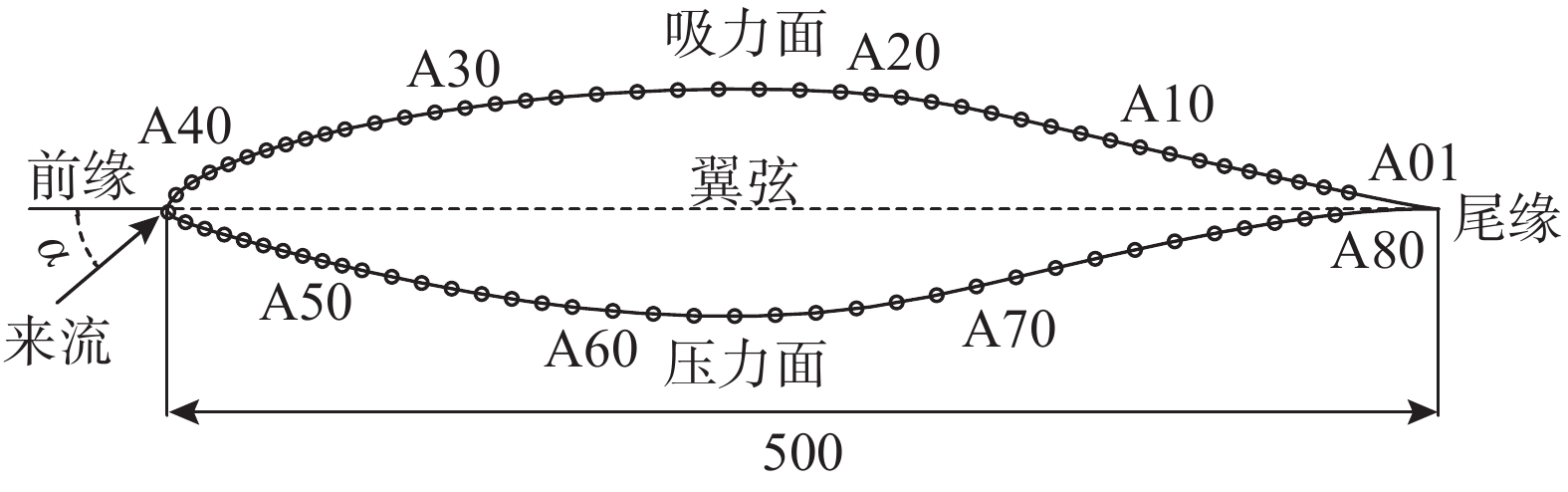
风洞试验是获取翼型二维气动数据的可靠手段^[13]，风洞试验在石家庄铁道大学风工程研究中心STU-1风洞的低速试验段内进行，试验段宽4.38 m、高3.0 m、长24.0 m，最大风速30.0 m/s，背景湍流度小于等于0.4%。根据风洞试验段的尺寸和NREL S810翼型的外形，加工制作等截面试验模型，模型弦长为0.5 m、展向长1.7 m。在试验模型中间截面位置处沿径向布置80个测压孔，采用刚性模型测压试验研究翼型的气动荷载，测压孔布置如图1所示。

图  1  模型测压孔布置　/mm

Figure  1.  Layout of model pressure taps

下载: 全尺寸图片 幻灯片

试验模型安装如图2所示。采用眼镜蛇三维脉动风速测量仪(Cobra Probe)测量来流风速，根据风速时程计算得到来流湍流度；同时测量洞体内温度、相对湿度和大气压，计算得到试验雷诺数。使用64通道微型压力扫描阀测量翼型模型表面压力，量程为±2500 Pa，精度为±0.03%。通过压力扫描阀测得的压力数据由DTC Initium数据采集系统进行采集，试验采样时间为30 s，频率为330 Hz。

图  2  模型安装实体

Figure  2.  Schematic diagram of model installation

下载: 全尺寸图片 幻灯片

1.2   试验工况

受地表粗糙度的影响，中原山区复杂地形70 m高度处湍流度最高达到13%^[14]。新疆复杂山区地形70 m高度处湍流度最大达到7.8%^[15]。重庆地区起伏不平地区几十米高度处稳定层结顺风向湍流度可达12%^[16]。考虑实际复杂山区地形风力机轮毂高度处湍流强度，确定试验湍流度范围为0.0%~13.0%。

在模型上游设置单平面格栅，包括条形格栅和网状格栅，通过调整格栅的间隙大小来改变湍流强度。单平面格栅具体参数如表1和图3所示，通过调节格栅板条的宽度a和b及格栅板条的间距M和N来得到不同湍流度的来流风场。单平面格栅位置固定在距离转盘中心7 m处，经测量得到，通过格栅产生的湍流近似各向同性，试验实现的最大湍流强度为13%，其余工况湍流强度分别为10.0%、8.5%、4.6%、2.3%和均匀流。

表  1  单平面格栅参数

Table  1.  Parameters of single plane grid

种类	横间距 M/mm	纵间距 N/mm	横板宽 a/mm	纵板宽 b/mm	与模型距离 D/m	湍流度 Iu/(%)
1	−	−	−	−	−	≤0.4
2	1275.0	−	−	75	32	2.3
3	337.5	337.5	75	75	7	4.6
4	225.0	−	−	75	32	5.0
5	600.0	600.0	150	150	7	8.5
6	375.0	750.0	150	150	7	10.0
7	375.0	375.0	150	150	7	13.0

下载: 导出CSV 

| 显示表格

图  3  单平面格栅尺寸示意图

Figure  3.  Dimension of single plane grid

下载: 全尺寸图片 幻灯片

2   试验结果分析

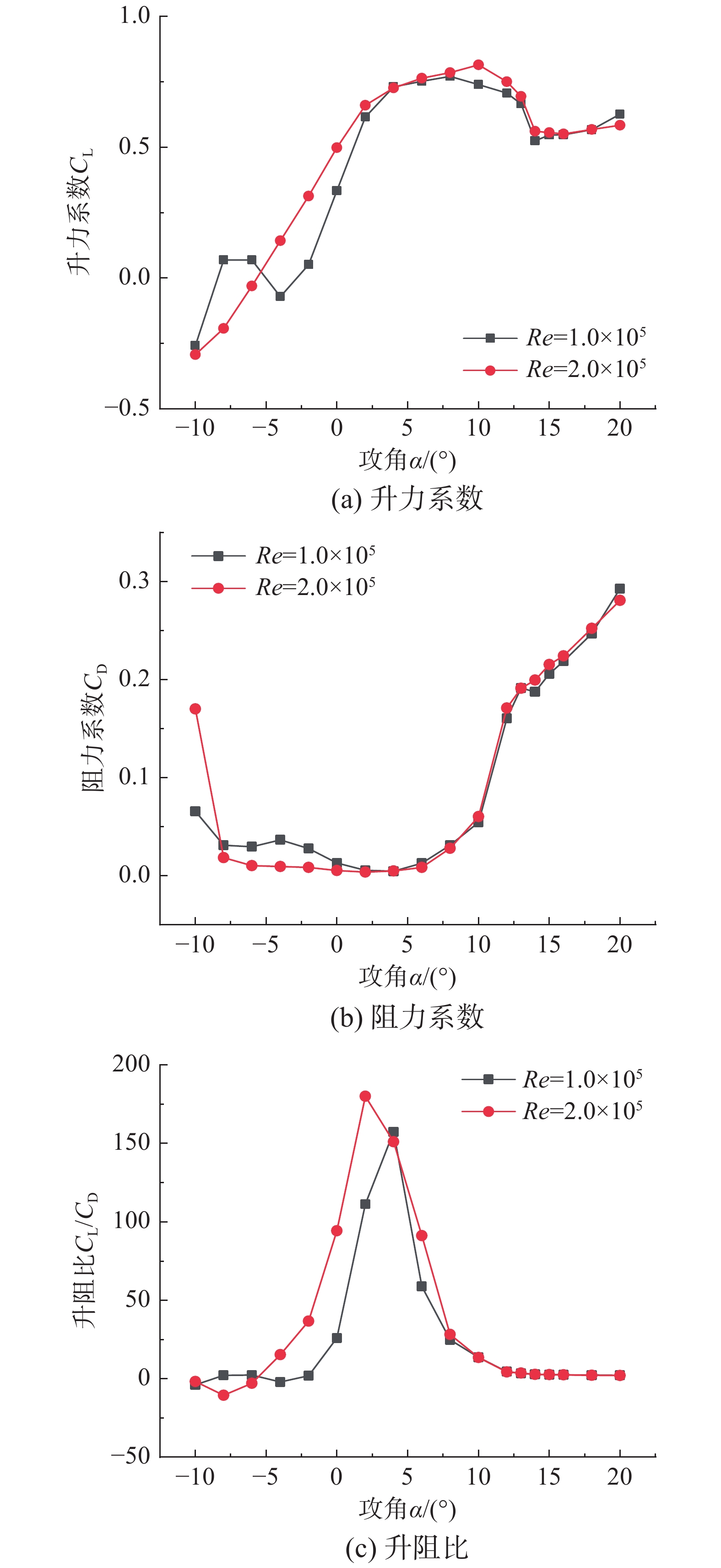
均匀流工况下，如图4(a)所示，雷诺数较小时(Re=1.0×10⁵)，升力系数在负攻角−10°~−4°范围内有一段突升和突降，之后随攻角增大升力系数上升，直至到达最大升力系数0.77后开始失速，失速攻角为10°；当雷诺数增大到2.0×10⁵时，翼型最大升力系数增加至0.81，失速攻角仍为10°。

阻力系数随雷诺数的变化如图4(b)所示，雷诺数较小时(Re=1.0×10⁵)时，在失速攻角处阻力系数为0.05，后随攻角增加阻力系数迅速升高，直至20°时达到0.29；当雷诺数增大为2.0×10⁵时，阻力系数几乎不变。

升阻比随雷诺数变化如图4(c)所示，雷诺数为1.0×10⁵时，升阻比在4°攻角时达到最大，为157.46；当雷诺数增大为2.0×10⁵时，最大升阻比对应的攻角前移至2°，并且升阻比增加到180.2。

图  4  均匀流下随雷诺数变化的升阻力系数及升阻比曲线

Figure  4.  Curves of lift coefficient, drag coefficient and lift drag ratio varying with Reynolds number at uniform flow

下载: 全尺寸图片 幻灯片

如图5所示，在小雷诺数工况(Re=1.0×10⁵)，提高来流湍流度至I_u=2.3%，与均匀流相比，翼型升力系数发生了明显的失速延迟，失速攻角后移至12°；湍流度继续增大至I_u=4.6%，翼型的升力系数出现了显著提升，并且在失速攻角12°时，对应的升力系数最大值为1.09，较均匀流最大升力系数增大了41.6%；随着来流湍流度的继续增大，翼型升力系数又开始逐渐降低，当I_u=8.3%时，与I_u=4.6%工况相比，升力系数下降幅度达到19.3%~36.6%，失速继续延迟，失速攻角后移至13°，对应的升力系数最大值为0.77，较均匀流最大升力系数保持不变；当来流湍流度I_u≥10%时，翼型升力系数继续降低，与均匀流相比，I_u=10.0%升力系数下降幅度为11.3%~36.4%，I_u=13.0%升力系数下降幅度为0.6%~49.3%。且失速攻角仍继续后移，I_u=10.0%时的失速攻角为15°，对应的升力系数最大至为0.62，较均匀流最大升力系数降低了19.5%；而当I_u=13.0%时，升力系数随攻角的增加变化较为平缓，在−10º~20º试验攻角范围内未出现明显的失速攻角。

图  5  Re=1.0×10⁵时湍流度对翼型气动性能的影响

Figure  5.  Effect of turbulence intensity on aerodynamic performance of airfoils at Re=1.0×10⁵

下载: 全尺寸图片 幻灯片

当来流湍流度小幅度增大至I_u=2.3%，翼型的阻力系数变化不大。来流湍流度增至I_u=4.6%，与均匀流相比，翼型的阻力系数出现了显著增高，增大幅度为20.9%~47.4%，在攻角20°时，对应点最大阻力系数为0.39，相对于均匀流时增大了34.3%；随着湍流度的逐渐增大，翼型阻力系数开始降低，当I_u=8.3%时，与I_u=4.6%工况相比，阻力系数下降幅度达到26.3%~43.0%，在失速攻角13°时，阻力系数为0.13，较均匀流下降了38.0%；当来流湍流度I_u≥10%时，翼型的阻力系数继续下降，与均匀流相比，来流湍流度为I_u=10.0%时，阻力系数下降幅度为19.4%~62.5%，来流湍流度为I_u=13.0%时，阻力系数下降幅度达到28.2%~64.1%。

增加湍流度至I_u=2.3%，最大升阻比开始下降至96.15，相较于均匀流工况降低了38.9%，但对应的攻角不变；继续增加湍流度，最大升阻比开始上升，增加来流湍流度至I_u=4.6%，最大升阻比上升至136.99，但仍较均匀流低13.0%，对应的攻角前移至0°附近；当湍流增加至5.0%时，最大升阻比上升至683.90，较均匀流上升334.3%，最大升阻比攻角后移至2°附近；当来流湍流度I_u≥8.3%时，翼型最大升阻比又开始下降，但仍显著大于均匀流工况，与I_u=5.0%相比，I_u=8.3%升阻比下降9.3%，I_u=10.0%升阻比下降11.2%，I_u=13.0%升阻比下降40.4%。

如图6所示，在大雷诺数工况(Re=2.0×10⁵)，提高来流湍流度至I_u=2.3%，与均匀流相比，翼型升力系数没有发生明显的变化，失速攻角仍为10°；湍流度继续增大至I_u=4.6%，翼型的升力系数出现了显著提升，增大幅度为22.8%~98.4%，失速攻角后移至12°，对应的升力系数最大值为1.14，较均匀流最大升力系数增大了51.8%；随着来流湍流度的继续增大，翼型升力系数又开始逐渐降低，当I_u=8.5%时，与I_u=4.6%工况相比，升力系数下降幅度达到11.9%~47.3%，失速继续延迟，失速攻角后移至13°，对应的升力系数最大值为0.91，较均匀流最大升力系数增大了30.9%；当来流湍流度I_u≥11%时，翼型升力系数继续降低，与均匀流相比，I_u=11.0%升力系数下降幅度为I_u=13.0%，升力系数下降幅度为31.1%~63.2%。且失速攻角仍继续后移，I_u=11.0%时的失速攻角为15º；而当I_u=13.0%时，升力系数随攻角的增加变化较为平缓，在−10º~20º试验攻角范围内未出现明显的失速攻角。

图  6  Re=2.0×10⁵时湍流度对翼型气动性能的影响

Figure  6.  Effect of turbulence intensity on aerodynamic performance of airfoils at Re=2.0×10⁵

下载: 全尺寸图片 幻灯片

当来流湍流度小幅度增大至I_u=2.3%，翼型的阻力系数变化不大。来流湍流度增至I_u=4.6%，与均匀流相比，翼型的阻力系数出现了显著增高，增大幅度为5.0%~49.0%，在攻角20°时，对应点最大阻力系数为0.42，相对于均匀流时增大了50.0%；随着湍流度的逐渐增大，翼型阻力系数开始降低，当I_u=8.5%时，与I_u=4.6%工况相比，阻力系数下降幅度达到21.9%~36.7%，在失速攻角13°时，阻力系数为0.14，较均匀流下降了25.0%；当来流湍流度I_u≥11%时，翼型的阻力系数继续下降，与均匀流相比，来流湍流度为I_u=11.0%时，阻力系数下降幅度为15.6%~71.5%，来流湍流度为I_u=13.0%时，阻力系数下降幅度达到47.6%~85.2%。

增加湍流度至I_u=2.3%，最大升阻比开始下降至159.99，相较于均匀流工况降低了11.1%，但对应的攻角不变；增加来流湍流度至I_u=4.6%，最大升阻比开始下降至159.99，相较于均匀流工况降低了11.1%，对应的攻角不变；当湍流增加至5.0%时，最大升阻比上升至499.43，较均匀流上升177.4%，最大升阻比攻角后移至4°附近；当来流湍流度I_u≥8.5%时，翼型最大升阻比又开始下降，与I_u=5.0%相比，I_u=8.3%升阻比下降55.0%，I_u=10.0%升阻比下降11.2%，I_u=13.0%升阻比下降40.4%。

在I_u=2.3%时，雷诺数较小时(Re=1.0×10⁵)，失速攻角为12°，雷诺数增大至2.0×10⁵，失速攻角前移至10°。但此时雷诺数的增加，对阻力系数和升力系数影响较小，可显著提升最大升阻比；在I_u=4.6%时，雷诺数从1.0×10⁵增加到2.0×10⁵时，最大升力系数从1.09增加至1.14，最大阻力系数从0.39增加至0.42，最大升阻比从136.99增至159.99，对应的攻角相同。

湍流度增至I_u=8.5%，随着雷诺数的增大，最大升力系数从0.77增加至0.91，失速攻角处的阻力系数从0.13增加至0.14，但最大升阻比显著降低，最大升阻比对应的攻角均为2°；湍流度增至I_u=11.0%，随着雷诺数的增大，最大升力系数从0.62增至0.66，失速攻角处的阻力系数从0.13增加至0.14。最大升阻比显著降低，从607.33降至223.24，最大升阻比对应的攻角从2°后移至6°。

I_u=13.0%时，随着雷诺数的增大，最大升力系数从0.56降至0.40，最大阻力系数从0.20降至0.15。最大升阻比从407.83降至282.92，其所对应的攻角从2°后移至6°。

3   结论

以大型风力机专用翼型NREL S810为研究对象，通过在不同雷诺数下对均匀流环境及有湍流环境下的数据进行分析，分析了雷诺数增加对均匀流气动性能的影响、湍流度增加对气动性能的影响以及雷诺数和湍流度对翼型气动性能的综合影响，得到如下结论：

(1) 在均匀流工况下，随着雷诺数的增大，翼型升力系数增加，失速攻角和阻力系数基本不变，最大升阻比对应的攻角前移。

(2) 随着来流湍流度的增大，翼型的升力系数和阻力系数均呈先增大后减小的变化趋势，当湍流度为4.6%时增加至最大，之后开始下降；而最大升阻比会随湍流度的增加先减小后增大再减小。

(3) 仅在I_u=2.3%时，雷诺数的增加会延缓失速延迟。随着雷诺数的增加，翼型的升力系数和阻力系数呈先增大再减小的趋势，当湍流度I_u≤11%时，随着雷诺数的增加，升、阻力系数增加；当湍流度I_u>11%时，随着雷诺数的增加，升、阻力系数减小。随着雷诺数的增加，最大升阻比先增大再减小，并且最大升阻比对应的攻角呈先前移再后移的趋势。