流线型箱梁涡激振动的气动力演化规律

韩原; 李震; 王仰雪; 邵林媛; 靖洪淼; 刘庆宽

doi:10.6052/j.issn.1000-4750.2022.06.S037

流线型箱梁涡激振动的气动力演化规律

韩原^1,,
李震^1,,
王仰雪^1,,
邵林媛^1,,
靖洪淼^{1, 2, 3,},
刘庆宽^{1, 2, 3, ,}

1.
石家庄铁道大学土木工程学院，河北，石家庄 050043
2.
石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室，河北，石家庄 050043
3.
河北省风工程和能源利用工程技术创新中心，河北，石家庄 050043

基金项目: 国家自然科学基金项目(51778381)；科技冬奥专项项目(21475402D)；河北省高端人才项目(冀办[2019]63号)；河北省青年科学基金项目(E2021210063)；河北省研究生创新项目(CXZZBS2023136)

详细信息

作者简介:
韩　原(1991−)，男，山东人，博士生，主要从事桥梁风致振动与控制研究(E-mail: hanyuan@stdu.edu.cn)

李　震(1996−)，男，河北人，硕士生，主要从事桥梁风致振动与控制研究(E-mail: lz95770@163.com)

王仰雪(1998−)，男，安徽人，硕士生，主要从事桥梁风致振动与控制研究(E-mail: wyxpeaksnow@163.com)

邵林媛(1996−)，女，辽宁人，硕士生，主要从事桥梁风致振动与控制研究(E-mail: sly@stdu.edu.cn)

靖洪淼(1990−)，男，山东人，讲师，博士，主要从事桥梁风致振动与控制、山区桥位风环境研究(E-mail: jhm@stdu.edu.cn)

通讯作者:
刘庆宽(1971−)，男，河北人，教授，博士，博导，主要从事桥梁与结构的风荷载、风致振动与控制研究(E-mail: lqk@stdu.edu.cn)

中图分类号: U441+.3
计量
- 文章访问数: 195
- HTML全文浏览量: 27
- PDF下载量: 38
出版历程
- 收稿日期: 2022-06-18
- 修回日期: 2022-12-25
- 网络出版日期: 2023-01-31
- 刊出日期: 2023-06-24

EVOLUTIONARY OF AERODYNAMIC CHARACTERISTICS AROUND STREAMLINED BOX GIRDER DURING VERTICAL VORTEX-INDUCED VIBRATION

HAN Yuan^1,,
LI Zhen^1,,
WANG Yang-xue^1,,
SHAO Lin-yuan^1,,
JING Hong-miao^{1, 2, 3,},
LIU Qing-kuan^{1, 2, 3, ,}

1.
School of Civil Engineering, Shijiazhuang Tiedao University, Shijiazhuang, Heibei 050043, China
2.
State Key Laboratory of Mechanical Behavior and System Safety of Traffic Engineering Structures, Shijiazhuang Tiedao University, Shijiazhuang, Hebei 050043, China
3.
Innovation Center for Wind Engineering and Wind Energy Technology of Hebei Province, Shijiazhuang, Hebei 050043, China

摘要

摘要: 涡激振动是大跨度流线型箱梁桥在低风速下常见的风致振动形式，对桥梁结构的疲劳寿命和行车舒适性有较大影响。为揭示流线型箱梁涡激振动机理，有必要研究其涡激振动的气动力演化规律。以某流线型箱梁桥为对象，通过同步测振测压的风洞试验方法，获得了+5°风攻角下主梁模型的涡激振动响应及表面测点风压时程，对比分析了涡激振动前、涡激振动振幅上升区、涡激振动振幅极值点、涡激振动振幅下降区和涡激振动后五个不同阶段模型表面的平均风压系数、脉动风压系数和涡激力的变化规律。结果表明：在涡激振动的不同阶段，流线型箱梁表面平均风压系数变化不大，而脉动风压系数分布具有明显的演化过程。涡激力在涡激振动振幅上升区、涡激振动振幅极值点及涡激振动振幅下降区有明显的卓越频率，且与结构自振频率相近，涡激振动前和涡激振动后无明显卓越频率。涡激力卓越频率对应的振幅与涡激振动位移振幅正相关，两者同在涡激振动振幅极值点处达到最大。
- 流线型箱梁 /
- 风洞试验 /
- 涡激振动 /
- 气动力 /
- 演化规律
Abstract: The vortex-induced vibration (VIV) is a common form of wind-induced vibration of long span streamlined box-girder bridge under low wind speed. It has a great influence on the fatigue life and driving comfort of a bridge structure. In order to reveal the VIV mechanism of a streamlined box girder, it is necessary to study the aerodynamic evolution law of VIV of a streamlined box girder. Taking a streamlined box-girder bridge as an example, a wind tunnel test was conducted to obtain the VIV response and pressure time-history data from pressure measurement points on the experimental model for the angles of attack +5°. The changes of mean values of wind pressure coefficient, of root-mean-square (RMS) values of wind pressure coefficients and, of vortex-induced force (VIF) amplitude spectrum in different vortex-induced stages are analyzed. Those stages include pre-VIV stage, ascent stage, extreme amplitude point, descent stage, and post-VIV stage. It is found that mean values of wind pressure coefficients have little change, however, the distribution of RMS values of wind pressure coefficients has obvious changes. The VIF has obvious predominant frequencies in the ascent stage, at the extreme amplitude point, and in the descent stage. These frequencies are similar to the natural vibration frequency of the structure. However, there is no considerable predominant frequency in pre-VIV stage and post-VIV stage. The amplitude corresponding to the dominant frequency of VIF is positively correlated with the amplitude of VIV and reaches the maximum at the extreme amplitude point.
- streamlined box girder /
- wind tunnel tests /
- vortex-induced vibration /
- aerodynamic forces /
- evolutionary characteristics

HTML全文

涡激振动是大跨度桥梁在低风速时容易出现的自激限幅振动。涡激振动由于其限幅特性，不会导致桥梁结构短期内突然垮塌，但其发生风速通常较低，高频次的出现会增加桥梁结构疲劳破坏的风险^[1-3]。国内外多座大跨度桥梁，如丹麦的大带东桥，加拿大的Wye大桥，日本的东京海湾大桥和我国的鹦鹉洲大桥、九江长江大桥都曾发生过较大幅度的涡激振动^[4]。影响涡激振动产生的因素多且复杂，目前对涡激振动的发生机理尚未研究透彻。PAIDOUSSIS等^[5]对比分析了不同主梁断面形式下涡激振动的发生机理，归纳出主梁涡激振动的4种典型涡脱形式：梁顶涡脱、梁尾涡脱、交错涡脱和梁顶撞击涡脱。LARSEN和LAROSE^[6]以流线型箱梁断面为研究对象，发现梁底涡脱也是一种造成涡激振动发生的涡脱形式。HU等^[7]基于流线型闭口箱梁断面研究了模型各区域气动力对涡激力的贡献值，从气动力的角度揭示了涡激振动发生机理。刘小兵等^[8]在均匀流场中对扁平箱梁进行了阶段模型测振试验，发现与涡激振动锁定区间外相比，涡激力在涡振锁定区间内有更强的展向相关性。胡传新等^[9]分析了不同雷诺数下流线闭口箱梁气动力时频特性，发现箱梁表面分布气动力与涡激力相关性的空间分布有明显的雷诺数效应。流线型箱梁涡激振动过程中，漩涡脱落的变化会导致表面气动力的变化，继而影响涡激振动响应的变化。因此，从表面气动力演化的角度揭示涡激振动机理是很有必要的。本文基于同步测振测压风洞试验，研究了流线型箱梁在涡激振动前、涡激振动振幅上升区、涡激振动振幅极值点、涡激振动振幅下降区、涡激振动后阶段的气动力演化特性，揭示了涡激振动过程中振幅变化的机理。

1 风洞试验设计及涡激振动响应测试

1.1 主梁断面参数介绍及模型设计

以象山港大桥为研究对象，主梁为流线型箱梁，桥面宽28.8 m，梁高3.5 m。综合考虑风洞尺寸及阻塞度等因素，模型何缩尺比采用1∶30，长宽比采用2∶1，表层蒙皮和桥面栏杆材料选用ABS板材，骨架由钢管和加劲肋板组成。模型刚度满足实验要求，质量满足相似条件。主梁节段模型尺寸如图1所示。

图 1 主梁节段模型断面图　/mm

Figure 1. Geometrical sizes of a bridge sectional model

下载: 全尺寸图片幻灯片

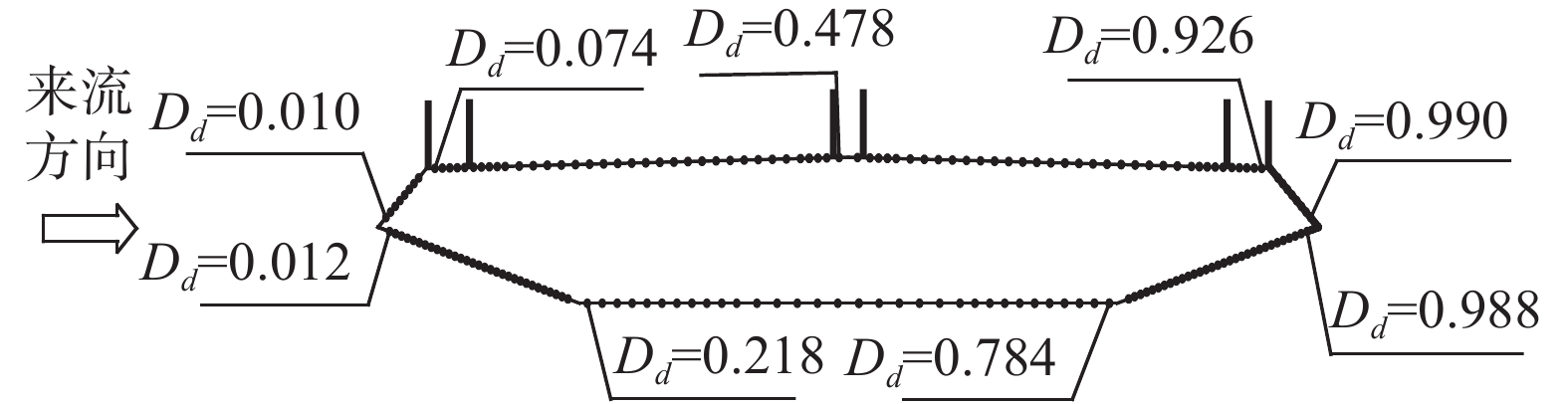
模型环向布置180个风压测点，测点间距7 mm~24 mm不等，对风压变化敏感部位进行测点加密，为了方便描述测点位置及其风压系数的对应关系，定义测点的无量纲距离D_d如式(1)所示：

${{D}_{{d}}}=\frac{{{d}_{i}}}{{D}}$

(1)

式中： ${d_i}$ 为第i个测压点沿其所在模型表面到模型最上游端的周向距离；D为模型最上游端沿待定义测点所在模型表面到最下游端的周向距离。测点具体布置如图2所示。

图 2 测点无量纲间距示意图

Figure 2. Dimensionless distance diagram of measuring points

下载: 全尺寸图片幻灯片

1.2 试验设备介绍

风洞试验在风工程研究中心STDU-1多功能大气边界层风洞低速试验段进行。低速试验段断面尺寸4.38 m×3.00 m，试验风速为1.5 m/s~30 m/s，流场达到了优秀边界层风洞标准。通过调节弹簧刚度可以改变系统的自振频率，本次试验模型自振频率调整为1.92 Hz。每个刚臂两端分别布置一个激光位移计，记录激光位移计与刚臂下边缘之间距离变化时程数据。模型测振同时进行模型表面风压测量，风压测量系统由微型压力扫描阀和数据处理设备组成。图3为试验模型安装图。为了减小支架系统等干扰，在模型两侧各安装了1块端板，端板长宽约为主梁宽高的1.5倍和3.5倍。

图 3 试验模型安装图

Figure 3. Test model installation diagram

下载: 全尺寸图片幻灯片

1.3 涡激振动振幅试验结果分析

试验在均匀流场中进行，完成了+5°攻角下的同步测振测压试验。激光位移计采集的位移数据经过处理可得到模型涡激振动响应。

将来流风速和涡激振动振幅进行无量纲化处理，模型竖向涡激振动响应如图4所示。折减风速 $U'$ 如式(2)所示，无量纲振幅 $Z'$ 如式(3)所示。

图 4 模型竖向涡激振动响应

Figure 4. Vertical VIV response of model

下载: 全尺寸图片幻灯片

$U' = \frac{U}{{fB}}$

(2)

$Z' = \frac{Z}{B}\quad$

(3)

式中：U为试验中的来流风速；f为模型系统的竖弯自振频率；B为模型断面梁高；Z为振幅。

取折减风速14.63、17.12、18.94、19.52和20.72作为涡激振动前、涡激振动振幅上升区、涡激振动振幅极值点、涡激振动振幅下降区和涡激振动后阶段的代表风速。以下如无说明，以折减风速点代表涡激振动不同阶段。

2 主梁模型气动力演化规律分析

模型表面的风压分布可以表征模型周围的空气绕流情况，将各测点风压与其相邻两测点距离的1/2相乘可得到模型表面分布气动力，将风压无量纲化可得到风压系数^[10-11]。对比涡激振动前、涡激振动振幅上升区、涡激振动振幅极值点、涡激振动振幅下降区和涡激振动后模型表面的平均风压系数、脉动风压系数以及涡激力幅值谱，分析得到模型竖向涡激振动过程气动力演化规律。风压系数C_pi(t)定义如式(4)所示：

$C_{pi}^{}(t) = \frac{{P_i^{}(t) - P}}{{1/2\rho U_{}^2}}$

(4)

式中：P为前方来流的静压；U为前方来流的速度；ρ为空气密度； $P_i^{}(t)$ 为测得的模型表面测点压力信号的时间序列。

2.1 测点平均风压系数分析

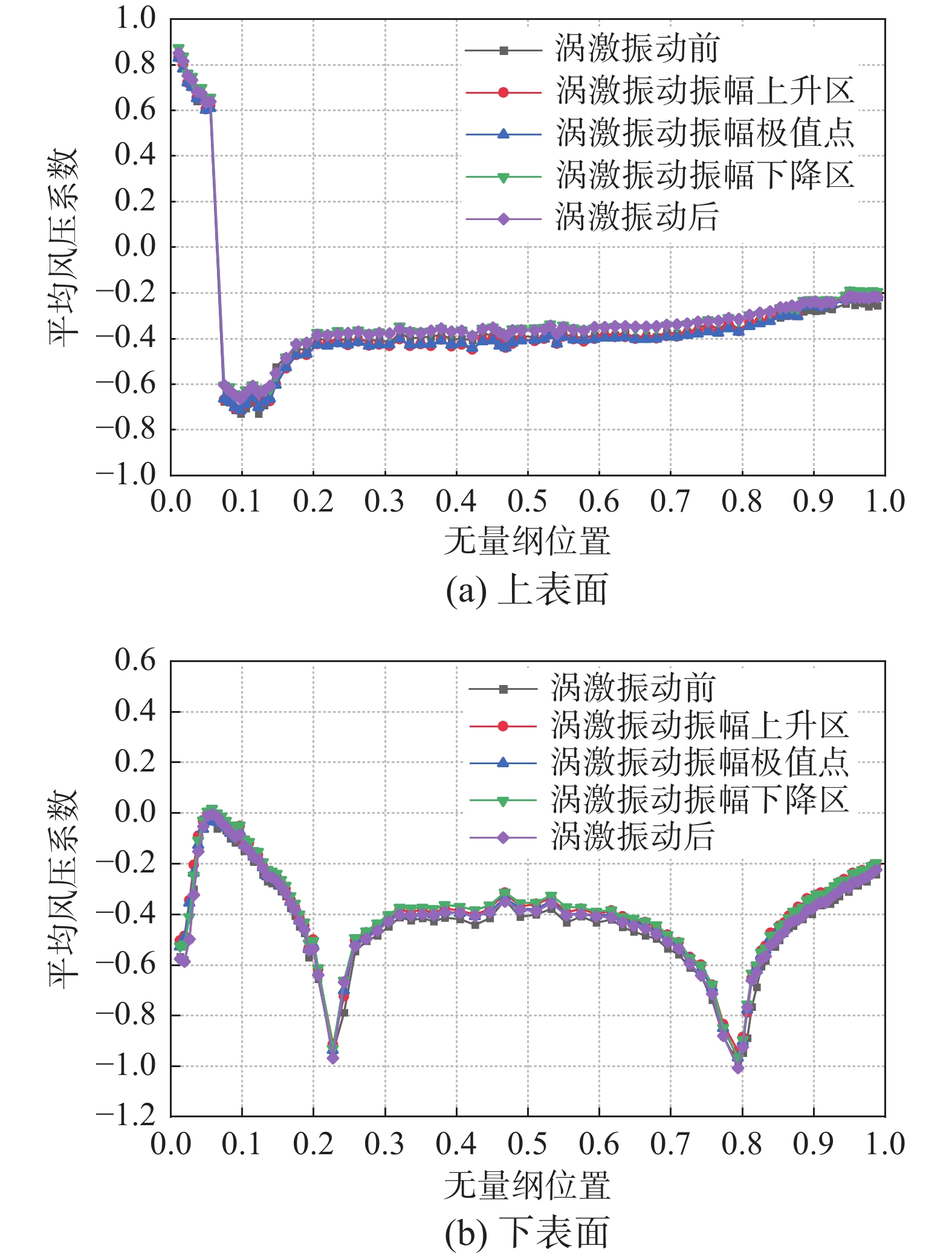
模型表面平均风压系数可以表征气流在模型表面的分离与再附着情况。正压表示模型表面受压力作用，负压表示表面受吸力作用。涡激振动过程模型表面平均风压系数空间分布演化如图5所示。由图可见，涡激振动过程中模型表面平均风压分布规律没有明显变化，迎风侧风嘴上部及下表面D_d=0.0511附近为正压区，其余位置均为负压区，说明在迎风侧风嘴上部两端出现了气流分离，气流分离后在下表面D_d=0.0511附近发生了再附着，之后很快又发生了分离，其余位置未出现气流再附着现象。

图 5 涡激振动过程模型表面平均风压系数

Figure 5. Mean values of wind pressure coefficient of VIV process model surface

下载: 全尺寸图片幻灯片

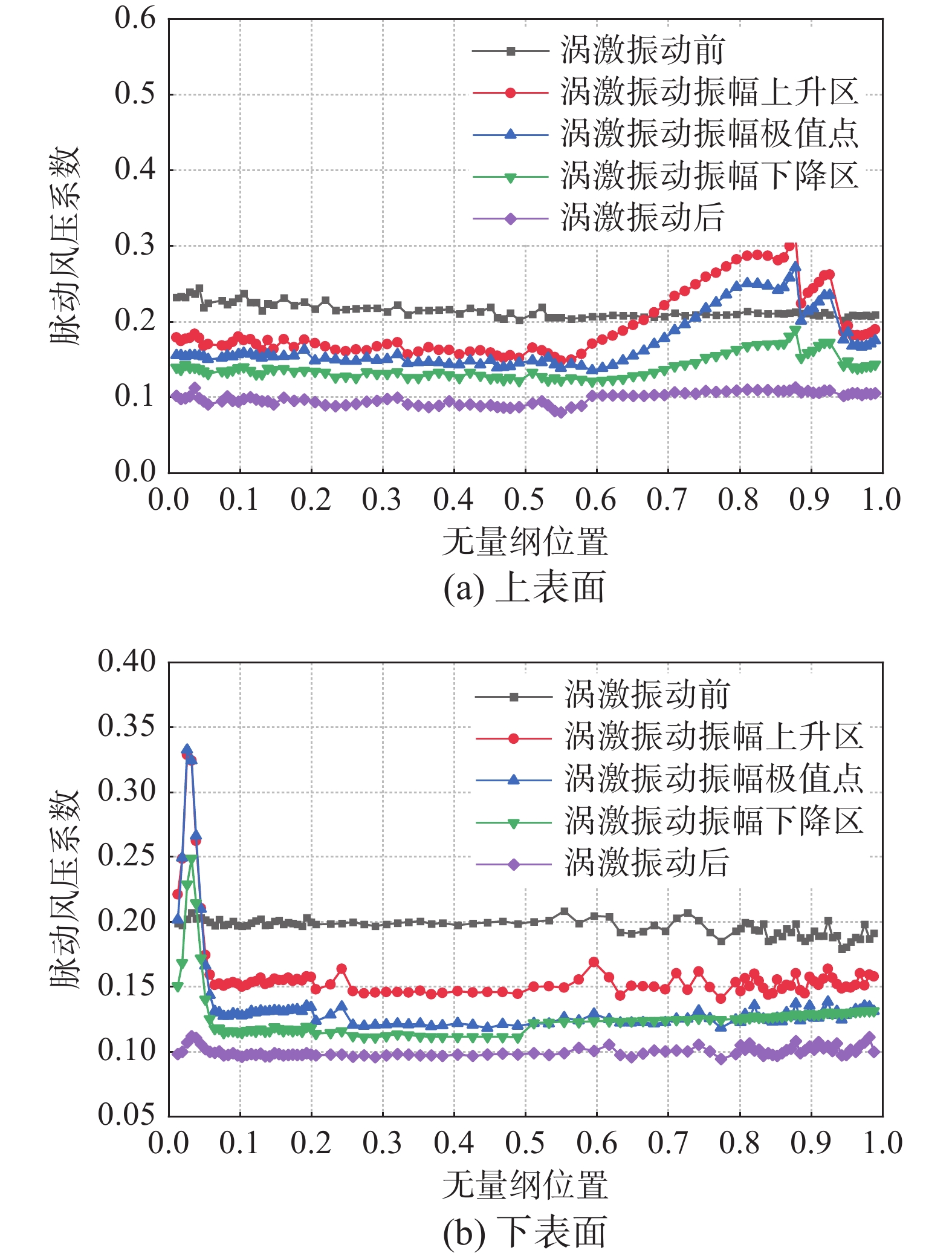
2.2 测点脉动风压系数分析

模型涡激振动过程中，动荷载主要由风压脉动部分提供。涡激振动过程模型测点脉动风压系数空间分布，如图6所示。脉动风压系数空间分布规律具有明显的变迁过程。涡激振动发生前和涡激振动发生后，同一涡激振动阶段内，各测点脉动风压系数差别不大。在涡激振动振幅上升区、涡激振动振幅极值点和涡激振动振幅下降区，均在上表面后部、迎风侧斜腹板顶部表现出测点脉动风压系数迅速增大的特征，这是由于，在这些位置出现了规律的旋涡脱落，增加了风压的不稳定性。

图 6 涡激振动过程模型测点脉动风压系数

Figure 6. RMS values of wind pressure coefficient of VIV process model surface

下载: 全尺寸图片幻灯片

2.3 涡激力幅频分析

模型体轴坐标系下气动升力可通过压力积分法计算得出，再经过坐标变换即得风轴坐标系下模型气动升力。将模型风轴坐标系下的气动升力减去升力均值，即得到涡激力，各阶段涡激力幅值谱如图7所示。在涡激振动前阶段，涡激力幅值谱无明显卓越频率；进入涡激振动振幅上升区，出现明显的卓越频率1.90 Hz，与结构自振频率相近，对应涡激力振幅为1.19 N/m；在涡激振动振幅极值点，频谱分布与涡激振动振幅上升区相似，卓越频率对应涡激力振幅为1.66 N/m，较涡激振动上升区提高了39.50%；进入涡激振动振幅下降区后，频谱分布无明显变化，但卓越频率对应涡激力振幅急剧减小为0.58 N/m，较涡激振动振幅极值点下降了65.06%；涡激振动后阶段，未出现明显卓越频率。可见，卓越频率对应涡激力振幅与涡激振动位移振幅正相关，在涡激振动振幅极值点处达到最大。涡激力在涡激振动前和涡激振动后无明显卓越频率；在涡激振动振幅上升区、涡激振动振幅极值点及涡激振动振幅下降区有明显的卓越频率，且与结构自振频率相近。

图 7 涡激振动过程模型涡激力幅值谱

Figure 7. Amplitude spectrum of VIV process model

下载: 全尺寸图片幻灯片

3 结论

本文进行了流线型箱梁涡激振动同步测振、测压风洞试验，从模型涡激振动幅度、测点平均风压系数、测点脉动风压系数和涡激力的角度，研究了流线型箱梁涡激振动过程中气动力演化特性，主要结论如下：

(1) 在涡激振动过程中，流线型箱梁表面脉动风压系数分布具有明显的演化过程。涡激振动前及涡激振动后脉动风压系数分布均匀；涡激振动振幅上升区、涡激振动振幅极值点、涡激振动振幅下降区上表面后部脉动风压系数大幅增加。

(2) 涡激力在涡激振动振幅上升区、涡激振动振幅极值点及涡激振动振幅下降区有明显的卓越频率，且与结构自振频率相近，而在涡激振动前和涡激振动后无明显卓越频率。涡激力卓越频率对应振幅与涡激振动振幅正相关，两者同在涡激振动振幅极值点处达到最大。

图 1 主梁节段模型断面图　/mm

Figure 1. Geometrical sizes of a bridge sectional model

下载: 全尺寸图片幻灯片

图 2 测点无量纲间距示意图

Figure 2. Dimensionless distance diagram of measuring points

下载: 全尺寸图片幻灯片

图 3 试验模型安装图

Figure 3. Test model installation diagram

下载: 全尺寸图片幻灯片

图 4 模型竖向涡激振动响应

Figure 4. Vertical VIV response of model

下载: 全尺寸图片幻灯片

图 5 涡激振动过程模型表面平均风压系数

Figure 5. Mean values of wind pressure coefficient of VIV process model surface

下载: 全尺寸图片幻灯片

图 6 涡激振动过程模型测点脉动风压系数

Figure 6. RMS values of wind pressure coefficient of VIV process model surface

下载: 全尺寸图片幻灯片

图 7 涡激振动过程模型涡激力幅值谱

Figure 7. Amplitude spectrum of VIV process model

下载: 全尺寸图片幻灯片

参考文献(11)

[1]	陈政清, 黄智文. 大跨度桥梁竖弯涡振限值的主要影响因素分析[J]. 中国公路学报, 2015, 28(9): 30 − 37. doi: 10.3969/j.issn.1001-7372.2015.09.005 CHEN Zhengqing, HUANG Zhiwen. Analysis of main factors influencing allowable magnitude of vertical vortex-induced vibration of long-span bridges [J]. China Journal of Highway and Transport, 2015, 28(9): 30 − 37. (in Chinese) doi: 10.3969/j.issn.1001-7372.2015.09.005
[2]	李玲瑶, 余志武, 何旭辉, 等. 基于可靠度理论的桥梁涡激振动概率性评价[J]. 工程力学, 2015, 32(10): 154 − 160,168. doi: 10.6052/j.issn.1000-4750.2014.04.0280 LI Lingyao, YU Zhiwu, HE Xuhui, et al. Probabilistic evaluation of vortex-induced vibration of bridges based on reliability theory [J]. Engineering Mechanics, 2015, 32(10): 154 − 160,168. (in Chinese) doi: 10.6052/j.issn.1000-4750.2014.04.0280
[3]	喻梅, 廖海黎, 李明水, 等. 基于经验线性涡激力的桥梁涡激振动TMD控制[J]. 工程力学, 2013, 30(6): 269 − 274. doi: 10.6052/j.issn.1000-4750.2012.08.0630 YU Mei, LIAO Haili, LI Mingshui, et al. Suppression of vortex-induced vibration of bridges using TMD based on linear empirical vortex-shedding forces model [J]. Engineering Mechanics, 2013, 30(6): 269 − 274. (in Chinese) doi: 10.6052/j.issn.1000-4750.2012.08.0630
[4]	葛耀君, 赵林, 许坤. 大跨桥梁主梁涡激振动研究进展与思考[J]. 中国公路学报, 2019, 32(10): 1 − 18. doi: 10.19721/j.cnki.1001-7372.2019.10.001 GE Yaojun, ZHAO Lin, XU Kun. Review and reflection on vortex-induced vibration of main girders of long-span bridges [J]. China Journal of Highway and Transport, 2019, 32(10): 1 − 18. (in Chinese) doi: 10.19721/j.cnki.1001-7372.2019.10.001
[5]	PAIDOUSSIS M P, PRICE S J, DE LANGRE E. Fluid-structure interactions: Cross-flow-induced instabilities [M]. Cambridge: Cambridge University Press, 2010.
[6]	LARSEN A, LAROSE G L. Dynamic wind effects on suspension and cable-stayed bridges [J]. Journal of Sound and Vibration, 2015, 334: 2 − 28. doi: 10.1016/j.jsv.2014.06.009
[7]	HU C X, ZHAO L, GE Y J. Mechanism of suppression of vortex-induced vibrations of a streamlined closed-box girder using additional small-scale components [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2019, 189: 314 − 331. doi: 10.1016/j.jweia.2019.04.015
[8]	刘小兵, 张海东, 王彦彪. 扁平箱梁涡激力的展向相关特性研究[J]. 工程力学, 2016, 33(增刊 1): 239 − 243, 250. doi: 10.6052/j.issn.1000-4750.2015.05.S049 LIU Xiaobing, ZHANG Haidong, WANG Yanbiao. Study on spanwise correlation of vortex-induced forces on a flat box girder [J]. Engineering Mechanics, 2016, 33(Suppl 1): 239 − 243, 250. (in Chinese) doi: 10.6052/j.issn.1000-4750.2015.05.S049
[9]	胡传新, 赵林, 陈海兴, 等. 流线闭口箱梁涡振气动力的雷诺数效应研究[J]. 振动与冲击, 2019, 38(12): 118 − 125. doi: 10.13465/j.cnki.jvs.2019.12.017 HU Chuanxin, ZHAO Lin, CHEN Haixing, et al. Reynolds number effects on aerodynamic forces of a streamlined closed-box girder during vortex-induced vibrations [J]. Journal of Vibration and Shock, 2019, 38(12): 118 − 125. (in Chinese) doi: 10.13465/j.cnki.jvs.2019.12.017
[10]	汪家继, 樊健生, 聂建国, 等. 大跨度桥梁箱梁的三分力系数识别研究[J]. 工程力学, 2016, 33(1): 95 − 104. doi: 10.6052/j.issn.1000-4750.2014.06.0475 WANG Jiaji, FAN Jiansheng, NIE Jianguo, et al. Computationial study on static coefficients of box girder section for long-span bridges [J]. Engineering Mechanics, 2016, 33(1): 95 − 104. (in Chinese) doi: 10.6052/j.issn.1000-4750.2014.06.0475
[11]	刘圣源, 胡传新, 赵林, 等. 中央开槽箱梁断面扭转涡振全过程气动力演化特性[J]. 工程力学, 2020, 37(6): 196 − 205. doi: 10.6052/j.issn.1000-4750.2019.08.0478 LIU Shengyuan, HU Chuanxin, ZHAO Lin, et al. Aerodynamic force evolution characteristics around the central-slotting box girder during the whole torsional vortex-induced vibration process [J]. Engineering Mechanics, 2020, 37(6): 196 − 205. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.08.0478

施引文献(2)

期刊类型引用(1)

王滨璇，孙一飞，胡波，韩原，刘庆宽. 风攻角对流线型主梁涡振特性影响的试验研究. 工程力学. 2024(S1): 222-227 .

本站查看

其他类型引用(1)

资源附件(0)

图(7)

计量

文章访问数: 195
HTML全文浏览量: 27
PDF下载量: 38
被引次数: 2

1 风洞试验设计及涡激振动响应测试
1.1 主梁断面参数介绍及模型设计
1.2 试验设备介绍
1.3 涡激振动振幅试验结果分析
2 主梁模型气动力演化规律分析
2.1 测点平均风压系数分析
2.2 测点脉动风压系数分析
2.3 涡激力幅频分析
3 结论

流线型箱梁涡激振动的气动力演化规律

通讯作者: 刘庆宽(1971−)，男，河北人，教授，博士，博导，主要从事桥梁与结构的风荷载、风致振动与控制研究(E-mail: lqk@stdu.edu.cn)

计量

出版历程