超高性能混凝土(Ultra-high performance concrete，简称UHPC)是一种新型的水泥基复合材料，具有超高强度、高韧性和优异耐久性等优点^[1-2]，但延性较差。将UHPC置于钢管中形成钢管超高性能混凝土(Ultra-high performance concrete-filled steel tube，简称UHPCFST)，核心UHPC因受到钢管约束处于三向受压状态，其延性显著增强，强度和韧性也将进一步提升^[3]。UHPCFST具有承载力高、延性好等优点，可减小构件截面尺寸、减轻结构自重，能够满足现代工程结构向着高耸、大跨、重载方向发展的需求。此外，在UHPC中掺入适量粗骨料可减少胶凝材料用量，降低材料造价，增强抗自收缩能力和整体稳定性^[4]。

目前，国内外学者对UHPCFST构件的受力性能进行了广泛研究，但主要针对其轴压性能^[5-6]、纯弯性能^[7-8]和抗震性能^[9-11]。王震等^[12]根据力平衡和变形协调原理，建立了圆钢管UHPC短柱极限承载力计算模型，并基于Mander模型，提出了圆钢管约束UHPC单轴受压本构模型。XU等^[13]和颜燕祥等^[14]考察了钢纤维和聚丙烯纤维掺量、钢管壁厚对UHPCFST短柱轴压性能的影响，基于极限平衡理论和变形协调原理，建立了圆形和方形UHPCFST短柱轴压极限承载力计算公式。CHEN等^[15]研究了UHPCFST短柱的轴压性能，并与普通钢管混凝土柱进行对比，发现钢管对UHPC的约束增强作用弱于普通混凝土。HOANG等^[16-17]研究了约束系数、径厚比对圆形UHPCFST构件承载能力和延性的影响，提出了UHPCFST短柱轴压极限承载能力计算公式。韦建刚等^[5]进行了钢管约束UHPC短柱轴压试验，发现高强钢管的局部鼓曲和UHPC的脆性得到明显改善。此外，文献[18-19]对UHPCFST构件的受弯性能进行研究，评价了现有规范的适用性。现有关于UHPCFST构件受力性能的研究主要侧重于轴压性能和受弯性能，而关于UHPCFST中长柱偏心受压性能的试验研究尚未见报道。

本文以长径比和偏心距作为变化参数，设计了7根圆形钢管含粗骨料超高性能混凝土(简称CA-UHPCFST)试件，对其偏心受压性能开展试验研究，通过将实测极限承载力与规范计算结果进行对比，给出了适合圆形CA-UHPCFST中长柱偏压极限承载力计算的设计规程，为其工程应用提供参考。

1   试验概况

1.1   试件设计与制作

本试验共设计了7个圆形CA-UHPCFST中长柱试件，主要考虑了长径比L/D(3.5、8、12、16)和偏心距e(0 mm、15 mm、30 mm、45 mm)这2个变化参数。试件基本参数见表1，表中试件编号“LC8E30”的含义如下：“LC”表示中长柱；“8”表示长径比为8；“E30”代表偏心距为30 mm。按照设计长度制作空钢管，确保钢管两端齐平，以消除因端部不平而产生的初始偏心，在试件底部焊接尺寸为140 mm×140 mm×10 mm的端板，试件加载前焊接另一端端板。

表  1  试件基本参数

Table  1.  Parameters of specimens

试件编号	D/mm	t/mm	L/mm	L/D	fy/MPa	As/mm2	fck/MPa	Ac/mm2	e/mm	Nu/kN
LC8E00	114	6	912	8	406	2034	124	8167	0	1520
LC8E15	114	6	912	8	406	2034	124	8167	15	1133
LC8E30	114	6	912	8	406	2034	124	8167	30	863
LC8E45	114	6	912	8	406	2034	124	8167	45	645
SC3.5E30	114	6	400	3.5	406	2034	124	8167	30	965
LC12E30	114	6	1368	12	406	2034	124	8167	30	742
LC16E30	114	6	1824	16	406	2034	124	8167	30	636
注：D、t、L分别为钢管的直径、壁厚和试件长度；L/D为长径比；fy为钢材的屈服强度；fck为CA-UHPC的立方体抗压强度；As、Ac分别为钢管和核心CA-UHPC的横截面面积；e为偏心距；Nu为实测极限承载力。

下载: 导出CSV 

| 显示表格

1.2   试验材料

钢材均采用Q390无缝钢管，外径为114 mm，壁厚为6 mm。参照《金属材料 拉伸试验 第1部分：室温试验方法》(GB /T 228.1−2010)^[20]，在30 t万能试验机上对钢材进行拉伸试验。实测钢管的屈服强度为406 MPa，极限抗拉强度为589 MPa，弹性模量为206 GPa，泊松比为0.284。

本试验采用娲石牌P.O52.5普通硅酸盐水泥，矿物掺和料采用硅灰和粉煤灰，其中硅灰的比表面积为22 m²/g，SiO₂的含量为92%；粉煤灰采用麻城一级粉煤灰，颜色呈深灰色；细骨料为天然河沙，粒径小于1.5 mm，细度模数为2.6；粗骨料采用粒径为5 mm~16 mm的花岗岩碎石。减水剂为中建商品混凝土有限公司提供的聚羧酸高效减水剂(简称SP)，减水率为35%，固含量为40%。采用武汉新途工程纤维制造有限公司生产的镀铜平直型钢纤维和聚丙烯纤维(简称PPF)，其中钢纤维直径为0.2 mm，长度为13 mm，抗拉强度≥2200 MPa；聚丙烯纤维长度为19 mm，直径为0.048 mm，抗拉强度为400 MPa，密度为0.91 kg/m³。含粗骨料超高性能混凝土(简称CA-UHPC)的配合比见表2。参照《活性粉末混凝土》(GB/T 31387−2015)^[21]对CA-UHPC的力学性能进行测试，实测立方体抗压强度为124 MPa，轴心抗压强度为112 MPa，弹性模量为46 GPa，峰值应变为2732 με。

表  2  CA-UHPC配合比

Table  2.  Mix proportion of CA-UHPC /(kg/m³)

水泥	硅灰	粉煤灰	水	SP	钢纤维	PPF	砂	碎石
449	104	138	124	17	157	0.9	760	750

下载: 导出CSV 

| 显示表格

1.3   试验装置及加载方案

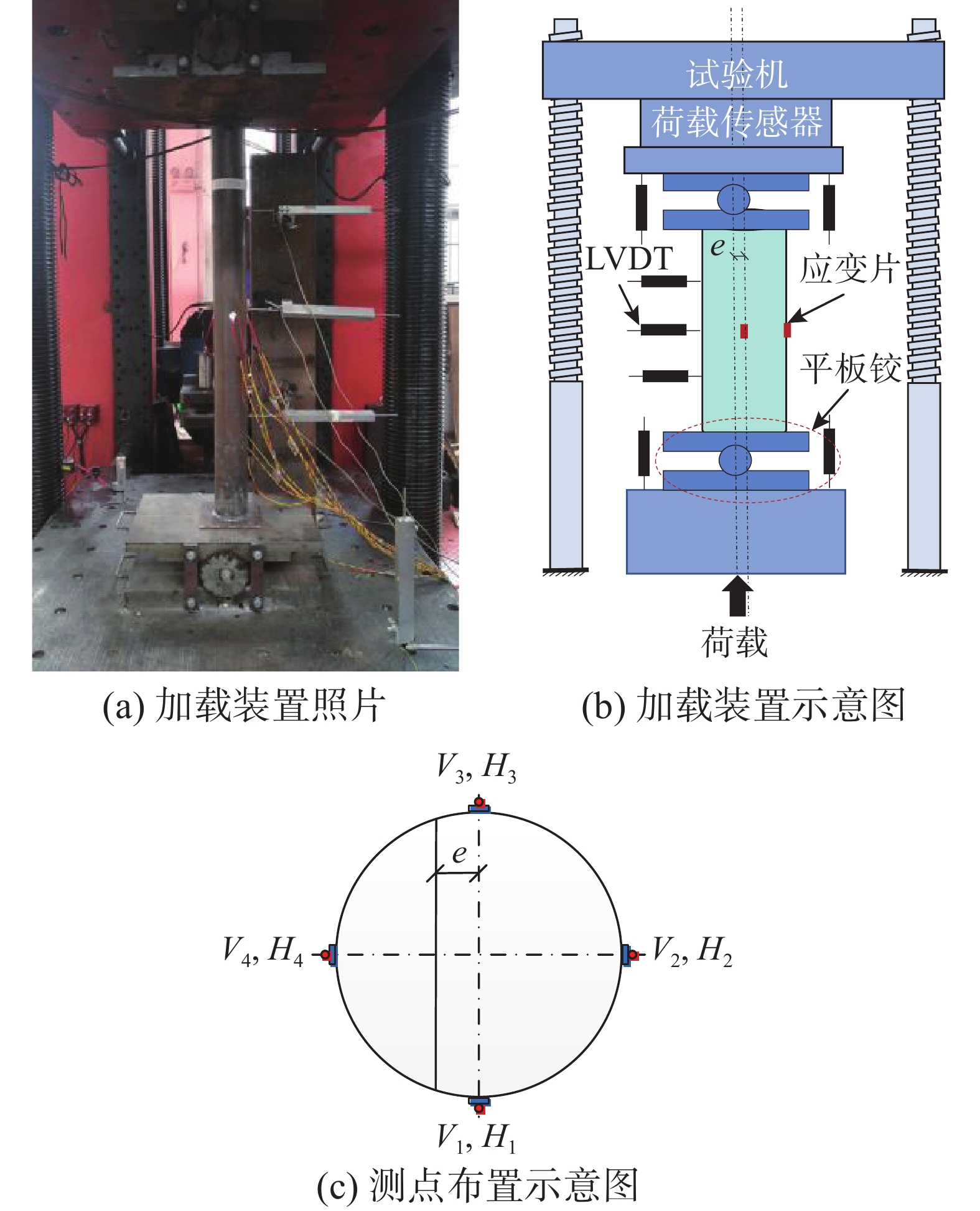
试验在武汉大学土木建筑工程学院土木工程实验中心的500 t压力试验机上进行。偏心荷载通过固定在试验机上的平板铰施加，平板铰中心线与试验机中心线重合，偏心距通过调整平板铰中心线与试件中心线的距离设置。在试件半高处截面对称布置4组90°应变花，测量钢管表面纵向和横向应变。在试件底部和顶部竖向布置4个位移计测量轴向压缩变形，沿高度方向四等分点处水平布置3个位移计测量侧向挠曲变形。试验加载装置及测点布置示意图如图1所示。荷载由电脑自带采集系统采集，应变片和位移计数据由东华DH 3816N静态应变采集系统采集，采样频率为2 Hz。

为保证试件、平板铰、试验机之间良好接触，对试件进行预加载，幅值为200 kN。正式加载采用分级加载制度，达到预估极限荷载前，每级荷载约为预估极限荷载的1/10，加载速率为5 kN/s，每级持荷2 min；当荷载达到预估极限荷载的90%后，采用位移加载，加载速率为1 mm/min；进入下降段后，降低加载速率，采取慢速连续加载。当荷载下降至峰值荷载的70%或侧向挠曲变形过大而不能继续加载时，结束试验。

图  1  试验装置及测点布置示意图

Figure  1.  Test setup and layout of measuring points

下载: 全尺寸图片 幻灯片

2   试验结果与分析

2.1   试验现象与破坏形态

在荷载达到峰值荷载的85%~95%之前，试件表面无明显变化，试件处于弹性阶段。由于核心CA-UHPC具有较高的受压比例极限，在达到峰值荷载之前，荷载随轴向压缩变形的增加呈线性增加，荷载-位移曲线趋于线性。进入弹塑性阶段后，受压区半高截面处钢管表面的铁锈开始脱落，钢管径向膨胀急剧增加，试件产生轻微的侧向挠曲。达到峰值荷载时，核心混凝土发出压碎的声音，试件中部呈现明显的侧向弯曲，长径比越大，峰值荷载时侧向挠曲越明显。进入下降阶段后，承载力迅速下降，侧向挠曲变形加剧，试件最终呈现整体弯曲失稳破坏。其中部分长径比为8的试件，受压区中部因受到核心混凝土的挤压而产生局部鼓曲。

圆形CA-UHPCFST中长柱在偏心受压下的破坏形态如图2所示。可看出，长径比较小的试件呈弯曲失稳和局部压屈破坏，长径比超过12的试件表现为整体弯曲失稳破坏。随长径比和偏心距的增加，失稳现象变得更加明显。采用氧割的方式剥开试件中部1/3高度范围的钢管，观察核心CA-UHPC的破坏形态，如图2所示。可看出，核心混凝土受压区仅有少量肉眼可见的纵向压碎裂纹，受拉区存在较多的细小横向裂纹，随着长径比和偏心距的增加，核心CA-UHPC受拉区和受压区微裂纹的数量减少，裂纹的宽度和深度也减小。

图  2  CA-UHPCFST中长柱及核心混凝土破坏形态

Figure  2.  Failure modes of CA-UHPCFSTs and concrete core

下载: 全尺寸图片 幻灯片

2.2   荷载-轴向变形曲线

图3给出了CA-UHPCFST中长柱在偏心受压下的荷载-轴向变形关系曲线。可看出，随着偏心距的增加，荷载-轴向变形曲线在弹性阶段的斜率逐渐减小，极限承载力随之降低，下降段趋于平缓，而峰值荷载对应的轴向压缩变形随偏心距的增加变化规律不明显。在相同偏心距下，随长径比的增加，刚度和极限承载力逐渐降低，下降段更加陡峭，但长径比对弹性阶段曲线斜率和极限荷载对应的轴向压缩变形值影响较小。此外，由图3(b)可看出，长径比为3.5的短柱在相同偏心距下其初始刚度和极限承载力均高于中长柱试件，曲线的下降段更加平缓，延性更好。

图  3  荷载-轴向变形曲线

Figure  3.  Load versus axial displacement curves

下载: 全尺寸图片 幻灯片

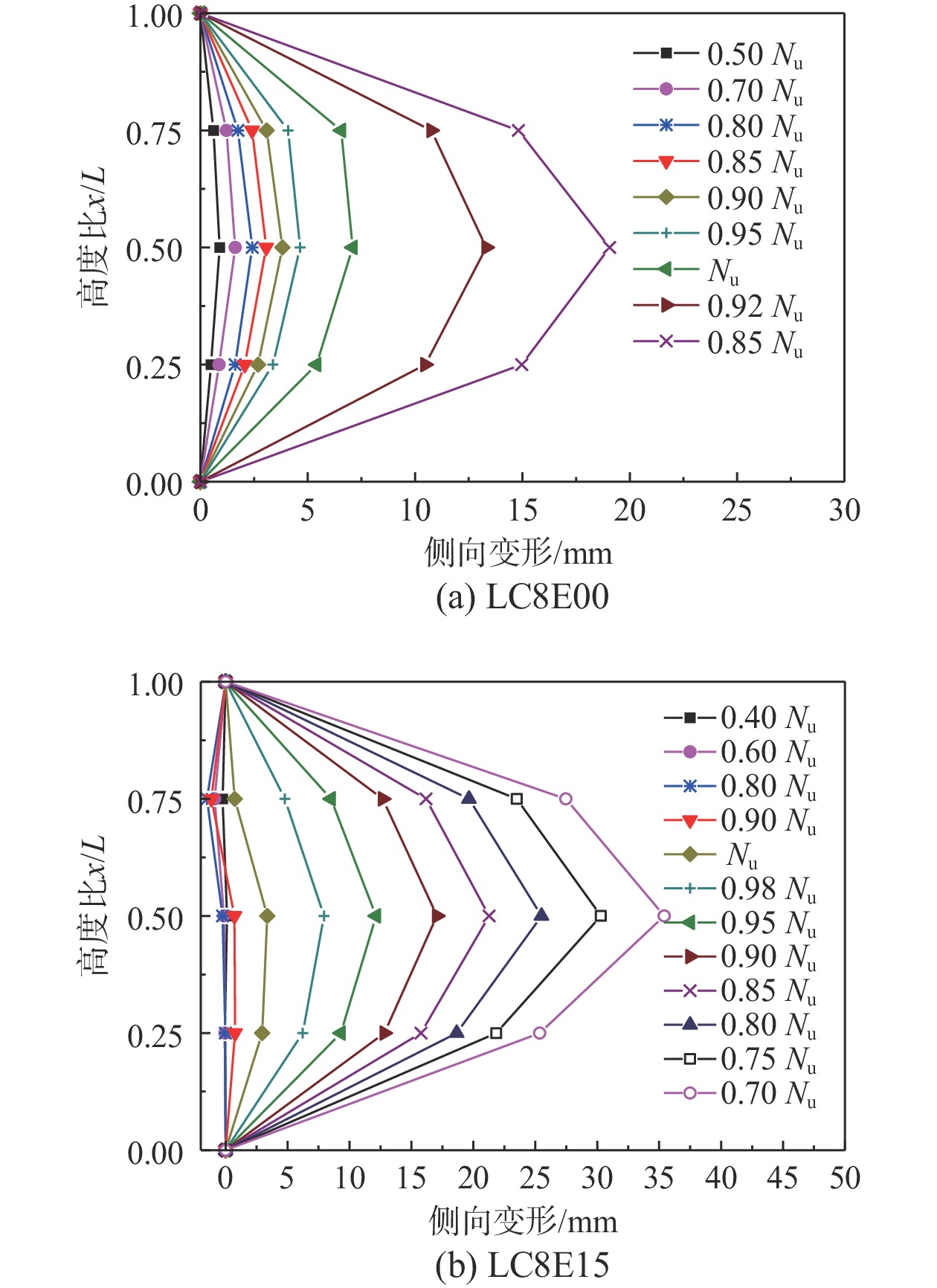
2.3   荷载-侧向挠度分布曲线

图4给出了各级荷载下试件的侧向挠度分布曲线，其中纵坐标$x/L$表示各侧向挠度测量点至柱底距离与试件高度的比值，横坐标为不同荷载水平下各测点的侧向挠度。可看出，在弹性阶段，侧向挠度曲线分布密集，表明此阶段偏心受压中长柱的侧向挠曲变形较小，试件侧向挠度增长缓慢且呈非对称式发展，部分甚至呈“S”形分布。由于在弹性阶段，二阶效应不明显，短柱和中长柱近似为轴心受压，试件径向膨胀使得位移计的读数为负值。而随长径比和偏心距的增加，侧向挠度在弹性阶段的变形值逐渐减小，曲线分布更加密集，近似于半波正弦分布。进入弹塑性阶段后，侧向挠曲变形加快，负的变形值逐渐减小变为正值，而正的变形值持续增加。当荷载达到峰值荷载后，由于试件处于偏心受压状态且二阶效应加剧，致使柱中截面的附加弯矩迅速增加，导致侧向挠曲急剧增加，侧向挠曲近似半波正弦分布。此外，随长径比和偏心距的增加，试件在相同荷载水平下的侧向挠曲变形值增大。

2.4   荷载-应变曲线

图5为圆形CA-UHPCFST中长柱在偏心受压下柱中截面荷载-应变曲线。可看出，不同长径比试件半高处截面钢管应变发展特征相似。在弹性阶段，钢管表面应变线性增加，纵向应变增加的速率大于横向应变。进入弹塑性阶段后，长径比为8的试件在偏心距为0 mm、15 mm、30 mm时，钢管受压侧的应变超过了钢材屈服应变，表明钢管半高处截面在试件进入弹塑性阶段后达到屈服；而当偏心距为45 mm时，荷载达到极限荷载的90%时钢管半高处截面应变超过钢材屈服应变，表明中长柱在达到极限荷载时钢管均屈服，在偏心荷载下发生弹塑性失稳破坏。长径比为12和16的长柱试件达到极限荷载时，半高处钢管纵向应变均小于钢材屈服应变，表明钢管尚未屈服，试件发生弹性失稳破坏。达到极限荷载后，中长柱半高处截面的应变均有增长，而随长径比和偏心距的增加，荷载-应变曲线下降段变得陡峭，截面塑性发展越不明显。

下载: 全尺寸图片 幻灯片

  4  典型试件侧向挠度分布曲线

  4.  Lateral deflection distribution curves of slender columns

下载: 全尺寸图片 幻灯片

下载: 全尺寸图片 幻灯片

  5  偏心受压CA-UHPCFST中长柱荷载-应变曲线

  5.  Load-strain curves of CA-UHPCFST slender columns under eccentric compression

下载: 全尺寸图片 幻灯片

图6为CA-UHPCFST中长柱半高处截面在各级荷载下纵向应变分布。可看出，受压侧边缘应变增长快于受拉侧，加载过程中柱半高处纵向应变的发展满足平截面假定。此外，对于偏心距为0 mm、15 mm、30 mm的中长柱，截面纵向应变在弹性阶段均为压应变，表明全截面处于受压状态。进入弹塑性阶段后，整个截面仍处于全截面受压状态，应变读数均为负数。达到极限荷载后，受拉侧边缘逐渐由受压转变为受拉，半高处截面由全截面受压转变为一侧受压和一侧受拉，受拉侧边缘应变片读数随偏心距的增加而增大，试件中性轴越靠近截面形心轴。随着荷载的增加，截面中性轴逐渐向形心轴移动。在相同偏心距下，随着长径比的增加，截面受压侧和受拉侧边缘应变片的读数均随之减小，由于长径比和偏心距的增加使得二阶效应变得显著，试件趋于弹性失稳破坏，复合截面性能得不到充分发挥，核心混凝土受压区压碎和受拉区开裂现象不明显。

下载: 全尺寸图片 幻灯片

  6  中长柱半高处截面纵向应变分布

  6.  Longitudinal strain distributions at mid-height section of specimens

下载: 全尺寸图片 幻灯片

2.5   极限承载力

图7给出了不同长径比和偏心距下圆形CA-UHPCFST中长柱偏心受压极限承载力。可看出，随长径比的增加，试件极限承载力逐渐降低，长径比由3.5增加至8、12和16时，极限承载力分别下降了10.6%、23.1%和34.1%。由于长径比的增加，加剧了二阶效应对极限承载力的影响，且试件内部的初始缺陷也随之增加，导致试件趋于弹性失稳破坏。由图7(b)可看出，对于长径比为8的中长柱，偏心距由0 mm增加至15 mm、30 mm、45 mm，极限承载力分别下降了34.2%、75.9%和128.7%，表明CA-UHPCFST中长柱的极限承载力随偏心距的增加而减小。由此可见，偏心距对CA-UHPCFST中长柱极限承载力的影响高于长径比。

图  7  试件极限承载力

Figure  7.  Ultimate carrying capacities of specimens

下载: 全尺寸图片 幻灯片

2.6   延性

延性可用于反映结构构件的塑性变形能力，参考文献[22]中评价钢管纤维混凝土柱延性的方法，延性系数可定义为：$\mu {\text{ = }}{\varDelta _{0.85{\text{u}}}}/{\varDelta _{\text{u}}}$，其中${\varDelta _{0.8{\text{u}}}}$和${\varDelta _{\text{u}}}$分别表示荷载达到极限承载力和下降至峰值荷载85%时对应的变形值。

图8给出了不同长径比和偏心距下圆形CA-UHPCFST试件延性系数。可看出，长径比由3.5增加至8、12和16，其延性系数分别下降了29.9%、39.3%和43.6%，表明试件的延性系数随长径比的增加而减小。由图8(b)可知，中长柱的延性系数随偏心距的增加呈先增加后减小的趋势，偏心距由0 mm增加至15 mm、30 mm和45 mm，延性系数分别增加了29.5%、54.4%和27.5%。

图  8  试件延性系数

Figure  8.  Ductility factors of specimens

下载: 全尺寸图片 幻灯片

3   极限承载力计算

目前，国内外对钢管混凝土承载力的计算进行了广泛研究并取得了丰硕成果，各个国家均颁布了相关设计规范和规程，给出了钢管混凝土构件极限承载力计算方法。本文分别采用CECS 28−2012^[23]、DL/T 5085−1999^[24]、AISC−LRFD^[25]和GB 50936−2014^[26]计算圆形CA-UHPCFST中长柱偏心受压极限承载力，并将计算结果与试验结果进行对比，如表3所示。

由表3可看出，CECS 28−2012和AISC−LRFD计算结果偏保守，N_uc/N_u的平均值分别为0.935和0.737，方差为0.067和0.101，变异系数分别为0.072和0.137；DL/T 5085−1999的计算结果高于实测值，偏不安全；GB 50936−2014计算结果的平均值为1.049，方差为0.035，变异系数为0.033，计算结果与试验结果最为接近，且离散性较小，适用于预测圆形钢管含粗骨料超高性能混凝土中长柱偏心受压极限承载力。

表  3  规范公式计算值与实测值对比

Table  3.  Comparisons between the calculated values of codes with the experimental results

试件编号	L/D	e/mm	Nu/kN	CECS 28−2012			DL/T 5085−1999			AISC−LRFD			GB 50936−2014
				Nuc/kN	Nuc/Nu		Nuc/kN	Nuc/Nu		Nuc/kN	Nuc/Nu		Nuc/kN	Nuc/Nu
LC8E00	8	0	1520	1553	1.021		2095	1.386		1274	0.847		1682	1.115
LC8E15	8	15	1133	1008	0.856		1157	0.983		805	0.684		1190	1.051
LC8E30	8	30	863	745	0.863		857	0.993		576	0.668		880	1.019
LC8E45	8	45	645	591	0.891		682	1.028		449	0.676		698	1.050
SC3.5E30	3.5	30	965	968	1.003		949	0.984		593	0.615		968	1.003
LC12E30	12	30	742	653	0.935		780	1.117		555	0.794		793	1.068
LC16E30	16	30	636	582	0.980		706	1.188		524	0.882		661	1.040
平均值				0.935			1.096			0.737			1.049
标准差				0.067			0.147			0.101			0.035
变异系数				0.072			0.134			0.137			0.033
注：L/D表示长径比；e为偏心距；Nuc和Nu分别为极限承载力规范计算值和实测值。

下载: 导出CSV 

| 显示表格

4   结论

本文以长径比和偏心距为变化参数，通过8根圆形钢管含粗骨料超高性能混凝土中长柱偏心受压性能试验研究，得到主要结论如下：

(1)中长柱在偏心受压下发生局部屈曲的弹塑性失稳破坏，长柱发生整体弯曲弹性失稳破坏；钢纤维的掺入可减轻核心CA-UHPC受压区压碎程度，受拉区裂纹的数量和深度均明显减小；随长径比和偏心距的增加，核心CA-UHPC受压区和受拉区裂纹的数量均减小。

(2)圆形CA-UHPCFST试件长径比由3.5增加至8、12、16，极限承载力分别下降了10.6%、23.1%和34.1%，偏心距由0 mm增加至15 mm、30 mm和45 mm，极限承载力分别减小了34.2%、75.9%和128.7%。试件延性系数随长径比的增加而降低，随偏心距的增加呈先增大后减小的趋势。

(3) CECS 28−2012和AISC-LRFD预测极限承载力偏保守，DL/T 5085−1999高估了偏心受压极限承载力，GB 50936−2014的预测结果与试验实测值吻合较好，建议采用该标准的计算方法预测圆形钢管含粗骨料超高性能混凝土中长柱偏心受压极限承载力。