由于曲梁结构具有造型优美、施工简便及受力性能好等优点，已被广泛应用于土木工程、航空航天、工业机械等领域^[1]。在实际工程中，曲梁不可避免地会受到动力荷载的作用(如地震作用、风荷载、移动荷载等)，动力学分析是这类结构计算分析的重要内容。与直梁相比，由于受到曲率的影响，曲梁的动力特性很复杂，目前缺乏对其进行较为精确分析的方法。因此，建立一套精确、可靠的计算方法，高效地获得曲梁动力学问题的精确解，具有十分重要的意义。

DEN HARTOG^[2]最早使用Rayleigh-Ritz法得到了圆弧拱面内振动的频率。BICKFORD和STROM^[3]运用传递矩阵法对曲梁面内和面外自由振动进行了研究。基于精确的动力刚度法， HOWSON和JEMAH^[4]、TSENG等^[5]分析了曲梁的面内自振特性。叶康生和殷振炜^[1]、YANG等^[6]和袁驷等^[7]采用有限元这一应用范围广泛的数值方法研究了曲梁的面内自由振动。虽然国内外学者对曲梁的自由振动特性做了大量的研究，关于其强迫振动的研究则相对不足。吴玉华和楼文娟^[8]采用虚拟激励法与Galerkin法对水平随机地震作用下弹性圆拱的随机响应进行了研究。EFTEKHARI^[9]运用基于微分求积法得到了移动集中荷载作用下曲梁的瞬态响应。但文献[8]和文献[9]都是基于Euler曲梁理论，没有考虑剪切变形和转动惯量的影响。

状态空间法通过选择能量对偶的两类物理量如位移和内力作为状态变量，能将描述结构力学特性的控制方程整理成简洁的矩阵形式^[10]，即状态方程。这种方法具有计算效率高、易于编程等优点，已被广泛地应用于结构的静力和动力分析中^[11-13]。然而，在曲梁的强迫振动分析中尚鲜见报道。

本文基于Timoshenko曲梁理论，通过选择合适的状态变量，建立了圆弧曲梁面内动力学问题的状态空间列式，并给出了固有频率和振动模态的求解过程。采用SHEN等^[11]和LIU等^[13]的方法，即通过引入辛内积，建立了普通边界条件下圆弧曲梁振动模态关于质量和旋转惯量的正交关系式。基于所建立的正交关系式，运用模态叠加法导出了非齐次状态方程即强迫振动方程的解析解，并得到了圆弧曲梁在竖向移动荷载作用下的瞬态响应。最后，给出了数值算例，结果表明采用本文方法进行圆弧曲梁面内动力学分析是十分精确和可靠的。

1   状态方程列式

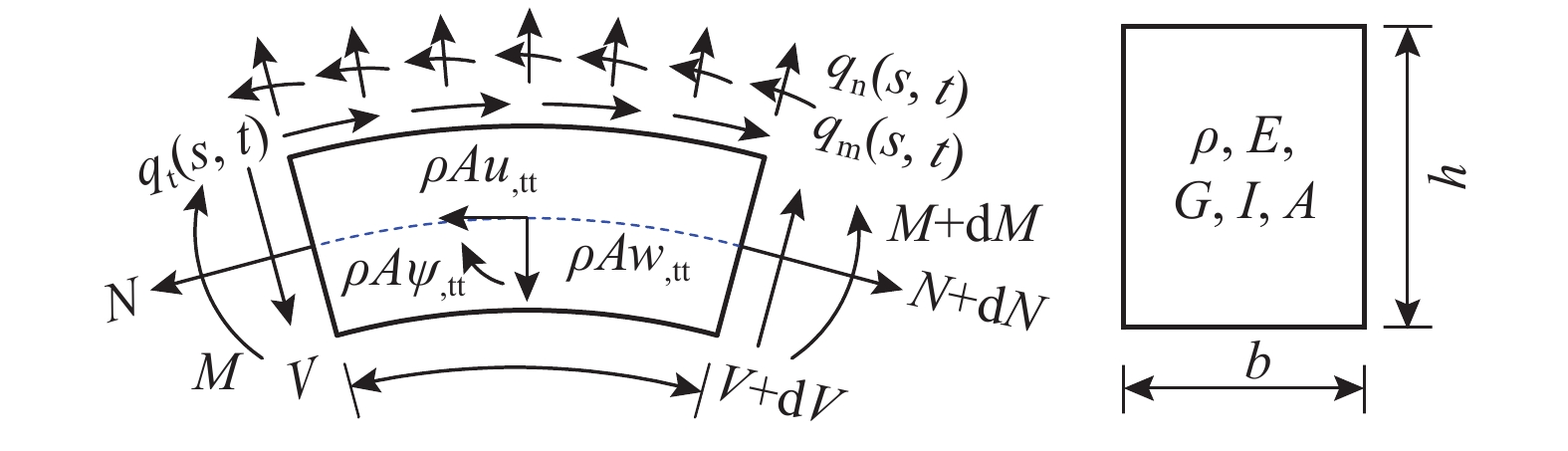
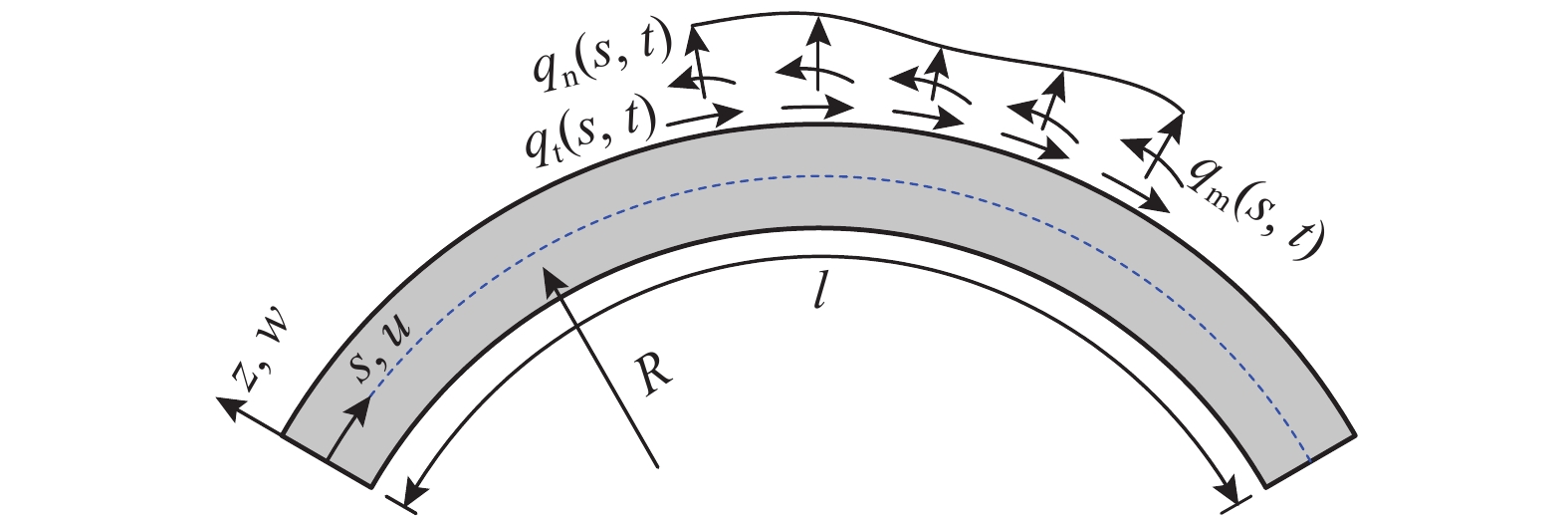
考虑任意动力荷载作用下的圆弧曲梁，如图1所示，其中曲线长度和半径为分别为$l$和$R$。沿曲梁中曲线建立坐标轴$s$轴，将$s$轴逆时针旋转90°得到法向坐标轴${\textit{z}}$轴。$u$、$w$分别是轴线上的环向位移和径向位移，$\psi$为截面的转角，${q_{\rm{t}}}$、${q_{\rm{n}}}$和${q_{\rm{m}}}$分别为作用在曲梁轴线上的环向分布荷载、径向分布荷载以及分布弯矩。

曲梁的微元及其横截面示意图如图2所示。$M$、$V$、$N$分别为整个截面上的弯矩、剪力和轴力，弯矩$M$正方向的选取是为了保证弯矩在相应的正转角上做正功；$A$、$I$分别为截面面积和截面惯性矩，并且有$A = bh$，$I = {{b{h^3}}/ {12}}$，$b$、$h$分别为截面的宽度和高度；$\rho$、$E$、$G$分别是密度、弹性模量和剪切模量，并且有$G = {E / {[2(1 + \nu )]}}$，$\nu$为泊松比。根据微元的平衡，可以得到：

图  1  平面圆弧曲梁模型

Figure  1.  Planar circularly curved beam model

下载: 全尺寸图片 幻灯片

图  2  曲梁微元及其横截面

Figure  2.  Infinitesimal element and typical cross-section of a curved beam

下载: 全尺寸图片 幻灯片

根据Timoshenko曲梁基本理论^[14]，弯矩$M$、剪力$V$和轴力$N$可以表示为：

式中，$\kappa$为截面剪切修正系数。

将式(1)和式(2)整理成矩阵的形式，即可得到曲梁面内动力学问题的状态方程：

式中：${\boldsymbol{v}} = \left[ {w\quad u\quad \psi \quad V\quad N} \quad M \right]^{\rm{T}}$为状态向量，上标${\text{T}}$为矩阵的转置；系统矩阵${\boldsymbol{A}}$、惯性力列向量${{{{\boldsymbol{q}}}}_1}$、荷载列向量${\boldsymbol{q}}_2$的表达式分别为：

本文在这里之所以选择${\boldsymbol{v}} = \left[ {w\quad u\quad \psi \quad V\quad N} \quad M \right]^{\rm{T}}$为状态向量：一方面是因为它与边界条件和连续性条件直接相关；另一方面在后续的模态关于质量和旋转惯量的正交关系式证明中，为了利用辛内积的概念，必须将三个广义力和相应的三个广义位移形成一一对应的共轭物理量，即剪力对应于径向位移、轴力对应于环向位移、弯矩对应于转角，并要使得广义力在相应的广义位移上做正功^{[11, 13]}。

2   自由振动分析

2.1   状态方程的解

对于曲梁面内自由振动问题，可假设：

式中：$\omega$为固有频率(圆频率)；${{\overline {\boldsymbol{v}}}}(s)$为${{{\boldsymbol{v}}}}$的振幅向量。将式(7)代入式(3)，并且令${{{{\boldsymbol{q}}}}_2} = {\boldsymbol{0}}$，得到：

式中：

如果曲梁的几何、材料属性沿轴线方向是不变的，即系统矩阵${{{\boldsymbol{H}}}}$的元素都是常数，则可采用传统传递矩阵法对状态方程式(8)进行求解，得到其解为：

式中，${{\text{e}}^{{{{\boldsymbol{H}}}}s}}$为传递矩阵。

2.2   固有频率及振动模态

在式(10)中令$s = l$，得到：

式中，${{\boldsymbol{T}}} = {{\text{e}}^{{{{\boldsymbol{H}}}}l}}$为曲梁两端状态向量间的传递矩阵。

对于两端简支的曲梁，其边界条件可以表示为：

将式(12)代入式(11)，可以得到：

式中，${T_{ij}}$为矩阵${\boldsymbol{T }}$第$i$行第$j$列的元素。式(13)是一个齐次线性方程组，有非零解的条件是其系数矩阵行列式的值为0，即：

式(14)为两端简支曲梁的频率方程，它是一个关于频率$\omega$的超越方程，可以采用二分法来搜索它的根^[15]。一旦求得某一阶频率后，将其代回式(13)，即可求得在$s = 0$处的状态向量(包含一个任意常数因子)，再通过式(10)可确定曲梁内任意位置处的状态向量，这样就可以确定该频率对应的振动模态(也包含一个任意常数因子)。对于其他边界条件，同样能求得相应的频率和振动模态。

2.3   模态关于质量和旋转惯量的正交关系式

为了运用模态叠加法计算曲梁在动力荷载作用下的响应，必须建立振动模态关于质量和旋转惯量的正交关系式。本节将采用SHEN等^[11]和LIU等^[13]的方法，即基于状态空间列式和辛内积的概念来进行推导。首先考察对应于两个不同模态的状态向量${{{\overline {\boldsymbol{v}}}}_i}$和${{{\overline {\boldsymbol{v}}}}_j}$，定义如下辛内积：

式中，${\boldsymbol{J}} = \left[ {\begin{matrix} {\boldsymbol{0}}&{{{\boldsymbol{I}}_{3 \times 3}}} \\ { - {{\boldsymbol{I}}_{3 \times 3}}}&{\boldsymbol{0}} \end{matrix}} \right]$为单位辛矩阵，${{\boldsymbol{I}}_{3 \times 3}}$为三阶单位矩阵。可以证明单位辛矩阵具有如下性质：${{\boldsymbol{J}}^{\text{T}}} = - {\boldsymbol{J}}$，${{\boldsymbol{J}}^{\text{2}}} = - {{\boldsymbol{I}}_{6 \times 6}}$，${{\boldsymbol{I}}_{6 \times 6}}$是六阶单位矩阵。

状态向量${{{\overline {\boldsymbol{w}}}}_i}$和${{{\overline {\boldsymbol{w}}}}_j}$对应于两个不同频率的振动模态，因此有：

式中：

对于第$i$阶模态和第$j$阶模态，将式(16)两边同时左乘${{\overline {\boldsymbol{v}}}}_j^{\text{T}}{{{\boldsymbol{J}}}}$和${{\overline {\boldsymbol{v}}}}_i^{\text{T}}{{{\boldsymbol{J}}}}$，并在曲梁的整个弧长上进行积分，然后将两式相减，可以得到：

对式(18)左边进行分部积分并利用${{{{\boldsymbol{J}}}}^{\text{T}}} = - {{{\boldsymbol{J}}}}$，可以得到：

由式(18)和式(19)可以得到：

考虑实际工程中常见的3种边界条件，即简支(S)、固支(C)和自由(F)，它们可以分别表示为：

将这些边界条件代入式(21)，可以得到：

式(22)就是曲梁的两个不同模态关于质量和旋转惯量的正交关系式。

3   强迫振动分析

3.1   模态叠加法

本节将采用模态叠加法研究曲梁的强迫振动问题，为此，假设：

式中，${{\overline {\boldsymbol{W}}}}(s)$、${\boldsymbol{\eta }}(t)$分别为模态矩阵和广义坐标矢量，可分别定义为：

式中，${{{\overline {\boldsymbol{w}}}}_k}(s)$为第$k$阶模态。将式(24)的第一式代入式(8)，可以得到：

式中，${\boldsymbol{M}}(s)$是$6 \times n$阶矩阵，并且只有第4行、第5行、第6行的元素是非零的，即：

将式(23)代入式(3)，得到：

式中，${\boldsymbol{V}}(s)$为$6 \times n$阶矩阵，并且只有第4行、第5行、第6行的元素是非零的，即：

将式(25)代入式(27)，可以得到：

将式(29)两边同时乘以${[{{\overline{\boldsymbol{ W}}}}(s)]^{\text{T}}}{\boldsymbol{J}}$，并在曲梁整个弧长上对$s$进行积分，得到：

利用模态关于质量和旋转惯量的正交关系式(22)，得到：

式中：

关于${\eta _k}(t)$的微分方程的通解可用杜哈梅积分表示为：

式中，${\eta _k}(0)$、$\displaystyle \frac{{{\text{d}}{\eta _k}(0)}}{{{\text{d}}t}}$为曲梁的初始条件，若初始时曲梁处于静止状态，则有${\eta _k}(0) = \displaystyle\frac{{{\text{d}}{\eta _k}(0)}}{{{\text{d}}t}} = 0$。

3.2   竖向移动集中荷载作用下的动力响应

考虑曲梁上作用一个沿着梁轴线移动的竖向集中荷载，大小为${P_{\rm m0}}$，方向竖直向上为正，竖直向下为负，移动速率为$c$，${t_{\rm{d}}} = {l \mathord{\left/ {\vphantom {l c}} \right. } c}$为移动荷载作用在梁轴线上的时间，那么该动力荷载可以表示为：

式中：$\delta ( \cdot )$为Dirac Delta函数；$y'(ct)$为$s = ct$处曲梁轴线的斜率。将式(35)代入式(32)，得到：

当$0 \leqslant t < {t_{\rm{d}}}$时，移动荷载仍然作用在曲梁上，且初始时曲梁处于静止状态，即初始条件为${\eta _k}(0) = \displaystyle \frac{{{\text{d}}{\eta _k}(0)}}{{{\text{d}}t}} = 0$，那么由式(34)可以得到${\eta _k}(t)$的表达式为：

当$t \geqslant {t_{\rm{d}}}$时，移动荷载已经移出曲梁外，此时的解是由初始条件${\eta _k}({t_{\rm{d}}})$和$\displaystyle\frac{{{\text{d}}{\eta _k}({t_{\rm{d}}})}}{{{\text{d}}t}}$引起的自由振动，即：

这样，可以分时段求得圆弧曲梁在竖向移动荷载作用下的瞬态响应：

4   数值算例

4.1   自由振动

考虑四种不同边界条件下(SS：两端简支；CC：两端固支；CS：一端固支一端简支；CF：一端固支一端自由)的等截面圆弧曲梁，其轴线为1/4圆弧，曲梁的基本参数如下：$l = 1.1781\;{\text{m}}$，$R = 0.75\;{\text{m}}$，$E = 70\;{\text{GPa}}$，$\kappa = 0.85$，${{\kappa G} \mathord{\left/ {\vphantom {{\kappa G} E}} \right. } E} = 0.3$，$A = 4\;{{\text{m}}^{\text{2}}}$，$I = 0.01\;{{\text{m}}^{\text{4}}}$，$\rho = 2777\;{{{\text{kg}}} \mathord{\left/ {\vphantom {{{\text{kg}}} {{{\text{m}}^3}}}} \right. } {{{\text{m}}^3}}}$。表1给出了SS圆弧曲梁的前10阶无量纲频率值$\omega {l^2}\sqrt {{{\rho A} \mathord{\left/ {\vphantom {{\rho A} {EI}}} \right. } {EI}}}$，并将其与YANG等^[6]、EISENBERGER和EFRAIM^[16]的无量纲频率值进行对比。从表1可以看出，本文方法计算结果与文献[6]、文献[16]计算结果吻合得很好，特别是几乎与文献[16]的结果完全相同，从而验证了本文方法在进行自由振动分析时的正确性。表2还给出了CC、CS和CF这三种边界条件下圆弧曲梁的前10阶无量纲频率$\omega {l^2}\sqrt {{{\rho A} \mathord{\left/ {\vphantom {{\rho A} {EI}}} \right. } {EI}}}$。

表  1  SS圆弧曲梁前10阶无量纲频率值$\omega {l^2}\sqrt {{{\rho A} \mathord{\left/ {\vphantom {{\rho A} {EI}}} \right. } {EI}}}$

Table  1.  The first 10 dimensionless frequencies $\omega {l^2}\sqrt {{{\rho A} \mathord{\left/ {\vphantom {{\rho A} {EI}}} \right. } {EI}}}$ of the SS circularly curved beam

频率阶数	本文	文献[6]	文献[16]		频率阶数	本文	文献[6]	文献[16]
1阶	29.280	29.306	29.280		6阶	143.618	143.679	143.618
2阶	33.305	33.243	33.305		7阶	156.666	156.629	156.666
3阶	67.124	67.123	67.124		8阶	190.477	190.596	190.477
4阶	79.971	79.950	79.971		9阶	225.361	225.349	225.361
5阶	107.851	107.844	107.851		10阶	234.524	234.809	234.524

下载: 导出CSV 

| 显示表格

表  2  CC、CS和CF三种边界条件下圆弧曲梁前10阶无量纲频率值$\omega {l^2}\sqrt {{{\rho A} \mathord{\left/ {\vphantom {{\rho A} {EI}}} \right. } {EI}}}$

Table  2.  The first 10 dimensionless frequencies $\omega {l^2}\sqrt {{{\rho A} \mathord{\left/ {\vphantom {{\rho A} {EI}}} \right. } {EI}}}$ of the circularly curved beams under three different boundary conditions (CC, CS and CF)

频率 阶数	CC	CS	CF		频率 阶数	CC	CS	CF
1阶	35.073	32.218	3.630		6阶	147.261	145.802	114.519
2阶	41.149	36.758	15.535		7阶	160.291	158.232	123.581
3阶	79.582	73.458	40.245		8阶	195.774	193.194	162.277
4阶	79.994	79.993	54.414		9阶	225.365	225.363	188.304
5阶	117.748	112.969	82.707		10阶	237.933	236.264	204.282

下载: 导出CSV 

| 显示表格

4.2   竖向移动集中荷载

考察竖向移动荷载作用下圆弧曲梁的动力响应，曲梁轴线为1/2圆弧，其基本参数如下：$R = 2\;{\text{m}}$，$b = 0.1\;{\text{m}}$，$h = 0.05\;{\text{m}}$，$E = 200\;{\text{GPa}}$，$\kappa = {5 / 6}$，$\nu = 0.3$，$\rho = 7800\;{{{\text{kg}}} / {{{\text{m}}^3}}}$。竖向移动荷载为${P_{m0}} = - 1\;{\text{kN}}$，移动速度为$c = 5\;{{\text{m}} / {\text{s}}}$。表3给出了采用状态空间法和模态叠加法计算SS、CC和CS这三种边界条件下圆弧曲梁跨中径向最大位移的收敛性，从表3可以看出，取前10阶模态完全可以满足精度要求。EFTEKHARI^[9]给出的SS和CC边界条件下曲梁跨中径向最大位移分别为−0.73 mm和−0.45 mm，与本文的结果吻合得很好，从而验证了运用本文方法进行强迫振动分析时的正确性。图3给出了三种边界条件下跨中径向位移和环向位移随时间的变化曲线，从图3中可以看出，SS边界条件下跨中位移最大，而CC边界条件下跨中位移最小。

表  3  竖向移动集中荷载作用下圆弧曲梁跨中径向最大位移计算的收敛性

Table  3.  Convergence of the maximum radial deflection at mid-span of the circularly curved beams under vertical moving concentrated load /mm

边界 条件	模态阶数
	1阶	2阶	3阶	4阶	5阶	6阶	7阶	8阶	9阶	10阶
SS	0.00	−0.67	−0.67	−0.71	−0.71	−0.72	−0.72	−0.73	−0.73	−0.73
CC	0.00	−0.41	−0.41	−0.43	−0.43	−0.45	−0.45	−0.45	−0.45	−0.45
CS	−0.25	−0.60	−0.62	−0.64	−0.64	−0.65	−0.65	−0.66	−0.66	−0.66

下载: 导出CSV 

| 显示表格

图  3  竖向移动集中荷载作用下圆弧曲梁的动力响应

Figure  3.  Dynamic responses of the circularly curved beams under vertical moving concentrated load

下载: 全尺寸图片 幻灯片

5   结论

针对圆弧曲梁面内动力学问题，本文基于所建立的状态空间列式给出了固有频率和振动模态的求解过程。根据SHEN等^[11]和LIU等^[13]的方法，通过引入辛内积，建立了普通边界条件下圆弧曲梁振动模态关于质量和旋转惯量的正交关系式。基于所建立的正交关系式，运用模态叠加法给出了强迫振动方程的解析解，并具体考察了圆弧曲梁在竖向移动集中荷载作用下的瞬态响应。得到主要结论如下：

(1)本文得到的圆弧曲梁自由振动频率、移动荷载下的强迫振动响应与已有结果吻合得很好，证明本文方法是十分精确和可靠的。

(2)本文方法很容易扩展到几何、材料属性沿梁轴线方向是变化的曲梁面内动力学分析中，可以为研究复杂结构的振动问题提供一种有效的分析工具。