EXPERIMENTAL STUDY ON THE INFLUENCE OF RAILINGS ON AERODYNAMIC FORCE OF STREAMLINED MAIN GIRDER
-
摘要: 针对流线型箱梁对风荷载作用比较敏感的情况，以具有典型流线型箱梁断面的象山港大桥为工程背景，通过风洞测压试验方法，研究了施工态和成桥态主梁的平均阻力系数、平均升力系数和平均力矩系数随雷诺数Re的变化情况，同时也分析了桥面临空侧栏杆高度变化对主梁三分力系数的影响规律。研究结果表明：施工态的主梁平均升力系数与平均力矩系数会随着风攻角的增大而增大；成桥态的主梁三分力系数在涡振区间内(Re=2.92×104~4.05×104)变化较为复杂；随着雷诺数的增大，平均升力系数和平均力矩系数基本上呈现出栏杆高度越大其系数越大的趋势。Abstract: In view of the sensitivity of streamlined main girder to wind load, Xiangshangang Bridge with typical streamlined box girder section was taken as the research object, and performed wind tunnel test on a sectional model. The variations of average drag coefficient, average lift coefficient and average moment coefficient with Reynolds number were studied for the construction and completion conditions of bridge girder section. At the same time, the influence of different railings height on the variation of three-component force coefficient of main girder was analyzed. The result shows that the average life coefficient and the average moment coefficient of the bridge at construction condition increase with the increase of wind attack angle; The variation of the three-component coefficients of the bridge in the vortex vibration range (Re=2.92×104-4.05×104) is complicated; with the increase of Reynolds number, the average lift coefficient and the average moment coefficient basically show a trend that the greater the height of the railings, the greater the coefficient.
-
桥梁对风荷载的敏感程度随着跨径的增大更加明显。桥梁结构气动外形的改变会显著影响结构周围的流场形态，进而改变大跨度桥梁的风致振动响应。在桥梁抗风研究中，气动力是对涡振响应分析、静风荷载及稳定性评价的重要指标参数，气动力系数的取值会影响桥梁抗风设计。因此，研究桥梁气动外形的改变对气动力的影响对提高桥梁的抗风性能有重大意义。
影响桥梁结构气动外形的主要因素有：桥梁的附属设施，如栏杆的截面类型、高度、倾斜角度和透风率等[1-6]，以及检修车轨道的尺寸和分布位置等[7-10]。通常会通过改变主梁的风嘴角度[11]、斜腹板角度[12-13]、中央开槽处理[14]，或者设置导流板[15]、扰流板[16]、稳定板[17]等，来改变主梁的气动外形来改善主梁涡振性能。
气动力受雷诺数Re影响明显，研究代表如：李加武等、金挺等[18-20]研究发现流线型主梁存在明显的三分力雷诺数效应；MATSUDA等[21]发现低雷诺数的气动力结果偏大；任若松等[22]发现桥梁结构的细微变化对气动力的雷诺数效应影响较小。因此，本文对Re=2.0×104~14.7×104的施工态主梁和Re=1.9×104~9.7×104的成桥态主梁的气动力变化规律进行了研究，并分析了栏杆高度的变化对气动力的影响。
1 主梁风洞试验概况
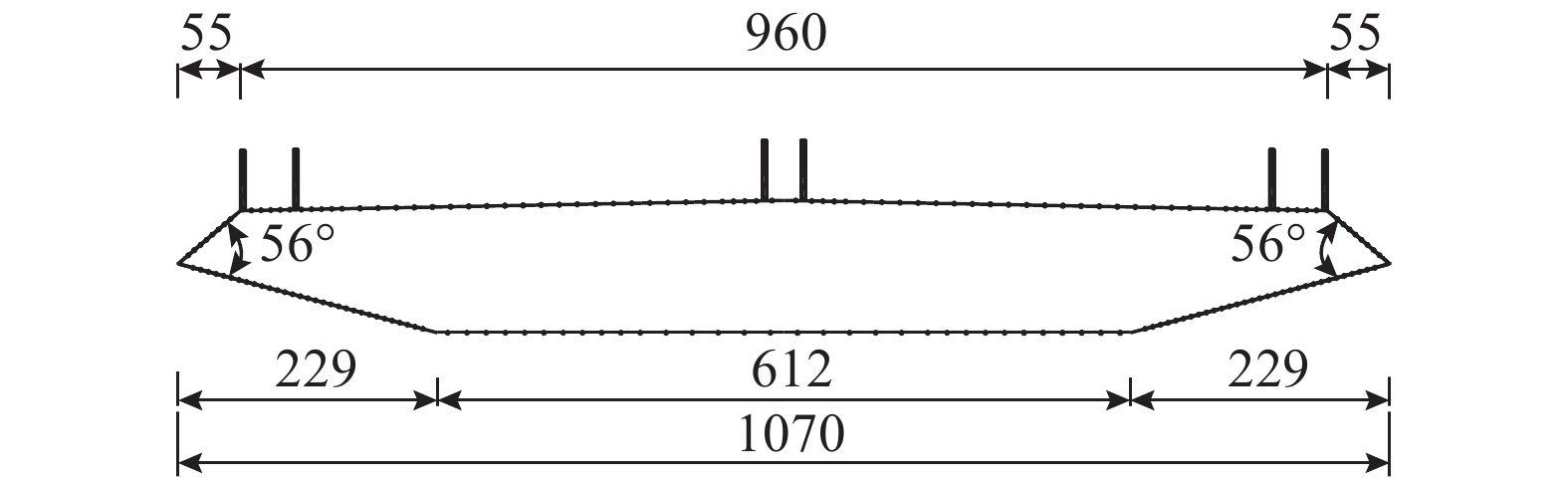
试验在石家庄铁道大学STU-1风洞低速试验段内进行，该试验段宽4.4 m、高3.0 m、长24.0 m，最大风速达30.0 m/s，背景紊流度小于0.4%[23]。以具有典型流线型断面的宁波象山港大桥为工程背景，主梁的宽高比为9.7、风嘴角度为56°。考虑试验段截面尺寸限制和模型的尺寸效应等因素[24-25]，制作缩尺比为1∶30的主梁节段模型，模型长L=2140 mm、宽B=1070 mm、高D=117 mm。在模型跨中位置布置一圈测压点，分上、下表面共180个测压点，在试验段内进行动态测压试验，主梁节段模型尺寸及测点布置示意图如图1所示。
在试验段内搭建弹性悬挂系统(见图2)，还原实桥的振动形式，系统主要由刚性支撑、花篮螺栓、弹簧、刚臂和主梁节段模型等组成。测压试验中使用美国PSI公司生产的微型ESP压力扫描阀和数据处理设备组成的风压测试、采集和处理系统，每个扫描阀有64个通道，量程为±2500 Pa，采样频率为330 Hz，采样时间30 s。每根测压管长度一致，消除了因管路长度对试验结果的影响。
试验在均匀流场中进行，在0°、±3°、±5°攻角下进行测压试验，分别测试了施工态主梁(桥面无栏杆)、成桥态主梁(桥面有栏杆，临空侧栏杆高H = 0.45D，D为梁高)的表面风压数据。此外，还测试了桥面临空栏杆高度为H=0.35D和H=0.56D的成桥风压数据。通过测压试验，分析桥面有无栏杆及栏杆高度的改变对流线型主梁气动力的影响。
2 不同主梁状态对气动力的影响
对主梁表面所测得的风压数据进行积分[26]，可算得气动力的均值和时程值。雷诺数Re是流体惯性力与粘性力的比值，反映流体的基本特征，在不同雷诺数下，流经同一结构的流场会发生变化，导致结构的气动性能和风振特性改变。气动力包括阻力系数、升力系数和力矩系数。计算公式如下：
Re=惯性力粘性力=ρUDμ=UDν (1) CD=FD0.5ρU2D (2) CL=FL0.5ρU2B (3) CM=FM0.5ρU2B2 (4) 式中：ρ为空气密度；U为来流平均风速；D为模型梁高；μ为流体动力粘性系数；ν为运动粘性系数；FL为整个节段模型所受平均升力；FD为节段模型所受平均阻力；FL为节段模型所受平均力矩；B为模型梁宽；CD、CL、CM分别为平均阻力系数、平均升力系数和平均力矩系数。
2.1 施工态主梁
施工态主梁是指桥梁在施工阶段的过程中，桥面上未安装附属设施时的状态。不同风攻角下，施工态主梁三分力系数随雷诺数的变化曲线如图3所示。由图3可见，阻力系数在风攻角
α =−5°时最大，在风攻角α =0°时最小，两者差值在0.2左右。在−5°、−3°和0°风攻角下，平均阻力系数随着雷诺数的增大缓慢增大。然而，在风攻角α =+3°、+5°时平均阻力系数随着雷诺数的增大而减小；风攻角越大平均升力系数越大，在非负攻角时平均升力系数随着雷诺数的增大而增大，负攻角时随着雷诺数的增大而减小；平均力矩系数的变化规律与平均升力系数的规律相同。不同的是，在非负攻角时平均力矩系数为正值，负攻角时为负值，而平均升力系数的数值在各攻角下均为负值。![]()
图 3 施工态主梁三分力系数随雷诺数的变化曲线Figure 3. Curves of three component coefficients at constructing state of bridge girder with Reynolds number2.2 成桥态主梁
成桥态主梁是在施工态主梁的桥面上安装栏杆(忽略检修车轨道等附属设施)。安装栏杆后，成桥态的主梁节段模型发生明显了的涡激振动现象，因此三分力系数的变化趋势较施工态主梁相比较而言复杂许多。图4给出了成桥态主梁三分力系数随雷诺数的变化曲线。由图可见，在涡振区间内(Re=2.92×104~4.05×104)平均阻力系数在风攻角
α =+3°、+5°时呈现先减小后增大的趋势，平均升力系数在风攻角α =0°、+3°、+5°时呈现先增大后减小的趋势。而平均力矩系数随着雷诺数的增大而减小，且风攻角越大力矩系数越大。![]()
图 4 成桥态主梁三分力系数随雷诺数的变化曲线Figure 4. Curves of three component coefficients at completed state of bridge girder with Reynolds number3 不同栏杆高度对主梁气动力的影响
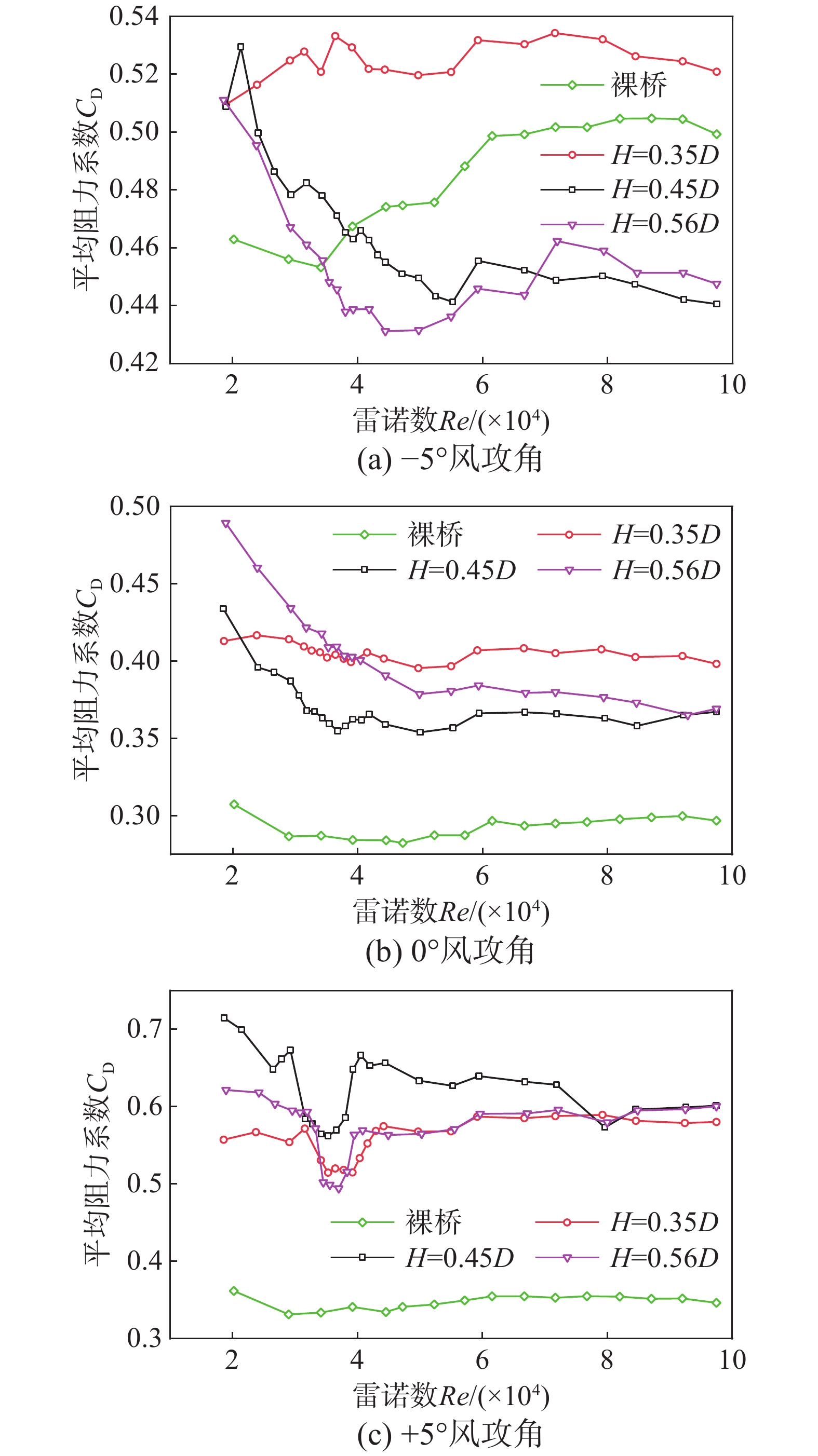
3.1 不同栏杆高度对阻力系数的影响
图5给出了−5°、0°、+5°风攻角下栏杆高度对阻力系数随雷诺数变化的影响，文中所改变的栏杆高度是桥面临空侧人行道栏杆。当风攻角
α =−5°时，栏杆高0.35D主梁的平均阻力系数最大，其数值在0.52左右，栏杆高0.45D和栏杆高0.56D的平均阻力系数小于栏杆高0.35D。当Re>3.92×104时，施工态主梁的平均阻力系数大于栏杆高0.45D和栏杆高0.56D，但小于栏杆高0.35D；当风攻角α = 0°时，成桥态主梁断面的平均阻力系数明显大于施工态。在1.84×104<Re<3.78×104时，三种不同栏杆高度的平均阻力系数大小顺序为：0.56D>0.35D>0.45D，当Re>3.78×104时，0.35D>0.56D>0.45D；当风攻角α =+5°时，安装栏杆后平均阻力系数明显增大，在1.84×104<Re<7.95×104时，栏杆高0.45D时平均阻力系数较大，另两者平均阻力系数相当，当Re>7.95×104时，不同高度栏杆的平均阻力系数相近。![]()
图 5 不同栏杆高度、不同风攻角时平均阻力系数随雷诺数的变化曲线Figure 5. Curves of mean drag coefficient with Reynolds Number at different railing heights and attack angles3.2 不同栏杆高度对平均升力系数的影响
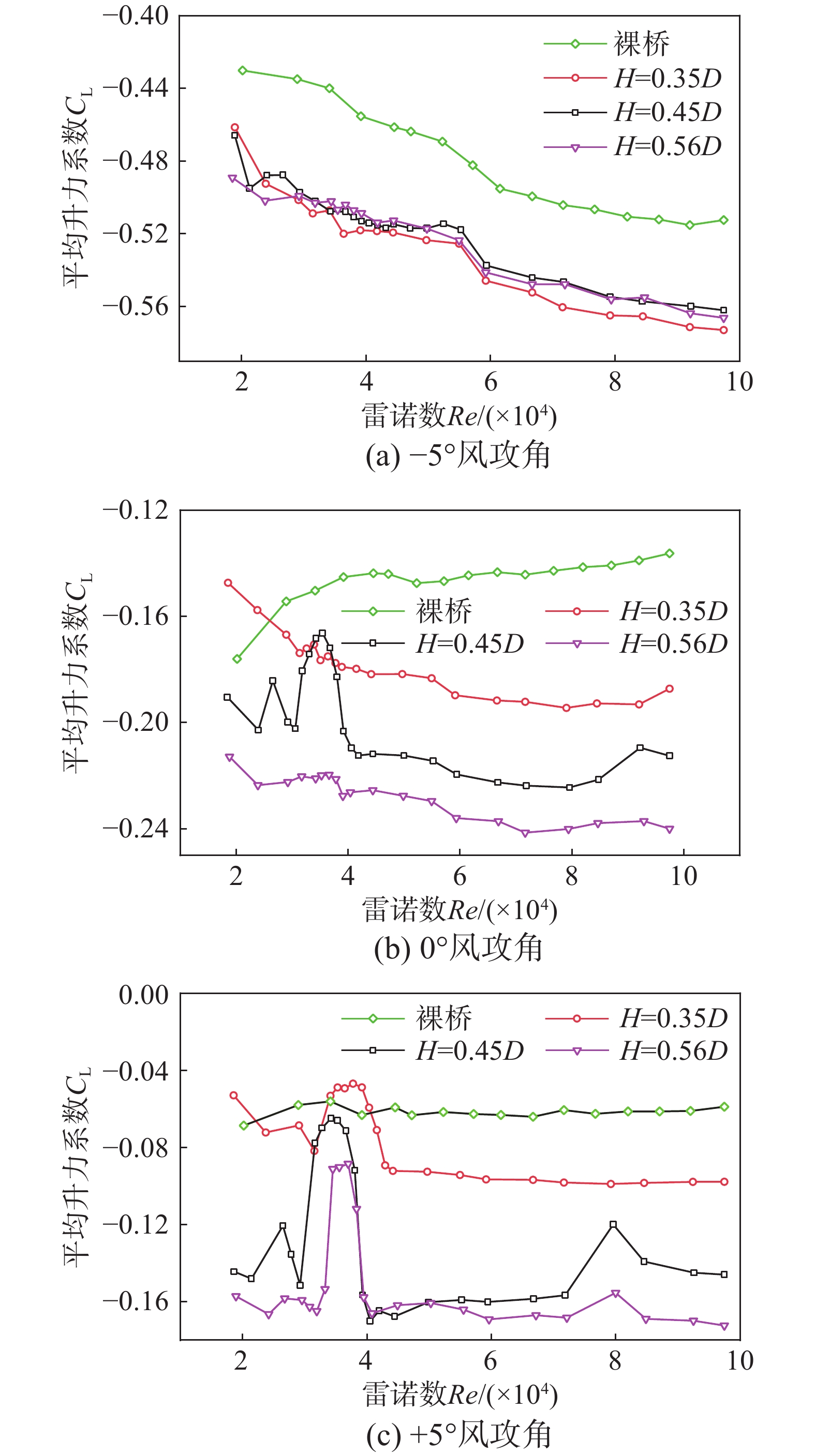
由图6可见，安装不同高度的栏杆后，基本上在所有的雷诺数范围内平均升力系数都有所降低。在风攻角
α =−5°时，不同栏杆高度主梁的平均升力系数十分相近，随着攻角的增大，不同高度栏杆主梁的平均升力系数发生变化。在风攻角α =0°、+5°时，大趋势上呈现着主梁栏杆高度越低平均升力系数越低，在局部上存在些许差异，具体表现在：在风攻角α =0°时，在涡振区间内，栏杆高0.45D时平均升力系数出现峰值现象，在3.31×104<Re<3.80×104时，栏杆高0.45D的平均升力系数超越了栏杆高0.35D；在风攻角α =+5°时，在涡振区间内(Re=2.92×104~4.05×104)有栏杆的主梁断面平均升力系数都出现峰值现象，在3.41×104<Re<4.10×104范围内，栏杆高0.35D的平均升力系数大于裸梁。在3.69×104<Re<5.02×104范围内，栏杆高0.45D和0.56D的平均升力系数基本一致。![]()
图 6 不同栏杆高度、不同风攻角时平均升力系数随雷诺数的变化曲线Figure 6. Curves of mean moment coefficient with Reynolds Number at different railing heights and attack angles3.3 不同栏杆高度对平均力矩系数的影响
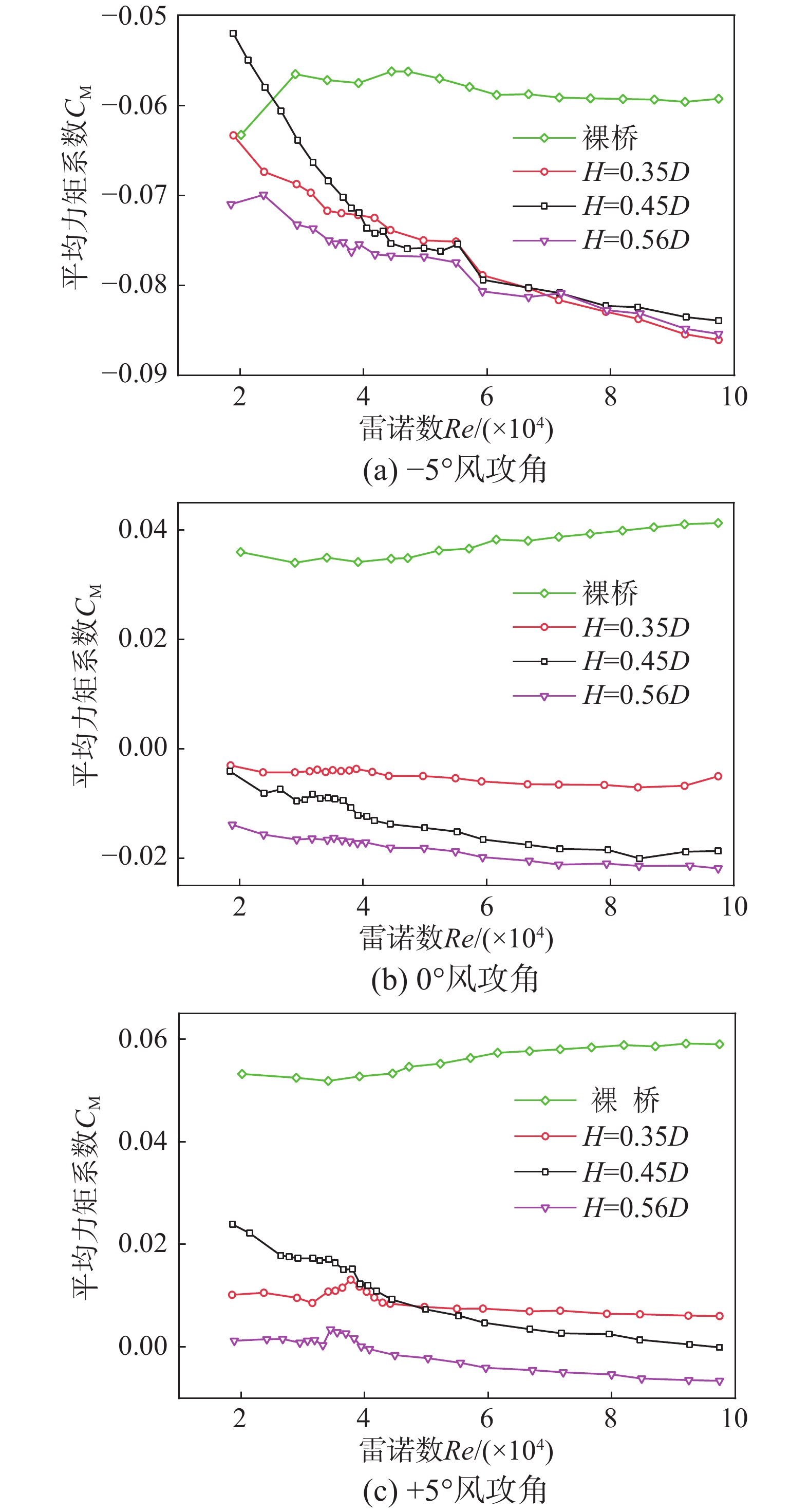
由图7给出的不同高度栏杆下平均力矩系数的变化规律，总体上可见，裸桥的平均力矩系数大于成桥的平均力矩系数。在风攻角
α =−5°时，1.84×104<Re<3.92×104范围内，不同高度栏杆之间栏杆高0.45D的平均力矩系数最大，且随着雷诺数的增大下降趋势最大。栏杆高0.45D的平均力矩系数最小，随着雷诺数的增大，下降趋势较为缓和。当Re>3.92×104时，随着雷诺数的增大，不同高度栏杆主梁之间的平均力矩系数基本一致。在风攻角α =0°、+5°时，平均力矩系数的整体变化趋势同样成呈现出随着栏杆高度增大而减小的趋势，不同的是在风攻角α =+5°时，1.84×104<Re<3.92×104范围内，栏杆高0.45D的平均力矩系数大于栏杆高0.35D。![]()
图 7 不同栏杆高度、不同风攻角时平均力矩系数随雷诺数的变化曲线Figure 7. Curves of mean lift coefficient with Reynolds number at different railing heights and attack angles4 结论
通过主梁节段模型风洞动态测压试验方法，研究了施工态主梁和不同高度栏杆的成桥态主梁三分力系数随雷诺数的变化趋势，得到的主要结论如下：
(1) 施工态主梁：非正攻角的平均阻力系数与非负攻角的平均升力系数和平均力矩系数，随着雷诺数的增大系数增大。平均阻力系数在风攻角
α =0°时最小，平均升力系数与平均力矩系数随着风攻角的增大而增大。(2) 成桥态主梁：成桥断面的三分力系数变化在涡振区间(Re=2.92×104~4.05×104)内较裸桥而言复杂，在涡振区间内，当风攻角
α =+3°和α =+5°时，平均阻力系数呈现先减小后增大的趋势，在非负攻角的时平均升力系数呈现处先增大后减小的趋势。成桥断面的平均力矩系数，随着雷诺数的增大而减小。(3) 不同风攻角下，不同栏杆高度的平均阻力系数随雷诺数的变化趋势不同。随着雷诺数的增大，平均升力系数和平均力矩系数基本上呈现栏杆高度越大其系数越大的趋势。
-
![]()
图 3 施工态主梁三分力系数随雷诺数的变化曲线
Figure 3. Curves of three component coefficients at constructing state of bridge girder with Reynolds number
![]()
图 4 成桥态主梁三分力系数随雷诺数的变化曲线
Figure 4. Curves of three component coefficients at completed state of bridge girder with Reynolds number
![]()
图 5 不同栏杆高度、不同风攻角时平均阻力系数随雷诺数的变化曲线
Figure 5. Curves of mean drag coefficient with Reynolds Number at different railing heights and attack angles
![]()
图 6 不同栏杆高度、不同风攻角时平均升力系数随雷诺数的变化曲线
Figure 6. Curves of mean moment coefficient with Reynolds Number at different railing heights and attack angles
-
[1] LARSEN A, ESDAHL S, ANDERSEN J E, et al. Storebælt suspension bridge–vortex shedding excitation and mitigation by guide vanes [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2000, 88(2/3): 283 − 296.
[2] ZHAN J, XIN D B, OU J P, et al. Experimental study on suppressing vortex-induced vibration of a long-span bridge by installing the wavy railings [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2020, 202: 104205. doi: 10.1016/j.jweia.2020.104205
[3] XIN D B, ZHAN J, ZHANG H F, et al. Control of vortex-induced vibration of a long-span bridge by inclined railings [J]. Journal of Bridge Engineering, 2021, 26(12): 04021093. doi: 10.1061/(ASCE)BE.1943-5592.0001803
[4] 刘庆宽, 王仰雪, 孙一飞, 等. 栏杆高度对流线型箱梁涡振性能影响的试验研究 [J/OL]. 湖南大学学报(自然科学版). https://kns.cnki.net/kcms/detail/43.1061.N.20221020.1046.002.html, 2022-11-29. LIU Qingkuan, WANG Yangxue, SUN Yifei, et al. Experimental study on the influence of railings with different heights on vortex-induced vibration performance of streamlined box girder [J/OL]. Journal of Hunan University (Natural Sciences). https://kns.cnki.net/kcms/detail/43.1061.N.20221020.1046.002.html, 2022-11-29. (in Chinese)
[5] 王仰雪, 刘庆宽, 靖洪淼, 等. 倾斜栏杆对流线型箱梁涡激振动性能影响的试验研究[J]. 振动与冲击, 2023, 42(6): 232 − 239. doi: 10.13465/j.cnki.jvs.2023.06.028 WANG Yangxue, LIU Qingkuan, JING Hongmiao, et al. Experimental study on the influence of inclined railings on the vortex-induced vibration performance of a streamlined box girder [J]. Journal of Vibration and Shock, 2023, 42(6): 232 − 239. (in Chinese) doi: 10.13465/j.cnki.jvs.2023.06.028
[6] 王仰雪, 孙一飞, 刘庆宽, 等. 栏杆透风率对流线型箱梁涡振特性影响的风洞试验研究[C]. 广州: 第30届全国结构工程学术会议论文集(第Ⅱ册), 2021: 89 − 93. WANG Yangxue, SUN Yifei, LIU Qingkuan, et al. Influence of railing ventilation rate on characteristics of vortex induced vibration of streamlined box girder [C]. Guangzhou: Proceedings of the 31st National Conference on Structural Engineering (NO. Ⅱ), 2021: 89 − 93. (in Chinese)
[7] BATTISTA R C, PFEIL M S. Reduction of vortex-induced oscillations of Rio–Niterói bridge by dynamic control devices [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2000, 84(3): 273 − 288. doi: 10.1016/S0167-6105(99)00108-7
[8] 黄林, 董佳慧, 王骑, 等. 检修车轨道位置与导流板对宽体扁平钢箱梁涡振性能影响研究 [J/OL]. 西南交通大学学报. https://kns.cnki.net/kcms/detail/51.1277.U.20210929.0857.002.html, 2022-11-29. HUANG Lin, DONG Jiahui, WANG Qi, et al. Study on the influence of maintenance rail position and guide vane on vortex-induced vibration performance of wide flat steel box girder [J/OL]. Journal of Southwest Jiaotong University. https://kns.cnki.net/kcms/detail/51.1277.U.20210929.0857.002.html, 2022-11-29. (in Chinese)
[9] 李春光, 张记, 樊永波, 等. 宽幅流线型钢箱梁涡振性能气动优化措施研究[J]. 桥梁建设, 2017, 47(1): 35 − 40. LI Chunguang, ZHANG Ji, FAN Yongbo, et al. Study of aerodynamic optimization measures for vortex-induced vibration performance of wide streamlined steel box girder [J]. Bridge Construction, 2017, 47(1): 35 − 40. (in Chinese)
[10] LAIMA S, LI H, CHEN W L, et al. Effects of attachments on aerodynamic characteristics and vortex-induced vibration of twin-box girder [J]. Journal of Fluids and Structures, 2018, 77: 115 − 133. doi: 10.1016/j.jfluidstructs.2017.12.005
[11] 李春光, 毛禹, 韩艳, 等. 窄幅边主梁斜拉桥涡振性能及气动控制措施研究[J]. 铁道科学与工程学报, 2022, 19(5): 1347 − 1354. doi: 10.19713/j.cnki.43-1423/u.T20210501 LI Chunguang, MAO Yu, HAN Yan, et al. Vortex induced vibration performance and aerodynamic control measures of cable stayed bridge with narrow side girder [J]. Journal of Railway Science and Engineering, 2022, 19(5): 1347 − 1354. (in Chinese) doi: 10.19713/j.cnki.43-1423/u.T20210501
[12] 王德智. 闭口钢箱梁几何外形的空气动力性能优化[D]. 上海: 同济大学, 2013. WANG Dezhi. Geometrical optimization of closed boxgirders based on aerodynamic performance [D]. Shanghai: Tongji University, 2013. (in Chinese)
[13] 孙延国, 廖海黎, 李明水. 基于节段模型试验的悬索桥涡振抑振措施[J]. 西南交通大学学报, 2012, 47(2): 218 − 223, 264. doi: 10.3969/j.issn.0258-2724.2012.02.008 SUN Yanguo, LIAO Haili, LI Mingshui. Mitigation measures of vortex-induced vibration of suspension bridge based on section model test [J]. Journal of Southwest Jiaotong University, 2012, 47(2): 218 − 223, 264. (in Chinese) doi: 10.3969/j.issn.0258-2724.2012.02.008
[14] 刘圣源, 胡传新, 赵林, 等. 中央开槽箱梁断面扭转涡振全过程气动力演化特性[J]. 工程力学, 2020, 37(6): 196 − 205. LIU Shengyuan, HU Chuanxin, ZHAO Lin, et al. Aerodynamic force evolution characteristics around the central-slotting box girder during the whole torsional vortex-induced vibration process [J]. Engineering Mechanics, 2020, 37(6): 196 − 205. (in Chinese)
[15] LARSEN A, SAVAGE M, LAFRENIÈRE A, et al. Investigation of vortex response of a twin box bridge section at high and low Reynolds numbers [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(6/7): 934 − 944.
[16] 朱乐东, 张海, 张宏杰. 多孔扰流板对半封闭窄箱梁涡振的减振效果[J]. 实验流体力学, 2012, 26(3): 50 − 55. doi: 10.3969/j.issn.1672-9897.2012.03.009 ZHU Ledong, ZHANG Hai, ZHANG Hongjie. Mitigation effect of multi-orifice flow-disturbing plate on vortex-induced resonance of narrow semi-closed box deck [J]. Journal of Experiments in Fluid Mechanics, 2012, 26(3): 50 − 55. (in Chinese) doi: 10.3969/j.issn.1672-9897.2012.03.009
[17] 贺耀北, 周洋, 华旭刚. 双边钢主梁-UHPC组合梁涡振抑制气动措施风洞试验研究[J]. 振动与冲击, 2020, 39(20): 142 − 148. doi: 10.13465/j.cnki.jvs.2020.20.019 HE Yaobei, ZHOU Yang, HUA Xugang. A wind tunnel test on aerodynamic measures for vortex-induced vibration suppression of a bilateral steel-UHPC composite beam [J]. Journal of Vibration and Shock, 2020, 39(20): 142 − 148. (in Chinese) doi: 10.13465/j.cnki.jvs.2020.20.019
[18] 李加武, 张宏杰, 韩万水. 斜拉桥风致响应的雷诺数效应[J]. 中国公路学报, 2009, 22(2): 42 − 47. doi: 10.3321/j.issn:1001-7372.2009.02.008 LI Jiawu, ZHANG Hongjie, HAN Wanshui. Wind-induced response of cable-stayed bridge with consideration of reynolds number effect [J]. China Journal of Highway and Transport, 2009, 22(2): 42 − 47. (in Chinese) doi: 10.3321/j.issn:1001-7372.2009.02.008
[19] 李加武, 林志兴, 项海帆. 桥梁断面三分力系数的雷诺数效应[J]. 同济大学学报(自然科学版), 2004, 32(10): 1328 − 1333. doi: 10.3321/j.issn:0253-374X.2004.10.013 LI Jiawu, LIN Zhixing, XIANG Haifan. Reynolds number effect of mean force coefficient of two kinds of typical bridge deck section [J]. Journal of Tongji University (Natural Science), 2004, 32(10): 1328 − 1333. (in Chinese) doi: 10.3321/j.issn:0253-374X.2004.10.013
[20] 金挺, 林志兴. 扁平箱形桥梁断面斯特罗哈数的雷诺数效应研究[J]. 工程力学, 2006, 23(10): 174 − 179. doi: 10.3969/j.issn.1000-4750.2006.10.033 JIN Ting, LIN Zhixing. Reynolds number effects on strouhal number of flat-box girder bridge decks [J]. Engineering Mechanics, 2006, 23(10): 174 − 179. (in Chinese) doi: 10.3969/j.issn.1000-4750.2006.10.033
[21] MATSUDA K, COOPER K R, TANAKA H, et al. An investigation of Reynolds number effects on the steady and unsteady aerodynamic forces on a 1:10 scale bridge deck section model [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89(7/8): 619 − 632.
[22] 任若松, 梁新华, 刘小兵, 等. 准流线型桥梁断面气动力特性的雷诺数效应研究[J]. 工程力学, 2020, 37(增刊 1): 139 − 144. doi: 10.6052/j.issn.1000-4750.2019.04.S023 REN Ruosong, LIANG Xinhua, LIU Xiaobing, et al. Study on Reynolds number effect of aerodynamic characteristics of quasi-streamlined bridge section [J]. Engineering Mechanics, 2020, 37(Suppl 1): 139 − 144. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.04.S023
[23] 刘庆宽. 多功能大气边界层风洞的设计与建设[J]. 实验流体力学, 2011, 25(3): 66 − 70. doi: 10.3969/j.issn.1672-9897.2011.03.015 LIU Qingkuan. Aerodynamic and structure desigh of multifunction boundary-layer wind tunnel [J]. Journal of Experiments in Fluid Mechanics, 2011, 25(3): 66 − 70. (in Chinese) doi: 10.3969/j.issn.1672-9897.2011.03.015
[24] 温青, 华旭刚, 池俊豪, 等. 端部条件和长宽比对矩形断面节段模型涡激振动的影响[J]. 振动工程学报, 2020, 33(4): 653 − 659. doi: 10.16385/j.cnki.issn.1004-4523.2020.04.002 WEN Qing, HUA Xugang, CHI Junhao, et al. Effects of end conditions and aspect ratios on vortex-induced vibration for a rectangular sectional model [J]. Journal of Vibration Engineering, 2020, 33(4): 653 − 659. (in Chinese) doi: 10.16385/j.cnki.issn.1004-4523.2020.04.002
[25] 李永乐, 陈星宇, 汪斌, 等. 扁平箱梁涡激共振阻塞效应及振幅修正[J]. 工程力学, 2018, 35(11): 45 − 52, 78. doi: 10.6052/j.issn.1000-4750.2017.07.0576 LI Yongle, CHEN Xingyu, WANG Bin, et al. Blockage-effects and amplitude conversion of vortexinduced vibration for flat-box girder [J]. Engineering Mechanics, 2018, 35(11): 45 − 52, 78. (in Chinese) doi: 10.6052/j.issn.1000-4750.2017.07.0576
[26] 李加武, 林志兴, 金挺. 压力积分法在桥梁断面雷诺数效应研究中的应用[J]. 振动工程学报, 2006, 19(4): 505 − 508. doi: 10.3969/j.issn.1004-4523.2006.04.013 LI Jiawu, LIN Zhixing, JIN Ting. Application of pressures integration in effeets of bridge decks [J]. Journal of Vibration Engineering, 2006, 19(4): 505 − 508. (in Chinese) doi: 10.3969/j.issn.1004-4523.2006.04.013
-
期刊类型引用(5)
1. 滕培松，吴聪，向敏，刘小兵. 主桁倾角对倒梯形钢桁梁气动特性的影响分析. 河北科技大学学报. 2024(02): 217-224 . 
百度学术
2. 韩鹏，常幸，邵林媛，孙一飞，褚泽楷，刘庆宽. 带肋斜拉索涡激振动和气动力特性的试验研究. 工程力学. 2024(S1): 136-141 . 本站查看
3. 王滨璇，孙一飞，胡波，韩原，刘庆宽. 风攻角对流线型主梁涡振特性影响的试验研究. 工程力学. 2024(S1): 222-227 . 本站查看
4. 于春放，靖洪淼，张记涛，许浩然，乔明哲，刘庆宽. 不同雷诺数下4∶1圆角矩形柱气动力特性及流场数值模拟研究. 工程力学. 2024(S1): 332-338 . 本站查看
5. 刘庆宽，王仰雪，孙一飞，李震，韩原，靖洪淼. 栏杆高度对流线型箱梁涡振性能影响的试验研究. 湖南大学学报(自然科学版). 2023(07): 140-150 . 百度学术
其他类型引用(4)
下载:
计量
- 文章访问数: 184
- HTML全文浏览量: 61
- PDF下载量: 30
- 被引次数: 9
