CALCULATION METHOD FOR STABILITY OF SELF-BEARING MASONRY WALL IN HIGH AND WIDE SPACE
-
摘要:
以弹性力学薄板屈曲理论为基础,采用能量法并选取满足边界条件的挠曲试函数,借助Python软件自编计算程序,推导了对边简支对边自由板、三边简支一边自由板及四边简支板在轴向均布荷载作用下的屈曲临界承载力计算公式,采用有限元模型分析对结果进行验证,并给出屈曲特征系数ξ与高宽比r的简化关系式。基于面外抗弯刚度和面内轴向刚度相等原则,将带构造柱和圈梁的砌体墙由非均匀各向异性材料等效成各向同性材料,并验证等效模型用于墙体屈曲分析的可靠性。提出可用于不同平面布置形式自承重砌体墙的稳定性设计验算方法,并给出其在两个实际工程中的应用。该文方法操作简便,可考虑砌体墙不同边界条件、构造柱和圈梁布置、自承重墙三角形轴力分布特点等影响,相关结论可供类似工程设计参考。
Abstract:Based on the elastic buckling theory, the energy method is adopted and the deflection test functions satisfying the boundary conditions are selected, the formulas for calculating the buckling critical bearing capacity of thin plates under uniformly distributed axial loads are derived with the aid of computational programs developed in Python, and three different boundary cases are considered: opposite sides simply supported and other sides free, three sides simply supported one side free and, four sides simply supported. The results are verified by finite element analysis, and the simplified calculation formulas between ξ of buckling characteristic coefficient and aspect ratio r of plate are developed. Based on the principle that the out-of-plane flexural stiffness and in-plane axial stiffness of masonry walls are equal, the non-uniform anisotropic material of masonry wall with constructional columns and ring beams is equivalent to isotropic material, and the reliability of equivalent model for wall buckling analysis is verified. The stability design method of self-bearing masonry wall with different arrangement is proposed, and its application in two practical projects is discussed. The method presented is easy to operate and to consider the influence of different boundary conditions of masonry walls, the effect of constructional columns and ring beams, and the distribution characteristic of triangular axial forces of self-bearing walls. The conclusions can be used as a reference for similar engineering design.
-
我国《砌体结构设计规范》(GB 50003−2011),以下简称《砌规》[1]通过限制高厚比的构造措施来保证墙体稳定性,普通墙体考虑构造柱及自承重墙的修正系数后高厚比限值通常小于30,故对于200 mm厚的建筑砌体隔墙,当层高超过6 m时其高厚比验算将难以满足规范要求。随着对建筑物功能要求的不断提高,在会议会展中心、商场影院、体育场馆、高铁站厅等公共建筑中出现越来越多的大层高大空间结构,若仍按《砌规》验算方法来控制墙厚,墙厚的增加不仅增加结构自重、极大地影响建筑使用空间,而且十分不经济。高厚比限值主要基于墙体强度承载力与稳定承载力相等的原则得出,而实际上自承重墙的荷载很小,其强度承载力并未充分发挥,《砌规》高厚比限值不适用于自承重墙,采用墙体稳定承载力的直接计算方法来指导工程设计会更为合理和经济。
以往关于砌体墙稳定性的研究[2-4]多关注墙顶作用荷载的情况,而自承重墙主要承受自重,即为轴向均布荷载,因此有必要研究荷载分布形式对稳定性的影响。轴向均布荷载下一维杆件的稳定性问题已有一定的研究成果,例如,李亮等[5]利用能量法推导了竖向均布荷载作用下悬臂杆的屈曲临界荷载简化计算公式,黄开志等[6]采用近似求解静力平衡微分方程的方法得出不同边界条件压杆在轴向均布荷载下稳定性计算公式,田炜烽等[7]采用基于数值拟合的等效力法来求解任意分布轴力作用下框架柱弹性稳定问题。对于轴向均布荷载下二维墙体的稳定性研究成果还较少,蔚博琛等[8]基于能量法建立了一字形墙肢考虑自重时平面外失稳的计算方法,但其研究的一字墙实质仍是一维受力问题。
砌体墙厚度一般远小于其他两个方向的尺寸,可简化为薄板,墙体在自重荷载下的失稳模态是沿厚度方向的弯曲变形,稳定性破坏通常发生在材料进入塑性之前,因此砌体墙稳定性问题可类比弹性力学的薄板压曲问题[9]。砌体墙为复杂的非均匀各向异性材料,在采用薄板压曲问题的相关计算理论和方法前,需对其进行匀质化等效。对于纯砌体,可将其视为由周期性介质规律组合而成的材料,并通过研究等效体积单元的特性来得到等效匀质材料的参数[10-14],但对于带构造柱和圈梁的墙体该方法难以适用。本文参考带肋梁增强的构造异性结构的拟板法[15-16],基于面外抗弯刚度和面内轴向刚度相等原则对带构造柱和圈梁的砌体墙进行各向同性等效,而后基于薄板压曲理论来求解不同边界和荷载条件下的墙体稳定性问题。
1 轴向均布荷载下矩形薄板的压曲
根据弹性力学理论[17],薄板压曲临界荷载可采用静力法(求解平衡微分方程)、能量法(如瑞利-里兹法)或数值法(如有限元法)进行计算。一般只有极少数情况可采用静力法得到理论结果,随着计算机技术的发展,采用数值法虽然容易求得满足工程应用精度的结果,但难以得到显示的计算公式表达,因此可将其作为理论计算的辅助验证手段。本文采用能量法和数值拟合相结合的方法来推导轴向均匀分布荷载下矩形薄板压曲临界荷载的计算公式,考虑3种边界情况,分别是:对边简支对边自由、三边简支一边自由、四边简支。
采用能量法时需先设定满足位移边界条件的薄板压曲挠度ω,为了提高计算精度,ω可采用级数形式,即:
ω=∑mCmωm (1) 式中:ωm为满足位移边界条件的函数;Cm为互不依赖的待定系数,其值由最小势能原理确定。板在微弯状态下的总势能Π是板的应变能U和外力势力W之和,即:
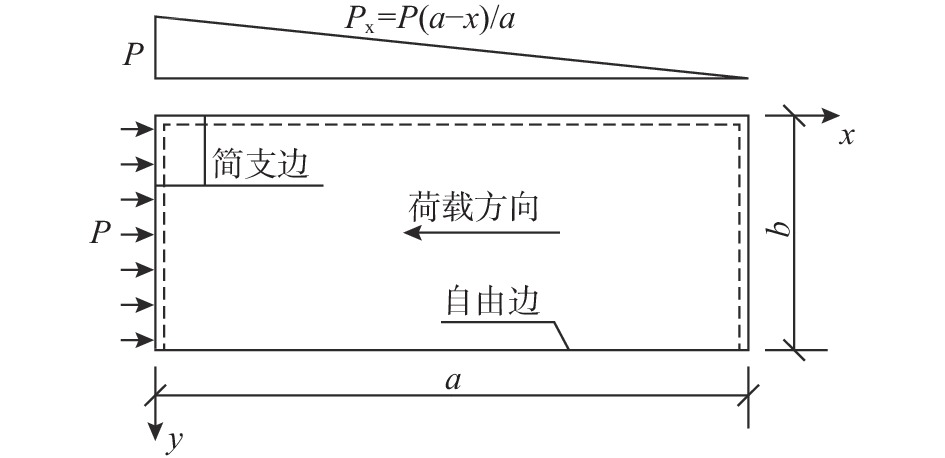
Π=U+W (2) U=D2∫a0∫b0{(∂2ω∂x2+∂2ω∂y2)2−2(1−ν)⋅[∂2ω∂x2⋅∂2ω∂y2−(∂2ω∂x∂y)2]}dxdy,W=−12∫a0∫b0[Fx(∂ω∂x)2+Fy(∂ω∂y)2+2Fxy∂ω∂x⋅∂ω∂y]dxdy (3) 式中:D=Et312(1−ν2)为板的抗弯刚度,其中E为弹性模量,t为板厚,ν为泊松比;a、b为板的高度和宽度,参考图1;Fx、Fy为板中面沿x、y轴方向单位宽度的拉压力;Fxy为板中面单位宽度的顺剪力。
1.1 对边简支对边自由板
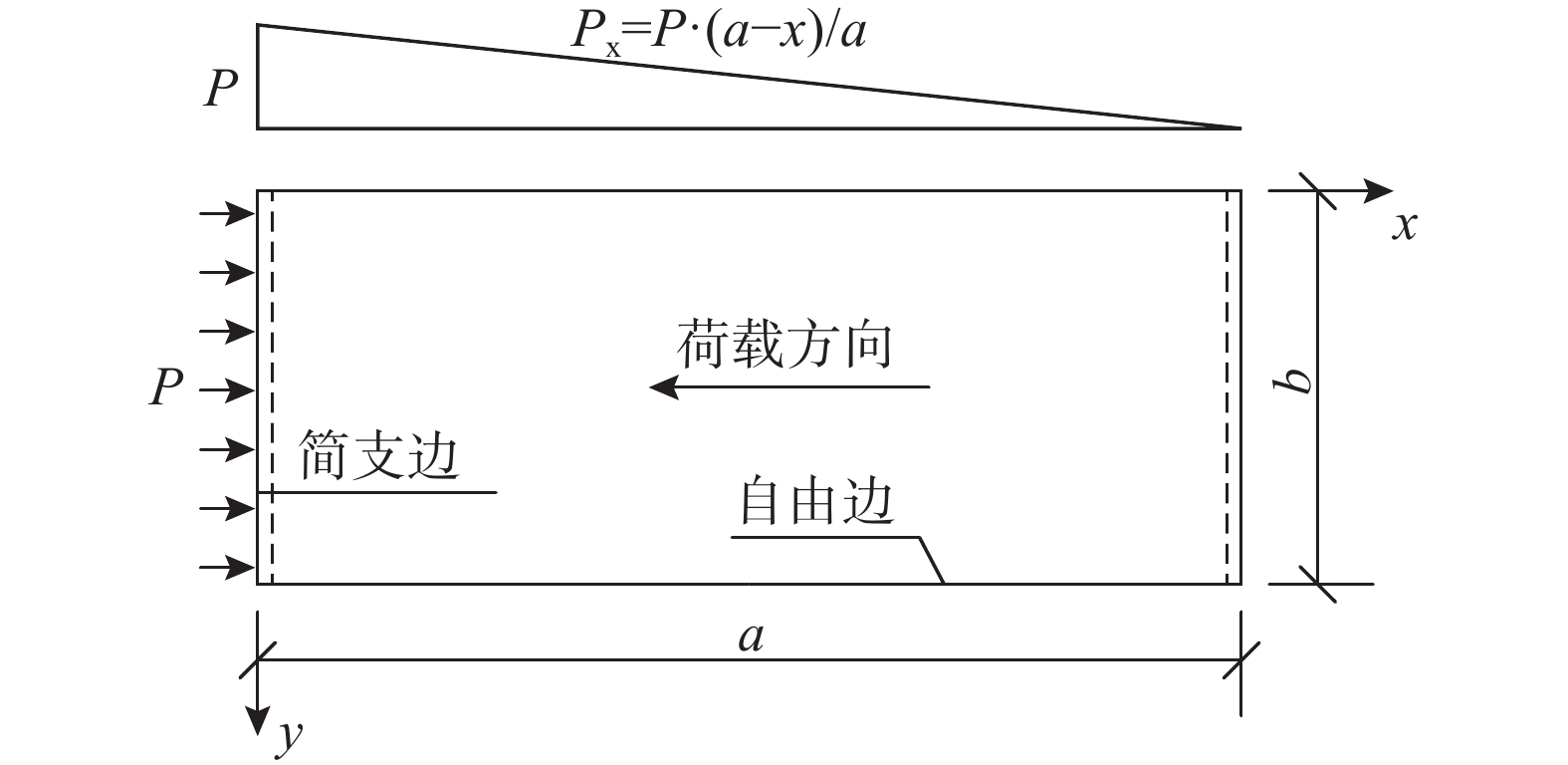
计算简图如图1所示,板承受沿-x方向的均布荷载作用,则板内轴力为三角形分布,设底部单位宽度板的反力为P,则横轴坐标x处单位宽度板的轴力为Px=P(a−x)/a。设失稳临界状态时板的挠度表达式如下:
ω=∑mCmsinmπxa (4) 容易验证式(4)满足板的位移边界条件。
由于∂ω∂y=0,式(3)中U可简化为:
U=D2∫a0∫b0(∂2ω∂x2)2dxdy (5) 即计算结果表达式与泊松比ν无关。
取式(4)的前两项计算,即m=1、2,并将Fx=Px、Fy=0、Fxy=0代入式(3)和式(5),可得应变能U和外力势能W分别为:
U=π4Db4a3(C21+16C22) (6) W=−Pb72a(9π2C21+160C1C2+36π2C22) (7) 根据势能驻值原理,可得到:
∂Π∂C1=(π4Db2a3−π2Pb4a)C1−20Pb9aC2=0∂Π∂C2=−20Pb9aC1+(8π4Dba3−π2Pba)C2=0 (8) 由于C1、C2不同时为0,故上面关于C1、C2的线性方程组的行列式应为0,观察上述方程的系数特点,令P=ξπ2Da2,代入后整理得到特征方程如下:
ξ2−12.5437ξ + 20.0699 = 0 (9) 解得ξ=1.8825,或ξ=10.6611(舍去)。为校核该结果的误差大小,可对式(4)取更多项次进行计算,由于积分运算量较大,笔者通过开源软件Python及其符号运算库SymPy[18]编程处理,势能求解主要采用了积分函数integrate( )和微分函数diff( ),特征方程的求解采用solve( )函数,最后得到当m取3项时ξ=1.8819,当m取4项时ξ=1.8814,可见增加计算项次后结果差异很小,说明假定的挠度表达式(4)收敛性良好。
为验证上述结果的可靠性,采用SAP2000软件建立与图1对应的有限元屈曲分析模型,计算参数如下:E=5 GPa、10 GPa,t=100 mm、200 mm,ν=0.15,b=5 m,单位面积自重荷载q=1 kN/m2,高宽比r=a/b的取值区间为[0.5~6],采用薄壳单元,网格划分尺寸取0.25 m。根据有限元计算得到的第一阶屈曲因子,可计算出临界荷载,进而反算出系数ξ,结果如图2所示,其中“E10t100”表示E=10 GPa,t=100 mm,其余类似。可知:① 系数ξ与弹性模量E和墙厚t无关,原因是有限元模型的屈曲临界荷载始终与E和t3成正比,反算系数ξ值时会直接约分掉;② 有限元分析得到的系数ξ在[1.89~1.84]之间,与能量法计算推导的结果吻合良好,验证了理论计算方法的正确性。对于工程应用而言可取ξ=1.8,即对边简支对边自由板的临界荷载Pcr计算如下:
Pcr=ξπ2Da2,ξ=1.8 (10) 类比两端简支细长杆的欧拉临界荷载计算公式Pcr=π2EIl2(l为杆长,EI为杆的抗弯刚度)可知,荷载P作用在构件顶部与荷载1.8P沿构件高度均匀分布引起的失稳效应相当。
1.2 三边简支一边自由板
如图3所示,荷载分布与图1相同,但其中一个侧边改为简支,另一侧边仍为自由边。设失稳临界状态时板的挠度表达式如下:
ω=∑mCmysinmπxa (11) 容易验证式(11)满足板的位移边界条件。
参考文献[10]中给出的不同边界下矩形薄板临界荷载表达式的形式,令P=Kπ2Db2、r=ab,取泊松比ν=0.15。计算过程与1.1节相同,当式(11)取m=1、2两项计算时,可得到K的特征方程为:
r4K2−(2.5927r4+12.5437r2)K+1.3398r4+12.9636r2+20.0699=0 (12) 在式(12)中代入不同的r值即可求出对应的K。同样地,为校核计算结果的误差大小,对式(11)增加m的计算项次,笔者采用Python编程处理。另外,建立与图3对应的有限元屈曲分析模型来反算K值,计算参数同1.1节,同样可以验证系数K与弹性模量E和墙厚t无关。另外,考虑到常规砌体材料泊松比ν的取值范围为0.15~0.20,在图4中也给出ν=0.20的计算结果。
可见:① 增加m的项次后计算结果差异很小,说明假定的挠度表达式(11)收敛性良好;② 有限元分析结果与能量法推导结果吻合良好,验证了理论计算方法的正确性;③ K值随泊松比增大而有所减小,但差异在5%以内。为方便工程应用,可采用简化的式(13)来计算K:
K=1.8r2+0.7 (13) 即三边简支一边自由板临界荷载Pcr为:
Pcr=Kπ2Db2=ξπ2Da2 (14) ξ=a2b2K=1.8+0.7a2b2 (15) 1.3 四边简支板
图1中的两条自由边改成简支边,即得到四边简支板的计算简图,荷载分布不变。由于临界荷载是板保持微弯状态的最小荷载,荷载沿-x向作用,y向变形应是半波,故设失稳临界状态时板的挠度表达式如下:
ω=∑mCmsinπybsinmπxa (16) 容易验证式(16)满足板的位移边界条件。
参考文献[9],可以证明此时式(3)中U的第二项积分结果为0,故简化为:
U=D2∫a0∫b0(∂2ω∂x2+∂2ω∂y2)2dxdy (17) 即计算结果表达式与泊松比ν无关。
与1.2节类似,对式(16)取不同的计算项次,并采用Python编制计算程序,可得到K-r的关系。另外,建立有限元屈曲分析模型来反算K值,有限元计算参数同1.1节,同样可以验证系数K与弹性模量E和墙厚t无关。计算结果对比如图5。
可见:① 随着高宽比r的增加,需要相应增加m的项次才能得到准确的结果,比如,当r=2时,m取4项或以上时的结果均是接近的,而当r=4时,m需取6项或以上时结果才是接近的,这与1.1节、1.2节的规律不同,原因是前两种边界条件下板沿x向的屈曲形态均接近半波变形,而四边简支板的屈曲形态是底部集中变形,如图6所示,因此当r增加时四边简支板的挠度函数需要取更多的项次才能描述其实际变形情况;② 能量法推导结果较有限元分析结果偏大,但偏差基本在5%以内,验证了理论计算方法的正确性。为方便工程应用,可采用简化的式(18)来计算K:
K=1.8r2+4.4 (18) 即四边简支板临界荷载Pcr为:
Pcr=Kπ2Db2=ξπ2Da2 (19) ξ=a2b2K=1.8+4.4a2b2 (20) 2 砌体墙等效各向同性
砌体墙通常包含砌块、砂浆、构造柱及圈梁等组成部分,材料性质复杂,且实际工程中还要考虑墙体厚度、构造柱和圈梁截面大小及间距等变化,在计算软件日臻完善的今天可以通过建立精细有限元模型[19-20]来得到即定参数下的墙体稳定承载力,但此方法耗时较大,难以用于直接指导工程设计。如果对砌体墙进行材料各向同性等效,则可采用第1节推导的结果来进行砌体墙稳定性计算。本文等效计算基于以下假定条件:① 砌体墙各组成部分的材料均假定为弹性;② 砌块和砂浆采用整体化模拟,不考虑灰缝、马牙槎等影响;③ 构造柱和圈梁均匀分布且平均面外刚度接近。
2.1 等效计算方法
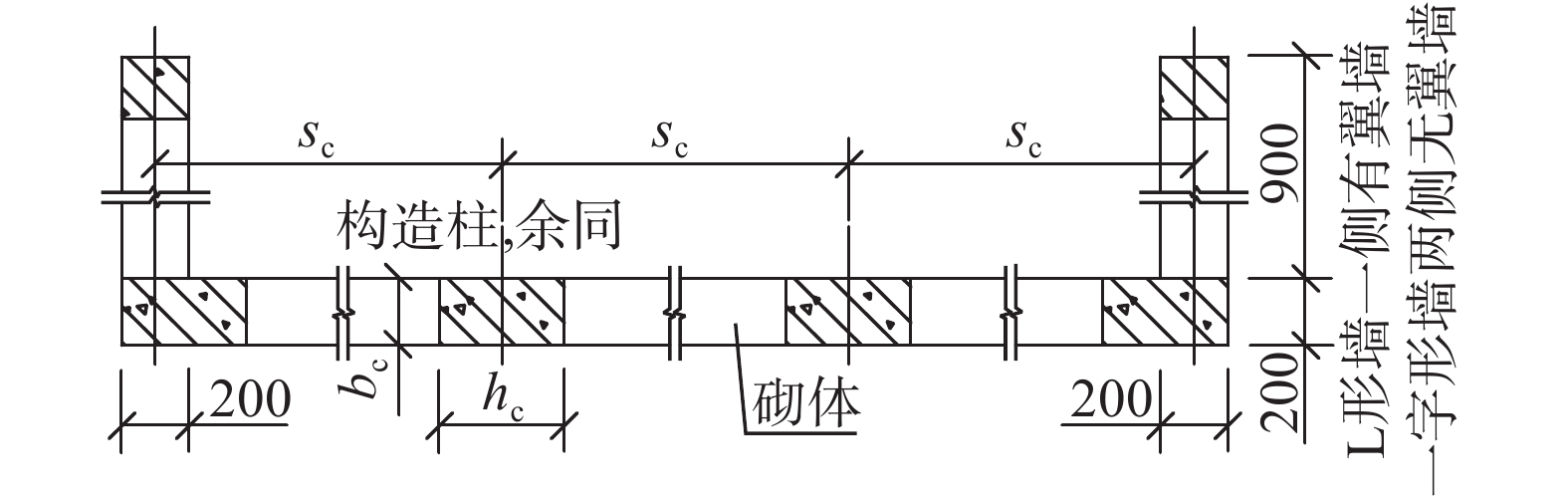
对于构造柱和圈梁均匀布置的墙体,参数示意如图7,并设:砌体墙厚tm,弹性模量Em;构造柱截面bc×hc,间距sc;圈梁截面bb×hb,间距sb;圈梁和构造柱弹性模量均为Ec。取sc宽度范围带构造柱的砌体墙计算,考虑板的泊松效应,可得等效板单位宽度的抗弯刚度D1和轴向刚度H1分别为:
D1=[(sc−hc)Emt3m12(1−ν2)+Echcb3c12]/sc (21) H1=[Em(sc−hc)tm+Echcbc]/sc (22) 同样地,可取sb高度范围的砌体进行等效计算,只需将式(21)、式(22)中的构造柱参数换成圈梁对应参数即可,相应地得到等效板单位宽度的抗弯刚度D2和轴向刚度H2。一般情况下当圈梁和构造柱的截面尺寸或间距不同时沿宽度和高度等效得到的结果并不相同,一字形墙失稳模态为单向弯曲变形,其等效计算只需考虑D1、H1,其余情况墙体失稳模态为双向弯曲变形,其等效计算应取两个方向的平均值,即:
Deq=D1+κD22=Eeqt3eq12(1−ν2eq) (23) Heq=H1+κH22=Eeqteq (24) 式中,Eeq、νeq、teq、Deq、Heq分别为等效各向同性材料板的弹性模量、泊松比、厚度、单位宽度的抗弯刚度和轴向刚度,并取νeq =ν。对一字形墙取κ=0,其余情况取κ=1。
由式(23)、式(24)可得:
teq=√12(1−ν2)(D1+κD2)H1+κH2 (25) 将teq代入式(24)即可求得:
Eeq=H1+κH22teq (26) 除一字形墙外,为避免两个方向的刚度差异较大导致上述等效产生较大误差,圈梁与构造柱的平均面外抗弯刚度应接近,即按式(27)控制圈梁和构造柱的截面和间距:
EcIbsb = αEcIcsc (27) 式中:Ib=hbb3b12,Ic=hcb3c12,α≈1。
当砌体墙面积较小或构造柱、圈梁非均匀布置时,按上述等效计算可能带来一定的误差,此时可取整片墙进行等效计算,只需将式(21)、式(22)稍作调整改为式(28)、式(29)即可:
D1=[(B−∑ihci)Emt3m12(1−ν2)+∑iEchcib3ci12]/B (28) H1=[(B−∑ihci)Emtm+∑iEchcibci]/B (29) 式中:B为整片墙的宽度;hci、bci为各构造柱的高度和宽度,转角位置的构造柱计1/2。同样地,可按整片墙高进行水平向等效得到D2、H2,计算过程类似。
2.2 等效模型有限元验证
为验证砌体墙等效各向同性计算方法的可靠性,采用SAP2000软件建立一字形、L形、槽形三种平面形式的墙体有限元屈曲分析模型,分别代表两边支承板、三板支承板及四边支承板的屈曲模态形式。墙体平面示意见图8,计算参数见表1,各形式墙体分别进行6 m、10 m、14 m、18 m四种不同高度的建模计算。以10 m高槽形墙为例,有限元模型三维示意见图9,其中:模型A为实际结构模型,墙体采用壳单元,构造柱和圈梁采用梁单元;模型B为等效模型,采用壳单元;两模型边界条件相同,即底部约束3个方向(X、Y、Z)的平动自由度,顶部约束2个方向(X、Y)的平动自由度,侧边无约束。模型按5.0 kN/m2均布自重荷载进行−Z向加载,并进行此荷载工况下的整体屈曲分析。
表 1 墙体计算参数Table 1. Calculation parameters of masonry walls编号 砌体
墙厚
tm/mm砌体
弹性模量
Em/MPa构造柱
截面
bc×hc/mm构造
柱间距
sc/mm圈梁截面
bb×hb/
mm圈梁间距
sb/mm混凝土
弹性模量
Ec/MPa算例1 200 2200 200×400 3000 200×300 2000 25500 算例2 200 2200 300×400 3000 300×300 2000 25500 对不同形式、高度和构造柱尺寸的墙体进行有限元模型的屈曲分析,得到第一阶屈曲因子,计算结果见图10,图中墙体编号C-10表达槽形墙、高度10 m,其余类似。由结果可知:① 模型A和模型B的计算结果接近,最大差异约12%;② 当构造柱和圈梁的宽度增加时模型B和模型A的结果比值有增大的趋势,说明构造柱、圈梁形成的框架等效成壳单元后刚度有所偏大,原因在于等效壳单元的面内抗剪刚度大,另外构造柱端部为单节点铰接,无扭转刚度,等效成壳后为多节点线约束,相当于增加了扭转刚度。整体而言,2.1节给出的砌体墙等效为各向同性弹性板的方法可行,等效计算具有较好的精度。
3 砌体墙稳定性设计公式
根据前述推导,轴向均匀分布荷载作用下矩形薄板屈曲临界荷载可统一表达为:
Pcr=ξπ2Da2 (30) 不同板边界条件下的ξ值按式(10)、式(15)、式(20)计算。参考《高层建筑混凝土结构技术规程》(JGJ 3−2010)[21]附录D关于剪力墙的稳定性计算方法,考虑到材料的弹塑性、荷载的长期性及荷载偏心距、墙体施工垂直度偏差等影响,取竖向荷载设计值不大于理论计算临界值的1/10。设层高为h,采用等效各向同性的材料参数,并取π21−ν2≈10,可得:
P⩽ (31) 式中:P为轴向均匀分布荷载作用下墙底单位宽度的轴力设计值;ξ根据不同边界条件按下述取值:
1) 单片独立墙肢按对边简支对边自由板计算,取ξ=1.8。
2) T形、L形、槽形和工字形墙的翼缘及T形墙的腹板(图11),按三边简支一边自由板计算ξ:
\xi = 1.8 + 0.7{\left( {\frac{h}{{{b_{\text{f}}}}}} \right)^2} (32) 式中:bf取单侧翼缘高度bfi的大值,对于T形墙的腹板则取腹板高度bw。
3) 槽形和工字形墙的腹板(图11),按四边简支板计算ξ:
\xi = 1.8 + 4.4{\left( {\frac{h}{{{b_{\text{w}}}}}} \right)^2} (33) 4 工程应用
4.1 案例1
长沙某国际会议中心采用钢框架结构,建筑地上整体为3层,典型层高为13 m和18 m,局部有夹层区域层高为9 m。建筑设计要求隔墙采用A5.0蒸压加气混凝土砌块和Mb5.0专用砌筑砂浆。如按高厚比限值30进行估算,则层高18 m时砌体墙厚度将达到600 mm,这将极大地影响建筑使用功能并增加结构自重。结构设计时通过加密、加大构造柱和圈梁来增强砌体墙整体稳定性。圈梁宽度同墙厚,高度为250 mm,沿竖向的布置间距为2 m。砌体墙及构造柱典型布置如图12所示,构造柱沿墙长均匀分布,门洞高度2.3 m,洞顶均设置截面同圈梁的过梁。构造柱和圈梁混凝土等级C30,弹性模量Ec=30 GPa,砌体弹性模量Em=2.2 GPa。考虑砌体自重、抹灰、装修吊挂等荷载,墙厚200 mm、300 mm时对应荷载标准值分别为4.5 kN/m2、5.5 kN/m2。
不考虑门洞影响,按本文提出的计算方法和有限元模拟分析分别对图12所示典型隔墙进行稳定性验算,有限元建模方式同图9的模型A,毎个算例中的纵、横墙及结构柱等构件均整体建模考虑。结果如表2所示:① 由P1/ P2的结果可知式(31)的计算结果与有限元结果接近;② 由P1/ P的结果可知承载力安全系数均大于1,说明砌体墙稳定性满足设计要求;③ 墙W1的公式计算结果偏保守,原因是本文第一章推导中假定板边界为理想简支,而实际上与之相连的墙体会提供一定的弯曲刚度。
表 2 某国际会议中心典型砌体隔墙稳定性验算结果Table 2. Stability calculation results of typical masonry walls in an International conference center编号 层高
h/m等效弹性
模量Eeq /MPa等效墙厚
teq /mm稳定
系数ξ计算临界荷载{P_1} = \xi \dfrac{{{E_{{\text{eq}}}}t_{{\text{eq}}}^3}}{{12{h^2}}}\Bigg/(kN/m) 有限元结果
P2/(kN/m)荷载设计值
P/(kN/m)\dfrac{{{P_1}}}{{{P_2}}} \dfrac{{{P_1}}}{P} W1 9 5953 200 2.81 137.6 192.9 52.7 0.71 2.61 W2 9 7115 200 5.94 347.9 398.0 52.7 0.87 6.61 W3 9 5344 200 4.64 204.1 238.8 52.7 0.85 3.88 W4 13 5274 200 9.87 205.3 191.9 76.1 1.07 2.70 W5 13 5522 300 12.34 268.8 311.3 76.1 0.86 3.53 W6 12 6648 200 1.80 187.0 194.0 85.8 0.96 2.18 W4 18 5482 200 17.27 194.8 183.4 105.3 1.06 1.85 W5 18 5730 200 22.00 259.4 303.8 105.3 0.85 2.46 注:P为墙底轴力设计值,荷载分项系数取1.3;P2为有限元屈曲分析一阶临界荷载的1/10。 4.2 案例2
海口某国际会展中心采用带支撑钢框架结构,建筑地上整体为1层(局部设置夹层),建筑隔墙采用A5.0蒸压加气混凝土砌块砌筑,局部隔墙最大高度20 m。圈梁宽度同墙厚,高度为200 mm,沿竖向的布置间距为2 m。砌体墙及构造柱典型布置如图13所示,构造柱沿墙长均匀分布,门洞高度2.4 m,洞顶均设置截面同圈梁的过梁,构造柱和圈梁混凝土等级C25。砌体自重、抹灰、装修吊挂等荷载标准值合计为4.0 kN/m2。
隔墙稳定性验算结果见表3,由表可知:① 稳定性安全系数P1/ P的结果均大于1,说明墙体稳定性满足设计要求;② 墙W7和W9布置相同,但W9有限元分析的稳定承载力比W7大40%左右,原因是W9两侧有距离较近的框架柱,框架柱刚度大,对W9的水平向弯曲变形产生较强的约束作用。
表 3 某国际会展中心典型砌体隔墙稳定性验算结果Table 3. Stability calculation results of typical masonry walls in an international convention and exhibition center编号 层高
h/m等效弹性
模量Eeq /MPa等效墙厚
teq /mm稳定
系数ξ计算临界荷载{P_1} = \xi \dfrac{{{E_{{\text{eq}}}}t_{{\text{eq}}}^3}}{{12{h^2}}}\Bigg/(kN/m) 有限元结果
P2/(kN/m)荷载设计值
P/(kN/m)\dfrac{{{P_1}}}{{{P_2}}} \dfrac{{{P_1}}}{P} W7 20.0 4707 200 15.11 118.5 144.0 104.0 0.82 1.14 W8 20.0 5172 200 55.97 482.4 452.7 104.0 1.07 4.64 W9 20.0 4707 200 15.11 118.5 200.2 104.0 0.59 1.14 W10 6.7 3490 200 1.80 93.3 97.8 34.8 0.95 2.68 注:P为墙底轴力设计值,荷载分项系数取1.3;P2为有限元屈曲分析一阶临界荷载的1/10。 4.3 施工过程控制措施
砌体隔墙在砌筑过程中存在砂浆强度尚未达到设计值、墙顶与主体结构的拉结作用尚未形成等情况,其边界条件及受力状态与正常使用情况有所不同,为保证超高砌体墙施工过程的稳定性,建议采取以下措施:
1) 在墙体面外设置临时支撑以减小施工过程中墙体的计算高度,比如采用钢管扣件脚手架、剪刀撑和抛撑等方式搭设稳定的砌筑操作平台,墙体与操作平台之间设置临时拉结措施。
2 )沿墙高分段砌筑,每段高度不超过4 m,且纵横墙整体同步施工,每个分段砌筑完成后即浇筑本段墙的构造柱及圈梁,待构造柱及圈梁混凝土达到不低于75%设计强度后再进行下一分段的砌筑。
3) 墙砌至板、梁附近后,应留一定空隙,间隔7 d以上待下部砌体沉实后再用斜砌法敲紧填实,墙顶与梁或板设间距不超过1 m的拉结筋。
4) 砌体与主体结构柱、构造柱、圈梁之间设置间距约0.5 m的拉结筋,构造柱纵筋在柱脚及柱顶对应主体结构位置提前预埋。
上述措施已应用到工程案例1和案例2中,最终效果良好,目前上述工程均已完成竣工验收并正式投入使用。
5 结论
本文以稳定计算理论为基础,推导了轴向均布荷载作用下不同边界矩形薄板的压曲临界荷载计算公式,采用匀质化等效手段,将薄板计算公式应用到自承重砌体墙稳定性验算中,并对相关计算结果进行有限元模拟验证。主要结论如下:
(1)基于能量法并选取满足边界条件的挠曲试函数,借助Python软件自编计算程序,本文得到了对边简支对边自由板、三边简支一边自由板及四边简支板在轴向均布荷载作用下屈曲特征值K、ξ的计算公式。有限元分析结果与能量法推导结果吻合良好,验证了本文方法的正确性。
(2)基于面外抗弯刚度和面内轴向刚度相等原则,本文提出一种将带构造柱和圈梁的砌体墙等效成各向同性材料的方法,有限元对比分析表明等效模型用于屈曲分析具有较好的精度,可以满足工程应用需要。
(3) 根据平面布置形式的不同,采用等效各向同性材料,将砌体墙归类成不同边界条件弹性板的计算,并提出墙体稳定性计算公式。两个实际工程的应用结果表明,本文方法操作简便,可考虑砌体墙不同边界条件、构造柱和圈梁布置、自重墙三角形轴力分布特点等影响;计算结果合理,可用于指导类似工程设计。
本文理论推导基于弹性材料假定,虽然采用有限元模型进行了结果验证,但材料的非线性行为尚未做讨论,这也是后续进一步研究的重点。
-
表 1 墙体计算参数
Table 1 Calculation parameters of masonry walls
编号 砌体
墙厚
tm/mm砌体
弹性模量
Em/MPa构造柱
截面
bc×hc/mm构造
柱间距
sc/mm圈梁截面
bb×hb/
mm圈梁间距
sb/mm混凝土
弹性模量
Ec/MPa算例1 200 2200 200×400 3000 200×300 2000 25500 算例2 200 2200 300×400 3000 300×300 2000 25500 表 2 某国际会议中心典型砌体隔墙稳定性验算结果
Table 2 Stability calculation results of typical masonry walls in an International conference center
编号 层高
h/m等效弹性
模量Eeq /MPa等效墙厚
teq /mm稳定
系数ξ计算临界荷载{P_1} = \xi \dfrac{{{E_{{\text{eq}}}}t_{{\text{eq}}}^3}}{{12{h^2}}}\Bigg/(kN/m) 有限元结果
P2/(kN/m)荷载设计值
P/(kN/m)\dfrac{{{P_1}}}{{{P_2}}} \dfrac{{{P_1}}}{P} W1 9 5953 200 2.81 137.6 192.9 52.7 0.71 2.61 W2 9 7115 200 5.94 347.9 398.0 52.7 0.87 6.61 W3 9 5344 200 4.64 204.1 238.8 52.7 0.85 3.88 W4 13 5274 200 9.87 205.3 191.9 76.1 1.07 2.70 W5 13 5522 300 12.34 268.8 311.3 76.1 0.86 3.53 W6 12 6648 200 1.80 187.0 194.0 85.8 0.96 2.18 W4 18 5482 200 17.27 194.8 183.4 105.3 1.06 1.85 W5 18 5730 200 22.00 259.4 303.8 105.3 0.85 2.46 注:P为墙底轴力设计值,荷载分项系数取1.3;P2为有限元屈曲分析一阶临界荷载的1/10。 表 3 某国际会展中心典型砌体隔墙稳定性验算结果
Table 3 Stability calculation results of typical masonry walls in an international convention and exhibition center
编号 层高
h/m等效弹性
模量Eeq /MPa等效墙厚
teq /mm稳定
系数ξ计算临界荷载{P_1} = \xi \dfrac{{{E_{{\text{eq}}}}t_{{\text{eq}}}^3}}{{12{h^2}}}\Bigg/(kN/m) 有限元结果
P2/(kN/m)荷载设计值
P/(kN/m)\dfrac{{{P_1}}}{{{P_2}}} \dfrac{{{P_1}}}{P} W7 20.0 4707 200 15.11 118.5 144.0 104.0 0.82 1.14 W8 20.0 5172 200 55.97 482.4 452.7 104.0 1.07 4.64 W9 20.0 4707 200 15.11 118.5 200.2 104.0 0.59 1.14 W10 6.7 3490 200 1.80 93.3 97.8 34.8 0.95 2.68 注:P为墙底轴力设计值,荷载分项系数取1.3;P2为有限元屈曲分析一阶临界荷载的1/10。 -
[1] GB 50003−2011, 砌体结构设计规范 [S]. 北京: 中国建筑工业出版社, 2011. GB 50003−2011, Code for design of masonry structures [S]. Beijing: China Architecture & Building Press, 2010. (in Chinese)
[2] SANDOVAL C, ROCA P, BERNAT E, et al. Testing and numerical modelling of buckling failure of masonry walls [J]. Construction and Building Materials, 2011, 25(12): 4394 − 4402. doi: 10.1016/j.conbuildmat.2011.01.007
[3] SANDOVAL C, ROCA P. Study of the influence of different parameters on the buckling behaviour of masonry walls [J]. Construction and Building Materials, 2012, 35: 888 − 899.
[4] BAKEER T. Empirical estimation of the load bearing capacity of masonry walls under buckling – Critical remarks and a new proposal for the Eurocode 6 [J]. Construction and Building Materials, 2016, 113: 376 − 394. doi: 10.1016/j.conbuildmat.2016.03.063
[5] 李亮, 李国强. 轴向均布荷载下弯剪型竖向悬臂杆的屈曲临界荷载简化算法[J]. 西安建筑科技大学学报(自然科学版), 2013, 45(6): 817 − 821, 828. doi: 10.15986/j.1006-7930.2013.06.015 LI Liang, LI Guoqiang. Simplified algorithm of buckling critical load for shear-bending cantilever rod under axially uniformly distributed load [J]. Journal of Xi'an University of Architecture & Technology (Natural Science Edition), 2013, 45(6): 817 − 821, 828. (in Chinese) doi: 10.15986/j.1006-7930.2013.06.015
[6] 黄开志, 陈小亮. 考虑轴向均布载荷时压杆的稳定性计算[J]. 力学与实践, 2015, 37(6): 744 − 749. HUANG Kaizhi, CHEN Xiaoliang. Calculating stability of long column while considering axial uniform load [J]. Mechanics in Enginering, 2015, 37(6): 744 − 749. (in Chinese)
[7] 田炜烽, 郝际平, 丁戈, 等. 任意分布轴力作用下框架柱弹性稳定的实用解法[J]. 工程力学, 2012, 29(2): 74 − 80. TIAN Weifeng, HAO Jiping, DING Ge, et al. A practical method for the elastic stability of frame column under random distribution axial force [J]. Engineering Mechanics, 2012, 29(2): 74 − 80. (in Chinese)
[8] 蔚博琛, 张敬书, 于晓旭, 等. 楼梯间外纵墙一字形墙肢的稳定性问题及处理[J]. 工程力学, 2019, 36(8): 133 − 140. doi: 10.6052/j.issn.1000-4750.2018.07.0403 WEI Bochen, ZHANG Jingshu, YU Xiaoxu, et al. Stability analysis and strengthening of rectangular longitudinal exterior wall in staircases [J]. Engineering Mechanics, 2019, 36(8): 133 − 140. (in Chinese) doi: 10.6052/j.issn.1000-4750.2018.07.0403
[9] 蒋耀华, 倪玉双. 基于薄板稳定问题的砌体墙板高厚比限值[J]. 沈阳大学学报(自然科学版), 2021, 33(1): 61 − 67. doi: 10.16103/j.cnki.21-1583/n.2021.01.009 JIANG Yaohua, NI Yushuang. Limiting value of height-to-thickness ratio of masonry wall with plate stability [J]. Journal of Shenyang University (Natural Science), 2021, 33(1): 61 − 67. (in Chinese) doi: 10.16103/j.cnki.21-1583/n.2021.01.009
[10] CECCHI A, SAB K. A multi-parameter homogenization study for modeling elastic masonry [J]. European Journal of Mechanics / A Solids, 2002, 21(2): 249 − 268. doi: 10.1016/S0997-7538(01)01195-0
[11] PENG B, WANG D D, ZONG G, et al. Homogenization strategy for brick masonry walls under in-plane loading [J]. Construction and Building Materials, 2018, 163: 656 − 667. doi: 10.1016/j.conbuildmat.2017.12.133
[12] 倪玉双, 杨伟军, 梁建国. 基于三维匀质化的砌体墙板平面外性能研究 [J]. 应用力学学报, 2014, 31(4): 631 − 637, 14. NI Yushuang, YANG Weijun, LIANG Jianguo. Research on the out-of-plane mechanical properties of masonry wall with three-dimensional homogenization [J]. Chinese Journal of Applied Mechanics, 2014, 31(4): 631 − 637, 14. (in Chinese)
[13] 蒋宇洪, 杨娜, 白凡. 基于RVE单元的藏式古建石砌体均质化研究[J]. 工程力学, 2020, 37(7): 110 − 124. doi: 10.6052/j.issn.1000-4750.2019.08.0461 JIANG Yuhong, YANG Na, BAI Fan. Research on the homogenization of Tibetan ancient stone masonry based on RVE elements [J]. Engineering Mechanics, 2020, 37(7): 110 − 124. (in Chinese) doi: 10.6052/j.issn.1000-4750.2019.08.0461
[14] DROUGKAS A, SARHOSIS V, D'ALESSANDRO A, et al. Homogenisation of masonry structures subjected to seismic loads through matrix / inclusion micromechanics [J]. Structures, 2022, 38: 375 − 384. doi: 10.1016/j.istruc.2022.02.016
[15] 金晖, 邓宗白. 能量法研究矩形填充多孔材料夹芯层面内等效模量[J]. 力学季刊, 2009, 30(2): 330 − 336. doi: 10.15959/j.cnki.0254-0053.2009.02.021 JIN Hui, DENG Zongbai. Research on equivalent modulus of sandwich core plane for rectangular fill materials use energy method [J]. Chinese Quarterly of Mechanics, 2009, 30(2): 330 − 336. (in Chinese) doi: 10.15959/j.cnki.0254-0053.2009.02.021
[16] 黄川腾, 王志军, 邓然, 等. 考虑剪切变形的箱型空心楼盖拟板法研究[J]. 工程力学, 2015, 32(12): 198 − 207. doi: 10.6052/j.issn.1000-4750.2014.05.0437 HUANG Chuanteng, WANG Zhijun, DENG Ran, et al. Study on analogue slab method considering shear deformation for box-filler hollow floor [J]. Engineering Mechanics, 2015, 32(12): 198 − 207. (in Chinese) doi: 10.6052/j.issn.1000-4750.2014.05.0437
[17] 徐芝纶. 弹性力学—下册 [M]. 第四版. 北京: 高等教育出版社, 2006. XU Zhilun. Elasticity—Volume 2 [M]. 4th ed. Beijing: Higher Education Press, 2006. (in Chinese)
[18] SymPy Development Team, SymPy documentation (Release 1.7) [CP]. https://github.com/sympy/sympy/releases?page=2, 2020.
[19] ZENG B W, LI Y, NOGUEZ C C. Modeling and parameter importance investigation for simulating in-plane and out-of-plane behaviors of un-reinforced masonry walls [J]. Engineering Structures, 2021, 248: 113233.
[20] ASAD M, ZAHRA T, THAMBOO J, et al. Finite element modelling of reinforced masonry walls under axial compression [J]. Engineering Structures, 2022, 252: 113594.
[21] JGJ 3−2010, 高层建筑混凝土结构技术规程 [S]. 北京: 中国建筑工业出版社, 2010. JGJ 3−2010, Technical specification for concrete structures of tall building [S]. Beijing: China Architecture & Building Press, 2010. (in Chinese)
-
期刊类型引用(2)
1. 张国刚,唐盛华,方志. 斜拉桥环境激励模态参数识别不确定性试验研究. 公路. 2024(01): 93-103 .  百度学术
百度学术
2. 张国刚,唐盛华,方志,金耀. 斜拉桥锤击法模态参数识别不确定性的试验研究. 公路. 2023(11): 139-147 .  百度学术
百度学术
其他类型引用(0)



 下载:
下载: