浸没边界(IB)方法由PESKIN^[1]提出，是计算流体力学中强大和高效的方法之一^[2]，将边界对流场的作用模化为彻体力源项^[3]，大幅减少网格生成的工作量，并保留了结构网格拓扑清晰、并行化简单等特点^[4]，常应用于模拟边界条件复杂的流动及流固耦合问题^[5]。浸没边界方法一般基于笛卡尔坐标系背景网格，固体模型和流体计算域都位于计算域内，通过设置流固标记区分，并采用相同形式的算法求解。因此应用浸没边界方法模拟燃烧流场时需要计算原本无需求解的固体域网格点的信息。对于外部流动问题或简单几何中的内流模拟，位于固体区域的网格点较少，浪费的计算资源可忽略。对于流道复杂的多连通域中的湍流燃烧模拟，位于固体区域的点往往占总网格数的很大一部分，若不采取局部加密或优化计算域等措施，应用浸没边界方法求解此类问题时会造成严重的计算资源浪费。部分学者对此提出了解决方案，ANUPINDI等^[6]采用大量小体积的分块按照流体区域形状覆盖几何模型，此方法增加了分块难度，并且经DELORME等^[7]的测试，其网格利用率提升不大。ZELICOURT等^[8]重设流体网格点索引，但重设后在拓扑上与非结构网格相同，需要重新设计算法并失去了结构网格拓扑清晰的优点。ZHU等^[9]采用开源软件按图形分块并行，在分块后计算效率得到一定程度的提升，但需要重新设计并行框架。

燃气轮机燃烧室为典型的多连通域，其流道结构复杂且存在大量重要的小尺度结构。燃烧室精细化设计需要结合高保真、高效的两相湍流燃烧数值模拟，而大规模高质量网格的划分是燃烧室高分辨率仿真的难点之一^[10]。两相湍流燃烧数值模拟基础研究大多基于贴体结构网格，JONES等^[11-12]及曾家等^[13]采用贴体结构网格模拟简化的燃气轮机燃烧室中的两相湍流燃烧现象，大幅简化燃烧室结构后，贴体结构网格的划分仍较为复杂。贴体结构网格拓扑结构限制了算法对复杂几何模型的适应能力。TACHIBANA等^[14]及CHENG等^[15]采用非结构网格研究某燃烧室中两相湍流燃烧现象，非结构网格能提高网格的几何适应能力但存在拓扑不清晰，存在寻址时间长，收敛难度大，梯度项计算复杂，同分辨率网格总数多的缺点^[16]。而应用非贴体结构网格结合浸没边界方法，可在保留结构网格拓扑清晰，计算效率高等优点的同时，解决复杂几何模型网格生成问题。近年来超算算力的提升和大规模并行技术的发展满足了浸没边界法对壁面附近网格高分辨率的需求，在复杂结构燃烧室的湍流燃烧模拟中应用浸没边界法成为可能，王方等^[10]利用传统笛卡尔坐标系下的浸没边界法成功对复杂结构燃烧室进行了大涡模拟，但计算域中大量的固体网格点严重影响了浸没边界法应用于燃烧室模拟的效率。

高保真的几何再现是高保真数值模拟的基础，在例如燃气轮机燃烧室等多连通域复杂结构内的湍流燃烧数值模拟中，利用浸没边界方法能够解决该类结构中网格生成困难问题，但传统笛卡尔坐标系下的浸没边界法求解复杂结构的内流问题时效率低下。本文在曲线坐标系下的结构网格中应用离散力法实现Neumann边界条件。模拟时以流体域外轮廓为基础生成曲线坐标系结构网格，并对旋流器等关键位置进行局部加密，再经坐标变换后求解。这种方法在提高网格点利用率的同时保留了浸没边界法网格划分简单、拓扑清晰等优点。本文首先通过模拟双旋流燃烧室检验本方法的可行性和准确性，之后实现对真实燃气轮机环形燃烧室的单头部模型中两相湍流燃烧现象的高保真数值模拟，对比本方法与笛卡尔坐标系浸没边界方法的求解效率。

1   计算模型与方法

为了将曲线坐标系下的浸没边界方法结合大涡模拟-概率密度函数输运方程湍流燃烧模型(LES-TPDF)并应用于多连通域燃烧室中的湍流燃烧模拟，首先需要将燃烧室几何以网格标记的形式映射到背景网格中，用于区分流体计算域和固体网格点。在此基础上，需要在经过坐标变换和离散后的控制方程组中添加源项，从而在曲线坐标系下实现浸没边界方法。

1.1   IB网格标记生成方法

根据几何模型生成网格标记是在两相湍流燃烧数值模拟中应用浸没边界方法的基础。本文中参考光线追踪中的常用的Möller-Trumbore算法^[17]，以计算域中背景网格坐标为基础，扫描STL (STereoLithography)格式的几何模型，根据扫描线与几何模型交点个数设置网格标记。

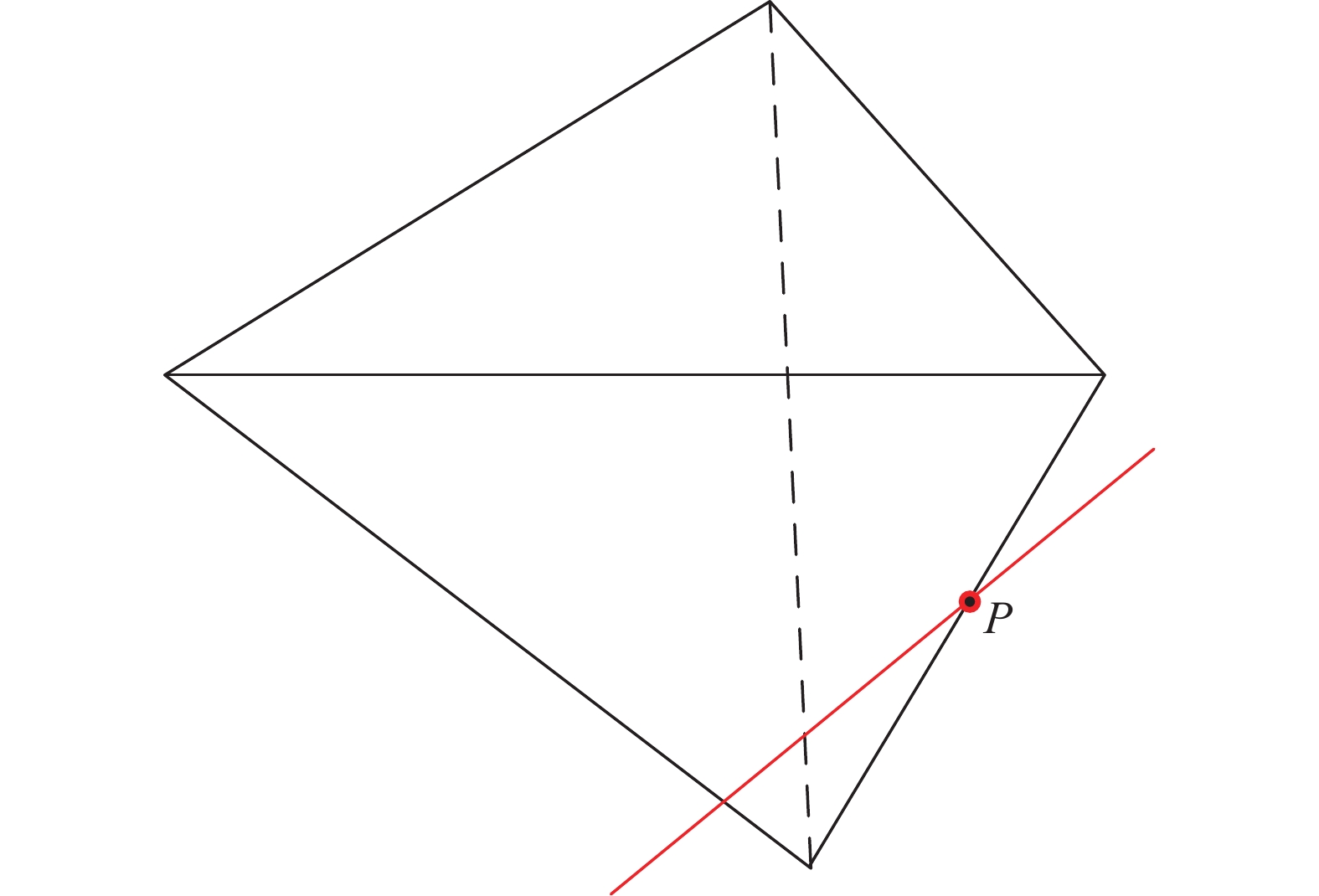
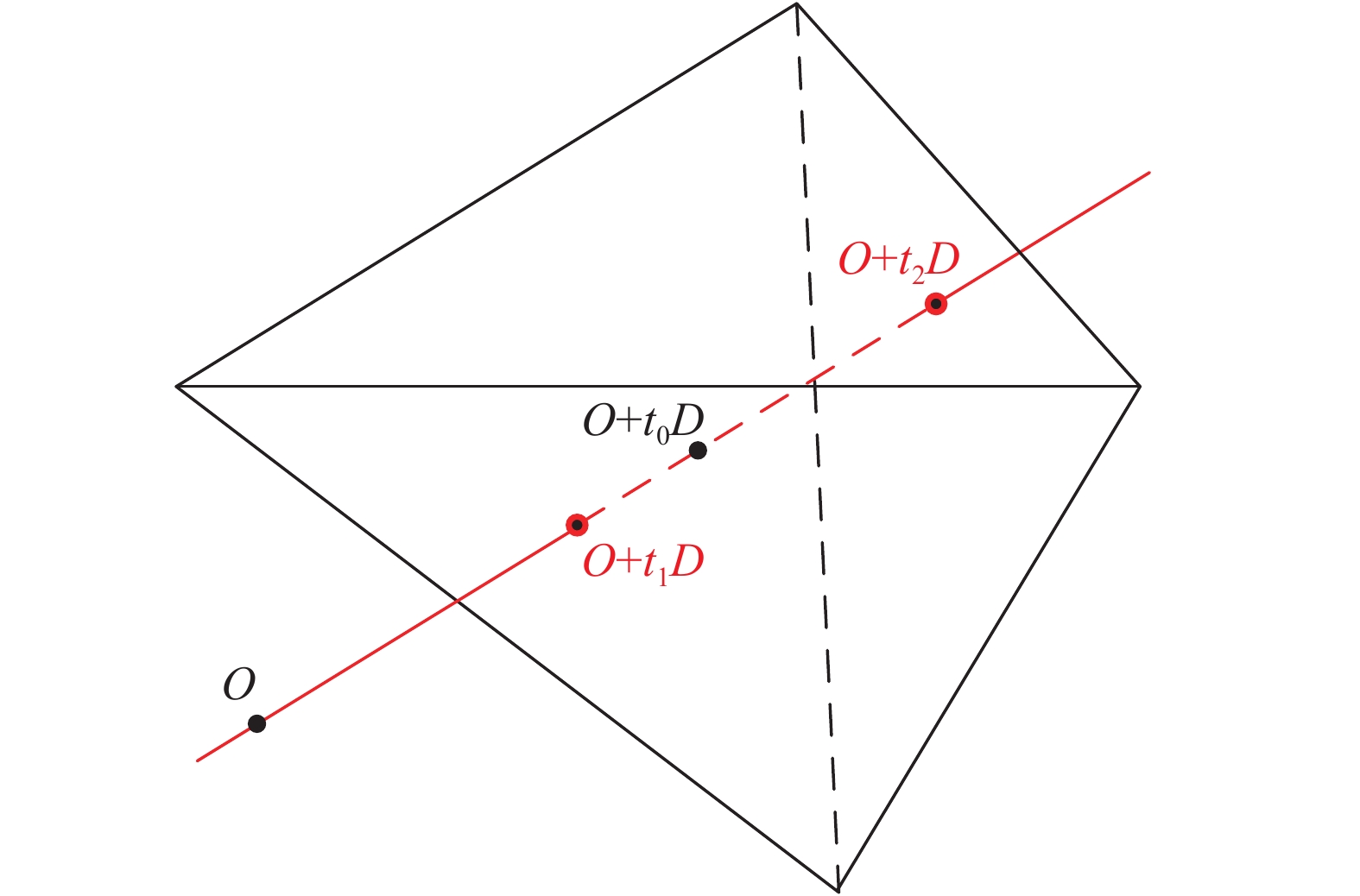
扫描直线上任一点可记为${\boldsymbol{P}} = {\boldsymbol{O}} + t{\boldsymbol{D}}$，其中${\boldsymbol{O}}$为起始点，${\boldsymbol{D}}$为扫描方向，$t$为任意实数。若背景网格中的某一点可表示为${\boldsymbol{O}} + {t_0}{\boldsymbol{D}}$，扫描线与几何体有两个交点，分别为${\boldsymbol{O}} + {t_1}{\boldsymbol{D}}$和${\boldsymbol{O}} + {t_2}{\boldsymbol{D}}$，若${t_1} < {t_0} < {t_2}$或${t_2} < {t_0} < {t_1}$，则该网格点位于几何体内，否则该点位于几何体外，如图1所示，依此标记该网格点的流固情况。

图  1  扫描算法示意图

Figure  1.  Schematic diagram of scanning algorithm

下载: 全尺寸图片 幻灯片

为提高效率，若背景网格对应坐标系中存在直线坐标轴，则平行于该坐标轴并以其他两个方向上的点为扫描点分组生成扫描直线。根据坐标范围选取几何模型中可能与该扫描线存在交点的三角面集合，将该集合中第$n$个三角面的三个顶点记为${{\boldsymbol{P}}_{0n}}$、${{\boldsymbol{P}}_{1n}}$和${{\boldsymbol{P}}_{2n}}$，有：

其中，${b_1}$和${b_2}$为任意实数，式(1)可写为：

由Cramer法则和向量混合积可得：

再令${{\boldsymbol{E}}_1} = {{\boldsymbol{P}}_{1n}} - {{\boldsymbol{P}}_{0n}}$，${{\boldsymbol{E}}_2} = {{\boldsymbol{P}}_{2n}} - {{\boldsymbol{P}}_{0n}}$，${\boldsymbol{S}} = {\boldsymbol{O}} - {{\boldsymbol{P}}_{0n}}$，${{\boldsymbol{S}}_1} = {\boldsymbol{D}} \times {{\boldsymbol{E}}_2}$，${{\boldsymbol{S}}_2} = {\boldsymbol{S}} \times {{\boldsymbol{E}}_1}$，可将式(3)简化为：

同理：

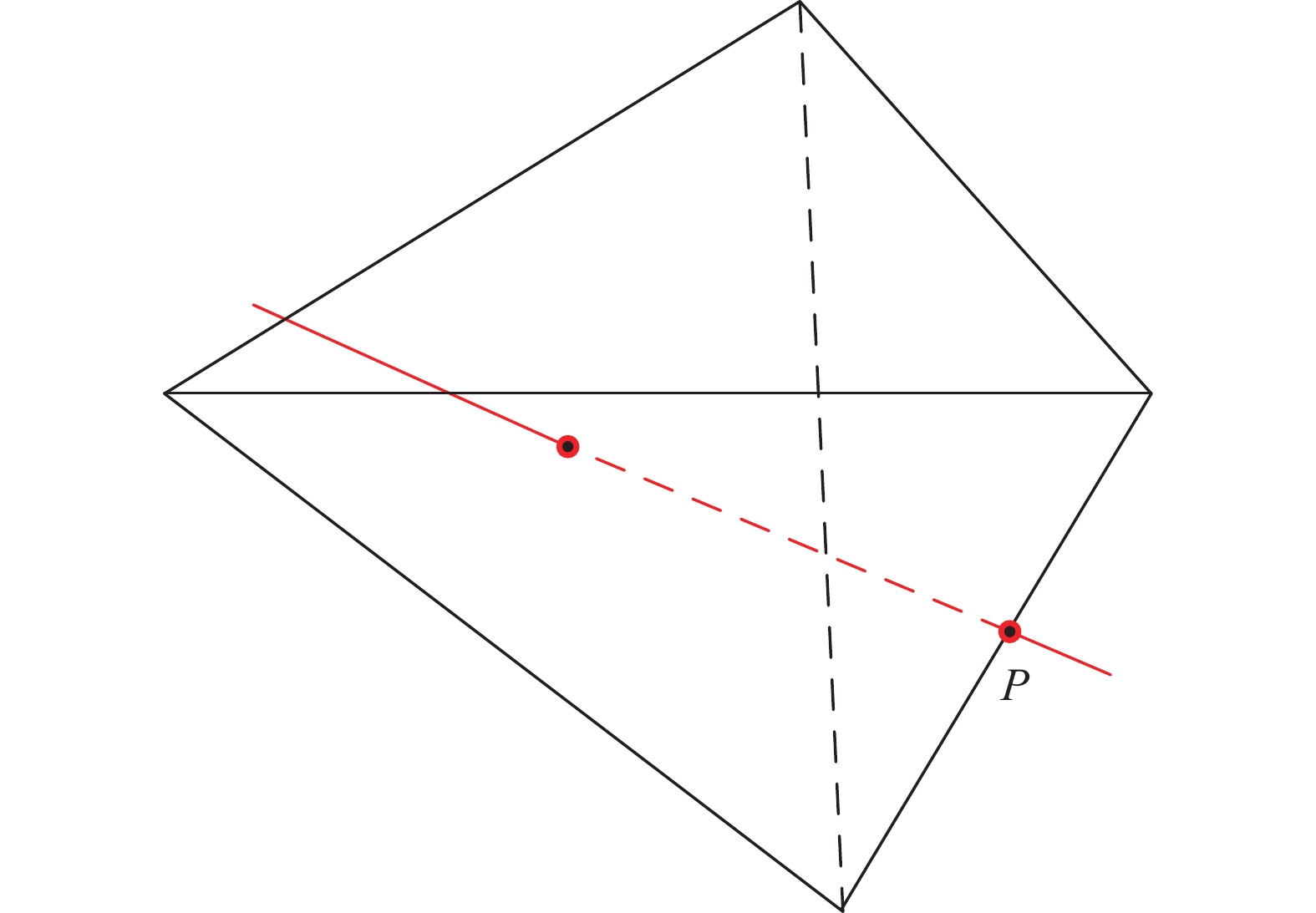
之后，判断是否满足${b_1} \geqslant 0$，${b_2} \geqslant 0$，${b_1} + {b_2} \geqslant 0$三个条件。若满足，则扫描线与当前三角面存在交点，且交点坐标为${\boldsymbol{P}} = {\boldsymbol{O}} + t{\boldsymbol{D}}$。

对于某一条扫描线，若它与模型存在两个或多个坐标相同的交点，则扫描线与模型的边线有交点，需要分两种情况讨论。第一种情况为坐标相同的交点对应的不同三角面法向量在扫描线上投影方向相反，此时扫描线与模型擦边而过，对应交点是无效的，应当舍弃，如图2所示。

图  2  扫描线与模型擦边而过示意图

Figure  2.  Schematic diagram of the scan line passing by the model

下载: 全尺寸图片 幻灯片

第二种情况为坐标相同的交点对应的不同三角面法向量在扫描线上投影方向相同，此时扫描线经边线(或边角点)穿入模型内部，对应交点是有效的，如图3所示。

图  3  扫描线经边线穿入模型内示意图

Figure  3.  Schematic diagram of scan line edge penetration into the model

下载: 全尺寸图片 幻灯片

遍历全部可能与该扫描线存在交点的三角面集合后，根据交点集合判定扫描线上全部网格点的流固情况。

1.2   LES-TPDF结合曲线坐标系浸没边界方法

大涡模拟采用滤波函数过滤流场中的变量，直接求解尺度大于滤波尺度的变量并用亚网格模型模化尺度小于滤波尺度的变量，其精度高于雷诺平均方法且计算量低于直接数值模拟方法，近年来被广泛应用于工程中^[18-19]。概率密度函数输运方程湍流燃烧模型求解湍流燃烧问题时能在不假设低维流形条件下完全封闭化学反应源项，相较其他燃烧模型更为准确并且可结合复杂化学反应机理。浸没边界方法能够大幅降低网格生成与分块的工作量，本文利用坐标变换在曲线坐标系中应用浸没边界方法避免因燃烧室流道复杂而导致固体区域网格过多，提高求解效率。用于坐标变换的Jacobian矩阵记为${\boldsymbol{J}}$，其中：

式中：${x_i}$为背景网格所对应的曲线坐标系中的坐标；${\xi _i}$为坐标变换后的笛卡尔坐标系中的坐标。在大涡滤波后的N-S方程组中应用链式法则，可得坐标变换后的连续方程、动量方程、标量输运方程分别为：

式中：$\overline \rho$为平均密度；${\mu _{\rm t}}$为分子粘度与亚网格湍流粘度之和；${\tilde u_j}$为密度加权滤波后的${x_j}$方向的速度分量；$t$为时间；${\boldsymbol{\phi}}$为包括物质浓度和混合物焓在内的标量集合形成的矢量；$A$为六面体网格某一面的面积，用Gauss-Ostrogradskii定理将守恒方程在体积$\partial V$上积分，得积分形式的守恒方程组：

式中，${G_k}$为控制体某方向上的流量，采用散度形式近似得到方程中的对流项。坐标系变换中非正交性产生的交叉导数项通过显式方法计算，并加入源项。通过前一时间步的质量守恒方程的解计算非线性项。以上的离散方法产生了对于通用变量的准线性方程组：

式中：$a$为系数；$\tilde \phi$为密度加权滤波后的通用变量；$\sum\nolimits_{\alpha = {\rm S,N,W,E,L,R}} {{{\tilde \phi _\alpha }}{a_\alpha }}$为六面体网格中当前网格点紧邻的六个网格点的对流扩散项，需要结合浸没边界网格标记求解；下标$\rm P$表示当前网格点；下标$\alpha$可取$\rm S,N,W,E,L,R$，表示与当前网格点相邻的六个网格点；${S_{\rm P}}$代表源项，包含所有不能用面通量表示的项，并且依赖于${{\tilde \phi _{\rm P}}}$。

本文通过处理离散方程系数阵隐式地实现Neumann边界条件。根据浸没边界网格标记寻找紧贴固体网格的流体网格。若某一流体边界网格的南方向(S)网格为固体壁面，对于离散形式的动量方程，首先向其中加入彻体力源项$S_{{\rm{IBM}}}^{{\rm{momentum}}} = - {{\tilde \phi _{\rm S}}}{a_{\rm S}}$，离散形式动量方程变为：

${S}_{{\rm{IBM}}}^{{\rm{momentum}}}$中包含了未知量${{\tilde \phi _{\rm S}}}$，可在求解离散方程前令${a_{\rm S}} = 0$实现。这种处理相当于求解${{\tilde \phi _{\rm P}}}$过程中${{\tilde \phi _{\rm S}}}$恒为0，即无滑移边界条件。

此外，为修正壁面附近的速度分布，用壁面函数法求解并隐式加入由壁面切应力$\tau$形成的源项${{\tilde \phi _{\rm P}}}{a_\tau } + {S_\tau }$，即：

采用SIMPLE(Semi-Implicit Method for Pressure Linked Equations)算法求解动量方程和连续方程。在求解由连续方程得到的压力修正方程时，压力增量梯度在某边界网格点北方向的分量可表示为：

对于靠近浸没边界固壁区域的流体单元(包括与固壁相隔一个流体单元的网格)，下标$\rm P$对应网格为流体域，即$\left( {\Delta p} \right)_{\rm P}^{}$位于流体计算域。若$\left( {\Delta p} \right)_{\rm N}^{}$、$\left( {\Delta p} \right)_{\rm S}^{}$、$\left( {\Delta p} \right)_{\rm NN}^{}$、$\left( {\Delta p} \right)_{\rm SS}^{}$四项中存在两个位于流场中的单元，则根据这两个单元求解压力增量梯度，否则$\left. \dfrac{{\partial \Delta p}}{{\partial {\xi _1}}}\right|_{\rm N} = 0$。对于压力修正方程中的压力平滑算子，采用相同的方法求解。之后，根据压力增量梯度的近似更新网格面上的质量通量，对于浸没边界上的流体网格，其与固壁相邻面的质量通量(如$G_1^{}{|_{\rm N}}$)恒为0。网格中心速度采用两倍网格尺度($2\Delta$)近似，最终得到修正后的速度场。

对于包含流场中各物质浓度和混合物焓值在内的标量输运方程，其边界均为零梯度边界条件。可通过向离散方程中加入源项$S_{{\rm{IBM}}}^{{\rm{scalar}}} = {{\tilde \phi _{\rm P}}}{a_{\rm S}} - {{\tilde \phi _{\rm S}}}{a_{\rm S}}$，离散形式的标量输运方程变为：

$S_{{\rm{IBM}}}^{{\rm{scalar}}}$中包含未知量${{\tilde \phi _{\rm P}}}$和${{\tilde \phi _{\rm S}}}$，可以通过在求解离散方程前先令${a_{\rm P}} = {a_{\rm P}} - {a_{\rm S}}$，再令${a_{\rm S}} = 0$实现。这种处理使离散方程中原有的${{\tilde \phi _{\rm S}}}{a_{\rm S}}$变为${{\tilde \phi _{\rm P}}}{a_{\rm S}}$，相当于在求解过程中${{\tilde \phi _{\rm S}}}$恒等于${{\tilde \phi _{\rm P}}}$，即实现零梯度边界条件。

为了求解各物质浓度和混合物焓的亚网格分布，需求解随机变量集合的输运方程：

式中：${{\boldsymbol{\zeta}} ^m}$为第$m$个欧拉随机场中的随机变量集合，其样本空间为标量集合$\tilde {\boldsymbol{\phi}}$；$K( {{{\boldsymbol{\zeta}} ^m}} )$为对流扩散项；$Sto( {{{\boldsymbol{\zeta}} ^m}} )$为随机项；$M( {{{\boldsymbol{\zeta}} ^m},\tilde {\boldsymbol{\phi }}} )$为小尺度混合项；$\dot \omega ( {{{\boldsymbol{\zeta}} ^m}} )$为化学反应源项。随机变量不存在亚网格分布，其输运方程与标量输运方程相比多出了随机项和小尺度混合项，这两项以源项的形式加入到式(18)中。其中小尺度混合项是亚网格的，与浸没边界网格标记的分布无关，而随机项以网格间随机输运的形式形成显式源项：

式中：${{\boldsymbol{u}}^{Sto}}$为随机速度，由Weiner过程定义，与流场无关。因此在定义随机输运时，若$i$方向相邻网格被标记为固体域，则令$u_i^{Sto} = 0$。

对于喷雾燃烧的情况，由于求解时固体域由浸没边界网格标记组成，用拉格朗日法求解粒子轨迹时需要再次采用Möller-Trumbore求交算法获得喷雾液滴粒子与真实壁面碰撞时的交点并计算反弹轨迹。对于式(4)~式(6)，在粒子与真实壁面碰撞时应当满足${b_1} \geqslant 0$，${b_2} \geqslant 0$，${b_1} + {b_2} \geqslant 0$，${b_1} + {b_2} \leqslant 0$，还需满足粒子按原速度在当前时间步和下一时间步分别位流体区域和固体区域。

本文在基于LES-TPDF(Large-Eddy Simulation-Transported Probability Density Function，大涡模拟-概率密度函数输运方程)模型的AECSC 2.0 (Aero Engine Combustor Simulation Code 2.0)软件^[20-22]湍流燃烧算法的基础上结合曲线坐标系下的浸没边界方法，开发出基于浸没边界方法的航空发动机燃烧室数值模拟软件AECSC-IBM (Aero Engine Combustor Simulation Code based on Immersed Boundary Method)并应用于多连通域内的湍流燃烧模拟。

2   算例模拟结果与讨论

2.1   双旋流燃烧室两相湍流燃烧模拟

真实燃气轮机燃烧室通常流道结构复杂，实验测量和数值模拟都较为困难。因此，通常建立实验室规模的模型燃烧室替代真实燃烧室作为研究对象，为数值模拟程序提供实验检验数据并为工程中燃烧室性能模拟提供测量值参考。旋流器是燃气轮机燃烧室中最为关键的结构之一，本文选取MEIER等^[23]设计的双旋流燃烧室(GTMC)作为模拟对象，采用曲线坐标系下的浸没边界方法结合LES-TPDF湍流燃烧模型分别模拟其冷态流动工况和喷雾燃烧工况。不同于工程中实际应用的燃烧室，GTMC燃烧室结构简单，对其划分贴体结构网格是可实现的，本文将基于曲线坐标坐标系浸没边界方法开发得到的AECSC-IBM软件模拟得到的数据与实验数据，以及曾家等^[13]利用基于贴体结构网格的AECSC 2.0软件及商业软件FLUENT的模拟结果进行对比，以检验本方法应用于燃烧室数值模拟的准确性。

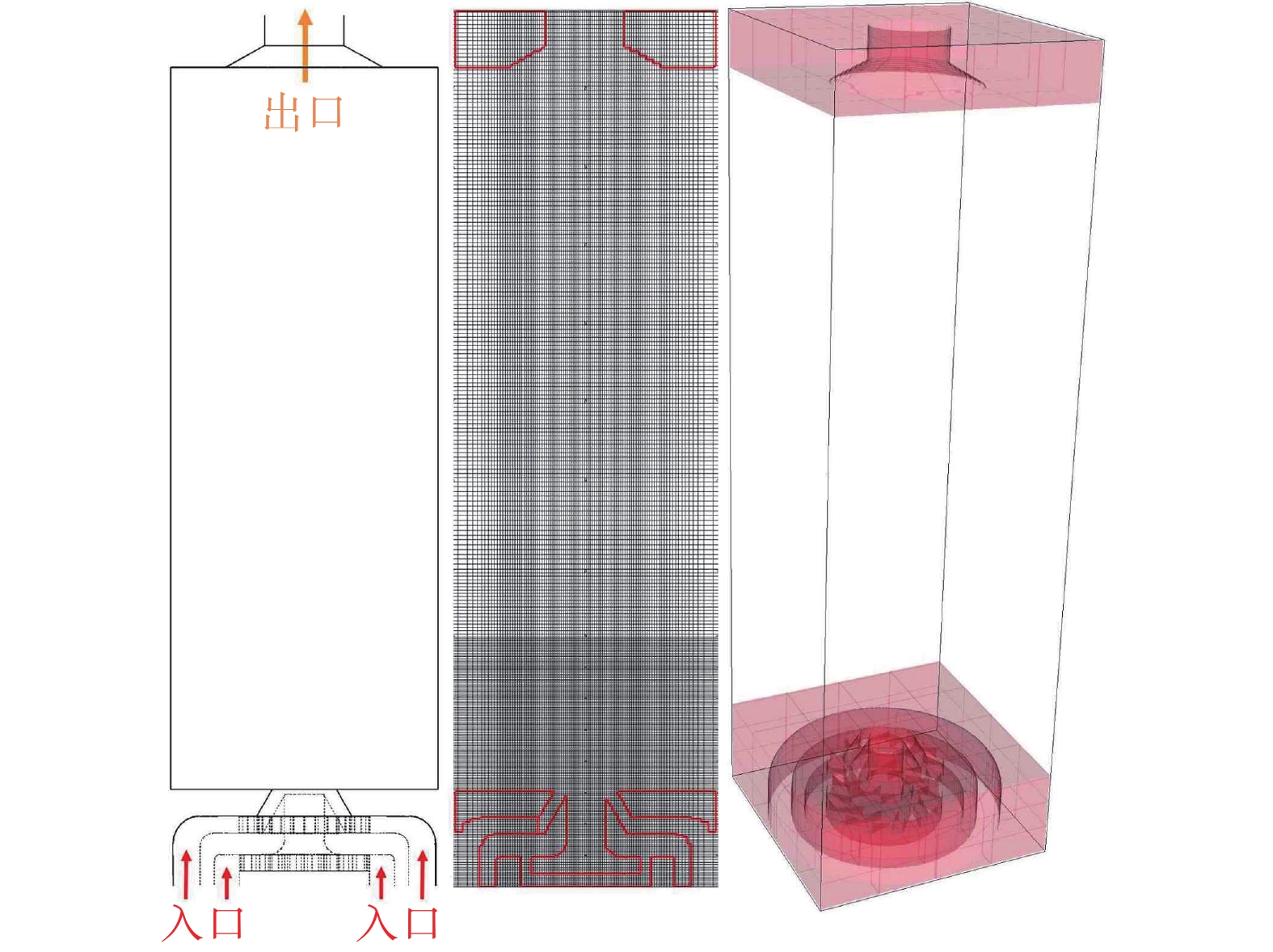
本文所模拟的双旋流燃烧室几何结构如图4所示，其长度为$264{\text{ mm}}$，燃烧室内垂直于旋流器轴线的截面为边长$102{\text{ mm}}$的正方形。进口空气分为两部分经中心旋流器和外旋流器进入燃烧室。煤油燃料经燃油管道和垂直槽道进入燃烧室，液滴速度与旋流器轴线方向夹角31°。中心旋流器、外旋流器以及燃油通道的几何结构如图5所示。

图  4  双旋流燃烧室几何结构示意图^[23]

Figure  4.  Schematic diagram of the geometric structure of the double-swirler combustor^[23]

下载: 全尺寸图片 幻灯片

图  5  旋流器与燃油通道几何结构示意图^[23]

Figure  5.  Schematic diagram of the geometry of the swirler and the fuel passage^[23]

下载: 全尺寸图片 幻灯片

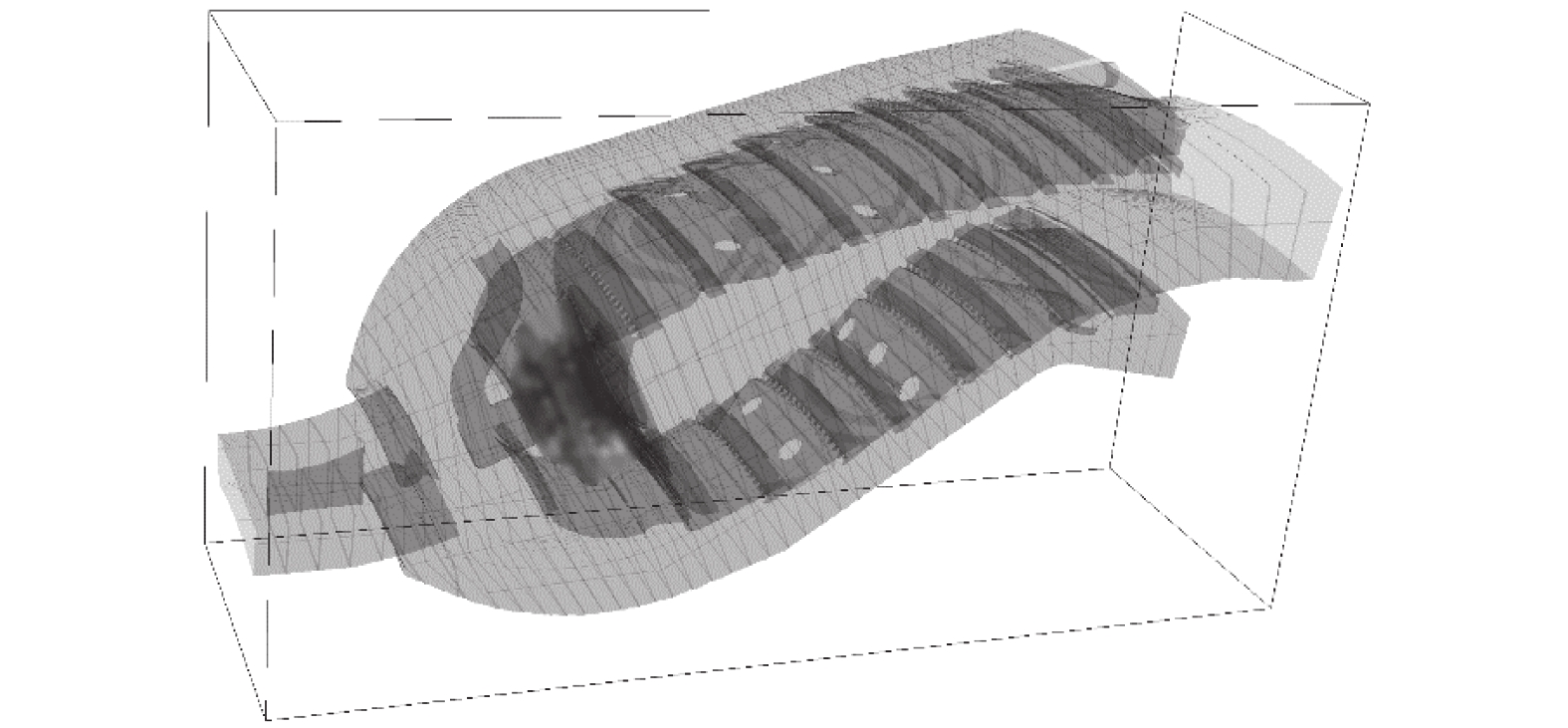
应用本方法模拟双旋流燃烧室中的湍流燃烧现象时，空气从内外两个进口以1∶1.65的比例^[13]进入内外旋流器。参考贴体网格模拟时的网格尺度，以$349$万的背景网格为基础，并在背景网格中利用曲线坐标系对旋流器附近局部加密，扫描燃烧室几何模型并生成浸没边界网格标记。计算双旋流燃烧室算例时采用的几何模型、背景网格与扫描得到的浸没边界网格标记如图6所示。

图  6  计算采用的双旋流燃烧室几何模型与网格

Figure  6.  Double-swirler combustor geometry model and mesh used for calculation

下载: 全尺寸图片 幻灯片

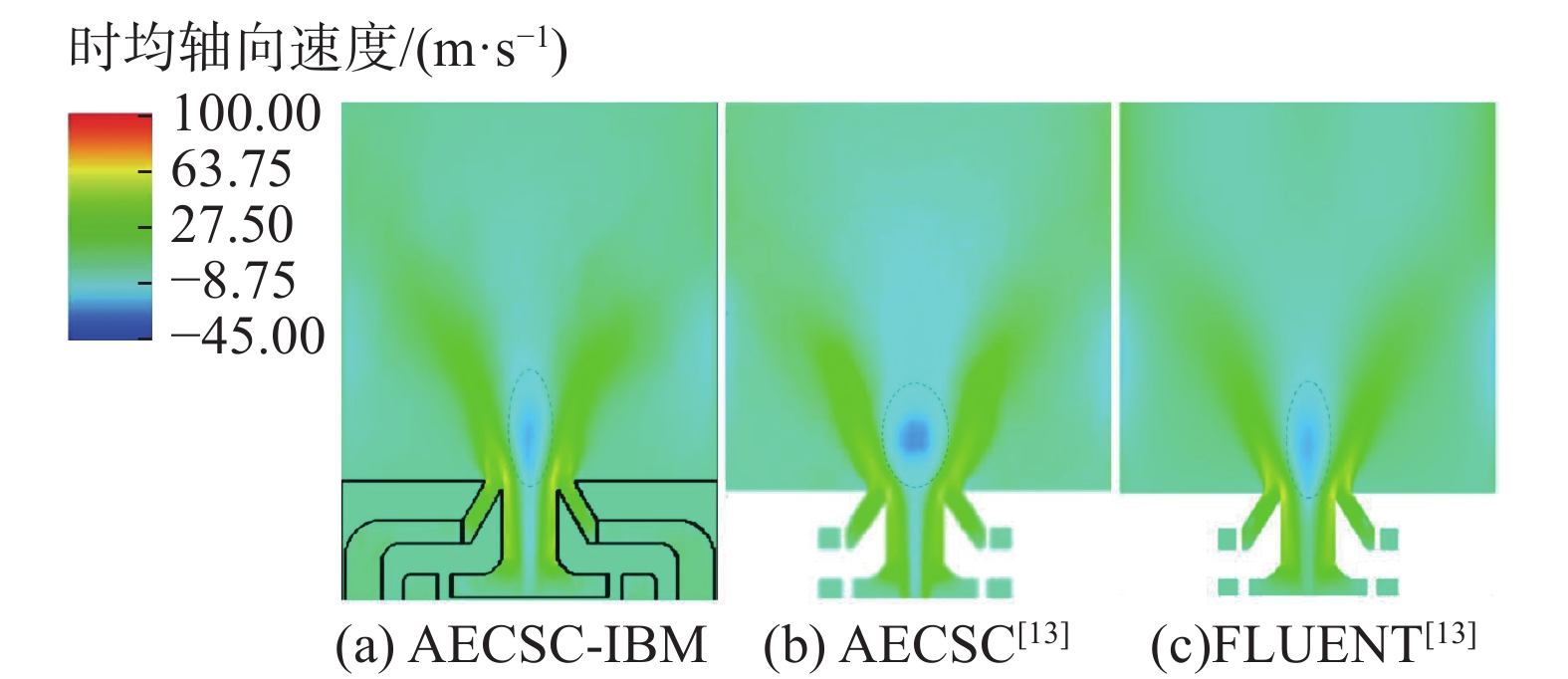
对于冷态工况，进口空气压强为$0.4{\text{ MPa}}$，温度为$295{\text{ K}}$，进口总流量$82{\text{ g/s}}$。采用大涡模拟结合本浸没边界方法，并采用$64$核并行求解得到冷态流场，其三维速度矢量与流线如图7所示。

图  7  冷态工况速度矢量图与流线图

Figure  7.  Velocity vector diagram and streamline diagram in cold condition

下载: 全尺寸图片 幻灯片

图8对比了基于本方法的AECSC-IBM软件模拟得到的旋流器出口轴向速度时均分布及采用相同数量贴体网格的AECSC及FLUENT软件模拟结果^[13]，图中用虚线标记了回流区大致形状，本浸没边界方法模拟的双旋流燃烧室回流区形状接近FLUENT软件模拟结果，而AECSC模拟得到的回流区则更宽。

图9对比了采用本浸没边界方法的双旋流燃烧室冷态工况时均速度分布模拟结果(AECSC-IBM)与贴体网格的AECSC和FLUENT模拟结果，以及实验数据。横坐标${X}$代表径向测点与旋流器轴线的距离，纵坐标${Z}$代表在轴向上与旋流器出口平面之间的距离。

图  8  冷态工况时均轴向速度云图

Figure  8.  Mean axial velocity cloud diagram in cold condition

下载: 全尺寸图片 幻灯片

图  9  冷态工况时均轴向速度对比

Figure  9.  Comparison of average axial velocity in cold condition

下载: 全尺寸图片 幻灯片

采用式(21)中的方法计算平均相对误差，以径向为例：${\rm{Erro}}{{\rm{r}}_U}$为径向速度分量$U$的平均相对误差；${U_{{\rm{CAL}}}}$为该方向上计算得到的速度分量；${U_{{\rm{EXP}}}}$为实验得到的速度分量；${n_{{\rm{EXP}}}}$为实验测点个数。得到双旋流燃烧室时均速度分布的平均相对误差如表1所示：

表  1  双旋流燃烧室算例时均速度平均相对误差

Table  1.  Time-averaged velocity average relative error of the double-swirler combustor

高度/mm	速度方向	本方法		贴体结构网格方法
		AECSC-IBM/(%)		AECSC/(%)	FLUENT/(%)
2	轴向	13.8		15.4	15.1
5	轴向	12.0		11.7	11.4
10	轴向	21.2		9.7	15.8
2	切向	15.4		14.2	11.2
5	切向	11.6		9.9	11.2
10	切向	18.0		19.2	14.3
2	径向	36.6		75.3	34.5
5	径向	16.9		15.3	11.9
10	径向	18.0		14.3	10.2

下载: 导出CSV 

| 显示表格

由图10中的时均轴向速度分布以及表2中计算得到的相对误差可知，基于本曲线坐标系浸没边界方法模拟得到的速度场与实验值接近，时均速度的误差与采用贴体网格的AECSC和FLUENT模拟结果的误差相当。

图  10  旋流器出口2 mm处时均轴向速度对比

Figure  10.  Comparison of the time-averaged axial velocity at 2 mm from the outlet of the cyclone

下载: 全尺寸图片 幻灯片

表  2  旋流器出口2 mm处时均轴向速度与实验值相对误差

Table  2.  The relative error between the time-averaged axial velocity and the experimental value at 2 mm from the outlet of the cyclone

位置	本方法		贴体结构网格方法
	AECSC-IBM/(%)		AECSC/(%)	FLUENT/(%)
峰值1	0.8		21.7	27.9
峰值2	12.6		2.7	6.2
谷值	3.0		0.3	3.9
峰值3	13.5		11.0	10.4
峰值4	5.1		20.5	22.4

下载: 导出CSV 

| 显示表格

靠近旋流器出口位置的轴向速度分布与实验数据之间的误差大小反应了数值方法对旋流器附近流场的解析能力。从高度$2{\text{ mm}}$处实验值的轴向速度分布中可发现，在${X}$轴正负方向分别存在两个速度轴向速度峰值，在切向速度和径向速度分布图的对应位置上也存在相邻的两对峰值。在结合旋流器模型，这两个峰值分别由内旋流器与外旋流器形成，曲线坐标系浸没边界方法模拟得到的轴向速度中，靠近轴线(${X} = 0$)的峰值略高于远离轴线的轴向速度峰值，这与实验结果相符，而其他两种软件用贴体网格得到的结果与之相反。在高度$2{\text{ mm}}$处轴向速度的峰值位置，采用贴体结构网格的AECSC和FLUENT软件模拟得到的峰值处时均轴向速度均方根误差分别为$14.3{\text{% }}$和$16.7{\text{% }}$，而采用本浸没边界方法模拟得到的均方根误差为$6.6{\text{% }}$。本方法在靠近旋流器出口的测点位置轴向速度精度优于贴体网格，可能与贴体网格在旋流器出口附近网格质量较低有关。而在其他截面本方法的精度略差于贴体网格，可能与本浸没边界方法在流固边界位置的处理方法有关。

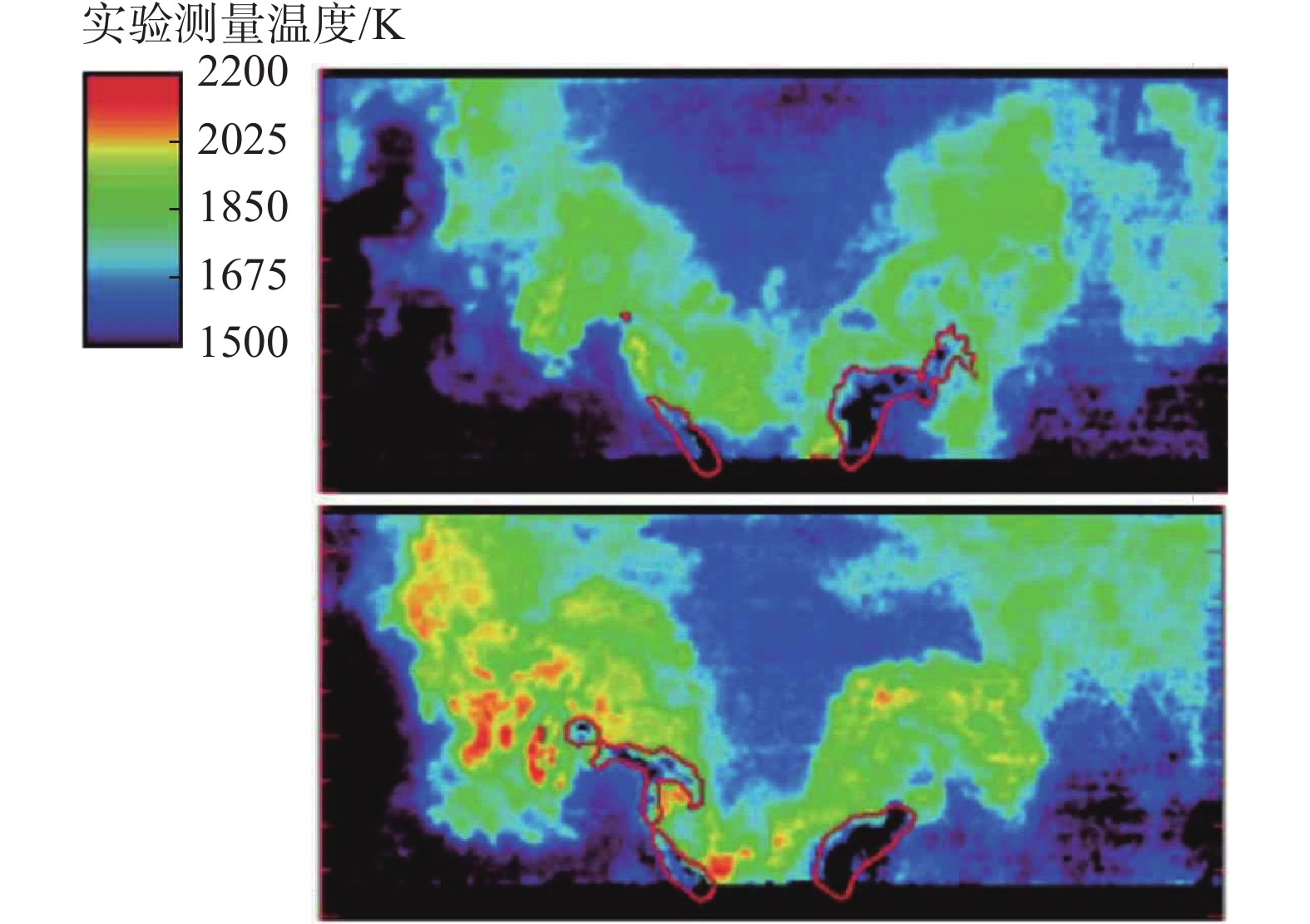
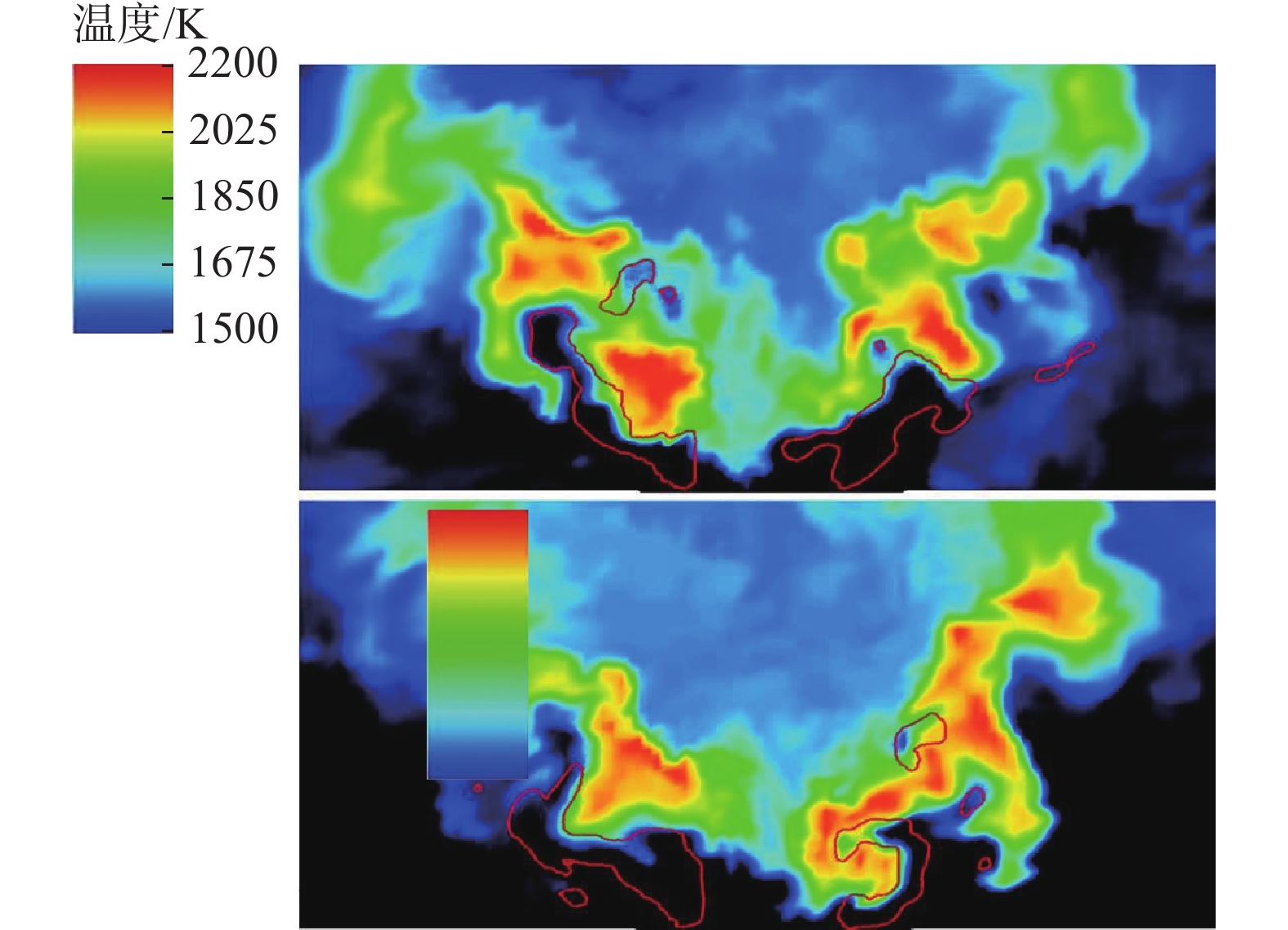
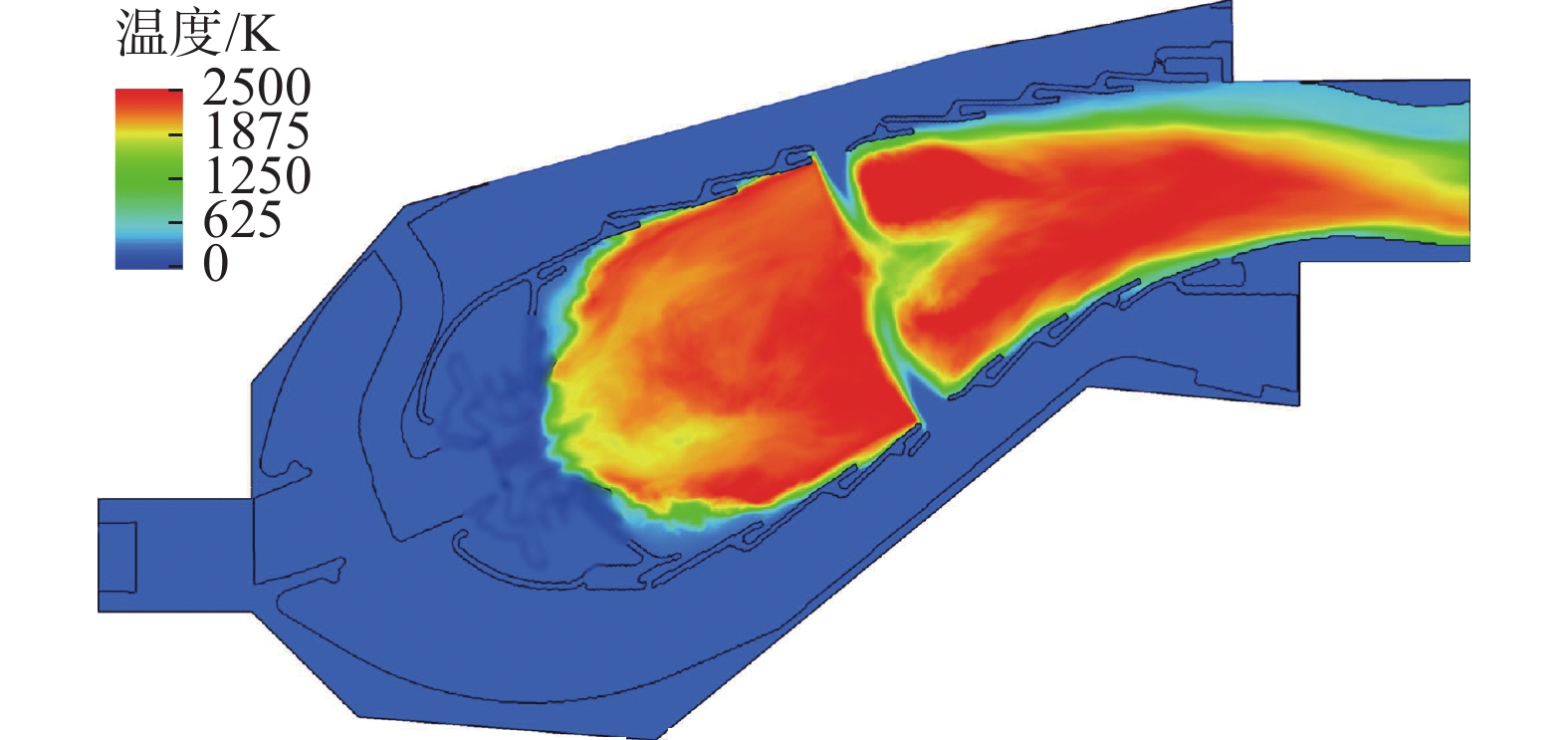
双旋流燃烧室算例的冷态工况测试表明本方法结合LES能够准确模拟复杂结构内湍流流动现象，在此基础上，应用本方法结合LES-TPDF湍流燃烧模型对双旋流燃烧室的喷雾燃烧工况进行模拟。在该燃烧室热态实验中，采用航空煤油Jet-A作为燃料，燃料流量为$3{\text{ g}}/{\text{s}}$，进口空气压强$0.4{\text{ MPa}}$，温度为$550{\text{ K}}$，流量为$60{\text{ g}}/{\text{s}}$，由于实验未提供喷雾液滴粒子详细数据，这里参考采用贴体网格模拟本算例时假定的粒子数据^[13]，其中煤油液滴粒子的初速度为$50{\text{ m}}/{\text{s}}$，温度为$380{\text{ K}}$，Sauter平均直径(Sauter Mean Diameter，SMD)为$15$。两相湍流燃烧的瞬态温度场与煤油质量分数等值线的实验照片和模拟结果分别如图11和图12所示，时间平均温度场实验照片和模拟结果分别如图13和图14所示。

图  11  瞬态温度云图与煤油浓度等值线实验照片^[23]

Figure  11.  Experimental photos of transient temperature nephogram and isoline of kerosene mass fraction^[23]

下载: 全尺寸图片 幻灯片

温度云图可反映出湍流流动、液滴蒸发以及化学反应之间的相互作用。在瞬态温度云图中旋流器出口附近，由于煤油液滴蒸发吸热，形成靠近燃油喷嘴的低温区。液滴蒸发后在回流区附近进行较强烈的燃烧反应，并在喷雾锥面后侧形成高温区。在时均温度云图中，由于液滴最初从喷嘴喷出时SMD较大，蒸发出气相煤油较少，燃烧反应放热较少，结合蒸发的吸热作用导致温度较低。之后液滴粒子在与湍流流动相互作用下破碎和蒸发，燃烧反应增强，在时均温度云图实验照片中可看到耳垂形的高温区。在模拟结果中，温度分布与实验照片相似，模拟中液滴蒸发较快，耳垂形高温区相比实验提前，更靠近旋流器出口。

图  12  瞬态温度云图与煤油浓度等值线模拟结果

Figure  12.  Simulation results of transient temperature nephogram and isoline of kerosene mass fraction

下载: 全尺寸图片 幻灯片

图  13  时均温度云图实验照片^[23]

Figure  13.  Experimental photo of time-average temperature nephogram^[23]

下载: 全尺寸图片 幻灯片

图  14  时均温度云图模拟结果

Figure  14.  Simulation results of time-average temperature nephogram

下载: 全尺寸图片 幻灯片

对双旋流燃烧室的冷态流动模拟和两相湍流燃烧模拟表明，本方法能够处理复杂几何结构，应用本方法的AECSC-IBM软件能够精确地模拟包含旋流器等复杂结构的燃烧室中的湍流流动及燃烧化学反应。与采用贴体网格相比，浸没边界结合利用曲线坐标系进行局部加密的方法在含旋流器等复杂结构的燃烧室模拟中大幅降低了网格生成工作量，并且能保证旋流器等结构所在位置的合适的网格密度和高的网格质量。

2.2   真实航空燃气轮机燃烧室两相湍流燃烧模拟

选取某型号真实全环形航空燃气轮机燃烧室的单头部模型(局部模糊处理)，如图15所示，应用本曲线坐标系中的浸没边界方法对其进行湍流流动与喷雾燃烧模拟，以检验本方法在工程实际应用中的可行性。本文选取的航空燃气轮机全环形燃烧室几何结构复杂，旋流器与火焰筒等部件上存在大量小尺度结构，且流道形状不规则，对于复杂结构内部湍流及燃烧数值模拟具有一定代表性。

图  15  某型航空燃气轮机燃烧室单头部模型^[10]

Figure  15.  Single head model of a certain type of aviation gas turbine combustor^[10]

下载: 全尺寸图片 幻灯片

本算例中，经压气机压缩过的空气密度为$3.955{\text{ kg}}/{{\text{m}}^3}$，压强为$790\;216.58{\text{ Pa}}$，温度为$696.01{\text{ K}}$，以$121.07{\text{ m}}/{\text{s}}$的速度沿${X}$轴的正方向流入扩压器。为了测试本曲线坐标系中的浸没边界方法相比采用笛卡尔坐标系的浸没边界方法在求解复杂几何内流问题时的优势，本文首先基于这两种方法进行冷态流动模拟。为了保证网格分辨率足够，设置笛卡尔坐标系中的全场网格尺度为均匀的$0.5{\text{ mm}}$^[10]。对于曲线坐标系中的背景网格，将全场网格尺度限制在不大于$0.5{\text{ mm}}$。在以上条件下划分得到两种坐标系下的背景网格，其中笛卡尔坐标系下网格总数为$5425$万，曲线坐标系下网格总数为$4637$万。在背景网格基础上扫描燃烧室几何生成网格标记，如图16和图17所示。图18和图19分别为笛卡尔坐标系网格和曲线坐标系网格中的浸没边界网格标记，二者均准确映射了单头部燃烧室几何模型。

图20和图21分别展示了笛卡尔坐标系网格与曲线坐标系网格的并行分块情况中央截面示意图，其中燃烧室曲线外侧区域被标记为无需求解的固体域。在笛卡尔坐标系背景网格中，$38.3{\text{% }}$的并行分块内完全为固体域，此外还有大量固体域占比很高的分块，提高了并行计算负载均衡的难度，造成了计算资源浪费。

图  16  笛卡尔坐标系下中央截面背景网格及网格标记图

Figure  16.  The background grid and grid marking diagram of the central section in the Cartesian coordinate system

下载: 全尺寸图片 幻灯片

图  17  曲线坐标系下中央截面背景网格及网格标记图

Figure  17.  The background grid and grid marking diagram of the central section in the curvilinear coordinate system

下载: 全尺寸图片 幻灯片

图  18  笛卡尔坐标系中三维浸没边界网格标记

Figure  18.  3D immersion boundary mesh labeling in Cartesian coordinates

下载: 全尺寸图片 幻灯片

图  19  曲线坐标系中三维浸没边界网格标记

Figure  19.  3D immersion boundary mesh labeling in curvilinear coordinates

下载: 全尺寸图片 幻灯片

求解时，采用对应于网格分块的$512$个CPU，利用MPI框架并行计算。如表3所示，采用笛卡尔网格时，每千步约需$6.6$小时，采用曲线坐标系时，每千步约需$2.8$小时。可发现采用曲线坐标系浸没边界方法求解时总网格数为采用笛卡尔坐标系的$84.8\text{%}$，而求解时间则大幅缩短为采用笛卡尔坐标系时的$42.9{\text{% }}$，这可能与网格数过多时并行效率下降等因素有关。

图  20  笛卡尔坐标系下中央截面并行块划分情况示意图

Figure  20.  Schematic diagram of the parallel block division of the central section in the Cartesian coordinate system

下载: 全尺寸图片 幻灯片

图  21  曲线坐标系下中央截面并行块划分情况示意图

Figure  21.  Schematic diagram of the parallel block division of the central section in the curvilinear coordinate system

下载: 全尺寸图片 幻灯片

表  3  笛卡尔坐标系与曲线坐标系算例的网格与并行数据

Table  3.  Grid and parallel data of cases in Cartesian and curvilinear coordinates

网格与并行数据	笛卡尔坐标系	曲线坐标系
网格尺度$\Delta {\rm /mm}$	$\Delta \equiv 0.5$	$\Delta \leqslant 0.5$
总网格数	$5.425 \times {10^7}$	$4.637 \times {10^7}$
并行分块数	$512$	$512$
每千步计算时间/h	$6.6$	$2.8$

下载: 导出CSV 

| 显示表格

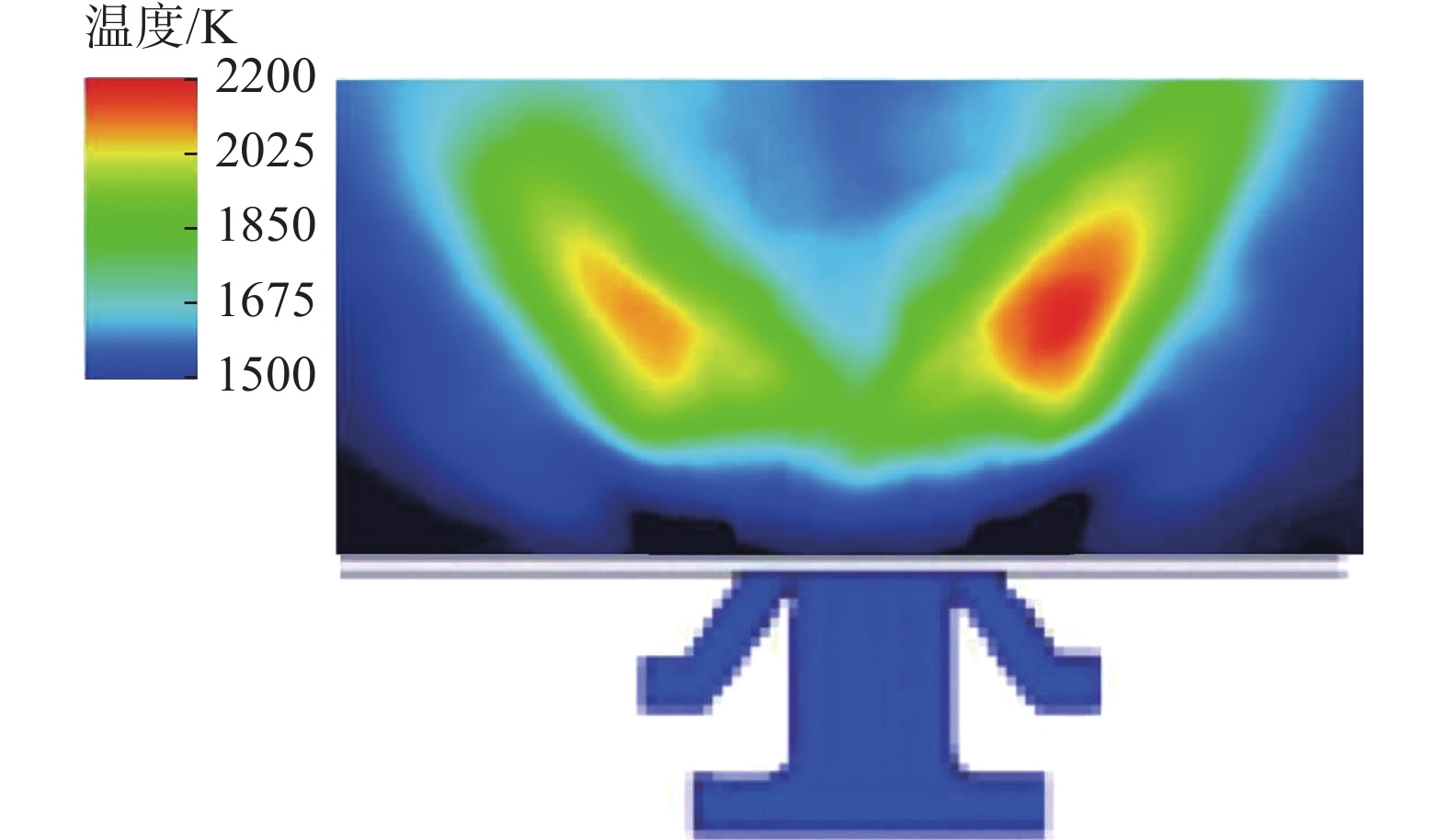
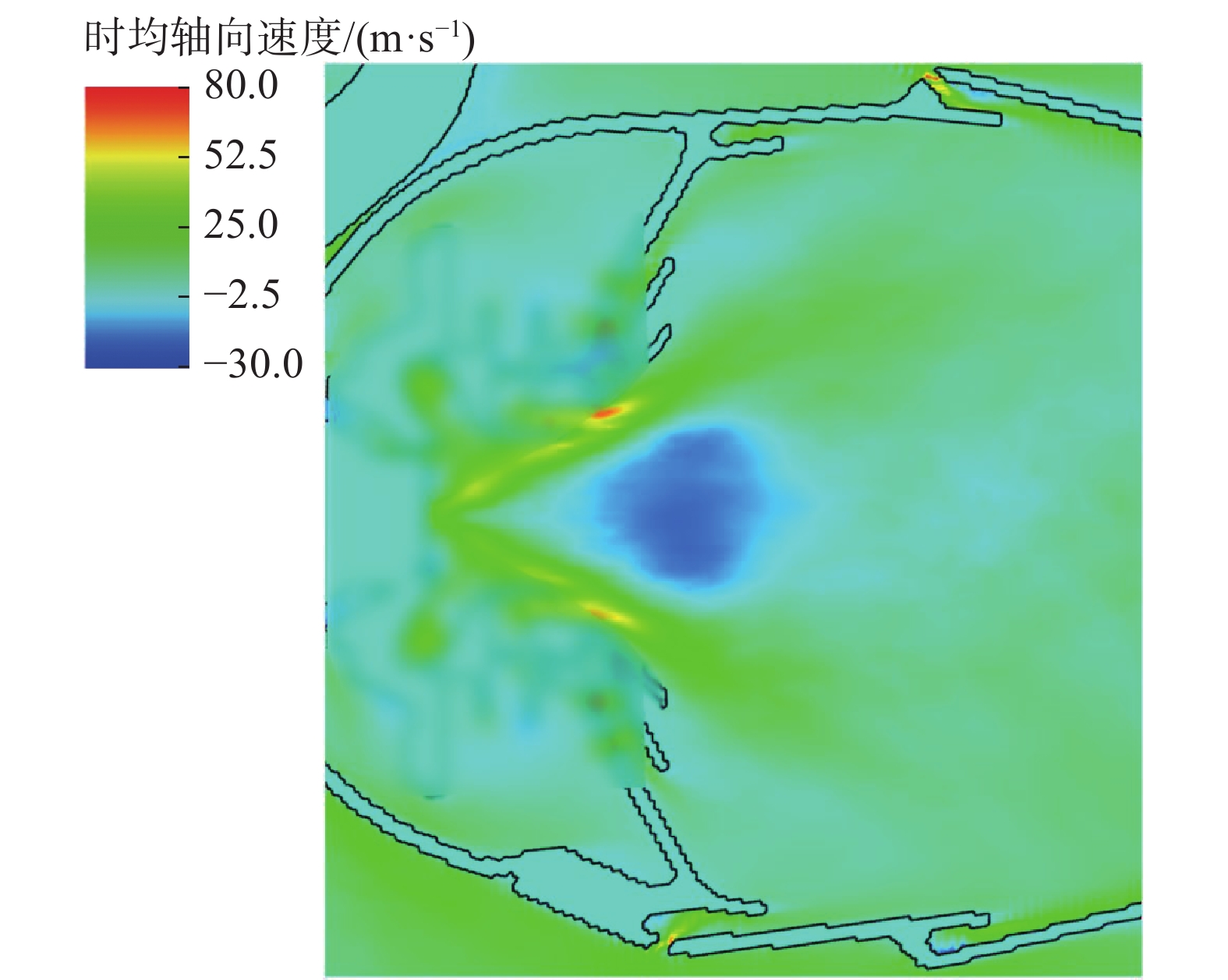
采用本曲线坐标系中的浸没边界方法能够大幅节约复杂结构内湍流流动模拟所需的计算资源。基于该方法模拟真实燃气轮机燃烧室中的湍流燃烧现象，以检验其精度并探索其应用于工程中的可行性。在本文模拟的燃烧室中，初始温度$400{\text{ K}}$的燃油经半径$3{\text{ mm}}$的喷咀以$0.0077{\text{ kg}}/{\text{s}}$的流量和$39.5$的SMD值沿与旋流器轴线夹角60°的方向呈锥形喷出，并采用热沉积模型模拟电火花点火。点火一段时间后，得到充分发展的湍流燃烧场。其中稳定燃烧状态的燃烧室中央截面的流场速度矢量如图22所示。

燃烧室中央截面的瞬态温度云图如图23所示，由图可知，温度较低燃油从喷咀喷出后形成一段低温区，之后燃油蒸发并在主燃孔附近位置剧烈燃烧，放出大量热导致温度升高，掺混孔流入的冷空气使温度局部下降，之后未反应完全的碳氢化合物在掺混孔后方继续燃烧放热。火焰筒内外壁存在大量冷却孔，外部冷空气经小孔形成温度较低的气膜以避免火焰筒温度过高。

图  22  燃烧室中央截面瞬态速度云图

Figure  22.  Transient velocity nephogram of the central section of the combustor

下载: 全尺寸图片 幻灯片

图  23  燃烧室中央截面瞬态温度云图

Figure  23.  Transient temperature nephogram of the central section of the combustion chamber

下载: 全尺寸图片 幻灯片

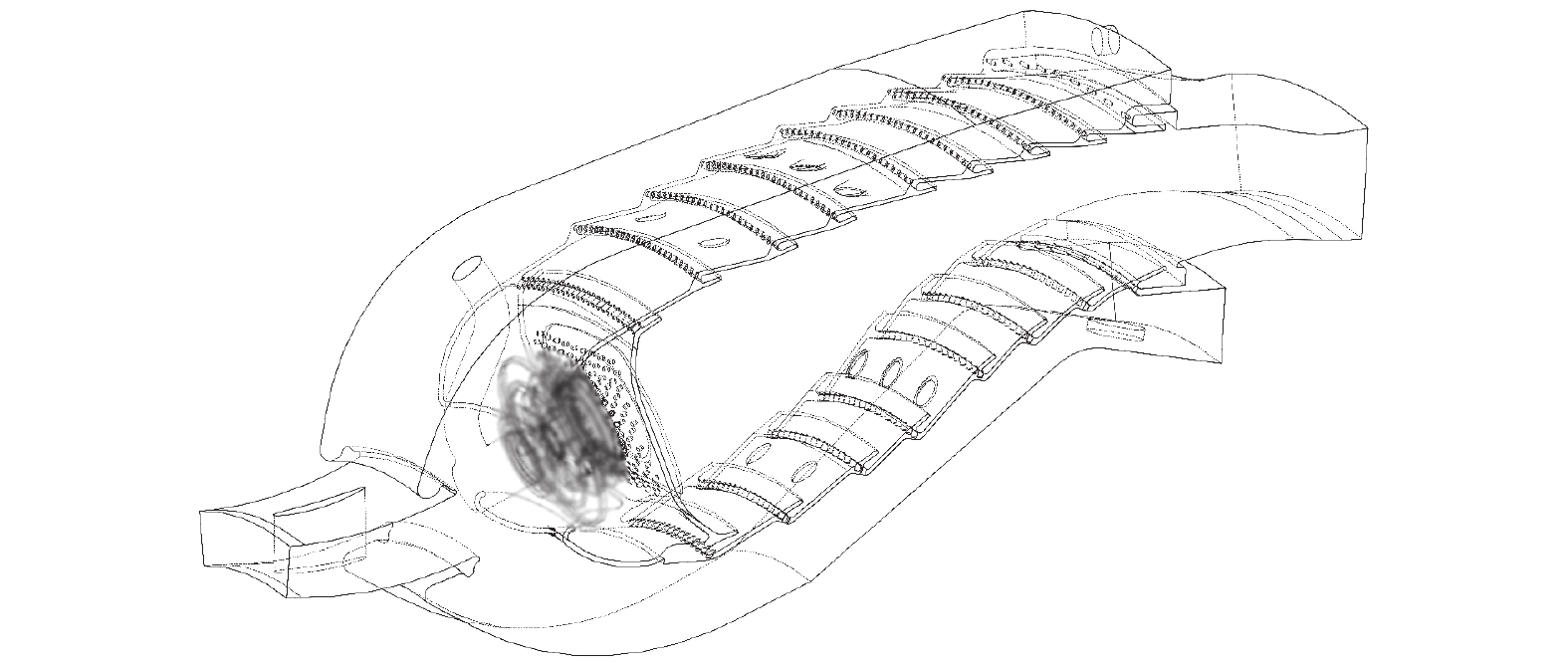
燃烧室的旋流器功能重要而结构复杂，其产生如图24中蓝色区域所示的回流区，使火焰稳定。采用本曲线坐标系浸没边界方法能够求解以上所述的结构附近的湍流流动与燃烧反应，使得对复杂结构燃烧室的高保真模拟成为可能。

对模拟中的湍流燃烧场进行统计和时间平均，得到时均温度分布，如图25所示。对于结构复杂的真实燃烧室，在喷雾燃烧时内部温度较高，对其内部进行实验测量非常困难，因此利用本方法模拟得到的湍流燃烧场可为燃烧室设计提供详细流动和化学反应等信息作为参考。时均温度云图明显地表现出旋流器产生的高温回流区，在主燃孔附近的剧烈反应导致的高温，掺混孔以及火焰筒壁面的冷却孔形成的低温区域。燃烧室出口附近靠近壁面的位置温度较低，出口径向温度分布的最高温度位于径向相对高度的$0.2$~$0.4$，与实验数据相符。

图  24  回流区附近时均轴向速度云图

Figure  24.  Time-average axial velocity nephogram near the recirculation zone

下载: 全尺寸图片 幻灯片

图  25  燃烧室中央截面时均温度云图

Figure  25.  Time-average temperature nephogram of the central section of the combustion chamber

下载: 全尺寸图片 幻灯片

在时均温度场的基础上，对燃烧室出口温度作周向平均，形成沿径向的温度分布曲线，并于实验得到的数据对比，如图26。其中红色曲线为利用本曲线坐标系下的浸没边界方法结合LES-TPDF湍流燃烧模型得到的出口温度分布，黑色圆点表示实验中六个测点测量得到的温度。由图可知利用本方法模拟得到的出口径向温度分布与实验值基本一致，计算可得均方根误差(RMSE)为$11.7{\text{% }}$。本文所模拟的真实航空燃气轮机环形燃烧室单头部模型内部几何结构复杂，且湍流流动与燃烧化学反应存在强烈非线性的相互作用，浸没边界网格对复杂边界及其附近流动的解析，煤油液滴的破碎蒸发的求解，煤油燃料组分及化学反应机理的简化等因素都可造成数值模拟时的误差。采用本曲线坐标系浸没边界方法结合LES-TPDF湍流燃烧模型模拟本算例中的燃烧室时，能够精确分辨燃烧室细节结构及获得燃烧室内的三维湍流燃烧场，并且计算资源的利用效率高于传统笛卡尔坐标系下的浸没边界方法，最终得到的温度分布与实验值的误差较小，因此，本方法应用于复杂构型内湍流燃烧数值模拟可为实际工程中燃烧室的设计提供参考。

图  26  燃烧室出口径向温度分布模拟值与实验值

Figure  26.  Simulation and experimental value of radial temperature distribution at the combustion chamber outlet

下载: 全尺寸图片 幻灯片

3   结论

本文提出一种应用于多连通域内高效率、高保真湍流燃烧数值模拟的曲线坐标系浸没边界方法，利用曲线坐标系和坐标变换减少固体网格点占比并实现网格局部加密，将此方法应用于复杂结构燃烧室中两相湍流燃烧的数值模拟中，检验其精度和对计算效率的提升效果。

本方法在双旋流燃烧室模拟中，模拟得到的速度场与燃烧场与实验贴合较好，模拟精度较高。在最靠近旋流器出口截面(高度$2{\text{ mm}}$)轴向速度的峰值位置，采用浸没边界方法模拟得到的均方根误差为$6.6{\text{% }}$，优于采用同规模贴体结构网格的自研软件AECSC(误差$14.3{\text{% }}$)和商业软件FLUENT(误差$16.7{\text{% }}$)在该位置的模拟结果。

在某型真实航空燃气轮机全环形燃烧室的单头部模型的模拟中，在网格最低分辨率相同(全场网格尺度$\Delta {\leqslant} 0.5{\text{ mm}}$)时，采用曲线坐标系背景网格时的总网格数降低为采用笛卡尔坐标系背景网格时的$84.8\text{%}$。采用相同的$512$个CPU核心计算相同的时间步数，采用曲线坐标系IB方法求解消耗的时间为笛卡尔坐标系IB方法的$42.9{\text{% }}$。采用本方法减少了无需求解的固体区域在计算域中的占比，大幅提高了计算效率。利用本方法模拟燃烧室中的两相湍流燃烧，出口径向温度分布的均方根误差为$11.7{\text{% }}$。

真实燃烧室往往为流道结构复杂的多连通域，本方法在解决真实燃烧室数值模拟中网格生成及分块困难的问题的同时，利用曲线坐标系和坐标变换减少固体区域在计算域中所占的比例，提高了浸没边界方法应用于复杂流道内流问题的求解效率，节省了计算资源。综上所述，本文提出的曲线坐标系浸没边界方法对于多连通域内流问题的高保真、高效模拟具有一定学术价值和工程应用前景。