基于解析二阶盲辨识的结构工作模态分析及真假模态区分

李涧鸣; 包腾飞; 周喜武; 高瑾瑾; 顾昊

doi:10.6052/j.issn.1000-4750.2022.03.0222

基于解析二阶盲辨识的结构工作模态分析及真假模态区分

李涧鸣^{1, 2,},
包腾飞^{1, 2, 3, ,},
周喜武^4,,
高瑾瑾^5,,
顾昊^{1, 2,}

1.
河海大学水文水资源与水利工程科学国家重点实验室，南京 210098
2.
河海大学水利水电学院，南京 210098
3.
三峡大学水利与环境学院，宜昌 443002
4.
江苏省水利工程科技咨询股份有限公司，南京 210029
5.
水利部交通运输部国家能源局南京水利科学研究院，南京 210029

基金项目: 国家重点研发计划项目(2018YFC1508603)；国家自然科学基金项目(51739003)；中央高校基本科研业务费专项资金项目(2018B623X14)；江苏省研究生科研与实践创新计划项目(KYCX18_0592)；中国博士后基金项目(2021M701044)

详细信息

作者简介:
李涧鸣(1992−)，男(土家族)，湖北人，博士生，主要从事结构振动测试、模态分析和健康监测研究(E-mail: lijianming@hhu.edu.cn)

周喜武(1976−)，男，黑龙江人，高工，硕士，主要从事水利、岩土工程仿真和模型试验研究(E-mail: 850394549@qq.com)

高瑾瑾(1993−)，女，湖北人，工程师，博士，主要从事水利工程仿真和计算力学研究(E-mail: gaojinjinhhu@outlook.com)

顾　昊(1990−)，男，江苏人，副教授，博士，主要从事水工程安全监控与健康诊断研究(E-mail: ghao@hhu.edu.cn)

通讯作者:
包腾飞(1974−)，男，湖北人，教授，博士，博导，主要从事水工结构安全监控、评估和反馈分析研究(E-mail: baotf@hhu.edu.cn)

中图分类号: TU311.3
计量
- 文章访问数: 168
- HTML全文浏览量: 42
- PDF下载量: 42
出版历程
- 收稿日期: 2022-03-06
- 修回日期: 2022-08-06
- 网络出版日期: 2023-01-31
- 刊出日期: 2024-01-24

OPERATIONAL MODAL ANALYSIS UPON ANALYTIC SECOND-ORDER BLIND IDENTIFICATION AND DISCRIMINATION BETWEEN PHYSICAL AND SPURIOUS MODES

LI Jian-ming^{1, 2,},
BAO Teng-fei^{1, 2, 3, ,},
ZHOU Xi-wu^4,,
GAO Jin-jin^5,,
GU Hao^{1, 2,}

1.
State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Hohai University, Nanjing 210098, China
2.
College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China
3.
College of Hydraulic and Environmental Engineering, China Three Gorges University, Yichang 443002, China
4.
Jiangsu Province Water Engineering Sci-tech Consulting Co., Ltd., Nanjing 210029, China
5.
Nanjing Hydraulic Research Institute, National Energy Administration, Ministry of Transport, Ministry of Water Resources, Nanjing 210029, China

摘要

摘要:
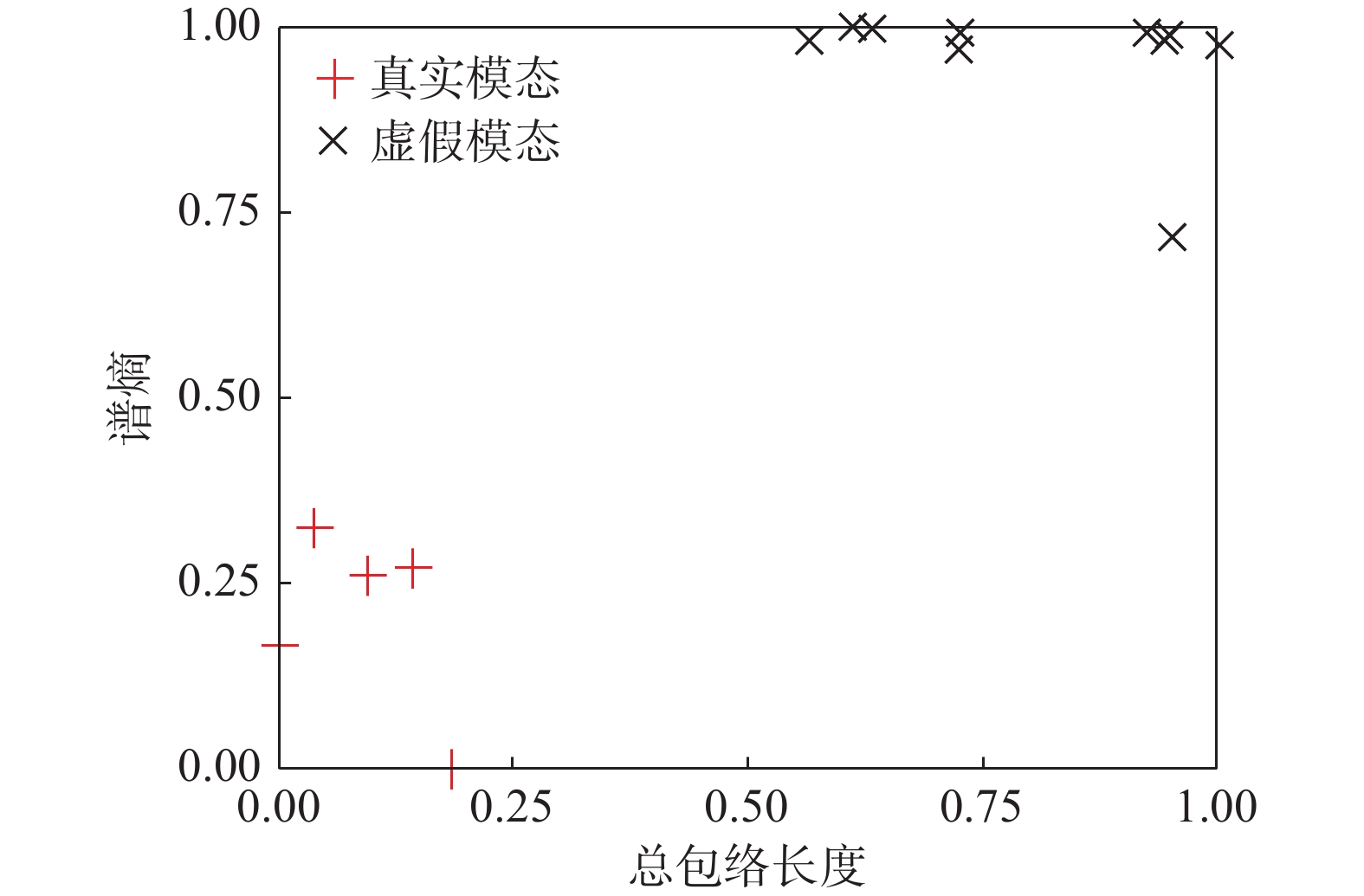
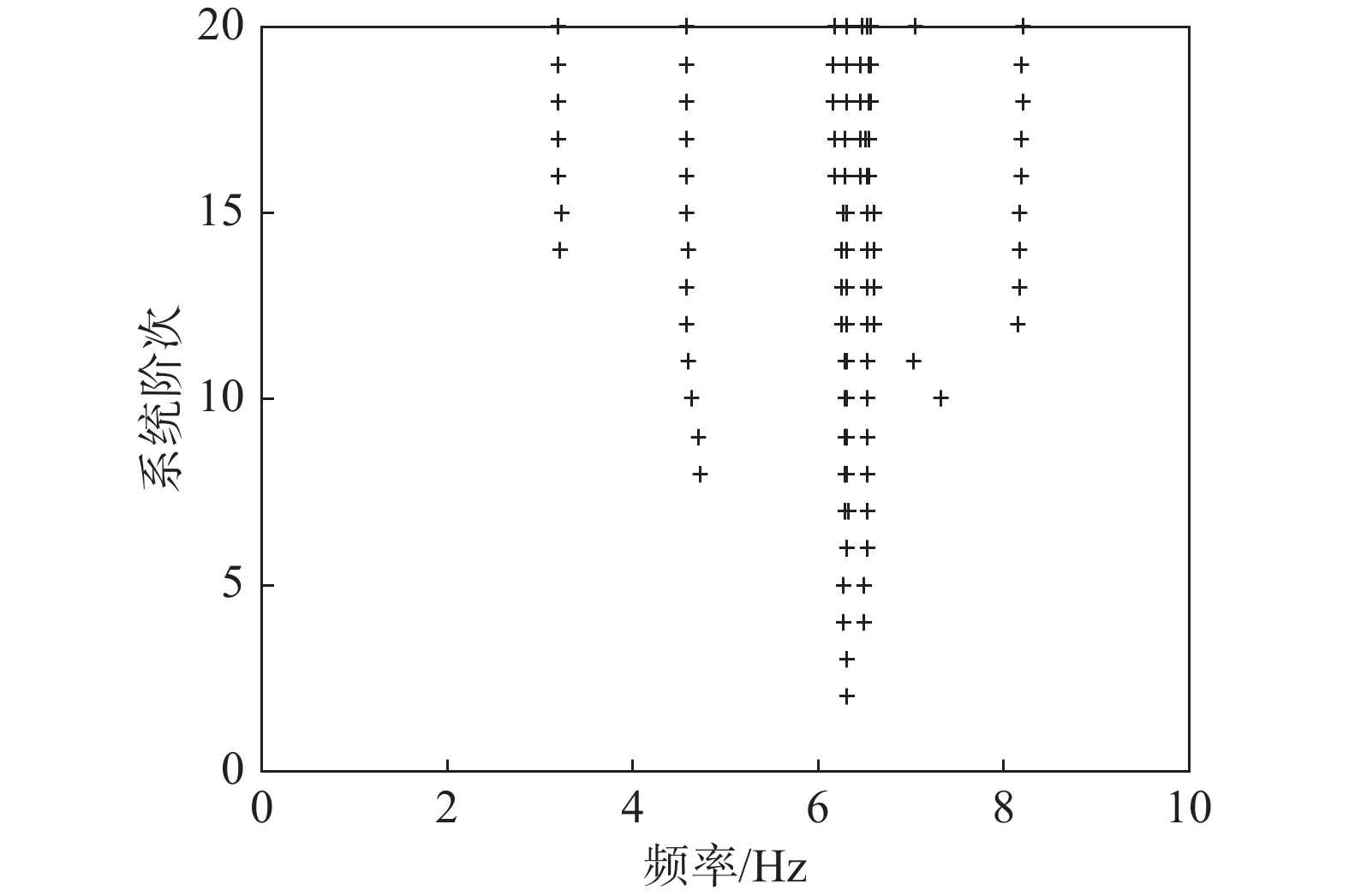
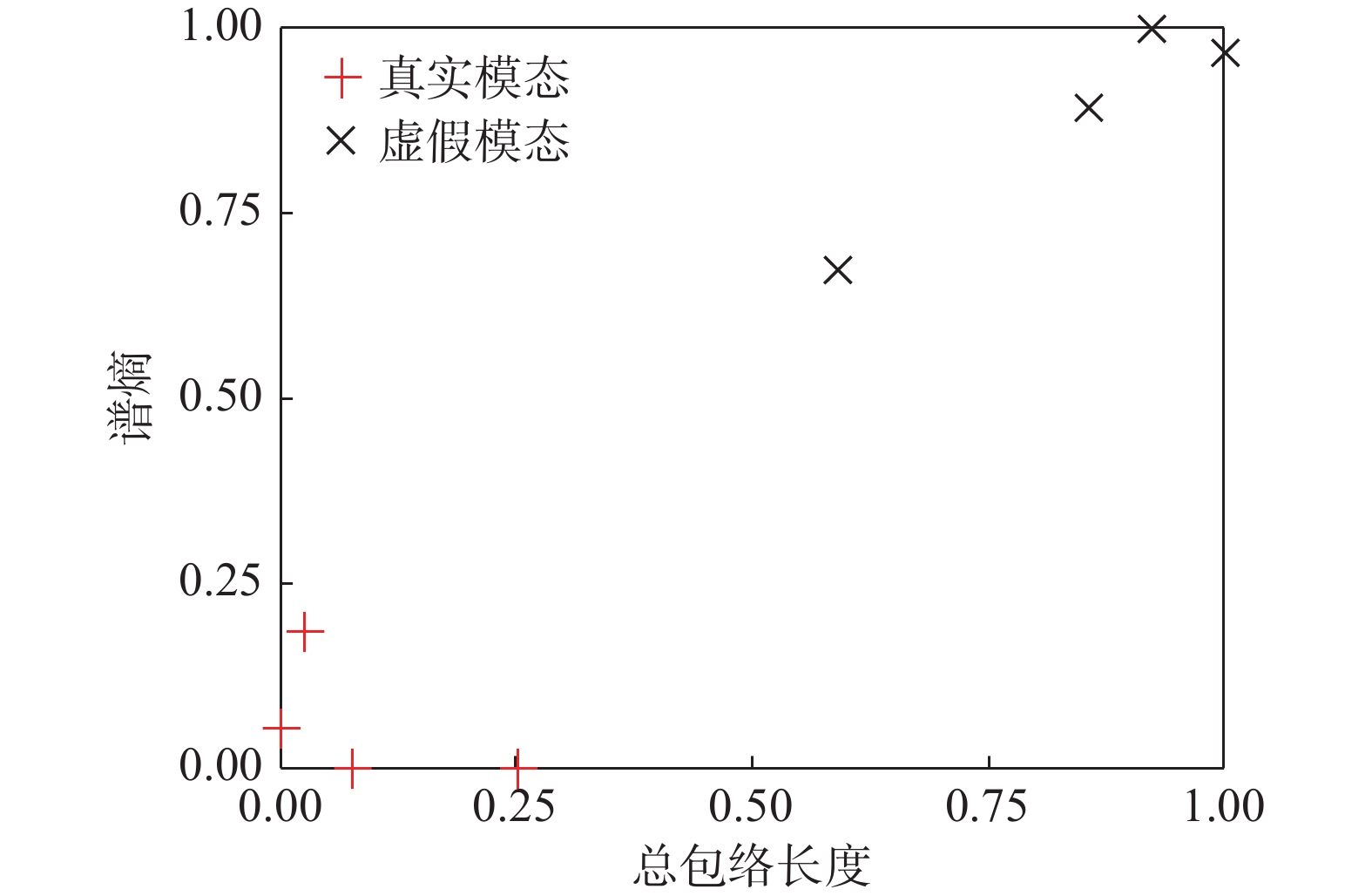
自动获取运行中的模态参数对于大型土木结构的健康状态实时在线监测具有重要意义。针对现有方法模态分辨困难的问题，提出了一种基于解析二阶盲辨识的工作模态分析方法，并相应提出了真假模态区分方法以实现模态参数自动识别。与传统方法不同，该方法无需引入稳定图，可直接从结构振动响应中有效分离出各阶模态响应。通过构造模态特征指标和K均值聚类实现真假模态自动区分，并采用频域参数拟合法估计模态参数。通过8自由度数值算例和混凝土重力拱坝工程实例对该文方法效果进行了验证。结果表明：该方法具有较好的模态自动分离和筛选能力，对固有频率、阻尼比和振型的识别精度均较高，尤其对于密集模态的识别具有显著优势。
- 结构健康监测 /
- 模态分析 /
- 二阶盲辨识 /
- 自动识别 /
- 混凝土坝
Abstract:
The automated extraction of operational modal parameters is of great importance to real-time health monitoring of large infrastructures. Regarding to the shortage of the existing methods in view of the difficulty of modes discrimination, an operational modal analysis method based on analytic second-order blind identification is proposed. A companion method to discriminate between physical and spurious modes for automated identification is also developed. Unlike traditional methods, the modal responses of each mode can be separated directly from structural vibration responses without using stabilization diagrams. Physical and spurious modes can be discriminated by introducing modal metrics and adopting K-means clustering. Modal parameters can then be estimated by the frequency domain parameter fitting method. The proposed method is validated by a numerical example of 8-DOF system and an engineering example of concrete arch-gravity dam. The results show that the method has preferable ability in automated modes separation and discrimination and, demonstrates high precision in the identification of natural frequencies, of damping ratios and, of mode shapes, showing remarkable advantages, especially in the appearance of closely spaced modes.
- structural health monitoring /
- modal analysis /
- second-order blind identification /
- automated identification /
- concrete dams

HTML全文

图 1 模态特征指标的K均值聚类结果

Figure 1. The result of K-means clustering for modal metrices

下载: 全尺寸图片幻灯片

图 2 主坝2600 m廊道加速度传感器布置图

Figure 2. Positions of accelerometers in the 2600 m dam gallery

下载: 全尺寸图片幻灯片

图 3 大坝60 min加速度时程曲线

Figure 3. Dam acceleration time series in 60 min

下载: 全尺寸图片幻灯片

图 4 模态特征指标的K均值聚类结果

Figure 4. The result of K-means clustering for modal metrices

下载: 全尺寸图片幻灯片

图 5 各阶模态响应的自相关函数

Figure 5. Autocorrelation functions of modal responses for each mode

下载: 全尺寸图片幻灯片

图 6 各阶模态响应的自功率谱密度函数

Figure 6. Auto power spectral density functions of modal responses for each mode

下载: 全尺寸图片幻灯片

图 7 本文方法的振型识别结果

Figure 7. Mode shapes results identified by the proposed method

下载: 全尺寸图片幻灯片

图 8 随机子空间的稳定图

Figure 8. Stabilization diagram of SSI

下载: 全尺寸图片幻灯片

表 1 本文方法识别的模态参数与理论值的比较

Table 1 Comparisons between modal parameters identified by the proposed method and theoretical values

模态阶次	固有频率/Hz			阻尼比			MAC/ (%)
模态阶次	理论值/ Hz	本文方法/ Hz	误差/ (%)	理论值/ (%)	本文方法/ (%)	误差/ (%)	MAC/ (%)
1	2.058	2.059	0.034	2.19	2.14	2.32	99.999
2	3.325	3.326	0.024	1.35	1.42	5.84	99.998
3	4.465	4.464	−0.028	1.26	1.26	0.01	99.992
4	5.212	5.210	−0.037	1.50	1.57	4.34	99.992

下载: 导出CSV

表 2 EFDD识别的模态参数与理论值的比较

Table 2 Comparisons between modal parameters identified by EFDD and theoretical values

模态阶次	固有频率			阻尼比			MAC/ (%)
模态阶次	理论值/ Hz	本文方法/ Hz	误差/ (%)	理论值/ (%)	本文方法/ (%)	误差/ (%)	MAC/ (%)
1	2.058	2.058	0.014	2.19	2.38	8.39	99.999
2	3.325	3.326	0.022	1.35	1.25	−7.37	99.999
3	4.465	4.464	−0.039	1.26	1.23	−2.68	99.956
4	5.212	5.210	−0.011	1.50	1.18	−21.44	99.974

下载: 导出CSV

表 3 频域参数拟合法计算表

Table 3 Calculation table of frequency domain parameter fitting method

模态阶次	${\omega _1}$	${\omega _2}$	${\omega _3}$	${\omega _4}$	${\omega _5}$	${\omega _6}$	${\omega _7}$	${\boldsymbol{P}}({\omega _1})$	${\boldsymbol{P}}({\omega _2})$	${\boldsymbol{P}}({\omega _3})$	${\boldsymbol{P}}({\omega _4})$	${\boldsymbol{P}}({\omega _5})$	${\boldsymbol{P}}({\omega _6})$	${\boldsymbol{P}}({\omega _7})$	${\lambda _r}$
1	18.71	19.19	19.66	20.14	20.62	21.10	21.58	0.03+0.04i	0.05+0.03i	0.06+0.02i	0.08−0.01i	0.05−0.05i	0.03−0.03i	0.02−0.03i	−0.92+19.99i
2	27.34	27.82	28.30	28.78	29.26	29.74	30.22	0.02+0.04i	0.03+0.05i	0.06+0.04i	0.09+0.003i	0.06−0.03i	0.04−0.03i	0.02−0.03i	−0.78+28.69i
3	37.41	37.89	38.37	38.85	39.33	39.81	40.29	0.03+0.03i	0.04+0.04i	0.06+0.03i	0.08+0.004i	0.07−0.04i	0.04−0.04i	0.03−0.04i	−1.00+38.99i
4	39.33	39.81	40.29	40.77	41.25	41.73	42.21	0.01+0.03i	0.02+0.04i	0.04+0.04i	0.07+0.02i	0.06−0.01i	0.05−0.02t	0.04−0.03i	−1.04+40.89i
5	50.36	50.84	51.32	51.80	52.28	52.76	53.24	0.03+0.05i	0.07+0.05i	0.08+0.02i	0.09−0.003i	0.08−0.05i	0.04−0.05i	0.03−0.04i	−0.99+51.65i
注：i为虚数单位。

下载: 导出CSV

表 4 本文方法和EFDD方法识别的模态参数

Table 4 Modal parameters identified by the proposed method and EFDD

模态阶次	固有频率/Hz		阻尼比/(%)		MAC/(%)	振型描述
模态阶次	本文方法	EFDD	本文方法	EFDD	MAC/(%)	振型描述
1	3.185	3.184	4.60	5.62	97.98	对称
2	4.567	4.580	2.71	2.18	99.61	反对称
3	6.207	6.260	2.55	2.20	85.23	对称
4	6.510	−	2.54	−	−	对称
5	8.222	8.232	1.91	1.95	98.02	反对称

下载: 导出CSV

参考文献(16)

[1]	刘宇飞, 辛克贵, 樊健生, 等. 环境激励下结构模态参数识别方法综述[J]. 工程力学, 2014, 31(4): 46 − 53. doi: 10.6052/j.issn.1000-4750.2012.11.0873 LIU Yufei, XIN Kegui, FAN Jiansheng, et al. A review of structure modal identification methods through ambient excitation [J]. Engineering Mechanics, 2014, 31(4): 46 − 53. (in Chinese) doi: 10.6052/j.issn.1000-4750.2012.11.0873
[2]	PEREIRA S, REYNDERS F, MAGALHÃES F, et al. The role of modal parameters uncertainty estimation in automated modal identification, modal tracking and data normalization [J]. Engineering Structures, 2020, 224: 111208. doi: 10.1016/j.engstruct.2020.111208
[3]	ZINI G, BETTI G, BARTOLI G. A quality-based automated procedure for operational modal analysis [J]. Mechanical Systems and Signal Processing, 2022, 164: 108173. doi: 10.1016/j.ymssp.2021.108173
[4]	杨志林, 罗漪, 王海峰. 基于数据库的优化随机子空间法识别精度评价[J]. 工程力学, 2023, 40(4): 116 − 128, 192. doi: 10.6052/j.issn.1000-4750.2021.10.0769 YANG Zhilin, LUO Yi, WANG Haifeng. Identification accuracy evaluation of optimized random subspace method based on database [J]. Engineering Mechanics, 2023, 40(4): 116 − 128, 192. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.10.0769
[5]	施袁锋, 朱正言, 陈鹏, 等. 基于EM算法和模态形式的状态空间模型自降阶工作模态分析[J]. 工程力学, 2021, 38(9): 15 − 25. doi: 10.6052/j.issn.1000-4750.2020.08.0618 SHI Yuanfeng, ZHU Zhengyan, CHEN Peng, et al. Operational modal analysis using EM algorithm and modal-form state-space model with auto model order reduction [J]. Engineering Mechanics, 2021, 38(9): 15 − 25. (in Chinese) doi: 10.6052/j.issn.1000-4750.2020.08.0618
[6]	何定桥, 杨军. 基于HHT的结构模态参数自动化识别方法和试验验证[J]. 工程力学, 2022, 39(11): 109 − 122. doi: 10.6052/j.issn.1000-4750.2021.06.0466 HE Dingqiao, YANG Jun. An automatic structural modal parameters identification method based on HHT and its experimental verification [J]. Engineering Mechanics, 2022, 39(11): 109 − 122. (in Chinese) doi: 10.6052/j.issn.1000-4750.2021.06.0466
[7]	MAGALHÃES F, CUNHA Á, CAETANO E. Online automatic identification of the modal parameters of a long span arch bridge [J]. Mechanical Systems and Signal Processing, 2009, 23(2): 316 − 329. doi: 10.1016/j.ymssp.2008.05.003
[8]	REYNDERS E, HOUBRECHTS J, DE ROECK G. Fully automated (operational) modal analysis [J]. Mechanical Systems and Signal Processing, 2012, 29: 228 − 250. doi: 10.1016/j.ymssp.2012.01.007
[9]	郑沛娟, 林迪南, 宗周红, 等. 基于图论聚类的随机子空间模态参数自动识别[J]. 东南大学学报(自然科学版), 2017, 47(4): 710 − 716. doi: 10.3969/j.issn.1001-0505.2017.04.014 ZHENG Peijuan, LIN Dinan, ZONG Zhouhong, et al. Automatic stochastic subspace identification of modal parameters based on graph clustering [J]. Journal of Southeast University (Natural Science Edition), 2017, 47(4): 710 − 716. (in Chinese) doi: 10.3969/j.issn.1001-0505.2017.04.014
[10]	张永祥, 刘心, 褚志刚, 等. 基于随机子空间法的模态参数自动提取[J]. 机械工程学报, 2018, 54(9): 187 − 194. ZHANG Yongxiang, LIU Xin, CHU Zhigang, et al. Autonomous modal parameter extraction based on stochastic subspace identification [J]. Journal of Mechanical Engineering, 2018, 54(9): 187 − 194. (in Chinese)
[11]	祝青鑫, 王浩, 茅建校, 等. 基于聚类分析的桥梁结构模态参数自动识别方法[J]. 东南大学学报(自然科学版), 2020, 50(5): 837 − 843. doi: 10.3969/j.issn.1001-0505.2020.05.007 ZHU Qingxin, WANG Hao, MAO Jianxiao, et al. Automated modal parameter identification method for bridges based on cluster analysis [J]. Journal of Southeast University (Natural Science Edition), 2020, 50(5): 837 − 843. (in Chinese) doi: 10.3969/j.issn.1001-0505.2020.05.007
[12]	BELOUCHRANI A, ABED-MERAIM K, CARDOSO J F, et al. A blind source separation technique using second-order statistics [J]. IEEE Transactions on Signal Processing, 1997, 45(2): 434 − 444. doi: 10.1109/78.554307
[13]	PONCELET F, KERSCHEN G, GOLINVAL J C, et al. Output-only modal analysis using blind source separation techniques [J]. Mechanical Systems and Signal Processing, 2007, 21(6): 2335 − 2358. doi: 10.1016/j.ymssp.2006.12.005
[14]	MCNEIL S. An analytic formulation for blind modal identification [J]. Journal of Vibration and Control, 2011, 18(14): 2111 − 2121.
[15]	LI J M, BAO T F, VENTURA C E. An automated operational modal analysis algorithm and its application to concrete dams [J]. Mechanical Systems and Signal Processing, 2022, 168: 108707. doi: 10.1016/j.ymssp.2021.108707
[16]	BRINCKER R, ZHANG L M, ANDERSEN P. Modal identification of output-only systems using frequency domain decomposition [J]. Smart Material and Structures, 2001, 10(3): 441 − 445. doi: 10.1088/0964-1726/10/3/303